«2a. Пространство. Время. Движение»

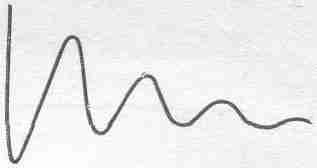
Гармонический осциллятор, к изучению ко­торого мы сейчас переходим, будет встречаться нам почти всюду; хотя мы начнем с чисто меха­нических примеров грузика на пружинке, ма­лых отклонений маятника или каких-то других механических устройств, на самом деле мы бу­дем изучать некое дифференциальное уравне­ние. Это уравнение непрестанно встречается в физике и в других науках и фактически описы­вает столь многие явления, что, право же, стоит того, чтобы изучить его получше. Такое уравне­ние описывает колебания грузика на пружинке, колебания заряда, текущего взад и вперед по электрической цепи, колебания камертона, порождающие звуковые волны, аналогичные колебания электронов в атоме, порождающие световые волны. Добавьте сюда уравнения, описывающие дей­ствия регуляторов, например поддерживающих заданную температуру термостата, сложные взаимодействия в химиче­ских реакциях и (уже совсем неожиданно) уравнения, от­носящиеся к росту колонии бактерий, которых одновременно и кормят и травят ядом, или к размножению лис, питаю­щихся кроликами, которые в свою очередь едят траву, и т. д. Мы привели очень неполный список явлений, которые описы­ваются почти теми же уравнениями, что и механический осцил­лятор. Эти уравнения называются линейными дифференциаль­ными уравнениями с постоянными коэффициентами. Это урав­нения, состоящие из суммы нескольких членов, каждый из которых представляет собой производную зависимой величины по независимой, умноженную на постоянный коэффициент. Таким образом,

называется линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами (все аn — посто­янные).

§ 2. Гармонический осциллятор

Пожалуй, простейшей механической системой, движение которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является масса на пружинке. После того как к пружинке подвесят грузик, она немного рас­тянется, чтобы уравновесить силу тяжести. Проследим теперь за вертикальными отклонениями массы от положения равнове­сия (фиг. 21.1).

Фиг. 21.1. Грузик, подвешенный на пружинке.

Простой пример гармонического ос­циллятора.