6. Электродинамика
Глава 15 ВЕКТОРНЫЙ ПОТЕНЦИАЛ
§ 1. Силы, действующие на петлю с током; энергия диполя
§ 2. Механическая и электрическая энергии
§ 3. Энергия постоянных токов
§ 4. В или А?
§ 5. Векторный потенциал и квантовая механика
§ 6. Что истинно в статике, но ложно в динамике?
§ 1. Силы, действующие на петлю с током; энергия диполя
В предыдущей главе мы изучали магнитное поле, создаваемое маленькой прямоугольной петлей, по которой течет ток. Мы нашли, что это поле диполя с дипольным моментом, равным
m= IA,(15.1)
где I — сила тока, a A — площадь петли. Момент направлен по нормали к плоскости петли, так что можно писать и так:
m=IАn,
где n — единичный вектор нормали к площади А.
Петли с током, или магнитные диполи, не только создают магнитные поля, но и сами подвергаются действию силы, попав в магнитное поле других токов. Рассмотрим сперва силы, действующие на прямоугольную петлю в однородном магнитном поле. Пусть ось z направлена по полю, а ось y лежит в плоскости петли, образующей с плоскостью xy угол q (фиг. 15.1). Тогда магнитный момент петли, будучи нормальным к ее плоскости, образует с магнитным полем тоже угол q.
Раз токи на противоположных сторонах петли текут в противоположные стороны, то и силы, действующие на них, тоже направлены врозь, а суммарная сила равна нулю (в однородном поле). Но благодаря силам, действующим на стороны, обозначенные на фиг. 15.1 цифрами 1 и 2, возникает вращательный момент, стремящийся вращать петлю вокруг оси у. Величина этих сил Flи F2 такова:
F1=F2=IBb.
Фиг. 15.1. Прямоугольная петля с током I в однородном поле В, направленном по оси z.
Действующий на нее вращательный момент равен t=mXB, где магнитный момент m=Iab.
Их плечо равно
так что вращательный момент
Вращательный момент может быть записан и векторно:
(15.2)
То, что вращательный момент дается уравнением (15.2), мы показали пока только для довольно частного случая. Но результат, как мы увидим, верен для маленьких петель любой формы. Полезно напомнить, что и для вращательного момента, действующего на электрический диполь, мы получили соотношение подобного же рода:
Сейчас нас интересует механическая энергия нашей петли, по которой течет ток. Раз есть момент вращения, то энергия, естественно, зависит от ориентации петли. Принцип виртуальной же работы утверждает, что момент вращения — это скорость изменения энергии с углом, так что можно написать
Подставляя t =+mBsinq и интегрируя, мы вправе принять за энергию выражение
(Знак минус стоит потому, что петля стремится развернуть свой момент по полю; энергия ниже всего тогда, когда m и В параллельны.)
По причинам, о которых мы поговорим позже, эта энергия не есть полная энергия петли с током. (Мы, к примеру, не учли энергии, идущей на поддержание тока в петле.) Поэтому мы будем называть ее Uмех, чтобы не забыть, что это лишь часть энергии. И, кроме того, постоянную интегрирования в (15.3) мы вправе принять равной нулю, все равно ведь какие-то другие виды энергии мы не учли. Так что мы перепишем уравнение так:
(15.4)
Опять получилось соответствие с электрическим диполем, где было
(15.5)
Только в (15.5) электрическая энергия — и вправду энергия, а Uмехв (15.4) — не настоящая энергия. Но все равно ее можно применять для расчета сил по принципу виртуальной работы. Надо только предполагать, что ток в петле (или по крайней мере магнитный момент m) остается неизменным при повороте.
Для нашей прямоугольной петли можно показать, что Uмех соответствует также работе, затрачиваемой на то, чтобы внести петлю в поле. Полная сила, действующая на петлю, равна нулю лишь в однородном поле, а в неоднородном все равно останутся какие-то силы, действующие на токовую петлю. Внося петлю в поле, мы вынуждены будем пронести ее через места, где поле неоднородно, и там будет затрачена работа. Будем считать для упрощения, что петлю вносят в поле так, что ее момент направлен вдоль поля. (А в конце, уже в поле, ее можно повернуть как надо.)
Вообразите, что мы хотим двигать петлю в направлении x, т. е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.
Фиг. 15.2. Петлю проносят через поле В (поперек него) в направлении x.
Рассчитаем сначала работу переноса каждой стороны по отдельности, а затем все сложим (вместо того, чтобы складывать силы до интегрирования). Силы, действующие на стороны 3 и 4, направлены поперек движения, так что на эти стороны работа не тратится. Сила, действующая на сторону 2, направлена по x и равна 1bВ(x); чтобы узнать всю работу против действия магнитных сил, нужно проинтегрировать это выражение по x от некоторого значения х, где поле равно нулю, скажем, от х = -Ґ до теперешнего положения х2:
(15.6)
Подобно этому, и работа против сил, действующих на сторону 1,равна
(15.7)
Чтобы вычислить каждый интеграл, надо знать, как В(х) зависит от х. Но ведь сторона 1 при движении рамки расположена все время параллельно стороне 2 на одном и том же расстоянии от нее, так что в ее интеграл входит почти вся работа, затраченная на перемещение стороны 2. Сумма (15.6) и (15.7) на самом деле равна
(15.8)
Но, попав в область, где В на обеих сторонах 1 и 2 почти одинаково, мы имеем право записать интеграл в виде
где В — поле в центре петли. Вся вложенная механическая энергия оказывается равной
Это согласуется с выражением для энергии (15.4), выбранным нами прежде.
Конечно, тот же вывод получился бы, если бы мы до интегрирования сложили все силы, действующие на петлю. Если бы мы обозначили через В1поле у стороны 1 а через В2— поле у стороны 2, то вся сила, действующая в направлении х, оказалась бы равной
Если петля «узкая», т. е. если В2и В1не очень различаются между собой, то можно было бы написать
Так что сила была бы равна
(15.10)
Вся работа, произведенная внешними силами над петлей, равнялась бы
а это опять -mB. Но теперь нам становится понятно, почему получается, что сила, действующая на небольшую токовую петлю, пропорциональна производной магнитного поля, как это следовало ожидать из
Другой наш результат состоит в следующем. Хоть и не исключено, что не все виды энергии вошли в формулу Uмех= m·B (ведь это просто некоторая имитация энергии), ею все же можно пользоваться, применяя принцип виртуальной работы, чтобы узнать, какие силы действуют на петли с постоянным током.
§ 2. Механическая и электрическая энергии
Теперь мы хотим пояснить, почему энергия Uмех, о которой говорилось в предыдущем параграфе, не настоящая энергия, связанная с постоянными токами, почему у нее нет прямой связи с полной энергией всей Вселенной. Правда, мы подчеркнули, что ею можно пользоваться как энергией, когда вычисляешь силы из принципа виртуальной работы, при условии, что ток в петле (и все прочие токи) не меняется. Посмотрим теперь, почему же все так выходит.
Представим, что петля на фиг. 15.2 движется в направлении +х, а ось z примем за направление В. Электроны проводимости на стороне 2 будут испытывать действие силы, толкающей их вдоль провода, в направлении у. Но в результате их движения по проводу течет электрический ток и имеется составляющая скорости vyв том же направлении, в котором действует сила. Поэтому над каждым электроном каждую секунду будет производиться работа Fyvy , где vy — компонента скорости электрона, направленная вдоль провода. Эту работу, совершаемую над электронами, мы назовем электрической. Оказывается, что когда петля движется в однородном поле, то полная электрическая работа равна нулю, потому что на одной части петли работа положительная, а на другой — равная ей отрицательная. Но при движении контура в неоднородном поле это не так — тогда остается какой-то чистый избыток одной работы над другой. Вообще-то эта работа стремится изменить поток электронов, но если он поддерживается неизменным, то энергия поглощается или высвобождается в батарейке или в другом источнике, сохраняющем ток постоянным. Вот именно эта энергия и не учитывалась, когда мы вычисляли Uмех в (15.9), потому что в наши расчеты входили только механические силы, действующие на провод.
Вы можете подумать: но сила, действующая на электроны, зависит от того, насколько быстро движется провод; быть может, если бы провод двигался достаточно медленно, этой электрической энергией можно было бы вообще пренебречь. Действительно, скорость, с какой высвобождается электрическая энергия, пропорциональна скорости провода, но все же полная выделенная энергия пропорциональна к тому же еще и времени, в течение которого проявлялась эта скорость. В итоге полная выделенная электрическая энергия пропорциональна произведению скорости на время, а это как раз и есть пройденное расстояние. Каждому пройденному в поле расстоянию отвечает заданное, и притом одно и то же, количество электрической работы.
Возьмем кусок провода единичной длины, по которому течет ток I. Провод движется перпендикулярно самому себе и магнитному полю В со скоростью v;провод. Благодаря наличию тока сами электроны обладают скоростью дрейфа vдрейфвдоль провода. Компонента магнитной силы, действующей на каждый электрон в направлении дрейфа, равна qe vпровод В. Значит, скорость, с какой производится электрическая работа, равна Fvдрейф = (qevпроводВ)vдрейф. Если на единице длины провода имеется N проводящих электронов, то вся величина электрической работы, производимой в секунду, такова:
Но Nqеvдрейф равно току I в проводе, так что
И поскольку ток поддерживается неизменным, то силы, действующие на электроны проводимости, не ускоряют их; электрическая энергия переходит не к электронам, а к тому источнику, который сохраняет силу тока постоянной.
Но заметьте, что сила, действующая на провод, равна IB; значит, IBvпровод — это механическая работа, выполняемая над проводом в единицу времени, dUмех/dt = IBvпровод. Отсюда мы заключаем, что механическая работа перемещения провода в точности равна электрической работе, производимой над источником тока, так что энергия петли остается постоянной!
Это не случайность. Это следствие закона, с которым мы уже знакомы. Полная сила, действующая на каждый из зарядов в проводе, равна
Скорость, с которой производится работа, равна
(15.12)
Если электрического поля нет, то остается только второе слагаемое, а оно всегда равно нулю. Позже мы увидим, что изменение магнитных полей создает электрические поля, так что наши рассуждения применимы лишь к проводам в постоянных магнитных полях.
Но тогда почему же принцип виртуальной работы дает правильный ответ? Потому, что пока мы не учитывали полную энергию Вселенной. Мы не включали в рассмотрение энергию тех токов, которые создают магнитное поле, с самого начала присутствующее в наших рассуждениях.
Но представим себе полную систему, наподобие изображенной на фиг. 15.3,а, где петля с током I вдвигается в магнитное поле B1 созданное током I2 в катушке. ТокI1, текущий по петле, тоже будет создавать какое-то магнитное поле В2 близ катушки. Если петля движется, то поле В2 изменяется. В следующей главе мы увидим, что изменяющееся магнитное поле создает поле Е, и это поле действительно начнет действовать на заряды в катушке. Эту энергию мы обязаны включить в наш сводный баланс энергий.
Мы, конечно, могли бы подождать говорить об этом новом вкладе в энергию до следующей главы, но уже сейчас можно оценить его, если применить соображения принципа относительности.
Фиг. 15.3. Вычисление энергии маленькой петли в магнитном поле.
Приближаем петлю к неподвижной катушке и знаем, что электрическая энергия петли в точности равна и противоположна по знаку произведенной механической работе. Иначе говоря,
Теперь предположим, что мы смотрим на происходящее с другой точки зрения: будем считать, что петля покоится, а катушка приближается к ней. Тогда катушка движется в поле, созданном петлей. Те же рассуждения приведут к выражению
Механическая энергия в обоих случаях одна и та же — она определяется только силой, действующей между двумя контурами.
Сложение двух уравнений дает
Полная энергия всей системы равна, конечно, сумме двух электрических энергий и взятой один раз механической энергии. В итоге выходит
Полная энергия всей системы — это на самом деле Uмех со знаком минус. Если нам нужна, скажем, полная энергия магнитного диполя, то следует писать
И только тогда, когда мы потребуем, чтобы все токи оставались постоянными, можно использовать лишь одну из частей энергии Uмех (всегда равную истинной анергии со знаком минус) для вычисления механических сил. В более общих задачах надо соблюдать осторожность, чтобы не забыть ни одной из энергий. Сходное положение наблюдалось и в электростатике. Мы показали там, что энергия конденсатора равна Q2/2C. Когда мы применяем принцип виртуальной работы, чтобы найти силу, действующую между обкладками конденсатора, то изменение энергии равно Q2/2, умноженному на изменение в 1/С, т. е.
(15.14)
А теперь предположим, что нам надо было бы подсчитать работу, затрачиваемую на сближение двух проводников, но при другом условии — что напряжение между ними остается постоянным. Тогда правильную величину силы мы могли бы получить из принципа виртуальной работы, если бы поступили немного искусственным образом. Раз Q = CV, то полная энергия равна 1/2 CV2. Но если бы мы ввели условную энергию, равную —1/2CV2, то принцип виртуальной работы можно было бы применить для получения сил, полагая изменение этой условной энергии равным механической работе (это при условии, что напряжение V
считается постоянным). Тогда
(15.15)
а это то же самое, что написано в уравнении (15.14). Мы получаем правильный ответ, хотя пренебрегаем работой, которую электрическая система тратит на постоянное поддержание напряжения. И здесь опять электрическая энергия ровно вдвое больше механической и имеет обратный знак.
Итак, если мы ведем расчет искусственно, пренебрегая тем фактом, что источник потенциала должен тратить работу на то, чтобы напряжение оставалось неизменным, то все равно мы приходим к правильному результату. Это в точности соответствует положению дел в магнитостатике.
§ 3. Энергия постоянных токов
Зная, что Uполн = -Uмех, используем этот факт, чтобы найти истинную энергию постоянных токов в магнитных полях. Начать можно с истинной энергии небольшой токовой петельки. Обозначая Uполнпросто через U, напишем
U = m·В.(15.16)
Хотя эту энергию мы подсчитали только для плоской прямоугольной петли, все это верно и для плоской петельки произвольной формы.
Энергию контура произвольной формы можно найти, представив себе, что он состоит из небольших токовых петель. Скажем, имеется провод в форме петли Г (фиг. 15.4). Натянем на эту петлю поверхность S, а на ней наметим множество петелек, каждую из которых можно считать плоской. Если заставить ток I циркулировать по каждой петельке, то в итоге выйдет то же самое, как если бы ток шел только по петле Г, ибо токи на всех внутренних линиях взаимно уничтожатся. Система небольших токов физически не будет отличима от исходного контура, и энергия должна быть той же, т. е. должна быть равна сумме энергий всех петелек.
Если площадь каждой петельки Dа, то ее энергия равна IDаBn, где Bn — компонента В, нормальная к Dа. Полная энергия равна U = SIBnDа.
Фиг. 15.4. Энергию большой петли в магнитном поле можно считать суммой энергий маленьких петелек.
В пределе, когда петли становятся бесконечно малыми, сумма превращается в интеграл, и
(15.17)
где n — единичная нормаль к da,
Если мы положим В = СXA, то поверхностный интеграл можно будет связать с контурным (по теореме Стокса):
(15.18)
где ds — линейный элемент вдоль Г. Итак, мы получили энергию контура произвольной формы:
(15.19)
В этом выражении А обозначает, конечно, векторный потенциал, возникающий из-за токов (отличных от тока / в проводе), которые создают поле В близ провода.
Далее, любое распределение постоянных токов можно считать состоящим из нитей, идущих вдоль тех линий, по которым течет ток. Для любой пары таких контуров энергия дается выражением (15.19), где интеграл взят вокруг одного из контуров, а векторный потенциал А создан другим контуром. Полная энергия получается сложением всех таких пар. Если вместо того, чтобы следить за парами, мы полностью просуммируем по всем нитям, то каждую энергию мы засчитаем дважды (такой же эффект мы наблюдали в электростатике), и полную энергию можно будет представить в виде
(15.20)
Это соответствует полученному для электростатической энергии выражению
(15.21)
Значит, мы можем считать А, если угодно, своего рода потенциальной энергией токов в магнитостатике. К сожалению, это представление не очень полезно, потому что оно годится только для статических полей. В действительности, если поля со временем меняются, ни выражение (15.20), ни выражение (15.21) не дают правильной величины энергии.
§ 4. B или А?
В этом параграфе нам хотелось бы обсудить такой вопрос: что такое векторный потенциал — просто полезное для расчетов приспособление (так в электродинамике полезен скалярный потенциал) или же он как поле вполне «реален»? Или же «реально» лишь магнитное поле, так как только оно ответственно за силу, действующую на движущуюся частицу?
Для начала нужно сказать, что выражение «реальное поле» реального смысла не имеет. Во-первых, вы вряд ли вообще полагаете, что магнитное поле хоть в какой-то степени «реально», потому что и сама идея поля — вещь довольно отвлеченная. Вы не можете протянуть руку и пощупать это магнитное поле. Кроме того, величина магнитного поля тоже не очень определенна; выбором подходящей подвижной системы координат можно, к примеру, добиться, чтобы магнитное поле в данной точке вообще пропало.
Под «реальным» полем мы понимаем здесь вот что: реальное поле — это математическая функция, которая используется нами, чтобы избежать представления о дальнодействии. Если в точке Р имеется заряженная частица, то на нее оказывают влияние другие заряды, расположенные на каком-то удалении от Р. Один прием, которым можно описать взаимодействие,— это говорить, что прочие заряды создают какие-то «условия» (какие — не имеет значения) в окрестности Р. Если мы знаем эти условия (мы их описываем, задавая электрическое и магнитное поля), то можем полностью определить поведение частицы, нимало не заботясь после о том, что именно создало эти условия.
Иными словами, если бы эти прочие заряды каким-то образом изменились, а условия в Р, описываемые электрическим и магнитным полем в точке Р, остались бы прежними, то движение заряда тоже не изменилось бы. «Реальное» поле тогда есть совокупность чисел, заданных так, что то, что происходит в некоторой точке, зависит только от чисел в этой точке и нам больше не нужно знать, что происходит в других местах. Именно с таких позиций мы и хотим выяснить, является ли векторный потенциал «реальным» полем.
Вас может удивить тот факт, что векторный потенциал определяется не единственным образом, что его можно изменить, добавив к нему градиент любого скаляра, а силы, действующие на частицы, не изменятся. Однако это не имеет ничего общего с вопросом реальности в том смысле, о котором мы говорили, К примеру, магнитное поле как-то меняется при изменении относительного движения (равно как и Е или А). Но нас нисколько не будет заботить, что поле можно изменять таким образом. Нам это безразлично; это никак не связано с вопросом о том, действительно ли векторный потенциал—«реальное» поле, пригодное для описания магнитных эффектов, или же это просто удобный математический прием.
Мы должны еще сделать кое-какие замечания о полезности векторного потенциала А. Мы видели, что им можно пользоваться в формальной процедуре расчета магнитных полей заданных токов, в точности как j может применяться для отыскания электрических полей. В электростатике мы видели, что j давалось скалярным интегралом
(15.22)
Из этого j мы получали три составляющих Е при помощи трех дифференцирований. Обычно это было легче, чем вычислять три интеграла в векторной формуле
(15.23)
Во-первых, их три, а во-вторых, каждый из них вообще-то немного посложнее, чем (15.22).
В магнитостатике преимущества не так ясны. Интеграл для А уже сам по себе векторный:
(15.24)
т. е. здесь написаны три интеграла. Кроме того, вычисляя ротор А для получения В, надо взять шесть производных и расставить их попарно. Сразу не ясно, проще ли это, чем прямое вычисление
(15.25)
В простых задачах векторным потенциалом часто бывает пользоваться труднее, и вот по какой причине. Предположим, нас интересует магнитное поле В в одной только точке, а задача обладает какой-то красивой симметрией. Скажем, нам нужно знать поле в точке на оси кольцевого тока. Вследствие симметрии интеграл в (15.25) легко возьмется и вы сразу получите В. Если бы, однако, мы начали с А, то пришлось бы вычислять В из производных А, а для этого надо было бы знать А во всех точках по соседству с той,которая нас интересует. Большая же часть их не лежит на оси симметрии, интеграл для А усложняется. В задаче с кольцом, например, пришлось бы иметь дело с эллиптическими интегралами. В подобных задачах А, разумеется, не приносит большой пользы. Во многих сложных задачах, бесспорно, легче работать с А, но в общем трудно было бы доказывать, что эти технические облегчения стоят того, чтобы начать изучать еще одно векторное поле.
Мы ввели А потому, что оно действительно имеет большое физическое значение. Оно не просто связано с энергиями токов (в чем мы убедились в последнем параграфе), оно — «реальное» физическое поле в том смысле, о котором мы говорили выше. В классической механике силу, действующую на частицу, очевидно, можно записать в виде
F = q(E+vXB), (15.26)
так что, как только заданы силы, движение оказывается полностью определенным. В любой области, где В = 0, хотя бы А и не было равно нулю (например, вне соленоида), влияние А ни в чем не сказывается. Поэтому долгое время считалось, что А — не «реальное» поле. Оказывается, однако, что в квантовой механике существуют явления, свидетельствующие о том, что поле А на самом деле вполне «реальное» поле, в том смысле, в каком мы определили это слово. В следующем параграфе мы покажем, что все это значит.
§ 5. Векторный потенциал и квантовая механика
Когда мы от классической механики переходим к квантовой, то наши представления о важности тех или иных понятий во многом меняются. (Кое-какие из этих понятий мы уже рассматривали раньше.) В частности, постепенно сходит на нет понятие силы, а понятия энергии и импульса приобретают первостепенную важность. Вместо движения частиц, как вы помните, речь теперь идет уже об амплитудах вероятностей, которые меняются в пространстве и времени. В эти амплитуды входят длины волн, связанные с импульсами, и частоты, связываемые с энергиями. Импульсы и энергии определяют собой фазы волновых функций и по этой-то причине они важны для квантовой механики.
Фиг. 15.5. Интерференционный опыт с электронами.
Вместо силы речь теперь идет о том, каким образом взаимодействие меняет длину волны. Представление о силе становится уже второстепенным, если вообще о нем еще стоит говорить. Даже когда, к примеру, упоминают о ядерных силах, то на самом деле, как правило, работают все же с энергиями взаимодействия двух нуклонов, а не с силой их взаимодействия. Никому не приходит в голову дифференцировать энергию, чтобы посмотреть, какова сила. В этом параграфе мы хотим рассказать, как возникают в квантовой механике векторный и скалярный потенциалы. Оказывается, что именно из-за того, что в квантовой механике главную роль играют импульс и энергия, самый прямой путь введения в квантовое описание электромагнитных эффектов — сделать это с помощью А и j.
Надо сперва слегка напомнить, как действует квантовая механика. Мы снова вернемся к описанному в вып. 3, гл. 37, воображаемому опыту, в котором электроны испытывали дифракцию на двух щелях. На фиг. 15.5 показано то же устройство. Электроны (все они обладают примерно одинаковой энергией) покидают источник и движутся к стенке с двумя узкими щелями. За стенкой находится «защитный» вал — поглотитель с подвижным детектором. Этот детектор предназначен для измерения частоты I, с которой электроны попадают в небольшой участок поглотителя на расстоянии х от оси симметрии. Частота эта пропорциональна вероятности того, что отдельный электрон, вылетевший из источника, достигнет этого участка «вала». Вероятность обладает распределением сложного вида (оно показано на рисунке), которое объясняется интерференцией двух амплитуд, по одной от каждой щели. Интерференция двух амплитуд зависит от их разности фаз. Иными словами, когда амплитуды равны С1еiф1и С2еiф2, разность фаз d=Ф1-Ф2 определяет интерференционную картину [см. вып. 3, гл. 29, уравнение (29.12)]. Если расстояние от щелей до экрана равно L, а разность длин путей электронов, проходящих через две щели, равна а (как показано на фигуре), то разность фаз двух волн дается отношением
(15.27)
Как обычно, мы полагаем l= l/2p, где l — длина волны, отвечающая пространственному изменению амплитуды вероятности. Для простоты рассмотрим лишь те значения х, которые много меньше L; тогда можно будет принять
и
(15.28)
Когда х равно нулю, то и d равно нулю; волны находятся в фазе, а вероятность имеет максимум. Когда d равно п, волны оказываются в противофазе, интерферируя деструктивно, и вероятность достигает минимума. Так электронная интенсивность получает волнообразный вид.
Теперь мы хотим сформулировать тот закон, которым в квантовой механике заменяется закон силы F=qvXВ. Этот закон будет определять собой поведение квантовомеханических частиц в электромагнитном поле. Раз все происходящее определяется амплитудами, то закон должен будет объяснить, как сказывается на амплитудах влияние магнитного поля; с ускорениями же частиц мы больше никакого дела иметь не будем. Закон этот состоит в следующем: фазу, с какой амплитуда достигает детектора, двигаясь по какой-то траектории, присутствие магнитного поля меняет на величину, равную интегралу от векторного потенциала вдоль этой траектории, умноженному на отношение заряда частицы к постоянной Планка. То есть
Если бы магнитного поля не было, то наблюдалась бы какая-то определенная фаза прибытия. Если же где-то появляется магнитное поле, то фаза прибытия возрастает на величину интеграла в (15.29).
Хотя для наших теперешних рассуждений в этом нет необходимости, заметим все же, что влияние электростатического поля тоже выражается в изменении фазы, равном интегралу по времени от скалярного потенциала j со знаком минус:
Эти два выражения справедливы лишь для статических полей, но, объединив их, мы получим правильный результат для любого, статического или динамического, электромагнитного поля. Именно этот закон и заменяет собой формулу F= q(E+vXВ). Мы сейчас, однако, будем говорить только о статическом магнитном поле.
Положим, что опыт с двумя щелями проводится в магнитном поле. Мы хотим узнать, с какой фазой достигают экрана две волны, пути которых пролегают через две разные щели. Их интерференция определяет то место, где окажется максимум вероятности. Фазу волны, бегущей по траектории (1), мы назовем Ф1; а через Ф1 (В = 0) обозначим фазу, когда магнитного поля нет. Тогда после включения поля фаза достигает величины
(15.30)
Аналогично, фаза для траектории (2) равна
(15.31)
Интерференция волн в детекторе зависит от разности фаз
Разность фаз в отсутствие поля мы обозначим d (В = 0); это та самая разность, которую мы подсчитали в уравнении (15.28). Кроме того, мы замечаем, что из двух интегралов можно сделать один, идущий вперед по пути (1), а назад — по пути (2); этот замкнутый путь будет обозначаться (1—2). Так что получается
(15.33)
Это уравнение сообщает нам, как под действием магнитного поля изменяется движение электрона; с его помощью мы можем найти новые положения максимумов и минимумов интенсивности.
Прежде чем сделать это, мы хотим, однако, поставить один интересный и важный вопрос. Вы помните, что в вектор-потенциальной функции есть некоторый произвол. Две разные вектор-потенциальные функции А и А', отличающиеся на градиент Сy некоторой скалярной функции, представляют одно и то же магнитное поле (потому что ротор градиента равен нулю). Они поэтому приводят к одной и той же классической силе qvXВ. Если в квантовой механике все эффекты зависят от векторного потенциала, то какая из многих возможных А-функций правильна?
Ответ состоит в том, что в квантовой механике продолжает существовать тот же произвол в А. Если в уравнении (15.33) мы заменим А на А' = А+Сy, то интеграл от А превратится в
Интеграл от Сy вычисляется по замкнутому пути (1—2); но интеграл от касательной составляющей градиента по замкнутому пути всегда равен нулю (по теореме Стокса). Поэтому как А, так и А' приводят к одним и тем же разностям фаз и к одним и тем же квантовомеханическим эффектам интерференции. И в классической, и в квантовой теории важен только ротор 4; любая функция А, у которой ротор такой, как надо, приводит к правильной теории.
Тот же вывод становится очевидным, если мы используем результаты, приведенные в гл. 14, § 1. Там мы показали, что контурный интеграл от А по замкнутому пути равен потоку В через контур, в данном случае потоку между путями (1) и (2). Уравнение (15.33) можно, если мы хотим, записать в виде
где под потоком В, как обычно, подразумевается поверхностный интеграл от нормальной составляющей В. Результат зависит только от В, т. е. только от ротора А.
Но раз результат можно выражать и через В и через А, то может создаться впечатление, что В удерживает свои позиции «реального» поля, а А все еще выглядит искусственным образованием. Но определение «реального» поля, которое мы вначале предложили, основывалось на идее о том, что «реальное» поле не смогло бы действовать на частицу на расстоянии. Мы же беремся привести пример, в котором В равно нулю (или по крайней мере сколь угодно малому числу) в любом месте, где частицы могут оказаться, так что невозможно представить себе, что В непосредственно действует на них.
Вы помните, что если имеется длинный соленоид, по которому течет электрический ток, то поле В существует внутри него, а снаружи поля нет, тогда как множество векторов А циркулирует снаружи соленоида (фиг. 15.6). Если мы создадим такие условия, что электроны будут проходить только вне соленоида (только там, где есть А), то, согласно уравнению (15.33),
соленоид будет все же влиять на их движение.
Фиг. 15.6. Магнитное поле и векторный потенциал длинного соленоида.
По классическим же воззрениям это невозможно. По классическим представлениям сила зависит только от В. Чтобы узнать, течет ли по соленоиду ток, частица должна пройти сквозь него. А квантовая механика утверждает, что наличие магнитного поля в соленоиде можно установить, просто обойдя его, даже не приближаясь к нему вплотную!
Представьте, что мы поместили очень длинный соленоид малого диаметра прямо тут же за стенкой между двумя щелями (фиг. 15.7). Диаметр соленоида должен быть намного меньше расстояния d между щелями. В этих обстоятельствах дифракция электронов на щели не приведет к заметным вероятностям того, что электроны проскользнут где-то близ соленоида. Как же все это повлияет на наш интерференционный эксперимент?
Сравним два случая: когда ток по соленоиду идет и когда тока нет. Если тока нет, то нет ни В ни А, и получается первоначальная картина электронных интенсивностей вдоль поглотителя.
Фиг. 15.7. Магнитное поле способно влиять на движение электронов, даже когда оно существует только в области, еде вероятность обнаружить электрон пренебрежимо мала.
Если мы включим ток и создадим внутри соленоида магнитное поле В, то снаружи появится поле А. Возникнет сдвиг в разности фаз, пропорциональный циркуляции А вне соленоида, а это означает, что картина максимумов и минимумов сдвинется на другое место. Действительно, раз поток В между любыми двумя путями постоянен, то точно так же постоянна и циркуляция А. Для любой точки прибытия фаза меняется одинаково; это соответствует тому, что вся картина сдвигается по х на постоянную величину, скажем, на х0. Эту величину х0легко подсчитать. Максимальная интенсивность возникает там, где разность фаз двух волн равна нулю. Подставляя вместо d выражение (15.32) или (15.33), а вместо d (B=0) выражение (15.28), получаем
(15.35)
или
(15.36)
Картина при наличии соленоида будет выглядеть так, как показано на фиг. 15.7. По крайней мере так предсказывает квантовая механика.
Недавно был проделан точно такой же опыт. Это чрезвычайно сложный опыт. Длина волны электронов крайне мала, поэтому прибор должен быть миниатюрным, иначе интерференции не заметишь. Щели должны лежать вплотную друг к другу, а это означает, что нужен необычайно тонкий соленоид. Оказывается, что при некоторых обстоятельствах кристаллы железа вырастают в виде очень длинных и микроскопически тонких нитей. Если эти железные нити намагнитить, они образуют маленький соленоид, у которого нет снаружи магнитного поля (оно проявляется только на концах). Так вот, был проделан опыт по интерференции электронов с железной нитью, помещенной между двумя щелями, и предсказанное смещение электронной картины подтвердилось.
А тогда поле А в нашем смысле уже «реально». Вы можете возразить: «Но ведь там есть магнитное поле». Да, есть, но вспомните нашу исходную идею — «реально» только такое поле, которое, чтобы определить собой движение частицы, должно быть задано в том месте, где она находится. Поле В в нити действует на расстоянии. Если мы не хотим, чтобы его влияние выглядело как действие на расстоянии, мы должны пользоваться векторным потенциалом.
Эта проблема имеет интересную историю. Теория, которую мы изложили, была известна с самого возникновения квантовой механики, с 1926 г. Сам факт, что векторный потенциал появляется в волновом уравнении квантовой механики (так называемом уравнении Шредингера), был очевиден с того момента, как оно было написано. В том, что он не может быть заменен магнитным полем, убеждались все, кто пытался это проделать; друг за другом все убеждались, что простого пути для этого не существует. Это ясно и из нашего примера, когда электрон движется по области, где нет никакого поля, и тем не менее подвергается воздействию. Но, поскольку в классической механике А, по-видимому, не имело непосредственного, важного значения и, далее, из-за того, что его можно было менять добавлением градиента, люди еще и еще раз повторяли, что векторный потенциал не обладает прямым физическим смыслом, что даже в квантовой механике «правами» обладают только электрические и магнитные поля. Когда оглядываешься назад, кажется странным, что никто не подумал обсудить этот опыт вплоть до 1956 г., когда Бом и Аронов впервые предложили его и сделали весь вопрос кристально ясным. Все это ведь всегда подразумевалось, но никто не обращал на это внимания. И многие были просто потрясены, когда всплыл этот вопрос. Вот по этой-то причине кое-кто и счел нужным поставить опыт и убедиться, что все это действительно так, хотя квантовая механика, в которую все мы верим вот уже сколько лет, давала вполне недвусмысленный ответ. Занятно, что подобные вещи могут тридцать лет быть на виду у всех, но из-за определенных предрассудков относительно того, что существенно, а что нет, могут всеми игнорироваться.
Сейчас мы хотим немного продолжить наш анализ. Мы продемонстрируем связь между квантовомеханической и классической формулами, чтобы показать, почему оказывается, что при макроскопическом взгляде на вещи все выглядит так, как будто частицы управляются силой, равной произведению qv на ротор А. Чтобы получить классическую механику из квантовой, нам нужно рассмотреть случаи, когда все длины волн малы по сравнению с расстояниями, на которых заметно меняются внешние условия (например, поля). Мы не будем гнаться за общностью доказательства, а только покажем все на очень простом примере. Обратимся снова к тому же опыту со щелями. Но теперь вместо того, чтобы втискивать все магнитное поле в узкий промежуток между щелями, представим себе такое магнитное поле, которое раскинулось позади щелей широкой полосой (фиг. 15.8). Возьмем идеализированный случай, когда в узкой полосе шириной w, много меньшей L, магнитное поле однородно. (Это легко устроить, надо только подальше отнести поглотитель.) Чтобы подсчитать сдвиг по фазе, мы должны взять два интеграла от А вдоль двух траекторий (1) и (2).
Фиг. 15.8. Сдвиг интерференционной картины из-за наличия полоски магнитного поля.
Как мы видели, они различаются просто на поток В между этими путями. В нашем приближении поток равен Bwd. Разность фаз для двух путей поэтому равна
(15.37)
Мы замечаем, что в принятом приближении сдвиг фаз не зависит от угла. Так что опять-таки эффект сводится к сдвигу всей картины вверх на величину Dx. Из формулы (15.28)
Подставляя d-d (В = 0) из (15.37), получаем
(15.38)
Такой сдвиг равноценен тому, что все траектории отклоняются на небольшой угол а (см. фиг. 15.8), равный
(15.39)
По классическим воззрениям мы тоже должны были ожидать, что узкая полоска магнитного поля отклонит все траектории на какой-то маленький угол, скажем a' (фиг. 15.9,а). Когда электроны проходят через магнитное поле, они подвергаются действию поперечной силы qvXВ в течение времени wlv. Изменение их поперечного импульса просто равно ему самому, так что
(15.40)
Фиг. 15.9. Отклонение частицы из-за прохождения ее через магнитное поле.
Угловое отклонение (фиг. 15.9,6) равно отношению этого поперечного импульса к полному импульсу р. Мы получаем
: Этот результат можно сравнить с уравнением (15.39), в котором та же величина вычислялась квантовомеханически. Но связь между классической и квантовой механикой в том и состоит, что частице с импульсом р ставится в соответствие квантовая амплитуда, изменяющаяся как волна длиной l. = h/p. В соответствии с этим уравнением а и а' оказываются идентичными; и классические и квантовые выкладки приводят к одному и тому же.
Из этого анализа мы видим, как получается, что векторный потенциал, который в квантовой механике появляется в явном виде, вызывает классическую силу, зависящую только от его производных. В квантовой механике существенна только интерференция между соседними путями; в ней всегда оказывается, что эффект зависит только от того, как сильно поле А меняется от точки к точке, а значит, только от производных А, а не от него самого. Несмотря на это, векторный потенциал А (наряду с сопровождающим его скалярным потенциалом j), по-видимому, приводит к более прямому описанию физических процессов. Чем глубже мы проникаем в квантовую теорию, тем яснее и прозрачней нам это становится. В общей теории — квантовой электродинамике — в системе уравнений, заменяющих собой уравнения Максвелла, векторные и скалярные потенциалы уже считаются фундаментальными величинами. Векторы Е и В постепенно исчезают из современной записи физических законов: их вытесняют А и j.
§ 6. Что истинно в статике, но ложно в динамике?
Наше исследование статических полей близится к концу. В этой главе мы опасно близко подошли к такому пункту, когда уже следует подумывать о том, что случится, если поля начнут меняться со временем. Толкуя о магнитной энергии, нам едва удалось избежать этого, да и то потому, что мы прикрылись релятивистскими соображениями. Даже при этом наша трактовка проблемы энергии выглядела несколько искусственно и, пожалуй, даже таинственно, потому что мы игнорировали тот факт, что движущиеся катушки должны на самом деле создавать меняющиеся поля. Теперь самое время перейти к изучению полей, меняющихся во времени, к тому, что составляет предмет электродинамики. Мы проделаем это в следующей главе. Однако прежде следует подчеркнуть некоторые моменты.
Хотя мы и начали этот курс с того, что представили полные и точные уравнения электромагнетизма, мы сразу же принялись изучать какие-то вырезанные куски, потому что так было легче. Большим преимуществом является возможность начать с простой теории статических полей и лишь потом перейти к более сложной теории, включающей динамические поля. При этом приходится с самого начала учить меньше нового материала и остается время потренировать мозги, поразмять свои умственные мускулы, прежде чем приступить к задачам потруднее.
Но в таком процессе кроется одна опасность — пока мы не услышали весь рассказ целиком, в нас может укорениться и выдать себя за полную та неполная истина, которую мы успели усвоить; в голове все перепутается: то, что верно всегда, и то, что справедливо только временами. Поэтому в табл. 15.1 мы даем сводку важнейших формул, которых мы касались, отделяя в ней те, что верны в общем случае, от тех, которые соблюдаются только в статике, но ложны в динамике. Эта сводка содержит намеки на то, куда мы собственно с вами путь держим; изучая динамику, мы должны будем детально развить то, что пока приходилось описывать без доказательства.
Пожалуй, здесь стоит сделать несколько замечаний по поводу самой таблицы. Прежде всего вы должны обратить внимание, что уравнения, с которых мы начали, это правильные уравнения, в этом месте мы вас не вводим в заблуждение. Формула для электромагнитной силы (часто именуемой силой Лоренца) F = q(E+vXВ) также правильна. Ошибочен только закон Кулона; он годится только для статики. Четыре уравнения Максвелла для Е и В тоже правильны. Уравнения, принятые нами в статике, ошибочны, потому что мы выбросили из них все члены с производными по времени.
Закон Гаусса С·E = r/e0 остается, но ротор Е в общем случае не равен нулю. Значит, Е нельзя всегда приравнивать к градиенту скаляра — электростатического потенциала. Мы увидим, что скалярный потенциал все же остается, но это уже величина, которая меняется во времени и должна употребляться для полного описания электрического поля только вместе с векторным потенциалом. Конечно, уравнения, управляющие этим новым скалярным потенциалом, также оказываются новыми.
Мы вынуждены также распроститься с представлением о том, что Е в проводниках равно нулю. Когда поля меняются, заряды в проводниках, вообще говоря, не успевают перестраиваться так, чтобы поле все время обращалось в нуль. Они приходят в движение, но никогда не достигают равновесия. Единственное общее утверждение таково: электрические поля создают токи в проводниках. Итак, в переменных полях проводники не являются эквипотенциальными поверхностями. Отсюда также следует, что представление о емкости нельзя сделать универсальным.
Раз магнитных зарядов не бывает, дивергенция В всегда равна нулю. Так что В можно всегда приравнивать СXА. (Выходит, что меняется не все!) Но В генерируется не только токами; СXВ пропорционально плотности тока плюс новое слагаемое dE/dt. Это означает, что А связано с токами новым уравнением. Оно связано и с j. Если мы для собственного удобства воспользуемся свободой выбора С·А, то уравнения для А и j можно будет записать так, что они приобретут простой и изящный вид. Поэтому мы выдвигаем требование, чтобы c2С·А было равно -дj/dt, и тогда дифференциальные уравнения для А или для j оказываются такими, как в таблице.
Потенциалы А и j все еще можно выразить в виде интегралов от токов и зарядов, но это уже не те же самые интегралы, что были в статике. Удивительнее всего, однако, то, что правильный вид интегралов похож на прежний, статический, но с одним небольшим видоизменением, имеющим ясный физический смысл.
Когда мы берем интегралы, чтобы получить потенциалы в некоторой точке, скажем в точке (1) на фиг. 15.10, то мы обязаны использовать значения j и r в точке (2) в более раннее время t' = t-r12/c. Как и следовало ожидать, влияние точки (2) на точку (7) распространяется со скоростью с. Это небольшое видоизменение позволяет отыскивать поля изменяющихся токов и зарядов, потому что, как только мы узнаем А и j, то В получается, как и раньше, как СXА, а Е = -Сj-dA/dt.
Наконец, вы видите из таблицы, что некоторые выводы, полученные в статике (например, вывод о том, что плотность энергии в электрическом поле равна e0E2/2), остаются справедливыми и в электродинамике. Не надо обманывать себя и думать, что все это естественно. Правильность любой формулы, выведенной в статическом случае, должна в динамике доказываться сызнова. Например, мы знаем, что объемный интеграл от rj тоже дает электростатическую энергию. Но это верно только в статике.
В свое время мы детально разберем все эти вопросы; пока же полезно держать в уме эту сводку, чтобы знать, что не грех и позабыть, а что следует считать справедливым всегда.
*Если поле В выходит из плоскости рисунка, то поток, в соответствии с его определением, будет отрицательным, а х0— положительным.
Глава 16 ИНДУЦИРОВАННЫЕ ТОКИ
§ 1. Моторы и генераторы
§ 2. Трансформаторы и индуктивности
§ 3. Силы, действующие на индуцируемые токи
§ 4. Электротехника
§ 1. Моторы и генераторы
Открытие тесной связи между электричеством и магнетизмом, происшедшее в 1820 г., было поистине волнующим событием — ведь до того они считались совершенно независимыми. Сначала открыли, что токи в проводах создают магнитные поля, а затем в том же году обнаружили, что на провода в магнитном поле действуют силы.
Волнение было вызвано тем, что возникающую механическую силу можно использовать в машине для выполнения какой-то работы. Сразу же после этого замечательного открытия люди начали конструировать электромоторы, заставив работать на себя силы, действующие на провода с током. Принцип устройства электромотора схематически показан на фиг. 16.1. Постоянный магнит (обычно в нем имеется несколько частей из мягкого железа) создает магнитное поле внутри двух щелей. Конец каждой щели представляет собой северный или южный полюсы, как показано на схеме. Прямоугольная рамка из медной проволоки помещается так, что одной из своих сторон она попадает в каждую щель. Когда по рамке проходит ток, то в обеих щелях он идет в противоположных направлениях, так что силы оказываются направленными противоположно и создают в рамке вращательный момент вокруг изображенной на схеме оси. Если рамка закреплена на оси так, что она может вращаться, то ее можно подсоединить к шкивам или шестеренкам и заставить производить полезную работу.
Ту же идею можно использовать и при конструировании чувствительных приборов для электрических измерений.
Фиг. 16.1. Схематическое изображение простого электромагнитного мотора.
Так что немедленно после открытия закона сил точность электрических измерений намного возросла. Прежде всего вращательный момент такого мотора может быть значительно увеличен для данного тока, если заставить его проходить по нескольким виткам, а не по одному. Кроме того, рамку можно установить так, чтобы она вращалась под действием очень малого момента, укрепив ее ось в тщательно сделанных подшипниках, либо подвешивая ее на тончайшей проволоке или кварцевой нити. Тогда даже чрезвычайно слабый ток заставит катушку повернуться, и для малых углов величина поворота будет пропорциональна току. Угол поворота можно измерить, приклеив к рамке стрелку или (для очень тонких приборов) прикрепив маленькое зеркальце к рамке и отмечая сдвиг его изображения на шкале. Такие приборы называют гальванометрами. Вольтметры и амперметры работают по тому же принципу. Те же идеи могут быть применены в большом масштабе для создания мощных моторов, производящих механическую работу. Рамку можно заставить вращаться много, много раз, если с помощью укрепленных на оси контактов каждые пол-оборота менять направление тока в ней на противоположное, Тогда момент силы будет всегда направлен в одну и ту же сторону. Маленькие моторчики постоянного тока именно так и устроены. В моторах больших размеров постоянного или переменного тока постоянные магниты часто заменяют электромагнитами, и питаются они от источника электрической энергии.
Осознав, что электрический ток рождает магнитное поле, многие "сразу же предположили, что так или иначе магниты должны тоже создавать электрические поля. Для проверки этого предположения были поставлены различные эксперименты. Например, располагали два провода параллельно друг другу и по одному из них пропускали ток, пытаясь обнаружить ток в другом проводе. Мысль заключалась в том, что магнитное поле сможет как-то протащить электроны вдоль второго провода по закону, который должен формулироваться как-то так: «одинаковое стремится двигаться одинаковым образом». Но, пропуская по одному проводу самый большой ток и используя самый чувствительный гальванометр, обнаружить ток во втором проводе не удалось. Большие магниты тоже не давали никакого эффекта в расположенных поблизости проводах. Наконец, в 1840 г. Фарадей открыл существенную особенность, которую раньше упускали из виду,— электрические эффекты возникают только тогда, когда что-нибудь изменяется, Если в одной из двух проволок ток меняется, то в другой тоже наводится ток, или же если магнит движется вблизи электрического контура, то там возникает ток. Мы говорим теперь, что токи в этих случаях индуцируются. В этом и состояло явление индукции, открытое Фарадеем. Оно преобразило довольно скучную область статических полей в увлекательную динамическую область, в которой происходит огромное число удивительных явлений. Эта глава посвящена качественному описанию некоторых из них. Как мы увидим, можно довольно быстро попасть в очень сложные ситуации, трудно поддающиеся подробному количественному анализу. Но это неважно. Наша главная задача в этой главе — сначала познакомить вас с кругом относящихся сюда явлений. Тщательный анализ мы проделаем немного позже.
Из того, что мы уже знаем, нам легко понять кое-что о магнитной индукции, то, что не было известно во времена Фарадея. Мы знаем о существовании действующей на движущийся заряд силы vXВ, которая пропорциональна его скорости в магнитном поле. Пусть у нас есть проволока, которая движется вблизи магнита (фиг. 16.2), и пусть мы подсоединили концы проволоки к гальванометру. Когда проволока проходит над полюсом магнита, стрелка гальванометра сдвигается.
Магнит создает вертикальное магнитное поле, и, когда мы двигаем проволоку поперек поля, электроны в проволоке чувствуют силу, направленную вбок, т. е. перпендикулярно нолю и направлению движения. Сила толкает электроны вдоль проволоки. Но почему же при этом приходит в движение стрелка гальванометра, который расположен так далеко от этой силы? Да потому, что электроны, испытывающие магнитную силу, начинают двигаться и толкают (за счет электрического отталкивания) другие электроны, находящиеся чуть дальше по проволоке, а те в свою очередь отталкивают еще более удаленные электроны и так далее на большое расстояние.
Фиг. 16.2. Движение провода в магнитном поле создает ток (это регистрирует, гальванометр).
Любопытная штука.
Это так удивило Гаусса и Вебера, построившего впервые гальванометр, что они попытались определить, как далеко распространяются силы по проволоке. Они протянули проволоку поперек всего города, и один ее конец Гаусс присоединил к батарее (батареи были известны раньше генераторов), а Вебер наблюдал, как сдвигается стрелка гальванометра. И они обнаружили способ передавать сигналы на большое расстояние — это было рождение телеграфа! Разумеется, здесь нет прямого отношения к индукции, здесь речь шла о способе передачи тока по проволоке, о том, действительно ли ток продвигается за счет индукции или нет.
Предположим теперь, что в установке, изображенной на фиг. 16.2, мы проволоку оставляем в покое, а двигаем магнит. И снова наблюдаем эффект на гальванометре. Фарадей еще обнаружил, что движение магнита под проволокой (один способ) вызывает такой же эффект, как и движение проволоки над магнитом (другой способ). Но когда движется магнит, то на электроны проволоки уже больше не действует сила v X В. Это и есть то новое явление, которое открыл Фарадей. Сегодня мы можем попытаться понять его с помощью принципа относительности.
Мы уже поняли, что магнитное поле магнита возникает за счет его внутренних токов. Поэтому мы ожидаем появления такого же эффекта, если вместо магнита на фиг. 16.2 взять катушку из проволоки, по которой течет ток. Если двигать провод мимо катушки, то гальванометр обнаружит ток, равно, как и в том случае, когда катушка движется мимо провода. Но существует и еще более удивительная вещь: если менять магнитное поле катушки не за счет ее движения, а за счет изменения в ней тока, то гальванометр снова покажет наличие эффекта. Например, если расположить проволочную петлю рядом с катушкой (фиг. 16.3), причем обе они неподвижны, и выключить ток, то через гальванометр пройдет импульс тока. Если же снова включить ток в катушке, то стрелка гальванометра качнется в противоположную сторону.
Всякий раз, когда через гальванометр в установке, показанной на фиг. 16.2 или 16.3, проходит ток, в проводе в каком-то одном направлении возникает результативное давление на электроны. В разных местах электроны могут толкнуться в разные стороны, но в одном направлении напор оказывается больше, чем в другом. Учитывать нужно только давление электронов, просуммированное вдоль всей цепи. Мы называем этот результирующий напор электронов электродвижущей силой (сокращенно э. д. с.) цепи. Более точно э. д. с. определяется как тангенциальная сила, приходящаяся на один заряд, проинтегрированная по длине провода, вдоль всей цепи. Открытие Фарадея целиком состояло в том, что э. д. с. в проводе можно создать тремя способами: двигая провод, двигая магнит вблизи провода или меняя ток в соседнем проводе.
Обратимся снова к простому прибору, изображенному на фиг. 16.1, только теперь не будем пропускать ток через проволоку, чтобы придать ей вращение, а будем крутить рамку с помощью внешней силы, например рукой или с помощью водяного колеса. При вращении рамки ее провода движутся в магнитном поле, и мы обнаруживаем в цепи рамки э. д. с.
Фиг. 16.3. Катушка с током возбуждает ток в другой катушке, если первая катушка перемещается или если ток в ней меняется.
Мотор превратился в генератор.
Индуцированная э. д. с. возникает в катушке генератора за счет ее движения. Величина э. д. с. дается простым правилом, открытым Фарадеем. (Сейчас мы просто сформулируем это правило, а несколько позднее разберем его подробно.) Правило такое: если магнитный поток, проходящий через петлю (этот поток есть нормальная составляющая В, проинтегрированная по площади петли), меняется со временем, то э. д. с. равна скорости изменения потока. Мы будем в дальнейшем называть это «правилом потока». Вы видите, что, когда катушка на фиг. 16.1 вращается, поток через нее изменяется. Вначале, скажем, поток идет в одну сторону, а когда катушка повернется на 180°, тот же поток идет сквозь катушку по-другому. Если непрерывно вращать катушку, поток сначала будет положительным, затем отрицательным, потом опять положительным и т. д. Скорость изменения потока должна тоже меняться. Следовательно, в катушке возникает переменная э. д. с. Если присоединить два конца катушки к внешним проводам через скользящие контакты, которые называются контактными кольцами (просто, чтобы провода не перекручивались), мы получаем генератор переменного тока.
А можно с помощью скользящих контактов устроить и так, чтобы через каждые пол-оборота соединение между концами катушки и внешними проводами становилось противоположным, так что когда э. д. с. изменит свой знак, то и соединение станет противоположным. Тогда импульсы э. д. с. будут всегда толкать ток в одном направлении вдоль внешней цепи. Мы получаем так называемый генератор постоянного тока.
Прибор, изображенный на фиг. 16.1, может быть либо мотором, либо генератором. Связь между моторами и генераторами хорошо демонстрируется с помощью двух одинаковых «моторов» постоянного тока с постоянными магнитами, катушки которых соединены двумя медными проводами. Если ручку одного из «моторов» поворачивать механически, он становится генератором и приводит в движение второй как мотор. Если же поворачивать ручку второго, то генератором уже становится он, а первый работает как мотор. Итак, здесь мы встречаемся с интересным примером нового рода эквивалентности в природе: мотор и генератор эквивалентны. Количественная эквивалентность на самом деле не совсем случайна. Она связана с законом сохранения энергии.
Другой пример устройства, которое может работать либо для создания э. д. с., либо воспринимать действие э. д. с., представляет собой приемная часть обычного телефона, т. е. «слухофон». Первоначальный телефон Белла состоял из двух таких «слухофонов», соединенных двумя длинными проводами.
Фиг. 16.4. Приемное или передающее устройство телефона.
Основной принцип этого устройства показан на фиг. 16.4. Постоянный магнит создает магнитное поле в двух сердечниках из мягкого железа и в тонком железном диске — мембране, которая приводится в движение звуковым давлением. При движении мембрана изменяет величину магнитного поля в сердечниках. Следовательно, поток через катушку проволоки, намотанной вокруг одного из сердечников, изменяется, когда звуковая волна попадает на мембрану. Тогда в катушке возникает э. д. с. Если концы катушки присоединены к цепи, в ней устанавливается ток, который представляет собой электрическое изображение звука.
Если концы катушки на фиг. 16.4 присоединить двумя проводами к другому такому же устройству, то по второй катушке потечет меняющийся ток. Этот ток создаст меняющееся магнитное поле и заставит меняться и силу притяжения железной мембраны. Она начнет дрожать и породит звуковые волны, подобные тем, которые колебали первую мембрану. С помощью маленьких кусочков железа и меди человеческий голос передается по проводам!
(Приемники в современных домашних телефонах похожи на только что описанный, а вот передатчики используются уже улучшенные, чтобы получить большую мощность. Это «микрофоны с угольной мембраной», в которых звуковое давление изменяет электрический ток от батарей.)
§ 2. Трансформаторы и индуктивности
Одна из наиболее интересных сторон открытий Фарадея заключается совсем не в том, что э. д. с. возникает в движущейся катушке, это мы можем понять с помощью магнитной силы qXВ. Главное — в том, что изменение тока в одной катушке создает э. д. с. во второй катушке. И уж совсем удивительно, что величина э. д. с., наведенной во второй катушке, дается тем же самым «правилом потока»: э. д. с. равна скорости изменения магнитного потока сквозь катушку. Возьмем, например, две катушки (фиг. 16.5), каждая из которых намотана на отдельную стопку железных пластинок (с их помощью можно создать более сильные магнитные поля).
Фиг. 16.5. Две катушки, намотанные на стопки железных пластинок, позволяют зажечь лампочку, не соединяя ее прямо с генератором.
Присоединим теперь одну из катушек — катушку а — к генератору переменного тока. Непрерывно меняющийся ток создает непрерывно меняющееся магнитное поле. Такое изменяющееся магнитное поле генерирует переменную э. д. с. во второй катушке — катушке b. Эта э. д. с., например, способна заставить гореть электрическую лампочку.
В катушке bэ. д. с. меняется с частотой, конечно, равной частоте первого генератора. Но ток в катушке b может быть больше или меньше тока в катушке а. Ток в катушке b зависит от индуцированной в ней э. д. с. и от сопротивления и индуктивности остальной части ее цепи. Эта э. д. с. может быть меньше э. д. с. генератора, если, скажем, изменение потока мало. Или же э. д. с. в катушке b может оказаться много больше э. д. с. генератора, если на катушку 6 навить много витков, ибо в этом случае в данном магнитном поле поток через катушку будет больше. (Можно, если хотите, сказать об этом иначе — в каждом витке э. д. с. одна и та же, и поскольку полная э. д. с. равна сумме э. д. с. отдельных витков, то большое число витков в совокупности создает большую э. д. с.)
Такая комбинация двух катушек (обычно с набором железных пластинок, повышающих магнитное поле) называется трансформатором. Он может «трансформировать» одну э. д. с. (называемую еще «напряжением») в другую.
Эффекты индукции возникают и в одной отдельной катушке. Например, в установке, изображенной на фиг. 16.5, меняющийся поток проходит не только через катушку b, которая зажигает лампочку, но и через катушку а. Меняющийся ток в катушке а создает меняющееся магнитное поле внутри нее самой, и поток этого поля непрерывно изменяется, так что в катушке а получается самоиндуцированная э. д. с.
Э. д. с., действующая на ток, возникает тогда, когда его собственное магнитное поле растет, или в общем случае, если его собственное поле изменяется каким угодно образом. Этот эффект называется самоиндукцией.
Когда мы ввели «правило потока», утверждающее, что э. д. с. равна скорости изменения потока, мы не определяли направление э. д. с. Существует простое правило (называемое правилом Ленца) для определения направления э.д. с.: э. д. с. стремится препятствовать всякому изменению потока. Иначе говоря, направление наведенной э. д. с. всегда такое, что, если бы ток пошел в направлении э. д. с., он создал бы поток поля В, препятствующий изменению поля В, создающего эту э. д. с. Правилом Ленца можно пользоваться, чтобы найти направление э. д. с. в генераторе, показанном на фиг. 16.1, или в обмотке трансформатора (фиг. 16.3).
В частности, если ток в отдельной катушке (или в любом проводе) меняется, возникает «обратная» э. д. с. в цепи. Эта э. д. с. действует на заряды, текущие в катушке а на фиг. 16.5, препятствуя изменению магнитного поля, и поэтому направлена так, чтобы препятствовать изменению тока. Она стремится сохранить ток постоянным; э. д. с. противоположна току, когда ток увеличивается, и направлена по току, когда он уменьшается. При самоиндукции ток обладает «инерцией», потому что эффекты индукции стремятся сохранить поток постоянным точно так же, как механическая инерция стремится сохранить скорость тела неизменной.
Любой большой электромагнит обладает большой самоиндукцией. Пусть, например, к катушке большого электромагнита присоединена батарея (фиг. 16.6) и пусть установилось большое магнитное поле. (Ток достигает постоянной величины, определяемой напряжением батареи и сопротивлением провода катушки.)
Фиг. 16.6. Включение электромагнита в цепь.
Лампочка открывает проход току в момент отключения, препятствуя возникновению слишком большой э.д.с. на контактом выключателя.
Но теперь предположим, что мы пытаемся отсоединить батарею, разомкнув выключатель. Если бы мы на самом деле разорвали цепь, ток быстро уменьшился бы до нуля и в процессе уменьшения создал бы огромную э. д. с. В большинстве случаев такой э. д. с. оказывается вполне достаточно, чтобы образовалась вольтова дуга между разомкнутыми контактами выключателя. Возникающее большое напряжение могло бы нанести вред катушке, да и вам, если бы именно вы размыкали выключатель! По этим причинам электромагниты обычно включают в цепь примерно так, как показано на фиг. 16.6. Когда переключатель разомкнут, ток не меняется быстро, а продолжает течь через лампу, оставаясь постоянным за счет э. д. с. от самоиндукции катушки.
§ 3. Силы, действующие на индуцируемые токи
Вы, вероятно, наблюдали великолепную демонстрацию правила Ленца с помощью приспособления, изображенного на фиг. 16.7. Это электромагнит точно такой же, как катушка а на фиг. 16.5. На одном конце электромагнита помещается алюминиевое кольцо. Если с помощью переключателя подсоединить катушку к генератору переменного тока, то кольцо взлетает в воздух. Силу, конечно, порождают токи, индуцируемые в кольце. Тот факт, что кольцо отлетает прочь, показывает, что токи в нем препятствуют изменению поля, проходящего через кольцо. Когда у магнита северный полюс находится сверху, индуцированный ток в кольце создает внизу северный полюс. Кольцо и катушка отталкиваются точно так же, как два магнита, приложенные одинаковыми полюсами. Если в кольце сделать тонкий разрез по радиусу, сила исчезает — убедительное доказательство того, что она действительно обусловлена токами в кольце.
Фиг. 16.7. Проводящее кольцо сильно отталкивается электромагнитом, когда в нем меняется ток.
Фиг. 16.8. Электромагнит вблизи идеально проводящей плоскости.
Если вместо кольца у края электромагнита поместить алюминиевый или медный диск, то и он отталкивается; индуцированные токи циркулируют в материале диска и снова вызывают отталкивание.
Интересный эффект, в основе похожий на предыдущий, возникает с листом идеального проводника. В «идеальном проводнике» ток совсем не встречает сопротивления. Поэтому возникшие в нем токи могут течь не переставая. Фактически малейшая э. д. с. создала бы сколь угодно большой ток, а это на самом деле означает, что в нем вообще не может быть э. д. с. Любая попытка создать магнитный поток, проходящий сквозь такой лист, вызовет токи, образующие противоположно направленные поля В — все со сколь угодно малыми э. д. с., так что никакого потока не будет.
Если к листу идеального проводника мы поднесем электромагнит, то при включении тока в магните в листе возникают токи (называемые вихревыми токами), и никакой магнитный поток не пройдет. Линии поля будут иметь вид, показанный на фиг. 16.8. То же самое произойдет, если к идеальному проводнику поднести постоянный магнит. Поскольку вихревые токи создают противоположные поля, магниты от проводника отталкиваются. Поэтому оказывается возможным подвесить постоянный магнит в воздухе над листом идеального проводника, изготовленного в форме тарелки (фиг. 16.9). Магнит будет поддерживаться в воздухе за счет отталкивания индуцированных вихревых токов в идеальном проводнике. При обычных температурах идеальных проводников не существует, но некоторые материалы при достаточно низких температурах становятся идеальными проводниками.
Фиг. 16.9. Магнитная палочка отталкивается вихревыми токами и повисает над чашей из сверхпроводника.
Так, при температуре ниже 3,8° К олово становится идеальным проводником; тогда оно называется сверхпроводником.
Если проводник, показанный на фиг. 16.8, не вполне идеальный, то возникнет некоторое сопротивление течению вихревых токов. Токи будут постепенно замирать, и магнит медленно опустится. В неидеальном проводнике, чтобы течь дальше, вихревым токам необходима некоторая э. д. с., а для возникновения э. д. с. поток должен непрерывно меняться. Поток магнитного поля постепенно проникает в проводник.
В обычном проводнике имеются не только силы отталкивания за счет вихревых токов, но могут быть и боковые силы. Например, если мы передвигаем магнит над проводящей поверхностью, вихревые токи создают тормозящую силу, потому что индуцированные токи препятствуют изменению потока. Такие силы пропорциональны скорости и похожи на силы вязкости.
Эти эффекты хорошо наблюдаются на приборе, изображенном на фиг. 16.10. Квадратная медная пластинка укреплена на конце стержня, образуя маятник. Пластинка качается взад и вперед между полюсами электромагнита. Когда магнит включается, движение маятника неожиданно прекращается. Как только металлическая пластинка попадает в зазор магнита, в ней индуцируется ток, который стремится помешать изменению потока через пластинку. Если бы пластинка была идеальным проводником, токи были бы столь велики, что они снова вытолкнули бы пластинку и она отскочила бы назад. В медной же пластинке имеется некоторое сопротивление, поэтому токи' сначала заставляют пластинку почти намертво застыть, когда она начинает входить в поле. Затем, по мере того как токи замирают, пластинка продолжает медленно двигаться в магнитном; поле и останавливается совсем.
Схема вихревых токов в медном маятнике поясняется фиг. 16.11. Сила и расположение токов весьма чувствительны к форме пластинки. Если, скажем, вместо медной пластинки взять другую, в которой имеется ряд узких щелей (фиг. 16.12), то эффекты вихревых токов сильно уменьшатся. Маятник проходит сквозь магнитное поле лишь с небольшой тормозящей силой
Фиг. 16.10. Торможение маятника указывает на силы, возникающие благодаря вихревым токам.
Причина в том, что токи в каждой части пластинки возбуждаются меньшими по величине потоками и, следовательно, эффекты сопротивления каждой петли оказываются большими. Чем меньше токи, тем меньше и торможение. Вязкий характер силы проявится еще более наглядно, если медную пластинку поместить между полюсами магнита и затем отпустить ее. Пластинка не падает, она просто медленно опускается. Вихревые токи оказывают сильное сопротивление движению, точь-в-точь как вязкое сопротивление меда.
Если мы не будем протаскивать проводник мимо магнита, а попробуем вращать его в магнитном поле, то в нем в результате тех же эффектов возникнет тормозящий момент. И наоборот, если вращать магнит, меняя местами его полюса, вблизи проводящей плоскости или кольца, то кольцо повернется за магнитом, токи в кольце создадут момент, стремящийся повернуть кольцо вместе с магнитом.
Фиг. 16.11. Вихревые токи в медном маятнике.
Фиг. 16.12. Эффекты от вихревых токов сильно снижаются, если в пластинке прорезать щели.
Поле, весьма похожее на поле вращающегося магнита можно создать с помощью устройства из катушек (фиг. 16.13). Мы берем железный тор (т. е. железное кольцо в виде бублика) и наматываем на него шесть катушек. Направив ток так, как показано на фиг. 16.13, а, через обмотки 1 и 4, мы получим магнитное поле в направлении, указанном стрелками. Если мы теперь переключим ток на обмотки 2 и 5, то магнитное поле будет направлено уже по-другому (фиг. 16.13, б). Продолжая так действовать, мы получаем последовательность полей, изображенных на остальных частях нашего рисунка. Если процесс проводить плавно, то получится «вращающееся» магнитное поле. Подсоединив катушки к сети трехфазного тока (а она дает именно такую последовательность токов), мы легко получим требуемую последовательность токов. «Трехфазный ток» создается генератором, использующим принцип фиг. 16.1, за тем исключением, что на оси симметрично укрепляются три рамки, т. е. каждая под углом 120° к соседней. Когда рамки вращаются как единое целое, э. д. с. максимальна в одной рамке, затем в другой и т. д. в правильной последовательности. Трехфазный ток имеет много практических преимуществ. Одно из них заключается в возможности получить вращающееся магнитное поле. Момент, действующий на проводник со стороны такого вращающегося поля, легко обнаруживается на металлическом кольце, поставленном на изолирующей подставке прямо над тором (фиг. 16.14). Вращающееся поле вызывает вращение кольца вокруг вертикальной оси. Здесь видны те же основные элементы, которые имеются в больших промышленных трехфазных индукционных моторах.
Фиг. 16.13. Создание вращающегося магнитного поля.
Другой тип индукционного мотора показан на фиг. 16.15. Это устройство непригодно для практических высокоэффективных моторов, но иллюстрирует основной принцип. Электромагнит М, состоящий из пачки прокатанных железных листов, на которую навита спиральная обмотка, питается от генератора переменного тока. Магнит создает переменный поток поля 15 сквозь алюминиевый диск. Если имеются только эти две компоненты (см. фиг. 16.15, а), у нас еще нет мотора. В диске имеются вихревые токи, но они симметричны и момента не возникает. (Диск будет немного нагреваться за счет токов индукции.)
Фиг. I6.14. С помощью вращающегося поля (фиг. 16.13) можно придать кольцу из проводника вращающий момент.
Фиг. 16.15. Простой пример индукционного мотора с затененным полюсом.
Если теперь мы закроем только одну половину магнитного полюса алюминиевой пластинкой (фиг. 16.15, б), то диск начнет вращаться и мы получим мотор. Действие его связано с двумя эффектами вихревых токов. Во-первых, вихревые токи в алюминиевой пластинке препятствуют изменению потока сквозь нее, поэтому магнитное поле над пластинкой всегда отстает от поля над непокрытой частью полюса. Этот так называемый эффект «затененного полюса» создает поле, которое в «затененной» области меняется совсем так же, как и в «незатененной», за исключением постоянного запаздывания во времени. Эффект в целом такой, как будто имеется вдвое более узкий магнит, постоянно передвигающийся из незатененной области в затененную. Во-вторых, меняющиеся поля взаимодействуют с вихревыми токами диска, создавая в нем момент силы.
§ 4. Электротехника
Когда Фарадей впервые опубликовал свое замечательное открытие о том, что изменение магнитного потока создает э. д. с., его спросили (как спрашивают, впрочем, всякого, кто открывает какие-то новые явления): «Какая от этого польза?» Ведь все, что он обнаружил, было очень странным — в проводе возникал крошечный ток, когда он двигал провод возле магнита. Какая же может быть от этого «польза»? Фарадей ответил: «Какая может быть польза от новорожденного?»
А теперь вспомните о тех громадных практических применениях, к которым привело его открытие. Все, что мы описывали,— отнюдь не игрушки; это примеры, выбранные по большей части так, чтобы представить принцип той или иной практической машины. Например, вращающееся кольцо во вращающемся поле — индукционный мотор. Существует, конечно, известная разница между кольцом и практически используемым индукционным мотором. У кольца момент очень мал; протяните руку и вы можете остановить его. В хорошем моторе детали должны быть лучше пригнаны: магнитное поле не должно так щедро «растрачиваться» в воздухе. Во-первых, с помощью железа поле концентрируется. Мы не говорили о том, как это делает железо, но оно способно увеличить магнитное поле в десятки и тысячи раз по сравнению с полем одной медной катушки. Во-вторых, зазоры между частями железа делаются небольшими; с этой целью железо даже встраивается внутрь вращающегося кольца. Словом, все направлено на то, чтобы получить наибольшие силы и максимальную эффективность, т. е. превратить электрическую мощность в механическую, и такое «кольцо» уже нельзя будет удержать рукой.
Задача уменьшения зазоров и установление самого практичного режима работы есть дело инженерной науки. Она требует серьезного изучения проблем конструирования, хотя никаких новых принципов получения силы не существует. Но от основных принципов до практического и экономичного проектирования — долгий путь. И именно тщательная инженерно-конструкторская работа сделала возможным такую грандиозную вещь, как гидростанция Боулдер Дэм и все, что с ней связано.
Что такое Боулдер Дэм? Огромная река, перегороженная бетонной стеной. Но что это за стена! Изогнутая в виде идеально плавной кривой, тщательно рассчитанная так, чтобы как можно меньше бетона сдерживало напор реки. Стена утолщается книзу, образуя чудесную форму, которой любуются художники, но которую способны оценить только инженеры, потому что они понимают, насколько это хорошо. Они знают, что утолщение определяется тем, как растет давление воды на глубине. Но мы отвлеклись от электричества.
Затем вода реки забирается в огромную трубу. Уже само по себе это замечательное инженерное сооружение. По трубе вода передается к «водяному колесу» — огромной турбине — и заставляет колесо вращаться. (Еще одно достижение техники.) Но зачем крутят колеса? Они присоединены к невероятно запутанной мешанине из железа и меди (там все перекручено и переплетено). Все сооружение состоит из двух частей — одна крутится, а другая — стоит. Все это сложное сооружение сделано из немногих материалов, главным образом из железа и меди, а также из бумаги и шеллака, служащих изоляцией. Вращающееся чудовище. Генератор. Откуда-то из этого месива железа и меди вылезает несколько медных концов. Плотина, турбина, железо, медь — все собрано вместе для того, чтобы на этих медных полосках появилось нечто особенное — э. д. с. Затем медные полосы проходят небольшой путь и закручиваются несколько раз вокруг другого куска железа, образуя трансформатор; на этом их работа кончается.
Но вокруг этого же куска железа обвивается еще один медный кабель, который не соединяется непосредственно с полосами, пришедшими от генератора; он проходит поблизости от полос и забирает их з. д. с. Трансформатор превращает энергию, которая имела сравнительно низкое напряжение, необходимое для эффективной работы генератора, в очень высокое напряжение, которое лучше всего подходит для экономичной передачи электроэнергии по длинным кабелям.
И все должно быть исключительно эффективным — не может быть ничего лишнего, никаких потерь. Почему? Через все эти устройства протекает вся электрическая энергия, которая используется в стране. Если пропадет всего один или два процента энергии — подумайте, как много это составит. Если в трансформаторе остается только один процент энергии, то она должна куда-то деваться. Если бы, например, она выделялась в виде тепла — все устройство расплавилось бы.
Из Боулдер Дэм выходит во всех направлениях несколько дюжин медных стержней — длинных, очень длинных стержней толщиной, пожалуй, с вашу руку и длиной в сотни миль. Узкие медные дороги, несущие энергию гигантской реки. Затем эти дороги разветвляются... трансформаторов становится еще больше... иногда они подходят к большим генераторам, переводящим ток в другие формы... иногда к машинам, выполняющим важные промышленные работы... к новым трансформаторам... Затем все новые и новые разветвления и ответвления... пока, наконец, река не распределится по всему городу; она крутит моторы, создает тепло, свет, изготовляет приборы. Чудо рождения горячего огня из холодной воды на расстоянии более 600 миль — и все это благодаря особым образом собранным кусочкам железа и меди. Большие моторы для проката стали и крошечные моторчики для бормашины. Тысячи маленьких колесиков, крутящихся под действием большого колеса в Боулдер Дэм. Остановите большое колесо, и все остальные колесики замрут; огни потухнут.
Но этого мало. Те же явления, которые помогают взять грандиозную мощь реки и распределить ее по всей округе, пока в конце концов несколько капель реки закрутят бормашину, снова приходят на помощь при создании исключительно тонких приборов... для определения неуловимо слабых токов... для передачи голосов, музыки и изображений... для вычислительных машин... для автоматических машин фантастической точности.
Все это возможно потому, что тщательно продумано устройство из меди и железа — эффективно созданы магнитные поля... железные блоки диаметром в 2 метра, вращающиеся с зазором в 2 миллиметра... рассчитаны правильно пропорции меди, чтобы получить оптимальную эффективность... выдуманы странные формы, которые все служат своим целям, так же как форма плотины.
Если археолог будущего когда-нибудь раскопает Боулдер Дэм, он, вероятно, восхитится красотой ее линий. А исследователь — гражданин какой-то великой цивилизации Будущего, посмотрев на генераторы и трансформаторы, скажет: «Заметьте, как красивы формы каждой железной детали. Подумайте, сколько мысли вложено в каждый кусочек меди».
Здесь проявляется сочетание могущества техники и тщательного расчета. В генераторе осуществляется то, что нигде более в природе не встречается. Правда, силы индукции появляются и в других случаях. Несомненно, где-то вокруг Солнца и звезд действуют эффекты электромагнитной индукции. Возможно (хотя и не наверное), что магнитное поле Земли поддерживается каким-то гигантским аналогом электрического генератора, который работает на токах, циркулирующих в недрах Земли. Но нигде нет такого сочетания движущихся частей, которые могли бы порождать электрическую энергию, как это делается в генераторе,— непрерывно и очень экономично.
Вы, возможно, думаете, что конструирование электрических генераторов уже не представляет интереса, что это уже мертвая наука, ведь все они давно созданы. Почти совершенные генераторы или моторы можно взять просто с полки. Но даже если бы это было и так, нужно восхищаться чудесной законченностью решения проблемы. Однако осталось немало и нерешенных задач. И даже генераторы и моторы становятся снова проблемой. Возможно, что скоро для решения проблемы распределения электрической энергии понадобится использовать всю область низких температур и сверхпроводников. Будут созданы новые оптимальные установки с учетом радикально новых факторов. Возможно, энергетические сети будущего будут мало похожи на сегодняшние.
Итак, вы видите, что при изучении законов индукции можно заняться бесчисленным множеством приложений и проблем. Конструирование электрических машин само по себе может стать задачей всей жизни. Мы не будем слишком углубляться в этот вопрос, но мы должны осознать то, что открытие закона индукции неожиданно связало теорию с огромным числом практических применений. Область эта принадлежит инженерам и тем ученым прикладной науки, которые занимаются детальной разработкой различных приложений. Физика дает им лишь основу — основные законы, не зависящие от того, к чему они применяются. (Создание этой основы еще далеко не закончено, потому что предстоит еще подробно рассмотреть свойства железа и меди. Немного позже мы увидим, что физика может кое-что сказать и о них.)
Современная электротехника берет свое начало с открытий Фарадея. Бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить.
Глава 17 ЗАКОНЫ ИНДУКЦИИ
§ 1. Физика индукции
§ 2. Исключения из «правила потока»
§ 3. Ускорение частицы в индуцированном электрическом поле; бетатрон
§ 4. Парадокс
§ 5. Генератор переменного тока
§ 6. Взаимная индукция
§ 7. Самоиндукция
§ 8. Индуктивность и магнитная энергия
§ 1. Физика индукции
В предыдущей главе мы описали множество явлений, которые показали, что эффекты индукции весьма сложны и интересны. Сейчас мы хотим обсудить основные законы, управляющие этими эффектами. Мы уже определяли э. д. с. в проводящей цепи как полную силу, действующую на заряды, просуммированную по всей длине цепи. Более точно, это тангенциальная компонента силы на единичный заряд, проинтегрированная по всему проводу вдоль цепи. Следовательно, эта величина равна полной работе, совершаемой над единичным зарядом, когда он обходит один раз вокруг цепи.
Мы дали также «правило потока», которое утверждает, что э. д. с. равна скорости изменения магнитного потока сквозь такую цепь проводников. Давайте посмотрим, можем ли мы понять, почему это так. Прежде всего рассмотрим случай, когда поток меняется из-за того, что цепь движется в постоянном поле.
На фиг. 17.1 показана простая проволочная петля, размеры которой могут меняться. Петля состоит из двух частей — неподвижной U-образной части (а) и подвижной перемычки (b), которая может скользить вдоль двух плеч U. Цепь всегда замкнута, но площадь ее может меняться. Предположим, что мы помещаем эту петлю в однородное магнитное поле так, что плоскость U оказывается перпендикулярной полю. Согласно правилу, при движении перемычки в петле должна возникать э. д. с., пропорциональная скорости изменения потока сквозь петлю. Эта э. д. с. будет порождать в петле ток. Мы предположим, что сопротивление проволоки достаточно велико, так что токи малы.
Фиг. 17.1. В рамке наводится э.д.с., если поток меняется за счет изменения площади рамки при перемещении перемычки b.
Тогда магнитным полем от этого тока можно пренебречь.
Поток через петлю равен wLB, поэтому «правило потока» дало бы для э. д. с. (ее обозначим через о)
где v — скорость смещения перемычки.
Нам следовало бы понимать этот результат и с другой точки зрения, отправляясь от магнитной силы vXB, действующей на заряды в движущейся перекладине. Эти заряды будут чувствовать силу, касательную к проволоке и равную vB для единичного заряда. Она постоянна вдоль длины w перемычки и равна нулю в остальных местах, поэтому интеграл равен
E= -wvB,
что в точности совпадает с результатом, полученным из скорости изменения потока.
Приведенное доказательство можно распространить на любой случай, когда магнитное поле постоянно и провода движутся. Можно в общем виде доказать, что для любой цепи, части которой движутся в постоянном магнитном поле, э. д. с. равна производной потока по времени независимо от формы цепи.
Ну а что произойдет, если петля будет неподвижна, а магнитное поле изменится? На этот вопрос мы не можем ответить с помощью тех же аргументов. Фарадей открыл (поставив опыт), что «правило потока» остается справедливым независимо от того, почему меняется поток.
Сила, действующая на электрические заряды, в общем случае дается формулой F = q(E+vXB); новых особых «сил за счет изменения магнитного поля» не существует. Любые силы, действующие на покоящиеся заряды в неподвижной проволоке, возникают за счет Е. Наблюдения Фарадея привели к открытию нового закона о связи электрического и магнитного полей: в области, где магнитное поле меняется со временем, генерируются электрические поля. Именно это электрическое поле и гонит электроны по проволоке, и, таким образом, оно-то и ответственно за появление э. д. с. в неподвижной цепи, когда магнитный поток изменяется.
Общий закон для электрического поля, связанного с изменяющимся магнитным полем, такой:
(17.1)
Мы назовем его законом Фарадея. Он был открыт Фарадеем, но впервые в дифференциальной форме записан Максвеллом в качестве одного из его уравнений. Давайте посмотрим, как из этого уравнения получается «правило потока» для цепей. Используя теорему Стокса, этот закон можно записать в интегральной форме
(17.2)
где, как обычно, Г — произвольная замкнутая кривая, a S — любая поверхность, ограниченная этой кривой. Вспомним, что здесь Г — это математическая кривая, зафиксированная в пространстве, a S — фиксированная поверхность. Тогда производную по времени можно вынести за знак интеграла:
(17.3)
Применяя это соотношение к кривой Г, которая идет вдоль неподвижной цепи проводников, мы получаем снова «правило потока». Интеграл слева — это э. д. с., а в правой части с обратным знаком стоит скорость изменения потока, проходящего внутри контура. Итак, соотношение (17.1), примененное к неподвижному контуру, эквивалентно «правилу потока».
Таким образом, «правило потока» согласно которому э. д. с. в контуре равна взятой с обратным знаком скорости, с которой меняется магнитный поток через контур, применимо, когда поток меняется за счет изменения поля или когда движется контур (или когда происходит и то, и другое). Две возможности —«контур движется» или «поле меняется» — неразличимы в формулировке правила. Тем не менее для объяснения правила в этих двух случаях мы пользовались двумя совершенно разными законами: vXB для «движущегося контура» и СXЕ = -dB/dt для «меняющегося поля».
Мы не знаем в физике ни одного другого такого примера, когда бы простой и точный общий закон требовал для своего настоящего понимания анализа в терминах двух разных явлений. Обычно столь красивое обобщение оказывается исходящим из единого глубокого основополагающего принципа. Но в этом случае какого-либо особо глубокого принципа не видно. Мы должны воспринимать «правило» как совместный эффект двух совершенно различных явлений.
На «правило потока» мы должны посмотреть следующим образом. Вообще говоря, сила на единичный заряд равна F/q = Е+vXB. В движущихся проводниках сила возникает за счет v. Кроме того, возникает поле Е, если где-либо меняется магнитное поле. Эти эффекты независимы, но э. д. с. вокруг проволочной петли всегда равна скорости изменения магнитного потока сквозь петлю.
§ 2. Исключения из «правила потока»
Здесь мы приведем несколько примеров, частично известных Фарадею, которые показывают, как важно ясно понимать разницу между двумя эффектами, ответственными за возникновение наведенной э. д. с. Наши примеры включают те случаи, когда «правило потока» неприменимо либо потому, что вообще никаких проводов нет, либо потому, что путь, избираемый индуцированными токами, проходит внутри объема проводника.
Вначале сделаем важное замечание: та часть э. д. с., которая возникает за счет поля Е, не связана с существованием физической проволоки (в отличие от части vXВ). Поле Е может существовать в пустом пространстве, и контурный интеграл от него по любой воображаемой линии в пространстве есть скорость изменения потока В через эту линию.
Фиг. 17.2. При вращении диска слагаемое vXB порождает э.д.с., но поток сквозь цепь не меняется.
Фиг. 17.3. При повороте пластинок в однородном магнитном поле поток может сильно меняться, но э.д.с. не возникает.
(Заметьте, что это совсем непохоже на поле Е, создаваемое статическими зарядами, так как в электростатике контурный интеграл от Е по замкнутой петле всегда равен нулю.)
Теперь опишем случай, когда поток через контур не меняется, а э. д. с. тем не менее существует. На фиг. 17.2 показан проводящий диск, помещенный в магнитное поле и который может вращаться на неподвижной оси. Один контакт приделан к оси, а другой трется о внешний край диска. Цепь замыкается через гальванометр. Когда диск вращается, «контур» (в смысле места в пространстве, где текут токи) всегда остается тем же самым. Но часть «контура» проходит в диске, в движущемся материале. Хотя поток по контуру постоянен, э. д. с. все же есть, в этом можно убедиться по отклонению гальванометра. Ясно, что здесь перед нами случай, когда за счет силы vXB в движущемся диске возникает э. д. с., которая не может быть равна изменению потока.
В качестве обратного примера мы сейчас рассмотрим несколько необычный случай, когда поток через «контур» (снова в смысле того места, где текут токи) изменяется, а э. д. с. отсутствует. Представим себе две металлические пластины со слегка изогнутыми краями (фиг. 17.3), помещенные в однородное магнитное поле, перпендикулярное их плоскости. Каждая пластина присоединена к одному из полюсов гальванометра, как показано на фигуре. Пластины образуют контакт в одной точке Р, так что цепь замкнута. Если теперь повернуть пластины на небольшой угол, точка контакта сдвинется в Р'.
Если мы вообразим, что «цепь» замкнута внутри пластин по пунктирной линии, то по мере поворота пластины взад и вперед магнитный поток через этот контур изменяется на большую величину. Но поворот может произойти от незначительного движения, тогда vXB очень мало и э. д. с. практически отсутствует. В этом случае «правило потока» бессильно. Оно справедливо лишь для контуров, материал которых остается неизменным. Когда материал контура меняется, приходится обращаться снова к основным законам. Правильное физическое содержание всегда дается двумя основными законами:
§ 3. Ускорение частицы в индуцированном электрическом поле; бетатрон
Мы уже говорили, что э. д. с., созданная изменяющимся магнитным полем, может существовать даже в отсутствие проводников; т. е. магнитная индукция возможна без проводов. Мы можем представить себе э. д. с. вдоль произвольной математической кривой в пространстве. Она определяется как тангенциальная компонента Е, проинтегрированная вдоль кривой. Закон Фарадея гласит, что этот контурный интеграл равен скорости изменения магнитного потока через замкнутую кривую [соотношение (17.3)].
В качестве примера действия такого индуцированного электрического поля мы сейчас рассмотрим движение электрона в изменяющемся магнитном поле. Представим себе магнитное поле, которое всюду на плоскости направлено по вертикали (фиг. 17.4). Магнитное поле создается электромагнитом, но детали нас здесь интересовать не будут. В нашем примере мы предположим, что магнитное поле симметрично относительно некой оси, т. е. напряженность магнитного поля зависит только от расстояния до оси.
Фиг. 17.4. Электрон ускоряется в аксиально-симметричном магнитном поле, зависящем от времени.
Магнитное поле меняется также со временем. Представим теперь, что электрон в этом поле движется по круговой траектории постоянного радиуса с центром на оси поля. (Позже мы увидим, как можно создать такое движение.) Меняющееся магнитное поле создает электрическое поле Е, касательное к орбите электрона, которое будет двигать его по окружности. Вследствие симметрии это электрическое поле всюду на окружности принимает одну и ту же величину. Если орбита электрона имеет радиус r, то контурный интеграл от Е по орбите равен скорости изменения магнитного потока через окружность. Контурный интеграл от Е равен просто величине Е, умноженной на длину окружности 2pr. Магнитный поток, вообще говоря, дается интегралом. Обозначим через Bср — среднее магнитное поле внутри окружности; тогда поток равен этому среднему магнитному полю, умноженному на площадь круга.
Мы получим (отвлекаясь от знака)
Поскольку мы предположили, что r—величина постоянная, то Е пропорционально производной по времени от среднего поля:
(17.4)
Электрон будет чувствовать электрическую силу qE и будет ею ускоряться. Помня, что на основании точного релятивистского уравнения движения скорость изменения импульса пропорциональна силе, имеем
(17.5)
Для принятой нами круговой орбиты электрическая сила, действующая на электрон, всегда направлена по движению, поэтому полный импульс будет расти со скоростью, даваемой равенством (17.5). Комбинируя (17.5) и (17.4), можно связать скорость изменения импульса с изменением среднего магнитного поля:
(17.6)
Интегрируя по t, получаем следующее выражение для импульса электрона:
(17.7)
где р0 — импульс, с которым электрон начинает двигаться, a DBcp — последующее изменение Bср. Работа бетатрона — машины, ускоряющей электроны до больших энергий, основана именно на этой идее.
Чтобы понять, как работает бетатрон, необходимо представлять себе принцип движения электрона по окружности. В гл. 11 (вып. 1) мы уже обсуждали этот принцип. Если на орбите электрона создать магнитное поле В, возникнет поперечная сила qvXB, которая при соответствующем выборе В может заставить электрон двигаться по предположенной орбите. В бетатроне эта поперечная сила вызывает движение электрона по круговой орбите постоянного радиуса. Мы можем определить, каким должно быть магнитное поле на орбите, опять с помощью релятивистского уравнения движения, но на этот раз для поперечной компоненты силы. В бетатроне (см. фиг. 17.4) поле В перпендикулярно v, поэтому поперечная сила равна qvB. Таким образом, сила равна скорости изменения поперечной компоненты импульса pt:
(17.8)
Когда частица движется по окружности, Скорость изменения поперечного импульса равна величине полного импульса, умноженной на w — угловую скорость вращения (согласно аргументам, приведенным в гл. 11, вып. 1):
(17.9)
где, поскольку движение круговое,
(17.10)
Полагая магнитную силу равной поперечному ускорению, имеем
(17.11)
где Ворб — поле при радиусе, равном r.
В приведенном в действие бетатроне импульс электрона, согласно выражению (17.7), растет пропорционально Bср, и чтобы электрон продолжал двигаться по собственной окружности, равенство (17.11) должно по-прежнему выполняться вместе с ростом импульса электрона. Величина Bopб должна расти пропорционально импульсу р. Сравнивая (17.11) с (17.7), определяющим р, мы видим, что должно выполняться следующее соотношение между Вср — средним
магнитным полем внутри орбиты радиуса r и магнитным полем Вор6 на орбите:
(17.12)
Для правильной работы бетатрона нужно, чтобы среднее магнитное поле внутри орбиты росло в два раза быстрее магнитного поля на самой орбите. При этих условиях с ростом энергии частицы, увеличивающейся за счет индуцированного электрического поля, магнитное поле на орбите растет как раз со скоростью, нужной для удержания частицы на окружности.
Бетатрон используется для разгона электронов до энергий в десятки или даже в сотни миллионов электронвольт. Однако по ряду причин для ускорения электронов до энергий, много больших нескольких сот миллионов электронвольт, эта машина становится невыгодной. Одна из этих причин — трудность достижения на практике требуемой высокой величины среднего магнитного поля внутри орбиты, а вторая — несправедливость формулы (17.6) для очень больших энергий, так как в ней не учитывается потеря энергии частицей за счет излучения электромагнитной энергии (так называемое синхротронное излучение, см. гл. 34, вып. 3). По этим причинам ускорение электронов до самых больших энергий — до многих миллиардов электрон-вольт — совершается посредством машины другого рода, называемой синхротроном.
§ 4. Парадокс
Теперь мы хотели бы предложить вам некий кажущийся парадокс. Парадокс возникает тогда, когда при одном способе рассуждений получается один ответ, а при другом способе — совсем другой, так что мы остаемся в неведении, что же собственно должно быть на самом деле. Разумеется, в физике никогда не бывает настоящих парадоксов, потому что существует только один правильный ответ; по крайней мере мы верим, что природа поступает только единственным способом (и именно этот способ, конечно, правильный). Поэтому в физике парадокс — всего лишь путаница в нашем собственном понимании. Итак, вот наш : парадокс.
Представим, что мы конструируем прибор (фиг. 17.5), в котором имеется тонкий круглый пластмассовый диск, укрепленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток / от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен. Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток.
Фиг. 17.5. Повернется ли диск, если ток I прекратится?
После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую
скорость.
Но можно рассуждать и по-другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.
Хотелось бы предостеречь вас, что правильный ответ не зависит от всяких несущественных факторов, таких, как несимметричное положение батареи, например. В самом деле, вы можете представить себе, скажем, такой идеальный случай: соленоид сделан из сверхпроводящей проволоки, через которую проходит ток. После того как диск тщательно установлен неподвижным, температуру соленоида медленно начинают повышать. Когда температура проволоки достигнет переходного значения между сверхпроводимостью и нормальной проводимостью, ток в соленоиде обратится в нуль вследствие сопротивления проволоки. Поток, как и раньше, упадет до нуля и вокруг оси возникнет электрическое поле. Мы хотели бы также предостеречь вас, что решение не простое, но это и не обман. Когда вы разберетесь в этом, вы обнаружите важный закон электромагнетизма.
§ 5. Генератор переменного тока
В оставшейся части этой главы мы применим принципы, изложенные в § 1 для анализа ряда явлений, обсуждавшихся в гл. 16. Сначала мы рассмотрим подробно генератор переменного тока. Такой генератор в основном состоит из проволочной катушки, вращающейся в однородном магнитном поле. Тот же самый результат может быть достигнут с помощью неподвижной катушки в магнитном поле, направление которого вращается по способу, описанному в предыдущей главе. Мы рассмотрим лишь первый случай. Пусть имеется круглая катушка из проволоки, которая может вращаться вокруг оси, проходящей вдоль одного из ее диаметров. И пусть эта катушка помещена в магнитное поле, перпендикулярное оси вращения (фиг. 17.6). Представим себе, что оба конца катушки выведены на внешнюю цепь с помощью каких-нибудь скользящих контактов.
Благодаря вращению катушки магнитный поток через нее будет меняться. Поэтому в цепи катушки появится э. д. с. Пусть S —- площадь катушки, а q — угол между магнитным полем и нормалью к плоскости катушки. Тогда поток через катушку равен
BScosq. (17.13)
Если катушка вращается с постоянной угловой скоростью w, то q меняется со временем как wt. Тогда э. д. с. о в катушке равна
или
(17.14)
Если мы выведем провода из генератора на некоторое расстояние от вращающейся катушки, в место, где магнитное поле равно нулю или хотя бы не меняется со временем, то ротор от Е в этой области будет равен нулю, и мы сможем определить электрический потенциал. В самом деле, если ток не уходит из генератора, то разность потенциалов V между двумя проводами будет равна э. д. с. вращающейся катушки, т. е.
Фиг. 17.6. Катушка из проволоки, вращающаяся в однородном магнитном поле,— основная идея генератора переменного тока.
Разность потенциалов в проводах меняется как sinwt. Такая меняющаяся разность потенциалов называется переменным напряжением.
Поскольку между проводами имеется электрическое поле, они должны быть электрически заряжены. Ясно, что э. д. с. генератора выталкивает лишние заряды в провода, пока их электрическое поле не становится достаточно сильным, чтобы в точности уравновесить силу индукции. Если посмотреть на генератор со стороны, то покажется, будто два провода электростатически заряжены до разности потенциалов V, а заряды как бы меняются со временем, создавая переменную разность потенциалов. Есть и еще одно отличие от того, что наблюдается в случае электростатики. Если присоединить генератор к внешней цепи, по которой может проходить ток, мы обнаружим, что э. д. с. не позволяет проводам разряжаться, а продолжает подпитывать их зарядами, когда из них уходит ток, стремясь сохранить на проводах одну и ту же разность потенциалов. Если генератор подключен к цепи, полное сопротивление которой равно R, ток в цепи будет пропорционален э. д. с. генератора и обратно пропорционален R. Поскольку э. д. с. синусоидально изменяется со временем,
то и ток делает то же самое. Возникает переменный ток
Схема такой цепи приведена на фиг. 17.7.
Мы можем также заметить, что э. д. с. определяет количество энергии, поставляемое генератором. Каждый заряд в проводе получает в единицу времени энергию, равную F·v, где F — сила, действующая на заряд, a v — его скорость. Пусть теперь количество движущихся зарядов на единице длины провода равно n; тогда мощность, выделяющаяся в элементе ds провода, равна
Фиг. 17.7. Цепь с генератором переменного тока и сопротивлением.
В проводе скорость v всегда направлена вдоль ds, так что мощность можно переписать в виде
Полная мощность, выделяемая во всей цепи, есть интеграл от этого выражения по всей петле:
(17.15)
Вспомним теперь, что qnv — это ток I и что э. д. с. определяется как интеграл от F/q по всей цепи. Мы получаем
(17.16)
Когда в катушке генератора имеется ток, на нее непременно действуют механические силы. В самом деле, мы знаем, что вращающий момент, действующий на катушку, пропорционален ее магнитному моменту, напряженности магнитного поля В и синусу угла между ними. Магнитный момент есть ток катушки, умноженный на ее площадь. Поэтому вращающий момент равен
(17.17)
Скорость, с которой должна совершаться механическая работа, чтобы поддерживать вращение катушки, есть угловая скорость w, умноженная на вращающий момент силы:
(17.18)
Сравнивая это выражение с (17.14), мы видим, что затраты механической работы в единицу времени, требуемые для вращения катушки против магнитных сил, в точности равны eI — электрической энергии, поставляемой
э. д. с. генератора в единицу времени. Вся механическая энергия, расходуемая в генераторе, появляется в виде электрической энергии в цепи.
В качестве другого примера токов и сил, обусловленных индуцированной э. д. с., проанализируем, что же происходит в установке, показанной на фиг. 17.1. Имеются U-образная проволока и скользящая перемычка, расположенные в однородном магнитном поле, перпендикулярном плоскости параллельных проволок. Теперь предположим, что «дно» U (левая часть фиг. 17.1) сделано из проволоки с большим сопротивлением, тогда как две боковые проволоки сделаны из хорошего проводника вроде меди — в этом случае нам не надо беспокоиться об изменении сопротивления цепи при движении перекладины. Как и раньше,
э. д. с. цепи равна
(17.19)
Ток в цепи пропорционален этой э. д. с. и обратно пропорционален сопротивлению цепи:
(17.20)
Благодаря этому току на перемычку будет действовать магнитная сила, пропорциональная длине перемычки, току в ней и магнитному полю:
(17.21)
Подставляя I из (17.20), получаем для силы
(17.22)
Мы видим, что сила пропорциональна скорости перемещения перемычки. Направление силы, как легко понять, противоположно скорости. Такая «пропорциональная скорости» сила, похожая на силу вязкости, получается всякий раз, когда движущиеся проводники создают индуцированные токи в магнитном поле. Вихревые токи, о которых мы говорили в предыдущей главе, приводят также к силам, действующим на проводники и пропорциональным скорости проводника, хотя такие случаи в общем дают более сложные распределения токов, которые трудно анализировать.
При конструировании механических систем часто бывает удобно располагать тормозящими силами, пропорциональными скорости. Вихревые токи дают один из наиболее удобных способов получения таких зависящих от скорости сил.
Пример применения подобных сил можно найти в обычном домашнем счетчике — ваттметре. Там имеется тонкий алюминиевый диск, вращающийся между полюсами постоянного магнита. Этот диск приводится в движение маленьким электромотором, вращающий момент которого пропорционален мощности, потребляемой в электросети квартиры. Вихревые токи в диске вызывают силу сопротивления, пропорциональную скорости. Следовательно, скорость диска устанавливается пропорциональной скорости потребления электроэнергии. С помощью счетчика, присоединенного к вращающемуся диску, подсчитывается число оборотов диска. Так определяется полная потребленная энергия, т. е. число использованных ватт-часов.
Согласно формуле (17.22), сила от индуцированных токов, т. е. всякая сила от вихревых токов, обратно пропорциональна сопротивлению. Сила тем больше, чем лучше электропроводность материала. Причина, разумеется, заключается в том, что при малом сопротивлении э. д. с. создает больший ток, а большие токи дают большие механические силы.
Из наших формул мы можем увидеть, как механическая энергия превращается в электрическую энергию. Как и раньше, электрическая энергия, выделяемая в сопротивлении цепи, есть произведение eI, Работа в единицу времени, совершаемая при движении перекладины, есть произведение силы, действующей на перекладину, на ее скорость. Используя для силы выражение (17.21), получаем работу в единицу времени:
Мы видим, что она действительно равна произведению $I, которое мы получаем из (17.19) и (17.20). Снова механическая работа появляется в виде электрической энергии.
§ 6. Взаимная индукция
Теперь нам нужно рассмотреть случай, когда проволочные катушки неподвижны, а меняются магнитные поля. Описывая образование магнитного поля токами, мы рассматривали только случай постоянных токов. Но если токи меняются медленно, магнитное поле в каждый момент будет примерно такое же, как магнитное поле постоянного тока. Мы будем считать в этом параграфе, что токи всегда меняются достаточно медленно, и можно сказать, что это утверждение справедливо.
На фиг. 17.8 показано устройство из двух катушек, с помощью которого можно продемонстрировать основные эффекты, ответственные за работу трансформатора. Катушка 1 состоит из проводящей проволоки, свитой в виде длинного соленоида. Вокруг этой катушки и изолированно от нее навита катушка 2, состоящая из нескольких витков проволоки. Если теперь по катушке 1 пропустить ток, то, как мы знаем, внутри нее появится магнитное поле. Это магнитное поле проходит также сквозь катушку 2. Когда ток в катушке 1 меняется, магнитный поток тоже будет меняться, и в катушке 2 появится индуцированная э.д.с. Эту индуцированную э.д.с. мы сейчас и вычислим.
В гл. 13, § 5 (вып. 5) мы видели, что магнитное поле внутри длинного соленоида однородно и равно
(17.23)
где N1 — число витков в катушке 1, I1 — ток в ней, а l — её длина. Пусть поперечное сечение катушки 1 равно S, тогда поток поля В равен его величине, умноженной на S. Если в катушке 2 имеется N2 витков, то поток проходит по катушке N2 раз. Поэтому э. д. с. в катушке 2 дается выражением
.(17.24)
Единственная меняющаяся со временем величина в (17.23) есть I1. Поэтому э. д. с. дается выражением
(17.25)
Мы видим, что э. д. с. в катушке 2 пропорциональна скорости изменения тока в катушке 1. Константа пропорциональности — по существу геометрический фактор двух катушек, называется коэффициентом взаимной индукции и обозначается обычно m21. Тогда (17.25) записывается уже в виде
(17.26)
Предположим теперь, что нам нужно было бы пропустить ток через катушку 2 и нас интересует, чему равна э. д. с. в катушке 1. Мы вычислили бы магнитное поле, которое повсюду пропорционально току I2. Поток сквозь катушку I зависел бы от геометрии, но был бы пропорционален току I2. Поэтому
Фиг. 17.8. Ток в катушке 1 создает магнитное поле, проходящее через катушку 2.
Фиг. 17.9. Любые две катушки обладают взаимной индукцией m, пропорциональной интегралу от ds1·ds2· (1/r12).
э. д. с. в катушке 1 снова была бы пропорциональна dI2/dt. Мы можем записать
(17.27)
Вычисление m 12 было бы труднее, чем те вычисления, которые мы проделали для m 21. Мы не будем сейчас им заниматься, потому что дальше в этой главе мы покажем, что m 12 обязательно равно m 21.
Поскольку поле любой катушки пропорционально текущему в ней току, такой же результат получился бы и для любых двух катушек из проволоки. Выражения (17.26) и (17.27) приобрели бы одинаковую форму, и только постоянные m 12 и m 21 были бы другие. Их значения будут зависеть от формы катушек и их относительного положения.
Предположим, нам нужно найти коэффициент взаимной индукции между двумя произвольными катушками, например показанными на фиг. 17.9. Мы знаем, что общее выражение для э. д. с. в катушке 1 можно записать так:
где В — магнитное поле, а интеграл берется по поверхности, ограниченной контуром 1. В гл. 14, § 1 (вып. 5) мы видели, что поверхностный интеграл от В можно свести к контурному интегралу от векторного потенциала. В нашем случае
как контурный интеграл по контуру цепи 2:
(17.29)
где I2 — ток в цепи 2, а r12 — расстояние от элемента цепи ds2 к точке на контуре 1, в которой мы вычисляем векторный потенциал (см. фиг. 17.9). Комбинируя (17.28) и (17.29), можно выразить э. д. с. в цепи 1 как двойной контурный интеграл:
В этом выражении все интегралы берутся по неподвижным контурам. Единственной переменной величиной является ток I2, который не зависит от переменных интегрирования. Поэтому его можно вынести за знак интеграла. Тогда э. д. с. можно записать как
где коэффициент m 12 равен
(17.30)
Из этого интеграла очевидно, что m 12 зависит только от геометрии цепей; он зависит от некоторого среднего расстояния между двумя цепями, причем в среднее с наибольшим весом входят параллельные отрезки проводников двух катушек. Нашу формулу можно использовать для вычисления коэффициента взаимной индукции любых двух цепей произвольной формы. Кроме того, она показывает, что интеграл для m 12 тождествен с интегралом для m 21. Таким образом, мы показали, что оба коэффициента одинаковы. Для системы только с двумя катушками коэффициенты m 12 и m 21 часто обозначают символом m без значков и называют просто коэффициентом взаимной индукции:
m 12= m 21 = m.
§ 7. Самоиндукция
При обсуждении индуцированных э. д. с. в двух катушках на фиг. 17.8 и 17.9 мы рассмотрели лишь случай, когда ток проходит либо в одной катушке, либо в другой. Если токи имеются одновременно в обеих катушках, то магнитный поток, пронизывающий каждую катушку, будет представлять сумму двух потоков, существующих и по отдельности, поскольку к магнитным полям применим принцип суперпозиции. Поэтому э. д. с. в каждой катушке будет пропорциональна не только изменению тока в другой катушке, но и изменению тока в ней самой.
Фиг. 17.10. Цепь с источником напряжения и индуктивностью (а) и аналогичная ей механическая система (б).
Таким образом, полную э. д. с. в катушке 2 следует записать в виде
(17.31)
""Аналогично, э. д. с. в катушке 1 будет зависеть не только от изменяющегося тока в катушке 2, но и от изменяющегося тока в ней самой:
(17.32)
Коэффициенты m 22 и m 11 всегда отрицательны. Обычно пишут
(17.33)
где ж1 и ж 2называют коэффициентами самоиндукции двух катушек (или индуктивностями).
Конечно, э. д. с. самоиндукции будет существовать даже для одной катушки. Любая катушка сама по себе обладает коэффициентом самоиндукции ж и ее
э. д. с. будет пропорциональна скорости изменения тока в катушке. Обычно считают, Что э. д. с. и ток одной катушки положительны, если они направлены одинаково. При этом условии для отдельной катушки
можно написать
(17.34)
Знак минус указывает на то, что э. д. с. противодействует изменению тока, ее часто называют «обратной э. д. с.».
Поскольку любая катушка обладает самоиндукцией, противодействующей изменению тока, ток в катушке обладает своего рода инерцией. Действительно, если мы хотим изменить ток в катушке, мы должны преодолеть эту инерцию, присоединяя катушку к какому-то внешнему источнику, например батарее или генератору (фиг. 17.10, а). В такой цепи ток / связан с напряжением V соотношением
(17.35)
Это соотношение имеет форму уравнения движения Ньютона для частицы в одном измерении. Поэтому мы можем исследовать его по принципу «одинаковые уравнения имеют одинаковые решения». Таким образом, если поставить в соответствие напряжение V от внешнего источника приложенной внешней силе F, а ток I в катушке скорости v частицы, то коэффициент индукции катушки жбудет соответствовать массе т частицы (фиг. 17,10, б).
Таблица 17.1 · СОПОСТАВЛЕННЫЕ ВЕЛИЧИНЫ
§ 8. Индуктивность и магнитная энергия
Продолжая аналогию предыдущего параграфа, мы отметили в таблице, что в соответствии с механическим импульсом p=mv (скорость изменения которого равна приложенной силе) должна существовать аналогичная величина, равная
ж I, скорость изменения которой V. Разумеется, мы не имеем права говорить, что ж I — это настоящий импульс цепи; на самом деле это вовсе не так. Вся цепь может быть неподвижна и вообще не иметь импульса. Просто ж I аналогично импульсу mv в смысле удовлетворения аналогичным уравнениям.
Точно так же кинетической энергии 1/2mv2 здесь соответствует аналогичная величина 1/2ж 2. Но здесь нас ждет сюрприз. Величина 1/2aж I2 — действительно есть энергия и в электрическом случае. Так получается потому, что работа, совершаемая в единицу времени над индуктивностью, равна VI, а в механической системе она равна Fv — соответствующей величине. Поэтому в случае энергии величины не только соответствуют друг другу в математическом смысле, но имеют еще и одинаковое физическое значение.
Мы можем проследить это более подробно. В (17.16) мы нашли, что электрическая работа в единицу времени за счет сил индукции есть произведение э. д. с. и тока:
Подставляя вместо e ее выражение через токи из (17.34), имеем
(17.38)
Интегрируя это уравнение, находим, что энергия, которая требуется от внешнего источника, чтобы преодолеть э. д. с. самоиндукции и создать ток (что должно равняться накопленной энергии U), равна
(17.37)
Поэтому энергия, накопленная в индуктивности, равна 1/2ж I2.Применяя те же рассуждения к паре катушек, изображенных на фиг. 17.8 или 17.9, мы можем показать, что полная электрическая энергия системы дается выражением
(17.38)
В самом деле, начиная с тока I=0 в обеих катушках, можно вначале включить ток I1 в катушке 1, оставляя I2=0. Совершенная работа как раз равна l/2ж 1l12. Но теперь, включая I2, мы совершаем не только работу 1/2ж 2I22 против э. д. с. в цепи 2, но еще и добавочное количество работы —m I1I2, которая есть интеграл
от э. д. с. m(dIz/dt) в цепи 1, умноженный на теперь уже постоянный ток I1 в этой цепи.
Пусть теперь нам нужно найти силу между любыми двумя катушками, по которым идут токи I1 и I2. Прежде всего мы могли бы использовать принцип виртуальной работы, взяв вариацию от энергии (17.38). Мы должны помнить, конечно, что при изменении относительного положения катушек единственной меняющейся величиной является коэффициент взаимной индукции m. Тогда мы могли бы записать уравнение виртуальной работы в виде
Это уравнение ошибочно, потому что, как мы видели раньше, в него включено только изменение энергии двух катушек и не включена энергия источников, которые поддерживают постоянными значения токов I1и I2. Мы понимаем теперь, что эти источники должны поставлять энергию для компенсации индуцированных э. д. с. в катушках во время их движения. Если мы хотим правильно применить принцип виртуальной работы, то должны включить и эти энергии. Но мы видели, что можно сделать и короче — использовать принцип виртуальной работы, помня, что полная энергия — это взятая с обратным знаком энергия Uмех (то что мы называем «механической энергией»). Поэтому силу можно записать в виде
(17.39)
Тогда сила между катушками дается выражением
Воспользуемся выражением (17.38) для энергии системы из двух катушек, чтобы показать, какое интересное неравенство существует между взаимной индукцией m и коэффициентами самоиндукции ж 1 и ж 2двух катушек. Ясно, что энергия двух катушек должна быть положительной. Если мы начинаем с нулевых токов в обеих катушках и увеличиваем эти токи до некоторых значений, то тем самым мы увеличиваем энергию всей системы. В противном случае токи самопроизвольно возрастут и будут отдавать энергию остальному миру — вещь невероятная! Далее, наше выражение для энергии (17.38) можно с
таким же успехом записать в следующей форме:
(17.40)
Это просто алгебраическое преобразование. Эта величина должна быть всегда положительна при любых значениях I1 и I2. В частности, она должна быть положительна, когда I2 вдруг примет особое значение:
(17.41)
Но при таком значении I2 первое слагаемое в (17.40) равно нулю. Если энергия положительна, то последнее слагаемое в (17.40) должно быть больше нуля. Мы получаем требование, что
Таким образом, мы доказали общее соотношение, что величина взаимной индукции m любых двух катушек обязательно меньше или равна геометрическому среднему двух коэффициентов самоиндукции (сам m может быть положителен или отрицателен в зависимости от выбора знаков для токов It и I2):
(17.42)
Соотношение между m и коэффициентами самоиндукции обычно записывают в виде
(17.43)
Постоянную k называют коэффициентом связи. Если большая часть потока от одной катушки проходит через другую катушку, то коэффициент связи близок к единице; мы говорим, что катушки «сильно связаны». Если катушки значительно удалены друг от друга или же все устроено так, что взаимное проникновение их потоков очень мало, коэффициент связи становится близок к нулю, а коэффициент взаимной индукции очень мал.
Для вычисления взаимной индукции двух катушек мы дали формулу (17.30), которая представляет собой двойной контурный интеграл по обеим цепям. Мы могли бы подумать, что та же формула применима и для вывода коэффициента самоиндукции одной катушки, если оба контурных интегрирования проводить по одной и той же катушке. Однако это не так, потому что при интегрировании по двум катушкам знаменатель r12 под знаком интеграла стремится к нулю, когда два элемента длины находятся в одной точке. Коэффициент самоиндукции, получаемый из этой формулы, оказывается бесконечным. Происходит это потому, что формула наша — приближенная, и справедлива она только для поперечных сечений проводов в обеих цепях, малых по сравнению с расстоянием от одной цепи до другой. Ясно, что это приближение для отдельной катушки не годится. На самом деле оказывается, что индуктивность отдельной катушки стремится логарифмически к бесконечности, когда диаметр ее проволоки становится все меньше и меньше.
Значит, мы должны поискать другой способ вычисления коэффициента самоиндукции одной катушки. При этом надо учесть распределение токов внутри проводника, потому что его размеры — важный параметр. Но мы не будем считать полную индуктивность, а сосчитаем лишь ту ее часть, которая связана с расположением проводников, и не будем учитывать часть, связанную с распределением токов. Пожалуй, самый простой способ найти такую индуктивность — это использовать магнитную энергию. Ранее, в гл. 15, § 3, мы нашли выражение для магнитной энергии распределения стационарных токов:
(17.44)
Если известно распределение плотности тока j, то можно вычислить векторный потенциал А, а затем, оценив интеграл (17.44), получить энергию. Эта энергия равна магнитной энергии самоиндукции, l/2ж I2. Приравнивая их, получаем формулу для индуктивности:
(17.45)
Мы, конечно, ожидаем, что индуктивность есть число, зависящее только от геометрии цепи, а не от тока / в цепи. Формула (17.45) действительно приводит к такому результату, потому что интеграл в ней пропорционален квадрату тока — ток входит один раз от j и еще раз от векторного потенциала А. Интеграл, деленный на I2, зависит от геометрии цепи, но не от тока I.
Выражению (17.44) для энергии распределения токов можно придать совсем другую форму, иногда более удобную для вычислений. Кроме того, как мы увидим позже, именно эта форма важна, потому что она справедлива в более общем случае. В формуле (17.44) и А и j можно связать с В, поэтому можно надеяться, что энергия выразится через магнитное поле — точно так же, как нам удалось связать электростатическую энергию с электрическим полем. Начнем с подстановки e0c2СXВ вместо j. Заменить А мы не можем с той же легкостью, потому что нельзя обратить B=СXA, чтобы выразить А через В. Можно только
записать
(17.46)
Любопытно, что при некоторых ограничениях этот интеграл можно превратить в
(17.47)
Чтобы увидеть это, выпишем подробно типичный множитель. Предположим, что мы взяли множитель (СXB)zAz, входящий в интеграл (17.46). Выписывая полностью компоненты, получаем
(имеются, конечно, еще два интеграла того же сорта). Проинтегрируем теперь первый множитель по х, интегрируя по частям,
Теперь предположим, что наша система (имея в виду источники и поля) — конечная, так что, когда мы уходим на большие расстояния, все поля стремятся к нулю. Тогда при интегрировании по всему пространству подстановка ByAzна пределах интеграла дает нуль. У нас остается только В (дАг/дх); это, очевидно, есть часть от By(СXA)yи, значит, от В·(СXA). Если вы выпишите остальные пять множителей, то увидите, что (17.47) на самом деле эквивалентно (17.46).
А теперь мы можем заменить (СXA) на В и получить
(17.48)
Мы выразили энергию в магнитостатическом случае только через магнитное поле. Выражение тесно связано с формулой, которую мы нашли для электростатической энергии:
(17.49)
Эти две энергетические формулы выделены потому, что иногда ими удобнее пользоваться. Обычно есть и более важная причина: оказывается, что для динамических полей (когда Е и В меняются со временем) оба выражения (17.48) и (17.49) остаются справедливыми, тогда как другие данные нами формулы для электрической и магнитной энергий перестают быть верными — они годятся лишь для статических полей.
Если нам известно магнитное поле В одной катушки, мы можем найти коэффициент самоиндукции, приравнивая выражение для энергии (17.48) и 1/2жI2. Посмотрим, что получится в результате для индуктивности длинного соленоида. Раньше мы видели, что магнитное поле в соленоиде однородно и В снаружи равно нулю. Величина поля внутри равна В=nI/e0с2, где n — число витков на единицу длины намотки, а I — ток. Если радиус катушки r, а длина ее L (мы считаем, что L очень велика, чтобы можно было пренебречь краевыми эффектами, т. е. L >>r), то внутренний объем равен pr2L. Следовательно, магнитная энергия равна
что равно 1/2^I2. Или
(17.50)
* Кстати, это не единственный способ установления соответствия между механическими и электрическими величинами.
* Мы пренебрегаем всеми тепловыми потерями энергии в сопротивлении катушки. Эти потери требуют дополнительных затрат энергии источника, но не меняют энергии, которая тратится на индуктивность.
Глава 18 УРАВНЕНИЯ МАКСВЕЛЛА
§ 1. Уравнения Максвелла
§ 2. Что дает добавка
§ 3. Все о классической физике
§ 4. Передвигающееся поле
§ 5. Скорость света
§ 6. Решение уравнений Максвелла; потенциалы и волновое уравнение
§ 1. Уравнения Максвелла
В этой главе мы вернемся к полной системе из четырех уравнений Максвелла, которые мы приняли как отправной пункт в гл. 1 (вып. 5). , До сих пор мы изучали уравнения Максвелла небольшими частями, кусочками; теперь пора уже прибавить последнюю часть и соединить их все воедино. Тогда мы будем иметь полное и точное описание электромагнитных полей, которые могут изменяться со временем произвольным образом. Все сказанное в этой главе, если даже оно и будет противоречить чему-то сказанному ранее, правильно, а то, что говорилось ранее в этих случаях, неверно, потому что все высказанное ранее применялось к таким частным случаям, как, скажем, случаи постоянного тока или фиксированных зарядов. Хотя всякий раз, когда мы записывали уравнение, мы весьма старательно указывали ограничения, легко позабыть все эти оговорки и слишком хорошо заучить ошибочные уравнения. Теперь мы можем изложить всю истину, без всяких ограничений (или почти без них).
Все уравнения Максвелла записаны в табл. 18.1 как словесно, так и в математических символах. Тот факт, что слова эквивалентны уравнениям, должен быть сейчас вам уже знаком — вы должны уметь переводить одну форму в другую и обратно.
Первое уравнение — дивергенция Е равна плотности заряда, деленной на eо,— правильно всегда. Закон Гаусса справедлив всегда как в динамических, так и в статических полях. Поток Е через любую замкнутую поверхность пропорционален заключенному внутри заряду. Третье уравнение — соответствующий общий закон для магнитных полей.
Уравнения Максвелла
(Поток Е через замкнутую поверхность) = (Заряд внутри нее)/e0
(Интеграл от Е по замкнутому контуру) = -d/dt(Поток В сквозь контур)
(Поток В через замкнутую поверхность) = 0
с2 (Интеграл от В по контуру)=(Ток в контуре) /e0 + d/dt(Поток Е сквозь контур)
(Поток заряда через замкнутую поверхность) =-d/dt(Заряд внутри нее)
Закон силы
F = q(E+vXB)
Закон движения
(Закон Ньютона, исправленный Эйнштейном}
Гравитация
Поскольку магнитных зарядов нет, поток В через любую замкнутую поверхность всегда равен нулю. Второе уравнение СXE=-dB/dt — это закон Фарадея, и обсуждался он в последних двух главах. Он тоже верен в общем случае. Но последнее уравнение содержит нечто новое. Раньше мы встречались только с частью его, которая годится для постоянных токов. В этом случае мы говорили, что ротор В равен j/e0c2, но правильное общее уравнение имеет новый член, который был открыт Максвеллом.
До появления работы Максвелла известные законы электричества и магнетизма были такими же, как те, что мы изучали в гл. 3—14 (вып. 5) и гл. 15—17. В частности, уравнение для магнитного поля постоянных токов было известно только в виде
(18.1)
Максвелл начал с рассмотрения этих известных законов и выразил их в виде дифференциальных уравнений, так же как мы поступили здесь. (Хотя символ С еще не был придуман, впервые, в основном благодаря Максвеллу, стала очевидной важность таких комбинаций производных, которые мы сегодня называем ротором и дивергенцией.) Максвелл тогда заметил, что в уравнении (18.1) есть нечто странное. Если взять дивергенцию от этого уравнения, то левая сторона обратится в нуль, потому что дивергенция ротора всегда равна нулю. Таким образом, это уравнение требует, чтобы дивергенция j также была равна нулю. Но если дивергенция j равна нулю, то полный ток через любую замкнутую поверхность тоже равен нулю.
Полный ток через замкнутую поверхность равен уменьшению заряда внутри этой поверхности. Он наверняка не может быть всегда равен нулю, так как мы знаем, что заряды могут перемещаться из одного места в другое. Уравнение
(18.2)
фактически есть наше определение j. Это уравнение выражает самый фундаментальный закон — сохранение электрического заряда: любой поток заряда должен поступать из какого-то запаса. Максвелл заметил эту трудность и, чтобы избежать ее, предложил добавить dE/dt в правую часть уравнения (18.1); тогда он и получил уравнение IV в табл. 18.1:
Во времена Максвелла еще не привыкли мыслить в терминах абстрактных полей. Максвелл обсуждал свои идеи с помощью модели, в которой вакуум был подобен упругому телу. Он пытался также объяснить смысл своего нового уравнения с помощью механической модели. Теория Максвелла принималась очень неохотно, во-первых, из-за модели, а, во-вторых, потому, что вначале не было экспериментального подтверждения. Сейчас мы лучше понимаем, что дело в самих уравнениях, а не в модели, с помощью которой они были получены. Мы можем только задать вопрос, правильны ли эти уравнения или они ошибочны. Ответ дает эксперимент. И уравнения Максвелла были подтверждены в бессчетных экспериментах. Если мы отбросим все строительные леса, которыми пользовался Максвелл, чтобы построить уравнения, мы придем к заключению, что прекрасное здание, созданное Максвеллом, держится само по себе. Он свел воедино все законы электричества и магнетизма и создал законченную и прекрасную теорию.
Давайте покажем, что добавочный член имеет тот самый вид, который требуется, чтобы преодолеть обнаруженную Максвеллом трудность. Взяв дивергенцию его уравнения (IV в табл. 18.1), мы должны получить, что дивергенция правой части равна нулю:
(18.3)
Во втором слагаемом можно переставить порядок дифференцирования по координатам и времени, так что уравнение может быть переписано в виде
(18.4)
Но, согласно первому из уравнений Максвелла, дивергенция Е равна r/e0. Подставляя это равенство в (18.4), мы придем к уравнению (18.2), которое, как мы знаем, правильно. И наоборот, если мы принимаем уравнения Максвелла (а мы принимаем их потому, что никто никогда не обнаружил эксперимента, который опроверг бы их), мы должны прийти к выводу, что заряд всегда сохраняется.
Законы физики не дают ответа на вопрос: «Что случится, если заряд внезапно возникнет в этой точке, какие будут при этом электромагнитные эффекты?». Ответ дать нельзя, потому что наши уравнения утверждают, что такого не происходит. Если бы это случилось, нам понадобились бы новые законы, но мы не можем сказать, какими бы они были. Нам не приходилось наблюдать, как ведет себя мир без сохранения заряда. Согласно нашим уравнениям, если вы внезапно поместите заряд в некоторой точке, вы должны принести его туда откуда-то еще. В таком случае мы можем говорить о том, что произошло.
Когда мы добавили новый член в уравнение для ротора Е, мы обнаружили, что им описывается целый новый класс явлений. Мы увидим также, что небольшая добавка Максвелла к уравнению для СXB имеет далеко идущие последствия. Мы затронем лишь некоторые из них в этой главе.
§ 2. Что дает добавка
В качестве нашего первого примера рассмотрим, что происходит со сферически симметричным радиальным распределением тока. Представим себе маленькую сферу с нанесенным на ней радиоактивным веществом. Это радиоактивное вещество испускает наружу заряженные частицы. (Мы можем представить также большой кусок желе с маленьким отверстием в центре, в которое с помощью шприца впрыскиваются какие-то заряды и из которого заряды медленно просачиваются.)
Фuг18.1. Каково магнитное поле сферически симметричного тока?
В любом случае мы имели бы ток, который повсюду направлен по радиусу наружу. Будем считать, что величина его одинакова во всех направлениях.
Пусть полный заряд внутри сферы произвольного радиуса r есть Q(r). Если плотность радиального тока при таком же радиусе равна j(r), то уравнение (18.2) требует, чтобы Q уменьшалось со скоростью
(18.5)
Спросим теперь о магнитном поле, создаваемом токами в этом случае. Предположим, мы начертили какую-то петлю Г на сфере радиуса r(фиг. 18.1). Сквозь петлю проходит какой-то ток, поэтому можно ожидать, что магнитное поле циркулирует в направлении, указанном на фигуре.
И сразу возникает затруднение. Как может поле В иметь какое-то особое направление на сфере? При другом выборе петли Г мы бы заключили, что ее направление прямо противоположно указанному. Поэтому возможна ли какая-либо циркуляция В вокруг токов?
Нас спасают уравнения Максвелла. Циркуляция В зависит не только от полного тока, проходящего сквозь петлю Г, но и от скорости изменения со временем электрического потока через нее. Должно быть так, чтобы эти две части как раз погашались. Посмотрим, получается ли это.
Электрическое поле на расстоянии r должно быть равно Q(г)/4pe0r2, пока, как мы предположили, заряд распределен симметрично. Поле радиально, и скорость его изменения тогда равна
(18.6)
Сравнивая это с (18.5), мы видим, что для любого расстояния
(18.7)
В уравнении IV (табл. 18.1) оба члена от источника погашаются и ротор В равен всегда нулю. Магнитного поля в нашем примере нет.
В качестве второго нашего примера рассмотрим магнитное поле провода, используемого для зарядки плоского конденсатора (фиг. 18.2). Если заряд Q на пластинах со временем изменяется (но не слишком быстро), ток в проводах равен dQ/dt. Мы ожидаем, что этот ток создаст магнитное поле, которое окружает провод. Конечно, ток вблизи провода должен создавать обычное магнитное поле, оно не может зависеть от того, где идет ток.
Предположим, мы выбрали петлю Г1 в виде окружности с радиусом r (фиг. 18.2, а). Контурный интеграл от магнитного поля будет равен току I, деленному на e0с2. Мы имеем
(18.8)
Все это мы получили бы для постоянного тока, но результат не изменится, если учесть добавку Максвелла, потому что для плоской поверхности S внутри окружности электрического поля нет (считая, что провод очень хороший проводник). Поверхностный интеграл от dE/dt равен нулю.
Предположим, однако, что теперь мы медленно продвигаем кривую Г1 вниз. Мы будем получать всегда тот же самый результат до тех пор, пока не нарисуем кривую вровень с пластинами конденсатора
Фиг. 18.2. Магнитное поле вблизи заряжаемого конденсатора.
Тогда ток I будет стремиться к нулю. Исчезнет ли при этом магнитное поле? Это было бы очень странно. Давайте поглядим, что говорит уравнение Максвелла для кривой Г, которая представляет собой окружность радиуса r, плоскость которой проходит между пластинами конденсатора (фиг. 18.2, б). Контурный интеграл от В вокруг Г есть 2prB. Он должен быть равен производной по времени потока Е, проходящего сквозь плоскую поверхность круга S2. Этот поток Е, как мы знаем из закона Гаусса, должен быть равен
произведению 1/e0 на заряд Q на одной из пластин конденсатора. Мы имеем
(18.9)
Это очень хорошо. Результат тот же, что мы нашли в (18.8). Интегрирование по меняющемуся электрическому полю 'дает то же магнитное поле, что и интегрирование по току в проводе. Конечно, как раз об этом и говорит уравнение Максвелла. Легко видеть, что так должно быть всегда, если применить наши рассуждения к двум поверхностям 81и S'1, ограниченным одной и той же окружностью Г1 на фиг. 18.2, б. Сквозь S1проходит ток /, но нет электрического потока. Сквозь S1нет тока, но есть электрический поток, меняющийся со скоростью I/e0. То же поле В получится, если мы применим уравнение IV (табл. 18.1) к каждой поверхности.
Из нашего обсуждения добавки, введенной Максвеллом, у вас могло сложиться впечатление, что она добавляет немного — просто подправляет уравнения в согласии с тем, что мы уже ожидали. Это верно, пока мы рассматриваем уравнение IV само по себе, ничего особенно нового не появляется. Слова само по себе, однако, весьма важны. Небольшое изменение, введенное Максвеллом в уравнение IV в сочетании с другими уравнениями, на самом деле дает много нового и важного. Но прежде чем заняться этим вопросом, поговорим подробнее в табл. 18.1.
§ 3. Все о классической физике
В табл. 18.1 сведено все, что знала фундаментальная классическая, физика, т. е. та физика, которая была известна до 1905 г. В одной этой таблице есть все. С помощью этих уравнений можно понять все достижения классической физики.
Прежде всего, мы имеем уравнения Максвелла, записанные как в расширенном виде, так и в короткой математической форме. Затем есть сохранение заряда, которое даже записано в скобках, потому что сохранение заряда можно вывести из имеющихся полных уравнений Максвелла. Так что в таблице имеются даже небольшие излишки. Дальше мы записали закон для силы, поскольку все имеющиеся электрические и магнитные поля ничего не говорят нам до тех пор, пока мы не знаем, как они действуют на заряды. Однако, зная Е и В, мы можем найти силу, действующую на объект с зарядом q, который движется со скоростью v. Наконец, имеющаяся сила ничего не говорит нам, пока мы не знаем, что происходит, когда сила ускоряет что-то; нам необходимо знать закон движения, который говорит, что сила равна скорости изменения импульса. {Помните? Об этом говорилось в начале курса.) Мы даже включили эффекты теории относительности, записав импульс в виде р=m0vЦ(1-v2/c2).
Но если мы действительно хотим законченности, нам следует добавить еще один закон — закон тяготения Ньютона? и мы поставили его в конце.
Итак, в одной небольшой таблице мы собрали все фундаментальные законы классической физики, даже хватило места выписать их словами и еще с некоторым излишком. Это великий момент. Мы покорили большую высоту. Мы на вершине К-2, мы почти подготовлены покорить теперь Эверест, т. е. квантовую механику.
В основном мы пытались научиться понимать эти уравнения. А теперь, когда мы собрали их воедино, мы собираемся разобраться, что означают эти уравнения, что нового скажут они о том, чего мы еще не поняли. Мы много потрудились, чтобы вскарабкаться к этой точке. Это потребовало больших усилий, а теперь мы собираемся начать приятное путешествие — спуск с горы в долину, там мы увидим все, чего мы достигли.
§ 4. Передвигающееся поле
А теперь о новых следствиях. Они возникают из сопоставления всех уравнений Максвелла. Сначала давайте посмотрим, что произошло бы в особенно простом случае. Предположим, что изменяется только одна координата у всех величин, т. е. рассмотрим задачу одного измерения.
Случай этот показан на фиг. 18.3. Перед нами заряженный лист, помещенный на плоскости yz. Сначала он неподвижен, а затем мгновенно приобретает скорость и в направлении у и движется с этой постоянной скоростью. Вас может беспокоить присутствие такого «бесконечного» ускорения, но фактически это не имеет значения; просто представьте себе, что скорость достигает значения и очень быстро. Итак, мы внезапно получаем поверхностный ток J (J — ток на единицу ширины в z-направлении). Чтобы упростить проблему, предположим, что имеется еще неподвижный лист, заряженный противоположно и наложенный на плоскость yz, так что электростатические эффекты отсутствуют.
Фиг. 18.3. Бесконечная заряженная плоскость неожиданно приводится в поступательное движение.
Возникают магнитное и электрическое поля, распространяющиеся от плоскости с постоянной скоростью.
Представим себе также (хотя на фигуре мы показали лишь то, что происходит в конечной области), что лист простирается до бесконечности в направлениях ±у и ±z. Другими словами, здесь мы имеем случай, когда тока нет, а затем внезапно появляется однородный лист с током. Что же произойдет?
Мы знаем, что, когда имеется лист с током в положительном y-направлении, возникнет магнитное поле, направленное в отрицательном z-направлении при х>0 и в положительном z-направлении при х<0. Мы могли бы найти величину В, используя тот факт, что контурный интеграл от магнитного поля будет равен току на e0с2. Мы получили бы, что В-J/2e0с2 (поскольку ток I в полосе шириной w равен Jw, а контурный интеграл от В есть 2Вw).
Так мы определяем поле вблизи листа для малых значений х, но, поскольку мы считаем лист бесконечным, хотелось бы получить с помощью тех же рассуждений магнитное поле подальше (для больших значений х). Однако это означало бы, что в момент, когда мы включаем ток, магнитное поле внезапно изменяется повсюду от нуля до конечной величины. Но погодите! При внезапном изменении магнитного поля возникают огромные электрические эффекты. (Как бы оно ни менялось, электрические эффекты возникнут.) Так что в результате движения заряженного листа создается меняющееся магнитное поле и, следовательно, должны возникнуть электрические эффекты.
Фиг. 18.4. Зависимость величины В (или E) от х. а — спустя время t после начала движения заряженной плоскости; б — поля от заряженной плоскости, начавшей двигаться в момент t= Т в сторону отрицательных у; в — сумма а и б.
Если электрические поля образовались, они должны начинаться с нуля и меняться к какому-то значению. Возникнет некая производная dE/dt, которая будет вносить вклад вместе с током J в создание магнитного поля. Так разные уравнения зацепляются друг за друга, и мы должны попытаться найти решения для всех полей сразу.
Рассматривая уравнения Максвелла порознь, нелегко сразу получить решение. Поэтому сначала мы сообщим вам ответ, а затем уже проверим, действительно ли оно удовлетворяет уравнениям. Ответ: Поле В, которое мы вычислили, на самом деле создается прямо вблизи листа с током (для малых х). Так и должно быть, потому что если мы проведем крошечную петлю вокруг листа, то в ней не будет места для прохождения электрического потока. Но поле В подальше (для больших х) сначала равно нулю. Оно в течение некоторого времени остается нулевым, а затем внезапно включается. Короче говоря, мы включаем ток и немедленно вблизи него включается магнитное поле с постоянным значением В; затем включенное поле В распространяется от области источника. Через некоторое время появляется однородное магнитное поле всюду, вплоть до некоторого значения х, а за ним оно равно нулю. Вследствие симметрии оно распространяется как в положительном, так и в отрицательном x-направлении.
Фиг.18.5. То же, что на фиг. 18.3 (вид сверху).
Поле Е делает то же самое. До момента t=0 (когда мы включаем ток) поле повсюду равно нулю. Затем, спустя время t, как Е, так и В постоянны вплоть до расстояния х = vt, а за ним равны нулю. Поля продвигаются вперед, подобно приливной волне, причем фронт их движется с постоянной скоростью, которая оказывается равной с, но пока мы будем называть ее v. Изображение зависимости величины Е или В от х (как они кажутся в момент t) показано на фиг. 18.4, а. Если снова посмотреть на фиг. 18.3 в момент t, то мы увидим, что область между x=±vt «занята» полями, но они еще не достигли области за ней. Мы снова подчеркиваем — мы предполагаем, что лист заряжен, а следовательно, поля Е и В простираются бесконечно далеко в у- и z-направлениях. (Мы не можем изобразить бесконечный лист, поэтому мы показываем лишь то, что происходит в конечной области.)
Теперь мы хотим проанализировать количественно то, что происходит. Чтобы сделать это, рассмотрим два поперечных разреза: вид сверху, если смотреть вниз вдоль оси у (фиг. 18.5), и вид сбоку, если смотреть назад вдоль оси z (фиг. 18.6). Начнем с вида сбоку. Мы видим заряженный лист, движущийся вверх; магнитное поле направлено внутрь страницы для +x и от страницы для -х, а электрическое поле направлено вниз всюду, вплоть до x=± vt.
Посмотрим, согласуются ли такие поля с уравнениями Максвелла. Сначала нарисуем одну из тех петель, которыми мы пользовались для вычисления контурного интеграла, скажем прямоугольник Г2 на фиг. 18.6.
Фиг. 18.6. То же, что на фиг. 18.3 (вид сбоку).
Заметьте, что одна сторона прямоугольника проходит в области, где есть поля, а другая — в области, до которой поля еще не дошли. Через эту петлю проходит какой-то магнитный поток. Если он изменяется, должна появиться э. д. с. вдоль петли. Если волновой фронт движется, мы будем иметь меняющийся магнитный поток, поскольку поверхность, внутри которой существует поле В, непрерывно увеличивается со скоростью v. Поток внутри Г2 равен произведению В на ту часть поверхности внутри Г2) где есть магнитное поле. Скорость изменения потока (поскольку величина В постоянна) равна величине поля, умноженной на скорость изменения поверхности. Скорость изменения поверхности найти легко. Если ширина прямоугольника Г2 равна L, то поверхность, в которой В существует, меняется как LvDt за отрезок времени Dt (см. фиг. 18.6). Скорость изменения потока тогда равна BLv. По закону Фарадея она должна быть равна контурному интегралу от Е вокруг Г2, который есть просто EL. Мы получаем равенство
(18.10)
Таким образом, если отношение Е к В равно v, то рассматриваемые нами поля будут удовлетворять уравнению Фарадея. Но это не единственное уравнение; у нас есть еще одно, связывающее Е и В:
(18.11)
Чтобы применить это уравнение, посмотрим на вид сверху, изображенный на фиг. 18.5. Мы уже видели, что это уравнение дает нам значение В вблизи заряженного листа. Кроме того, для любой петли, нарисованной вне листа, но позади волнового фронта, нет ни ротора В, ни j или меняющегося поля Е, так что уравнение там справедливо. А теперь посмотрим, что происходит в петле Г1, которая пересекает волновой фронт, как показано на фиг. 18.5. Здесь нет токов, поэтому уравнение (18.11) можно записать в интегральной форме так:
(18.12)
Контурный интеграл от В есть просто произведение В на L. Скорость изменения потока Е возникает только благодаря продвигающемуся волновому фронту. Область внутри Г1, где Е не равно нулю, увеличивается со скоростью vL. Правая сторона (18.12) тогда равна vLE. Уравнение это приобретает вид
(18.13)
Мы имеем решение, когда поля В и Е постоянны за фронтом, причем оба направлены под прямыми углами к направлению, в котором движется фронт, и под прямыми углами друг к другу. Уравнения Максвелла определяют отношение Е к В. Из (18.10) и (18.13) получаем
Но одну минутку! Мы нашли два разных выражения для отношения Е/В. Может ли такое поле, как мы описываем, действительно существовать? Имеется лишь одна скорость v, для которой оба уравнения могут быть справедливы, а именно v = с. Волновой фронт должен передвигаться со скоростью с. Вот пример, когда электрическое возмущение от тока распространяется с определенной конечной скоростью с.
А теперь спросим, что произойдет, если мы внезапно остановим заряженный лист, после того как он двигался в течение короткого времени Т? Увидеть, что случится, можно с помощью принципа суперпозиции. У нас был ток, равный нулю, а затем его внезапно включали. Мы знаем решение для этого случая. Теперь мы собираемся добавить другой ряд полей. Мы берем другой заряженный лист и внезапно начинаем его двигать в противоположном направлении с той же скоростью, только спустя время Т после начала движения первого листа. Полный ток от двух листов вместе сначала равен нулю, потом он включается в течение времени Т, затем выключается снова, потому что оба тока погашаются. Так мы получаем прямоугольный «импульс» тока.
Новый отрицательный ток создает такие же поля, как и положительный, но с обратными знаками и, разумеется, с запаздыванием во времени Т. Волновой фронт по-прежнему движется со скоростью с. В момент времени t он достигает расстояния x=±c(t- Т) (см. фиг. 18.4, б). Итак, мы имеем два «куска» поля, перемещающихся со скоростью с (см. фиг. 18.4, а и б). Соединенные поля будут такими, как показано на фиг. 18.4, в. Для х>сt поля равны нулю, между х=с(t-Т) и x=ct они постоянны (со значениями, которые мы нашли выше), и для x<c(t-Т) они снова равны нулю.
Короче говоря, мы получаем маленький кусочек поля толщиной сТ, который покинул заряженный лист и передвигается через все пространство сам по себе. Поля «оторвались»; они распространяются свободно в пространстве и больше не связаны каким-то образом с источником. Куколка превратилась в бабочку!
Как же эти совокупности электрического и магнитного полей могут сохранять сами себя? Ответ: За счет сочетания эффектов из закона Фарадея СXE=-dВ/dt и нового члена, добавленного Максвеллом c2СX B=dE/dt. Они не могут не сохранять себя. Предположим, что магнитное поле исчезло бы. Тогда появилось бы меняющееся магнитное поле, которое создавало бы электрическое поле. Если бы это электрическое поле попыталось исчезнуть, то изменяющееся электрическое поле создало бы магнитное поле снова. Следовательно, за счет непрерывного взаимодействия — перекачивания туда и обратно от одного поля к другому — они должны сохраняться вечно. Они не могут исчезнуть. Они сохраняются, вовлеченные в общий танец — одно поле создает другое, а второе создает первое,— распространяясь все дальше и дальше в пространстве.
§ 5. Скорость света
У нас есть волна, которая уходит от материального источника и движется со скоростью с (это скорость света). Вернемся немного назад. Исторически не было известно, что коэффициент c в уравнениях Максвелла тот же, что и скорость распространения света. Это была просто константа в уравнениях. Мы назвали ее с c самого начала, так как знали, что в конце концов должно получиться. Мы не думаем, что было бы разумнее сначала заставить вас выучить формулы с разными константами, а затем вернуться обратно и подставить с повсюду, где оно должно стоять. С точки зрения электричества и магнетизма, однако, мы прямо начинаем с двух констант e0 и с2, которые появляются в уравнениях электростатики и магнитостатики:
(18.14)
и
(18.15)
Если взять любое произвольное определение единицы заряда, можно экспериментально определить постоянную e0, входящую в уравнение (18.14), скажем, измеряя силу между двумя неподвижными единичными зарядами по закону Кулона. Мы должны также определить экспериментально постоянную e0с2, которая появляется в уравнении (18.15), что можно сделать, скажем, измерив силу между двумя единичными токами. (Единичный ток означает единичный заряд в секунду.) Отношение этих двух экспериментальных постоянных есть с2 — как раз другая «электромагнитная постоянная».
Заметим теперь, что постоянная с2 получается одна и та же независимо от того, какова выбранная наша единица заряда. Если мы выберем «заряд» в два раза больше (скажем, удвоенный заряд протона), то в нашей «единице» заряда e0 должна уменьшиться в четыре раза. Когда мы пропускаем два таких «единичных» тока по двум проводам, в каждом проводе будет в два раза больше «зарядов» в секунду, так что силы между двумя проводами будут в четыре раза больше. Постоянная e0с2 должна уменьшиться в четыре раза. Но отношение e0с2/e0 не меняется.
Следовательно, непосредственно из экспериментов с зарядами и токами мы находим число с2, которое оказывается равным квадрату скорости распространения электромагнитных возбуждений. Из статических измерений (измеряя силы между двумя единичными зарядами и между двумя единичными токами) мы находим, что с=3,00·108 м/сек. Когда Максвелл впервые проделал это вычисление со своими уравнениями, он сказал, что совокупность электрического и магнитного полей будет распространяться с этой скоростью. Он отметил также таинственное совпадение — эта скорость была равна скорости света. «Мы едва ли можем избежать заключения,— сказал Максвелл,— что свет — это поперечное волнообразное движение той же самой среды, которая вызывает электрические и магнитные явления».
Так Максвелл совершил одно из великих обобщений физики! До него был свет, было электричество и был магнетизм. Причем два последних явления были объединены экспериментальными работами Фарадея, Эрстеда и Ампера. Потом внезапно свет не стал уже больше «чем-то еще», а был электричеством и магнетизмом в новой форме, небольшими кусками электрического и магнитного полей, которые распространяются в пространстве самостоятельно.
Мы обращали ваше внимание на некоторые черты этого особого решения, которые, однако, справедливы для любой электромагнитной волны: магнитное поле перпендикулярно направлению движения фронта волны; электрическое поле также перпендикулярно направлению движения фронта волны; и два вектора Е и В перпендикулярны друг другу. Далее, величина электрического поля Е равна произведению с на величину магнитного поля В. Эти три факта — что оба поля поперечны направлению распространения, что В перпендикулярно Е и что Е=сВ — верны вообще для любой электромагнитной волны. Наш частный случай — хороший пример, он показывает все основные свойства электромагнитных волн.
§ 6. Решение уравнений Максвелла; потенциалы и волновое уравнение
Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.
Начнем с С·В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В — есть ротор чего-то. Поэтому, если вы записали
B = СXA, (18.16)
то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А', если A'=A+Сty, где y— любое скалярное поле, потому что ротор Сy — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)
Теперь разберем закон Фарадея СXE= -dB/dt, потому что он не содержит никаких токов или зарядов. Если мы запишем В как СXA и продифференцируем по t, то сможем переписать закон Фарадея в форме
СXE = - d/dtСXA.
Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде
(18.17)
Мы видим, что Е+дА/дt — это вектор, ротор которого равен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было СXE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от -j (минус для технических удобств). То же самое сделаем и для E+дA/дt; мы полагаем
(18.18)
Мы используем то же обозначение j, так что в электростатическом случае, когда ничто не меняется со временем и dA/dt исчезает, Е будет нашим старым -Сj. Итак, закон Фарадея можно представить в форме
(18.19)
Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал j и векторный потенциал А, который, разумеется, представляет три функции.
Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим А на A'=A+Сy? В общем, Е должно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и j вместе по правилам
(18.20)
Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.
Раньше мы выбирали С·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.
Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники r и j. Раз мы можем определить А и j из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.
Начнем с подстановки уравнения (18.19) в С·E=r/e0; получаем
это можно записать еще в виде
(18.21)
Таково первое уравнение, связывающее j и А с источниками, Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:
а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):
Первый член можно переписать, используя алгебраическое тождество Vx (СXA) = С (С·A)-С2A; мы получаем
(18.22)
Не очень-то оно простое!
К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для j разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая
(18.23)
Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:
(18.24)
И. наше уравнение (18.21) для j принимает такую же форму:
(18.25)
Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит j, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (d/dt)2, когда мы раскроем ее, то обнаружим
(18.26)
Это уравнение имеет приятную симметрию по х, у, z, t; здесь (-1/с2) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.
Уравнения Максвелла привели нас к нового типа уравнению для потенциалов j и А, но с одной и той же математической формой для всех четырех функций j, Ах, Ауи Аг. Раз мы научились решать эти уравнения, то можем получить В и Е изСXЕ и-Сj-dA/dt. Мы приходим к другой форме электромагнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.
Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме
и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что j и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность j и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.
С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и j в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные уравнения в терминах Е и В. Но они — по ту сторону горы, на которую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе, — нас ожидают новые, прекрасные пейзажи.
*Это не совсем так. Поля могут быть «поглощены», если попадут в область, в которой есть заряды.
Это значит, что где-то могут быть созданы другие поля, которые наложатся на эти поля и «погасят»их в результате деструктивной интерференции (см. гл. 31, вып. 3)
* К-2— вторая по высоте вершина мира в северо-западных отрогах Гималаев, называемых Каракорум.—- Прим. ред.
*Выбор значения С·А называется «выбором калибровки». Изменение А за счет добавления Сy называется «калибровочным преобразованием». Выбор (18.23) называют «калибровкой Лоренца».
Глава 19 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
Добавление, сделанное после лекции
Когда я учился в школе, наш учитель физики, по фамилии Бадер, однажды зазвал меня к себе после урока и сказал: «У тебя вид такой, как будто тебе все страшно надоело; послушай-ка об одной интересной вещи». И он рассказал мне нечто, что мне показалось поистине захватывающим. Даже сейчас, хотя с тех пор прошла уже уйма времени, это продолжает меня увлекать. И всякий раз, когда я вспоминаю о сказанном, я вновь принимаюсь за работу. И на этот раз, готовясь к лекции, я поймал себя на том, что вновь анализирую все то же самое. И, вместо того чтобы готовиться к лекции, я взялся за решение новой задачи. Предмет, о котором я говорю,— это принцип наименьшего действия.
Вот что сказал мне тогда мой учитель Бадер: «Пусть, к примеру, у тебя имеется частица в поле тяжести; эта частица, выйдя откуда-то, свободно движется куда-то в другую точку. Ты подбросил ее, скажем, кверху, а она взлетела, а потом упала.
От исходного места к конечному она прошла за какое-то время. Попробуй теперь какое-то другое движение. Пусть для того, чтобы перейти «отсюда сюда», она двигалась уже не так, как раньше, а вот так:
но все равно очутилась на нужном месте в тот же самый момент времени, что и раньше».
«И вот,— продолжал учитель,— если ты подсчитаешь кинетическую энергию в каждый момент времени на пути частицы, вычтешь из нее потенциальную энергию и проинтегрируешь разность по всему тому времени, когда происходило движение, то увидишь, что число, которое получится, будет больше, чем при истинном движении частицы.
Иными словами, законы Ньютона можно сформулировать не в виде F=ma, а вот как: средняя кинетическая энергия минус средняя потенциальная энергия достигает своего самого наименьшего значения на той траектории, по которой предмет двигается в действительности от одного места к другому.
Попробую пояснить тебе это чуть понятнее.
Если взять поле тяготения и обозначить траекторию частицы x(t), где х — высота над землей (обойдемся пока одним измерением; пусть траектория пролегает только вверх и вниз, а не в стороны), то кинетическая энергия будет 1/zm(dx/dt)2, а потенциальная энергия в произвольный момент времени будет равна mgx.
Теперь я для какого-то момента движения по траектории беру разность кинетической и потенциальной энергий и интегрирую по всему времени от начала до конца. Пусть в начальный момент времени ttдвижение началось на какой-то высоте, а кончилосъ в момент t2 на другой определенной высоте.
Тогда интеграл равен
Можно подсчитать разность потенциальной и кинетической энергий на таком пути... или на любом другом. И самое поразительное — что настоящий путь это тот, по которому этот интеграл наименьший.
Давай проверим это. Для начала разберем такой случай: у свободной частицы вовсе нет потенциальной энергии. Тогда правило говорит, что при переходе от одной точки к другой за заданное время интеграл от кинетической энергии должен оказаться наименьшим. А это значит, что частица обязана двигаться равномерно. (И это правильно, мы же с тобой знаем, что скорость в таком движении постоянна.) А почему равномерно? Разберемся в этом. Если бы было иначе, то временами скорость частицы превысила бы среднюю, а временами была бы ниже ее, а средняя скорость была бы одинаковой, потому что частице надо было бы дойти «отсюда сюда» за условленное время. Например, если тебе нужно попасть из дому в школу на своей машине за определенное время, то сделать это можно по-разному: ты можешь сперва гнать, как сумасшедший, а в конце притормозить, или ехать с одинаковой скоростью, или сначала можешь даже отправиться в обратную сторону, а уж потом повернуть к школе, и т. д. Во всех случаях средняя скорость, конечно, должна быть одной и той же — частное от деления расстояния от дома до школы на время. Но и при данной средней скорости ты иногда двигался слишком быстро, а иногда чересчур медленно. А средний квадрат чего-то, что отклоняется от среднего, как известно, всегда больше квадрата среднего; значит, интеграл от кинетической энергии при колебаниях скорости движения всегда будет больше, нежели при движении с постоянной скоростью. Ты видишь, что интеграл достигнет минимума, когда скорость будет постоянной (при отсутствии сил). Правильный путь таков.
Предмет же, подброшенный в поле тяжести вверх, сперва поднимается быстро, а потом все медленнее. Происходит это потому, что он обладает и потенциальной энергией, а наименьшего значения должна достигать разность между кинетической и потенциальной энергиями.
Раз потенциальная энергия возрастает по мере подъема, то меньшая разность получится, если как можно быстрее достичь тех высот, где потенциальная энергия велика. Тогда, вычтя из кинетической энергии этот высокий потенциал, мы добьемся уменьшения среднего. Так что выгоднее такой путь, который идет вверх и поставляет добрый отрицательный кусок за счет потенциальной энергии.
Но, с другой стороны, нельзя ни двигаться слишком быстро, ни подняться слишком высоко, потому что на это потребуется чересчур много кинетической энергии. Надо двигаться достаточно быстро, чтобы подняться и спуститься за определенное время, имеющееся в твоем распоряжении. Так что не следует стараться взлететь слишком высоко, а просто надо достичь какого-то разумного уровня. В итоге оказывается, что решение есть своего рода равновесие между желанием раздобыть как можно больше потенциальной энергии и желанием как можно сильней уменьшить количество кинетической энергии — это стремление добиться максимального уменьшения разности кинетической и потенциальной энергий».
Вот и все, что сказал мне мой учитель, потому что он был очень хороший учитель и знал, когда пора остановиться. Сам я, увы, не таков. Мне трудно остановиться вовремя. И поэтому вместо того, чтобы просто разжечь в вас интерес своим рассказом, я хочу запугать вас, хочу, чтобы вам стало тошно от сложности жизни,— попробую доказать то, о чем я рассказал. Математическая задача, которую мы будем решать, очень трудна и своеобразна. Имеется некоторая величина S, называемая действием. Она равна кинетической энергии минус потенциальная, проинтегрированная по времени:
Не забудьте, что и п. э. и к. э.— обе функции времени. Для любого нового мыслимого пути это действие принимает свое определенное значение. Математическая задача состоит в том, чтобы определить, для какой кривой это число меньше, чем для других.
Вы скажете: «О, это просто обычный пример на максимум и минимум. Надо подсчитать действие, продифференцировать его и найти минимум».
Но погодите. Обычно у нас бывает функция какой-то переменной и нужно найти значение переменной, при котором функция становится наименьшей или наибольшей. Скажем, имеется стержень, нагретый посредине. По нему растекается тепло и в каждой точке стержня устанавливается своя температура. Нужно найти точку, где она выше всего. Но у нас речь идет совсем об ином — каждому пути в пространстве отвечает свое число, и предполагается найти тот путь, для которого это число минимально. Это совсем другая область математики. Это не обычное исчисление, а вариационное (так его называют).
В этой области математики имеется много своих задач. Скажем, окружность обычно определяют как геометрическое место точек, расстояния которых от данной точки одинаковы, но окружность можно определить и иначе: это та из кривых данной длины, которая ограничивает собою наибольшую площадь. Любая другая кривая такого же периметра ограничивает площадь меньшую, чем окружность. Так что если поставить задачу: найти кривую данного периметра, ограничивающую наибольшую площадь, то перед нами будет задача из вариационного исчисления, а не из того исчисления, к которому вы привыкли.
Итак, мы хотим взять интеграл по пути, пройденному телом. Сделаем это так. Все дело в том, чтобы вообразить себе, что существует истинный путь и что любая другая кривая, которую мы проведем,— не настоящий путь, так что если подсчитать
для нее действие, то получится число, превышающее то, которое мы получим для действия, соответствующего настоящему пути.
Итак, задача: найти истинный путь. Где он пролегает? Один из способов, конечно, мог бы состоять в том, чтобы подсчитать действие для миллионов и миллионов путей и потом посмотреть, при каком пути это действие наименьшее. Вот тот путь, при котором действие минимально, и будет настоящим.
Такой способ вполне возможен. Однако можно сделать проще. Если имеется величина, обладающая минимумом (из обычных функций, скажем, температура), то одно из свойств минимума состоит в том, что при удалении от него на расстояние первого порядка малости функция отклоняется от минимального своего значения только на величину второго порядка. А в любом другом месте кривой сдвиг на малое расстояние изменяет значение функции тоже на величину первого порядка малости. Но в минимуме легкие уходы в сторону в первом приближении не приводят к изменению функции.
Это-то свойство мы и собираемся использовать для расчета настоящего пути.
Если путь правильный, то кривая, чуть-чуть отличная от него, не приведет в первом приближении к изменению в величине действия. Все изменения, если это был действительно минимум, возникнут только во втором приближении.
Это легко доказать. Если при каком-то отклонении от кривой возникают изменения в первом порядке, то эти изменения в действии пропорциональны отклонению. Они, по всей вероятности, увеличат действие; иначе это не был бы минимум. Но раз изменения пропорциональны отклонению, то перемена знака отклонения уменьшит действие. Выходит, что при отклонении и одну сторону действие возрастает, а при отклонении в обратную сторону — убывает. Единственная возможность того, чтобы это действительно был минимум,— это чтобы в первом приближении никаких изменений не происходило и изменения были бы пропорциональны квадрату отклонения от настоящего пути.
Итак, мы пойдем по следующему пути: обозначим через x(t) (с чертой внизу) истинный путь — тот, который мы хотим найти. Возьмем некоторый пробный путь x(t), отличающийся от искомого на небольшую величину, которую мы обозначим h(t).
Идея состоит в том, что если мы подсчитаем действие S на пути x(t), то разность между этим S и тем действием, которое мы вычислили для пути x(t) (для простоты
оно будет обозначено S), или разность между S и S, должна быть в первом приближении по h нулем. Они могут отличаться во втором порядке, но в первом разность обязана быть нулем.
И это должно соблюдаться для любой h. Впрочем, не совсем для любой. Метод требует принимать во внимание только те пути, которые все начинаются и кончаются в одной и той же паре точек, т. е. всякий путь должен начинаться в определенной точке в момент t1 и кончаться в другой определенной точке в момент t2. Эти точки и моменты фиксируются. Так что наша функция h(отклонение) должна быть равна нулю на обоих концах: h(t1)=0 и h(t2)=0. При этом условии наша математическая задача становится полностью определенной.
Если бы вы не знали дифференциального исчисления, вы могли бы проделать такую же вещь для отыскания минимума обычной функции f(x). Вы бы задумались над тем, что случится, если взять f(x) и прибавить к х малую величину h, и доказывали бы, что поправка к f(x) в первом порядке по h должна в минимуме быть равна нулю. Вы бы подставили x+h вместо х и разложили бы f(x+h) с точностью до первой степени h. . ., словом, повторили бы все то, что мы намерены
Итак, идея наша заключается в том, что мы подставляем x(t)=x(t)+- h(t) в формулу для действия
где через V(x) обозначена потенциальная энергия. Производная dx/dt — это, естественно, производная от x(t) плюс производная от h(t), так что для действия я получаю такое выражение:
Теперь это нужно расписать подетальней. Для квадратичного слагаемого я получу
Но постойте-ка! Ведь мне не нужно заботиться о порядках выше первого. Я могу убрать все слагаемые, в которых есть h2 и высшие степени, и ссыпать их в ящик под названием «второй и высшие порядки». Из этого выражения туда попадет только одна вторая степень, но из чего-то другого могут войти и высшие. Итак, часть, связанная с кинетической энергией, такова:
Дальше нам нужен потенциал V в точках x+h. Я считаю т) малой и могу разложить V(x) в ряд Тэйлора. Приближенно это будет V(x); в следующем приближении (из-за того, что здесь стоят обычные производные) поправка равна h, умноженной на скорость изменения V по отношению к x; и т. д.:
Для экономии места я обозначил через V производную F по х. Слагаемое с h2 и все, стоящие за ним, попадают в категорию «второй и высшие порядки». И о них больше нечего беспокоиться. Объединим все, что осталось:
Если мы теперь внимательно взглянем на это, то увидим, что два первых написанных здесь члена отвечают тому действию S, которое я написал бы для искомого истинного пути х. Я хочу сосредоточить ваше внимание на изменении S, т. е. на разности между S и тем S, которое получилось бы для истинного пути. Эту разность мы будем записывать как dS и назовем ее вариацией S. Отбрасывая «второй и высшие порядки», получаем для dS
Теперь задача выглядит так. Вот передо мной некоторый интеграл. Я не знаю еще, каково это х, но я твердо знаю, что, какую h я ни возьму, этот интеграл должен быть равен нулю. «Ну что ж,— подумаете вы,— единственная возможность для этого — это чтобы множитель при h был равен нулю». Но как быть с первым слагаемым, где есть dh/dt? Вы скажете: «Если h обращается в ничто, то и ее производная такое же ничто; значит, коэффициент при dh/dt должен тоже быть нулем». Ну это не совсем верно. Это не совсем верно потому, что между отклонением h и его производной имеется связь; они не полностью независимы, потому что h (t) должно быть нулем и при ttи при t2.
При решении всех задач вариационного исчисления всегда пользуются одним и тем же общим принципом. Вы чуть сдвигаете то, что хотите варьировать (подобно тому, как это сделали мы, добавляя h), бросаете взгляд на члены первого порядка, затем расставляете все так, чтобы получился интеграл в таком виде: «сдвиг (h), умноженный на что получится», но чтобы в нем не было никаких производных от h(никаких dh/dt). Непременно нужно так все преобразовать, чтобы осталось «нечто», умноженное на h. Сейчас вы поймете, отчего это так важно. (Существуют формулы, которые подскажут вам, как в некоторых случаях можно это проделать без каких-либо выкладок; но они не так уж общи, чтобы стоило заучивать их; лучше всего проделывать выкладки так, как это делаем мы.)
Как же я могу переделать член dh/dt, чтобы в нем появилось h? Я могу добиться этого, интегрируя по частям. Оказывается, что в вариационном исчислении весь фокус в том и состоит, чтобы расписать вариацию S и затем проинтегрировать по частям так, чтобы производные от h исчезли. Во всех задачах, в которых появляются производные, проделывается такой же фокус.
Припомните общий принцип интегрирования по частям. Если у вас есть произвольная функция f, умноженная на dh/dt и проинтегрированная по t, то вы расписываете производную от hf:
В интересующем вас интеграле стоит как раз последнее слагаемое, так что
В нашей формуле для dS за функцию f принимается произведение т на dx/dt; поэтому я получаю для dS выражение
В первый член должны быть подставлены пределы интегрирования t1и t2. Тогда я получу под интегралом член от интегрирования по частям и последний член, оставшийся при преобразовании неизменным.
А теперь происходит то, что бывает всегда,— проинтегрированная часть исчезает. (А если не исчезает, то нужно переформулировать принцип, добавив условия, обеспечивающие такое исчезновение!) Мы уже говорили, что h на концах пути должна быть равна нулю. Ведь в чем состоит наш принцип? В том, что действие минимально при условии, что варьируемая кривая начинается и кончается в избранных точках. Это значит, что h(t1)=0 и h(t2)=0. Поэтому проинтегрированный член получается равным нулю. Мы собираем воедино остальные члены и пишем
Вариация S теперь приобрела такой вид, какой мы хотели ей придать: что-то стоит в скобках (обозначим его F), и все это умножено на h(t)и проинтегрировано от t1до t2.
У нас вышло, что интеграл от какого-то выражения, умноженного на h(t), всегда равен нулю:
Стоит какая-то функция от t; умножаю ее на h(t) и интегрирую ее от начала до конца. И какова бы ни была h, я получаю нуль. Это означает, что функция F(t)равна нулю. В общем-то это очевидно, но я на всякий случай покажу вам один из способов доказательства.
Пусть в качестве h (t) я выберу нечто, что равно нулю всюду, при всех t, кроме одного, заранее выбранного значения t. Оно
остается нулем, пока я не
дойду до этого t,
затем оно подскакивает на мгновение и сразу же осаживает назад. Если вы берете интеграл от этой h, умноженной на какую-то функцию F, то единственное место, в котором вы получите что-то ненулевое,— это там, где h (t) подскакивало; и у вас получится значение F в этом месте на интеграл по скачку. Сам по себе интеграл по скачку не равен нулю, но после умножения на F он должен дать нуль. Значит, функция в том месте, где был скачок, должна оказаться нулем. Но ведь скачок можно было сделать в любом месте; значит, F должна быть нулем всюду.
Мы видим, что если наш интеграл равен нулю при какой угодно h, то коэффициент при h должен обратиться в нуль. Интеграл действия достигает минимума на том пути, который будет удовлетворять такому сложному дифференциальному уравнению:
На самом деле оно не так уж сложно; вы его уже встречали прежде. Это просто F=ma. Первый член — это масса, умноженная на ускорение; второй — это производная от потенциальной энергии, т. е. сила.
Итак, мы показали (по крайней мере для консервативной системы), что принцип наименьшего действия приводит к правильному ответу; он утверждает, что путь, "обладающий минимумом действия,— это путь, удовлетворяющий закону Ньютона.
Нужно сделать еще одно замечание. Я не доказал, что это минимум. Может быть, это максимум. На самом деле это и не обязательно должен быть минимум. Здесь все так же, как в «принципе кратчайшего времени», который мы обсуждали, изучая оптику. Там тоже мы сперва говорили о «кратчайшем» времени. Однако выяснилось, что бывают положения, в которых это время не обязательно «кратчайшее». Фундаментальный принцип заключается в том, чтобы для любых отклонений первого порядка от оптического пути изменения во времени были бы равны нулю; здесь та же самая история. Под «минимумом» мы на самом деде подразумеваем, что в первом порядке малости изменения величины S при отклонениях от пути должны быть равны нулю. И это не обязательно «минимум».
Теперь я хочу перейти к некоторым обобщениям. В первую очередь всю эту историю можно было бы проделать и в трех измерениях. Вместо простого x я тогда имел бы x, у и z как функции t, и действие выглядело бы посложнее. При трехмерном движении вы должны использовать полную кинетическую энергию: (m/2), умноженное на квадрат всей скорости. Иначе говоря
Кроме того, потенциальная энергия теперь является функцией x, у и z. А что можно сказать о пути? Путь есть некоторая кривая общего вида в пространстве; ее не так легко начертить, но идея остается прежней. А как обстоит дело с h? Что ж, и h имеет три компоненты. Путь можно сдвигать и по x, и по у, и по z, или во всех трех направлениях одновременно. Так что h теперь вектор. От этого сильных усложнений не получается. Раз нулю должны быть равны лишь вариации первого порядка, то можно провести расчет последовательно с тремя сдвигами. Сперва можно сдвинуть h только в направлении x и сказать, что коэффициент должен обратиться в нуль. Получится одно уравнение. Потом мы сдвинем h в направлении у и получим второе. Затем сдвинем в направлении z и получим третье. Можно все, если угодно, проделать в другом порядке. Как бы то ни было, возникает тройка уравнений. Но ведь закон Ньютона — это тоже три уравнения в трех измерениях, по одному для каждой компоненты. Вам предоставляется самим убедиться, что это все действует и в трех измерениях (работы здесь не так много). Между прочим, можно взять какую угодно систему координат, полярную, любую, и сразу получить законы Ньютона применительно к этой системе, рассматривая, что получится, когда произойдет сдвиг h вдоль радиуса или по углу, и т. д.
Метод может быть обобщен и на произвольное число частиц. Если, скажем, у вас есть две частицы и между ними действуют какие-то силы и имеется взаимная потенциальная энергия, то вы просто складываете их кинетические энергии и вычитаете из суммы потенциальную энергию взаимодействия. А что вы варьируете? Пути обеих частиц. Тогда для двух частиц, движущихся в трех измерениях, возникает шесть уравнений. Вы можете варьировать положение частицы 1 в направлении x, в направлении у и в направлении z, и то же самое проделать с частицей 2, так что существует шесть уравнений. И так и должно быть. Три уравнения определяют ускорение частицы 1 через силу, действующую на нее, а три других — ускорение частицы 2 из-за силы, действующей на нее. Следуйте всегда тем же правилам игры, и вы получите закон Ньютона для произвольного числа частиц.
Я сказал, что мы получим закон Ньютона. Это не совсем верно, потому что в закон Ньютона входят и неконсервативные силы, например трение. Ньютон утверждал, что та равно всякой F. Принцип же наименьшего действия справедлив только для консервативных систем, таких, где все силы могут быть получены из потенциальной функции. Но ведь вы знаете, что на микроскопическом уровне, т. е. на самом глубинном физическом уровне, неконсервативных сил не существует. Неконсервативные силы (такие, как трение) появляются только от того, что мы пренебрегаем микроскопическими сложными эффектами: просто слишком много частиц приходится анализировать. Фундаментальные же законы могут быть выражены в виде принципа наименьшего действия.
Позвольте перейти к дальнейшим обобщениям. Положим, нас интересует, что будет, когда частица движется релятивистски. Пока мы не получили правильного релятивистского уравнения движения; F=ma верно только в нерелятивистских движениях. Встает вопрос: существует ли в релятивистском случае соответствующий принцип наименьшего действия? Да, существует. Формула в релятивистском случае такова:
Первая часть интеграла действия — это произведение массы покоя m0 на с2 и на интеграл от функции скорости Ц(1-v2/c2). Затем вместо того, чтобы вычитать потенциальную энергию, мы имеем интегралы от скалярного потенциала j и от векторного потенциала А, умноженного на v, Конечно, здесь приняты во внимание только электромагнитные силы. Все электрические и магнитные поля выражены в терминах j и А. Такая функция действия дает полную теорию релятивистского движения отдельной частицы в электромагнитном поле.
Конечно, вы должны понимать, что всюду, где я написал v, прежде чем делать выкладки, следует подставить dx/dt вместо vxи т. д. Кроме того, там, где я писал просто х, у, z, вы должны представить себе точки в момент t: x(t), y(t), z(t). Собственно, только после таких подстановок и замен v у вас получится формула для действия релятивистской частицы. Пусть самые умелые из вас попытаются доказать, что эта формула для действия действительно дает правильные уравнения движения теории относительности. Позвольте лишь посоветовать для начала отбросить А, т. е. обойтись пока без магнитных полей. Тогда вы должны будете получить компоненты уравнения движения dp/dt=-qСj, где, как вы, вероятно, помните, p=mv/Ц(l-v2/с2).
Включить в рассмотрение векторный потенциал А намного труднее. Вариации тогда становятся несравненно более сложными. Но в конце сила оказывается равной тому, чему следует: q(E+vXB). Но позабавьтесь с этим сами.
Мне хотелось бы подчеркнуть, что в общем случае (к примеру, в релятивистской формуле) под интегралом в действии уже не стоит разность кинетической и потенциальной энергий. Это годилось только в нерелятивистском приближении. Например, член m0c2Ц(1-v2/с2) — это не то, что называют кинетической энергией. Вопрос о том, каким должно быть действие для произвольного частного случая, может быть решен после некоторого числа проб и ошибок. Это задача того же типа, что и определение, каковы должны быть уравнения движения. Вы просто должны поиграть с известными вам уравнениями и посмотреть, можно ли их написать в виде принципа наименьшего действия.
Еще одно замечание по поводу терминологии. Ту функцию, которую интегрируют по времени, чтобы получить действие S, называют лагранжианом ж. Это функция, зависящая только от скоростей и положений частиц. Так что принцип наименьшего действия записывается также в виде
где под xiи viподразумеваются все компоненты координат и скоростей. Если вы когда-нибудь услышите, что кто-то говорит о «лагранжиане», знайте, что речь идет о функции, применяемой для получения S. Для релятивистского движения в электромагнитном поле
Кроме того, я должен отметить, что самые дотошные и педантичные люди не называют S действием. Его именуют «первой главной функцией Гамильтона». Но читать лекцию о «принципе наименьшей первой главной функции Гамильтона» было свыше моих сил. Я назвал это «действием». Да к тому же все больше и больше людей называют это «действием». Видите ли, исторически действием было названо нечто другое, не столь полезное для науки, но я думаю, что разумнее изменить определение. Теперь и вы начнете именовать новую функцию действием, а вскоре и все вообще станут называть ее этим простым именем.
Теперь я хочу сообщить вам по поводу нашей темы кое-что, похожее на те рассуждения, которые я вел по поводу принципа кратчайшего времени. Существует разница в самом существе закона, утверждающего, что некоторый интеграл, взятый от одной точки до другой, имеет минимум,— закона, который сообщает нам что-то обо всем пути сразу, и закона, который говорит, что когда вы двигаетесь, то, значит, есть сила, приводящая к ускорению. Второй подход докладывает вам о каждом вашем шаге, он прослеживает ваш путь пядь за пядью, а первый выдает сразу какое-то общее утверждение обо всем пройденном пути. Толкуя о свете, мы говорили о связи этих двух подходов. Теперь я хочу объяснить вам, отчего должны существовать дифференциальные законы, если имеется такой принцип — принцип наименьшего действия. Причина вот в чем: рассмотрим действительно пройденный в пространстве и времени путь. Как и прежде, обойдемся одним измерением, так что можно будет начертить график зависимости x от t. Вдоль истинного пути S достигает минимума. Положим, что у нас есть этот путь и что он проходит через некоторую точку а пространства и времени и через другую соседнюю точку b.
Теперь, если весь интеграл от t1 до t2 достиг минимума, необходимо, чтобы интеграл вдоль маленького участочка от а до b тоже был минимальным. Не может быть, чтобы часть от а до b хоть чуточку превосходила минимум. Иначе вы могли бы подвигать туда-сюда кривую на этом участочке и снизить немного значение всего интеграла.
Значит, любая часть пути тоже должна давать минимум. И это справедливо для каких угодно маленьких долек пути. Поэтому тот принцип, что весь путь должен давать минимум, можно сформулировать, сказав, что бесконечно малая долька пути — это тоже такая кривая, на которой действие минимально. И если мы возьмем достаточно короткий отрезок пути — между очень близкими друг к другу точками а и b,— то уже неважно, как меняется потенциал от точки к точке вдали от этого места, потому что, проходя весь ваш коротенький отрезочек, вы почти не сходите с места. Единственное, что вам нужно учитывать,— это изменение первого порядка малости в потенциале. Ответ может зависеть только от производной потенциала, а не от потенциала в других местах. Так, утверждение о свойстве всего пути в целом становится утверждением о том, что происходит на коротком участке пути, т. е. дифференциальным утверждением. И эта дифференциальная формулировка включает производные от потенциала, т. е. силу в данной точке. Таково качественное объяснение связи между законом в целом и дифференциальным законом.
Когда мы говорили о свете, то обсуждали также вопрос: как все-таки частица находит правильный путь? С дифференциальной точки зрения это понять легко. В каждый момент частица испытывает ускорение и знает только то, что ей положено делать в это мгновение. Но все ваши инстинкты причин и следствий встают на дыбы, когда вы слышите, что частица «решает», какой ей выбрать путь, стремясь к минимуму действия. Уж не «обнюхивает» ли она соседние пути, прикидывая, к чему они приведут — к большему или к меньшему действию? Когда мы на пути света ставили экран так, чтобы фотоны не могли перепробовать все пути, мы выяснили, что они не могут решить, каким путем идти, и получили явление дифракции.
Но верно ли это и для механики? Правда ли, что частица не просто «идет верным путем», а пересматривает все другие мыслимые траектории? И что если, ставя преграды на ее пути, мы не дадим ей заглядывать вперед, то мы получим некий аналог явления дифракции? Самое чудесное во всем этом — то, что все действительно обстоит так. Именно это утверждают законы квантовой механики. Так что наш принцип наименьшего действия сформулирован не полностью. Он состоит не в том, что частица избирает путь наименьшего действия, а в том, что она «чует» все соседние пути и выбирает тот, вдоль которого действие минимально, и способ этого выбора сходен с тем, каким свет отбирает кратчайшее время. Вы помните, что способ, каким свет отбирает кратчайшее время, таков: если свет пойдет по пути, требующему другого времени, то придет он с другой фазой. А полная амплитуда в некоторой точке есть сумма вкладов амплитуд для всех путей, по которым свет может ее достичь. Все те пути, у которых фазы резко различаются, ничего после сложения не дают. Но если вам удалось найти всю последовательность путей, фазы которых почти одинаковы, то мелкие вклады сложатся, и в точке прибытия полная амплитуда получит заметное значение. Важнейшим путем становится тот, возле которого имеется множество близких путей, дающих ту же фазу.
В точности то же происходит и в квантовой механике. Законченная квантовая механика (нерелятивистская и пренебрегающая спином электрона) работает так: вероятность того, что частица, выйдя из точки 1 в момент t1, достигнет точки 2 в момент t2, равна квадрату амплитуды вероятности. Полная амплитуда может быть записана в виде суммы амплитуд для всех возможных путей — для любого пути прибытия. Для любого x(t), которое могло бы возникнуть для любой мыслимой воображаемой траектории, нужно подсчитать амплитуду. Затем их все нужно сложить. Что же мы примем за амплитуду вероятности некоторого пути? Наш интеграл действия говорит нам, какой обязана быть амплитуда отдельного пути. Амплитуда пропорциональна eiS/h, где S — действие на этом пути. Это значит, что если мы представим фазу амплитуды в виде комплексного числа, то фазовый угол будет равен S/h,. Действие S имеет размерность энергии на время, и у постоянной Планка размерность такая же. Это постоянная, которая определяет, когда нужна квантовая механика.
И вот как все это срабатывает. Пусть для всех путей действие S будет весьма большим по сравнению с числом h. Пусть какой-то путь привел к некоторой величине амплитуды. Фаза рядом проложенного пути окажется совершенно другой, потому что при огромном S даже незначительные изменения S резко меняют фазу (ведь h чрезвычайно мало). Значит, рядом лежащие пути при сложении обычно гасят свои вклады. И только в одной области это не так — в той, где и путь и его сосед— оба в первом приближении обладают одной и той же фазой (или, точнее, почти одним и тем же действием, меняющимся в пределах h). Только такие пути и принимаются в расчет. А в предельном случае, когда постоянная Планка h стремится к нулю, правильные квантовомеханические законы можно подытожить, сказав: «Забудьте обо всех этих амплитудах вероятностей. Частица и впрямь движется по особому пути — именно по тому, по которому S в первом приближении не меняется». Такова связь между принципом наименьшего действия и квантовой механикой. То обстоятельство, что таким способом можно сформулировать квантовую механику, было открыто в 1942 г. учеником того же самого учителя, мистера Бадера, о котором я вам рассказывал. [Первоначально квантовая механика была сформулирована при помощи дифференциального уравнения для амплитуды (Шредингер), а также при помощи некоторой матричной математики (Гейзенберг).]
Теперь я хочу потолковать о других принципах минимума в физике. Есть очень много интересных принципов такого рода. Я не буду их все перечислять, а назову еще только один. Позже, когда мы доберемся до одного физического явления, для которого существует превосходный принцип минимума, я расскажу вам о нем. А сейчас я хочу показать, что необязательно описывать электростатику при помощи дифференциального уравнения для поля; можно вместо этого потребовать, чтобы некоторый интеграл обладал максимумом или минимумом. Для начала возьмем случай, когда плотность зарядов известна повсюду, а нужно найти потенциал j в любой точке пространства. Вы уже знаете, что ответ должен быть такой:
Другой способ утверждать то же самое заключается в следующем: надо вычислить интеграл U*
это объемный интеграл. Он берется по всему пространству. При правильном распределении потенциала j(x, у, z) это выражение достигает минимума.
Мы можем показать, что оба эти утверждения относительно электростатики эквивалентны. Предположим, что мы выбрали произвольную функцию j. Мы хотим показать, что когда в качестве j мы возьмем правильное значение потенциала j плюс малое отклонение f, то в первом порядке малости изменение в U* будет равно нулю. Так что мы пишем
здесь j — это то, что мы ищем; но мы проварьируем j, чтобы увидеть, каким он должен быть для того, чтобы вариация U* оказалась первого порядка малости. В первом члене U* нам нужно написать
Единственный член первого порядка, который будет меняться, таков:
Во втором члене U* подынтегральное выражение примет вид
изменяющаяся часть здесь равна rf. Оставляя только меняющиеся члены, получим интеграл
Дальше, руководствуясь нашим старым общим правилом, мы должны очистить интеграл от всех производных по f. Посмотрим, что это за производные. Скалярное произведение равно
Это нужно проинтегрировать по x, у и по z. И здесь напрашивается тот же фокус: чтобы избавиться от df/dx, мы проинтегрируем по х по частям. Это приведет к добавочному дифференцированию j по х. Это та же основная идея, с помощью которой мы избавились от производных по t. Мы пользуемся равенством
Другой способ утверждать то же самое заключается в следующем: надо вычислить интеграл U*
это объемный интеграл. Он берется по всему пространству. При правильном распределении потенциала j(x, у, z) это выражение достигает минимума.
Мы можем показать, что оба эти утверждения относительно электростатики эквивалентны. Предположим, что мы выбрали произвольную функцию j. Мы хотим показать, что когда в качестве j мы возьмем правильное значение потенциала j плюс малое отклонение f, то в первом порядке малости изменение в U* будет равно нулю. Так что мы пишем
здесь j — это то, что мы ищем; но мы проварьируем j, чтобы увидеть, каким он должен быть для того, чтобы вариация U* оказалась первого порядка малости. В первом члене U* нам нужно написать
Единственный член первого порядка, который будет меняться, таков:
Во втором члене U* подынтегральное выражение примет вид
изменяющаяся часть здесь равна rf. Оставляя только меняющиеся члены, получим интеграл
Дальше, руководствуясь нашим старым общим правилом, мы должны очистить интеграл от всех производных по f. Посмотрим, что это за производные. Скалярное произведение равно
Это нужно проинтегрировать по x, у и по z. И здесь напрашивается тот же фокус: чтобы избавиться от df/dx, мы проинтегрируем по x по частям. Это приведет к добавочному дифференцированию j по x. Это та же основная идея, с помощью которой мы избавились от производных по t. Мы пользуемся равенством
Проинтегрированный член равен нулю, так как мы считаем f равным нулю на бесконечности. (Это отвечает обращению h в нуль при t1и t2. Так что наш принцип более точно формулируется следующим образом: U* для правильного j меньше, чем для любого другого
j(х, у, z), обладающего теми же значениями на бесконечности.) Затем мы проделаем то же с у и с z. Наш интеграл DU* обратится в
Чтобы эта вариация была равна нулю при любом произвольном f, коэффициент при f должен быть равен нулю. Значит,
Мы вернулись к нашему старому уравнению. Значит, наше «минимальное» предложение верно. Его можно обобщить, если слегка изменить выкладки. Вернемся назад и проинтегрируем по частям, не расписывая все покомпонентно. Начнем с того, что напишем следующее равенство:
Продифференцировав левую часть, я могу показать, что она в точности равна правой. Это уравнение подходит для того, чтобы провести интегрирование но частям. В нашем интеграле DU* мы заменяем Сj·Сf на —fС2j+С·(fС j) и затем интегрируем это по объему. Член с дивергенцией после интегрирования по объему заменяется интегралом по поверхности:
А поскольку мы интегрируем по всему пространству, то поверхность в этом интеграле лежит на бесконечности. Значит, f=0, и мы получаем прежний результат.
Только теперь мы начинаем понимать, как решать задачи, в которых мы не знаем, где расположены все заряды. Пусть мы имеем проводники, на которых как-то распределены заряды. Если потенциалы на всех проводниках зафиксированы, то наш принцип минимума все еще разрешается применять. Интегрирование в U* мы проведем только по области, лежащей снаружи всех проводников. Но раз мы не можем на проводниках менять j, то на их поверхности f=0, и поверхностный интеграл
тоже равен нулю. Остающееся объемное интегрирование нужно проделывать только в промежутках между проводниками.
И мы, конечно, снова получаем уравнение Пуассона
Мы, стало быть, показали, что наш первоначальный интеграл U* достигает минимума и тогда, когда он вычисляется в пространстве между проводниками, каждый из которых находится при фиксированном потенциале [это значит, что каждая пробная функция j(х, у, z) должна равняться заданному потенциалу проводника, когда (х, у, z) — точки поверхности проводника]. Существует интересный частный случай, когда заряды расположены только на проводниках. Тогда
и наш принцип минимума говорит нам, что в случае, когда у каждого проводника есть свой заранее заданный потенциал, потенциалы в промежутках между ними пригоняются так, что интеграл U* оказывается как можно меньше. А что это за интеграл? Член Сj — это электрическое поле. Значит, интеграл — это электростатическая энергия. Правильное поле и есть то единственное, которое из всех полей, получаемых как градиент потенциала, отличается наименьшей полной энергией.
Я хотел бы воспользоваться этим результатом, чтобы решить какую-нибудь частную задачу и показать вам, что все эти вещи имеют реальное практическое значение. Предположим, что я взял два проводника в форме цилиндрического конденсатора.
У внутреннего проводника потенциал равен, скажем, V, а у внешнего— нулю. Пусть радиус внутреннего проводника будет равен а, а внешнего — b. Теперь мы можем предположить, что распределение потенциалов между ними — любое.
Но если мы возьмем правильное значение j и вычислим
, то должна получиться энергия системы 1/2CV2.
Так что с помощью нашего принципа можно подсчитать и емкость С. Если же мы возьмем неправильное распределение потенциала и попытаемся этим методом прикинуть емкость конденсатора, то придем к чересчур большому значению емкости при фиксированном V. Любой предполагаемый потенциал j, не точно совпадающий с истинным его значением, приведет и к неверной величине С, большей, чем нужно. Но если неверно выбранный потенциал j является еще грубым приближением, то емкость С получится уже с хорошей точностью, потому что погрешность в С — величина второго порядка по сравнению с погрешностью в j.
Предположим, что мне неизвестна емкость цилиндрического конденсатора. Тогда, чтобы узнать ее, я могу воспользоваться этим принципом. Я просто буду испытывать в качестве потенциала разные функции j до тех пор, пока не добьюсь наинизшего значения С. Допустим, к примеру, что я выбрал потенциал, отвечающий постоянному полю. (Вы, конечно, знаете, что на самом деле поле здесь не постоянно; оно меняется как 1/r.) Если поле постоянно, то это означает, что потенциал линейно зависит от расстояния. Чтобы напряжение на проводниках было каким нужно, функция j должна иметь вид
Эта функция равна V при r=а, нулю при r=b, а между ними имеется постоянный наклон, равный —V/(b-а). Значит, чтобы определить интеграл U*, надо только помножить квадрат этого градиента на e0/2 и проинтегрировать по всему объему. Проведем этот расчет для цилиндра единичной длины. Элемент объема при радиусе r равен 2prdr. Проводя интегрирование, я нахожу, что моя первая проба дает такую емкость:
Интеграл здесь просто равен
Так я получаю формулу для емкости, которая хотя и неправильна, но является каким-то приближением:
Конечно, она отличается от правильного ответа C=2pe0/ln(b/a), но в общем-то, она не так уж плоха. Давайте попробуем сравнить ее с правильным ответом для нескольких значений b/а. Вычисленные мною числа приведены в следующей таблице
Даже когда b/a=2 (а это приводит уже к довольно большим отличиям между постоянным и линейным полем), я все еще получаю довольно сносное приближение. Ответ, конечно, как и ожидалось, чуть завышен. Но если тонкую проволочку поместить внутри большого цилиндра, то все выглядит уже гораздо хуже. Тогда поле изменяется очень сильно и замена его постоянным полем ни к чему хорошему не приводит. При b/а=100 мы завышаем ответ почти вдвое. Для малых b/а положение выглядит намного лучше. В противоположном пределе, когда промежуток между проводниками не очень широк (скажем, при b/а=1,1), постоянное поле оказывается весьма хорошим приближением, оно дает значение С с точностью до десятых процента.
А теперь я расскажу вам, как усовершенствовать этот расчет. (Ответ для цилиндра вам, разумеется, известен, но тот же способ годится и для некоторых других необычных форм конденсаторов, для которых правильный ответ вам может быть и не известен.) Следующим шагом будет подыскание лучшего приближения для неизвестного нам истинного потенциала j. Скажем, можно испытать константу плюс экспоненту j и т. д. Но как вы узнаете, что у вас получилось лучшее приближение, если вы не знаете истинного j? Ответ: Подсчитайте С; чем оно ниже, тем к истине ближе. Давайте проверим эту идею. Пусть потенциал будет не линейным, а, скажем, квадратичным по r, а электрическое поле не постоянным, а линейным. Самая общая квадратичная
форма, которая обращается в j =0 при r=b и в j =V при r=а, такова:
где a — постоянное число. Эта формула чуть сложнее прежней. В нее входит и квадратичный член, и линейный. Из нее очень легко получить поле. Оно равно просто
Теперь это нужно возвести в квадрат и проинтегрировать по объему. Но погодите минутку. Что же мне принять за a? За j я могу принять параболу, но какую? Вот что я сделаю: подсчитаю емкость при произвольном a. Я получу
Это выглядит малость запутанно, но так уж выходит после интегрирования квадрата поля. Теперь я могу выбирать себе а. Я знаю, что истина лежит ниже, чем все, что я собираюсь вычислить. Что бы я ни поставил вместо a, ответ все равно получится слишком большим. Но если я продолжу свою игру с а и постараюсь добиться наинизшего возможного значения С, то это наинизшее значение будет ближе к правде, чем любое другое значение. Следовательно, мне теперь надо подобрать а так, чтобы значение С достигло своего минимума. Обращаясь к обычному дифференциальному исчислению, я убеждаюсь, что минимум С будет тогда, когда a=-2b/(b+а). Подставляя это значение в формулу, я получаю для наименьшей емкости
Я прикинул, что дает эта формула для С при различных значениях b/а. Эти числа я назвал С (квадратичные). Привожу таблицу, в которой сравниваются С (квадратичные) с С (истинными).
Например, когда отношение радиусов равно 2:1, я получаю 1,444. Это очень хорошее приближение к правильному ответу, 1,4423. Даже при больших b/а приближение остается довольно хорошим — оно намного лучше первого приближения. Оно остается сносным (завышение только на 10%) даже при b/а=10:1. Большое расхождение наступает только при отношении 100:1. Я получаю С равным 0,346 вместо 0,267. С другой стороны, для отношения радиусов 1,5 совпадение превосходное, а при b/a=1,1 ответ получается 10,492065 вместо положенного 10,492070. Там, где следует ожидать хорошего ответа, он оказывается очень и очень хорошим.
Я привел все эти примеры, во-первых, чтобы продемонстрировать теоретическую ценность принципа минимального действия и вообще всяких принципов минимума, и, во-вторых, чтобы показать вам их практическую полезность, а вовсе не для того, чтобы подсчитать емкость, которую мы и так великолепно знаем. Для любой другой формы вы можете испробовать приближенное поле с несколькими неизвестными параметрами (наподобие а) и подогнать их под минимум. Вы получите превосходные численные результаты в задачах, которые другим способом не решаются.
Добавление, сделанное после лекции
Мне не хватило времени на лекции, чтобы сказать еще об одной вещи (всегда ведь готовишься рассказать больше, чем успеваешь). И я хочу сделать это сейчас. Я уже упоминал о том, что, готовясь к этой лекции, заинтересовался одной задачей. Мне хочется вам рассказать, что это за задача. Я заметил, что большая часть принципов минимума, о которых шла речь, в той или иной форме вытекает из принципа наименьшего действия механики и электродинамики. Но существует еще класс принципов, оттуда не вытекающих. Вот пример. Если сделать так, чтобы токи протекали через массу вещества, удовлетворяющего закону Ома, то токи распределятся в этой массе так, чтобы скорость, с какой генерируется в ней тепло, была наименьшей. Можно также сказать иначе (если температура поддерживается постоянной): что скорость выделения энергии минимальна. Этот принцип, согласно классической теории, выполняется даже в распределении скоростей электронов внутри металла, по которому течет ток. Распределение скоростей не совсем равновесно [см. гл. 40 (вып. 4), уравнение (40.6)], потому что они медленно дрейфуют в стороны. Новое распределение можно найти из того принципа, что оно при данном токе должно быть таково, что развивающаяся в секунду за счет столкновений энтропия уменьшится настолько, насколько это возможно. Впрочем, правильное описание поведения электронов должно быть квантовомеханическим. Так вот в чем состоит вопрос: должен ли этот самый принцип минимума развивающейся энтропии соблюдаться и тогда, когда положение вещей описывается квантовой механикой? Пока мне не удалось это выяснить.
Вопрос этот интересен, конечно, и сам по себе. Подобные принципы возбуждают воображение, и всегда стоит попробовать выяснить, насколько они общи. Но мне необходимо это знать и по более практической причине. Вместе с несколькими коллегами я опубликовал работу, в которой с помощью квантовой механики мы примерно рассчитали электрическое сопротивление, испытываемое электроном, пробирающимся сквозь ионный кристалл, подобный NaCl. [Статья об этом была напечатана в Physical Review, 127, 1004 (1962) и называется «Подвижность медленных электронов в полярных кристаллах».] Но если бы существовал принцип минимума, мы могли бы воспользоваться им, чтобы сделать результат намного более точным, аналогично тому как принцип минимума емкости конденсатора позволил нам добиться столь высокой точности для емкости, хотя об электрическом поле наши сведения были весьма неточными.
* Эта лекция никак не связана со всем остальным. Она прочитана лишь для того, чтобы отвлечься от основной темы и немного передохнуть. (Перевод надписей, сделанных на доске, приведен около рисунков, над стрелками.— Прим. ред.)
Глава 20 РЕШЕНИЯ УРАВНЕНИЙ МАКСВЕЛЛА В ПУСТОМ ПРОСТРАНСТВЕ
§ 1. Волны в пустом пространстве; плоские волны
§ 2. Трехмерные волны
§ 3. Научное воображение
§ 4. Сферические волны
Повторить: гл. 47 (вып. 4) «Звук, Волновое уравнение»; гл. 28 (вып. 3) «Электромагнитное излучение»
§ 1. Волны в пустом пространстве; плоские волны
В гл. 18 мы достигли того, что уравнения Максвелла появились в полном виде. Все, что есть в классической теории электрических и магнитных полей, вытекает из четырех уравнений:
Когда мы свели все эти уравнения воедино, мы обнаружили новое знаменательное явление: поля, создаваемые движущимися зарядами, могут покинуть источник и отправиться путешествовать в пространстве. Мы рассмотрели частный случай, когда внезапно включается целая бесконечная плоскость. После того как в течение времени t шелток, возникают однородные электрические и магнитные поля, простирающиеся от плоскости на ct. Предположим, что по плоскости yz течет ток в направлении +yс поверхностной плотностью J. Электрическое поле будет иметь только y-компоненту, а магнитное — только z-компоненту. Величина компонент поля будет равна
(20.2)
для положительных x, меньших ct. Для больших x поля равны нулю. Равные по величине поля простираются на то же расстояние от плоскости в направлении отрицательных y. На фиг. 20.1 показан график зависимости величины полей от x в момент t. С течением времени «волновой фронт» в ct распространяется вдоль х с постоянной скоростью с.
Фиг. 20.1. Зависимость электрического и магнитного полей от х через t сек после того, как была включена заряженная плоскость.
Теперь представим себе такую последовательность событий. На мгновение мы включаем ток единичной силы, а затем внезапно увеличиваем его силу втрое и поддерживаем его на этом уровне. Как же будут теперь выглядеть поля? Это можно узнать таким образом. Во-первых, надо представить ток с единичной силой, включенный при t=0 и больше не менявшийся. Тогда поля при положительных х будут иметь вид, представленный на фиг. 20.2, а. Затем надо задать себе вопрос, что произойдет, если в момент t1 включить постоянный ток силой в две единицы?
В этом случае поля станут вдвое больше, чем прежде, но отойдут по х только на промежуток c(t-t1) (фиг. 20.2, б). Складывая эти два решения (по принципу суперпозиции), мы получаем, что сумма источников — это ток силой в одну единицу с момента нуль до момента t1и ток в три единицы в более поздние моменты. В момент t поля меняются вдоль х так, как показано на фиг. 20.2, в.
Возьмем теперь более сложную задачу. Рассмотрим ток, имевший сначала силу в одну единицу, а затем достигший силы в три единицы и выключенный. Каковы будут поля от такого тока? Решение можно получить точно так же, как и раньше,
Фиг. 20.2. Электрическое поле плоскости с током.
а — одна единица тока включена в момент t=0; б—две единицы тока включены в момент t=t1; в — суперпозиция а и б.
Фиг. 20.3. Если сила источника тока меняется так, как на рисунке (а), то в момент t электрическое поле как функция от х приобретает другой вид (б).
т. е. складывая решения трех разных задач. Сперва найдем поля постоянного тока единичной силы (эту задачу мы уже решали). Потом узнаем поля от тока двойной силы. И, наконец, возьмем решение для полей токов с силой в минус три единицы. Сложив все три решения, мы получим ток силой в одну единицу от t=0 до какого-то более позднего момента, скажем, до t1, затем ток силой в три единицы до момента t2, а потом ток, равный нулю, т. е. выключенный. График зависимости тока от времени показан на фиг. 20.3, а. Складывая три решения для электрического поля, мы видим, что его изменения с расстоянием х в данный момент t подобны изображенным на фиг. 20.3, б. Поле в точности отображает собой ток. Распределение поля в пространстве есть точное отражение изменений тока со временем, но только нарисованное задом наперед. По мере того как проходит время, вся картина перемещается наружу со скоростью с, так что получается ломтик полей, который движется к положительным х и хранит в себе всю историю перемен тока. Если бы мы находились где-то на расстоянии многих километров, мы могли бы лишь по изменению электрического или магнитного поля безошибочно рассказать, как менялся ток в источнике.
Заметьте также, что даже после того, как вся деятельность в источнике прекратилась и все заряды исчезли, а токи сошли на нет, наш ломтик полей продолжает свое путешествие через пространство. Получается распределение электрических и магнитных полей, которое существует независимо от токов и зарядов. Это и есть тот новый эффект, который следует из полной системы уравнений Максвелла. Мы можем, если нужно, представить только что проделанный анализ в строго математической форме, написав, что электрическое поле в данном месте и в данное время пропорционально току в источнике, но не в то же время, а в более ранний период [t-(x/с)]. Можно написать
Вас удивит, если я скажу, что мы уже выводили это уравнение раньше (с другой точки зрения), когда говорили о теории показателя преломления. Тогда нам нужно было представить себе, какие поля создаст слой колеблющихся диполей в тонком плоском диэлектрике, если диполи приводятся в движение электрическим полем падающей электромагнитной волны. Задача наша состояла в расчете комбинированного поля начальной волны и волн, излучаемых колеблющимися диполями. Как же мы смогли тогда рассчитать поля, создаваемые движущимися зарядами, не зная уравнений Максвелла? Мы тогда приняли в качестве исходной (без вывода) формулу для полей излучения, создаваемых на больших расстояниях от ускоряемого точечного заряда. Если вы заглянете в гл. 31 (вып. 3), то увидите, что выражение (31.10) — это как раз наше выражение (20.3), которое мы только что написали. Хотя прежний наш вывод относился только к большим расстояниям от источника, теперь мы видим, что тот же результат верен и вблизи источника.
Сейчас мы хотим взглянуть в общем виде на поведение электрических и магнитных полей в пустом пространстве вдалеке от источников, т. е. от токов и зарядов. Очень близко от них (так близко, что источники за время запаздывания передачи не успевают сильно измениться) поля очень похожи на те, которые получились у нас в электростатике или магнитостатике. Но если перейти к таким большим расстояниям, что запаздывание станет заметным, то природа полей может радикально отличаться от тех решений, которые мы нашли. Когда поля значительно удаляются ото всех источников, они начинают в некотором смысле приобретать свой собственный характер. Так что мы вправе приступить к обсуждению поведения полей в области, где нет ни токов, ни зарядов.
Предположим, что нас интересует род полей, которые могут существовать в областях, где и r и j равны нулю. В гл. 18 мы видели, что физику уравнений Максвелла можно также выразить на языке дифференциальных уравнений для скалярного и векторного потенциалов:
(20.4)
(20.5)
Если r и j равны нулю, то эти уравнения упрощаются:
(20.6)
(20.7)
Стало быть, в пустом пространстве и скалярный потенциал j, и каждая компонента векторного потенциала А удовлетворяют одному и тому же математическому уравнению. Пусть буквой y (пси) мы обозначили любую из четырех величин j, Ах, Ау, Аг; тогда нам нужно изучить общие решения уравнения
(20.8)
Его называют трехмерным волновым уравнением — трехмерным потому, что функция y может в общем случае зависеть от х, у и z и следует учитывать изменения по каждой из этих координат. Это становится ясным, если мы выпишем явно три члена оператора Лапласа:
(20.9)
В пустом пространстве электрические и магнитные поля Е и В тоже удовлетворяют волновому уравнению. Так, поскольку B=СXА, дифференциальное уравнение для В можно получить, взяв ротор от уравнения (20.7). Раз лапласиан — это скалярный оператор, то порядок операций вычисления лапласиана и ротора можно переставлять:
Точно так же можно переставлять и вычисление rot и d/dt:
Из этого мы получаем следующее дифференциальное уравнение
для В:
(20.10)
Тем самым выясняется, что компонента магнитного поля В удовлетворяет трехмерному волновому уравнению. Подобно этому, из того факта, что Е=-Сj-dAJdt, следует, что электрическое поле Е в пустом пространстве удовлетворяет трехмерному волновому уравнению
(20.11)
Все наши электромагнитные поля подчиняются одному и тому же уравнению (20.8). Можно еще спросить: каково самое общее решение этого уравнения? Однако прежде, чем решать этот трудный вопрос, сначала посмотрим, что можно сказать в общем случае о тех решениях, в которых по у и по z ничего не меняется. (Всегда сначала беритесь за простые случаи, чтобы было видно, чего следует ожидать, а уж потом можете переходить к случаям посложней.) Предположим, что величина полей зависит только от х, так что по у и по z поля не меняются. Мы, следовательно, опять рассматриваем плоские волны и должны ожидать, что получатся те же результаты, что и в предыдущей главе. И мы действительно получим в точности те же самые ответы. Вы можете спросить: «Но зачем снова делать то же самое?» Это важно, во-первых, потому, что мы не доказали, что найденные нами волны представляют собой самое общее решение для плоских волн, и, во-вторых, потому что наши поля произошли от источника тока особого вида. Сейчас мы хотели бы выяснить такой вопрос: каков самый общий вид одномерной волны в пустом пространстве? Мы не узнаем этого, если будем рассматривать тот или иной источник особого вида, нам нужна большая общность. Кроме того, на этот раз мы будем работать не с интегральной формой уравнений, а с дифференциальной. Хотя итог одинаков, это прекрасный случай поупражняться в выкладках и убедиться в том, что не имеет значения, каким путем идти. Вы должны уметь действовать любым путем, потому что, наткнувшись на трудную задачу, вы часто обнаруживаете, что годится лишь один из многих способов расчета.
Можно было бы прямо рассмотреть решение волнового уравнения для какой-нибудь из электромагнитных величин. Вместо этого мы начнем прямо с начала, с уравнений Максвелла для пустого пространства, и вы убедитесь в их тесной связи с электромагнитными волнами. Так что мы отправляемся от уравнений (20.1), полагая, что в них токи и заряды равны нулю. Они обращаются в
(20.12)
Распишем первое уравнение покомпонентно:
(20.13)
Мы предположили, что по у и z поле не меняется, так что два последних члена равны нулю. Тогда, согласно (20.13),
(20.14)
Решением его является постоянное в пространстве Ех(компонента электрического поля в направлении х). Взглянув на уравнение IV в (20.12) и полагая, что В тоже не изменяется вдоль y и z, вы убедитесь, что Ехпостоянно и во времени. Таким полем может оказаться постоянное поле от какого-то заряженного конденсатора вдали от этого конденсатора. Нас сейчас не занимают такие неинтересные статические поля; мы интересуемся лишь динамически изменчивыми полями. А для динамических полей Ех=0.
Итак, мы пришли к важному результату о том, что при распространении плоских волн в произвольном направлении электрическое поле должно располагаться поперек направления своего распространения. Конечно, у него еще остается возможность каким-то сложным образом изменяться по координате х.
Поперечное поле Е можно всегда разбить на две компоненты, скажем на у и z. Так что сначала разберем случай наличия у электрического ноля только одной поперечной компоненты. Для начала возьмем электрическое поле, направленное по у, т. е. с нулевой z-компонентой. Ясно, что, решив эту задачу, мы всегда сможем разобрать и тот случай, когда электрическое поле всюду направлено по z. Общее решение можно всегда представить в виде суперпозиции двух таких полей.
Какими простыми стали теперь наши уравнения! Теперь единственная ненулевая компонента электрического поля — это Еу, и все производные (кроме производных по х) тоже равны нулю. Остатки уравнений Максвелла выглядят чрезвычайно просто.
Рассмотрим теперь второе из уравнений Максвелла [т. е. II из (20.12)]. Расписав компоненты rot E, получаем
здесь x-компонента СXE равна нулю, потому что равны нулю производные по у и z; y-компонента тоже равна нулю: первый член потому, что все производные по z равны нулю, а второй потому, что Ez=0. Единственная не равная нулю компонента rot E — это z-компонента, она равна дЕу/дх. Полагая, что три компоненты СXE равны соответствующим компонентам —dB/dt, мы заключаем, что
(20.15)
(20.16)
Поскольку временные производные как x-компоненты магнитного поля, так и
y-компоненты магнитного поля равны нулю, то обе эти компоненты суть попросту постоянные поля и отвечают найденным раньше магнитостатическим решениям. Ведь кто-то мог оставить постоянный магнит возле того места, где распространяются волны. Мы будем игнорировать эти постоянные поля и положим Вхи Вyравными нулю.
Кстати, о равенстве нулю x-компонент поля В мы должны были бы заключить и по другой причине. Поскольку дивергенция В равна нулю (по третьему уравнению Максвелла), то мы, прибегая при рассмотрении электрического поля к тем же доводам, что и выше, должны были бы прийти к выводу, что продольная компонента магнитного поля не может изменяться вдоль х. А раз мы такими однородными полями в наших волновых решениях пренебрегаем, то нам следовало бы положить Вхравным нулю. В плоских электромагнитных волнах поле В, равно как и поле Е, должно быть направлено поперек направления распространения самих волн.
Равенство (20.16) дает нам добавочное утверждение о том, что если электрическое поле имеет только y-компоненту, то магнитное поле имеет только z-компоненту. Значит, Е и В перпендикулярны друг другу. Именно это и наблюдалось в той волне особого типа, которую мы уже рассмотрели.
Теперь мы готовы использовать последнее из уравнений Максвелла для пустого пространства [т. е. IV из (20.12)1. Расписывая покомпонентно, имеем
(20.17)
Из шести производных от компонент В только dBz/dx не равна нулю. Так что три уравнения просто дают
(20.18)
Итог всей нашей деятельности состоит в том, что отличны от нуля только по одной компоненте электрического и магнитного полей и эти компоненты обязаны удовлетворять уравнениям (20.16) и (20.18). Эти два уравнения можно объединить в одно, если первое из них продифференцировать по х, а второе— по t; тогда левые стороны уравнений совпадут (с точностью до множителя с2). И мы обнаруживаем, что Е подчиняется уравнению
(20.19)
Мы уже встречали это дифференциальное уравнение, когда изучали распространение звука. Это волновое уравнение для одномерных волн.
Заметьте, что в процессе вывода мы получили больше, чем содержится в (20.11). Уравнения Максвелла дали нам информацию и о том, что у электромагнитных волн есть только компоненты поля, расположенные под прямым углом к направлению распространения волн.
Вспомним все, что нам известно о решениях одномерного волнового уравнения. Если какая-то величина ш удовлетворяет одномерному волновому уравнению
(20.20)
то одним из возможных решений является функция ш (x, t),
имеющая вид
(20.21)
т. е. функция одной-единственной переменной (x-ct). Функция i(x-ct) представляет собой «жесткое» образование вдоль оси х, которое движется по направлению к положительным х со скоростью с (фиг. 20.4). Так, если максимум функции f приходится на нулевое значение аргумента, то при t=0 максимум ш оказывается при x=0. В более поздний момент, скажем при t=10, максимум ш окажется в точке х=10 с. Когда время движется, максимум тоже движется в сторону возрастания х со скоростью с. Порой удобнее считать, что решение одномерного волнового уравнения является функцией от (t-х/с). Однако в сущности это одно и то же, потому что любая функция от (t-х/с)— это
также функция от (x-ct):
Покажем, что f(x-ct) действительно есть решение волнового уравнения. Поскольку f зависит лишь от одной переменной — переменной (x-ct), то мы будем через f' обозначать производную f по этой переменной, а через f"— вторую производную.
Фиг. 20.4. Функция f(x-ct) представляет неизменный «контур», движущийся в направлении возрастания х со скоростью с.
Дифференцируя (20.21) по х, получаем
потому что производная от (x-ct) no x равна единице. Вторая производная ш no x равна
(20.22)
А производные ш no t дают
(20.23)
Мы убеждаемся, что ш действительно удовлетворяет одномерному волновому уравнению.
Вы недоумеваете: «Откуда же вы взяли, что решением волнового уравнения является f(x-ct)? Мне эта проверка задним числом совсем не нравится. Нет ли прямого пути отыскать решение?» Хорошо, вот вам прямой путь: знать решение. Можно, конечно, «испечь» по всей науке прямые математические аргументы, тем более, что мы знаем, каким должно быть решение, но с таким простым, как у нас, уравнением игра не стоит свеч. Со временем вы сами дойдете до того, что, как только; увидите уравнение (20.20), тут же будете представлять себе f(x-ct)=шв качестве решения. (Подобно тому, как сейчас при виде интеграла от x2dx у вас сразу всплывает ответ x3/3.)
На самом деле вы должны представлять себе немножко больше. Решением является не только любая функция от (x-ct), но и функция от (х+сt). Из-за того, что в волновом уравнении с встречается только в виде с2, изменение знака с ничего не меняет. И действительно, самое общее решение одномерного волнового уравнения — это сумма двух произвольных функций, одной от аргумента (x-ct), а другой от (x+ct):
(20.24)
Первое слагаемое дает волну, движущуюся по направлению к положительным х, второе — произвольную волну, бегущую к отрицательным х. Общее решение получается наложением двух таких волн, существующих одновременно.
● ● ●
Следующий забавный вопрос решите сами. Возьмем функцию ш в виде
ш=coskxcoskct.
Эта функция не имеет вида f(x-ct) или g(x+ct). Но прямой подстановкой в (20.20) легко убедиться, что она удовлетворяет волновому уравнению. Но как же мы тогда смеем говорить, что общее решение имеет вид (20.24)?
● ● ●
Применяя эти выводы о решении волнового уравнения к y-компоненте электрического поля Еу, мы заключаем, что Е может меняться по х произвольным образом. Всякое поле, которое существует в самом деле, можно всегда рассматривать как сумму двух картин. Одна волна плывет через пространство в каком-то направлении со скоростью с, причем связанное с нею магнитное поле перпендикулярно к электрическому; другая волна бежит в противоположном направлении с той же скоростью. Такие волны отвечают хорошо нам известным электромагнитным волнам — свету, радиоволнам, инфракрасному излучению, ультрафиолету, рентгеновским лучам и т. д. Мы уже изучали очень подробно излучение света. Так как все, чему мы тогда научились, применимо к любым электромагнитным волнам, то теперь нет нужды рассматривать подробно поведение этих волн.
Пожалуй, стоит лишь сделать несколько замечаний о поляризации электромагнитных волн. Раньше мы решили рассмотреть частный случай электрического поля с одной только y-компонентой. Имеется, конечно, и другое решение для волн, бегущих в направлении +х или -х, т. е. решение, при котором электрическое поле обладает одной лишь z-компонентой. Так как уравнения Максвелла линейны, общее решение для одномерных волн, распространяющихся в направлении х, есть сумма волн Еyи волн Еz. Общее
решение суммируется следующими формулами:
(20.25)
У подобных электромагнитных волн направление вектора Е не неизменно: оно как-то произвольно смещается по спирали в плоскости yz. Но в каждой точке магнитное поле всегда перпендикулярно к электрическому и к направлению распространения.
Если присутствуют только волны, бегущие в одном направлении (скажем, в положительном направлении х), то имеется простое правило, говорящее об относительной ориентации электрического и магнитного полей. Правило состоит в том, что векторное произведение ЕXВ (которое, как известно, является вектором, поперечным и к Е, и к В) указывает направление, куда бежит волна. Если Е совмещать с В правым поворотом, то вектор поворота показывает направление вектора скорости волны. (Позже мы увидим, что вектор ЕXВ имеет особый физический смысл: это вектор, описывающий течение энергии в электромагнитном поле.)
§ 2. Трехмерные волны
А теперь обратимся к трехмерным волнам. Мы уже знаем, что вектор Е удовлетворяет волновому уравнению. К тому же выводу легко прийти, отправляясь прямо от уравнений Максвелла. Предположим, что мы исходим из уравнения
и берем ротор от обеих частей:
(20.26)
Вы помните, что ротор от ротора любого вектора может быть записан в виде суммы двух членов, один из которых содержит дивергенцию, а другой — лапласиан:
Но в пустом пространстве дивергенция Е равна нулю, так что остается только член с лапласианом. Далее, из четвертого уравнения Максвелла в пустом пространстве [см. (20.12)] производная по времени от C2(СXB) равна второй производной Е по t:
Тогда (20.26) обращается в
Это и есть трехмерное волновое уравнение. Расписанное во всей красе, оно выглядит так:
Как же нам найти общее решение этого уравнения? Ответ таков: все решения трехмерного волнового уравнения могут быть представлены в виде суперпозиции уже найденных нами одномерных решений. Мы получили уравнение для волн, бегущих в направлении х, предположив, что поле не зависит от у и z. Конечно, имеются и другие решения, в которых поля не зависят от x и z,— это волны, идущие в направлении у. Затем существуют решения, не зависящие от х и y; они представляют волны, движущиеся в направлении z. Или в общем случае, поскольку мы записали наши уравнения в векторной форме, трехмерное волновое уравнение может иметь решения, которые являются плоскими волнами, бегущими, вообще говоря, в любом направлении. Кроме того, раз уравнения линейны, то одновременно может распространяться сколько угодно плоских волн, бегущих в каких угодно направлениях. Таким образом, самое общее решение трехмерного волнового уравнения является суперпозицией всех видов плоских волн, бегущих во всех возможных направлениях.
Попытайтесь представить себе, как выглядят сейчас электрические и магнитные поля в нашей аудитории. Прежде всего здесь имеется постоянное магнитное поле; оно возникло от токов внутри нашей Земли, от постоянного земного магнетизма. Затем здесь имеются какие-то нерегулярные, почти статические электрические поля. Они скорей всего созданы электрическими зарядами, появляющимися из-за того, что кто-то ерзает на своем стуле или трется рукавами о стол (словом, в результате трения). Кроме того, здесь есть еще и другие магнитные поля, вызванные переменными токами в электропроводке,— поля, которые меняются с частотой в 50 гц в такт с работой генератора на городской электростанции. Но еще больший интерес представляют электрические и магнитные поля, меняющиеся быстрее. К примеру, там, где свет падает из окна, освещая стены и пол, имеются небольшие колебания электрического и магнитного полей, перемещающиеся за секунду на 300 000 км. По комнате еще распространяются инфракрасные волны, идущие от ваших горячих голов к холодной доске с формулами. Да! Мы еще позабыли об ультрафиолетовом свете, о рентгеновских лучах и о радиоволнах, которые проносятся по комнате.
Через комнату скользят электромагнитные волны, которые несут в себе джазовую музыку. Проносятся и волны, модулированные серией импульсов, представляющих картины событий, которые происходят сейчас в других местах света, или картины воображаемых явлений, происходящих при растворении воображаемого аспирина в воображаемых желудках. Чтобы убедиться в реальности этих волн, достаточно просто включить электронную аппаратуру, которая превращает эти волны в изображения и звуки.
Если мы займемся дальнейшим анализом еще более слабых колебаний, то заметим мельчайшие электромагнитные волны, пришедшие в нашу комнату с огромных расстояний. В ней существуют мельчайшие колебания электрического поля, гребни которых отстоят друг от друга примерно на фут, а источник их удален отсюда на миллионы миль. Эти волны передаются на Землю с межпланетной станции Маринер II, которая как раз проходит сейчас где-то мимо Венеры. Ее сигналы несут сводку всей той информации, которую ей удалось ухватить у планеты (информации, полученной от электромагнитных волн, дошедших от Венеры к станции).
И есть здесь еще едва заметные колебания электрических и магнитных полей от волн, возникших в миллиардах световых лет отсюда, в галактиках, находящихся в удаленнейших уголках Вселенной. В том, что это действительно так, убедились, «заполнив комнату проволокой», т. е. соорудив антенны величиной с эту комнату. Так были замечены радиоволны, дошедшие до нас из мест, находящихся за пределами досягаемости крупнейших оптических телескопов. Кстати, даже эти оптические телескопы всего лишь простые собиратели электромагнитных волн. А то, что мы называем звездами, лишь заключения — заключения, выведенные из единственной физической реальности, которую мы до сих пор от них получали, из тщательного изучения бесконечно сложных волновых движений электрических и магнитных полей, достигающих Земли.
В аудитории имеются, конечно, еще другие разные поля — от молний, вспыхивающих где-то вдалеке отсюда, от заряженных частиц в космических лучах в тот момент, когда они проносятся сквозь комнату, и еще поля и еще... Представляете, какая сложная штука все эти электрические поля в пространстве вокруг нас! И все они подчиняются трехмерному волновому уравнению.
§ 3. Научное воображение
Я просил вас представить себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку.
Чтобы получить представление об электромагнитном поле, требуется более высокая степень воображения. Почему? Да потому что для того, чтобы невидимые ангелы стали доступны пониманию, мне нужно только чуть-чуть изменить их свойства — я делаю их слегка видимыми, и тогда я уже могу увидеть и форму их крыльев, и их тела, и их нимбы. Как только мне удалось представить себе видимого ангела, то необходимая для дальнейшего абстракция (состоящая в том, чтобы почти невидимых ангелов представить себе совершенно невидимыми) оказывается сравнительно легким делом.
Вы можете тоже сказать: «Профессор, дайте мне, пожалуйста, приближенное описание электромагнитных волн, пусть даже слегка неточное, но такое, чтобы я смог увидеть их так, как я могу увидеть почти невидимых ангелов. И я видоизменю эту картину до нужной абстракции».
Увы, я не могу этого сделать для вас. Я просто не знаю как. У меня нет картины этого электромагнитного поля, которая была бы хоть в какой-то степени точной. Я узнал об электромагнитном поле давным-давно, 25 лет тому назад, когда я был на вашем месте, и у меня на 25 лет больше опыта размышлений об этих колеблющихся волнах. Когда я начинаю описывать магнитное поле, движущееся через пространство, то говорю о полях Е и В, делаю руками волнистые движения и вы можете подумать, что я способен их видеть. А на самом деле, что я при этом вижу? Вижу какие-то смутные, туманные, волнистые линии, на них там и сям надписано Е и В, а у других линий имеются словно какие-то стрелки, то здесь, то там на них есть стрелки, которые исчезают, едва в них вглядишься. Когда я рассказываю о полях, проносящихся сквозь пространство, в моей голове катастрофически перепутываются символы, нужные для описания объектов, и сами объекты. Я не в состоянии дать картину, хотя бы приблизительно похожую на настоящие волны. Так что, если вы сталкиваетесь с такими же затруднениями при попытках представить поле, не терзайтесь, дело обычное.
Наша наука предъявляет воображению немыслимые требования. Степень воображения, которая теперь требуется в науке, несравненно превосходит то, что требовалось для некоторых прежних идей. Нынешние идеи намного труднее вообразить себе. Правда, мы используем для этого множество средств. В ход пускаются математические уравнения и правила, рисуются различные картинки. Вот сейчас я ясно осознаю, что всегда, когда я завожу речь об электромагнитном поле в пространстве, фактически перед моим взором встает своего рода суперпозиция всех тех диаграмм на эту тему, которые я когда-либо видывал. Я не воображаю себе маленьких пучков линий поля, снующих туда и сюда; они не нравятся мне потому, что если бы я двигался с иной скоростью, то они бы исчезли. Я не всегда вижу и электрические, и магнитные поля, потому что временами мне кажется, что гораздо правильнее была бы картина, включающая векторный и скалярный потенциалы, ибо последние, пожалуй, имеют больший физический смысл, чем колебания полей.
Быть может, вы считаете, что остается единственная надежда на математическую точку зрения. Но что такое математическая точка зрения? С математической точки зрения в каждом месте пространства существует вектор электрического поля и вектор магнитного поля, т. е. с каждой точкой связаны шесть чисел. Способны ли вы вообразить шесть чисел, связанных с каждой точкой пространства? Это слишком трудно. А можете вы вообразить хотя бы одно число, связанное с каждой точкой пространства? Я лично не могу! Я способен себе представить такую вещь, как температура в каждой точке пространства. Но это, по-видимому, вообще вещь представимая: имеется теплота и холод, меняющиеся от места к месту. Но, честное слово, я не способен представить себе число в каждой точке.
Может быть, поэтому стоит поставить вопрос так: нельзя ли представить электрическое поле в виде чего-то сходного с температурой, скажем, похожего на смещения куска студня? Сначала вообразим себе, что мир наполнен тонкой студенистой массой, а поля представляют собой какие-то искривления (скажем, растяжения или повороты) этой массы. Вот тогда можно было бы себе мысленно вообразить поле. А после того, как мы «увидели», на что оно похоже, мы можем отвлечься от студня. Именно это многие и пытались делать довольно долгое время. Максвелл, Ампер, Фарадей и другие пробовали таким способом понять электромагнетизм. (Порой они называли абстрактный студень «эфиром».) Но оказалось, что попытки вообразить электромагнитное поле подобным образом на самом деле препятствуют прогрессу. К сожалению, наши способности к абстракциям, к применению приборов для обнаружения поля, к использованию математических символов для его описания и т. д. ограниченны. Однако поля в известном смысле — вещь вполне реальная, ибо, закончив возню с математическими уравнениями (все равно, с иллюстрациями или без, с чертежами или без них, пытаясь представить поле въяве или не делая таких попыток), мы все же можем создать приборы, которые поймают сигналы с космической ракеты или обнаружат в миллиарде световых лет от нас галактику, и тому подобное.
Вопрос о воображении в науке наталкивается зачастую на непонимание у людей других специальностей. Они принимаются испытывать наше воображение следующим способом. Они говорят: «Вот перед вами изображены несколько людей в некоторой ситуации. Как вы представляете, что с ними сейчас случится?» Если вы ответите: «Не могу себе представить», они могут счесть вас за человека со слабым воображением. Они проглядят при этом тот факт, что все, что допускается воображать в науке, должно согласовываться со всем прочим, что нам известно: что электрические поля и волны, о которых мы говорим, это не просто удачные мысли, которые мы вызываем в себе, если нам этого хочется, а идеи, которые обязаны согласовываться со всеми известными законами физики. Недопустимо всерьез воображать себе то, что очевидным образом противоречит известным законам природы. Так что наш род воображения — весьма трудная игра. Надо иметь достаточно воображения, чтобы думать о чем-то никогда прежде не виденном, никогда прежде не слышанном. В то же время приходится, так сказать, надевать на мысли смирительную рубашку, ограничивать их условиями, вытекающими из наших знаний о том, какому пути на самом деле следует природа. Проблема создания чего-то, что является совершенно новым и в то же время согласуется со всем, что мы видели раньше,— проблема чрезвычайно трудная.
Но раз уж зашла об этом речь, я хочу остановиться на том, в состоянии ли мы себе представить красоту, которую мы не можем видеть. Это интересный вопрос. Когда мы глядим на радугу, она нам кажется прекрасной. Каждый, увидав ее, воскликнет: «О радуга!». (Смотрите, как научно я подхожу к вопросу. Я остерегаюсь именовать что-то восхитительным, пока нет экспериментального способа определить это.) Ну, а как мы описывали бы радугу, если бы были слепыми? А ведь мы слепы, когда измеряем коэффициент отражения инфракрасных лучей от хлористого натрия или когда говорим о частоте волн, пришедших от некоторой невидимой глазу галактики. Тогда мы чертим график, рисуем диаграмму. К примеру, для радуги подобным графиком была бы зависимость интенсивности излучения от длины волны, измеренная спектрофотометром под всевозможными углами к горизонту. Вообще говоря, подобные измерения должны были бы приводить к довольно пологим кривым. И вот в один прекрасный день кто-то обнаружил бы, что при какой-то определенной погоде, под некоторыми углами к горизонту спектр интенсивности как функция длины волны начал себя вести странно — у него появился пик. Если бы угол наклона прибора чуть-чуть изменился, максимум пика перешел бы от одной длины волны к другой. И вот через некоторое время в физическом журнале для слепых появилась бы техническая статья под названием «Интенсивность излучения как функция угла при некоторых метеоусловиях». В этой статье был бы график типа, показанного на фиг. 20.5. «Автор заметил,— говорилось бы, быть может, в статье,— что под большими углами основная часть радиации приходится на длинные волны, а под меньшими максимум излучения смещается к коротким волнам». (Ну, а мы бы сказали, что под углом 40° свет преимущественно зеленый, а под углом 42° — красный.)
Но находите ли вы график, приведенный на фиг. 20.5, восхитительным? В нем ведь содержится существенно больше различных деталей, чем мы в состоянии постичь, когда видим радугу: наши глаза не могут схватить доподлинную форму спектра. А вот глазам радуга все же кажется восхитительной. Хватает ли у вас воображения, чтобы в спектральных кривых увидеть всю ту красоту, которую мы видим, смотря на радугу? У меня — нет.
Фиг. 20.5. Зависимость интенсивности электромагнитных волн от длины волны под тремя углами (отсчитываемыми от направления, противоположного направлению на Солнце).
Доступно наблюдению лишь в определенных метеорологических условиях.
Но представим себе, что у меня имеется график зависимости коэффициента отражения кристаллов хлористого натрия от длины волны в инфракрасном участке спектра и от угла. Я могу вообразить себе, как это представилось бы моим глазам, обладай они способностью видеть в инфракрасном свете. Должно быть, это был бы какой-то яркий, насыщенный «зеленый цвет», на который накладывались бы отражения от поверхностей «металлически-красных» тонов. Это выглядело бы поистине великолепно, но я не знаю, способен ли я, взглянув на график коэффициента отражения NaCl, снятый на каком-то приборе, сказать, что он столь же прелестен.
Но, с другой стороны, хоть мы и не можем видеть красоту тех или иных частных измерений, мы можем утверждать, что постигаем своеобразную красоту уравнений, описывающих всеобщие физические законы. Например, в волновом уравнении (20.9) очень красива та правильность, с какой в нем расположены х, у, z и t. И эта приятная симметрия появления х, у, z, t намекает на ту величественную красоту, которая таится в четырех равнозначных координатах, в возможности того, что у пространства есть четырехмерная симметрия, в возможности проанализировать ее и развить специальную теорию относительности. Так что существует еще интеллектуальная красота, ассоциируемая с уравнениями.
§ 4. Сферические волны
Мы видели, что существуют решения волнового уравнения, отвечающие плоским волнам, и что любая электромагнитная волна может быть описана как суперпозиция многих плоских волн. В определенных случаях, однако, удобнее описывать волновое поле в другой математической форме. Я хотел бы сейчас разобрать теорию сферических волн — волн, которые соответствуют сферическим поверхностям, расходящимся из некоторого центра. Когда вы бросаете камень в пруд, то по водной глади побежит рябь в виде круговых волн — это двумерные волны. Сферические волны похожи на них, только распространяются они во всех трех измерениях.
Прежде чем начать описание сферических волн, немного займемся математикой. Пусть имеется функция, зависящая только от радиального расстояния r точки от начала координат, иными словами, сферически симметричная функция. Обозначим ее ш(r), где под r подразумевается
т. е. расстояние от начала координат. Чтобы узнать, какие функции ш (r) удовлетворяют волновому уравнению, нам понадобится выражение для лапласиана ш. Значит, нам нужно найти сумму вторых производных ш по х, по у и по z. Через ш'(r) мы обозначим первую производную i|) по r, а через ш"(r) — вторую. Сначала найдем производные по х. Первая производная равна
Вторая производная по х равна
Частные производные r по x можно получить из
так что вторая производная ш no x принимает вид
(20.28)
Точно так же и
(20.29)
(20.30)
Лапласиан равен сумме этих трех производных. Вспоминая,
что x2+y2+z2=r2, получаем
(20.31)
Часто бывает удобнее записывать уравнение в следующей
форме:
(20.32)
Проделав дифференцирование, указанное в (20.32), вы убедитесь, что правая часть здесь та же, что и в (20.31).
Если мы хотим рассматривать сферически симметричные поля, которые могут распространяться как сферические волны, то величины, описывающие поля, должны быть функцией как r, так и t. Предположим, что нам нужно знать, какие функции ш(r, t) являются решениями трехмерного волнового уравнения
(20.33)
Поскольку ш(г, t) зависит от пространственных координат только через г, то в качестве лапласиана можно использовать выражение (20.32). Но для точности, поскольку ш зависит также и от t, нужно дифференцирование по r записывать в виде частной производной. Волновое уравнение обращается в
Его и предстоит нам решать. Оно выглядит сложнее, чем в случае плоских волн. Но заметьте, что если умножить это уравнение на r, то получится
(20.34)
Это уравнение говорит нам, что функция r ш удовлетворяет одномерному волновому уравнению по переменной r. Используя часто подчеркивавшийся нами общий принцип, что у одних и тех же уравнений и решения одни и те же, мы приходим к выводу, что если r ш окажется функцией одного только (r-ct), то оно явится решением уравнения (20.34). Итак, мы обнаруживаем, что сферические волны обязаны иметь вид
Или, как мы видели раньше, можно в равной степени считать r ш имеющим форму
Деля на r, находим, что характеризующая поле величина ш (чем бы она ни была) имеет вид
(20.35)
Такая функция представляет сферическую волну общего вида, распространяющуюся от начала координат со скоростью с. Если на минуту забыть об r в знаменателе, то амплитуда волны как функция расстояния от начала координат в каждый данный момент обладает определенной формой, которая распространяется со скоростью с. Однако r в знаменателе говорит нам, что по мере того, как волна распространяется, ее амплитуда убывает пропорционально 1/r. Иными словами, в отличие от плоской волны, амплитуда которой остается при движении все время одной и той же, амплитуда сферической волны беспрерывно спадает (фиг. 20.6).
Фиг. 20.6. Сферическая волна ш=f(t-r/с)/r.
а — зависимость ш от r при t=tl и ma же волна в более поздний момент времени t2; б — зависимость ш от t при r=r1 и та же самая волна на расстоянии r2.
Этот факт легко понять из простых физических соображений.
Мы знаем, что плотность энергии в волне зависит от квадрата амплитуды волны. По мере того как волна разбегается, ее энергия расплывается на все большую и большую площадь, пропорциональную квадрату радиуса волны. Если полная энергия сохраняется, плотность энергии должна убывать как 1/r2, а амплитуда — как 1/r. Поэтому формула (20.35) для сферической волны вполне «разумна».
Мы игнорировали другое возможное решение одномерного волнового уравнения
или
Это тоже сферическая волна, но бегущая внутрь, от больших r к началу координат.
Тем самым мы делаем некоторое специальное предположение. Мы утверждаем (без какого-либо доказательства), что волны, создаваемые источником, всегда бегут только от него. Поскольку мы знаем, что волны вызываются движением зарядов, мы настраиваемся на то, что волны бегут от зарядов. Было бы довольно странно представлять, что прежде чем заряды были приведены в движение, сферическая волна уже вышла из бесконечности и прибыла к зарядам как раз в тот момент, когда они начали шевелиться. Такое решение возможно, но опыт показывает, что, когда заряды ускоряются, волны распространяются от зарядов, а не к ним. Хоть уравнения Максвелла предоставляют обеим волнам равные возможности, мы привлекаем добавочный факт, основанный на опыте, что «физическим смыслом» обладает только расходящаяся волна.
Нужно, однако, заметить, что из этого добавочного предположения вытекает интересное следствие: мы теряем при этом симметрию относительно времени, которая есть у уравнений Максвелла. Как исходные уравнения для Е и В, так и вытекающие из них волновые уравнения при изменении знака t не меняются. Эти уравнения утверждают, что любому решению, которое отвечает волне, бегущей в одну сторону, отвечает столь же правильное решение для волны, бегущей в обратную сторону. И утверждая, что мы намерены брать в расчет только расходящиеся сферические волны, мы делаем тем самым важное дополнительное предположение. (Очень тщательно изучалась такая электродинамика, в которой обходятся без этого дополнительного предположения. Как это ни удивительно, но во многих обстоятельствах она не приводит к физически абсурдным результатам. Однако обсуждение этих идей теперь увлекло бы нас чересчур в сторону. Мы поговорим об этом подробнее в гл. 28.)
Нужно упомянуть еще об одном важном факте. В нашем решении для расходящейся волны (20.35) функция ш в начале координат бесконечна. Это как-то необычно. Мы бы предпочли иметь такие волновые решения, которые гладки повсюду. Наше решение физически относится к такой ситуации, когда в начале координат располагается источник. Значит, мы нечаянно сделали одну ошибку: наша формула (20.35) не является решением свободного волнового уравнения (20.33) повсюду; уравнение (20.33) с нулем в правой части решено повсюду, кроме начала координат. Ошибка вкралась оттого, что некоторые действия при выводе уравнения при r=0 «незаконны».
Покажем, что ту же самую ошибку легко сделать и в электростатике. Допустим, что нам нужно решить уравнение электростатического потенциала в пустом пространстве С2j=0. Лапласиан равен нулю, потому что мы предположили, что никаких зарядов нигде нет. Но как обстоит дело со сферически симметричным решением уравнения, т. е. с функцией j, зависящей только от r? Используя для лапласиана формулу (20.32), получаем
Умножив это выражение на r, приходим к уже интегрировавшемуся уравнению
Проинтегрировав один раз по r, мы увидим, что первая производная rj равна постоянной, которую мы обозначим через а;
Еще раз проинтегрировав, мы получим для rj формулу
где b — другая постоянная интегрирования. Итак, мы обнаружили, что решение для электростатического потенциала в пустом пространстве имеет вид
Что-то здесь явно не так. Мы же знаем решение для электростатического потенциала в области, где нет электрических зарядов: потенциал всюду постоянен. Это соответствует первому слагаемому в решении. Но имеется еще и второй член, подсказывающий нам, что в потенциал дает вклад нечто, меняющееся как 1/r. Мы знаем, однако, что подобный потенциал соответствует точечному заряду в начале координат. Стало быть, хоть мы и думали, что нашли решение для потенциала в пустом пространстве, наше решение фактически дает нам также поле точечного источника в начале координат. Вы замечаете сходство между тем, что сейчас произошло, и тем, что произошло тогда, когда мы искали сферически симметричное решение волнового уравнения? Если бы в начале координат действительно не было ни зарядов, ни токов, то не возникли бы и сферически расходящиеся волны. Сферические волны должны вызываться источниками в начале координат. В следующей главе мы исследуем связь между излучаемыми электромагнитными волнами и вызывающими их токами и напряжениями.
Глава 21 РЕШЕНИЯ УРАВНЕНИЙ МАКСВЕЛЛА С ТОКАМИ И ЗАРЯДАМИ
§ 1. Свет и электромагнитные волны
§ 2. Сферические волны от точечного источника
§ 3. Общее решение уравнений Максвелла
§ 4. Поля колеблющегося диполя
§ 5. Потенциалы движущегося заряда; общее решение Льенара и Вихерта
§ 6. Потенциалы заряда, движущегося с постоянной скоростью;
формула Лоренца
Повторить: гл. 28 (вып. 3) «Электромагнитное излучение»; гл. 31 (вып. 3)
«Как возникает показатель преломления»; гл. 34 (вып. 3)
«Релятивистские явления в излучении»
§ 1. Свет и электромагнитные волны
В предыдущей главе мы видели, что среди решений уравнений Максвелла есть электромагнитные волны. Свету, радио, рентгеновским лучам и т. д. отвечают электромагнитные волны отличающиеся только длиной волны. Мы уже подробно изучали различные явления, связанные со светом. В этой главе мы хотим связать оба вопроса и показать, что уравнения Максвелла действительно могли служить основой для изучения свойств света.
Наше изучение света мы начали с того, что выписали уравнение для электрического поля, создаваемого зарядом, который мог как-то произвольно двигаться. Уравнение имело вид
[см. гл. 28 (вып. 3), выражение (28.3)].
Если заряд движется произвольным образом, то электрическое поле, которое существует в некоторой точке, в настоящий момент зависит только от положения и движения заряда в более ранний момент времени, отстающий на интервал, необходимый для того, чтобы свет, двигаясь со скоростью с, прошел расстояние r' от заряда до точки поля. Иными словами, если вам нужно знать электрическое поле в точке (1) в момент t, вы должны подсчитать положение (2') заряда и его движение в момент (t-r'1с} [где r' — расстояние до точки (1)] из положения заряда (2') в момент (t—r/с).
Фиг. 21.1. Поля в точке (1) в момент t зависят от того положения (2'), которое заряд q занимал в момент (t — r'/с).
Штрихи здесь напоминают вам, что r' — это так называемое «запаздывающее расстояние» от точки (2') к точке (1), а вовсе не теперешнее расстояние между точкой (2) — положением заряда в момент t — и точкой поля (1) (фиг. 21.1). Заметьте, что сейчас по-иному определяется направление единичного вектора еr. В гл. 28 и 34 (вып. 3) мы уславливались, что r (и, стало быть, еr) будет показывать на источник. Теперь же мы следуем определению, используемому в формулировке закона Кулона, по которому r направлено от заряда [в точке (2)] к точке (1) поля. Единственное отличие в том, что новое r (и еr) противоположно старому.
Мы видели также, что если скорость заряда v всегда много меньше с и если рассматриваются только точки, сильно удаленные от заряда, так что в (21.1) существенно лишь последнее слагаемое, то поля можно также записать в виде
и
Рассмотрим более детально, что дает полное уравнение (21.1). Вектор еr — это единичный вектор, направленный от «запаздывающей» точки (2') к точке (1). Тогда первое слагаемое дает то, чего следовало бы ожидать, если бы заряд в своем «запаздывающем» положении создавал кулоново поле,— это можно назвать «запаздывающим кулоновым полем». Электрическое поле обратно пропорционально квадрату расстояния и направлено от «запаздывающего» положения заряда (т. е. по вектору еr').
Но это только первое слагаемое. Остальные напоминают нам, что законы электричества не утверждают, что все поля, оставаясь, как и были, статическими, начинают просто запаздывать (а такое утверждение порой приходится слышать). К «запаздывающему кулонову полю» надо добавить два других слагаемых.
Второе говорит, что к запаздывающему кулонову полю надо сделать «поправку», равную быстроте изменения запаздывающего кулонова поля, умноженной на r'/с, т. е. на само запаздывание. Этот множитель как бы стремится скомпенсировать запаздывание в первом. Два первых слагаемых соответствуют вычислению «запаздывающего кулонова поля» и затем экстраполяции его в будущее, на время r'/с, т. е. как раз к моменту t! Экстраполяция линейна, как если бы мы предположили, что «запаздывающее кулоново поле» будет по-прежнему изменяться со скоростью, рассчитанной для заряда в точке (2'). Если поле меняется медленно, эффект запаздывания почти полностью сводится на нет поправочным слагаемым, и оба слагаемых вместе приводят к величине электрического поля, очень близкой к «мгновенному кулонову полю» заряда, находящегося в точке (2).
Наконец, в формуле (21.1) имеется еще третье слагаемое — вторая производная единичного вектора еr'. Изучая явление света, мы по существу использовали тот факт, что вдали от заряда два первых слагаемых убывают как обратный квадрат расстояния и на больших расстояниях оказываются слишком слабыми по сравнению с третьим, которое убывает как 1/r. Поэтому мы сосредоточили наше внимание на последнем слагаемом и показали, что оно (опять-таки на больших расстояниях) пропорционально компоненте ускорения заряда, поперечной к линии зрения. (Кроме того, почти всюду ранее мы рассматривали только случай, когда заряды двигались нерелятивистски. Релятивистские эффекты рассматривались только в гл. 34, вып. 3.)
Теперь нужно попробовать связать эти две вещи. У нас есть уравнения Максвелла и есть формула (21.1) для поля точечного заряда. Естественно спросить, эквивалентны ли они? Если мы сможем вывести (21.1) из уравнений Максвелла, то действительно поймем связь света с электромагнетизмом. Вывод ее и есть главная цель этой главы.
Выясняется, что полного вывода мы сделать не можем — чересчур сложные математические детали не позволят нам выйти с поля боя без потерь. Но все же мы подойдем к цели достаточно близко, так что вы легко поймете, как может быть установлена интересующая нас связь. Мы опустим лишь некоторые математические детали. Математика этой главы может показаться некоторым из вас довольно сложной, и, возможно, вам даже станет скучно следить внимательно за выводом. Но мы все же считаем, что очень важно связать то, что вы учили раньше, с тем, что вы изучаете сейчас, или по крайней мере продемонстрировать, как эта связь может быть установлена. Если вы не забыли прежние главы, то обратите внимание на то, что всякий раз, как мы принимали некоторое высказывание за исходную точку обсуждения, мы заботливо объясняли, является ли это высказывание новым «допущением», т. е. отражает ли оно основной закон природы или же его можно в конечном счете вывести из каких-то других законов. Дух этих лекций обязывает нас обсудить связь менаду светом и уравнениями Максвелла. Может быть, вам будет кое-где и трудно — с этим уж ничего не поделаешь: другого пути не существует.
§ 2. Сферические волны от точечного источника
В гл. 18 мы установили, что уравнения Максвелла можно решать подстановкой
(21.2)
и
(21.3)
где j и А обязаны удовлетворять уравнениям
(21.4)
и
(21.5)
и, кроме того, условию
(21.6)
Найдем теперь решение уравнений (21.4) и (21.5). Для этого надо уметь решать уравнение
(21.7)
где величина s (которая называется источником) известна. Ясно, что для уравнения (21.4) s соответствует r/e0, a ш—это j, а для уравнения (21.5) s соответствует jx/e0с2, если ш — это Ах, и т. д. Но нас интересует чисто математическая задача решения (21.7) безотносительно к тому, каков физический смысл ш и s. Там, где r и j равны нулю (это место называется «пустотой»), там потенциалы j и А и поля Е и В удовлетворяют трехмерному волновому уравнению без источников; математическая форма этого уравнения такова:
(21.8)
В гл. 20 мы видели, что решения этого уравнения могут представлять волны разных сортов: плоские волны, бегущие в x-направлении я|;=f(t-x/с); плоские волны, бегущие вдоль у или вдоль z или в любом другом направлении; сферические
(21.9)
(Решения можно записать иначе — например в виде цилиндрических волн, разбегающихся от оси.)
Мы тогда заметили, что физически формула (21.9) относится не совсем к пустоте: в начале координат должны быть какие-то заряды, иначе расходящаяся волна не получилась бы. Иными словами, формула (21.9) есть решение уравнения (21.8) всюду, кроме непосредственной окрестности точки r=0, где (21.9) представляет собой решение полного уравнения (21.7), в правой части которого стоят источники. Давайте теперь посмотрим, что это за уравнение, т. е. какого рода источник s в уравнении (21.7) должен вызвать волну типа (21.9).
Предположим, что имеется сферическая волна (21.9) и поглядим, во что она превращается при очень малых r. Тогда запаздыванием -r/с в f(t-r/с) можно пренебречь, и поскольку функция f плавная, ш превращается в
(21.10)
Итак, ш в точности похоже на кулоново поле заряда, расположенного в начале координат. Мы знаем, что для небольшого сгустка заряда, ограниченного очень малой областью близ начала координат и имеющего плотность r,
где Q=∫rdV. Такой потенциал j удовлетворяет уравнению
Следуя тем же расчетам, мы должны были бы сказать, что ш из выражения (21.10) удовлетворяет уравнению
(21.11)
где s связано с f формулой
при
Единственная разница в том, что в общем случае s, а, стало быть, и S может оказаться функцией времени.
Далее очень важно то, что если ш удовлетворяет (21.11) при малых r, то оно удовлетворяет также и (21.7). По мере приближения к началу координат зависимость шот r типа 1/r приводит к тому, что пространственные производные становятся очень большими. А производные по времени остаются теми же. [Это просто производные f(t) по времени.] Так что, когда r стремится к нулю, множителем d2ш/dt2в уравнении (21.7) по сравнению с С2ш можно пренебречь, и (21.7) становится эквивалентным уравнению (21.11).
Подытоживая, можно сказать, что если функция источника s(t) из уравнения (21.7) сосредоточена в начале координат и ее общая величина равна
(21.12)
то решение уравнения (21.7) имеет вид
(21.13)
Влияние слагаемого с d2ш/dt2в (21.7) сказывается лишь на появлении запаздывания (t-r/с) в потенциале кулонова типа.
§ 3. Общее peшeниe уравнений Максвелла
Мы нашли решение уравнения (21.7) для «точечного» источника. Теперь встает новый вопрос: Каков вид решения для рассредоточенного источника? Ну, это решить легко; всякий источник s(x, у, z, t) можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s(x, у, z, t)dV. Поскольку (21.7) линейно, суммарное поле представляет собой суперпозицию полей от всех таких элементов источника.
Используя результаты предыдущего параграфа [см. (21.13)], мы получим, что в момент t поле dm в точке (х1, y1, z1) [или, короче, в точке (1)], создаваемое элементом источника sdV в точке (х2> у2, z2) [или, короче, в точке (2)],выражается формулой
где r12 — расстояние от (2) до (1). Сложение вкладов от всех частей источника означает, конечно, интегрирование по всей области, где s№0, так что мы имеем
(21.14)
Иначе говоря, поле в точке (1) в момент времени t представляет собой сумму всех сферических волн, испускаемых в момент t-r12/c всеми элементами источника, расположенного в точке (2). Выражение (21.14) является решением нашего волнового уравнения для любой системы источников.
Теперь мы видим, как получать общее решение уравнений Максвелла. Если подразумевать под шскалярный потенциал j, то функция источника s превращается в r/e0. А можно считать, что ш представляет одну из трех компонент векторного потенциала А; тогда s означает соответствующую компоненту j/e0c2. Стало быть, если во всех точках известна плотность нарядов r(х, у, z, t) и плотность тока j(х, у, z, t), то решения уравнении (21.4) и (21.5) можно выписать немедленно:
(21.15)
(21.16)
Поля Е и В получатся дифференцированием потенциалов [используются выражения (21.2) и (21.3)]. Кстати, можно проверить явно, что j и А, полученные из (21.15) и (21.16), действительно удовлетворяют равенству (21.6).
Мы решили уравнения Максвелла. В любых обстоятельствах, если только заданы токи и заряды, из этих интегралов можно определить потенциалы, а затем, продифференцировав их, получить поля. Тем самым с теорией Максвелла покончено. И это позволяет нам также замкнуть круг и вернуться к нашей теории света, потому что достаточно только подсчитать электрическое поле движущегося заряда, чтобы связать все это с нашей прежней теорией света. Все, что нам остается сделать,— это взять движущийся заряд, вычислить из этих интегралов его потенциал и затем из -Сj-dA/dt, дифференцируя, найти Е. Мы должны получить формулу (21.1). Работы придется проделать много, но принцип ясен.
Итак, мы дошли до центра электромагнитной вселенной. У нас в руках полная теория электричества, магнетизма и света, полное описание полей, создаваемых движущимися зарядами, и многое, многое другое. Все сооружение, воздвигнутое Максвеллом, во всей его полноте, красе и мощи сейчас перед нами. Это, пожалуй, одно из величайших свершений физики. И чтобы напомнить о его важности, мы переписываем все формулы вместе и обводим их красивой рамкой.
§ 4. Поля колеблющегося диполя
Мы пока еще не провели обещанного вывода формулы (21.1) для электрического поля движущегося точечного заряда. Даже зная то, что мы уже знаем, этот вывод все равно проделать нелегко. Нам не удалось обнаружить формулы (21.1) нигде, ни в каких книжках и статьях (кроме первых выпусков этих лекций). Это свидетельствует о том, что вывод ее не прост. (Поля движущегося заряда записывались неоднократно и в других видах, которые все, конечно, эквивалентны.) Мы ограничимся поэтому здесь тем, что просто покажем на нескольких примерах, что (21.15) и (21.16) приводят к тем же результатам, что и (21.1). Первым делом мы покажем, что при том единственном условии, что движение заряженной частицы является нерелятивистским, (21.1) приводит к правильной величине полей. (Уже этот частный случай покрывает 90% всего того, что было сказано о явлении света.)
Рассмотрим такую ситуацию, когда имеется сгусток зарядов, каким-то образом перемещающийся в небольшой области; требуется найти создаваемые им где-то вдалеке от этого места поля.
Можно поставить вопрос и иначе: мы найдем поле на произвольном расстоянии от точечного заряда, который почти незаметно колеблется вверх и вниз. Поскольку свет обычно испускают такие нейтральные тела, как атомы, то мы будем считать, что наш колеблющийся заряд q расположен вблизи неподвижного, равного по величине, но противоположного по знаку заряда. Если расстояние между центрами зарядов равно d, то у зарядов появится дипольный момент p=qd, который мы будем считать функцией времени. Следует ожидать, что поблизости от зарядов запаздыванием поля можно будет пренебречь; электрическое поле будет в точности таким же, как и то, которое получалось раньше для электростатического диполя [но, конечно, с мгновенным дипольным моментом p(t)]. Однако при большом удалении в формуле для поля должно появиться добавочное слагаемое, которое меняется как 1/r и зависит от того, каково ускорение заряда в направлении, поперечном к лучу зрения. Посмотрим, получится ли у нас этот результат. Начнем с вычисления векторного потенциала А при помощи (2.16). Пусть плотность зарядов в сгустке есть r(х, у, z) и весь он движется все время со скоростью v. Тогда плотность тока j(x, у, z) равна vr(x,y, z). Удобно систему координат расположить так, чтобы ось z была направлена по v; тогда геометрия нашей задачи изобразится так, как показано на фиг. 21.2. Нас интересует интеграл
(21.17)
Если размеры заряда-сгустка на самом деле намного меньше, чем r12, то r12 в знаменателе можно положить равным r (расстоянию от центра сгустка) и вынести r за знак интеграла. Кроме того, мы собираемся положить и в числителе r12=r, хотя это и не совсем верно. А неверно это потому, что на самом деле, скажем, полагается брать j в верхней части сгустка совсем не в тот момент, когда в нижней, а немного в другое время.
Фиг. 21.2. Потенциалы в точке (1) даются интегралами от плотности заряда r.
Полагая r12=r в j(t-r12/с), мы вычисляем плотность тока для всего сгустка в одно и то же время (t-r/с). Это приближение годится лишь тогда, когда скорость v заряда много меньше с. Мы, стало быть, ведем расчет в нерелятивистском случае. После замены j на rv интеграл (21.17) превращается в
Раз скорость всех зарядов в сгустке одна и та же, этот интеграл просто равен v/r, умноженному на общий заряд q. Но qv — это как раз dp/dt (скорость изменения дипольного момента), только надо ее, конечно, определять в более раннее время (t-r/с). Запишем эту величину так: p(t-r/с). Итак, мы получаем для векторного потенциала
Мы узнали, что ток в меняющемся диполе создает векторный потенциал в форме сферических волн, источник которых обладает силой р’/4pe0с2.
Теперь из B=СXA можно получить магнитное поле. Поскольку р’ направлен по оси z, у А есть только z-компонента; в роторе остаются только две ненулевые производные. Значит, Вх=дАг/ду и В=—дАz/дх. Поглядим сперва на Вх:
(21.19)
Чтобы продифференцировать, вспомним, что r=Ц(x:2+y2+z2), так что
Но мы помним, что дr/ду=y/r; значит, первое слагаемое даст
(21.21)
что убывает как 1/r2, т. е. как поле статического диполя (потому что в данном направлении у/r постоянно).
Второе слагаемое в (21.20) приводит к новому эффекту. Если провести в нем дифференцирование, то получится
(21.22)
где р” — просто вторая производная р по t. Вот это-то получающееся от дифференцирования числителя слагаемое и ответственно за излучение. Во-первых, оно описывает поле, убывающее на расстоянии как i/r, во-вторых, зависит от ускорения заряда. Теперь вам должно быть ясно, как мы собираемся получить формулу типа (21.1'), описывающую световое излучение.
Явление это настолько интересно и важно, что стоит немного подробнее разобраться в том, откуда берется это «радиационное» слагаемое. Мы начинали с выражения (21.18), зависящего от r как 1/r и тем самым похожего на кулонов потенциал (если не обращать внимания на запаздывающий множитель в числителе). Почему же когда мы, желая получить поле, дифференцируем по пространственным координатам, то не получаем просто поля вида 1/r2 (конечно, с соответствующей временной задержкой)?
А вот почему. Представьте, что диполь приведен в колебательное движение вверх и вниз. Тогда
Если начертить график зависимости Аrот r в каждый данный момент, то получится кривая, показанная на фиг. 21.3. Амплитуда в пиках убывает как 1/r, но, кроме того, еще имеются пространственные колебания, которые ограничены огибающей вида 1/r. Пространственные производные в формуле пропорциональны наклону кривой. Из фиг. 21.3 видно, что встречаются намного более крутые наклоны, чем наклон самой кривой 1/г. Очевидно, что при данной частоте наклоны в пиках пропорциональны амплитуде волны, меняющейся как 1/r. Тем самым объясняется степень спадания радиационного слагаемого с расстоянием.
Все это получается оттого, что временные вариации в источнике превращаются в пространственные вариации, когда волны начинают разбегаться в стороны, магнитные же поля зависят от пространственных производных потенциала.
Фиг. 21.3. Зависимость величины А от r в момент t для сферической волны от колеблющегося диполя.
Теперь возвратимся назад и закончим наши расчеты магнитного поля. Для Вхмы получили (21.21) и (21.22). Поэтому
(21.1')
С помощью точно таких же выкладок мы придем к
И все это можно объединить в одну красивую векторную формулу:
(21.23)
А теперь взгляните на нее. Прежде всего на больших удалениях (когда r велико) следует принимать в расчет только р. Направление В дается вектором pXr, перпендикулярным и к радиусу r, и к ускорению (фиг. 21.4). Все сходится с тем, что получилось бы из формулы (21.1').
Теперь посмотрите (к этому мы не привыкли) на то, что происходит поблизости от заряда. В гл. 14, § 7 (вып. 5) мы вывели закон Био и Савара для магнитного поля элемента тока. Мы нашли, что элемент тока jdV привносит в магнитное поле следующий вклад:
(21.24)
Вы видите, что эта формула с виду очень похожа на первое слагаемое в (21.23), если только вспомнить, что р — это ток. Но разница все же есть. В (21.23) ток надо подсчитывать в момент (t-r/с), а в (21.24) этого нет. На самом деле, однако, (21.24) для малых r все еще годится, потому что второе слагаемое в (21.23) стремится уничтожить эффект запаздывания из первого слагаемого. Вместе оба они приводят при малых r к результату, очень близкому к (2124).
Фиг. 21.4. Поля излучения В и Е колеблющегося диполя.
В этом можно убедиться следующим образом. Когда r мало, (t-r/с) не очень отличается от t, и в (21.23) скобки можно разложить в ряд Тэйлора. Первый член разложения дает
n в том же порядке по r/с
Если их сложить, члены с р уничтожатся и слева останется незапаздывающий ток р, т. е. р(t) плюс члены порядка (r/с)2 и выше [например, 1/2(r/с)2Р"']. Эти члены при достаточно малых r (малых настолько, что за время r/с ток р заметно не меняется) будут очень малы.
Стало быть, (21.23) приводит к полям, очень похожим на те, которые дает теория с мгновенным действием, гораздо более похожим на них, чем на поля теории с мгновенным действием и с задержкой; эффекты задержки первого порядка компенсируются вторым членом. Статические формулы очень точны, намного более точны, чем вам могло бы показаться. Конечно, компенсация чувствуется только вблизи от заряда. Для далеких точек эти поправки уже ничего не спасают, потому что временное запаздывание приводит к очень большим эффектам и в конечном счете к важному члену 1/r — к эффекту излучения.
Перед нами все еще стоит задача расчета электрического поля и доказательства того, что оно совпадает с (21.1'). Правда, уже чувствуется, что на больших расстояниях ответ получится такой, как надо. Мы знаем, что вдали от источников, где возникает распространяющаяся волна, Е перпендикулярно к В (и к r), как на фиг. 21.4, и что с В=Е. Значит, Е пропорционально ускорению р", как и предсказывалось формулой (21.1').
Чтобы получить электрическое поле на всех возможных расстояниях, нужно найти электростатический потенциал. Когда мы подсчитывали интеграл токов для А, желая получить (21.18), то сделали приближение: мы пренебрегли малозаметным изменением r в члене с запаздыванием. Для электростатического потенциала этого делать нельзя, потому что тогда у нас получилось бы {/r, умноженное на интеграл от плотности заряда, т. е. на константу. Такое приближение чересчур грубо. Надо обратиться к высшим порядкам. И вместо того, чтобы путаться в этих прямых расчетах высших приближений, можно поступить иначе — определить скалярный потенциал из равенства (21.6), используя уже найденное значение векторного потенциала. Дивергенция А в этом случае просто равна dAJdz, поскольку Ахи Ayтождественно равны нулю. Дифференцируя точно так же, как это делалось выше при вычислении В, получаем
Или в векторных обозначениях
Из равенства (21.6) получается уравнение для j:
Интегрирование по t просто убирает надо всеми р по одной точке:
(Постоянная интегрирования отвечала бы некому наложенному статическому полю, которое, конечно, может существовать, но мы считаем, что у выбранного нами колеблющегося диполя статического поля нет.) Теперь мы можем из
найти электрическое поле Е. После утомительных (хоть и прямых) выкладок [при этом нужно помнить, что p(t-r/с) и его производные по времени зависят от х, у и z через запаздывание r/с] мы получаем
где
(21.27)
Это выглядит довольно сложно, но интерпретируется просто. Вектор р* — это дипольный момент с запаздыванием и с «поправкой» на запаздывание, так что два члена с р* в (21.26) при малых r дают просто статическое поле диполя [см. гл. 6 (вып. 5), выражение (6.14)]. Когда r велико, то член с р преобладает над остальными, и электрическое поле пропорционально ускорению зарядов в направлении поперек r и само направлено вдоль
проекции р на плоскость, перпендикулярную к r.
Этот результат согласуется с тем, что мы получили бы, применяя формулу (21.1'). Конечно, эта формула — более общая; она годится для любого движения, а не только для малозаметных движений, для которых запаздывание r/с в пределах всего источника можно считать постоянным [как (21.26)]. Во всяком случае, теперь мы укрепили столбами все наше прежнее изложение свойств света, за исключением лишь некоторых вопросов из гл. 34 (вып. 3), которые связаны с последней частью выражения (21.26). Мы можем теперь перейти к получению поля быстродвижущихся зарядов. Это приведет нас к релятивистским эффектам [гл. 34 (вып. 3)].
§5. Потенциалы движущегося заряда; общее решение Льенара и Вихерта
В предыдущем параграфе мы пошли на упрощение при вычислении интеграла для А, рассматривая только небольшие скорости. Но при этом мы шли таким путем, которым легко можно прийти и к новым выводам. Поэтому сейчас мы заново предпримем расчет потенциалов точечного заряда, движущегося уже, как ему захочется (даже с релятивистской скоростью). Как только мы получим этот результат, у нас в руках окажутся электромагнитные свойства электрических зарядов во всей их полноте. Даже формулу (21.1') можно будет тогда легко получить, взяв только нужные производные. И наш рассказ удастся, наконец, довести до конца. Итак, запаситесь терпением!
Попробуем подсчитать в точке (х1, у1, z1) скалярный потенциал j(1), создаваемый точечным зарядом (вроде электрона), движущимся любым, каким угодно образом. Под «точечным» зарядом подразумевается очень маленький заряженный шарик, такой маленький, как только можно себе представить, с плотностью заряда р(х, у, z). Потенциал j можно найти из (21.15):
(21.28)
На первый взгляд кажется (и почти все так и подумают), что ответ состоит в том, что интеграл от r по такому «точечному» заряду равен просто общему заряду q, т. е. что
Через r'12здесь обозначен радиус-вектор от заряда в точке (2) к точке (7), измеренный в более раннее время (t—r12/c). Эта формула ошибочна.
Фиг. 21.5. «Точечный» заряд (рассматриваемый как небольшое распределение зарядов в форме куба), движущийся со скоростью v к точке (1).
Правильный ответ такой:
(21.29)
где vr' — компонента скорости заряда, параллельная r12, т. е. направленная к точке (1). Сейчас я объясню, почему это так. Чтобы легче было следить за моими доводами, я сперва проведу расчет для «точечного» заряда в форме небольшого заряженного кубика, который движется к точке (1) со скоростью v(фиг. 21:5). Сторона куба будет а, это число пусть будет много меньше r12 [расстояния от центра заряда до точки (1)].
Чтобы оценить величину интеграла (21.28), мы вернемся к основному определению: запишем его в виде суммы
(21.30)
где ri — расстояние от точки (1) к i-му элементу объема DVi, а ri-— плотность заряда в DVi в момент ti=(t-ri/с). Поскольку все ri>>а, удобно будет выбрать все DVi в виде тонких прямоугольных ломтиков, перпендикулярных к r12 (фиг. 21.6).
Предположим, что мы начали с того, что взяли элементы объема DVi некоторой толщины w, много меньшей а.
Отдельные элементы объема будут выглядеть так, как показано на фиг. 21.7, а. Их нарисовано гораздо больше, чем нужно, чтобы закрыть весь заряд. А сам заряд не показан, и по весьма существенной причине. Где его нужно нарисовать? Ведь для каждого элемента объема DVi надо брать r в свой момент t~(t-r/с). Но раз заряд движется, то для каждого элемента объема DVi он окажется в другом месте!
Начнем, скажем, с элемента объема 1 на фиг. 21.7, а, выбранного так, чтобы в момент tl = (t-r1/с) «задняя» грань заряда пришлась на DVi (фиг, 21.7, б).
Фиг. 21.6, Элемент объема DVi, используемый для вычисления потенциалов.
Фиг. 21.7. Интегрирование r(t-r'/c)dV для движущегося заряда.
Тогда, вычисляя r2DV2, нужно взять положение заряда в несколько более позднее время t2=(t- r2/c) и заряд к этому времени сместится в положение, показанное на фиг. 21.7, в. Так же будет с DV3, DV4 и т. д. Вот теперь можно подсчитывать сумму.
Толщина каждого DVi- равна w, а объем wa2. Поэтому каждый элемент объема, накладывающийся на распределение заряда, содержит в себе заряд wa2r, где r — плотность заряда внутри куба (мы считаем ее однородной). Когда расстояние от заряда до точки (1) велико, то можно все ri в знаменателях положить равными некоторому среднему значению, скажем, взятому с учетом запаздывания положению r' центра куба. Сумма (21.30) превращается в
где DVN—тот последний элемент DVi, который еще накладывается на распределение зарядов (см. фиг. 21.7, д). Сумма тем самым равна
Но ra3 — просто общий заряд q, a Nw—длина b, показанная на фиг. 21.7, д. Получается
(21.31)
А чему же равно b? Это длина куба зарядов, увеличенная на расстояние, пройденное зарядом за время от t1=(t-r1/с) до tN=(t—rN/с). Это расстояние, пройденное зарядом за время
А поскольку скорость заряда равна v, то пройденное расстояние равно vDt = vb/c. Но длина b — само это расстояние плюс a:
Отсюда
Здесь, конечно, под v подразумевается скорость в «запаздывающий» момент t' = (t-r'/с); это можно указать, записав [1—v/c]зап; тогда уравнение (21.23) для потенциала принимает вид
Это согласуется с тем, что было предположено в (21.29). Появился поправочный множитель. Он появился потому, что в то время, как наш интеграл «проносится над зарядом», сам заряд движется. Когда заряд движется к точке (1), его вклад в интеграл увеличивается в b/а раз. Поэтому правильное значение интеграла равно q/r', умноженному на b/а, т.е. на 1/[1—v/c]зan.
Если скорость заряда направлена не к точке наблюдения (1), то легко видеть, что важна только составляющая его скорости в направлении к точке (1). Если обозначить эту составляющую скорости через vr, то поправочный множитель запишется в виде 1/[1-vr/с]зап. Кроме того, проделанный нами анализ в равной степени проходит для распределения заряда любой формы (это не обязательно должен быть куб). Наконец, поскольку «размер» а заряда не вошел в окончательный итог, то тот же результат получится, если заряд стянется до любых размеров, вплоть до точки. Общий результат состоит в том, что скалярный потенциал точечного заряда, движущегося с произвольной скоростью,
(21.32)
Это уравнение часто пишут в эквивалентном виде:
(21.33)
где r — вектор, соединяющий заряд с той точкой (1), в которой вычисляется потенциал j, а все величины в скобках надо вычислять в «запаздывающий» момент времени t'=(t—r'/c).
То же самое получается и тогда, когда по (21.16) вычисляют А для точечного заряда. Плотность тока равна rv, а интеграл от r — тот же, что и в j. Векторный потенциал равен
(21.34)
Потенциалы точечного заряда в этой форме были впервые получены Льенаром и Вихертом. Их так и называют: потенциалы Льенара — Вихерта.
Чтобы замкнуть круг и вернуться к формуле (21.1), теперь нужно только подсчитать Е и В из этих потенциалов (при помощи B=СXA и Е=-Сj-dA/dt). Теперь остается одна арифметика. Впрочем, арифметика эта довольно запутанна, так что мы не будем приводить здесь детали счета. Придется поверить мне на слово, что формула (21.1) эквивалентна выведенным нами потенциалам Льенара — Вихерта.
*Если у вас достаточно времени и вам не жаль бумаги, то попытайтесь проделать это самостоятельно. Вот вам парочка советов: во-первых, не забывайте, что производные r' довольно запутанны, ведь они суть функции от t'! Во-вторых, не пытайтесь вывести формулу (21.1); лучше проделайте в ней все дифференцирования и затем сопоставьте то, что у вас получится, с выражением для Е, полученным из потенциалов (21.33) и (21.34).
§ 6. Потенциалы заряда, движущегося с постоянной скоростью; формула Лоренца
Применим теперь потенциалы Льенара — Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория относительности ведет свое начало от теории электричества и магнетизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)]— это открытия, сделанные Лоренцем при исследовании уравнений электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потенциалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым теорию Максвелла.
Пусть имеется заряд, движущийся вдоль оси х со скоростью v (фиг. 21.8). Нас интересуют потенциалы в точке Р(х, у, z). Если (=0 — момент, в который заряд проходит через начало координат, то в момент t заряд окажется в точке x—vt, y=z=0. А нам нужно знать его положение с учетом запаздывания, т. е. положение в момент
(21.35)
где r' — расстояние от заряда до точки Р в этот запаздывающий момент. В это более раннее время t' заряд был в x=vt', так что
(21.36)
Чтобы найти r' или t', это уравнение надо сопоставить с (21.35). Исключим сперва r', решив (21.35) относительно r' и подставив в (21.36). Возвысив затем обе части в квадрат,
т. е. квадратное уравнение относительно t'. Раскрыв скобки и расположив члены по степеням t', получим
Фиг. 21.8. Определение потенциала в точке Р заряда, движущегося равномерно вдоль оси х.
Отсюда найдем
Чтобы получить r', надо это t' подставить в
Теперь мы уже можем найти j из выражения (21.33), имеющего вид
(21.38)
(ввиду того, что v постоянно).
Составляющая v в направлении r' равна v(x-vt')/r', так что v·r' просто равно v(x-vt'), а весь знаменатель равен
Подставляя (1-v2/c2)t' из (21.37), получаем
Это уравнение становится более понятным, если переписать его в виде
Векторный потенциал А — это такое же выражение, но с добавочным множителем v/c2:
В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца. Если бы заряд находился в начале координат в своей собственной системе покоя, то его потенциал имел бы вид
А мы смотрим на него из движущейся системы координат, и нам кажется, что координаты следует преобразовать с помощью формул
Это обычное преобразование Лоренца. Лоренц вывел его тем же самым способом, каким пользовались и мы.
Но что можно сказать о добавочном множителе 1/Ц(1-v2/с2), который появился перед дробью в (21.39)? И кроме того, как появляется векторный потенциал А, если он в системе покоя частицы повсюду равен нулю? Мы вскоре покажем, что А и j вместе составляют четырехвектор, подобно импульсу р и полной энергии U частицы. Добавка 1/Ц(1—v2/c2) в (21.39)—это тот самый множитель, который появляется всегда, когда преобразуют компоненты четырехвектора, так же как плотность заряда r преобразуется в r/Ц(1-v2/c2). Собственно из формул (21.4) и (21.5) почти очевидно, что А и j суть компоненты одного четырехвектора, потому что в гл. 13 (вып. 5) уже было показано, что j и r — компоненты четырехвектора.
Позднее мы более подробно разберем относительность в электродинамике; здесь мы хотели только показать, как естественно уравнения Максвелла приводят к преобразованиям Лоренца. Поэтому не надо удивляться, узнав, что законы электричества и магнетизма уже вполне пригодны и для теории относительности Эйнштейна. Их не нужно даже как-то особо подгонять, как это приходилось делать с ньютоновой механикой.
* С обратным знаком. См. дальше.— Прим. ред.
*Формула была выведена Р. Фейнманом в 1950 г. и приводится иногда в лекциях как удобный способ расчета синхротронного излучения.

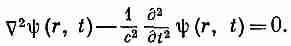

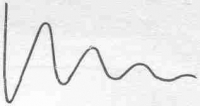
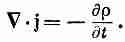

Комментарии к книге «6. Электродинамика», Ричард Филлипс Фейнман
Всего 0 комментариев