Али Альмоссави Хакни рутину. Как алгоритмы помогают справляться с беспорядком, не тупить в супермаркете и жить проще
Посвящается Фатиме
МОЖНО ВЕСЬ ДЕНЬ ПЛАВАТЬ В МОРЕ ЗНАНИЙ, НО ТАК И НЕ ПРОМОКНУТЬ.
Нортон Джустер «Призрачная будка»Ali Almossawi
BAD CHOICES: How Algorithms Can Help You Think Smarter and Live Happier
Copyright © 2017 by Ali Almossawi
© Черепанов В., перевод на русский язык, 2018
© ООО «Издательство «Эксмо», 2018
* * *
Из этой книги вы узнаете:
• как расставить приоритеты при походе в магазин
• как уместить свою мысль в ограниченное количество знаков в Твиттере
• как быстро отсортировать почту
• как найти свой размер одежды на распродаже
• как составить крутой плейлист
Предисловие
Знаете ли вы, когда Ричард Фейнман начал разрабатывать свои знаменитые уравнения, которые принесли ему Нобелевскую премию? Он увидел, как кто-то подбрасывает тарелку в воздух. Знаете ли вы, как Джон фон Нейман сконструировал основные части своего электронного компьютера? Он взял за основу идею своего друга о том, как воспоминания сохраняются в мозге человека. В курсе ли вы, что вид кривляющегося и кричащего орангутанга в клетке навел Чарльза Дарвина[1] на гениальные мысли? У Фейнманна, фон Неймана, Дарвина и других ученых есть одна общая черта: они видели физику, математику и науку повсюду, далеко за пределами своих лабораторий.
Даже если вы не собираетесь стать нобелевским лауреатом, в повседневной жизни есть много вещей, которые можно записать в виде алгоритма. Вы постоянно применяете алгоритмы для решения различных задач: ищете ли вы пару к носку в куче вещей, решаете ли, когда поехать за продуктами, определяете приоритетность задач на день и так далее. Алгоритм – это последовательность точных шагов, при помощи которой в конкретный промежуток времени достигается намеченная цель. Реализация этой последовательности может начаться с приложения усилий и энергозатрат, но подразумевается, что в итоге ваши действия принесут определенную пользу. Все это характеристики алгоритма.
Поразительно, но тексты на вавилонских глиняных табличках 1800–1600 годов до н. э. показывают, что древние вавилоняне использовали алгоритмы, скажем, при вычислении сложного процента или расчете ширины и длины резервуара. Иными словами, жизнь вавилонян складывалась из точной последовательности операций. Эти операции требовали определенных усилий, подразумевали конечный результат и приносили пользу.
Алгоритмы встречаются в работах ученых, которые на протяжении многих веков вносили вклад в развитие математики. После появления компьютеров эти характеристики позволили ЭВМ выполнять задачи предсказуемым способом.
Несмотря на важность алгоритмов в нашей повседневной жизни, почти вся посвященная им литература описывает исключительно их научное применение. Многие авторы игнорируют практическую пользу и эффективность многих алгоритмов. Простые ежедневные задачи можно выполнять разными способами, и чем больше мы знаем таких способов, тем легче достигаем результата. Это можно сравнить с развитием интуиции, которой мы все обладаем. И тут на помощь приходит эта книга.
Цель книги – познакомить вас с алгоритмом мышления при решении повседневных задач и показать, что все эти подходы сравнимы друг с другом. Например, два метода нахождения рубашки нужного размера на вешалке можно описать графически (см. рисунок).[2]
Графики такого вида (их называют линейными и логарифмическими) и есть те самые схемы, которые мы будем строить и обсуждать в этой книге. Бывает, что оба подхода одинаково действенны, когда у нас всего несколько предметов, но их эффективность меняется по мере того, как количество предметов растет.
В этой книге мы рассмотрим с точки зрения алгоритмов двенадцать знакомых каждому мест, включая гостиную, мастерскую и универмаг, где нужно будет выполнить ряд заданий. После каждого рисунка следует описание сцены и комментарий. Мы приведем по крайней мере два возможных способа выполнения фундаментального задания: один – медленный, другой – быстрый. Чтобы понять разницу между ними, надо все время помнить заголовок книги, отчасти навеянный рассуждениями ученого Дональда Кнута о «хороших» алгоритмах, которые можно считать быстрыми или эффективными.[3]
Введение
Для чего нужны относительные величины?
Сравнения – чрезвычайно мощная штука. Одно из первых абстрактных понятий, которые усваивают дети, – разница между большим и маленьким. Когда ребенок спрашивает: «А какого размера тот титанозавр из Музея естественной истории?», то ответ типа «Не очень большой. Всего семнадцать футов в высоту» мало что скажет малышу. Зато он поймет такое объяснение: «Если бы Сюзан, Маргарет и Яша встали друг другу на плечи, то Яша, наверное, смог бы дотянуться до нижней челюсти ящера».
Возможно, умение оперировать относительными величинами – врожденная способность, поскольку ею обладают все дети. Последние эксперименты показывают, что мозг ребенка проявляет такую же активность в ответ на изменения размера изображения, как и при изменении количества образов. Результаты других экспериментов, проведенных в отдаленных уголках мира, говорят, что люди, избежавшие напасти формального образования, судят о количестве предметов при помощи относительных величин.
Из всех подвидов человека разумного ярче всего эта интуиция выражена у ученых-компьютерщиков. Именно она помогает им быстро выбирать лучший из методов решения проблемы. Выходит, способность видеть мир в относительных величинах дает вам преимущество в профессиональной деятельности. Например, условные обозначения математических действий, выученные в начальной школе, остаются в вашем арсенале мышления на протяжении всего школьного курса и за пределами стен учебных заведений, в том числе и в быту.
Именно это обстоятельство стало основной причиной написания этой книги. В школе и колледже я часто прибегал к сравнениям, оценкам, прикидкам и приблизительным величинам для понимания различных терминов и концепций. Я не осмеливался никому признаться в этом, потому что такие методы выглядели слишком простыми. И только прочитав книги «Самый странный человек»[4] и «Общество разума», я узнал, что не я один считаю полезным этот тип мышления. Позже я познакомился с работой «Искусство озарения в науке и инженерном деле» и другими книгами, посвященными этой идее.
Я надеюсь, что моя книга поможет вам лучше мыслить и понимать побочные эффекты этой методики. Она не будет учить вас, как лучше находить пары носков – этой интуитивной способностью обладают почти все люди. Скорее она заставит вас задуматься: «Надо же, я и не знал, что о носках можно рассуждать в таких категориях». Похоже, критическое, алгоритмическое мышление – высокоэффективный инструмент, который влияет на наше поведение, меняя его в лучшую сторону.
Зачем фокусироваться на повседневных задачах?
Алгоритмы могут быть сложными, но они очень важны и так или иначе являются частью нашей жизни. Анализируя те сферы нашего бытия, которые служат хорошими моделями для различных алгоритмов, мы вырабатываем подход, который приносит больше пользы.
Алгоритмы не оторваны от реальности. Не случайно многие объяснения в этой книге сопровождаются иллюстрациями. Рассказывать о чем-либо при помощи рисунков удобно не только потому, что они добавляют красок и эмоций в однообразное повествование. Изображения погружают человека в знакомую среду, включают его в процесс. Вы становитесь способны на более сложные суждения и более интенсивное мышление, когда соединяете новую информацию с известной. Именно поэтому аналогии – очень эффективный инструмент.
Алгоритмы интерактивны. Если вы посмотрите на историю человечества, то обнаружите, что многие известные люди получали образование, поступая учениками к какому-либо мастеру, а не просто сидели за партами и списывали примеры с доски. Алгоритмы часто называют готовыми рецептами, но, по-моему, использование готовых решений больше похоже именно на списывание: это скучное, механическое и бессодержательное занятие. В такой модели ученика рассматривают как некий сосуд, а задача инструктора – наполнить его знаниями. Еще одна метафора: пользоваться готовыми решениями – все равно что смотреть комедию со смехом за кадром, где кто-то другой веселится за вас.
В этой книге каждый урок представлен в виде сценария или плана на целый день. Такой план заставляет вас развивать собственный подход путем погружения и проигрывания различных ситуаций, проговаривания их; он помогает вам в мыслях выйти за пределы ежедневной рутины. Интерактивный подход делает чтение увлекательнее и дает читателю более полезный обучающий опыт. Мои самые яркие детские воспоминания об учебе – это беседы с родителями или с учителем. Все они понимали, что в обучении процесс так же важен, как способности.
Я допускаю возможность разных итогов. Один из моих любимых афоризмов об обучении принадлежит Фрэнсису Бэкону:[5] «Второстепенная и неочевидная польза не менее важна, чем признанный всеми положительный результат». На каждый вопрос существует не один ответ. Представьте себе некий музей науки – родители читают надписи на экспонатах и пересказывают их детям как могут. Никто не приходит в этот мир готовым ученым, никто не покидает его, зная все; но каждый обретает что-то ценное за счет своего опыта.
Алгоритмическое мышление в повседневной жизни
1 Найди пару носку
Баронесса Марджи Вана родилась в некогда влиятельной венской семье, но недавно ее обвинили в контрабанде шоколадных яиц «Kinder Surprise» в США. Сейчас она работает гувернанткой по программе языкового обмена в Берне. Впервые в жизни ей предстоит разобрать кучу белья. Марджи обескуражена тем, что все члены семьи, где она проживает, каждые полчаса бросают в корзину для белья пару носков. Найти и разложить носки по парам – дело непростое. При этом у всех разные размеры и каждый предпочитает определенный цвет.
Подсказка. Здесь может быть поставлено сразу несколько задач, но начинайте с самой главной.
Вы когда-нибудь задумывались над тем, какой важной функцией с точки зрения биологии является человеческая память? Когда кто-то откидывается на спинку стула, прикладывая одну руку ко лбу и закрывая глаза в попытке вспомнить стихи, уравнение или телефонный номер, – это сама суть человека. Представьте, какие мучения ждали бы нас в жизни без этой замечательной способности – и как без нее живут люди, страдающие слабоумием. Для начала вам бы пришлось каждый раз заново заполнять голову одними и теми же знаниями, как герою фильма «Помни».[6]
Я затронул этот вопрос в самом начале, потому что быстрые методы решения проблем улучшают память.[7] Вспомните компьютерную программу «AlphaGo», которая недавно победила чемпиона по игре в го благодаря способности учиться не только у экспертов-людей, но и у самой себя, накапливая в памяти все больше информации.[8] Иначе говоря, многие быстрые способы решения проблем, с которыми мы познакомимся в этой книге, помогают избежать выполнения одних и тех же однообразных действий по многу раз.
Но не будем забегать вперед. Вернемся к бедной старой Марджи Ване. Итак, ей надо собрать в пары носки, сваленные в огромную кучу одежды. Давайте сфокусируемся на одной из нескольких задач и рассмотрим два возможных способа решения.
ЦЕЛЬ: РАЗЛОЖИТЬ ПО ПАРАМ НОСКИ В КУЧЕ БЕЛЬЯ
МЕТОД 1: ВЫБРАТЬ НОСОК. ПОИСКАТЬ ЕМУ ПАРУ В ГРУДЕ БЕЛЬЯ. ОТЛОЖИТЬ ОБА НОСКА В СТОРОНУ. ВЗЯТЬ ДРУГОЙ НОСОК. ПОИСКАТЬ ЕМУ ПАРУ В ГРУДЕ БЕЛЬЯ. ОТЛОЖИТЬ ОБА НОСКА В СТОРОНУ. И ТАК ДАЛЕЕ.
МЕТОД 2: ВЫБЕРИТЕ НОСОК. ОТЛОЖИТЕ ЕГО В СТОРОНУ. ВЫБЕРИТЕ ДРУГОЙ НОСОК. ЕСЛИ ОН ПОДХОДИТ К ПЕРВОМУ, ОБЪЕДИНИТЕ ИХ. ВЫЛОЖИТЕ В РЯД НОСКИ БЕЗ ПАРЫ. ПОДБЕРИТЕ К НИМ НОСКИ СОВПАДАЮЩЕГО ЦВЕТА И РАЗМЕРА.[9]
Прежде чем читать дальше, проработайте эти варианты, используя ручку и бумагу или любой другой реквизит. Подумайте о том, какую цель преследует каждый отдельный шаг на примере сцен, перечисленных ниже.
Если в куче всего четыре носка, то неважно, какой метод будет использовать Марджи: она быстро справится с задачей. А теперь представьте, что перед ней лежит сотня носков. Если она выберет первый метод, то с большой вероятностью будет снова и снова натыкаться на один и тот же носок, поскольку он остается в общей куче. Вытащив его в первый раз, она не извлечет из него никакой информации.
При использовании второго метода перед ней вырастет шеренга носков без пары, и, следовательно, она будет брать каждый носок из кучи вещей всего один раз. Второй метод оказывается быстрее, потому что он опирается на память – точнее говоря, на то, что мы иногда называем справочными таблицами, или сверхоперативной памятью.
Полезно представить справочную таблицу как сборник уникальных идентификаторов – клавиш, каждая из которых указывает на какую-либо связанную с ней информацию. Вы в буквальном смысле видите надписи на клавишах. Мы называем этот тип представления парой «ключ—значение».
В случае с носками наши клавиши скорее всего будут цветными. Когда Марджи находит красный носок, она ищет тот же цвет среди непарных. Найдя его, она может вводить дополнительные идентификаторы/признаки, например стиль или оттенок. Если пара так и не найдена, она создает новую область под названием «красное» с единственным красным носком в ней.
Как эти два метода соотносятся друг с другом?[10] Мы уже заметили, что работа по методу 1 сильно замедляется по сравнению с методом 2 по мере увеличения носков в куче. На самом деле существует гораздо больше способов решения задачи. Но нам сейчас важно показать, чем именно эти два метода радикально отличаются друг от друга, не упоминая другие, чья эффективность может находиться где-то посередине. К примеру, Марджи могла бы применить принцип Дирихле – то есть вытаскивать по шесть носков из кучи одновременно и подбирать пары таким способом.
Вытаскивая носок из кучи, мы достаточно быстро сможем подобрать ему пару. Кратковременная память большинства людей прекрасно работает с группами, насчитывающими плюс-минус десять предметов, а именно такими величинами мы оперируем в данный момент. Натыкаясь на носок, который мы уже откладывали в сторону, мы должны воскликнуть: «А, да – я его уже видел!» Если вы когда-нибудь играли в карточную игру «Память», преимущества и недостатки этой системы должны быть вам хорошо знакомы.
Если бы у нас было гораздо больше носков разных типов и цветов, то ряд непарных оказался бы таким длинным, что нам пришлось бы заново пересматривать всю их последовательность каждый раз, когда мы вытаскиваем из кучи новый. Это трудоемко и долго, особенно если искомый предмет оказывается в самом конце.
В 1953 году математик Ханс Питер Лун, работавший в корпорации «IBM», выдвинул идею, которая положила начало созданию альтернативной структуры, облегчающей потенциальную замедленность, присущую любому комплексному поиску. Эта структура иногда называется ассоциативным массивом, или хеш-таблицей (посыплем еще немного соли на раны старушки Марджи). Хеш-таблица делает то же, что и массив: она сохраняет вещи в коллекции, но использует более строгую последовательность (например, большой черный носок всегда идет после красного носка) для немедленного так называемого поиска за постоянное время.[11]
Он называется непрерывным, потому что не зависит от длины последовательности. Впрочем, это не всегда так. Многие вещи в программном обеспечении, к неудовольствию исследователей и практиков, не подчиняются фундаментальным законам – в отличие от природы. Но здесь мы допускаем, что из-за малого числа несопоставимых носков синапсы Марджи будут возбуждаться быстро и вызывать почти немедленную реакцию.
Как мы увидим позже, непрерывный поиск чаще всего происходит в тех случаях, когда можно смоделировать задание при помощи формулы, которая избавляет от необходимости выполнять его снова и снова, перебирая все существующие позиции.[12] Известно, что формула, используемая с хеш-таблицами, называется хеш-функция. Ее работа – поместить вещь в кучу так, чтобы потом можно было вытащить ее из памяти достаточно быстро.
Но отложим эти соображения в сторону. Суть в том, что подход, который использует одни и те же знания повторно, может быть быстрее, чем тот, который их не использует. Это особенно полезно знать, когда речь идет о выполнении каких-либо повторяющихся операций. Например, вы выбираете в магазине коробку свеч в виде букв для именинного пирога вашей дочери. Или же вы собрались постирать, и вам нужно отделить белое постельное белье от цветного и нижнего. Или вы пытаетесь составить самое длинное слово из определенного набора букв, как в британском телешоу «Каунтдаун».
В каждой из этих ситуаций вы спросите себя: можно ли сделать это задание быстрее, используя память – свою собственную или общечеловеческую? В примере с кучей носков, составляя ряд носков без пары, мы договорились, что у нас не может быть больше пяти их типов. В примере с коробкой свеч мы бы выбрали любые подходящие нам четыре буквы, когда мы натыкаемся на них, а не искали бы отдельно L или U и так далее.
В случае с грязной одеждой удобнее складывать ее в три разные корзины, чтобы не перебирать перед стиркой. А в ситуации с самым длинным словом можно взять первое пришедшее на ум слово и посмотреть, нельзя ли удлинить его путем склонения или перевода в форму множественного числа. Здесь наш первоначальный выбор служит как бы префиксом[13] (взятым из памяти) к последующим словам.
Есть замечательная структура под названием префиксное дерево, которая именно это и делает. Она пользуется тем, что цифры и номера имеют общие префиксы, чтобы производить такие операции, как проверка орфографии и автокоррекция слов, которые вы вводите в строку поиска слишком быстро и при этом делаете ошибки.
РАЗВЕ НЕ ЗДОРОВО, ЧТО ОБЫДЕННОЕ СТАНОВИТСЯ УВЛЕКАТЕЛЬНЫМ, СТОИТ ТОЛЬКО ПОДОЙТИ К НЕМУ ИНАЧЕ?!
2 Выбери свой размер
На следующий день после Рождества медсестра Эппи Тоам из шотландского городка Инвернесс рано утром пришла к местному универмагу в ожидании новогодней распродажи. У Эппи довольно распространенный размер одежды, и она хочет первой ворваться в магазин, чтобы успеть ухватить все блузки своего размера. Ей нужно делать все быстро. Ситуация может выйти из-под контроля. В прошлом году во время такой распродажи 15 человек получили травмы, а потом пришлось вызывать военных, чтобы прекратить давку. Как Эппи может повысить свои шансы заполучить нужные блузки, до того как они попадут в чужие руки?
Подсказка. Рассматривайте этот пример, доводя его до абсурда. Что, если стойки с одеждой будут располагаться по всей ширине магазина?
Если мы ищем что-то среди большого количества одежды, то нужно ли просматривать всю коллекцию? Другими словами, если у нас 100 вещей, должны ли мы просмотреть все 100, то есть занимает ли такая операция линейное время? Смысл линейной функции в том, что если для нахождения чего-то в куче из 100 вещей нужна минута, то можно ожидать, что у нас уйдет две минуты на поиск нужной вещи в куче из 200 предметов гардероба.
Обычно так и происходит. Однако коллекция может обладать одним интересным качеством, а именно: она поддается сортировке, что позволяет найти вещь по алгоритму логарифмического времени, примерно за 7 шагов, а не за 100. Вспомните, что логарифм – это всего лишь нечто обратное экспоненте. Составляя компьютерные программы, мы предполагаем, что основание логарифма есть 2, поэтому логарифм 100 это log2 100, то есть получается примерно 7. Это значительное улучшение можно увидеть, переходя от линейного времени к логарифмическому. Поэтому логарифм и является таким важным понятием, особенно когда мы говорим о скорости роста. К этому мы будем часто возвращаться в следующих главах.
Для начала давайте представим, как Эппи носится по магазину с сияющим от гордости и тщеславия лицом. Шарф развевается, ее боевые крики вырываются сквозь стиснутые зубы и отражаются от стен универмага. Она все утро готовилась к этому моменту.
ЦЕЛЬ: НА ВЫБРАННОЙ ВЕШАЛКЕ НАЙТИ БЛУЗКУ СВОЕГО РАЗМЕРА.
МЕТОД 1: ДЛЯ ВЫБРАННОЙ ВЕШАЛКИ. ПРОСМОТРЕТЬ ВСЕ БЛУЗКИ ОДНУ ЗА ДРУГОЙ.
МЕТОД 2: ДЛЯ ВЫБРАННОЙ ВЕШАЛКИ. НАЧНИТЕ ИСКАТЬ СВОЙ РАЗМЕР В СЕРЕДИНЕ ВЕШАЛКИ. ЕСЛИ ТАМ ВИСЯТ БЛУЗКИ РАЗМЕРОМ БОЛЬШЕ, НУЖНО ПОЙТИ НАЛЕВО. ЕСЛИ ЖЕ РАЗМЕРЫ МЕНЬШЕ – НАПРАВО.
Вот так можно наглядно сравнить эти два метода. Очевидно, что поиски по методу 1 станут значительно медленнее, чем по методу 2, по мере увеличения количества блузок на вешалке.
Как вы уже, вероятно, догадались, в методе 2 выгодно используется знание двух фактов. Во-первых, блузки, скорее всего, отсортированы по размерам. А во-вторых, поскольку у Эппи ходовой размер, то скорее всего нужные ей блузки висят где-то в середине вешалки. Зная это, можно не только начать с середины, но и передвигаться влево или вправо своеобразными скачками, каждый раз сокращая коллекцию вдвое. Такой подход и есть визитная карточка алгоритма логарифмического времени.[14] Это та самая интуиция, которую мы используем, чтобы найти нужное слово в словаре, или имя в телефонном справочнике, или статью в энциклопедии. Те же интуитивные знания мы будем применять, если заснем над скучной книгой и захотим на следующий день возобновить чтение с того же места. В целом можно охарактеризовать этот подход как принцип отбрасывания ненужной информации.
ЭППИ НАХОДИТ СВОЙ РАЗМЕР ЗА 4 ШАГА.
ЭППИ НАХОДИТ СВОЙ РАЗМЕР ЗА 2 ШАГА.
Для нас наиболее важной информацией о логарифмах является то, что они медленно растут, как вы видели из предыдущих графиков. Мы предпочитаем решения, которые растут медленно, потому что это означает, что наш метод не так сильно зависит от количества предметов. Эппи скорее всего найдет нужную вещь на вешалке с сотней блузок менее чем за 7 шагов, а на гипотетической вешалке с тысячью блузок – всего за 10 шагов или около того, что не так уж плохо. Этот метод логарифмического поиска чего-либо в отсортированной группе предметов часто называют бинарным поиском. Он значительно эффективнее метода 1, известного под названием линейный поиск, и благодаря ему Эппи приобрела кучу новых блузок своего размера.
3 Поход за продуктами
Ян Патой – бывший учитель английской словесности, лингвист. Он пенсионер и живет на востоке Лондона. Несколько лет назад он упал, и теперь у него сильно болит спина. Он не любит выходить на улицу, потому что боится соседской собаки, но ему приходится иногда совершать вылазки за продуктами. В Лондоне часто идет дождь, а старые кости Яна не выносят сырости. Как свести к минимуму количество походов в магазин в неделю, чтобы не умереть с голода?
Есть такой комедийный скетч с двумя Ронни[15] – клиент приходит в скобяную лавку и читает список вещей, которые ему нужно купить. Вместо того чтобы дождаться конца списка, владелец магазина каждый раз хватает названную вещь, и все заканчивается тем, что у продавца едет крыша.
Запомните эту сценку.[16] Мы еще вернемся к ней. Но сначала давайте посмотрим, как Ян может решить, насколько часто ему ходить в магазин.
ЦЕЛЬ: СОВЕРШАТЬ КАК МОЖНО МЕНЬШЕ ВЫЛАЗОК В МАГАЗИН В ТЕЧЕНИЕ НЕДЕЛИ.
МЕТОД 1: ОБНАРУЖИТЬ, ЧТО КАКОЙ-ТО ПРОДУКТ ЗАКАНЧИВАЕТСЯ И ОТПРАВИТЬСЯ ЗА НИМ В МАГАЗИН.
МЕТОД 2: СОСТАВЛЯТЬ СПИСОК ЗАКОНЧИВШИХСЯ ПРОДУКТОВ. ПОЙТИ В МАГАЗИН, КОГДА СПИСОК ДОСТИГНЕТ ОПРЕДЕЛЕННЫХ РАЗМЕРОВ ИЛИ КОГДА ЗАКОНЧИТСЯ КАКОЙ-НИБУДЬ ЖИЗНЕННО ВАЖНЫЙ ПРОДУКТ, НАПРИМЕР ШОКОЛАДНЫЕ БАТОНЧИКИ «КИТ-КАТ».[17]
Вот уже знакомый нам график, где можно посмотреть и сравнить эффективность этих двух методов.
Одна из интерпретаций этой сцены звучит так: важно избегать повторяющейся работы. К примеру, секретарша, которой нужно подшить десять различных отчетов, может сделать дырки во всех десяти листах сразу, а не мучиться с каждым по отдельности. Или же – почему бы не намылить все грязные тарелки разом и не вымыть их вместе, вместо того чтобы тереть и прополаскивать по очереди. Или порезать луковицу вдоль, прежде чем начать шинковать ее поперек. Или оснастить новые высотные здания диспетчерской системой, которая сажает в один лифт пассажиров, едущий на тот же этаж.
Внимательный исследователь может сделать еще одно наблюдение, и оно имеет отношение к походу Яна в продуктовый магазин. Давайте поговорим об этом.
В информационных технологиях есть много способов хранения набора данных. Мы рассмотрели основные способы на примере массива разнопарных носков. Затем во второй сцене мы увидели, как массив может максимизировать какое-либо качество, а именно – возможность поиска путем сортировки контента. Вспомните отсортированные в нужном порядке рубашки на вешалках. Именно это делают структуры данных, или абстрактные типы данных, как их иногда называют. Они повышают значение одного или нескольких свойств, которые нас интересуют, обычно за счет других, не столь важных для нас. Пример: безопасность и удобство работы. Приложение, которое запрашивает у вас пароль каждый раз, когда вы нажимаете на кнопку, возможно, гарантирует большую безопасность, но оно менее удобно в использовании.
Структура, которая, на мой взгляд, заслуживает внимания, известна под именем стек. Стек выводит на первый план качество предмета, который находится сверху, независимо от того, сколько позиций расположено ниже. Так, увидев в кафе стопку газет, вы возьмете просматривать только верхнюю, потому что знаете, что она свежая, а вас интересуют самые последние новости. Точно так же и со стеками: нас интересует то, что находится на самом верху.
В случае с Яном его когнитивный стек состоит из продуктов, которые закончились у него дома. Когда в верхней позиции оказывается «Кит-Кат», Ян решает пойти в магазин и очистить верх стека. Таким образом он постоянно убирает верхние элементы, пока весь стек не очистится. Закончившийся «Кит-Кат» становится триггером для начала очистки стека. До наступления этого момента Ян может спокойно добавлять другие позиции в список и заниматься своими делами.
Наше воспоминание о скетче в исполнении двух Ронни тоже здесь к месту. Оно позволяет владельцу магазина построить воображаемый стек, возможно, по одному для каждого ряда полок, чтобы не лазать вверх и вниз по лестнице много раз. Если бы клиент прочитал весь список нужных товаров, владелец построил бы свои стеки, исходя из расположения полок, создавая позиции для стека каждого ряда.
В 1946 году Алан Тюринг опубликовал научную статью, где представил концепцию стека, используя термин «закапывание». Как отмечает Эндрю Ходжес, автор биографии Тюринга, идея оказалась новостью для фон Неймана. Вот небольшая выдержка из работы Тюринга:
«Как производится закапывание и откапывание? Есть много способов. Один – вести список таких заметок в одной или нескольких стандартных линиях задержки (1024), где самая недавняя запись становится последней. Положение самой недавней записи хранится в фиксированном временном хранилище, и эта ссылка изменяется каждый раз, когда зависимая позиция начинается или заканчивается».
Этот поразительный текст рассказывает о том, как концепции, которые мы сегодня считаем интуитивными, вообще появились на свет. Они стали очевидными, только когда кто-то изучил различные проблемы, пытаясь найти их решение. Возможно, вам захочется прочитать об эффекте Флинна – он назван по имени Джима Флинна, предположившего, что человек становится умнее отчасти благодаря тому, что его интуитивное мышление зреет и становится более изощренным и сложным. У людей, рождающихся сегодня, в мозг уже встроена способность к интуиции, более совершенная, чем та, что была у их предков.
Поэтому бывает смешно читать старые тексты и трактаты – они показывают нам, как далеко мы продвинулись. Помню, я открыл однажды «Руководство по хорошим манерам для детей» авторства Дезидериуса Эразмуса, изданную в 1530 году, и нашел такой совет: «Не давайте соплям скапливаться в носу, так поступают только неряхи. Еще Сократа критиковали за этот порок». Для человека из XXI столетия это правило выглядит само собой разумеющимся, но в контексте того времени оно блистало новизной.
Разговор Тюринга о вспомогательных операциях напоминает еще одну жизненную ситуацию, где стеки были бы полезны. Представьте, что на следующее утро к дому Яна подъезжает почтальон и не смотрит ему в глаза. По щекам почтальона катятся слезы, а губы дрожат от обиды.
«Простите, не сделал ли я чего-то такого, что обидело вас?» – спрашивает Ян.
«Ну, вообще-то сделали. Так и есть», – сказал почтальон, отводя взгляд.
Как же Яну вспомнить, каким образом он обидел почтальона? Ему нужно изучить верхние пункты из нужного стека воспоминаний – стека под названием «почтальон». Причина наверняка кроется в их последнем общении.
Есть ли в нашей повседневной жизни вещи, которые работают как стеки? Как насчет Всемирной паутины? Каждый раз, когда вы кликаете по ссылке, вы помещаете данный сайт в стек. Заходя на эту ссылку еще раз, вы берете веб-адрес из стека. Вам все равно, сколько сайтов вы посетили, пока вы можете вернуться к последнему и от него к другому, стоящему раньше, и так далее.
Можно надеяться, что Ян сумеет разобраться в своем стеке, чтобы внести поправки в манеру общения с почтальоном, и научится лучше определять, когда ему идти за продуктами.
4 Выход из лабиринта
Как-то раз один портной, грек по имени Иоаннис, заблудился в собственной мастерской. Мастерская пользовалась большой популярностью среди афинян, а сам Иоаннис имел репутацию скряги и скопидома. Ситуация осложнялась тем, что помещение располагалось на обширном участке земли, постепенно занимая его, по мере того как Иоаннис в течение 30 лет строил новые проходы и ставил стеллажи для удовлетворения своей страсти к накопительству. И вот он попался: сидит в созданном им же самим лабиринте, заваленном хламом, а вокруг выстроились полки с бесконечными рядами ниток, одежды и разломанных швейных машин. Как же Иоаннису найти путь обратно? Или ему суждено погибнуть здесь?
Есть еще одна греческая история. Когда родился Минотавр, полубык-получеловек, великий архитектор Дедал построил лабиринт, куда было заточено это злое и коварное существо.
«Оказавшись внутри, он бродил по извилистым тропинкам, но так никогда и не нашел выхода. В это место периодически отправлялись молодые афиняне, которых отдавали на съедение Минотавру. И не было у них никакой возможности спастись».
К счастью для Тесея, который тоже должен был стать жертвой Минотавра, дочь царя Ариадна влюбилась в него и разработала план его побега.
Она послала за Дедалом и велела ему показать выход из лабиринта. Тесею она обещала спасение, если он возьмет ее в Афины и там женится на ней. Ариадна дала ему ключ, полученный от Дедала, и клубок пряжи, который Тесей должен был прикрепить к двери и разматывать нить по мере продвижения. Так он и сделал и, конечно же, когда понадобилось, смог проделать путь в обратном направлении. Он смело прошел по лабиринту, нашел Минотавра спящим, убил его и вышел наружу».
Запомните эту историю. Мы скоро вернемся к ней снова. А пока давайте опишем три метода, которые Иоаннис мог бы использовать, чтобы найти выход из мастерской.
ЦЕЛЬ: ВЕРНУТЬСЯ К ВЫХОДУ
МЕТОД 1: ИДТИ ПО ПРОХОДАМ. СВОРАЧИВАТЬ НАУГАД, ПОКА НЕ НАЙДЕШЬ ВЫХОД.
МЕТОД 2: ДЕРЖАСЬ ПРАВОЙ РУКОЙ ЗА СТЕНУ, ИДТИ ВДОЛЬ НЕЕ, СВОРАЧИВАЯ КАЖДЫЙ РАЗ ТОЛЬКО НАПРАВО.
МЕТОД 3: ВЗЯТЬ С ПОЛКИ КАТУШКУ С НИТКАМИ И РАЗМАТЫВАТЬ ЕЕ ПО МЕРЕ ДВИЖЕНИЯ ПО ПРОХОДУ. ЕСЛИ ПОПАДЕШЬ В ТУПИК ИЛИ НАТКНЕШЬСЯ НА СВОЮ ЖЕ НИТКУ, ТО ПОВЕРНУТЬ НАЗАД И ПОЙТИ ПО ДРУГОМУ ПРОХОДУ.
Метод 1 имитирует путь мыши в лабиринте. Никаких продвинутых умственных способностей для него не требуется – просто беспорядочное хождение от одной точки до другой, пока по случайности не наткнешься на кусок сыра. Иногда его так и называют – метод беспорядочной мыши. Как вы можете догадаться, результат достигается крайне медленно.
Метод 2 немного интереснее, хотя тоже довольно прост. Здесь Иоаннис идет по стене, держась за нее рукой, и находит дорогу к выходу. Почему это срабатывает? Потому что, если развернуть стены лабиринта, получится прямая линия, и, шагая вдоль нее, когда-нибудь достигнешь конца.[18]
Хоть метод 2 и быстрее метода 1, его проблема в том, что в лабиринте могут быть так называемые островки или петли – внутренние стены, которые не соединены с внешними. В 1820 году граф Стэнхоуп построил в Чевенинге (Кент) первый садовый лабиринт с такими петлями. Его целью было создать лабиринт, из которого нельзя выйти по методу 2.
Таким образом, в некоторых лабиринтах этот метод, известный как стенохождение или правило правой руки,[19] может подвести человека и не привести к желаемому результату.
Краткое отступление. Интересно, что Чарльз Дарвин почти двадцать лет изучал все возможные контраргументы к своей теории эволюции, прежде чем опубликовал «Происхождение видов». Исследование такого масштаба сродни хождению по лабиринту, где развилки тропинок соответствуют предположениям,[20] где тупики означают, что аргумент не выдерживает критики, а выход – понимание, что вывод верен. Оказалось, что этот когнитивный подход к аргументам и контраргументам также работает, если применять его для поиска выхода из реального лабиринта. И это в точности то, что мы видим в методе 3 и в истории о нити Ариадны.
При помощи этого метода Иоаннес ведет обратный учет, который помогает ему тянуть нить: когда он попадает в тупик, он может вернуться и пойти по другому пути.[21] Возможность вернуться к месту пересечения ходов и попробовать более удачный путь гарантирует, что Иоаннес рано или поздно найдет дорогу обратно. Эта стратегия нахождения выхода из лабиринта называется алгоритм Тремо, ей мы обязаны французскому математику Эдуарду Лукасу и его книге «Математические рекреации», изданной в 1882 году.
Недавние исследования доказывают, что другие существа (например, муравьи) тоже могут использовать что-то типа метода обратного отслеживания для нахождения пути, если тропинка обрывается. Этот способ быстрее метода 1 и помогает выбраться из замкнутых петель в отличие от метода 2.
Заметьте, что эти три метода полезны, только когда главная цель – выбраться из лабиринта. Есть и другие способы поисков выхода, которые могут быть гораздо быстрее, однако при их применении требуется знать, как устроен лабиринт. Кроме того, методы, которые мы рассмотрели, не гарантируют нахождения самого короткого пути из лабиринта.
В мире есть десятки настоящих лабиринтов, некоторые простираются на многие мили, и там усвоенные нами уроки можно применить на практике. Но вышеперечисленные методы могут пригодиться и в других ситуациях. В более общем виде идея прохода от одной точки до другой в замкнутом пространстве, похожем на лабиринт, выглядит так. Это сеть или график как альтернативный способ описания лабиринта, где проходы – края, а пересечения – вершины, находятся в ядре многих приложений, которыми мы пользуемся и полагаемся на них каждый день. Приложение, которое знает, как соединены дороги – OpenStreetMap, например, – может подсказать кратчайший путь от вашего дома до пляжа. Веб-сайт, который знает, как связаны люди, места и вещи – скажем, Google’s Knowledge Grap, – дает лучшие результаты поиска: интернет-сайт, который знает, кто ваши друзья – Facebook или LinkedIn, например, – может догадаться, с кем еще вы знакомы, а программа, которая знает, как соединены ее компоненты и модули – скажем, Firefox, – предвидит, где вероятнее всего проявятся дефекты в будущем, основываясь на паттернах и плотности соединений.
Даже роботы-пылесосы служат хорошим примером. Не все они одинаковы. Уровень сложности зависит от того, как много пространства они способны охватить. Самые простые пылесосы бродят беспорядочными линиями или кругами, в то время как более продвинутые сначала составляют карту комнаты, определяя, где находятся стены, углы и повороты, а потом ездят взад-вперед по принципу решетки. Иными словами, когда робот знает, как лучше всего добраться с одного конца комнаты в другой, это приближает его цель, а результат – более чистая комната.[22]
В случае с Иоаннисом он выберется из лабиринта и не сойдет с ума, независимо от того, каким методом воспользуется. Но если он продолжит бесконтрольно копить хлам, а его лавка будет и дальше разрастаться, то ему придется все время ходить по ней с клубком ниток в кармане.
5 Сортировка почты
Чарли Магна не успевает закончить свои почтовые дела. Сейчас уже середина дня, июль, Кейптаун. Температура 45 °C. К тому же рассеянный и неуклюжий Чарли выронил коробку с отсортированными письмами и перемешал пачки, которые нужно доставить 33 адресатам в его округе. Но и это не все: у почтальона повышенная чувствительность к солнечному свету, а он забыл кепку и солнцезащитные очки дома. Стоя на коленях на раскаленной гальке, он собирает конверты и пытается разложить их в нужном порядке, чтобы закончить работу, прежде чем на коже появятся волдыри.
Подсказка: подумайте, как можно разбить одну большую проблему на несколько маленьких.
Порядок поможет нам управиться с задачей быстрее. Представьте, что было бы, если бы местная газета не анонсировала предстоящие события по дням недели. Если бы серии телесериала, которые вы планируете посмотреть, не перечислялись в телепрограмме. Как было бы досадно тратить время на поиски следующего эпизода, вместо того чтобы посмотреть очередную историю о неудавшемся наркодилере, получившем еще один удар от жестокой вселенной.
Давайте посмотрим, как Чарли может справиться со своей неожиданной поблемой.
ЦЕЛЬ: СНОВА РАЗЛОЖИТЬ РАССЫПАННЫЕ ПАЧКИ КОНВЕРТОВ В НУЖНОМ ПОРЯДКЕ
МЕТОД 1: ПОЛОЖИТЬ ОДНУ ПАЧКУ НА ЗЕМЛЮ ПЕРЕД СОБОЙ. ВЗЯТЬ ВТОРУЮ ПАЧКУ, И, ЕСЛИ МЕСТО ЖИТЕЛЬСТВА АДРЕСАТА БЛИЗКО К ПЕРВОМУ, ПОМЕСТИТЬ ЕЕ СЛЕВА. И ТАК ДАЛЕЕ, ПОКА САМЫЕ БЛИЗКИЕ АДРЕСА НЕ ОКАЖУТСЯ СЛЕВА ОТ ЛИНИИ, А САМЫЕ ДАЛЕКИЕ – СПРАВА.
МЕТОД 2: РАЗЛОЖИТЕ ПАЧКИ КОНВЕРТОВ В РЯД ПЕРЕД СОБОЙ. РАЗДЕЛИТЕ ИХ ТАК, ЧТОБЫ СПРАВА И СЛЕВА ОКАЗАЛОСЬ ОДИНАКОВОЕ КОЛИЧЕСТВО КОНВЕРТОВ. ЗАТЕМ РАЗДЕЛИТЕ КАЖДУЮ ГРУППУ ПОПОЛАМ. КЛАДИТЕ БЛИЗКИЙ АДРЕС СЛЕВА, А ДАЛЕКИЙ – СПРАВА. ЗАТЕМ ДЕЛАЙТЕ ЭТО ДЛЯ КАЖДОЙ ПАРЫ ПАР И ТАК ДАЛЕЕ.
Вот как эти два метода выглядят на графике:
В реальной жизни при сортировке каких-либо вещей вручную, как это делает Чарли, допустимы некоторые вариации метода 1, которые он скорее всего использовал бы. Как мы видели из прежних сравнительных графиков, общее правило таково: для сортировки нескольких вещей годится любой метод. И только когда предметов много, один из методов может оказаться намного лучше другого. Хотя метод 2 не всегда имеет практическую корреляцию в реальной жизни, по крайней мере при сортировке, мы обсудим общий подход в концептуальных терминах.[23]
Для начала заметим, что метод 1 несет в себе определенный ритм. Чарли берет одну пачку конвертов, затем просматривает другие пачки, чтобы определить, куда ее положить. Затем он берет другую пачку конвертов, просматривает остальные пачки и так далее. Мы видели подобный подход раньше, когда разбирали носки, не так ли? Разница в том, что с каждым конвертом Чарли просматривает все другие только один раз, в то время как с носками Марджи могла потратить много времени, выискивая к каждому пару в куче белья.
Подход Чарли в методе 1 – характерная черта алгоритма с квадратичным временем.[24] Каждый раз, когда у вас есть набор предметов (независимо от того, одинаковые ли они или разные) и вы перебираете их все в поисках одного, у вас есть алгоритм с квадратичным временем. Другие примеры подобного алгоритма – примерка нескольких рубашек с целью выбрать подходящую к вашим брюкам или сравнение списка покупок с продуктами на полке в магазине.
В информационных технологиях многие простые способы сортировки данных протекают в квадратичном времени. Подобно методу 1 Чарли, они все работают путем сравнивания смежных пунктов и перемещения их в зависимости от того, какой больше, а какой меньше. Все подходы, построенные на принципе сравнения прилегающих точек, в среднем происходят в квадратичном времени (n2). Иначе говоря, если n – количество конвертов, мы можем описать функцию, которая располагает эти конверты в нужном порядке с помощью сравнения, как «ограниченные n2», то есть в среднем (это ключевое слово!) мы не можем это сделать быстрее. Существует также сортировка методом вставок, методом выделения и пузырьковым методом.
Когда я впервые услышал о сортировке, будучи 16-летним школьником, я сперва не понял, что может быть лучше метода с квадратичным временем. График показывает, что метод 2 значительно быстрее, чем метод 1, поэтому стоит сортировать элементы в субквадратичном времени.
Общий подход к субквадратичному способу сортировки подразумевает такие методы, как разделение и присваивание, то есть разбивание группы предметов на более мелкие группы и сортировку этих групп.[25] Разделение группы пополам есть логарифмический метод, как мы видели ранее, а помещение предметов в одну группу снова – линейный, так как мы берем один предмет один раз. Этот подход к сортировке называют линейно-логарифмическим, и можно представить, что он гораздо быстрее, чем метод с квадратичным временем и немного медленнее, чем метод с линейным временем.[26] Его можно называть лог-линейным, или просто n log n, – этот порядок складывается из времени, затрачиваемого на разделение группы (log n) и на компоновку предметов заново (n). При умножении они дают n log n. Слово «линейно-логарифмический» образовано из двух: «линейный» и «логарифмический». Это создает концепцию, более сложную, чем составляющие ее части, – совсем как с Джедвардом.[27]
Два хорошо известных линейно-логарифмических алгоритма – сортировка слиянием, изобретенная Джоном фон Нейманом в 1945 году, и быстрая сортировка, придуманная Тони Хоаром в 1959 году. Метод 2 для Чарли сходен с сортировкой слиянием. Этап разделения соответствует раскладыванию пачек конвертов на отдельные кучки. А этап обратного слияния – сравнению и совмещению этих пачек. На последнем этапе в первый раз у нас остается набор двух упорядоченных групп. Во второй раз мы получаем уже четыре упорядоченные группы. В случае с Чарли процесс будет выглядеть так:
Заметьте, как он переходит от набора неотсортированных конвертов в первом этапе к набору отсортированных конвертов, хоть и одного размера, на втором. На каждом последующем этапе он совмещает группы, создавая все более длинные ряды отсортированных конвертов, пока у него не останется один ряд, содержащий все конверты. Если мы рассмотрим поближе один из таких этапов, например этап 4, то сможем увидеть, как происходит слияние.
И все же метод 2 – лучший выбор исходя из увеличения скорости, которого он позволяет достичь. Преимущество Чарли в том, что у него всего 33 пачки конвертов для сортировки. Любой метод спасет его от недельных страданий из-за обожженной кожи. Если бы у него было больше конвертов, то скоростной метод 2 оказался бы более предпочтителен, и Чарли, несомненно, извлек бы пользу от знания, как быстрее сортировать почту. Ну, а пока он заканчивает свой рабочий день.
ЗАВЕРШАЯ РАЗВОЗКУ ПОЧТЫ, ЧАРЛИ СЧАСТЛИВ КАК НИКОГДА: СЕГОДНЯ ОН УЗНАЛ КОЕ-ЧТО НОВОЕ. «ВЕЗДЕ ЕСТЬ МЕСТО ДЛЯ ОТКРЫТИЙ, – ГОВОРИТ ОН СЕБЕ, – ДАЖЕ ТАМ, ГДЕ НЕ ОЖИДАЕШЬ».
ПОЛЬЗУЙТЕСЬ НА ЗДОРОВЬЕ. ТОНИ ХОАР. ИЗОБРЕТАТЕЛЬ МЕТОДА БЫСТРОЙ СОРТИРОВКИ
6 Стань крутым
Фой недавно переехал в Эшленд. Несмотря на ухоженную бородку-эспаньолку и непременный атрибут при выходе в свет – последний номер журнала «New Yorker» (он носит его под мышкой и никогда не читает, но любит небрежно бросить перед собой на столик в кафе или ресторане); несмотря на все это, он остается аутсайдером на новом месте. Его неизменный ответ на любой серьезный вопрос «Милтон бы не пришел в восторг от этого, поверьте мне», очень скоро начинает звучать банально и претенциозно. «Что вы думаете о новой книге Карла Ова Кнаусгарда?» – Милтон бы не пришел в восторг от этого, поверьте мне». «Вам понравился новый сингл Адели, Фой?» – «Милтон бы не пришел в восторг от этого, поверьте мне».
Переживая за свой имидж, Фой стремится стать настоящим знатоком культуры и искусства. Для начала он решил ознакомиться с наиболее известными представителями музыкального мира и купаться в их славе. Но, оказавшись перед огромным выбором дисков в музыкальных магазинах Эшленда, он растерян и не знает, что делать.
ЦЕЛЬ: ИЗУЧИТЬ ПОПУЛЯРНУЮ МУЗЫКУ.[28]
МЕТОД 1: ВЫБРАТЬ ПОПУЛЯРНОГО ИСПОЛНИТЕЛЯ ИЛИ ИСПОЛНИТЕЛЬНИЦУ И ПОЗНАКОМИТЬСЯ С ЕГО ИЛИ ЕЕ ПЕСНЯМИ, ПОТОМ НАЙТИ ЕЩЕ ОДНОГО И ИЗУЧИТЬ ЕГО ТВОРЧЕСТВО И ТАК ДАЛЕЕ.
МЕТОД 2: ПОЙТИ В МУЗЫКАЛЬНЫЙ МАГАЗИН, ВЫБРАТЬ КУЧУ ПЕСЕН И ПРОСЛУШАТЬ ИХ.
Давайте начнем со способов приобретения новых знаний о музыке.
Можно выбрать метод 1, исходя из того, что веб-сайты то и дело подсовывают нам рекомендации, основанные на анализе наших предпочтений. Этот подход известен как анализ связей и гласит: если имеется набор предметов, содержащих что-то общее, будь то песни, фильмы, люди или запчасти для машины, то, анализируя отношения между этими элементами – их связи, мы можем ответить на вопрос «Какой из этих элементов наиболее важен?». Именно в этом мы сейчас заинтересованы больше всего.
Самый простой пример – цитаты. Частое цитирование и большое количество публикаций, упоминающих некую работу, считаются хорошим показателем, подтверждающим ее важность. Этот подход приписывания более высокой значимости участникам, на которых ссылаются другие, помог Google вырваться на передовые позиции. Их результаты на первой странице выглядят для пользователей более значимыми, чем те, что следуют за ними.
Мы изучим два типа связей: степень, с которой вещи связаны друг с другом, и насколько похожи друг на друга эти связанные элементы.
Степень: допустим, у нас есть богатая коллекция, сборник всех песен мира, и мы можем выделить те пары песен, где автор одной повлиял на другого. Мы посмотрим, кто из них творил раньше или обратимся к информации, опубликованной в открытом доступе. Наша схема будет первоначально иметь такой вид:
Если мы сделаем это со всеми песнями, то в конечном итоге у нас получится много кругов и связей или целая сеть. Но в этой сети не хватает важной части, а именно – непрямых ссылок. Если Боб Марли повлиял на Эрика Клэптона, а тот оказал влияние на Пола Маккартни, то резонно предположить, что влияние Боба Марли распространяется также и на Пола Маккартни. Чтобы отследить эти непрямые ссылки, выполним процедуру, известную под названием умножение матриц. Мы размещаем всех исполнителей на квадратной матрице, ставим точку каждый раз, когда артист слева повлиял на артиста в верхней строке и потом поднимаем матрицу каждого по мере роста его влияния, постоянно отслеживая более давний набор ссылок. Когда мы уже не можем идти дальше (это называется достижением транзитивного замыкания матрицы), мы суммируем все данные и получаем что-то похожее на такую схему.
Посчитав количество точек в ряду каждого исполнителя, мы узнаем имена тех, кто сильнее повлиял на других, и сможем выстроить список самых влиятельных артистов и их песен.
Нельзя применить ту же последовательность шагов к деталям машины. Здесь точка может означать техническую зависимость: колесо зависит от оси, а ось – от шасси. Однако метод анализа связей поможет ответить на вопрос типа: «Поступает много жалоб. Мы думаем, что все дело в сложности этой модели. Можете ли вы сделать список наиболее тесно соединенных между собой частей?» Колесо связано с двумя другими частями прямо или опосредованно. Связаны ли они с четырьмя другими узлами, или пятью, или десятью? Большое число связей для певца отражает его значимость. Но для узлов машины много связей – это плохой показатель, так как он может указывать на потенциальную склонность машины к поломкам.
Все вышесказанное может послужить в качестве отправной точки. Переходя из одного жанра в другой, мы движемся от наиболее влиятельного исполнителя ко второму по значимости и так далее. Если на каком-то этапе мы захотим сравнивать песни, то нужно будет изменить подход.
Один из способов определить, какие песни похожи на конкретную мелодию – послушать, что пели до того, как она была написана. Один из способов определить, какие исполнители похожи, скажем, на Боба Марли, – изучить аудиторию: сколько людей, которые слушают Эрика Клэптона, также слушают и Боба Марли? Сколько людей, которые слушают Стиви Уандера, также слушают и Боба Марли? И так далее. Если мы рассмотрим таким образом каждого артиста и ранжируем результаты от большего к меньшему, то у нас появится представление, кто из певцов больше всех похож на Марли. В этом процессе много тонкостей, и его можно усовершенствовать более продвинутыми методами. Например, применяя так называемый коэффициент Жаккара, а не просто считая певцов, мы избежим искажения результатов из-за исполнителей, у которых слишком много поклонников.
Вы видите результат анализа, полученного данным методом, каждый раз, когда ищете что-нибудь в поисковике. То же самое происходит, если вам вешают лапшу на уши в новостях на сайтах социальных сетей, рекомендуют «вещи, которые вы можете захотеть купить» на коммерческом ресурсе, или предлагают общаться «с людьми, которые могут вас заинтересовать» на профессиональном сайте. Газеты тоже занимаются чем-то подобным, составляя статью в стиле, используемом людьми, для которых она предназначена, и затем сравнивая, насколько эта статья похожа на другие. Все сервисы, предоставляющие услуги по просмотру видео, построены на прогнозировании и отборе роликов, которые могут понравиться подписчику, и на контенте, похожем на его любимые ролики. Недавно компания Netflix сообщила в своем блоге, что факторы, принимаемые во внимание при рекомендации фильмов и телешоу, включают в себя не только определенный тип контента (например, «Вы смотрите передачи по научной фантастике, вам может понравиться и другая такая же передача»), но также регион, в котором живет зритель («Вы смотрите кулинарное шоу, но вы находитесь в Индии, так что вам могут понравиться болливудские фильмы»). Подсчитано, что 80 % роликов, просмотренных на сайте Netflix, – это результат рекомендаций пользователям. Как мы видели в главе 4, соединение таких связей с правильным анализом могут породить открытие.[29]
Метод 2 предполагает случайную выборку. В музыкальном магазине вы подходите к коробке и вытаскиваете оттуда сразу несколько дисков. Как и при любой случайной выборке, вы не можете узнать, насколько близки выбранные диски к разделу музыки, который вам нужен. Даже если вы сразу наткнетесь на популярную музыку, вы не сможете это понять. Работая с результатами анализа связей, мы уже не должны полагаться на случайные догадки о том, с чего начать поиск.
Если бы Фою были доступны эти технологические преимущества, мы могли бы представить два метода на примере следующих графиков. Метод 1 требует в худшем случае линейного времени, а на метод 2 уйдет постоянное количество времени. Метод 2 – линейный (в худшем случае), так как Фою придется теоретически прослушать все песни в мире, прежде чем он найдет ту, которая ему нужна. Метод 1 – постоянный, потому что независимо от количества песен в мире Фой начинает свой путь с наиболее популярных произведений.
Чтобы увидеть, насколько универсален прикладной метод решения задачи Фоя, давайте рассмотрим пример из абсолютно другой сферы – политики. Вплоть до XIX века американская политическая система выглядела совершенно иначе. Во время выборов улицы были заполнены мужчинами (женщины не обладали правом голоса до 1920 года), которые проводили демонстрации, выпивали – и голосовали. Но позже голосование стало менее публичным актом, и политикам пришлось самим искать себе избирателей. В 1890 году Уильям Дженнингс Брайан придумал способ, который можно, вероятно, назвать первым примером рассылки, – что-то вроде базы данных своих сторонников. В ХХ веке такие базы распространились повсеместно, а к XXI их уже освоили все партии, поскольку они помогают воздействовать на людей, исходя из их потребительских привычек.
Эта многовековая тенденция доказывает: для политических партий, если они хотят эффективно вербовать избирателей и в конечном счете экономить деньги и время, важно знать, где искать свой электорат. Вместо того чтобы распространять агитацию на всю страну, более эффективно адресовать ее тем людям, которые с большей вероятностью поддержат их программу.
Этот подход применяется в самых разных сферах, где существует проблема охвата аудитории и влияет сегодня практически на всех пользователей популярных веб-сайтов и сервисов.
Что все это значит для Фоя? Повысил ли он свой культурный уровень, к чему так стремится? Мы не знаем этого, так как нашей задачей было помочь ему начать путешествие, а не достичь цели.
Одна из ловушек, подстерегающая того, кто вознамерился научиться чему-то новому, заключается в том, что он рискует не с того начать. Это может привести к неудачам, разочарованию в предмете интереса или же к прекращению начатого дела. Результат анализа связей, инновации, поддерживаемые Интернетом и в скором будущем, вероятно, электронными приборами, которые смогут общаться между собой, – это один из способов для любопытных людей вроде Фоя обрести новые знания. В случае с Фоем технология, которая проанализирует миллионы песен, поможет ему приобщиться к миру культурных и просвещенных людей гораздо быстрее, чем если бы он ею не пользовался. Он уже подписался на рассылку встреч местных клубов любителей музыки, поэтому все выглядит обнадеживающе.
ОСВАИВАЙ ВСЕ ЭТО, ФОЙ. ПУТИ ЖИЗНИ, КАК СКАЗАЛ БЫ УСАТЫЙ НЕМЕЦКИЙ ФИЛОСОФ, РЕДКО БЫВАЮТ ПРОСТЫМИ. НО ЗА ТРУДНОСТЯМИ СЛЕДУЕТ ВОЗНАГРАЖДЕНИЕ.
7 Обнови статус
Некто Дуэйн отправился в поход по Скалистым горам Канады. Здесь кристально чистые озера с бирюзовой водой прячутся в лесной чаще, а в воде отражается все величие грандиозных гор и деревьев. Птицы щебечут, порхая в чистом небе, а с запада дует нежный бриз. В такие моменты кажется, что весь наш мир – царство тишины и покоя. Как будто нигде не льются реки крови, нет всемирного потепления и нищеты. «Идеалисты правы, – шепчет проплывающая в небе тучка, – несомненно, правы».
И все же мысли Дуэйна витают далеко отсюда. Сегодня утром, когда группа выдвинулась из Ванкувера, ему довелось стать свидетелем необычного зрелища. Он видел, как утка прохаживалась вдоль берега, виляя хвостом, как будто танцевала румбу. С тех пор нет ему покоя – он изо всех сил старается составить смешное, но в то же время короткое предложение, чтобы описать всю прелесть сцены, используя не более 140 символов. Такое ограничение диктует прибор, созданный для того, чтобы расширить нашу свободу. Дуэйн не может подвести армию незнакомцев, на чье восхищение он рассчитывает.
Мозг, как утверждают нейрологи, обладает способностью выделять во всем отличительные черты. Когда в тихой комнате вы слышите какой-то шум, ваш мозг фиксируется на нем. Если вы находитесь в шумной комнате и слышите звук, непохожий на другие шумы, то ваше сознание непременно вычленит его. Информация, которая встречается часто, обычно рассматривается мозгом как менее значимая, и он отфильтровывает ее поток.
Метод, которого придерживаются многие, печатая эсэмэски с пропуском часто встречающихся букв, например гласных, частично основан на положении из теории информации. Оно гласит, что «длжна передвться тлько инфрмция сущствнная для ншго понмния». Благодаря избыточности языка предыдущее предложение понятно, потому что пропущенные буквы можно угадать. Поэтому, когда нам надо сократить текст и не потерять суть, как в случае с Дуэйном, такой подход вовсе не так уж плох. Именно так мы делали до появления системы упрощенного набора текста.[30] Но вместе с экономией места этот подход приводит к потере данных, пусть неинформативных и несущественных.
До сих пор мы говорили о более быстрых или более медленных способах выполнения задач, а сейчас речь пойдет о вещах, которые занимают больше или меньше места. Этот баланс важен для оценки различных подходов к решению проблем: часто ученые-компьютерщики сравнивают скорость разных методов (временна́я сложность выполнения задачи), но иногда оценивают, как много памяти или места на диске эти методы занимают (пространственная сложность).
ЦЕЛЬ: СОЧИНИТЬ ОСТРОУМНУЮ ФРАЗУ-СТАТУС, КОТОРАЯ СОДЕРЖИТ НЕ БОЛЬШЕ 140 СИМВОЛОВ.
МЕТОД 1: ЗАМЕНЯТЬ ДЛИННЫЕ СЛОВА НА КОРОТКИЕ, НО МЕНЕЕ ТОЧНЫЕ.
МЕТОД 2: ОПУСКАТЬ ЧАСТО ВСТРЕЧАЮЩИЕСЯ БУКВЫ, НАПРИМЕР ГЛАСНЫЕ, В НЕКОТОРЫХ СЛОВАХ.
Поразительно, но у метода 2 есть аналог в информационных технологиях. В 1952 году ученый Дэвид А. Хаффман изобрел способ сокращения пространства, необходимого для хранения данных. В отличие от прежних методов алгоритм Хаффмана не требовал удаления информации, а концентрировался на оптимизации.
Компьютеры хранят словесную информацию, кодируя буквы алфавита, цифры и другие символы и занося их в таблицу, где им присваиваются числовые значения. Эти значения затем сохраняются в том виде, какой понимает компьютер, – он называется бинарным, или двоичным, кодом. Каждый символ в нем представлен в виде кода, который может состоять из семи бит. Например, буква «а» английского алфавита имеет значение 97, а в двоичном коде запись этого числа выглядит так:
1100001
Буква «b» имеет значение 98 и в двоичном коде она такая:
1100010
Если бы нам нужно было представить слово «hans» в двоичном коде, то оно бы выглядело так (каждая буква занимает 7 бит, всего 28 бит):
1101000 1100001 1101110 1110011
То обстоятельство, что символы имеют двойные коды одинаковой длины (в нашем случае 7 бит), позволяет легко декодировать бинарную цепочку. Все, что нам нужно сделать, – считывать каждые семь бит и затем, используя таблицу соответствий, перекодировать их в слова английского языка.
Но Хаффман был хитер. Он посмотрел на эти семь бит и сказал: «Конечно, должен быть способ сжимать данные». Друзья отговаривали его. «Нет, Хаффман, – говорили они. – Этого нельзя сделать. Ты слишком многого хочешь. Не рвись в герои». Но Хаффман не слушал их. Он был готов броситься с головой в неизвестность, чтобы изобрести другое бинарное представление набора символов.
Вместо использования бинарных кодов с фиксированной длиной Хаффман стал применять бинарные коды разной длины. Он опирался на факт, что некоторые символы встречаются в письменной речи чаще, чем другие, поэтому он присвоил этим часто встречающимся буквам меньшие величины. Соответственно они имели более короткий бинарный код, а реже встречающиеся символы – более длинный.
Например, для нашего набора данных частота встречаемости символов распределяется так, как показано на таблице слева.
Буква «е» встречается нам 705 раз, буква «а» – 605 раз и так далее. Заметьте, что символы отсортированы сверху вниз в порядке убывания частоты. Согласно подходу Хаффмана, нужно взять пару символов с наименьшей частотой встречаемости, сложить их значения, сохраняя результат в новом вре́менном символе, а затем отсортировать набор. Процесс повторяется, пока у нас больше не останется пар символов.
В конечном итоге получается дерево, где каждый узел (символ) соединен с парой узлов, на основе которых он образовался, с двумя краями. Если мы произведем такую операцию с приведенным выше набором данных, то в конечном итоге получим что-то вроде схемы, где мы сначала соединяли «f» и «j», затем результат этого действия совмещали с «l» и так далее. Каждая колонка, начиная со второй, представляет собой один шаг алгоритма.
Когда мы преобразуем схему в дерево, все становится яснее. Оптимизированный двоичный код символа – это цепочка, которую мы получаем, считывая биты с самого верхнего, или корневого,[31] узла и двигаясь ниже к узлу символа. Каждый раз, когда мы двигаем дерево влево, мы прибавляем ноль к двоичному коду символа, а при движении вправо добавляем единицу. Поэтому буква «е» заканчивается двухбитным двоичным кодом 11, а буква «f» представляет собой пятибитный код 10001. Приписывание 1 или 0 к дочернему узлу дерева Хаффмана производится факультативно, то есть литера «е» может быть закодирована как «01», а не как 11. Несмотря на то что двоичные коды не всегда уникальны, они считаются наиболее оптимальными. В любом случае дерево Хаффмана отсылается адресату вместе с сообщением, чтобы получатель знал, как его раскодировать.
Вот список оптимизированных двоичных кодов. Заметьте, что самые частые буквы имеют наиболее короткие коды.
Как же будет выглядеть слово «hans» в двоичном коде?
001 01 101 000
Для такой записи нам понадобилось 11 бит, а не 28. Это открытие заставляет вспомнить историю почти столетней давности о том, как передавали сообщения по телеграфу. Способ Самюэля Морзе кодировать буквы также был основан на том, насколько часто эти буквы встречались в английском языке. Морзе определял частоту различных букв не в ходе бесед с учеными или анализа данных – он просто считал литеры в шрифтовой каретке наборщика в типографии. Так что в следующий раз, когда какой-нибудь умник начнет критиковать ваши методы исследования, не отступайте.
Техники компрессии данных, подобные кодированию методом Хаффмана, чрезвычайно важны в современном мире. Оптимальное использование пространства означает, что вебсайты будут загружаться быстрее, веб-серверы могут сжимать файлы, прежде чем рассылать их по сети, а современные браузеры сумеют легко распаковывать их. Если место ограниченно, любое увеличение скорости имеет значение.
Компрессия также означает, что фильмы (то есть файлы формата MPEG-2), изображения (файлы формата JPEG) и песни (файлы формата МРЗ) могут занимать меньше пространства, что позволит сэкономить деньги на их хранении и пересылке. Аудиофайлы типа МРЗ интересны в том плане, что их сжатие основано на удалении того диапазона аудиосигналов, который человеческое ухо не может услышать из-за особенностей своего анатомического строения. Например, оно не воспринимает частоту свыше 20 000 Гц.
В следующий раз, когда вы будете разговаривать по голосовой или видеосвязи с высоким качеством звука и изображения, подумайте о том, что ваша беседа стала возможной благодаря конверсии. Технология достигла такого уровня, что вашему приложению нужно всего лишь послать данные по сети, а потом либо догадаться о содержании, либо реконструировать оставшуюся часть на другом конце. На самом деле компрессия помогает снизить барьер использования технологий.
Все это хорошо. Но что там с Дуэйном и его читателями? Останутся ли они довольны? К счастью, да. Парень удачно выкрутился из ситуации и успешно описал сцену – событие, его юмор и важное сообщение, предназначенное для тех, кто хотел его услышать. Сила написанного слова – вот за что был сожжен на костре Уильям Тиндейл.[32] Парень обновляет свой статус, и сотни нетерпеливых пользователей получают долгожданный хит.
«В фантастическом походе с самого рассвета. Лучшее: утки устроили бесплатное шоу».
Остается надеяться, что умение Дуэйна сжимать сообщения без потери важной информации всегда будет приводить к такому же успешному результату. Если нет, уткам придется его научить.
8 Как все успеть?
Кви Ноа работает в Сент-Луисе, в фирме сельскохозяйственных технологий, которая специализируется на продаже генетически модифицированных семян. Она всего лишь скромная секретарша, и ее босс дал ей кучу заданий, которые нужно закончить к концу недели. Отчетный день – пятница. Осталось всего два дня. Если Кви не выполнит все задания вовремя, ей не разрешат пойти на ежегодный корпоратив в субботу. Этот банкет – единственное мероприятие в жизни фирмы, во время которого начальники и подчиненные общаются на равных. Для Кви это шанс «на людей посмотреть и себя показать». Если ей повезет, то она получит повышение, на которое так давно надеется. Что же ей делать?
Справляться с растущим потоком задач – одно из самых важных умений в жизни взрослого человека. Только подумайте, как много книг и статей вам нужно будет прочитать по теме эффективного планирования рабочего времени, чтобы умело распределять рабочую нагрузку. Кви хорошо знает, что успеть все вовремя – задача непростая, которая потребует напряжения всех сил. Давайте рассмотрим для нее несколько способов достичь цели.
ЦЕЛЬ: ВЫПОЛНИТЬ ВСЕ ЗАДАНИЯ К КОНЦУ НЕДЕЛИ.
МЕТОД 1: ПОРАБОТАТЬ НЕМНОГО НАД ОДНИМ ЗАДАНИЕМ. ПЕРЕКЛЮЧИТЬСЯ НА ДРУГОЕ. ПОРАБОТАТЬ НЕМНОГО. ПЕРЕКЛЮЧИТЬСЯ НА СЛЕДУЮЩЕЕ. И ТАК ДАЛЕЕ.
МЕТОД 2: ОТСОРТИРОВАТЬ ЗАДАНИЯ ОТ САМОГО ПРОСТОГО ДО САМОГО СЛОЖНОГО. НАЧАТЬ С ПРОСТОГО. КОГДА ОНО БУДЕТ СДЕЛАНО, ПЕРЕЙТИ КО ВТОРОМУ ПРОСТОМУ. И ТАК ДАЛЕЕ.
МЕТОД 3: РАССОРТИРОВАТЬ ЗАДАНИЯ ПО ПРИОРИТЕТНОСТИ. НАЧАТЬ С САМОГО ВАЖНОГО. КОГДА ОНО БУДЕТ ЗАКОНЧЕНО, ПЕРЕЙТИ К СЛЕДУЮЩЕМУ ПО ВАЖНОСТИ. И ТАК ДАЛЕЕ.
Все эти методы наверняка знакомы. Применяя метод 1, мы используем единицы времени, чтобы определять, когда переключиться с одного задания на другое. Например, у нас три набора заданий по трем различным предметам в школе, и все нужно сдать до конца недели. Можно посвятить утро одному предмету, день – второму, а вечером заняться третьим. На следующий день повторяем эту схему и так далее, пока не будут готовы все задания. Этот метод распределения времени – хороший пример того, как современные операционные системы справляются с многочисленными приложениями, и его иногда называют контекстным переключением. Диспетчер следит за текущими процессами,[33] отводит им определенное время, а потом контролирует, чтобы каждый процесс умещался в предписанный ему хронометраж.
Переключение между процессами происходит так плавно, что при наблюдении за операционной системой создается впечатление, будто они протекают параллельно. Сегодня при наличии многоядерных процессоров так оно и есть. Четырехъядерный процессор может одновременно вести четыре процесса, и контекстуальное переключение ему требуется только тогда, когда процессов запускается больше, чем у него ядер.
Это напоминает приложение параллельной обработки, которое имеет аналог в реальной жизни и называется конвейерной обработкой. Набор взаимосвязанных заданий распределяется и выполняется так, чтобы оптимизировать имеющиеся в наличии ресурсы. Например, вы с двумя вашими друзьями вдруг вспомнили, что забыли приготовить мешки с подарками для гостей, а вечеринка вот-вот закончится. Чтобы сделать как можно больше мешков в единицу времени, эффективно применить что-то вроде конвейерного метода: вы пишете поздравления на мешке, один друг складывает в него подарки, а второй – завязывает мешки лентой. Это лучше других подходов, когда один или оба ваших друга будут ждать, пока вы подпишете все мешки. Распределение заданий важно, но до определенной степени: как однажды написал Фред Брукс, девять женщин не родят ребенка за один месяц.
При современных характеристиках «железа» мы не замечаем границ возможностей контекстуального переключения. Между тем каждый раз, когда система его выполняет, ей нужно придержать состояние последнего процесса, очистить регистры и удалить передаваемые данные, а затем загрузить новое состояние процесса.[34]
Для человека когнитивная нагрузка, которая сопровождает этот тип переключения, может быть довольно серьезной. Одно из препятствий на пути обеспечения продуктивности – необходимость прервать текущее занятие, переключиться на что-то срочное, а затем вернуться к предыдущему делу. Операционная система работает подобным образом, запуская так называемый обработчик прерываний, который может временно остановить текущий процесс, чтобы либо передать ему некоторые данные, которых ждет система, либо изменить приоритетность задач.
Если время прерывания достаточно велико, мы можем побороться, приводя разум в состояние, необходимое для выполнения оригинального задания. Контекстное переключение имеет определенные преимущества – оно гарантирует, что мы поработаем по крайней мере над какой-то частью каждого задания. В то же время, когда задача имеет временные рамки, стратегия «Не пропускать ни одного задания» грозит разочарованием и переутомлением.
Метод 2 – это подход, знакомый многим любителям откладывать на потом. В соответствии с ним нужно оставлять сложные задачи под самый конец, а вначале делать только самое простое. Его преимущество в том, что он приносит множество небольших, но быстрых побед. Его часто называют жадным алгоритмом, но этот термин необязательно подразумевает пренебрежение какими-либо делами. Он просто подчеркивает, что алгоритм пытается достичь максимального результата за счет минимума усилий.
Удачное применение жадного алгоритма – найти самую быструю дорогу из одной точки в другую, например, между двумя городами. Мы спрашиваем себя в каждом пункте: «До какого города здесь ближе всего?» Это хороший способ принимать решения, хотя он может помешать вам увидеть оптимальные пути на ранних этапах путешествия. Мы уже встречали разновидность такого подхода в главе 4, хотя Иоаннис просто хотел выбраться из лабиринта и не задумывался, сколько времени у него это займет.
Об алгоритмах поиска кратчайшего пути написано много, и здесь есть несколько соперничающих друг с другом подходов. Один из самых известных называется алгоритмом Дейкстры. Он был создан в 1959 году голландским ученым-компьютерщиком Эдсгером В. Дейкстрой. В более общем виде этот класс алгоритмов известен как алгоритмы поиска по графу.
Другое применение жадных алгоритмов, которое стоит отметить, – это поиск потенциальных совпадений в массиве текста, часто с целью заменить совпавшие символы другими. Например, в тексте есть словосочетание «Джесса Джессика», и мы хотим унифицировать разные варианты написания этого имени. Команда «Искать сочетание «Джесс»», после которой стоит набор других букв, оканчивающийся на «а», даст нам все встречающиеся формы написания этого имени (Джесса Джессика), а не отдельные имена («Джесса», «Джессика»). Поисковик совпадений остановится на последней «а», а не на первой. Иногда это полезно, хоть в данном случае у нас другая цель поиска.
Представьте, что вы едете по незнакомой дороге и видите знак, который показывает, сколько километров до трех окрестных городов. Вы можете поддаться искушению и поехать в ближайший из них.
Нежадный алгоритм сложнее и часто приносит лучшие результаты. Можно увидеть его аналог в военных действиях, где быстрый успех, например защита столицы, приносится в жертву ради более важной победы. Вспомните, как русская армия обошлась с армией Наполеона в 1812 году.
Нежадный алгоритм может быть охарактеризован как длинная, или затянувшаяся, игра. Wall Street Journal недавно опубликовал статью о чемпионах по скрабблу из Нигерии. Их победа была обусловлена не обширным словарным запасом, а интуитивной практикой выбора более коротких слов. Вместо того чтобы подбирать семи- и восьмибуквенные слова, которые приносят больше очков, нигерийские игроки обнаружили, что игра четырех- и пятибуквенными словами приводит к улучшению стратегии в долгосрочной перспективе. Они сохраняли самые сочетаемые буквы для будущих раундов, когда им выпадали не лучшие варианты из мешка. Вот отрывок из статьи, рисующий преимущества такого подхода:
«Британцы лидируют со словом «утверждение», которое дало им 86 очков, но в следующие пять раундов им удавалось выбирать слова, которые приносили меньше 30 очков. После слова «анкета» (93) мистер Джигере вырвался вперед. В финале счет был 449 против 432. Члены команды-победительницы подняли своего чемпиона на руки и понесли по комнате под популярную нигерийскую песню «Мы победили».
Метод 3 устраняет один из недостатков метода 2, фокусируясь на задачах, которые действительно важны. Мы составляем список задач, событий или чего-либо еще и располагаем их по приоритету. Заметьте, что «приоритетность» бывает и функцией «времени завершения», поэтому можно сказать, что метод 2 также располагает задачи в соответствии с их приоритетом. Возьмем, к примеру, принтер. Если в очереди на печать стоит 10 документов по 50 страниц каждый, а за ними идет один одностраничный документ, то, возможно, для принтера имеет смысл поставить последнюю задачу в приоритет, а не заставлять ее ждать до самого конца печати. Разделение двух методов показывает, что приоритетность иногда базируется на других свойствах, а не только на времени выполнения.
Получая новое задание, мы можем поместить его не в конец списка, а куда-нибудь в середину – в зависимости от приоритетности. Включение нового пункта в середину списка приоритетных задач порой приводит к увеличению времени, пока вы стираете старые задачи, освобождая место под новые. В главе 12 мы поговорим о том, как компьютер выбирает способ хранения такого списка (который часто называют очередью с приоритетом), чтобы такие вставки совершались достаточно быстро. Часто в повседневной жизни этот алгоритм наиболее эффективен.
Вот как все три метода выглядят на графике:
При условии, что задачи не зависят друг от друга (то есть очередность выполнения более ранних заданий не связана с временем выполнения последующих задач), все три метода Кви займут одинаковое время.[35] Как было упомянуто в главе 1, мы сравниваем основные операции во всех трех методах, то есть оцениваем, сколько времени Кви тратит на работу над задачами. Если бы мы вместо этого рассматривали, скажем, время, которое уходит у Кви на составление и ведение ее списка задач, то мы бы сказали, что метод 1 занимает постоянное время, то есть 0, а метод 2 и метод 3 занимают в худшем случае логарифмический объем времени. Для чего концентрироваться на одном наборе опций и приносить в жертву другой? Возможно, потому первый набор больше способствует достижению итоговой цели по сравнению со вторым, поскольку составление и ведение списка заданий – не такое уж сложное дело.[36] Больше об этом будет рассказано в главах 10 и 12.
Недостаточно смотреть на относительные величины; когда речь идет о результате задания, все становится существенным. Это относится и к алгоритмам, исполняемым за постоянное время. Представьте работника парковки, который хочет впихнуть как можно больше машин в ряд, чтобы эффективнее использовать пространство. Все ваши алгоритмы по выезду с парковки могут быть таковыми, но уровень сервиса разительно отличается. Например, если не оставлять свободного проезда, то парковщику придется в худшем случае убрать восемь других машин, чтобы добраться до нужного авто. Если оставлять проезд свободным все время, то придется убирать максимум три машины. Введение временных ограничений на то, когда можно оставлять или забирать машины, с правилом «без привилегий на въезд и выезд» позволит вообще не убирать другие машины при возвращении авто клиенту.
Если Кви не удастся выполнить задание в полном объеме, то какой результат будет для нее вторым по значимости? Если она решит уделять больше внимания высокоприоритетным задачам, то вдруг первое же задание, за которое она возьмется, займет целую неделю? Можно ли это совместить?[37] Такие вопросы порой порождают творческие и оригинальные решения.
Отступление: в романе Кейго Хигашино «Страсть подозреваемого Х» (2005) учитель математики говорит о решении геометрической задачи путем превращения ее в алгебраическую, чтобы понять, как оценивают его студенты свои пробелы в знаниях. Это удивительное напоминание о том, насколько легко принимать прочитанное как данность, не оспаривая его. Мы интерпретируем новую информацию тем способом, который соответствует имеющимся у нас знаниям. Это явление ученый-компьютерщик Алан Кай назвал релятивизацией. Оно может стать и пороком, и добродетелью, в зависимости от того, как ее использовать.
9 Как починить ожерелье?
Джо – независимая ремесленница. Она продает свои поделки на рынке в Нью-Мехико, или на Индейском рынке, как его часто называют на рекламных плакатах. Много лет она страдает от ревматоидного артрита, поэтому ей все труднее зарабатывать на жизнь. Ее работа связана с ручным трудом: она изготавливает на заказ ожерелья с именами. Прилавок Джо расположен рядом со входом на рынок, и она убеждает каждого посетителя, что лучший подарок, который можно купить на рынке, это ожерелье с именем любимого человека или своим собственным.
Маленькая девочка поддалась на ее уговоры. «Меня зовут Жаклин», – говорит она. Джо приступает к работе, нанизывая бусины на простой кусок шпагата, к которому на концах приклеивается застежка. Она отдает законченную вещь девочке, но та мотает головой. Ей не нравится ожерелье. «Простите, но в моем имени две буквы «к». Разве вы не знали, что детям теперь модно давать оригинальные имена?» Бедная Джо!
В главе 1 мы говорили о массивах как о способе хранить группы элементов, которые могут быть быстро просмотрены в линейном времени. А в главе 3 мы узнали, что есть алгоритмы для выполнения заданий, на которые уходит постоянное количество времени независимо от величины задания. Сейчас мы поговорим об алгоритме, который концентрируется на возможности добавлять и удалять элементы в любых точках и за постоянное время. Для начала давайте рассмотрим два способа, при помощи которых Джо может исправить ожерелье Жаклин.
ЦЕЛЬ: ДОБАВИТЬ ШАРИК С ПРОПУЩЕННОЙ БУКВОЙ НА ОЖЕРЕЛЬЕ.
МЕТОД 1: РАССТЕГНУТЬ ОЖЕРЕЛЬЕ, УДАЛИТЬ ВСЕ БУСИНЫ, ПОКА НЕ ДОБЕРЕШЬСЯ ДО БУКВЫ «К» ИЛИ «Л». ДОБАВИТЬ ПРОПУЩЕННУЮ БУКВУ, НАНИЗАТЬ ОСТАЛЬНЫЕ БУСИНЫ.
МЕТОД 2: РАЗРЕЗАТЬ ОЖЕРЕЛЬЕ МЕЖДУ БУКВАМИ «К» И «Л». ВСТАВИТЬ БУКУ «К» НА ЛЮБОЙ ИЗ ОТРЕЗКОВ. СКРЕПИТЬ ШПАГАТ КЛЕЕМ.
У массивов есть недостатки – элементы, которые появляются рядом друг с другом, так же рядом и хранятся в памяти. Если возникает необходимость вставить новый элемент между двумя другими, мы не можем сделать это просто так: нам придется сдвинуть все элементы, расположенные после этой точки, чтобы освободить место для нового. Так поступают в соответствии с методом 1. Джо нужно по очереди удалить бусины с любого конца ожерелья, пока она не доберется до места, где должна стоять дополнительная бусина. Потом она нанизывает ее на шпагат и ставит на место все остальные. Процесс займет вдвое больше времени, если имя заказчика будет длиннее в два раза.[38]
Новизна метода 2 состоит в том, что кусок шпагата может быть разрезан в любой точке и затем связан или склеен. Это важное свойство шпагата, потому что – и в этом мы сейчас убедимся – оно позволяет нам устранить главный недостаток массивов, в которых добавление или удаление элемента означает высокие трудозатраты. До определенного момента метод 1 может оказаться лучшим: чего стоит удаление одной-двух бусин по сравнению с разрезанием шпагата и связыванием двух концов? Но вряд ли его преимущество сохранится, если в ожерелье окажется больше бусин.
В информатике существует структура, которая проявляет именно это свойство, и вот как она выглядит:
У нас есть группа элементов, но мы больше не ограничены необходимостью хранить их рядом друг с другом. Вместо этого каждый элемент в группе просто указывает на другой, стоящий рядом с ним. Эта связь, или же ссылкамежду каждой парой элементов, очень похожа на шпагат Джо. И теперь, если мы хотим добавить элемент, нам не нужно больше освобождать для него место. Мы можем просто видоизменить соответствующие ссылки. То же самое относится и к удалению элементов.
Эта структура, разработанная еще в 50-е годы, известна под названием связный список. Она стала основой для многих приложений в вычислительной технике из-за ее эффективности при вставке и удалении элементов из группы в заданной точке. Например, в главе 8 мы упомянули, что принтер может ставить задания в очередь, хранить их в списке и решать, поместить ли менее объемные задания перед другими. Эффективным способом для этого будет создание очереди с использованием связного списка.
По-прежнему следует помнить, что мы концентрируемся на фундаментальных операциях. Есть и другие операции, такие как поиск элемента, который мы хотим добавить после нового. В большинстве случаев время, затраченное на поиск этого элемента как в массиве, так и в списке, будет одинаковым.
Другое приложение – текстовый редактор. Он выбирает, представить ли текст в документе через сохранение его в виде строк в связном списке. Тогда, передвигая строчки или добавляя новые между уже имеющимися, программа просто меняет ссылки на строки, а не физически передвигает их в памяти. Деталь, которая восхищает нас больше всего, – ссылки идут один раз, от каждого пункта к следующему.
В некоторых случаях, как в примере с текстовым редактором, строка выигрывает не только от знания того, какая строчка идет за ней, но и от того, какая стоит перед нею. Когда курсор находится на конкретной строке и мы двигаем его наверх, наш редактор следует по ссылке к предыдущей строке, а не возвращается к началу связного списка (известного как заголовок), чтобы двигаться от узла к узлу. Модификация до связного списка приводит к появлению структуры под названием двунаправленный связный список. Название, похоже, придумано тем же весельчаком, который окрестил портативную радиостанцию «walkie-talkie» – «гуляй-болтай».
Джо, конечно, не пасует перед трудностями, но все равно она выиграет, узнав о быстром способе исправить ожерелье. Кстати, точно так же сценаристы правили свои сценарии до изобретения компьютерных программ и текстовых редакторов. Они разрезали лист и прилепляли к нему нужный кусок.
Вот как метод Джон выглядит на графике.
10 Возьми коробку
Людвик продает компьютерные товары в магазине на Миссион-Стрит. Он живет рядом на 14-м этаже сорокаэтажного жилого комплекса, где все помещения общего пользования находятся под видеонаблюдением. Чтобы зарабатывать и покрывать расходы на растущую аренду, Людвик часто подбирает картонные коробки из склада утильсырья в своем доме и использует их для отправки модулей памяти клиентам за границу. Помещение для утиля есть на каждом этаже здания.
Недавно поступил заказ, который нужно выполнить сегодня, а почта закрывается через 15 минут. Людвику нужно срочно найти картонную коробку для посылки.
ЦЕЛЬ: ПРОЙТИ КАК МОЖНО МЕНЬШЕ ЭТАЖЕЙ, ЧТОБЫ НАЙТИ ПУСТУЮ КОРОБКУ.
МЕТОД 1: ПЕРЕХОДИТЬ С ЭТАЖА НА ЭТАЖ В ПОИСКАХ КОРОБКИ.
МЕТОД 2: ПОПРОСИТЬ ВАХТЕРА ПОСМОТРЕТЬ ЗАПИСИ КАМЕР ИЗ ПОМЕЩЕНИЙ УТИЛЬСЫРЬЯ.
Давайте обсудим, как Людвику достичь цели и найти коробку в своем здании.
Метод 1 – это внутренний алгоритм Людвика. Он начинает с верхнего этажа и идет вниз, преодолевая по одному лестничному пролету. Время, которое потребуется для выполнения задания по этому методу, можно разделить пополам, если попросить друга просмотреть четные этажи, а сам Людвик в это время займется нечетными. Но такой алгоритм остается линейно-временным по причинам, которые мы рассмотрим немного позже.
Метод 2 предлагает более удачный алгоритм и позволяет Людвику выяснить, в какой из комнат есть пустые коробки, если он попросит вахтера просмотреть записи камер. Такой алгоритм дает возможность найти пустую коробку в постоянное время, а не в линейное, так как для этого придется посетить только один этаж. Звонок на вахту – постоянная единовременная цена, которую заплатит Людвик, чтобы избежать линейного роста времени.
Возможно, настал момент обсудить способ, с помощью которого мы измеряем скорость роста. В этой книге мы намеренно идем на упрощение ради ясности. Но все равно важно понимать, что есть разные пути для описания скорости роста определенного алгоритма или функции. Один из них известен как «нотация большой теты» (Big-Theta Notation) и характеризует функцию посредством установки верхнего и нижнего предела. Для большого числа элементов он означает, что функция может расти не быстрее, чем линейная функция (n) или логарифмическая функция (log n), и не медленней, чем другие функции,[39] с которыми она связана.
Поэтому мы позволяем себе утверждать: «Бинарный поиск лучше линейного, потому что в худшем случае он занимает логарифмическое время». Как мы видели в главе 2, бинарный поиск (метод логарифмического времени) позволяет нам найти рубашку на вешалке с сотней рубашек за семь шагов, а на гипотетической вешалке с тысячью рубашками – всего за десять шагов или около того. Сравните это с сотней и тысячью шагов соответственно в случае линейного поиска.
Есть два момента, которые предполагает нотация большой теты. Первое: она опускает коэффициенты, объясняя, что их значения становятся непоследовательными по мере увеличения количества предметов.[40] Итак, степень роста n или n/2 будет характеризоваться линейным временем и записываться как θ(n) – читается «большая тета n». Второе: большая тета рассматривает только главный член в функции, предполагая, что он максимально воздействует на результат функции по отношению к другим членам. До сих пор мы называли этот главный член основной операцией. Приводя пример из информатики, профессор Марк Вайсе разъясняет этот вопрос:
В функции 10N3+N2+40N+80, для N =1 000 величина функции есть 10 001 040 080, из которых 10 000 000 000 приходится на член 10N3.
Итак, если метод 1 заставляет Людвика посетить этаж, где он живет, скажем, два раза, мы охарактеризуем время, которое уходит у него на достижение цели в худшем случае как t(n)=n+1, где +1 обозначает этот дополнительный визит, и он записывается в нотации большой теты как θ(n).
Это допущение требует нескольких оговорок.
Например, бывают случаи, в которых второстепенные члены оказывают серьезное влияние на функцию. Вспомните Джо и ее ожерелье из главы 9. Мы сконцентрировались на добавлении бусин и рассматривали первый метод как линейно-временной, а второй – как постоянно-временной и при этом более привлекательный. Мы по умолчанию признавали, что склеивание свободных концов шпагата было простым заданием – но если клею нужно пять минут, чтобы схватиться? Повлияет ли это на выбор Джо? Такие постоянные величины наиболее заметны, когда мы имеем дело с малым числом элементов и должны учитывать их наличие.
Две другие нотации, которые дополняют большую тету и оперируют при тех же условиях, – большая омега и большая о. Большая омега устанавливает нижнюю границу функции для достаточно большого значения n, то есть она говорит, что наша функция может расти не медленней, чем ее нижняя граница. Большая о определяет верхнюю границу функции для достаточно большого значения n, то есть говорит о том, что наша функция может расти не быстрее, чем верхняя граница. Конечно, в действительности функция может расти медленней, чем верхний предел и, таким образом, быть более привлекательной, но большое о – пессимист и воплощение закона Сода.[41]
Когда мы говорим о скорости роста алгоритма, мы имеем в виду его действенность в худшем случае, когда он тесно связан, по оценке большой теты. Заметьте, что любой уровень скрытности, двуличия, обмана, который мы допускаем в этой книге, порождает компромисс. Важно знать, что в реальности больше нюансов, чем в теории, – об этом можно прочитать в источниках, перечисленных в конце книги. Что касается Людвика, то различия в двух алгоритмах очевидны, что делает решение его проблемы достаточно легким.
11 Заполни полки
Терри учится на втором курсе престижного вуза Medlock High в Беверли-Хиллз (Калифорния). Он наказан (оставлен после занятий) за затеянную на лекции по социологии провокационную дискуссию на тему «Не во всем должны быть авокадо и капуста». В качестве воспитательной меры куратор отправил Терри в школьную библиотеку и велел выставить книги на только что купленную полку. Старая полка недавно обрушилась, и около 250 книг оказалось на полу. Все, что нужно сделать второкурснику-бунтарю, – выстроить книги на полке в алфавитном порядке по фамилиям авторов. Терри собирается вечером сходить в кино с друзьями и не хочет застрять в университете до полуночи. Ему удастся все сделать, но нельзя терять ни минуты.
ЦЕЛЬ: ВЫСТАВИТЬ ВСЕ КНИГИ НА ПОЛКУ В АЛФАВИТНОМ ПОРЯДКЕ.
МЕТОД 1: ВЗЯТЬ КНИГУ И ПОСТАВИТЬ ЕЕ НА ПОЛКУ. ВЗЯТЬ ДРУГУЮ И ПОСТАВИТЬ ЕЕ ПЕРЕД ИЛИ ПОСЛЕ ПЕРВОЙ, В ЗАВИСИМОСТИ ОТ ФАМИЛИИ АВТОРА. И ТАК ДАЛЕЕ.
МЕТОД 2: ИСПОЛЬЗОВАТЬ КНИЖНЫЕ ДЕРЖАТЕЛИ, ЧТОБЫ ОСТАВЛЯТЬ МЕСТО ПОСЛЕ КАЖДОЙ БУКВЫ АЛФАВИТА, ЗАТЕМ СТАВИТЬ КНИГИ, ПЕРЕМЕЩАЯ ДЕРЖАТЕЛИ ПО МЕРЕ НАДОБНОСТИ.
Давайте вначале решим, как Терри может поступить с заданием. Мы видели в главе 15, что подходы к сортировке, которые строятся на сравнении смежных элементов и определении, какой из них больше, а какой меньше, занимают квадратичное время. Мы говорили, что примеры такого подхода на практике включают в себя сортировку вставкой, сортировку выбором и пузырьковую сортировку и что все они работают, используя образец с минимальными различиями. Метод 1 Терри – это тот же подход, что и метод 1 Чарли из главы 5.
Здесь интересно, что усовершенствованный метод Терри не останавливается на алгоритме разбивания, как в случае с Чарли. Он модифицирует оригинальный алгоритм квадратичного времени. Это происходит при внедрении относительно простой инновации. Если мы возьмем такой алгоритм, как сортировка вставкой, мы обнаружим, что самым медленным действием будет помещение элемента на правильное место. Каждый раз после того, как мы делаем это, приходится менять расположение всех последующих элементов, передвигая их один за другим.
Что происходит при применении метода 2 Терри? Он заранее учитывает эти сдвиги, создавая пустые пространства по всей длине полки через равные промежутки. Найдя нужное место для вставляемой книги, Терри, вероятнее всего, передвинет лишь несколько других книг. Чем больше и шире эти свободные пространства, тем меньше книг ему придется сдвигать каждый раз.
Эта модернизация метода сортировки путем вставки ведет от алгоритма квадратичного времени к линейно-логарифмическому «с высокой вероятностью», как выразился его автор, и называется библиотечной сортировкой. Вспомните идею из главы 10: расставление книжных держателей по полке может сделать этот подход медленнее, если книг мало, но при их достаточно большом количестве он обладает преимуществом перед альтернативным алгоритмом.
Вот как два этих подхода выглядят на графике:
Возможно, мы лучше поймем выигрышность этого подхода, рассмотрев альтернативный, чуть более ограниченный сценарий. Вот какую мрачную картину рисуют авторы библиотечной сортировки: технологическая индустрия накрылась медным тазом, мир устал от ее глупых идей. Тысячи уволенных работников нашли убежище в некоем месте, где применяют свои таланты в обмен на бесплатную пиццу с приправами. Приток специалистов привел в восторг университеты по всей стране. Все рады, кроме архивариуса в том самом колледже. Да, пятнадцать лет назад его звали Терри. Он заведует полками с ячейками, которые промаркированы именами всех выпускников кафедры, расположенными в алфавитном порядке, и затем двигает поверх всех остальных лейблов один.
Теперь, когда частота движения ячеек достигла космической скорости, Терри вспомнил об алгоритме, который он применял когда-то в школе. Он признает, что подобный подход поможет снизить его стресс за счет высвобождения свободного пространства. И вот он создает пустые кармашки между занятыми ячейками.[42]
Недавнее упоминание о «высокой вероятности» подводит нас к важной теме и одновременно сути этой главы. Прежде мы мимоходом упоминали о «худших случаях» и «средних случаях» для разных алгоритмов. Эти существенные показатели позволяют спрогнозировать, сколько времени уйдет у определенного алгоритма на перебор всего ряда элементов.
Время осуществления алгоритма зависит от многих условий. Например, в коде мы можем столкнуться с присутствием логических ветвей (если это не ваш случай, то пропустите этот абзац). Исходя из того, какой путь выбран, время пробега может варьироваться. Хороший пример – быстрая сортировка, которая упомянута в главе 5. При быстрой сортировке разделение начинается в первую очередь с выбора опорного элемента. Этот элемент используется для разделения массива данных на две группы: в одной содержатся элементы меньше опорного, в другой – больше него. Когда опорный элемент выбирается наугад, быстрая сортировка в среднем случае проходит в логарифмическом времени. Если опорный элемент слишком велик или слишком мал, быстрая сортировка может идти в квадратичном времени в худшем случае. Это изменение в производительности происходит из-за того, что опорный элемент не справляется с разделением массива элементов на каждом этапе, и приходится проверять почти каждый элемент на каждом из тех этапов, которые, как мы видели в ранних главах, являются атрибутами квадратичного алгоритма.
Анализ быстрой сортировки показывает, что алгоритм имеет высокую вероятность прохождения в линейно-логарифмическом времени. Мы знаем, что нужно сделать, чтобы достичь этого, – убедиться, что опорный элемент не является самым верхним или самым нижним в массиве. Таким образом элемент с усредненным значением применим практически для всех случаев и может гарантировать, что быстрая сортировка пройдет в линейно-логарифмическом времени.
Но иногда вероятной гарантии все же недостаточно. Если наш алгоритм работает с таким приложением, как управление космическим шаттлом, или представляет угрозу для чьей-то жизни, регулирует работу инфузионного насоса или дефибриллятора, то показатель наихудшего случая будет нас сильно беспокоить. Классификация потенциального результата полезна и в других приложениях, применимых в повседневной жизни.
Для Терри средний случай линейно-логарифмического времени более чем предпочтителен, хотя поиск по его алгоритму в худшем случае будет проходить в квадратичном времени. Сейчас ему не о чем волноваться. Пока у него достаточно книжных разделителей, он успевает в кино вовремя.
12 В супермаркете
Вурзма Моне до недавнего времени работал менеджером в фонде управления инвестиционными бумагами. Непостижимое решение стать рэпером возникло у него после того, как он прочитал в одной из школ лекцию о страховке кредиторов от дефолта. Беседа прошла под лозунгом «Кем работает мой отец», и к полудню Вурзма решил вести более осмысленную жизнь. Он ходит в местный супермаркет каждые две недели и часто ловит себя на том, что бродит по проходам из одного конца в другой в поисках нужных ему вещей из списка покупок. Туда-сюда, туда-сюда – у него уходит целая вечность на покупки. Визит в магазин еще больше затягивается из-за странной походки Вурзмы, которая мало походит на «крутую пацанскую» и больше напоминает ребят, которые своим видом будто говорят: «Я пропустил очередную консультацию у психотерапевта». Другие рэперы сразу замечают это несоответствие, и хрупкое доверие к Вурзме со стороны уличной продвинутой молодежи еще больше слабеет. Ему надо перестать выглядеть идиотом и избавиться от мыслей, обрекающих его на смехотворное существование.
Вурзма находится на перепутье. Но у нас хорошая новость: похоже, мы знаем, как ему помочь, и в этой главе рассмотрим варианты, о которых уже говорили в предыдущих главах. Есть два способа, которые Вурзма может использовать, бродя по супермаркету в поисках продуктов из списка.
ЦЕЛЬ: СВЕСТИ К МИНИМУМУ КОЛИЧЕСТВО РЯДОВ, ПО КОТОРЫМ НУЖНО ПРОЙТИ.
МЕТОД 1: ПРОСМОТРЕТЬ ВЕСЬ СПИСОК ПОКУПОК ПО ПУНКТАМ.
МЕТОД 2: ПОДГОТОВИТЬ СПИСОК ЗАРАНЕЕ, ЧТОБЫ ВСЕ БЫЛО РАЗЛОЖЕНО ПО КАТЕГОРИЯМ. ПРОСМАТРИВАТЬ ОДНУ КАТЕГОРИЮ ЗА ДРУГОЙ, СОВЕРШАЯ ПОКУПКИ.
Я положу свой массив в твой массив, чтоб ты не стартовал, не спросив
До сих пор мы говорили о массивах как о фундаментальной структуре, предназначенной для хранения набора элементов. В главе 6 мы ввели еще одну полезную структуру под названием матрица, которая также нужна для хранения групп элементов. Но здесь они сохраняются в двух измерениях, а не в одном. Что общего у этих двух структур? А то, что массив может быть преобразован в матрицу. Все, что нужно для этого сделать, – вместо сохранения литер (как, например, цифра, буква или слово) в каждом расположении сохранить массив. Массив массивов называется двумерным, или в более общем виде многомерным массивом.
Многомерные массивы позволяют нам с Вурзмой сделать одну полезную вещь – сохранить список покупок в двух измерениях, что позволит нашему герою двигаться по любому подмассиву в зависимости от отдела, в котором он сейчас находится.
Итак, список покупок из простого перечня пунктов становится списком категорий, причем каждая из них, в свою очередь, представляет собой список пунктов.[43] Поскольку продукты в магазине обычно группируются по категориям, Вурзма может просто отправиться в ту часть магазина, где находятся, например, предметы личной гигиены, пробежаться по массиву под названием «личная гигиена» и взять нужные ему вещи со стеллажа. То же самое – для всех остальных покупок. Вот как занимаются шопингом по методу 2. Если бы Вурзма использовал обычный список – массив, как в методе 1, то он бы бродил примерно 13 минут от одного ряда к другому, в худшем случае – просто изучая полки.
Вурзма проходит мимо всех стеллажей для покупки одного предмета из списка. Если n – число проходов, а m – количество пунктов в списке, тогда n/2 × m=(nxm/2). Иными словами, для покупки 20 вещей Вурзма проходит через 20 рядов 20 раз. Принимая во внимание, что для прохождения каждого ряда требуется 2 секунды, то потерянное время составит до 13 минут. С методом 2 его общее время на ходьбу между рядами составляет примерно минуту, так как он не появляется в одном и том же ряду больше одного раза. Вурзма в лучшем случае проходит все ряды один раз, то есть n/2. Так что для приобретения 20 наименований покупок Вурзма, идя от одного ряда к другому, теряет меньше минуты.
Заметьте, что метод 1 не выглядит в точности как сортировка по квадратичному времени, которую мы видели в главах 5 и 11. Он следует шаблону, заставляя Вурзму в худшем случае пройти по всем рядам в магазине для каждой покупки в его списке. Вот как сравниваются два метода:
Бум-бум-бум, делай это часто и пожалеешь, как герой книги Мураками
В главе 1 мы говорили о хеш-таблицах и о том, как они полезны, когда нам нужно провести быстрый обзор и не беспокоиться о порядке. Разговор о многомерных массивах дает нам прекрасную возможность расширить наше знание о хеш-таблицах. Раньше мы принимали на веру, что хеш-функция всегда отмечает позицию элемента, назначая ему уникальное местоположение в хеш-таблице, и именно благодаря этому гарантируется его быстрое нахождение в любое время. В реальности хеш-функция может столкнуться с таким явлением, как коллизия, при которой соответствующее место в хеш-таблице уже занято другим элементом. Это происходит либо потому, что хеш-функция неидеальна, то есть не работает правильно и не обеспечивает единообразного распределения значений хеш-функции, либо у нас больше элементов для хранения, чем может вместить таблица. Степень заполнения хеш-таблицы называется коэффициентом заполнения и равна нулю, когда хеш-таблица пуста, или единице, когда она заполнена.
В таких случаях есть несколько способов разрешения коллизии. Один из них известен под названием метод цепочек. Во время создания цепочки возникает не хеш-таблица элементов, а хеш-таблица группы элементов. Таким образом, когда происходит коллизия, соответствующий пункт перемещается в конец группы и поэтому не происходит непреднамеренной перезаписи данных.
Итак, у нас есть хеш-таблица, которая представляет собой группу групп элементов. Когда наша хеш-функция находит место, в котором имеется множество элементов, нам приходится перебрать их все, пока не найдется искомый. Этот процесс, конечно, полностью прозрачен для пользователя.
Думаешь, куда пойти потом? не волнуйся, я тебе покажу направление, так что поторопись
Нужно подчеркнуть еще одну вещь: многомерный массив заранее навязывает нашим элементам приоритет, а именно – расстояние от входа магазина до конкретного ряда, где находится нужная вам вещь. Возможно, пора расширить наши знания об очередях с приоритетом, о которых мы упоминали мимоходом в главе 8. Там мы говорили, что, когда вы составляете некий приоритизированный список элементов, а после нужно добавить к нему новый элемент, может понадобиться стереть некоторые части списка, чтобы освободить место. Довольно скоро дело заходит в тупик, и вы обнаруживаете, что нужно делать новый список. Как может машина составить такой список с эффективностью, которую мы ждем от нее?
Мы уже видели структуры, оптимизированные для быстрого просмотра (массивы) и вставки элементов в произвольных точках (связные списки). Теперь подробнее рассмотрим очередь с приоритетом, которая оптимизирована для добавления элемента высшего приоритета[44] к коллекции в логарифмическое время. Она называется очередью, даже если не является таковой в привычном представлении, то есть когда первый предмет, вставший в очередь, первым же из нее выходит.[45] Вместо этого вы можете представить очередь с приоритетом как некое подземное растение, которое пускает только один побег за один раз и позволяет проходящим мимо людям сорвать его.
Когда мы принимаемся за задание высшего приоритета, дерево перестраивается и выталкивает наверх задание второй приоритетности, и так далее. Этот способ описания очереди с приоритетом называется пирамидой. Мы не можем объяснить принцип пирамиды при помощи аналогии, но это замечательная структура. Нам стоит оценить, как она умеет перестроиться и вытолкнуть наверх элемент первоочередной приоритетности в логарифмическом времени, обеспечивая возникновение вставок также в логарифмическом времени.
Давайте смоделируем приоритизированный список в виде пирамиды.
Заметьте, что пирамида представляет собой как бы дерево из узлов. У них есть две особенности. Первое: каждый узел имеет более низкий приоритет, чем родительский.[46] Поэтому пункт с самым большим приоритетом, то есть продукт, расположенный ближе всего ко входу в магазин, помещен на самом верху. Ничего больше не сообщается о порядке других узлов, таких как узлы, которые находятся на одном уровне. Есть другие структуры, они гарантируют, что все узлы в древоподобной структуре упорядочиваются, как бинарное дерево поиска, полезное в ситуациях, которые мы описывали в главе 2.
Второе свойство: каждый узел имеет два дочерних, с возможным исключением самых низших узлов. Этот структурный инвариант гарантирует, что высота пирамиды, то есть самый длинный возможный путь, не будет превышать log n, где n есть номер элементов в пирамиде.
Вот что происходит, когда Вурзма берет коробку перчаток – вещь, которая, как мы определили, лежит ближе всего ко входу, – и хочет узнать, что из списка взять следующим.
Как только мы удалили наивысший узел, первое свойство пирамиды уничтожается и активируется алгоритм повторной перестройки, который подразумевает замену пустого корневого узла последним узлом в пирамиде. Далее следует проверка нового корневого узла и его сравнение с дочерними, чтобы понять, нужно ли их поменять. Эта проверка и замена производятся с каждой парой, состоящей из родительского узла и самого малого из двух дочерних узлов все время, по мере продвижения к последнему узлу в пирамиде. Заметьте, что этот процесс перестройки пирамиды занимает логарифмическое время[47] и приводит к тому, что следующая самая близкая вещь оказывается наверху.
То же самое происходит, если нам нужно вставить новый приоритетный пункт в список, не стирая и не передвигая другие без необходимости, за log n число движений. Мы добавляем новый пункт в конец пирамиды и затем меняем местами с его родительским узлом, если он вдруг оказывается больше, чем новый пункт. Мы продолжаем менять их при необходимости до самого корневого узла.
В этой книге мы говорили об элегантных подходах, которые может использовать компьютер при решении какой-либо задачи. Нужно снова вспомнить о них, чтобы подчеркнуть: алгоритмы могут иметь все свойства, присущие искусству, – красоту, изящество и грацию. Если вы достигнете более продвинутых областей, где алгоритмы играют большую роль, обращайте внимание не только на результаты и производительность, но и на способы их составления. В мире искусственного интеллекта приложения алгоритмов включают в себя постановку более быстрых диагнозов в больнице, спасение жизни пациентов или исследования, дающие представление о геноме человека. В мире теории игр приложения работают на компании кратковременной аренды автомобилей, где принимают решения, как объединить пассажиров, которым нужно одновременно ехать одинаковым маршрутом. Мир компьютерного будущего занимается проектировкой беспилотных автомобилей или изобретает новые способы обработки изображений, выходящие за рамки простых трансформаций яркости и контраста. Приложениям нет границ в прикладном использовании.
Что же касается Вурзмы, то его карьера рэпера скоро начнется. Никто прежде не думал о сочинении рэпа как о массивах, хеш-таблицах и очередях с приоритетом. А ведь это может быть круто! Вурзме предстоит рассказать об этом своему сыну, которого он хочет поразить своим выступлением на рэп-баттле, в тот день, когда мальчику исполнится 11, то есть на следующей неделе. Да, что-то может пойти наперекосяк. Но самое главное: Вурзма стал быстрее управляться с покупками и делает все так хорошо, что его готовящийся к выпуску сингл пронизан самомнением. Вот и молодец.
Больше никаких игр, никаких шуток, я новый человек,
Феникс, возрожденный из пепла,
Давай начистоту, как Билл Хикс,[48]
Я так быстр, что трудно поверить, от варенья до салфеток «Клинекс»,
Хлеб, молоко и мед, органический сахар и печенье-ассорти,
Вижу: все глядят на меня, в удивлении и шоке,
Но твой стыд слишком велик, чтобы ты смог признать это,
И это норм,
Ты лишь критик себя самого,
А я – киношка Майкла Бея.[49]
Заключительные мысли
Когда Фейнманна однажды спросили, как ему удалось развить свою легендарную способность молниеносно решать задачи, он ответил, что применял к ним различные способы, то есть смотрел на них под разным углом зрения. Использование аналогий – один из способов рассмотреть задачу, отождествление – другой, диалектический метод – третий. Для Фейнманна, который всегда был шоуменом, выдуманная история была способом удивить аудиторию – и по-новому взглянуть на задачу.
В искусстве есть аналогичный подход к решению задач. Умение нарисовать сцену с различных точек без потери деталей здесь считается огромным достоинством. Интересно, что это стало возможным благодаря инновации итальянского архитектора и скульптора Брунеллески в период Возрождения. Разрабатывая математический способ передачи линейной перспективы, Брунеллески создал идеально точный рисунок баптистерии Святого Иоанна во Флоренции. Предметы, которые располагались ближе, выглядели больше, находящиеся дальше – меньше, а линии плиток сходились в одной точке. Такие фрески, как «Вручение ключей» авторства Пьетро Перуджино и «Афинская школа» Рафаэля, – прекрасные более поздние примеры применения этого метода.
Мы начали с того, что концентрация на относительных величинах и каждодневных задачах помогает сделать сложные задания более выполнимыми. В какой-то мере они создают в голове своеобразные триггеры, которые напоминают нам о необходимости постоянно делать выбор. В следующий раз, когда вы увидите гору вещей, которую нужно отсортировать, вы, наверное, подумаете: «Ага, хорошее и плохое, быстрое и медленное, квадратичное и линейно-логарифмическое». Ваши сын, дочь, племянница или племянник могут спросить вас, что такое бинарный поиск, и вы подумаете: «Ага, свобода, Уильям Уолас, Эппи Тоам, рубашки на вешалке». Такие ассоциации легко и весело запоминать. Умение выбирать между хорошим и плохим поможет вам: вы будете знать, как выглядит спектр вариантов для выполнения конкретного задания.
Сегодня слово «алгоритм» можно услышать от многих людей, подобно тому как словосочетание «большой массив данных» было в ходу несколько лет назад. Я надеюсь, что после прочтения этой книги вы поняли, что эта концепция – не причуда. Ее корни в истории, как мы видели при обсуждении вавилонских табличек. Это вневременная концепция, поэтому о ней стоит поговорить, разобрать ее и, что важнее всего, показать, как можно использовать алгоритм в качестве инструмента эффективного мышления.
Благодарности
Каждый, кто приложил руку к этой книге, сделал ее лучше. Я обязан многим Сету Фишману за доведение проекта до ума за такое короткое время. Я также в долгу перед Мелани Тортороли, которая придумала броский заголовок, и благодарен ей за выбор нужного направления, озарение и редактуру. Джорджину Лейкок я благодарю за правки, мысли и дельные предложения. Я благодарен издательству «Викинг» и Джону Мюррею за предоставленные мне привилегии. Отдельная благодарность моему помощнику, работающему на треть ставки, талантливому Алехандро Джиральдо за его рисунки и Сэму Пенроузу, Елене Глассман и Марку Рейду за то, что нашли время просмотреть рукопись и высказать свое мнение о ней. Ссылкой на язык Бейсик, упомянутой в главе 11, я обязан Марку. За помощь в работе над этой книгой я благодарен Марку Сурману, который дал добро этому проекту на ранних стадиях, Питеру Норвигу, который поделился своими мыслями, как представить первую версию, и Елене Глассман, которая познакомила меня с работами Питера.
И прежде всего я благодарен своей жене Дане и своим родителям.
Узнать больше
О темах и концепциях, рассмотренных в этой книге, можно узнать больше, прочитав хотя бы несколько работ из приведенного ниже списка.
Ambrose, Susan A., et al. How Learning Works: Seven Research-Based Principles for Smart Teaching. New York: John Wiley & Sons, 2010.
Книга адресована преподавателям колледжа и содержит прекрасные советы о том, как облегчить процесс обучения. Она опирается на научные методы и теоретическую базу.
Avirgan, Jody. A History of Data in American Politics (Part 1): William Jennings Bryan to Barack Obama. FiveThirtyEight, /a-history-of-data-in-american-politics-part-1-william-jennings-bryanto-barack-obama.
Здесь больше политики, чем науки. Статья рассматривает историю американской политики, исходя из таких понятий, как память, данные и связи.
Bacon, Francis. The Advancement of Learning. London: J. M. Dent & Sons, 1984.
В этой книге есть запомнившийся мне пример, который послужил вступлением к цитате, использованной в Предисловии: «Теннис – игра сама по себе бесполезная, но она делает глаз быстрым, а тело – гибким. Точно так же в математике побочный результат не менее важен, чем искомый и главный».
Bender, Michael A., Martin Farach-Colton, and Miguel A. Mosteiro. Insertion Sort Is O(n log n). Theory of Computing Systems 39 no.3 (2006): 391–97.
Рекомендуется тем, кто хочет больше узнать о методе библиотечной сортировки, упомянутой в главе 11.
Brooks, Frederick P. The Mythical Man-Month: Essays on Software Engineering, Anniversary Edition. 1975. Reprint, Reading, MA: Addison-Wesley Longman, 1995.
Книга рассказывает об управлении проектами в контексте разработки программного обеспечения, доказывая, что усиление проекта кадровыми ресурсами не всегда приносит пользу.
Buck, Jamis, and Jacquelyn Carter. Mazes for Programmers: Code Your Own Twisty Little Passages. Dallas, TX: The Pragmatic Programmers, 2015.
Исчерпывающее изложение об алгоритмах создания и распутывания лабиринтов. Эта книга попалась мне в конце 2015 года, когда я решал, продолжать ли мне работать над обучением алгоритмам с помощью историй или заняться чем-то другим. Меня вдохновило, что некоторые работы Джамиса посвящены тем же темам.
Celma, Oscar. Music Recommendation. Music Recommendation and Discovery: The Long Tail, Long Fail and Long Play in the Digital Music Space. Berlin: Springer-Verlag, 2010, 43–85.
Здесь больше говорится о музыкальных открытиях, чем о теме, которую мы обсуждали в главе 6. Хороший источник для знакомства с миром цифровой музыки.
Dehaene, Stanislas. The Number Sense: How the Mind Creates Mathematics. New York: Oxford University Press, 1999.
Когда я только начинал изучать когнитивную психологию, мне встретилась работа Жана Пиаже («Формирование детского интеллекта…» и так далее). Позже я узнал из передачи Radiolab об исследованиях Станисласа и был увлечен идеями о том, как работает и развивается сознание ребенка.[50]
Demaine, Erik, and Srinivas Devadas. 6.006–Introduction to Algorithms. MIT OpenCourseWare, 2011.
Бесплатные видеолекции, подробно и доступно рассматривающие тему алгоритмов во всех ее аспектах.
Dennett, Daniel C. Intuition Pumps and Other Tools for Thinking. New York: W. W. Norton, 2013.
Я полюбил эту книгу с тех пор, как слушал ее за рулем во время поездки из Калифорнии во Флориду. Рекомендую прочесть хотя бы две первые главы об основных инструментах мышления.
Diagram Group. Comparisons. New York: St. Martin’s Press, 1980.
Рабочее название для книги было «Сравнения», с отсылкой к этой книге, которая представляет собой сборник фактов с иллюстрациями и схемами – именно так, как я люблю.
Erasmus, Desiderius. A Handbook on Good Manners for Children: De Civilitate Morum Puerilium Libellus. Edited by Eleanor Merchant. London: Preface, 2008.
Пока я не посмотрел мини-сериал Би-би-си «Волчий зал», я не догадывался, что Дезидериус был другом Ганса Гольбейна-младшего, который написал канонические портреты Томаса Мора, Томаса Кромвеля и многих других. Моя любимая цитата из Томаса Мора: «Все, что у меня есть, – это земля, на которой я стою. Эта земля и есть Томас Мор. Возьми ее, если хочешь». А вот что я люблю у Дезидериуса: «Некоторые учат детей сдерживать позывы выпускать газы. Но вредить своему здоровью из вежливости – это вовсе не хорошие манеры. Если можете, отойдите в сторону. Если нет, вспомните старую мудрость – заглушать пуканье кашлем».
Согласно одному апокрифическому переводу, этот пассаж завершается словами: «Кто с этим спорит, тот это поддерживает».
Feynman, Richard Phillips, and Ralph Leighton. What Do You Care What Other People Think?: Further Adventures of a Curious Character. New York: W. W. Norton, 2001.
Эта и следующая книги важны для тех, кто хочет знать, каким видел мир такой выдающийся ученый, как Фейнманн. Я впервые прочитал их в 2005-м, будучи нелюдимым аспирантом в Питсбурге, и они навсегда изменили мой взгляд на жизнь.
Feynman, Richard Phillips, Ralph Leighton, and Edward Hutchings. Surely You’re joking, Mr. Feynman!: Adventures of a Curious Character. New York: W. W. Norton, 1997. Fredricks, Jennifer A., Phyllis C. Blumenfeld, and Alison H. Paris. School Engagement: Potential of the Concept, State of the Evidence. Review of Educational Research 74 no. 1 (Spring 2004): 59–109.
Мне понравилось в этой статье обсуждение вовлеченности и того, что может увлечь учеников в классе.
Freire, Paulo. Pedagogy of the Oppressed. England: Penguin Books, 1996. First published in 1970 by The Continuum Publishing Company.
Образ студента как сосуда рожден «банковской» моделью обучения Фрейре. Разговор о предписании (в противовес выбору) как о средстве угнетения поразил меня в свое время, как и рассуждения о том, что критическое осмысление своей личности и целей обучения – истинные инструменты эмансипации. Это чрезвычайно поучительная книга.
Gefter, Amanda. The Man Who Tried to Redeem the World with Logic. Nautilus, Feb. 5, 2015.
Великие идеи рождаются в неожиданных местах. В этом эссе подробно рассказано про Уолтера Питтса и его вклад в когнитивную неврологию. Пример Неймана в Предисловии заимствован отсюда.
Gordon, Deborah M. The Collective Wisdom of Ants. Scientific American, Feb. 1, 2016.
Пример о муравьях, находящих путь домой, в главе 4 взят из этой работы.
Hamilton, Edith. Mythology: Timeless Tales of Gods and Heroes, 1942. Boston: Little, Brown, 2012.
Отсюда взята история о Тесее для главы 4.
Hinshaw, Drew, and Joe Parkinson. For World’s Newest Scrabble Stars, SHORT Tops SHORTER. Wall Street Journal, May 19, 2016.
Пример из главы 8 о контринтуитивном подходе при игре в Скраббл приведен в этой статье.
Hodges, Andrew. Alan Turing: The Enigma. New York: Audible Studios, 2012.
О работе Тьюринга и его коллег в криптографическом центре Блетчли-парк в 1940-х годах стоит почитать, так как она перекликается с некоторыми затронутыми нами концепциями. Например, инновация, значительно сократившая время работы «Бомбы Тьюринга» – программы для раскодирования сообщений немецкой шифровальной машины Enigma, – определяла настройку, с которой следовало начать.
Holt, Jim. Numbers Guy: Are Our Brains Wired for Math? New Yorker, March 3, 2008.
Еще один полезный текст о работе Станисласа Деана. Здесь я впервые встретил выражение «голый купол головы».
Knuth, Donald E. Ancient Babylonian Algorithms. Communications of the ACM 15, no. 7 (1972): 671–77.
Пример древневавилонских алгоритмов взят из этой статьи.
The Art of Computer Programming, Volume 1: Fundamental Algorithms. Reading, MA: Addison-Wesley, 1973.
The Art of Computer Programming, Volume 3: Sorting and Searching. Reading, MA: Addison-Wesley, 1973.
Книги профессора Кнута – не для слабонервных, но они представляют собой блестящее сочетание исторического контекста с математическим подходом.
Papert, Seymour. Mindstorms: Children, Computers, and Powerful Ideas. 2nd ed. New York: Basic Books, 1993.
Я обратился к Сеймуру Паперту, чтобы больше узнать о конструкционизме – теории, вдохновленной конструктивизмом Пиаже. Паперт считает исследование, а также групповую и проектную деятельность основой обучения. Его работы повлияли на мои идеи, которые впоследствии вылились в эту книгу.[51]
Poundstone, William, ed. Labyrinths of Reason: Paradox, Puzzles, and the Frailty of Knowledge. New York: Doubleday, 2011.
Пример лабиринта Стэнхоупа в главе 4 взят из этой книги.
Sedgewick, Robert, and Kevin Wayne. Algorithms. 4th ed. Reading, MA: Addison Wesley, 2011.
Если вы решили прочесть только одну книгу об алгоритмах, советую выбрать именно эту. Ее графики прекрасно помогают понять, как работают алгоритмы.
Simon, Herbert A. The Sciences of the Artificial. 3rd ed. Cambridge, MA: MIT Press, 1999.
Разговор о разных подходах в Предисловии отчасти навеян рассуждениями Герберта Саймона об «удовлетворительных решениях».
Spangher, Alexander. Building the Next New York Times Recommendation Engine. Open, New York Times, August 11, 2015.
В этом блоге подробно рассмотрено, как работает рекомендательный механизм для текстовых документов.[52]
Turing, Alan M. Proposals for the Development in the Mathematics Division of an Automatic Computing Engine (ACE). Report E882, Executive Committee, NPL, February 1946.
Отрывок в главе 3 взят из этого текста.
Vanderbilt, Tom. How Your Brain Decides Without You. Nautilus, Nov. 6, 2014.
Утверждение в главе 8 о том, что мы интерпретируем новую информацию на основе уже известной, заимствовано из этой работы.
Wagner, Tony, and Ted Dintersmith. Most Likely to Succeed: Preparing Our Kids for the Innovation Era. New York: Simon & Schuster, 2015.
Мысль о том, что те, кто внес самый серьезный вклад в цивилизацию, по большей части слушали своих учителей, а не «списывали решение», взята из этой книги. Это замечательная книга об обучении.
Weiss, Mark Allen. Data Structures and Problem Solving Using Java. 3rd ed. Reading, MA: Addison-Wesley Longman, 2002.
Пример о главных членах функции в главе 10 взят из этой книги.
Wilson, Brent G. Constructivist Learning Environments: Case Studies in Instructional Design. Englewood Cliffs, NJ: Educational Technology, 1996.
Изучая психологию развития, я нашел этот текст о конструктивизме, конкретнее – о том, как исследование и игра помогают когнитивному развитию.
Wing, Jeannette M. Computational Thinking. Communications of the ACM 49, no. 3 (2006): 33–35.
Работая над рукописью этой книги, я встретил статью своего бывшего профессора и был рад, что она увлечена той же идеей. В ее публикации рассказывается о перспективах алгоритмического мышления.
Темпы роста
Одна из тем этой книги – сравнение альтернативных подходов к выполнению одного и того же задания. Почти в каждой главе мы сравнивали одно с другим, используя диаграмму темпов роста. Графики на этих диаграммах были преднамеренно не маркированы. Вот свод темпов роста от самого медленного (лучшее) до самого быстрого (худшее).
ПОСТОЯННОЕ ВРЕМЯ: при данном количестве элементов; если удвоить его, то время, требующееся для выполнения этого задания, останется тем же.
ЛОГАРИФМИЧЕСКОЕ ВРЕМЯ: для достаточно большого числа элементов; если удвоить их количество, то время, требующееся для выполнения задания, увеличится приблизительно на единицу.
ЛИНЕЙНОЕ ВРЕМЯ: для достаточно большого числа элементов; если удвоить их количество, время увеличится примерно вдвое.
ЛИНЕЙНО-ЛОГАРИФМИЧЕСКОЕ ВРЕМЯ: для достаточно большого числа элементов; если удвоить их количество, то время увеличится примерно вдвое и возрастет на один.
КВАДРАТИЧНОЕ ВРЕМЯ: для достаточно большого числа элементов; если удвоить их количество, то время увеличится в квадрате.
ЭКСПОНЕНТНОЕ ВРЕМЯ: для достаточно большого числа элементов; если мы увеличим его всего лишь на одну единицу, то время на выполнение этого задания вырастет примерно вдвое! Самая бледная линия с левого края каждой схемы в этой книге обозначает график экспонентного времени.
* * *
Примечания
1
Ричард Фейнманн (1918–1988) – американский физик-теоретик; Джон фон Нейман (1903–1957) – венгерский и американский математик; Чарльз Дарвин (1809–1888) – автор теории эволюции (прим. ред.).
(обратно)2
Все линии изображены на графике двойного логарифмического масштаба, поэтому они имеют такой вид (прим. автора).
(обратно)3
Важно в самом начале отметить, что эти характеристики не всегда применимы к другим сферам жизни, например к учебе, где скорость – не главное. По моему опыту та обучающая среда, которая требует от студентов работать быстро, настраивает их на неудачу (прим. автора).
(обратно)4
В этой книге есть смешной отрывок об Оливере Хивсайде, остром на язык отшельнике, чей подход к математике проектирования отличался особой прагматичностью. Инженеры хвалили метод Хивсайда, но математики смеялись над ним из-за недостатка точности. У Хивсайда же не было времени проявлять дотошность («Стоит ли мне отказываться от ужина, если я не понимаю, как происходит пищеварение?»). (Прим. автора.)
(обратно)5
Фрэнсис Бэкон (1561–1626) – один из крупнейших философов Нового времени, основоположник эмпиризма и английского материализма (прим. ред.).
(обратно)6
«Помни» («Memento») – фильм Джонатана Нолана (2000). Главный герой, переживший тяжелую травму головы, не может ничего удержать в памяти больше 15 минут.
(обратно)7
Факт, который часто описывают фразой «торговать памятью за деньги» (прим. автора).
(обратно)8
Этот подход был впервые применен в Университете Торонто десять лет назад, и сейчас его называют глубоким обучением (прим. автора).
(обратно)9
Заметьте, что, применяя оба метода, мы не занимаемся отделением носков от не-носков, поскольку наше задание – разобраться только с носками (прим. автора).
(обратно)10
Есть более сложные методы изучения скорости роста. Один из них – узнать, не растет ли определенный метод быстрее, чем показанная скорость (известная под названием большое-о), или медленнее, чем показанная скорость (известная как большое-Ώ, т. е. «большая омега»). Другой метод – посмотреть, описывают ли скорости роста лучшие, худшие или средние случаи. Мы поговорим обо всех этих случаях позже (прим. автора).
(обратно)11
В этом примере Марджи не особенно заботится о том, в каком порядке лежат неразобранные носки. Все, что ее беспокоит, – все носки должны быть отложены в одну сторону.
(обратно)12
Например, найти сумму первых чисел n было бы сложно, если бы вы проходились по этим n-числам один за другим, каждый раз суммируя пары. Гораздо удобнее использовать вместо этого формулу n x (n+1)/2 (прим. автора).
(обратно)13
Префикс в информатике – начало строки программы (прим. ред.).
(обратно)14
Сходным образом процесс многократного удвоения чисел от 1 до n логарифмичен, поскольку мы можем сделать не более чем log n скачков, прежде чем получим n. Например, сколько лет уйдет на зарабатывание 1 млн долларов, если начать с 1 доллара и каждый год удваивать его? Можно посчитать это вручную или же применить log2 1 000 000 = 19,93 года (прим. автора).
(обратно)15
«Два Ронни» – популярный в 1970-е годы британский комедийный сериал с актерами Ронни Баркетом и Ронни Корбеттом (прим. ред.).
(обратно)16
Ее можно посмотреть здесь: bookofbadchoices.com/links/ronnies. Интересующая нас последовательность событий происходит ближе к середине ролика (прим. автора).
(обратно)17
Здесь может быть реклама любого другого продукта (прим. автора).
(обратно)18
Иллюстрации, приведенные ниже, навеяны рисунками Джемиса Бака. См. ссылки в конце книги (прим. автора).
(обратно)19
Вариант – правило левой руки, когда человек следует по стене, держась за нее левой рукой (прим. автора).
(обратно)20
Аргумент состоит из ряда положений, называемых тезисами. Каждый из них либо правдив, либо ложен (прим. автора).
(обратно)21
Он также может отмечать места пересечения ходов куском мела или оставлять там лоскутки ткани.
(обратно)22
В марте 2016 года в номере американского кулинарного журнала Cook's Illustrated сравнение разных подходов было проиллюстрировано фотографиями работающих роботов-пылесосов, сделанными с длинной выдержкой.
(обратно)23
Не все можно объяснить на примерах, да и не всегда это нужно (прим. автора).
(обратно)24
Он называется квадратичным, потому что время, которое требуется для сортировки конвертов, повышается на порядок n2 с увеличением их количества – скажем, 100 секунд для 10 конвертов, 10 000 секунд для 100 конвертов и так далее (прим. автора).
(обратно)25
Процесс также включает в себя концепцию под названием «рекурсия», которую мы не будем рассматривать в этой книге, но с которой стоит ознакомиться (прим. автора).
(обратно)26
Вспомните, что логарифмы растут медленно (прим. автора).
(обратно)27
Джедвард (Jedward) – ирландский поп-дуэт братьев-близнецов Джона и Эдварда Граймсов (оба род. 1991) (прим. ред.).
(обратно)28
Под популярной музыкой мы подразумеваем музыку тех исполнителей, которые вдохновили других артистов или имели последователей; но можно иметь в виду что-то более простое, например музыку в стиле поп. Главный вопрос: «Как выбрать самое важное из этих песен?» (Прим. автора.)
(обратно)29
При выдаче рекомендаций важно учитывать долговременный эффект. В случае с Фоем целесообразно советовать ему что-либо, зная его цель, но вообще стоит задуматься: всегда ли хорошо смотреть однотипные шоу? Читать одинаковые книги, слушать одних и тех же экспертов? Не ограничивает ли это человека, не мешает ли ему это жить полноценной жизнью, наслаждаясь ею во всем ее великолепии? Алгоритмы есть отражение людей, стоящих за ними. Всегда нужно помнить о человеческих предрассудках, которые проявляются не только в том, что мы делаем и говорим, но и в том, что мы создаем (прим. автора).
(обратно)30
Некоторые комментаторы популярных сайтов занимаются этим до сих пор (прим. автора).
(обратно)31
В информатике деревья рисуются корнями вверх, а их ветви тянутся вниз в отличие от обычных деревьев (прим. автора).
(обратно)32
Уильям Тиндейл (1494–1536) – английский ученый, протестантский реформатор и переводчик Библии. Сожжен на костре как еретик.
(обратно)33
Каждое приложение, которое вы запускаете, порождает процессы, которые система должна затем контролировать (прим. автора).
(обратно)34
Заметьте, что в большинстве современных браузеров при открытии каждого нового окна начинается новый отдельный процесс, поэтому вы видите многочисленные вводы в одном и том же браузере на вашем мониторе или в окне задач (прим. автора).
(обратно)35
Это утверждение не всегда верно (прим. автора).
(обратно)36
Это тоже относительно. Подумайте о собирании теннисных мячей после матча. Что важнее: расстояние, которое вы проходите, или количество наклонов? Для некоторых важнее первое, поэтому они будут искать короткие пути к мячам; для других, у кого, например, болит спина, – второе. Такой человек выберет альтернативный подход: сгонит все мячи к сетке, а потом подберет их разом (прим. автора).
(обратно)37
Дуглас Карл Энгельбарт, изобретатель компьютерной мыши, писал о процессе постановки вопроса: «Достаточно ли важны эти задания, чтобы начать именно с них?»
(обратно)38
Вдвое больше времени – это наихудший вариант, если пропущенная буква находится в середине (прим. автора).
(обратно)39
Вспомните, что чем медленнее растет функция, тем более она привлекательна (прим. автора).
(обратно)40
Этого, конечно, может и не случиться. Иногда влияние больших констант на функцию незначительно (прим. автора).
(обратно)41
Закон Сода – популярный в Англии предшественник «законов Мэрфи»; гласит, что все самое худшее, что может случиться, непременно случается. Аналогичен известному в русской культуре «закону бутерброда», или «закону подлости» (прим. ред.).
(обратно)42
Первый язык, на котором я начал программировать, был Бейсик. Недавно, разговаривая с другом, я вспомнил, что номера строк в нем обычно имели «пробелы». Строка 2 шла не за строкой 1, а строка 20 необязательно следовала за строкой 10 и так далее. Этот разговор позволил программисту добавить новые строки между существующими, избегая перенумерации всех строк (прим. автора).
(обратно)43
Любой интересный набор данных будет скорее всего аналогичен многомерному массиву, рассматриваемому как множественные столбцы, которые статистик использовал бы для различных видов анализа (прим. автора).
(обратно)44
На самом деле она выдвигает на поверхность самый маленький (или самый большой) элемент, но в данном случае мы используем это свойство для обнаружения самого высокоприоритетного элемента (прим. автора).
(обратно)45
Структура, которая удовлетворяет списку, организованному по принципу «последним вошел – первым вышел», существует и даже имеет аналоги в повседневной жизни. Вспомните, как в продуктовых магазинах скоропортящиеся продукты ставят на переднюю полку, причем более лежалые помещаются вперед, а недавно доставленные – назад (прим. автора).
(обратно)46
За исключением самого высокого узла – корневого, – так как у него нет родительского узла (прим. автора).
(обратно)47
Вспомните, что n=10 и так log2 10=3.
(обратно)48
Ульям Мелвин «Билл» Хикс (1961–1994) – американский стендап-комик и социальный критик.
(обратно)49
Майкл Бей (род. 1965) – один из самых кассовых режиссеров в мире; автор фильмов «Армагеддон», «Скала», «Плохие парни», сериала «Трансформеры» и т. д. (прим. ред.)
(обратно)50
Radiolab – передача, посвященная выдающимся явлениям в науке, психологии и др. (прим. ред.)
(обратно)51
Конструкционное обучение построено на создании интеллектуальных моделей познания окружающего мира. Конструкционисты пропагандируют систему обучения, в которой новая информация опирается на имеющиеся знания; студенты работают над проектами из разных областей под руководством преподавателей, без лекций и пошаговых инструкций. Конструктивизм – одно из течений современной философии науки, гласящее, что познание происходит путем построения интерпретации (модели) мира. Возникло в конце 70-х – начале 80-х гг. XX в. (прим. ред.).
(обратно)52
Рекомендательный механизм/рекомендательная система – программа, которая анализирует профиль пользователя с целью выяснить, какие объекты могут быть ему интересны (прим. ред.).
(обратно)

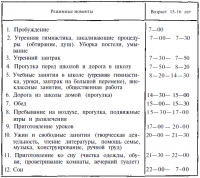







Комментарии к книге «Хакни рутину. Как алгоритмы помогают справляться с беспорядком, не тупить в супермаркете и жить проще», Али Альмоссави
Всего 0 комментариев