Версия текста 1.10. (с) 2018
Введение
Как сказал еще Галилей, “Книга природы написана на языке математики”, и с этим сложно не согласиться. Математика это универсальный язык науки, это базовые принципы, на которых построена вся Вселенная. 2+2=4 независимо от того, верим мы в это или нет, знаем мы это или нет, существуем мы вообще или нет, и это будет верно не только для нас, но и для жителя Альфы Центавра.
Из этого следует важное правило: математические законы нельзя придумать, их можно только открыть. Треугольник подчинялся теореме Пифагора еще до того, как Пифагор открыл и сформулировал известную теорему. Число Пи было вычислено в древнем Китае, но его значение было таким всегда - еще до того как появился не только Китай, но и наша планета Земля.
Именно поэтому я надеюсь, что кто-то из читателей с помощью этой книги откроет для себя в математике что-то новое. Увы, в представлении большинства, математика - это достаточно скучная наука, вероятно так ее преподают в школе. Если кто-то с помощью этой книги найдет для себя что-то новое, можно считать что время было потрачено не зря.
Эта книга не задачник, а скорее сборник рассказов о тех или иных математических вопросах. Т.к. математические примеры без цифр бессмысленны, “практическая” часть дается на языках программирования Python и Си.
Номер версии в заголовке указан не случайно. Эта книга не закончена, и по мере появления каких-то новых интересных вопросов она будет дополняться. Желающие также могут присылать свои истории или задачи по адресу dmitryelj@gmail.com, наиболее интересные из них будут включены в текст. Обо найденных неточностях также просьба писать на этот адрес.
Книга распространяется бесплатно в электронном виде, в различных форматах (PDF, FB2) ее можно скачать по ссылке . Там же доступен и архив с примерами программ.
Приятного чтения.
Елисеев Дмитрий
История версий текста
04.2017 - 1.0
09.2017 - 1.1, 1.2 - добавлены главы 19 и 20 про нейронные сети
11.2017 - 1.3, добавлена глава 21 про фракталы
11.2017 - 1.4, дополнена глава 7 про магические квадраты, добавлены главы 22 и 23 про “горн Гавриила” и построение графиков функций, в “Приложения” добавлен пример оптимизации кода на Python.
12.2017 - 1.5, дополнена глава 4 про шарообразность Земли.
01.2018 - 1.6, добавлена глава 24 про точность компьютерных вычислений, глава 25 про календарь, добавлено Приложение 4.
03.2018 - 1.7, добавлена глава 21 про использование библиотеки TensorFlow.
04.2018 - 1.8, добавлена глава 27 про азартные игры.
04.2018 - 1.9, добавлена глава 28 про теорему Пифагора.
10.2018 - 1.10, добавлена глава 29 про abc-гипотезу, дополнена глава про простые числа, дополнена глава о “магических квадратах”, улучшено форматирование кода.
1. Основы языков Python и Си
Математика немыслима без расчетов и примеров вычислений. Примеры в данной книге иллюстрируются фрагментами кода на языке Python. Этот язык удобен тем, что он очень прост и подходит для начинающих, поэтому кратко рассмотрим как им пользоваться.
Для использования языка Python нужно установить интерпретатор языка с сайта / или воспользоваться онлайн-версией, например на странице . Все примеры из книги тестировались на Python версии 2.7.
Для запуска Python-программы необходимо:
- Сохранить файл в Блокноте с любым именем и расширением .py, например test1.py.
- Открыть консоль (нажать Win+R и набрать cmd), в консоли набрать команду (без кавычек) “python путь_к_файлу.py”, например “python C:\PythonApps\test1.py”.
Как более удобный вариант, можно скачать бесплатную среду разработки PyСharm community edition, и редактировать и запускать файлы в ней. Скачать PyСharm можно со страницы /.
Кстати, чтобы запустить короткую программу на Python, ее необязательно сохранять в файл, код можно ввести непосредственно в интерпретатор. Для этого достаточно запустить (Win+R) программу python.exe и просто ввести подряд соответствующие строки:
Для запуска программы на языке Си, ее сначала надо сохранить файле с расширением .c, и выполнить команду “gcc имя_файла.c”. Будет создан exe-файл, который можно запустить. Бесплатный компилятор С/C++ можно установить с помощью утилиты mingw-get, скачать которую можно на странице /. Также можно воспользоваться и любой онлайн-версией c++ компилятора, например этой.
Минимальная программа на Си выглядит так:
#include <stdio.h>
int main()
{
printf("Hello world\n");
return 0;
}
Рассмотрим простые примеры использования.
Объявление и вывод переменных
Python: достаточно ввести имя и значение.
x = 3
y = 10
print("x=", x)
print(x+y)
В отличие от языка С++, тип переменной будет определен автоматически, указывать его не нужно. Его можно при необходимости узнать, введя print (type(x)).
Важно иметь в виду, что синтаксис функции print в версиях Python 2.7 и 3.0 разный. В Python 2.7 можно написать print x, y, но в Python 3.0 такой код вызовет ошибку, нужно использовать круглые скобки и писать print(x, y). Код со скобками будет работать в обеих версиях Python, поэтому в примерах используется именно он.
И еще один момент насчет вывода значений. По умолчанию Python может выдавать ошибку при использовании русских букв, нужно указывать кодировку символов. Чтобы избежать этого и сделать код короче, во многих примерах будут по возможности указываться английские или “международные” аббревиатуры.
Cи: необходимо явно указать тип и значение переменной.
int x = 3;
int y = 10;
printf("x=%d\n", x);
printf("%d\n", x+y);
Циклы
В отличие от того же С++ или Java, циклы в Python задаются отступами, что после других языков программирования может быть непривычным. Часть кода, находящаяся внутри цикла, будет выполнена заданное количество раз.
Python
Вывод чисел от 1 до 9:
for p in range(1,10):
print(p)
Для сравнения, вот такой код без отступов работать не будет, и это важно помнить, например при копировании кода из этой книги:
for p in range(1,10):
print(p)
Вывод чисел от 1 до 9 с шагом 2:
for p in range(1,10,2):
print(p)
Кстати, в Python 2.7 функция range возвращает объект “список”, и соответственно выделяет память заданного размера. Для большинства примеров в книге это не критично, но если нужно написать код типа for p in range(1,10000000), то range следует заменить на xrange, в противном случае программа вполне может занять гигабайт памяти даже на простом с виду цикле. Для Python 3.xx это не требуется.
Си
Вывод чисел от 1 до 9:
for(int i=1; i<10; i++) {
printf("%d\n", i);
}
Вывод чисел от 1 до 9 с шагом 2:
for (int i=1; i < 10; i += 2) {
printf("%d\n", i);
}
Массивы
Массив это линейный набор чисел, с которыми удобно выполнять однотипные операции, например вычисление суммы или среднего арифметического.
Python:
Объявляем массив чисел:
values = [1,2,3,5,10,15,20]
Добавляем элемент в массив:
values.append(7)
Выводим массив на экран:
print(values)
Выводим элементы массива построчно:
for p in values:
print(p)
Это же можно сделать с помощью индексов (нумерация элементов массива начинается с 0):
for i in range(0, len(values)):
print(values[i])
Можно получить и значение и индекс сразу, иногда это удобно.
for i, item in enumerate(mylist):
print(i, item)
Можно создать массив определенного размера, заполненный определенными числами. Создадим массив из 100 элементов, заполненный нулями.
values = [0.0] * 100
print(values)
Есть немного более сложный, но и более гибкий вариант создания массива. Создадим массив из 100 элементов, заполненный нулями:
values = [0.0 for i in range(100)]
Создадим массив, заполненный числами 0,1,..,99:
values = [i for i in range(100)]
Создадим массив, заполненный квадратами чисел:
values = [i*i for i in range(100)]
Создать двухмерный массив в Python также несложно:
matrix4x4 = [ [0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0]]
matrix4x4[0][0] = 1
print(matrix4x4)
Аналогично вышеописанному способу, можно создать 2х-мерный массив 100x100:
values100x100 = [[0.0 for j in range(100)] for i in range(100)]
Си:
Динамические массивы поддерживаются только в C++, статические массивы создаются так:
int values[7] = {1, 2, 3, 5, 10, 15, 20};
for (int i=0; i < 7; i++) {
printf("%d\n", values[i]);
}
При желании можно слегка схитрить, если максимальный размер массива заранее известен.
int values[255] = {1, 2, 3, 5, 10, 15, 20}, cnt = 7;
for (int i=0; i < cnt; i++) {
printf("%d\n", values[i]);
}
values[cnt] = 7;
cnt++;
Можно пользоваться динамическим распределением памяти, хотя это немного сложнее:
int *valuesArray = (int *)malloc(10 * sizeof(int));
valuesArray[0] = 1;
valuesArray[1] = 3;
valuesArray[2] = 15;
valuesArray = (int *)realloc(valuesArray, 25 * sizeof(int));
valuesArray[20] = 555;
valuesArray[21] = 777;
for (int i=0; i < 25; i++) {
printf("%d\n", valuesArray[i]);
}
free(valuesArray);
Важно заметить, что неинициализированные значения массива, например valuesArray[16], будут содержать “мусор”, некие значения которые были до этого в памяти. Си достаточно низкоуровневый язык, и такие моменты нужно учитывать. Хорошим тоном является инициализация всех переменных при их описании. Вот такой код формально не содержит ошибок:
int x;
printf("x=%d\n", x);
Однако при его запуске выведется значение 4196608, или 0, или 32, результат непредсказуем. В большой программе такие ошибки может быть сложно найти, тем более что проявляться они могут не всегда.
Арифметические операции
Сложение, умножение, деление:
x1 = 3
x2 = (2*x1*x1 + 10*x1 + 7)/x1
Возведение в степень:
x3 = x1**10
print(x1, x2, x3)
Переменную также можно увеличить или уменьшить:
x1 += 1
x1 -= 10
print(x1)
Остаток от деления:
x2 = x1 % 6
print (x2)
Условия в Python кстати, задаются отступами, аналогично циклам:
print (x1)
if x1 % 2 == 0:
print("x1 четное число")
else:
print("x1 нечетное число")
Подсчитаем сумму элементов массива:
values = [1,2,3,5,10,15,20]
s = 0
for p in values:
s += p
print(s)
Этот способ математически корректный, но медленный - лучше для этого можно воспользоваться встроенной функцией sum:
values = [1,2,3,5,10,15,20]
print(sum(values))
В Си вычисление суммы элементов массива выглядит так:
int sum = 0;
for(int i=0; i<cnt; i++) {
sum += values[i];
}
printf("Sum=%d\n", sum);
Для более сложных операций в Python необходимо подключить модуль math. Вычисление квадратного корня:
import math
print(math.sqrt(x3))
Python может делать вычисления с большими числами, что достаточно удобно:
import math
x1 = 12131231321321312312313131124141
print(10*x1)
print(math.sqrt(x1))
Можно вывести даже факториал числа 1024, что не сделает ни один калькулятор:
import math
print(math.factorial(1024))
Пожалуй, этого не хватит чтобы устроиться на работу программистом, но вполне достаточно для понимания большинства примеров в книге.
Используем Jupiter Notebook
Большинство примеров в книге написаны на языке Python. Однако, кроме описанного выше “классического” способа запуска программ, есть другой, весьма популярный сейчас способ - использование “записных книжек”, или notebooks. Такая система работает для языка Python, и называется Jupiter Notebook. Идея состоит в интерактивном редактировании страницы с кодом и текстом, где по сути, программа, больше похожа на текст книги. Это может быть удобно для каких-то экспериментов, где можно пробовать фрагменты кода и сразу видеть результат.
Для установки Jupiter Notebook для Windows достаточно ввести команду C:\Python27\Scripts\pip.exe install jupyter. Затем достаточно ввести команду jupyter notebook - запустится сервер, а в браузере откроется визуальный редактор, где можно редактировать код и видеть результат. По умолчанию редактор покажет файлы в текущем каталоге, выглядеть это может примерно так.
Файлы .ipynb - это файлы “записных книжек”, которые мы можем открыть.
Создадим новый файл, нажав кнопку New в правой части экрана. Появляется окно где мы можем писать код и тут же выполнять его, нажав кнопку Run. Кроме кода можно писать и текстовые комментарии (поддерживается даже форматирование как в HTML). Таким образом, эта система объединяет и редактор, и интерпретатор Python, и также позволяет сразу видеть результаты работы.
Для примера построим график функции количества простых чисел (подробнее в гл.5).
“Записную книжку” Jupiter можно сохранить, закрыть, переименовать и пр.
В данной книге такой способ запуска Python-программ не используется, но кому-то он может оказаться более удобным. Ну а сейчас вернемся к математике.
2. Математические фокусы
Для “разминки” рассмотрим несколько фокусов, имеющих отношение к числам. Никаких особых сложностей в них нет, но их знание поможет развеселить или удивить знакомых знанием математики.
Умножение в уме числа на 11
Рассмотрим простой пример:
26*11 = 286
Сделать это в уме просто, если взять сумму чисел и поместить в середину:
26*11 = 2 [ 2+6 ] 6
Аналогично 43*11 = 473, 71*11 = 781 и так далее.
Чуть длиннее расчет, если сумма чисел больше либо равна 10. Но и тогда все просто: в середину кладется младший разряд, а 1 уходит в старший разряд:
47*11 = [4] [4+7=11] [7] = [4+1] [1] [7] = 517
94*11 = [9] [9+4=13] [4] = [10] [3] [4] = 1034
Возведение в квадрат числа, оканчивающегося на 5
Подсчитать это тоже просто. Если число рассмотреть как пару NM, то первая часть результата - это число N, умноженное на (N+1), вторая часть числа - всегда 25.
352 = [3*4] [25] = 12 25
Аналогично:
252 = [2*3] 25 = 625 852 = [8*9] 25 = 7225 и так далее.
Отгадывание результата
Попросим человека загадать любое число. Например 73. Затем чтобы еще больше запутать отгадывающего, попросим сделать следующие действия:
- удвоим число (146)
- прибавляем 12 (158)
- разделим на 2 (79)
- вычтем из результата исходное число (79-73 = 6)
В конце мы отгадываем, что результат - 6. Суть в том, что число 6 появляется независимо от того, какое число загадал человек.
Математически, это доказывается очень просто:
(2*n + 12)/2 - n = n + 6 - n = 6, независимо от значения n.
Отгадывание чисел
Есть другой фокус с отгадыванием чисел. Попросим человека загадать трехзначное число, числа в котором идут в порядке уменьшения (например 752). Попросим человека выполнить следующие действия:
- записать число в обратном порядке (257)
- вычесть его из исходного числа (752 - 257 = 495)
- к ответу добавить его же, только в обратном порядке (495 + 594)
Получится число 1089, которое “фокусник” и объявляет публике.
Математически это тоже несложно доказать.
- Любое число вида abc в десятичной системе счисления представляется так:
abc = 100*a + 10*b +c.
- Разность чисел abc - cba:
100*a + 10*b +c + 100 - 100*c-10*b - a = 100*a - 100*c - (a - c) = 100*(a-c) - (a-c)
- Т.к. по условию a - c > 0, то результат можно записать в виде:
100*(a-c) - (a-c) = 100*(a-c) - 100 + 90 + 10 - (a-c) = 100*(a-c-1) + 10*9 + (10-a+c)
Мы узнали разряды числа, получающегося в результате:
a1=a-c-1, b1 = 9, c1 =10-a+c
- Добавляем число в обратном порядке:
a1b1c1 + c1b1a1 = 100*(a-c-1) + 10*9 + (10-a+c) + 100* (10-a+c) + 10*9 + a-c-1
Если раскрыть все скобки и сократить лишнее, в остатке будет 1089.
Еще один несложный фокус с угадыванием чисел весьма популярен в Интернете. Его описание проще привести в виде скриншота страницы:
Неподготовленный зритель недоумевает, как квадрат “угадывает” число, хотя принцип очень прост, и объясняется школьной арифметикой. Если вычесть из любого числа xy составляющие его числа, результат будет равен 10*x + y - x - y = 9*x. Т.е. какое бы число не загадал зритель, результат всегда будет соответствовать номерам 9, 18, 27 и пр. Эта картинка и показывается при клике на черном квадрате.
3. Число Пи
Вобьем в стену гвоздь, привяжем к нему веревку с карандашом, начертим окружность. Как вычислить длину окружности? Сегодня ответ знает каждый школьник - с помощью числа Пи. Число Пи - несомненно, одна из основных констант мироздания, значение которой было известно еще в древности. Оно используется везде, от кройки и шитья до расчетов гармонических колебаний в физике и радиотехнике.
Сегодня достаточно нажать одну кнопку на калькуляторе, чтобы увидеть его значение:
Pi = 3.1415926535… Однако, за этими цифрами скрывается многовековая история. Что такое число Пи? Это отношение длины окружности к ее диаметру. То что это константа, не зависящая от самой длины окружности, знали еще в древности. Но чему она равна? Есть ли у этого числа какая-то внутренняя структура, неизвестная закономерность? Узнать это хотели многие. Самый простой и очевидный способ - взять и измерить. Примерно так вероятно и поступали в древности, точность разумеется была невысокой. Еще в древнем Вавилоне значение числа Пи было известно как 25/8. Затем Архимед предложил первый математический метод вычисления числа Пи, с помощью расчета вписанных в круг многоугольников. Это позволяло вычислять значение не «напрямую», с циркулем и линейкой, а математически, что обеспечивало гораздо большую точность. И наконец в 3-м веке нашей эры китайский математик Лю Хуэй придумал первый итерационный алгоритм — алгоритм, в котором число вычисляется не одной формулой, а последовательностью шагов (итераций), где каждая последующая итерация увеличивает точность. С помощью своего метода Лю Хуэй получил Пи с точностью 5 знаков: π = 3.1416. Дальнейшее увеличение точности заняло сотни лет. Математик из Ирана Джамшид ибн Мас‘уд ибн Махмуд Гияс ад-Дин ал-Каши в 15-м веке вычислил число Пи с точностью до 16 знаков, а в 17-м веке голландский математик Лудольф вычислил 32 знака числа Пи. В 19-м веке англичанин Вильям Шенкс, потратив 20 лет, вычислил Пи до 707 знака, однако он так и не узнал, что в 520-м знаке допустил ошибку и все последние годы вычислений оказались напрасны (в итерационных алгоритмах хоть одна ошибка делает все дальнейшие шаги бесполезными).
Что мы знаем о числе Пи сегодня? Действительно, это число весьма интересно:
- Число Пи является иррациональным: оно не может быть выражено с помощью дроби вида m/n. Это было доказано только в 1761 году.
- Число Пи является трансцендентным: оно не является корнем какого-либо уравнения с целочисленными коэффициентами. Это было доказано в 1882 году.
- Число Пи является бесконечным.
- Интересное следствие предыдущего пункта: в числе Пи можно найти практически любое число, например свой собственный номер телефона, вопрос лишь в длине последовательности которую придется просмотреть. Можно подтвердить, что так и есть: скачав архив с 10 миллионами знаков числа Пи, я нашел в нем свой номер телефона, номер телефона квартиры где я родился, и номер телефона своей супруги. Но разумеется, никакой “магии” тут нет, лишь теория вероятности. Можно взять любую другую случайную последовательность чисел такой же длины, в ней также найдутся любые заданные числа.
И наконец, перейдем к формулам вычисления Пи, т.к. именно в них можно увидеть красоту числовых взаимосвязей - то, чем интересна математика.
Формула Лю-Хуэя (3й век):
Формула Мадхавы-Лейбница (15 век):
Формула Валлиса (17 век):
Формула Мэчина (18 век):
Попробуем вычислить число Пи по второй формуле. Для этого напишем простую программу на языке Python:
sum = 0.0
sign = 1
for p in range(0, 33):
sum += 4.0*sign/(1 + 2*p)
print(p, sum)
sign = -sign
Запустим программу в любом онлайн-компиляторе языка Питон (например ). Получаем результат:
Шаг Значение
0 4.0
1 2.666666666666667
2 3.466666666666667
3 2.8952380952380956
4 3.3396825396825403
5 2.9760461760461765
6 3.2837384837384844
7 3.017071817071818
8 3.2523659347188767
9 3.0418396189294032
10 3.232315809405594
11 3.058402765927333
12 3.2184027659273333
13 3.0702546177791854
14 3.208185652261944
15 3.079153394197428
16 3.200365515409549
17 3.0860798011238346
18 3.1941879092319425
19 3.09162380666784
20 3.189184782277596
21 3.0961615264636424
22 3.1850504153525314
23 3.099944032373808
24 3.1815766854350325
25 3.1031453128860127
26 3.1786170109992202
27 3.1058897382719475
28 3.1760651768684385
29 3.108268566698947
30 3.1738423371907505
31 3.110350273698687
32 3.1718887352371485
Как можно видеть, сделав 32 шага алгоритма, мы получили лишь 2 точных знака. Видно что алгоритм работает, но количество вычислений весьма велико. Как известно, в 15м веке индийский астроном и математик Мадхава использовал более точную формулу, получив точность числа Пи в 11 знаков:
Попробуем воспроизвести ее в виде программы, чтобы примерно оценить объем вычислений.
Первым шагом необходимо вычислить √12. Возникает резонный вопрос - как это сделать? Оказывается, уже в Вавилоне был известен метод вычисления квадратного корня, который сейчас так и называется “вавилонским”. Суть его в вычислении √S по простой формуле:
Здесь x0 - любое приближенное значение, например для √12 можно взять 3.
Запишем формулу в виде программы:
from decimal import Decimal
print ("Квадратный корень:")
number = Decimal(12)
result = Decimal(3)
for p in range(1, 9):
result = (result + number/result)/Decimal(2)
difference = result**2 - number
print(p, result, difference)
sqrt12 = result
Результаты весьма интересны:
Шаг Значение Погрешность
1 3.5 0.25
2 3.464285714285714 0.00127
3 3.464101620029455 3.3890E-8
4 3.464101615137754 2.392873369E-17
Результат: √12 = 3.464101615137754
Как можно видеть, сделав всего 4 шага, можно получить √12 с достаточной точностью, задача вполне посильная даже для ручных расчетов 15 века.
Наконец, запрограммируем вторую часть алгоритма - собственно вычисление Пи.
sum = Decimal(1)
sign = -1
for p in range(1,32):
sum += Decimal(sign)/Decimal((2*p+1)*(3**p))
sign = -sign
print(p, sqrt12*sum)
print("Result:", sqrt12*sum)
Результаты работы программы:
Шаг Значение
1 3.079201435678004077382126829
2 3.156181471569954179316680000
3 3.137852891595680345522738769
4 3.142604745663084672802649458
5 3.141308785462883492635401088
6 3.141674312698837671656932680
7 3.141568715941784242161823554
8 3.141599773811505839072149767
9 3.141590510938080099642754230
10 3.141593304503081513121460820
11 3.141592454287646300323593597
12 3.141592715020379765581606212
13 3.141592634547313881242713430
14 3.141592659521713638451335328
15 3.141592651733997585128216671
16 3.141592654172575339199092210
17 3.141592653406165187919674184
18 3.141592653647826046431202391
19 3.141592653571403381773710565
20 3.141592653595634958372427485
21 3.141592653587933449530974820
22 3.141592653590386522717511595
23 3.141592653589603627019680710
24 3.141592653589853940610143646
Уже на 24м шаге мы получаем искомые 11 знаков числа Пи. Задача явно требовала больше времени чем сейчас, но вполне могла быть решена в средние века.
Современные формулы не столь просты внешне, зато работают еще быстрее. Для примера можно привести формулу Чудновского:
Для сравнения, те же 24 итерации по этой формуле дают число Пи со следующей точностью:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249.
Если сделать 100 итераций и вычислить 1000 знаков Пи, то можно увидеть так называемую “точку Фейнмана”:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420207
Это последовательность “999999”, находящаяся на 762м знаке от начала. Желающие могут поэкспериментировать дальше самостоятельно с помощью программы на языке Python:
from math import factorial
from decimal import *
def chudnovsky(n):
pi = Decimal(0)
k = 0
while k < n:
pi += (Decimal(-1)**k) * (Decimal(factorial(6*k)) /
((factorial(k)**3) * (factorial(3*k)))*
(13591409 + 545140134*k)/(640320**(3*k)))
k += 1
print("Шаг: {} из {}".format(k, n))
pi = pi * Decimal(10005).sqrt()/4270934400
pi = pi**(-1)
return pi
# Требуемая точность (число знаков)
N = 1000
getcontext().prec = N
val = chudnovsky(N/14)
print(val)
Эта программа не оптимизирована, и работает довольно-таки медленно, но для ознакомления с сутью алгоритма этого вполне достаточно. Кстати, с помощью формулы Чудновского два инженера Александр Йи и Сингеру Кондо в 2010 году объявили о новом мировом рекорде вычисления Пи на персональном компьютере: 5 трлн знаков после запятой. Компьютеру с 12 ядрами, 97Гб памяти и 19 жесткими дисками потребовалось 60 дней для выполнения расчетов.
На этом мы закончим с числом Пи, хотя с ним конечно, связано куда больше интересных фактов. Например 3 марта (т.е. 03.14) отмечается международный “день числа Пи”, ну а другие факты читатели могут поискать самостоятельно.
4. Вычисление радиуса Земли
О том, что Земля круглая сегодня знает каждый школьник, и никого не удивить таким видом планеты из космоса.
Однако в историческом плане, увидеть планету свысока мы смогли совсем-совсем недавно. Как же мог греческий ученый Эратосфен измерить радиус Земли, в 240 году до нашей эры? Оказывается мог, используя 2 научных “инструмента” - транспортир и верблюда, ну и разумеется, математику.
Эратосфен жил в Александрии - крупнейшем городе того времени, центром науки и искусств древнего мира. В Александрии по преданию, находился маяк высотой 120 метров - даже сегодня такое сооружение не просто построить, а в то время маяк считался одним из 7 чудес света. Эратосфен же был не только ученым, но и хранителем Александрийской библиотеки, содержащей до 700000 книг.
Читая труды по географии, Эратосфен нашел интересный факт - в городе Сиене в день летнего солнцестояния Солнце стоит так высоко, что предметы в полдень не отбрасывают тени. Другой может и не обратил бы на это внимание, но Эратосфен не зря интересовался и математикой и астрономией. Он знал что в его городе Александрии тень в этот же день имеет другой угол. Эратосфен дождался солнцестояния, измерил угол солнечных лучей и получил величину 7,2 градуса.
Что это значит? Объяснение данному факту могло быть только одно - Земля круглая, и угол падения солнечных лучей в разных точках Земли в одно время различается.
Картинка с сайта physicsforme.com
Дальше, как говорится, дело техники. Зная примерное расстояние между Сиеном и Александрией (которое было известно из времени в пути каравана верблюдов) и угол, легко получить длину всей окружности. К чести Эратосфена, его результат отличается от сегодняшнего всего лишь на 1%. Так, задолго до эпохи авиации и воздухоплавания, человек впервые смог измерить радиус планеты, даже при этом не отрываясь от нее. Увидеть настоящую кривизну Земли сумели лишь пилоты стратостатов в начале 20 века, более чем через 2000 лет после описанного опыта.
Разумеется, повторить подобный эксперимент сегодня легко может любой школьник. Нужно лишь сделать простейший угломер из транспортира и отвеса, и с помощью знакомых в другом городе, сделать измерения высоты Солнца в двух точках в одно и то же время.
Может ли Земля быть плоской?
Как ни странно об этом писать в 21 веке, но оказывается, до сих пор есть люди, верящие в плоскую Землю. По их мнению, Земля плоская, а Солнце и Луна вращаются вокруг северного полюса, как показано на рисунке.
Вероятно, это началось как чья-то шутка, но к сожалению, немало людей, которые не очень дружили в школе с физикой и математикой, приняли все за чистую монету. Есть даже общество Flat Earth Society, члены которого всерьез уверены в “теории заговора”, и в том что все вокруг их обманывают, в том числе и NASA. Может ли такое быть? Попробуем разобраться.
1) Действительно, человек слишком мал по сравнению с Земным шаром, и “на глаз” увидеть кривизну Земли невозможно. Но это вовсе не является доказательством “плоскости” Земли - просто радиус Земли для человека слишком велик, чтобы его увидеть. Геометрически это легко вычислить.
Как известно, дистанция видимого горизонта для человека - около 5км, а радиус Земли примерно 6000км (6000000м). По теореме Пифагора (см.картинку ниже), при R=6000000 и d=5000, длина гипотенузы R+h = 6000.002.08м, т.е. прирост высоты h по сравнению с плоскостью - всего лишь 2м. Угол вершины треугольника со сторонами 5000м и 2м, составит всего лишь 0.022°, это величина которую “на глаз” невозможно заметить.
В то же время, 2 метра - эта величина которую разумеется, можно измерить. Это демонстрировали, в частности, на канале Discovery Science, направив луч лазера параллельно поверхности воды. На катере было отчетливо видно, что пятно от луча при удалении поднялось вверх, что и должно быть в теории.
Основная сложность такого опыта - обеспечение параллельности луча Земле с точностью до сотых градуса, что в домашних условиях повторить сложно. Именно поэтому в youtube были опубликованы разные “опровержения” - очевидно, что направив луч не параллельно, можно получить любые результаты.
И наконец, в их втором тесте, взлетающий с другого берега озера вертолет, наблюдался в телескоп, и действительно появлялся “из под” поверхности озера.
Ну и наконец, даже не имея лазера и вертолета, можно увидеть данный эффект с помощью бинокля, смотря на удаляющийся корабль на берегу моря.
Скриншот с youtube показывает тот же эффект:
Впрочем, об этом эффекте знали и древние греки, а вот некоторые современные люди, увы, забыли.
Кстати, формула дальности горизонта активно используется связистами, т.к. УКВ-радиоволны распространяются только в прямой видимости. Именно поэтому дальность приема FM станций относительно невелика, и составляет порядка 50км.
2) Очевидно, что гипотеза висящего в космосе “блина”, над центром которого вращается Солнце, не выдерживает никакой критики с точки зрения всех законов физики - такая система в принципе не может быть устойчивой, “солнце” тут же упало бы на “землю”, а куски “земли” в итоге, под действием сил тяготения собрались бы в итоге вместе, и образовали бы - что? Правильно, шар.
3) Как увидел еще Галилей, планеты и их спутники подчиняются законам небесной механики. Некоторые могут считать, что NASA фальсифицирует результаты, но посмотреть на небо может любой желающий.
Данный снимок Юпитера сделан в телескоп автором с балкона:
На нем четко видно шар Юпитера и вращающиеся вокруг него спутники. Если выбрать удачное время, можно увидеть и прохождение тени спутника по поверхности планеты. Если подождать некоторое время, то можно увидеть и вращение самого Юпитера, он вращается весьма быстро.
Так что, к сожалению для любителей плоской Земли, плоских дискообразных планет в небе не наблюдается, проверить это с телескопом может любой желающий. Считать что все планеты таки круглые, а только Земля плоская - это противоречило бы и логике и здравому смыслу.
4) Приверженцы теории верят, что NASA фальсифицирует снимки Земли из космоса. Однако увидеть их тоже может любой желающий - достаточно RTL-SDR приемника ценой 20$ и самодельной антенны, чтобы принять сигналы метеоспутников NOAA. Они постоянно передаются со спутников в открытом виде на частоте 137МГц, и услышать их может любой желающий, с помощью обычной рации и программы Orbitron (программа нужна чтобы узнать точное время пролета спутника). Подключив приемник к компьютеру, можно декодировать сигнал и получить изображение, передаваемое спутником в данный момент:
5) Запустить ракету в космос действительно сложно и дорого. Однако обычный метеозонд можно приобрести на ebay за 20-30$, что позволит запустить фотокамеру с GPS-трекером на высоту 20-25км. Этот опыт вполне доступен, и его делали даже школьники. На такой высоте шарообразность Земли уже не вызывает сомнений.
Таким образом, благодаря математике, геометрии и здравому смыслу, мы таки можем убедиться что Земля не может быть плоской - даже несмотря на то, что мы не видим этого невооруженным глазом.
Кстати, как подсказывает гугл, кривизну Земли все-таки наблюдали невооруженным глазом альпинисты, находящиеся в горах Перу на высоте 6000м. Для этого им пришлось натянуть ровную нить, чтобы сравнить ее с изгибом горизонта, все-таки изгиб на такой высоте еще весьма мал.
5. Простые числа
Каждый знает, что простые числа — такие числа, которые делятся только на единицу и самих себя. Но так ли они просты, как кажутся, и актуальны ли сегодня? Попробуем разобраться.
То, что существуют числа, которые не делятся ни на какое другое число, люди знали еще в древности. Последовательность простых чисел имеет следующий вид:
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 …
Доказательство того, что этих чисел бесконечно много, дал еще Евклид, живший в 300 г до н.э. Примерно в те же годы уже известный нам греческий математик Эратосфен, придумал довольно-таки простой алгоритм получения простых чисел, суть которого была в последовательном вычеркивании чисел из таблицы. Те оставшиеся числа, которые ни на что не делились, и были простыми. Алгоритм называется «решето Эратосфена» и за счет своей простоты (в нем нет операций умножения или деления, только сложение) используется в компьютерной технике до сих пор.
Видимо, уже во время Эратосфена стало ясно, что какого-либо четкого критерия, является ли число простым, не существует — это можно проверить лишь экспериментально. Существуют различные способы для упрощения процесса (например, очевидно, что число не должно быть четным), но простой алгоритм проверки не найден до сих пор, и скорее всего найден не будет: чтобы узнать, простое число или нет, надо попытаться разделить его на все меньшие числа.
Это несложно записать в виде программы на языке Python:
import math
def is_prime(n):
if n % 2 == 0 and n > 2:
return False
for i in range(3, int(math.sqrt(n)) + 1, 2):
if n % i == 0:
return False
return True
# Вывод всех простых чисел от 1 до N
N = 100
for p in range(1, N, 2):
if is_prime(p): print(p)
# Вывод результата, является ли заданное число простым
print(is_prime(2147483647))
Желающие могут поэкспериментировать с программой самостоятельно.
Подчиняются ли простые числа каким-либо законам? Да, и они довольно любопытны. Так, например, французский математик Мерсенн еще в 16 веке обнаружил, что много простых чисел имеет вид 2N — 1, эти числа названы числами Мерсенна. Еще незадолго до этого, в 1588 году, итальянский математик Катальди обнаружил простое число 219 — 1 = 524287 (по классификации Мерсенна оно называется M19). Сегодня это число кажется весьма коротким, однако даже сейчас с калькулятором проверка его простоты заняла бы не один день, а для 16 века это было действительно огромной работой. На 200 лет позже математик Эйлер нашел другое простое число 231 — 1 = 2147483647. Необходимый объем вычислений каждый может представить сам. Он же выдвинул гипотезу, названную позже «проблемой Эйлера», или «бинарной проблемой Гольдбаха»: каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел. Например, можно взять 2 четных числа 123456 и 888777888. С помощью компьютера можно найти их сумму в виде двух простых чисел: 123456 = 61813 + 61643 и 888777888 = 444388979 + 444388909. Точное доказательство этой теоремы не найдено до сих пор, хотя с помощью компьютеров она была проверена до чисел с 18 нулями.
Кстати, последовательность простых чисел Мерсенна 2N-1 имеет следующий вид:
M2=3, M3=7, M5=31, M7=127, M13=8191, M17=131071, M19=524287, M31=2147483647, ...
При этом показатели N, что удивительно, сами тоже являются простыми числами (доказательство этой теоремы можно найти в интернете):
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, ...
Существует и другая теорема, называемая теоремой Ферма-Эйлера, открытая в 1640 году, которая говорит о том, что если простое число имеет вид 4*k+1, то оно может быть представлено в виде суммы квадратов других чисел. Так, например, в нашем примере простое число 444388909 = 4*111097227 + 1. И действительно, с помощью компьютера можно найти, что 444388909 = 19197*19197 + 8710*8710. Теорема была доказана Эйлером лишь через 100 лет.
И наконец Бернхардом Риманом в 1859 году была выдвинута так называемая «Гипотеза Римана» о количестве распределения простых чисел, не превосходящих некоторое число. Эта гипотеза не доказана до сих пор, она входит в список семи «проблем тысячелетия», за решение каждой из которых Математический институт Клэя в Кембридже готов выплатить награду в один миллион долларов США.
Так что с простыми числами не все так просто. Есть и удивительные факты. Например, в 1883 г. русский математик И.М.Первушин из Пермского уезда доказал простоту числа 261 — 1 = 2305843009213693951. Даже сейчас компьютеру с запущенной вышеприведенной программой требуется несколько минут на проверку данного числа, а на то время это была поистине гигантская работа.
Кстати интересно, что существуют люди, обладающие уникальными способностями мозга — так например, известны аутисты, способные находить в уме (!) 8-значные простые числа. Как они это делают, непонятно. Такой пример описывается в книге известного врача-психолога Оливера Сакса “Человек, который принял жену за шляпу”. По некоторым предположениям, такие люди обладают способностью “видеть” числовые ряды визуально, и пользуются методом “решета Эратосфена” для определения, является ли число простым или нет.
Еще два интересных простых числа: 73939133 и 1979339333. Они интересны тем, что если от них убирать правую цифру, то каждое новое число - тоже простое:
73939133 - 7393913 - 739391 - 73939 - 7393 - 739 - 73 - 7
1979339333 - 197933933 - 19793393 - 1979339 - 197933 - 19793 - 1979 - 197 - 19 - 1
Для нахождения всех подобных чисел можно написать несложную программу, использующую написанную ранее функцию is_prime:
for v in xrange(10000001, 99999999, 2):
v0, v1, v2, v3, v4, v5, v6, v7 = v, v/10, v/100, v/1000, v/10000,
v/100000, v/1000000, v/10000000
if is_prime(v7) and is_prime(v6) and is_prime(v5) and is_prime(v4) and
is_prime(v3) and is_prime(v2) and is_prime(v1) and is_prime(v0):
print v0, v1, v2, v3, v4, v5, v6, v7
Несколько сотен лет математикам известна другая, не менее оригинальная последовательность, где все числа простые:
31 331 3331 33331 333331 3333331 33333331
Дальше ряд заканчивается, число 333333331 = 17*19607843, простым не является.
Желающие могут проверить самостоятельно, не обладают ли другие последовательности (51, 551, 61, 661 и пр) такими же свойствами.
Еще одна интересная гипотеза была выдвинута Ферма, который предположил, что все числа вида
являются простыми. Эти числа называются “числами Ферма”. Однако, это оказалось верным только для 5 первых чисел: F0=3, F1=5, F2=17,F3=257, F4=65537. В 1732 году Эйлер опроверг гипотезу, найдя разложение на множители для F5: F5= 641·6700417. Существуют ли другие простые числа Ферма, пока неизвестно до сих пор. Такие числа растут очень быстро (для примера, F7=340282366920938463463374607431768211457), и их проверка является непростой задачей даже для современных компьютеров.
Актуальны ли простые числа сегодня? Еще как! Простые числа являются основой современной криптографии, так что большинство людей пользуются ими каждый день, даже не задумываясь об этом. Любой процесс аутентификации, например, регистрация телефона в сети, банковские платежи и прочее, требуют криптографических алгоритмов. Суть идеи тут крайне проста и лежит в основе алгоритма RSA, предложенного еще в 1975 году. Отправитель и получатель совместно выбирают так называемый «закрытый ключ», который хранится в надежном месте. Этот ключ представляет собой, как, наверное, читатели уже догадались, простое число. Вторая часть — «открытый ключ», тоже простое число, формируется отправителем и передается в виде произведения вместе с сообщением открытым текстом, его можно опубликовать даже в газете. Суть алгоритма в том, что не зная «закрытой части», получить исходный текст невозможно.
К примеру, если взять два простых числа 444388979 и 444388909, то «закрытым ключом» будет 444388979, а открыто будут передано произведение 197481533549433911 (444388979*444388909). Лишь зная вторую половинку, можно вычислить недостающее число и расшифровать им текст.
В чем хитрость? А в том, что произведение двух простых чисел вычислить несложно, а вот обратной операции не существует — если не знать первой части, то такая процедура может быть выполнена лишь перебором. И если взять действительно большие простые числа (например, в 2000 символов длиной), то декодирование их произведения займет несколько лет даже на современном компьютере (к тому времени сообщение станет давно неактуальным). Гениальность данной схемы в том, что в самом алгоритме нет ничего секретного — он открыт и все данные лежат на поверхности (и алгоритм, и таблицы больших простых чисел известны). Сам шифр вместе с открытым ключом можно передавать как угодно, в любом открытом виде. Но не зная секретной части ключа, которую выбрал отправитель, зашифрованный текст мы не получим. Для примера можно сказать, что описание алгоритма RSA было напечатано в журнале в 1977 году, там же был приведен пример шифра. Лишь в 1993 году при помощи распределенных вычислений на компьютерах 600 добровольцев, был получен правильный ответ.
Числа Мерсенна
Про простые числа Мерсенна уже упоминалось ранее, они достаточно интересны, чтобы остановиться на них подробнее. Это числа, вычисляемые по формуле N = 2n - 1.
Но не все так просто. Во-первых, не все числа такого вида являются простыми, была доказана теорема, что число N простое, только если n является простым. Однако, это необходимое но не достаточное условие, к примеру 11 простое число, а 211-1 = 2047 = 23·89 простым не является.
Используя вышенаписанную функцию is_prime, получить первые 9 чисел Мерсенна весьма просто.
m = 0
for p in range(2, 32):
if is_prime(p) and is_prime(2**p - 1):
m += 1
print("M{} = {} (p={})".format(m, 2**p - 1, p))
С помощью программы легко получить первые 10 чисел Мерсенна.
M1 = 3 (22-1)
M2 = 7 (23-1)
M3 = 31 (25-1)
M4 = 127 (27-1)
M5 = 8191 (213-1)
M6 = 131071 (217-1)
M7 = 524287 (219-1)
M8 = 2147483647 (231-1)
M9 = 2305843009213693951 (261-1)
Однако, проверка таких чисел на языке Python занимает весьма приличное время - даже нахождение числа M10 может занять более получаса.
К счастью для нас, еще в начале прошлого века математики Люка в 1870г и Лемер в 1930г доказали теорему о том, что простоту числа Мерсенна можно узнать, проверяя лишь остатки от деления определенной последовательности (подробнее можно прочитать в Википедии). Этот тест выполняется в тысячи раз быстрее, и позволяет проверять числа гораздо большей длины.
Полный текст программы приведен ниже.
import math, time
def is_prime(n):
if n % 2 == 0 and n > 2:
return False
for i in range(3, int(math.sqrt(n)) + 1, 2):
if n % i == 0:
return False
return True
def is_mersenne_prime(p):
# Lucas-Lehmer 2^p-1 number primality test
if p == 2:
return True
else:
m_p = 2**p - 1
s = 4
for i in range(3, p+1):
s = (s ** 2 - 2) % m_p
return s == 0
m = 0
for p in range(2, 100):
if is_prime(p) and is_mersenne_prime(p):
t_start = time.time()
res = is_mersenne_prime(p)
m += 1
val = 2**p - 1
print("M{} = {} (p={}, T={})".format(m, val, p, time.time() - t_start))
В программу также добавлен вывод времени расчета для каждого числа.
Интересно заметить, что простота числа M25 = 221701-1 была доказана студентами Noll и Nickel в 1978г с помощью университетского компьютера, и это “открытие” попало даже в телевизионные новости. Сейчас с помощью вышеприведенной программы, это число можно сделать даже на 20-долларовом компьютере Raspbery Pi, сама проверка занимает не более минуты.
С помощью 2х вышеприведенных функций легко проверить такое число Мерсенна:
bp = 2**21701 - 1
print(bp, is_mersenne_prime(21701))
Нельзя не признать, что само число 221701-1 выглядит достаточно внушительно:
44867916611904333479495141036159177872720902372938861301036480447512785609158053637162018395920183108689149613973035533621134551674715287880007134345347194681025732056939825423723521750452980127215084299527266875706892007262798468825185681532142985720637290299313726344463257416449344509835102458816789016394945893696705168502436180232259551672603295389186364437045681350697590862198047118901225352609650331560624641680529360950276322519541199378781611887950368067065467094570602703933944508795918017973611326798274338403964825448745270434393258865935311826270281291301767537362073560471706796018086986188192305477308263143033689309402401116023184218739861793173381674293624039080146446533167893142403441626243986354829868152963856856097613981370008545290902178852760181267516916666189196652889272405457548015727583223936389690623948268629738406595342536881770621194098884299042222510205198907427651269590866489020849331593183544730378438673619905441075619665362094087700417583472204239335761771260615063239687136058218014855376128809648109025328444692060981149171853122623214490315199270347679840250650446624361158632712607371820441076129040576076156413981966443384174935945557589269550551384444249641738589326431062350244259749888495427561113138125373546749571089212977055534105306317668036525450115619994704703080975001831039096328170193148671686659220369588362291591980963840251182084839045643052580945876198697254235294718583716788165976228557375284260972377346244685323620326927812128869122804644917707943186384476057711810558228653120572801809938250702311789320142979213175068746598525343177694757992501015403459055756096150131796369342571712916973547166474698856592132612717244249685861542410597610354729550125380584497109056463991926448357223209008827764713220228439775757230755516658614028292960947522709456751199752268424383084190316769975828969408161512929731166188774631973942613003505328030528435929861943028814647224393409604332129915709479716480001751152901047730022099226496393622633345405009361146955156338963448113785646130979933903537929751619768669550563002423706161236691536299577305442116055910462682405728304933022695634876033547918117176704431651372729753611485207957283097607765933169252913861287726833830000755907168496373643201886627226059186824987046158950280121480310106220821760865120562920439756658081153617726352709131801387158672559847396101178548655217308890158788609324326427919178121708326042669857675282709609677929532780738060001705557411238564945972873592110131239116174462947424279402757853073650206058072089139080813381552120237889176959032725532187981806390188976611966923383780080589571180304127953763426872458894003176440733448130784320760858250357720163697308151884697269173048039142351116460009341135465682559795451407065757164712682892684340399927996841540378943787439234382545562253973300003977291497945580368468642313784723553952911754115108385290054865563784523161325911184338403975092561182541488447059744171236348865292897919507096247432485742758096709852132553243687088002636637356883647209281384466468348661473539477676114713952390574283871138643608927689646270265436227072361361556969326026972555137795806131512078396392381117163021488319719122953967241849650035686516897636532829829413559438271078909648012546818155830670649731025924561052079518365511691315910359549578098542021850858860195694976630351366074278129451101792937644085504395275589852388064138602439346909569031381270272833205694814223411334423565977453887542395353485301546284835327702006873689327611630437966491140077951840154972590243416512380587609900111470825767310676939441942826834427612997756892340669203408743659224466633723212596650417249730825215118303577011272768581293371366148392778532335573122542905472394542069919985611732624482347646980930805586007081976261003097963198812882873782621377463926668786498204922447802136607398552526766227205124310008056632919363553194966717056709446690809053625020657218419836547624618595375352039018705449062959037038925284556675116361168237279922207920794703117075921951295707710873733317931433110923531405719416365240907518118794096775462324423434250371711420947553571555908465792580645089870615111865933553809003552706994499748706917899889082891225016257753453229705906397483096836459677640750701051127649136815511445021677568414826304009394300853762240103073543616073297109679097852591173721376034038403903797326084264850909622924265141840684883798695123898530601713627917934581206083528373369371952855787986368194089909153037760311683730584329384267492189510884229753903906808988993523259437606901944039838823315225488711871355530334671879703287493612171018890720047791219983006575690550227543246901734749051876793980240930546447655515405860615566182339568500526080685358056916078877218441535928716267560418132595102517522928981353833074067246933111570873295331815501725771241383698605105802286768924861382741652271179538064625778814288737402101220075694269814240934893379113612806306410045157701609671517543787442511524203121293023260598375610136932287924468473569626893292863959506611559181514200293625478634965230187600993204860736747921056014359652196606989325320755082356901630669240688685505174445515739151017185696401582807173431580481627122423292641208991071222953038343766541925054971737959169869292375645057151727543470106206531135735154136115144300015873080448570355596137321380062748881332031472142823024949510022409370177712994235289702790490255826941441774321618772576455298250619988354955614763200793811728997204477597638052792510878225745663494703701392574625552528908681553926116252158243953964293657171414581341823547346468074289772645946104841180801333621512150598625594195401601933368973292090945435953301875202828322848138663871822530516790587144451339179411203328134884327892252621182901800244630979609876813374281202935998128401633959108387881070976339195584757402099414224321539543476019604874975720230127703172732861447718691961098975942332752633167063512960112700154075209382155551695503282689329429789346503176351007528609841743736084042408094015850910964618482805649640269394165006760210370817982850495571836159005709917919149733735278914364020463842602726375487527643414975692020200079346255666615166515258291939313433912222614621242014153365037286833662921186290423547789663783785467893012638041082143785487398866487992341179948504338667781255945413472465246231194881401316071628427281713042247869185631200192333698966933544361629391311041730956501694662754558875644345191269279600693551809271956450264294092857410828353511882751
К счастью для нас, язык Python может работать с большими числами неограниченной длины, ну и мощность современных компьютеров достаточно велика. Сама проверка этого числа методом Люка-Лемера заняла всего лишь 15с, разумеется, для компьютеров и программистов в 1978г это было гораздо более сложной задачей.
Изучение чисел Мерсенна продолжается энтузиастами и сейчас. Самым большим на момент написания книги простым числом, является число М49 = 274207281 - 1, содержащее 22 338 618 знаков. А в начале 2018 года было найдено 50е число Мерсенна М50 = 277232917-1. Его проверка заняла на 32-ядерном сервере Xeon 82 часа. Существует даже сеть распределенных вычислений , присоединиться к которой может любой желающий, для этого достаточно установить на компьютер программу для расчета.
Кстати, вывести число 277232917-1 совсем несложно с помощью Python. Само вычисление числа проблем не составляет, а вот стандартная функция print для таких длинных чисел не работает - результата дождаться так и не удалось. Однако, число можно вывести посимвольно, если каждый раз выводить остаток от деления на 10, и уменьшать число во столько же раз.
bp2 = 2**77232917 - 1
while True:
print(bp2%10, end='')
bp2 = bp2/10
if bp2 == 0: break
Разумеется, только вывод на экран таким способом займет порядка нескольких часов. Второй недостаток программы в том, что число выводится задом наперед, т.к. первыми выводятся самые младшие разряды, после вывода данные в файле придется перевернуть. Зато мы все-таки можем посмотреть, как выглядит самое больше найденное число Мерсенна (в перевернутом виде) в современной истории: 1709712679608160372856311737129564169399997264989729636740737…
Впрочем, все это уже сделали за нас, уже готовое число M50 можно просто скачать по ссылке , размер файла составляет 23Мбайт.
В завершение темы простых чисел, приведем вид так называемой “спирали Улама”. Математик Станислав Улам открыл ее случайно в 1963 году, рисуя во время скучного доклада на бумаге числовую спираль и отмечая на ней простые числа:
Как оказалось, простые числа образуют вполне повторяющиеся узоры из диагональных линий. В более высоком разрешении изображение выглядит так (картинка с сайта ):
В общем, можно предположить что далеко не все тайны простых чисел раскрыты и до сих пор.
6. Совершенные числа
Еще одно удивительное свойство мира чисел было доказано еще Евклидом: если число вида 2p-1 является простым (уже известное нам число Мерсенна), то число 2P-1(2p-1) является совершенным, т.е. равно сумме всех его делителей.
Рассмотрим пример для p=13:
213-1 = 8191. Как показывает приведенная ранее программа, 8191 - действительно простое число.
212*(213-1) = 33550336.
Чтобы найти все делители числа и их сумму, напишем небольшую программу:
def is_perfect(n):
sum = 0
for i in range(1, int(n/2)+1):
if n % i == 0:
sum += i
print(i)
print("Сумма", sum)
return sum == n
is_perfect(33550336)
Действительно, 33550336 делится на числа 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8191, 16382, 32764, 65528, 131056, 262112, 524224, 1048448, 2096896, 4193792, 8387584, 16775168. И сумма этих чисел равна искомому 33550336.
Совершенные числа встречаются довольно-таки редко, их последовательность согласно Википедии, образует вид:
6,
28,
496,
8128,
33 550 336,
8 589 869 056,
137 438 691 328,
2 305 843 008 139 952 128,
2 658 455 991 569 831 744 654 692 615 953 842 176,
Кстати, еще Эйлер доказал, что все совершенные числа имеют только вид 2p-1(2p-1). А вот нечетных совершенных чисел пока не обнаружено, но и не доказано что их не существует. Интересно проверить этот факт практически. Совершенное число 137438691328 обнаружил еще немецкий математик Иоганн Мюллер в 16 веке. Сегодня такое число несложно проверить на компьютере.
Во-первых, слегка оптимизируем приведенную выше программу. Как нетрудно видеть, если число N делится нацело на P, то мы “автоматом” сразу находим и второй делитель N/P. Например, если 10 делится нацело на 2, то оно делится и на 10/2=5. Это позволяет заметно сократить число вариантов перебора. Во-вторых, используем тип чисел Decimal, позволяющий использовать большие числа. Обновленная программа выглядит так:
from decimal import *
def is_perfect(n):
s = Decimal(1)
p = Decimal(2)
while p < n.sqrt()+1:
if n % p == 0:
s += p
if p != n/p: s += n/p
p += 1
return s == n
print(is_perfect(Decimal('137438691328')))
Запускаем, программа работает - число '137438691328' действительно является совершенным. Оно делится на 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524287, 1048574, 2097148, 4194296, 8388592, 16777184, 33554368, 67108736, 134217472, 268434944, 536869888, 1073739776, 2147479552, 4294959104, 8589918208, 17179836416, 34359672832 и 68719345664, сумма этих чисел равна 137438691328. Однако, проверка “совершенности” данного числа заняла … 54 секунды. Это конечно быстро по сравнению с 16м веком, но совершенно недостаточно чтобы проверить все числа, хотя бы до миллиарда. Значит пора использовать более тяжелую артиллерию - перепишем программу на языке Си. Все-таки Python это интерпретатор, и работает заметно медленнее. Получаемый код не намного сложнее:
#include <string.h>
#include <math.h>
#include <stdbool.h>
#include <stdint.h>
bool isPerfect(unsigned long long int n) {
unsigned long long int sum = 1, i;
for(i=2; i<=sqrt(n)+1; i++)
{
if (n%i==0) {
sum += i;
if (i != n/i) {
sum += n/i;
}
}
}
return sum == n;
}
int main() {
unsigned long long int n = 137438691328LL;
bool res = isPerfect(n);
printf("%d\n", res);
return 0;
}
Компилируем программу с помощью компилятора gcc, запускаем получившийся exe-файл: время выполнения меньше секунды, уже гораздо лучше. Теперь несложно поменять функцию main для перебора всех чисел от 1 до 200000000000. В код также добавлен вывод промежуточных результатов каждые 1000000 итераций, чтобы видеть ход выполнения программы.
int main() {
unsigned long long int MAX = 200000000000LL;
unsigned long long int p;
for (p=1; p<MAX; p++) {
if (isPerfect(p))
printf(" %llu ", p);
if (p % 1000000 == 0)
printf("*%llu,%llu*", 100*p/MAX, p);
}
}
Увы, для таких чисел как 200000000000, скорости обычного компьютера все равно недостаточно. Примерно за час работы программы, было перебрано лишь 100млн вариантов, а для перебора всех 200млрд понадобился бы не один день. Желающие могут продолжить процесс самостоятельно, однако с уверенностью можно сказать что в диапазоне от 1 до 100000000 действительно нет совершенных чисел кроме 6, 28, 496, 8128 и 33550336.
Проверка числа 2 305 843 008 139 952 128 является непростой задачей даже для современного компьютера - во-первых, в языке C/C++ нет встроенных типов данных для столь большого числа, а во-вторых, число вариантов перебора слишком велико.
Разумеется, выше было приведено самое простое решение “в лоб”, можно оптимизировать и саму программу, например разбить вычисление на несколько процессорных ядер, однако данная задача выходит за рамки этого материала. Немного про параллельные вычисления будет рассказано в конце книги.
7. Магический квадрат
Еще одна старинная математическая головоломка - магический квадрат. Магическим называют квадрат, заполненный неповторяющимися числами так, что суммы чисел по горизонталям, вертикалям и диагоналям одинаковы. Такие квадраты известны давно, самым старым из известных является магический квадрат Ло Шу, изображенный в Китае в 2200г до нашей эры.
Если подсчитать количество точек, то можно перевести квадрат в современный вид, изображенный справа.
Магический квадрат 4х4 был обнаружен в индийских надписях 11 века:
И наконец, известный квадрат 4х4, изображенный на гравюре немецкого художника Дюрера “Меланхолия”. Этот квадрат изображен не просто так, 2 числа 1514 указывают на дату создания гравюры.
Как можно видеть, уже математики прошлого умели строить магические квадраты разной размерности. Интересно рассмотреть их свойства.
Сумма чисел магического квадрата размера NxN зависит только от N, и определяется формулой:
Это несложно доказать, т.к. сумма всех чисел квадрата равна сумме ряда 1..N2. Действительно, для квадрата Дюрера M(4) = 34, что можно посчитать на картине. Для квадратов разной размерности суммы равны соответственно: M(3) = 15, M(4) = 34, M(5) = 65, M(6) = 111, M(7) = 175, M(8) = 260, M(9) = 369, M(10) = 505.
Напишем программу для построения магических квадратов размерности N. Первый подход будет “в лоб”, напрямую. Создадим массив, содержащий все числа от 1 до N2 и получим все возможные перестановки этого массива. Их число довольно-таки велико, и составляет 1*2*..*N = N! вариантов. Также для каждого массива необходимо проверить, является ли он “магическим”, т.е. выполняется ли требование равенства сумм.
Для получения всех перестановок воспользуемся алгоритмом, описанным здесь - -cpp.ru/permutation/.
Код программы приведен ниже:
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def next_set(arr, n):
j = n - 2
while j != -1 and arr[j] >= arr[j + 1]: j -= 1
if j == -1:
return False
k = n - 1
while arr[j] >= arr[k]: k -= 1
swap(arr, j, k)
l = j + 1
r = n - 1
while l < r:
swap(arr, l, r)
l += 1
r -= 1
return True
def is_magic(arr, n):
for i in range(0, n):
sum1, sum2, sum3, sum4 = 0, 0, 0, 0
for j in range(0, n):
sum1 += arr[i * n + j]
sum2 += arr[j * n + i]
sum3 += arr[j * n + j]
sum4 += arr[(n - j - 1) * n + j]
if sum1 != sum2 or sum1 != sum3 or sum1 != sum4 or
sum2 != sum3 or sum2 != sum4 or sum3 != sum4:
return False
return True
def show_squares(n):
N = n * n
arr = [i + 1 for i in range(N)]
cnt = 0
while next_set(arr, N):
if is_magic(arr, n):
print(arr)
cnt += 1
return cnt
# Требуемая размерность
cnt = show_squares(3)
print("Число вариантов:", cnt)
Программа выдала 8 вариантов для N=3, время вычисления составило 2 секунды:
[2, 7, 6, 9, 5, 1, 4, 3, 8] [6, 1, 8, 7, 5, 3, 2, 9, 4]
[2, 9, 4, 7, 5, 3, 6, 1, 8] [6, 7, 2, 1, 5, 9, 8, 3, 4]
[4, 3, 8, 9, 5, 1, 2, 7, 6] [8, 1, 6, 3, 5, 7, 4, 9, 2]
[4, 9, 2, 3, 5, 7, 8, 1, 6] [8, 3, 4, 1, 5, 9, 6, 7, 2]
Действительно, как известно, существует только 1 магический квадрат 3х3:
Остальные являются лишь его поворотами или отражениями (очевидно что при повороте квадрата его свойства не изменятся).
Теперь попробуем вывести квадраты 4х4. Запускаем программу… и ничего не видим. Как было сказано выше, число вариантов перебора для 16 цифр равняется 16! или 20922789888000 вариантов. На моем компьютере полный перебор такого количества занял бы 1089 дней!
Однако посмотрим на магический квадрат еще раз:
Суммы всех элементов по горизонтали и вертикали равны. Из этого мы легко можем записать равенство его членов:
x11 + x12 + x13 + x14 = x21 + x22 + x23 + x24
x11 + x12 + x13 + x14 = x14 + x24 + x34 + x44
x11 + x12 + x13 + x14 = x13 + x23 + x33 + x43
x11 + x12 + x13 + x14 = x12 + x22 + x32 + x42
x11 + x12 + x13 + x14 = x11 + x21 + x33 + x44
x11 + x12 + x13 + x14 = x31 + x32 + x33 + x34
И наконец, общая сумма: т.к. квадрат заполнен числами 1..16, то если сложить все 4 строки квадрата, то получаем 4S = 1+..+16 = 136, т.е. S=34 (что соответствует приведенной в начале главы формуле).
Это значит, что мы легко можем выразить последние элементы через предыдущие:
x14 = S - x11 - x12 - x13
x24 = S - x21 - x22 - x23
x34 = S - x31 - x32 - x33
x41 = S - x11 - x21 - x31
x42 = S - x12 - x22 - x32
x43 = S - x13 - x23 - x33
x44 = S - x14 - x24 - x34
Что это дает? Очень многое. Вместо перебора 16 вариантов суммарным количеством 16!=20922789888000 мы должны перебрать лишь 9 вариантов, что дает 9!=362880 вариантов, т.е. в 57657600 раз меньше! Как нетрудно догадаться, мы фактически выразили крайние строки квадрата через соседние, т.е. уменьшили размерность поиска с 4х4 до 3х3. Это же правило будет действовать и для квадратов большей диагонали.
Обновленная программа выглядит более громоздко (в ней также добавлены проверки на ненулевые значения и проверки на уникальность элементов), зато расчет происходит в разы быстрее. Здесь также используется возможность работы со множествами в языке Python, что легко позволяет делать перебор нужных цифр в цикле:
set(range(1,16+1)) - множество чисел [1..16]
set(range(1,16+1)) - {x11} - множество чисел [1..16] за исключением x11.
Также добавлена простая проверка на минимальность суммы: очевидно, что сумма всех элементов не может быть меньше чем 16+1+2+3 = 22.
cnt = 0
digits = set(range(1,16+1))
for x11 in digits:
for x12 in digits - {x11}:
for x13 in digits - {x11,x12}:
for x14 in digits - {x11,x12,x13}:
s = x11 + x12 + x13 + x14
if s < 22: continue
for x21 in digits - {x11,x12,x13,x14}:
for x22 in digits - {x11,x12,x13,x14,x21}:
for x23 in digits - {x11,x12,x13,x14,x21,x22}:
x24 = s - x21 - x22 - x23
if x24 <= 0 or x24 in [x11,x12,x13,x14,x21,x22,x23]: continue
for x31 in digits - {x11,x12,x13,x14,x21,x22,x23,x24}:
for x32 in digits - {x11,x12,x13,x14,x21,x22,x23,x24,x31}:
for x33 in digits - {x11,x12,x13,x14,x21,x22,x23,x24,x31,x32}:
x34 = s - x31 - x32 - x33
x41 = s - x11 - x21 - x31
x42 = s - x12 - x22 - x32
x43 = s - x13 - x23 - x33
x44 = s - x14 - x24 - x34
if x34 <= 0 or x41 <= 0 or x42 <= 0 or
x43 <= 0 or x44 <= 0: continue
data = [x11, x12, x13, x14, x21, x22, x23, x24, x31,
x32, x33, x34, x41, x42, x43, x44]
if len(data) != len(set(data)): continue
if is_magic(data, 4):
print data
cnt += 1
print cnt
В результате, программа проработала всего лишь около часа (вместо 3х лет!), всего было выведено 7040 квадратов размерностью 4х4. Разумеется, большинство из них являются поворотами или отражениями друг друга. Было доказано что уникальных квадратов всего 880.
Кстати, приведенную выше программу можно еще оптимизировать.
Во-первых, заменим операции поиска во множестве вида if x21 in set([x11, x12, x13]) прямым сравнением if x21 != x11 and x21 != x12… Программа получается немного более громоздкой, зато такие операции выполняются быстрее - программа работает быстрее примерно на 10%.
Во-вторых, как можно увидеть, операции со множествами выполняются в цикле множество раз. Например, в коде
for x11 in digits:
for x12 in digits - {x11}:
for x13 in digits - {x11, x12}:
каждый раз формируется множество digits - {x11}, затем digits - {x11, x12} и т.д. Если вынести множества в отдельные переменные, число операций можно сократить, хотя это и делает код более громоздким:
for x11 in digits:
s11 = digits - {x11}
for x12 in s11:
s12 = s11 - {x12}
for x13 in s12:
При таком способе, на каждом шаге из множества вычитается только одна новая цифра, а не все заново.
И наконец, как было показано выше, сумма чисел магического квадрата может быть вычислена заранее по известной формуле - для N=4 она равна 34. Это позволяет избавиться от цикла по x14, заменив его простым выражением x14 = s - x11 - x12 - x13, что ускорит программу примерно в 10 раз. В итоге наших действий, программа работает всего лишь несколько минут вместо часа, прирост скорости весьма заметный.
Полный текст программы можно найти в архиве с файлами под названием “07 - magic4.py”.
Вспомним теперь магический квадрат Дюрера, в его строке есть цифры 1514, соответствующие году создания гравюры. С помощью программы можно решить еще одну задачу: посмотреть сколько всего возможно квадратов с такими цифрами. Здесь число вариантов перебора меньше, т.к. еще 2 цифры фиксированы. Оказывается, помимо “авторского”, возможны всего 32 варианта, например:
1 15 14 4 2 15 14 3
5 11 8 10 5 10 7 12
12 6 9 7 11 8 9 6
16 2 3 13 16 1 4 13
Интересно, что верхний ряд помимо цифр 15 и 14 может содержать либо 1,4 либо 2,3, других вариантов нет. Разные варианты содержат лишь перестановки этих цифр.
Если же говорить о квадратах большей размерности, то число вариантов перебора для них получается слишком большим. Так для квадрата 5х5, даже если выразить крайние члены через соседние, получаем 4х4 остающихся клеток, что даст нам те же самые 16! вариантов перебора. В архиве с книгой приложен файл “07 - magic5.c” для расчета квадратов 5х5, но автору так и не хватило терпения дождаться всех результатов. Заметно ускорить вычисления можно, лишь перенеся вычисления на GPU, об этом будет рассказано отдельно.
В качестве примера алгоритма построения квадратов любой нечетной размерности без полного перебора, можно назвать так называемый сиамский метод, известный уже с 17 века. Его описание можно найти в Википедии, пример программы на языке Python можно найти в приложении к книге.
Для N=9, программа сгенерировала следующий квадрат:
47 58 69 80 1 12 23 34 45
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35
Существует множество других алгоритмов построения, например метод Франклина, Россера, Рауз-Болла, желающие могут поискать их самостоятельно.
И наконец, можно вспомнить так называемые “пандиагональные” магические квадраты. Это квадраты, в которых учитываются суммы также “косых” диагоналей, которые получаются если вырезать квадрат из бумаги и склеить его в тор. Желающие могут добавить в программу вывод таких квадратов самостоятельно.
8. Магический квадрат из простых чисел
Существует еще одна разновидность магического квадрата - составленного из простых чисел. Пример такого квадрата показан на рисунке:
29
131
107
167
89
11
71
47
149
Приведенную выше программу легко модифицировать для такого расчета: достаточно лишь заменить множество digits = set(range(1,16+1)) на другое, содержащее простые числа.
Для примера будем искать квадраты среди трехзначных простых чисел от 101 до 491.
Заменим в предыдущей версии программы строку digits = set(range(1,16+1)) на
primes = [ 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163,
167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251,
257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443,
449, 457, 461, 463, 467, 479, 487, 491 ]
digits = set(primes)
Таких квадратов нашлось 40, например:
233
167
389
419
263
107
137
359
293
Сумма чисел равна вполне красивому числу 789.
Т.к. число вариантов перебора больше, программа работает дольше. Время поиска составило 724с для Python-версии и 316c для программы на C++.
Если же рассматривать минимально возможный квадрат из простых чисел, то его сумма равняется тоже вполне “красивому” числу 111:
7
61
43
73
37
1
31
13
67
Примером квадрата 4х4 может быть квадрат с также “красивой” суммой 222:
97
41
73
11
17
47
83
75
59
79
13
71
49
55
53
65
9. Числа Фибоначчи
Возьмем 2 числа: 0 и 1. Следующее число рассчитаем как сумму предыдущих чисел, затем повторим процесс.
Мы получили последовательность, известную как числа Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...
Эта последовательность была названа в честь итальянского математика 12 века Леонардо Фибоначчи. Фибоначчи рассматривал задачу роста популяции кроликов. Если предположить, что новорожденная пара кроликов 1 месяц растет, через месяц начинает спариваться, и затем через каждый месяц дает потомство, то количество пар кроликов несложно подсчитать:
Как можно видеть, число пар образует как раз те самые числа Фибоначчи. Сама последовательность Фибоначчи кажется простой. Но чем она интересна? Пример с кроликами не случаен - эти числа действительно описывают множество природных закономерностей:
- Множество растений имеют количество лепестков, равное одному из чисел Фибоначчи. Количество листьев на стебле также может описываться этим законом, например у тысячелистника.
- Другое известное изображение - спираль Фибоначчи, которая строится по похожему принципу соотношения размеров прямоугольников:
Это изображение также часто встречается в природе, от раковин моллюсков, до формы атмосферного циклона или даже спиральной галактики.
Для примера достаточно взять фотографию циклона из космоса, и наложить обе картинки вместе:
- Если взять и разделить друг на друга 2 любых соседних члена последовательности, например 233/377, получится число 0,618. Случайно это или нет, но это число - то самое “золотое сечение”, считающееся наиболее эстетичной пропорцией.
Числа Фибоначчи несложно вывести в программе на языке Python:
from decimal import *
def printNumbers(n):
i1 = Decimal(0)
i2 = Decimal(1)
for p in range(1, n + 1):
print("F({}) = {}".format(p, i2))
fib = i1 + i2
i1 = i2
i2 = fib
getcontext().prec = 100
N = 100
printNumbers(N)
Интересно заметить, что растет последовательность Фибоначчи весьма быстро, уже F(300) = 222232244629420445529739893461909967206666939096499764990979600.
10. Высота звуков нот
Еще в древности человек заметил, что натянутая струна порождает колебания звука. Во времена Пифагора было замечено, что струны издают мелодичный звук, если их длина соотносится как небольшие целые числа (1:2, 2:3, 3:4 и т. д.). Звук от струны длиной 2/3 дает чистую квинту, 3/4 струны дает кварту а половина струны - октаву.
Рассмотрим струну с условной длиной = 1. Будем умножать длину струны на 3/2, если полученное число больше 2, разделим еще на 2.
1
3/2 = 1,5
1.5 * 3/2 = 2.25, 2.25/2 = 1,125 = 9/8
9/8 * 3/2 = 1,6875 = 27/16
Похожий ряд, если его упорядочить по возрастанию, называется пифагоровым строем:
“до” - 1
“ре” - 9/8
“ми” - 81/64
“фа” - 4/3
“соль” - 3/2
“ля” - 27/16
“си” - 243/128
“до” - 2
Он также называется квинтовым, т.к. ноты получались увеличением на квинту, т.е. на 3/2. Считается, что этот строй использовался еще при настройке лир в древней Греции, и сохранился вплоть до средних веков. Названия нот разумеется, были другие - современные названия придумал только через 1000 лет итальянский теоретик музыки Гвидо д’Ареццо в 1025 г..
Разумеется, в древней Греции никто не знал про частоту колебаний звука, зато древние греки были хорошими геометрами, и проблем с умножением и делением у них не было. Современная теория колебаний струны появилась гораздо позже, работы Эйлера и Д’Аламбера были написаны в 1750х годах.
Как математически определяются частоты звуков нот? Сейчас мы знаем, что октава (от “до” до “до” следующей октавы) - это умножение частоты на 2 (или укорочение струны в 2 раза). Для остальных нот с 18 века используется так называемый “хорошо темперированный строй”: октава делится на 12 равных промежутков, а последовательность частот образует геометрическую прогрессию.
Для одной октавы получаются следующие коэффициенты: 1,0594, 1,1224, 1,1892, …, 2. На клавиатуре они отображаются всем известным образом, образуя 12 полутонов:
Таким образом, если знать частоту любой ноты, все остальные легко рассчитываются по вышеприведенной формуле.
Очевидно, что “базовая” частота может быть любой. Традиционно принято например, что частота камертона ноты “Ля” 440Гц. Остальные ноты первой октавы:
ДО
261.6
ДО#
277
РЕ
293.7
РЕ#
311
МИ
329.6
ФА
349.2
ФА#
370
СОЛЬ
392
СОЛЬ#
415
ЛЯ
440
ЛЯ#
466
СИ
494
Интересно заметить, что квинта в этой системе имеет соотношение частот 27/12 = 1.49, что чуть-чуть отличается от “пифагорейского” чистого тона с соотношением 1.5. На слух “современная квинта” имеет небольшие биения 0,5Гц, соответствующие разности частот 392 - 392.4. До сих пор есть любители исполнения старинной музыки в квинто-терцевом строе, называемым “чистым”. В 18м же веке дебаты между приверженцами “старого” и “нового” строя были довольно-таки острыми. Впрочем, преимущества равномерно темперированного строя в виде четкого соотношения между частотами нот и возможности транспонирования музыки в любую другую тональность “без потери качества” оказались решающими. Сейчас “чистый строй” имеет лишь историческое значение, и используется лишь иногда для исполнения старинных произведений.
И традиционно, программа на языке Python, выводящая частоты полутонов в обе стороны от ноты “Ля”:
import math
freq_la = 440
for p in range(-32,32):
freq = freq_la*math.pow(2, p/12.0)
print(p, freq)
11. Вращение планет
Еще в древней Греции ученые знали, что планеты движутся по небу, но каким образом? Сотни лет господствовала геоцентрическая система мира - в центре была Земля, вокруг которой по окружностям двигались Луна, планеты (на то время их было известно 5) и Солнце:
Такая система казалась вполне логичной и интуитивно понятной (даже сейчас люди говорят что солнце “всходит” и “заходит”), однако не объясняла астрономам почему планеты движутся по небу неравномерно, и временами даже в обратную сторону.
Вот так, к примеру, выглядит перемещение по небу планеты Марс, что никак не укладывается в теорию движения по кругу:
Впрочем геоцентрическая система просуществовала более 1500 лет, только в 16м веке Коперник издал свой труд «О вращениях небесных сфер», где описывал вращение планет по круговым орбитам вокруг Солнца. Однако проблемой было то, что и при этой схеме фактические движения планет не совпадали с расчетными.
Объяснить это не мог никто, пока в 1600 году немецкий математик Иоганн Кеплер не стал изучать многолетние результаты наблюдений, сделанные астрономом Тихо Браге. Кеплер был великолепным математиком, но и у него ушло несколько лет чтобы понять суть и вывести законы, которые и сейчас называются законами Кеплера.
Как оказалось, движение планет подчиняется 3м математическим законам:
1) Планеты движутся по эллиптическим орбитам, в одном из фокусов эллипса находится Солнце
2) Планеты движутся неравномерно: скорость планеты увеличивается при движении к Солнцу и уменьшается в обратном направлении. Но за равные промежутки времени вектор движения описывает равные площади: площади участков “А” одинаковы:
3) Квадраты периодов обращений планеты пропорциональны кубу расстояний до орбиты:
Кеплер считал, что весь мир подчиняется гармонии, и что солнечная система больше похожа на часовой механизм, чем на божественное творение. Найденные им законы не только красивы и гармоничны, но и совпали с реальными наблюдениями (уже позже выяснилось, что законы Кеплера могут быть выведены из законов Ньютона и закона всемирного тяготения, желающие могут найти доказательства в Википедии).
Что касается Марса, то его орбита более вытянутая, чем орбита Земли, чем и объясняется разница как в скорости движения, так и в яркости планеты. Картинка с сайта журнала “Наука и жизнь”:
Кстати, эта картинка хорошо объясняет, почему только некоторые годы благоприятны для запуска космических кораблей к Марсу - те годы, в которые расстояние между планетами минимально.
12. Парадоксы теории вероятности
На интуитивном уровне понимание теории вероятности довольно-таки просто. Возьмем кубик с 6 гранями, подбросим и посмотрим какая грань выпала. Интуитивно ясно, что вероятность выпадения 1 грани из 6 будет 1/6. Действительно, вероятностью называют отношение числа равновероятных событий к числу всех возможных вариантов:
Какова вероятность что выпадут 2 цифры подряд? Она равна произведению вероятностей: (1/6)*(1/6) = 1/36.
Вроде все просто, однако несмотря на простоту, есть довольно-таки много задач, где математика не всегда совпадает с бытовым “здравым смыслом”. Рассмотрим несколько таких парадоксов.
Дети мистера Смита
Эту задачу описывал Мартин Гарднер. Известно что у мистера Смита двое детей, и один из них мальчик. Какова вероятность, что второй из них тоже мальчик? Интуитивно кажется, что вероятность пола ребенка всегда равна 1/2, но не все так просто.
Рассмотрим возможные варианты семей с двумя детьми:
- мальчик-мальчик
- мальчик-девочка
- девочка-мальчик
- девочка-девочка
Исходя из списка вариантов, ответ понятен. Вариант “девочка-девочка” по условию не подходит. Всего остается 3 варианта семей где есть мальчик (М+М, М+Д, Д+М), значит вероятность что второй ребенок окажется мальчиком, равна 1/3.
Бросание кубика
Вернемся к бросанию кубика. Допустим, мы бросили кубик 5 раз, и все разы выпала цифра “3”. Какова вероятность, что мы бросим кубик еще раз, и выпадет снова цифра “3”?
Ответ прост. Интуитивно кажется, что вероятность такого события очень мала. Но в реальности кубик не имеет какой-либо встроенной “памяти” на предыдущие события. Какие бы числа не выпадали до текущего момента, вероятность нового числа также равна 1/6 (а вот если говорить о вероятности выпадения такой серии “в целом”, то она действительно равна 1/(6*6*6*6*6*6) = 1/46656.
Кстати, такая вероятность это много или мало? Интуитивно кажется что мало, и в принципе оно так и есть. Одному человеку пришлось бы бросать кубик каждые 10 секунд 4 дня, чтобы дождаться выпадения 6 цифр подряд. Однако если рассматривать большие числа, то такие вероятности становятся неожиданно большими. Например, если 6 раз кубик бросят все 5 миллионов жителей Петербурга, то 6 цифр подряд выпадут примерно у 100 человек - довольно-таки значительное количество. Это на самом деле важный момент: даже довольно-таки маловероятные события гарантированно произойдут, если речь идет о большом числе попыток. Это важно при прогнозировании таких событий как ДТП, аварии, катастрофы, и прочие негативные явления, которые в большом городе увы, не редкость. По этой же причине редкие заболевания эффективнее лечить в большом городе - редкая болезнь, встречающаяся 1 раз на 100000 человек, может практически не встречаться в небольшом городе и у врачей не будет опыта борьбы с ней, а в мегаполисе таких больных наберется в несколько раз больше.
Парадокс Монти Холла
Этот известный парадокс хорошо описан в Википедии.
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, открывает одну из оставшихся дверей, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Интуитивно кажется, что если автомобиль спрятан за одной из дверей, то вероятность его найти равна 1/3, и смена двери ничего не даст. Однако это неверно.
Принцип прост: если игрок изначально правильно указал дверь с автомобилем (а вероятность этого действительно ⅓), то замена двери приведет его к проигрышу. Однако в обеих других случаях изначального выбора неверной двери (а вероятность этого ⅔) смена двери приведет к выигрышу. Таким образом, смена двери приведет к выигрышу с вероятностью ⅔ вместо ⅓.
Парадокс дней рождений
Допустим, в организации работает 24 человека. Какова вероятность что хотя бы двое отмечают день рождения в один и тот же день? Интуитивно кажется, что эта вероятность весьма мала и будет равна 24/365, но и в этом случае интуиция ошибается. В реальности, мы должны рассматривать количество пар, которые могут образовать данные люди. Это число довольно-таки велико, например, если обозначить 5 человек как ABCDE, то количество возможных пар будет 10 (AB, AC, AD, AE, BC, BD, BE, CD, CE, DE), а для группы из 24 человек возможно 276 пар.
Для точного расчета воспользуемся принципом произведения вероятностей. Вероятность того, что для 2х людей день рождения не совпадает, равна 364/365. Для 3х человек вероятность что все дни не совпадут, равна произведению 364/365 * 363/365, и так далее. Для n-человек формула приведена в Википедии:
(n! - обозначение факториала, n! = 1*2*..*(n-1)*n)
Нужная нам вероятность обратного события равна обратной величине:
Вывести все значения несложно с помощью программы на Python:
import math
def C(n):
return 1000 - 1000*math.factorial(365)/(math.factorial(365 - n)*365**n)
for n in range(3, 50):
print("{} - {}%").format(n, 0.1 * C(n))
365! это очень большое число, поэтому здесь использованы целочисленные вычисления языка Python, уже затем значение было переведено в проценты.
В результате получаем следующую таблицу:
3 0.0082 4 0.0163 5 0.0271
6 0.0404 7 0.0562 8 0.0743
9 0.0946 10 0.1169 11 0.1411
12 0.1670 13 0.1944 14 0.2231
15 0.2529 16 0.2836 17 0.3150
18 0.3469 19 0.3791 20 0.4114
21 0.4436 22 0.4756 23 0.5072
24 0.5383 25 0.5686 26 0.5982
27 0.6268 28 0.6544 29 0.6809
30 0.7063 31 0.7304 32 0.7533
33 0.7749 34 0.7953 35 0.8143
36 0.8321 37 0.8487 38 0.8640
39 0.8782 40 0.8912 41 0.9031
42 0.9140 43 0.9239 44 0.9328
45 0.9409 46 0.9482 47 0.9547
48 0.9605 49 0.9657 50 0.9703
Как видно из таблицы, уже при количестве сотрудников 50 человек, хотя бы 1 день рождения почти гарантированно совпадет (вероятность 97%), а для 24 человек получаем вероятность равную 0.538, т.е. более 50%.
13. Поверхность Луны
Посмотрим на фотографию поверхности Луны. Эта фотография была сделана автором через телескоп с балкона:
Что мы видим? Очевидно, лунную поверхность, покрытую кратерами, оставшимися от предыдущих столкновений метеоритов с Луной.
Казалось бы, причем здесь математика? При том, что столкновение с метеоритом - случайное событие, его частота подчиняется теории вероятности. На Луне нет атмосферы, нет эрозии и ветра, поэтому лунная поверхность - идеальная “книга”, в которой записаны события последних десятков тысяч лет. Изучая поверхность Луны, можно подсчитать какого размера объекты падали на ее поверхность.
Исследование поверхности Луны камерами высокого разрешения ведется и сейчас. Было подсчитано, что за последние 7 лет на Луне образовались не менее 220 новых кратеров. Это важно еще и потому, что данные подсчеты помогут оценить опасность для Земли.
Есть ли кратеры на Земле? Разумеется есть. Данная фотография сделана вовсе не на Луне или на Марсе, а в США:
Так называемый Аризонский кратер возник около 50тыс лет назад после падения метеорита диаметром 50 метром и весом 300 тысяч тонн. Диаметр кратера составляет более километра. В Сибири находится кратер Попигай размером 100км, он был открыт в 1946 году.
Разумеется, такие большие кратеры довольно-таки редки. Последнее же падение крупного метеорита было по историческим меркам весьма недавно, всего лишь около 100 лет назад. В 1908г в тунгусской тайге упал метеорит, мощность взрыва оценивалась от 10 до 50 мегатонн. По отзывам, взрывная волна обогнула земной шар, а световые явления в атмосфере были столь сильны, что в Лондоне ночью можно было читать газету. Лишь по случайности падение метеорита пришлось на малонаселенные районы Сибири - если бы удар был чуть раньше или позже, такой мощности хватило бы, чтобы полностью уничтожить город размером с Санкт-Петербург. Совсем же недавно, в 2013 году, метеорит размером около 20 метров разрушился в атмосфере, а его многочисленные обломки упали в районе Челябинска. Пострадало примерно 1500 человек, в основном от выбитых ударной волной стекол. По оценкам NASA суммарная мощность составила до 400 килотонн.
Увы, то, что для определенного района Земли может быть катастрофой, для космоса совершенно заурядный момент. Это лишь вопрос времени, достаточно посмотреть на поверхность Луны. По одной из гипотез, 66 миллионов лет назад наша планета столкнулась с большим астероидом, в результате чего было уничтожено 75% видов живых существ, в том числе и динозавры. Поэтому задача наблюдения и прогнозирования астероидной опасности должна быть в обязательном списке дел для человечества, если мы не хотим повторить их судьбу.
14. Так ли случайны случайные числа?
В каждом языке программирования существует функция генерации случайных чисел. Они используются в различных областях, от игр до криптографии или генерации паролей.
На языке Python вывести случайное число можно так:
import random
print(random.randint(0,9))
Но как это работает? Задача вывода действительно случайного числа далеко не так проста как кажется. Чтобы вывести что-то на компьютере, это что-то надо сначала запрограммировать. Но очевидно, что задать формулой случайный, хаотический процесс, невозможно - по определению формула и хаос противоречат друг другу. Именно поэтому числа на самом деле являются псевдослучайными - они лишь похожи на случайные, а в реальности являются результатом вполне конкретного алгоритма.
Одним из наиболее популярных и простых алгоритмов, является линейный конгруэнтный метод (linear congruential generator). Его формула проста:
Рассмотрим пример реализации на языке Python:
x = 123456789
m = 2**31 - 1
for p in range(10):
x = (1103515245*x + 12345) % m
print(x)
Программа действительно выводит числа, которые вполне похожи на случайные: 295234770, 465300796, 1475666158, 588454008, 929838277, 50298429, 1089988954, 698778454, 2010473888, 36125306. Как нетрудно догадаться, при повторном запуске программы числа будут одни и те же. Чтобы числа не повторялись, такой генератор обычно инициализируют значением текущего системного времени.
Увы, такой генератор имеет определенные недостатки: во-первых, его последовательность рано или поздно начинает повторяться, во-вторых, он не является криптостойким - зная текущее значение, можно вычислить следующее, что к примеру, может позволить злоумышленнику узнать “случайно” сгенерированный пароль по его первым буквам.
Существуют другие алгоритмы генерации псевдослучайных чисел, например на основе простых чисел Мерсенна (Mersenne Twister generator). Существуют также аппаратные генераторы случайных чисел, например такая функция присутствует в процессорах Intel. Есть даже сайт , с помощью которого можно сгенерировать случайную последовательность чисел. По заверениям авторов, они используют 3 радиоприемника, настроенных на частоту шума атмосферных помех.
Разумеется, в большинстве обычных программ, например при написании компьютерной игры, “качеством” случайных чисел можно пренебречь, встроенные алгоритмы вполне неплохи. Но при разработке специализированного ПО, где вопрос криптостойкости имеет значение, стоит уже обратить внимание на то, насколько надежен применяемый алгоритм.
15. Распределение случайных величин
С теорией вероятности связан еще один интересный момент - законы распределения случайных величин. Огромное количество процессов в реальности подчиняются всего лишь нескольким законам распределения.
Равномерное распределение
Возьмем игральный кубик и бросим его много раз. Очевидно, что вероятность выпадения каждого числа одинакова. На графике это можно изобразить примерно так:
Другим примером может быть время ожидания автобуса. Если человек пришел на остановку в случайное время, то период ожидания может быть любым, от нуля до максимума интервала движения.
Нормальное распределение
Возьмем группу людей, например в 100 человек, и измерим их рост. Очевидно, что будет некоторое количество людей небольшого роста, некоторое количество высоких людей, совсем мало очень высоких, и совсем мало очень низких. Такое распределение естественно для многих объектов, не только людей, потому оно и называется нормальным.
Формула нормального распределения совпадает с формулой Гаусса:
Подбирая коэффициенты, можно получить разные виды распределения.
Касаемо роста людей, согласно сайту , график роста для мужчин и женщин имеет следующий вид:
Распределение Пуассона
Следующий вид распределения не менее интересен. Рассмотрим события, происходящие с некоторой известной интенсивностью независимо друг от друга, например приход покупателей в магазин. Допустим, в магазин приходит в среднем 10 покупателей в минуту. Какова вероятность, что в какой-то момент времени в магазин придет 20 покупателей?
Вероятность таких событий описывается распределением Пуассона:
График распределения имеет примерно такой вид (в нашем примере λ=10):
Этим же распределением описываются различные случаи, от вероятности неисправностей (если 0.01% телевизоров имеют неисправность, какова вероятность что в партии из 20 штук окажется 2 неисправных телевизора), до скорости роста колоний в чашке Петри.
Вернемся к нашему примеру с 20 покупателями. В интернете можно найти таблицы значений Пуассона для λ=10. По ним можно найти, что вероятность прихода сразу 20 человек составляет 0,19%.
16. Измерение скорости света
С бытовой точки зрения, скорость света практически мгновенна. Действительно, свет за секунду может обогнуть Землю 8 раз, а за 2 секунды пролетает расстояние от Земли до Луны. Поэтому до 17 века про реальную скорость света никто не знал. Как же ее вычислили?
Сегодня опыт по измерению скорости света можно провести даже в школе - достаточно длинного куска кабеля, генератора импульсов и осциллографа. Действительно, задержка сигнала в куске кабеля длиной 50м, будет равна 50/300000000, или 0.016мкс - величина которую покажет даже дешевый осциллограф с максимальной частотой 10-20МГц. Но как же это сделали в 17 веке, когда не было не то что осциллографов, даже до появления лампы накаливания было еще 200 лет ожидания? Помогли астрономия, геометрия, и разумеется, математика.
Говоря точнее, помогло наблюдение Юпитера и его спутников. Спутники Юпитера были открыты еще Галилеем, увидеть их может каждый, даже с балкона в небольшой телескоп. С увеличением около 300х они видны примерно так:
Период вращения спутников Юпитера невелик, и составляет примерно 2 дня. Уже в 17м веке измерение времени было достаточно точным (маятниковые часы изобрел голландский физик и математик Гюйгенс в 1657г), чтобы датский астроном Олаф Ремер в 1676 году обнаружил расхождение расчетного и реального положения спутника примерно в 16 минут (величина, которую трудно не заметить даже при технологиях 17 века). Для измерения орбит спутников Юпитера Ремер использовал момент, когда спутник входит в тень Юпитера - момент, который можно измерить довольно-таки точно.
Как догадался Ремер, запаздывание во времени было связано с движением Земли по орбите.
Картинка с сайта -light.info:
В момент второго измерения расстояние до Юпитера больше примерно на диаметр орбиты Земли (период обращения Юпитера вокруг Солнца - 12 лет, что гораздо больше земного). Это и приводило к тому, что свет от Юпитера приходил с большим запаздыванием, чем при первом измерении. Сделав подсчеты, Ремер получил значение скорости света в 220000км/c. В то время конечность скорости света казалась настолько невероятной, что после публикации во французской академии наук далеко не все поверили молодому ученому. Разумеется, последующие измерения подтвердили правильность метода.
Более точное значение было получено лишь через 200 лет, французский физик Луи Физо с помощью зубчатого колеса и двух зеркал получил значение в 312000км/c. Расстояние между зеркалами было 8,6км, одно зеркало было расположено в доме отца Физо недалеко от Парижа, второе зеркало было расположено на Монмартре. Физо нашел такую скорость вращения колеса, при котором луч света проходящий через зубец колеса затемнялся, что означало что запаздывание света соответствует скорости вращения колеса.
Кстати, по последним данным, не только свет, но и гравитационные волны тоже распространяются с той же скоростью, при визуальных и “гравитационных” наблюдениях слияний черных дыр расхождений не было обнаружено.
17. Можно ли своими глазами увидеть прошлое?
С предыдущим вопросом связан простой забавный факт. Можно ли лично своими глазами увидеть событие, происходящее например, миллион лет назад? Да, и это очень просто сделать - достаточно посмотреть на небо.
Как наверное читатели уже догадались, все дело в скорости света. Расстояние от Земли до Солнца составляет 150млн километров, свет преодолевает его за 8 минут. Таким образом, когда мы смотрим на небо, мы видим Солнце таким, каким оно было 8 минут назад. Смотря на Юпитер, мы видим его с запаздыванием примерно в полчаса. Расстояние до других звезд гораздо больше. Сириус мы видим таким, каким он был 8 лет назад, звезда Вега имеет расстояние в 25 световых лет, столько нужно свету чтобы долететь до Земли. Туманность Андромеды мы видим с запаздыванием в 2.5 миллиона лет - время сопоставимое с периодом жизни мамонтов и первобытных людей. Если бы там висело гигантское зеркало, в котором отражалась бы Земля, гипотетически можно было бы их увидеть, хотя такого размера телескоп конечно же физически невозможен.
А если серьезно, то данный факт запаздывания света очень помогает астрономам изучать историю Вселенной - наблюдая удаленные галактики, находящиеся на расстоянии миллиардов световых лет, мы видим их в прошлом - их свет шел до нас эти самые миллиарды лет. И таким образом, чем мощнее телескоп, тем дальше во времени он позволяет заглянуть, тем самым, позволяя видеть то время, когда и галактики и звезды еще были молодыми.
С другой стороны, в запаздывании света есть и большой минус. Даже если будут созданы космические корабли, способные долететь до другой звезды, обмениваться сообщениями с космонавтами придется с тем же запаздыванием. К примеру, радиосообщение до Сириуса дойдет до получателя через 8,6 лет, и столько же придется ждать ответа. Уже сейчас можно поговорить по телефону с астронавтами на МКС (в 2015 году британский астронавт Тим Пик ошибся номером, и удивил неизвестную женщину вопросом “Здравствуйте, это Земля?”), а вот для Марса время задержки составит около 15 минут - так что поговорить по телефону или по Скайпу с марсианской колонией было бы невозможно.
18. Сколько вольт в электросети?
Глупый вопрос, подумают многие. Каждый школьник в России знает что напряжение в сети 220 вольт (в США каждый школьник знает что напряжение в сети 110 вольт). Полезно привести такую картинку:
Кстати, в 90е годы, когда поездки за границу только становились доступными, некоторые привозили американскую электронику, но работала она зачастую не долго, из-за того что сетевое напряжение отличается в 2 раза. А сейчас даже чуть больше, по российскому стандарту 2003 года, напряжение в сети должно составлять 230В. Предельно допустимым отклонением считается 10%, т.е. значения 210-250В в принципе возможны.
Но вопрос заголовка не в этом. Будем для простоты считать напряжение равным “условным” 220 вольт. Однако подключим осциллограф к электросети, и увидим примерно такую картинку:
Что это значит? Где “наши” 220 вольт?
Все просто (хотя и не совсем). Ток в сети переменный - он меняет свое направление с частотой 50 раз в секунду. В отличие к примеру, от батарейки - если на ней написано 1.5 вольта, это значит что на ней действительно 1.5 вольта и направление тока не меняется. Но вернемся к розетке. Ток в нее подается не просто так, а с целью выполнения какой-либо работы. Как измерить работу переменного тока, который в разные моменты времени движется то в одну, то в другую сторону? Для этого было введено понятие действующего напряжения - величины постоянного тока, способного выполнить ту же работу (например нагрев спирали электроплитки). Напряжение, которое показывает осциллограф - называется амплитудным. Эти величины связаны простой формулой:
220 умноженное на √2, дает как раз 310В. Разумеется, обычный тестер откалиброван в “бытовых” единицах, в режиме измерения переменного тока он покажет 220В. А если выпрямить напряжение, например диодным мостиком, то тестер покажет как раз 310В постоянного тока.
И еще немного про переменный ток. Откуда берется напряжение в 380 вольт? Ток от трансформатора подается по нулевому проводу и 3м фазам: это 3 линии, напряжение в которых сдвинуто на разный угол друг относительно друга.
Картинка из Википедии:
Нулевой провод - общий. В квартиры подается напряжение с одной из фаз, значением в стандартные 220 вольт. Это напряжение называется фазным. Если же используется 3х-фазная сеть целиком, то напряжение между двумя фазами, например в точках a и с на рисунке, составляет как раз 380 вольт. Это напряжение называется линейным.
Математически, оба напряжения связаны простой формулой:
Действительно, 220*√3 = 380.
Кстати, обрыв нулевого провода в доме - серьезная неисправность, из-за чего в квартиры может быть подано линейное напряжение, составляющее те самые 380В. Такой случай произошел лично с автором, впрочем ущерб оказался невелик, перегорели лишь настенные электронные часы и несколько блоков питания. Но при отсутствии в доме людей это может привести и к пожару, такие случаи не редкость. Так что тем, у кого в квартире старая проводка, рекомендуется установить в электрощиток устройство защиты от перенапряжения, его цена невелика, и явно дешевле ремонта в квартире.
19. Нейронные сети
Нейроны - биологическая основа всей разумной жизни на Земле, и казалось, бы при чем здесь математика? При том, что как выяснилось еще в 50е годы, модель нейрона математически очень проста:
Нейрон состоит из определенного числа “входов” (синапсов), каждый из которых имеет определенный весовой коэффициент Wij, собственно ячейки нейрона, суммирующей значения “входов”, некоторой функции активации (упрощенно говоря, нейрон переходит в “активное” состояние, если сумма больше некоторого порога), и выхода (аксона), который в свою очередь, может передать сигнал на следующий нейрон.
Можно написать, что:
Sum = w11*x1 + w12*x2 + … + w1n*xn
Out = f(Sum)
В качестве функции активации f часто используется “сигмоида” (хотя бывают и другие варианты):
Как можно видеть, все весьма просто - математически нейрон лишь чуть сложнее чем обыкновенный сумматор. Выходы нейрона благодаря функции активации лежат в диапазоне 0..1.
Что может делать один нейрон? Практически ничего полезного, но если объединить их в сеть, возможности возрастают кардинально. Например, сеть из 6 нейронов уже способна воспроизвести любую логическую функцию, что мы сейчас и продемонстрируем.
Рассмотрим структуру сети, называемую “многослойный перцептрон” (multilayer perceptron):
Как можно видеть, она состоит из входного слоя нейронов (input layer), скрытого слоя (hidden layer) и выходного слоя (output layer). Каждый нейрон скрытого слоя соединен со всеми входными нейронами, плюс введено дополнительное “смещение” (bias), которое можно представить как нейрон, вход которого всегда = 1 и вес равен константе (например 0.5). Дальше структура повторяется. Количество входных, выходных и скрытых нейронов может быть различно.
Процесс перехода сигнала по сети называется прямым распространением (forward propagation). Допустим, на входе имеются значения: x1 = 0, x2 = 1. Тогда прямое распространение выглядит так:
Шаг-1: передача сигнала от входа во внутренний (hidden) слой
h1 = f(x1*w1 + x2*w2 + 0.5*1)
h2 = f(x1*w3 + x2*w4 + 0.5*1)
Шаг-2: передача сигнала от внутреннего в наружный (output) слой
o1 = f(h1*w5 + h2*w6 + 0.5*1)
o2 = f(h1*w7 + h2*w8 + 0.5*1)
Собственно и все, мы подали на вход сети сигнал “х” и получили на выходе сигнал “о”. Однако внимательный читатель может задать вопрос - а как задаются коэффициенты w1, w2,..,w8? Это собственно, самое интересное и сложное, процесс настройки параметров сети и называется обучением. Задавая различные наборы входных и выходных данных, мы можем обучить сеть воспроизводить требуемые нам функции. Для данного типа сетей используется так называемый алгоритм обратного распространения (back propagation). Его суть в модификации коэффициентов w от конца сети к началу, примерно это можно выразить так:
Шаг-0: Значение коэффициентов w1..w8 заполняются некоторыми случайными величинами.
Шаг-1: Берем набор входных данных, получаем значения выхода (output) методом уже рассмотренного “прямого распространения”.
Шаг-2: Сравниваем значения output с “целевыми” значениями (target). Для удобства сравнения часто используется функция квадрата разности: Err = (output - target)2
Шаг-3: Модифицируем “выходные” коэффициенты w5..w8 так, чтобы значение Err уменьшалось. Для этого используется метод так называемого “градиентного спуска”: функцию output всей нейронной сети в целом легко можно выразить как последовательность сумм и произведений (x1*w1 + x2*w2 …), это значит, что продифференцировав ее по нужному весовому параметру, легко найти производную, например dOutput/dw5. Как известно, производная показывает направление роста функции, что нам и нужно - мы можем изменить параметр w5 на величину, обратную производной.
Шаг-4: Выполняем аналогичный процесс для “входных” коэффициентов w1..w4, формулы тут примерно аналогичны предыдущему пункту.
Шаги 1..4 повторяются до тех пор, пока ошибка не станет меньше некоторой величины. Этот процесс весьма медленный, и может требоваться несколько тысяч итераций, однако выполняется он лишь однократно. Далее коэффициенты можно сохранить, и сеть уже обучена воспроизводить указанный при обучении набор данных. Эти весовые коэффициенты фактически и являются аналогом нейронных связей, появляющихся после обучения в “биологической” сети.
Более подробно формулы с примерами вычислений можно найти здесь. А мы рассмотрим программу на языке Python, реализующую данный метод.
import math, random
class MLP(object):
def __init__(self, n_in, n_hidden, n_out):
self.n_in = n_in
self.n_hidden = n_hidden
self.n_out = n_out
# Входные данные: массив [n_in + 1] инициализирован значениями 1.0
self.inputLayer = [1.0] * (n_in + 1)
# Веса входного-скрытого слоя: матрица [n_in+1]x[n_hidden] заполнена 0..1
self.wIH = [[random.random() for x in range(n_in + 1)] for y in range(n_hidden)]
# Скрытые нейроны: [n_hidden + 1]
self.hiddenLayer = [1.0] * (n_hidden + 1)
# Веса нейронов скрытого-выходного слоя: [n_hidden+1]x[n_out], 0..1
self.wHO = [[random.random() for x in range(n_hidden + 1)] for y in range(n_out)]
# Выходной слой: массив
self.outputLayer = [1.0] * n_out
def printValues(self):
print "Network: input/hidden/output: {}/{}/{}".format(self.n_in, self.n_hidden, self.n_out)
print "Вход", self.inputLayer
print "wIH", self.wIH
print "Скрытый слой", self.hiddenLayer
print "wHO", self.wHO
print "Выход", self.outputLayer
def printOutput(self):
print "Вход", self.inputLayer
print "Выход", self.outputLayer
def sigmoid(self, x):
# Функция активации
return 1.0 / (1.0 + math.exp(-x))
def derivative(self, x):
# Производная функции активации
return x * (1 - x)
def forwardPass(self, x):
# Прямое распространение
# Input
for p in range(len(x)):
self.inputLayer[p] = x[p]
# Input-Hidden
for h in range(self.n_hidden):
sum = 0.0
for i in range(len(self.inputLayer)):
sum += self.inputLayer[i] * self.wIH[h][i]
self.hiddenLayer[h] = self.sigmoid(sum)
# Hidden-Output
for o in range(self.n_out):
sum = 0.0
for h in range(len(self.hiddenLayer)):
sum += self.hiddenLayer[h] * self.wHO[o][h]
self.outputLayer[o] = self.sigmoid(sum)
def backPass(self, input, target):
# Обратное распространение
# Формулы основаны на статье
# /a-step-by-step-backpropagation-example/
learn_rate = 0.5
# Output->hidden layer adjust weights
for o in range(self.n_out):
for h in range(self.n_hidden):
deout = -(target[o] - self.outputLayer[o])
der = self.derivative(self.outputLayer[o])
hid = self.hiddenLayer[h]
der = deout * der * hid
prev = self.wHO[o][h]
self.wHO[o][h] -= learn_rate * der
# Hidden->input layer adjust weights
for h in range(self.n_hidden):
for i in range(self.n_in):
derSum = 0.0
for o in range(self.n_out):
deout = -(target[o] - self.outputLayer[o])
derOut = self.derivative(self.outputLayer[o])
der = deout * derOut * self.wHO[o][h]
derSum += der
derH = self.derivative(self.hiddenLayer[h])
derI = self.inputLayer[i]
der = derSum * derH * derI
prev = self.wIH[h][i]
self.wIH[h][i] -= learn_rate * der
def calcError(self, x, target):
# Вычисление ошибки: 0.5*Sum(dV^2)
err = 0.0
for p in range(self.n_out):
err += 0.5 * ((self.outputLayer[p] - target[p]) ** 2)
return err
Как можно видеть, создан класс MLP, принимающий на входе 3 параметра: число входных нейронов, число скрытых нейронов, число выходных нейронов.
Рассмотрим пример использования этой сети для логической функции XOR. Как известно, она имеет следующую таблицу истинности:
Таким образом, в нашей сети будет 2 входных параметра (их еще называют “характеристиками”) и 1 выходной. Количество скрытых нейронов пусть будет 2.
Код на языке Python выглядит следующим образом.
mlp = MLP(n_in=2, n_hidden=2, n_out=1)
print("Тренировка сети")
inputs = [[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]]
targets = [[0.0], [1.0], [1.0], [0.0]]
N = 500000
for p in range(N):
rand_index = random.randrange(0, len(inputs))
mlp.forwardPass(inputs[rand_index])
mlp.backPass(inputs[rand_index], targets[rand_index])
err = mlp.calcError(inputs[rand_index], targets[rand_index])
if p % 10000 == 0:
print("Step", p, "error", err)
print("")
print("Done")
mlp.printValues()
print("")
print("Результаты")
mlp.forwardPass([0.0, 0.0])
mlp.printOutput()
mlp.forwardPass([0.0, 1.0])
mlp.printOutput()
mlp.forwardPass([1.0, 0.0])
mlp.printOutput()
mlp.forwardPass([1.0, 1.0])
mlp.printOutput()
Как можно видеть, мы создаем сеть с заданными параметрами, затем выполняем большое количество раз функции прямого и обратного распространения. При каждом вызове функции backPass коэффициенты чуть корректируются в сторону уменьшения ошибки.
В результате получаем следующие наборы параметров W:
Wih = [[10.276084, 9.57721341, 0.11424834], [0.86694222, 0.86379, 0.728575]]
Who = [53.976871, -61.523507, 0.13521682]
Напомним, что весовые коэффициенты фактически соответствуют нейронным связям, возникающим в “настоящих” биологических сетях. Тестирование показывает, что обученная сеть действительно воспроизводит функцию XOR практически достоверно, лишь с небольшой погрешностью:
Input [0.0, 0.0], output [0.0000266]
Input [0.0, 1.0], output [0.95193190]
Input [1.0, 0.0], output [0.95074983]
Input [1.0, 1.0], output [0.07137252]
Как показывает тестирование, если увеличить число скрытых нейронов до 3х, обучение происходит гораздо быстрее, и не требует столь большого числа итераций. Уже 50000 итераций достаточно для приемлемой точности, лог программы выглядит примерно так:
Network: input/hidden/output: 2/3/1
Train phase:
Step 0 error 0.418338057819
Step 10000 error 0.00320960246906
Step 20000 error 0.00115714673178
Step 30000 error 0.00176164027913
Step 40000 error 4.34585435915e-05
wIH [[6.243515, -4.35533, 0.1199493], [5.040033, 5.132244, 0.35661004], [-4.4208235, 6.207919, 0.2522050]]
wHO [-11.2227881, 14.0531446, -11.2731065, 0.9389702]
Test phase:
Input [0.0, 0.0], output [0.0436959]
Input [0.0, 1.0], output [0.9712140]
Input [1.0, 0.0], output [0.9721711]
Input [1.0, 1.0], output [0.0075550]
Как можно видеть, даже такая простая нейронная сеть, изначально заполненная случайными коэффициентами, смогла обучившись на наборе данных, корректно воспроизвести его. Разумеется, количество как входов, так и выходов, может быть другим, функция XOR была взята лишь для наглядности.
Разумеется, описанная выше сеть является очень простой, в качестве более сложного примера можно привести архитектуру так называемой “сверточной сети” (convolutional neural network, CNN). Такая сеть “разбивает” входные данные на фрагменты, каждый из которых в свою очередь выделяет на изображении следующими подсетями какие-то ключевые детали. Подобные сети используются например, в задачах распознавания образов, в частности, рукописного текста.
Фото с сайта
Несмотря на всю сложность (сети могут содержать тысячи нейронов, а их обучение может занимать не один день), принципы функционирования модели нейрона в общем, практически те же, что и в вышеописанной функции XOR.
И еще один философский вопрос, который может возникнуть при рассмотрении нейронных сетей - возможен ли искусственный интеллект, сможет ли компьютер мыслить. Ответ не так прост как кажется. С физической точки зрения - ответ однозначно “да”. По отдельности нейроны нашего мозга состоят из весьма простых компонентов, и нет никакого принципиального запрета смоделировать их работу на компьютере. С алгоритмической точки зрения - узнать как работает самосознание, пока что никто не смог, данный вопрос еще открыт, как для математиков, так и для физиологов. Таким образом, запрограммировать на компьютере процесс мышления пока невозможно, но лишь потому, что собственно принцип еще неизвестен. Впрочем, учитывая скорость развития современных технологий, можно предположить что это лишь вопрос времени, причем возможно не очень дальнего. Хорошо это или нет - вопрос другой, выходящий за рамки данного текста. Ну и для понимания сложности данной задачи - для симуляции лишь 1% человеческого мозга (а это 1.7млрд нервных клеток и 10.4трлн синапсов) в течении 1 секунды, в 2013 году понадобилось 40 минут расчетов на суперкомпьютере из 82000 процессоров.
Что касается нейронных сетей, рассмотренных выше (MLP, CNN), то разумеется, никаким сознанием они обладать не могут, такие сети могут лишь научиться выполнять какую-то одну, пусть и весьма сложную, задачу. Тут еще важно не путать два принципиально разных момента - можно создать “симулятор чата”, загрузив в компьютер сотни тысяч фраз и ответов на них, и даже человек не сможет отличить такого “собеседника” от живого (что-то похожее работает например, в Siri), но полноценным интеллектом с собственным сознанием (есть даже термин “strong AI”) это не является.
20. Нейронные сети - распознавание текста
Рассмотрим практический пример - распознавание выше написанной нейронной сетью рукописного текста. Для тренировки сети воспользуемся имеющейся в открытом доступе базой MNIST, содержащей 60000 черно-белых рукописных изображений цифр размером 28x28пкс.
Выглядят изображения примерно так:
Массив изображений каждой цифры хранится в виде чисел float в диапазоне от 0 до 1, длина массива равна 28х28 = 784 значения. Кстати, при выводе массива в консоль форма цифры вполне узнаваема:
(картинка соответствует числу “5”)
Всего таких чисел, как было сказано, 60000, что вполне хватит для тренировки нашей сети.
Воспользуемся уже готовым классом MLP, изменим лишь некоторые параметры:
- Число входов будет равно 28х28 = 784, т.к. на вход нейросети будет подаваться массив целиком.
- На выходе нейросеть должна давать значения от 0 до 9, однако мы не можем получить значение > 1, так что воспользуемся другим путем: нейросеть будет иметь 10 выходов, где “1” будет соответствовать указанной цифре. Т.е. для числа “0” мы получим [1,0,0,0,0,0,0,0,0,0], для “1” [0,1,0,0,0,0,0,0,0,0], и так далее.
- Число скрытых нейронов мы берем наугад, например 48. Это значение мы позже можем скорректировать по результатам тестирования сети.
В итоге, мы имеем такую структуру сети:
Рассмотрим подробнее программу на языке Python.
Тренировка сети
Создаем нейронную сеть и подготавливаем 2 массива тестовых данных (исходные и целевых значения). Массив “digits” загружается из зараннее подготовленного текстового файла базы MNIST. Для каждой цифры содержится исходный массив в 784 цифры, и правильное значение числа, которое и будет использоваться для тренировки.
mlp = MLP(n_in=28 * 28, n_hidden=48, n_out=10)
print "1. Загрузка данных"
with open("digitsMnist.txt", 'rb') as fp:
digits = cPickle.load(fp)
print "2. Подготовка данных"
batch = 50
inputs = []
targets = []
for p in range(batch):
data = digits[p]["data"]
resulVal = digits[p]["result"]
# Конвертация целевого числа в массив: “3” => [0,0,0,1,0,0,0,0,0,0]
result_flat = [0.0] * 10
result_flat[resulVal] = 1.0
inputs.append(data)
targets.append(result_flat)
Собственно тренировка ничем по сути не отличается от предыдущего примера с функцией XOR. Т.к. процесс идет несколько часов, были также добавлены функции сохранения и чтения состояния сети, чтобы процесс можно было прервать и затем продолжить. Прервать тренировку можно в любой момент нажатием Ctrl+C. Для удобства визуализации процесса выводится суммарная ошибка по всем тестируемым цифрам.
print "3. Обучение"
mlp.load()
try:
N = 10000
for p in range(N):
errSum = 0.0
for d in range(batch):
mlp.forwardPass(inputs[d])
mlp.backPass(inputs[d], targets[d])
errSum += mlp.calcError(inputs[d], targets[d])
print "Step", p, "error", errSum
except KeyboardInterrupt:
pass
mlp.save()
Всего было проведено около 50000 итераций на блоке размером 50 цифр, весь массив в 60000 цифр не использовался. Обучение сети заняло порядка 2х часов на компьютере с Core i7. Разумеется, этот проект учебный, и программа никак не оптимизирована по быстродействию. С использованием специальных фреймворков типа Keras тренировка такой сети занимает не более 5 минут.
Тестирование сети
И наконец, тестирование. В качестве теста, “от руки” была нарисована цифра “3”, которая получилась в виде массива примерно такой:
t = [[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,1,1,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] +
[ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ]]
Следующий код выводить на экран цифру, и значения параметров выходного слоя:
for digit in t:
printDigit(digit)
mlp.forwardPass(digit)
mlp.printOutput()
Результат весьма интересен:
[0.019443, 0.0102247, 0.0091067, 0.467039, 0.0000103, 0.0150096, 0.0008709, 0.0004573, 0.655264, 0.0867915]
На тренировочных значениях сеть должна была выдавать “1” в том разряде, который соответствует “загаданному” числу. И хотя нигде явным образом это не планировалось и специально не программировалось, сеть выдала максимальные значения в тех разрядах массива, где “по ее мнению”, степень схожести максимальна. Как можно видеть, эти разряды соответствуют числам “3” и “8”, что визуально действительно похоже на нарисованное число. Строго говоря, результат не совсем верный, картинка больше похожа на “3” чем на ”8”, но и тренировка не была закончена полностью.
Для следующего теста число нейронов было увеличено до 128, а количество итераций обучения было увеличено до 75000.
Результаты теста на том же массиве:
[0.0044085, 0.219943, 0.0118179, 0.816858, 0.0002372, 0.06267359, 0.0008674, 0.00020319, 0.55439027, 0.00061541]
Максимальное значение теперь действительно соответствует числу “3”, можно сказать что сеть работает как задумывалось.
Для тех кто захочет поэкспериментировать самостоятельно, исходный текст программы и база чисел MNIST находятся в архиве, ссылка на который есть в начале книги.
21. Использование библиотеки TensorFlow
Говоря о математических вычислениях и нейронных сетях, нельзя не упомянуть библиотеку TensorFlow - эта библиотека была специально создана в Google для расчетов в области машинного обучения. Изначально она предназначалась только для использования внутри Google, но затем исходные коды TensorFlow были опубликованы для всех желающих. Библиотека достаточно сложна в использовании, но позволяет получить неплохие результаты.
Для установки TensorFlow для Windows необходимо:
- Установить 64-битную версию Python (дистрибутив можно скачать по ссылке -365/)
- Запустить из консоли команду pip3 install tensorflow
Рассмотрим использование Tensorflow на простом примере: умножение двух массивов. Исходный код приведен ниже.
import tensorflow as tf
# Initialize two constants
x1 = tf.constant([1,2,3,4])
x2 = tf.constant([5,6,7,8])
# Multiply
task = tf.multiply(x1, x2)
# Intialize the Session
session = tf.Session()
# Print the result
print(session.run(task))
# Close the session
session.close()
Сохраним программу в файле tf1.py и запустим, набрав в консоли python3 tf1.py (обратим внимание на цифру “3” в версии Python).
Разберем код программы подробнее. Функция tf.constant позволяет создать константу, в нашем случае это массив со значениями x1 = [1,2,3,4]. Аналогично создается массив x2. Наконец, команда task = tf.multiply(x1,x2) умножает два массива. Казалось бы все пока просто - но не совсем. Если мы напишем print(task), то никакого результата не увидим, на экран отобразится лишь что-то типа Tensor(“Mul:0”, dtype=int32). На самом деле, в памяти TensorFlow формируется так называемый “граф вычислений” (computation graph). Как уже упоминалось, Python - это интерпретатор, и работает довольно-таки медленно, поэтому библиотека TensorFlow формирует в памяти собственную модель данных для вычислений. Для того, чтобы получить реальный результат, мы должны создать объект Session, и запустить в нем вычисления командой session.run(task). Когда вычисления произведены, сессию можно закрыть командой session.close().
Разумеется, можно вычислять не только константы. Рассмотрим пример использования переменных.
import tensorflow as tf
k = tf.constant(2)
a = tf.placeholder(tf.int32)
b = tf.placeholder(tf.int32)
m = tf.multiply(k, a)
task = tf.add(m, b)
session = tf.Session()
print(session.run(task, feed_dict={a: 2, b: 3}))
print(session.run(task, feed_dict={a: [10,11], b: [3,4]}))
session.close()
Здесь мы задаем граф вычислений по формуле a*k + b, где a и b - это переменные, для указания этого используется специальный тип placeholder. Теперь, при вычислении командой session.run мы можем передать различные параметры, например a=2 и b=3:
print(session.run(task, feed_dict={a: 2, b: 3}))
>> 7
Можно даже передать массивы в качестве параметра:
print(session.run(task, feed_dict={a: [10,11], b: [3,4]}))
> [23, 26]
Библиотека TensorFlow поддерживает множество различных операций, например, вычисления с матрицами, ну и разумеется, большое количество функций предназначено специально для обработки данных и машинного обучения. Вернемся к предыдущей главе, и перепишем нашу нейронную сеть, распознающую текст. За основу исходного кода был взят готовый пример из -Examples/tree/master/examples желающие могут изучить приведенные там примеры более подробно.
Код целиком приведен ниже:
import tensorflow as tf
import _pickle as cPickle
# Prepare training data
training_epochs = 500
learning_rate = 0.001
inputs = []
targets = []
with open("digitsMnist.txt", 'rb') as fp:
digits = cPickle.load(fp)
print("Digits loaded:", len(digits))
inputs = list(map(lambda x: x["data"], digits))
def arrayFromDigit(data):
result = data["result"]
# Convert value to array: "3" => [0,0,0,1,0,0,0,0,0,0]
result_flat = [0.0]*10
result_flat[result] = 1.0
return result_flat
targets = list(map(arrayFromDigit, digits))
# Network Parameters
n_hidden_1 = 48 # 1st layer number of neurons
n_input = 784 # MNIST data input (img shape: 28*28)
n_classes = 10 # MNIST total classes (0-9 digits)
model_path = "model_mlp.ckpt"
# tf Graph input
X = tf.placeholder("float", [None, n_input])
Y = tf.placeholder("float", [None, n_classes])
# Store layers weight & bias
weights = {
'h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
'out': tf.Variable(tf.random_normal([n_hidden_1, n_classes]))
}
biases = {
'b1': tf.Variable(tf.random_normal([n_hidden_1])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
# Create model
def multilayer_perceptron(x):
# Hidden fully connected layer with 256 neurons
layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1'])
# Output fully connected layer with a neuron for each class
out_layer = tf.matmul(layer_1, weights['out']) + biases['out']
return out_layer
# Construct model
logits = multilayer_perceptron(X)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=Y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)
# Initializing the variables
init = tf.global_variables_initializer()
# Save/restore model
saver = tf.train.Saver()
session = tf.Session()
session.run(init)
# Training cycle
for p in range(training_epochs):
_, c = session.run([train_op,loss_op], feed_dict={X:inputs, Y:targets})
if p % 50 == 0:
print("Step {} of {}".format(p, training_epochs))
print("Training Finished!")
# Save model (optional)
# save_path = saver.save(sess, './' + model_path)
# print("Model saved in file: %s" % save_path)
# Restore model weights from previously saved model (optional)
# saver.restore(sess, model_path)
# print("Model restored from file: %s" % save_path)
# Use model
pred = tf.nn.softmax(logits) # Apply softmax to logits
print("")
t = [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,1,1,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ]
res = session.run(pred, feed_dict={X: [t]})
print("Result:", res[0])
session.close()
Как можно видеть, суть практически не отличается от описанного в главе 19. Мы создаем модель в функции multilayer_perceptron, состоящую из входных данных x, скрытого слоя layer_1 и выходного слоя out_layer. Мы также имеем массивы weights и biases. Далее, весь громоздкий код тренировки сети, который был написан в главе 19, здесь не нужен - он уже реализован в TensorFlow, нам достаточно вызвать функцию optimizer.minimize в цикле тренировки.
Опционально, готовую модель можно сохранить и загрузить, чтобы не тренировать ее каждый раз, этот код закомментирован. И наконец, мы берем цифру “3” из предыдущего примера, и запускаем уже готовую сеть для распознавания.
Результаты работы программы показаны на рисунке:
Обучение сети заняло … 20 секунд вместо 2х часов - что показывает кардинальный прирост в быстродействии по сравнению с неоптимизированным кодом на Python, выходные данные соответствуют “нарисованной” цифре “3”.
22. Фракталы
Фракталы - интересные математические объекты, которые долгое время не замечались математиками. В 1872 году, объекты такого типа впервые описал немецкий математик Карл Вейерштрасс, “придумавший” функцию следующего вида:
Это непрерывная функция, но при этом не являющаяся гладкой, для нее невозможно вычислить производную ни в одной из точек.
В Википедии можно найти ее график:
Во времена Вейерштрасса математики назвали такую функцию “оскорблением здравого смысла”, практической применимости не мог найти никто. Лишь через 100 лет, в историческом плане совсем недавно, в 1975 году, математик Мандельброт ввел термин “фрактал”. Фракталы стали широко известны после выхода в 1977 году его книги “Фрактальная геометрия природы” - как оказалось, такие структуры распространены в природе гораздо чаще, чем это можно представить. От ветвей деревьев или рисунка береговой линии, до сосудов человека или колебаний курса акций - все эти процессы имеют природу, схожую с фрактальной.
Основное свойство фракталов - самоподобие, увеличенный фрагмент повторяется большое (в идеале бесконечное) число раз. Простейший пример, знакомый каждому - ветви дерева. Возьмем линию, которая через определенное расстояние делится надвое, для каждой из половинок повторим вышеуказанное правило. Получим знакомый рисунок:
Другим примером служит так называемый “парадокс береговой линии”. При измерении длины государственной границы между Испанией и Португалией, выяснилось, что по измерениям из Португалии, длина границы составила 987км, а по измерениям с Испанской стороны - 1214км. Т.к. противоречие было налицо, им заинтересовался английский математик Льюис Ричардсон, который выяснил, что все дело в масштабе - чем меньше масштаб, тем больше получается длина. Поразительным оказалось то, что при теоретически бесконечном масштабе, длина линии также будет бесконечной!
Впрочем, фигуры такого типа были известны и раньше (хотя их рассматривали скорее как математический курьез), например описанная в 1904 году кривая Коха. Построить ее весьма просто: возьмем линию, разделим ее в центре равносторонним треугольником, для каждой новой линии повторим процесс:
Эта фигура теоретически также имеет конечную площадь, но при этом бесконечную длину края. Также как и функция Вейерштрасса, кривая Коха нигде не дифференцируема. Также очевидно, что при увеличении любого фрагмента кривой Коха, он не будет отличаться от “оригинала”, деление будет продолжаться и дальше.
Если замкнуть 3 такие линии, получится так называемая “снежинка Коха”. Нарисовать ее несложно на языке Python, благодаря встроенной библиотеке рисования Turtle. Она позволяет управляя виртуальной “черепашкой”, рисовать примитивы простыми командами, типа “повернуть на угол” или “сдвинуться на расстояние”.
Для рисования линии Коха, нам потребуются всего 3 команды: сдвинуться вперед, повернуть на 60 градусов, и повернуть на -60 градусов. Повторив процедуру 3 раза, мы получим “снежинку Коха”.
Код на языке Python выглядит так:
import turtle
def koch(size, order):
if order > 0:
koch(size/3, order - 1)
turtle.left(60)
koch(size/3, order - 1)
turtle.right(120)
koch(size/3, order - 1)
turtle.left(60)
koch(size/3, order - 1)
else:
turtle.forward(size)
turtle.ht()
turtle.speed(20)
for i in range(3):
koch(size=400, order=4)
turtle.right(120)
turtle.exitonclick()
В результате работы программы мы получаем следующую картинку:
Можно увеличив количество итераций и размер картинки, убедиться что шаблон повторяется.
Может возникнуть вопрос, как длина линии может быть бесконечной при конечной длине. Примерной аналогией может быть сумма ряда:
S = 0.9 + 0.09 + 0.009 + …
Как нетрудно догадаться, сам по себе ряд бесконечный, но его сумма стремится ко вполне определенному числу 0.999999… = 1.
“Снежинка Коха” интересна своей простотой, но есть и более сложные варианты фракталов. Рассмотрим множество Мандельброта, которое строится по следующему алгоритму: для каждой точки c=x + j*y на комплексной плоскости, эта точка попадает в множество при условии что ряд Zn+1 = Zn2 + c не расходится при z0 = 0.
Рассмотрим пример.
При c = (0,0) = 0 + 0j, ряд очевидно, всегда равен нулю, т.е. не расходится, значит точка (0,0) попадает в множество.
При с = (0.5, 0.5) = 0.5 + 0.5j, получаем следующие значения:
Z0 = 0
Z1 = Z0 + c = 0.5+0.5j
Z2 = Z1 + c = 0.5+1j
Z3 = Z2 + c = -0.25+1.5j
Z4 = Z3 + c = -1.6875-0.25j
Z5 = Z4 + c = 3.28515625+1.34375j
Z6 = Z5 + c = 9.48658752+9.32885j
Легко видеть, что ряд расходящийся, числа увеличиваются, значит (0.5, 0.5) не попадает в множество.
При с = (0.25, 0.25) = 0.25 + 0.25j, имеем следующий ряд:
Z0 = 0
Z1 = Z0 + c = 0.25+0.25j
Z2 = Z1 + c = 0.25+0.375j
Z3 = Z2 + c = 0.171875+0.4375j
Z4 = Z3 + c = 0.088134+0.400390625j
Z5 = Z4 + c = 0.09745508+0.32057666j
Z6 = Z5 + c = 0.15672809+0.31248365j
Z7 = Z6 + c = 0.17691766+0.34794993j
Z8 = Z7 + c = 0.160230+0.37311697j
Z9 = Z8 + c = 0.1364575+0.36956959j
Как можно видеть, ряд не расходится, т.е. точка (0.25, 0.25) попадает в множество.
Разумеется, вручную делать такие проверки было бы крайне неудобно, собственно это одна из основных причин, по которой фракталы не были известны до появления компьютеров. Чтобы заметить какие-либо закономерности фрактальной природы, необходима возможность их автоматического рисования. Кстати, сам Мандельброт работал в IBM и имел доступ к весьма мощным компьютерам своего времени.
На языке Python проверку попадания точки в множество легко записать в виде функции. Для нас удобно то, что Python умеет работать с комплексными числами, что делает запись кода более короткой.
Сама функция имеет следующий вид:
def countMandelbrotIterationsForPt(pt):
z = 0
c = pt
threshold = 64
for iteration in xrange(threshold):
z = z*z + c
if abs(z) > 4:
break
return iteration
Здесь вычисляется 64 итерации, которых вполне достаточно чтобы определить, является ли ряд расходящимся или нет.
Чтобы сохранить весь фрактал, нужно перебрать все точки в диапазоне [-2, 2], программа, сохраняющая фрактал в файл, приведена ниже:
from PIL import Image
points = 1000
img = Image.new('RGB', (2*points,2*points), "black")
pixels = img.load()
# Range.X: -2..2,
# Range.Y: -2..2
for ix in xrange(-points, points, 1):
for iy in xrange(-points, points, 1):
pt = complex(2.0*ix/points, 2.0*iy/points)
i = countMandelbrotIterationsForPt(pt)
if i > 16:
colR, colG, colB = 4*i, 4*i, 0
if colR >= 255: colR = 255
if colB >= 255: colB = 255
if colB >= 255: colB = 255
img_x = points + ix
img_y = points + iy
pixels[img_x, img_y] = (colR, colG, colB)
if ix % 10 is 0:
print "Done: {}%".format(100.0*(ix + points)/(2*points))
img.save("fractal.png")
Как можно видеть, программа содержит 2 вложенных цикла ix, iy, затем значение преобразуются в комплексное число, для которого и выполняется описанная выше функция проверки.
Результат выполнения программы для 1000 точек, показан на рисунке:
Если в несколько раз увеличить количество точек, можно увидеть структуру верхней части более детально:
Немного изменив формулу, можно получить другие виды фракталов. Например, множество Жюлиа, описывается также, но Z0 = pt, и c = const. Казалось бы, небольшое отличие, приводит к совершенно другому рисунку фрактала:
Кстати, этот рисунок напоминает сорт цветной капусты “Романеско”:
Наконец, если в формуле фрактала Мандельброта Zn+1 = Zn2 + c, вычислять абсолютное значение Z*Z в виде (|a| + j|b|)*(|a| + j|b|), мы получим фрактал с названием “горящий корабль”:
Сложно сказать, насколько форма напоминает корабль, верхняя часть под увеличением скорее напоминает береговую линию, видимую с высоты:
Кстати, фрактальные алгоритмы - неотъемлемая часть современных методов рисования ландшафтов, таких как горы, деревья, облака и пр, эти объекты действительно имеют фрактальную природу.
В youtube можно найти интересные трехмерные визуализации фракталов, например, набрав в поиске “mandelbrot 3d”:
Для желающих поэкспериментировать самостоятельно, исходные коды программы генерации фракталов, приведены в приложении к книге. В приложении также есть готовые изображения фракталов, сгенерированные с высоким разрешением более 10000х10000 пикселов.
23. Горн Гавриила
В математике есть некоторые парадоксы, связанные с бесконечностью.
Так называемый “Горн Гавриила” (Gabriel's Horn) - это фигура, образованная функцией y = 1/x, если создать из нее 3х-мерную фигуру:
Интерес данного объекта в том, что “горн” имеет конечный объем - но при этом бесконечную площадь поверхности. Если бы такая фигура существовала в реальности, ее можно было бы заполнить краской, а вот покрасить целиком не получилось бы.
Действительно, формулы площади (V) и объема (A) “горна” легко найти в Википедии:
Из них видно, что при a = ∞, V становится равным ℼ, а A действительно стремится к бесконечности.
24. Построение графиков функций
Очень многие закономерности гораздо легче исследовать графически. Очень просто и эффективно строить графики с помощью языка Python и библиотеки matplotlib.
Выведем графики функций y = x2 и у = 0.5x2.
import matplotlib.pyplot as plt
plt.title('Graph')
plt.xlabel('X')
plt.ylabel('Y')
x_values = range(0,10)
y_values1 = map(lambda x: 0.5*x*x, x_values)
y_values2 = map(lambda x: x*x, x_values)
plt.axis([0, 10, 0, 20]) # xmin, xmax, ymin, ymax
plt.plot(x_values, y_values1, 'ro', label='0.5*x*x')
plt.plot(x_values, y_values2, marker='o', linestyle='--', label='x*x')
plt.legend()
plt.show()
Результат работы программы выглядит так:
Как можно видеть, мы имеем массив входных данных x_values = range(0,20), и 2 массива выходных данных y_values1 и y_values2, вычисляемых по соответствующим формулам. Все остальное за нас делает библиотека matplotlib. Команда plt.plot выводит график на экран, причем можно задать разные варианты оформления. Команда выводит подсказку (“легенду”), и является опциональной. Команды plt.title, plt.xlabel и plt.ylabel задают названия графика и осей. Команда plt.show выводит окно с графиком на экран.
Рассмотрим более сложный пример.
Выведем график так называемой “функции распределения простых чисел”, показывающий количество простых чисел меньше либо равных числу x.
Программа вывода графика выглядит так:
import matplotlib.pyplot as plt
import math
def is_prime(n):
if n % 2 == 0 and n > 2:
return False
for i in xrange(3, int(math.sqrt(n)) + 1, 2):
if n % i == 0:
return False
return True
def get_primes(n):
cnt = 0
for i in xrange(1, n):
if is_prime(i):
cnt += 1
return cnt
N = 400
x_values = range(2, N)
y_values = map(lambda n: get_primes(n), x_values)
plt.axis([0, N, 0, N/4])
plt.plot(x_values, y_values, 'ro', markersize=1)
plt.show()
Кстати, согласно Википедии, еще в 18м веке Гауссом и Лежандром было высказано предположение что функция распределения простых чисел выглядит так:
Это легко проверить графически, добавив строчку вывода второго графика:
plt.plot(x_values,map(lambda n:n/math.log(n),x_values), marker='o', linestyle='--')
Окончательный график выглядит так:
С помощью библиотеки numpy строить графики еще проще.
График функции sin(t) в диапазоне 0..2𝜋:
import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 2.0, 0.01)
s = np.sin(2*np.pi*t)
plt.plot(t, s)
plt.show()
Важно заметить, что t здесь - не одно число, а целый массив - в данном примере используется возможность numpy работать непосредственно с массивами.
И наконец, с помощью matplotlib можно строить даже 3х-мерные графики функции двух переменных, для этого используется модуль mplot3d:
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import math
fig = plt.figure()
ax = fig.gca(projection='3d')
# Axis
ax.set_xlabel('X')
ax.set_xlim(0, 20)
ax.set_ylabel('Y')
ax.set_ylim(0, 20)
ax.set_zlabel('Z')
ax.set_zlim(0, 20)
# Graph
for x in range(0,20):
for y in range(0,20):
z = 10*math.sin(0.1*x + 0.1*y)
ax.scatter(x, y, z, c='r', s=1)
plt.show()
Результат показан на рисунке:
Интересно отметить кросплатформенность кода на Python - приведенная выше программа работает и на Windows и на OSX без каких-либо изменений.
25. Точность компьютерных вычислений
Запустим интерпретатор Python и введем простую программу:
a1 = 0.5 - 0.4
a2 = 1.5 - 1.4
print a1
print a2
Получим результаты 0.1 и еще раз 0.1. Пока все логично.
Введем новую команду:
print a1 == a2
В результате получаем … False. 0.1 != 0.1? Как такое может быть?
Чтобы убедиться, что значения не равны, введем:
print a1 - a2
Получаем вовсе не 0, как хотелось бы, а -1.1102230-16. Почему так? Разберемся.
Полученный результат - вовсе не ошибка, а вполне известная особенность компьютерных вычислений с вещественными числами. Любое число в языке программирования имеет свой определенный тип. Обычно это или целое число (1,2,3…), или так называемое число с плавающей точкой (1.1, 2.5, 3.8,...).
С целыми числами все просто - в памяти компьютера они хранятся в двоичном виде как суммы степеней 2. Например для числа “5”:
5 = 0*128 + 0*64 + 0*32 + 0*16 + 0*8 + 1*4 + 0*2 + 1*1 = 00000101b.
Любое десятичное число можно перевести в двоичное “туда” и “обратно”, соответствие тут однозначно, никакой потери точности нет. Ограничения лишь в количестве используемых байт, например для 1 байта (8 бит) максимальное число будет 128+64+32+16+8+4+2+1 = 255. Для 2х бит максимально хранимое значение равно 65535, для 4х бит 2147483647, и так далее.
C вещественными числами все сложнее. Для их хранения используется так называемый стандарт IEEE-754. Согласно этому стандарту, значения хранятся в так называемом формате “чисел с плавающей точкой”, состоящем из трех величин - знака (+ или -), мантиссы и экспоненты.
value = (1 + b0/2 + b1/4 + b2/8 + b3/16 + … ) * 2e-127
(b - биты мантиссы, e - экспонента)
К примеру, значение 3.14 в двоичном виде будет храниться так: 01000000010010001111010111000011. Первый 0 - это знак (+), 1000000 = 128 - это экспонента, а 10010001111010111000011 - это мантисса.
Достаточно проверить первые несколько чисел:
(1 + 1/2 + 1/16 + ...) * 2128-127 = 3.14
Ключевая особенность таких чисел - это их ограниченная точность, ведь на мантиссу и экспоненту отводится вполне определенное число бит. Ошибка весьма невелика, но тем не менее она есть. Например, число 0.5 будет храниться как 00111111000000000000000000000000, что действительно дает 0.5. А вот 0.6 будет храниться как 00111111000110011001100110011010, что в результате дает 0.60000002384185791015625.
Разумеется, записывая в языке программирования строку a=0.6, пользователь не задумывается о битах. Но как в поговорке про суслика, мы его не видим, а он есть.
Введем команды в языке Python:
a = 0.8
print a
Получим 0.8 - команда print достаточно “умна” чтобы округлить результат. Но сделаем вывод с большим числом знаком после запятой:
print("{0:.20f}".format(a))
Получим 0.8000000000000004441, что как говорится, и требовалось доказать.
Что с этим делать? Ну в общем-то ничего. Реальная ошибка в точности достаточно мала, чтобы это было проблемой. Но при желании можно использовать типы данных большей точности, правда ценой увеличения объема памяти и замедления скорости вычислений. Например, в С++ можно выбрать между типами float и double, второй имеет большую точность, но занимает больше памяти.
В целом, выполняя вычисления на компьютере, следует помнить что:
1) Если есть возможность использовать целочисленные вычисления - лучше использовать их, это помимо точности, эффективнее как по быстродействию, так и по занимаемой памяти.
2) Вещественные числа нельзя сравнивать оператором ==, как было показано выше, результат будет неверен. К примеру, следующий код не будет работать:
a = 0.5
b = 0.4
if a-b == 0.1:
print "0.1!"
Вместо этого достаточно убедиться, что результат мал:
if abs(a-b-0.1) < 1e-8:
print "0.1!"
3) Для денежных расчетов, где ошибки округления весьма нежелательны и баланс должен сойтись, существуют специальные библиотеки и типы данных, например библиотека python-money для Python.
4) Если все-таки желательно повысить точность, в Python можно использовать тип Decimal. Он хранит, по возможности, все значимые биты числа.
from decimal import Decimal
a = Decimal("0.5")
b = Decimal("0.4")
print a-b == Decimal("0.1")
Данная программа действительно вернет True. Но достигается это за счет значительного (до 10 раз или даже выше) замедления скорости расчета, да и не для всех вычислений это работает, например для уже упомянутого числа 1/3 точное значение сохранить невозможно. Но для таких случаев можно хранить числа в виде дробей, сохраняя и числитель и знаменатель. В общем, единого решения тут нет, каждый случай нужно рассматривать отдельно.
Но опять же, стоит повторить, что в большинстве случаев можно не беспокоиться - точности стандартных типов данных вполне достаточно. К примеру, если сохранить в переменной расстояние от Москвы до Владивостока, равное 9136.9км, то ошибка округления составит 10-11м, что лишь немногим больше размера одного атома. Скорее всего, такой ошибкой можно пренебречь.
26. Математика и календарь
Еще одна большая тема, где соединяются математика, астрономия и реальная жизнь - это наш обычный календарь. Например, часто можно услышать что високосный год считается “тяжелым”. Может ли такое быть?
Для начала, вспомним что Земля вращается по эллиптической орбите вокруг Солнца (что обеспечивает смену времен года), и в то же время, вокруг своей оси (что обеспечивает чередование дней). Второй период всем известен, и составляет 24 часа, а вот первый период известен уже не всем, и составляет 365.242187 суток. А в году, как известно, 365 дней.
На картинке это выглядит примерно так:
Первую неточность в календаре знали уже в древнем Риме, еще во времена Юлия Цезаря. Каждые 4 года добавлялся один день, чтобы скомпенсировать те самые недостающие 1/4 суток. В какой именно год добавлять - несложно догадаться, что принципиальной разницы тут нет, главное чтобы число лет было кратно 4. Можно даже добавлять по 2 дня каждые 8 лет, принципиально это ни на что не повлияет. Может ли високосный год быть “тяжелее” другого, соседнего? Очевидно что нет, т.к. все равно, какой именно год считать високосным - это лишь общепринятая условность, и на орбиту Земли выбор года никак не влияет.
Но если с орбитой все более-менее понятно, то с календарем не все оказалось так просто. Внимательный читатель наверное заметил, что разница в 0.242187 суток вовсе не кратна ¼. И совершенно справедливо. В юлианском календаре год оказывался длиннее астрономического на 11.2 минуты. Казалось бы немного, но за 128 лет накапливался целый день разницы. Впрочем, в древние времена ритм жизни был не столь быстр как сейчас, и ошибку заметили … только спустя 1.5 тысячи лет, когда “набежало” уже более 10 дней разницы. Это стало заметно не только астрономам - такой сдвиг календаря влиял и на даты посевов, и на празднование дней равноденствия. Тогда, в 1582 году папа Григорий XIII ввел новый календарь, названный теперь “григорианским” - в нем убрано часть високосных годов. Современное правило звучит так: год високосный, если он делится на четыре без остатка, но если он делится на 100 без остатка, это не високосный год, но если он делится без остатка на 400, это високосный год. Таким образом, 1996, 2000, 2004 - високосные годы, но 1900й год високосным не был. Правило выглядит запутанным, но зная, что день разницы накапливается за 128 лет, нетрудно понять почему именно так. Каждый 100й год 1 день “убирается” чтобы скомпенсировать разницу, набегающую за 100 лет, но каждый 400й год делается еще одно исключение, чтобы скомпенсировать оставшиеся 28 лет.
Кстати, в России увы, исчисление европейской точностью не отличалось. Юлианский календарь использовался в России аж до 1918 года, суммарная “набежавшая” разница составила 13 суток, что и составляет разницу между “старым” и “новым” стилем (лишь Турция и Египет приняли новый календарь еще позже, в 1927 году).
Так что теперь мы знаем причину, почему все отмечают “старый новый год” именно 13 января - это тот самый промежуток, который накопился за почти 2000 лет из “всего лишь” 11 минутной разницы между реальным и календарным годами.
Является ли григорианский календарь абсолютно точным? Нет, но дополнительных високосных дней никто уже не вводит, это было бы слишком запутанно. Вместо этого, по необходимости, просто чуть корректируют текущее время, например 1 июня 2015 года, по международному соглашению, день длился на 1 секунду дольше - секунда была добавлена для компенсации разницы календарного и астрономического времени. С 1972 года такие поправки вводились 25 раз.
27. Можно ли выиграть в азартные игры?
Одним из “классических” примеров использования теории вероятности являются азартные игры. Собственно, многие из статистических расчетов изначально и возникли из-за желания понять такие процессы, как например, бросание кубика. Посмотрим, какова вероятность выиграть в ту или иную азартную игру.
Игральные кости
Самый наверное, интуитивно простой и понятный вариант - есть кубик с метками от 1 до 6, и вероятность выпадения того или иного числа равна 1/6.
Но играть таким способом было бы скучно, поэтому популярны игры с более сложными правилами. Популярной азартной игрой является крэпс, на рисунке приведена картинка игрового стола. Как можно видеть, там много всего, но мы не будем вдаваться в глубокие тонкости.
Каждый ход игры состоит из бросания двух кубиков, набранные очки суммируются. Как написано в статье / “Правила игры незамысловаты: игрок кидает две кости, и, если сумма очков на них равна 7 или 11, он выигрывает, если 2, 3 или 12 — проигрывает. Когда на кубиках выпадает другая сумма, шутер бросает их до выигрышной или проигрышной комбинаций”.
Посмотрим, сколько можно выиграть таким способом. Для этого необязательно идти в казино, для симуляции игры воспользуемся Python. Напишем функцию для одного броска:
import random
def shoot():
return random.randint(1,6) + random.randint(1,6)
Напишем функцию симуляции одного хода по вышеописанным правилам.
def move():
while True:
val = shoot()
print("Dice roll:", val)
if val == 7 or val == 11:
return True
if val == 2 or val == 3 or val == 12:
return False
Зададим нашему виртуальному игроку начальную сумму в 100 у.е., и запустим процесс игры. Пусть наш игрок сделает 100 ставок, каждый раз по 1у.е.
money_total = 100
win = 0
loose = 0
for p in range(100):
bet = 1
step = move()
if step is True:
money_total += bet
win += 1
else:
money_total -= bet
loose += 1
print("Win", win, "Loose", loose, "Money", money_total)
Запускаем симуляцию 100 игр и удивляемся результату, игрок выиграл, причем с заметным отрывом побед от поражений: Win 63, Loose 37, Money 126.
Увеличиваем число игр до 1000 и запускаем еще раз, игрок опять выиграл: Win 680, Loose 320, Money 460.
Понятно, что что-то здесь не так - игра, в которой игрок был бы всегда в плюсе, вряд ли была бы популярной в казино, оно бы просто разорилось. Попробуем разобраться.
Интуитивно кажется, что при бросании кубика вероятность выпадения любой грани равновероятна. И это действительно так, но в случае одного кубика. Если кубиков два, то все становится гораздо сложнее. К примеру, число 7 может выпасть как 3+4, 2+5, 1+6, а вот число 12 может выпасть только в виде комбинации 6+6.
Построим в Jupyter notebook график выпадения сумм от 1 до 12 для 100 бросков:
from matplotlib import pyplot as plt
%matplotlib inline
y = [ shoot() for v in range(100) ]
plt.hist(y)
Предположение подтвердилось, и суммы из центра действительно выпадают чаще. Таким образом, числа 7 и 11 действительно выпадают чаще чем 2,3 или 12. И вероятность получить выигрышную комбинацию “7 или 11” действительно выше.
Как такое может быть? Увы, ответ прост - автор процитированной выше статьи просто не разобрался досконально в правилах игры. Текст “правила игры незамысловаты: игрок кидает две кости, и, если сумма очков на них равна 7 или 11, он выигрывает, если 2, 3 или 12 — проигрывает” весьма далек от правды, и правила совсем не так незамысловаты как кажутся.
Реальные правила для ставки на pass line оказались несколько сложнее (есть и другие виды ставок, желающие могут разобраться самостоятельно).
Ход-1: Делается бросок. Если выпадает 7 или 11, игрок выигрывает, если 2, 3 или 12, игрок проигрывает. Если выпадает другое число, оно запоминается под названием point.
Ход-2: Делается бросок. Если выпадает 7, то игрок проиграл. Если выпадает point то игрок выиграл. Если выпадают другие числа, ход повторяется (в это время игроки могут также делать ставки на другие числа).
Действительно, все чуть сложнее, чем описывалось в изначальном варианте. Допишем функцию симуляции с учетом более точных правил.
def move():
point = 0
while True:
val = shoot()
if point == 0:
# First move
if val == 7 or val == 11:
return True
if val == 2 or val == 3 or val == 12:
return False
point = val
else:
# 2..N move
if val == 7:
return False
if val == point:
return True
Результат теперь более похож на правду: за 100 игр игрок выиграл 43 раза, проиграл 57 раз, баланс в конце игры составил 86у.е. от изначальных 100. Интересно и то, что число выигрышей оказалось довольно-таки велико, и составляет лишь немногим менее 50%. Это грамотная стратегия с точки зрения казино - она позволяет поддерживать интерес участника к игре (все время проигрывать было бы неинтересно), но в то же время баланс прибыли казино остается положительным, а баланс денег игрока - соответственно, отрицательным.
Посмотрим подробнее, что получается для симуляции в 100 игр.
- Шанс выиграть на первом шаге выпал примерно в 20 случаях.
- Шанс проиграть сразу на первом шаге выпал в 15 случаях
- В остальных 65 случаях игра продолжается, и тут все хитро: выбор происходит из двух чисел, 7 и point, но как было видно из графика выше, вероятность выпадения “проигрышной” цифры 7 максимальна, что в общем-то и требовалось доказать.
Интересно заметить, что шанс выигрыша в 45% - довольно-таки высок. Так можно ли выиграть? В краткосрочном периоде, да, например, в другой симуляции игроку “повезло”, и он за 100 игр увеличил свой виртуальный капитал со 100 до 112уе.
Но уже следующая симуляция показала отрицательный баланс: игрок уменьшил свое состояние со 100 до 88уе, потеряв, кстати, те же самые 12уе, “выигранные” в предыдущий раз.
Если увеличить число итераций до 1000, то можно увидеть как может выглядеть денежный баланс игрока в долгосрочной перспективе:
Понятно, что при шансе выигрыша каждой игры менее 50%, результирующая сумма денег на счету игрока будет постепенно уменьшаться, а сумма прибыли казино постепенно увеличиваться. На графике кстати, видны всплески и падения, и может возникнуть резонный вопрос - можно ли их предсказать? Увы нет, т.к. бросания кубика - это независимые друг от друга события, и предыдущие результаты никак не влияют на следующие. Можно еще раз повторить главную мысль - можно выиграть один или даже несколько раз, но в долгосрочном периоде остаться в плюсе у казино невозможно, правила игры составлены так что баланс будет не в пользу игрока.
В игре крэпс есть и другие виды ставок, желающие могут проанализировать их самостоятельно.
Американская рулетка
Следующий популярный вид азартных игр - рулетка, рассмотрим ее американский вариант.
Игровое поле рулетки делится на 38 ячеек: 36 зон с цифрами + 2 зоны “zero” и “double zero”. Брошенный на рулетку шарик очевидно, остановится в одной из зон. Игрок может делать разнообразные ставки, видов которых более 10, рассмотрим некоторые из них.
Черное-белое (или чет-нечет)
Игрок выигрывает, если названная им ставка совпала. Очевидно, что вероятность черного или белого была бы 50/50, если бы не два поля zero - при попадании на них ставка проигрывает. Как и в случае с крэпсом, это делает вероятность выигрыша лишь чуть менее 50% - но этого “чуть” достаточно, чтобы быть в минусе.
Напишем функцию симуляции хода с помощью случайных чисел от 1 до 38, последние 2 цифры будем считать за “зеро”.
def move_roulette1():
val = random.randint(1, 38)
if val == 37 or val == 38:
return False
return val % 2 != 0
Запустим симуляцию для 100 игр, код тот же самый что и в симуляции крэпса, поменяем только вызов функции.
money_total = 100
win = 0
loose = 0
for p in range(100):
bet = 1
step = move_roulette1()
if step is True:
money_total += bet
win += 1
else:
money_total -= bet
loose += 1
print("Win", win, "Loose", loose, "Money", money_total)
Результат: игрок выиграл 46 раз и проиграл 54 раза. На графике видно, что у игрока были и “взлеты” и “падения”, но итоговый баланс все равно негативный.
Чем больше мы играем, тем глубже мы уходим в минус, а казино соответственно, в плюс:
Ставка на конкретный номер
Игрок также может поставить на определенный номер, ставка при выигрыше составляет 35:1. Это кажется большим, но нетрудно догадаться, что шанс выпадения определенного номера рулетки 1:38, т.е. опять же, чуть меньше.
Допишем функцию ставки на конкретный номер:
def move_roulette2(num):
val = random.randint(1,38)
return val == num
Симуляция, будем считать что игрок ставит на число 10:
money_total = 100
win = 0
loose = 0
for p in range(100):
bet = 1
step = move_roulette2(10)
if step is True:
money_total += 35*bet
win += 1
else:
money_total -= bet
loose += 1
print("Win", win, "Loose", loose, "Money", money_total)
В результате, игрок выиграл 2 раза и проиграл 98 раз, итоговый баланс -28у.е.
Ставка на два номера
Можно поставить на два номера - шанс выигрыша выше, но зато ставка меньше и составляет 17:1.
Напишем функцию:
def move_roulette3(num1, num2):
val = random.randint(1,38)
return val == num1 or val == num2
За 100 попыток нашей симуляции игрок выиграл 3 раза и проиграл 97 раз, баланс составил -46у.е.
Существуют и другие виды ставок, например, на 4 номера с коэффициентом 1:8, желающие могут поэкспериментировать самостоятельно. Как нетрудно догадаться, все коэффициенты рассчитаны так, чтобы игрок оказался в минусе. Кажется заманчивым поставить 1уе на номер, чтобы выиграть целых 35уе. Но сумма выигрыша увеличивается в 35 раз, а шанс выигрыша уменьшается в 38 раз - итоговый баланс все равно будет в пользу казино.
Лото 6 из 45
Следующее, что интересно проверить, это лото. Принцип игры довольно прост - в барабане находятся 45 шаров, выпадают случайным образом 6 из них. Цена билета составляет 100р, а выигрыш зависит от количества угаданных шаров. Примерный порядок сумм выигрыша таков: 2 угаданных шара дают выигрыш в 100р, 3 угаданных шара дают 300р, 4 шара - 3000р, 5 шаров - 300.000р и 6 шаров - суперприз порядка 10.000.000р.
Для начала напишем программу выбрасывания шаров:
def lottery(values):
balls = range(1, 45+1)
b1 = balls.pop(random.randint(0, len(balls)-1))
b2 = balls.pop(random.randint(0, len(balls)-1))
b3 = balls.pop(random.randint(0, len(balls)-1))
b4 = balls.pop(random.randint(0, len(balls)-1))
b5 = balls.pop(random.randint(0, len(balls)-1))
b6 = balls.pop(random.randint(0, len(balls)-1))
s = [b1,b2,b3,b4,b5,b6]
# print s
res = list(set(s) & set(values))
return len(res)
Из массива balls 6 раз “достается” случайный элемент, затем определяется число элементов пересечений двух множеств. Затем построим график суммарного выигрыша от количества купленных билетов. Для простоты будем считать что игрок ставит на одни и те же числа (тем более, что это ни на что не влияет).
money = []
money_total = 0
for p in xrange(N):
val = lottery([3,7,12,18,33,28])
if val == 2:
money_total += 100
if val == 3:
money_total += 300
if val == 4:
money_total += 3000
if val == 5:
money_total += 300000
if val == 6:
money_total += 3000000
money.append(money_total)
x = range(0, N)
price = map(lambda x: ticket_price*x, x)
from matplotlib import pyplot as plt
%matplotlib inline
plt.plot(price, money)
Интересно проанализировать работу программы. Если купить 100 билетов (суммарная потраченная сумма будет 10.000р), то это дает около 14 угаданных “двойных” шаров и один угаданный “тройной”. Суммарный выигрыш составляет около 2.000р при потраченных 10.000р.
График выигрыша от потраченной суммы получился практически линейным:
Получается, что если купить билетов на миллион, выигрыш составит 250тыс. “Суперприз” в симуляции так не разу и не выпал, хотя теоретически, он конечно возможен. Кстати, как написано в правилах, призовой фонд составляет 50% с проданных билетов, но “суперприз” выпадает далеко не всегда, так что как и в случае с казино, организаторы разумеется, в выигрыше.
В завершении этой главы, интересно сравнить принципиально разный психологический подход к играм. В лотерее выигрыши потенциально велики, но весьма редки. В казино подход обратный — ставки настроены так, что человек будет выигрывать максимально часто. Условно, сделав 10 игр в казино, человек выиграет 4 раза и проиграет 6 раз. Это позволяет игроку не терять интерес к игре, но в любом случае общий баланс остается негативным — человек будет много раз выигрывать, но и чуть-чуть больше проигрывать.
В итоге, может ли существовать «выигрышная стратегия» в таких случайных играх? Очевидно нет, т.к. ни кость, ни шарик, ни лотерейные билеты, не имеют памяти, и их поведение не зависит от предыдущих итераций. Кстати, этот момент важно помнить - интуитивно, проиграв несколько раз, человек может решить, что вот сейчас-то он “точно” выиграет. Увы нет - рулетка или кубик не имеют памяти, и “не знают” о количестве предыдущих попыток, каждая игра по сути начинается с чистого листа. Можно ли выиграть в азартные игры? Как показывает, симуляция, в принципе можно, теория вероятности допускает. Но недолго — стоит начать играть 2й, 3й,… Nй раз, как баланс пойдет вниз. В долгосрочной перспективе выиграть у казино невозможно.
28. Теорема Пифагора
Теорему Пифагора, можно надеяться, знает каждый школьник. Она была известна еще до нашей эры, и говорит о том, что для прямоугольного треугольника со сторонами a,b,c выполняется равенство a2 + b2 = c2.
Ничего сложного, в этом разумеется, нет. Интерес тут представляет другое - так называемые “пифагоровы тройки” - наборы из целых чисел, удовлетворяющие теореме Пифагора. Если например, мы возьмем треугольник со сторонами a=1 и b=2, то с будет равна 2.236, что не является целым числом. А вот треугольник со сторонами a=3 и b=4 удовлетворяет данному условию (с=5).
Таких наборов достаточно много, например (3,4,5), (5,12,13), (8,15,17) и пр. Интересно посмотреть на них графически - для чего отметим соответствующие точки (3,4, 5,12 и пр) на плоскости. Для вывода напишем простую программу на языке Python - просто переберем все пары X,Y, и отметим точками те, для которых выполняется целочисленное равенство.
import math
import matplotlib.pyplot as plt
r_max = 20
pt_x, pt_y = [], []
cnt = 0
for x in range(1, r_max):
for y in range(1, r_max):
d = math.sqrt(x*x + y*y)
if d.is_integer():
print x, y, d
pt_x.append(x)
pt_y.append(y)
cnt += 1
print("CNT:", cnt)
plt.plot(pt_x, pt_y, 'ro', markersize=1)
plt.axhline(0, color='black')
plt.axvline(0, color='black')
plt.show()
Полученная картинка для чисел от 1 до 20 показана на рисунке. Ей соответствуют треугольники со сторонами 3,4,5, 6,8,10, 5,12,13, 9,12,15, 8,15,17 и 12,16,20. Некоторые треугольники, например 6,8,10 являются умножением на 2 предыдущей тройки 3,4,5. Те тройки, которые не имеют таких пар, называются примитивными.
Если увеличить количество точек по оси, то мы увидим вполне красивый периодический узор:
Разумеется, изображение является симметричным, его можно продлить и в сторону отрицательных чисел.
Интересно заметить проявляющиеся параболические дуги, узор которых является довольно-таки сложным.
Можно оставить на картинке только примитивные пары, при этом количество точек станет заметно меньше, зато параболический узор становится гораздо заметнее.
Кстати, для более высоких степеней N > 2 выражение an + bn = cn уже не имеет решений для целых чисел. Это так называемая “Великая теорема Ферма”, которая занимала умы математиков не одну сотню лет. Теорема была полностью доказана лишь в 1995г Эндрю Уайлсом, а доказательство занимает 130 страниц.
29. ABC-гипотеза
Еще один интересный пример из теории чисел - так называемая ABC-гипотеза. Она была сформулирована в 1985г, и до сих пор является одной из нерешенных задач.
Гипотеза формируется довольно-таки просто: для любого числа s>1 существует ограниченное множество троек взаимно простых чисел A+B = C, таких что (rad(A)*rad(B)*rad(C))s < C.
Операция rad(N) называется радикалом, и определяется как произведение всех простых чисел, из которых можно составить число N:
rad(7) = 7 (7 = 1*7)
rad(8) = 2 (8 = 2*2*2)
rad(10) = 10 (10 = 5*2)
rad(17) = 17 (17 = 17*1)
rad(30) = 30 (30 = 2*3*5)
Числа называются взаимно простыми, если они не имеют одинаковых простых множителей, например 3 и 20 взаимно-простые (3=3, 20=2*2*5), а 12 и 15 нет (12=2*2*3, 15=3*5).
Так вот, ABC-гипотеза говорит о том, что если взять некое число S>1, например 1.2, то количество равенств A,B,C, удовлетворяющих описанному условию, будет ограниченным. Пример такой тройки чисел: 1+8=9.
Действительно, rad(1)=1, rad(8)=2, rad(9)=3, и 3 > (1*2)1.2.
Интерес гипотезы, во-первых, в том, что таких равенств мало, для большинства чисел неравенство не выполняется. Например, если взять наугад, равенство 10+6=16, то (rad(10)*rad(6)*rad(16))1.2 = (10*6*2)1.2 = 312.6, > 16.
Во-вторых, доказать эту гипотезу чрезвычайно сложно. На момент написания книги, только один японский математик Синъити Мотидзуки попытался доказать ее, но это доказательство занимает 500 страниц, и его корректность пока что никто не смог подтвердить (у некоторых ученых были сомнения в его корректности, да и разобраться в таком объеме непросто).
Также считается, что на основе этой гипотезы могут быть доказаны другие известные теоремы, так что ее доказательство было бы важным для математики в целом.
Разумеется, мы здесь не претендуем на доказательство гипотезы, но можем проверить некоторые значения на языке Python.
Для начала, возьмем функцию нахождения простых множителей числа N.
def prime_factors(n):
factors = []
while n % 2 == 0:
factors.append(int(2))
n = n / 2
for i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide n
while n % i == 0:
factors.append(int(i))
n = n / i
if n > 2:
factors.append(int(n))
return factors
Как можно видеть, функция последовательно делит числа, и если остаток от деления равен 0, результат заносится в массив. Отдельно проверяются два частных случая - если число четное (делится на 2) и если число простое (ни на что не делится кроме себя). В результате функция возвращает массив чисел, напримем для 8 это будет [2,2,2] (2*2*2 = 8).
Следующий шаг - напишем функцию вычисления радикала. Для этого мы воспользуемся множеством (set), которое хранит неповторяющиеся элементы массива prime_factors.
def rad(n):
result = 1
for num in set(prime_factors(n)):
result *= num
return result
Третья функция - проверка на то, что 3 числа являются взаимно простыми, и у них нет общих делителей.
def not_mutual_primes(a,b,c):
fa, fb, fc = set(prime_factors(a)), set(prime_factors(b)), set(prime_factors(c))
return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and
len(fb.intersection(fc)) == 0
Здесь мы пользуемся функцией нахождения пересечения множеств языка Python.
Написанных 3х функций достаточно, чтобы написать функцию вывода троек чисел A,B,C:
def calculate(N):
S = 1.2
cnt = 0
for a in range(1, N):
for b in range(1, N):
if b < a: continue
c = a+b
if not_mutual_primes(a, b, c):
if c > (rad(a*b*c))**S:
print("{} + {} = {}".format(a, b, c))
cnt += 1
print("N: {}, CNT: {}".format(N, cnt))
return cnt
Как написано в условии задачи, количество таких троек должно быть ограниченно. Мы можем вывести график количества троек от максимального значения N, тогда будет примерно видно, как быстро он растет.
import matplotlib.pyplot as plt
x_values = range(1,2000,25)
y_values = list(map(calculate, x_values))
plt.plot(x_values, y_values, 'ro', label='count(N), S=1.2')
plt.legend()
plt.show()
Как можно видеть, количество троек реально мало - в диапазоне до 2000 их всего 10:
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
5 + 1024 = 1029
13 + 243 = 256
49 + 576 = 625
81 + 1250 = 1331
На графике это хорошо видно, более того, видно что рост графика замедляется, и число троек скорее всего, действительно ограничено для любого диапазона чисел.
Приложение 1 - Вычисления с помощью видеокарты
Еще 20 лет назад, во времена процессоров 80386, пользователям приходилось покупать математический сопроцессор, позволяющий быстрее выполнять вычисления с плавающей точкой. Сейчас такой сопроцессор покупать уже не надо - благодаря прогрессу в игровой индустрии, даже встроенная видеокарта компьютера имеет весьма неплохую вычислительную мощность. Например, даже бюджетный видеочип Intel Graphics 4600 имеет 20 вычислительных блоков, что превышает количество ядер “основного” процессора. Разумеется, каждое ядро GPU по отдельности слабее CPU, но здесь как раз тот случай, когда количество дает преимущество над качеством. Вычисления с помощью GPU сейчас очень популярны - от майнинга биткоинов до научных расчетов, диапазон ценовых решений также различен, от “бесплатной” встроенной видеокарты до NVIDIA Tesla ценой более 100тыс рублей. Поэтому интересно посмотреть, как же это работает.
Есть две основные библиотеки для GPU-расчетов - NVidia CUDA и OpenCL. Первая обладает большими возможностями, однако работает только с картами NVIDIA. Библиотека OpenCL работает с гораздо большим числом графических карт, поэтому мы рассмотрим именно ее.
Основной принцип GPU-расчетов - параллельность вычислений. Данные, хранящиеся в “глобальной памяти” (global & constant memory) устройства, обрабатываются модулями (каждый модуль называется “ядром”, или “kernel”), каждый из которых работает параллельно с другими. Модуль имеет и свою собственную память для промежуточных данных (private memory). Так это выглядит в виде блок-схемы:
Таким образом, если задача может быть разбита на небольшие блоки, параллельно обрабатывающие небольшой фрагмент блока данных, такая задача может эффективно быть решена на GPU.
Для запуска OpenCL-программы из Python, необходимо поставить библиотеку pyopencl, скачать ее дистрибутив можно со страницы . Для установки библиотеки под Windows необходимо скачать файл и ввести команду pip install pyopencl-2018.1.1+cl12-cp27-cp27m-win_amd64.whl для 64-разрядной версии Python, или pip install pyopencl‑2018.1.1+cl12‑cp27‑cp27m‑win32.whl для 32-разрядной.
Для тестирования pyopencl можно запустить программу, выводящую информацию о системе:
import pyopencl as cl
for plat in cl.get_platforms():
print 'Platform: {}'.format(plat.name)
print 'Version: ' + plat.version
devices = plat.get_devices(cl.device_type.ALL)
print 'Devices:'
for dev in devices:
print('\t{} ({})'.format(dev.name, dev.vendor))
flags = [('Version', dev.version),
('Type', cl.device_type.to_string(dev.type)),
('Memory (global), MB', str(dev.global_mem_size/(1024*1024))),
('Memory (local), KB', str(dev.local_mem_size/1024)),
('Max work item dims', str(dev.max_work_item_dimensions)),
('Max work group size', str(dev.max_work_group_size)),
('Max compute units', str(dev.max_compute_units)),
('Driver version', dev.driver_version),
('Device available', str(bool(dev.available))),
('Compiler available', str(bool(dev.compiler_available)))]
for name, flag in flags:
print '\t\t{0:<25}{1:<10}'.format(name + ':', flag)
Если pyopencl и драйвер видеокарты установлен корректно, мы увидим на экране примерно такой вывод (программа запускалась на Macbook Pro):
Platform: Apple
Version: OpenCL 1.2 (Sep 12 2017 16:28:17)
Devices:
Iris Pro (Intel)
Version: OpenCL 1.2
Type: GPU
Memory (global), MB: 1536
Memory (local), KB: 64
Max work item dims: 3
Max work group size: 512
Max compute units: 40
Driver version: 1.2 (Oct 4 2017 01:28:36)
Device available: True
Compiler available: True
Программа удобна своей кросс-платформенностью, один и тот же код может работать и на OSX и на Windows без каких-либо изменений.
Рассмотрим пример: сформировать массив простых чисел от 1 до N. Для решения такой задачи можно использовать алгоритм “решето Эратосфена”, но мы в учебных целях будем решать задачу напрямую, проверяя каждое число отдельно.
Код программы:
import pyopencl as cl
import pyopencl.array as cl_array
import numpy, time
type = cl.device_type.GPU # cl.device_type.CPU
platform = cl.get_platforms()[0]
devices = platform.get_devices(device_type=type)
ctx = cl.Context(devices)
queue = cl.CommandQueue(ctx)
prg = cl.Program(ctx, """
__kernel void primes(__global int *results)
{
int gid = get_global_id(0);
if (gid < 2) return;
int num = gid + 1;
for(int p=2; p<=num/2 + 1; p++) {
if ((num % p) == 0) {
return;
}
}
int val = atomic_add(&results[0], 1);
results[val+1] = num;
}
""").build()
N = 500000
results = numpy.zeros(N, dtype=numpy.int32)
dest_dev = cl_array.to_device(queue, results)
size = (results.shape[0]-1,)
prg.primes(queue, size, None, dest_dev.data)
res = dest_dev.get()
count = res[0]
primes = numpy.sort(res[1:count+1])
print "Found prime numbers:", count
# for p in primes:
# print p
Разберем текст программы подробнее.
1. Мы создаем контекст устройства , передав ему в качестве параметра тип устройства device_type.GPU. Переменная типа CommandQueue хранит очередь команд, которые будут посланы на устройство.
2. Класс cl.Program получает в качестве параметра программу ядра (kernel) и компилирует ее с помощью вызова функции build. Функция primes написана на языке Си, и будет выполняться параллельно на всех ядрах видеокарты.
3. С помощью функции numpy.zeros мы создаем заполненный нулями массив размера N, затем копируем его на видеокарту с помощью вызова dest_dev = cl_array.to_device. Важно понимать, что существуют две разных копии массива - один в памяти компьютера, второй на видеокарте, с которым и будут выполняться вычисления.
4. Вызовом функции prg.primes выполняется параллельный расчет на видеокарте. При этом в качестве параметра функция получает массив, общий для всех экземпляров функции. Библиотека OpenCL сама распараллеливает вызовы функций, общее количество вызовов равно числу элементов массива, а для получения конкретного идентификатора мы используем функцию get_global_id. В нашем случае идентификатор соответствует числу, которое мы хотим проверить.
5. Если простое число найдено, мы кладем его в глобальный массив results. Но т.к. несколько ядер работают с одним массивом одновременно, мы должны быть уверены что данные будут сохранены корректно, для этого мы используем функцию atomic_add. Первую ячейку массива мы таким образом используем для хранения количества найденных простых чисел.
6. Когда выполнение программы завершено, мы загружаем данные обратно с помощью функции dest_dev.get(). Т.к. ядра запускались параллельно, то простые числа лежат в массиве вперемешку, чтобы их отсортировать, мы вызываем функцию numpy.sort.
Как можно видеть, процесс довольно-таки громоздкий, но оно того стоит. Однопоточная программа, написанная на Си с таким же кодом, выполнялась 14 секунд. Вышеприведенная программа, запускаемая на видеокарте, выполнила расчет за 1.2 секунды.
Разумеется, еще раз стоит повторить, что “игра стоит свеч” лишь в том случае, если задача хорошо распараллеливается на небольшие блоки, в таком случае выигрыш будет заметен.
Рассмотрим теперь тот же код, но написанный с помощью библиотеки pycuda. Разумеется, выполнить его смогут только владельцы видеокарт NVIDIA.
import pycuda.driver as cuda
import pycuda.autoinit
from pycuda.compiler import SourceModule
import numpy, time
# Define kernel
mod = SourceModule('''
__global__ void primes(int *results, int maxVal) {
int gid = blockDim.x*blockIdx.x + threadIdx.x;
if (gid < 2 || gid >= maxVal) return;
int num = gid + 1;
for(int p=2; p<=num/2 + 1; p++) {
if ((num % p) == 0) {
return;
}
}
int val = atomicAdd(&results[0], 1);
results[val+1] = num;
}''')
N = 500000
n, grid = 1 + N/512, 512
# Host array
h_array = numpy.zeros(n*grid, dtype=numpy.int32)
# Copy host array to device array
d_array = cuda.mem_alloc(h_array.nbytes)
cuda.memcpy_htod(d_array, h_array)
# Invoke kernel
func = mod.get_function("primes")
func(d_array, numpy.int32(N), block=(n, 1, 1), grid=(grid, 1))
# Copy device array to host array
cuda.memcpy_dtoh(h_array, d_array)
count = h_array[0]
primes = numpy.sort(h_array[1:count+1])
print "Found prime numbers:", count
# for p in primes:
# print p
Как можно видеть, принцип тот же. Единственная разница состоит в том, что “вручную” пришлось указать размер блока в 512 значений, и весь массив разбить на блоки, используя параметр grid - библиотека OpenCL делала этот процесс автоматически. И разумеется, синтаксис и названия функций разных библиотек тоже разные, хотя суть остается примерно та же.
Приложение 2 - Тестирование скорости языка Python
Язык Python очень удобен своей краткостью и лаконичностью, возможностью использования большого количества сторонних библиотек. Однако, один из его минусов, который может быть ключевым для математических расчетов - это быстродействие. Python это интерпретатор, он не создает exe-файл, что разумеется, сказывается на скорости выполнения программы.
Рассмотрим простой пример: рассчитаем сумму квадратов чисел от 1 до 1000000. Также выведем время выполнения программы.
Программа на языке Python выглядит так:
import time
start_time = time.time()
s = 0
for x in xrange(1,1000001):
s += x*x
print("Sum={}, T={}s".format(s, time.time() - start_time))
Результаты работы:
Sum = 333333833333500000, T = 0.47s
Учитывая, что чисел всего миллион, не так уж и быстро. Попробуем ускорить программу, для этого по возможности используем функции встроенных библиотек. Они зачастую написаны на С, и работают быстрее.
import time
start_time = time.time()
l = xrange(1000001)
s = sum(x*x for x in l)
print("Sum = {}, T = {}s".format(s, time.time() - start_time))
Результаты работы:
Sum = 333333833333500000, T = 0.32s
Быстрее, но лишь чуть-чуть.
Заметно лучший результат можно получить, используя профессиональную математическую библиотеку numpy, хотя она довольно сложна для новичков.
import numpy as np
start_time = time.time()
a = np.arange(1,1000001, dtype=np.uint64)
s = np.sum(a ** 2)
print("Sum = {}, T = {}s".format(s, time.time() - start_time))
Результат 0.008с - в 40 раз быстрее “обычного” Python-кода.
И наконец, призываем “тяжелую артиллерию”: перепишем программу на языке Cи.
Код выглядит так:
#include <stdio.h>
#include <time.h>
int main() {
clock_t start = clock();
unsigned long long int sum = 0, i;
for (i = 1; i < 1000001; i + +) {
sum += i * i;
}
clock_t end = clock();
printf("Sum = %llu, T = %fs", sum, (float)(end - start)/CLOCKS_PER_SEC);
return 0;
}
Как можно видеть, он ненамного сложнее python-версии. Перед запуском программы, ее надо скомпилировать, выполнив команду C:\GCC\bin\gcc.exe "Appendix-2 - speedTest.c" -o"Appendix-2 - speedTest". Результат очевиден: T = 0.007 секунд. И еще чуть-чуть: добавляем флаг оптимизации по скорости, выполнив команду C:\GCC\bin\gcc.exe "Appendix-2 - speedTest.c" -o"Appendix-2 - speedTest" -O3. Результат: 0.0035 секунд, разница в быстродействии более 100 раз!
Увы, в более сложных задачах такого прироста реально не бывает (в последнем примере очень короткий код, который видимо полностью помещается в кеш-памяти процессора), но на некоторое улучшение быстродействия можно рассчитывать. Хотя переписывание программы - это крайний случай, сначала целесообразно поискать стандартные библиотеки, которые возможно уже решают данную задачу. К примеру, следующий код на языке Python вычисляет сумму элементов массива за 0.1с:
a = xrange(1000001)
s = 0
for x in a:
s += x
print(s)
Можно использовать встроенную функцию sum:
a = range(1000001)
s = sum(a)
print(s)
Данный код выполняется за 0.02 секунды, т.е. в 5 раз быстрее первого варианта.
Вопрос, что выбрать, на самом деле, не так однозначен - язык Си быстрее, но и сложнее в использовании. Если заранее известно, что задача состоит в обработке большого набора чисел (например поиск простых чисел или магических квадратов), то может быть более целесообразным сразу писать программу на Си или С++, в принципе это не намного сложнее, а работать программа будет быстрее. С другой стороны, при наличии в программе сложной логики или структур данных, написание ее на Python будет гораздо проще. Поэтому, на практике целесообразно прототип программы делать на языке Python, и только в том случае, если проблема быстродействия становится критичной и не решаемой доступными средствами, переходить на более низкоуровневые средства разработки. Также рекомендуется поискать решения среди уже написанных Python-библиотек - для многих задач такие библиотеки уже написаны на языке C++, и их можно использовать, и они работают довольно-таки быстро.
Для тех, кто захочет максимально широко использовать Python в математических расчетах, крайне рекомендуется ознакомиться с библиотекой numpy, она является стандартом де-факто для всех серьезных расчетов.
Теперь посмотрим, как еще можно ускорить Python-программу с помощью многопоточности и других хитростей.
Приложение 3 - Пример ускорения Python-программы
Рассмотрим практический пример сравнения скорости вычислений на Python. Допустим, есть массив целых чисел, для каждого числа надо найти количество его делителей.
Функцию нахождения делителей числа будем использовать “как есть”, без какой-либо оптимизации: перебираем все числа, если число делится без остатка, увеличиваем счетчик.
def get_dividers(n):
divs = 0
for i in xrange(1, n+1):
if n % i == 0:
divs += 1
return divs
Рассмотрим способы решения задачи. Исходные данные: массив целых чисел:
values = [41212317, 4672313, 4342311, 46512319, 51212317, 5672313, 5342311, 56512319]
Способ-1
Решение “в лоб” (заодно показан способ измерения времени выполнения).
import timeit
start_time = timeit.default_timer()
res = []
for v in values:
res.append(get_dividers(v))
print(res)
print("T =", timeit.default_timer() - start_time)
Время выполнения кода на компьютере с процессором Core i7: 10c.
Способ-2
Используем функцию map, позволяющую применить функцию сразу к массиву.
res = map(get_dividers, values)
print(list(res))
Время выполнения: те же 10с, пока мы выиграли разве что в краткости записи.
Способ-3
Используем многопоточность, класс multiprocessing.Pool, позволяющий разбить вычисления над массивом на несколько потоков (способ работает только в Python 3).
if __name__ == '__main__':
p = multiprocessing.Pool(processes=4)
res = p.map(get_dividers, values)
print(list(res))
Время выполнения: 3.7с, что уже лучше. Интересно, что несмотря на разбивку на 4 процесса, реальное время выполнения уменьшилось лишь вдвое. Многопоточные вычисления - достаточно дорогостоящая в плане накладных расходов операция, множество ресурсов процессора тратится на синхронизацию и передачу данных между процессами.
Способ-4
Используем библиотеку параллельных вычислений ipyparallel. Она имеет большие возможности, даже позволяет производить вычисления параллельно на нескольких компьютерах.
Перед тестом запустим сервер вычислений на том же компьютере, командой
ipcluster start -n 4.
Код запуска вычислений не намного больше:
import ipyparallel as ipp
rc = ipp.Client()
dv = rc[:]
res = dv.map_sync(get_dividers, values)
print(list(res))
Как можно видеть, синтаксис практически тот же, библиотека сама делает всю работу по распараллеливанию вычислений. Впрочем, время выполнения практически то же - 3.4с, ведь мы выполняем вычисления на одном компьютере. При желании читатели могут повторить эксперимент с несколькими компьютерами самостоятельно, описание процесса есть на странице .
Способ-5
Как говорилось еще в начале книги, Python - это интерпретатор, и код выполняется достаточно медленно. Кардинально повысить скорость можно, используя компиляцию программы перед выполнением, что было реализовано в библиотеке Numba. Ее можно установить, выполнив команду pip install numba.
Метод очень простой и эффективный, и практически не требует изменения кода: всего лишь добавляем перед описанием функции ключевое слово @numba.jit.
Данный код скопирован в отдельный файл Appendix3_test2.py:
import numba
@numba.jit
def get_dividers(n):
divs = 0
for i in xrange(1, n+1):
if n % i == 0:
divs += 1
return divs
Запуск ничем не отличается от предыдущего варианта:
res = map(test2.get_dividers, values)
print(list(res))
Время выполнения в обычном, однопоточном режиме - 1.5с. Это уже заметная разница!
И наконец, повторяем вышеописанные процедуры, но функцию заменяем на новый вариант.
Многопоточность:
p = multiprocessing.Pool(processes=8)
res = p.map(test2.get_dividers, values)
Время выполнения: 1.04c.
И последний вариант, библиотека ipyparallel:
res = dv.map_sync(test2.get_dividers, values)
print(list(res))
Время выполнения: 0.57c.
Таким образом, по сравнению с изначальным вариантом, мы увеличили скорость расчетов почти в 20 раз, при этом сам код изменять или переписывать практически не пришлось.
В целом, можно предложить следующий алгоритм оптимизации вычислений на языке Python:
1) По возможности, стараться использовать встроенные функции, имеющиеся в библиотеках math, numpy и др. Они уже написаны на C или C++, и работают максимально эффективно.
2) Использовать библиотеку numba, указав в начале функции префикс @numba.jit. Это самый простой и “безболезненный” способ, он чуть увеличит время запуска программы, но скорость расчетов может вырасти в 10 раз. Правда, этот способ не поможет, если код уже состоит только из вызовов встроенных функций из п1. Если же код содержит циклы, условия, другие проверки, то скорость выполнения вырастет значительно.
3) Если скорость расчета нужно еще увеличить, переходим к более тяжелой артиллерии - многопоточности. Используя библиотеку multiprocessing, можно разбить вычисления на несколько ядер процессора - это может увеличить скорость в 2-4 раза. Но важно иметь в виду, что межпроцессное взаимодействие - сама по себе довольно-таки долгая операция, так что делать ее имеет смысл для действительно долго выполняющихся фрагментов кода. Небольшая функция, вызывающаяся много раз в разных потоках, будет работать в итоге даже медленнее за счет дополнительных “накладных расходов”.
4) И наконец, если скорость расчета нужно еще увеличить, можно разбить вычисления на несколько компьютеров в сети, используя библиотеку ipyparallel. Как и в предыдущем случае, заранее следует продумать структуру алгоритма, чтобы производить вычисления крупными блоками, это сделает метод более эффективным.
5) Если необходимо обработать большой объем данных, целесообразно рассмотреть вычисления на видеокарте (GPU). За счет параллельности обработки, можно запустить программу одновременно на нескольких сотнях ядер видеокарты, что может дать огромный прирост в скорости. Такие библиотеки (OpenCL и CUDA) есть практически под все видеокарты, имеющиеся сегодня в продаже.
Кстати, заранее бывает довольно сложно предсказать, насколько хорошо сработает тот или иной метод. Более того, результат может оказаться даже хуже чем был, если например накладные расходы на передачу данных превышают выигрыш. Поэтому каждый шаг оптимизации следует обязательно проверять тестами, чтобы убедиться, что процесс идет в правильном направлении.
Приложение 4 - Тестирование программы на языке Fortran-90
Язык Фортран всегда считался специализированным для математических вычислений. Его первая версия появилась в IBM еще в 1957 году, более-менее современными версиями являются Fortran 90 и Fortran 2003.
Поскольку и сейчас существует версия gfortran под Linux и OSX, стало интересно сравнить быстродействие программ. Отдельного компьютера с Linux у меня не было, так что программа была запущена на Raspberry Pi. Один и тот же код без проблем компилировался и под Linux и под OSX.
В качестве теста использовалась несложная программа вычисления числа Пи по формуле Валлиса.
Программа на С выглядит так:
Appendix4_test1.c
#include <stdio.h>
double wallis_formula(unsigned long int count)
{
double pi = 1.0, num;
unsigned long int i;
for (i=1; i<=count; i++)
{
num = 4.0*i*i;
pi *= num/(num - 1);
}
return pi*2;
}
int main() {
unsigned long int input_count = 100000000;
double result = wallis_formula(input_count);
printf("Calc done: %.20f\n", result);
return 0;
}
Программа, переписанная на Fortran 90 выглядит немного непривычно, если не сказать, архаично:
Appendix4_test1.f90:
function wallisSeries() result(pi)
real(8) :: pi
real(8) :: num
integer :: ITERATIONS = 100000000
pi = 1.0
do i = 1,ITERATIONS
num = 4.0*i*i
pi = pi*num/(num - 1)
end do
pi = 2*pi
end function
program hello
real(8) :: wallisSeries
print *, "Calc done:", wallisSeries()
end program hello
Впрочем, несмотря на другой синтаксис, основная структура кода та же.
Ключи компиляции также похожи:
gcc -o Appendix4_test1_c Appendix4_test1.c -Ofast
gfortran -o Appendix4_test1_f Appendix4_test1.f90 -Ofast
Результаты запуска обеих программ оказались весьма интересными.
Raspberry Pi
$ gfortran -o Appendix4_test1_f Appendix4_test1.f90 -Ofast
$ time ./Appendix4_test1_f
Calc done: 3.1415926364809641
real 2.222s
$ gcc -o Appendix4_test1_c Appendix4_test1.c -Ofast
$ time ./Appendix4_test1_c
Calc done: 3.14159264306626218044
real 3.441s
Как можно видеть, программа на Си оказалась где-то на 30% медленнее. Все-таки более простой код Fortran позволяет легче получить более эффективный код. Но на OSX с gcc последней версии все оказалось по-другому.
OSX
$ time ./Appendix4_test1_f
Calc done: 3.1415926364809641
real 0.788s
$ time ./Appendix4_test1_c
Calc done: 3.14159264306626218044
real 0.434s
Тут уже наоборот, Си вырвался вперед. Возможно, более современный компилятор создает более эффективный код, также возможно, что более эффективно используются команды современных процессоров. Второе интересное отличие - значения в крайних знаках Пи отличаются, видимо реализация расчетов с плавающей точкой в двух языках слегка отличаются (те, кто читал главу 24, поймут в чем дело).
Из всего этого следует несколько выводов. Фортран все-таки устаревший язык, и в общем случае, переписывать программу с Си на Фортран, надеясь ее ускорить, смысла нет - прироста производительности не будет. По читаемости и удобству написания кода Фортран тоже проигрывает - все-таки прогресс в создании компиляторов за последние 20 лет весьма значителен. Но с другой стороны, использование Фортран может быть целесообразно на каких-то специализированных устройствах, если современные компиляторы недоступны. Или в тех случаях, когда уже есть большое количество готовых библиотек, которые в противном случае, пришлось бы переписывать.
Заключение
На этом данная книга закончена, хотя надеюсь, что не навсегда - по возможности и по мере появления новых идей, новые главы будут дописываться. Автор надеется, что хоть немного удалось познакомить читателей с увлекательным миром математики и программирования.
Продолжение следует.
Обо найденных неточностях или дополнениях просьба писать на электронную почту dmitryelj@gmail.com. Наличие новой версии можно проверить на странице .
Fueled by Johannes Gensfleisch zur Laden zum Gutenberg




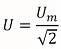

Комментарии к книге «Рассказы о математике с примерами на языках Python и C», Дмитрий Витальевич Елисеев
Всего 0 комментариев