Игнаси Белда «Мир математики» № 33 «Разум, машины и математика. Искусственный интеллект и его задачи»
Предисловие
Я не боюсь компьютеров.
Я боюсь их отсутствия.
Айзек Азимов
Уже несколько десятилетий искусственный интеллект занимает умы не только ученых, но и широкой публики. Что правда, а что вымысел во всех этих фильмах и романах с говорящими роботами, автономными машинами и автоматическими системами, которые действуют почти как люди?
В этой книге мы раскроем некоторые тайны искусственного интеллекта и коротко расскажем о том, что такое «искусственная жизнь». Ждать ли нам в ближайшем будущем появления говорящих машин и автономных разумных систем, или робот еще не скоро сравнится с человеком? Ответ на этот и многие другие вопросы вы узнаете из книги, которую держите в руках.
В ней мы расскажем о четырех основных сферах применения искусственного интеллекта: поиске, обучении, планировании и автоматических рассуждениях. Также в главе 5 мы поговорим об анализе данных — одной из областей, где искусственный интеллект находит наибольшее применение. В нашу цифровую эпоху анализ данных крайне важен, ведь сегодня ежесекундно генерируются миллиарды байт данных, которые были бы бесполезны без интеллектуальных средств, позволяющих преобразовать эти байты в знания.
Наконец, в главе 6 мы погрузимся в бездны искусственной жизни, поговорим о том, что такое живой организм, и выясним, возможно ли вообще создание живых разумных организмов. Отвечая на эти вопросы, мы приведем практические примеры того, как современный человек каждый день сталкивается с искусственной жизнью.
Завершая предисловие, отметим, что хотя вычислительные науки и относятся к прикладной математике, мы в этой книге постарались все же перенести на задний план математическую и аналитическую основу нашего повествования, чтобы сделать эту увлекательную тему более понятной. Кажется, мы достигли определенного успеха, потому что, читая эту книгу, наш редактор, авторитетный специалист в области популярной математики, не раз и не два задавал вопрос: действительно ли мы пишем о математике? Да, эта книга — о математике, и более того, без математики все описанное в ней не могло бы появиться.
17 ноября 2067 года
Полемика вокруг мер, принятых Центральным компьютером
В европейских столицах состоялись массовые акции протеста, направленные против сокращения расходов на социальные программы.
Париж, Брюссель, Барселона, Милан, Порту, Мюнхен и многие другие европейские города серьезно пострадали в ходе беспорядков и массовых акций, направленных против мер, утвержденных Центральным компьютером (ЦК).
Новое законодательство напрямую затронет европейский средний класс, так как согласно принятым законам продолжительность отпусков сократится на 10 % — с 200 дней в год до 180, температура в жилых помещениях будет снижена на 1 °C — с 25 до 24 °C, а субсидирование пятого робота-помощника для каждого гражданина будет прекращено, что повлечет за собой снижение расходов по этой социальной программе на 20 %.
Принятие представленного пакета законов обеспечит экономию в 8 трлн евро, которые будут направлены на повышение добычи на шахтах Марса и Венеры, как указано в заявлении ЦК, который уже 34 года железной рукой правит Европейским союзом.
Как известно, согласно Конституции Европейского союза, пересмотренной 39 лет назад и утвержденной на референдуме, вся законодательная, исполнительная и судебная власть передана ЦК, который по вычислительным способностям, объему памяти и скорости анализа значительно превосходит любые группы экспертов-людей. Эффективность пакета законов, принятых ЦК, подтвердили различные автоматические аналитики (АА) из основных независимых систем автоматического анализа (НСАА).
Тем не менее представители населения утверждают, что эти законы ущемляют гражданские свободы и стали ответной мерой на решительный отказ людей ратифицировать Всеобщую декларацию прав роботов и автономных машин.
Внутри Центрального компьютера ЦК управляется когнитивной картой, включающей триллионы переменных, каждая из которых заключена в одном из так называемых нейронов. При постройке ЦК каждый нейрон был связан с соседними, в результате образовалась огромная нейронная сеть. Она непрерывно модифицируется: при наступлении нового события меняется и значение переменной, соответствующей этому событию, после чего, как при цепной реакции, изменяются значения нейронов, связанных с этой переменной.
Графически такую нейронную сеть можно сравнить бассейном, куда упал камень. В месте соударения камня с водой силы поверхностного натяжения практически мгновенно передаются другим молекулам на поверхности воды. Так возникают волны, которые распространяются по всей поверхности бассейна, а затем постепенно затухают.
При постройке ЦК в его когнитивную карту были внесены квадриллионы элементов данных, собранных за всю историю человечества. Далее когнитивная карта автоматически построила связи между нейронами на основе всего опыта, накопленного людьми.
После того как была выстроена нейронная сеть, ЦК начал использовать ее не только для контроля над Европейским союзом, но и для принятия решений с помощью системы автоматических рассуждений. Эта система способна выдвигать гипотезы и предсказывать их последствия. Продолжая приведенную ранее аналогию, можно сказать, что мы бросаем камень в копию исходного бассейна и наблюдаем за тем, как меняется поверхность воды. Если эффект от предполагаемых изменений оказывается положительным, изменения вступают в силу.
Можно сказать, что система автоматических рассуждений ЦК представляет собой алгоритм поиска.
Если ЦК обнаруживает, что необходимо решить какую-то проблему, он разворачивает комбинаторное дерево, отражающее все политические, социальные, экономические и даже военные действия, которые можно предпринять. Учитывая сложность политической деятельности, это дерево уже через несколько миллисекунд содержит несколько миллионов ответвлений, и если процесс его формирования не прекратится, то всего за несколько секунд число ветвей дерева будет превышать число атомов во Вселенной. Допустим, что наша цель — снизить дефицит бюджета на 1,5 %.
Скорость современных квантовых суперкомпьютеров такова, что комбинаторное дерево всего за несколько секунд становится бесконечно большим. Разумеется, провести расчеты над бесконечным деревом невозможно, поэтому ЦК использует различные средства, чтобы «отрубить» ветви, которые очевидно не приведут к желаемой цели. К примеру, если мы хотим снизить дефицит бюджета, но при этом не планируем повышать налоги и/или стимулировать экономический рост путем увеличения бюджета, то цели мы не достигнем. Следовательно, все ветви дерева, не ведущие к требуемой цели, можно отсечь. Подобные эвристические методы решения проблем были созданы автоматически на основе данных за прошлые периоды.
Позднее группа европейских экспертов по общественным наукам подробно проанализировала эти методы. К удивлению скептиков, доля изменений, внесенных экспертами в первые версии эвристических методов, составила всего 0,003 %. Экспертный анализ занял пять лет, в то время как на автоматический вывод всех эвристических методов ушло всего три дня.
Система автоматического вывода эвристик основывалась на эволюционных алгоритмах, то есть на интеллектуальных системах, предлагающих случайные решения (в нашем случае каждым решением была предложенная эвристика), которые постепенно уточнялись в ходе процесса, имитирующего эволюцию в природе согласно законам Дарвина. Решения, наиболее приспособленные к среде, — это решения, оставившие наибольшее число потомков.
Иными словами, эвристики, в наибольшей степени подкрепленные данными прошлых периодов, имеют больше шансов получить распространение в ходе этой виртуальной эволюции и оставить потомство.
Теперь остается подождать, пока не станет ясно, что меры, предложенные Hercules v3.4, действительно будут благоприятны для общества, как неизменно происходило в последние 34 года. Без сомнения, качество нашей жизни существенно возрастет.
Как уже догадался читатель, представленная выше статья полностью выдумана и очень далека от реальности. Но возможен ли подобный сценарий через 50 лет — сценарий, при котором все важные решения, определяющие судьбу человечества, принимают, претворяют в жизнь и анализируют мыслящие машины?
На Кипре, где сложилась крайне нестабильная военная и экономическая обстановка, исследователи из местного университета и Банка Греции уже предложили систему на основе когнитивных карт, позволяющую предсказывать воздействие на ситуацию изменений, представленных каждой стороной конфликта — греческой, турецкой, НАТО, Евросоюзом и так далее.
Чтобы получить более точное представление о том, насколько правдоподобна изложенная выше газетная статья, посмотрим, каких успехов уже добились исследователи, которые занимаются искусственным интеллектом, и сильно ли отличается нынешнее положение дел от описанного сценария. Добро пожаловать в удивительный мир искусственного интеллекта, где математика, вычисления и философия идут рука об руку и уже вплотную подошли к границе, отделяющей человека от машины.
Глава 1. Что такое искусственный интеллект
Существует довольно много научно-фантастических фильмов, в которых действуют автономные машины, способные самостоятельно принимать решения. Но каково в действительности развитие искусственного интеллекта? Неужели и правда близок тот час, когда мы своими глазами сможем увидеть картины, изображенные в «Космической одиссее 2001 года» или в фильме «Я, робот»?
Прежде чем начать наш рассказ, дадим точное определение искусственному интеллекту. Трактовка слова «искусственный» разногласий не вызывает: «искусственный» означает «не природный», то есть «созданный по воле человека». А что такое «интеллект»? Согласно большинству словарей, это слово имеет множество значений, среди которых выделяются «способность понимать», «способность решать задачи», «способность учиться из опыта и адаптироваться к новым ситуациям».
И различные определения этого понятия показывают всю его сложность.
Психологи и философы пытаются определить и измерить интеллект на протяжении многих веков. Но все предложенные ими определения довольно трудно применить не к людям, а к другим объектам. К примеру, обладает ли интеллектом компьютерная программа, способная синхронизировать и координировать работу всех систем самолета, позволяющая со стопроцентной надежностью прокладывать курс в зависимости от текущих требований? Возможно, что да. Но можно ли сказать, что интеллектом обладает комар? Это насекомое ведь тоже способно синхронизировать и координировать работу всех своих органов и со стопроцентной надежностью прокладывать курс в зависимости от текущих требований.
Тест Тьюринга
Практическое решение, позволяющее определить, обладает ли машина интеллектом, первым предложил в 1950 году математик Алан Тьюринг, который считается одним из создателей искусственного интеллекта. В основе его теста лежит очень простая идея: если машина во всем ведет себя подобно мыслящему существу, то она должна обладать интеллектом.
Тест Тьюринга проводится следующим образом. Человек и машина располагаются в разных комнатах и не могут видеть друг друга. После этого человек печатает на клавиатуре ряд вопросов для машины, а та выдает на монитор ответ. Если человек считает, что беседует с человеком, то оцениваемая им машина разумна и, следовательно, обладает искусственным интеллектом.
Человек, задающий вопросы машине (X), использует систему, препятствующую визуальному контакту. Таким образом, он может определить, кто его собеседник — машина или человек — только по ответам на вопросы.
Разумеется, тест Тьюринга вызвал шквал критики со стороны некоторых теоретиков. Можно ли сказать, что машина разумна, только потому, что она способна отвечать на вопросы с помощью огромного словаря вопросов и ответов? Быть может, интеллект — это нечто большее, и он подразумевает, к примеру, наличие сознания?
* * *
АЛАН ТЬЮРИНГ (1912–1954)
Английский математик и философ Алан Тьюринг благодаря множеству фундаментальных открытий считается одним из создателей не только искусственного интеллекта, но и всей современной информатики.
Во время Второй мировой войны Тьюринг занимался криптоанализом и стал одним из главных действующих лиц в операции по взлому шифров машины «Энигма». Успешное завершение этой операции позволило союзникам узнавать обо всех перемещениях нацистских войск.
Основным теоретическим вкладом Тьюринга в вычислительные науки стала так называемая машина Тьюринга — теоретическая модель универсальной вычислительной машины, способной обрабатывать любые входные данные и получать выходное значение за конечное время. Машина Тьюринга состоит из бесконечной ленты с записанными на ней символами, а также управляющего устройства, которое может смещаться вдоль ленты вправо или влево, считывать записанные на ней символы, стирать их и записывать новые. Также машина Тьюринга содержит правила, определяющие действия управляющего устройства для любого символа, записанного на ленте. В практической информатике эти правила соответствуют компьютерной программе, а лента — системе ввода-вывода и регистру о состоянии выполнения программы.
Сегодня при создании новых языков программирования, например С, Pascal, Java и других, прежде всего нужно доказать, что они являются Тьюринг-полными, то есть эквивалентны машине Тьюринга.
Ученый покончил с собой, не выдержав преследования британских властей. На суде Тьюринг отказался от адвоката, сочтя, что ему не в чем оправдываться, и был признан виновным, что в конечном итоге привело его к самоубийству. В 2009 году Гордон Браун, который в то время занимал пост премьер-министра Великобритании, публично принес извинения от имени британского правительства за преследования, которым подвергся Алан Тьюринг в последние годы жизни.
* * *
Главным критиком теста Тьюринга стал философ Джон Сёрль, предложивший эксперимент под названием «китайская комната». Представьте себе, что человек, не знающий ни слова по-китайски, помещен в закрытую комнату в торговом центре Шанхая. Посетителей торгового центра приглашают задать этому человеку вопросы, записав их на бумаге и передав записку через специальное отверстие. Под рукой у человека в закрытой комнате находится словарь, в котором указаны все китайские иероглифы, содержащиеся во всех возможных вопросах, которые только могут задать посетители. Молодой человек снаружи пишет на листе бумаги вопрос на китайском языке: «Там внутри тепло?» и просовывает записку в комнату. Человек внутри смотрит на иероглифы, находит их в словаре и выбирает возможный ответ на вопрос. Далее он перерисовывает нужные иероглифы на новый лист и возвращает ответ автору вопроса. Ответ на китайском языке звучит так: «Нет, вообще тут очень холодно». Логично, что и задающий вопрос молодой китаец, и остальные участники эксперимента получат корректные ответы на своем родном языке и сочтут, что человек в запертой комнате прекрасно владеет китайским. Однако на самом деле все ответы были составлены на основе словаря соответствий, а запертый человек не понял ни единого иероглифа.
Может ли произойти так, что машина, которая пройдет тест Тьюринга, обманет нас, как человек, сидящий в китайской комнате? Нет, это невозможно. «Китайская комната» — некорректный эксперимент: в нем люди, сидящие в комнате, не знают китайского, но отвечают на вопросы с помощью руководства, созданного кем-то, кто знает китайский и смог составить полный перечень вопросов и ответов.
Сегодня новая технология считается интеллектуальной, если она позволяет решить задачу творчески, что всегда считалось исключительной способностью человеческого мозга. Ярким примером технологии, которая кажется интеллектуальной, но не считается таковой, являются первые экспертные системы, созданные в 1960-е годы. Экспертная система — это компьютерная программа, реализованная по определенным сложным правилам, которая может автономно осуществлять контроль над другими системами. Примером можно считать компьютерную программу с огромным списком симптомов различных заболеваний, на основе которых она может назначить нужное лечение. Тем не менее такая система неспособна вывести новое правило из уже известных или при необходимости предложить нестандартную терапию. Следовательно, эта система не обладает креативностью и ее нельзя назвать интеллектуальной.
Интеллектуальная компьютерная система удовлетворяет отчасти субъективным требованиям: так, она должна иметь возможность обучаться, уметь оптимизировать математические функции со множеством параметров (измерений) на огромном интервале (области определения) или планировать использование огромного объема ресурсов с учетом ограничений.
Подобно остальным областям науки и техники, со временем в искусственном интеллекте возникли специализированные дисциплины и были выделены пять больших разделов.
1. Поиск.
2. Обучение.
3. Планирование.
4. Автоматические рассуждения.
5. Обработка естественного языка.
В разных областях искусственного интеллекта применяются порой одни и те же технологии и алгоритмы. Расскажем о каждом из разделов подробно.
* * *
МОЖНО ЛИ СЫМИТИРОВАТЬ ИНТЕЛЛЕКТ? ШАХМАТЫ, КАСПАРОВ И DEEP ВLUЕ
Шахматы — классическая комбинаторная задача, для решения которой с самого момента создания информатики безуспешно предпринимались попытки применить интеллектуальные методы, позволившие бы компьютеру одержать победу над игроками-людьми. Почему же нельзя сымитировать интеллект в такой игре, как шахматы? Представьте, что мы ввели в компьютер правила игры и он построил множество всех возможных ходов. Далее мы можем последовательно определить оптимальный ход в каждой возможной позиции. Число возможных ходов имеет порядок 10123, и это больше, чем количество всех электронов во Вселенной! Следовательно, только для хранения результатов объем памяти компьютера должен превышать Вселенную! Как видите, в примере с шахматами, в отличие от «китайской комнаты», сымитировать интеллект при помощи перечня всех возможных ходов абсолютно невозможно.
Наибольшую известность среди всех шахматных компьютеров приобрел компьютер Deep Blue и его противостояние с Гарри Каспаровым. Суперкомпьютер Deep Blue, запрограммированный для игры в шахматы, в 1996 году впервые в истории обыграл чемпиона мира. Вначале в шести партиях победу одержал Каспаров со счетом 4:2. Чемпиону противостояла машина, способная анализировать 100 миллионов ходов в секунду. Затем против Каспарова выступила вторая версия компьютера, Deeper Blue, способная анализировать уже 200 миллионов ходов в секунду. На этот раз победу одержал компьютер, однако Каспаров был уверен, что в определенный момент машине все же помог человек. Ситуация выглядела так: Каспаров пожертвовал пешку, чтобы затем начать контратаку. Компьютер не мог обнаружить эту ловушку, так как его расчеты распространялись на ограниченное число ходов вперед и он не мог увидеть зарождающуюся контратаку Каспарова.
Однако машина не поддалась на эту уловку, что вызвало у шахматиста подозрения. После завершения партии он попросил обнародовать протоколы операций, выполненных компьютером. Компания IBM ответила согласием, однако в конечном итоге протоколы так и не были представлены публике.
Созданный компанией IBM суперкомпьютер Deep Blue, одержавший победу над чемпионом мира по шахматам.
Поиск
Под поиском здесь понимается поиск оптимального решения определенной задачи.
После определения задачи с помощью математической функции речь пойдет об оптимизации функций, то есть о поиске входных параметров, при которых результирующее значение будет оптимальным. Для решения некоторых задач требуется оптимизировать несколько функций одновременно, при этом определить эти функции и ограничить их значения непросто. Для автоматической системы оптимизация функций представляет сложную задачу, особенно если функция не задана аналитически и ее примерный вид можно определить лишь на основе нескольких множеств значений. Часто бывает, что рассматриваемая функция имеет несколько сотен параметров, либо вычисление множеств ее значений очень трудоемко, либо множества ее значений содержат шум, то есть в определенных точках пространства являются неточными.
В подобных сложных сценариях используется искусственный интеллект. Человек способен решать сложные многомерные математические функции благодаря интуиции — классическим примером служат функции подобия. Представьте, что вам знакомы более 500 человек. Если вы увидите фотографию какого-то человека, то мгновенно сможете сказать, знаком ли он вам, и даже назвать его имя. Эта с виду простая операция решается путем оптимизации функции, описывающей разницу между лицами, которые вы помните, и изображенным на фотографии. Каждое лицо описывается тысячами параметров: цвет глаз, соотношение размеров рта и носа, наличие веснушек и так далее. Наш мозг способен определять все эти характеристики и сравнивать их с характеристиками всех знакомых нам людей. Мозг оценивает параметры лица на фотографии, сравнивает их с параметрами лиц всех знакомых людей и определяет, для какого человека различие между этими параметрами будет наименьшим. Также мозг определяет, когда различие между параметрами настолько мало, что можно сказать: на фотографии изображен один из знакомых людей. И все эти операции мозг выполняет менее чем за секунду. Однако для компьютера распознавание лиц — крайне сложная операция, и ему для решения этой же задачи потребуется несколько минут.
* * *
ГО — ОДНА ИЗ ВЕЛИЧАЙШИХ НЕРЕШЕННЫХ ЗАДАЧ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА
Игра го — прекрасный пример комбинаторной задачи, в которой выбор оптимального хода в заданной позиции вполне по силам даже игроку среднего уровня, но крайне сложен для компьютера.
Сегодня еще ни одна компьютерная программа не смогла без форы обыграть профессионального игрока в го.
Правила этой стратегической китайской игры крайне просты, однако по ходу партий постоянно возникают невероятно сложные сценарии. В го играют на доске, разделенной линиями на квадраты размером 19 х 19. Два игрока по очереди ставят фишки белого и черного цвета на свободные пересечения линий доски. Если одна или несколько фишек оказываются полностью окруженными фишками другого цвета, то «захваченные» фишки снимаются с доски. Игрок может в любой момент передать право хода противнику, но если оба они передают право хода два раза подряд, партия заканчивается, и победителем признается тот, кто на момент прекращения партии имел более выгодную позицию.
С точки зрения математики го — стратегическая игра, подобная шахматам. Однако если компьютер все же оказался способен одержать верх над чемпионом мира по шахматам, то программы для игры в го едва ли одолеют игрока-любителя. Происходит это по трем причинам. Во-первых, доска для игры в го более чем в пять раз просторнее шахматной доски, следовательно, потребуется проанализировать большее число ходов. Во-вторых, каждый ход может повлиять на несколько сотен последующих, поэтому компьютер не может прогнозировать развитие партии в долгосрочной перспективе. Наконец, в шахматах фигуры снимаются с доски по одной и обладают определенной ценностью, поэтому можно довольно точно оценить выгоду оттого или иного хода. В го, напротив, выгода, получаемая от взятия фишки соперника, зависит оттого, какие именно фишки снимаются с доски, что определяется их текущим расположением.
Доска и фишки для игры в го. Последние традиционно называются камнями.
Положение фишек на доске в одной из партий финала чемпионата мира, прошедшего в 2002 году, где встретились Чхве Мёнхун (белые) и Ли Седоль.
* * *
Почему мы называем этот раздел искусственного интеллекта поиском, если речь идет о численной оптимизации? К поиску относятся задачи и другого типа, к примеру, так называемые комбинаторные задачи. Их решения образованы различными элементами, которые могут сочетаться между собой и порождать комбинаторное пространство. Решение такой задачи определяется оптимальным множеством элементов. Хороший пример комбинаторной задачи — шахматная партия. Оптимальным решением этой задачи будет последовательность ходов, ведущих к выигрышу.
Еще один классический пример — так называемая задача о ранце, в которой нужно уложить в рюкзак различные предметы. В этом случае решением будет совокупность предметов с минимальным общим весом и максимальной ценностью. И вновь комбинаторная задача, относительно простая для человека, часто оказывается крайне сложной для компьютера.
Одна из множества информационных систем, используемых для распознавания образов, в данном случае — для распознавания лиц. На иллюстрации изображена разработка японской компании NEC.
Обучение
Следующий раздел искусственного интеллекта — обучение. Является ли интеллектуальной система, способная обучаться на основе предшествующего опыта? Вернемся к примеру с автоматической системой диагностирования, в которую введено множество симптомов, соответствующих определенным заболеваниям. Этот процесс ввода информации, содержащей различные внутренние связи, называется обучением. После того как система обучена, она способна найти в памяти любой симптом и определить, какое заболевание ему соответствует. Обучение такой системы основано на запоминании, и ее нельзя назвать интеллектуальной. Цель обучения интеллектуальных систем — сформировать способность формулировать обобщения, то есть выводить некие правила, которые затем можно будет применить для решения новых задач.
Автоматическое обучение стало одним из самых обширных разделов искусственного интеллекта. В университетах, исследовательских центрах и компаниях ежедневно совершаются новые открытия в этой области, ведь, с одной стороны, в различных областях знаний и промышленности очень велика потребность в экспертных системах, а с другой — программировать полезные экспертные системы очень сложно.
Обучение интеллектуальной экспертной системы производится на основе последовательности случаев и соответствующих им решений. После обучения система способна выводить правила и нормы, описывающие исходные случаи, и для любого нового случая она сможет найти новое решение. Экспертную систему можно считать интеллектуальной, только если она умеет автоматически обучаться и формулировать обобщения. Иными словами, система не должна требовать ручного ввода правил, а после обучения она ведет себя подобно эксперту в своей предметной области.
Позднее мы расскажем о способах применения экспертных систем более подробно. Мы приведем несколько показательных примеров современных экспертных систем, например систем, используемых для прогнозирования просрочки платежей по ипотеке, систем раннего обнаружения злокачественных опухолей или систем автоматической классификации нежелательных электронных писем (спама).
Автоматическая классификация электронной почты с целью отделить спам от корректных сообщений — одна из областей применения экспертных систем.
Планирование
Третий крупный раздел искусственного интеллекта — планирование. Человек обладает способностью строить планы с незапамятных времен. Можно сказать, что человек и выжил-то благодаря планированию. Если мы перенесемся в палеолит, то и там встретимся с проблемой, требующей планирования: как распределить наличный объем пропитания между числом потребителей — членов племени? Кому отдать сочное мясо, богатое калориями: тем, кто собирает ягоды, или охотникам?
А если один из собирателей — женщина на последних месяцах беременности? Все эти вопросы соответствуют так называемым ограничениям системы, то есть обстоятельствам, которые следует учитывать при составлении плана.
Ограничения делятся на обязательные и необязательные. В нашем примере с доисторическим племенем лучшие куски мяса должны доставаться тем, кто больше всего нуждается в этом. Однако не случится ничего страшного, если самому сильному охотнику в один из дней не достанется самый сочный кусок. Конечно, эта ситуация не может повторяться постоянно, но уж один-то день охотник может потерпеть.
Следовательно, это необязательное ограничение.
В качестве примера обязательного ограничения приведем распределение ресурсов университета (то есть аудиторий и преподавателей) в течение учебного года. Потребителями ресурсов будут студенты, изучающие, например, математический анализ, торговое право, физику и другие предметы. При распределении ресурсов нужно учесть, что студенты, изучающие торговое право и физику, не могут одновременно занимать, например, аудиторию 455. Заведующий кафедрой математического анализа также не может преподавать торговое право, так как не имеет необходимой квалификации. В этом примере описанные ограничения являются обязательными.
Таким образом, при разработке интеллектуального алгоритма планирования важнейшую роль играет возможность или невозможность нарушить накладываемые ограничения.
* * *
ЗАДАЧА КОММИВОЯЖЕРА
Порой определенная задача может быть отнесена к тому или иному разделу искусственного интеллекта в зависимости оттого, с какой стороны мы подойдем к ее решению. Хорошим примером является задача коммивояжера (Travelling Salesman Problem, или TSP), которую можно решить путем поиска или планирования.
Формулировка этой задачи звучит так: для данного множества городов, дорог между ними и расстояний нужно найти маршрут коммивояжера, проходящий через все города. Коммивояжер не может заезжать в один и тот же город дважды и при этом он должен преодолеть наименьшее расстояние. Как читатель может догадаться, в зависимости от расположения маршрутов между городами коммивояжер обязательно посетит какой-либо город дважды, следовательно, это условие можно считать несущественным.
Пример графа городов, связанных между собой. Расстояние между городами в километрах указано на ребрах графа.
Автоматические рассуждения
Четвертый раздел искусственного интеллекта — автоматические рассуждения.
Именно они привлекают наибольшее внимание широкой публики и часто становятся главной темой научной фантастики. Тем не менее автоматическим рассуждениям как отдельной дисциплине дала начало не слишком увлекательная задача об автоматическом доказательстве математических теорем.
Часто выдвигаются новые теоремы, которые требуется доказать или опровергнуть. Доказательство теорем может быть крайне сложным. Именно это произошло с великой теоремой Ферма (согласно ей, если n — целое число, большее двух, то несуществует ненулевых натуральных чисел, удовлетворяющих равенству zn = хn + уn) — на доказательство этой теоремы ушло более 200 лет!
В 1956 году экономист Герберт Саймон (1916–2001) и инженер Аллен Ньюэлл (1927–1992) совместно разработали машину под названием Logic Theorist, способную доказывать нетривиальные теоремы математической логики. Разумеется, появление этой машины стало вехой в развитии искусственного интеллекта и вновь вызвало философскую дискуссию о возможности создания мыслящих машин. Эта дискуссия, конечно же, повлияла на литературу и кино 1960—1970-х годов, породив образы мыслящих машин, враждебных человеку. Согласно философу Памеле МакКордак, Logic Theorist доказывает: машина способна выполнять задачи, которые cчитаются творческими и подвластными исключительно человеку.
Гэрберт Саймон (слева) и Аллен Ньюэлл за игрой в шахматы, 1958 год.
В Logic Theorist использовались так называемые символьные системы, созданные математиками, чтобы придать смысл некоторым выражениям и уйти от произвольных обозначений. К примеру, мы можем утверждать: высказывание «быть человеком» означает «быть смертным», что можно записать математически как А —> В, где символ А эквивалентен высказыванию «быть человеком», символ —> — «означает», а В равносильно высказыванию «быть смертным». «Быть человеком означает быть смертным» — это произвольное высказывание, которое записывается выражением А —> В. После формализации всех произвольных членов выполнять операции с ними намного проще с точки зрения математики и информатики.
Для упрощения математических действий символьные системы опираются на аксиомы, из которых выводятся теоремы. Преимущество символьных систем в том, что они являются формальными и однозначно определенными, поэтому программировать их сравнительно просто. Рассмотрим пример:
Сократ — человек.
Все люди смертны.
Следовательно, Сократ смертен, поскольку он — человек.
Если мы запишем эти высказывания в формальном виде, они будут выглядеть так:
А: Сократ
В: человек (люди)
А —> В
С: смертен (смертны)
В —> С
Если А —> В и В —> С, то А —> С, то есть Сократ смертен.
В этом случае правило вывода под названием «гипотетический силлогизм» позволяет заключить, что А —> С истинно, если А —> В и В —> С.
Тем не менее число вариантов, полученных при автоматическом и систематическом выводе теорем на основе аксиом и правил вывода, будет опасно близко к числу атомов во Вселенной. По этой причине в машине Logic Theorist использовались эвристические рассуждения, то есть методы нечеткого прогнозирования, которые помогали выбрать лучшие производные высказывания среди возможных. Отобранные высказывания определяли правильную последовательность выводов, позволявших прийти от аксиом к доказательству теорем.
Рассмотрим практический пример. Мы хотим знать, смертен ли Сократ. Нам известны следующие исходные аксиомы:
А: Сократ
В: болельщик «Олимпиакоса
С: грек
D: человек
Е: смертен
А —> С
С —> D
A —> D
С —> Б
D —> E
Определим, истинно или ложно А —> Е, с помощью «грубой силы», то есть путем перебора всех возможных сочетаний. Имеем:
А —> С —> D —> Е
A —> С —> В
A —> D —> E
Мы выполнили семь логических операций, взяв за основу всего пять аксиом и одно правило вывода — гипотетический силлогизм. Легко догадаться, что в сценариях, содержащих больше аксиом и правил вывода, число возможных сочетаний может оказаться столь велико, что на получение доказательств уйдут годы. Чтобы решить эту проблему так, как это сделали Саймон и Ньюэлл, используем эвристическое рассуждение (или эвристику). В нашем примере эвристика подскажет: если мы хотим доказать, что некий человек смертен, нет необходимости заводить разговор о футболе (А —> С —> В).
И символьные, и эвристические системы широко используются для решения практических задач, а не только для автоматического доказательства теорем.
Приведем еще один пример использования эвристик. На каждом ходу в шахматной партии существует в среднем 37 возможных вариантов. Следовательно, если компьютерная программа будет анализировать партию на восемь ходов вперед, на каждом ходу ей придется рассмотреть 378 возможных сценариев, то есть 3512479453921 ходов — более 3,5 млрд вариантов. Если компьютер тратит на анализ каждого варианта одну микросекунду, то при анализе партии всего на восемь ходов вперед (достаточно простая задача для профессионального шахматиста) мощный компьютер будет думать над каждым ходом больше двух с половиной лет!
Для ускорения процесса нужны какие-то улучшения, которыми и будут эвристики. Эвристики — это правила прогнозирования, позволяющие исключить из рассмотрения ходы, которые ведут к очень невыгодной позиции и поэтому нецелесообразны. Уже благодаря тому, что эвристики позволяют исключить из рассмотрения несколько абсурдных ходов, число анализируемых вариантов существенно сокращается. Таким образом, эвристики — это средства прогнозирования, основанные на интуиции программиста, которые играют столь важную роль в большинстве интеллектуальных систем, что в значительной степени определяют их качество.
* * *
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Математическая логика — раздел математики, занимающийся изучением схем и принципов рассуждений. Это дисциплина, в которой на основе различных правил и методов определяется корректность аргумента. Логика широко используется в философии, математике и информатике как средство проверки корректности имеющихся утверждений и вывода новых. Математическая логика была создана на основе аристотелевой логики Джорджем Булем, автором новой алгебры, которую впоследствии назвали булевой, и Огастесом де Морганом, сформулировавшим законы логики с помощью новой, более абстрактной нотации.
В последние 50 лет математическая логика пережила бурный рост, и на ее основе возникла современная логика, которую следует отличать от классической логики, или логики первого порядка. Формально логика первого порядка рассматривает только конечные выражения и правильно построенные формулы. В ней нет места бесконечным множествам и неопределенности.
Сколь бы сложными ни казались выражения, записанные на доске, в них очень редко используются символы, значение которых выходит за рамки логики первого порядка.
* * *
В последние годы непрерывно развиваются автоматические рассуждения, и теперь интеллектуальные системы способны рассуждать в условиях недостатка информации (неполноты), при наличии противоречивых исходных утверждений (в условиях неопределенности) или в случаях, когда при вводе новых знаний в систему объем совокупных знаний о среде необязательно возрастает (в условиях немонотонности).
Крайне мощным инструментом для работы в этих областях является нечеткая логика — разновидность математической логики, в которой высказывания необязательно абсолютно истинны или абсолютно ложны. Если в классической математической логике о любом высказывании всегда можно сказать, истинно оно или ложно (к примеру, ложным будет высказывание «некий человек не смертен», а истинным — «все люди смертны»), то в нечеткой логике рассматриваются промежуточные состояния. Так, если раньше говорили, что Крез не беден, это автоматически означало, что он богат, а если говорили, что Диоген не богат, это означало, что он беден (в этом примере классическая логика явно дискриминирует представителей среднего класса!). Применив нечеткую логику, мы можем сказать, что Аристотель богат со степенью, например, 0,6.
* * *
ДЖОРДЖ БУЛЬ (1815–1864) И ЕГО ЛОГИКА
Если Алана Тьюринга называют одним из отцов современной информатики, то Джорджа Буля можно назвать ее дедом. Этот британский философ и математик создал булеву алгебру — основу современной компьютерной арифметики, которая, в свою очередь, является фундаментом всей цифровой электроники.
Буль разработал систему правил, которые посредством математических методов позволяют выражать и упрощать логические задачи, в которых допускается только два состояния — «истина» и «ложь». Три основные математические операции булевой алгебры — это отрицание, объединение («или») и пересечение («и»). Отрицание, обозначаемое символом заключается в смене значения переменной на противоположное. К примеру, если А = «Аристотель — человек», то ¬А = «Аристотель — не человек». Объединение, обозначаемое символом v — это бинарная операция, то есть операция, в которой для получения результата требуются два аргумента. Результатом объединения будет истина, если один из двух аргументов истинный.
К примеру: «Верно ли, что сейчас вы либо читаете, либо ведете машину?». Ответом на этот вопрос будет «Да, верно», поскольку сейчас вы читаете эту книгу. Но если бы вы вели машину и не читали книгу, то ответ также был бы утвердительным. Он был бы утвердительным и в том случае, если бы вы, пренебрегая всеми соображениями безопасности, вели машину и читали эту книгу одновременно.
Третья операция — пересечение, обозначаемая символом , также является бинарной. Если мы переформулируем предыдущий вопрос и скажем «Верно ли, что сейчас вы читаете и ведете машину?», то ответом будет «Да, верно» только в том случае, если вы будете читать за рулем.
На основе трех указанных операций можно определить другие, более сложные, например исключающее «или» (), результат которой в нашем случае будет истинным только тогда, когда мы либо читаем книгу, либо ведем машину, но не выполняем оба эти действия одновременно. Операция не принадлежит к основным операциям булевой алгебры, так как ее можно выразить через три основные операции А В = (А ¬ В) v (¬ А В).
В цифровой электронике «истина» и «ложь» обозначаются единицей и нулем. Этим значениям соответствует наличие электрического тока в цепи (1) либо его отсутствие (0). Логические операции выполняются с помощью сочетаний транзисторов. Именно благодаря применению транзисторов в интегральных схемах в последние 40 лет информатика развивается столь быстрыми темпами.
Микропроцессор вашего домашнего компьютера, который можно назвать его мозгом, содержит сотни миллионов транзисторов, расположенных на площади всего лишь в несколько квадратных сантиметров!
Обработка естественного языка
Понимание человеческого языка и использование его при коммуникации — одна из важнейших нерешенных задач этой области знаний. Если искусственная система сможет понимать как языки программирования, так и человеческий язык, это поможет сделать машины более «человечными». Обработка естественного языка означает не только преобразование звуков в фонемы и письменные знаки, но и понимание смысла сообщаемых понятий (как в письменной, так и в устной форме) и выполнение с ними каких-либо действий.
Первые важные открытия в сфере обработки естественного языка совершил инженер Джозеф Вейценбаум (1923–2008), который в 1964–1966 годах разработал программу «Элиза». Пользователи могли задавать вопросы этой компьютерной программе, моделировавшей работу психотерапевта, а «Элиза», казалось, понимала их смысл, так как выдавала более или менее осмысленные ответы. Ниже приведена запись реального разговора между автором этой книги и «Элизой»:
Игнаси Белда: Мне нужен отпуск.
Элиза: Что означает для тебя отпуск?
Игнаси Белда: Я мог бы проводить больше времени с женой.
Элиза: Расскажи мне подробнее о своей семье.
Игнаси Белда: У меня есть только жена.
Элиза: Ты говоришь, что у тебя только одна жена?
Игнаси Белда: Да, я не полигамен.
Элиза: Ты кажешься позитивным.
Игнаси Белда: Мою жену зовут Лайа.
Элиза: А кто еще принадлежит к твоей семье?
Игнаси Белда: Больше никто.
Элиза: На самом деле никто?
Игнаси Белда: Да.
Элиза: Ты уверен?
Игнаси Белда: Абсолютно.
Как видите, настоящие психологи могут спать спокойно — «Элиза» еще не скоро сможет лишить их работы. Тем не менее с 1960-х годов обработка естественного языка развивается быстрыми темпами, и сегодня существуют методы решения столь разных задач, как определение плагиата, автоматический перевод текстов или очеловечивание интерфейсов взаимодействия людей и машин. Заинтересованный читатель может поговорить с «Элизой» на сайте .
И наконец, управление тем, что известно
Грамотное структурирование знаний крайне важно. Например, представим, что нас спросили, кто занимает должность мэра в американском городе Остин в штате Техас. Если мы не живем в этом регионе США, то наверняка сразу же ответим: «Не знаю». А система, в которой знания структурированы недостаточно хорошо, например любой персональный компьютер, потратит несколько минут на анализ всех документов на жестком диске, чтобы определить, не содержится ли в них имя мэра этого американского города. Интеллектуальная или псевдоинтеллектуальная система должна отвечать на этот вопрос так же быстро и четко, как человек. Для этого знания, хранящиеся в системе, должны быть четко структурированы и легко доступны.
При решении практических задач требуется не только грамотное структурирование знаний, но и наличие адекватных инструментов, позволяющих просматривать сохраненные знания и поддерживать их в упорядоченном виде. Именно эту базу знаний система использует в качестве основы при автоматических рассуждениях, поиске, обучении и так далее. Следовательно, база знаний интеллектуальной системы изменяется, поэтому интеллектуальным системам необходимы средства контроля знаний, которые, к примеру, позволят разрешать возможные противоречия, устранять избыточность и даже обобщать понятия.
Чтобы четко контролировать знания, содержащиеся в базе, необходима метаинформация, описывающая их внутреннее представление. Знать, как представлены знания, очень важно, так как они могут быть структурированы множеством способов, и информация о структуре хранимых знаний может оказаться крайне полезной.
Следует учитывать и разграничение знаний: при работе с нашей базой знаний будет полезна информация о том, какие области и в какой мере эта база охватывает.
Человек легко справится с неполнотой знаний, но информационной системе необходимо очень четко указать, что ей известно, а что — нет. Поэтому одним из первых методов управления базами знаний стало допущение замкнутости мира (англ. CWA — Closed World Assumption). Это допущение предложил Раймонд Рейтер в 1978 году. Он взял за основу простое утверждение, которое, однако, имело важные последствия: «Единственные объекты, которые могут удовлетворять предикату Р, — те, что должны удовлетворять ему». Иными словами, все знания, не зафиксированные в системе, неверны.
Допустим, нас спросили, работает ли некий человек в определенной компании.
Чтобы узнать ответ, мы обращаемся к списку сотрудников, и если нужного человека в списке нет, то говорим, что он не работает в компании.
Допущение замкнутости мира в свое время существенно упростило работу с базами знаний. Однако читатель наверняка догадался, что это допущение имеет важные ограничения: если в реальной жизни нам неизвестен какой-либо факт, это не означает, что он автоматически будет ложным. Вернемся к примеру со списком сотрудников компании. Возможно, человек, работающий в организации, не указан в списке по ошибке или потому, что список устарел? Еще один недостаток допущения замкнутости мира заключается в том, что при работе с ним необходимо использовать чисто синтетические рассуждения.
Представьте, что у нас есть следующих список одиноких людей и людей, состоящих в браке:
Холост (-а) Хуан
Холост (-а) Мария
В браке Давид
Если кто-то спросит систему, холост ли Хорхе, система ответит отрицательно, так как Хорхе нет в списке холостяков. Составим новый список вида:
Не в браке Хуан
Не в браке Мария
В браке Давид
Вновь спросим систему, женат ли Хорхе, и вновь получим отрицательный ответ.
Система не содержит информации о семейном положении Хорхе, поэтому она позволяет сделать противоречивый вывод: Хорхе не одинок и вместе с тем не состоит в браке. Очевидно, что допущение замкнутости мира некорректно применять при неопределенности знаний или в случае их неполноты, поэтому сегодня это допущение используется только в частных случаях.
Наконец, мы не можем закончить разговор о работе с базами знаний, не упомянув о системах поддержки истинности (TMS, от англ. Truth Maintenance Systems).
Эти системы обеспечивают непротиворечивость баз знаний. Они особенно полезны при использовании немонотонных рассуждений, то есть методов, при которых база знаний постепенно увеличивается или уменьшается по ходу рассуждений. Системы поддержки истинности делятся на две группы: системы вертикального поиска и системы горизонтального поиска. Системы первой группы обходят базу знаний в поисках противоречий от общего к частному. При обнаружении противоречия они проходят ранее пройденный путь в обратном направлении. Системы горизонтального поиска, напротив, формулируют различные параллельные сценарии или гипотезы так, что из полученного множества контекстов по мере обнаружения противоречий последовательно исключаются отдельные варианты. Иными словами, для данного возможного контекста (представьте себе определенную позицию в шахматной партии) системы горизонтального поиска определяют сценарии, к которым можно прийти из текущей ситуации (в примере с шахматами этими сценариями будут возможные ходы), и исключают те, что оказываются противоречивыми. В шахматной партии противоречивым сценарием будет ход, при котором компьютер окажется в очень невыгодной позиции, поскольку цель компьютера — одержать победу, а неудачный ход противоречит этой цели.
Глава 2. Поиск
Как создаются новые лекарства? Еще совсем недавно фармацевты готовили медикаменты вручную, а их единственными помощниками были бумага и карандаш.
Они создавали и оптимизировали химическую структуру лекарства и в специальных лабораториях синтезировали и испытывали все новые и новые их версии, чтобы подтвердить, действительно ли возросла эффективность таблеток. Этот метод проб и ошибок отчасти объясняет, почему стоимость разработки нового лекарства в среднем составляет 1 млрд долларов.
При создании нового средства, как правило, синтезируется новая молекула, взаимодействующая с неким белком и в конечном итоге нейтрализующая его действие.
В живых организмах белки участвуют в метаболическом каскаде — последовательности реакций. Следовательно, если молекула нейтрализует действие одного из белков, участвующих в интересующей нас последовательности реакций, каскад будет нарушен, а молекула станет хорошим лекарством.
В этом упрощенном сценарии лекарство препятствует взаимодействию белка-мишени с белком с и нарушает метаболический каскад.
Чтобы нейтрализовать один из этих белков, необходимо, чтобы молекулы лекарства соединялись с ним определенным образом. Следовательно, большая часть усилий при создании нового медикамента направлена на то, чтобы новая молекула присоединялась к активному центру нужного белка — мишени.
Чтобы определить, действительно ли молекула лекарства соединяется с молекулой белка, необходимо измерить энергию их взаимодействия. Энергия взаимодействия между молекулой-кандидатом и белком-мишенью — это энергия, которую необходимо приложить для сохранения связи в системе. К примеру, если мы хотим, чтобы магнит держался на двери холодильника, нам не нужно постоянно прикладывать какую-то силу. Достаточно мощный магнит, только поднеси его к дверце, сам по себе притянется к ней с определенной силой. В этом случае говорят: для того чтобы магнит оставался прикрепленным к дверце холодильника, требуется приложить отрицательную энергию.
Разумеется, молекула лекарства, которая не образует связи с молекулой белка-мишени, не окажет лечебного воздействия: такая молекула будет свободно перемещаться по кровеносной системе или тканям, никак не решая задачу нейтрализации белка. А хорошим лекарством будет соединение, для которого энергия взаимодействия будет отрицательной и минимально возможной, — это говорит нам о том, насколько сильно притягиваются молекулы лекарства и белка. Следовательно, основной параметр, значение которого следует оптимизировать при разработке нового лекарства, это энергия взаимодействия.
Подобные задачи, решение которых заключается в определении ряда оптимальных параметров (например, какой шахматной фигурой нужно сделать ход, чтобы выиграть партию, или какими должны быть положение и размеры балок моста, чтобы снизить стоимость строительства и повысить прочность конструкции), объединяются в категорию задач поиска. При этом часто требуется найти параметры, обеспечивающие максимальное значение некой математической функции. В этом случае поиск называется оптимизацией.
Об этом говорил еще Дарвин
Чаще других для решения задач поиска применяется метод эволюционных вычислений. При этом происходит оптимизация значений функций различной сложности, подобно тому как живые организмы эволюционируют, чтобы повысить выживаемость в окружающей среде.
Идею эволюционных вычислений предложил исследователь Джон Холланд в 1975 году в своей книге «Адаптация в естественных и искусственных системах» (Adaptation in Natural and Artificial Systems). Позднее западные ученые обнаружили, что немецкие инженеры уже использовали подобные стратегии для оптимизации формы сопл первых реактивных двигателей самолетов во время Второй мировой войны. Эволюционные вычисления охватывают широкий спектр методов и алгоритмов, целиком основанных на законах естественной эволюции, предложенных Дарвином. Согласно его законам, лучше всего к жизни в определенной среде подготовлены особи, которые демонстрируют более высокую выживаемость и, как следствие, оставляют больше потомства.
В этой аналогии с законами естественной эволюции особям соответствуют возможные решения задачи. Эволюционные алгоритмы сначала оценивают пригодность каждой «особи», а затем определяют, каким будет их «потомство» — второе поколение решений. В ходе итеративного процесса особи из последующих поколений оцениваются, отбираются и скрещиваются между собой, формируя новые поколения особей. Этот процесс заканчивается после выполнения установленных для задачи критериев останова. Таким образом, любой эволюционный алгоритм состоит из пяти основных этапов: инициализации, оценки, отбора, размножения и замещения, как показано на следующей схеме.
Различия между эволюционными алгоритмами определяются тем, как именно реализован каждый из этих основных этапов.
* * *
ДАРВИН И ЛАМАРК: ДВА РАЗНЫХ ВЗГЛЯДА НА ЭВОЛЮЦИЮ
Жан Батист Пьер Антуан де Моне Ламарк (1744–1829) — французский натуралист, который совершил революцию в биологии, предложив классификацию живых организмов в зависимости от их сложности, а также четко разделив органический и неорганический мир. Еще одним его вкладом в науку стало создание первой биологической теории эволюции, изложенной в книге «Философия зоологии», которая была опубликована в 1809 году, за 50 лет до того, как свою теорию эволюции предложил Дарвин.
Теория Ламарка, в отличие от дарвиновской, основывается на наследовании приобретенных признаков, то есть на способности отдельных особей передавать потомкам приобретенные на протяжении жизни полезные признаки, которые способствуют адаптации к окружающей среде. Различия между теориями эволюции Ламарка и Дарвина прекрасно демонстрирует их объяснение длинной шеи жирафа. Согласно Ламарку, жирафы, которые выше всех вытягивали шею и развивали мышцы, чтобы дотянуться до съедобных листьев на высоких ветках деревьев, передавали этот признак своему потомству, которое продолжало развивать эти мышцы, и в конце концов шеи жирафов достигли нынешних размеров. Согласно теории Дарвина, напротив, жираф, родившийся с самой длинной шеей или с более мощными мышцами, передаст эти признаки потомству независимо оттого, какие усилия он предпринимал при жизни.
Хотя гипотезы Ламарка были отвергнуты в пользу теории Дарвина, не так давно их правильность была подтверждена для некоторых частных случаев. К примеру, известно, что мать, организм которой после пережитой болезни выработал особые антитела, может передать их детям, которые получат иммунитет к этой болезни. Таким образом, здесь мы имеем дело с наследованием признаков, приобретенных при жизни в результате адаптации к окружающей среде.
Карикатура на Ламарка, изображенного в виде жирафа.
Инициализация
Инициализация популяции — отдельный этап, достаточно независимый от используемого эволюционного алгоритма. Инициализация определяется скорее особенностями рассматриваемой задачи — присутствием в ней ограничений, которые следует учитывать, или, напротив, полным отсутствием представления о том, как должно выглядеть «хорошее» решение, в результате чего инициализация выполняется абсолютно случайным образом. Существуют задачи, в которых случайная инициализация предпочтительнее, однако особи первого поколения должны обладать определенными различиями, чтобы охватить все возможные решения.
На этом этапе особенно важно представление знаний об особи, так как оно в значительной степени определит оставшуюся часть эволюционного алгоритма.
Чаще всего особи представляются в виде хромосом. Это новое понятие заимствовано у природы: хромосома представляет собой последовательность генов, а каждый ген — число, обозначающее часть решения.
Рассмотрим в качестве примера алгоритм, цель которого — увеличение емкости картонной коробки при наименьшем расходе картона на ее изготовление. Если мы используем эволюционный алгоритм, то хромосомы, посредством которых мы представим решение, будут иметь три гена: длину, ширину и высоту. При инициализации будет создана популяция коробок произвольных размеров, представленных в виде троек чисел, заключенных в допустимых интервалах. В ходе работы алгоритма популяции коробок будут эволюционировать до тех пор, пока не будет найдена оптимальная коробка в соответствии с установленными критериями.
Оценка
Следующий этап после инициализации — оценка. Обычно считается, что это важнейшая часть эволюционного алгоритма, так как именно она определяет задачу, которую требуется решить. На первом шаге оценки воссоздается решение: информация из хромосомы (генотипа) каждой особи используется для моделирования решения (фенотипа), представленного особью. Целью оценки может быть как простое вычисление объема картонной коробки по известным размерам, как в нашем примере, так и чрезвычайно сложные и дорогостоящие расчеты, к примеру моделирование жесткости конструкции при проектировании моста.
После воссоздания фенотипа необходимо оценить полученное решение. Каждой особи присваивается свое значение приспособленности, которое на последующих этапах эволюционного алгоритма поможет отличить хорошие решения от плохих.
Оценка фенотипов может быть сложной, дорогостоящей и даже зашумленной.
Иными словами, при решении некоторых сложных задач приспособленность одного и того же фенотипа при разных оценках будет различаться. Шум, который также можно назвать ошибкой, неизменно присутствует в задачах, в которых оценка приспособленности используется для численного моделирования. К примеру, при моделировании сопротивления усталости металлов, из которых изготавливаются детали двигателей внутреннего сгорания, решение математических уравнений, описывающих усталость металла, оказывается столь дорогостоящим, что моделирование более выгодно. При этом вполне возможно, что результаты повторного моделирования для каждой детали будут отличаться.
Использование генетических алгоритмов для проектирования деталей двигателей внутреннего сгорания, осуществленное компанией Honda в 2004 году, показало: процесс оценки отличался высоким уровнем шума и неточностью, а также был весьма длительным — расчет приспособленности для каждой особи в популяции занимал восемь часов.
* * *
УПИТАННЫЕ ПТИЦЫ С ОСТРОВА МАВРИКИЙ И ДАВЛЕНИЕ ОТБОРА
Когда исследователи в XVII веке впервые прибыли на остров Маврикий, они обнаружили неожиданный дар небес — упитанных птиц с вкусным мясом, которых стали называть додо. Крылья этих птиц были слишком маленькими, а лапы — слишком короткими, поэтому они не могли ни улететь, ни убежать от охотников. Исследователи безжалостно охотились на додо, а кошки, собаки, крысы и другие животные, завезенные человеком на остров, разоряли гнезда птиц и питались их яйцами.
Додо полностью вымерли менее чем за сто лет, и сегодня эти милые и безобидные птицы известны нам только по рисункам и гравюрам. Додо никогда не испытывали необходимости эволюционировать, а когда они столкнулись с давлением отбора, птицам попросту не хватило времени на то, чтобы справиться с ним. Давление отбора — движущая сила эволюции. Без него живые существа не имеют достаточно стимулов для того, чтобы приспособиться к среде, они не испытывают необходимости развивать оптимальное поведение или другие признаки. В разные годы естествоиспытатели документально описали различные виды, которые, очевидно, находились в похожей ситуации: они обитали в среде, изобиловавшей пропитанием, где отсутствовали хищники, а межвидовая конкуренция была слабой.
Все эти факторы препятствовали появлению признаков, которые были присущи похожим видам, обитавшим в более конкурентных средах.
В отсутствие хищников и при избытке пропитания в изолированной экосистеме острова додо не нужны были сильные крылья и мощные лапы. Кстати, в дословном переводе с португальского «додо» означает «глупый». Кто знает, возможно, додо стали «глупыми» именно из-за того, что отсутствовало давление отбора?
Додо на гравюре XVII века.
Отбор
Следующий этап эволюционного алгоритма, выполняемый после оценки особей текущего поколения, — это отбор. Его цель — выделить лучших особей, которые оставят потомство. Процесс отбора лучших особей является основой естественной эволюции. Интенсивность этого процесса называется давлением отбора. Давление отбора тем больше, чем меньше доля особей, переходящих в следующее поколение.
Однако можно доказать, что если мы применим столь простую стратегию, как прямой отбор лучших особей, то давление отбора будет слишком велико. При значительном давлении отбора эволюционные алгоритмы обычно работают не слишком хорошо, так как завершают работу на локальных, а не глобальных оптимумах.
Главное преимущество эволюционных алгоритмов — возможность получить хорошие решения на больших областях поиска, или, говоря математическим языком, возможность найти оптимумы функций, как правило, многомерных и имеющих несколько локальных или глобальных максимумов. Если давление отбора при эволюционной оптимизации слишком велико, то есть если мы хотим найти решение слишком быстро, для чего выберем лучших особей и ограничимся поверхностным рассмотрением, то алгоритм завершит работу слишком рано, а его результатами будут локальные, а не глобальные оптимумы.
Этап отбора идеально подходит для моделирования давления отбора в эволюционных алгоритмах. В пределе, когда давление отбора будет наибольшим, производится единичный отбор — иными словами, из текущего поколения выбирается только одна особь, на основе которой образуется следующее поколение. Другим предельным случаем будет полностью случайный отбор, при котором приспособленность особей не учитывается. Логично, что следует выбрать некую промежуточную стратегию, при которой производится отбор лучших особей для размножения и вместе с тем присутствует некоторая степень случайности, позволяющая рассмотреть альтернативные варианты. При такой стратегии с определенной вероятностью может быть выбрана любая, даже самая неприспособленная особь. Сегодня применяются три стратегии отбора, обладающие этими свойствами: рулетка, ранговая селекция и турнирная селекция.
Метод селекции, основанный на принципе колеса рулетки, достаточно прост. Он заключается в том, что каждая особь может быть выбрана с вероятностью, пропорциональной ее приспособленности по отношению к приспособленности остальных особей. Следовательно, если нужно отобрать 10 особей, колесо рулетки потребуется вращать 10 раз.
В примере на рисунке представлено восемь особей и значения их функции приспособленности в процентах от целого. Как вы можете догадаться, при каждом вращении рулетки вероятность выбора определенной особи будет пропорциональной отношению ее значения функции приспособленности к целому. Метод рулетки не исключает возможность выбора менее приспособленных особей — они всего лишь будут выбираться с меньшей вероятностью. Если мы будем вращать колесо рулетки 10 раз, то несколько раз обязательно выберем приспособленных особей, но также вероятно, что несколько раз выбранные особи будут не самыми конкурентоспособными. Именно возможность выбора неконкурентоспособных особей делает генетические алгоритмы столь мощными: это позволяет следовать несколькими путями одновременно, открывать другие варианты, выявлять множество различных максимумов, а в долгосрочной перспективе — находить хорошее локальное решение, а в лучшем случае — глобальный максимум.
Еще одна стратегия отбора, пригодная для решения сложных задач, — это ранговая селекция. При ее использовании отбирается n копий наиболее приспособленной особи, n — 1 — второй по порядку и так далее до n = 0. Эта стратегия исключает вероятность того, что некая «сверхособь» снизит вероятность отбора прочих особей.
(«Сверхособью» называется особь, далекая от оптимальной, но намного превышающая по своим параметрам прочих особей из своего поколения.) Наличие сверхособей приводит к тому, что популяция оказывается скученной возле нее, и улучшить результаты становится невозможно.
Третья стратегия, турнирная селекция, заняла монопольное положение среди стратегий отбора, используемых при решении реальных задач, благодаря выгодным математическим свойствам и высокой гибкости при моделировании давления отбора. При турнирной селекции используется тот же принцип, что и при объединении спортивных команд в пары при игре на выбывание. Особи отбираются попарно случайным образом, и оптимальной считается та особь, которая побеждает в этом воображаемом турнире. Следовательно, при турнирной селекции необходимо отобрать столько пар, сколько особей необходимо выбрать. Почему эта стратегия считается очень гибкой при моделировании давления отбора? Что произойдет, если мы будем организовывать «турниры» не между двумя, а между n особями? Что если в турнире будет одерживать верх не одна, а m особей? В таком случае говорят, что проводится турнир n: m. С увеличением n давление отбора будет повышаться, с увеличением m — понижаться.
Чтобы лучше понять схему проведения турнира, представьте себе начальные этапы футбольной Лиги чемпионов. Они проводятся по схеме 4:2 — футбольные команды объединяются произвольным образом в группы по четыре, а две лучшие переходят в следующий этап. Конечно, в примере с Лигой чемпионов нельзя говорить о действительно случайном турнире, так как при формировании групп учитываются определенные критерии — так, в одну группу не могут попасть две команды из одной страны. Однако мы тоже можем вводить свои правила при использовании эволюционных алгоритмов, что будет определять тот или иной тип эволюции.
Часто используется правило, согласно которому в одном турнире соперничают максимально похожие особи. Алгоритм способен находить оптимальные значения функции со множеством оптимумов.
Эти роботы-крабы определяют участки с максимальной освещенностью. У одного из этих роботов нет ног, у другого их сразу четыре. Создатель роботов, Джош Бонгард из Вермонтского университета, описал их поведение с помощью эволюционного генетического алгоритма и смог показать, что они действовали лучше, чем классические роботы, созданные с той же целью.
Размножение
После отбора особей, которые оставят потомство, наступает этап размножения.
Существует несколько систем размножения, которые необязательно являются важнейшими составляющими эволюционных алгоритмов, но на самом деле конкретный эволюционный алгоритм получает свое название в зависимости от того, какая система размножения в нем используется. К примеру, генетические алгоритмы, о которых мы поговорим чуть позже, представляют собой эволюционные алгоритмы, в которых для размножения особей применяется скрещивание с мутациями.
Генетические алгоритмы — самые популярные среди всех эволюционных алгоритмов благодаря тому, что они оптимально сочетают сравнительно невысокую сложность программирования и хорошие результаты. Размножение путем скрещивания с мутациями тесно связано с основными понятиями генетики. В генетическом алгоритме каждая особь представлена хромосомой, а каждая хромосома представляет собой последовательность генов. При скрещивании хромосом двух особей сначала случайным образом определяется точка, которая делит хромосомы на две половины.
Далее эти четыре половины (две для каждой из родительских особей) скрещиваются между собой, и образуется два потомка. Первый потомок содержит первую половину хромосомы первой родительской особи (назовем ее отцом) и вторую половину хромосомы второго родителя (матери). Второй потомок будет содержать первую половину хромосомы матери (до точки пересечения) и вторую половину хромосомы отца.
После получения потомства проводится мутация, при которой с очень маленькой вероятностью (как правило, около 5 %) несколько генов в новых хромосомах изменяются случайным образом. В теории и на практике можно показать, что без мутаций генетические алгоритмы не слишком способствуют оптимизации — результатами их работы обычно становятся субоптимумы функции, то есть локальные максимумы. Благодаря мутациям генетические алгоритмы совершают небольшие случайные прыжки в пространстве поиска. Если результаты этих прыжков окажутся не слишком многообещающими, то в ходе эволюции они будут отброшены, в противном случае — закрепятся в наиболее приспособленных особях следующих поколений.
* * *
ГРЕГОР МЕНДЕЛЬ И ГЕНЕТИКА
Австрийский монах Грегор Мендель (1822–1884) открыл и в 1866 году опубликовал первые законы наследования. Эти законы, открытые по результатам скрещивания нескольких видов гороха и известные сегодня как законы Менделя, описывают передачу определенных признаков от родителей к потомкам. С открытием этих законов в генетике и науке вообще появилось важное понятие — доминантные и рецессивные гены.
Мендель в ходе своих экспериментов зафиксировал окрас горошин у различных видов гороха. Первое поколение он получил путем скрещивания растений, приносивших желтые горошины, с растениями, приносившими зеленые горошины. Мендель заметил, что растения, полученные в результате скрещивания, имеют только желтые горошины. Но позднее он обнаружил, что при скрещивании этих растений между собой растения следующего поколения в большинстве своем имеют желтые горошины, однако, к удивлению ученого, у некоторых растений горошины вновь имели зеленый цвет. Соотношение растений с желтыми и зелеными горошинами равнялось 3:1. Проведя аналогичные эксперименты для других признаков, Мендель пришел к выводу: существуют гены, которые доминируют над другими и тем самым подавляют их проявление.
Существование доминантных и рецессивных генов объясняло, почему скрещивание особей с одним и тем же выраженным геном может давать потомство с другим выраженным геном — оба родителя являются носителями рецессивного гена, который подавляется доминантным. Несмотря на то что в свое время труды Менделя не получили широкой известности, в них были заложены основы генетики — науки, которая сыграла определяющую роль в развитии современной медицины.
Замещение
Завершающий этап эволюционного цикла — замещение. Его цель — выбрать, какие особи из предыдущего поколения будут замещены новыми, полученными на этапе размножения. Чаще всего заменяются все особи из предыдущего поколения, за исключением лучшей, которой дается возможность «прожить» еще одно поколение. Этот метод, известный как элитизм, несмотря на крайнюю простоту и некоторую неестественность, оказался удивительно эффективным.
Также было предложено множество других стратегий замещения особей. Обратите внимание, что вновь, как и на этапе отбора, можно смоделировать то или иное давление отбора в зависимости от того, как будут выбираться особи для замещения.
Если мы всегда будем выбирать всех особей популяции и замещать их новыми, давление отбора будет отсутствовать. А если мы будем отбирать только неприспособленных особей популяции для замещения, то давление отбора крайне возрастет.
С другой стороны, на этом этапе также эффективны политики видообразования, то есть методы, упрощающие определение различных решений для задач с несколькими оптимумами. Наиболее популярным среди таких методов является метод замещения посредством цитирования (niching). Суть его состоит в том, что для каждой новой полученной особи производится отбор особей предыдущего поколения, сильнее всего схожих с ней. В следующее поколение переходит только лучшая из этой группы схожих особей.
Мы рассказали о некоторых наиболее популярных методах, применяемых на каждом из этапов эволюционных алгоритмов. Следует понимать, что существует и множество других методов.
* * *
ЭВОЛЮЦИОННЫЕ АЛГОРИТМЫ ЛАМАРКА
Двойственность теорий Дарвина и теорий Ламарка проявляется и в эволюционных алгоритмах.
Отметим, что обе теории оказались крайне эффективными для решения задач оптимизации. Чаще всего используются дарвиновские эволюционные алгоритмы, описанные в этой главе, а алгоритмы, созданные согласно теориям Ламарка, содержат дополнительный этап между оценкой и отбором. Этот этап заключается в краткой локальной оптимизации, имитирующей обучение или адаптацию особи к окружающей среде перед достижением репродуктивного возраста.
Локальная оптимизация, как правило, представляет собой небольшие мутации, применяемые к каждой особи. После мутации оценивается изменение приспособленности. Если приспособленность повысилась, мутация подтверждается, и цикл «мутация-оценка» повторяется вновь.
Если же мутация привела к снижению приспособленности особи, она отвергается, после чего цикл «мутация-оценка» повторяется начиная с состояния, предшествовавшего мутации. Первые эволюционные алгоритмы, построенные согласно теории Ламарка, получили название эволюционных стратегий. Как мы уже упоминали, они использовались немецкими инженерами во время Второй мировой войны для оптимизации сопл двигателей первых реактивных самолетов.
Практический пример: поиск эффективного лекарства
Как вы уже увидели, используя методы оптимизации, основанные на природных процессах, ученые добились огромных успехов в области искусственного интеллекта. Не так давно эволюционные вычисления при изготовлении лекарств позволили добиться заметных успехов. Напомним, что при создании медикаментов целью исследователей является подбор соединения, для которого энергия связи с определенным белком будет отрицательной и минимально возможной. Искомое соединение должно сформировать внутри нашего организма неразрывную связь с белком-мишенью, чтобы их неодолимо тянуло друг к другу, как сладкоежек тянет к карамели.
Рассмотрим, как действует эволюционный алгоритм при оптимизации молекул во время разработки лекарств. Сначала требуется инициализировать популяцию молекул. На этом этапе молекулы обычно формируются случайным образом. Для простоты будем рассматривать поколения всего из трех молекул, хотя обычно их число в одном поколении достигает нескольких сотен.
Далее произведем оценку молекул, рассчитав энергию взаимодействия каждой из них с белком-мишенью. Для этого используются различные вычислительные методы. Один из них (мы не будем подробно описывать принцип его действия) называется молекулярным докингом — это трехмерное моделирование, в ходе которого оценивается, сможет ли молекула образовать связь при встрече с мишенью и какой будет энергия этой связи. Возникает любопытная ситуация: при использовании эволюционного алгоритма для поиска идеальной молекулы на одном из его этапов мы вновь применяем эволюционный алгоритм, чтобы оценить качество молекулы по сравнению с остальными. Результатом докинга являются оцененные молекулы.
Следующий этап — отбор, который можно организовать, например, путем турнирной селекции. В ходе турнирной селекции случайным образом формируются пары молекул, после чего производится оценка их энергии взаимодействия и принимается решение о том, какие молекулы останутся, а какие — отсеются. Напомним, что энергия взаимодействия должна быть отрицательной и принимать минимально возможное значение.
Следующий этап эволюционного алгоритма — размножение, в ходе которого на основе отобранных молекул создаются новые, сочетающие в себе свойства молекул предыдущего поколения. Так, путем скрещивания двух молекул, отобранных на предыдущем шаге, создаются две новые молекулы.
На следующей иллюстрации показано, как две молекулы делятся.
И, наконец, путем соединения частей этих молекул образуются две новые молекулы.
На этапе замещения особи первого поколения замещаются новыми, созданными на предыдущем этапе. Наиболее популярный и простой метод замещения — элитизм, при котором замещаются все молекулы предыдущего поколения за исключением одной, наиболее приспособленной. В нашем случае новое поколение будет состоять из двух молекул, полученных в результате скрещивания, и одной молекулы из предыдущего поколения с энергией взаимодействия, равной —8.
После замещения эволюционный цикл завершается и повторяется необходимое число раз. Иными словами, дальше производится оценка молекул второго поколения, затем среди них отбираются лучшие, и так далее, после чего формируется третье поколение молекул. Процесс повторяется, пока не будет достигнуто заранее определенное число поколений или популяция не сойдется, то есть 90 % особей не будут представлять собой одну и ту же молекулу.
Разумеется, мы приводим упрощенное описание процесса, а в действительности все обстоит намного сложнее. Но скажите, разве сам процесс не прекрасен?
Глава 3. Машинное обучение
Четверг, 6 мая 2010 года, 9:30 утра. Начинаются торги на американских фондовых биржах. Этот день ничем не отличался от остальных: утренняя сессия прошла без каких-либо аномалий. Но в 14:45 без явной причины некоторые самые важные рыночные котировки за несколько секунд обвалились. Даже с учетом высокой волатильности, характерной для финансовых рынков в период нестабильности, этот обвал был достаточно неожиданным: акции некоторых наиболее крупных и надежных компаний потеряли в цене более 60 %, а весь американский и, как следствие, мировой финансовый рынок обрушился за несколько минут. Индекс Доу-Джонса (один из наиболее популярных биржевых индексов) потерял 9,2 %, что стало крупнейшим падением в течение одного дня торгов за всю историю (этот день позже будет назван черным вторником). Позднее падение стабилизировалось, и индекс снизился «всего» на 3,2 %, но в результате за несколько секунд безвозвратно исчезли триллионы долларов.
Первые признаки обвала были обнаружены на Нью-Йоркской фондовой бирже.
Было предложено множество объяснений, но точная причина черного вторника до сих пор неизвестна. Согласно одной из гипотез, которую поддерживает большинство финансовых аналитиков, причиной обвала стала деятельность высокочастотных трейдеров (HFT — от англ. High Frequency Traders), однако рыночные регуляторы традиционно отвергали эту версию. Высокочастотные трейдеры — это автоматические интеллектуальные системы купли-продажи акций и финансовых инструментов, способные принимать решения в течение нескольких микросекунд. Сегодня системами высокочастотной торговли совершается 50 % всех международных финансовых операций.
Но как может информационная система, интеллектуальная или нет, принимать столь масштабные решения так быстро? Любой начинающий инвестор знает, что котировки ценных бумаг на финансовых рынках зависят от бесконечного множества социальных, экономических и политических факторов, начиная от последних заявлений финского министра занятости о регулировании труда в стране и заканчивая непредвиденным снижением спроса на сырье в связи с потеплением на юге Германии. Как может информационная система учитывать такой объем информации, чтобы принимать, казалось бы, интеллектуальные решения о покупке или продаже акций, причем всего за несколько секунд? Вот в чем вопрос.
Машинное обучение — один из главнейших столпов искусственного интеллекта. Мы не осознаем этого, но большинство сценариев, с которыми мы сталкиваемся каждый день, полностью контролируются мыслящими машинами. Но прежде чем начать работу, машины должны пройти обучение.
Пример обучения: диагностика опухолей
Диагностика опухолей — один из примеров, когда искусственный интеллект может оказаться крайне полезным. Прохождение маммографии с целью предотвращения рака груди является (или должно быть) регулярной практикой для взрослых женщин. Маммография — это всего лишь радиография молочных желез, позволяющая распознать аномалии, которые могут быть злокачественными опухолями. Поэтому всякий раз, когда радиолог при маммографии выявляет подобную аномалию, он проводит более подробный анализ, для которого требуется биопсия, или изъятие тканей из организма — намного более дорогостоящая и болезненная процедура, чем маммография.
Положительные результаты биопсии в 10 % случаев оказываются ложными — иными словами, при маммографии обнаруживается аномалия, однако биопсия не показывает никаких следов опухоли. Поэтому врачам крайне важно иметь в своем распоряжении средства, позволяющие свести к минимуму эти 10 % ложноположительных результатов, — чтобы снизить не только расходы на здравоохранение, но и стресс от обследования.
С другой стороны, наблюдаются и ложноотрицательные результаты, когда маммография не показывает никаких аномалий, но у пациента уже развилась опухоль. Крайне важно, чтобы новые средства диагностики позволяли снизить число как ложноположительных, так и ложноотрицательных случаев. Как вы узнаете чуть позже, снизить число ложноотрицательных случаев намного сложнее, чем ложноположительных, при этом последствия ложноотрицательных случаев намного серьезнее.
Представьте, что онколог анализирует результаты маммографии пациента, чтобы определить наличие признаков опухоли. В общем случае он выполняет следующие действия.
1. Анализ результатов маммографии и выявление наиболее важных параметров с целью определения новой проблемы. Множество выявленных параметров позволяет описать сложившуюся ситуацию.
2. Поиск иных результатов маммографии, обладающих похожими свойствами, которые были ранее получены самим врачом или приведены в специальной литературе.
3. Установление диагноза с учетом диагнозов для множества схожих результатов маммографии.
4. Наконец, при необходимости консультация с коллегами для подтверждения диагноза.
3. Запись диагноза в базу для последующего использования в будущем.
Описанная процедура полностью совпадает с одним из самых популярных методов прогнозирования, используемых в искусственном интеллекте, называется он «рассуждение по прецедентам», или CBR (от англ. Case-Based Reasoning). Рассуждение по прецедентам заключается в решении новых задач путем поиска аналогий с уже решенными задачами. После того как выбрано наиболее схожее решение, оно адаптируется к особенностям новой задачи, поэтому рассуждение по прецедентам помогает не только анализировать данные, но и достигать более общей цели — интеллектуального решения задач на основе анализа данных.
* * *
ХАРАКТЕРИСТИКИ, ИСПОЛЬЗУЕМЫЕ ПРИ ОБНАРУЖЕНИИ ОПУХОЛЕЙ ГРУДИ
Рассуждение по прецедентам, подобно другим интеллектуальным методам, может применяться для обнаружения злокачественных опухолей при маммографии. Так как входными данными в любом из подобных методов являются числа, необходим промежуточный этап, который заключается в автоматическом извлечении числовых данных из медицинских изображений. При обнаружении опухолей груди обычно производятся измерения некоторых часто встречающихся элементов молочных желез, называемых микрокальцинатами, которые представляют собой микроскопические скопления кальция в тканях. Для обнаружения злокачественных микрокальцинатов в молочных железах обычно используются следующие характеристики: площадь, периметр, компактность (соотношение между площадью и периметром), число отверстий, неровность (величина, описывающая неправильную форму микрокальцината), длина, ширина, вытянутость (соотношение между длиной и шириной) и положение центра тяжести микрокальцината.
* * *
Подобно тому как эксперт хранит накопленные знания в памяти или в блокнотах, в рассуждении по прецедентам используется структура данных под названием «память прецедентов», где хранятся ранее проанализированные случаи. Схема рассуждения по прецедентам представлена на следующем рисунке.
Первая фаза рассуждения по прецедентам, извлечение, состоит в поиске в памяти прецедентов решений задач, наиболее схожих с текущей. В нашем примере цель извлечения — найти прошлые результаты маммографии, по своим характеристикам схожие с полученными при обследовании.
Далее проводится адаптация — попытка адаптировать обнаруженное решение к рассматриваемому случаю. Предположим, что логистической компании необходимо перевезти груз из Лиссабона в Рим, и для оптимизации маршрута используется рассуждение по прецедентам. На первом этапе в памяти прецедентов будет произведен поиск ранее выполненных перевозок по наиболее похожим маршрутам.
Допустим, в памяти прецедентов содержится уже оптимизированный маршрут между Мадридом и Миланом. Следовательно, большая часть нового маршрута будет уже известной, и останется лишь оптимизировать путь от Лиссабона до Мадрида и от Милана до Рима. Оптимизацию этих двух небольших частей общего маршрута можно провести другими, классическими методами. Использование уже известного маршрута Мадрид — Милан при прокладке нового маршрута Лиссабон — Рим и представляет собой суть этапа адаптации.
Далее выполняется проверка, в ходе которой эксперт-человек анализирует диагноз, поставленный машиной. На этом этапе человек и машина работают вместе, что способствует непрерывному улучшению качества работы машины и повышению точности результатов. Диагностирование раковых опухолей крайне важно, поэтому руководители системы здравоохранения не передают решение этой задачи автоматическим средствам, не требующим участия человека.
На последнем этапе рассуждения по прецедентам следует определить, стоит ли включать решение, утвержденное экспертом, в память прецедентов? Иными словами, достаточно ли оно репрезентативно, чтобы включить его в набор результатов маммографии, которые будут использоваться для диагностики опухолей в будущем?
Итог рассуждений по прецедентам (и рассуждений эксперта) будет успешным только при корректном прохождении всех четырех перечисленных этапов. На каждом из этапов необходимо учитывать следующие основные аспекты.
— Критерий извлечения: не все предыдущие результаты одинаково полезны.
Следует определить, какие прецеденты нужно выбрать при рассмотрении нового случая. Для этого необходимо ввести метрики, или расстояния, позволяющие оценить схожесть нового случая и тех, что хранятся в памяти. К примеру, при анализе результатов маммографии для нового случая с помощью этих математических метрик определяется, какой из уже известных результатов больше всего схож с анализируемым.
— Критерий достоверности: для каждой предметной области характерны определенная сложность и уровень риска. В примере с диагностированием опухолей очевидно, что цена, которую необходимо заплатить в случае ложноотрицательного результата, намного выше, чем если врач посчитает доброкачественную опухоль злокачественной. Поэтому крайне важно иметь механизмы определения критериев, позволяющих гарантировать достоверность результата.
— Критерий проверки: проверка предложения требует вмешательства эксперта. В примере с анализом результатов маммографии в силу особой важности процедуры проверку производит эксперт-радиолог.
— Критерий сохранения знаний: способность решать задачи напрямую связана с имеющимся опытом их решения. Следовательно, необходимо четко обеспечить непротиворечивость знаний как при включении новых случаев, так и при устранении уже имеющихся, вносящих противоречия.
Все перечисленные выше аспекты имеют общую основу — накопленный опыт системы. Желательно, чтобы память прецедентов обладала следующими свойствами:
— компактность: память не должна содержать ни избыточных случаев, ни шума, иначе рассматриваемая ситуация будет искажена, а при подборе случаев, наиболее схожих с рассматриваемым, возникнут ошибки;
— репрезентативность: нельзя решить задачу, о которой ничего не известно, поэтому необходимо иметь репрезентативные примеры всех возможных аспектов предметной области. Только так мы гарантируем, что наше видение реальности при решении задачи будет полным;
— ограниченность: скорость работы системы напрямую зависит от того, с каким числом элементов она работает. Размер памяти определяет, способна ли система дать ответ в разумное время.
Три вышеперечисленных свойства можно свести к следующей предпосылке: необходимо располагать минимально возможным множеством независимых инцидентов, полностью описывающих предметную область.
Еще один пример: онлайн-маркетинг
С ростом популярности интернета маркетинг радикально изменился, и сегодня на смену массовому маркетингу пришел персонализированный. К примеру, когда вы открываете интернет-сайты, то видите перед собой рекламные объявления или баннеры, которые не являются ни случайными, ни статическими — напротив, различные инструменты анализируют поведение пользователя и отображают ему персонализированную рекламу в зависимости от его текущих интересов.
Каждый, кто получал электронную почту в Gmail, почтовом сервисе Google, замечал, что сбоку всегда показывается реклама, связанная с содержанием полученного письма. А если вы на прошлой неделе искали гостиницу в Париже, то не удивляйтесь, если сегодня на одной из интернет-страничек перед вами появится реклама таких гостиниц.
Все механизмы, которые использует Google и другие компании этой сферы для управления онлайн-маркетингом, представляют собой интеллектуальные инструменты, которые мгновенно и автоматически, без вмешательства человека, принимают решения о том, какую рекламу показать пользователю. Если бы в этом процессе каким-то образом участвовали люди, то выполнить в секунду десятки миллионов маркетинговых действий было бы невозможно, а речь ведь идет о цифрах именно такого порядка.
Многие считают наиболее интеллектуальным средством онлайн-маркетинга механизм предложения похожих книг, используемый компанией Amazon. Этот же механизм используют в похожих целях и другие компании, например компания Yahoo в своем Radio LAUNCHcast, где песни, положительно оцененные пользователем, фиксируются в его профиле, и в будущем система предлагает песни, которые прослушали и положительно оценили другие пользователи с похожими профилями.
Действие этой системы можно увидеть на сайте Amazon всякий раз, когда вы ищете какой-то определенный товар: независимо от того, зарегистрированы вы на сайте или нет, вы увидите раздел «Купившие этот товар также покупают» («Customers who bought this item also bought…»). Этот механизм, кажущийся тривиальным, на самом деле крайне сложен и относится к искусственному интеллекту. Он вовсе не ограничивается простым просмотром корзин покупок других пользователей, которые приобрели просматриваемый вами товар.
Раздел «Похожие товары» на странице интернет-магазина Amazon.
Классическое средство решения задач такого типа — так называемые байесовские сети. Крупнейший в мире научно-исследовательский институт, занимающийся изучением байесовских сетей, — это Microsoft Research Institute, где рассматриваются возможности их применения не только в онлайн-маркетинге, но и в других областях. В частности, байесовские сети применяются для автоматической адаптации интерфейса Windows в зависимости от особенностей работы и предпочтений пользователя.
Идея, на которой основаны байесовские сети, такова: существуют цепочки событий, которым с определенной вероятностью сопутствуют другие цепочки событий.
Именно поэтому байесовские сети называют сетями — они представляют собой сплетенные друг с другом цепочки вероятностных зависимостей. Рассмотрим пример с покупкой книг.
* * *
ДРУГИЕ СПОСОБЫ ИСПОЛЬЗОВАНИЯ АВТОМАТИЧЕСКОГО МАРКЕТИНГА
Автоматический маркетинг применяется не только в интернете: сегодня его используют банки, телекоммуникационные компании и даже супермаркеты. К примеру, кто не видел скидочные купоны в супермаркетах, где мы делаем покупки на неделю? Логично, что нам обычно дают купоны не на товары, которые мы и так всегда покупаем (разумеется, при условии, что скидочная программа организована правильно), а на товары, которые выбирают другие покупатели примерно с тем же набором покупок, что и мы. Таким образом мы узнаем о товарах, которые никогда раньше не покупали, и после первой покупки они могут занять постоянное место в нашей корзине. Подобным образом действуют и другие компании, в частности в сфере финансов и телекоммуникаций: с учетом нашего профиля они часто предлагают новые продукты, которые, возможно, будут нам интересны.
Супермаркет в Нью-Йорке.
* * *
В представленной сети видно, что 98 % клиентов, купивших книгу «Я, робот», также приобрели роман «Основание». И напротив, ни один из тех, кто купил «Дюну», не приобрел «Гордость и предубеждение», поэтому между этими двумя книгами не существует никакой связи. Если система обнаруживает, что клиент недавно купил книгу «Я, робот» и теперь ищет информацию о книге «Основание», в разделе рекомендаций он увидит «Дюну» и «Контакт», так как их приобрела значительная доля покупателей, купивших первые две книги. Все вышеперечисленные действия образуют индивидуальную маркетинговую кампанию для каждого клиента, цель которой — повышение продаж. В ходе этих кампаний покупателям автоматически предлагаются два товара, о существовании которых они, возможно, и не подозревали. Система располагает обширной информацией о прошлых покупках и формирует представленную выше сеть причинно-следственных связей для рекомендации новых товаров.
Системе также известно, что рекламировать «Гордость и предубеждение» тому,
кто покупает научно-фантастические романы (а именно это происходит при классических маркетинговых кампаниях), — пустая трата времени. В рамках традиционной маркетинговой кампании выход нового издания «Гордости и предубеждения» мог быть объявлен, к примеру, в тематической программе о книгах, выходящей в эфир в 23:00 на канале, посвященном культуре. Но даже если бы маркетологи верно выбрали программу и время ее выхода в эфир так, чтобы ее с большой вероятностью посмотрели люди, заинтересованные в продукте, на многих любителей научной фантастики реклама не произвела бы никакого эффекта. При использовании статического канала маркетинга, например телевидения, радио или афиш на улицах, рекламодатель не может определить индивидуальный профиль клиента. И даже если профиль клиента известен, рекламодатель не располагает необходимыми средствами для того, чтобы адаптировать рекламу для каждого из нас.
Мозг робота: нейронные сети
Робототехника — одна из самых сложных областей инженерии, и не только потому, что в простой руке робота используется множество сервоприводов и электронных устройств. Ее сложность связана с тем, что траектории движения подвижных частей робота определяются путем сложных математических расчетов. В некоторых случаях все расчеты выполняются в искусственном мозге робота, состоящем, подобно мозгу высших живых организмов, из нейронных сетей. Но в случае с роботами речь идет об искусственных нейронах.
Схематичное изображение нейрона человеческого мозга.
Понятия «нейронная сеть» и «искусственный нейрон» появились не так давно, и эйфория по отношению к ним уже не раз сменялась разочарованием. Эти понятия возникли как составляющие алгоритма Threshold Logic Unit (блок пороговой логики), который был предложен Уорреном Маккалоком и Уолтером Питтсом в 1940-е годы и имел большой успех. Искусственный нейрон, по сути, представляет собой инкапсуляцию указанного алгоритма. Специалисты описывают искусственный нейрон следующим образом:
Вход1 —> X1
Вход2 —> Х2
…
Входi —> Xi
Если > Пороговое значение,
то Выход <— 1
иначе Выход <— 0
На обычном языке это означает: нейрон возбуждается тогда и только тогда, когда стимул, то есть сумма произведений (Xi∙Весi), превышает определенное пороговое значение.
Как вы можете видеть, нейрон крайне прост, поскольку требует лишь нескольких арифметических действий и одну операцию сравнения. Простота искусственных нейронов способствовала их реализации в микрочипах. К концу 90-х годов стала возможной полная реализация искусственных нейронных сетей исключительно в аппаратном обеспечении. Сегодня эти микрочипы используются при изготовлении электронных прогнозных устройств, к примеру, приборов, позволяющих определить причину недомогания плачущего ребенка.
Искусственный нейрон функционирует аналогично естественному. Но основная сложность нейронных сетей заключается в двух элементах, которые должны согласовываться между собой. Именно от них зависит, сможет ли нейронная сеть делать более или менее точные прогнозы. Эти два элемента — вес входных сигналов и пороговое значение. Трудоемкая корректировка этих значений, по результатам которой для ряда входных значений нейрон должен выдавать желаемое выходное значение, называется обучением. Прорыв в обучении нейронов совершил Фрэнк Розенблатт в конце 1950-х, предложив модель нейрона, способного корректировать веса и пороговое значение. Модель Розенблатта получила название перцептрон.
С точки зрения биологии реальный нейрон ведет себя почти так же: каждый нейрон имеет множество входов, куда поступают электрические сигналы от других нейронов (соединения между нейронами называются синапсами), затем определяется, превышают ли эти стимулы порог чувствительности. При этом следует учитывать, что некоторые синапсы важнее других (важность синапсов описывается с помощью весов, о которых мы упоминали выше). Если порог чувствительности превышен, то по аксону проходит электрический сигнал (в случае с искусственным нейроном аналогом этого сигнала будет выходное значение).
Перцептрон оказался полезным при прогнозировании: он способен предсказать, к какому классу принадлежит заданная выборка. Классическим примером является задача о растениях рода ирис, в которой рассматриваются выборки трех видов: ирис щетинистый (Iris setosa), ирис разноцветный (Iris versicolor) и ирис виргинский (Iris virginica). Каждая выборка описывается четырьмя параметрами: длиной и шириной лепестков, длиной и шириной чашелистиков. Цель задачи — определить, к какому виду принадлежат растения из новой выборки. Для решения будем использовать три перцептрона, каждый из которых настроен на обнаружение одного из трех видов. Таким образом, если новая выборка содержит растения вида ирис щетинистый, то всего один перцептрон вернет значение 1, два других — 0.
По порядку: ирис щетинистый, ирис разноцветный и ирис виргинский.
В зависимости от формы и размеров лепестков и чашелистиков система способна определить, к какому виду принадлежат цветы.
Читатель, возможно, задается вопросом: почему для решения задачи об ирисах нельзя использовать методы статистики? И действительно, эта задача так проста, что ее можно решить классическими методами статистики, к примеру, методом главных компонент. Но обратите внимание, что перцептрон и статистические методы описывают две принципиально различные схемы рассуждений, и описанная перцептроном, возможно, точнее соответствует естественным рассуждениям.
При решении задачи об ирисах методами статистики мы получили бы правила вида «если длина лепестков находится на интервале между указанными значениями, а ширина — между другими указанными значениями, весьма вероятно, что выборка принадлежит к виду Х». Перцептрон же рассуждает следующим образом: «если длина лепестков находится на интервале между указанными значениями, а ширина — между другими указанными значениями, весьма вероятно, что выборка принадлежит к виду X. Но если чашелистики слишком коротки, то размеры лепестков уже не имеют значения, так как выборка будет принадлежать к виду У».
Иными словами, при взвешивании входных значений для принятия решений одни данные могут иметь больший вес, чем другие, однако при достижении предельных значений входные данные, ранее считавшиеся неважными, начинают играть важную роль.
Нейроны группируются…
Несмотря на прорыв, которым стало открытие перцептрона и грандиозные перспективы его применения, ученые вскоре обнаружили: перцептроны нельзя использовать для решения линейно неразделимых задач (к несчастью, именно к этой группе относится большинство задач реальной жизни). По этой причине в 1980-е годы в адрес нейронных сетей прозвучало немало критики, а участники дебатов порой переходили от научных рассуждений к личным оскорблениям оппонентов.
К великому разочарованию ученых, эти споры пришлись на «темные века» в истории искусственного интеллекта — период, отмеченный существенным снижением выделяемых средств на исследования в США и Европе.
Во-первых, общество поняло, что идеи, изображенные в «Космической одиссее 2001 года», еще долго не найдут воплощения. Во-вторых, американские государственные организации, которые возлагали большие надежды на искусственный интеллект, считая, что он поможет одержать верх в холодной войне, постигла неудача. Разочарование ждало и тех, кто связывал свои ожидания с системами автоматического перевода, крайне важными для изучения советских технических документов. Когда стала понятна неэффективность перцептронов для решения линейно неразделимых задач, финансирование исследований в этой области существенно снизилось. Однако ученые продолжили исследования, хотя и опасаясь насмешек со стороны недоброжелателей.
В течение многих лет считалось, что создание сверхразумных компьютеров, подобных HAL 9000 из фильма «Космическая одиссея 2001 года», более чем реально. Увы, вскоре наступило разочарование.
* * *
ЛИНЕЙНАЯ НЕРАЗДЕЛИМОСТЬ
Рассмотрим ситуацию, когда выборки могут принадлежать к одной из двух категорий, каждая из которых описывается двумя дескрипторами (следовательно, двумя входными значениями).
Нарисуем график для восьми выборок.
На этом графике кругами белого цвета отмечены выборки категории А, черными — выборки категории В. Нетрудно провести линию, разделяющую категории, — именно эту операцию проводит перцептрон при корректировке порогового значения и весов входных значений. Но что произойдет, если мы рассмотрим синтетическую задачу, предметом которой является операция XOR? XOR — это логическая операция, соответствующая исключающему «или», которая описывается следующим соотношением:
Теперь график будет выглядеть так:
Теперь уже нельзя провести линию, отделяющую белые круги от черных, следовательно, эта задача является линейно неразделимой. Перцептрон нельзя корректно обучить для решения такой простой логической задачи, как задача XOR.
* * *
Решение проблемы линейной неразделимости было найдено в конце 80-х годов.
Оно было столь очевидным и естественным, что даже странно, почему никто не додумался до него раньше. Решение нашла сама природа еще несколько миллионов лет назад: достаточно связать между собой различные перцептроны, сформировав так называемую нейронную сеть.
На следующем рисунке изображена нейронная сеть, состоящая из трех слоев нейронов: первый слой — входной, второй — скрытый, третий и последний — выходной. Эта нейронная сеть называется сетью прямого распространения, так как поток данных в ней всегда направлен слева направо, а синапсы не образуют циклов.
Нейронная сеть может быть сколь угодно сложной, иметь произвольное число скрытых слоев и, кроме того, содержать связи, которые идут в обратном направлении и тем самым моделируют некую разновидность памяти. Ученые построили нейронные сети, содержащие до 300 тысяч нейронов — столько, сколько содержит нервная система земляного червя.
В нейронной сети процесс обучения усложняется, поэтому инженеры разработали множество методов обучения. Один из самых простых — метод обратного распространения ошибки, давший название отдельной разновидности нейронных сетей, в которой он используется. Суть этого метода состоит в снижении ошибки выходного значения нейронной сети путем корректировки весов входных значений синапсов в направлении справа налево по методу градиентного спуска. Иными словами, сначала весам всех синапсов нейронной сети присваиваются произвольные значения, после чего на вход сети подается выборка, выходное значение для которой известно (такая выборка называется обучающей). Как и следовало ожидать, в этом случае выходное значение будет случайным. Далее, начиная с нейронов, близких к выходу, и заканчивая нейронами входного слоя, начинается корректировка весов связей.
Цель этой корректировки — приблизить выходное значение нейронной сети к реальному известному значению.
Эта процедура повторяется несколько сотен или тысяч раз для всех обучающих выборок. Когда обучение для всех выборок завершено, говорят, что прошла эпоха обучения. Далее процесс обучения может быть повторен на протяжении еще одной эпохи для тех же обучающих выборок. Как правило, при обучении рассматривается несколько десятков выборок. Этот процесс подобен реальному обучению, когда человек вновь и вновь видит одни и те же данные.
* * *
ОПАСНОСТЬ ПЕРЕОБУЧЕНИЯ
Система прогнозирования, в которой применяется машинное обучение, формулирует прогнозы путем обобщения предшествующего опыта. Следовательно, система, неспособная совершать обобщения, становится бесполезной.
Если процесс обучения повторяется слишком много раз, наступает момент, когда веса подобраны столь точно и система настолько адаптировалась к обучающим выборкам, что прогнозы формулируются не путем обобщения, а на основе запомненных случаев. Система становится способной выдавать корректные прогнозы для обучающих выборок, но всякий раз, когда на вход будет подаваться иная выборка, полученный прогноз окажется некорректным. Такая ситуация называется переобучением.
Нечто похожее происходит с ребенком, который не учится умножать, а запоминает таблицу умножения. Если мы попросим его найти произведение двух чисел из таблицы, он ответит без запинки, но если мы попросим его перемножить два других числа, ребенок задумается.
Таблицы умножения — прекрасный пример обучения путем запоминания.
* * *
С годами архитектура нейронных сетей и методы обучения усложнялись. Постепенно возникло множество разновидностей нейронных сетей для решения самых разных задач реальной жизни. Сегодня наиболее часто используются нейронные сети Хопфилда, в которых реализован механизм запоминания под названием «ассоциативная память».
Схема нейронной сети Хопфилда.
В ассоциативной памяти информация упорядочена по содержанию. Следовательно, для доступа к ней необходимо указать содержание информации, а не ее физическое расположение, как при чтении с жесткого диска или из оперативной памяти компьютера.
Другой тип нейронных сетей, широко используемых сегодня, это самоорганизующиеся карты Кохонена. Нейронные сети этого типа содержат новаторское решение: их обучение происходит не под наблюдением. Напротив, сама сеть учится на своих ошибках.
…и мозг начинает работать
В физике существует отдельная дисциплина, инверсная кинематика, которая занимается расчетом движений, необходимых для того, чтобы переместить предмет из точки А в точку В. По мере внесения в систему новых степеней свободы сложность расчетов (различных операций над матрицами) возрастает экспоненциально.
Рассмотрим в качестве примера роботизированную руку с выдвижным манипулятором, способную вращаться в четырех местах. Если мы будем решать матричные уравнения инверсной кинематики классическим способом, то даже суперкомпьютеру потребуется несколько часов на то, чтобы определить, как именно необходимо сместить руку в каждом направлении, чтобы переместить инструмент, закрепленный в манипуляторе, из точки А в точку В.
Таким образом, при реализации роботизированных систем, способных изменять траектории движения в реальном времени, классические методы решения матричных уравнений неприменимы. Если речь идет о роботах, систематически выполняющих одни и те же задачи (это могут быть роботы на сборочном конвейере автомобильного завода), то можно заранее рассчитать и последовательно запрограммировать работу моторов и выдвижного манипулятора. Но если мы хотим сконструировать роботизированную руку, способную действовать автономно и координировать движения в зависимости от ситуации (представьте себе роботов, которые используются на космических кораблях, в хирургии или первых экспериментальных домашних роботов), то нам потребуются более передовые системы, способные быстро вычислять, как именно должны двигаться детали робота, чтобы выполнить поставленную задачу.
На сегодняшний день при создании роботов такого типа эффективно используются нейронные сети с обратным распространением ошибки. В нашем примере нейронная сеть, обученная управлять движениями робота, будет иметь столько выходных нейронов, сколько роботу доступно степеней свободы. Каждый выходной нейрон указывает, на сколько нужно сместиться в каждом направлении, чтобы переместиться из начальной точки в конечную.
Значительное неудобство этого метода по сравнению с классическими подходами состоит в том, что нейронная сеть должна пройти длительное обучение, сравнимое с обучением человека, который в детстве учится ходить. Для человека, уже овладевшего этим навыком, не представляет трудности решать на каждом шаге сложные физические уравнения кинематики и переставлять ноги, не теряя равновесия.
При классическом обучении нейронных сетей с обратным распространением ошибки вновь и вновь рассматриваются десятки тысяч примеров и сотни тысяч возможных траекторий. И для каждой из рассматриваемых траекторий нейронная сеть обучается приводить в действие различные моторы, чтобы робот переместился из начальной точки в конечную.
После завершения обучения нейронной сети говорят, что она усвоила сенсомоторную карту. В результате центр управления роботом может с высочайшей точностью решать задачи инверсной кинематики всего за несколько миллисекунд.
Мозг усложняется
Успехи в использовании нейронных сетей привели к тому, что уже в XXI веке они стали стандартным инструментом решения множества задач. Однако нейронные сети обладают серьезными недостатками.
Первый из них — переобучение. Второй — большое число параметров, значения которых следует задавать вручную, случайным образом, до начала обучения нейронной сети. Здесь основная проблема заключается в том, что не существует каких-либо руководств и методик, описывающих, как именно следует задавать значения параметров. В результате на решение этой задачи приходится тратить значительные человеческие и технические ресурсы и в большинстве случаев прибегать к старому проверенному методу проб и ошибок. Третий недостаток, носящий скорее философский, нежели практический характер, заключается в том, что мы не понимаем, как именно рассуждает обученная нейронная сеть. Этому не придавалось особого значения до тех пор, пока нейронные сети не стали в полной мере применяться для решения реальных задач. Если мы, к примеру, используем нейронную сеть для контроля антиблокировочной системы автомобиля (ABS), то вполне логично, что инженеры хотят до мельчайших подробностей понимать, как рассуждает нейронная сеть, — только так они могут быть уверены, что тормоза не откажут ни в одной из многих тысяч возможных ситуаций.
Нейронная сеть формулирует прогнозы, однако неизвестно, как именно она при этом рассуждает. Некоторые сравнивают нейронные сети с магическим кристаллом.
С конца 90-х годов многие специалисты по теории вычислений интенсивно работают над созданием новых вычислительных методов, которые позволят устранить эти недостатки или хотя бы снизить их негативный эффект. Окончательное решение в начале XXI века предложила группа под руководством Владимира Вапника из знаменитой компании AT&T Bell Labs, специализирующейся на телекоммуникациях и производстве электроники. Вапник разработал метод опорных векторов (англ. SVM — Support Vector Machine), при котором для решения линейно неразделимых задач вводятся новые, искусственные измерения, позволяющие преобразовать исходную задачу в линейно разделимую.
Метод опорных векторов лишен большинства недостатков нейронных сетей, поэтому сегодня он пришел им на смену практически во всех областях компьютерных технологий. Тем не менее нейронные сети до сих пор используются в промышленности, в частности в робототехнике, благодаря простой аппаратной реализации.
Нужны ли экзамены?
Как вы уже знаете, машинное обучение может применяться во всех областях науки и техники. Но можно ли пойти дальше и применить его в образовании? Как преподаватель определяет уровень знаний учеников? Можно ли автоматизировать некоторые субъективные критерии, которые используют школьные учителя и университетские преподаватели для оценки знаний учащихся? Можно ли спрогнозировать уровень знаний ученика, не проводя экзаменов? На все эти вопросы поможет ответить дерево принятия решений.
Исчезнет ли подобная картина в будущем? Этого наверняка хотят многие студенты.
Деревья принятия решений крайне просты, но очень эффективны для распознавания образов. Они позволяют выяснить, какие переменные играют определяющее значение при отнесении выборки к тому или иному классу. Рассмотрим пример. Допустим, что мы хотим спрогнозировать оценки студентов и располагаем следующими исходными данными.
Хорошее дерево принятия решений, составленное с учетом этих данных, может выглядеть следующим образом.
* * *
ИНФОРМАЦИОННОЕ ДЕРЕВО
Дерево — это структура данных, которая очень широко используется в инженерном деле, так как позволяет строить иерархии данных. При работе с деревьями используются особые понятия.
Данные, представленные в дереве, называются узлами. Эти узлы, представляющие единицы информации, делятся на разные уровни и связываются между собой ветвями. Узел, связанный с узлом более высокого уровня, называется потомком, узел, связанный с узлом низшего уровня, — родителем. Узлы, не имеющие потомков, называются листьями.
* * *
В этом случае посещаемость не является определяющей переменной, поэтому не представлена в виде узла дерева. Существуют различные методологии, позволяющие определить, является ли переменная модели дискриминантной (иными словами, можно ли разделить выборку на группы в зависимости от значений этой переменной). В основе одной из самых популярных методологий лежит понятие энтропии Шеннона. В рамках этой методологии для каждого уровня дерева определяется переменная, порождающая меньше всего энтропии. Именно эта переменная и будет дискриминантной для рассматриваемого уровня. Рассмотрим метод подробнее.
Энтропия Шеннона S рассчитывается по следующей формуле:
Попробуем применить это понятие в нашей задаче об экзаменах. На первом уровне дерева необходимо проанализировать энтропию, порождаемую каждой переменной. Первая переменная — «оценка за предыдущий предмет». Если мы разделим выборки в зависимости от значений этой переменной, получим два подмножества выборок. Для первого подмножества энтропия Шеннона будет равна
SОценка за предыдущий предмет ниже средней = -0,75∙log(0,75) — 0,25∙log(0,25) = 0,56,
так как среди студентов, которые в прошлом году получили оценку ниже средней, не сдали экзамен 75 %, сдали — 25 %. Для второго множества энтропия Шеннона будет равна
SОценка за предыдущий предмет ниже средней = -0,33∙log(0,33) — 0,67∙log(0,67) = 0,64,
так как треть студентов, которые в прошлом году получили оценку выше средней, не сдали экзамен, две трети студентов — сдали.
Подобные расчеты повторяются для каждой переменной. Следующая переменная — «посещаемость». Для простоты установим граничное значение посещаемости, равное 95 %. В этом случае
SПосещаемость выше 95 % = -0,6∙log (0,6) — 0,4∙log(0,4) = 0,67;
SПосещаемость выше 95 % = -0,5∙log (0,5) — 0,5∙log(0,5) = 0,69
Наконец, рассмотрим переменную «сданные задания» и вновь для простоты разобъем выборку на 2 группы, выделив тех, кто сдал больше и меньше 60 % заданий.
Имеем:
SСдано более 60 % заданий = -0,75∙log(0,75) — 0,25∙log(0,25) = 0,56;
и
SСдано более 60 % заданий = -1∙log(1) = 0
Следовательно, наилучшей дискриминантной переменной будет последняя, так как энтропия подмножеств, выделенных на ее основе, равна 0,56 и 0.
В этом случае все представители обучающей выборки, сдавшие менее 60 % заданий, не сдали экзамен, следовательно, эту ветвь дерева можно не рассматривать.
Но другая ветвь содержит одинаковое число студентов, сдавших и не сдавших экзамен. Следовательно, необходимо продолжить анализ, не учитывая уже дискриминированные выборки.
Теперь остались только две переменные, которые могут повлиять на итоговое решение: «оценка за предыдущий предмет» и «посещаемость». Значения энтропии Шеннона для групп, выделенных в зависимости от значений первой дискриминантной переменной, таковы:
SОценка за предыдущий предмет ниже средней = -0,5∙log (0,5) — 0,5∙log (0,5) = 0,69;
SОценка за предыдущий предмет ниже средней = -1∙log(1) = 0
Если мы рассмотрим переменную «посещаемость»,
SПосещаемость выше 95 % = -0,33∙log (0,33) — 0,67∙log (0,67) = 0,64;
SПосещаемость выше 95 % = -1∙log(1) = 0
В качестве дискриминантной переменной мы выберем «посещаемость», так как для нее характерна меньшая энтропия.
Метод построения деревьев принятия решений и, следовательно, метод обучения деревьев прост и элегантен, однако обладает двумя значительными недостатками.
Первый из них состоит в том, что задачи с большим числом переменных решаются очень медленно. Второй, более серьезный, заключается в том, что результатом работы алгоритма будет не глобальный, а локальный оптимум. Иными словами, так как дерево всегда анализируется не полностью, а по отдельным уровням, возможно, что на каком-то этапе определенная переменная будет выбрана потому, что она снижает энтропию на своем уровне, однако при выборе другой переменной общее решение будет более оптимальным.
Чтобы повысить качество решений, получаемых с помощью деревьев, часто используются так называемые леса: с помощью различных методов производится обучение нескольких деревьев, а итоговый прогноз формируется с учетом результатов, полученных для каждого дерева..
В рамках этого подхода при обучении леса деревья принятия решений чаще всего строятся путем случайного выбора переменных. Иными словами, если мы хотим обучить 100 деревьев, составляющих лес, то для каждого дерева выберем пять случайных переменных и произведем обучение только с этими пятью переменными. Этот приближенный метод носит поэтическое название random forest («случайный лес»).
Глава 4. Автоматическое планирование и принятие решений
Описанные ниже события могли произойти в любой день.
14:32 — грузовик, двигавшийся по второстепенной дороге с превышением скорости, перевернулся. Водитель получил сильный ушиб головы.
14:53 — на место аварии прибыли пожарные и скорая помощь, которые за несколько минут извлекли из машины водителя в бессознательном состоянии и с серьезной черепно-мозговой травмой.
15:09 — машина скорой помощи прибыла в больницу, где реаниматологи диагностировали смерть мозга водителя.
15:28 — была установлена личность водителя, о его смерти сообщили родственникам.
16:31 — группа психологов связалась с семьей погибшего, чтобы оказать эмоциональную поддержку и получить согласие на передачу донорских органов, не пострадавших при аварии.
16:36 — после непродолжительных споров родственники согласились передать врачам почки умершего (далее — донора).
16:48 — бригада хирургов начала удаление почек и их обследование. Параллельно с этим администрация больницы улаживала необходимые бюрократические формальности.
17:24 — после завершения операции в информационную систему были введены биологические данные донора и характеристики его органов.
Так начинается трансплантация органов.
Как происходит трансплантация
17:24 — информационная система мгновенно определила двух реципиентов донорских почек, отправила им уведомление и выделила необходимые ресурсы для перевозки. В первом случае для перевозки почки в соседний город на расстояние 30 километров потребовалось подготовить машину скорой помощи. Во втором случае почка была доставлена самолетом в город, находящийся в 450 километрах, где действовала иная автономная медицинская система. Перевозка второй почки из больницы в ближайший аэропорт была произведена на вертолете. Все необходимые мероприятия были проведены информационной системой автоматически. Одновременно с этим система выполнила большую часть юридических процедур в соответствии с требованиями систем здравоохранения в городах донора и реципиента.
18:10 — началась первая операция по пересадке почки в больнице соседнего города.
19:03 — началась вторая операция в городе, расположенном в 450 километрах.
21:00 — оба реципиента получили необходимые лекарства и иммунодепрессанты.
Обе операции прошли успешно.
Почему испанская система пересадки донорских органов считается одной из лучших в мире? Какие особенности этой системы отличают ее от систем других стран с более высоким уровнем развития науки и техники? Почему Европейская комиссия рассматривает возможность внедрения испанской модели во всех странах Евросоюза? Как уже читатель наверняка догадался, испанская процедура трансплантации основана на мощной интеллектуальной системе, доступ к которой имеют все больницы страны. Эта система не только учитывает потребности и характеристики каждого реципиента и все логистические детали, но также сложность и неоднородность правовых норм, связанных с пересадкой органов, в разных регионах.
Указанная интеллектуальная система состоит из множества относительно простых узкоспециализированных информационных систем, формирующих мощный «коллективный разум» (так называемая многоагентная система). Именно поэтому Испания в сфере трансплантации органов занимает первое место в мире. Система координирования трансплантации, как правило, имеет многоуровневую структуру, в которой выделяются национальный, зональный, региональный уровни и отдельные больницы. На уровне отдельных больниц данные реципиентов могут распределяться по сети больниц или же содержаться в централизованном хранилище данных.
В силу указанных выше особенностей существует множество интеллектуальных агентов, управляющих информацией обо всех реципиентах. С этими агентами непрерывно обмениваются данными другие интеллектуальные агенты, которые задействуются всякий раз, когда становятся доступны донорские органы. Другие агенты системы занимаются самыми разными аспектами, к примеру планируют и распределяют логистические ресурсы для перевозки органов или решают административные вопросы согласно требованиям различных региональных систем здравоохранения.
* * *
ГОЛУБИНЫЙ РЕЙТИНГ
Известнейшая компания Google пользуется огромным авторитетом в мире компьютерных технологий и искусственного интеллекта. Священный Грааль Google — алгоритм, используемый для ранжирования результатов поиска, к которому несколько миллионов раз в секунду обращаются пользователи со всего мира. Этот алгоритм привлек огромный интерес, и в Google поступило столько обращений с просьбами опубликовать его, что утром 1 апреля 2002 года на главной странице поисковика была размещена ссылка, которая вела на описание алгоритма ранжирования. Этот алгоритм назывался pigeon ranking («голубиный рейтинг»), и такое название было выбрано не случайно. В статье, расположенной по ссылке, объяснялось, что Google располагал установками, заполненными PC (от английского pigeon cluster — «голубиный кластер»; это же сокращение обозначает «персональный компьютер»). Перед каждым голубем находились экран и клавиатура. В описании алгоритма указывалось, что всякий раз, когда пользователь вводит запрос в Google, все сайты, удовлетворяющие поисковому запросу, отображаются перед одним из голубей, который затем начинает клевать кнопки на клавиатуре. После этого сайты упорядочиваются в зависимости оттого, сколько раз голубь нажмет на кнопки.
В этой же статье объяснялось, как Google работает с голубями, как они живут и в каких условиях содержатся. Также упоминалось, что в Google пробовали использовать других пернатых, в частности кур и хищных птиц, но больше всего для выполнения задачи подошли именно голуби.
Автор статьи даже осмелился указать, что пусть ни один голубь еще не стал членом Конституционного суда, была доказана их эффективность как авиадиспетчеров и футбольных арбитров.
Многие инженеры и конкуренты Google не сразу поняли, что статья была опубликована 1 апреля — в День смеха, который отмечается в многих странах, в том числе в США.
* * *
Упрощенный пример сети агентов, отвечающей за координацию перевозки органов.
Подобная многоагентная интеллектуальная архитектура обладает множеством преимуществ. В частности, эта система является отказоустойчивой — если один или сразу несколько агентов откажут, система будет по-прежнему способна решать задачи за счет саморегулирования и задействования других агентов. Еще одно важное преимущество подобной архитектуры заключается в использовании относительно простых, но узкоспециализированных агентов, на основе которых можно выстроить интеллектуальную систему, способную за несколько секунд решать сложные междисциплинарные задачи.
* * *
АГЕНТНО-ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ
Компьютерное программирование — быстро развивающаяся дисциплина. На сегодняшний день существует пять больших семейств языков программирования, наиболее популярным из которых является семейство объектно-ориентированных языков. В объектно-ориентированном программировании все сущности представлены с помощью особых единиц информации, называемых объектами. Объекты имеют ряд атрибутов, где хранят информацию о самих себе, и способны выполнять с этой информацией некоторые операции. Объектно-ориентированное программирование требует вмешательства координаторов, которые обладают интеллектом и постоянно направляют запросы тем или иным объектам при решении задач. Неизменно предполагается, что объект — это элемент, не обладающий интеллектом, который ожидает указаний. Но не так давно мощное развитие получило новое направление программирования — агентно-ориентированное. В нем «неразумные» объекты превращаются в намного более интеллектуальные и автономные агенты, и одновременно снижается роль координатора.
Планирование — основа всего
Планирование использования ресурсов для успешного решения тех или иных задач может оказаться крайне сложным даже для опытного человека. Такое планирование используется во всех областях, начиная от не слишком важных задач, например планирования учебного расписания, распределения аудиторий, лабораторий и аудиовизуальных материалов, и заканчивая крайне важным планированием ресурсов при тушении лесных пожаров или борьбе с другими стихийными бедствиями.
Автоматические рассуждения крайне просты для человека, но невероятно сложны для машин. По сути, способность рассуждать в немалой степени является отличительным признаком людей, и ключевые особенности рассуждений до сих пор не слишком понятны нейробиологам. Для имитации рассуждений человека инженеры разработали ряд очень интересных приемов, которые применяются, к примеру, при тушении лесных пожаров.
Сегодня многие пожарные службы используют системы планирования с искусственным интеллектом. Как правило, при обнаружении лесного пожара средних размеров специалисту экстренной службы требуется до полутора часов на разработку плана тушения. Этот план подробно описывает все действия, которые следует выполнять всеми доступными средствами в зависимости от характеристик местности, погодных условий и так далее. Однако специалисты часто сталкиваются со следующей проблемой: условия в районе пожара непрерывно меняются, и этот процесс идет так быстро, что человек попросту не успевает изменить план действий. В результате многие службы пытаются внедрить автоматизированные системы, способные составить план тушения пожара за несколько секунд. Система фиксирует такие параметры, как рельеф местности, погодные условия, проезды к зоне пожара, доступные авиационные и наземные средства, а также возможность координировать действия с другими подразделениями и центрами управления, на основе этих параметров она составляет план и отправляет его на проверку человеку-эксперту.
Тушение лесного пожара требует координирования многочисленных человеческих и материальных ресурсов.
Может случиться так, что в данный момент одна единица техники не задействована, и система предлагает два варианта: перевести ее в зону, где бушует пожар, либо отправить ее на тушение очагов пожара в другую, менее опасную область, расположенную ближе. Как система определит, какой из вариантов лучше? Логично, что конечная цель — потушить пожар, следовательно, кажется более естественным направить технику туда, где пожар сильнее. С другой стороны, на переброску тех ники может уйти несколько часов, а всего в нескольких минутах езды очаги пожара не представляют большой опасности, и их можно потушить относительно легко.
Как объективно оценить преимущества от тушения пожара в определенной области с учетом расстояния до нее и затраченного времени? Именно такой оценки требует классическая, неинтеллектуальная система планирования. Но при тушении пожара используется не одна, а несколько десятков единиц наземной и воздушной техники.
Также можно учесть новые переменные, например скорость ветра и прогноз погоды, возможные дожди, расположение жилья, природоохранных зон и так далее. При таком обилии переменных становится понятной огромная потребность в интеллектуальной системе, способной принимать решения с учетом всех перечисленных факторов и на основе нечетких параметров.
* * *
НЕЧЕТКАЯ ЛОГИКА
Нечеткая логика — раздел математической логики, приближающий логические действия и методы к естественным, человеческим рассуждениям. Как правило, в реальной ситуации ничто не делится на белое и черное, но в классической логике, в частности в булевой, переменные могут быть только истинными или ложными, что вынуждает рассматривать лишь крайности.
К примеру, на вопрос, хорошо или плохо играет вратарь футбольной команды из первого дивизиона чемпионата Казахстана, дать однозначный ответ нельзя: в сравнении с элитой мирового футбола он наверняка не слишком хорош, но по сравнению с вратарем моей районной команды он будет первоклассным игроком.
Поэтому переменные нечеткой логики принимают значения не «истина» или «ложь», а вещественные значения, заключенные на интервале от 0 до 1, где значению 1 соответствует «истина», 0 — «ложь». Если мы обозначим через 0 неспособность отразить любой удар, а через 1 — уровень лучшего вратаря мира, то вратарь казахской команды получит вполне достойную оценку в 0,73.
* * *
Для решения задач такого типа обычно используются классические алгоритмы поиска, применяемые в искусственном интеллекте, в частности поиск с возвратом (back-tracking) или метод ветвей и границ (branch-and-bound). Оба этих алгоритма действуют схожим образом: по сути, они разворачивают комбинаторное дерево и обходят его в поисках оптимального варианта. Развертывание комбинаторного дерева происходит достаточно просто. На первом этапе создается дерево, содержащее все возможные планы (вспомните понятия, которые мы объяснили в первой главе, рассказывая об интеллектуальном алгоритме, способном определять оптимальные ходы в шахматной партии). Далее с помощью интеллектуальных алгоритмов последовательно отсекаются те ветви, которым соответствуют нереальные планы либо планы, нарушающие ограничения или ведущие к неоптимальному решению.
Важное отличие метода поиска с возвратом от метода ветвей и границ заключается в том, что первый метод состоит в обходе дерева в глубину, второй — в обходе в ширину. Это различие крайне важно: в зависимости от представления задачи отсечение той или иной ветви может иметь разную эффективность.
Последовательное отсечение ветвей дерева по мере обхода абсолютно необходимо — в противном случае, как и почти во всех комбинаторных задачах, число планов, а значит, и число ветвей, будет так велико, что его нельзя будет обойти за разумное время. Чтобы ускорить отсечение ветвей, в методах, основанных на обходе дерева, обычно используются так называемые эвристики (или формальное представление интуитивных понятий), которые может применить специалист предметной области, чтобы определить: та или иная ветвь не приведет к нужному результату, и ее необходимо отсечь как можно скорее. Разумеется, если мы отсечем ветвь, которая соответствует неосуществимому плану, на раннем этапе алгоритма, то можем сэкономить несколько часов вычислений — с переходом на более высокие уровни число вариантов, которые необходимо проанализировать, возрастает экспоненциально.
Простой пример дерева планирования для игры «крестики-нолики».
* * *
ТЕОРЕМА «БЕСПЛАТНОГО ОБЕДА НЕ БЫВАЕТ»
Теорема под названием «бесплатного обеда не бывает» (no-free lunch) гласит: не существует алгоритма, позволяющего получить оптимальные решения всех возможных задач. Теорема получила свое любопытное название на основе метафоры о стоимости блюд в различных ресторанах. Допустим, что существует определенное число ресторанов (каждый из них обозначает определенный алгоритм прогнозирования), где в меню различным блюдам (каждое блюдо обозначает определенную задачу прогнозирования) сопоставлена цена (или качество решения этой задачи, которое позволяет получить рассматриваемый алгоритм). Человек, который любит поесть и при этом не прочь сэкономить, может определить, какой ресторан предлагает его любимое блюдо по самой выгодной цене. Вегетарианец, сопровождающий этого обжору, наверняка обнаружит, что его любимое вегетарианское блюдо в этом ресторане стоит намного дороже. Если обжора захочет полакомиться бифштексом, он выберет ресторан, где бифштекс подают по самой низкой цене. Но у его друга-вегетарианца при этом не останется другого выбора, кроме как заказать единственное вегетарианское блюдо в этом ресторане, пусть даже по заоблачной цене. Это очень точная метафора ситуации, когда необходимость использования определенного алгоритма для решения конкретной задачи приводит к гарантированно неоптимальным результатам. Исследователи прилагают огромные усилия для создания супералгоритма или суперметода, позволяющего составить идеальный план, но в конечном итоге неизменно сталкиваются с определенным множеством данных или контекстом, в котором оптимальные результаты показывает другой алгоритм.
Теорема имеет еще одно важное следствие: если мы тратим много сил на корректировку алгоритма, чтобы добиться идеальных результатов для определенных исходных данных, эти корректировки гарантированно приведут к ухудшению работы алгоритма для другого множества данных. Вывод: любой алгоритм будет либо работать идеально для небольшого числа случаев и плохо — во всех остальных, либо будет демонстрировать посредственные результаты во всех случаях. соответствует неосуществимому плану, на раннем этапе алгоритма, то можем сэкономить несколько часов вычислений — с переходом на более высокие уровни число вариантов, которые необходимо проанализировать, возрастает экспоненциально.
Выявление конфликтов
Остров Кипр, Средиземное море, январь 1997 года. Власти Кипра и Греции объявили об установке двух зенитно-ракетных комплексов С-300 класса «земля-воздух», закупленных в России, что стало серьезным усилением вооруженных сил обоих государств в рамках единого оборонного пространства.
Представители российского министерства обороны подтвердили, что переданные Кипру комплексы С-300 предназначены для выполнения исключительно оборонительных задач и никак не нарушат неустойчивый баланс сил между греческими и турецкими военными на острове.
Зенитно-ракетный комплекс С-300 на военном параде в России..
Турция, январь 1997 года. Турецкое правительство незамедлительно заявило, что установка ракет является серьезной угрозой безопасности страны, и объявило о принятии встречных мер. Кроме того, турецкие власти сообщили, что если ракеты коснутся кипрской земли, то это станет сигналом к началу военных действий на острове.
В ответ правительство Кипра перевело вооруженные силы в режим максимальной боевой готовности, который был снят лишь в июне того же года.
Весна 1997 года. Греческое правительство, в свою очередь, сочло, что установка ракет С-300 не поможет сдержать турецкую угрозу, так как ракеты были открыты для удара турецких войск и не уцелели бы в случае нападения. Следовательно, власти Греции посчитали, что любые попытки дестабилизировать ситуацию в регионе будут предприняты турецкой стороной, так как комплексы С-300 применяются исключительно для обороны.
В этот же период была проведена мобилизация греческой армии для поддержки кипрских войск на случай атаки со стороны Турции. Российские власти сохраняли нейтралитет, однако заявили, что на продажу двух комплексов С-300 не повлияет какое-либо вмешательство извне.
Турция начала интенсивные переговоры с союзниками по НАТО, но безуспешно. Затем турецкие власти решили начать сотрудничество с Израилем и обучить войска противодействию комплексам С-300.
Нестабильный регион в Восточном Средиземноморье.
Сентябрь 1997 года. Турецкий военный флот начал рейды в Восточном Средиземноморье с целью обнаружения судов, в частности российских военных кораблей, чтобы предотвратить доставку ракет. Россия и Греция оповестили Турцию о начале военных действий в случае атаки или морской блокады Кипра.
Декабрь 1997 года. Россия сосредоточила значительные военно-морские силы в регионе, в том числе авианосцы и подводные лодки. Предположительно их задачей была перевозка комплексов С-300 и уничтожение турецкого флота в случае попытки перехватить груз.
Январь 1998 года. Под давлением США и Великобритании и перед лицом турецкой угрозы власти Греции в итоге решили отказаться от установки ракет на Кипре. Ракеты С-300 были размещены на греческом острове Крит, а на Кипр были доставлены другие, менее мощные комплексы, переданные греческими властями правительству Кипра в обмен на С-300.
Результатом конфликта, который мог завершиться трагически и иметь самые серьезные последствия, стала дестабилизация отношений между Турцией и Кипром. Позиции греческого правительства, напротив, не пострадали.
Какую роль в этих событиях сыграл искусственный интеллект? Как можно предсказать и даже предотвратить тактические маневры, чтобы избежать угрозы начала военных действий, как в описанной ситуации? В 2005 году группой исследователей Кипрского университета была разработана сложная интеллектуальная система, основанная на нечетких когнитивных картах. При обучении системы использовались эволюционные алгоритмы, способные с высокой точностью предсказывать и моделировать политическую нестабильность. Эта система при анализе кипрского конфликта выделяет 16 переменных, начиная от «нестабильности/напряженности на Кипре» и заканчивая «влиянием международного сообщества». Кроме того, рассматриваются такие переменные, как «политическая поддержка со стороны Греции» или «усиление турецкой армии».
Нечеткая когнитивная карта — это нейронная сеть, в которой каждый нейрон показывает, как изменяется значение одной из переменных с течением времени.
К примеру, в определенный момент политическая поддержка со стороны Греции может быть довольно велика, и нейрон, соответствующий этой переменной, может содержать значение 92 %. Нейрон, соответствующий переменной «усиление турецкой армии», может содержать невысокое значение, к примеру 23 %.
С другой стороны, каждый нейрон связан с соседними с помощью ребер. Каждое ребро описывает вес причинно-следственной связи между нейронами, которые оно соединяет. К примеру, «политическая нестабильность на Кипре» влияет на «усиление турецкой армии» с величиной 0,32. Если политическая нестабильность в определенный момент составляет 50 %, это вызовет прямое усиление турецкой армии на 16 %, то есть на 0,32 ∙ 50 %. Также существуют отрицательные причинно-следственные связи: к примеру, переменная «решение Кипрского вопроса» влияет на переменную «политическая нестабильность на Кипре» с величиной —0,21.
Сложные причинно-следственные связи между нейронами системы (ее когнитивная карта содержит 45 связей) зафиксированы эволюционным алгоритмом, в котором каждая особь популяции представляет собой матрицу весов для 45 связей между переменными карты. Приспособленность каждой матрицы оценивается по тому, насколько точно она описывает эскалацию конфликтов, произошедших в прошлом.
Таким образом, после обучения системы с помощью подходящей матрицы весов исследователи смогли моделировать ситуации вида «что будет, если…» для поиска оптимального решения Кипрского вопроса. В статье, опубликованной авторами системы, было рассмотрено три сценария, на примере которых описывались прогнозы, составленные системой. В одном из случаев была рассмотрена ситуация, при которой турецкая армия навсегда покидала остров. Прогноз включал различные события, приводившие к постепенному росту напряженности, за которым в итоге следовали анархия и хаос.
* * *
ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ И ВОЙНЫ
В истории человечества войны были ключевым фактором технического прогресса во все времена, начиная с изготовления Архимедом военных машин во время Пунических войн и заканчивая развитием ядерной энергетики в период холодной войны.
Искусственный интеллект также изначально имел военное применение. Сами основы вычислительной техники были заложены в разгар Второй мировой войны, когда союзникам потребовалось расшифровать секретные коды нацистских войск.
Во время холодной войны важные открытия в этой области произошли из-за того, что требовалось перевести огромный объем научно-технических текстов с русского языка на английский, и для выполнения автоматического перевода появились техники обработки естественных языков.
В 1966 году был опубликован доклад Комитета по автоматической обработке языков (ALPAC — от англ. Automatic Language Processing Advisory Committee), в котором рекомендовалось прекратить государственное финансирование исследований, связанных с обработкой естественного языка. В качестве причины указывались неудовлетворительные результаты, полученные за 10 лет исследований.
Рассказывают (хотя вряд ли эти данные можно считать достоверными), что во время войны в Персидском заливе американские военные систематически производили бомбардировки всех целей, где, по оценкам интеллектуальной системы, были спрятаны самолеты противника.
По-видимому, решения принимались с помощью так называемых нейронных сетей Кохонена, о которых будет рассказано далее.
Машина «Энигма», применявшаяся во время Второй мировой войны для шифрования и расшифровки сообщений.
Глава 5. Анализ данных
Руководство крупной американской сети супермаркетов Osco несколько лет назад поставило перед службой информационных технологий задачу разработать систему, способную анализировать огромные объемы данных, генерируемых ежедневно.
Предполагалось, что в результате анализа станут понятны рыночные тенденции.
Сразу после заверения работы над системой была обнаружена удивительная тенденция: в период с 17:00 до 19:00 существенно возрастали совокупные продажи подгузников и пива. Иными словами, масса клиентов, приобретавших в это время подгузники, включали в свою продуктовую корзину и пиво. Эта тенденция сначала обеспокоила исследователей, однако вскоре нашлось и объяснение: клиенты с маленькими детьми не могут отправиться на футбол, баскетбол или бейсбол, поэтому они покупали пиво, чтобы пить его во время телевизионной трансляции матчей.
Как компания Osco использовала эту информацию? Полки с подгузниками и пивом были переставлены ближе друг к другу, и совокупные продажи обеих групп товаров значительно возросли. Этот пример использования информационных систем получил известность, и сегодня все крупные торговые сети используют хранилища данных и средства интеллектуального анализа для изучения тенденций рынка и запуска новых продуктов.
О том, что такое интеллектуальный анализ данных и хранилище данных, мы расскажем чуть позже. Пока лишь отметим, что анализ данных — это дисциплина, в которой изучаются способы извлечения информации из систематически собираемых сведений. В силу растущей сложности данных среды проводить подобный анализ с каждым разом становится все труднее, и сегодня интеллектуальный анализ данных выделяют в отдельную дисциплину на стыке искусственного интеллекта и статистики.
Анализ данных возник в XVIII веке одновременно с появлением первых современных государств, осуществлявших систематический сбор информации о населении и состоянии экономики. Интеллектуальный анализ данных появился значительно позже, в конце XX века, когда вычислительные мощности и новые методы искусственного интеллекта достигли уровня, достаточного для того, чтобы извлекать информацию из огромных объемов данных.
Интеллектуальный анализ данных
Результатом классического интеллектуального анализа данных является математическая модель, которая помогает объяснить выявленные в ходе анализа тенденции.
Также эта модель позволяет предсказать появление новых тенденций и даже провести классификацию или сегментирование данных на основе шаблонов поведения, выявить которые совсем не просто.
При интеллектуальном анализе результатом обработки данных является информация, из которой извлекаются знания.
Фундаментальные средства анализа данных основывались на понятиях, связанных с условной вероятностью и предложенных священником Томасом Байесом еще в XVIII веке. Проблема, которая серьезно осложняет анализ данных, заключается в том, откуда берутся сами данные. К примеру, представим, что мы хотим проанализировать сведения о пациентах, страдающих от раковых заболеваний, и обращаемся к архиву онко диспансера. Как правило, в подобных архивах содержится намного больше информации о больных пациентах, чем о здоровых, ведь источником данных является больница. Это исходное отклонение Байес выразил с помощью введенного им понятия условной вероятности, которое мы уже объясняли в предыдущей главе.
Результатом исследований условной вероятности Байеса стал ряд методов, позволяющих учесть это исходное отклонение и сделать точные выводы. В общем случае интеллектуальный анализ данных делится на следующие этапы.
1. Отбор множества данных. На этом этапе выбираются целевые переменные, на основе которых будут производиться сегментирование, классификация или прогнозирование, а также независимые переменные — данные, на основе которых будут строиться модели. Часто обработать все доступные данные невозможно, поэтому на этапе отбора необходимо произвести выборку данных для анализа.
2. Анализ особенностей данных. На этом этапе проводится первое простое изучение данных для выявления нетипичных значений, выходящих за разумные пределы. Также определяются переменные, которые не предоставляют важной информации для решения задачи.
3. Преобразование входных данных. На этом этапе обычно проводится нормализация данных, чтобы избежать серьезных ошибок на последующих этапах моделирования. Предположим, что в задаче рассматриваются две переменные — рост и вес жителей страны. Рост, скорее всего, будет указываться в сантиметрах или даже миллиметрах, вес — в килограммах. Если мы будем использовать нейронную сеть для моделирования этих данных, то получим некорректные результаты из-за больших различий во входных значениях (рост человека может достигать двух тысяч миллиметров, а вес редко превышает сто килограммов). Поэтому данные обычно преобразуются так, чтобы минимальное значение равнялось 0, максимальное — 1.
4. Моделирование. Это основной этап интеллектуального анализа данных. Методы анализа данных делятся на группы в зависимости от того, какие приемы используются на этом этапе. По этой причине моделирование обычно охватывает ряд средств и методологий, как правило, относящихся к мягким вычислениям (эта дисциплина изучает методы решения задач с неполными или неточными данными) и неизменно направленных на извлечение нетривиальной информации. Сюда относятся нейронные сети, метод опорных векторов и так далее.
5. Извлечение знаний. Часто на предыдущем этапе не удается мгновенно извлечь знания из данных. На этом этапе применяются различные инструменты, к примеру, позволяющие получить новые знания при помощи корректно обученной нейронной сети.
6. Интерпретация и оценка данных. Несмотря на интенсивное использование компьютерных методов в интеллектуальном анализе данных, этот процесс по прежнему далек от полной автоматизации. Значительная часть интеллектуального анализа данных выполняется вручную, а качество результатов зависит от опыта инженера. По этой причине после завершения процесса извлечения знаний необходимо проверить корректность выводов, а также убедиться, что они нетривиальны (к примеру, тривиальным будет знание о том, что рост всех людей заключен на интервале от 1,4 до 2,4 м). Также при реальном интеллектуальном анализе одни и те же данные анализируются при помощи разных методологий. На этом этапе производится сравнение результатов, полученных с помощью различных методов анализа и извлечения знаний.
* * *
ПАПА РИМСКИЙ — ПРИШЕЛЕЦ?
В 1996 году Ханс-Петер Бек-Борнхольдт и Ханс-Херманн Даббен в статье, опубликованной в престижном журнале Nature, рассмотрели вопрос: действительно ли Папа Римский — человек? Они рассуждали следующим образом: если мы выберем одного человека случайным образом, то вероятность того, что он будет Папой Римским, составит 1 к 6 миллиардам. Продолжим силлогизм: вероятность того, что Папа Римский — человек, равна 1 к 6 миллиардам.
Опровержение этих рассуждений привели Шон Эдди и Дэвид Маккей в том же самом журнале, применив условную вероятность. Они рассуждали следующим образом: вероятность того, что некий человек — Папа Римский, вовсе не обязательно равна вероятности того, что некий индивид — человек, если он — Папа Римский. Применив математическую нотацию, имеем:
Р(человек | Папа Римский) =/= р(Папа Римский | человек).
Если мы хотим узнать значение Р (человек | Папа Римский), нужно применить теорему Байеса. Получим:
Допустим, вероятность того, что некий индивид (житель планеты Земля) — пришелец, пренебрежимо мала ). Тогда вероятность того, что этот индивид — человек, стремится к 1 . Вероятность того, что пришелец будет избран Папой Римским, еще меньше (Р (Папа Римский | пришелец) < 0,001). Следовательно, можно со всей уверенностью утверждать, что
Проклятие размерности
Прекрасно известно, что интуиция, не подкрепленная размышлениями, — злейший враг статистики и теории вероятностей. Многие думают, что при анализе данных большой объем входных данных (но не выборок) позволит получить больше информации, а следовательно, и больше знаний. С этим заблуждением традиционно сталкиваются начинающие специалисты по интеллектуальному анализу данных, и распространено оно настолько широко, что специалисты называют его проклятием размерности.
Суть проблемы заключается в том, что при добавлении к математическому пространству дополнительных измерений его объем возрастает экспоненциально.
К примеру, 100 точек (102) — достаточная выборка для единичного интервала, при условии, что расстояние между точками не превышает 0,01. Но в кубе единичной стороны аналогичная выборка должна содержать уже 1000000 точек (106), а в гиперкубе размерностью 10 и с длиной стороны, равной 1, — уже 1020 точек. Следовательно, чтобы при добавлении новых измерений выборка по-прежнему охватывала пространство должным образом (иными словами, чтобы плотность математического пространства оставалась неизменной), объемы выборок должны возрастать экспоненциально. Допустим, что мы хотим найти закономерности в результатах парламентских выборов и располагаем множеством данных об избирателях и их предпочтениях. Часть имеющихся данных, к примеру рост избирателей, возможно, не будет иметь отношения к результатам голосования. В этом случае лучше исключить переменную «рост», чтобы повысить плотность выборок избирателей в математическом пространстве, где мы будем работать.
Именно проклятие размерности стало причиной появления целого раздела статистики под названием отбор характеристик (англ, feature selection). В этом разделе изучаются различные математические методы, позволяющие исключить максимально большой объем данных, не относящихся к рассматриваемой задаче. Методы отбора характеристик могут варьироваться от исключения избыточной или связанной информации до исключения случайных данных и переменных, имеющих постоянное значение (то есть переменных, значения которых на множестве выборок практически не меняются). В качестве примера приведем переменную «гражданство».
Логично, что ее значение будет одинаковым для всех или почти всех избирателей, следовательно, эта переменная не имеет никакой ценности.
Чаще всего используется такой метод отбора характеристик, как метод главных компонент. Его цель — определение проекции, в которой вариация данных будет наибольшей. В примере, представленном на следующем рисунке, две стрелки указывают две главные компоненты с максимальной вариацией в облаке точек. Максимальная вариация указана более длинной стрелкой. Если мы хотим снизить размерность данных, то две переменные, откладываемые на осях абсцисс и ординат, можно заменить новой переменной — проекцией выборок на компоненту, указываемую длинной стрелкой.
На этом графике стрелки указывают направления, в которых вариация данных будет наибольшей.
* * *
А ЭТО КТО? РАСПОЗНАВАНИЕ ЛИЦ
Многие современные фотоаппараты способны во время съемки распознавать лица. Например, цифровые фотоаппараты часто содержат функцию, позволяющую определить число лиц на фотографии и автоматически настроить параметры съемки так, чтобы все лица оказались в фокусе.
Социальная сеть Facebook также использует функцию распознавания лиц, способную определять людей на фотографиях, загружаемых пользователем. Как же действуют подобные функции?
Большинство функций распознавания лиц основаны на методе главных компонент. Сначала проводится обучение системы на множестве изображений различных лиц. В ходе обучения система определяет главные компоненты в результате анализа нескольких фотографий одного лица и множества фотографий всех лиц. В действительности система всего лишь запоминает наиболее характерные черты лица каждого человека, чтобы потом распознать его.
Таким образом, для нового изображения система извлекает информацию о главных компонентах и сравнивает ее с информацией о компонентах, полученной в ходе обучения. В зависимости от процента совпадения система способна определить, какая часть тела изображена на фотографии, лицо или нога, и даже распознать, какому человеку принадлежит это лицо.
* * *
Метод главных компонент заключается в поиске линейного преобразования, позволяющего получить новую систему координат для исходного множества выборок.
В этой системе координат первая главная компонента будет отражать наибольшую вариацию, вторая — следующую по величине вариацию и так далее. Число компонент может быть любым. Одно из преимуществ этого метода заключается в том, что на промежуточных этапах поиска компонент с наибольшей вариацией можно определить, какую часть вариации переменных объясняет каждая компонента. К примеру, первая главная компонента может объяснить 75 % вариации, вторая — 10 %, третья — 1 % и так далее. Так можно уменьшить размерность множества данных и при этом гарантировать, что новые измерения, которые придут на смену исходным, будут объяснять минимум вариации данных. Рекомендуется, чтобы вариация, в сумме описываемая выделенными компонентами, составляла около 80 %.
Несмотря на все преимущества и относительную простоту метода главных компонент (сегодня этот метод входит в стандартную поставку всех пакетов статистических программ), по мере увеличения числа измерений в модели сложность расчетов возрастает, и вычисления могут оказаться непосильными. В подобных случаях используются два других метода отбора характеристик: жадный прямой отбор (greedy forward selection) и жадное обратное исключение (greedy backward elimination). Оба этих метода обладают серьезными недостатками: они требуют выполнения огромного объема расчетов, при этом вероятность выбора наиболее подходящих характеристик невысока. Однако основная идея этих методов и ее реализация просты, а объем необходимых вычислений для большого числа измерений все же не так высок, как при использовании метода главных компонент. Это объясняет, почему жадный прямой отбор и жадное обратное исключение стали так популярны среди специалистов по интеллектуальному анализу данных.
* * *
ЖАДНЫЕ АЛГОРИТМЫ
Жадные алгоритмы — разновидность алгоритмов, в которых для определения следующего действия (при решении задач планирования, поиска или обучения) всегда выбирается вариант, ведущий к максимальному увеличению некоего градиента в краткосрочной перспективе.
Достоинство жадных алгоритмов заключается в том, что они способны очень быстро найти максимальное значение определенных математических функций. Для сложных функций, имеющих несколько максимумов, жадные алгоритмы, напротив, обычно останавливаются на одном из локальных максимумов, так как не могут оценить задачу в целом. В итоге жадные алгоритмы оказываются не вполне эффективны, так как результатом их работы часто является субоптимум функции.
* * *
Как следует из названия, один из этих методов является прямым, а другой — обратным, однако оба используют один принцип. Представьте, что мы хотим отобрать характеристики, точнее всего описывающие тенденции голосования на парламентских выборах. Имеем пять известных характеристик выборки: покупательная способность, родной город, образование, пол и рост избирателя. Будем использовать для анализа тенденций нейронную сеть. Применив жадный прямой отбор, выберем первую переменную в задаче и смоделируем данные с помощью нейронной сети, используя только эту переменную. После того как модель построена, оценим точность прогноза и сохраним полученную информацию. Повторим аналогичные действия для всех остальных переменных по отдельности. По завершении анализа выберем переменную, для которой были получены лучшие результаты, и повторим моделирование с последующей оценкой модели, но уже для двух переменных. Предположим, что лучшие результаты были получены для переменной «образование». Проверим все возможные сочетания переменных, в которых первой переменной будет «образование». Получим модели «образование и родной город», «образование и пол», «образование и рост». И вновь, проанализировав четыре сочетания, выберем лучшее из них, к примеру «образование и покупательная способность», после чего повторим описанные выше действия уже для трех переменных, две из которых будут фиксированы. Этот процесс будет повторяться до тех пор, пока с добавлением очередной переменной точность новой модели относительно предыдущей, содержащей на одну переменную меньше, не перестанет возрастать.
Жадное обратное исключение проводится прямо противоположным образом: в качестве исходной выбирается модель, содержащая все переменные, затем из нее последовательно исключаются переменные так, чтобы качество модели не ухудшалось.
Как можно догадаться, этот метод является не слишком интеллектуальным: он не гарантирует, что будет найдено наилучшее сочетание переменных, а также предполагает значительный объем вычислений, поскольку на каждом этапе необходимо выполнять моделирование заново.
Ввиду важных недостатков существующих методов отбора характеристик на специализированных конференциях постоянно предлагаются новые методы. Они обычно описываются тем же принципом, что и метод главных компонент, то есть заключаются в поиске новых переменных, которые замещают исходные и повышают плотность информации. Подобные переменные называются латентными. Они используются во множестве дисциплин, однако наибольшее распространение получили в общественных науках. Такие характеристики, как качество жизни в обществе, доверие участников рынка или пространственное мышление человека, — латентные переменные, которые нельзя измерить напрямую. Они измеряются и выводятся по результатам совокупного анализа других, более осязаемых характеристик. Латентные переменные обладают еще одним преимуществом: они сводят несколько характеристик в одну, тем самым уменьшая размерность модели и упрощая работу с ней.
Визуализация данных
Визуализация данных — дисциплина, изучающая графическое представление данных, как правило многомерных. Эта дисциплина стала популярной вскоре после образования современных государств, способных систематически собирать данные о развитии экономики, общества и производственных систем. В действительности визуализация данных и анализ данных — смежные дисциплины, так как многие средства, методы и понятия, используемые для упрощения визуализации, возникли в рамках анализа данных, и наоборот.
Возможно, автором первой известной визуализации статистических данных был Михаэль ван Лангрен, который в 1644 году изобразил на диаграмме 12 оценок расстояния между Толедо и Римом, предложенных 12 разными учеными. Слово «ROMA» («РИМ») указывает оценку самого Лангрена, а маленькая размытая стрелка, изображенная под линией примерно в ее центре, — корректное расстояние, вычисленное современными методами.
Еще в XVIII веке Джозеф Пристли составил диаграмму, где изобразил, в какое время жили некоторые выдающиеся деятели античности.
В том же столетии, благодаря трудам Иммануила Канта, который утверждал, что именно представление делает объект возможным, а не наоборот, стало понятно, что нельзя вести споры о знаниях или реальности, не учитывая, что эти самые знания и реальность создает человеческий разум. Так представление и визуализация данных заслуженно заняли важнейшее место в науке.
Позднее, во время Промышленной революции, начали появляться более сложные методы представления данных. В частности, Уильям Плейфэр создал методы, позволяющие представить изменение объемов производства, связав их с колебаниями цен на пшеницу и с величиной заработной платы при разных правителях на протяжении более 250 лет.
Благодаря вычислительной технике специалисты в сфере визуализации данных начали понимать, каким должно быть качественное представление данных для их быстрой интерпретации. Один из важнейших моментов, которые следует принимать во внимание (помимо самих данных, модели представления и графического движка, используемого для визуализации), — ограниченные способности восприятия самого аналитика, конечного потребителя данных. В мозгу аналитика происходят определенные когнитивные процессы, в ходе которых выстраивается ментальная модель данных. Однако эти когнитивные процессы страдают из-за ограниченности нашего восприятия: так. большинство из нас неспособны представить себе больше четырех или пять измерений. Чтобы упростить построение моделей, необходимо учитывать все эти ограничения. Качественная визуализация данных должна представлять информацию в иерархическом виде с различными уровнями подробностей. Также визуализация должна быть непротиворечивой и не содержать искажений. В ней следует свести к минимуму влияние данных, которые не содержат полезной информации или могут вести к ошибочным выводам. Рекомендуется дополнять визуализацию иными статистическими данными, указывающими статистическую значимость различной информации.
Для достижения всех этих целей используются стратегии, подобные рассмотренным в главе, посвященной анализу данных. Первая из них заключается в снижении размерности с помощью уже описанных методов, в частности, путем ввода латентных переменных. Вторая стратегия состоит в снижении числа выборок модели путем их разделения на значащие группы. Этот процесс называется кластеризацией (английское слово «кластер» можно перевести как «гроздь», «пучок»).
Кластерный анализ состоит в разделении множества результатов наблюдений на подмножества — кластеры, так, чтобы все результаты, принадлежащие к одному кластеру, обладали некими общими свойствами, необязательно очевидными. Кластеризация данных значительно упрощает их графическое представление, а также позволяет специалистам по визуализации понять изображаемые данные. Существует множество алгоритмов кластеризации, и каждый из них обладает особыми математическими свойствами, которые делают его пригодным для тех или иных типов данных.
Распознавание образов
В главе об анализе данных нельзя обойти стороной тему распознавания образов как одну из основных целей анализа. Для распознавания образов можно использовать все описанные выше средства: нейронные сети, метод опорных векторов, метод главных компонент и другие. Как вы видите, распознавание образов имеет непосредственное отношение к машинному обучению.
Цель системы-классификатора, подобно нейронной сети или методу опорных векторов, — предсказать, к какому классу относится данная выборка, то есть классифицировать ее. Поэтому системе-классификатору в целях обучения следует передать множество выборок известных классов. После обучения системы ей можно будет передавать для классификации новые выборки. Как и в описанных выше методах, начальное множество выборок известных классов обычно делится на два подмножества — обучающее и тестовое. Тестовое множество помогает проверить, не переобучена ли система.
При создании классификаторов применяются два подхода: мичиганский, предложенный исследователями из Мичиганского университета, и питтсбургский, появившийся, соответственно, в университете города Питтсбурга. В мичиганском подходе описывается эволюционный алгоритм, в котором в роли эволюционирующих особей выступают правила, каждое правило содержит множество условий и цель.
Класс выборки укажет правило, с набором условий которого совпадает выборка.
В питтсбургском подходе, напротив, каждая особь представляет собой множество правил, а приспособленность особи оценивается по средней ошибке для каждого из этих правил. Оба подхода, которые в немалой степени дополняют друг друга, имеют свои преимущества и недостатки. В последние 30 лет исследователи предлагают различные улучшения обоих подходов, чтобы компенсировать их неэффективность.
Практический пример: анализ продаж
Еще одна важная область применения искусственного интеллекта в бизнесе — это работа с хранилищами данных, которые широко используются предприятиями с большой клиентской базой и, следовательно, с большой базой выборок. Путем анализа базы выборок можно определить тенденции, закономерности и шаблоны поведения. Хранилище данных — это место, куда стекаются данные со всего предприятия, будь то данные о продажах, производстве, результатах маркетинговых кампаний, внешних источниках финансирования и так далее. Сегодня хранилища данных используются в таких областях, как банковская сфера, здравоохранение, розничная торговля, нефтепереработка, государственная служба и другие.
Создание и структурирование хранилища данных — сложная задача, на решение которой инженерам потребуется несколько месяцев и даже лет. После того как хранилище данных выстроено, структурировано и обеспечена его корректность, содержащиеся в нем данные изучаются и анализируются с помощью так называемых OLAP-кубов, которые в действительности представляют собой гиперкубы. OLAP-куб (от англ. OnLine Analytical Processing — «аналитическая обработка в реальном времени») — это многомерная структура данных, позволяющая очень быстро выполнять перекрестные запросы к данным различной природы. О LAP-куб можно считать многомерным вариантом электронной таблицы. К примеру, электронная таблица, в которой представлены данные о продажах молочных продуктов нашей компании в разных странах в прошлом году (в тысячах штук), может выглядеть так.
Если мы хотим получить данные о продажах в отдельные месяцы, нужно добавить к таблице третье измерение, в котором для каждого региона и типа продукции представленные данные будут разбиты на 12 месяцев.
Сформировав куб, мы сможем выполнять различные виды сложного анализа данных с учетом предварительно выстроенной структуры куба. Заметим, что основные затраты вычислительных ресурсов при использовании хранилища данных связаны не с самим анализом данных, а с построением множества гиперкубов. Гиперкубы могут отражать данные организации с учетом множества возможных сочетаний. Поэтому OLAP-кубы, как правило, строятся по ночам, а используются и анализируются на следующий день.
С помощью OLAP-кубов аналитики компании, производящей молочные продукты, могут ввести в систему новое измерение — погодные условия в каждый день года в каждом регионе, где продаются продукты компании. Это новое измерение позволит изучить уровень потребления различных продуктов в зависимости от температуры.
Располагая этими знаниями и прогнозами погоды, аналитики могут предсказать, какой объем всех видов продукции следует произвести в каждом регионе, чтобы свести запасы молочной продукции к минимуму. Отметим, что соблюдение температурного режима хранения молочных продуктов требует немалых расходов.
Часто измерения OLAP-кубов дополнительно усложняются, и в пределах одного измерения вводятся иерархии. Так, в предыдущем примере измерение, описывающее погоду, можно дополнить новой иерархией, например привести данные о погоде за каждый день или в каждом квартале, так как уровень потребления молочных продуктов будет гарантированно отличаться летом и зимой, в начале и в конце месяца.
Можно сформировать иерархию регионов и ввести как более крупные (Центральная Европа, Южная Европа), так и более мелкие области (Ломбардия, Бретань, Андалусия).
Разумеется, после завершения построения с помощью OLAP-кубов можно решать различные задачи визуализации данных, помимо очевидного анализа, о котором мы уже рассказывали. К примеру, можно изображать двухмерные сечения куба или отдельные «кубики» (небольшие многомерные части куба), складывать или вычитать значения в рамках иерархий и даже вращать куб, чтобы взглянуть на данные с другой стороны.
* * *
MICROSOFT RESEARCH
Сегодня крупнейшим коммерческим исследовательским центром мира, где ведутся работы по изучению искусственного интеллекта, является Microsoft Research. В этом центре работают авторитетные ученые, которые занимаются изучением столь важных вопросов, как машинное обучение или новые способы взаимодействия человека и машины. Microsoft Research имеет представительства в самых разных странах, в частности в Германии, США, Великобритании, Китае, Индии и Египте.
Специалисты центра являются мировыми лидерами в области использования байесовских сетей и других вероятностных методов в таких областях, как обнаружение нежелательных писем (спама) или интеллектуальная адаптация интерфейса информационных систем к шаблонам поведения пользователей.
Глава 6. Искусственная жизнь
Дать определение понятиям «жизнь» и «интеллект» трудно как с точки зрения биологии, так и с точки зрения философии. Возможно, это так же сложно, как и дать формальное определение интеллекта. В первой главе мы уже говорили о философских и математических дискуссиях, целью которых было определение понятия «интеллект»: это тест Тьюринга, «китайская комната», споры о творчестве и так далее.
Один из самых активных и авторитетных специалистов в этой области, Джон Холланд (род. 1929), также занимавшийся эволюционными алгоритмами, глубоко изучил этот вопрос и пришел к выводам, которые помогут нам определить, что такое жизнь.
Искусственная жизнь тесно связана с другим важным понятием в рамках искусственного интеллекта — так называемыми мягкими вычислениями (soft computing).
Мягкие вычисления — это совокупность средств и методов, как правило, имеющих непосредственные аналогии в природе, которые позволяют решать задачи высокой сложности путем обработки неполной и неточной информации. К таким методам относятся эволюционные алгоритмы, нейронные сети, нечеткая логика и так далее.
Мягкие вычисления оформились в отдельный раздел информатики в 1990-е годы и сегодня используются при решении задач, для которых эксперты не смогли найти оптимального решения. В некоторых случаях оптимальное решение подобных задач требует нескольких лет расчетов или использования данных, которые невозможно получить. Мягкие вычисления позволяют быстро найти неоптимальное, но достаточно хорошее решение задач такого типа. Сегодня мягкие вычисления используются для решения задач во всех областях науки и техники, начиная от биологии и заканчивая политологией.
Введение в искусственную жизнь
Одно из важнейших свойств системы, в которой есть «жизнь», таково: в ней должны присутствовать определенные условия, которые делают возможным появление самоорганизующихся систем, намного более сложных, чем их составные части.
Прекрасный пример такой системы — колония муравьев, в которой относительно несложное поведение простых элементов, муравьев, порождает полностью самоорганизующуюся систему — колонию, намного более сложную, чем сумма ее частей.
Еще одна характеристика жизни заключается в том, что живой организм должен уметь выживать в среде, в лучшем случае — оставить потомство. Чтобы организм можно было назвать живым, он должен иметь определенную неслучайную динамику, независимую от возможных изменений окружающей среды. Также живая система должна обладать повторяющимся, но неравномерным поведением. Иными словами, если действие нового процесса очевидно, но при этом он является циклическим, то сущность, в которой проявляется этот процесс, нельзя считать живой.
Утка Жакаде Вокансона (1709–1782) — возможно, первого инженера, занимавшегося искусственной жизнью.
Как читатель уже понял, определить жизнь и интеллект со всей математической точностью непросто. До сих пор не найден простой критерий, позволяющий выяснить, можно ли считать живым тот или иной искусственный либо естественный объект. Споры о сущности жизни выходят далеко за рамки математики и информатики.
Даже в биологии ученые до сих пор не пришли к единому мнению по некоторым вопросам, связанным с жизнью, к примеру, можно ли считать живым организмом вирус. И можно ли считать живым организмом компьютерный вирус? Проанализируем ситуацию: компьютерные вирусы очевидно обладают динамическим поведением, которое не является регулярным или циклическим. Но можно ли сказать, что компьютерные вирусы возникли естественным образом? Скорее всего нет, так как они созданы злоумышленником-программистом, в то время как обычные вирусы возникли естественным путем.
* * *
ВИРУСЫ И ПРИОНЫ
Вирусы это биологические системы, сами по себе не способные к размножению, поэтому большинство биологов не считает их живыми организмами, однако консенсус по этому вопросу до сих пор не достигнут. Существует множество видов вирусов, но все они обладают общим свойством — в них присутствует генетический материал, который вирусы передают хозяевам при заражении. В результате появляются новые копии вируса, разумеется, несущие в себе этот генетический материал. Копии вируса распространяются по организму хозяина и поражают новые и новые клетки.
Прионы, в свою очередь, еще более просты и не имеют генетического материала, однако способны передаваться от одного организма к другому. Механизм передачи прионов до сих пор неясен, но сегодня они представляют большой научный интерес, поскольку вызывают серьезные заболевания, например губчатую энцефалопатию крупного рогатого скота (коровье бешенство).
Прионы — это естественные белки с аномальной структурой. Вступая в контакт с другим белком в организме, прион вызывает изменения в его структуре. В результате затронутый белок перестает функционировать, а его аномальная структура передается другим белкам. Является ли прион живым организмом? По мнению биологов, нет.
Схема строения вируса.
* * *
«ЖИВЫЕ» ВЫЧИСЛЕНИЯ
В этой главе рассказывается об искусственных системах, имитирующих поведение живых организмов, а также о вычислительных системах, построенных на основе живых организмов.
Процессоры современных компьютеров состоят из сотен миллионов транзисторов, в которых все вычислительные операции выполняются с помощью электрических сигналов. Транзисторы — безжизненные объекты, изготовленные из неорганических элементов, например кремния.
Но можно ли заменить транзисторы живыми организмами, состоящими из клеток? В последнее время биологам и физикам удалось решить эту задачу и заставить живые клетки выполнять математические действия, подобно транзисторам. Следовательно, в будущем ученые смогут создать системы искусственной жизни на основе биологических вычислений. Станут ли компьютеры будущего живыми существами, которые будут питаться обычной едой, а не электричеством?
Сложные адаптивные системы
Чтобы упростить определение понятия «жизнь», некоторые эксперты предложили более общее понятие сложной адаптивной системы. Сложная адаптивная система — это агент или совокупность агентов, действующих совместно, при этом достаточно разумных, чтобы адаптироваться к окружающей среде, когда поведение других систем меняется. Под определение сложной адаптивной системы подпадает более широкий спектр живых систем, чем те, что приходят нам в голову, когда мы слышим термин «живой организм». К сложным адаптивным системам относятся иммунная система человека, торговая корпорация или целая экосистема. Пример с корпорацией достаточно любопытен, поскольку вряд ли ее можно считать «живой». Однако если тщательно подумать, то станет очевидно: корпорация рождается, растет, может оставить потомство и умереть. В большинстве европейских стран корпорации имеют почти такие же права и обязанности, как и обычные люди, да и названия у них схожи: если людей называют физическими лицами, то корпорации — юридическими лицами.
Ученые сходятся на том, что сложную адаптивную систему определяют семь характеристик: четыре свойства и три механизма. Сочетание этих основных характеристик порождает новые свойства и механизмы. Определение сложной адаптивной системы носит несколько более общий характер, чем определение самого понятия «жизнь» с точки зрения биологии: мы никогда не назвали бы финансовую компанию или город живыми. Поэтому неоднозначный термин «искусственная жизнь», определить который совсем не просто, обычно используется разве что в сенсационных заголовках и в рассуждениях дилетантов.
* * *
SIMCITY И СЛОЖНЫЕ АДАПТИВНЫЕ СИСТЕМЫ
Города — прекрасные примеры сложных адаптивных систем. Компьютерная игра SimCity, позволяющая строить города и симулировать их жизнь, — прекрасная возможность познакомиться со сложными адаптивными системами: сама игра наполняет города жителями, генерирует социальную и рыночную активность и ставит игрока перед сложными ситуациями, требующими решения (разрушение коммуникаций или стихийные бедствия).
Еще одна компьютерная игра, дающая возможность познакомиться со сложными адаптивными системами, — Civilization, ее цель — создать целую конкурентоспособную цивилизацию с городами, путями сообщения, оборонительными сооружениями, заключить торговые договоры с соседями, определить социальную и научную политику.
Город, построенный в игре SimCity.
Первое свойство: агрегирование
Агрегирование — это объединение простых сущностей, в результате которого образуется система, более сложная, чем сумма ее составных частей. Представьте себе муравейник и муравьев — адаптируемость всей колонии к изменениям среды намного выше, чем адаптируемость отдельного муравья. Простые сущности, образующие систему, называются агентами.
Агрегирование является рекурсивным процессом: агент, возникший в результате агрегирования других, более простых агентов, может объединиться с другими агентами того же или другого вида и образовать агрегированный агент второго уровня.
К примеру, результатом агрегирования конечной продукции, потребленной обществом, капиталовложений и государственных расходов будет валовый внутренний продукт страны.
Следует отметить, что коммуникация между элементами одной категории или между элементами, образующими объект более высокого уровня, не является частью агрегирования, однако без нее адаптация к среде невозможна.
Первый механизм: присвоение меток
Присвоение меток — механизм, активно упрощающий агрегирование агентов. Присвоение меток не только упрощает идентификацию агентов, но и помогает разрушить симметрию, часто возникающую при агрегировании в сложных системах. К примеру, если мы начнем вращать белый бильярдный шар в одном направлении и на его поверхности будут отсутствовать какие-либо метки, то наблюдатель едва ли сможет увидеть, что шар вращается, и тем более не сможет определить скорость вращения.
Если же мы нанесем на поверхность шара метку в любой точке за исключением тех двух, в которых ось вращения шара пересекает его поверхность, то наблюдатель легко сможет определить направление и скорость вращения.
Агенты при агрегировании помечаются множеством разных меток, начиная от штандартов с изображением орла — отличительных знаков римских легионов, и заканчивая сложными метками, которыми современные телекоммуникационные устройства помечают передаваемые сообщения (эти метки указывают, в каком порядке следуют части сообщения, чтобы получатель мог восстановить сообщение целиком, а также содержат сложные механизмы обнаружения возможных ошибок в сообщении или самой метке в процессе передачи). Разумеется, не все метки должны быть видимыми: к примеру, млекопитающие обоих полов, принадлежащие к определенным видам, в период спаривания выделяют невидимые глазу вещества — феромоны.
Метки упрощают избирательное взаимодействие между агентами, так как позволяют различать экземпляры одного и того же класса агентов или различные составные части агента. На основе меток возможна реализация фильтров, схем сотрудничества, а также видообразование. Агенты также могут сохранять агрегированное состояние, и их метки будут оставаться неизменными, даже если будут меняться составные части агента более высокого уровня. По сути, нанесение меток — механизм, упрощающий организацию агентов и коммуникацию между ними.
Второе свойство: нелинейность
Свойство линейности лежит в основе множества математических дисциплин, начиная от арифметики и заканчивая алгебраической топологией, не говоря уже о дифференциальном исчислении. Функция линейна, если ее значение представляет собой всего лишь взвешенную сумму ее аргументов (независимо от их значений). К примеру, функция 4х + 2у — z линейна, функция 4 sinx — 2y-z — нет.
Использование линейных методов в математике и инженерном деле настолько важно, что сегодня большая часть профессиональной деятельности любого инженера и ученого заключается в поиске линейных функций, максимально точно описывающих те или иные явления природы. К сожалению, ни один из этих методов неприменим для изучения сложных адаптивных систем. По сути, одна из важнейших особенностей таких систем заключается в том, что их совокупное поведение намного сложнее суммы поведений отдельных частей, из чего, по определению, следует нелинейность.
Прекрасный пример, иллюстрирующий нелинейности в природе и сложных адаптивных системах, — взаимодействие «производитель — потребитель» и его частный случай — взаимодействие «хищник — жертва». Представьте себе лес, где живет D хищников (например, лис) и Р жертв (например, зайцев). Если вероятность того, что лиса поймает зайца, равна с, то ежедневно в лапы лис попадает с∙Р∙D зайцев. К примеру, если с = 0,5, D = 3 и Р = 10, то лисы поймают с ∙Р∙D = 0,5∙3∙10 = 15 зайцев. Если число лис и зайцев увеличится вчетверо, число пойманных зайцев возрастет еще больше: с∙Р∙D = 0,5∙12∙40 = 240. Как видите, этот результат нельзя получить простым сложением числа хищников и жертв.
Даже в сравнительно простой ситуации нелинейность может серьезно повлиять на агрегированную систему. Поэтому всегда говорят, что совокупное поведение сложной адаптивной системы сложнее, чем поведение ее составных частей.
* * *
МОДЕЛЬ ЛОТКИ — ВОЛЬТЕРРЫ
Уравнения, описывающие пример с лисами и зайцами, могут значительно усложняться. Исследователь Альфред Джеймс Лотка описал, как изменятся эти уравнения, если мы будем учитывать колебания численности хищников и жертв с течением времени. Допустим, что D(t) и P(t) — численность хищников и жертв в момент времени t. В каждый момент времени рождается n и умирает m хищников. Следовательно, формула, описывающая изменение численности хищников с течением времени, записывается так: D(t + 1) = D (t) + nD(t) — mD(t). Аналогично изменение численности жертв описывается уравнением: Р(t + 1) = Р(t) + n'Р(t) — mV(t). Следует учесть, что рост числа жертв означает рост рождаемости хищников, что можно выразить, к примеру, с помощью постоянной r.
Число взаимодействий «жертва — хищник», как мы показали, равно cPD. Следовательно, новое уравнение, описывающее численность хищников, будет выглядеть так:
D(t+1) = D(t) + nD(t) — mD(t) + r[cP(t)∙D(t)]
Изменение численности жертв будет происходит прямо противоположным образом: при любом взаимодействии «хищник — жертва» численность жертв будет сокращаться. Уравнение численности жертв будет иметь вид:
P(t+1) = P(t) + r[P(t) — m'P(t) — r[cP(t)∙D(t)].
Если теперь мы зафиксируем значения постоянных и будем решать эти уравнения для последовательных моментов времени, то увидим, что D(t) и P(t) будут колебаться, а хищники и жертвы будут последовательно переживать циклы изобилия и голода.
График, описывающий колебания численности зайцев и лис с течением времени согласно модели Лотки — Вольтерры.
Третье свойство: формирование потоков
Потоки возникают на всех уровнях сложных адаптивных систем, где присутствуют узлы, носители и переносимые ресурсы. Ограничимся двумя примерами сложных адаптивных систем. Первый — центральная нервная система живого организма, где узлами являются нейроны, носителями — соединяющие их синапсы, а переносимым ресурсом — электрические импульсы. Второй пример — потоки в экосистеме, где узлами являются виды, носителем — пищевая цепь, а переносимым ресурсом — энергия, представленная в виде биохимических элементов (потребляемого белка, сахара и так далее).
В общем случае узлы являются средствами обработки ресурса, а связи определяют взаимодействия между узлами. Следует учесть, что в сложной адаптивной системе сеть взаимодействий может меняться, а узлы и связи могут возникать и исчезать.
Эти особенности и обеспечивают адаптируемость системы к среде и позволяют ей корректировать свое поведение в зависимости от текущей ситуации.
Нанесение меток — один из самых важных механизмов сложных адаптивных систем для определения потоков: метки могут определять, какие связи играют важнейшую роль при переносе ресурсов.
Потоки обладают двумя свойствами, представляющими интерес при изучении работы сложных адаптивных систем. Первое свойство заключается в том, что потоки вносят в систему эффект мультипликатора. К примеру, в такой сложной адаптивной системе, как экономика страны, перенос денег от одного узла к другому (например, между банками) исполняет роль денежного мультипликатора. Второе интересное свойство — способность создания циклов с целью переработки. Обратите внимание, как на схеме нелинейно возрастает объем промышленного производства в сложной адаптивной системе — производственной цепочке изготовления автомобилей — при переработке и в ее отсутствие.
В первом сценарии производитель стали преобразует железную руду в сталь с эффективностью 100 % (то есть с коэффициентом 1). Далее 50 %, то есть половина произведенной стали, используется для производства автомобилей, оставшиеся 50 % — для изготовления бытовой техники. Если мы для простоты предположим, что из каждой единицы стали изготавливается автомобиль или единица бытовой техники, то получим, что в конце потока будет произведено 5 автомобилей и 5 единиц бытовой техники.
Теперь рассмотрим сценарий, в котором благодаря переработке возникает эффект мультипликатора.
Во втором сценарии 75 % автомобилей перерабатывается. Следовательно, теперь производитель стали может повысить объемы производства, что в конечном итоге позволит выпускать больше автомобилей. Если на первом этапе переработке подвергалось 5 автомобилей, то с последовательным повышением производительности система стабилизируется на уровне 8 выпускаемых машин и 6 машин, подвергаемых переработке, на каждом цикле. Это означает, что производство стали возрастет до 16 единиц: 10 единиц будет выплавляться из 10 единиц железной руды, еще шесть будет получено в результате переработки автомобилей.
Четвертое свойство: разнообразие
Разнообразие — еще одна определяющая характеристика сложных адаптивных систем. В любой сложной адаптивной системе наблюдается значительное разнообразие агентов, которые совместно определяют шаблоны поведения системы. В качестве примера приведем тропический лес, где можно пройти полкилометра и не увидеть двух деревьев одного вида. Или рассмотрим такую сложную адаптивную систему, как целый город, к примеру Рим, где живут миллионы самых разных людей со своими занятиями и особенностями, где работают тысячи компаний, по большей части непохожих друг на друга, при этом каждая из этих компаний, в свою очередь, также представляет собой сложную адаптивную систему.
Такое разнообразие вовсе не случайно. Каждый агент в рамках системы занимает свою нишу, которая определяется его связями с соседними агентами. Если мы исключим из сложной адаптивной системы один агент, другие автоматически займут его место. Когда система прекращает адаптироваться к условиям среды, наступает стабильное состояние, иными словами наблюдается сходимость.
Разнообразие также наблюдается, когда агент или совокупность агентов занимают новые ниши, в результате чего сложная адаптивная система получает новые функциональные возможности. Хороший пример — мимикрия, в ходе которой, к примеру, цветки орхидей имитируют внешний вид насекомых, чтобы привлечь других насекомых — переносчиков пыльцы и сделать опыление более эффективным.
Цветки растения офрис пчелоносная имитируют насекомых, чтобы привлечь других насекомых — переносчиков пыльцы.
Однако главный вопрос звучит так: какой фактор допускает и даже стимулирует возникновение столь большого разнообразия в сложных адаптивных системах? При подробном изучении таких систем можно последовательно проследить, какие изменения они претерпевали в процессе возникновения того или иного агента, и тем самым понять роль отдельных агентов в системе. К примеру, когда в сложной адаптивной системе в результате адаптации возникают циклические потоки, что ведет к переработке ресурсов и повышению общей эффективности, в ней открываются ниши, где появляются новые, «перерабатывающие» агенты. Другой пример сценария, порождающего разнообразие, — рост предприятия: в процессе роста возникает необходимость в новых иерархиях и, следовательно, в агентах нового типа, которые будут отвечать за координацию действий на каждом уровне иерархии.
Второй механизм: внутреннее моделирование
Любая сложная адаптивная система способна создавать внутренние модели окружающей среды, позволяющие предсказать будущие события и изменения, которые должны произойти для успешной адаптации системы к этим событиям. Такие модели строятся на основе информационных потоков, поступающих в систему и вызывающих полезные изменения ее внутренней структуры. После того как модель построена, она помогает системе предсказывать, какие последствия будет иметь появление определенных закономерностей в среде. Но как система может представить накопленный опыт в виде моделей? Как система создаст модель для прогноза последствий будущих событий?
Оптимальной движущей силой для создания подобных моделей является давление отбора. Бактерия всегда «знает», что ей нужно следовать в направлении, где находится больше питательных веществ. Этот «инстинкт» описывается внутренней моделью, указывающей, что если бактерия будет следовать подобной схеме поведения, то с наибольшей вероятностью гарантирует себе пропитание. Бактерии, которые благодаря кодификации структур и иерархий внутренних агентов смогли создать подобные модели, имеют больше шансов оставить потомство и, следовательно, передать ему это отличительное свойство.
Существует два вида внутренних моделей: явные и неявные. В примере с бактерией, следующей инстинктам в поиске питания, мы имеем дело с неявной моделью, так как она не позволяет ни «думать», ни моделировать альтернативные варианты развития событий. Явные модели, свойственные высшим живым организмам, напротив, позволяют оценивать различные гипотетические сценарии и принимать оптимальные решения после анализа альтернативных вариантов. Примером явной модели в сложной адаптивной информационной системе может служить машина для игры в шахматы, способная анализировать сотни тысяч вариантов на каждом ходу.
Логично, что неявная модель создается и адаптируется к среде по законам эволюции, в то время как для явных моделей скорость адаптации намного выше.
Колония бактерий Escherichia coli, увеличенная в 10 000 раз. Каждая «палочка» обозначает бактерию.
Третий механизм: строительные блоки
Внутренняя модель сложной адаптивной системы, как правило, основывается на ограниченном множестве выборок, описывающих ситуации, произошедшие в прошлом. Эти выборки похожи, но каждая из них обладает определенной новизной. Как сложная адаптивная система может создавать на базе ограниченного предшествующего опыта внутренние модели, полезные в будущем? Ключ к этому парадоксу — использование так называемых строительных блоков, то есть элементов, на которые можно разложить любую систему, среду или сценарий. Рассмотрим в качестве примера финансовую организацию, которая идеально соответствует определению сложной адаптивной системы. Допустим, что организация должна принять решение, выдавать ли клиенту кредит. Главный вопрос заключается в том, сможет ли клиент вернуть кредит в условленный срок. Банк не представляет, сможет ли клиент совершать платежи по кредиту через 15 лет, так как не способен предсказывать будущее. Усложним ситуацию и предположим, что клиент не имеет кредитной истории, то есть банку о нем ничего не известно. В этом случае банк разложит проблему на составляющие и, проанализировав определяющие характеристики нового клиента — уровень его образования, должность, семейное положение и другие, — рассмотрит поведение клиентов со схожим профилем. Эти характеристики будут строительными блоками, описывающими сценарий, с которым столкнулся банк как сложная адаптивная система.
Способность сочетать строительные блоки для создания неявных внутренних моделей развивается по законам эволюции, а обучение явных внутренних моделей обычно проходит в гораздо более короткие сроки, хотя в природе такой способностью обладают только высшие живые организмы.
Клеточные автоматы
Классическим примером искусственной жизни (вернее, сложной адаптивной системы) в информатике являются клеточные автоматы. Клеточный автомат — достаточно простое понятие, предназначенное для изучения сложности высших систем.
Оно было предложено авторитетными математиками и друзьями Станиславом Уламом (1909–1984) и Джоном фон Нейманом (1903–1957).
Американский математик польского происхождения Станислав Улам.
Автоматы — это математические модели, которые для определенных входных значений запрограммированы на выполнение ряда инструкций. Иными словами, автомат — это обобщение алгоритма или компьютерной программы. Таким образом, в информатике автоматами является все, от программируемого микрочипа, способного выполнять определенные действия, и заканчивая операционной системой. Еще один пример автомата, о котором мы уже рассказывали, это машина Тьюринга.
Как правило, теоретические автоматы, подобные машине Тьюринга, — это устройства, фиксирующие входные сигналы и печатающие выходные значения на одномерных лентах. Автомат проходит вдоль ленты и считывает написанные на ней символы, как показано на рисунке. На основе считанных символов и заложенных в автомат инструкций он выполняет то или иное действие, к примеру, печатает на определенном участке ленты некий символ.
Два основных компонента машины Тьюринга — бумажная лента и устройство чтения-записи.
Клеточные автоматы представляют собой особый класс автоматов, которые не перемещаются по поверхности двухмерных лент. В них среда, содержащая входные и выходные значения, представляет собой плоскость, разделенную на клетки подобно шахматной доске, причем в каждой клетке расположен неподвижный клеточный автомат. Входную информацию в клеточном автомате содержат клетки, смежные с той, в которой он находится. Выходная информация фиксируется в клетке, где расположен сам клеточный автомат.
Каждый автомат, находящийся в одной из клеток доски, содержит ряд инструкций. К примеру, если число черных клеток, окружающих клетку, где расположен клеточный автомат, четно, он закрасит свою клетку в черный цвет, в противном случае — в белый. Поместив аналогичные автоматы во все клетки доски, мы получим различные рисунки, которые будут меняться в зависимости от того, в какой цвет разные автоматы будут закрашивать те или иные клетки.
Некоторые из бесконечного множества возможных конфигураций клеточного автомата порождают повторяющиеся узоры, как, например, в игре «Жизнь» Конвея.
Читатель найдет в интернете множество фигур, порождающих прекрасные рисунки, которые затем уничтожаются и создаются вновь, причем все подобные фигуры описываются очень простыми правилами.
Паровая машина Тьюринга. Рисунок, сделанный студентами Вашингтонского университета в одной из аудиторий.
* * *
КЛЕТОЧНЫЙ АВТОМАТ ДЖОНА КОНВЕЯ, ИЛИ ИГРА «ЖИЗНЬ»
Игра «Жизнь», придуманная Джоном Хортоном Конвеем (род. 1937), представляет собой клеточный автомат, который, несмотря на простоту, демонстрирует удивительное поведение. Правил, описывающих его работу, всего два. В них учитываются восемь клеток, смежных с каждой, а также состояние самой клетки, в которой расположен клеточный автомат.
Правило № 1: если у белой клетки три соседние с ней клетки имеют черный цвет, то эта клетка также окрашивается в черный цвет. В противном случае клетка остается белой.
Правило № 2: если клетка окрашена в черный, а две или три соседние с ней клетки также черного цвета, то клетка не меняет цвет. В противном случае она становится белой.
Если читатель знаком с основами программирования, мы советуем ему реализовать эти простые правила в программе, чтобы посмотреть на игру «Жизнь» в действии. Для всех остальных далее приведено несколько примеров.
Это одна из конфигураций, возникающих при программировании правил игры «Жизнь», известная как «планер». Она порождает следующую циклическую последовательность.
Как показано на иллюстрации, фигура t + 4 идентична фигуре t, но смещена на одну клетку вниз и вправо. Следовательно, в момент времени t + 9 «планер» (именно так называется фигура, изображенная на рисунке) вновь сместится вдоль диагонали, отмеченной на иллюстрации ниже.
Более сложная версия «планера». Если бы изображение было анимированным, вы смогли бы увидеть, что рисунки, расположенные под стрелкой, смещаются вдоль линии, отмеченной на иллюстрации.
Искусственные иммунные системы
Имитация разумного поведения природы всегда была источником вдохновения для инженеров, занимающихся искусственным интеллектом. В свое время природа подсказала человеку идею нейронных сетей и эволюционных алгоритмов, которые сыграли важнейшую роль в развитии искусственного интеллекта. О них мы уже рассказывали в прошлых главах. Аналогично возникли и другие модели, в частности искусственные иммунные системы, в которых предпринята попытка сымитировать поведение иммунной системы живых существ, или роевой интеллект — попытка смоделировать отдельное и простое поведение членов колонии (например, пчелиного роя), в совокупности демонстрирующих определенное поведение, которое можно назвать интеллектуальными.
Иммунная система животного представляет собой крайне эффективную систему распознавания образов и оптимизации. Для каждой новой задачи, которую необходимо решить (то есть для нового антигена, попадающего в тело), путем упорядоченного процесса проб и ошибок иммунная система быстро находит решение — антитело, способное распознать антиген.
Действие иммунной системы напоминает эволюционный процесс с одним отличием: при работе иммунной системы не происходит скрещивания различных решений с целью выявления среднего решения, сочетающего в себе достоинства родительских. Действие иммунной системы можно представить следующим образом.
1. Случайным образом генерируется обширное множество антител.
2. Оценивается пригодность каждого антитела, или его способность распознать антиген, попавший в организм.
3. На основе антител первого поколения по следующей схеме создается второе поколение.
1) Генерируется множество копий антител. Число копий каждого антитела пропорционально его пригодности. Иными словами, новое поколение будет содержать много копий очень эффективных антител, а неэффективные антитела будут присутствовать лишь в нескольких копиях или вовсе не попадут в следующее поколение.
2) В копии антител вносятся изменения (мутации, если использовать терминологию эволюционных алгоритмов) обратно пропорционально их эффективности. Иными словами, копии эффективных антител в новом поколении почти не изменятся, а копии неэффективных антител претерпят серьезные изменения.
4. Для новых антител, полученных на предыдущих этапах, вновь оценивается способность распознавать искомый антиген, после чего весь процесс повторяется, и создается новое поколение антител.
5. Когда биологическая система считает, что эффективное антитело для борьбы с антигеном найдено, процесс останавливается.
Описанный выше процесс создания антител в иммунной системе нетрудно адаптировать для решения других реальных задач. Единственный важный момент заключается в том, как правильно представить возможные решения проблемы, чтобы их можно было копировать и видоизменять. В этом случае рекомендуется следовать той же методологии, что и при использовании эволюционных алгоритмов, то есть кодировать решения с помощью хромосом, состоящих из генов. Хотя мы смешиваем терминологию из двух, на первый взгляд совершенно разных методов, описанный выше процесс применяется на практике. Искусственные иммунные системы все чаще используются для решения реальных инженерных задач, поскольку они позволяют эффективно оптимизировать решения, а также прекрасно адаптируются к архитектуре современных суперкомпьютеров и распределенных вычислений (в частности, грид-вычислений и облачных вычислений). При грид-вычислениях и облачных вычислениях ресурсы распределены в абстрактном и нечетком «облаке» компьютеров, очень мощных по отдельности, при этом обмен данными между ними необязательно должен быть эффективным. При централизованном контроле над иммунной системой оценка антител может производиться в облаке, а по завершении оценки следующее поколение антител будет создаваться центральной системой контроля. В этом сценарии наибольшие вычислительные затраты связаны с индивидуальной оценкой антител, именно поэтому она проводится в облаке. Создание новых поколений может выполняться последовательно с небольшими затратами в центральной системе.
Роевой интеллект
Создатели роевого интеллекта (англ, swarm intelligence) также черпали вдохновение в природе. Этот термин был введен Херардо Бени и Ван Цзином в конце 1980-х. Роевой интеллект основан на моделировании поведения множества отдельных простых сущностей таким образом, что их совокупное поведение может считаться интеллектуальным. Основная задача при реализации роевого интеллекта — определить, как именно отдельные сущности взаимодействуют со своими соседями и средой. Если эта политика взаимодействий определена корректно, то при агрегировании всех сущностей колонии, или роя, будет наблюдаться совокупное интеллектуальное поведение.
Рассмотрим практический пример, в котором имитируется поведение стаи птиц, кружащей в небе. Допустим, что мы хотим найти оптимум сложной математической функции, насчитывающей сотни измерений, со множеством локальных максимумов и минимумов. Вначале (то есть в момент времени t = 0) расположим сто «птиц» случайным образом, но вблизи друг от друга, на некоторой части области определения функции. Всякий раз, когда мы движемся вперед вдоль оси времени (t' = t + 1), каждая «птица» должна учитывать всего два параметра: направление (А), в котором располагается «центр масс» стаи, то есть среднее направление, указывающее, где находятся остальные члены стаи, чтобы не слишком отдаляться от них, и направление (В) максимального градиента функции, которую необходимо оптимизировать — так как мы хотим найти максимум функции, нужно определить, в каком направлении функция возрастает быстрее всего. На основе двух вычисленных направлений А и В рассчитывается третье, С = А + В. Каждая «птица» должна немного сместиться в этом направлении С. Так как все «птицы» подчиняются этим правилам поведения, стая будет двигаться вдоль графика функции, не слишком отдаляясь от него, в поисках глобального максимума. Преимущество использования группы «птиц» позволяет увеличить выборочное пространство и снизить вероятность попадания в локальные максимумы, далекие от глобального.
На рисунке черными точками обозначены различные «птицы» стаи, белой точкой — центр масс стаи. Стрелкой указано направление, в котором следует стая в поисках глобального максимума.
Роевой интеллект имитирует движение некоторых птиц, к примеру скворцов, которые собираются в огромные стаи, вычерчивающие в небе весьма любопытные фигуры.
Несмотря на инновационный характер роевого интеллекта, его полноценное использование для решения реальных задач только начинается. Сегодня активно рассматривается возможность применения роевого интеллекта в автоматически управляемых транспортных средствах. Наиболее интенсивные исследования в этой области ведутся в двух тесно связанных отраслях — авиакосмической и военной промышленности.
Области применения искусственной жизни
Искусственная жизнь — относительно новый раздел искусственного интеллекта, и многие области его применения только зарождаются. В будущем сложные задачи контроля, управления и планирования будут выполняться именно «живыми» системами, как это уже происходит на рынках ценных бумаг.
Теория игр
Теория игр — раздел математики, изучающий стратегии взаимодействия субъектов и процессы принятия решений. Конечная цель теории игр — определить оптимальные стратегии и спрогнозировать поведение субъектов в конкретных ситуациях.
Основы этой дисциплины заложили математики Джон фон Нейман и Оскар Моргенштерн во время холодной войны. Их целью был поиск оптимальных военных стратегий, однако теория игр быстро нашла применение в экономике, политике, этике, философии, биологии и, разумеется, вычислительной технике.
Теория игр крайне полезна при изучении сложных адаптивных систем, так как агенты, составляющие эти системы, часто должны соперничать или сотрудничать между собой для общего блага. При сотрудничестве часто происходит так, что отдельные усилия конкретного агента оказываются выше, чем общая выгода, пропорционально разделенная между всеми агентами, составляющими систему. Тем не менее эти отдельные усилия способны сыграть определяющую роль при достижении общего результата, который может на несколько порядков превышать индивидуальные усилия агентов. Таким образом, чтобы стимулировать адекватное поведение агентов, составляющих систему, и определить ее жизнеспособность на основе их поведения, необходимо использовать методы теории игр.
Знаменитый робот ASIMO, созданный в компании Honda, способен, подобно человеку, спускаться по лестнице и играть в футбол.
И вновь интеллектуальный анализ данных
Искусственная жизнь привлекательна и окутана тайной для непосвященных. Однако описанные нами понятия, которые скрываются за определением искусственной жизни, например клеточные автоматы, используются для решения достаточно прозаических инженерных задач, в частности для интеллектуального анализа данных, о котором мы уже рассказали. В задачах анализа данных для получения выводов требуется обрабатывать огромные объемы данных, что не под силу экспертам-людям. По этой причине для анализа обычно используются интеллектуальные информационные инструменты.
Анализ данных можно выполнить множеством средств, среди которых особое место занимают клеточные автоматы, так как они позволяют представить взаимосвязи между данными в пространстве. Допустим, что мы анализируем данные о продажах зонтов в конкретной стране. Сведения о продажах с разбивкой по клиентам могут быть обработаны без учета местоположения, в лучшем случае — разделены на категории по территориям: к примеру, клиент А из города X приобрел 20 единиц товара, клиент В из города У — 240 единиц, клиент С из города Z — 4530 единиц. В системе, где не учитывается территориальное распределение, города X, Y и Z — всего лишь категории, и мы никак не можем указать, что город X находится в 150 км к югу от Y, а Y — в 400 км южнее Z. Если мы будем учитывать эти данные, то станет понятно, что в северном регионе страны дожди идут чаще, а к югу продажи зонтов существенно снижаются.
Теперь представим данные о местоположении в виде таблицы, подобно тому, как это происходит при использовании клеточных автоматов. Постараемся связать расположение данных в таблице с реальным географическим местоположением регионов, откуда поступили данные о продажах. При таком представлении данных территориальное расположение можно учесть намного более интеллектуальным способом, чем при простом разбиении на категории.
После сведения данных в таблицу можно применить эволюционный алгоритм, позволяющий обнаружить правила, которые необходимо реализовать в клеточном автомате для анализа. Вернемся к примеру с продажами зонтов и дополним данные о продажах уровнем осадков в егионах. Мы можем разработать алгоритм, позволяющий получить множество правил, согласно которым раскрасим клетки таблицы в тот или иной цвет в зависимости от продаж зонтов в различных регионах, исключив влияние уровня осадков. Если мы представим данные о продажах на карте без учета уровня осадков, получим следующую картину.
Если мы исключим воздействие разного уровня осадков, карта будет выглядеть следующим образом.
На основе этих данных эксперт может определить, что объем продаж выше всего в центральных и южных регионах. Это означает, что уровень покупательной способности в этой части страны выше: из-за особенностей погоды зонты не являются товаром первой необходимости, однако люди готовы покупать их. Далее компания — продавец зонтов повысит цены в центре и на юге страны: хотя в этом регионе продажи меньше, люди покупают зонт не из необходимости, а как предмет роскоши, следовательно, менее чувствительны к цене.
Программирование роботов
Еще одна очень важная область, в которой используется искусственная жизнь и сложные адаптивные системы в целом, это программирование роботов. Постепенно широкому потребителю становятся доступными домашние роботы, способные пылесосить, протирать пол и даже определять вторжение посторонних в квартиру.
Такие роботы обычно мобильны, однако их перемещениями и действиями должна руководить интеллектуальная система. Рассмотрим роботов-пылесосов и покажем, как они соответствуют определению сложных адаптивных систем.
Робот-пылесос — один из самых известных домашних роботов.
— Агрегирование. Разумеется, эти роботы представляют собой агрегированные системы, так как содержат мотор, датчики присутствия, пылесос, устройство обработки данных, определяющее, в каком направлении должен двигаться робот, и так далее.
— Нанесение меток. Эти роботы могут присваивать метки различным элементам среды и взаимодействовать с ними. К примеру, если робот определяет, что некоторая область грязнее обычного, он помечает ее соответствующей меткой и прилагает больше усилий для ее уборки. Пользователь также может отметить зону, в которую робот не должен заходить, и он будет избегать этой зоны.
— Нелинейность. Поведение робота очевидно нелинейно, так как его части в совокупности способны решать намного более важные задачи, чем по отдельности. Мотор, колеса, пылесос и другие элементы робота независимо друг от друга не смогут провести уборку в доме без вмешательства человека, а когда все эти элементы объединены в сложную адаптивную систему, они способны убрать пыль самостоятельно.
— Потоки. Сам робот представляет собой сложную систему управления потоками информации, поступающей из внешней среды. Робот содержит ряд датчиков, которые фиксируют информацию о среде и указывают, что робот находится в особенно загрязненной области или перед ним располагается стена. Вся эта информация поступает в центральный процессор, который анализирует ее и отправляет сигналы различным деталям робота. Детали робота исполняют инструкции, изменяющие исходную среду, из которой изначально поступают сигналы. Если робот обнаруживает загрязненный участок, его процессор повышает мощность всасывания, а если робот сталкивается с препятствием, то процессор может дать указание совершить разворот.
— Разнообразие. Если робот наталкивается на препятствие, то ищет способы обойти его. Разнообразие заключается в том, что робот обходит препятствия по-разному — он постоянно чередует способы обхода, чтобы снизить вероятность попадания в бесконечный цикл.
— Внутренние модели. Робот содержит ряд неявных внутренних моделей: в начале работы он движется случайным образом, а по мере знакомства с территорией сосредотачивает внимание на особо пыльных участках.
— Строительные блоки. Роботы-пылесосы в своих внутренних моделях используют строительные блоки. К примеру, если робот сталкивается со стеной, он пытается обойти препятствие, затем понимает, что обойти стену нельзя, и применяет иную стратегию. Робот-пылесос не обучен адаптировать подобное поведение ко всем возможным типам стен или препятствий, напоминающих стены, он использует строительный блок под названием «стена» и при столкновении с ним следует определенной стратегии.
Эпилог
Предсказывать очень трудно. Особенно будущее.
Нильс Бор
Дочитав книгу до конца, читатель должен был получить некоторое представление о том, что является реальностью, а что — вымыслом в научно-фантастических рассказах, романах и фильмах, в которых часто изображаются мыслящие человекоподобные машины.
Сегодня искусственный интеллект представляет собой не более чем набор передовых средств, позволяющих быстро находить приближенные решения сложных задач на основе накопленного опыта, подобно тому, как это делает человек. Иногда подобные алгоритмы, которые стали доступны нам благодаря современной науке и технике, не чужды инновационного подхода и творчества. Однако машины, которые можно спутать с человеком, появятся еще не скоро, даже в тех областях, где исследователям удалось добиться наибольших успехов. И все же каждый день мы, сами того не осознавая, взаимодействуем с различными системами и устройствами, реализующими интеллектуальные алгоритмы, — это и системы управления европейскими поездами, и системы очистки сточных вод в большинстве крупных городов, и системы перевозок миллионов тонн грузов по планете.
Искусственный интеллект постепенно вошел в нашу жизнь. Рано или поздно настанет день, когда появятся машины, обладающие тем же уровнем креативности, ощущений и эмоционального интеллекта, что и человек. В день, когда это произойдет, мы поймем, что мы не одиноки.
Приложение. Разговор с «Элизой»
В первой главе мы уже привели короткий разговор с «Элизой» — «автоматическим психологом», созданным Джозефом Вейценбаумом. В этом приложении я приведу запись еще одного реального разговора, на этот раз более продолжительного, чтобы читатель смог оценить поведение программы в чуть более широком контексте.
Разумеется, все изложенные мной доводы абсолютно вымышленны и приведены в иллюстративных целях.
Элиза: Привет. Как дела? Расскажи о своей проблеме.
Игнаси Белда: У меня стресс.
Элиза: Как давно у тебя стресс?
Игнаси Белда: С тех пор, как мой редактор сказал, что я должен быстрее работать над книгой.
Элиза: А почему редактор требует, чтобы ты быстрее работал над книгой?
Игнаси Белда: Потому что он хочет, чтобы я закончил книгу до января.
Элиза: Это настоящая причина?
Игнаси Белда: Мне кажется, на редактора тоже оказывается давление.
Элиза: Можешь объяснить подробнее?
Игнаси Белда: Он сказал, что ему нужно достаточно книг для срочной публикации.
Элиза: И это объясняет, почему он хочет, чтобы ты быстрее работал над книгой?
Игнаси Белда: А что думаешь ты?
Элиза: Почему ты меня об этом спрашиваешь?
Игнаси Белда: Потому что это очевидно.
Элиза: А какие еще причины приходят тебе в голову?
Игнаси Белда: Мне кажется, что другие авторы задерживают сдачу рукописей.
Элиза: Ты имеешь в виду, что они задерживают сдачу рукописей по какой-то причине?
Игнаси Белда: Так сказал редактор.
Элиза: Тебе не кажется, что этому есть еще какая-то причина?
Игнаси Белда: Нет, все дело в том, что на него тоже оказывается давление.
Элиза: Ты несколько склонен к отрицанию.
Игнаси Белда: Почему ты так говоришь?
Элиза: Эта тема тебя интересует?
Игнаси Белда: Да, мне интересно знать, почему тебе кажется, будто я немного склонен к отрицанию.
Элиза: Я вижу.
Здесь автор устал ходить по кругу и прекратил разговор. Читатель заметил, что принцип действия программы в действительности очень прост. Первое, что пытается сделать «Элиза», получив новое утверждение, это поинтересоваться его причинами, затем причинами причин и так далее. Когда программа заходит в тупик, она пытается отвечать уклончивыми фразами вида «Ты несколько склонен к отрицанию» или «Я вижу».
Словарь
Автомат. Машина, необязательно имеющая физическое воплощение, которую можно запрограммировать так, что она будет определенным образом реагировать на поступающие входные сигналы.
Байесовская сеть. Математическая модель, основанная на вероятностных зависимостях между определенными событиями. Вероятностные зависимости описываются условной вероятностью — это понятие предложил священник Томас Байес в XVIII веке. Байесовские сети основаны на следующей идее: одним цепочкам событий с определенной вероятностью сопутствуют другие цепочки событий. Байесовские сети потому и называют сетями, что они представляют собой сплетенные друг с другом цепочки вероятностных зависимостей.
Булева логика. Математическая логика, основанная на булевой алгебре, в которой переменные могут принимать только два значения — «истина» и «ложь». На булевой логике основана вся современная цифровая электроника, за исключением последних разработок, связанных с квантовыми вычислениями.
Генетический алгоритм. Частный случай эволюционного алгоритма. В общем случае при использовании генетических алгоритмов решения рассматриваемой задачи представляются в виде последовательности битов. Последовательности (гены), описывающие лучшие решения (особи), скрещиваются между собой и мутируют, максимально точно имитируя процесс биологической эволюции. Генетические алгоритмы вошли в число первых эволюционных алгоритмов, которые способствовали росту популярности искусственного интеллекта.
Дерево принятия решений. Понятие, используемое в информатике для классификации статистических выборок. В основе классификации лежит анализ наиболее важных, или дискриминантных компонент, позволяющих однозначно отнести выборку к тому или иному классу. Деревья принятия решений очень просты и вместе с тем крайне эффективны для распознавания образов.
Интеллектуальный анализ данных. Раздел анализа данных, описывающий извлечение новых знаний и вывод неочевидных правил по итогам изучения больших объемов данных. При интеллектуальном анализе данных возможно установление отношений между данными, объем которых слишком велик, чтобы человек мог обработать их и сформулировать какую-либо гипотезу.
Кластеризация. Разбиение статистических выборок на группы согласно различным критериям. Цель методов кластеризации — интеллектуальное определение критериев разбиения выборки на подгруппы. Кластеризация используется множеством способов во всех научных дисциплинах.
Клеточный автомат. Частный случай программируемого автомата и простейший пример искусственной жизни. Клеточный автомат получает входные сигналы из смежных областей и в зависимости от окружающей среды действует тем или иным образом.
Латентная переменная. Статистическая переменная, описывающая несколько условий в выборке одновременно. Некоторые примеры часто применяемых латентных переменных — «богатство» общества или благосостояние населения. Эти переменные повышают плотность информации, так как сводят несколько простых переменных воедино. Существуют автоматические методы создания латентных переменных, в частности метод главных компонент, который позволяет не только создавать подобные переменные, но и выбирать те, для которых вариация данных будет наибольшей.
Машина Тьюринга. Частный случай программируемого автомата, который принимает входные значения, записанные на бесконечной ленте, и содержит устройство чтения-записи, способное перемещаться вдоль этой ленты. Предполагается, что машина Тьюринга — универсальная вычислительная машина, хотя это до сих пор не доказано математически. Машина Тьюринга — математическая абстракция, которая широко используется в теории коммуникаций: если в данном языке программирования возможна реализация машины Тьюринга, то с его помощью можно реализовать любой алгоритм.
Метод главных компонент. Этот метод, также обозначаемый англоязычной аббревиатурой РСА, — популярный метод статистики, используемый для определения компонент, или переменных, при которых вариация изучаемых данных является наибольшей.
Метод опорных векторов. Мощный и популярный математический метод, разработанный ученым Владимиром Вапником в начале XXI века. Метод опорных векторов позволяет классифицировать статистические выборки путем ввода новых «искусственных» измерений на множестве данных рассматриваемой задачи. Название метода связано с тем, что для классификации статистических данных определяются векторы — опоры гиперплоскости, которые лучше всего разделяют между собой выборки разных классов.
Нейронная сеть. Математическая модель, представляющая собой сеть искусственных нейронов, которые можно обучить для решения задач классификации. Нейронные сети имитируют поведение нервной системы живых существ, также состоящей из обученных нейронов.
Переобучение. Переобучение наблюдается в случае, когда алгоритм классификации в результате обучения оказывается не способным обобщать и может лишь запоминать. При переобучении алгоритм способен корректно классифицировать только выборки, запомненные во время обучения. Переобучение обычно происходит в случае, когда процесс обучения алгоритма оказывается слишком длительным. При агрегировании десятков или сотен подобных алгоритмов общий интеллект нелинейно возрастает и в итоге становится весьма высоким.
Разнообразие. Понятие, рассматриваемое в эволюционных вычислениях для определения генетической изменчивости популяции (множества предложенных решений) эволюционного алгоритма и ее эволюции с течением времени. Изучение генетического разнообразия крайне важно для определения оптимальной конфигурации алгоритма, результатом которой будет не локальный, а глобальный оптимум.
Роевой интеллект. Сложная искусственная система, используемая для решения определенных задач. Суть роевого интеллекта — программирование автоматов особым образом, позволяющим наделить их примитивным «интеллектом».
Универсальная вычислительная машина. Устройство, способное выполнить любой алгоритм. Универсальная вычислительная машина — математическая абстракция, позволяющая доказать, что в новом языке программирования или электронном устройстве можно реализовать все функции, необходимые для его использования.
Эволюционные вычисления. Дисциплина, изучающая эволюционные алгоритмы, их оптимальную конфигурацию и способы применения для решения задач. См. также Эволюционный алгоритм.
Эволюционный алгоритм. Метод поиска и оптимизации, основанный на принципах естественного отбора. В рамках эволюционного алгоритма выдвигаются возможные решения задачи, которые затем оцениваются, и путем сравнения лучших из них определяется оптимальное решение.
Экспертная система. Первые интеллектуальные компьютерные программы, которые представляли собой «экспертов» в той или иной области. Рассуждения этих программ ограничены знаниями, введенными в систему во время программирования. Экспертные системы почти не способны к обу чению по результатам нового опыта, поэтому в настоящее время практически не используются.
Энтропия Шеннона. Математическое понятие, широко используемое в телекоммуникациях для определения «беспорядочности», или энтропии, сигнала. Энтропия Шеннона представляет собой меру, описывающую число различных символов и частоту их появления в сигнале или источнике данных. Также применяется в криптографии и при сжатии данных.
Библиография
CASTI, J.L., El quinteto de Cambridge, Madrid, Taurus, 1998.
GOLDBERG, D.E., Genetic Algorithms in Search, Optimization, and Machine Learning, Boston, Addison-Wesley, 1989.
—: The Design of Innovation. Lessons from and for Competent Genetic Algorithms, Norwell, Kluwer Academic Publishers, 2002.
HOLLAND, J.H., Adaptation in Natural and Artificial Systemst Cambridge/Londres, MIT Press/Bradford Books, 1992.
—: Emergence. From Chaos to Order, Cambridge, Perseus Books, 1998.
—: Hidden Order. How Adaptation Builds Complexity, Reading, Perseus Books, 1995.
McElreath, R., Robert, B., Mathematical Models of Social Evolution. A Guidefor the Perplexed, Chicago, The University of Chicago Press, 2007.
* * *
Научно-популярное издание
Выходит в свет отдельными томами с 2014 года
Мир математики
Том 33
Игнаси Белда
Разум, машины и математика.
Искусственный интеллект и его задачи
РОССИЯ
Издатель, учредитель, редакция:
ООО «Де Агостини», Россия
Юридический адрес: Россия, 103066,
г. Москва, ул. Александра Лукьянова, д. 3, стр. 1
Письма читателей по данному адресу не принимаются.
Генеральный директор: Николаос Скилакис
Главный редактор: Анастасия Жаркова
Выпускающий редактор: Людмила Виноградова
Финансовый директор: Наталия Василенко
Коммерческий директор: Александр Якутов
Менеджер по маркетингу: Михаил Ткачук
Менеджер по продукту: Яна Чухиль
Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт , по остальным вопросам обращайтесь по телефону бесплатной горячей линии в России:
в 8-800-200-02-01
Телефон горячей линии для читателей Москвы:
в 8-495-660-02-02
Адрес для писем читателей:
Россия, 600001, г. Владимир, а/я 30,
«Де Агостини», «Мир математики»
Пожалуйста, указывайте в письмах свои контактные данные для обратной связи (телефон или e-mail).
Распространение:
ООО «Бурда Дистрибьюшен Сервисиз»
УКРАИНА
Издатель и учредитель:
ООО «Де Агостини Паблишинг» Украина
Юридический адрес: 01032, Украина,
г. Киев, ул. Саксаганского, 119
Генеральный директор: Екатерина Клименко
Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт , по остальным вопросам обращайтесь по телефону бесплатной горячей линии в Украине:
® 0-800-500-8-40
Адрес для писем читателей:
Украина, 01033, г. Киев, a/я «Де Агостини»,
«Мир математики»
Украïnа, 01033, м. Киïв, а/с «Де Агостiнi»
БЕЛАРУСЬ
Импортер и дистрибьютор в РБ:
ООО «Росчерк», 220037, г. Минск,
ул. Авангардная, 48а, литер 8/к,
тел./факс: (+375 17) 331-94-41
Телефон «горячей линии» в РБ:
® + 375 17 279-87-87 (пн-пт, 9.00–21.00)
Адрес для писем читателей:
Республика Беларусь, 220040, г. Минск,
а/я 224, ООО «Росчерк», «Де Агостини»,
«Мир математики»
КАЗАХСТАН
Распространение:
ТОО «КГП «Бурда-Алатау Пресс»
Издатель оставляет за собой право увеличить рекомендуемую розничную цену книг. Издатель оставляет за собой право изменять последовательность заявленных тем томов издания и их содержание.
Отпечатано в соответствии с предоставленными материалами в типографии:
Grafica Veneta S.p.A Via Malcanton 2
35010 Trebaseleghe (PD) Italy
Подписано в печать: 16.07.2014
Дата поступления в продажу на территории России: 02.09.2014
Формат 70 х 100 / 16. Гарнитура «Academy».
Печать офсетная. Бумага офсетная. Печ. л. 5.
Уcл. печ. л. 6,48.
Тираж: 28 900 экз.
© Ignasi Belda, 2011 (текст)
© RBA Collecionables S.A., 2011
© ООО «Де Агостини», 2014
ISBN 978-5-9774-0682-6
ISBN 978-5-9774-0728-1 (т. 33)


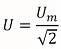


Комментарии к книге «Разум, машины и математика», Игнаси Белда
Всего 0 комментариев