Китайгородский Александр Исаакович «ФОТОНЫ И ЯДРА» «ФИЗИКА ДЛЯ ВСЕХ» Книга 4
Предисловие
Этой 4-й книгой серии «Физика для всех» заканчивается рассмотрение основ физики.
Что понимать под этим неопределенным словом «основы»?
Прежде всего те фундаментальные законы, на которых покоится все здание физики. Их не так много, так что можно даже перечислить: законы движения классической механики; законы термодинамики; законы, содержащиеся в уравнениях Максвелла и командующие над зарядами, токами и электромагнитными полями; законы квантовой физики и теория относительности.
Законы физики, как и всего естествознания, имеют эмпирическую природу. Мы приходим к ним путем наблюдения и эксперимента. Опытом устанавливается множество первичных фактов: строение вещества из атомов и молекул, ядерная модель атома, волново-корпускулярный аспект материи… Как число фундаментальных законов, так и число основных фактов и понятий, которые нужны для их описания, не так уж велико и во всяком случае ограничено.
За последние десятилетия физика разрослась настолько, что лица, работающие в разных ее областях, перестают понимать друг друга, как только разговор выходит за рамки того, что их объединяет в одну семью, — за пределы законов и понятий, лежащих в основе всех разделов физики. Отдельные главы физики тесно переплелись с техникой, с другими частями естествознание, с медициной и даже с гуманитарными науками. Неудивительно, что они оформились в самостоятельные дисциплины.
Вряд ли кто-либо будет спорить, что изложению областей прикладной физики должно предшествовать обсуждение основных законов и фактов. Но столь же очевидно, что разные авторы, в зависимости от своего индивидуального вкуса и узкой специальности, будут отбирать и компоновать материал, нужный для построения фундамента физики, каждый по-своему. На суд читателя выносится один из возможных вариантов изложения основ физики.
О круге читателей серии «Физика для всех» уже говорилось в предисловии к первым выпускам. Эти книги написаны для представителей всех профессий, желающих вспомнить физику, представить себе ее современный облик, оценить влияние на научно-технический прогресс и значение для формирования материалистического взгляда на мир. Многие страницы книг заинтересуют учителей физики и школьников, которые полюбили физику. Надо думать, что кое-что интересное для себя найдут в этих книгах и те читатели, которых отпугивают алгебраические формулы.
Разумеется, эта серия книг не имеет в виду, что кто-либо будет с их помощью изучать предмет. Для этого существуют учебники.
Книга «Фотоны и ядра» должна, по мысли автора, показать читателю, как работают законы электромагнитного поля и квантовой физики при рассмотрении поведения электромагнитных волн разной длины. Перед тем как перейти к разговору об атомных ядрах, читатель получит представление о волновой механике и специальной теории относительности. После изложения основных фактов, касающихся строения атомного ядра, мы перейдем к разговору о волнующей человечество теме об источниках энергии на Земле. И, наконец, закончим повествование кратким рассказом о физике Вселенной.
Малый объем книги не позволил остановиться на многих традиционных темах. Старому пришлось уступить место новому.
А. И. Китайгородский
Глава 1 Мягкое электромагнитное излучение
ОБМЕН ЭНЕРГИЕЙ ПУТЕМ ИЗЛУЧЕНИЯ
Мягким мы называем то электромагнитное излучение, длины волн которого лежат примерно в интервале от 0,1 до 100 мкм. При этом надо сделать еще одну оговорку. Говоря о мягком излучении, мы будем иметь в виду электромагнитные волны, которые создаются не радиотехническими способами. Эта оговорка необходима, ибо чисто радиотехническими методами можно «залезть» в область мягкого излучения.
Довольно часто мягкое излучение называют также световым. Пользуясь этим термином, надо не забывать, что видимый свет занимает лишь узкий участок длин волн, который для «среднего» человеческого глаза лежит в пределах от 380 до 780 нм (0,38—0,78 мкм).
Если дальше мы будем пользоваться термином «свет», то только в широком смысле слова, ибо законы, справедливые для видимого участка спектра, верны и для всех остальных представителей мягкого излучения.
Напомним также, что излучение более коротковолновое, чем видимый свет, носит название ультрафиолетового, а более длинноволновое — инфракрасного.
Теперь мы можем перейти к теме параграфа.
Как нам известно, существуют три способа обмена теплом. Явления носят названия теплопроводности, тепловой конвекции и теплового излучения. Для того чтобы исследовать обмен энергией, происходящий за счет теплового излучения, надо посмотреть, как ведут себя тела, находящиеся в вакууме (исключена конвекция) на некотором расстоянии друг от друга (исключена теплопроводность).
Опыт показывает, что если два или много тел образуют замкнутую систему (читатель помнит, что это означает отсутствие обмена энергией с предметами, которые в систему не входят), то температуры этих тел выравниваются. Каждое из тел системы является одновременно и излучателем, и поглотителем. Происходят бесчисленные акты переходов атомов и молекул с более высокого уровня на низкий (при этом испускается соответствующий фотон) и с более низкого уровня на высокий (фотон поглощается). В обмене энергией участвуют фотоны всех энергий, или, что то же самое, электромагнитные волны всех длин.
Разумеется, тело не поглощает всю энергию, которая на него падает. Могут быть такие тела, которые в большей степени рассеивают или пропускают через себя те или иные лучи. Но это дела не меняет: тепловое равновесие все равно наступает рано или поздно.
Условие теплового равновесия требует, чтобы отношение энергии поглощения к энергии испускания волны определенной длины было одинаковым для всех тел. Эту теорему строго доказал в 1860 г. немецкий физик Густав Кирхгоф (1824–1887). Для разных температур отношение может меняться, но если температура задана, оно будет одинаковым для фотонов заданной энергии.
Теорема в достаточной степени ясная. Можно сказать, что и в доказательстве она не нуждается. Смысл закона состоит в том, что число поглощенных фотонов данного сорта (т. е. данной энергии) при тепловом равновесии равно числу излученных фотонов того же сорта.
Отсюда следует такое правило: если предмет сильно поглощает какие-либо лучи, то эти же лучи он сильно излучает.
Это правило помогает предсказать условия, при которых наступит тепловое равновесие. Почему мало нагреется под действием солнечных лучей вода, заключенная в бутыль с посеребренными стенками, и сильно нагреется вода в фляжке из черного стекла? Объяснение очевидно: тело черного цвета сильно поглощает лучи, их энергия пойдет на повышение температуры, тепловое равновесие установится после сильного нагрева. Напротив, посеребренная поверхность является превосходным отражателем. Предмет поглощает мало энергии, нагревание будет идти лишь медленным темпом, равновесие установится при низкой температуре.
А теперь, так сказать, «переверните» опыт. Налейте горячую воду в обе фляжки и поставьте их в холодильник. В каком случае охлаждение произойдет быстрее? Быстрее нагрев, быстрее и охлаждение. Больше энергии поглощается, больше и отдается.
Очень эффектны опыты с цветной керамикой. Если предмет окрашен в зеленый цвет, то это значит, что черепок поглощает все цвета, кроме зеленого. Ведь глаз видит те световые лучи, которые отражаются или рассеиваются веществом. Теперь раскалим черепок. Каким мы его увидим? Ответ у вас уже на кончике языка: он нам представится фиолетовым, ибо фиолетовый — цвет, дополнительный к желто-зеленому. Про цвет говорят, что он дополнительный к такому-то, если в смеси эти два цвета дают белый.
Термин «дополнительные цвета» ввел в науку еще Ньютон, когда он с помощью стеклянной призмы разложил белый свет в спектр.
ИЗЛУЧЕНИЕ НАКАЛЕННЫХ ТЕЛ
Хорошо известно, что кусок металла, который начинают греть, сначала раскаляется докрасна, потом добела. Большинство химических веществ раскалить не удается. Они либо плавятся, либо разлагаются. Так что все сказанное ниже в основном относится к металлам.
Наиболее примечательным обстоятельством является то, что спектр излучения всех нагретых тел мало специфичен. Дело тут в следующем. Из основного закона об энергетических уровнях ясно, что спектр, излучения и спектр поглощения тела должны совпадать. Металлы непрозрачны для всей области спектра мягкого излучения. Отсюда следует, что они должны и излучать фотоны всех энергий.
Можно сказать и иначе: сплошной спектр возникает по той причине, что в многоатомной системе энергетические уровни атомов слились в перекрывающиеся полосы. В такой системе возможны любые энергетические переходы, т. е. любые разности энергий m-го и n-го уровней Еm — Еn, а значит, и любые частоты излучения и поглощения. На рис. 1.1 показан вид спектра раскаленного тела для нескольких температур (мы привели теоретические кривые, справедливые для так называемого абсолютно черного тела).
Надо сказать, что теоретический вывод формы такой кривой, сделанный Планком в 1900 г., явился первым шагом в становлении квантовой физики. Чтобы получить совпадение теории с опытом, Планку пришлось допустить, что излучение и поглощение света происходят порциями. Планк не решился на следующий шаг, а именно на утверждение, что вполне правомерно говорить о частицах света — фотонах. Этот шаг был сделан Эйнштейном в 1905 г.
МАКС ПЛАНК (1858–1947) — выдающийся немецкий ученый, положивший начало квантовой теории. Пытаясь найти математическое выражение, которое правильно описывало бы спектральное распределение излучения абсолютно черного тела, Планк показал, что такая формула может быть получена введением в теорию «кванта действия». Планк допустил, что тело испускает энергию порциями, равными произведению константы, которая впоследствии получила его имя, на частоту света.
И только в 1913 г. Бор ввел представление о квантовании энергии. Что же касается логически стройной теории теплового излучения, то ее становление надо датировать 1926 г.
Сначала обсудим вид этих кривых, а потом уже поговорим о теории. Прежде всего обратим внимание на то, что по мере повышения температуры площадь под кривой быстро растет. Какой физический смысл имеет площадь, обнимаемая кривой излучения? Строя график, подобный приведенному на рисунке, говорят, что по оси ординат отложена интенсивность излучения для данной длины волны. Но что значит «для данной длины волны» — имеется ли в виду, скажем, 453 нм или 453,2 нм? А может быть, 453,257859987654 нм? Надеюсь, читателю ясно, что, говоря «для данной длины волны», ведут речь о маленьком интервале длин волн. Уславливаются, скажем, что это будет интервал, равный 0,01 нм. Отсюда следует, что физический смысл имеет не ордината, а столбик с основанием 0,01 нм. Площадь этого столбика равняется энергии, излученной волнами, имеющими длину в интервале, например, от 453,25 до 453,26 нм. Разбив на такие столбики всю площадь, которую охватывает кривая, и сложив их площади, мы получим суммарную интенсивность всего спектра. На этом примере я объяснил операцию, которая математиками называется интегрированием. Итак, площадь под кривой дает полную интенсивность излучения. Оказывается, она пропорциональна четвертой степени температуры.
На рисунке, который мы обсуждаем, видно, что с ростом температуры меняется не только площадь, обнимаемая кривой, но происходит сдвиг ее максимума влево, т. е. в область ультрафиолета.
Связь длины волны света в микрометрах, соответствующей наиболее интенсивному излучению (поглощению), с температурой в кельвинах дается следующей формулой:
λмакс = 2886/Т
При низких температурах максимум лежит в инфракрасной области. Вот поэтому инфракрасное излучение называют иногда тепловым. Замечательным обстоятельством является то, что мы располагаем приборами, способными почувствовать тепловое излучение, исходящее от тел, температура которых комнатная и даже ниже комнатной. Современная техника умеет «видеть» в полной темноте. Этой же способностью обладают некоторые животные. Странного тут ничего нет, ибо инфракрасные лучи имеют в принципе те же свойства, что и видимые.
В частности, не следует забывать, что любое животное является источником излучения. Зачастую говорят о том, что можно «почувствовать» в темноте присутствие человека. Это не мистика. Просто тот, кто «чувствует», обладает обостренным восприятием тепловых лучей.
Не могу удержаться, чтобы не рассказать читателю одну интересную историю, показывающую, что с тепловыми лучами надо считаться и тогда, когда в житейском понимании этого слова источниками лучей являются ненагретые тела. Несколько лет назад мне предложили разобраться в опытах, которые производил один человек, выдававший себя, за «мага», способного останавливать движение мотора силой своей воли. Моя задача заключалась в том, чтобы найти этим опытам (кудесники XX века любят прибегать к наукообразной терминологии и называют их телекинезом) рациональное объяснение.
Схема опыта показана на рис. 1.2.
На оси моторчика вращалось крылышко, и оно действительно останавливалось, когда «маг» садился рядом с коробкой, в которую была выведена ось мотора. Я быстро выяснил, что любой человек, подсевший к коробке с моторчиком, оказывал на крылышко такое же влияние. Остановка крылышка происходила через 10–15 мин. Останавливался не мотор, как утверждал «маг», а именно крылышко. Таким образом, было очевидно, что силе сцепления оси мотора с крылышком препятствует какая-то другая сила, связанная с присутствием человека.
Я показал, что крылышко можно остановить почти мгновенно, если поднести к стенке коробки электрическую лампу. Стало ясным, что дело в тепле, которое излучает тело человека. Пустив в коробку струю табачного дыма, я продемонстрировал, что внутри коробки возникают конвекционные потоки воздуха, которые направлены именно таким образом, чтобы воспрепятствовать крылышку вращаться. Точные измерения показали, что на стороне коробки, обращенной к человеку, возникает температура примерно на один градус выше, чем на далекой от него стороне коробки.
Инфракрасные лучи, исходящие от тела, нагретого до 60–70 °C, каждый может почувствовать, поднося ладонь. Разумеется, надо устранить тепловую конвекцию. Нагретый воздух поднимается кверху, а вы поднесите ладонь снизу. В этом случае можете быть уверены в том, что ощутили именно тепловые лучи.
Прежде чем расстаться с тепловыми лучами, поясним, почему большим прогрессом явился переход от электрической лампы накаливания с угольной нитью к современной лампе с вольфрамовой питью. Все дело в том, что угольную нить можно довести до температуры; 2100 К, а вольфрамовую — до 2500 К. Почему эти 400 К так важны? Все дело в том; что цель лампы накаливания — не греть, а давать свет. Следовательно, надо добиться такого положения, чтобы максимум кривой приходился на видимое излучение. Как видно из графика, идеалом было бы располагать такой нитью, которая выдерживала бы температуру поверхности Солнца, 6000. К. Но даже переход от 2100 К к 2500 К повышает долю энергии, приходящейся на видимое излучение, от 0,5 до 1,6 %
ТЕОРИЯ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
Если система излучающих и поглощающих тел замкнута, то «газ» фотонов, с помощью которых тела обмениваются энергией, должен быть в равновесии с атомами, дающими жизнь этим фотонам. Число фотонов с энергией hv зависит от того, сколько атомов находится на уровне E1 и сколько на уровне Е2. Эти числа при равновесии неизменны.
Но равновесие носит динамический характер, поскольку одновременно идут процессы и возбуждения, и излучения. Каким-либо образом — то ли благодаря соударению с другой частицей, то ли из-за поглощения пришедшего извне фотона — атом или атомная система перебирается на высокий уровень. В этом возбужденном состоянии система существует некоторое неопределенное время (обычно измеряемое долями секунды), а затем возвращается на низкий уровень. Этот процесс называют самопроизвольным излучением. Атом ведет себя, как шарик, который с трудом удается удерживать на остроконечной вершине горки сложного профиля: ничтожное дуновение — и равновесие нарушено. Шарик скатывается в ямку, большей частью в самую глубокую, из которой его можно извлечь лишь сильным ударом. Про атом, спустившийся на самую низкую ступеньку, говорят: атом находится в стабильном состоянии.
Запомним, однако, что кроме положений «на вершине» и «в глубокой яме» существует еще и промежуточная ситуация: шарик может находиться в неглубокой ложбине, откуда его можно вызволить если не легким дуновением, то во всяком случае небольшим толчком. Такое положение (называется метастабильным. Так что кроме возбужденного и стабильного существует еще и третий вид уровней энергии — метастабильный.
Итак, переходы будут происходить в обе стороны. То один, те другой атом будут перебираться на верхний уровень. Через мгновение они будут спускаться на низкий уровень, излучая свет. Но в то же время другие атомы получат энергию и поднимутся на верхние уровни.
Закон сохранения энергии требует, чтобы число переходов сверху вниз равнялось числу переходов снизу вверх. Чем определяется число переходов вверх? Двумя факторами: во-первых, числом атомов, находящихся на нижнем этаже, и, во-вторых, числом ударов, которые поднимут их на верхний этаж. Ну, а число переходов вниз? Оно определяется, конечно, числом атомов, находящихся на верхнем этаже, и вроде бы больше ни от чего не зависит. Именно так сначала полагали физики-теоретики. Но концы с концами у них сходились плохо. Число переходов вверх, зависящее от двух множителей, росло с температурой куда быстрее, чем число переходов вниз, которое зависело только от одного фактора. Модель, казалось бы очевидная, приводила к нелепице. Получалось, что рано или поздно все атомы будут загнаны на верхний уровень: система атомов будет находиться в неустойчивом состоянии, а излучения не будет.
Вот этот невозможный вывод и выудил Эйнштейн в 1926 г. из рассуждений своих предшественников. Видимо, на переходы атомов с верхнего этажа на нижний влияет еще какое-то обстоятельство. Оставалось предположить, что кроме спонтанного (самопроизвольного) перехода на низкий уровень существует и переход вынужденный.
Что такое вынужденное излучение? Вот что это. Система находится на верхнем уровне. От нижнего уровня ее отделяет разность энергий E2 — E1 = h∙v. Оказывается, если на систему падает фотон с энергией, равной hv, то он заставит систему перейти на нижний уровень. Сам падающий фотон при этом не поглотится, а пойдет дальше в том же направлении в сопровождении нового, порожденного им, в точности такого же фотона.
Не надо искать логики в этом рассуждении. Было озарение, догадка… А о ее справедливости должен судить опыт. С помощью предположения о вынужденном (стимулированном) излучении удается вывести количественную формулу, дающую график излучения в функции длины волны для нагретого тела. Теория блестяще совпадает с опытом и поэтому оправдывает выдвинутую гипотезу.
Интересно, что практические выводы из факта существования вынужденного излучении, приведшие к открытию лазеров, были сделаны спустя много лет.
ОПТИЧЕСКИЕ СПЕКТРЫ
Вообще говоря, любое тело является источником мягкого электромагнитного излучения. С помощью спектрографа — прибора, основной частью которого является призма или дифракционная решетка, — свет разлагается в спектр. Спектр может оказаться сплошным, полосатым, линейчатым. Спектры раскаленных твердых тел очень похожи друг на друга. Да и раскалить до свечения можно лишь небольшое число веществ. Разумеется, редкостью является раскаленная жидкость. Весьма информативными являются спектры излучения газов. Таковы спектры лучей, приходящих к нам от далеких звезд.
Важнейшие сведения о структуре Вселенной принесены на Землю световыми лучами звездной материи, находящейся в газообразном состоянии.
В земных условиях нетрудно создать спектры излучения атомов. Атомы заставляют светиться, либо пропуская через газ ток, либо нагревая газ. Следует отметить, что таким способом можно изучать спектры только атомов, но не спектры молекул. Прежде чем газ начнет светиться, молекулы распадутся на атомы. Поэтому, если исследователя интересуют жидкости или твердые тела, то он изучает спектры поглощения. В конечном счете картина определяется системой энергетических уровней. Переходы сверху вниз или снизу вверх несут одинаковые сведения. Надо действовать так, как удобней.
Спектры, состоящие из отдельных четких линий, мы получим лишь от газа или разбавленного раствора. Во 2-й книге говорилось о том, что поведение растворенных молекул напоминает во многих отношениях поведение газа. Это справедливо и для оптической спектроскопии. К сожалению, имеет место влияние растворителя на характер спектра, но, сопоставляя вид спектров молекул, растворенных в разных веществах, можно учесть это влияние и «вытянуть» из эксперимента дактилоскопию растворенной молекулы.
Получить характерный спектр — еще не значит установить систему энергетических уровней молекулы. Однако для многих практических целей это и не требуется. Располагая альбомом, в котором собраны данные о спектрах (т. е. список спектральных линий и их интенсивностей, или кривые зависимости интенсивности от частоты) какого-либо семейства химических веществ, снимая спектр неизвестного вещества и сопоставляя опытную картину картинками из альбома, мы узнаем вещество совершенно таким же образом, как по рисунку бороздок на пальце определяют преступника.
В последнее время оптический спектральный анализ получил соперника в лице радиоспектроскопии. Радиоспектроскопические методы уступают пока что (и это «пока» будет, видимо, длиться недолго) оптическим по чувствительности, но зато в огромное число раз превосходят оптические методы по возможностям идентификации и количественного анализа смесей веществ.
В нашу задачу не входит знакомство с конкретными спектрами веществ. Достаточно познакомить читателя с картиной уровней энергии атомов водорода и припципиальной схемой энергетических уровней свободной молекулы.
На рис. 4.3 изображена система энергетических уровней водорода. Обращаю ваше внимание на характерное сгущение уровней по мере увеличении расстояния от нулевой черты.
Кстати, не следует думать, что обозначенный на схеме нуль — это «настоящий» нуль. Разумеется, невозбужденный атом водорода обладает определенной энергией. Но поскольку в спектрах проявляются разности энергий, то отсчет удобно вести от нижней черты. В зависимости от силы полученного «щелчка» атом может подняться на любой из «этажей», ненадолго задержаться в этом неравновесном состоянии и далее любым из двух возможных способов (спонтанное или вынужденное излучение) опуститься вниз.
Возникающий спектр удобно разбить на ряд «серий». Каждая серия подчинена своему нижнему уровню. В видимой части лежит так называемая серия Бальмера. Ее объяснение было первым триумфом теории строения атома Нильса Бора.
НИЛЬС БОР (1885–1962) — знаменитый датский физик. Создал первую квантовую модель атома и таким образом открыл закон квантования энергии. Активно участвовал в разработке принципов квантовой механики. Показал принципиальную неприменимость к микромиру понятий подходящих для описания поведения макроскопических тел. Внес большой вклад в теорию строения атомного ядра.
Не все энергетические переходы равновероятны. Чем выше вероятность перехода, тем сильнее соответствующая линия. Есть и запрещенные переходы.
Большим торжеством физиков-теоретиков явилось то, что они исчерпывающим образом объяснили спектр атомов водорода, решая знаменитое уравнение квантовой механики, выведенное в 1926 г. Эрвином Шредингером.
На спектры атомов влияют внешние поля. Линии расцепляются на несколько компонент под действием электрического поля (эффект Штарка) и под действием магнитного (эффект Зеемана). Мы не станем объяснять эти интересные явления. Скажем лишь, что разобраться в некоторых из них удалось только после того, как Гаудсмит и Уленбек предположили, что электрон обладает спином. О том, как спин обнаруживает себя в опытах непосредственно, уже говорилось в 3-й книге.
И, наконец, последнее замечание, касающееся картинки энергетических уровней. Мы видим, что предел, к которому подходят уровни, обозначен числом 13,53. Что это за число? Это ионизационное напряжение. Если помножить заряд электрона на величину этого напряжения в вольтах, то мы получим величину работы, которую надо затратить, чтобы оторвать электрон от ядра, иными словами, чтобы разрушить атом водорода.
Спектры атомов возникают в результате электронных переходов. Как только мы переходим от атомов к молекуле, сразу же возникает необходимость в учете еще двух составляющих энергии. Молекула может вращаться, атомы молекулы могут совершать колебания по отношению друг к другу. Все эти виды энергии тоже квантуются, они могут иметь лишь определенные дискретные значения. Таким образом, энергетическое состояние молекулы описывается состоянием ее электронного облака (электронный уровень), состоянием колебательного движения (колебательный уровень) и состоянием вращения (вращательный уровень). Приходится оперировать тремя типами данных — так сказать, номером дома, этажа и квартиры.
Но что играет роль этажа, а что — квартиры? Какие энергетические уровни разделены большими промежутками, а какие малыми? На эти вопросы отвечает рис. 1.4.
На схеме показаны два электронных уровня е' и е' (номера домов). Этажи — колебательные уровни — помечены буквой v, а номера квартир — вращательные уровни — буквой j. Правда, такая нумерация домов не принята. Используется, как известно, сплошная нумерация квартир, а мы при описании спектров молекулы нумеруем квартиры на каждом этаже, начиная с нуля.
Как видите, промежутки между вращательными уровнями самые маленькие, а наибольшей является разность между электронными уровнями (е' и е").
Положим, у молекулы возможны электронные уровни, лежащие при 100, 200, 300…. единицах энергии, колебательные уровни — при 10, 20, 30…. единицах, вращательные — при 1, 2, 3…. единицах; тогда молекула, находящаяся на втором электронном уровне, первом колебательном и третьем вращательном, будет иметь энергию 213 единиц.
Итак, энергия молекулы может быть задана в виде
Е = Еэл + Екол + Евр.
Частота излученного или поглощенного света будет всегда соответствовать разности (значок Δ) двух уровней, т. е.
v = (1/h)∙(ΔЕэл + ΔЕкол + ΔЕвр).
Хотелось бы выделить такие переходы, при которых меняется только один «сорт» энергии. Практически это возможно, только для вращательных переходов, и мы легко поймем, почему.
Начнем исследовать поглощение электромагнитных воли группой молекул с самых длинных волн, т. е. с палых порций энергии hv. До тех пор, пока величина кванта энергии не станет равной расстоянию между двумя ближайшими уровнями, молекула поглощать не будет. Постепенно увеличивая частоту, мы дойдем до квантов, способных поднять молекулу с одной «вращательной» ступеньки на другую. Это произойдет, как показывает опыт, в области микроволн (край радиодиапазона), или, иначе говоря, в области, далекого инфракрасного спектра. Длины волн порядка 0,1–1 мм будут поглощаться молекулами. Возникнет чисто вращательный спектр.
Новые явления произойдут тогда, когда мы направим на вещество излучение, обладающее квантами энергии, достаточными для перевода молекулы с одного колебательного уровня на другой. Однако мы никогда не получим чисто колебательного спектра, т. е. такую серию переходов, при которой номер вращательного уровня сохранялся бы. Напротив, переходы с одного колебательного уровня на другой будут затрагивать различные вращательные уровни. Скажем, переход с нулевого (самого низкого) колебательного уровня на первый может состоять в подъеме с третьего вращательного уровня на второй или со второго на первый и т. д. Таким образом, возникнет колебательно-вращательный спектр. Мы будем наблюдать его в инфракрасном свете (3—50 мкм). Все переходы с одного колебательного уровня на другой будут мало отличаться по энергии и дадут в спектре группу очень близких линий. При малом разрешении эти линии сольются в одну полосу. Каждая полоса соответствует определенному колебательному переходу.
Мы попадем в новую спектральную область, в область видимого света, когда энергия кванта станет достаточной для перевода молекулы с одного электронного уровня на другой. И здесь, разумеется, невозможны ни чисто электронные переходы, ни электронно-колебательные. Возникнут сложные переходы, в которых энергетический переход сопровождается переменой и «дома», и «этажа», и «квартиры». Поскольку колебательно-вращательный’ переход представляет собой полосу, то спектр в видимой области будет практически сплошным.
Характеристические спектры атомов и молекул долгие годы исполняли (и продолжают исполнять и сегодня) скромную роль помощников в деле определения химического, строения и состава веществ. Революционные события и области спектроскопии произошли совсем недавно.
ЛАЗЕРНОЕ ИЗЛУЧЕНИЕ
Первые тридцать лет нашего века ознаменованы фантастическими успехами теоретической физики. В эти годы были открыты такие важнейшие законы природы, как законы механики больших скоростей, законы строения атомного ядра, законы квантовой механики. Последующие сорок лет демонстрируют не менее феноменальные успехи приложения теории к практике. В эти годы человечество научилось извлекать энергию из атомных ядер, получило в свое распоряжение полупроводниковые транзисторы, революционизирующие радиотехнику и приведшие к созданию ЭВМ, и овладело лазерной техникой. Эти три приложения, по сути дела, и привели к событиям, которые именуют научно-технической революцией.
В этом параграфе речь пойдет о лазерах. Задумаемся над обстоятельствами, которые не позволяют нам, действуя традиционными методами, создать сильный направленный пучок света.
Самый мощный свет, собранный в предельно узкий пучок, расходится и теряет свою интенсивность на расстояниях. И лишь в научно-фантастическом романе Алексея Толстого герой придумывает «гиперболоид», позволяющий создавать лучи, способные жечь, резать, нести громадную энергию на далекое расстояние. Разумеется, можно изготовить такое вогнутое зеркало, которое создаст параллельный пучок света. Для этого надо в фокус зеркала поместить точечный источник. Но точечный — это математическая абстракция. Ну, пусть не точечный, а просто небольшой. Однако, даже накалив шарик до 6000 К (а больше ни один материал не выдерживает), мы получим пучок света жалкой интенсивности. А как только начнем, увеличивать размеры источника, так сразу же вместо параллельного пучка лучей получим веер световых «нитей» и интенсивность луча прожектора будет быстро убывать с расстоянием.
Итак, первое препятствие на пути создания сильного луча — это то, что атомы излучают свет во все стороны. Первое, но не последнее. Атомы и молекулы излучают, так сказать, не сговариваясь друг с другом. Поэтому лучи, исходящие из разных атомов, отправляются в путешествие несогласованно, не дожидаясь друг друга. Это приводит к тому, что излучения разных атомов не совпадают по фазе. A раз так, то лучи от разных атомов будут зачастую уничтожать друг друга. Последнее, как вы вспоминаете, происходит тогда, когда горб одной волны приходится на впадину другой.
Вот эти препятствия и удается преодолеть, создав лазерное излучение. Слово «лазер» — это сокращенное английское название: Light Amplification by Stimulated Emission of Radiation, что означает: усиление света с помощью стимулированного излучения.
Идея складывается из нескольких элементов. Прежде всего мы вспоминаем, что наряду со спонтанный излучением существует вынужденное. Как было сказано, этот вид излучения возникает тогда, когда фотон света встречается с возбужденным атомом. Если энергия возбуждения атома в точности равна энергии фотона, то фотон заставляет атом высветиться. Атом переходит на более низкий уровень и излучает фотон. Замечательной особенностью стимулированного излучения является то, что этот фотон будет таким же, как тот, который его породил, не только в отношении своей энергии; он отправится в путь с той же фазой и в том же направлении.
Второй элемент идеи состоит в следующем. Если систему излучающих атомов заключить в трубку, донышки которой находятся на определенном расстоянии друг от друга и могут явиться зеркалами для тех фотонов, которые нас интересуют, то мы можем за счет путешествий фотонов туда-обратно постепенно собрать в этом сосуде множество фотонов, порожденных одинаково возбужденными атомами.
Третий элемент идеи заключается в том, чтобы подольше удержать атомы в возбужденном состоянии, а затем после такой «накачки» заставить все атомы высветиться одновременно. Осуществление идеи лазера, т. е. размножение одного фотона и получение миллиардов тождественных, неотличимых по своим свойствам фотонов, должно привести к созданию светового луча беспрецедентной интенсивности. Такой пучок размывался бы в ничтожной степени, и на поперечное сечение луча приходилась бы огромная энергия.
Но как этого добиться? В течение долгих десятилетий никто не догадывался. Еще в 30-х годах важные соображения на этот счет были высказаны В. А. Фабрикантом; позднее настойчивые усилия будущих лауреатов Нобелевской премии советских ученых А. М. Прохорова и Н. Г. Басова и американского физика Ч. Таунса привели к созданию лазеров.
Положим, система обладает двумя энергетическими уровнями. Большинство атомов или молекул находится на нижнем уровне. Тепловые удары могут на короткое время перевести молекулу на верхний уровень. Но такое положение будет длиться недолго — молекула высветится. При этом подавляющее большинство атомов перейдет на нижний уровень спонтанно. Стимулированные переходы на нижний — уровень будут редки, так как возбужденных частиц мало.
Положим, удалось найти вещество, атомы которого обладают тремя энергетическими уровнями, обозначенными на рис. 1.5 цифрами 1, 2, 3.
Расстояние 1–3 соответствует частоте излучения зеленого света, расстояние 1–2 соответствует частоте красного света. Допустим, что вероятность перехода с уровня 3 на уровень 2 в тысячи раз больше частоты перехода с уровня 2 на уровень 1. Будем облучать вещество зеленым светом. Атомы поднимутся на третий этаж, спонтанными переходами перейдут на уровень 2 и задержатся на этом уровне. Этот переход называется безызлучательным. Выделившаяся энергия переходит в колебательную энергию атомов. Продолжим нашу фантазию и представим себе, что удалось большинство атомов перевести на уровень 2. Мы добились инверсии заселенности, т. е. «ненормальной» заселенности. Верхние уровни 2 заселены гуще, чем нижние 1 — явление, которое невозможно, когда процессом распоряжается одно лишь тепловое движение.
Переход с уровня 2 на более низкий уровень 1 все же начнет происходить. Соответствующий фотон будет встречать на своем пути другие атомы, находящиеся на возбужденном уровне 2. Такая встреча приведет не к поглощению, а к созданию нового фотона. К первому, случайно образовавшемуся фотону 2–1 будут присоединяться такие же фотоны стимулированного излучения.
Возникает поток фотонов 2–1. Все эти фотоны будут в точности одинаковы и создадут луч огромной интенсивности.
Такой процесс и удалось воспроизвести исследователям, фамилии которых мы назвали. Исторически первым был создан рубиновый лазер. Схема уровней, показанная на рисунке, как раз и характеризует рубин с примесью атомов хрома.
Для создания лазера необходим источник возбуждения, который производит «накачку» лазера, т. е. переводит атомы на высший уровень.
Если источником лазерного излучения является твердое тело, то оно изготовляется в виде цилиндра, основания которого играют роль зеркал. В случае жидкостей или газов создается трубка с зеркалами у основания колонки. Осуществляя микрометрическую подачу зеркал, фиксируя таким образом длину колонки, можно поставить в хорошие условия только те фотоны, целое число длин волн которых укладывается вдоль длины колонки. Только в этом случае все волны складываются.
Пожалуй, основная особенность лазера состоит в возможности создания остронаправленного потока излучения. Лазерный луч может иметь практически любое поперечное сечение. Технически это достигается тем, что луч заставляют путешествовать по узкому стеклянному капилляру достаточно большой длины. Фотоны, идущие под углом к оси капилляра, не примут, участия в процессе размножения фотонов. Резонансная полость (т. е. зеркала, отражающие фотоны то в одном, то в другом направлении в тот период работы лазера, пока идет накачка атомов) размножает только фотоны одного направления. В некоторых случаях; не удовлетворяясь угловой расходимостью пучка порядка одного градуса, на пути выпущенного на волю луча ставят еще дополнительную линзу.
Лазерная установка, когда речь идет о создании больших мощностей, — сложное инженерное сооружение. В колонке создается первоначальный импульс, затем он может быть подан на усилители, которые работают на том же принципе, что и первоначальная колонка, но накачиваются независимо от первичной колонки. Мы не будем останавливаться на этих деталях. Нас интересуют физические принципы накачки и создания лазерного излучения. А они могут существенно различаться, как это показывают рис. 1.6–1.8 со схемами действия лазеров, с помощью которых сегодня получают лучи максимальной мощности.
На рис. 1.6 показана схема так называемого неодимового лазера. Название может ввести в заблуждение. Телом лазера является не металл неодим, а обычное стекло с примесью неодима. Ионы атомов неодима беспорядочно распределены среди атомов кремния и кислорода. Накачка производится лампами-молниями. Лампы дают излучение в пределах длин волн от 0,5 до 0,9 мкм. Возникает широкая полоса возбужденных состояний.
Совершенно условно она изображена пятью черточками. Атомы совершают безызлучательные переходы на верхний лазерный уровень (на этой и на других двух схемах он помечен цифрой 2). Каждый переход дает разную энергию, которая» превращается в колебательную энергию всей «решетки» атомов.
Лазерное излучение, т. е. переход на пустой нижний уровень, помеченный цифрой 1, имеет длину волны 1,06 мкм.
Показанный пунктиром переход с уровня 1 на основной уровень «не работает». Энергия выделяется в виде некогерентного излучения.
Неодимовый лазер позволяет получить фантастическую мощность, равную 1012 Вт. Энергия выдается импульсами, которые длятся 0,1 нс.
Молодым конкурентом, стал лазер, использующий переходы в возбужденных атомах иода (рис. 1.7).
Рабочим веществом является газ C3F7I. И здесь для накачки употребляются лампы-молнии, но физические процессы иные. Для накачки используется ультрафиолетовый свет с длиной волны 0,25 мкм. Под действием этого излучения происходит диссоциация молекул. Замечательным является то обстоятельство, что атомы иода, отрываясь от молекулы, оказываются в возбужденном состоянии! Как видите, это совсем другой способ достижения инверсии заселенности. Рабочий переход 2 —> 1 приводит к лазерному излучению с длиной волны 1,3 мкм, после чего происходит воссоединение атома иода с молекулярным остатком.
Вероятно, читатель слыхал, что широко используются гелий-неоновые лазеры. С их помощью получают достаточно сильный инфракрасный луч с длиной волны 1,13 мкм. Эти лазеры не принадлежат к числу рекордсменов по мощности. Поэтому мы приводим схему уровней для другого лазера, работающего на смеси азота и углекислого газа (рис. 1.8).
Но прежде чем перейти к ее описанию, надо ответить на естественный вопрос: зачем надо пользоваться смесью газов? Ответ таков: одни атомы и молекулы проще возбудить, а другие легче высвечиваются. Так что в лазере, работающем на смеси, в основном накачиваются энергией частицы одного сорта, столкновениями они передают энергию другим атомам или молекулам, а уже эти последние создают лазерный луч.
B ходу системы, состоящие более чем из двух газов. В частности, и в лазере, где основная роль принадлежит азоту и углекислому газу, кроме этих двух веществ целесообразно использовать различные добавки, в том числе гелий.
Накачка лазера, в котором «работают» молекулы СО2, производится способом, отличным от двух описанных. Смесь газов помещается в газоразрядную трубку, напряжение подается достаточно высокое для того, чтобы система перешла в состояние плазмы. Быстро движущиеся электроны возбуждают колебания молекул азота. Схема показывает скачок этой молекулы на верхний этаж. Не безразлично, какое напряжение приложено к электродам. Оптимальной энергией для возбуждения молекул азота является энергия около 2 эВ.
Молекула азота играет роль лишь посредницы. Сама она не дает излучения, а полученную от электронов энергию передает молекуле СО2 и переводит ее на верхний лазерный уровень.
Верхними лазерными уровнями 2 являются «квартиры третьего этажа» молекул СО2. Время жизни молекулы газа на верхнем лазерном уровне — около 0,001 с. Это совсем не мало, и молекула имеет достаточно большой шанс дождаться встречи с фотоном подходящей энергии, который вынудит ее поселиться этажом ниже.
Надо заметить, что «межквартирные» переходы много чаще переходов между «этажами». Время жизни на вращательном уровне измеряется десятимиллионными долями секунды. Это удачное обстоятельство приводит к тому, что заселение квартир каждого этажа можно считать стабильным. Поэтому с помощью технического приема, о котором мы говорили, — создания подходящего расстояния между зеркалами, — удается выделить какой-либо один переход — допустим, с шестой квартиры третьего этажа в пятую квартиру второго.
Конструктор лазера должен располагать исчерпывающими сведениями о времени существования атома на том или другом подуровне и о вероятностях перехода. Тогда он сможет выбрать оптимальное излучение данной газовой смеси. Лазер, работающий на углекислом газе, настраивают обычно на длину волны 10,5915 мкм.
Для хорошей работы лазера надо чтобы молекулы не задерживались на нижнем лазерном уровне. Так сказать, сделал свое дело, дай место другому. Так вот, при давлении 1 мм. рт. ст. молекулы углекислого газа испытывают 100 соударений в секунду, освобождающих уровень. Соответствующие цифры при наличии гелия и воды — 4000 и 100 000. Разница огромная.
Подбирая подходящие примеси к углекислому газу, можно существенней влиять на мощность прибора. Как будто бы именно такой лазер специалисты считают золотым медалистом.
Лазер, работающий на СО2, дает луч, который можно фокусировать на площадь 0,004 см2 с интенсивностью 1000 кВт/см2 при постоянном режиме и 1 000 000 кВт/см2 в импульсном режиме при времени импульса, равном 1 нс.
Поиск подходящих материалов для лазеров является своего рода искусством. Надо обладать хорошей интуицией, выдумкой, памятью, чтобы создать эффективно действующий лазер.
Исключительно большая интенсивность и когерентность лазерного излучения революционизировали многие области техники. Производство лазеров за последнее десятилетие превратилось в важнейшую отрасль промышленности. Лазеры находят себе применение как генераторы излучения, передающие не только энергию, но и информацию. Ведется интенсивное исследование возможностей применения лазеров для создания термоядерной реакции. В практику вошли применения лазера как ножа, как инструмента для проведения тончайших хирургических операций, как средства для разделения изотопов. О некоторых применениях лазера мы поговорим в ходе дальнейшего изложения.
ЛЮМИНЕСЦЕНЦИЯ
Тепловое излучение является универсальным свойством всех тел. Тепловые лучи излучаются телом при любой температуре, начиная от абсолютного нуля. Тепловой спектр — сплошной и изображается кривой, характер которой мы обсудили. Правда была приведена кривая для черного тела, но кривая для окрашенных тел в принципе мало чем отличается от кривой для черных. Разница лишь в том, что у окрашенных тел кривая будет искажена. Но общее возрастание энергии излучения при росте температуры и смещение максимума в левую сторону (если по оси абсцисс отложены длины волн) являются общим законом.
Любое излучение состоит в переходе с более высокого энергетического уровня на более низкий. Но причины возбуждения атомов или молекул могут быть разными. В случае теплового излучения это удары, получаемые частицами вещества благодаря тепловому движению.
Но это не единственная причина, заставляющая тело излучать волны. Явление люминесценции, к описанию которого мы переходим, имеет другую природу. Этим явлением охватывают процессы возбуждения молекул, не связанные с повышением температуры тела. Причинами возбуждения частиц могут быть встречи с пучками фотонов или электронов, механические удары, трение и т. д.
Люминесцируют практически все вещества, Но лишь некоторые вещества — люминофоры — светятся ярко и имеют практическое значение.
Люминофоры используются как материалы, которыми покрываются экраны телевизоров и осциллографов. В этом случае свечение происходит под ударами электронов. Очень эффектно люминесцируют вещества под действием ультрафиолетового излучения. Энергия падающего фотона должна быть во всяком случае больше энергии излучаемого фотона. Так что падающий квант энергии может принадлежать невидимой части спектра, а излученный — видимой.
Миллиардные доли примесей люминесцирующего вещества заговорят о себе, если вещество облучить ультрафиолетом. Поэтому люминесцентный анализ используется иногда как средство химического анализа. С его помощью обнаруживаются следы нежелательных загрязнений.
Люминофорами покрываются стенки ламп дневного света.
Различают два вида люминесценции — флуоресценцию и фосфоресценцию. Флуоресценция — высвечивание атома или молекулы, происходящее без задержки молекулы на возбуждённом уровне. Напротив, фосфоресценция есть явление, которое может произойти с большим запозданием. Это случается, если при возбуждении система переходит на метастабильный уровень, переходы с которого вниз имеют малую вероятность. Излучение происходит, как правило, после того, как молекула сначала поглотит энергию и поднимется на верхний уровень, а потом уже произойдет высвечивание, причем переход на низший уровень совершается без остановки на промежуточном, метастабильном.
Несколько слов об электролюминесценции, происходящей в некоторых полупроводниковых диодах на границе р-n-слоя. Это интересное явление имеет огромное практическое значение, так как с его помощью можно изготовить полупроводниковые лазеры. В основе лежит следующий факт: электрон и дырка полупроводника могут воссоединиться (рекомбинировать) с излучением фотона.
Чтобы такие переходы происходили непрерывно, надо пропускать через диод электрический ток. Задача состоит в том, чтобы отыскать подходящий материал, который удовлетворяет нескольким требованиям. Прежде всего, ток должен, если так можно выразиться, впрыскивать электроны в полупроводник р-типа, т. е. в полупроводник, который содержит больше дырок, либо должен накачивать дырки в кристалл n-типа. Сказанное есть условие необходимое. Но другие факторы, такие, например, как скорость перехода с верхнего на нижний уровень, могут играть решающую роль. Встречаются такие случаи, когда все факторы благоприятствуют переходу электрона сверху вниз и возникает электролюминесценция.
Особенно удачным для создания электролюминесценции оказался полупроводник арсенид галлия. Он даст достаточное количество фотонов. Фотоны распространяются вдоль р-n-границы. Два участка диода, перпендикулярные границе, полируются, и этим создается резонансная полость. Фотоны, образующиеся при рекомбинации дырки и электрона, оказываются синфазными, и при достаточно больших токах излучение становится таким же, как у лазеров, описанных выше, со всеми вытекающими отсюда следствиями в отношении остроты, направленности и поляризации излучения.
Полупроводниковые лазеры работают в диапазоне волн от ультрафиолета до далекого инфракрасного света и широко используются для самых разнообразных целей.
Глава 2 Оптические приборы
ПРИЗМА
Арсенал приборов, которыми пользуются в лабораториях и промышленности, меняется столь быстро, что исследователь, по каким-то причинам оставивший научную деятельность на пару десятков лет, а затем возвратившийся к своей работе, был бы вынужден учиться заново. Но и сейчас, и, вероятно, в далеком будущем он всегда встретится со своими старыми знакомыми — призмой и линзой. Поэтому напомним читателю простые законы, которым подчиняется ход светового луча при встрече с этими предметами, изготовленными из прозрачных материалов. Впрочем, прозрачность — понятие относительное. Для иных электромагнитных волн прозрачны дерево и бетон.
Законы встречи луча с телами, которые способны отражать и преломлять этот луч, просты до тех пор, пока не заявит о себе волновой аспект света. Они сводятся к закону отражения (угол падения равен углу отражения) и закону преломления света.
Как известно, падая на границу двух сред, луч света отклоняется от первоначального направления. Углы падения i и преломления r связаны соотношением
n = sin i/sin r
Этот закон был установлен тщательными измерениями физиком Виллебордом Снеллиусом (1580–1626), профессором университета в Лейдене. Содержание его курса лекций, в которых рассказывалось о явлениях встречи света с прозрачными телами, было хорошо известно узкому в то время кругу европейских ученых.
Вероятно, по этой причине с насмешкой была принята современниками статья Рене Декарта (1596–1650), опубликованная в 1637 г. под названием «Рассуждение о методе направления разума для поиска научных истин», в которой он вроде, бы «доказал» этот закон с помощью довольно странных для нас рассуждений. Туманные фразы Декарта отнюдь не привели, в трепет восхищения его коллег. А то обстоятельство, что в результате своих рассуждений Декарт пришел к правильной формуле, объясняли весьма просто: подгонкой рассуждений под результат, который был уже известен ранее. Так что Декарту пришлось вытерпеть и обвинение в плагиате.
Пожалуй, можно присоединиться к скептическому отношению современников к этой статье. Декарт рассматривает мяч, брошенный на слабую сетку. Мяч прорывает сетку, и теряет половину своей скорости. Тогда, — пишет великий философ, — движение мяча совершенно отличается от его предназначения в одну или в другую сторону. Понять, что сие означает, трудновато. Возможно, этой фразой Декарт хотел сказать, что горизонтальная составляющая скорости движения мяча не меняется., а вертикальная меняется, поскольку именно в этом направлении сетка препятствует движению мяча.
Но возвратимся к закону преломления. Углы i и r принято откладывать от положения нормали так, как показано на ряс. 2.1.
Величина n, называемая показателем преломления, зависит от сред, о которых идет речь. Чтобы сравнивать тела по их оптическим свойствам, удобно составить таблицу показателей преломления для случая падения луча из воздуха (если быть педантичным, то следует сказать: из вакуума) в среду. В этом случае угол преломления всегда будет меньше угла падения, а значит; показатель преломления будет больше единицы.
Показатель преломления, вообще говоря, расчет с плотностью среды. Так, у алмаза показатель преломления равен 2,4, а у льда 1,3.
Я не стану уделять место таблице показателей преломления. Но если бы мне пришлось это сделать, то я должен был бы указать, для какой длины волны света приводятся данные. Показатель преломления зависит от длины волны. Это важное явление, лежащее в основе действия ряда приборов, разлагающих электромагнитное излучение в спектр, носит название дисперсии.
Если свет падает из более плотной среды в менее плотную, то может произойти полное внутреннее отражение. В этом случае показатель преломления меньше единицы. По мере возрастания угла падения угол преломления будет все больше и больше приближаться к 90°. При условии
sin r = 1, sin i = n
свет перестанет проходить во вторую сроду, а будет полностью отражаться от границы раздела. Для воды угол полного внутреннего отражения равен 49°.
Преломление света плоской пластинкой можно использовать для того, чтобы «сдвинуть», луч, оставив его параллельным caмомy себе. А с помощью призмы луч света можно повернуть.
Если читатель захочет вспомнить вывод формулы угла поворота D луча, то найдет его в школьном учебнике. Вывод требует лишь знания элементарной геометрии, но он очень громоздкий, в особенности если проделать его для толстой призмы и любого, значения угла встречи луча с призмой. Простая формула получается в том случае, если призма тонкая, а угол падения луча на грань призмы не слишком отличается от прямого. Если так, то
D = (n — 1)∙p
где p — угол между гранями призмы.
С помощью призмы в конце XVII века великий изотоп впервые доказал, что белый свет не монохроматичен, а состоит из лучей разных цветов. Сильнее всего отклоняются фиолетовые лучи, слабее всего — красные. Именно поэтому мы говорим «ультрафиолетовые» и «инфракрасные» лучи, а не инфрафиолетовые и ультракрасные.
Научный мир узнал об открытии Ньютона в 1672 г. В описании своих опытов Ньютон ясен и точен. Здесь виден его гений. Что же касается словесного обрамления, то понять его — труд великий. Лишь мучительно пробираясь сквозь лес слов, удается установить одно: хотя автор обещал описывать факты и не создавать гипотез (знаменитое ньютоновское «гипотезис нон финго»), своего обещания он не выполнял. Многие аксиомы и определения, вроде: «луч света — это его мельчайшая часть», звучат на редкость странно для современного уха.
Пока что несет свою службу в химии спектрограф, основной частью которого является ньютонова призма. Материал должен обладать большой дисперсией. Призмы для спектрографа готовят из кварца, флюорита, каменной соли. Исследуемый свет пропускают через щель, которая расположена в главной фокальной плоскости входной линзы. Поэтому на призму падает параллельный пучок света. Фотоны различной частоты пойдут в разных направлениях. Вторая, выходная линза соберет одинаковые фотоны в одной точке фокальной плоскости. При желании можно на спектр посмотреть глазом. Для этого надо поставить матовое стекло. Можно спектр сфотографировать.
В настоящее время спектр регистрируют с помощью самописцев. Вдоль спектра скользит приемник энергии — фотоэлемент или термоэлемент, дающий ток, сила которого пропорциональна интенсивности света.
Этот ток заставляет отклоняться подвижную часть записывающего устройства точно таким же образом, как ток гальванометра отклоняет его стрелку. К отклонившейся части приспосабливается перо; оно пишет спектр на рулоне бумаги, разворачивающейся с постоянной скоростью.
ЛИНЗА
Существует, большая отрасль промышленности, которая изготовляет линзы. Прозрачные тела, ограниченные двумя сферическими поверхностями или одной сферической и одной плоской, встречаются самых разных размеров. В некоторых приборах используются линзы размером с десятикопеечную монету, в больших телескопах диаметр линзы может быть равен нескольким метрам. Изготовление больших линз — это великое искусство, ибо хорошая линза должна быть однородной.
Конечно, каждый из читателей держал линзу в руках и знает основные ее особенности. Линза увеличивает предмет, линза фокусирует лучи. При помощи линзы, поставленной на пути солнечного луча, легко зажечь клочок бумаги. Линза «собирает» лучи в одну точку. Это фокус линзы.
То, что параллельные, лучи сходятся в одной точке, и, наоборот, то, что линза создает параллельный пучок лучей, если точечный источник света поместить в фокусе линзы, доказывается с помощью закона преломления и простых геометрических соображений.
Если точка находится не в фокусе, а на расстоянии а от центра линзы, то исходящие от нее лучи соберутся на расстоянии а'. Эти два расстояния связаны известной формулой:
(1/a) + (1/a') = 1/f
здесь f — фокусное расстояние линзы.
Нетрудно показать, что лучи света, идущие от предмета, расположенного дальше двойного фокусного расстояния, создадут его перевернутое и уменьшенное в отношении а'/а изображение между фокусом и двойным фокусным, расстоянием.
Если перенести предмет в ту позицию, которую занимало изображение, то изображение перейдет в положение, которое занимал предмет. Работает так называемый принцип обратимости хода лучей.
Когда мы используем линзу как лупу, предмет лежит между линзой и ее фокусом. В этом случае изображение не переворачивается и лежит по ту же сторону, что и предмет (рис. 2.2).
Напоминаю различие между случаем лупы и двумя предыдущими примерами: лупа создаёт «мнимое» изображение, а при иных размещениях предмета мы получаем изображения, которые можно увидеть на экране или сфотографировать. С полным основанием мы их называем действительными.
Увеличение лупы тем больше, чем меньше ее фокусное расстояние. Предельные возможности лупы довольно скромные: угол зрения, под которым видно мнимое изображение, удается сделать от силы в 20–30 раз большим угла зрения, под которым мы видим предмет невооруженным глазом.
Многие оптические приборы были бы крайне простыми и состояли бы из одиночных линз, если бы не ряд неизбежных дефектов. Мы хотим чтобы параллельный пучок белого света собирался линзой в одной точке. Но этому мешает явление дисперсии. Ведь фотоны разного цвета будут отклоняться линзой в разных направлениях. В результате вместо точки мы получим растянутую вдоль оси линзы цветную линию. Это хроматическая аберрация.
Другой бедой является сферическая аберрация. Лучи, которые идут ближе к оси линзы, будут фокусироваться в более далекой точке, чем лучи, путь которых лежит подальше от оси.
По-разному ведут себя лучи, падающие на поверхность линзы под большими и малыми углами. Вместо точки мы получаем светящееся ядро, смещенное в сторону от правильной позиции. От ядра отходит хвост. Этот эффект называется комой. Слово «кома» в переводе с греческого означает нечто вроде «распущенные волосы».
На этом далеко не кончается перечень искажений, которые дает одиночная линза. Рассматривая квадрат, мы увидим четырехугольник, вершины которого соединены дугами, «проваленными» внутри. Происходит это потому, что лучи, исходящие из вершин квадрата и из середин его сторон, будут преломляться по-разному.
Большие неприятности доставляет конструкторам оптический приборов дефект, который называют астигматизмом. Если точка лежит вдалеке от главной оптической оси линзы, то ее изображение расщепится на две полоски, перпендикулярные друг другу и смещенные в противоположные стороны по отношению к позиции идеального изображения.
Есть и другие искажения. Специалисты в области производства линз сводят обычно все виды искажений к семи основным типам. Из них мы упомянули лишь пять.
Как это сплошь и рядом бывает в технике, при создании хорошей линзы мы должны избрать некое компромиссное решение. Совершенно ясно, что с размером линзы будут возрастать искажения, но, с другой стороны, освещенность изображения (т. е. число фотонов видимого света, приходящихся на единицу площади) пропорциональна квадрату диаметра линзы (т. е. ее площади). Но это еще не все. Допустим, что предмет, который изображает линза, находится далеко. Тогда изображение соберется в фокусе. Чем меньше фокусное расстояние, тем размер изображения будет меньше. Иными словами, поток света, исходящий из предмета, соберется на меньшей площади. Значит, освещенность будет обратно пропорциональна фокусному расстоянию.
По этим двум причинам светосилой линзы называют квадрат отношения ее диаметра к фокусному расстоянию.
Наименьшим фокусным расстоянием обладают толстые линзы — линзы, поверхности которых образованы малыми радиусами. Но именно такие линзы будут давать наибольшие искажения. Значит, увеличение светосилы линзы — будь то за счет ее размера, будь то за счет радиуса кривизны — приводит к плохому качеству изображения. Нелегкую задачу приходится решать техникам.
ФОТОАППАРАТ
Простейший фотоаппарат представляет собой линзу, играющую роль окошка в темном ящике. Изображение, даваемое линзой, фиксируется фотопластинкой, расположенной против окошка.
Но простая линза создает искаженное изображение. Поэтому она заменяется сложной системой линз, которая должна уничтожить оптические несчастья всех сортов. Эта система носит название фотообъектива.
Как же можно избавиться от искажений? Достаточно давно было предложено пользоваться системой линз, подобранных таким образом, чтобы дефекты каждой из них компенсировались дефектами других. Этот принцип получения «плюса» умножением двух «минусов» оказывается возможным осуществить для уничтожения всех семи дефектов с помощью всего лишь трех линз. Однако это лишь в принципе. Для создания наиболее совершенного изображения пользуются более сложными комбинациями. Одна из них (далеко не самая сложная) показана на рис. 2.3. Эта система вогнутых и выпуклых линз способна давать неискаженное изображение при значительном варьировании степени увеличения. Первая и третья компоненты системы перемещаются друг по отношению к другу, чем достигается непрерывное изменение фокусного расстояния в три раза.
Фотоаппарат нуждается в несложном приспособлении, позволяющем «наводить аппарат на фокус». Для этого надо иметь возможность менять расстояние между центром объектива и фотопленкой. Еще до сих пор сохранились фотоаппараты, в которых камера выполняется в форме гармоники, которую можно сжать. И надо сказать, что такие аппараты дают совсем неплохие снимки.
В современном фотоаппарате, умещающемся на ладошке, эта операция выполняется изящнее: винтовым движением оправы объектива. Как ясно из рассуждения о светосиле линзы, качество изображения улучшается, если мы уменьшим елико возможно зрачок камеры. Это достигается с помощью диафрагмы переменного диаметра. Размер диафрагмы мы выбираем так, чтобы он был поменьше, но пропускал достаточно света, чтобы дать хорошее изображение при заданной экспозиции.
Почему так забавно выглядят фотографии, снятые в те времена, когда фототехника была еще в пеленках? Так и чувствуется, что люди на фотоснимке застыли в напряженных позах. Объяснение весьма простое: фотограф вынужден был прибегать к большим экспозициям. Поэтому ему и приходилось изрекать сакраментальное: «Спокойно, снимаю».
Борьба за получение хорошего изображения при минимальной экспозиции ведется двумя путями. Первый путь — это совершенствование объектива. Делается это не только за счет подбора геометрии линз, составляющих объектив. В объективе, составленном из нескольких линз, чуть ли не половина света отражается. Это приводит, во-первых, к потере освещенности изображения и, во-вторых, создает световой фон, который уменьшает контрастность изображения. Борются с этим явлением приемом, который носит название просветления оптики. На поверхность линз наносятся тончайшие пленки. Благодаря явлению интерференции доля отраженного света резко уменьшается. Объективы с просветленной оптикой легко узнать: их стекло имеет голубоватый оттенок.
Второй путь улучшения фотоснимка — это совершенствование, фотографической пленки.
Скажем несколько слов о фотохимическом процессе, приводящем к образованию изображения. Фоточувствительный слой представляет, собой желатину, в которую вкраплены кристаллики бромистого серебра с небольшой примесью иодистого серебра. Величина кристаллических зернышек колеблется в пределах от одной тысячной до одной десятитысячной миллиметра. Число зерен, приходящихся на 1 см2, пленки, лежит в пределах от десятка до сотен тысяч. Если рассматривать фотоэмульсионный слой в микроскоп, то можно увидеть, что зернышки расположены довольно тесно.
Фотоны, попадающие на зерно эмульсии, разрушают связи между атомами серебра и атомами галоида. Число атомов серебра, получивших свободу, строго пропорционально числу фотонов, упавших на пленку. Фотограф подбирает такую выдержку, при которой разрушается значительное число связей между атомами серебра и брома. Но в то же время экспозиция не должна быть слишком велика. Большая экспозиция приведет к тому, что связи между атомами серебра и брома у всех кристалликов будут разрушены полностью. Тогда после проявления все кристаллики выделят все серебро, которое в них содержалось, и пластинка будет одинаково черной во всех местах.
При правильной экспозиции на фотопластинке возникает скрытое изображение предмета. В каждом зернышке число разорванных связей пропорционально числу фотонов, пришедших к этому зерну. Процесс проявления состоит в том, чтобы дать возможность объединиться потенциально свободным атомам серебра. При этом количество выделившегося серебра на негативе после проявления пленки будет пропорционально интенсивности света.
Из сказанного очевидно, что мельчайшие детали, которые показывает фотография объекта, никак не могут быть больше величины кристаллического зернышка бромистого серебра.
После того как пластинка проявлена, ее закрепляют. Этот процесс состоит в удалении неразложившегося бромистого серебра. Если мы не удалим эти неразложившиеся зерна, то, вынув негатив на свет, мы его «засветим»; ведь в этом случае зерна выделят полностью все содержащееся в них серебро.
Физика получения позитивного изображения столь очевидна, что мы не станем на ней останавливаться.
Техника современной цветной фотографии далеко не проста и заслуживает большого восхищения. Что же касается физики этого процесса, то она совсем не сложна. Модель восприятия цвета, которая предлагалась еще в середине XVIII века, вполне справедлива. Глаз человека обладает рецепторами трех цветов: красного, зеленого и синего. Комбинируя эти цвета в различных пропорциях, можно создать ощущение любого цвета. Соответственно со сказанным для получения цветного изображения надо располагать трехслойной пленкой. Верхний слой должен быть чувствительным к синим лупам, средний — к зеленым, а нижний — к красным. Как химики добиваются такого положения вещей, мы рассказывать не будем. Цветной негатив превращают в цветной позитив, используя опять же трехслойную фотобумагу.
ГЛАЗ
Глаз, созданный природой, является великолепным физическим прибором. Возможности различать десятки тысяч цветовых оттенков, видеть на далеком и близком расстояниях, ощущать двумя глазами объёмные соотношения предмета, чувствительность к весьма незначительным световым интенсивностям — все это свойства, которые сделают честь прибору самого высокого класса. Правда, глаз человека видит лишь небольшой участок спектра. Глаза ряда животных в некоторой степени лишены этого недостатка.
Устройство глаза напоминает устройство фотоаппарата. Роль объектива играет хрусталик, имеющий форму двояковыпуклой линзы. Хрусталик мягок и способен изменять свою форму под действием мышц, которые его охватывают. В этом состоит процесс аккомодации глаза, позволяющий одинаково хорошо видеть близкие и далекие предметы. С возрастом хрусталик твердеет, а мускулы слабеют, в связи с этим человеку необходимы очки «для дали» и «для чтения».
Изображение предмета проецируется на заднюю стенку глаза. Глазной нерв передает это ощущение в мозг.
Нормальный глаз молодого человека способен рассмотреть в деталях предмет, расположенный на расстоянии не меньшем, чем 10 см. С возрастом возникает обычно дальнозоркость, и это расстояние увеличивается до 30 см.
Перед хрусталиком находится зрачок, который играет роль диафрагмы фотоаппарата. Размеры зрачка могут меняться в пределах от 1,8 до 10 мм.
Роль фотопластинки, на которой образуется изображение, играет сетчатая оболочка, имеющая очень сложное строение. Под сетчатой оболочкой помещается зрительный эпителий, состоящий из светочувствительных клеток, которые носят название палочек и колбочек. Вы можете сравнить число этих клеток с числом зерен бромистого серебра в фотопластинке. Число зрительных клеток превышает сто миллионов. Поскольку человек способен различать цвета, то ясно, что зрительные клетки обладают неодинаковой чувствительностью к различным участкам спектра. К тому же результату мы придем, если будем полагать, что клетки делятся на классы, восприимчивые, к разным участкам спектра.
Если зрение нормальное, то задний фокус глаза в спокойном состоянии находится на сетчатке. Если он лежит перед сетчаткой, то человек близорук; если за сетчаткой, то человек страдает дальнозоркостью. К этим двум распространенным дефектам приводит слишком большая или слишком малая толщина хрусталика. Встречаются люди, страдающие астигматизмом. В этом случае в нормальном состоянии хрусталик не имеет правильной формы тела, ограниченного двумя сферическими поверхностями.
Все эти дефекты исправляются очками, которые должны совместно с хрусталиком дать оптическую систему, фокусирующую изображение предмета на сетчатку.
Линзы очков характеризуют числом диоптрий. Диоптрия — единица оптической силы линзы, а оптическая сила обратно пропорциональна фокусному расстоянию. Оптическая сила в диоптриях равна единице, поделенной на фокусное расстояние в метрах. Фокусные расстояния рассеивающих линз, которые применяют для своих очков близорукие люди, отрицательны.
Угол зрения глаза много больше, чем нам кажется. Ряд событий, происходящих под углом 90° в каждую сторону от прямого взгляда, фиксируется непосредственно подсознанием. Это обстоятельство приводит зачастую людей к ошибочному мнению, что они «чувствуют» взгляд прохожего, не видя его. Глаз плохо распознает предметы, которые он видит под углом, меньшим, чем одна, минута дуги. И это при хорошем освещении.
ПОЛЯРИЗАТОР
Световая волна является волной электромагнитной. Как было сказано в 3-й книге, наглядными экспериментами можно продемонстрировать, что вектор электрического поля перпендикулярен направлению луча. Если этот же факт трактовать, рассматривая свет в корпускулярном аспекте, то следует сказать, что частица света — фотон — представляет собой не шарик, а стрелочку. В ряде сложных расчетов физики-теоретики приходили к заключению, что фотон обладает спином (равным 1). Таким образом, представление фотона стрелочкой весьма естественно.
Обычный луч света — это поток фотонов, спины которых расположены беспорядочно. Такой луч света называется неполяризованным. Однако в ряде случаев мы имеем дело с пучком фотонов, у которых все спины смотрят в одну сторону, или, говоря на другом языке, имеем дело с электромагнитными волнами, электрический вектор которых имеет вполне определенное направление. Такие лучи называются поляризованными.
Один из способов получения поляризованных лучей состоит в том, что луч света заставляют пройти через низкосимметричный кристалл. Такие кристаллы, ориентированные надлежащим образом по отношению к падающему лучу, обладают способностью расщеплять естественный луч на два луча, поляризованные в двух взаимно перпендикулярных направлениях
К сожалению, я не могу дать читателю даже слабое представление о том, почему так происходит. Это связано с тем, что молекулы кристалла по-разному «встречают» волны с разно расположенными электрическими векторами. Но боюсь, что от этой фразы вам легче не стало. Смею лишь заверить, что теория расщепления лучей существует, и притом это очень хорошая теория, которая описывает все детали этого интересного явления. В частности, можно предсказать, как будет меняться картина прохождения света, если мы будем подставлять кристалл под разными углами к световому лучу.
Расщепив неполяризованный луч на два поляризованных, мы далее можем без особого труда добиться такого положения вещей, чтобы один из этих лучей ушел куда-нибудь в сторону. Сделав это, мы получим прибор, который называется николем, по имени его создателя английского физика Уильяма Николя (1768–1851). Прибор был предложен еще в 1820 г. Интересно отметить, что все объяснения поляризаций света давались в то время на корпускулярном языке и считались превосходным подтверждением корпускулярной теории света Ньютона.
Вскоре были обнаружены явления интерференции и дифракции, которые столь естественно объяснялись на волновом языке, что теория световых корпускул была погребена. Но… прошло столетие, и теория возродилась, как птица Феникс из пепла, — правда, уже в гораздо более скромном обличии лишь одного из двух аспектов электромагнитного поля.
Если на пути света поставить поляризатор, то интенсивность луча упадет, как и следовало ожидать, в два раза. Но самое интересное явление, которое и доказывает существование поляризации, произойдет тогда, когда на пути луча мы поставим второй такой же прибор. Его называют анализатором, хотя он ничем не отличается от первого николя. Начнем теперь поворачивать николь около луча света. Окажется, что интенсивность света, прошедшего через два николя, при некотором взаимном положении николей остается той же, что и в отсутствие николей. Мы говорим: в этом положении николи параллельны. Теперь начнем поворачивать анализатор. Когда мы повернем его на 90°, свет перестанет проходить. Мы скажем: николи скрещены.
В промежуточном положении, когда второй николь будет повернут от параллельного положения на угол α, интенсивность будет равна 1/2 I∙cos2 α. Формула легко объясняется, если принять, что вектор электрического поля разложился на две компоненты — одну перпендикулярную, а другую параллельную «щели» анализатора. Ну, а интенсивность пропорциональна квадрату амплитуды волны, т. е. квадрату электрического вектора. Поэтому изменение интенсивности света и должно происходить по закону квадрата косинуса.
Анализ поляризованного света имеет ряд практических применений. Представим себе, что николи скрещены, а между ними помещено прозрачное тело, которое способно поворачивать электрический вектор волны. Тогда произойдет просветление наблюдаемого поля. Такой способностью обладают тела, находящиеся под напряжением. В зависимости от величины напряжения поворот светового вектора, а вместе с ним и просветление поляка скрещенными николями будут различными. Мы увидим красивые картинки (и притом окрашенные, так как фотоны разного цвета ведут себя по-разному), которые позволяют судить о напряжениях в образце или о том, ориентированы или нет молекулы образца. Это ценные сведения, и поэтому хороший микроскоп снабжен двумя николями, чтобы изображение предмета можно было рассматривать в поляризованном свете.
Информация о структуре будет намного богаче. Поворачивать электрический вектор световой волны умеют и растворы многих веществ, например сахарные. При этом угол поворота оказывается строго пропорциональным количеству сахара в растворе. Так что можно приспособить поляриметр для измерения содержания, сахара, такие приборы называются сахариметрами, и их можно найти почти в любой химической лаборатории.
Этими двумя примерами не исчерпывается применение поляриметров, но приведенные два, пожалуй, являются главными.
МИКРОСКОП И ТЕЛЕСКОП
Оптическая часть микроскопа состоит из окуляра и объектива. Окуляр — это линза, к которой мы приближаем глаз; объектив почти касается рассматриваемого предмета. Предмет помещается на расстоянии, несколько большем фокусного расстояния объектива. Между объективом и окуляром возникает перевернутое увеличенное изображение. Надо, чтобы оно оказалось между окуляром и фокусом окуляра. Окуляр играют роль лупы. Можно доказать, что увеличение микроскопа равно произведению увеличений, которые дают окуляр и объектив по отдельности.
На первый взгляд может показаться, что с помощью микроскопа можно рассмотреть сколь угодно мелкие детали предмета. Почему бы, например, не сделать фотографию, увеличивающую размеры в тысячи раз, затем рассмотреть ее в микроскоп, и получить уже увеличение в миллион раз, и так далее.
Такого рода рассуждение не выдерживает критики. Прежде всего напомним, что увеличение фотографических картинок ограничено размером зернышка фотопленки. Ведь каждый кристаллик бромистого серебра действует как целое. Читатель, без сомнения, видел сильно увеличенные фотографии и замечал, что увеличение вовсе не приводит к уточнению картины, а только размазывает детали.
Но если мы сможем избежать операции фотографирования и будем увеличивать изображение оптическими способами, к чему имеется полная возможность (никто не мешает увеличивать число линз), то мы быстро убедимся, что и в этом случае большое увеличение не имеет смысла. Предел полезному увеличению любого прибора дает волновой аспект электромагнитного поля. Рассматриваем ли мы предмет через увеличительное стеклышко, просто глазом, с помощью микроскопа или телескопа — все равно во всех этих случаях световая волна, идущая от светящейся точки, должна пройти через отверстие. Но при этом возникает явление дифракции, т. е. отклонение светового луча от прямого пути. Луч в той или иной степени «заглядывает за угол». Поэтому изображение точки никогда не будет точкой, а будет пятнышком. И как ни стараться, невозможно сделать размер этого пятна меньшим длины волны света.
Существенно уметь прикинуть, при каких условиях ход электромагнитной волны заметно отклоняется от прямолинейного пути.
Если обозначить через х линейное отклонение от прямого пути, наблюдаемое на расстоянии f от источника излучения, а размер препятствия или отверстия, которое находится на пути следования луча, равен а, то имеет место следующее соотношение:
x = λ∙f/a
Здесь λ — длина волны. Из этого уравнения следует, что дифракцию можно наблюдать и от мельчайших частиц, и от небесных тел. Все зависит от того, о волнах какой длины и о каких расстояниях идет речь. То же самое можно сказать и об отверстиях. Вовсе не обязательно иметь дело с крошечными отверстиями, чтобы наблюдать дифракцию. Скажем, отверстие, в которое пролезет теннисный мяч, позволит наблюдать дифракционные явления, но, правда, лишь на расстояниях порядка сотен метров.
Простенькое уравнение, которое мы привели, позволяет судить о предельных возможностях микроскопов и телескопов.
Микроскоп не разрешает нам разглядеть детали предмета с большей точностью, чем микрометр. Ну, а детали миллиметрового размера мы видим невооруженным глазом. Отсюда ясно, что, пользуясь оптическим микроскопом, нет смысла добиваться увеличения больше чем в тысячу раз.
Но, это ограничение касается оптического микроскопа. Вот если бы удалось сконструировать микроскоп, который мог работать не со световыми лучами, а с какими-либо другими, у которых длина волны была бы меньшей, то полезное увеличение микроскопа возросло бы. Такой микроскоп давно создан и работает во многих научных лабораториях. Это электронный микроскоп. Длина волны электронов может быть выбрана очень маленькой (см. с. 112).
С помощью электронного микроскопа удается видеть детали строения вещества, измеряемые десятимиллионными долями миллиметра. Биологи увидели молекулы ДНК — те самые длинные молекулы, с помощью которых наследственные черты передаются от родителей их потомству. Видны молекулы белков, можно разобраться в структуре мембран клеток, увидеть детали строения мышечных волокон. Я привожу лишь одну рекордную фотографию (рис. 2.4), которая с увеличением большим, чем в 3 миллиона, показывает кристаллическую решетку минерала пирофиллита. Видно расстояние между плоскостями кристалла, равное 4,45 А°.
Предел возможностям электронного микроскопа связан не с его разрешающей способностью — мы можем без труда уменьшить длину волны электронов. Все дело в контрастности изображения: изучаемую молекулу надо положить на подложку, а она ведь сама состоит из молекул. На фоне молекул подложки трудно разглядеть ту молекулу, которая нас интересует.
Электронный микроскоп — сложный и дорогой прибор. Обычно его «рост» — порядка полутора метров. Электроны разгоняются высоким напряжением. А за счет чего создается увеличение? Принцип тот же, что и у оптического микроскопа. Увеличение создается линзами. Но, разумеется, эти «линзы» совсем не похожи на линзы обычного микроскопа. Электроны фокусируются электрическими полями, приложенными к металлическим пластинам с отверстиями, а также магнитными полями, созданными катушками.
Существует множество различных технических приемов, помогающих создать изображение. При помощи микротомов изготовляются тончайшие срезы, рассматриваемые на просвет, молекулы на подложке оттеняются путем осаждения на них паров металлов. Можно также получить «реплику» образца, т. е. покрыть его тончайшей пленкой прозрачного материала, а затем стравить сам объект.
Электронная микроскопия — большой и важный раздел физики, ей стоило бы посвятить отдельную главу. Но малый объем сочинения гонит меня вперед.
Мысли о том, что при помощи выпуклых стекол можно рассматривать удаленные предметы, высказывались еще в XVI веке. Тем не менее мы не ошибемся, если припишем открытие телескопа (вернее — подзорной трубы) великому Галилею. Она была построена в июле 1609 г., и уже через год Галилей опубликовал свои первые наблюдения звездного неба.
Как и микроскоп, зрительная труба (телескоп-рефрактор) является в принципе комбинацией тех же двух линз — объектива, обращенного к предмету, и окуляра, обращенного к глазу. Так как рассматривается бесконечно удаленный предмет, то его изображение создается в фокальной плоскости объектива. Фокальная плоскость окуляра совпадает с плоскостью объектива, и из окуляра выходят пучки параллельных лучей.
Возможности телескопа растут с увеличением диаметра объектива. Так, например, большим телескопам доступны на Луне кратеры диаметром 1 км, в небольшие же телескопы обычно можно рассмотреть кратеры диаметром 150 км.
В астрономической обсерватории мы найдем не только телескопы-рефракторы. Придется наверняка познакомиться и с телескопом-рефлектором. Поскольку мы рассматриваем далекие предметы и требуется собрать лучи в фокусе, то для этой цели можно воспользоваться не сферической линзой, а сферическим зеркалом. Преимущество очевидно: мы избавляемся от хроматической аберрации. Недостатки зеркального телескопа связаны лишь с трудно осуществимыми высокими требованиями, предъявляемыми к поверхности зеркала.
Разумеется, и у телескопа имеется предел полезного увеличения, связанный с волновым аспектом света. Луч далекой звезды размывается в кружок, и это дает предел угловому расстоянию между звездами, которые мы можем разглядеть в телескоп. Желание увеличить возможности телескопа и здесь связано с увеличением его диаметра. Вероятно, предельные возможности телескопов лежат где-то близко к одной десятой секунды дуги.
В последние годы на помощь телескопам пришла новая техника. Астрономы изучают небо, фиксируя весь спектр электромагнитных волн, которые присылает нам космос. Немного мы поговорим о вторжении современной физики в тихую обитель звездочетов в гл. 7.
ИНТЕРФЕРОМЕТРЫ
Как уже неоднократно подчеркивалось, электромагнитное поле обладает волновым аспектом. Так же точно волновым аспектом обладают потоки частиц — электронов, нейтронов, протонов. Звук является результатом механических смещений среды, происходящих по закону волны. Общим для всех этих физических процессов является возможность приписать любому излучению длину волны, частоту и скорость распространения, связанные уравнением с = λ∙v. Простейшее излучение монохроматично, т. е. описывается одной длиной волны. В общем случае излучение представляет собой сложный спектр, т. е. сумму волн разной длины и разной интенсивности.
Волновой аспект излучения проявляется в двух явлениях: при сложении волн, прошедших разные пути, а также при рассеянии телами, встречающимися по пути луча. Важный частный случай рассеяния волн — это дифракция. Сложение волн носит название интерференции.
Здесь речь пойдет об интерференции света. Это явление лежит в основе действия приборов, которые помогают точно измерять расстояния, а также некоторые другие физические величины. Приборы, использующие явление интерференции для прикладных целей, и носят название интерферометров.
Принцип измерения расстояний сводится к подсчету числа волн, укладывающихся на измеряемом отрезке.
На первый взгляд может показаться, что такие измерения проводить несложно. Возьмем два источника света и сведем их лучи в одну точку. В зависимости от того, придут ли волны в точку наблюдения «горб к горбу» или «горб к впадине», создастся светлое или темное пятно. Поставим теперь задачу измерить расстояние, на которое мы хотим переместить один из источников света. При таком перемещении фазовые соотношения двух волн в точке наблюдения будут меняться. Нам остается лишь считать количество смен света на темноту, и тогда, учитывая геометрию опыта и зная длину волны света, вычислим без труда величину перемещения.
В принципе все верно. Но, действуя таким способом, мы не будем наблюдать картины чередования света и темноты. Экран будет все время оставаться светлым. Итак, простой опыт не удался.
Совершено несомненным является такой результат: два луча света, испускаемые разными источниками, сведенные в одну точку, всегда будут усиливать друг друга. Так, может быть, волновая теория неверна?
Нет, теория верна, электромагнитному излучению присущ волновой аспект. Но мы попытались действовать, сделав неверное предположение. Для того чтобы наблюдалась интерференция, необходимо, чтобы между складывающимися волнами все время сохранялась неизменная разность фаз. А ведь фазовые соотношения даже между волнами, исходящими от двух атомов одного и того же источника, совершенно, случайны. Мы уже говорили, что атомы света выбрасывают фотоны, не «договариваясь» друг с другом о своем поведении. Следовательно, два разных источника излучают несогласованно, или, как говорят, создают некогерентное излучение.
Но не оказывается ли тогда согласованное, т. е. когерентное, излучение чем-то вроде Синей птицы? Не оказывается!
Решение проблемы исключительно красиво и в то же время крайне просто, как большинство оригинальных идей: надо заставить излучение атома складываться с самим собой! А для этого требуется расщепить луч, идущий от каждого источника, на две части, заставить эти две части одного луча пройти разные пути, а затем уже свести в одну точку. Вот при этом условии мы, наблюдая интерференцию и меняя разности путей частей расщепленного луча, и вправду можем измерить интересующие пас перемещение и длину, подсчитывая число чередований света и темноты.
Мы описали принцип, лежащий в основе интерферометрических измерений, открытый еще в 1815 г. французским физиком Огюстеном Френелем (1788–1827). Рассмотрим теперь способы, лежащие в основе действия интерферометров, с помощью которых расщепляют луч и создают разности хода между расщепленными частями луча.
Остановимся поподробней на интерференции лучей света, отраженных от внешней и внутренней сторон прозрачной пластинки или пленки. Явление заслуживает внимания как по своей практической значимости, так и потому, что наблюдается в природе. Кроме того, на этом примере легко уясняются многие важные понятия, которыми мы пользуемся при описании световых и других электромагнитных волн.
Рис. 2.5 позволяет вычислить сдвиг фаз между такими двумя лучами. Разность фаз определяется разностью хода, т. е. разностью путей, пройденных двумя лучами.
Как видно из чертежа, разность хода x = 2d∙cos r. Но как перейти от разности хода лучей к разности фаз, которая определяет, будут ли две волны усиливать или ослаблять друг друга?
Поговорим с читателем, которого не пугает формула косинуса. Колебание светового вектора в любой точке пространства, можно записать следующим образом: A cos 2π∙v∙t. Сдвиг по фазе, на угол φ означает необходимость добавления этого угла к аргументу косинуса. Если мы хотим сравнить фазы точек одной и той же волны, разделенных расстоянием х, то нам надо учесть, сколько длин волн укладывается на этом участке, и полученное число умножить на 2π. Эта величина и будет фазовым сдвигом. Итак, φ = 2π∙x/λ.
Теперь вернемся к интерференции лучей в пластинке. Выражение для разности хода мы записали. Значит, остается лишь поделить эту величину на λ. Но… стоп. Кто нам сказал, что длина волны света в пустоте и внутри прозрачной пластинки одинакова? Напротив, у нас есть все основания подозревать, что с волной что-то происходит, когда она переходит из одной среды в другую. Ведь существует явление дисперсии: фотоны разной частоты ведут себя по-разному. Частота, длина волны и скорость ее распространения, связаны равенством c = v∙λ. Какие же из этих величин меняются, когда волна попадает в другую среду? На этот вопрос отвечает опыт.
Можно непосредственно измерить скорость распространения волны в теле и убедиться в том, что показатель преломления, заставляющий волну изменять направление своего движения при косом падении на поверхность раздела двух сред, равен отношению скоростей распространения света в них. В случае, если одна из сред — воздух (точнее — вакуум),
n = c/v.
где с — принятое обозначение скорости света в пустоте, a v — скорость распространения в среде. Ну, а дальше? Какой из двух параметров — частота или длина волны — меняется при переходе света из воздуха в среду? Чтобы объяснить результаты интерференционных опытов, необходимо предположить, что частота фотона остается неизменной, а длина волны меняется. Поэтому для показателя преломления справедлива также формула
n = λ0/λ,
где λ0— длина волны в воздухе.
Вот теперь мы уже знаем всё, для того чтобы записать разность фаз между лучами в описываемом опыте с пластинкой. Поскольку один из лучей шел в воздухе, а второй — в стекле, то разность фаз будет равна
Что же можно измерить, изучая интерференцию лучей в пластинке? Формула отвечает на этот вопрос. Если известна толщина, то можно определить показатель преломления материала. Если известно значение n, то можно с очень большой точностью (доли длины световой волны) найти толщину, и, наконец, можно измерять длины волн разной «цветности».
Если пластинка имеет переменную толщину, материал ее всюду однороден и угол падения практически одинаков для рассматриваемого участка пластинки, то интерференция будет обнаружена в виде так называемых полос равной толщины. На неровной пластинке возникнет система темных и светлых (или радужных в случае белого света — ведь фотон каждой цветности будет вести себя по-своему) полос, обрисовывающих места равной толщины. В этом состоит объяснение цветных разводов, которые мы так часто видим на пленках нефти или масла, разлитых на воде.
Очень красивые полосы равной толщины легко наблюдать на мыльной пленке. Сделайте проволочную рамку. Опустите ее в мыльный раствор и выньте. Мыло стекает, и в верхней части пленка будет тоньше, чем в нижней. На пленке появятся цветные горизонтальные полосы.
Интерференционный метод широко применяется для измерения малых расстояний или малых изменений расстояний. Он позволяет заметить изменения толщины, меньшие сотых долей длины световой волны. В интерференционных измерениях неровностей на поверхности кристалла удается достигнуть точности порядка 10-7 см.
Широко распространен этот метод в оптической промышленности. Если, скажем, нужно проверить качество поверхности стеклянной пластинки, то это делается рассмотрением полос равной толщины воздушного клина, создаваемого испытуемой пластинкой с идеально плоской поверхностью. Если прижать эти две пластинки с одного края, то образуется воздушный клин. Если обе поверхности плоские, то линии равной толщины будут параллельными прямыми.
Представим себе, что на испытуемой пластинке имеется впадина или бугор. Тогда линии равной толщины искривятся и будут обходить дефектное место. При изменении угла падения света полосы движутся в ту или другую сторону в зависимости от того, бугром или впадиной является дефект. На рис. 2.6 показано, как выглядит поле микроскопа в этих случаях. Оба рисунка соответствуют дефектным образцам. У первого дефект расположен справа у самого края, а у второго — слева.
Точные измерения показателей преломления вещества могут быть проделаны при помощи интерференционных рефрактометров. В этих приборах наблюдается интерференция между двумя лучами, которые по возможности отдалены друг, от друга.
Положим, что на пути одного из лучей установлено тело длиной l и с показателем преломления n. Если показатель преломления среды есть n0, то оптическая разность хода изменится на Δ = l∙(n — n0). Два луча сводят в одну, точку при помощи фокусирующей линзы. Какую же картину будем мы наблюдать в зрительной трубе? Систему светлых и темных полос. Но это не полосы равной толщины, которые видны невооруженным глазом. Система полос, возникающая, в рефрактометре, имеет другое происхождение. Ведь исходный пучок света не идеально параллельному, а слегка расходящийся. Значит, падать на пластинку лучи, составляющие конус, будут под слегка разными углами.
Интерференционные события будут проходить одинаково у лучей одинакового наклона. Они и соберутся в одном месте фокальной плоскости зрительной трубы. Если разность хода между расщепленными частями пучка будет меняться, то полосы придут в движение. При изменении разности хода на величину Δ через окуляр трубы пройдут Δ/λ, полос.
Точность метода очень велика, ибо смещение в 0,1 полосы улавливается без труда. При таком смещении Δ = 0,1∙λ = 0,5∙10-5 см, что на длине l = 10 см позволит зафиксировать изменение показателя преломления на 0,5∙10-6.
Необходимо рассказать теперь об интерферометре другого типа, не использующего явление преломления. Это интерферометр, созданный американским физиком Альбертом Майкельсоном (1852–1931). Трудно переоценить ту роль, которую он сыграл в истории физики (я рискну даже на более сильное утверждение: в истории человеческой мысли). С помощью этого интерферометра был впервые установлен факт исключительной важности: скорость света в направлениях вдоль и поперек земной орбиты одинакова. Это значит, что скорость света не складывается со скоростью движения лампы, дающей световую вспышку, по тем правилам, по которым складывается скорость пули со скоростью сдвижения стрелка с ружьем. Открытие этого замечательного факта привело к становлению теории относительности, к коренному пересмотру смысла основных научных понятий — длины, времени, массы, энергии. Но об этом речь у нас впереди. А об интерферометре Мендельсона нам стоит поговорить сейчас, так как его значимость определяется не только местом, занимаемым в истории физики, но и тем, что до сего времени простые принципы, лежащие в основе его конструкции, используются для измерения длин и расстояний.
В этом приборе параллельный пучок монохроматического света падает на плоскопараллельную пластинку P1 (рис. 2.7), покрытую со штрихованной стороны полу прозрачным слоем серебра. Эта пластинка поставлена под углом 45° к падающему от источника лучу и делит его на два, один из которых идет параллельно падающему лучу (к зеркалу M1), а другой — перпендикулярно (к зеркалу М2).
Разделенные лучи падают на оба зеркала перпендикулярно и возвращаются в те самые места полупрозрачной пластинки, из которых они вышли. Каждый луч, вернувшийся от зеркала, повторно расщепляется на пластинке. Часть света возвращается в источник, а другая часть поступает в зрительную трубу. На рисунке видно, что луч, идущий от зеркала, стоящего напротив трубы, три раза проходит через стеклянную пластинку с полупрозрачным слоем. Поэтому для обеспечения равенства оптических путей луч, идущий от зеркала М1, пропускается через компенсационную пластинку P2, идентичную первой, но без полупрозрачного слоя.
В поле зрения трубы будут наблюдаться круговые кольца, соответствующие интерференции в воздушном слое (толщина которого равна разности расстояний зеркал от места расщепления лучей) первичных лучей, образующих конус. Перемещение одного из зеркал (например, зеркала М2 в положение, показанное пунктиром) на четверть длины волны будет соответствовать переходу от максимума к минимуму, т. е. вызовет смещение картины на полкольца. Это может быть отчетливо отмечено наблюдателем. Таким образом, в фиолетовых лучах чувствительность интерферометра больше чем 100 нм.
Появление на сцене лазеров произвело революцию в технике интерферометрии.
Дело заключается в следующем. Время излучения атома равно 10-8—10-9 с. Единичный акт излучения состоит в испускании цуга волн. Поскольку время излучения столь мало, то, несмотря на большую скорость света, цуг очень короткий. Когда мы расщепляем луч на части, то интерферировать могут только две части одного и того же цуга волн. Это значит, что один отрезок синусоиды должен существенно перекрыться с другим отрезком. Но для этого, разумеется, необходимо, чтобы разность хода между расщепившимися частями луча была значительно меньше длины цуга.
Максимальная разность хода между лучами, при которой может наблюдаться интерференция, носит название когерентной длины. Для света это доли миллиметра.
Но смотрите, сколь разительно меняется ситуация при лазерном излучении. Лазер непрерывного действия создает фотоны стимулированного излучения, отправляющиеся в путешествие в одной и той же фазе. Или, говоря на волновом языке, цуги волн, исходящие из равных атомов, накладываются друг на друга, создавая как бы единую волну. Когерентная длина практически становится неограниченной и во всяком случае измеряется метрами и километрами (идеал, как всегда, недостижим; но я не стану останавливаться на различных факторах, влияющих на когерентную длину).
Пользуясь лазерным светом, можно строить интерферометры, позволяющие решать задачи, которые ранее считались неосуществимыми. Так, скажем, при обычном источнике света зеркало интерферометра Майкельсона можно смещать лишь на величины порядка миллиметра. Если же световой луч создается лазером, то путь луча, падающего на зеркало М1, может быть равен нескольким сантиметрам, а луча, отраженного от М2,— десяткам метров.
Интерферометры для контроля сферичности линз могут быть изготовлены с одной-единственной поверхностью сравнения, в то время как, используя обычный свет, с изменением радиуса испытываемой линзы приходилось менять и эталон сравнения (так как нельзя было работать с большими разностями хода). Мы уже не говорим о том, что интерференционные картины стали несравненно ярче, а поэтому анализируются легко и более точно.
Возможность обходиться без компенсации оптического пути одного из лучей позволяет изготовлять интерферометры совершенно нового типа. Становится возможным следить за смещениями плотин, геологическим дрейфом, колебаниями земной коры. Отражая лазерный свет от объектов, находящихся на большом расстоянии, и заставляя его интерферировать с исходным, можно производить точные измерения скорости движения таких объектов.
ЛАЗЕРНЫЕ ИНСТРУМЕНТЫ
Устройство, создающее лазерный луч, конечно, можно назвать прибором, поскольку оно применяется для анализа, контроля, наблюдений. Однако, в отличие от других оптических приборов, несравненно большее значение лазер имеет в промышленности. Использование лазеров настолько всеобъемлюще, что мы будем к нему неоднократно возвращаться. В этом параграфе мы остановимся на применениях лазера для обработки материалов. Если не нужна большая мощность, то можно воспользоваться компактным неодимовым лазером. Сердцем этого лазера является, как уже говорилось, стекло, легированное неодимом. Стеклянный стержень имеет длину 50 мм и диаметр 4 мм. Вспышка света, производящего накачку, дается ксеноновои лампой. Для того чтобы избежать потерь световой энергии, лампа и стержень заключены в цилиндрическую камеру, которая охлаждается водой.
Для разнообразных применений этого или подобного инструмента важны следующие его свойства: возможность локализации энергии на исключительно малой площади, возможность точной дозировки порции энергии, возможность подачи энергии без применения каких-либо проводов дли контактов.
Характерно применение лазера в часовой промышленности. Всем хорошо известно, что часы изготовляются на «камнях». Возможно, читатель и не знает, для чего нужны в часах маленькие рубины, но что их количество определяет качество часов — ему, конечно, известно. В рубиновых шайбах надо буравить отверстия. Без помощи лазера эта операция занимала несколько минут для каждого камня. Теперь процесс полностью автоматизирован и занимает доли секунды. Если учесть, что число камней, нужных промышленности, измеряется многими миллионами в год, то значение этого использования инструмента становится совершенно очевидным.
Тем же целям служит лазер в алмазной промышленности. При изготовлении алмазных камней для протяжки или бурения лазер применяется как инструмент, с помощью которого камню можно придать любой профиль и проделать в нем отверстие вплоть до размера в несколько микрометров!
Но я прервал разговор о производстве часов. Лазер оказывает ему еще одну большую услугу: приваривает пружину к часовому механизму. Вполне очевидно, что и во всех других областях промышленности, где требуется точечная сварка (а современная техника имеет в этом крайнюю нужду), может о большим успехом использоваться лазерный луч. Огромным достоинством тончайшего луча является, то, что нет заботы об охране и охлаждении частей, соседствующих с местом, подлежащим сварке.
Уже тривиальным стало использование лазерного инструмента как ножа для вырезывания любых контуров на любом материале.
Упомянем об одной неожиданной области применения лазера: для реставрации мраморных скульптур. Атмосфера XX века, увы, — далеко не чистый воздух. Различные вредные газы, и прежде всего окись серы, образуют на мраморе черную корку. Корка эта пориста и поэтому как губка впитывает влагу и дополнительные дозы вредных веществ. Удаление корки механическими, и химическими средствами может привести к порче скульптуры. Действуя же лазером в импульсном режиме, удаляют корку не затронув мрамора.
При помощи лазера на углекислом газе осуществляется рост кристаллов без тиглей. Процесс этот не нов. Токи высокой частоты применялись уже давно для такого выращивания кристаллов, но не для диэлектриков, обладающих слишком малой теплопроводностью. При помощи лазеров сейчас растят без тиглей кристаллы ниобатов и других очень нужных веществ. Важность безтигельного роста кристаллов для нужд микроэлектроники невозможно переоценить, ибо миллионные доли примесей могут сыграть отрицательную роль; а избавиться от того, чтобы какие-либо «вредные» атомы не перешли из материала тигля в кристалл, практически невозможно.
Я не буду останавливаться на описании конструкции соответствующего аппарата. О росте кристаллов шла речь во 2-й книге. Как и в случае токов высокой частоты, луч лазера создает небольшую расплавленную зону, которая медленно подводит вещество к растущему кристаллу. Мне кажется вероятным, что использование лазера потеснит другие методы выращивания кристаллов.
ФОТОМЕТРИЯ
Каждый источник света можно охарактеризовать энергией, которую он излучает. Однако во многих случаях нас интересует только та часть потока энергии, которая приводит к зрительному ощущению. Такой особенностью обладают, как мы говорили, электромагнитные волны, длины которых лежат в пределах примерно от 380 до 780 нм.
Воспринимаемый мозгом свет характеризуется яркостью и цветом. Если сопоставить зрительные ощущения, которые создаются светом равной интенсивности, но разной длины волны, то окажется, что наиболее ярким глазу представляется источник света, дающий волну длиной 555 нм, что соответствует зеленому цвету.
Восприятие света можно характеризовать кривой видимости (рис. 2.8), которая показывает (в относительных единицах) чувствительность нормального глаза к волнам различной длины. Однако техники оставляют эту кривую вне внимания и предоставляют глазу выносить суждение об интегральной силе света.
Идя по этому пути, надо выбрать какой-то эталонный источник света, а затем сравнивать с ним другие источники. За единицей силы света долго сохранялось название свечи, ибо первые попытки выбора эталона как раз и заключались в том, чтобы подобрать некое стандартное пламя свечи. Не приходится и говорить, как это трудно сделать.
Международный эталон, принятый на сегодня, представляет собой раскаленное черное тело. Материалом служит платина. Черное тело испускает свет, излучаемый платиной, нагретой до температуры плавления, т. е. до 2046 К, через небольшое отверстие.
Единица силы света получила название канделы («свеча» по-латыни). Международное определение старается избежать прямого указания на температуру свечения (чтобы не внести ошибки, связанные с измерением температуры). Поэтому кандела определяется так: если в качестве источника взять платину, находящуюся в состоянии затвердевания при нормальном атмосферном давление, то площадь 1/610-5 м2 дает в направлении, перпендикулярном поверхности, силу света, равную одной канделе.
На достаточно больших расстояниях, источник света представляется точкой. Именно в этих случаях и удобно измерять силу света. Построим около точечного источника сферу, выделим на этой поверхности участок площадью S. Поделив S на квадрат расстояния от центра, мы получим так называемый телесный угол. Единицей телесного угла является стерадиан. Если на сфере радиусом один метр вырезается площадка S = 1 м2, то телесный угол равен одному стерадиану.
Световым потоком называют силу света точечного источника, умноженную на величину телесного угла.
Пусть вас не смущает то обстоятельство, что световой поток обращается в нуль, когда речь идет о параллельных лучах. В подобных случаях понятием светового потока не пользуются.
За единицу светового потока принимается люмен, равный потоку, который посылает точечный источник с силой света в одну канделу в угол, равный одному стерадиану. Суммарный световой поток, излучаемый точкой во все стороны, будет равняться 4π лм.
Сила света характеризует источник света вне зависимости от его поверхности. В то же время совершенно ясно, что впечатление будет различным в зависимости от протяженности источника. Поэтому пользуются понятием яркости источника. Это — сила света, отнесенная к единице поверхности источника света. Яркость измеряется в стильбах: один стильб равен канделе, поделенной на квадратный сантиметр.
Один и тот же источник света принесет равную световую энергию к странице раскрытой книги в зависимости от того, где он находится. Для читателя важно, какова освещенность участка письменного стола, на котором лежит книга. Если размер источника невелик (точечный источник), то освещенность равна силе света, поделенной на квадрат расстояния от источника. Почему на квадрат? Ответ ясен: световой поток остается неизменным внутри заданного телесного угла, как бы далеко мы ни ушли от светящейся точки. Ну, а площадь сферы и площадь участка, вырезаемого заданным телесным углом, будут шести обратно пропорционально квадрату расстояния. Это простое правило называют законом обратных квадратов. Изменив расстояние читаемой книги от маленькой лампочки с 1 до 10 м, мы уменьшим освещенность страницы книги в сто раз.
Единица освещенности — люкс. Такую освещенность создает поток света, равный 1 лм, на площади в 1 м2.
Освещенность в безлунную ночь равна 0,0003 лк. Так что когда мы говорим: «ни зги не видно», то определяем освещенность, этой самой «зги». В лунную ночь освещенность равна — 0,2 лк. Чтобы читать, не напрягая глаз, требуется освещенность 30 лк. При киносъемке включают мощные прожекторы и доводят освещенность предметов до 10 000 лк.
Но мы ничего еще не сказали о приборах, которые служат для измерения, световых потоков и освещенностей. В настоящее время такие измерения — не проблема. Фактически мы действуем именно так, как надо было бы поступить, дав новое определение канделы. Мы измеряем энергию, падающую на фотоэлемент, а шкалу фотоэлемента градуируем в люксах с учетом кривой видности.
Существовавшие в прошлом веке фотометры работали по принципу сравнения яркостей двух освещенных смежных площадок. На одну из них падал свет, силу которого мы хотели измерить. С помощью нехитрых приспособлений световой поток уменьшали в известное число раз так, чтобы в конце концов смежные площадки были освещены одинаково.
ГОЛОГРАФИЯ
Создание лазеров знаменует новую эпоху в развитии науки и техники. Трудно найти такую область знания, в которой стимулированное излучение не открыло бы новые возможности.
В 1947 г. Д. Габор предложил использовать когерентный свет для получения изображения объекта совершенно новым способом. Новая техника, получившая название голографии, коренным, образом отличается от фотографии. Голография становится возможной только лишь благодаря особенностям стимулированного излучения, отличающим его от обычного света.
Еще раз подчеркнем, что при лазерном излучении почти все фотоны совпадают по всем своим признакам — частоте, фазе, поляризации и направлению распространения. Лазерный луч размывается в ничтожной степени, т. е. можно получить чрезвычайно тонкий луч на больших расстояниях от источника, лазерному лучу свойственна очень большая когерентная длина (длина цуга волн). Благодаря последнему обстоятельству (оно-то и важно для голографии) возможна интерференция расщепленных лучей с большой разностью хода.
Верхняя часть рис. 2.9 поясняет технику получения голограммы.
Наблюдаемый объект освещается широким несильным (чтобы не повредить объект) лазерным лучом. Один и тот же луч рассеивается объектом и отражается зеркалом, которое создает так называемую опорную волну. Две волны накладываются. Происходит интерференция, картина которой фиксируется фотопластинкой.
Взгляните на рис. 2.10.
Сверху показан объект, а под ним — его «изображение». Мы не оговорились: эта сложная комбинация темных и светлых колец, называемая голограммой, действительно является изображением объекта, но только изображением скрытым. Голограмма содержит полную информацию об объекте, точнее — полные сведения об электромагнитной волне, рассеянной шахматными фигурками. Фотография не содержит таких всеобъемлющих сведений. Лучший фотоснимок точно передает все сведения об интенсивности рассеянных лучей. Но ведь волна, рассеянная любой точкой объекта, полностью характеризуется не только своей интенсивностью (амплитудой), но и фазой. Голограмма — это интерференционная картина, и каждая светлая или темная линия говорит нам не только об интенсивности, но и о фазе лучей, пришедших от объекта в соответствующие места фотопластинки.
Как и любую фотопластинку, голограмму проявляют, закрепляют и хранят сколько угодно времени. Когда нам захочется полюбоваться на снятый объект, мы облучим, как это показано на нижней части рис. 2.9, голограмму светом того же лазера, восстановив геометрическое расположение, имевшее место при съемке: луч лазера направим так, как шел луч, отраженный от зеркала. Тогда там, где находился объект, возникнет изображение предмета, в идеале тождественное той картине, которую видел глаз.
Теории получения голограммы мы не можем касаться. Основная идея состоит в том, что при освещении голограммы возникают рассеянные волны, обладающие теми же амплитудами и фазами, которые создали эту голограмму. Эти волны складываются в волновой фронт, тождественный тому волновому фронту, который создал голограмму. Происходит своеобразная реконструкция волны при освещении голограммы в тех же условиях, в которых освещался объект. Благодаря этому создается изображение объекта.
Исследования в области голографии продолжаются. Сейчас имеется возможность получать цветные изображения. Возможно улучшить результаты, снимая несколько голограмм с разных позиций. Наконец (и это, пожалуй, самое важное), оказывается, что можно рассматривать голограммы, не прибегая к лазеру.
Имеются книги, трактующие предмет голографии в деталях. Голография заслуживает внимания по той причине, что является очень емким способом хранения трехмерной информации об объекте. Последнее слово в этой области еще не сказано, и будущее покажет в какой мере, голография войдет в быт и в технику.
Глава 3 Жесткое электромагнитное излучение
ОТКРЫТИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
К рентгеновским лучам относят излучение, занимающее участок электромагнитного спектра примерно от нескольких десятков до сотых долей нанометра. Еще более жесткие, т. е. более коротковолновые лучи называются гамма-лучами.
Как мы уже говорили, названия участков электромагнитного спектра довольно условны. Тот или иной термин используют, руководствуясь не столько величиной длины волны, сколько характером источника излучения. Чаще всего термин «рентгеновские лучи» используют для излучения, возникающего при встрече потока, электронов с препятствием.
Вильгельм Конрад Рентген (1845–1923) открыл этот вид излучения 8 ноября 1895 г. В эти годы многие физики мира исследовали потоки электронов, возникающие в откачанных стеклянных трубках (некоторые из этих трубок были изображены на рис. 2.6 в. 3-й книге). В сосуд впаивались два электрода. К ним подводилось высокое напряжение. То, что от катода такой трубки распространяются какие-то лучи, подозревалось, довольно давно. Еще в самом начале XIX века различные исследователи наблюдали вспышки внутри трубки, свечение стекла. Опытами Вильгельма Гитторфа (1844–1914) и Уильяма Крукса (1832–1919) вполне отчетливо было доказано, что речь идет о лучах. Все учебники обошла фотография трубки Крукса с крестом, которую он создал в 1879 г., через десять лет после Гитторфа. Крест отбрасывал на стекло отчетливую тень. Этот изящный опыт, доказывает, что от катода идут какие-то лучи и распространяются они прямолинейно. Когда на стеклo падают лучи, оно светится, тонкий слой металла поглощает это излучение.
То, что катодные лучи представляют собой поток электронов) было доказано Дж. Дж. Томсоном в 1897 г. Способом, о котором мы рассказали в 3-й книге, ему удалось определить отношение заряда к массе электрона. Прошло еще 10–15 лет, и стало ясным, что электрон является мельчайшей частицей электричества.
Но мы повторяемся и уходим в сторону. Сейчас нас интересует открытие, сделанное Рентгеном. Однако этим повторением хотелось подчеркнуть, что открытие Рентгена предшествовало пониманию природы лучей, исходящих от катода. Собственно говоря, именно из-за этой неясности, Рентген и работал с различными трубками, отличавшимися взаимным расположением мест впайки электродов и формой стеклянной оболочки.
Мельчайшие подробности событий вечера 8 ноября 1895 г. хорошо известны. Рентген накинул кусок черной материи на трубку, погасил свет в комнате и собрался идти домой, забыв выключить рубильник. Бросив взгляд на прибор, с которым он работал, Рентген заметил, что светится лежащий рядом с трубкой обладающий способностью люминесцировать экран с синеродистым барием. Рентген вернулся, выключил рубильник — свечение пропало. Включил рубильник — экран опять засветился. Рентген знал, что в трубке той конструкции, с которой он работал, катодные лучи не могут пройти через чехол, накинутый на трубку, да еще пробежать через большой слой воздуха. Значит… значит, обнаружено новое, до сих пор не известное излучение.
Первое сообщение о своем открытии Рентген отправил в журнал в конце года. За это время он сумел настолько детально изучить свойства новых лучей, что, по сути дела, до открытия дифракции рентгеновских лучей (1912 г.), о чем у нас речь впереди, ничего нового и отношении икс-лучей обнаружено не было. Название «рентгеновские лучи» принято не везде: французы, англичане и американцы удержали название, которое дал открытому им излучению сам Рентген: икс-лучи.
Наиболее замечательным свойством рентгеновских лучей, свойством, которое Рентген исследовал и проиллюстрировал в первую очередь, является их способность проходить через материалы, непрозрачные для света. (Рис. 3.1 напоминает, что такого рода изошутки появились в большом количестве спустя каких-нибудь 2–3 месяца после первых публикаций Рентгена.)
Проникающая способность рентгеновских лучей оказывает неоценимые услуги медицине. Становится также возможным обнаружение дефектов в промышленных изделиях. Поразительные результаты рентгенографии являются следствием того, что разные по плотности вещества поглощают рентгеновские лучи по-разному. Чем легче атомы вещества, тем меньше они поглощают лучи.
Довольно быстро было установлено, что проницаемость тел по отношению к лучам растет с возрастанием напряжения на трубке. Напряжения, которые обычно применяются при рентгеновских просвечиваниях, лежат в пределах от нескольких десятков до нескольких сотен киловольт.
Изучив свойства рентгеновских лучей, исследователи установили, что причиной их возникновения является торможение потока электронов препятствием. Занятно, что долгое время рентгеновскую трубку изготовляли с тремя электродами. Против катода впаивался «антикатод», о который и ударялись электроны. Анод помещался сбоку. Через несколько лет сообразили, что это никчемное усложнение, и в настоящее время в трубку впаиваются два электрода. Пучок электронов тормозится анодом, поверхность которого обычно делается скошенной. В этом случае пучок рентгеновских лучей направляется в соответствующую сторону. Если поверхность анода будет, встречать пучок электронов под прямым углом, то лучи пойдут, от анода во все стороны, что приведет к потере в интенсивности.
Просвечивание рентгеновскими лучами совершило настоящую революцию в промышленности и особенно в медицине. Техника рентгеновского просвечивания в настоящее время весьма усовершенствована. Меняя расположение изучаемого объекта по отношению к рентгеновской трубке, можно получить несколько картин, с помощью которых удается не только установить расположение дефекта в проекции, но и определить глубину его залегания.
В зависимости от того, какие материалы или ткани подлежат исследованию, целесообразно применять иногда более жесткое (т. е. более проникающее), а иногда и совсем мягкое излучение. Главная задача — достигнуть контрастности: надо увидеть дефект, который даже незначительно отличается по плотности от основного материала.
Закон поглощения рентгеновских лучей, как и закон поглощения любого излучения, достаточно очевиден. Нас интересует, как изменится интенсивность луча (напомним, что интенсивность — это энергия, отнесенная к единице времени и единице площади) после прохождения пластинки толщиной d. Так как я пишу эту книгу для читателя, который не знает интегрального исчисления, то мне придется ограничиться формулировкой этого закона для прохождения лучом пластинок малой толщины. Толщина «мала» в том случае, если интенсивность падает незначительно, скажем на 1 %. Для такого примера закон прост: доля поглощенного излучения прямо пропорциональна толщине пластинки. Если интенсивность уменьшилась от значения I0 до значения I, то это простое правило запишется так:
(I — I0) = μ∙d
Коэффициент пропорциональности μ носит название коэффициента поглощения.
А вот простой вопрос, который я много раз задавал на экзаменах: в каких единицах измеряется, коэффициент поглощения? Сообразить нетрудно. Единицы измерения с обеих сторон равенства должны быть одинаковы. Это ведь ясно. Нельзя же сказать, что больше, 10 кг или 5 м. Сравнивать, можно килограммы с килограммами, амперы о амперами, эрга в эргами. Значит, в любом равенстве справа и слева должны стаять числа, выражаемые в одних ж тех же единицах.
Но в левой части нашего равенства записана так называемая безразмерная величина. Сказав, что доля поглощения излучения равна 1/30 или 0,08, мы этим все сказали. Единицы измерения «сократились» при делении интенсивности на интенсивность. Но если так, то и с правой стороны равенствах должна стоять безразмерная величина. Так как толщины измеряются в сантиметрах (или других единицах длины), то коэффициент поглощения выражается в обратных сантиметрах т. е. в см-1.
Допустим, что луч проходит через пластину толщиной 10 см, терян лишь 1?% интенсивности. Левая часть равенства равна 1/100. Значит, в этом примере коэффициент поглощения равен 0,001 см-1. А вот если лучи мягкие и теряют процент энергии, уже пройдя через фольгу толщиной в микрометр (0,0001 см), то коэффициент поглощения будет равен 100 см-1.
Физики не- располагают хорошей теорией для установлении формулы коэффициента поглощения. Укажу лишь, что коэффициент поглощения примерно пропорционален кубу длины волны рентгеновского излучения и кубу атомного номера вещества, через которое луч проходит.
Поскольку длины волн рентгеновских лучей весьма малы, то частоты колебания электромагнитных волн велики. Эта значит, что рентгеновский квант hv несет большую энергию. Этой энергии не только достаточно для химических реакций, приводящих к почернению эмульсии фотопластинки и к созданию свечения фосфоресцирующих экранов (на это способны и световые лучи), но ее с избытком хватает и на то, чтобы разрушать молекулы. Другими словами, рентгеновские лучи ионизуют воздух и другие среды; через которые они проходят.
Теперь несколько слов о гамма-лучах. Этот термин мы используем, когда речь идет о коротковолновом излучении, возникающем при радиоактивном распаде. Забегая вперед, скажем, что гамма-лучи исходят из естественных радиоактивных веществ и создаются искусственными элементами. В ядерном реакторе, конечно, возникает гамма-излучение. Сильные и очень жесткие гамма-лучи возникают при взрыве атомной бомбы.
Ввиду того, что гамма-лучи могут иметь очень малую длину волны, коэффициент их поглощения может быть очень малым. Так, например, гамма-лучи, которые излучаются при распаде радиоактивного кобальта, способны пройти через десятки сантиметров стали.
Коротковолновое электромагнитное излучение, способное разрушать молекулы, в существенных дозах очень опасно для организма. Поэтому от рентгеновских и гамма-лучей нужна защита. Чаще всего для этой цели используют свинец. Стены рентгеновских кабинетов покрывают специальной штукатуркой, содержащей соли бария.
Гамма-лучи, так же как и рентгеновские, могут быть использованы для просвечивания. Обычно прибегают к гамма-лучам радиоактивных веществ, которые являются «золой» ядерного горючего. Их достоинством по сравнению с рентгеновскими лучами является большая проникающая способность, но главное — это возможность использовать в качестве источника излучения маленькую ампулку, которую можно поместить в места, недоступные для рентгеновской трубки.
РЕНТГЕНОСТРУКТУРНЫЙ АНАЛИЗ
В 1912 г. Рентген был руководителем кафедры физики Мюнхенского университета. Проблемы, касающиеся природы икс-лучей, обсуждались на этой кафедре неустанно. Надо сказать, что Рентген, будучи сам физиком-экспериментатором, относился с большим уважением к теории. На кафедре физики Мюнхенского университета трудилось много талантливых теоретиков, которые ломали себе голову над тем, что представляют собой рентгеновские лучи.
Разумеется, были сделаны попытки выяснить природу рентгеновских лучей, исследуя их прохождение через дифракционную решетку. (Напомним читателю, что представляет собой дифракционная решетка, с помощью которой однозначно доказывается волновая природа света и вдобавок весьма точно определяется длина волны того или иного излучения.
Один из способов изготовления такой решетки состоит в том, что на стеклянную пластинку, покрытую слоем алюминия, мягким резцом из слоновой кости при помощи специальных машин наносятся штрихи. Штрихи должны отстоять на строго одинаковых расстояниях друг от друга. Хорошая решетка должна обладать малым периодом (общая ширина щели и непрозрачного промежутка) и большим числом штрихов. Удается довести это число до сотен тысяч, при этом на 1 мм приходится более тысячи штрихов.
При помощи линзы сильный точечный источник света дает параллельный пучок света, который падает на решетку под прямым углом. Из каждой щели лучи выходят во все стороны (иными словами — каждая щель становится источником сферической волны). Но лишь в избранных направлениях волны от всех щелей будут синфазны. Для взаимной поддержки требуется чтобы разность хода равнялась целому числу длин волн. Сильные лучи пойдут в направлениях под углом а, подчиняющихся условию
а∙sin α = n∙λ,
где n — целое число, а — период решетки. Читатель легко выведет эту формулу без нашей помощи.
Целое число n называют порядком спектра. Если на решетку падает монохроматический луч, то мы получим в фокальной плоскости окуляра несколько линий, разделенных темными промежутками. Если свет состоит из волн разной длины, то решетка создает несколько спектров — первого, второго и т. д. порядков. Каждый последующий спектр будет более растянут, чем предыдущий.
Поскольку длина волны света того же порядка, что-и расстояние между щелями, то дифракционные решетки разлагают свет (притом не только видимый, но также ультрафиолетовый и в особенности хорошо инфракрасный) в спектры. С их помощью можно проводить детальный спектральный анализ.
Но в отношении рентгеновских лучей дифракционные решетки вели себя как система открытых дверей. Рентгеновские лучи проходили через них не отклоняясь. Можно было предполагать, что рентгеновские лучи являются потоком частиц. Но не возбранялось думать, что рентгеновское излучение — это такое же электромагнитное излучение, как и свет, но только длина волны λ много короче. И правда, предположим, что λ очень мала. Если так, то согласно условию дифракции от линейной оптической решетки а∙sin α = n∙λ все n лучей, идущие под углами отклонения α, практически сольются, и дифракция не будет заметна. Но сделать дифракционную решетку с щелями, отстоящими друг от друга на расстоянии а, равном миллионным долям микрометра, вещь невозможная. Как же быть? Физик Макс Лауэ (1879–1960) еще в самом начале своей научной деятельности был уверен, что рентгеновские лучи — это электромагнитное излучение. Его знакомый кристаллограф, с которым они часто беседовали, был убежден, что кристалл представляет собой трехмерную решетку атомов. В одной из бесчисленных бесед на научные темы Лауэ решил сопоставить свою идею о природе рентгеновских лучей с представлением о кристалле как о решетке. «А вдруг расстояния между атомами кристалла и длина волны рентгеновских лучей — величины одного порядка?» — подумал Лауэ.
Может ли трехмерная решетка заменить линейную решетку щелей? Ответ на этот вопрос был не очевиден; тем не менее Лауэ решил попробовать. Первый опыт был совсем прост. Диафрагмировали пучок рентгеновских лучей. На пути лучей поставили крупный кристалл, а рядом с кристаллом — фотографическую пластинку. Правда, не очень ясно было, куда ставить пластинку, поскольку кристалл все же не линейная решетка. Место для пластинки было выбрано неудачное, и некоторое время опыт не получался. Забавно, что в правильное положение пластинка была поставлена случайно, по ошибке.
Эта случайность, конечно, особой роли в открытии не сыграла. Дело в том, что параллельно с попытками обнаружить явление на опыте Лауэ разрабатывал теорию явления. Вскоре ему удалось распространить теорию линейной дифракционной решетки на трехмерный случай. Из теории следовало, что дифракционные лучи будут возникать лишь при некоторых определенных ориентациях кристалла по отношению к падающему лучу. Из теории вытекало также, что наиболее интенсивными должны быть лучи отклоненные под небольшим углом. Отсюда следовало, что фотопластинку надо ставить за кристаллом, перпендикулярно падающему лучу.
Одними из первых обратили внимание на открытое явление англичане — отец и сын Брэгги. Оба носили одно имя — Уильям. Они немедленно повторили опыт Лауэ, дали его теории очень простую и наглядную интерпретацию и показали на большом числе простых примеров, что открытие Лауэ может быть использовано как метод изучения атомной структуры вещества.
Ознакомим читателя с основными идеями рентгеноструктурного анализа и дадим представление о методе определения структуры кристалла, следуя которому можно измерить расстояния между атомами с точностью до одной сотой ангстрема, дать картину пространственного расположения атомов в молекуле и выяснить характер упаковки молекул в кристалле.
Положим, что кристалл установлен на специальном держателе и вращается около некоторой оси. Рентгеновский луч падает под прямым углом к оси вращения. Что же при этом происходит? Рассмотрим дифракционные явления, происходящие при падении рентгеновского луча на кристалл, так как если бы рассеивающим центром являлся увел решетки.
Отец и сын Брэгги показали, что рассеяние рентгеновских лучей узлами решетки эквивалентно своеобразному избирательному (т. е. происходящему лишь при некоторых дискретных значениях угла) отражению лучей от систем узловых плоскостей, на которые может быть разбита решетка.
Пусть луч, представляющий собой электромагнитную волну определенной длины, падает на кристалл под каким-то углом. Для разных систем плоскостей этот угол будет разным. Мы вправе полагать, что любая атомная плоскость отразит рентгеновскую волну по закону: угол падения равен углу отражения. Но имеется существенное отличив от оптического луча. Рентгеновский луч, в отличие от света, проникает в глубь кристалла. Это означает, что отражение луча будет происходить не только от внешней поверхности, а от всех атомных плоскостей.
Рассмотрим одну из таких систем плоскостей, характеризующихся межплоскостным расстоянием d. Каждая из них будет «отражать» падающий луч под одним и тем же углом θ. Эти отраженные лучи должны интерферировать между собой, и сильный вторичный луч может возникнуть только в том случае, если лучи, отраженные от всех плоскостей семейства, будут распространяться в одной фазе. Иными словами, разность хода между лучами должна равняться целому числу длин волн.
На рис. 3.2 сделано геометрическое построение, из которого следует, что разность хода между соседними отраженными лучами равняется 2d∙sin θ. Следовательно, условие дифракции будет иметь вид
2d∙sin θ = n∙λ
Одновременно с Брэггами к этой формуле пришёл русский кристаллограф Г. В. Вульф, и она названа уравнением Брэгга-Вульфа (правильнее было бы употреблять первую фамилию во множественном числе, но так уж принято).
Кристалл можно разбить на системы плоскостей сколь угодно большим числом способов. Но эффективной для отражения окажется лишь система с таким межплоскостным расстоянием и ориентированная по отношению к падающем лучу таким образом, чтобы выполнялось уравнение Брэгга-Вульфа.
Очевидно, если луч монохроматический (т. е. электромагнитная волна имеет определенную длину), то при произвольном положении кристалла по отношению к лучу отражение может и не произойти. Однако, поворачивая кристалл, мы можем по очереди привести в отражающее положение разные системы плоскостей. Именно такой способ работы и оказался наиболее подходящим для практических целей.
Что же касается опыта Лауэ, то его удача определилась, тем, что на кристалл падал «белый спектр» рентгеновских лучей, т. е. поток волн, длины которых непрерывно распределены в некотором интервале (см. ниже). Поэтому, хотя в опыте Лауэ кристалл был неподвижен, разные системы плоскостей оказались в «отражающем» положении для волн различной длины. В настоящее время рентгеноструктурный анализ полностью автоматизирован. Маленький кристаллик (0,1–1 мм) закрепляют на специальной головке, которая может по заданной программе поворачивать кристалл, подставляя в отражающее положение одну за другой все его системы плоскостей. Каждая отражающая плоскость (так говорят для краткости, чтобы не повторять все время слово «система») характеризуется, во-первых, своим межплоскостным расстоянием, во-вторых, углами, которые она образует с осями элементарной ячейки кристалла (длины ребер и углы между ребрами ячейки измеряются в первую очередь и также автоматически), и, в-третьих, интенсивностью отраженного луча.
Чем больше атомов содержит молекула, тем, естественно, больше размеры элементарной ячейки. С этим усложнением растет и объем информации. Ведь число отражающих, плоскостей будет тем больше, чем больше ячейка. Число измеряемых отражений может колебаться от нескольких десятков до нескольких тысяч.
Мы обещали ознакомить читателя с основными идеями рентгеноструктурного анализа. Сначала, так сказать, перевернем проблему. Положим, что структура кристалла известна во всех деталях. Это значит, что мы знаем рисунок атомов, т. е. располагаем, сведениями о координатах всех атомов, образующих элементарную ячейку (пожалуйста, освежите в своей памяти те сведения о структуре кристалла, которые были даны во 2-й книге). Рассмотрим какую-либо систему отражающих плоскостей. Достаточно очевидно следующее. Если большинство атомов кристалла ляжет на плоскости, проходящие через узлы решетки, то все атомы будут рассеивать рентгеновские лучи в одной фазе. Возникнет сильный отраженный луч. Теперь представьте себе другой случай. Половина атомов попадает на узловые плоскости, а половина атомов находится как раз по середине между отражающими плоскостями. Тогда половина атомов рассеивает падающий луч в одной фазе, а половина — в противоположной. Отражения не произойдет!
Это два крайних случая. Во всех остальных мы будем получать, лучи разной интенсивности. Измерительный прибор — его называют автоматическим дифрактометром — способен измерить интенсивности отражений, отличающиеся в десять тысяч раз.
Интенсивность луча однозначно связана с расположением атомов между узловыми плоскостями. Формула, дающая, эту связь, слишком сложна, чтобы мы ее привели. Да это и не нужно. Сказанного выше в отношении двух крайних случаев достаточно, чтобы читатель поверил в существование такой формулы, в которой интенсивность представлена в функции координат всех атомов. Сортность, атомов также учитывается этой формулой, ибо чем больше электронов у атома, тем сильнее он рассеивает рентгеновские лучи.
В формулу, связывающую структуру и интенсивность отраженного луча, входят, конечно, и сведения об ориентации отражающей плоскости, а также о размерах элементарной ячейки. Таких уравнений мы можем записать столько, сколько измерено отражений.
Если структура известна, то интенсивности всех лучей могут быть рассчитаны и сопоставлены с опытом. Но ведь это не та задача, которую нам надо решить! Нужно справиться с обратной задачей: по сведениям об интенсивности нескольких десятков, или сотен, или тысяч отражений найти координаты всех атомов в ячейке. На первый взгляд может показаться, что при современных возможностях электронно-вычислительных машин никакой особой проблемы в решении этой обратной задачи не существует. Много уравнений? Ну так что же, вычислительная машина справится с их решением!
Однако дело обстоит далеко не так просто. Опытные данные — это интенсивности лучей. Интенсивность пропорциональна квадрату амплитуды. Формула связи, о которой шла речь, является, по сути дела, формулой интерференции. Волны, рассеянные всеми атомами кристалла, интерферируют между собой. Происходит сложение амплитуд волн, рассеянных всеми атомами. Вычисляется суммарная амплитуда, а интенсивность находится возведением амплитуды в квадрат. Такую задачу решить ничего не стоит. А как решить обратную? Извлечь квадратный корень из интенсивности, чтобы получить амплитуду? Правильно. Но у корня квадратного ведь два знака!
Надеюсь, вам становится ясной сложность задачи. Уравнений, из которых можно найти координаты атомов, у нас более чем достаточно. Но в правой части уравнения стоят числа известные с точностью до знака.
Казалось бы, дело безнадежное. И действительно, на первых порах исследователи и не пытались решать обратную задачу. Они действовали методом «проб и ошибок». Принимали на основании сведений о родственных структурах, что неизвестная структура выглядит так-то. Рассчитывали интенсивности десятка лучей, сравнивали с опытом. Ничего похожего? Ну что же, примем другую модель структуры.
Для простых случаев такой подход хоть и с трудом, но все же давал верные результаты. Но когда «структурщики» (таково жаргонное название этой группы исследователей) изучили практически все простые структуры, над возможностью решения обратной задачи пришлось крепко задуматься.
В середине 30-х годов догадались, что даже сложные структуры могут быть «решены» (я опять прибегаю к жаргонной фразе), если ограничиться изучением таких молекул, которые содержат много легких атомов и один тяжелый. Тяжелый атом содержит много электронов и рассеивает рентгеновские лучи много сильнее, чем легкие. Поэтому в первом, грубом приближении можно считать, что кристалл состоит только из тяжелых атомов. Если в ячейке один атом, то найти его координаты методом «проб и ошибок» труда не составит. Найдем его координаты и, полагая, что только он и хозяйничает в кристалле, выдвинем предположение, что знаки амплитуд, определенные для фиктивной структуры, состоящей только из тяжелых атомов, те же самые, что и для реальной структуры.
Важнейшим открытием, имеющим двадцатилетнюю давность, явилось доказательство теоремы о наличии связи между амплитудами отражений разных семейств плоскостей. Так, например, связаны между собой знаки амплитуд трех отражений, сдвинутых по фазе по отношению к узлу ячейки на величины α, β и α + β. Оказывается, если произведение cos α ∙ cos β ∙ cos (α + β) больше 1/8 по абсолютной величине, то оно обязательно имеет положительный знак. Можете проверить.
Развитие этой идеи привело к так называемым прямым методам структурного анализа. Даже в достаточно сложных случаях экспериментальный прибор можно соединить с вычислительной машиной, и машина будет «выдавать на-гора» структуру кристалла.
Когда знаки амплитуд отражения установлены, то определение координат атомов становится, как указывалось, задачей на решение большого числа уравнений со многими неизвестными. Важно при этом, чтобы число уравнений по крайней мере в десять, а лучше в сто раз превосходило бы число подлежащих определению координат атомов.
О технике решения этой системы уравнений я рассказывать не буду. Прибегают к обходному пути, который сводится к построению так называемых рядов Фурье электронной плотности. Изложить теорию рядов Фурье, да ещё в применении к проблеме определения структуры, можно, к сожалению, лишь для специально подготовленного читателя. Но мне кажется, что это и ни к чему. Свою задачу, по мере сил своих, я выполнил — разъяснил суть метода.
В каком виде выдает физик — специалист в области рентгеноструктурного анализа — сведения о структуре вещества, которые нужны химику? Представление об этом дает рис. 3.3, на котором показана очень простая структура вещества, называемая барбитуратом аммония.
Определение структуры подобной сложности в настоящее время является «детской» задачей. Такую структуру определит автомат без всякого вмешательства исследователя. Электронно-вычислительная машина может выдать результат и в виде чисел (значений координат атомов), и в виде картинок, похожих на приведенною. Атомы разного химического сорта обозначены кружками разных размеров. Но если исследователь желает, то ЭВМ выдаст картину электронной плотности. Каждый атом изображается так как географы обрисовывают линиями равных высот горные пики.
Только в нашем случае замкнутые линии — это не высоты, а кривые, указывающие на плотность электронов в данном месте. Вершиной «горного пика» является центр атома.
Приведенный рисунок — это крошечная доля того вклада, который внес в науку описанный нами метод. Успех метода очень велик. На сегодня определены структуры более 15 тысяч кристаллов, в том числе несколько десятков структур белков, молекулы которых состоят из многих тысяч атомов.
Определение структуры сложных молекул закладывает фундамент биологической химии и биологической физики. Эти науки находятся сейчас в бурном периоде развития. От них ждут открытия секретов жизни, болезней и смерти.
Рентгеноструктурный анализ, несмотря на свой, солидный, семидесятилетний возраст, остается на передней линии фронта науки.
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
В предыдущем параграфе мы походя упомянули, что можно встретиться с «белым» спектром и с монохроматическим лучом. Каким образом выяснить характер спектра жесткого электромагнитного излучения? Когда он бывает «белым», а в каких случаях монохроматическим?
Если диафрагмировать рентгеновские или гамма-лучи, исходящие из какого-либо источника (т. е, по ставить на пути излучения две заслонки с маленькими отверстиями), и заставить пучок падать на кристалл, то в наиболее общем случае возникнут несколько лучей, отраженных от плоскостей, оказавшихся в положении, удовлетворяющем уравнению Брэгга-Вульфа. Если установить кристалл так, чтобы какая-то его плоскость (дающая сильное отражение) совпадала с осью вращения специального прибора (рентгеновского спектрографа), а затем поворачивать кристалл так, чтобы эта плоскость подставлялась под падающий луч последовательно под всеми углами θ, то при каждом положении кристалла будет отражаться составляющая спектра определенной длины волны. «Принимать» эту отраженную волну мы можем либо с помощью ионизационного счетчика, либо можем ловить луч на фотопленку. Этим способом удается, во-первых, создать монохроматический луч любой длины волны, содержащийся в спектре излучения, и, во-вторых, исследовать спектр любого излучения.
Типичный спектр рентгеновской трубки с анодом из молибдена показан на рис. 3.4 (напряжение 35 кВ).
Можно сразу же прийти к заключению, что имеются какие-то две причины, которые приводят к созданию рентгеновского спектра. Действительно, мы видим, что наблюдающийся спектр является наложением острых пиков сплошную кривую. Конечно, происхождение этих пиков отличается от происхождения сплошной кривой.
Ораву же после того, как явление дифракции рентгеновских лучей было открыто, начались исследования рентгеновских спектров. Было установлено следующее. Сплошной спектр не характерен для материала анода и зависит от напряжения. Его особенностью является то, что он резко обрывается при некоторой минимальной длине волны. В сторону длинных волн, пройдя максимум, кривая спадает плавно, и «конца» спектра не видно.
Увеличивая напряжение на рентгеновской трубке, исследователи показали, что интенсивность сплошного спектра растет, а граница сдвигается в сторону коротких волн. При этом было установлено следующее очень простое равенство для граничной длины волны:
λмин = 12,34/U
На квантовом языке полученное правило формулируется без труда. Величина eU — это энергия, которую набирает электрон в своем путешествии от катода к аноду. Естественно, что электрон не может отдать энергии больше, чем эта величина. Если он передаст всю энергию на создание рентгеновского кванта (eU = hv), то после подстановки значения констант мы и получим (написанное выше- равенство (λ в ангстремах, U в киловольтах).
Поскольку возникает сплошной спектр, то отсюда следует, что электроны не обязательно отдают всю свою энергию на создание рентгеновских лучей. Опыт показывает, что большая часть энергии электронного пучка превращается в тепло. К. п. д. рентгеновской трубки очень низкий. Анод сильно разогревается, и его приходится охлаждать потоком воды, подаваемым внутрь анода.
Существует ли теория, объясняющая возникновение сплошного спектра рентгеновских лучей? Существует. Вычисления, которые мы, к сожалению, не можем провести, показывают, что из общих законов электромагнитного поля (из уравнений Максвелла), о которых у нас шла речь в 3-й книге, строго следует такой факт: если электроны тормозятся, то это ведет к возникновению сплошного спектра рентгеновских лучей. Соударение с твердым телом является несущественным обстоятельством. Можно затормозить электроны противополем и получить сплошное рентгеновское излучение без участия в этой игре материального анода.
Есть и еще одна возможность встретиться со сплошным рентгеновским спектром. Мы вспоминаем, что сплошной электромагнитный спектр излучается раскаленными телами. В земных условиях нам не приходится сталкиваться с рентгеновским спектром такого происхождения, ибо (сравните формулу, приведенную на с. 12) при самой высокой температуре раскаленного тела (несколько тысяч кельвинов, — ни одно твердое тело не выдерживает температуры большой) длина волны теплового излучения будет близка к половине микрометра.
Но не надо забывать о существовании плазмы. В искусственной плазме, создаваемой в земных условиях, и в звездах могут быть получены температуры, равные миллионам кельвинов. Тогда тепловой спектр электромагнитного излучения обнимет и рентгеновские лучи. Рентгеновские лучи, приходящие из космоса, помогают решать увлекательные задачи астрофизики.
Перейдем теперь к разговору об острых пиках, накладывающихся на кривую сплошного спектра. В отношении этих лучей было доказано как раз обратное правило — обратное по отношению к закону сплошного спектра. Места нахождения пиков, т. е. их длины волн, однозначно определяются материалом анода. Поэтому это излучение носит название характеристического.
Его происхождение непредвзято объясняется квантовой моделью атома. Электронные лучи рентгеновской трубки способны проникнуть внутрь атома вещества анода и вышибить из него электроны, которые находятся на самых низких энергетических уровнях. Как только освобождаемся низкий уровень, на него переходит какой-либо из электронов, более отдаленный от центра атома. Происходит излучение энергии в соответствии с основным квантовым законом Em — En = h∙v. Энергетические уровни расположены по-разному у разных атомов. Поэтому естественно, что возникающие спектры будут характеристическими.
Поскольку линии характеристического спектра наиболее сильные, то их и используют для рентгеноструктурного анализа. Сплошной спектр лучше всего «отсеять», т. е. перед тем, как заставить луч падать на изучаемый кристалл, надо отразить его от кристалла-монохроматора.
Поскольку спектры различных элементов характеристичны, то разложение луча в спектр можно использовать для целей химического анализа. Такой анализ называется рентгеноспектральным. Есть целый ряд областей, например изучение редкоземельных элементов, где рентгеноспектральный анализ буквально незаменим. Интенсивности спектральных рентгеновских характеристических линий позволяют с большой точностью определить процентное содержание того или иного элемента в смеси.
Нам остается сказать несколько слов о спектрах гамма-лучей. В земных условиях мы имеем дело с гамма-лучами, которые возникают при радиоактивном распаде, о котором у нас речь впереди. Радиоактивный распад может сопровождаться, а может и не сопровождаться гамма-излучением. Но какого бы типа ни был радиоактивный распад, спектр гамма-излучения будет характеристическим.
Если рентгеновские характеристические лучи возникают тогда, когда атом «спускается» с верхнего энергетического этажа на нижний, то гамма-лучи появляются в результате аналогичного перехода атомного ядра.
Гамма-спектры радиоактивных превращений хорошо изучены. Существуют таблицы, в которых можно найти точные данные о длине волны гамма-лучей, возникающих при альфа- или бета-превращениях того или иного радиоактивного изотопа.
РЕНТГЕНОГРАФИЯ МАТЕРИАЛОВ
Мне несколько раз приходится повторять, что с терминологией в науке дело обстоит не вполне благополучно. Наука развивается столь быстро, что содержание, вкладываемое в то или иное слово, меняется на глазах у одного поколения. И в то же время изменение терминологии связано с ломкой привычного. Невозможно изъять из обращения старые книги. Так что ничего не остается делать, кроме того, как строго оговаривать смысл, который вкладываешь в термин.
В настоящее время, когда говорят о рентгеноструктурном анализе, имеют в виду исследование атомной структуры кристаллов. Объектом изучения является монокристалл вещества.
Но польза от изучения структуры с помощью рентгеновских лучей далеко не исчерпывается решением этой задачи. Характерные и богатые информацией картины получают и в том случае, если снимают рентгенограммы с любых материалов, а не только с одиночных кристаллов. В этих случаях пользуются обычно термином «рентгенография».
Если на пути монохроматического рентгеновского луча поставить кусочек металлической фольги, то на плоской фотопластинке возникает система концентрических окружностей. Рентгенограмма такого типа называется дебаеграммой. Каково ее происхождение?
Большинство твердых тел состоит из маленьких кристалликов, беспорядочно ориентированных друг по отношению к другу. Когда расплав какого-либо вещества начинает застывать, то кристаллизация начинается одновременно из большого числа точек. Каждый кристаллик растет, «как ему хочется», и рост продолжается до тех пор, пока кристаллики не встретятся.
В каждом из кристалликов присутствуют одни и те же системы атомных плоскостей. Ведь по своей структуре кристаллики тождественны. Остановим свое внимание на какой-либо одной из систем плоскостей с межплоскостным расстоянием d. Кристалликов огромное множество (обычно линейный размер кристаллика твердого тела по порядку величины равен одной десятитысячной доле сантиметра), среди них, разумеется, найдутся и такие, плоскости которых находятся к падающему лучу под углом θ, удовлетворяющим условию Брэгга-Вульфа. Каждый из таких кристалликов даст пятнышко на фотопластинке. Отражение будут давать все кристаллики, нормали к плоскостям которых образуют конус (рис. 3.5).
Раз так, то и отраженные лучи лягут на конус. Пересечение этого конуса с фотопластинкой даст окружность. Измеряя радиусы этих окружностей и зная расстояние от объекта до фотопластинки, мы сразу же найдем брэгговский угол θ и сумеем рассчитать по такой рентгенограмме все межплоскостные расстояния вещества.
С помощью такой дифракционной картины мы сразу же отличим аморфное вещество от кристаллического. У аморфного вещества нет отражающих плоскостей. Поэтому на рентгенограмме мы не увидим системы резких дифракционных колец. Некоторый порядок в расположении молекул вещества имеется всегда, по той простой причине, что атомы не могут «налезать» друг на друга. Это приводит, как можно показать вычислениями, к тому, что на рентгенограмме аморфного вещества возникает одно, редко два размытых кольца.
Однако кольца, которые мы наблюдаем на рентгенограммах, дают нам еще целый ряд ценных сведений о строении материалов — металлов, полимеров, природных соединений. Если вещество состоит из крупных кристаллитов, то в таком случае дифракционное кольцо не будет сплошным, а будет состоять из отдельных маленьких пятнышек. Если кристаллиты расположены не беспорядочно, а ориентированы вдоль какой-нибудь оси или плоскости, как это бывает в металлических проволоках или листах, в полимерных нитях, в растительных волокнах, то об этом сразу же расскажут нам дифракционные кольца. Нетрудно попять, что при наличии преимущественных ориентаций кристаллитов отражения от атомных плоскостей не заполнят конус лучей непрерывно. Вместо колец мы увидим на рентгенограмме дуги. В том случае, если ориентация высокосовершенная, эти дуги могут выродиться в небольшие пятна.
Разумеется, детальное описание характера структуры по виду рентгенограммы является не такой уж простой задачей. И в этом случае метод «проб и ошибок» играет существенную роль. Исследователь придумывает модели структуры вещества, рассчитывает картины отражений рентгеновских лучей, которые должны были бы дать придуманные им модели, и, сопоставляя расчет с опытом, выбирает правильную картину структуры вещества.
Несколько условно в рентгенографии материалов различаются рассеяние под большими и рассеяние под малыми углами. Из формулы Брэгга-Вульфа, которую мы приводили выше, ясно, что рассеяние под большими углами происходит в том случае, если в структуре наблюдается периодичность через небольшие расстояния — скажем, 3—10 А°. Если же отраженные (или, можно говорить, рассеянные) рентгеновские лучи дают дифракционную картину, которая собирается около первичного луча, то это означает, что структура обладает периодичностью через большие расстояния.
В металловедении мы имеем дело в основном с дифракционными кольцами, расположенными под большими углами, поскольку они состоят из кристаллитов. Атомы кристаллитов образуют правильные решетки с ячейками, размеры которых имеют порядок единиц ангстремов.
В тех случаях, когда объектом исследования являются вещества, построенные из макромолекул, а к ним относится множество природных веществ, таких, скажем, как целлюлоза или ДНК, а также синтетические полимерные вещества, популярные названия которых — полиэтилен, нейлон, капрон и т. д. — превосходно знакомы любому читателю, не имеющему ни малейшего представления о химии, — в этих случаях мы сталкиваемся с чрезвычайно интересным обстоятельством. Иногда мы получим рентгенограммы, которые покажут нам кольца лишь большого диаметра. Иными словами, мы встретимся с таким же рассеянием под большими углами, как в металлах. А кой-когда мы не обнаружим колец большого диаметра, но увидим наличие дифракционных лучей, лишь незначительно отклонившихся от первичного направления. И, наконец, возможны и такие случаи, когда вещество обнаружит рентгеновское рассеяние как под большими, так и под малыми углами.
Малоугловым называют обычно рассеяние (я опять повторю, что деление на малоугловое рассеяние и рассеяние под большими углами несколько условно) в диапазоне от нескольких минут до 3–4°. Естественно, чем меньше угол дифракции, тем больше период повторяемости структурных элементов, которые эту дифракцию создали.
Рассеяние под большими углами обусловлено порядком в расположении атомов внутри кристаллитов. Что же касается малоуглового рассеяния, то оно связано с упорядоченным расположением довольно больших образований, которые называются надмолекулярными. Может случиться и так, что внутри этих образований, состоящих из сотен или тысяч атомов, нет никакого порядка. Но если такие крупные системы образуют одномерные, двумерные или трехмерные решетки, то рентгеновское малоугловое рассеяние расскажет об этом. Чтобы у читателя был зрительный образ, я предлагаю ему представить себе аккуратную конструкцию из мешков с картофелем. Чрезвычайно интересно и, вероятно, имеет глубокий смысл то обстоятельство, что мы встречаемся с таким «мешочечным» порядком в очень многих биологических системах. Например, длинные молекулы, образующие ткань мускулов, расположены так аккуратно, как карандаши кругового сечения в пачке. С исключительно высокой упорядоченностью этого типа мы сталкиваемся, как показывает рентгеновское малоугловое рассеяние, в мембранах клеток, в таких белковых системах, как вирусы, и т. д.
В теории дифракции существует интересная теорема, которую я не стану доказывать, но думаю, что она покажется естественной читателям. Можно строго показать, что вид дифракционной картины остается тем же самым, если в объекте, дающем дифракцию, поменять местами отверстия и непрозрачные промежутки. Иногда эта теорема заставляет исследователя помучиться. Это бывает тогда, когда он с одинаковым успехом может объяснить рентгеновское рассеяние как порами внутри вещества, так и чужеродными включениями. Изучение пор — их размера, формы, количества на единицу объема — представляет большой интерес для практиков. От этих особенностей структуры: синтетических волокон зависит в сильнейшей степени то, как они будут окрашиваться. Нетрудно догадаться, что неравномерное распределение пор явится причиной неравномерной окраски. Получится некрасивая ткань. Из всего сказанного достаточно очевидно, что рентгенография материалов является не только методом исследования вещества, но и методом технического контроля самых различных производств.
Глава 4 Обобщения механики
РЕЛЯТИВИСТСКАЯ МЕХАНИКА
Механика Ньютона, которую мы изложили в 1-й книге, является величайшим достижением человеческого гения. С ее помощью рассчитываются пути планет, траектории ракет, поведение механизмов. Развитие физики в XX веке показало, что законы ньютоновской механики имеют два ограничения: они становятся непригодными, когда речь идет о движении частиц малой массы; они перестают служить нам верой и правдой, когда речь идет о движении тел со скоростями, близкими к скорости света. Для малых частиц механику Ньютона заменяют так называемой волновой механикой, для быстро движущихся тел — релятивистской механикой.
Классическую механику приходится также несколько усложнить, когда мы сталкиваемся с очень большими силами тяготения. Непредставимо огромные поля тяготения, которые командуют поведением некоторых сверхплотных звезд, не разрешают ограничиться теми простыми формулами механики, с которыми читатель познакомился в 1-й книге. Но эти изменения мы оставим в стороне и остановимся на двух важнейших обобщениях, которые приходится делать, когда мы рассматриваем движения микрочастиц и когда изучаются движения со скоростями, близкими к скорости света.
Начнем с релятивистской механики. Путь к этой важной главе физики меньше всего напоминает прямую дорогу. Он не только извилист, но был проложен вроде бы через совсем другие страны. История началась с эфира. Вообще-то говоря, в конце XIX века физики благодушествовали. Учитель Макса Планка не советовал ему посвятить себя физике, ибо наука эта, по сути дела, закончена. Всего лишь два «пустяка» несколько портили вид стройного здания: не ладилось с объяснением излучения черного тела (разобравшись в этой «мелочи», физики пришли к открытию квантов), и потом портил настроение опыт Майкельсона. Этот эксперимент, доказавший что скорость света не складывается со скоростью Земли и одинакова во всех направлениях, заставил задуматься о свойствах эфира.
Мало кто сомневался в существовании некой тонкой материи, колебания которой и представляют собой электромагнитные волны. По прошествии ста лет кажется даже удивительным, что, несмотря на большое число несуразностей, к котором приводила «эфирная гипотеза», подавляющее большинство исследователей, и притом талантливых, незаурядных, шли на любые обходные маневры, вводили бездну дополнительных предположений, лишь бы спасти представление о свете как о движении невидимой субстанции.
Кто представлял себе эфир, как спокойное море, через которое пробираются планеты; кто думал, что эфир может увлекаться, как воздух, движущимися телами. Как ни странно, никто не высказывал, казалось бы, очевидной мысли, что колебания электрического и магнитного векторов происходят в точке, а потому не могут быть объяснены механическими смещениям. Как-то сводились концы с концами, строились теории в которых выводились формально правильные математические выражения (в них фигурировал пресловутый корень квадратный √(1 — (v/c)2), где v — скорость движения тела, а с — скорость света), но трактовались эти формулы неверно. Особенно большие огорчения доставил мыслителям опыт Майкельсона, который был впервые проделан в 1881 г. Используя интерферометр, устройство которого мы описывали в гл. 2, Майкельсон показал, что скорости света вдоль и поперек движения Земли по орбите практически одинаковы.
И этот убийственный для теории существования эфира факт не заставил ведущих физиков отказаться от веры в тончайшую материю, пронизывающую все тела. Считалось, что опыт Майкельсона заставляет нас распроститься с эфирным ветром. Ну, и пожалуйста. Картина мира будет еще краше, если считать эфир неподвижным и признать ньютоново абсолютное пространство, по отношению к которому совершают свой бег небесные тела.
Для объяснения опыта Майкельсона такие крупнейшие физики, как Джозеф Лармор (1857–1942) и Гендрик Антон Лоренц (1853–1928), применили гипотезу сокращения тел в направлении их движения. Однако логические противоречия и искусственность объяснения многих явлений, касающихся электродинамики, продолжали оставлять чувство неудовлетворенности.
Разрубить гордиев узел всех противоречий выпало на долю величайшего физика нашего столетия Альберта Эйнштейна (1879–1955).
АЛЬБЕРТ ЭЙНШТЕЙН (1879–1955) — гениальный ученый, творец теории относительности, революционизировавшей физическое мышление. В 1905 г. Эйнштейн публикует труд, посвященный специальной теории относительности. В 1907 г. им получена формула, связывающая энергию и массу тела. В 1915 г. Эйнштейн публикует общую теорию относительности. Из теории следовали новые законы тяготения и выводы о кривизне пространства.
Теорией относительности не исчерпывается вклад Эйнштейна в физику. Из работы Планка он делает вывод о существовании частицы света — фотона и показывает, каким образом можно с этих позиций объяснить ряд фундаментальных явлений, в том числе и фотоэффект.
Отправной точкой рассуждений Эйнштейна служил принцип относительности. Мало кто сомневался после Галилея, что в отношении механических движений все инерциальные системы равноправны (вернитесь, пожалуйста, к 1-й книге и освежите в памяти все, что было сказано по этому поводу). Получается как-то странно, да и несовершенно с эстетических позиций: для механических движений равноправие, а для электромагнитных его нет.
Откажемся от этой «некрасивой» точки зрения и примем, что принцип относительности верен для всех явлений.
А теперь задумаемся над результатом опыта Майкельсона. Попытки объяснить результат этого эксперимента, рассматривая распространение света в «эфире» наподобие распространения звука в воздухе, также не удовлетворяют Эйнштейна. Он чувствует, что «что-то» здесь не то. Собственно говоря, почему мы обязаны «подравнивать» свет и звук? Из-за того, что и тот и другой способны дифрагировать? Не такой уж сильный довод. Откажемся и от этой точки зрения и примем следующий постулат (на первый взгляд кажущийся диким): скорость света в вакууме одинакова с точки зрения всех наблюдателей, движущихся в разных инерциальных системах. В каком бы направлении ни бежала электромагнитная волна, какое бы тело ни послужило ее источником, земляне и инопланетяне, проживающие в другой галактике (как хочется многим фантазерам верить в их существование), измерят одну и ту же скорость — 299 792 км/с.
Вдоль прямолинейного участка железнодорожного пути катится вагон с неизменной скоростью v. Параллельно дороге идет шоссе. По нему в том же самом направлении, мчится мотоциклист. Инспектор ГАИ, пост которого расположен вблизи железной дороги, свистит вслед нарушителю — он промчался мимо него со скоростью u, куда большей, чем дозволено. Маленький радар, которыми теперь снабжены многие инспекторы, показывает 85 км/ч. Машинист поглядывает на мотоциклиста, который быстро нагоняет, а затем и обгоняет поезд. И этому наблюдателю нетрудно измерить скорость мотоциклиста. Она будет равна u' = 35 км/ч. Мне не надо доказывать читателю, что скорость поезда равна 50 км/ч. Справедлив закон сложения скоростей:
u = v + u'
И вот это, казалось бы сверхочевидное правило не подходит для светового луча. Фотоны движутся с одной и той же скоростью по отношению к двум наблюдателям, находящимся в разных инерциальных системах.
Гений Эйнштейна состоял в том, что он отказался от этого очевидного вывода не только для света, но желая сохранить единый подход ко всем физическим явлениям, как электромагнитным, так и механическим, взял на себя смелость отказаться от закона сложения скоростей для всех тел.
Разумеется, с подобных позиций опыт Майкельсона и объяснять нечего. Раз скорость света универсальна, значит, она будет одинаковой во всех направлениях — и вдоль земной орбиты, и поперек пути обращения Земли вокруг нашего светила.
Из сформулированных принципов сразу же следует что скорость света является максимальной скоростью[1].
Действительно, если скорость света не добавляется к скорости движения источника, значит, обогнать свет невозможно. Эйнштейн в своих воспоминаниях пишет, что еще в 1896 г. у него возник вопрос: «Если бы можно было погнаться за световой волной со скоростью света, то имели бы мы перед собой не зависящие от времени волновое поле? Такое все-таки кажется невозможным».
Итак, ни одно тело, ни одна частица не могут двигаться со скоростью большей, чем скорость света. Вдумайтесь, пожалуйста, в это утверждение. Ввиду его кажущейся парадоксальности повторим еще раз. Если на Земле или иной планете из одного места в другое отправляется в путешествие электромагнитная волна, то скорость распространения этой волны, измеренная земным наблюдателем и наблюдателем, пролетающим над Землей в ракете, движущейся с фантастической скоростью, будет одной и той же. Это же утверждение справедливо и для всякой частицы, движущейся со скоростью, равной скорости электромагнитных волн.
Свет — не исключение в теории Эйнштейна. Ну, а как происходит дело, когда скорость движущегося тела меньше скорости света? Очевидно, что и в этом случае простой принцип сложения скоростей, которым мы всегда так уверенно пользуемся, несправедлив. Но отклонение от обычного правила сложения скоростей начнет чувствоваться лишь тогда, когда скорость тела будет очень и очень велика
Релятивистская механика — таково название механики быстро движущихся тел — приводит к следующему правилу сложения скоростей:
Прикиньте, какими должны быть значения v и v', чтобы понадобились поправки к простому правилу сложения скоростей.
Как Обстоит дело, к примеру, с космическими полетами? Работает ли обычное правило сложения скоростей, когда речь идет о движениях со скоростью в десятки километров в секунду?
Как известно, весьма целесообразным является запуск «вторичной» ракеты с какого-либо космического корабля-ракетоносителя. Возможно, именно таким способом будут отправляться ракеты к окраинам Солнечной системы. Обозначим через v скорость космического корабля по отношению к Земле, через v' — скорость запущенной с него ракеты по отношению к космическому кораблю. Положим обе скорости v и v' равными 10 км/с. Подсчитаем теперь по точной формуле сложения скоростей, чему будет равна скорость ракеты по отношению к Земле. Тогда к единице в знаменателе надо добавлять дробь 102/(9∙1010) ~= 10-9. Поправка совершенно ничтожна, т. е. работает классическое правило сложения скоростей.
Какое же тогда практическое значение имеет релятивистская механика? Дойдем до ответа и на этот вопрос. А пока что потянем следствия из сформулированных гипотез. Поскольку приходится распроститься с принципом сложения скоростей, то мы уже готовы к тому, что придется внести существенные коррективы и в другие формулы механики.
Как подчеркивалось выше, решающую роль в становлении теории относительности сыграл опыт Майкельсона — опыт, которым было доказано, что скорость света вдоль и поперек движения Земли по солнечной орбите одна и та же.
Не будем рассматривать ход лучей в интерферометре Майкельсона. Ограничимся обсуждением более простых событий. Где-то на-Земле создана простенькая установка. На столбе на высоте l от земной поверхности установлен лазер. Его тончайший луч идет вдоль земного радиуса, отражается от положенного на земную поверхность зеркала, возвращается обратно и принимается фотоэлементом, который инженеры умудрились поместить таким образом, что мы вправе считать, что источник и приемник света находятся в одной точке.
На рис. 4.1 она обозначена буквой S.
При помощи ультрасовершенного секундомера можно зафиксировать два мгновения: первое, когда свет отправился в путешествие, и второе, когда он пришел к фотоэлементу. Два наблюдателя следят за этим явлением. Один находится тут же рядом с выдуманной нами установкой, а второго художник поместил на далекую звезду. Оба измеряют интервал времени τ между двумя событиями: уходом и возвращением света в точку S. Первый наблюдатель чертит картинку хода луча, проще которой и выдумать нельзя. Он полагает, что пути луча туда и обратно полностью совпадают. В справедливости своего рассуждения он убеждается с помощью равенства τ = 2∙l/с.
Звездный наблюдатель следит за вспышкой отправления света и за его приходом к фотоэлементу. Измеренный им промежуток времени равен τ. И он, чтобы проверить, всё ли правильно, строит картинку хода луча.
Но для него положения точки S в момент включения секундомера и в момент, когда он заметил реакцию фотоэлемента, не совпадают. Поэтому он строит другую картинку хода луча. Скорость Земли по отношению к себе звездный наблюдатель знает. Так что его чертежик изображает собой равносторонний треугольник, основание которого равно v∙τ, а высота равняется l. С помощью теоремы Пифагора звездный наблюдатель устанавливаем что путь, пройденный световым лучом, равен Этот путь равен c∙τ — ведь скорость света одинакова для всех наблюдателей. Раз так, то промежуток времени между двумя мгновениями будет равен
Что за неожиданный результат! Ведь с точки зрения земного наблюдателя этот же промежуток времени между теми же самыми событиями равен 2∙l/с.
Призовем на помощь логику и сделаем неизбежный вывод: время, которое отсчитывает покоящийся наблюдатель, отличается от времени, которое отсчитывает наблюдатель движущийся.
Время неподвижного наблюдателя называют собственным временем и обозначают τ0. Мы находим, что время наблюдателя, движущегося со скоростью v, связано с собственным временем выражением
То есть движущиеся часы идут медленнее неподвижных. Приняв основные постулаты теории, от этого вывода не спрячешься. А он ведет к такому на первый взгляд странному следствию, как необходимость отказаться от понятия одновременности.
А не получится ли так, что с точки зрения одного наблюдателя Джим выстрелил и Джон после этого упал, убитый пулей, а с точки зрения другого наблюдателя сначала упал убитый Джон, а затем выстрелил Джим? Смею заверить читателя, что релятивистская механика не ведет ни к каким несообразностям. Принцип причинности никогда не будет нарушен. И объяснить это можно было бы вполне популярно, но, к сожалению, объем книжки не позволяет этого сделать.
Но еще несколько слов надо сказать о парадоксе близнецов, который и до сего времени иногда приводят как доказательство несостоятельности теории. Ваня и Петя — близнецы. Петя прощается с Ваней и отправляется в космическое путешествие со скоростью, близкой к скорости света, и через некоторое время возвращается обратно. Петины часы идут медленнее. Поэтому оп вернется на Землю без морщин и седин и встретится со своим братом — дряхлым стариком.
Но организовать встречу, соблюдая те условия, при которых справедливы обсуждаемые нами формулы, к сожалению (или к радости — кому как), не удастся. Ведь для этого Пете надо изменить свою скорость на обратную, и поэтому выводы, относящиеся к инерциальным системам, к этому случаю не относятся.
Относительность времени не есть единственное следствие новой теории. Так же точно, как собственные часы наблюдателя идут быстрее всяких других, так и длина стержня l0, который вы держите в руках, максимальна. С точки зрения любого наблюдателя, который движется со скоростью v вдоль стержня, эта же длина равна l0∙√(1 — β2).
И в выражении для массы появляется все тот же корень. Масса m0 тела, которое наблюдатель «держит в руках», называется массой покоя. Она минимальна. Для движущегося наблюдателя
Вполне естественно, что масса возрастает с увеличением скорости. Действительно, раз у скорости есть предел, то по мере приближения к нему частицу все труднее и труднее ускорить. А ведь это и означает, что масса частицы растет.
С бóльшими скоростями, которые заставляли бы принимать во внимание отличие корня квадратного от единицы, в формулах расстояния и времени долгое время встречаться не приходилось. Лишь недавно удалось подтвердить справедливость формулы для времени.
А вот что касается зависимости массы от скорости, то она была обнаружена для потока электронов еще до появления статьи Эйнштейна. Формула для массы является в полном смысле слова технической формулой. Как мы увидим в следующем параграфе, без нее невозможно рассчитать и сконструировать современный ускоритель частиц. В этих очень дорогих машинах частицы разгоняется столь сильно, что корень квадратный становится куда более близким к нулю, чем к единице.
Формула зависимости массы от скорости была предложена впервые еще до Эйнштейна. До становления релятивистской механики она лишь трактовалась неверно.
Но знаменитое выражение Е = m∙с2, связывающее массу и энергию, было выведено Эйнштейном. Эта формула так же как и зависимости l, τ и m от скорости, строго следует из постулатов теории.
Умножим массу на квадрат скорости света. Для движущегося тела это будет m∙с2, а для того же тела в покое m0∙с2. Составим разность этих двух выражений:
Воспользуемся приближенным равенством, справедливость которого вы можете без труда проверить:
Разность, которую мы вычисляем, имеет вид
m∙с2 — m0∙с2 = m0∙v2/2
Как видите, она равняется кинетической энергии тела.
Раздумывая над этим равенством, Эйнштейн пришел к следующему фундаментальному заключению. Энергия движущегося тела может быть представлена выражением
Е = m∙с2.
Эта энергия складывается из энергии покоя и энергии движения. Не имея никаких сведений о структуре тела, не зная характера взаимодействия его частиц, можно утверждать, что его внутренняя энергия равна
U = m0∙с2.
Внутренняя энергия тела с массой 1 кг равна 1017 Дж. Такое количество тепла выделилось бы при сгорании 3 миллионов тонн угля. Как мы узнаем ниже, физики научились высвобождать лишь малую часть этой энергии, разрушая атомные ядра или заставляя их сливаться.
Подчеркнем, что уравнение Эйнштейна Е = m∙с2 относится не только к внутриядерной энергии. Уравнение универсально. Но здесь дело обстоит совершенно так же, как с часами космонавтов. Большей частью соотношение между энергией и массой не может быть проверено. Действительно, если нагреть 1 т молибдена на 1000 К, то масса возрастет на 3 миллионных доли грамма. Только огромная величина внутриядерных сил позволила убедиться в правильности уравнения Е = m∙с2.
Полезно, пожалуй, предупредить читателя об очень распространенной небрежной формулировке этого замечательного уравнения. Говорят: масса превращается в энергию; или еще хуже: материя превращается в энергию. На самом же деле формула Е = m∙с2 говорит следующее: какие бы взаимные превращения разных видов материи ни происходили, произошедшему в системе изменению энергии соответствует эквивалентное изменение массы. Энергия и масса являются двумя однозначно связанными характеристиками материи.
ЧАСТИЦЫ, СКОРОСТЬ КОТОРЫХ БЛИЗКА К СВЕТОВОЙ
Желание добраться до элементарных кирпичей, из которых построен мир, старо, как мир. Но долгие столетия этот предмет был подвластен только схоластическим рассуждениям мудрецов. Как только появились реальные возможности разрушать молекулы, атомы, атомные ядра, физики принялись за эту работу с вдохновением и настойчивостью. Работа эта не прекращается и по сей день, и, признаемся, пока что конца ей не видно.
Ясно, что для того, чтобы получить ответ на вопрос, из чего построен мир, надо разрушать частицы. Для этого нужны «снаряды», и чем большей энергией будут они обладать, тем больше надежды раскрыть эту тайну природы.
История производства быстрых частиц началась в 1932 г., когда сотрудники Резерфорда построили установку для получения протонов, которые разгонялись до энергий 500 кэВ. Затем последовали циклотроны, позволившие достигнуть энергий протонов, которые требовалось измерять уже мегаэлектронвольтами (напомним, что мега — миллион). На следующем этапе был изобретен синхротрон, позволивший разгонять протоны до миллиарда электронвольт. Началась эра гигаэлектронвольтов (гига — миллиард). Но теперь уже запроектированы машины, в которых счет пойдет на тысячи миллиардов электронвольт. В частности, физики, собиравшиеся в 1975 г. на международную конференцию (она происходила в Серпухове, где установлена одна из мощнейших машин этого типа), полагали, что надо было бы строить кольцевую машину с диаметром 16 км.
Но у читателя уже вертятся на кончике языка вопросы. В чем принцип действия таких машин? Почему им надо придавать кольцевую форму и, наконец, для чего они нужны?
По сути дела, ускорителем частиц является любой вакуумный прибор, к концам которого подведено высокое напряжение. Кинетическая энергия разогнавшейся до большой скорости частицы равна (впрочем, мы не в первый раз приводим эту формулу, но в этом беды нет: читатель ее тогда наверняка запомнит)
m∙v2/2 = e∙U
И рентгеновские, и телевизионные трубки можно назвать ускорителями.
Но на этом принципе особо больших скоростей не получишь. Термин «ускоритель» применяется тогда, когда речь идет о машинах, разгоняющих частицы до скоростей, близких к скорости света. Для этой цели надо заставить частицу проходить последовательно много полей. Сразу же легко сообразить, что линейный ускоритель малоудобен, ибо для того, чтобы получить какие-то жалкие десятки тысяч электронвольт, уже нужны пути, равные многим сантиметрам. Для достижения десяти миллиардов электронвольт нужна длина порядка десятка километров.
Нет, такое лобовое, решение проблемы не годится! В 1936 г. Эрнест Лоуренс (1901–1958) положил начало строительству современных кольцевых ускорителей, которые он назвал циклотронами. В одной установке объединяется ускорение частицы электрическим полем и ее многократное возвращение к ускоряющему промежутку с помощью магнитного поля.
Ускоритель Лоуренса похож на консервную банку, разрезанную на две части по диаметру. К двум половинкам прикладывается быстропеременное напряжение. Заряженное частицы ускоряются в те моменты, когда они проходят расстояния, разделяющие половинки прибора. Внутри «консервной банки» мы заставляем частицы двигаться по окружности, накладывая на прибор магнитное поле; линии индукции которого перпендикулярны ее дну. Как известно, в этом случае заряженная частица описывает окружность радиуса
R = m∙v/e∙H
Время одного оборота.
Т = 2π∙m/e∙H.
Для. того чтобы электрическое поле между двумя половинками машины «подхватывало» частицы, надо подобрать переменное напряжение так, чтобы его знак менялся как раз к тому моменту, когда частица подойдет к промежутку между половниками.
Заряды создаются в центре прибора (скажем, ионизация водорода создает протоны). Первая окружность будет иметь небольшой радиус. Однако каждая следующая окружность будет иметь больший радиус, поскольку, согласно приведенной формуле, он пропорционален скорости движения частицы.
На первый взгляд кажется, что, увеличивая размеры циклотрона, а вместе с этим и радиус кольцевой траектории, мы можем сообщить частице любую энергию. Достигнув желаемой энергии, нам останется лишь с помощью отклоняющей пластинки выпустить пучок, наружу. Дело обстояло бы идеально, если бы не зависимость массы от скорости. Формула Эйнштейна для массы, не имеющая, казалось когда-то, никакого практического значения, становится основной при расчетах кольцевых ускорителей.
Поскольку с возрастанием скорости масса частицы возрастает, то период обращения не остается неизменным, а растет. Частица начинает запаздывать. Она придет к ускоряющему промежутку не в тот момент, когда фаза напряжения изменится на 180°, а позже. По мере возрастания скорости мы придем к такому положению, что электрическое поле не только перестанет подхватывать частицы, но даже будет их тормозить.
Циклотрон позволил разгонять протоны примерно до 20 МэВ. Казалось бы, не так плохо. Но, как я уже сказал, физикам для их работы требуются все более и более мощные приборы. Ясно, что для достижения больших энергий нужно искать новые пути.
Вид формулы для периода обращения частицы подсказывает, какой путь надо избрать. С возрастанием скорости растет масса. Ну что же, значит, для поддержания периода надо увеличивать «в такт» напряженность магнитного поля. Однако это решение просто лишь на первый взгляд. Не надо забывать, что радиус обращения при каждом обороте частицы возрастает. Так что требуется, чтобы синхронное возрастание массы и магнитного поля было бы справедливо для частицы, проходящей последовательно окружности со все возрастающими радиусами. Внимательно поразобравшись в этой взаимосвязи величин, мы выясним, что найдутся такие «удачные» частицы, для которых, при некотором заданном темпе нарастания напряженности магнитного поля, это условие будет выполнено. А главное, окажется, что произойдет своеобразная автофазировка. Частица, у которой энергия больше, чем надо для радиуса ее обращения, будет замедляться из-за излишнего прироста массы; напротив, нехватка энергии приведет к ускорению.
Самыми простыми вычислениями, с помощью формул радиуса и периода обращения частицы, читатель может самостоятельно, убедиться, что именно так будет обстоять дело (задайте, темп увеличения напряженности магнитного поля, вычисляйте траектории частиц, постройте график — и вы почувствуете принцип автофазировки). А можете поверить мне на слово, что таким способом можно в принципе увеличивать скорость частиц до предела. Придется только использовать для ускорения импульсный метод. При возрастании напряженности поля установка работает. Обратный ход является холостым. Но мы не будем задерживаться на этом методе. Он является также пройденным этапом. Если сохранить этот принцип, то для создания современных ускорителей потребовалось бы изготовлять магниты массой в миллионы (!) тонн.
Современные кольцевые ускорители, называемые синхрофазотронами, осуществляют ускорение частиц, на одной орбите. Поэтому вся центральная часть магнита как бы вырезается. Работа в этих машинах также происходит импульсным методом. Согласованно меняют как напряженность магнитного поля, так и период электрического поля. Удачные частицы будут набирать скорость, двигаясь по строго кольцевой орбите. Менее удачные будут колебаться около хорошей орбиты, но все же будут набирать скорость.
В принципе ускорение можно довести до фантастических величин. Можно достичь скорости протонов, еле заметно отличающейся от скорости света.
Нам остается ответить на вопрос, зачем нужны такие машины. Ускоритель строят для того, чтобы разобраться в физике элементарных частиц. Чем выше энергия заряженных частиц, используемых как снаряды, бомбардирующие мишени, тем больше шансов найти законы взаимного превращения элементарных частиц.
Вообще-то говоря, мир построен всего лишь из трех частиц: электронов, протонов и нейтронов. Электрон пока что нет оснований считать составной частицей. Что же касается протонов и нейтронов, то они могут быть расщеплены на части. При разных столкновениях между «осколками» возникают новые частицы. Сегодня их насчитывается что-то около 250, и вся беда в том, что это число непрерывно растет по мере того, как возрастают мощности ускорителей. Специалисты в области физики элементарных частиц не теряют надежды найти что-то вроде системы Менделеева для элементарных частиц и свести их к небольшому числу, если так можно выразиться, «проточастиц», — удалось же сотню элементов и несколько сот их изотопов свести к комбинациям электронов, протонов и нейтронов.
Читатель вправе полюбопытствовать, какой же тогда смысл мы вкладывали во фразу: мир построен из трех частиц? Дело заключается в следующем. Совершенно устойчивыми частицами являются только протон и электрон. Нейтрон не вполне устойчив, если слово «устойчив» понимать житейски. Но время его жизни в мире частиц огромно: оно равно примерно 103 с. Что же касается множества остальных элементарных частиц, которые доставляют столько забот теоретикам, то их сроки жизни меньше 10-6 с. Разумеется, два последних числа не идут ни в какое сравнение.
Но тем не менее хочется привести в систему и эти короткоживущие обломки материи. Для элементарных частиц предлагалось много таких систем. Но как только на сцену выходил более мощный ускоритель, с его помощью обнаруживались новые явления, которые не укладывались в принятую схему.
В момент, когда пишутся эти строки, специалисты настроены оптимистически. Всю систему элементарных частиц удается как будто бы свести к «проточастицам», которые получили название кварков. Беда в том, что кварки, в отличие от электронов и протонов, не наблюдались и, вероятно, не могут наблюдаться в принципе. Чтобы создать «систему Менделеева» для элементарных частиц, кварку приходится придать электрический заряд, равный либо одной трети, либо двум третям заряда электрона, и приписать два дополнительных параметра, которым нельзя сопоставить какой бы то ни было образ. Эти параметры носят названия «странность» и «шарм»[2].
Автор этой книги не собирается останавливаться на проблемах, связанных с элементарными частицами. Он не делает этого не потому, что трудно популярно объяснить существующие схемы, а по той причине, что еще рано быть уверенными в их шарме и красоте. Не исключено, что появятся совсем новые идеи касательно элементарных частиц, совсем новые принципы подхода к этим крошечным участкам Вселенной, измеряемым (в сантиметрах) единицей, поделенной на единицу с тринадцатью нулями.
ВОЛНОВАЯ МЕХАНИКА
В 1923 г. в работе исключительной смелости и гениальной простоты французский физик Луи де Бройль писал: «В оптике в течение столетий слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым. Не делалась ли в теории микрочастиц обратная ошибка?» В этой работе де Бройль указал путь, следуя которому можно было связать с частицами волновые представления.
Его работу продолжает и завершает замечательный немецкий физик Эрвин Шредингер. А несколько позже, к 1926–1927 гг., становится ясным, что волновая механика и квантовая механика — по сути дела равнозначные термины. Эта новая механика представляет собой важнейший раздел физики, который учит нас, как рассматривать поведение микрочастиц в тех случаях, когда ни корпускулярный аспект, ни волновой недостаточны для трактовки событий.
Мы предупреждали читателя, что не следует слишком буквально понимать выражение «электромагнитная волна». И радиоизлучение, и свет, и рентгеновские лучи могут быть рассмотрены в двух аспектах: волновом и корпускулярном. Совершенно такое же утверждение справедливо и для потоков частиц. Хотя потоки частиц имеют четкие отличия от электромагнитного излучения (главное из них, то, что электроны, ядра, нейтроны и ионы могут двигаться с любыми скоростями, а фотоны — только со скоростью 300 000 км/с), этот вид: материи также выявляет в различных экспериментах то свойства волны, то свойства корпускул.
Какова же длина волны, которую надо приписать движущейся частице? С помощью рассуждений, которые в несколько упрощенном виде мы сейчас изложим, де Бройль показывает (вернее сказать, догадывается), чему должна быть равна длина волны, связанная с потоком частиц.
Обратимся к основным соотношениям, которые связывают корпускулярный аспект электромагнитного излучения с волновым. Порция энергии электромагнитного излучения, которую несет с собой фотон, выражается формулой E = h∙v. Энергия фотона, как и любой другой порции материи, подчиняется уравнению Эйнштейна. Таким образом, энергия фотона может быть представлена и формулой Е = m∙c2. Отсюда следует, что масса фотона[3] m = h∙v/c2. Умножая массу на скорость, мы получим значение импульса фотона:
p = h∙v/c = h/λ
Но нас интересует длина волны частицы, масса покоя которой отлична от нуля. Как догадаться, чему она равна? Допустить, что все приведенное рассуждение остается в силе; принять, что соотношение между импульсом и длиной волны является универсальным! Остается переписать это выражение в виде
λ = h/m∙v
Это и есть знаменитая формула де Бройля. Она показывает, что волновой аспект потока частиц должен проявляться особенно отчетливо, когда невелики масса и скорость частицы. Это и подтверждается опытом, ибо дифракцию частиц, оказывается, легко наблюдать в случае электронов и медленных нейтронов.
Проверка справедливости только что приведенного рассуждения, которое, кстати говоря, в свое время воспринималось как игра понятиями, вполне прямолинейна. Надо снять с одного и того же вещества рентгенограмму, электронограмму и нейтронограмму. Подогнав скорости частиц таким образом, чтобы длины волн были одинаковы во всех случаях, мы должны получить тождественные (в отношении радиусов колец) дебаеграммы. Так оно и оказывается.
В 1927 г. случайно осуществилась первая проверка формулы де Бройля. Американские физики Дэвиссон и Джермер производили опыты по рассеянию электронов на поверхности металлов, и при работе с прибором им случилось накалить объект. Объект был поликристаллическим, а после нагрева перекристаллизовался, теперь лучи рассеивались монокристаллом. Полученная картина была столь похожа на соответствующие рентгенограммы, что не было никакого сомнения в том, что электроны обладают способностью дифрагировать, как и рентгеновские лучи.
Достаточно скоро наблюдение электронной дифракции превратилось в метод исследования строения вещества, который во многих случаях оказывался более пригодным, чем рентгеноструктурный анализ. Основная область применения электронографии — это изучение структуры тонких пленок. Принципы ничем не отличаются от тех, которые мы обсуждали в гл. 3. Различие состоит в том, что электронные лучи рассеиваются электронами и ядрами, в то время как рентгеновские лучи рассеиваются только электронами.
Так как длина волны частицы обратно пропорциональна массе, то понятно, что дифракцию молекул наблюдать трудно. Во всяком случае до сих пор этого, сделано не было. Дифракцию протонов наблюдать можно, но она не представляет какого-либо интереса: для исследования объемной структуры протоны не годятся из-за малой проникающей способности, а для изучения поверхности лучше применять дифракцию электронов — она дает несравненно более богатую информацию о структуре.
Иначе обстоит дело с нейтронами. Исследование дифракции этих частиц стало предметом занятия многих ученых. Эта область науки получила название нейтронографии.
Получить нейтронограмму технически много труднее, чем рентгенограмму. Прежде всего, достаточно сильный пучок нейтронов подходящей длины волны (а длина волны регулируется скоростью нейтронов) можно создать лишь выводом этих частиц через специальный канал в атомном реакторе. Вторая трудность состоит в том, что рассеяние нейтронов невелико; они ведь легко проходят через вещество, не сталкиваясь с ядрами его атомов. Поэтому нужно работать с крупными кристаллами; размером порядка сантиметра. А такие кристаллы не так легко получить. И, наконец, третье обстоятельство: нейтроны не оставляют следа на фотопластинке, а в ионизационных приборах дают о себе знать лишь косвенно. Несколько слов о том, как считают нейтроны, мы скажем ниже.
Так почему все-таки исследователи занимаются нейтронографией? Дело заключается в том, что нейтроны, в отличие от рентгеновских лучей, не рассеиваются электродами, а отклоняются от своего пути при встречах с атомными ядрами. Можно привести много примеров веществ, атомы которых по числу электронов отличаются незначительно, а по свойствам ядер — резко. В подобных случаях рентгеновские лучи не различат атомов, а нейтронография приведет к успеху. А, пожалуй, самое главное обстоятельство — это то, что нейтроны сильно рассеиваются ядрами атомов водорода в то время как рентгеновские лучи способны установить расположение атомов водорода лишь с трудом: ведь у атома водорода всего лишь один электрон. А знать расположение этого атома очень важно. В огромном числе органических и биологических систем атом водорода связывает между собой части одной молекулы или соседние молекулы. Эта особая связь так и называется «водородной». Также вне конкуренции находится возможность нейтронографии отличать атомные ядра, обладающие различными магнитными свойствами. Всех этих причин достаточно для того, чтобы сделать нейтронографию важным методом исследования строения вещества.
ПРИНЦИП ГЕЙЗЕНБЕРГА
С тем, что свет и частицы обладают одновременно и волновыми, и корпускулярными свойствами, многие физики долгое время не могли примириться. Им казалось, что в этом дуализме содержится нечто, противоречащее теории познания. В особенности нетерпимым казался этим ученым принцип Гейзенберга.
Это важнейшее положение физики микромира устанавливает границы пригодности корпускулярного аспекта любых явлений, связанных с движением частиц вещества. Принцип Гейзенберга записывается в следующей форме;
Δx∙Δv > h/m
Здесь Δx и Δv — «размытость» нашего знания соответственно координаты и скорости движения (в направлении той же оси координат) сгустка материи, который мы рассматриваем в корпускулярном аспекте. Короче, Δx и Δv — это неопределенность в знании координаты и скорости частицы.
Необходимо подчеркнуть, что речь идет не о технических трудностях измерения. Приведенное соотношение связывает неопределенности, которые не удастся устранить в самом идеальном эксперименте. Сейчас лишь исторический интерес представляют различного рода схемы, которые предлагались для абсолютно точного измерения траектории и скорости движения частиц. Внимательным рассмотрением всегда можно было обнаружить принципиальный дефект схемы.
Попытаемся хотя бы несколькими словами пояснить, почему эксперимент не может дать большей точности, чем позволяет принцип Гейзенберга. Положим, что речь идет об определении положения частицы в пространстве. Чтобы узнать, где она находится, ее надо осветить. Как уже говорилось ранее, возможности различения деталей определяются длиной волны используемого излучения. Чем длина волны меньше, тем лучше. Но, уменьшая длину волны, мы увеличиваем частоту света, а значит, увеличиваем энергию фотона. Удар, который испытает рассматриваемая частица, лишит нас возможности вынести суждение о той скорости, которую она имела при встрече с фотоном.
Или еще один классический пример. Мы ставим на пути электрона узкую щель. Пролетев через щель, электрон падает на экран. Видна вспышка. Таким образом с точностью до ширины щели установлено местоположение электрона в момент, когда он проходил через отверстие. Погонимся за точностью. Для этой цели будем уменьшать размеры щели. Но тогда волновые свойства электрона начнут сказываться более резко (см. с. 49). Электрон может все дальше и дальше отклоняться от прямого пути. А это значит, что мы все в большей степени будем терять сведения о компоненте его скорости в направлении плоскости, в которой проделана щель.
Таких примеров можно придумать десятки, можно рассмотреть их количественно (что и делали физики в 30-х годах), и каждый раз будем приходить к приведенной выше формуле.
Обсудим оценки Δx и Δv, которые можно сделать в отношении частиц разной массы, пользуясь неравенством Гейзенберга.
Допустим, речь идет об электроне, принадлежащем атому. Можно поставить такой опыт, который установил бы, в каком месте находится электрон в данное мгновение? Поскольку размеры атома порядка 10-8 см, то это значит, что желательна точность, скажем, 10-9 см. Что же, в принципе (только в принципе) такой опыт осуществим. Но оценим с помощью неравенства потерю информации об этом электроне. Для электрона h/m примерно равно 7 см2/с, и для него принцип Гейзенберга запишется так: Δx∙Δv > 7. Итак, Δv > 7∙109 см/с, что совершенно бессмысленно, т. е. о скорости электрона ничего нельзя сказать.
Ну, а если попытаться узнать, скорость атомного электрона поточнее? И для этой цели можно придумать принципиально осуществимый эксперимент. Но тогда будет полностью потеряно знание о месте, где электрон находится.
Неравенство, примененное к атомному электрону, показывает, что корпускулярный аспект в этом случае не работает. Понятие траектории электрона лишено смысла, о путях перехода электрона с одного энергетического уровня на другой также сказать ничего нельзя.
Картина меняется в том случае, когда мы интересуемся движением электрона в ионизационных камерах. Трек, оставленный электроном, может быть зримым. Значит, есть у него траектория? Имеется! А как же связать это с предыдущим расчетом? И не надо связывать. Теперь все рассуждения надо провести заново. Толщина трека порядка 10-2 см. Следовательно, неопределенность в значении скорости даже для медленного электрона, который пролетает через камеру со скоростью около 1 км/с, практически пренебрежима по сравнению с этой величиной — она равна 7 м/с.
Эти числовые примеры показывают нам, что корпускулярный аспект начинает исчезать по мере того, как мы «приглядываемся» — стараемся разглядеть порцию материи подетальней.
О протонах и нейтронах можно весьма часто говорить как о частицах. Но если речь идет об их поведении внутри атомного ядра, которое имеет размер 10-13 см, то корпускулярный аспект не проглядывается.
Нетрудно также прикинуть, что в крупной молекуле с молекулярной массой порядка миллиона можно спокойно говорить как о горошинке. Такая молекула ведет себя как «честная» частица. Можно даже начертить траекторию ее теплового хаотического движения.
Давно прошло время, когда волново-корпускулярный дуализм воспринимался как нечто странное, нуждающееся в глубоком истолковании. Маститые ученые, даже такие, как Эйнштейн и Бор, яростно спорили о том, как надо трактовать столь «странное» поведение электронов и других частиц. В настоящее время подавляющее большинство естествоиспытателей не видит ничего особенного в использовании двух аспектов при описании различных явлений, в которых принимают участие электроны, ядра или фотоны.
Лет десять назад группа науковедов проводила анкетный опрос среди большой (около десяти тысяч человек) группы физиков. В числе прочих был задан вопрос: считает ли опрашиваемый, что проблема двух аспектов материи представляет интерес и не может считаться выясненной до конца? Только двадцать человек ответили, что они полагают, что неравенство Гейзенберга и прилегающие к нему проблемы, не являются истиной в последней инстанции.
Трудность примирения с этим важным законом природы объяснялась, видимо, логической ошибкой, лежащей в основе протеста, который формулировался так: «Не могу согласиться с тем, что поведение частички материи является непредсказуемым». Порочность фразы состоит в том, что о порции материи ведется речь как о частичке в обычном житейском понимании этого слова. На самом же деле порция материи идет ли речь о свете, микроволнах, электроне или ядре — вовсе не похожа на горошинку. Невозможно зрительно представить себе частицу материи. С этим ведь согласится каждый! Достаточно напомнить, что к электрону или протону неприменимы понятия цвета, твердости, температуры… Все эти свойства принадлежат лишь макроскопическим телам. Но если нельзя себе представить порцию материи, то тем более невозможно представить себе ее движение. Движение порции материи совмещает в себе два аспекта, волновой и корпускулярный. Поэтому непредсказуемым является лишь поведение одного из ее аспектов!
Квантовая механика (волновая механика; повторим еще раз, что это синонимы) дает нам сводку четких правил, с помощью которых мы можем предсказывать поведение порций материи. Описание частиц методами квантовой механики исчерпывающим образом отображает закономерности микромира. С ее помощью мы безошибочно предсказываем события; заставляем ее служить практике.
Конечно, это не означает, что в дальнейшем не будут открыты более общие законы природы, частным следствием которых станет современная квантовая механика, наподобие того как это произошло с механикой Ньютона. Эти общие законы должны быть пригодными для описания поведения частиц малой массы, движущихся с большими скоростями. Мы ждем с нетерпением — и надо признаться, ждем уже давно — создания теории, объединяющей все «механики» в одно целое. Для этой — увы, несозданной — теории даже имеется название: релятивистская квантовая механика.
Представляется удивительным, что каскад открытий, сделанных в первой четверти XX века, неожиданно приостановился. Читателю может показаться это утверждение странным. Но факт остается фактом. Несмотря на фантастический прогресс прикладных наук, несмотря на то, что за две последующие четверти столетия шла и идет высоким темпом научно-техническая революция, — несмотря на это, новых законов природы после открытия квантовой механики найдено не было… Придется подождать.
Глава 5 Строение атомных ядер
ИЗОТОПЫ
Мы рассказали в 3-й книге, как с помощью электрических и магнитных полей можно разделить пучок частиц, отличающихся отношением заряда к массе. Ну, а если заряды одинаковы, то становится возможным разделить частицы по величинам их масс. Для этой цели служит прибор, который носит название масс-спектрографа. Он широко применяется для химического анализа.
Схема этого прибора показана на рис. 5.1.
Идея его заключается в следующем. В электрическое поле конденсатора поступают частицы с разными значениями скоростей. Выделим мысленно группу частиц с одинаковым отношением e/m. Поток этих частиц попадает в электрическое поле и расщепляется: быстрые частицы отклонятся в электрическом поле меньше, медленные — больше. Веер этих частиц поступает теперь в магнитное поле, перпендикулярное чертежу. Оно включено так, чтобы отклонять частицы в противоположную сторону. И здесь быстрые частицы будут отклоняться меньше, а медленные — больше. Отсюда следует, что где-то за пределами поля, выделенный нами мысленно пучок одинаковых частиц опять соберется в одну точку — сфокусируется.
Частицы с иным значением e/m также соберутся в точку, но в другую. Расчет показывает, что фокусы для всех e/m расположатся весьма близко к некоторой прямой. Если вдоль этой прямой поместить фотографическую пластинку, то частицы каждого сорта дадут знать о себе отдельной линией.
С помощью масс-спектрографа были открыты изотопы. Честь открытия изотопов принадлежит Дж. Дж. Томсону. В 1912 г., изучая отклонение пучка ионов неона в электрическом и магнитном полях, этот исследователь обратил внимание на то, что пучок расщепляется на две части. Атомная масса неона (точнее, относительная атомная масса) была известна с достаточной точностью — она равнялась 20,200. Обнаружилось, что на самом деле, атомы неона бывают трех сортов. Они имеют массовые числа 20, 21 и 22 (массовые числа — относительные атомные массы, округленные до целого числа).
Поскольку химические свойства неона не зависели от его массы, то достаточно скоро физики уверились в том, что различия связаны лишь с ядром. Заряд ядра и число электронов одинаковы — значит, разные сорта атомов неона должны занимать одно и то же место в таблице Менделеева. Отсюда и название: изотопы, т. е. занимающие одинаковые места.
В 20-х годах масс-спектрограф приобрел современные черты и началось изучение изотопического состава всех элементов. Все без исключения элементы представляют собой смесь изотопов. Среди них есть такие, как водород или кислород, состоящие в основном из одного изотопа (водороде массовым числом 1—99,986 %, кислород с массовым числом 16–99,76 %). Но встречаются и элементы с иным соотношением изотопов. К таким относится, например, хлор (75 % изотопа с массовым числом 35 и 25 % с массовым числом 37). Имеются элементы, которые состоят из большого числа изотопов. Мы привели примеры стабильных изотопов. О радиоактивных (нестабильных, распадающихся) разновидностях одного и того же элемента речь впереди.
Достаточно быстро качество прибора возросло настолько, чтобы установить: массы изотопов выражаются целыми числами лишь с точностью до второй — четвертой цифр после запятой. О причинах этого отклонения мы расскажем ниже.
Поскольку на химическое поведение масса ядер не влияет, то ясно, что имеется много химических соединений, отличающихся изотопным составом. Говорят, что есть два сорта воды — обычная и тяжелая. В обычной воде присутствует изотоп водорода с массовым числом 1, а в тяжелой — так называемый дейтерий, изотоп водорода с массовым числом 2. Однако в природе, встречаются три изотопа кислорода с массовыми числами 16, 17 и 18; значит, вода является смесью молекул шести разных типов. Если молекулы вещества состоят из большого числа атомов, то число, изотопических разновидностей может измеряться десятками и сотнями.
Разделение изотопов является важной отраслью промышленности. Особенно большое значение оно имеет в ряде процессов, сопутствующих получению атомной энергии. Надо иметь возможность отделить тяжелую воду от легкой, разнести по разным приемникам атомы разных сортов ядерного горючего — урана, тория. Список подобных задач, которые индустрия ставит перед физиками, можно было бы продолжить.
Сложность состоит в том, что по своей электронной структуре, а значит и по химическим свойствам, атомы различаются крайне незначительно. Для легких атомов с очень большим трудом, применяя многоступенчатую химическую экстракцию, удается провести такое разделение. Для тяжелых атомов считалось возможным применение лишь физических методов, использующих малые различия в массе атомных ядер.
Наибольшим распространением до сегодняшнего дня пользуется метод газовой диффузии. Молекулы, содержащие изотопы разной массы, будут слегка отличаться по скорости прохождения через пористый барьер. Легкие молекулы пробираются через препятствия быстрее, чем тяжелые.
Разумеемся, можно прибегнуть и к разделению, основанному на принципе только что описанного масс-спектрографа. Но оба эти способа занимают много времени и применение их стоит больших денег.
Всего лишь несколько лет назад было показано, что разделение изотопов можно произвести принципиально новым методом, используя лазеры. Пригодность для этой цели лазера связана с тем, что с его помощью можно создать луч исключительно высокой монохроматичности. Различие в расстояниях между энергетическими уровнями, занимаемыми электронами двух изотопических разновидностей одного и того же элемента, разумеется, очень незначительно. Ведь оно обусловлено лишь массой ядра, поскольку заряды ядер двух изотопов одинаковы. А именно заряды и определяют в основном расположение электронных уровней. Луч лазера столь строго монохроматичен, что он способен привести в возбужденное состояние изотопы одного сорта и оставить в невозбужденном состоянии атомы другого сорта.
На рис. 5.2 изображены два процесса разделения изотопов с помощью лазера.
Газ атомов или молекул выходит из «отверстия печки. Луч лазера возбуждает атомы одной изотопной разновидности. Как правило, возбужденные атомы будут обладать электрическим или магнитным моментом. Поэтому неоднородное магнитное или электрическое поле уведет их в сторону (верхняя схема).
Второй метод используется в том случае, если возбужденные атомы быстро высвечиваются. В этом случае, проходя через пространство, освещаемое лазерным лучом, один и тот же атом возбуждается повторно, т. е. несколько раз испытывает неупругое столкновение с фотонами. Каждое поглощение фотона ведет к тому, что атом получает импульс, направленный в сторону действия лазерного луча. Атомы, способные возбудиться, просто выталкиваются кверху, в то время как атомы той разновидности, которая не поглощает фотоны, распространяются без отклонения.
Первый удачный опыт этого рода был проделан с пучком атомов бария, облучавшихся лазерным светом с длиной волны 0,55535 мкм. Поглощение одного фотона сдвигало атом на 0,8 см в течение 1 с при продольной скорости 50 000 см/c.
РАДИОАКТИВНОСТЬ
В 3-й книге было коротко рассказано, каким образом Резерфорд установил, что атом состоит из крошечного ядра и движущихся около него электронов. Теперь мы должны раскрыть перед читателем одну из важнейших страниц физики — ту, на которой записаны факты о строении атомного ядра из протонов и нейтронов. Как ни странно, но история этого открытия начинается за пятнадцать лет до того, как своими опытами по рассеянию, альфа-частиц тонкой фольгой Резерфорд доказал справедливость ядерной модели атома.
Верной 1896 г. французский физик Анри Беккерель (1852–1908) выяснил, что уран испускает лучи, действие которых, подобно рентгеновским лучам. Так же как и открытые за несколько месяцев перед этим икс-лучи Рентгена, урановые лучи засвечивают фотографические пластинки, проходят через непрозрачные предметы. Поглощение их пропорционально плотности предмета, помещенного между ураном и фотопластинкой. Если тело непрозрачно для этих лучей, то на пластинке образуются четкие контуры предмета. Урановые лучи, опять же как лучи Рентгена, способны ионизовать воздух; по ионизации воздуха можно очень хорошо оценивать их интенсивность.
Есть родственное в открытиях Беккереля и Рентгена — элемент случайности. Но один лишь случай никогда не является источником важного научного открытия. Как после открытия Рентгена нашлись люди, которые за несколько лет до него «видели» икс-лучи, так же и после открытия Беккереля выяснилось, что по крайней мере человека три наблюдали почернение фотопластинки, находившейся вблизи от солей урана. Но мало «увидеть»! Надо обратить внимание и надо выяснить настоящую причину явления. Это сделали Рентген и Беккерель, а не их предшественники. Потому они и заслужили честь и славу.
Путь к открытию Беккереля проходил через следующие этапы. Рентгеновские лучи в первых трубках, как мы это рассказывали, падали на стекло. Стекло флуоресцировало под действием катодных лучей. Поэтому естественно возникала мысль, что проникающие лучи являются спутниками флуоресценции. Беккерель и начал с того, что стал производить опыты с веществами, которые флуоресцируют под действием солнечного света. Довольно быстро он обнаружил, что проникающие лучи исходят из различных минералов, содержащих уран. Уже это было открытием. Но Беккерель не спешил сообщить о нем ученому миру. Опыты следовало повторить несколько раз. А тут, как назло, солнце упорно не появлялось на небе несколько дней. Фотопластинки вместе с исследуемыми минералами лежали в ожидании солнышка в ящике лабораторного стола. 1 марта 1896 г., наконец, выдался солнечный день. Можно было приступить к опытам. Но прежде чем начать работу, Беккерель решил проверить качество пластинок. Отправился в темную комнату, проявил одну из пластинок и увидел на ней четкие силуэты образцов минерала. А ведь флуоресценций-то никакой не было. Значит, дело не в ней.
Беккерель повторяет «темповые» опыты и убеждается в том, что его минералы являются источниками проникающего излучения, которое создается «само по себе» — без всякой помощи внешнего света.
Тщательный просмотр многих образцов приводит Беккереля к мысли, что источником лучей является уран. Если в минерале урана нет, то нет и проникающего излучения. Чтобы доказательство было полным, нужно исследовать чистый уран. А этот элемент — большая редкость: Беккерель достал уран у своего друга химика Муассана. На одном и том же заседании французской Академии наук Муассан рассказал о своем способе получения чистого урана, а Беккерель сообщил о том, что уран испускает лучи. Эти доклады были прочитаны 23 ноября 1896 г. Всего лишь пятьдесят лет отделяют это открытие от атомной бомбы, сброшенной над Хиросимой.
Прошел год. Осенью 1897 г. начинают свои опыты два молодых физика — супруги Кюри. Молодые энтузиасты работают в холодном сарае. Исследование химических особенностей образцов, дающих проникающую радиацию Беккереля, Мария Кюри (1867–1934) выбирает в качестве темы своей диссертации.
МАРИЯ СКЛОДОВСКАЯ-КЮРИ (1867–1984) — выдающаяся женщина-ученый. В 1898 г., исследуя излучение (природа которого в то время была неизвестна) урана и тория, выяснила, что в рудах этих элементов содержатся вещества, обладающие гораздо более сильной способностью к излучению. Ею были выделены полоний и радий. Мария Кюри и ее супруг Пьер Кюри ввели в обиход термин «радиоактивность». Открытия Марии Склодовской-Кюри были немедленно подхвачены Резерфордом и привели к установлению законов радиоактивного распада атомов.
Напряженный труд приводит к одному открытию за другим. Прежде всего обнаруживается, что кроме урана проникающие лучи дает и торий. Интенсивность лучей измеряется по силе ионизационного тока. Кюри подтверждает догадку Беккереля, что интенсивность проникающих лучей не зависит от того, в состав каких химических соединений входят уран и торий, а строго пропорциональна числу их атомов.
И вдруг осечка: урановая смоляная руда дает в четыре раза большую ионизацию, чем ей полагалось бы по количеству содержащегося в ней урана. Вот в момент таких поворотных пунктов и сказывается талант исследователя. Бесталанный человек не отказался бы от предположения, что во всем виноваты атомы урана. Но Мария Кюри понимает, что явление может быть объяснено и иначе. Ведь может статься, что в смоляной руде содержится в малом количестве неизвестный доселе химический элемент, который обладает способностью давать сильнейшее проникающее излучение. Догадка оказалась справедливой. Огромный, без преувеличения можно сказать — героический труд Кюри приводит к тому, что она выделяет сначала полоний (название не случайно: Мария Кюри — урожденная Склодовская, по национальности полька), а затем радий (лучистый). Радий оказался почти в тысячу раз активнее чистого урана.
Однако поведем наш разговор в более быстром темпе, не касаясь исторической последовательности событий.
После открытия радия были найдены и другие вещества, являющиеся источниками проникающих лучей. Все они получили название радиоактивных.
Что же представляет собой радиоактивное излучение?
В коробке, из которой был откачан воздух, помещался радиоактивный препарат, за ним — свинцовая заслонка со щелью. Луч проходил через щель, падал на фотопластинку и оставлял на ней след. Но как только коробка была помещена между полюсами магнита, на проявленной пластинке обнаружились три черточки. Радиоактивный луч разделился на три луча. Один отклонился в ту сторону, куда положено загибаться потоку отрицательно заряженных частиц, второй луч представлял собой поток положительных частиц. Третий луч не отклонялся. Видимо, он являлся родственником рентгеновского луча.
Методами, которые мы уже обсуждали, удалось доказать, что в общем случае радиоактивное излучение состоит из потока электронов (до того, как было выяснено, что это — электроны, лучи назывались бета-лучами), потока ядер атомов гелия (альфа-частицы) и жесткого электромагнитного излучения (гамма-лучи).
РАДИОАКТИВНЫЙ РАСПАД
Происходят ли какие-либо события с атомами, являющимися источниками радиоактивного излучения? Происходят. И события эти совершенно- поразительны. В 1902 г. тот же Резерфорд (об открытии структуры атома которым в 1911 г. мы рассказали уже давно, презрев историческую последовательность событий) доказывает, что в результате радиоактивного излучения происходит превращение одного сорта атомов в другой.
Резерфорд ожидал, что предположение, хотя и основанное на строгих опытных доказательствах, будет принято в штыки химиками. Действительно, ведь, доказывая наличие превращения атомов, мы посягаем на святая святых — на неделимость атома. Утверждая, что из урана можно получить свинец, мы осуществляем мечту алхимиков, которые заслужили «славу» ничуть не более почетную, чем астрологи.
Но под тяжестью доказательств противники быстро отступили, и через некоторое время явление естественного радиоактивного распада некоторых атомов было неоспоримо доказано как химическими, так, и физическими методами. В чем же заключается радиоактивное превращение?
Прежде всего, оказалось, что электронные лучи, входящие в состав радиоактивного излучения, выходят из ядра. Но если так, то заряд ядра увеличивается на единицу и радиоактивный атом превращается в следующий по порядку атом таблицы Менделеева.
Альфа-частица несет на себе двойной положительный заряд и имеет массу в четыре раза превышающую массу атома водорода. Если ядро выбрасывает такие частицы, то должно происходить «смещение» атома влево по порядку элементов в таблице Менделеева с соответствующим изотопическим превращением.
Совершенно тривиальным (вроде «веревка есть вервие простое») будет утверждение, что радиоактивному распаду подвержены неустойчивые атомы.
Мы не знаем, много ли сортов таких атомов существовало, когда начал остывать земной шар. Но нам превосходно известно, какие, неустойчивые атомы, можно разыскать сейчас в природе. Оказывается, что они являются членами трех кланов. Прародителями являются атом урана с массовым числом 238, атом урана с массовым числом 235 и атом тория с массовым числом 232.
На рис. 5.3 мы приводим первое семейство.
Первым превращением является переход 238U в 234Th, происходящий благодаря, выбрасыванию альфа-частиц. За ним следуют два бета-превращения, переводящие торий в протактиний, а протактиний опять в уран, но уже в изотоп с массовым числом 234. Далее следуют пять последовательных альфа-превращений, спускающих нас до неустойчивого изотопа свинца с массовым числом 214. Еще два «зигзага», и процесс распада заканчивается: изотоп свинца с массовым числом 206 является устойчивым.
Разрушение каждого отдельного атома является случайным. Есть атомы «счастливчики», которые обладают большим долголетием, а есть такие, которые живут мгновения.
Но в любом случав нельзя предугадать, когда произойдет превращение с данным атомом. Ведь мы не можем назвать день кончины нашего домашнего кота. Но у каждого вида животных существует свой средний срок жизни. Так же у каждого сорта атомов имеется весьма строгое среднее время существования. Впрочем, поведение атомов существенно отличается от жизни животных. Жизнь неустойчивых атомов, в отличие от среднего срока жизни живых существ, не зависит ни от каких внешних условий. Ничто не способно изменить среднее время распада. За каждую единицу времени распадается всегда одна и та же доля атомов:
ΔN/N = λ∙t
Эта формула годится лишь для случая? когда дробь ΔN/N невелика.
Величина λ является константой для каждого радиоактивного перехода. Вместо того, чтобы пользоваться этой константой, нагляднее характеризовать скорость процесса «временем полураспада», т. е. временем, которое требуется, чтобы половина какого-то количества радиоактивного вещества претерпела превращение. Это время для разных радиоактивных элементов может колебаться в огромных пределах. Так, период полураспада родоначальника рассмотренного нами семейства 238U составляет 4,5 млрд. лет. А вот половина атомов изотопа свинца с массовым числом 214 распадается за одну миллионную долю секунды.
ЯДЕРНЫЕ РЕАКЦИИ И ОТКРЫТИЕ НЕЙТРОНА
Радиоактивное превращение вполне аналогично химической реакции распада. Было химическое вещество, а затем под действием тепла или света распалось на два других. Скажем, углекислая кислота распалась на воду и углекислый газ. Так же точно в картине распада, который мы только что рассмотрели, ядро тория с массовым числом 230 распадается на ядро радия и ядро гелия.
Если возможен ядерный распад, то, наверное, должны существовать и ядерные реакции, происходящие по принципу
A + B —> С + D
Для того, чтобы произошла подобная химическая реакция, надо столкнуть молекулы веществ А и В. Для того, чтобы осуществить ядерную реакцию, надо столкнуть два атомных ядра.
Такие опыты и начали производиться с 1919 г. Резерфордом. До появления на сцену ускорителей частиц ядерные реакции осуществлялись путем бомбардировки какого-либо вещества альфа-частицами. После того как удалось получить мощные потоки протонов и других ядер, были открыты новые ядерные реакции. Стало ясным, что в принципе можно превратить изотоп любого химического элемента в другой. Можно получить и золото из других веществ. Мечта алхимиков стала явью.
Первой обнаруженной ядерной реакцией типа A + B —> С + D было превращение азота и гелия в кислород и водород. Вот как записывается подобная реакция:
147N + 42He — > 178O + 11H
Обратите внимание на то, что неизменными сохраняются суммы верхних цифр и суммы нижних цифр. Нижние цифры указывают заряд ядра, а верхние — массу, округленную до целого числа, т. е. массовые числа. Таким образом, строго действует закон сохранения электрического заряда. Закон сохранения массы осуществляется, как мы увидим ниже, лишь приближенно. Ну, а сумма массовых чисел сохраняется столь же строго, как и заряд.
Еще в 1920 г. Резерфорд высказал предположение, что должна существовать частица, лишенная электрического заряда и близкая по массе к протону. Резерфорду казалось, что иначе трудно понять, как положительно заряженная альфа-частица проникает в положительно заряженное ядро: ведь одноименно заряженные частицы отталкиваются.
ЭРНЕСТ РЕЗЕРФОРД (1871–1937) — замечательный английский физик, великий экспериментатор. Тонкими и оригинальными опытами показал, в чем заключается радиоактивный распад. Своими классическими опытами по рассеянию веществом потока альфа-частиц обосновал современную теорию строения атома как системы, состоящей из ядра и движущихся около него электронов. Продолжая свои опыты по бомбардировке ядрами различных мишеней, первый осуществил искусственное превращение элементов.
Частица без заряда, получившая название нейтрон, была открыта в 1932 г. Нетрудно понять, почему ее открытие задержалось. Ведь мы видим заряженные частицы по их следам (трекам), которые они оставляют в газе или фотоэмульсии благодаря их способности ионизировать попадающиеся на их пути молекулы. Но электрически нейтральная частица не взаимодействует с электронами, а потому и не оставляет на своем пути следов. Так что о существовании нейтронов можно судить лишь по вторичным эффектам.
Нейтрон был открыт при бомбардировке бериллия альфа-частицами. Эта реакция записывается так:
94Be + 42α — > 126C + 10n
Символ n принадлежит нейтрону. Но как же можно уверовать в существование частицы, которая сама не оставляет следов? По ее действиям. Представьте себе, что на зеленом сукне биллиардного стола находится невидимый глазу биллиардный шар. По столу катится видимый шар и вдруг «ни с того, ни с сего» отскакивает в сторону. Физик не может допустить, что его подводят законы сохранения энергии и импульса. Поэтому он делает вывод, что видимый шар натолкнулся на невидимый. Более того, пользуясь законами сохранения, он может определить все характеристики невидимого шара, выяснив, на какой угол отклонился от линии своего полета и как изменил свою скорость видимый шар.
Число нейтронов подсчитывают следующим образом. На пути нейтронного луча помещают вещество, содержащее атомы бора. При встрече с ядром бора нейтрон прекращает свое существование. Происходит следующая реакция:
105В + 10n —> 73Li + 42α.
Нейтрон пропал, а зато появилась альфа-частица. Регистрируя эти заряженные частицы, оставляющие видимый след в различного рода приемниках, мы сможем точно измерить интенсивность нейтронного луча.
Существует много других методов, которые позволяют с полной достоверностью определить все параметры, характеризующие нейтрон и вообще электрически нейтральную частицу. Совокупность точно согласующихся косвенных доказательств порою не менее убедительна, чем разглядывание видимых следов.
СВОЙСТВА АТОМНЫХ ЯДЕР
До открытия нейтрона физики полагали, что атомное ядро, построено из электронов и протонов. Это предположение таило в себе много противоречий, и попытки создания теории строения ядра были неудачными. Как только был найден нейтрон, возникающий при ядерных столкновениях, сразу появилась мысль, что атомное ядро построено не нейтронов и протонов. Впервые эта гипотеза была выдвинута советским физиком Д. Д. Иваненко.
С самого начала было ясно, что масса нейтрона если и не равна массе протона, то во всяком случае близка к ней. Поэтому тут же возникло четкое истолкование различий изотопов одного и того же элемента.
Как мы видим, каждому изотопу можно приписать два числа. Одно из них — это порядковый номер в таблице Менделеева Z, который равен числу протонов в ядре. Порядковый помер определяет поэтому число электронов, связанных с ядром. А раз так, то становится ясным, что порядковый номер и должен отвечать за химическое поведение элементов (ведь химические реакции не затрагивают ядер).
Что же касается массового числа, то оно равно общему числу нейтронов и протонов. Так что изотопы одного и того же элемента отличаются друг от друга числом нейтронов в ядре.
Очень точными опытами найдены характеристики обеих частиц, образующих ядро. Масса протона равна 1,6726∙10-24 г, т. е. она в 1836 раз больше массы электрона. Спин протона равен 1/2, а магнитный момент 1,41∙10-23 ед. СГС. Масса нейтрона незначительно больше массы протона, а именно равна 1,6749∙10-24 г. Спин нейтрона равен 1/2. Магнитный момент нейтрона антипараллелен спину и равен 0,966∙10-23 ед. СГС.
Спины и магнитные моменты атомных ядер исследуются разными методами: применяются оптическая спектроскопия, радиоспектроскопия, изучение отклонения пучков частиц в неоднородном магнитном поле. На общих принципах этих измерений мы останавливались в 3-й книге и в предыдущих главах этой книги. А сейчас мы ограничимся лишь изложением главных фактов, полученных за последние десятилетия большим отрядом физиков.
Прежде всего подчеркнем, что законы квантовой физики, касающиеся момента импульса; справедливы для всех частиц. Поэтому и для атомных ядер момент импульса может быть представлен формулой
Здесь величина h — постоянная Планка, с которой приходится встречаться во всех формулах квантовой физики.
Обычаю спином называют не это выражение, а параметр S. Теория строго доказывает, а опыт блестяще подтверждает, что спин любой частицы может равняться только 0, 1/2, 1, 3/2 и т. д.
Просматривая таблицы значений спинов различных атомных ядер (полученных, в разных опытах), мы обнаружим ряд интересных закономерностей. Прежде всего, у ядер, содержащих четное число протонов и четное число нейтронов, спин ядра равен нулю (4Не,; 12G, 16О). Число нуклонов (т. е. ядерных частиц), кратное четырем, вообще играет, видимо, большую роль. Во многих случаях, (но далеко не во всех) спин атомного ядра может быть получен следующим образом: отбрасываем, ближайшее к массовому числу А числе, кратное четырем, и умножаем оставшуюся разность на 1/2. Например: у лития-6 спин равен 2 х 1/2 = 1; 3/2 у лития-7; 1 у бора-10, 3/2 у бора-11.
Правилом является довольно очевидное обстоятельство: у ядер с четным массовым числом А спин целый или равен нулю, у ядер с нечетным А кратен 1/2.
Принцип Паули применим к протонам и нейтронам в ядре. Две тождественные частицы могут расположиться на одном уровне энергии лишь при условии антипараллельных спинов. Так как протон и нейтрон — разные частицы, то на одном уровне могут быть два протона и два нейтрона. В этой компактной группе со спином, равным нулю, мы узнаем ядро атома гелия (альфа-частицу).
Наличие спина означает наличие магнитного момента. Между механическим импульсом L и магнитным моментом М существует, как нам известно, прямая пропорциональность. При этом магнитный момент может быть либо параллелен, либо-антипараллелен спину.
БИЗОНЫ И ФЕРМИОНЫ
Мы несколько раз подчеркивали, что один энергетический уровень могут занять лишь две частицы с противоположно направленными спинами. Пришли пора сказать, что этот принцип (принцип Паули) справедлив лишь для одного класса частиц, который получил название фермионов. К фермионам относятся электроны, протоны и нейтроны. Следует также сказать, что всякая связанная система, состоящая из нечетного числа фермионов, также является фермионом. Второй сорт частиц называет бозонами. К ним относится фотон, некоторые короткоживущие элементарные частицы (такие, как, например пион), и, самое главное, к ним принадлежат все частицы, которые состоят из четного числа фермионов.
Число бозонов, находящихся на одном энергетическом уровне, не ограничено. Чтобы вы получше усвоили различие между бозонами и фермионами, мы приводим рис. 5.4. На этом рисунке каждый кружок символизирует пару частиц с противоположными спинами.
При очень низких температурах бозоны в основном собираются на самом низком уровне энергии. Фермионы расположены на этом рисунке в виде столбика.
Достаточно очевидно, что различия в поведении фермионов и бозонов наиболее отчетливо проявляются при низких температурах. При самых низких температурах число бозонов, расположенных в «подвале», может быть почти равным общему числу бозонов.
То, что сказано до сих пор, «понимать» не надо. Достаточно запомнить! Ибо сказанное есть истина в последней инстанции. Но я каждый раз испытываю сожаление, когда вынужден сообщать читателю без доказательства какие-либо положения, которые можно доказать, но лишь с помощью далеко не простых математических уравнений. Так вот оказывается, что бозоны в некоторых случаях могут, а в иных случаях не могут собираться на одном энергетическом уровне в больших количествах. Если они могут это сделать, то мы говорим, что произошла конденсация Бозе-Эйнштейна.
Когда большое число частиц оказывается на одном уровне, то в этом случае их движение становится идеально согласованным. Частицы-близнецы, не считаясь с тепловым хаосом, перемещаются совершенно тождественно.
Во 2-й книге мы рассказали об удивительной жидкости, обладающей при низкой температуре сверхтекучестью. Этой жидкостью является собрание атомов 4Не. Атомы этого изотопа — бозоны. При температуре 2,19 К происходит конденсация частиц, придающая жидкости поразительное свойство сверхтекучести. Потеря трения может быть грубо объяснена так: если только одному атому удалось пройти через тончайшую щель, то за ним послушно последуют и все другие.
Мы познакомились не с одним, а с двумя явлениями, где поток частиц движется, не считаясь с препятствиями. Сверхтекучее движение атомов 4Не напоминает электрический ток без сопротивления, который обнаруживается у многих металлов и сплавов также при низких температурах.
Но ведь электроны являются фермионами. Они не могут собраться в единый строй. Выход из положения был найден в 1956 г., когда американскими учеными была предложена теория, согласно которой ниже некоторой температуры электроны могут сцепляться в пары. Пара фермионов, как мы сказали с самого начала, — это бозон. Следовательно, сверхпроводимость появляется тогда, когда такие бозоны конденсируются на одном энергетическом уровне. Этим двум замечательным явлениям, сверхпроводимости и сверхтекучести, по сути дела дается одно и то же объяснение. Одна частица выбирает путь, который «протоптавшей и легче», и все другие следуют за ней.
Если идея превращения фермионов в бозоны за счет сцепления в пары справедлива, то, возникает законный вопрос: а не может ли изотоп 3Не, который обладает спином и является фермионом, также оказаться сверхтекучим, как и 4Не?
Было с самого начала очевидно, что если это явление и существует, то во всяком случае при температурах много более низких, чем температура перехода в сверхтекучее состояние основного изотопа 4Не. Причина ясна: ядро атома 3Не состоит из двух протонов и одного нейтрона. Значит, он на 25 % легче своего собрата. Поэтому, разумеется, тепловое движение 3Не будет более интенсивным и создание стройного марша бозонов станет возможным при более низких температурах. Но при каких? К сожалению, теория не могла предсказать температуры перехода 3Не в сверхтекучее состояние. Потребовалось фантастическое упорство и преодоление огромных трудностей, прежде чем в 1974 г. был получен сверхтекучий 3Не.
При какой же температуре происходит этот переход? Вот ответ, который стоило бы напечатать жирными буквами: при температуре, равной 0,0027 К. Может быть, читатель скажет: «Подумаешь, всего лишь на два градуса ниже температуры аналогичного перехода 4Не». О нет! Эти два градуса стоят много больше похолодания на два градуса, скажем, с температуры 20 до 18 °C. В этом житейском событии температура понизилась в 293/291 раза, а в случае, в котором мы ведем речь, температура понижена в 1000 раз. Это огромный успех экспериментальной физики и торжество теоретической, предсказавшей спаривание атомов 3Не в бозонную пару.
Зрительный образ помогает запоминанию. Для этого я привожу схему пары на рис. 5.5.
Магнитные моменты двух атомов направлены в одну сторону. Таким образом, переход 3Не в состояние конденсации Бозе-Эйнштейна должен сопровождаться скачкообразным изменением частоты магнитного резонанса. Ведь пара ведет себя как одно целое. Именно это и было обнаружено на опыте. Воистину блестящая страница физики, и было бы грешно не рассказать о ней читателю, несмотря на отсутствие возможности пояснить, при каких условиях и на основании каких причин происходит спаривание фермионов в бозонную пару.
МАССА И ЭНЕРГИЯ АТОМНОГО ЯДРА
Бегло было упомянуто, что массовое число округляет точное значение массы ядра до целого числа.
Сейчас принято выбирать атомную единицу массы (мы говорили об этом в 1-й книге) как 1/12 часть массы изотопа углерода 12С.
Относительные массы изотопов всех атомов отличаются от целых чисел хоть и незначительно, но столь существенно, что свалить эти различия на экспериментальные ошибки никак невозможно. Масса 1Н равна 1,00807, масса дейтерия вовсе не в два раза больше, а равна 2,01463.
Изучая внимательно таблицы масс изотопов, можно прийти к следующему важному выводу: масса ядра меньше суммы масс элементарных частиц, образующих ядро. Например, масса нейтрона 1,00888, масса протона 1,008807, масса двух нейтронов и двух протонов равна 4,0339 (в атомных единицах массы — 1 а. е. = 1,66∙10-27 кг). В то же время масса ядра атома гелия, который состоит из двух нейтронов и двух протонов, не равна этому числу, а равна 4,0038. Таким образом, масса ядра гелия меньше суммы масс составляющих ядро частиц на величину 0,0301 а. е. м., в тысячи раз превосходящую точность измерений.
Нет никакого сомнения, что эти малые различия имеют глубокий смысл. Но какой?
Ответ на этот вопрос принесла теория относительности. И появление ее на сцене в этот момент несомненно более эффектно, чем тогда, когда опыт подтвердил зависимость массы электрона от скорости его движения. То, что сумма масс протонов и нейтронов, составляющих ядро, меньше массы ядра, — явление, получившее название дефекта массы (плохой перевод с английского — масса ведь не «испортилась», а уменьшилась), — получает точную и ясную трактовку с помощью знаменитой формулы Е = mc2. Если система приобретает или теряет количество энергии ΔE, то масса этой системы соответственно возрастает или уменьшается на величину
Δm = ΔЕ/с2.
Дефект массы ядра (с точки зрения этого принципа) получает естественное истолкование: он является мерой энергии связи ядерных частиц.
Под энергией связи в химии и физике понимают ту работу, которую надо затратить для того, чтобы эту связь полностью нарушить. Если бы удалось разделить ядро на несколько частей, то масса системы возросла бы на величину дефекта массы Δm.
Разрушение ядра привело бы к выделению огромной энергии. Нетрудно прикинуть, что изменение массы на одну тысячную долю атомной единицы массы, т. е. на 1,66∙10-27 г, эквивалентно примерно 1 МэВ.
Зная атомную массу ядра, читатель без труда обнаружит следующий интересный факт. Если разделить энергию, связывающую протоны и нейтроны в ядре, на число частиц, то получится одно и то же число, а именно 8 МэВ, для всех ядер (кроме нескольких самых легких). Отсюда с несомненностью вытекает важное следствие: взаимодействуют лишь ближайшие протоны и нейтроны, т. е. ядерные силы действуют на коротких расстояниях. Они становятся практически равными нулю, если отойти от протона или нейтрона на расстояние порядка размера этих частиц (т. е. на 10-13 см).
Величину 8 МэВ поучительно сравнить с энергиями химической связи молекул. Эти последние равны обычно нескольким электронвольтам на атом. Значит, для расщепления молекулы на атомы надо затратить энергию в несколько миллионов раз меньшую, чем для расщепления ядра.
Из приведенных примеров ясно, что ядерные силы достигают огромных значений. Очевидно также, что ядерные силы представляют собой новый класс сил, так как они способны сцеплять частицы, заряженные одноименным электричеством. Ядерные силы не сводимы к электрическим.
Закономерности, которым подчиняются эти два рода сил, весьма и весьма различны. Электромагнитные силы убывают медленно, и приборы фиксируют электромагнитные поля на огромных расстояниях от заряженных частиц. Напротив, ядерные силы убывают с расстоянием очень быстро. Практически за пределами ядра они прекращают свое действие.
Другое важное различие состоит в том, что ядерные силы (примерно так же, как химические валентные силы) обладают свойством насыщения. Каждый нуклон, т. е. протон или нейтрон, взаимодействует с ограниченным числом ближайших соседей. Для электромагнитных сил такого ограничения не существует.
Значит, существуют три рода сил: гравитационные, электромагнитные и ядерные? Пока на этот вопрос нельзя ответить с определенностью. Физикам известен и четвертый вид сил, который получил неудачное название «слабого взаимодействия». О нем мы не будем рассказывать читателю, тем более, что есть надежда свести это взаимодействие к электромагнитным силам.
ЭНЕРГИЯ ЯДЕРНЫХ РЕАКЦИЙ
Мы выяснили два важных факта. Во-первых, между атомными ядрами могут происходить реакции по схемам, весьма схожим с теми, которые известны химикам; во-вторых, исходные ядра и возникшие новые частицы всегда будут несколько отличаться по массе (ибо сохраняется сумма массовых чисел, а не сумма масс ядер до и после реакции).
И кроме того, мы увидели, что самые ничтожные различия в массах будут сопровождаться выделением или поглощением огромных количеств энергии.
Энергии, которые выделяются или поглощаются при ядерных превращениях, не идут ни в какое сравнение с теплом химических реакций. Для образного сопоставления приведем следующие примеры. Один грамм угля при сгорании дает тепло, достаточное для того, чтобы нагреть до кипения полстакана воды. А вот какое количество тепла дает ядерное превращение: если бы удалось все ядра одного грамма бериллия разбить альфа-частицами, то выделилось бы тепло, достаточное для того, чтобы довести до кипения тысячу тонн воды.
Все это было превосходно известно Резерфорду и его сотрудникам. Но тем не менее Резерфорд считал совершенно неосуществимым использование ядерных реакций для практических целей (в то время никому из физиков не приходила в голову мысль о возможности цепных реакций). Подчеркнем, что в своем непредвидении революции, которую вызвало его открытие, он присоединился к Фарадею и Герцу, о чем уже упоминалось в 3-й книге как об интересной психологической загадке. Но так как мы знаем, что последовало за скромными опытами Резерфорда, то, разумеется, нам надо потратить немного места, дабы напомнить читателю, в чем состоит механизм выделения и поглощения энергии при реакциях.
Прежде всего мне хочется подчеркнуть не различие, а сходство химических и ядерных реакций.
Реакции такого типа, когда частицы А и В превращаются, в частицы С и D, выделяют или поглощают тепло в зависимости от того, образовались ли из медленных частиц быстрые или из быстрых медленные. Так дело обстоит в химических реакциях и точно так же в ядерных. И далее. Если из медленных частиц образовались быстрые, то, значит, кинетическая энергия системы возросла. Но закон сохранения энергии допускает это лишь в том случае, если потенциальная энергия системы уменьшилась. То есть в этом случае сумма внутренних энергий частиц А и В больше суммы внутренних энергий частиц С и D. Так обстоит дело в химических реакциях, точно так же ведут себя и внутренние энергии ядер.
Согласно закону Эйнштейна, уменьшение внутренней энергии однозначно связано с уменьшением массы. Увеличение внутренней энергии ведет к возрастанию массы. Так обстоит дело в химических реакциях, так обстоит дело и в реакциях ядерных.
Но в химии закон сохранения массы работает. Сумма масс молекул А и В равна сумме масс молекул С и D. А в ядерных реакциях это равенство не соблюдается. Значит, есть различие? Да ни в коем-случае. Разница лишь количественная. При химическом превращении изменения энергии, а значит, и массы столь незначительны (незначительны с точки зрения релятивистской теории), что изменения масс молекул нельзя обнаружить на опыте. Так что аналогия между обоими типами реакции стопроцентная.
Ввиду важности сказанного: (очень часто думают, что выделение ядерной энергии — это какой-то особый процесс; а думать так не следует) я приведу аналогичное рассуждение для случая, когда частица А разваливается на частицы В и С. Если частица делится на части «сама по себе», то говорят про частицу А, что она нестабильна. Если А — молекула, то про вещество говорят, что оно разлагается; если А — ядро, то вещество радиоактивно. В обоих случаях произойдет выделение тепла. Частицы В и С будут обладать какой-то кинетической энергией, которой ранее «не было». Эта энергия возникла из энергии потенциальной! Образно говоря, лопнула пружина, которая, соединяла частицы В и С в одно целое, а говоря научным языком — пропала энергия связи. За счет этой энергии связи, мы и получили быстро движущиеся частицы В и С, т. е. выделили энергию в форме тепла.
В случае химической реакции не обнаруживается различия в массе молекулы А и: сумме масс образовавшихся из нее молекул В и С ввиду малости энергии. Но в случае ядерных реакций это различие легко обнаружится на опыте. Ядра В и С будут отличаться по массе от ядра А на величину дефекта массы.
Сам по себе тот факт, что некая реакция дает тепло, ёще не означает, что она будет иметь практическое значение. Условие нестабильности системы, то обстоятельство, что исходное вещество находится на более высоком энергетическом уровне, чем продукты реакции, является, как говорят математики, условием необходимым, но не достаточным.
Мы подробно обсудили во 2-й книге, какие требования должны быть выполнены, чтобы вещество послужило в качестве химического топлива. Нам остается лишь продолжить аналогию между химическими и ядерными реакциями.
Итак, напомним: мало того, чтобы химическая реакция давала тепло, нужно, чтобы это тепло «поджигало» соседние молекулы.
Поэтому ясно, что, научившись сталкивать между собой атомные ядра с выделением огромных количеств энергии, физики ни в малейшей степени не подошли еще к созданию ядерного горючего.
В превращении с альфа-частицами бериллий или литий не ведут себя, как горючее. Они удовлетворяют первому требованию, предъявляемому к топливу: дают энергию. Литий и бериллий ведут себя так, как кусочки угля, каждый из которых надо поджигать отдельной спичкой.
Вплоть до конца 30-х годов создание ядерного горючего казалось совершенно безнадежной задачей.
ЯДЕРНАЯ ЦЕПНАЯ РЕАКЦИЯ
Начиная с 1934 г., работами, проведенными в основном итальянским физиком Энрико Ферми (1901–1954) и его учениками, было показано, что ядра атомов большинства элементов способны поглощать медленные нейтроны и в результате такого процесса становятся радиоактивными.
В то время были известны радиоактивные превращения, состоящие в излучении электронов и альфа-частиц (эти превращения сопровождаются гамма-излучением). Но в 1938 г. рядом исследователей (интересно, что у фундаментального открытия, о котором мы сейчас поведем речь, нет одного автора) было обнаружено, что в уране, активизированном нейтронами по методу Ферми, присутствует элемент, сходный с лантаном. Объяснение могло быть лишь одно: под действием нейтронов атом урана делится на две более или менее равные части. Исключительная важность этого открытия стала сразу же ясной. Дело в том, что к тому времени была известна следующая закономерность: чем больше атомный номер, тем больше в ядре нейтронов. В уране отношение числа нейтронов к числу протонов равно примерно 1,6. А для элементов таких, как лантан, находящихся в середине таблицы Менделеева, это отношение колеблется между 1,2 и 1,4.
Но если ядро урана делится на две примерно равные половинки, то ядра продуктов деления будут неизбежно содержать «лишнее» число нейтронов. Они будут выбрасывать нейтроны. А нейтроны и играют роль «спичек».
Становится ясной возможность цепной реакции. Первый расчет этого явления был дан в 1939 г. Драматический ход событий — пуск первого ядерного реактора, создание атомной бомбы и взрыв ее в Хиросиме — изложен во всех деталях в десятках книг. У нас нет места для описания этих событий, и мы изложим современное состояние вопроса!
Нам надо пояснить, во-первых, в чем состоит ядерная цепная реакция, во-вторых, как ее сделать управляемой и, в-третьих, в каком случае она приводит к взрыву.
На рис. 5.6 показана схема одной из важнейших реакций этого типа: деление ядра урана-235.
За первым нейтроном дело не встанет — он найдется в атмосфере. Но при желании иметь более действенную «спичку» можно воспользоваться ничтожным количеством смеси радия с бериллием.
Попадая в ядро урана-235, которое состоит из 92 протонов и 143 нейтронов, плотно упакованных в сфере радиусом около 10-12 см, нейтрон проникает в это ядро, образуя изотоп уран-236. Пришелец деформирует ядро. Через промежуток времени порядка 10-14 с две половинки ядра удерживаются лишь маленьким мостиком. Еще такой же маленький промежуток времени — и ядро делится на две части. Одновременно оба образовавшихся осколка выбрасывают из себя два-три (в среднем 2,56) нейтрона. Осколки разлетаются с колоссальной кинетической энергией. Один грамм урана-235 дает столько же энергии, сколько 2,5 т угля, иными словами, 22 000 кВт∙ч. Через 10-12 с ядра, образовавшиеся после деления, более или менее успокаиваются, излучив при этом восемь фотонов гамма-лучей. Возникшие ядра радиоактивны. В зависимости от того, какие осколки образовались, дальнейший процесс распада может продолжаться от секунд до многих лет с испусканием гамма-лучей и выбрасыванием электронов..
Рис. 5.7 показывает, что чаще всего ядро урана-235 делится на два неравных осколка.
Как видно из кривой, максимальное число делений приводит к образованию ядер с массовыми числами 141 и 95.
Набор возникших радиоактивных осколков во всяком случае весьма велик. Самые различные нужды промышленности в искусственных радиоактивных элементах могут быть удовлетворены.
Если нейтроны, образующиеся при делении одного ядра, будут способны делить ядра других атомов урана, то цепная реакция осуществима.
Так как вещество чрезвычайно «дырчато» в отношении своего ядерного строения, то весьма значительна вероятность того, что образовавшиеся при делении какого-либо ядра нейтроны покинут вещество, не произведя деления других ядер. Кроме того, следует учесть, что не всякая встреча ядер с нейтронами приведет к делению. Цепная реакция будет развиваться в том случае, если в каждый последующий момент число нейтронов, находящихся внутри куска вещества, будет таким же или большим, чем в предшествовавший момент времени. Это условие физик формулирует следующим образом: коэффициент размножения нейтронов, равный произведению числа нейтронов на вероятность встреч нейтрона с ядром и на вероятность захвата нейтрона ядром не должен быть меньше единицы.
Поэтому чистое атомное горючее имеет критическую массу. Если эта масса меньше критической, то можно спокойно (ну, скажем лучше, более или менее спокойно) носить этот кусок ядерного горючего в кармане. Тяжело не будет, так как критическая масса близка к килограмму.
Само собой разумеется, сколь важно знать величину критической массы. Первый расчет этой величины дал в 1939 г. Ф. Перрен, сын Жана Перрена. Этот расчет представляет сейчас лишь исторический интерес, ибо в то время еще не было известно, что данная реакция в природном уране невозможна, в каком бы количестве мы его ни взяли. Но понадобилось совсем немного времени, чтобы картина стала ясной. Цепная реакция в природном уране не идет из-за того, что нейтроны, получающиеся при делении ядер урана-235, поглощаются за счет «резонансного» захвата атомами урана-238 с образованием урана-239, который в результате двух последовательных бета-распадов переходит в нептуний и плутоний. Критической массой обладают только уран-235 и плутоний. Те вещества, которые обладают критической массой, и являются ядерным горючим. Таковы были сведения, которыми физики обладали уже в начале 40-х годов.
Если создать такую конструкцию, при которой нажатием кнопки можно объединить два куска ядерного горючего, каждый из которых имеет массу меньше критической, а объединенная масса выше критической, то произойдет взрыв. На этом простом принципе и работает атомная бомба.
А как поступить, если мы хотим управлять ходом реакции? Ответ достаточно очевиден: надо создать систему, в которой кроме атомов горючего находились бы другие атомы, поглощающие нейтроны и, так сказать, выводящие их из строя. Вполне годятся кадмиевые стержни. Кадмий сильно поглощает нейтроны, и, создав конструкцию, состоящую из стержней ядерного горючего и стержней кадмия, вдвигая и выдвигая их из тела ядерного реактора, или котла (такое название было дано этой системе), можно начать ядерную цепную реакцию, сделав коэффициент размножения нейтронов чуть больше единицы, а затем, доведя выделение тепла до желательного уровня, вдвинуть кадмиевые стержни так, чтобы коэффициент размножения стал в точности равным единице.
Глава 6 Энергия вокруг нас
ИСТОЧНИКИ ЭНЕРГИИ
В конечном счете вся энергия, которой мы можем распорядиться, приходит к нам от Солнца. В недрах нашего светила при температурах порядка миллионов кельвинов проходят реакции между атомными ядрами. Идет неуправляемый термоядерный синтез.
Человек научился осуществлять подобные реакции, сопровождающиеся баснословным выделением энергии в земных условиях. Это водородная бомба. Ведутся работы по созданию управляемого термоядерного синтеза, о котором у нас пойдет речь ниже.
Сейчас этими вводными фразами мы оправдываем то, что именно после разговора о строении ядер естественно перейти к беседе об источниках энергии на Земле.
В земных условиях мы можем добыть энергию тремя путями. Во-первых, извлечь ее за счет топлива — химического или ядерного. Для этой цели требуется создать цепную реакцию, в ходе которой происходило бы воссоединение или разрушение молекул или атомных ядер. Химическое топливо, имеющее пока что практическое значение, — это уголь, нефть, природный газ. Ядерное топливо — это уран и торий (разлом частиц) и легкие элементы — прежде всего водород (воссоединение частиц).
Второй путь — это превращение кинетической энергии в работу. Можно заставить производить работу водяные потоки. Гидроэнергия — «белый уголь» — становится важнейшим источником энергии, если заставить воду падать с большой высоты — построить плотину или использовать естественные водопады, такие, как Ниагарский. Этот же путь превращения энергии в работу заставляет вращаться крылья ветряных мельниц.
Мы увидим, что к воздушным потокам — «голубому углю» — надо отнестись со всей серьезностью. Ветряные мельницы возрождаются на новом техническом уровне и внесут заметную лепту в энергетическую кассу. К этой же категории источников энергии относится использование энергии приливных волн.
Законы термодинамики подсказывают нам и третье решение энергетической проблемы. В принципе всегда возможно построить двигатель, который использует разности температур. Как мы знаем, поток тепла, переходя от нагретого тела к холодному, может быть частично превращен в механическую работу. С разностями температуры мы встречаемся как в земной коре и в Мировом океане, так и в атмосфере. Углубляясь в земные недра, мы убедимся в том, что в любом месте земного шара наблюдается повышение температуры.
Все эти три возможности (еще раз повторим) возникают благодаря приходу на нашу планету излучения Солнца. Земля получает ничтожную долю энергии, которую несут солнечные лучи. Но и эта крошечная часть колоссальна, и ее хватит землянам не только на удовлетворение обыденных нужд, но и на осуществление самых фантастических проектов.
Но солнечную энергию можно использовать и непосредственно. Ведь мы научились превращать энергию излучения в электрический ток с помощью фотоэлементов. А получение электрического тока является наиболее важным путем использования энергии для практических целей.
Конечно, во многих случаях и внутренняя энергия вещества, и энергия движения водяных и воздушных потоков могут использоваться непосредственно, минуя стадию превращения в электрический ток. Но, пожалуй, во всех случаях, кроме движения самолетов и ракет, целесообразно получить от первичного источника электрическую энергию на электростанциях, а уж ее заставить служить нашим целям. Значение электрической энергии увеличится еще больше, когда мы научимся изготовлять легкие, маленькие и емкие аккумуляторы, которые заменят современные (тяжелые и малоемкие), стоящие в автомобилях.
Прежде чем перейти к конкретному обсуждению разных источников энергии, обратим внимание читателя еще раз на две важные классификации источников.
Прежде всего, важная граница раздела проходит между топливом и энергией Солнца, белого и голубого углей. В первом случае мы тратим безвозвратно запасы земных богатств. Что же касается Солнца, воздуха и воды, то они — даровые источники энергии. Даровые в том смысле, что использование их энергии не влечет за собой уменьшения каких бы то ни было земных ценностей. Работа ветряков не уменьшает количества воздуха на земном шаре, работа гидроэлектростанций не уменьшает глубины рек, не используются запасы земных веществ и при работе солнечных машин.
И еще одна проблема. Необходимо заботиться об охране окружающей нас флоры и фауны — это задача, важность которой невозможно переоценить. Сжигание топлива обладает не только тем недостатком, что обедняет Землю, оно еще вдобавок засоряет почву, воду и воздух огромным количеством вредных отбросов. И с гидроэлектростанциями в этом отношении дело обстоит не вполне благополучно. Изменение водного режима рек влияет на климат и губит существенную часть рыбного населения Земли.
Без всякого сомнения, оптимальным способом добычи энергии является прямое использование солнечного излучения.
После этих общих слов перейдем к более детальному обсуждению возможностей использования энергии в земных условиях и дадим читателю представление о числах, которые фигурируют в справочниках по энергетике.
Начнем с характеристики солнечной энергии. К границе атмосферы на каждый квадратный метр приходит энергия средней мощности около 1,4 кВт (если пересчитать эту величину для времени, равного 1 году, то получим около 1010 Дж энергии); такое количество тепла дают сотни килограммов угля. Сколько же тепла получает от Солнца весь земной шар? Подсчитав площадь Земли и учитывая неравномерное освещение солнечными лучами земной поверхности, получим около 1014 кВт. Это в 100 тысяч раз больше энергии, которую получают от всех источников энергии на Земле все фабрики, заводы, электростанции, автомобильные и самолетные моторы, короче — в 100 тысяч раз больше мощности энергии, потребляемой всем населением земного шара (порядка миллиарда киловатт).
До сего времени солнечная энергия используется совершенно незначительно. Рассуждали так: правда, подсчет наш дал огромную цифру, но ведь это количество энергии попадает во все места земной поверхности — и на склоны недоступных гор, и на поверхность океанов, занимающую бóльшую часть земной поверхности, и на пески безлюдных пустынь. Кроме того, совсем не так уж велико количество энергии, приходящейся на небольшую площадь. А ведь вряд ли целесообразно создавать приемники энергии, простирающиеся на квадратные километры. Наконец, заниматься превращением солнечной энергии в тепло имеет смысл в тех местностях, в которых много солнечных дней.
Энергетический голод и огромные успехи в производстве полупроводниковых фотоэлементов полностью изменили психологию энергетиков. Создано множество проектов и опытных установок, с помощью которых солнечные лучи фокусируются на тысячах (а в будущем — на миллионах и миллиардах) фотоэлементов. Техников не пугают пасмурные дни и поглощение лучей атмосферой. Нет сомнения, что прямому использованию солнечной энергии принадлежит большое будущее.
Так же точно изменилось наше отношение к голубому углю. Еще каких-нибудь двадцать лет назад говорилось: не будем возлагать больших надежд на ветер как источник энергии. Источник этот имеет тот же недостаток, что и солнечная энергия: количество энергии, приходящейся на единицу площади, относительно невелико; лопасти ветряной турбины, если создать такую для производства энергии в заводских масштабах, должны были бы достигнуть практически неосуществимых размеров. Не менее существенным недостатком является непостоянство силы ветра. Поэтому энергию ветра стоит использовать лишь в маленьких двигателях — «ветряках». Во время ветра они дают электроэнергию сельскохозяйственным машинам, освещают дома. Если образуется излишек энергии, он запасается в аккумуляторах. Эти излишки можно использовать в затишье. Конечно, полагаться на ветряк нельзя, — он может играть лишь роль вспомогательного двигателя.
Сегодня рассуждения инженеров, занятых проблемой борьбы с энергетическим голодом, совсем иные. Проекты электростанций, состоящих из тысяч регулярно расположенных «мельниц» с огромными крыльями, близки к осуществлению. Использование голубого, угля также внесет весомый вклад в книгу прихода энергии, нужной человечеству.
Даровым источником энергии является движущаяся вода — приливная волна океанов, непрерывно наступающая на сушу, и потоки речных вод, текущих к морям и океанам. Выработка электроэнергии на ГЭС в 1969 г. в СССР составила 115,2 млрд. кВт ч, в США — 253,3 млрд. кВт. ч, но водные ресурсы используются у нас только на 10,5 %, а в США на 37 %.
Приведенные цифры выработки электроэнергии на ГЭС весьма внушительны, но все-таки, если бы мы лишились угля, нефти и других источников энергии и перешли бы только на белый уголь — энергию рек, то пришлось бы уменьшить потребление энергии на земном шаре, даже сли бы на всех реках были построены все технически возможные гидроэлектростанции.
Ну, а приливная волна? Ее энергия весьма значительна, хотя примерно в десять раз меньше энергии рек. Увы, эта энергия пока что используется лишь в самой незначительной степени, пульсирующий характер приливов затрудняет ее использование. Однако советские и французские инженеры нашли практические пути к преодолению этой трудности. Теперь приливная электростанция обеспечивает выдачу гарантированной мощности в часы максимального потребления. Во Франции построена ПЭС на реке Ране, а в СССР — станция в Кислой Губе в районе Мурманска. Эта последняя послужит опытной моделью для сооружения проектируемых мощных (около 10 ГВт) приливных электростанций в заливах Белого моря.
Вода в океанах на больших глубинах имеет температуру, отличающуюся от температуры поверхностных слоев на 10–20 °C. Значит, можно построить тепловую машину, нагревателем которой в средних широтах явился бы верхний слой воды, а холодильником — глубинный. К.п.д. такой машины будет 1–2 %. Но это, конечно, тоже очень неконцентрированный источник энергии.
К числу даровых источников энергии относится геотермическая энергия. Не будем говорить о странах, богатых гейзерами. Они встречаются редко. Там, где они есть, их тепло используется для промышленных целей. Однако не следует забывать, что почти в любом месте земного шара, углубившись на 2–3 км, мы встретимся с температурами порядка 150–200 °C. Принцип создания геотермической электростанции самоочевиден. Надо пробурить два канала. В один из них будет поступать холодная вода, а из другого будет откачиваться горячая вода (рис. 6.1).
ТОПЛИВО
Все описанные до сих пор источники энергии обладают большими преимуществами по сравнению с топливом. Топливо сжигается. Использование энергии каменного угля, нефти, дерева — это невозвратимое уничтожение земных ценностей.
Каковы же запасы топлива на земном шаре? К обычному топливу, т. е. такому, которое горит от поднесенного огня, относятся уголь, нефть и подземный газ. Их запасы на земном шаре крайне малы. При современном расходовании нефти ее разведанные запасы придут к концу уже к началу следующего тысячелетия, то же относится и к газу. Запасов каменного угля несколько больше. Количество угля на Земле выражают цифрой в десять тысяч миллиардов тонн. Килограмм угля при сгорании дает несколько тысяч килокалорий тепла. (Разумеется, топливо бывает самого разного качества. Приведенная цифра — это своего рода единица измерения, как говорят единица условного топлива, которой пользуются при сопоставлении источников энергии разного происхождения.) Таким образом, общие энергетические запасы угля измеряются цифрой порядка 1020 ккал. Это примерно в тысячу раз больше годового потребления энергии.
Запас энергии на тысячу лет надо признать очень малым. Тысяча лет — это много только по сравнению с длительностью человеческой. жизни, а человеческая жизнь — ничтожное мгновение по сравнению с жизнью земного шара и с временем существования цивилизованного мира. Кроме того, потребление энергии на душу населения непрерывно растет. Поэтому, если бы запасы горючего сводились к нефти и углю, то положение дел на Земле с энергетическими запасами следовало бы считать катастрофическим.
Но разве обязательно ограничить химическое топливо теми веществами, которые мы находим в природе? Конечно, нет. В ряде случаев может оказаться, что синтетическое газообразное и жидкое топливо с выгодой заменяет нефть и газ.
В последние годы особое внимание уделяется промышленному производству водорода. Как горючее водород обладает многими достоинствами. Его можно добывать в неограниченных количествах разными путями. Он имеется всюду, так что нет проблемы транспортировки. Водород легко очищается от нежелательных примесей. В ряде случаев окажется более выгодным непосредственное использование тепла сгорания водорода. Можно миновать стадию превращения в электроэнергию.
Три основных процесса получения водорода представляются в настоящее время рентабельными: электролитический способ, термохимическое разложение и, Наконец, облучение водородсодержащих соединений нейтронами, ультрафиолетом и т. д. Оказывается экономически выгодным и получение водорода из угля и нефти в ядерных реакторах. В этих случаях можно предусмотреть передачу водорода к месту потребления по трубам, как это делается сейчас в отношении подземного газа.
Закончим на этом наш краткий обзор химических топлив и зададим вопрос: как обстоит дело с ядерным горючим? Каковы его запасы на Земле? Ведь его нужно так мало. Один килограмм ядерного горючего дает в 2,5 миллиона раз больше энергии, чем такое же количество угля.
Примерные расчеты показывают, что запасы потенциального ядерного горючего (из дальнейшего читатель поймет, почему мы воспользовались этим прилагательным) могут быть представлены следующими величинами: около 2 миллионов тонн урана и 4 миллиона тонн тория. Это вещества, из которых мы умеем сегодня извлекать энергию в атомных реакторах методом расщепления ядер. Прибавятся ли к ним другие вещества? Что же, это нельзя считать исключенным. Число ядерных реакций, дающих энергию, огромно. Вопрос лишь в том, как сделать реакцию цепной.
Пока поведем речь о том, что мы умеем делать сейчас. Как это следует из предыдущей главы, существует лишь одно-единственное встречающееся в природе вещество, которое является ядерным горючим. Это изотоп ypaн-235. Уран, который добывают на рудниках, содержит 99,3 % урана-238 и всего лишь 0,7 % урана-235.
На первый взгляд может показаться, что самая простая идея — это выделить нужный нам изотоп и создать, реакторы, состоящие из кусков или стержней этого вещества, вводя в реакционный объем контрольные стержни, поглощающие нейтроны, для управления ядерной реакцией.
Прежде всего следует отметить, что поглощать нейтроны, не давать им возможности участвовать в цепной реакции, невыгодно, если мы заботимся о мощности установки, т. е. хотим от единицы массы ядерного горючего получат как можно больше энергии в одну секунду. А вот замедлить нейтроны до тепловых скоростей — превратить «быстрые» нейтроны, образующиеся при развале ядра, в «медленные» — вот это весьма полезно для повышения эффективности работы котла, ибо ядра урана-235 поглощают медленные нейтроны с много большей вероятностью.
Если не говорить об опытных конструкциях, не вышедших за пределы лаборатории, то можно сказать, что в качестве замедлителя использовалась либо тяжелая вода, либо обычная вода. Тяжелая вода хороша тем, что она совсем не поглощает нейтронов. Но замедляет нейтроны она значительно хуже обычной.
Итак, самый простой, казалось бы, путь состоит в выделении изотопа уран-235. Мы уже говорили, что осуществление такого выделения будет стоить огромных денег. Ведь химические способы не годятся: речь идет о веществах, тождественных по своим химическим свойствам.
Наиболее рентабельным полагают сейчас метод центрифугирования. Перед тем как приступить к этой операции, надо получить какое-либо газообразное соединение урана. Единственным таким соединением, находящимся в газообразном состоянии при обычных температурах, является гексафлуорид урана. Различие в массах молекул газа, содержащих изотопы уран-238 и уран-235, столь незначительно, что лучшая центрифуга обогащает газ более легкими молекулами всего лишь на 12 %. Для того чтобы получить уран, содержащий 3 % изотопа уран-235 (такое топливо уже удобно использовать в ядерном реакторе), процесс надо повторить 13 раз. Ясно, что получение чистого изотопа уран-235 нельзя рассматривать как верное решение инженерной задачи.
Но имеется и другое, пожалуй, еще более важное соображение. Без урана-235 мы не превратим основную массу урана, а также торий в ядерное горючее. Вот поэтому мы и назвали их потенциальным горючим. Что же касается самого изотопа уран-235, то это топливо оттянет момент наступления энергетического голода на какие-нибудь сотни лет. Следовательно, если полагать, что человечество должно долгие столетия пользоваться ядерным горючим, то надо пойти другим путем.
Ядерное горючее можно производить в реакторе! В реакторе мы можем производить, во-первых, плутоний-239, который получается из урана-238, и, во-вторых, уран-233, получающийся из тория-232. Но начать дело без урана-235 никак нельзя.
Реакторы, производящие энергию и одновременно создающие новое горючее, называются бридерными. Можно добиться такой ситуации, когда реактор будет производись нового топлива больше, чем он потребляет, т. е., как говорят, сделать коэффициент воспроизведения большим единицы.
Итак, технически осуществимые пути использования всех запасов урана и тория нам известны. Следовательно, топлива, которым мы умеем пользоваться, хватит, по самым скромным оценкам, на многие тысячи лет.
И всё же… Приобщение к топливу урана и тория не решает принципиальную задачу освобождения человечества от энергетического голода — запасы минералов в земной коре ограничены.
Другое дело термоядерная реакция. Если удастся осуществить управляемый синтез легких ядер, добиться того, чтобы реакция поддерживала себя, то тогда мы действительно сможем сказать, что решили энергетическую проблему. Сколь реалистично решение этой задачи? В самое последнее время физики научились получать водородную плазму, находящуюся при температуре около 60 млн. кельвинов. Термоядерная реакция происходит при этой температуре. Но как сделать эту реакцию самоподдерживающейся, как осуществить термоядерный реактор — этого мы еще не знаем.
В Мировом океане запасено столько термоядерной энергии, что ее хватит для покрытия всех энергетических потребностей человечества в течение времени, превышающего возраст Солнечной системы. Вот уж действительно безграничный источник энергии.
Разговор о топливе окончен. Теперь перейдем к рассмотрению устройств, с помощью которых топливо заставляют работать.
ЭЛЕКТРОСТАНЦИИ
Разумеется, можно привести много примеров, когда непосредственное использование энергии не связано с получением электрического тока. Горит газ на кухне вашей квартиры, вздымается в небо ракета, движущаяся за счет отдачи продуктов сгорания топлива, да и старинные паровые двигатели кое-где находят себе применение. В ряде случаев целесообразно непосредственно превращать в движение и энергию, которую дают такие даровые источники, как ветер.
Но в подавляющем большинстве случаев нам нужен электрический ток. Нужен для того, чтобы давать свет, необходим для питания электрических двигателей, для создания электрической тяги, для обеспечения работы электросварочных и нагревательных печей, для зарядки аккумуляторов… И во всяком случае сегодня мы не мыслим, себе иной передачи энергии на расстоянии, как при помощи электрического тока. Поэтому, вероятно, не будет преувеличением сказать, что главной героиней техники по-прежнему остается электростанция.
По сей день существуют два основных промышленных способа приведения в движение вращающихся частей электрических машин — машин, производящих ток. Если эту работу выполняет энергия падающей воды, то мы говорим о гидроэлектростанциях (ГЭС); если движущей силой является давление пара на лопатки турбины, то мы говорим о теплоэлектростанциях (ТЭС).
Из класса ТЭС особо выделяют атомные электростанции (АЭС), хотя, по сути дела, они отличаются от обычных ТЭС лишь тем, что работают на другом горючем. Однако в обоих случаях мы получаем тепло, которое используем для получения пара.
Современный житель часто сталкивается с названием ТЭЦ — теплоэлектроцентраль или теплофикационные электростанции. ТЭЦ предназначены для снабжения потребителей не только электрической, но в первую очередь тепловой энергией в виде водяного пара или горячей воды.
Энергия падающей воды использовалась человеком с незапамятных времен. Водяное колесо древней мельницы является прообразом современной гидротурбины. Ударяясь в лопатку колеса, струя воды отдает ей часть своей кинетической энергии. Лопатка приходит в движение, колесо начинает вращаться.
Расположить лопатки колеса так, чтобы получить максимальный к. п. д., не так-то просто. Эту инженерную задачу решают специалисты по-разному в зависимости от условий падения воды. Разумеется, турбина будет (работать тем успешней, чем с большей высоты (а высоты эти достигают 300 м) обрушится на нее мощный водяной поток. Выполненные на высоком уровне современного инженерного искусства, гидравлические турбины проектируются на мощности, превышающие 500 МВт. Поскольку эти мощности создаются при довольно малых оборотах (порядка 100 в минуту), строящиеся сейчас гидравлические турбины поражают размерами и весом.
По направлению потока в рабочем колесе гидротурбины делятся на осевые и радиально-осевые. В Советском Союзе успешно работают гидротурбины радиально-осевого типа мощностью 508 МВт с диаметром рабочего колеса 7,5 м.
На гидростанциях вырабатывается сейчас самая дешевая электроэнергия, но их строительство обходится в несколько раз дороже тепловых станций и сооружаются они более длительное время. На гидростанциях установлены гидрогенераторы, которые приводятся во вращение гидравлической турбиной. Гидрогенераторы — очень большие синхронные машины, чаще всего с вертикальным валом. Диаметр ротора такой машины в 7—10 раз превышает его длину и в крупнейших машинах превосходит 15 м. Это необходимо для того, чтобы машина могла устойчиво работать при изменениях скорости гидравлической' турбины, приводящей ее во вращение. Ротор гидрогенератора имеет большое число явно выраженных полюсов. Так, генераторы Днепровской ГЭС имеют 72 полюса. Для питания обмотки полюсов постоянным током используется специальный генератор постоянного тока — возбудитель. Частота вращения гидрогенераторов невелика — 80—250 об/мин.
Гидрогенератор Красноярской ГЭС (мощностью 500 МВт) имеет частоту вращения 93,8 об/мин, диаметр его ротора 16 м, а масса 1640 т. Для Саяно-Шушенской ГЭС проектируется генератор на 650 МВт.
Как я уже говорил, использование гидроэнергии не обходится даром для окружающей среды. Но тем не менее преимущество ГЭС перед тепловыми станциями не подлежит сомнению. Прежде всего, ГЭС не потребляет топлива, запасы которого ничтожны. Но у тепловых электростанций имеется и еще один крупнейший недостаток. При превращении энергии топлива в электрическую, неизбежно значительная часть энергии уходит впустую.
Тем не менее что-нибудь около 80 % электроэнергии вырабатывается на тепловых станциях при помощи турбогенераторов, в которых силой является давление пара.
Для того чтобы к. п. д. генератора был большим, необходимо елико возможно увеличить температуру пара. Понятно, что этого можно достигнуть, лишь одновременно увеличивая давление. На современных ТЭС мощностью 200–300 МВт в турбины пускается пар, имеющий температуру 565 °C и давление 24 МПа.
Но почему надо стремиться к высоким температурам? Дело заключается в следующем. В паровой турбине мы в конечном счете используем то же самое явление, которое заставляет подпрыгивать неплотно пригнанную крышку чайника, когда в нем закипает вода. Иными словами, в паровой турбине происходит превращение тепловой энергий в механическую, а затем уже механической в электрическую. Так вот, при первом превращении (это можно строго доказать) теряется энергии не меньше, чем доля, равная отношению температуры окружающей среды к температуре пара (в кельвинах).
Весьма печально, что в современных устройствах для извлечения энергии приходится проходить через «тепловую ступень». Такой переход всегда связан с огромной потерей энергии, и идеальной электростанцией будущего станет такое предприятие, где энергия любого происхождения будет превращаться в электрическую энергию непосредственно. Пока эта важнейшая проблема не решена, нам остается лишь одно: стремиться к наиболее высоким температурам пара, газа или плазмы.
Как это ни сложно, но все же удается добиться на тепловых электростанциях к. п. д. около 40 %. Паротурбинный генератор — это электрическая машина с горизонтальным валом. Ротор изготовляется вместе с концами вала в виде одной поковки из специальной турбороторной стали, так как механические напряжения в нем из-за большой частоты вращения (3000 об/мин) достигают предельно допустимых для современных материалов значений. По той же причине ротор не имеет явно выраженных полюсов. На части его цилиндрической поверхности имеются пазы, в которые укладывается обмотка возбуждения. В пазах статора уложена трехфазная обмотка переменного тока.
По причине больших механических напряжений диаметр poтopa ограничен, поэтому для получения достаточной мощности приходится машину вытягивать в длину.
Первые отечественные турбогенераторы мощностью 500 кВт шли изготовлены в Ленинграде на заводе «Электросила» в 1925 г. А в 1964 г. «Электросила» выпустила турбогенератор мощностью, превышающей в 1000 раз свой первенец — 500 000 кВт.
Стремление получить большую мощность от одной машины без увеличения и без того уже огромных размеров привело к очень значительному усложнению. Так, для уменьшения потерь в обмотке статора ее выполняют из полых медных проводников, внутри которых пропускают воду. Обмотка возбуждения охлаждается водородом под давлением около 4 атм. Применение водорода, имеющего в 14 раз меньшую плотность, чем воздух, позволило увеличить мощность турбогенераторов на 15–20 %.
В Плане развития народного хозяйства на 1981–1985 гг. перед электротехнической промышленностью стоит задача освоить производство турбогенераторов мощностью 1–1,5 млн. кВт для тепловых и атомных электростанций.
Одна из наиболее интересных в мире электростанций создана в Советском Союзе. Называется она У-25 и дает в электросеть около 7000 кВт электроэнергии. Это самая большая в мире установка для генерирования электроэнергии методами магнитогидродинамики; сокращенно такие установки называют МГД. МГД-генератор не имеет вращающихся частей.
Идея, лежащая в основе действия этого интересного генератора, крайне проста. Поток ионов, обладающих значительной кинетической энергией (плазменная струя), проходит через магнитное поле наперерез линиям магнитной индукции. На ионы действует сила Лоренца. Напряженность индуцированного электрического поля, как нам известно, пропорциональна скорости ионного потока и величине магнитной индукции. Направлена э. д. с. перпендикулярно движению ионов. В этом направлении и возникает электрический ток, который замыкается через внешнюю нагрузку. Электроды, принимающие ток, находятся в непосредственном контакте с плазмой.
Электрическая энергия возникает за счет падения энергии плазменной струи. МГД-генератор позволяет довести к. п. д. электростанции до 60 % и более.
Критическим фактором при получении дешевой энергии от МГД является магнитное поле в канале. Это поле должно быть очень сильном. Обычный электромагнит с медной катушкой может создать такое поле, но он будет большим, сложным по конструкции и дорогостоящим; кроме того, он сам будет потреблять много электроэнергии. В связи с этим обратились к новой концепции конструирования магнитов со сверхпроводящей обмоткой. Такой магнит может создавать необходимое магнитное поле при небольшой затрате энергии и незначительном нагреве. Как показывают расчеты, большие затраты по получению температур, близких к абсолютному нулю, оправдывают себя.
Из беглого обзора, сделанного на предшествующих страницах, мы видим, что традиционные способы увеличения производства анергии еще не исчерпаны. Однако вряд ли можно признать, что человечество долгое время будет следовать этому пути.
Не говоря уже о том, что запасы топлива и возможности использования гидроэнергии близятся к концу, нельзя забывать о значительном влиянии на окружающую нас среду строительства новых электростанций. Экологи предупреждают о необходимости весьма осторожно относиться к вмешательству в жизнь рек. Обращают внимание энергетиков на огромные количества золы, которые выбрасываются в атмосферу при сгорании топлива. За год земная атмосфера принимает 150 млн. тонн золы, около 100 млн. тонн серы. Особенно тревожно увеличение в атмосфере количества углекислого газа. Каждый год оно возрастает на 20 млрд. тонн. За последние 100 лет содержание углекислого газа в атмосфере возросло на 14 %.
Имеются две причины этого роста: разрушение растительности на Земле и, самое главное, выбрасывание в атмосферу «газовой золы», образующейся при горении обычного топлива. Этот непрекращающийся рост может привести к пагубным последствиям, из которых наиболее важное — возрастание температуры атмосферы на 1,5–3 Кельвина, казалось бы, небольшое повышение температуры! Однако оно может привести к необратимому плавлению льдов, находящихся на полюсах. Климатологи полагают, что предельно допустимое дальнейшее возрастание количества углекислого газа в атмосфере не Должно превзойти нескольких десятков процентов.
ЯДЕРНЫЕ РЕАКТОРЫ
Как мы уже сказали, атомная электростанция относится к классу ТЭС. Отличие состоит в способе создания водяного пара, который направляется на лопатки турбины. С полным основанием можно термин «ядерный реактор» заменить словами «ядерный котел», подчеркивая этим родство, способов получения энергии.
Ядерному реактору, обычно придают форму цилиндрического здания. Стенки его должны быть очень толстыми и сделаны из материалов, поглощающих нейтроны и гамма-излучение. Реактор, который дает что-нибудь около 1000 МВт электрической энергии, в зависимости от используемого топлива, метода замедления нейтронов, способа отвода тепла может иметь различные размеры. Но во всех случаях эти размеры внушительные. Высота может достигать высоты 5—10-этажного дома, а диаметр будет порядка десяти метров.
Ядерная энергетика начала развиваться сразу же после окончания второй мировой войны. В Советском Союзе эти важнейшие исследования возглавил замечательный ученый и организатор Игорь Васильевич Курчатов.
ИГОРЬ ВАСИЛЬЕВИЧ КУРЧАТОВ (1903–1960) — видный советский физик, замечательный организатор, возглавлявший работу по разработке атомной проблемы в Советском Союзе. Начал свою научную деятельность в области физики твердого тела, создал учение о сегнетоэлектриках. В начале 30-х годов занялся исследованиями в области физики атомного, ядра. Под его руководством проведены важные работы в области изучения ядерной изомерии, резонансного поглощения нейтронов, искусственной радиоактивности.
И у нас, и за границей были испробованы самые различные конструкции. Прежде всего решается вопрос об изотопном составе используемого урана или другого ядерного горючего. Далее инженер должен решить, в каком виде он желает использовать горючее: в виде раствора солей урана или в виде твердых кусков. Твердому горючему элементу может быть придана различная форма. Можно работать с брусками, но более подходящими являются длинные стержни. Существенную роль играет геометрия расположения топливных элементов. Инженерный расчет поможет найти наиболее целесообразное расположение контрольных стержней, поглощающих нейтроны. Их перемещение (конечно, автоматическое) должно обеспечить нужное значение коэффициента размножения нейтронов.
Различие в поведении медленных (тепловых) нейтронов и быстрых нейтронов позволяет разбить типы, реакторов на две категории, а именно реакторы с замедлителем нейтронов и бридерные реакторы.
Реактор, в котором предусмотрено замедление нейтронов, может работать на природном уране. Количество замедлителя должно быть таким, чтобы не дать возможность значительному числу нейтронов поглощаться ядрами урана-238. А ведь этих ядер примерно в 140 раз больше, чем ядер урана-235. Если количество замедлителя будет малым, то нейтроны не будут успевать уменьшить свою скорость до тепловой, поглотятся ядрами урана-238 и цепная реакция не сможет продолжаться. Реактор, работающий на природном уране или уране, незначительно обогащенном ураном-235, будет все же создавать новое горючее — плутоний. Но его будет образовываться гораздо меньше, чем «сгорающих» ядер.
Пока что на атомных электростанциях используют реакторы на тепловых нейтронах. Наиболее часто применяют четыре типа реакторов: водо-водяные с обычной водой в качестве замедлителя и теплоносителя; графито-водяные с водяным теплоносителем и графитовым замедлителем; реакторы, в которых замедлителем является тяжелая вода, а теплоносителем обычная вода, и, наконец, графито-газовые реакторы.
Причина того, что специалисты в области атомной энергетики сосредоточили свое внимание на реакторах, работающих на тепловых нейтронах, видимо в том, что обогащение урана изотопом 235 является трудной задачей. Но надо помнить замечание, сделанное нами выше: используя в качестве горючего один лишь изотоп уран-235, мы лишаем себя возможности пустить в дело огромные запасы потенциального ядерного горючего.
В настоящее время намечается тенденция к переходу на ядерные реакторы другого типа, работающие на сильно обогащенном топливе и не использующие замедлителя нейтронов.
Допустим, что в котле имеется смесь, в которой на одну часть урана-235 приходится одна часть урана-238. В этом случае число нейтронов, выбывающих из цепной реакции благодаря захвату ураном-238, может быть бóльшим числа нейтронов, расщепляющих ядра урана-235 и продолжающих цепную реакцию. Такой реактор и будет бридерным. В зависимости от геометрии расположения стержней или кирпичей ядерного активного, и потенциального горючего, можно создать бридерный реактор с самым различным процентным отношением этих двух видов топлива и с разным коэффициентом воспроизведения.
Для того чтобы читатель имел представление о параметрах ядерных реакторов, приведем, два примера.
Рис. 6.2 дает общее представление об устройстве ядерного реактора, который в настоящее время используется на американских подводных лодках.
Охладителем является обычная вода. Поскольку обычная вода захватывает нейтроны примерно в 600 раз более эффективно, чем тяжелая вода, то такой реактор может работать только на уране-238, обогащенном ураном-235. Вместо природной доли 0,72 % в топливе этих реакторов содержится от 1 до 4 % урана-235. Реактор, способный давать 1100 МВт электрической энергий, имеет диаметр около 5 м, высоту 15 м и толщину стенок, около 30 см (5-этажный дом!). Если в такой реактор загрузить 80 т окиси урана с содержанием 3,2 % урана-235, то он будет работать 10–12 месяцев (после чего надо менять стержни). Вода в реакторе нагревается да 320 °C. Она циркулирует под давлением около 300 атм. Горячая вода превращается в пар и подается на лопасти турбины.
Остановимся теперь вкратце на французском проекте мощного бридерного реактора, получившем название Суперфеникс.
Предполагается в качестве топлива использовать смесь плутония-239 и урана-238. Замедлитель не будет использоваться, так что нейтроны не теряют скорости от момента своего рождения во время распада ядра до встречи с другим атомным ядром горючего материала.
То, что реактор работает на быстрых нейтронах, приводит к большой компактности. Ядро реактора не превосходит 10 м3. Таким образом, может выделяться большое количество тепла в единице объема.
Отвод тепла нельзя производить водой, поскольку она замедляет нейтроны. Для этой цели можно использовать жидкий натрий. Натрий плавится при температуре 98 °C и кипит при 882 °C при атмосферном давлении. Температура жидкого натрия по техническим причинам не должна быть выше 550 °C. Поэтому нет необходимости в повышении давления охлаждающей жидкости, к чему прибегают в тех случаях, когда охладителем является вода.
Размеры Суперфеникса такие: внутренний диаметр 64 м, высота около 80 м. Солидное 20-этажное здание! Ядро реактора представляет собой гексагональную призму, собранную (как пачка карандашей) из тонких стержней длиной 5,4 м. Стержни горючего материала перемежаются с контрольными стержнями.
У нас нет места (да и нет необходимости в книге по физике) описывать, каким образом организовано охлаждение ядра реактора. Достаточно сказать, что это делается в три приема. Первичный трубопровод — натриевый, он забирает тепло от реактора и отдает его в котел, откуда тепло передается второму, также натриевому трубопроводу, а затем третьему, по которому циркулирует водно-паровая смесь. Дальше — обычный путь к паровой турбине.
Расчеты показывают, что установка должна дать 3000 МВт тепловой мощности и 1240 МВт электрической.
Не могу не подчеркнуть еще раз, что необходимость превращать ядерную энергию в электрическую, проходя через тепловую стадию, оставляет чувство большой досады. Все равно, как если бы мы установили автомобильный двигатель с соответствующими приводами на обычной телеге. Но пока нет никакой идеи, как можно миновать эту стадию, создающую, пожалуй, основные трудности в строительстве атомных электростанций. К общему недостатку всех ТЭС здесь добавляется необходимость введения промежуточных трубопроводов. Ведь нужно исключить непозволительную радиоактивность пара, поступающего в турбину.
Приведем еще несколько данных для этого проекта. Максимальный поток нейтронов на 1 см2 в секунду должен равняться 6,2.1015. Коэффициент воспроизведения будет равен 1,24. Замена сгоревших элементов на новые должна производиться один раз в год. Быстрота потока жидкого натрия (техники говорят — массовый расход) 16,4 т/с (это в первичном трубопроводе). Выходящий перегретый пар будет выпускаться под давлением 18 МПа и при температуре 490 °C.
Скажем несколько слов о «золе» ядерного горючего. В результате деления ядер горючего возникает большое число радиоизотопов — этот процесс неуправляем; но мы имеем возможность получать любые изотопы, помещая в реактор какие-либо вещества. Поглощая нейтроны, они будут порождать новые атомы.
Разумеется, можно получать радиоизотопы и в ускорителях, подвергая материалы бомбардировке протонами или ядрами других элементов.
Число искусственных элементов, полученных к настоящему времени, весьма велико. Заполнились «пустые» места в таблице Менделеева: элементы с порядковыми номерами 61, 85 и 87 не имеют долгоживущих стабильных изотопов, и поэтому в природе их нет. Удалось и продлить таблицу Менделеева. Элементы с номером более высоким, чем 92, называются трансурановыми. Таблица Менделеева продлена до номера 105. Каждый трансурановый элемент получен в нескольких изотопических вариантах. Кроме новых химических элементов, изготовлено большое число радиоизотопов тех химических элементов, которые в своей стабильной форме встречаются в земной коре.
Ряд применений радиоизотопов известен уже много лет. Стерилизация продуктов гамма-лучами, дефектоскопия, создание генераторов электрической энергии, использующих электроны, возникающие при распаде… Список можно было бы продолжить.
Польза от радиоизотопов соизмерима, к сожалению, с хлопотами, которые они доставляют инженерам из-за необходимости защиты людей от радиоактивного излучения.
В золе ядерного горючего содержится 450 сортов атомов, среди них уран-237 и нептуний-239, которые превращаются в нептуний-237 и плутоний-239.
В отличие от угля или нефти, ядерное горючее не сгорает до конца. Ядерные реакторы работают в ряде случаев на обогащенном топливе с содержанием урана-235 между 2,5 и 3,5 %. Реактор прекращает в какой-то момент давать энергию, потому что в процессе распада образуется большое число изотопов, которые захватывают нейтроны и препятствуют продолжению реакции деления. При остановке реактора в ядерном горючем остается примерно 1 % урана-235 и несколько меньшее количество плутония-239.
Не приходится и говорить, что выбрасывать эту золу, содержащую столь значительное количество ценного горючего, крайне нецелесообразно. Поэтому с атомной электростанцией можно «спаять» большую химическую фабрику. Это предприятие должно быть полностью автоматизировано, поскольку приходится обрабатывать материалы, обладающие очень сильной радиоактивностью. Необходимость в серьезных мерах диктуется требованием оградить персонал от гамма-излучения.
На этих фабриках обработанные горючие элементы должны быть размельчены, растворены. Чистое горючее должно быть выделено (уран и плутоний) и возвращено для изготовления новых горючих элементов.
Остаются значительные количества бесполезного сильно радиоактивного раствора, которые надо где-то похоронить. При этом должна быть полная уверенность, что в течение многих столетий с местами захоронения не произойдет каких-либо драматических событий.
Специалисты настроены более или менее оптимистически. Полагают, что хранение бочек с радиоактивным раствором на глубинах порядка 1 км в специально подобранных для этого местах гарантирует 100 %-ную безопасность. Какие же места являются подходящими? Это должны решить геологи. Разумеется, подходят области, где исключается возможность землетрясений. Кроме того, нужно гарантировать отсутствие подземных водяных течений. Таким условиям удовлетворяют места соляных залежей. Нельзя просто сбрасывать бочки в километровый колодец. Для того чтобы обеспечить рассеяние тепла, выделяемого каждой бочкой, их надо размещать по крайней мере на расстоянии 10 м друг от друга.
ТЕРМОЯДЕРНАЯ ЭНЕРГИЯ
Как уже говорилось, химические и ядерные реакции очень схожи. Поскольку тепло выделяется не только при реакциях разложения, но зачастую и при соединении двух молекул в одну, то можно ожидать что и атомные ядра ведут себя подобным образом.
Ответить на вопрос, какие реакции слияния ядер могут оказаться энергетически выгодными, зная массы атомных ядер, совсем нетрудно.
Ядро дейтерия имеет массу 2,0146 а. е. м. Если два ядра сольются в одно; то образуется 4Не. Но его масса 4,0038, а не 4,0292. Избыток массы 0,0254 а. е. м. эквивалентен энергии, равной примерно 25 МэВ, или 4∙10-12 Дж. В 1 г дейтерия 0,3∙1024 атомов. Так что если бы такая реакция прошла, то 2 г дали бы 1018 Дж энергии!.. Оказывается, что наиболее перспективными являются реакции слияния тяжелых изотопов водорода — дейтерия, трития. Но и обычный водород тоже годится в качестве термоядерного горючего.
Термины, которыми мы пользуемся, носят совершенно условный характер. Во всех случаях речь идет о ядерной энергии. Но так уж сложилось, что энергию расщепления атомных ядер стали называть атомной энергией, а энергию слияния — термоядерной. Логики в этих терминах маловато. Но к ним привыкли.
«Термояд» (жаргонное слово) мог бы обеспечить землян энергией на миллионы лет, и при этом уровень воды в Мировом океане заметно бы не понизился. Так что можно считать термоядерную энергию даровой.
Но от идеи до ее осуществления дистанция огромная. Ведь все атомные ядра заряжены положительно. Ясно, чтобы подвести их на близкое расстояние друг к другу, нужна огромная энергия.
Откуда ее взять? Единственная возможность — это перевести вещество в состояние плазмы, т. е. оголить атомные ядра, а потом повысить температуру плазмы настолько, чтобы ядра начали соударяться (т. е. приблизились друг к другу на расстояние 10-13 см), презрев электрическое отталкивание.
Результат расчета крайне огорчителен. Предоставляю вам самим подсчитать величину энергии электростатического отталкивания по формуле е2/r, а затем прикинуть (для этого надо вспомнить формулу, которая связывает температуру с кинетической энергией любой частицы), каких температур надо достигнуть. Окажется, что десятков миллионов кельвинов.
Итак, надо создать высокотемпературную плазму. Есть два пути — один, по которому отряды физиков шагают уже более двух десятилетий, и другой, который лет на пятнадцать моложе.
Первый путь создания термоядерного реактора заключается в том, чтобы «загнать» плазму в «магнитную бутылку».
Если на газоразрядную трубку наложить магнитное поле, совпадающее по направлению с полем электрическим, то в такой трубке возникнет плазменный шнур. Заряженные частицы плазмы будут, как мы знаем, описывать спиральные траектории. Можно считать, что движение частиц складывается в один круговой поверхностный ток. Чем сильнее магнитное поле, тем меньше радиус плазменного шнура. Сила, которая действует на ток заряженных частиц со стороны магнитного поля, и есть причина образования шнура, не соприкасающегося со стенками газоразрядной трубки.
Таким образом, в принципе возможно создать плазму, которая «висит в воздухе».
Расчет показывает, что при начальном давлении водорода порядка 0,1 мм рт. ст., радиусе шнура 10 см и силе разрядного тока 500 000 А температура плазмы должна быть достаточной для того, чтобы начался термоядерный синтез.
На пути осуществления управляемой термоядерной реакции стоят очень большие трудности. Дело в том, что плазменный шнур по ряду причин оказывается весьма неустойчивым и расплывается через мгновения. Задача решается лишь в том случае, если удастся создать «магнитную бутыль» с «обратной связью»: требуется, чтобы случайные флуктуации, размывающие шнур, приводили к возникновению сил, которые стремились бы противодействовать размытию.
В середине 1978 г. группе американских физиков, работающих в Принстонском университете, удалось разогреть плазму до 60 млн. кельвинов. Этот успех был достигнут на разработанных в Советском Союзе «магнитных бутылях» (мы о них говорили в 3-й книге), получивших название «Токамак» (название происходит от сочетания трех слов: тороид, камера, магнит). Достигнутая температура достаточна для того, чтобы произошло слияние ядер дейтерия и трития.
Это большое достижение. Однако второй шаг еще не сделан. Не удается удержать горячую плазму достаточно длительное время. Пути технического осуществления этой задачи еще не очевидны. Создание управляемого термоядерного синтеза может оказаться задачей чрезвычайно дорогостоящей. Как бы то ни было, исследования в этой области продолжаются.
Ведутся работы по созданию управляемого термоядерного синтеза с помощью лазерного излучения. В настоящее время осуществлены лазеры с мощностью излучения около 1012 Вт, которая может быть, в виде световых импульсов длительностью 10-9—10-10 с, подана на вещество, которое мы хотим превратить в плазму. Естественно, что при падении света этой колоссальной мощности на твердое тело вещество мгновенно ионизуется и переходит в состояние плазмы. Надо добиться такого положения дел, чтобы создалась дейтериево-тритиевая плазма, имеющая температуру 108 К, и чтобы эта температура поддерживалась до тех пор, пока не начнется цепная реакция. Для осуществления этой задачу требуется создать плазму возможно большей плотности, чтобы увеличить число столкновений ядер.
На этих соображениях основывается схема реактора, показанная на рис. 6.3.
Твердый (замороженный) шарик, состоящий из изотопов водорода, падает в сосуде, откачанном до высокого вакуума. Когда шарик проходит через центр сосуда, включаются сильные лазеры, которые превращают твердое тело в плазму. Чтобы реактор заработал, надо добиться такой ситуации, при которой за промежуток времени между началом и концом реакции была бы выделена энергия, поддерживающая температуру, необходимую для протекания реакции. Расчеты показывают, что плотность плазмы должна быть выше плотности твердого тела в 103—104 раз, т. е. в 1 см3 должно находиться что-нибудь около 1026 частиц. Это сжатие лазер способен создать.
В принципе возможно получить нужную температуру и нужную плотность. Как будут разыгрываться события дальше? Энергия слияния ядер передается нейтронам, которые освобождаются при реакции. Эти нейтроны падают на литиевую оболочку сосуда. Литий через теплообменник передает энергию турбогенератору. Часть нейтронов реагирует с литием и производит тритий, который нужен как горючий материал.
Принцип прост. Но до его осуществления далеко, и притом вполне возможно встретиться с новыми неожиданными явлениями. Очень трудно пока что предсказать, какие требования надо предъявить к описанной установке, чтобы она превратилась в источник энергии. Исследователи уверены, что на пути создания столь большой мощности внутри малых объемов вещества будут открыты новые явления.
СОЛНЕЧНЫЕ ЛУЧИ
Превращение солнечной энергии в электрическую при помощи фотоэлементов известно уже давно. Однако до самого последнего времени никто не рассматривал возможности положить, это явление в основу действия электростанции. На первый взгляд такое предложение; может показаться дикой фантазией. Для того чтобы создать электростанцию мощностью 1000 МВт, надо настелить солнечные ячейки — так называют фотоэлементы, специально приспособленные для превращения солнечной энергии в электрическую, — на площадь 6 х 6 км2. И это в такой солнечной местности, как пустыня Сахара! A, скажем, в средней Европе, где солнечных дней не так уж много, площадь должна быть по крайней мере удвоена. Чистая фантазия, — воскликнет читатель; и в какую сумму обойдется такая электростанция!
Справедливое возражение. Но бросьте на другую чашу весов достоинства этого способа получения энергии. Мы не тратим никакого земного вещества и не загрязняем среду какими бы то ни было отходами. Не являются ли эти два довода столь сильными, чтобы заняться всерьез исследованием создания как можно более дешевых солнечных ячеек, а также способов оптимального размещения ячеек и фокусировки солнечных лучей? Многие исследователи убеждены не только в том, что проблема заслуживает серьезного внимания, но надеются, что именно на этом принципе и будут работать электростанции будущего. Так полагает и автор этой книги. Не исключено, что через несколько лет именно эту задачу назовут проблемой номер один.
Не преждевременен ли подобный оптимизм? Как обстоит дело сегодня? Прежде всего надо рассмотреть, какие солнечные ячейки может предложить промышленность уже сейчас.
Напомним рис. 6.4 принцип превращения солнечной энергии в электрический ток.
Ячейка состоит из полупроводникового р-n-слоя, зажатого между металлическими электродами. Солнечный свет создает свободные электроны и дырки, которые контактным напряжением отправляются в противоположные стороны и образуют ток.
Освоены три типа подобных ячеек. Гомоконтактные, в которых р-n-бисквит создается легированием кремния. Диффузионным процессом создается тонкий (0,3 мкм) n-слой и относительно толстый (300 мкм) р-слой. Гетероконтактные ячейки состоят из двух разных полупроводников. На металлическую подкладку напыляется n-слой сульфида кадмия толщиной 20–30 мкм, и химическими способами на его поверхности создается p-слой сернистой меди толщиной 0,5 мкм. Третий тип ячеек использует контактное напряжение между арсенидом галлия и металлом, разделенными тончайшей (0,002 мкм) пленкой диэлектрика.
Для оптимального использования энергии всего солнечного спектра подходят полупроводники с энергией связи электрона около 1,5 эВ. В принципе можно достичь к. п. д. солнечной ячейки 28 %.
Кремниевые гомоконтактные ячейки, которые обладают рядом технических преимуществ и изучены наиболее детально, дают к. п. д. от 11 до 15 %. Кремниевые солнечные ячейки производятся уже более двадцати лет. Материалом служит, кварцевый песок (окись кремния), из которого получают чистый кремний. Из него изготовляются монокристаллы толщиной 0,3 мм, имеющие форму круглой шайбы. В последние годы разработан процесс получения монокристаллической ленты. Хорошо освоена технология введения примесей, которая позволяет создавать в кремниевой шайбе p-слой. Для того чтобы солнечные лучи отражалась от кремния как можно меньше, поверхность покрывается тонкой пленкой окиси титана. При интенсивности света 100 мВт/см2 шайба создает напряжение 0,6 В. Плотность тока короткого замыкания равна 34 мА/см2. Различными способами можно собирать ячейки в батареи. Налажено производство кремниевых монокристаллических шайб диаметром 5–7,5 см. Их закрепляют между пластинами стекла. Соединяя их, можно собрать достаточно мощный источник тока.
Но возможна и разработка такого технологического процесса, при котором будут производиться ячейки много большей площади.
Главная причина, которая мешает в настоящее время использовать солнечные ячейки для промышленного получения энергии, — это дороговизна. Она вызывается необходимостью получения монокристаллической ленты высокого качества.
Возлагаются большие надежды на изготовление солнечных ячеек из тонких поликристаллических слоев. Такой процесс будет недорогим, но к.п.д. существенно понизится. Работа по поиску дешевых методов получения эффективных солнечных ячеек находится в самом разгаре.
Одновременно с этим исследователи ищут способы увеличить энергию, падающую на ячейку.
Созданы проекты электростанций, состоящих из 34 тысяч зеркал, которые отражают солнечные лучи и направляют их в приемник, находящийся на вершине башни высотой 300 м.
Если пользоваться концентрированной солнечной энергией, то надо позаботиться о том, чтобы на к. п. д. мало влияло повышение температуры ячейки. В этом отношении преимуществами обладают ячейки, изготовленные из арсенида галлия.
Рассматриваются предложения размещения электростанций, работающих за счет энергии солнечных, лучей, в горах на больших высотах, где обеспечены хорошие условия освещения Солнцем. В деталях разработан и проект создания электростанций, установленных на спутниках Земли.
Подобные космические электростанции могут получать энергию солнечных лучей без потерь и посылать ее в виде микроволн на Землю, где она будет превращаться в электроэнергию. На первый взгляд идея может показаться взятой из фантастического романа. И тем не менее инженеры серьезно относятся к проекту электростанций на спутнике размером 25x5 км3. На этой площади можно разместить 14 миллиардов фотоэлементов! Станция будет весить 100 000 т. Такая станция может дать энергии столько же, сколько десяток крупнейших атомных электростанций, т. е. что-то порядка 10 000 МВт.
Проекты разработаны в деталях, и их малые модели начинают испытываться.
Прошло всего лишь три года с момента выхода в свет первого издания этой книги. Однако рост внимания к нестандартным источникам энергии, тенденция современной техники освободиться от пользования источниками энергии, опасными или «грабящими» Земной шар, — явления, не подлежащие сомнению.
Закончу этот параграф выдержкой из репортажа с технической выставки в Японии, где демонстрировались различные модели «нестандартных» источников энергии («Литературная газета» от 29 июля 1981 r.):
«…Павильон, по форме напоминающий древнеегипетскую пирамиду. Стены из стеклянных блоков, оправленных в блестящие металлические рамы. Павильон сложен из 800 коллекторов солнечных лучей. Длина каждого коллектора 1820, ширина — 860 и толщина — 105 мм. Благодаря этим коллекторам солнце обогревало павильон площадью 4000 м2 и высотой с 5-этажный дом в марте и апреле, когда частенько выдавались холодные дни, а теперь, с наступлением лета, охлаждает залы и вдобавок производит за сутки 19 кг пищевого льда, используемого тут же в киосках с прохладительными напитками.
Соседний павильон не менее фантастичен по виду и столь же утилитарен по назначению. Разница лишь в том, что роль коллекторов солнечного тепла выполняют здесь не остекленные и наполненные водой блоки, а три тысячи вакуумных емкостей…
В одном из «солнечных павильонов» — сферическое зеркало. Его освещает мощный прожектор, имитирующий солнце. Собранное зеркалом тепло проходит несколько этапов превращения в электроэнергию, а она приводит в движение миниатюрный мотор. Строительство солнечных электростанций, работающих по такому принципу, начнется завтра, а сегодня проверяется, какой тип этих электростанций наиболее выгоден.
В окрестностях города Нио на острове Сикоку высится 69-метровая башня. На вершине — коллектор солнечных лучей, у подножия — генератор, вырабатывающий электричество. Рядом с башней — конкурирующая система. Она состоит из нескольких рядов параболических зеркал, каждое из которых самостоятельно концентрирует солнечные лучи. Собранная зеркалами энергия тоже направляется на генератор. В конце нынешнего года будет определено, какая система рентабельнее и, следовательно, пригоднее для нужд ближайшего будущего».
ЭНЕРГИЯ ВЕТРА
Воздушные массы земной атмосферы находятся в непрерывном движений. Циклоны, бури, постоянно дующие пассатные ветры, легкие бризы — многообразно проявление энергии потоков воздуха. Энергию ветра использовали для движения парусных судов и в ветряных мельницах еще в древние времена. Полная среднегодовая мощность воздушных потоков для всей Земли ни много ни мало 100 млрд. кВт.
Метеорологи хорошо осведомлены о скоростях ветра в различных местах земного шара и на разных высотах от земной поверхности. Ветер капризен; поэтому при всех прикидочных расчетах оперируют средней скоростью: 4 м/с на высоте 90 м — скромная оценка для прибрежной полосы.
Видимо, наиболее благоприятными селениями для использования голубой энергии являются те, которые расположены на берегах морей и океанов. Оказывается, что, рассчитывая на тихую погоду, Великобритания (она среди европейских стран самая богатая ветром) могла бы получить от ветра такое количество энергии, которое в шесть раз больше, чем ее производят сейчас все электростанции страны. А в Ирландии энергия ветров в сто раз превосходит потребление электрической энергии этой страной (впрочем, возможно, там не столь много ветра, сколь мало электростанций).
Каких-нибудь двадцать лет назад не возлагали больших надежд на ветер как источник энергии. Но тенденции современной энергетики меняются на наших глазах. Одна за другой создаются комиссии, задача которых — подумать об использовании даровых источников энергии. К богатствам земных недр относятся не так, как ранее: человечество начинает думать, что пришла пора позаботиться о целесообразном, а не хищническом использовании богатств, скрытых под земной корой. Поэтому и энергией ветра занялись всерьез. Трезво оценивая технические возможности, можно считать реальным использование долей процента от 100 млрд. кВт. Но и это очень много.
Созданы проекты гигантских «мельниц». Размах крыльев более 100 м, высота башни примерно такая же, скорость конца крыла мельницы около 500 км/ч. Мощность такой мельницы при обычной погоде достигает 1-3МВт. Несколько тысяч таких мельниц, работающих в стране, где сильный ветер не редкость, могут обеспечить ее энергией. В Западной Европе в 1973 г. было произведено 1261,6 млрд. кВт∙ч электрической энергии. В принципе (если не жалеть капитальных затрат) это малая часть той энергии, которую технически возможно взять у ветра! Строительство гигантских «ветряков» уже началось.
Расчеты показывают, что максимальную энергию ветряной двигатель дает тогда, когда ротор уменьшает скорость ветра на одну треть. Не надо думать, что ветряной двигатель должен обязательно копировать мельницу. Возможно применение роторов с вертикальной осью вращения. Ротор, показанный на рис. 6.6, может давать мощности порядка 20 кВт. Достоинство такого ротора — его независимость от направления ветра, недостаток в том, что он пригоден только тогда, когда сила ветра велика. Роторы такого типа изготовляются диаметром 5,5 м.
Вполне понятно, что генераторы, работающие за счет ветра, должны быть установлены на небольшой площади, но все же на таких расстояниях друг от друга, чтобы их взаимодействие не играло роли. Для того чтобы создать электростанцию мощностью 1000 МВт, нужна площадь порядка 5—10 км2.
Глава 7 Физика Вселенной
ИЗМЕРЕНИЕ РАССТОЯНИЙ ДО ЗВЕЗД
В настоящее время почти невозможно провести границу между астрономией и физикой. До тех пор, пока астрономы, вроде как географы, ограничивались описанием звездного неба, предмет астрономии мало привлекал внимание физиков. Однако картина радикально изменилась за последние десятилетия, в особенности после того, как начали проводиться наблюдения звездного неба со спутников и с Луны.
Если земная атмосфера не мешает, то удается принять все сигналы, приходящие к нам со всех уголков Вселенной. Это и потоки различных частиц, и электромагнитное излучение практически всего спектра — от гамма-лучей до радиоволн. Колоссально возросли возможности наблюдения звездного неба и в видимом свете.
Изучение потоков частиц и электромагнитного спектра безусловно относится к физике. Если добавить еще к этому, что изучение космоса сталкивает нас со множеством явлений, которым пока что не удается дать однозначного истолкования, если учесть, что мы можем и должны быть готовыми к тому, что физика Вселенной может привести к открытию новых законов природы, то становится ясным, почему исследователями звездного мира сейчас являются физики — физики по образованию и по методу мышления.
Мы начнем наш разговор о Вселенной с классической астрономической проблемы. Как измерить расстояния от Земли до небесных тел? Сейчас расстояния до Солнца и планет измеряются с очень большой точностью с помощью радиолокаторов. Среднее расстояние до Солнца равно 149 597 800±2000 км.
Но астрономы сумели промерить расстояния внутри планетной системы, а также до ближайших звезд (находящихся от Земли на расстоянии до 300 световых лет) и без помощи радара, пользуясь нехитрым в принципе методом, называемым триангуляцией.
Вдали от нас находится высокая башня. Добраться до нее трудновато. Ну, скажем, отделяют нас от башни непроходимые болота. Наведем зрительную трубу на башню, фиксируем это направление. Теперь отъедем на несколько километров по прямой линии, перпендикулярной к направлению на башню, и повторим наше наблюдение. Разумеется, теперь по отношению к далекому пейзажу башня будет видна под другим углом. Угол смещения называется параллаксом; расстояние, на которое мы отъехали от первой точки наблюдения, называется базисом. Параллакс измерен, базис известен. Строим прямоугольный треугольник и находим расстояние до башни. Вот этим методом и пользуются астрономы, определяя параллакс, наблюдая за светилом из двух обсерваторий, расположенных по прямой на расстоянии, равном радиусу Земли. При помощи сначала нехитрых приспособлений, а затем телескопов астрономы измеряли углы между направлениями на отдельные звезды (рис. 7.1). И обратили внимание на то, что можно отыскать группу звезд, которая движется по небу как одно целое. С каких позиций ни наблюдай, углы между направлениями остаются теми же самыми.
Но среди этих звезд зачастую находили какую-нибудь одну, которая явно смещалась по отношению к своим соседям. Принимая одну из «неподвижных» звезд как бы за точку отсчета, можно измерить угловое смещение звезды, менявшей свое расположение по отношению к неизменному созвездию. Этот угол смещения имеет смысл параллакса.
Еще в XVII веке, после изобретения Галилеем телескопа, астрономы измерили параллаксы планет, наблюдая их смещения по отношению к «неподвижным» звездам. Тогда подсчитали, что Земля отстоит от Солнца на расстоянии 140 млн. км. Совсем неплохая точность!
Для невооруженного глаза взаимное расположение звезд остается всегда неизменным. Но при помощи фотографии звездного неба с разных позиций можно обнаружить параллактическое смещение звезд. Если сделать две фотографии какого-либо участка звездного неба из одной и той же обсерватории с промежутком времени полгода, то расстояние между точками наблюдения будет равно почти 300 млн. км.
Измерения расстояний до звезд с помощью радара невозможны. Поэтому схема измерения, которую иллюстрирует рис. 7.1, вполне современна.
Такого рода снимки приводят нас к заключению, что есть звезды, которые заметно перемещаются по отношению к другим звездам. Было бы крайне нелогично допустить, что существуют звезды подвижные и звезды неподвижные. Напрашивается вывод, что те звезды, взаимное расположение которых сохранилось неизменным, находятся много дальше, чем блуждающая звезда. Как бы то ни было, мы получаем возможность с помощью хороших инструментов измерить параллаксы многих звезд. Измерения параллакса с точностью до одной сотой секунды дуги были проведены для многих звезд. Оказалось, что ближайшие из них находятся на расстояниях, больших одного парсека.
Один парсек есть расстояние, дающее угловое смещение в одну секунду, если за базис взять средний радиус земной орбиты. Легко подсчитать» что один парсек равен 30,26 триллиона километров.
Для измерения расстояний часто пользуются световыми годами. Один световой год — путь, который пройдет свет за год. Один парсек равен 3,26 светового года.
Параллактический метод применим до расстояний порядка сотен световых лет. А как измерить расстояния до более далеких звезд? Это оказывается уже совсем не простым делом, и уверенность в правильности приблизительных оценок (ручаться можно большей частью лишь за одну значащую цифру) получается сопоставлением результатов разных измерений.
Один из способов (а их много, и у нас нет возможности на них останавливаться) заключается в следующем. Если известно расстояние, до звезды R и видимая звездная величина m (мера освещенности, создаваемая звездой на Земле), то, пользуясь законом, согласно которому интенсивность изменяется обратно пропорционально квадрату расстояния от источника, можно вывести следующую формулу:
М = m — 5∙lg R + 5.
Здесь М есть так называемая абсолютная звездная величина. Это величина, которую имела бы звезда, если бы находилась от нас на некотором стандартном расстоянии, которое принимают равным 10 пк.
Мы с полным основанием полагаем, что эта формула справедлива и для далеких звезд. Но как ею воспользоваться для определения расстояния до звезды? Вот на этом-то самом интересном вопросе мы, к сожалению, и не можем остановиться подробнее: не хватает места в нашей маленькой книге. Оказывается, что для некоторой категории звезд удается построить график, который показывает как меняется отношение интенсивностей определенных пар линий звездного спектра в функции величины М. Ну, а интенсивности спектральных линий астрономы измерять умеют.
Для некоторых звезд, которые периодически меняют свой блеск (они принадлежат к классу так называемых цефеид), показано, что светимость, т. е. величина светового потока, заключенного в единице телесного угла (может относиться как к области спектра, так и к суммарному излучению), плавно возрастает с увеличением периода. Светимость, разумеется, строго связана с величиной М. Для этих переменных звезд их расстояние до наблюдателя устанавливается со значительной точностью.
А вот еще одна идея, которой можно воспользоваться для измерения «масштаба» Вселенной.
Звезды Вселенной не разбросаны во Вселенной как попало. На непредставимо огромных расстояниях от нас расположены различные звездные скопления? Они движутся по отношению к Солнечной системе самым разным образом. Это движение помогает нам определить расстояния до звездных скоплений. На помощь приходит эффект Доплера.
Формулы, которые мы рассматривали в 3-й книге, справедливы для любых колебаний. Поэтому частоты спектральных линий, наблюдаемые в спектре звезды, позволяют определить скорость ее движения в направлении от Земли или к ней. Так как с в формуле
есть скорость света 300 000 км/с, то понятно, что движение звезды должно быть достаточно быстрым, а спектрограф должен быть весьма высокого качества для того, чтобы мы обнаружили смещение спектральных линии.
Прошу заметить, что естествоиспытатель вполне уверен в том, что водород, находящийся в недрах звезды и заявляющий нам о своем присутствии в объекте, находящемся на невообразимо колоссальном расстоянии, — это такой же водород, как и тот, с которым мы имеем дело в земных условиях. Если бы звезда покоилась, то спектр водорода обязан был бы выглядеть совершенно так же, как спектр, который мы получаем от газоразрядной трубки (вот какова уверенность физика в единстве мира!). Но линии оказываются заметно сдвинутыми, и скорости галактик — это сотни, а то и десятки тысяч километров в секунду. Нет сомневающихся в приведенном объяснении. Да и как сомневаться? Ведь спектр водорода состоит из очень большого числа линий, и мы видим сдвиг не одной линии, а всех линий спектра в согласии с формулой Доплера.
Но вернемся к измерению звездных расстояний. Какую помощь может оказать нам знание скоростей движения звезд? Все просто… но, конечно, лишь в том случае, если мы заметим, что звезда за год сдвинулась (опять-таки по отношению к другим звездам, которые в данном измерении можно считать «неподвижными») на какое-то расстояние. Если дуговое перемещение звезды φ (перпендикулярно лучу света, который до нас доходит) известно, то, зная тангенциальную скорость, найдем расстояние до звезды R по формуле
R∙φ/t = v
Вместо t надо подставить время, которое ушло на перемещение звезды.
Но позвольте, скажет читатель, ведь в формулу входит тангенциальная скорость, а направление движения звезды нам не известно. Совершенно справедливое возражение. Поэтому приходится поступать следующим образом. Отбирается большое число звезд с одинаковым периодом изменения светимости. Для всех этих звезд измеряют лучевую скорость. Она будет колебаться от нуля (если звезда движется перпендикулярно лучу) до максимума (если звезда движется вдоль луча). Полагая, что в среднем тангенциальные и лучевые скорости одинаковы, можно подставить в написанную выше формулу среднее значение измеренных нами скоростей.
РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
В результате измерений расстояний, мы можем описать звездный мир следующим образом. Наблюдаемая Вселенная разбита на огромное число звездных скоплений, которые получили название галактик. Наша Солнечная система входит в Галактику, которую каждый видел на небе. Это Млечный Путь. Наша Галактика имеет форму диска, диаметр которого — около 100 тысяч световых лет. В Галактике что-нибудь около 1011 звезд разных типов. Солнце — одна из таких звезд, и находится наше светило на периферии Галактики. Звезды отдалены друг от друга на огромные расстояния. Расстояние между звездами в среднем в 10 миллионов раз превышает размер звезды. Для того чтобы добиться аналогичного разрежения в воздушном пространстве, надо было бы уменьшить плотность воздуха в 1018 раз.
Что же касается взаимного расположения галактик, то здесь картина иная. Средние расстояния между галактиками всего лишь в несколько раз больше размеров самих галактик.
Астрофизики, могут сообщить очень много деталей о характере взаимного движения звезд, принадлежащих одной галактике. На этом мы останавливаться не будем. Однако даже в книге, излагающей азбуку физики, мы не можем пройти мимо одного исключительно важного наблюдения. Достоверно установлено по изучению эффекта Доплера в спектрах, принадлежащих звездам разных галактик, что галактики разбегаются «от нас». При этом было показано, что скорость удаления галактики прямо пропорциональна расстоянию ее «от нас». Самые далекие видимые галактики движутся со скоростями, приближающимися к половине скорости света.
Почему я поставил в кавычки слова «от нас»? Да по той причине, что в этом утверждении кроется явно нечто несуразное. Подобная позиция могла бы удовлетворить лишь человека, верующего в то, что господь бог сотворил Землю и разместил вокруг нее звезды. Такая картина была принята в древние времена Аристотелем и господствовала в средние века. Вселенная имела границы, за которыми простиралось царство бога — эмпиреи.
Для современного человека совершенно неприемлема мысль о Вселенной, имеющей границы. Если есть граница, то сразу же следует вопрос: а что находится за ней? Так что нужно обойтись без представления о границе Вселенной. С другой стороны, никак нельзя поверить, что Земля или Солнце являются особыми телами во Вселенной. Это явно противоречит всем сведениям, добытым астрофизиками. Но ведь галактики разбегаются «от нас»! Как можно примирить с этим фактом наши требования к модели Вселенной? Хотим, чтобы у нее не было границ; желаем, чтобы она была более или менее однородна; требуем, чтобы картина Вселенной с точки зрения обитателя любой звезды была одной и той же.
Интеллектуальная необходимость в существовании такой модели привела Эйнштейна к следующему фундаментальному заключению. Геометрия Евклида, которой мы с успехом пользуемся в обыденной жизни, несправедлива, когда речь идет о непредставимо колоссальных расстояниях, с которыми мы сталкиваемся при изучении звездного мира. Отказ от геометрии Евклида означает отказ от наглядных моделей Вселенной. Ну что же, не в первый раз нам расставаться с возможностью наглядно представить себе окружающий нас мир.
Простившись с геометрией Евклида, мы можем предложить модель Вселенной, которая одновременно является замкнутой и в то же время не имеет ни границ, ни центра. В такой модели все точки пространства будут равноправными.
На первый взгляд может показаться, что Эйнштейн требует от нас очень большой жертвы. Мы так привыкли, что две параллельные линии никогда не пересекаются, что сумма квадратов катетов равна квадрату гипотенузы. Привыкли… Но, позвольте, вспомните уроки географии. На глобусе, изображающем земной шар, линии широт параллельны. А на географической карте? Вы вправе спросить, на карте какого типа. Ибо географические карты строятся различными способами. Если изобразить земной шар в виде двух полушарий, то параллели перестанут быть параллельными. Если прибегнуть к так называемой прямоугольной проекции, то расстояния между широтами перестанут быть равными. Какая уж тут геометрия Евклида!
Если желаете, то можете убедиться, что теорема Пифагора потерпела крах. На карте важнейших авиалиний я изобразил треугольник (рис. 7.2) Москва-Кейптаун-Лондон. Выбрал его потому, что случайно он на карте в точности прямоугольный. Значит, сумма квадратов катетов должна равняться квадрату гипотенузы. Как бы не так. Считайте: расстояния Москва-Лондон 2490 км, Москва-Кейптаун 10130 км и Лондон-Кейптаун 9660 км. Не работает теорема, не годится наша геометрия для географической карты.
Законы геометрии на плоскости, изображающей земной шар, отличаются от «обычных».
Рассматривая географическую карту полушарий, мы видим, что у нее есть «края». Но ведь это иллюзия. На самом деле, двигаясь по поверхности земного шара, мы никогда не доберемся до несуществующего «края Земли».
Существует анекдот. Маленький сын Эйнштейна спрашивает отца: «Папа, почему ты так знаменит?» Отец отвечает: «Мне повезло, я первый обратил внимание на то, что жук, ползая по глобусу, может обогнуть его по экватору и вернуться в исходную точку». Конечно, в такой форме открытия нет. Но перенести это соображение на трехмерное пространство Вселенной; утверждать, что она конечна и замкнута наподобие двумерной поверхности, ограничивающей глобус; сделать из этого вывод, что все точки Вселенной совершенно равноправны в том же смысле, что и все точки поверхности глобуса, — разумеется, это требует исключительной интеллектуальной смелости.
Отсюда такое заключение. Если мы, земляне, наблюдаем, что все галактики от нас разбегаются, то и житель планеты любой звезды будет видеть ту же картину. Он придет к тем же заключениям о характере движения звездного мира и измерит те же самые скорости галактик, что и обитатель Земли.
Модель Вселенной, предложенная Эйнштейном в 1917 г., является естественным следствием разработанной им так называемой общей теории относительности (ту часть теории, которую мы изложили в гл. 4, называют специальной).
Однако Эйнштейн не предполагал, что замкнутая Вселенная может изменять свои размеры. Это показал в 1922–1924 гг. советский ученый Александр Александрович Фридман (1888–1925). Оказалось, что теория требует либо расширения Вселенной, либо чередующихся расширений и сжатий. Во всяком случае она не может быть статической. Мы имеем право принять любую из этих двух точек зрения, т. е. либо предположить, что мы живем сейчас в эпоху расширения Вселенной, которой предшествовали чередовавшиеся сжатия и расширения, либо допустить, что Вселенная некое время тому назад (его можно рассчитать, оно оказывается равным нескольким десяткам миллиардов лет) представляла собой «космическое яйцо», которое взорвалось и с тех пор расширяется.
Надо отчетливо понимать, что вариант начального взрыва вовсе не связан с принятием сотворения мира. Может быть попытки заглянуть слишком далеко вперед и назад, а также на слишком большие расстояния неправомерны в рамках существующих теорий.
Рассмотрим в соответствии со схемой, представляющейся сейчас разумной, такой простой пример. Измеряем красное смещение спектральных линий излучения, приходящего к нам от далеких галактик. Пользуясь формулой Доплера, оцениваем скорости движения галактик. Чем дальше от нас галактики, тем быстрее они движутся. Телескоп сообщает скорости разбегания все более и более далеких галактик: десять тысяч километров в секунду, сто тысяч километров… Однако этому возрастанию значений скорости должен наступить предел. Ведь если галактика движется от нас со скоростью света, то мы ее в принципе не можем увидеть: частота света, вычисляемая по формуле Доплера, обратится… в нуль. От такой галактики свет до нас не доходит.
Каковы же максимальные расстояния, которые мы сумеем измерить, когда в нашем распоряжении окажутся сверхзамечательные приборы? Конечно, оценка может быть сугубо приблизительной. Во всяком случае жаловаться на то, что мы не можем заглянуть достаточно далеко, уж никак не приходится: число о котором идет речь, измеряется миллиардами световых лет!
Что же касается еще больших расстояний, то разговор о них, вероятно, лишен содержания. Можно сказать и так: в рамках сегодняшних представлений разговор о расстояниях, больших миллиардов световых лет, лишен физического смысла, поскольку нельзя предложить способ измерения.
Дело обстоит здесь вполне аналогично той ситуации, которая возникла с траекторией электрона: ее никак нельзя измерить просто потому, что представление о ней не имеет смысла.
ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Специальная теория относительности привела к необходимости ввести поправки в законы механики для тел, движущихся со скоростями, близкими к скорости света. Общая теория относительности вносит поправки в привычные представления о пространстве, когда речь идет об огромных расстояниях. Именно поэтому разговор об этой теории уместен в главе, посвященной физике Вселенной.
Общая теория относительности покоится на следующем принципе: нет таких экспериментов, с помощью которых можно было бы отличить движение тел под действием поля тяготения от движения в соответствующим образом подобранной неинерциальной системе отсчета.
Рассмотрим несколько простейших примеров. Мы находимся в лифте, который падает вниз с ускорением а. Выпустим из руки шарик и сообразим, какой характер будет иметь его падение. Как только шарик будет выпущен, начнется, с точки зрения инерциального наблюдателя, свободное падение с ускорением g. Так как лифт падает с ускорением то ускорение по отношению к полу лифта будет (g — а). Наблюдатель, находящийся в лифте, может описать движение падающего тела при помощи ускорения g' = g — a. Иначе говоря, наблюдатель в лифте может не говорить об ускоренном движении лифта, «изменив» ускорение поля тяжести в своей системе.
Теперь сравним два лифта. Один из них неподвижно висит над Землей, а другой движется в межпланетной пустоте с ускорением а по отношению к звездам. Все тела в неподвижном над Землей лифте обладают способностью свободно падать с ускорением g. Но такой же способностью обладают тела внутри межпланетного лифта. Они будут «падать» с ускорением — а на «дно» лифта.
Выходит, что действие поля тяжести и проявления ускоренного движения неотличимы.
Поведение тела в ускоренно движущейся системе координат равнозначно поведению тела в присутствии эквивалентного поля тяжести. Однако эта эквивалентность может быть полной, если мы ограничим себя наблюдениями на небольших участках пространства. Действительно, представим себе «лифт» с линейными размерами пола в тысячи километров. Если такой лифт неподвижно висит над земным шаром, то явления в нем будут происходить иначе, чем в том случае, когда лифт будет двигаться с ускорением а по отношению к неподвижным звездам. Это ясно из рис. 7.3: в одном случае тела падают косо на дно лифта, в другом случае — отвесно.
Таким образом, принцип эквивалентности справедлив для тех объемов пространства, в которых поле можно считать однородным.
Принцип эквивалентности поля тяготения с нужным образом подобранной локальной системой отсчета приводит к важному выводу: поле тяготения связано с кривизной пространства и искажением хода времени.
Два наблюдателя заняты измерением расстояния и промежутков времени. Их интересуют события, происходящие на вращающемся диске. Один наблюдатель находится на диске, а другой неподвижен (по отношению к звездам). Впрочем, работает только тот исследователь, который является, так сказать, жителем диска. Неподвижный наблюдатель лишь следит за работой своего коллеги.
Первый опыт заключается в измерении радиального расстояния, т. е. расстояния между двумя предметами, установленными на одном и том же радиусе диска на разных расстояниях от центра. Измерение производится обычным способом, а именно: между концами интересующего исследователей отрезка укладывается сколько-то раз стандартная линейка. С точки зрения обоих исследователей, длина линейки, расположенной перпендикулярно направлению движения, одна и та же. Поэтому между нашими двумя исследователями не возникнут разногласия по поводу длины радиального отрезка.
Теперь житель диска приступает ко второму опыту. Он желает измерить длину окружности. Линейку приходится укладывать вдоль движения. Конечно, надо учитывать кривизну окружности. Поэтому измерение следует проводить при помощи небольшой линейки, так, чтобы длину касательного отрезка можно было приравнять длине дуги. Наблюдатели не станут спорить о том, сколько раз уложилась линейка по длине окружности. Но тем не менее их мнения по поводу длины окружности разойдутся. Ведь неподвижный наблюдатель будет считать, что линейка сократилась, поскольку в этом втором опыте она расположена вдоль движения.
Итак, радиус окружности для обоих наблюдателей один и тот же, а длина окружности разная. Неподвижный наблюдатель приходит к выводу, что формула длины окружности 2π∙r неверна. Для меня, скажет неподвижный наблюдатель, длина окружности меньше, чем 2π∙r.
Этот пример показывает вам, как теория относительности приходит к отказу от евклидовой геометрии, или (это то же самое, сказанное другими словами) к представлению об искривлении пространства.
Аналогичные «безобразия» произойдут и с часами. Часы, закрепленные на разных расстояниях от оси вращения, идут с различной скоростью. Все они будут идти медленнее, чем неподвижные часы. При этом замедление тем больше, чем дальше от центра диска находятся часы. Неподвижный наблюдатель скажет, что пользоваться часами и линейками, если живешь на диске, можно лишь в том случае, если находишься на определенном расстоянии от центра. Пространство и время обладают локальными особенностями.
Теперь вспомним о принципе эквивалентности. Раз такие локальные особенности времени и пространства проявляются на вращающемся диске, значит, так же протекают явления и в поле тяготения. С диском дело обстоит так же, как и с лифтом, изображенным на рис. 7.3. Ускоренное движение неотличимо от движения в поле тяготения, направленного в сторону, обратную ускорению.
Таким образом, локальное искривление пространства и времени равносильно наличию поля тяготения.
Замкнутость Вселенной, о которой шла речь в предыдущем параграфе, несомненно может рассматриваться как подтверждение общей теории относительности. Однако читатель должен иметь в виду, что гипотеза о замкнутости Вселенной не является на сегодня единственно возможной.
Имеется возможность из хитроумных уравнений общей теории относительности вывести строгим математическим рассуждением ряд количественных следствий. Эйнштейн показал, что, во-первых, проходя вблизи Солнца, лучи света должны отклоняться. Луч, идущий в непосредственной близости от Солнца, должен отклониться на 1,75". Измерения дали величину 1,70. Во-вторых, орбита планеты Меркурий (вернее, ее перигелий) должна поворачиваться в своей плоскости. Расчет показывает, что это перемещение должно быть равно за столетие 43". Именно такое число и дают наблюдения. И еще одно предсказание, которое было подтверждено опытом: фотон тратит энергию (а значит, меняется частота света), преодолевая силы тяготения.
Общая теория относительности является одним из величайших завоеваний человеческого мышления. Ее создание сыграло огромную роль в развитии взглядов на Вселенную и революционизировало физику.
ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА
Физика Вселенной находится в стадии бурного развития. Ее никак нельзя назвать завершенной областью науки, как, скажем, механику малых скоростей или термодинамику. Поэтому не исключено, что при исследовании звезд будут открыты новые законы природы. Пока такого не произошло. Как бы то ни было, картина Вселенной, которую время от времени набрасывает тот или иной физик в популярной статье, все время терпит изменения. Так что и то, что я рассказываю в этой главе, возможно, будет пересмотрено через десяток-другой лет.
Уже давно астрономы понимали, что звезды бывают разные. При помощи телескопа, спектрографа и интерферометра удается определить много физических величин, которые могут быть занесены в паспорт звезды.
Как можно полагать по аналогии с земными опытами (ср. с. 12), характер спектра определяет температуру поверхности звезды. С этой температурой однозначно связан, наблюдаемый цвет звезды. Если температура 3000–4000 К, то цвет красноватый, если 6000–7000 К — желтоватый. Бледно-голубые звезды имеют температуру свыше 10000—12000 К. Выйдя в космические просторы, физики нашли звезды, максимум излучения которых лежит в области рентгеновских и даже гамма-лучей. Это означает, что температуры звезд могут достигать и миллионов кельвинов.
Другой важной характеристикой звезды является суммарная энергия достигающего нас спектра. Это светимость звезды. Колоссальные различия в светимости могут быть связаны с размером и массой звезды, с ее удаленностью от нас и с ее температурой.
Что касается химического состава звезд, то они представляют собой в основном водородно-гелиевые плазмы. Солнце — достаточно типичная звезда. Его химический сослав определен более или менее точно из вида спектров и из теоретических расчетов энергии излучения. Водород составляет 70 %, гелий 29 %. На долю других элементов приходится около 1 %.
В атмосфере многих звезд были обнаружены сильные магнитные поля, в тысячи раз большие магнитного поля Земли. Рассказывает об этом все тот же спектральный анализ, поскольку спектральные линии расщепляются в магнитных полях.
Межзвездная среда разрежена до немыслимых пределов. В одном кубическом сантиметре космоса находится один атом. Вспомните, что в 1 см3 воздуха, которым мы дышим, находится 2,7∙1019 молекул. Приведенная цифра — средняя. Существуют области пространства, где плотность межзвездного газа существенно выше средней. Кроме газа мы встречаемся и с пылью, которая состоит из частичек размером 10-4—10-5 см.
Следует полагать, что звезды образуются из газово-пылевой среды. Под влиянием сил тяготения некое облако начинает стягиваться в шар. Через сотни тысяч лет оно сожмется, а температура звезды повысится и сделает звезду видимой на небосводе. Разумеется, это время сильно зависит от размеров и соответственно от массы сгущающегося облака.
С продолжением сжатия температура в недрах звезды растет и достигает такого значения, при котором начинается термоядерная реакция. Четыре ядра атомов водорода превращаются в ядро атома гелия. Напомним, что при этом 4,0339 а.е.м. четырех атомов водорода превращаются в 4,0038 а.е.м. гелия. Выделяется энергия, эквивалентная 0,0301 а.е.м.
Выгорание водорода, которое происходит в центре звезды, может продолжаться разное время в зависимости от ее массы. Для Солнца это время равно 10–20 млрд. лет. Таков период стабильного состояния звезды. Силы гравитационного притяжения уравновешиваются внутренним давлением горячих ядер, которое пытается раздуть звезду. Так что звезда — это нечто вроде баллона со сжатым газом. Только роль стенок сосуда берут на себя силы тяготения.
Когда запасы водородного горючего начнут приходить к концу, внутреннее давление ослабнет. Ядро звезды начнет сжиматься.
Что же произойдет дальше? — спрашиваем мы у теоретика. Проделав соответствующие расчеты, теоретик отвечает, что дальнейшая судьба звезды зависит от того, удастся ли ей или нет сбросить с себя внешнюю оболочку. Если такой процесс окажется возможным и масса звезды станет раза в два меньше Солнца, то тогда создадутся силы, способные противостоять гравитационным. Образуется маленькая звезда с высокой температурой поверхности. Ее называют белым карликом.
Ну, а дальше? Опять-таки судьба звезды определяется ее массой. Если белый карлик имеет массу меньше, чем полторы массы Солнца, то он будет медленно умирать и никаких драматических событий не произойдет. Радиус будет уменьшаться, температура падать. В конце концов карлик превратится в холодную звезду размером с Землю. Такова «гибель» большинства звезд.
Но если масса белого карлика, образовавшегося после того, как звезда с выгоревшим топливом сбросила с себя оболочку, больше полутора солнечных масс, то сжатие не остановится на стадии белого карлика. Электроны сольются с протонами, и образуется нейтронная звезда, размер которой будет измеряться лишь несколькими десятками километров. Нейтронная звезда, должна, по расчетам, иметь температуру порядка десятка миллионов кельвинов. Максимум ее излучения лежит в области рентгеновских лучей.
Мы рассказали, что должно произойти со звездой, если ей удастся сбросить с себя внешнюю оболочку. Но математические уравнения не диктуют необходимость этого раздевания. Если же небесное тело сохранит массу порядка массы Солнца, то гравитационное притяжение просто уничтожит звезду. На месте, где была звезда, останется черная дыра.
На какой же стадии сжатия должно произойти уничтожение звезды и почему место, где она находилась получило название черной дыры?
Вспомним следующую простую закономерность, на которой основаны запуски ракет, уходящих с Земли в космос (см. 1-ю книгу). Чтобы покинуть Землю, нужна скорость 11 км/с. Величина этой скорости определяется уравнением
Из формулы ясно, что по мере сжатия шара определенной массы скорость, с которой ракета может уйти в космос с такого небесного тела, будет все время расти. Но ведь предельная скорость равна 300 000 км/с! Если звездный шар заданной массы сожмется до шарика, радиус которого равен
то выбраться из такого шара становится невозможным.
Иными словами, в место, где была звезда, может прийти все, что угодно, в том числе световой луч или луч другого электромагнитного излучения, а выбраться из дыры не удастся. Согласитесь, что название «черная дыра» вполне уместно. Нетрудно прикинуть по написанной формуле, что черные дыры с массами от 3 до 50 солнечных масс будут иметь размеры от 60 до 1000 км.
Теперь я остановлюсь более или менее детально на поисках черных дыр. Конечно, читатель может сказать, что это частный вопрос, которому не следовало бы уделять внимание в маленькой книге, посвященной всей физике. Но мне представляется поучительным сам метод подхода к этому поиску. Талант естествоиспытателя и проявляется в том, чтобы найти способы косвенных доказательств справедливости модели, свойства которой не могут быть доказаны непосредственно.
Задача действительно кажется на первый взгляд неимоверно сложной, если не неразрешимой. Разглядеть черное пятнышко размером в 1000 км на неимоверно больших расстояниях не под силу самому хорошему приору.
Советский физик Я. Б. Зельдович более чем 20 лет назад предложил начать поиск черных дыр, исходя из идеи, что их присутствие на небе должно влиять на поведение находящихся поблизости видимых тел. Вместе со своими сотрудниками он начал систематический просмотр звездных каталогов с тем, чтобы найти видимую звезду, вращающуюся около черной дыры. Такая звезда должна выглядеть одиночкой, а ее вращение приведет к тому, что спектральные линии будут периодически смещаться в красную или синюю сторону в зависимости от того, движется ли звезда от нас или к нам.
В эту работу включились исследователи и других стран, и было найдено некоторое число вроде бы подходящих звезд. Из величины доплеровского смещения можно грубо оценить массу звезды, около которой происходит вращение видимого спутника. Были отобраны невидимые кандидаты, масса которых была в три раза больше массы Солнца. Таким образом, речь не могла идти ни о белых карликах, ни о нейтронных звездах.
И все же этого недостаточно для утверждения, что такая экзотическая система, как черная дыра, действительно существует. Оппоненты могли выставить серию других объяснений периодического доплеровского смещения.
Однако имеется одно явление, которое можно призвать на помощь. Дело в том, что черная дыра обладает способностью втягивать в себя газ из своего спутника. При падении в черную дыру этот газ должен сильно разогреваться и излучать рентгеновские лучи. Правда, такую же оттяжку газа производят и нейтронные звезды, и белые карлики. Но их, как сказано выше, мы можем отличить от черной дыры по величине массы.
Совсем недавно была найдена звезда, удовлетворяющая всем требованиям, которым должен подчиняться спутник черной дыры. За этим открытием, без сомнения, последуют новые эксперименты и детальные теоретические расчеты, цель которых — предсказать особенности рентгеновского спектра, исходящего из окружения черной дыры. Ближайшее будущее должно показать, насколько часто эти поразительные «тела» встречаются во Вселенной. Есть основания полагать, что возможно существование крупных черных дыр и черных мини-дыр с массой порядка 1016 г. Такие дыры размером меньше атомного ядра могут неожиданно погибнуть, возвратив заключенную в них энергию. А ее достаточно, для того, чтобы удовлетворить в течение многих лет все нужды Земли в энергии. Какая великолепная тема для авторов научно-фантастических романов!
РАДИОАСТРОНОМИЯ
На фотографии, которая приведена на рис. 7.4, изображена параболическая радиоантенна. Она фокусирует падающие на нее параллельные радиолучи. Лучи собираются в точке, где помещен специальный приемник. Далее сигнал усиливается радиотехническими способами. Параболическая антенна, показанная на рисунке, установлена в городе Эффельсберге (ФРГ). С помощью этой антенны стометрового диаметра ведут совместные исследования ученые многих стран, в том числе и советские.
Подобные антенны обладают поразительной чувствительностью. Поворачивая их так, чтобы ось зеркала смотрела в интересующем нас направлении, мы в состоянии уловить потоки энергии порядка 10-28 Вт с/м2. Фантастично, не правда ли?!
Радиоастрономия привела к фундаментальным открытиям в области физики Вселенной.
Радиотелескопы установлены на Луне и на некоторых спутниках. Таким образом, поглощение и отражение электромагнитных волн атмосферой перестает быть препятствием для наблюдателя. Пока что имеются два «окна» в электромагнитном спектре. Одно из этих окон пропускает видимый свет, а другое — радиоизлучение в пределах длин волн от 2 см (15 000 МГц) до 30 м (10 МГц).
Погода не влияет на радиоастрономические наблюдения. Радионебо «выглядит» совсем иначе, чем то, которым мы любуемся ночью.
Радиоизлучение космоса — не очень сильное, и его изучение стало возможным лишь благодаря феноменальным успехам радиотехники. Достаточно сказать, что радиоизлучение Солнца в миллионы раз меньше по мощности чем излучение в световом диапазоне.
И несмотря на это, без радиоспектроскопии мы не смогли бы установить много важных фактов. Так, большую роль в понимании процессов, протекающих во Вселенной, играет измерение остаточного излучения взрывов «сверхновых» звезд.
Нейтральный водород излучает сильную волну длиной 21 см. Измерение интенсивности этого радиоизлучения позволило набросать картину распределения в космосе межзвездного газа и проследить за движением газовых, облаков.
Найдено большое число радиогалактик и квазаров, которые находятся от нас на предельно больших наблюдаемых расстояниях. Достаточно сказать, что красное смещение излучения, приходящего от этих источников достигает значения — 3,5. Красное смещение определяется как отношение разности принятой и испущенной длин волн к величине испущенной длины волны. Так что разность в 3,5 раза больше, чем длина волны излучения.
Радиометоды позволили заглянуть на самую окраину Вселенной. Радиоастрономические исследования позволили разобраться в природе космических лучей, поступающих к нам из небесных просторов.
КОСМИЧЕСКИЕ ЛУЧИ
Исследования, которые сейчас можно с удобствами производить в космосе, доказывают, что на нашу Землю непрерывно падает поток ядерных частиц, движущихся со скоростями, практически равными скорости света. Их энергия лежит в пределах 108—1020 эВ. Энергия порядка 1020 эВ превосходит на восемь порядков энергии, которые можно создать в самых мощных ускорителях!
В основном первичные космические лучи состоят из протонов (около 90 %); кроме протонов в них присутствуют и более тяжелые ядра. Разумеется, сталкиваясь с другими молекулами, атомами, ядрами, космические лучи способны создать элементарные частицы всех типов. Но астрофизиков интересует первичное излучение. Как создаются потоки частиц, обладающих такой энергией? Где лежат источники этих частиц?
Достаточно давно было доказано, что не Солнце является основным источником космического излучения. Но если так, то ответственность за создание космических лучей нельзя переложить и на другие звезды, поскольку в принципе они ничем не отличаются от Солнцу. Кто же виноват?
В нашей Галактике существует Крабовидная туманность, которая образовалась в результате взрыва звезды в 1054 г. (не надо забывать, что ученые следят за звездным небом не одну тысячу лет). Опыт показывает, что она является источником радиоволн и источником космических частиц. Это совпадение дает разгадку огромной энергии космических протонов. Достаточно допустить, что электромагнитное поле, образовавшееся в результате взрыва звезды, играет роль синхротрона, и тогда огромная энергия, которая набирается частицей, путешествующей по спирали вокруг линий магнитной индукции на протяжении тысяч световых лет, может достигнуть тех фантастических цифр, которые мы привели.
Расчеты показывают, что, пролетев расстояние, равное поперечнику нашей Галактики, космическая частица не может набрать энергии больше чем 1019 эВ. Видимо, частицы с максимальной энергией приходят к нам из других галактик.
Разумеется, нет никакой необходимости полагать, что только взрывы звезд приводят к появлению космических частиц. Любые звездные источники радиоволн могут быть одновременно источниками космических лучей.
Существование космических лучей было обнаружено еще в начале нашего века. Установив электроскопы на воздушном шаре, исследователь замечал, что разрядка электроскопа на больших высотах идет значительно быстрее, чем если этот старинный прибор, оказавший физикам немало услуг, помещен на уровне моря.
Стало ясным, что всегда происходящий спад листочков электроскопа не является следствием несовершенства прибора, а есть результат действия каких-то внешних факторов.
В 20-х годах физики уже понимали, что ионизация воздуха, которая снимала заряд с электроскопа, несомненно внеземного происхождения. Милликен первый уверенно, высказал такое предположение и дал явлению его современное название: космическое излучение.
В 1927 г. советский ученый Д. В. Скобельцын первый получил фотографию следов космических лучей в ионизационной камере.
Обычными способами, которые мы описывали ранее, была определена энергия космических частиц. Она оказалась огромной.
Изучая природу космических лучей, физики сделали ряд замечательных открытий. В частности, существование позитрона было доказано именно этим путем. Так же точно и мезоны — частицы с массой, промежуточный между массами протона и электрона, — были впервые обнаружены в космических лучах.
Исследования космических лучей продолжают оставаться одним из увлекательных занятий физиков.
* * *
Незавершенность астрофизики делает трудным ее изложение в одной главе небольшой книги, цель которой — ввести читателя в круг основных фактов и идей физической науки. Я выбрал из физических проблем, касающихся Вселенной, лишь несколько вопросов, которые казались мне наиболее интересными.
* * *
* * *
Примечания
1
Вообще-то говоря, релятивистской механике не противоречит существование частиц, движущихся со скоростями, сколь угодно большими, чем скорость света. Теоретики даже дали этим частицам название: тахионы. Однако если бы такие частицы существовали, то скорость света все равно осталась бы для них предельной, но только не максимальной, а, напротив, минимальной. Автор книги полагает, что теория тахионов — всего лишь изящная математическая игра. Если бы мир тахионов существовал, то на события, протекающие в нашей Вселенной, он в принципе не мог бы влиять… так же, как бог.
(обратно)2
В последние годы выяснилась необходимость в новом параметре, которому дали название «бьюти», т. е. красота.
(обратно)3
Масса фотона — это масса движущейся частицы; что касается массы покоя фотона, то она практически равна нулю; экспериментатор может поручиться, что она меньше 0,6∙10-20 МэВ. Отметим также, что соотношение для импульса фотона может быть непосредственно проверено измерениями давления света.
(обратно)


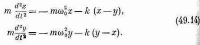
Комментарии к книге «Физика для всех. Книга 4. Фотоны и ядра», Александр Исаакович Китайгородский
Всего 0 комментариев