8a. Квантовая механика I
Глава 7 АММИАЧНЫЙ МАЗЕР
§ 1. Состояния молекулы аммиака
§ 2. Молекула в статическом электрическом поле
§ З. Переходы в поле, зависящем от времени
§ 4. Переходы при резонансе
§ 5. Переходы вне резонанса
§ 6. Поглощение света
§ 1. Состояния молекулы аммиака
В этой главе мы хотим обсудить применение квантовой механики в одном практическом устройстве — в аммиачном мазере. Вас может удивить, отчего это мы бросаем на полпути наше изложение формального аппарата квантовой механики и обращаемся к частной задаче. Но позже вы увидите, что многие черты этой частной задачи сплошь и рядом встречаются и в общей теории квантовой механики, так что детальное изучение задачи многому нас научит. Аммиачный мазер — это устройство для генерирования электромагнитных волн. Его действие основано на свойствах молекулы аммиака, о которых вкратце говорилось в предыдущей главе. Поэтому сначала мы подведем итоги тому, что нам уже известно.
Молекула аммиака имеет много состояний. Но мы будем считать ее системой с двумя состояниями (двухуровневой); сейчас нас интересует лишь то, что бывает, когда молекула находится в любом заданном состоянии вращения или поступательного движения. Физическую модель этих двух состояний можно наглядно представить себе следующим образом. Если вращать молекулу аммиака вокруг оси, проведенной через атом азота перпендикулярно плоскости атомов водорода, как показано на фиг. 7.1, мы обнаружим, что существуют два сорта состояний, которые не переходят друг в друга при таких поворотах и отличаются положением атома азота.
Фиг. 7.1. Физическая модель двух базисных состояний молекулы аммиака. Электрические дипольные моменты этих состояний равны m.
Азот может быть либо по одну сторону плоскости атомов водорода, либо по другую. Эти два состояния мы обозначаем |1> и |2>. Их мы выберем в качестве совокупности базисных состояний в нашем анализе поведения молекулы аммиака.
В системе с двумя базисными состояниями любое состояние |y> системы всегда может быть описано линейной комбинацией двух базисных состояний; это значит, что существует определенная амплитуда С1быть в одном базисном состоянии и амплитуда С2 быть в другом. Вектор состояния |y>можно записать в виде
где
Эта пара амплитуд меняется со временем согласно нашим гамильтоновым уравнениям — уравнениям (6.43). Используя симметрию двух состояний молекулы аммиака, мы полагаем H11=H22=E0и H12=H21=-А и получаем такое решение [см. (6.50) и (6.51)]:
Кинем теперь на эти решения более внимательный взгляд. Пусть сперва молекула была поставлена в состояние |y11>, для которого коэффициент b был равен нулю. Тогда при t=0 амплитуды оказаться в состояниях |1> и |2> одинаковы и останутся такими все время. Их фазы обе меняются во времени одинаково, с частотой (E0-A)/h. И точно так же, если бы мы поставили молекулу в состояние |y1>, для которого а=0, амплитуда C2равнялась бы C1с минусом, и это соотношение сохранилось бы навсегда — обе амплитуды менялись бы теперь во времени с частотой (E0+A)/h. Это все состояния, для которых связь между С1и С2не зависит от времени; других возможностей нет.
Мы нашли два частных решения, в которых амплитуды не меняются по величине и, более того, фазы меняются с одинаковой частотой. Это стационарные состояния по определению, данному в гл. 5, § 1, т. е. состояния с определенной энергией. Состояние |y11> обладает энергией Е11=Е0-А, а состояние |y1> — энергией E1=E0+A. Кроме этих, никаких стационарных состояний не существует, т. е. мы обнаруживаем, что у молекулы есть два уровня энергии, отличающиеся на 2А. (Подразумеваются, конечно, два уровня энергии для заданного состояния колебания и вращения, о которых говорилось в наших исходных допущениях.)
Если бы азот не мог перескакивать вверх или вниз, нам пришлось бы принять А равным нулю, и оба энергетических уровня (с энергией Е0)налезли бы один на другой. Истинные уровни не таковы; их среднее значение Е0, но они разведены на ±А, т. е. промежуток между энергиями двух состояний равен 2А. Поскольку А на самом деле мало, то и разница в энергиях очень мала.
Чтобы возбудить электрон внутри атома, требуются довольно высокие энергии, нужны фотоны оптического или ультрафиолетового диапазона. Чтобы возбудить вибрации молекул, требуются инфракрасные фотоны. Если речь идет о возбуждении вращений, различия в энергиях состояний соответствуют фотонам в далекой инфракрасной области. Но разность энергий 2А меньше их всех, меньше инфракрасных энергий, она приходится на микроволновой диапазон. Опытным путем было найдено, что существует пара уровней энергии с промежутком 10-4 эв, что отвечает частоте 24000 Мгц. Это, очевидно, означает, что 2A=hf, где f=24000 Мгц (отвечает волне длиной 11/4 см). Значит, перед нами молекула с переходами, которые вызывают испускание микроволн, а не свет в обычном смысле.
Для дальнейшей работы нам понадобится немного более удобное описание этих двух состояний с определенной энергией. Представим, что мы построили амплитуду С11из суммы двух чисел C1и С2:
Что бы это могло означать? Очень просто: это амплитуда того, что состояние |Ф> окажется в новом состоянии |//>, в котором амплитуды первоначальных базисных состояний равны между собой, Иначе говоря, когда мы пишем СII=<II |Ф>, то мы вправе абстрагироваться в уравнении (7.4) от |Ф>, поскольку оно выполняется при любых Ф, и писать
это означает то же самое, что и
Амплитуда того, что состояние (II} окажется в состоянии |1>, равна
а это, конечно, равняется просто единице, поскольку и |1>, и |2>суть базисные состояния. И амплитуда обнаружения состояния |II> в состоянии \2у тоже равна единице, так что у состояния |II> одинаковы амплитуды оказаться в каждом из базисных состояний |1> и |2>.
Но тут всплывает новая трудность. У состояния |II> полная вероятность оказаться то ли в одном базисном состоянии, то ли в другом получается больше единицы. Но это всего лишь означает, что вектор состояния неудачно «отнормирован». Чтобы исправить дело, надо вспомнить, что всегда для любого состояния обязано быть <II|II>=1. Использовав общее соотношение
полагая, что и Ф, и c суть состояние II, и суммируя по базисным состояниям |1> и |2>, получаем
Это даст, как положено, единицу, если мы изменим наше определение СII[см. уравнение (7.4)] и примем
Таким же путем можно построить и амплитуду
или
Эта амплитуда есть проекция состояния |Ф> на новое состояние |I>, обладающее амплитудами противоположного знака, для пребывания в состояниях |1> и |2>. А именно (7.6) означает то же самое, что и
или
откуда следует
Зачем все это нужно? С какой целью все это делается? Дело в том, что состояния |I> и |II> могут быть приняты за новую совокупность базисных состояний, особенно подходящую для описания стационарных состояний молекулы аммиака. Вы помните, что требования к совокупности базисных состояний были таковы:
Мы уже сами сделали так, чтобы было
Из (7.5) и (7.7) легко вывести, что и
Амплитуды СI=<I|Ф> и СII=<II|Ф> того, что любое состояние |Ф> окажется в одном из наших новых базисных состояний |I> и |II>, обязаны также удовлетворять гамильтонову уравнению вида (6.39). И действительно, если мы просто вычтем друг из друга два уравнения (7.2) и (7.3) и продифференцируем по t, то убедимся, что
А взяв сумму (7.2) и (7.3), увидим
Если за базисные состояния взять |I> и |II>, то гамильтонова матрица очень проста:
Заметьте, что каждое из уравнений (7.8) и (7.9) выглядит очень похоже на то, что получалось в гл. 6, § 6, для уравнения системы с одним состоянием. Они дают простую экспоненциальную зависимость от времени, отвечающую определенной энергии.
С ростом времени амплитуды пребывания в каждом из состояний ведут себя независимо.
Найденные нами раньше стационарные состояния |yI> и |yII> тоже являются, конечно, решениями уравнений (7.8) и (7.9). У состояния |yI> (для которого С1=-С2)
А у состояния |yII> (для которого С1=С2)
Пусть мы теперь умножили (7.10) на вектор состояния |/>; тогда получится
Вспомним, однако, что |I><I|=1; значит, это одно и то же, что сказать
Иначе говоря, вектор состояния стационарного состояния |yI> не отличается от вектора состояния базисного состояния |I> ничем, кроме экспоненциального множителя, связанного с энергией состояния. И действительно, при t=0
|yI>=|I>;
физическая конфигурация у состояния )/> та же самая, что и у стационарного состояния с энергией Е0+А. Точно так же для второго стационарного состояния получается
Состояние |II>— это просто стационарное состояние с энергией Е0-А при t=0. Стало быть, оба наших новых базисных состояния |I> и |II> физически имеют вид состояний с определенной энергией, но с изъятым экспоненциальным временным множителем, так что они могут быть приняты за базисные состояния, не зависящие от времени. (В дальнейшем нам будет удобно не отличать стационарные состояния |yI> и |yII> от их базисных состояний |I> и |II>, ведь различаются они только очевидными временными множителями.)
Подведем итог. Векторы состояний |I> и |II> — это пара базисных векторов, приспособленных для описания состояний молекулы аммиака с определенной энергией. Они связаны с нашими исходными базисными векторами формулами
Амплитуды пребывания в |I> и |II> связаны с С1и С2формулами
Всякое состояние может быть представлено линейной комбинацией |1> и |2>(с коэффициентами С1и С2) или линейной комбинацией базисных состояний с определенной энергией |I> и |II> (с коэффициентами СIи СII). Итак,
|Ф>=|1>С1+|2>С2, или
|Ф>=|I>СI+|II>СII.
Вторая формула дает нам амплитуды обнаружить состояние |Ф> в состоянии с энергией ЕI=Е0+А или в состоянии с энергией ЕII=Е0-А.
§ 2. Молекула в статическом электрическом поле
Если молекула аммиака находится в любом из двух состояний определенной энергии, а мы приложим к ней возмущение с частотой w, такой, что hw= EI-ЕП=2А, то система может перейти из нижнего состояния в верхнее. Или она может перейти из верхнего в нижнее и испустить фотон. Но для возбуждения таких переходов у вас должна быть физическая связь с состояниями — возможность возмущать систему. Должен существовать какой-то внешний механизм влияния на состояния, нечто вроде электрического или магнитного поля. В нашем частном случае эти состояния чувствительны к электрическому полю. На очереди, стало быть, у нас теперь проблема поведения молекулы аммиака во внешнем электрическом поле.
Для разбора этого поведения вернемся опять к первоначальной базисной системе |1> и |2> вместо |I> и |II>. Предположим, что имеется электрическое поле, направленное поперек плоскости атомов водорода. Пренебрежем на мгновение возможностью переброса атома азота вверх или вниз и зададим вопрос: верно ли, что энергия, этой молекулы в обоих положениях атома азота будет одинаковой? Вообще говоря, нет. Электроны стремятся к тому, чтобы находиться ближе к ядру азота, чем к ядрам водорода, так что водороды оказываются слегка положительно заряженными. Насколько — это зависит от деталей расположения электронов. Каково это распределение, точно представить очень трудно, но, во всяком случае, окончательный результат состоит в том, что у молекулы аммиака есть электрический дипольный момент, как показано на фиг.7.1. С его помощью можно продолжить дальнейший анализ, не интересуясь деталями направлений или величин смещений зарядов. Впрочем, чтобы наши обозначения не отличались от общепринятых, предположим, что электрический дипольный момент равен m и направлен от атома азота поперек плоскости атомов водорода.
Далее, когда азот перепрыгивает с одной стороны на другую, то центр масс не перемещается, а электрический дипольный момент переворачивается. В результате энергия в электрическом поле x будет зависеть от ориентации молекулы. При сделанном только что допущении потенциальная энергия будет выше тогда, когда атом азота будет удален от плоскости водородов в направлении поля, и ниже, когда он удален в обратную сторону; промежуток между обеими энергиями будет равен 2mx.
До этого места мы вынуждены были делать предположения о том, чему равны Е0и А, не зная, как подсчитать их. В соответствии со строгой физической теорией обязана существовать возможность вычисления этих констант, если известны положения и движения всех ядер и электронов. Но никто никогда не делал этого. В систему входит десяток электронов и четверка ядер, и задача чересчур сложна. Факт остается фактом: о молекуле этой никто не знает больше того, что знаем мы с вами. И все, что всякий может о ней сказать,— что в электрическом поле энергия двух состояний отличается и разность энергий пропорциональна электрическому полю. Коэффициент пропорциональности мы обозначили 2m, но его величина должна определяться экспериментально. Можно еще сказать, что молекула имеет амплитуду А перевернуться, но и она должна измеряться экспериментально. Никто не укажет нам точных теоретических значений m и А, потому что расчеты уж слишком сложны, чтобы честно их проделать.
Для молекулы аммиака в электрическом поле наше описание придется изменить. Если игнорировать амплитуду переброса молекулы из одной конфигурации в другую, то энергии двух состояний |1> и |2>обязаны быть равны (Е0±mx). Следуя процедуре, принятой в предыдущей главе, мы примем
Кроме того, предположим, что при интересующих нас электрических полях сами поля не сказываются заметно на геометрии молекулы и, стало быть, на амплитуде того, что атом азота перепрыгнет из одного положения в другое.
Поэтому можно принять, что Н12и H21 не изменились, т. е.
H12=H21=-А. (7.15)
Теперь с этими новыми значениями Нijнадо решать гамильтоновы уравнения (6.43). Мы могли бы их решить просто, как делали это прежде, но поскольку нам не раз, видимо, представится случай решать системы с двумя состояниями, то давайте уж решим их раз и навсегда в общем случае произвольного Нij, считая только, что со временем оно не меняется.
Мы ищем общее решение пары гамильтоновых уравнений
Это линейные дифференциальные уравнения с постоянными коэффициентами. Значит, всегда можно найти решения, являющиеся экспоненциальными функциями независимой переменной t. Сперва отыщем решения, в которых С1и С2 одинаково зависят от времени; возьмем пробные функции
Поскольку это решение отвечает состоянию с энергией E=hw,
то можно прямо написать
где Е пока неизвестна и должна быть определена так, чтобы дифференциальные уравнения (7.16) и (7.17) выполнялись. При подстановке С1и С2 из (7.18) и (7.19) в дифференциальные уравнения (7.16) и (7.17) производные дают просто -iE/h, умноженное на С1или C2, так что слева остается попросту ЕС1или ЕС2. Сокращая общие экспоненциальные множители, получаем
или после перестановки членов
У такой системы однородных алгебраических уравнений ненулевые решения для а1 и а2 будут лишь тогда, когда определитель, составленный из коэффициентов при а1и а2, равен нулю, т. е. если
Но когда уравнений два и неизвестных тоже два, то можно обойтись и без столь возвышенных представлений. Каждое из уравнений (7.20) и (7.21) дает отношение двух коэффициентов a1 и а2, и эти два отношения должны быть равны. Из (7.20) мы имеем
а из (7.21)
Приравнивая эти отношения, получаем, что Е должно удовлетворять равенству
(E-H11)(E-H22)-H12H21=0.
То же получилось бы и из (7.22). В любом случае для Е получается квадратное уравнение с двумя решениями:
Энергия E может иметь два значения. Заметьте, что оба они вещественны, потому что Н11и H22 вещественны, а Н12Н21, равное Н12H12=|H12|2, тоже вещественно, да к тому же положительно.
Пользуясь тем же соглашением, что и раньше, обозначим большую энергию EI, а меньшую ЕII. Имеем
Подставив каждую из этих энергий по отдельности в (7.18) и (7.19), получим амплитуды для двух стационарных состояний (состояний определенной энергии). Если нет каких-либо внешних возмущений, то система, первоначально бывшая в одном из этих состояний, останется в нем навсегда, у нее только фаза будет меняться.
Наши результаты можно проверить на двух частных случаях. Если H12=H21=0, то получается EI=H11 и EII=H22. А это бесспорно правильно, потому что тогда уравнения (7.16) и (7.17) не связаны и каждое представляет состояние с энергией H11 и H22. Далее, положив H11=H22=E0 и H21=H12=-А, придем к найденному выше решению:
еI=е0+а и еII=е0-а.
В общем случае два решения ЕIи ЕIIотносятся к двум состояниям; мы их опять можем назвать состояниями
У этих состояний С1и С2будут даваться уравнениями (7.18) и (7.19), где а1и а2 еще подлежат определению. Их отношение дается либо формулой (7.23), либо (7.24). Они должны также удовлетворять еще одному условию. Если известно, что система находится в одном из стационарных состояний, то сумма вероятностей того, что она окажется в |1>или |2>, должна равняться единице. Следовательно,
или, что то же самое,
Эти условия не определяют а1и а2 однозначно: остается еще произвол в фазе, т. е. в множителе типа еid. Хотя для а можно выписать общие решения, но обычно удобнее вычислять их в каждом отдельном случае.
Вернемся теперь к нашему частному примеру молекулы аммиака в электрическом поле. Пользуясь значениями Н11, H22 и Н12из (7.14) и (7.15), мы получим для энергий двух стационарных состояний выражения
Эти две энергии как функции напряженности x электрического поля изображены на фиг. 7.2.
Фиг. 7,2. Уровни энергии молекулы аммиака в электрическом поле.
Кривые построены по формулам (7.30):
Когда электрическое поле нуль, то энергии, естественно, обращаются в Е0±А. При наложении электрического поля расщепление уровней растет. Сперва при малых x оно растет медленно, но затем может стать пропорциональным $. (Эта линия — гипербола.) В сверхсильных полях энергии попросту равны
Тот факт, что у азота существует амплитуда переброса вверх — вниз, малосуществен, когда энергии в этих двух положениях сильно отличаются. Это интересный момент, к которому мы позже еще вернемся.
Теперь мы наконец готовы понять действие аммиачного мазера. Идея в следующем. Во-первых, мы находим способ отделения молекул в состоянии |I> от молекул в состоянии |II>. Затем молекулы в высшем энергетическом состоянии |I> пропускаются через полость, у которой резонансная частота равна 24000 Мгц. Молекулы могут оставить свою энергию полости (способ будет изложен позже) и покинуть полость в состоянии |II>. Каждая молекула, совершившая такой переход, передаст полости энергию E=EI-ЕII. Энергия, отобранная у молекул, проявится в виде электрической энергии полости.
Как же разделить два молекулярных состояния? Один способ такой. Аммиачный газ выпускается тонкой струйкой и проходит через пару щелей, создающих узкий пучок (фиг. 7.3).
Фиг. 7.3. Пучок молекул аммиака может быть разделен электрическим полем, в котором x2 обладает градиентом, перпендикулярным пучку.
Затем пучок пропускается через область, в которой имеется сильное поперечное электрическое поле. Создающие поле электроды изогнуты так, чтобы электрическое поле поперек пучка резко менялось. Тогда квадрат x·x электрического поля будет иметь большой градиент, перпендикулярный пучку. А у молекулы в состоянии |/> энергия с x2растет, значит, эта часть пучка отклонится в область меньших x2. Молекула же в состоянии |II>, наоборот, отклонится к области, где x2побольше, потому что ее энергия падает, когда x2растет.
Кстати, при тех электрических полях, которые удается генерировать в лаборатории, энергия mx всегда много меньше А. В этом случае корень в уравнении (7.30) приближенно равен
Во всех практических случаях энергетические уровни, стало быть, равны
и
и энергии с x2меняются линейно. Действующая на молекулы сила тогда равна
Энергия в электрическом поле у многих молекул пропорциональна x2. Коэффициент — это поляризуемость молекулы. Поляризуемость аммиака необычно высока: у него А в знаменателе очень мало. Стало быть, молекулы аммиака очень чувствительны к электрическому полю.
§ 3. Переходы в поле, зависящем от времени
В аммиачном мазере пучок молекул в состоянии |7> и с энергией ЕIпропускается через резонансную полость, как показано на фиг. 7.4.
Фиг. 7.4. Схематическое изображение аммиачного мазера.
Другой пучок отводится прочь. Внутри полости существует меняющееся во времени электрическое поле, так что нашей очередной задачей явится изучение поведения молекулы в электрическом поле, которое меняется во времени. Это совершенно новый род задач — задача с гамильтонианом, меняющимся во времени. Раз Htjзависит от x, то и Hijменяется во времени, и нам надлежит определить поведение системы в этих обстоятельствах.
Для начала выпишем уравнения, которые нужно решить:
Для определенности положим, что электрическое поле меняется синусоидально; тогда можно написать
На самом деле частота w берется всегда очень близкой к резонансной частоте молекулярного перехода w0=2A/h, но пока мы для общности будем считать w произвольной. Лучший способ решить наши уравнения — это, как и прежде, составить из C1и С2 линейные комбинации. Сложим поэтому оба уравнения, разделим на у 2 и вспомним определения СIи СIIиз (7.13), Получим
Вы видите, что это похоже на (7.9), но появился добавочный член от электрического поля. Равным образом, вычитая уравнения (7.36), получаем
Вопрос теперь в том, как решить эти уравнения. Это труднее, чем прежде, потому что x зависит от t; и действительно, при общем x (t)решение не представимо в элементарных функциях. Однако, пока электрическое поле мало, можно добиться хорошего приближения. Сперва напишем
Если бы электрического поля не было, то, беря в качестве gI и gII две комплексные постоянные, мы бы получили правильное решение. Ведь поскольку вероятность быть в состоянии |/ > есть квадрат модуля CI, а вероятность быть в состоянии |II> есть квадрат модуля СII, то вероятность быть в состоянии |I>или в состоянии |II> равна просто |gI|2 или |gII|2. Например, если бы система начинала развиваться из состояния |II> так, что gI было бы нулем, a |gII|2— единицей, то эти условия сохранились бы навсегда. Молекула из состояния |II> никогда бы не перешла в состояние |I>.
Польза записи решений в форме (7.40) состоит в том, что оно сохраняет свой вид и тогда, когда есть электрическое поле, если только mx меньше А, только gI и gII при этом станут медленно меняющимися функциями времени. «Медленно меняющиеся» означает медленно в сравнении с экспоненциальными функциями. В этом весь фокус. Для получения приближенного решения используется тот факт, что gI и gII меняются медленно.
Подставим теперь СIиз (7.40) в дифференциальное уравнение (7,39), но вспомним, что gI тоже зависит от t. Имеем
Дифференциальное уравнение обращается в
Равным образом уравнение для dCII/dt обращается в
Обратите теперь внимание, что в обеих частях каждого уравнения имеются одинаковые члены. Сократим их и умножим первое уравнение на
а второе на
. Вспоминая, что (EI- eii)=2А=hw0, мы в конце концов получаем
Получилась довольно простая пара уравнений — и пока еще точная. Производная от одной переменной есть функция от времени, умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.
Нас, по крайней мере сейчас, интересует только случай колеблющегося электрического поля. Взяв x(t) в форме (7.37), мы увидим, что уравнения для gI и gIIобратятся в
(it
И вот если x0достаточно мало, то скорости изменения gI и gIIтоже будут малы. Обе у не будут сильно меняться с t, особенно в сравнении с быстрыми вариациями, вызываемыми экспоненциальными членами. У этих экспоненциальных членов есть вещественные и мнимые части, которые колеблются с частотой w+w0 или w-w0. Члены с частотой w+w0 колеблются вокруг среднего значения (нуля) очень быстро и поэтому не дадут сильного вклада в скорость изменения g. Значит, можно сделать весьма разумное приближение, заменив эти члены их средним значением, т. е. нулем. Их просто убирают и в качестве приближения берут
Но даже и оставшиеся члены с показателями, пропорциональными (w-w0), меняются быстро, если только w не близко к w0. Только тогда правая сторона будет меняться достаточно медленно для того, чтобы набежало большое число, пока интегрируешь эти уравнения по t. Иными словами, при слабом электрическом поле изо всех частот представляют важность лишь те, которые близки к w0.
При тех приближениях, которые были сделаны для того, чтобы получить (7.45), эти уравнения можно решить и точно; но работа эта все же трудоемкая, и мы отложим ее на другое время, когда обратимся к другой задаче того же типа. Пока же мы их просто решим приближенно, или, лучше сказать, найдем точное решение для случая идеального резонанса w=w0 и приближенное — для частот близ резонанса.
§ 4. Нереходы при резонансе
Первым рассмотрим случай идеального резонанса. Если положить w=w0, то экспоненты в обоих уравнениях (7.45) станут равными единице, и мы просто получим
Если из этих уравнений исключить сперва gI, а потом gII, то мы увидим, что каждое из них удовлетворяет дифференциальному уравнению простого гармонического движения
Общее решение этих уравнений может быть составлено из синусов и косинусов. Легко проверить, что решениями являются следующие выражения:
где а и b — константы, которые надо еще определить так, чтобы они укладывались в ту или иную физическую ситуацию.
К примеру, предположим, что при t=0 наша молекулярная система была в верхнем энергетическом состоянии |I>, а это требует [из уравнения (7.40)], чтобы gI=1 и gII=0 при t=0. Для такого случая должно быть а=1 и b=0. Вероятность того, что молекула окажется в том же состоянии |I> в какой-то позднейший момент t, равна квадрату модуля gI, или
Точно так же и вероятность того, что молекула окажется в состоянии |II>, дается квадратом модуля gII:
Пока x мало и пока мы находимся в резонансе, вероятности даются простыми колебательными функциями. Вероятность быть в состоянии |I> падает от единицы до нуля и возрастает опять, а вероятность быть в состоянии |II> растет от нуля до единицы и наоборот. Изменение обеих вероятностей во времени показано на фиг. 7.5.
Фиг. 7.5. Вероятности обоих состояний молекулы аммиака в синусоидальном электрическом поле.
Нечего и говорить, что сумма обеих вероятностей всегда равна единице; ведь молекула всегда находится в каком-то состоянии.
Положим, что прохождение через полость занимает у молекулы время Т. Если сделать полость как раз такой длины, чтобы было mx0Т/h=p/2, то молекула, ныряющая в нее в состоянии |I>, наверняка вынырнет из нее в состоянии |II>. Если она вошла в полость в верхнем состоянии, то выйдет из полости в нижнем. Иными словами, ее энергия упадет, и эта потеря энергии не сможет перейти ни во что другое, а только в механизм, который генерирует поле. Детали, которые помогли бы вам разглядеть, как именно энергией молекулы питаются колебания полости, не так уж просты; однако нам и не нужно все эти детали изучать, потому что имеется принцип сохранения энергии. (Мы могли бы, если бы это было нужно, изучить их, но тогда нам пришлось бы иметь дело с квантовой механикой поля в полости наряду с квантовой механикой атома.)
Подытожим. Молекула входит в полость, поле полости, колеблющееся с как раз нужной частотой, индуцирует переходы с верхнего состояния на нижнее, и высвобождаемой энергией питается осциллирующее поле. В работающий мазер молекулы доставляют достаточно энергии для того, чтобы поддерживались колебания полости, ее хватает не только на то, чтобы возместить потери в полости, но и на то, чтобы небольшие избытки энергии извлекались из полости. Итак, молекулярная энергия превращается в энергию внешнего электромагнитного поля.
Вспомним, что перед входом в полость нам приходилось пользоваться фильтром, который разделял пучок так, что в полость входило только верхнее состояние. Легко показать, что, если бы мы начали с молекул в нижнем состоянии, процесс пошел бы в другую сторону и энергия от полости отбиралась бы. Если пустить в полость нефильтрованный пучок, то сколько молекул будет отбирать энергию от полости, столько же из них будет отдавать ей свою энергию, и в итоге ничего не случится. В настоящем мазере, конечно, не обязательно делать (mx0T/h) точно равным p/2. И при других значениях (кроме точных кратных p) существует какая-то вероятность переходов из состояния |I> в состояние |II>. Но при этих других значениях прибор уже не имеет к. п. д., равного 100%; многие из молекул, покидающие полость, могли бы снабдить ее энергией, но не сделали этого.
На самом деле и скорости молекул неодинаковы; они распределены по Максвеллу. Это означает, что идеальные периоды времени для разных молекул окажутся различными, и невозможно получить к. п. д., равный 100%, сразу для всех молекул. Вдобавок имеется еще одно усложнение, которое, правда, легко принять во внимание, но на этой стадии мы не будем им заниматься. Вы помните, что электрическое поле обычно меняется в полости от места к месту. Когда молекулы дрейфуют вдоль полости, электрическое поле близ молекул меняется как-то очень сложно, сложнее, чем предположенное нами обычное синусоидальное колебание. Ясно, что для точного решения задачи следовало бы воспользоваться более сложными интегрированиями, но общая идея остается прежней.
Можно мазеры устраивать и иначе. Не отделять прибором Штерна — Герлаха атомы в состоянии |I> от атомов в состоянии |II>, а собрать атомы в какой-то полости (в газообразном или твердом виде) и как-то переселить их из состояния |II> в состояние |I>. Один такой способ применяется в так называемом трехуровневом мазере. Для него используются атомные системы с тремя уровнями энергии (фиг. 7.6) и со следующими специальными свойствами.
Фиг. 7.6. Уровни энергии «трехуровневого» мазера.
Система поглощает излучение (скажем, свет) с энергией hw1и переходит от низшего уровня энергии ЕIIк какому-то более высокому уровню Е', а затем быстро испускает фотоны с энергией hw2 и переходит в состояние |/> с энергией ЕI. У состояния |I> большое время жизни, так что его населенность может возрасти; создаются условия, благоприятствующие работе мазера между состояниями |I> и |II>. Хотя такой прибор называют «трехуровневым» мазером, но сама мазерная процедура на самом деле происходит так же, как и у описанной нами двухуровневой системы.
Лазер — это всего-навсего мазер, действующий на световых частотах. «Полость» лазера обычно состоит попросту из двух зеркал, между которыми генерируются стоячие волны.
§ 5. Переходы вне резонанса
Наконец, хотелось бы выяснить, как изменяются состояния в условиях, когда частота полости, хотя и близка к w0, но не совпадает с ней. Эту задачу можно было бы решить точно, но мы не будем пытаться это делать, а обратимся к важному случаю малого электрического поля и малого промежутка времени Т, так что mx0T/h много меньше единицы. Тогда даже в случае уже изученного нами идеального - резонанса вероятность перехода очень мала. Будем исходить опять из того, что gI=1 и gII=0. Тогда мы вправе ожидать, что в течение всего времени Т наша величина gI останется близкой к единице, а gII будет малой по сравнению с единицей, и задача облегчается. Из второго уравнения (7.45) мы можем подсчитать gII, принимая gIравной единице и интегрируя от t=0 до t=T. Получается
Это та величина gII, которая стоит в (7.40), и она дает амплитуду того, что переход из состояния |I> в состояние |II> произойдет за время Т. Вероятность Р (I®II) такого перехода равна
|gII|2, или
Интересно начертить эту вероятность при фиксированном времени T как функцию частоты полости, чтобы посмотреть, насколько чувствительна она к частотам близ резонансной частоты w0. Кривая Р (I®II) показана на фиг. 7.7.
Фиг. 7.7. Вероятность перехода для молекулы аммиака как функция частоты.
(Вертикальная шкала была подогнана так, чтобы в пике была единица, для этого разделили на величину вероятности при w=w0.) С подобными кривыми мы встречались в теории дифракции, так что они должны быть вам знакомы. Кривая довольно резко падает до нуля при
(w-w0)=2p/T и никогда при больших отклонениях частоты снова не достигает заметной величины. Почти вся площадь под кривой лежит в пределах ±p/T. Можно показать [с помощью формулы
что площадь под кривой равна 2p/T и совпадает с площадью выделенного штрихованной линией прямоугольника.
Посмотрим, что это дает для реального мазера. Возьмем разумное время пребывания молекулы аммиака в полости, скажем 1 мсек. Тогда для f0=24000 Мгц можно подсчитать, что вероятность падает до нуля при отклонениях (f-f0)/f0=1/f0T, т. е. порядка 5·10-8. Очевидно, что для заметных вероятностей перехода частоты должны очень точно совпадать с w0. Этот эффект является основой той большой точности, которой можно достичь в «атомных» часах, работающих на принципе мазера.
§ 6. Поглощение света
Наше изложение применимо и к более общему случаю, чем аммиачный мазер. Мы ведь изучали поведение молекулы под влиянием электрического поля независимо от того, заключено оно в полость или нет. Просто можно было направить пучок «света» — микроволновой частоты — на молекулу и искать вероятность испускания или поглощения. Наши уравнения ничуть не хуже применимы и к этому случаю, но только лучше переписать их на языке интенсивности излучения, а не электрического поля. Если определить интенсивность как средний поток энергии через единицу площади в секунду, то из гл. 27 (вып. 6) следует
(Максимум x равен 2x0.) Вероятность перехода принимает вид
Обычно свет, освещающий подобную систему, не точно монохроматичен. Поэтому интересно решить еще одну задачу— подсчитать вероятность перехода, когда интенсивность света на единицу интервала частот равна и покрывает собой широкую полосу, включающую w0. Тогда вероятность перехода от |I> к |II> обратится в интеграл
Как правило, меняется с w медленнее, чем острый резонансный фактор. Эти две функции могут выглядеть так, как показано на фиг. 7.8.
Фиг. 7.8. Спектральная интенсивность может быть представлена своим значением при w0.
В таких случаях можно заменить ее значением в центре острой резонансной кривой и вынести из-под интеграла. Оставшийся интеграл — это просто площадь под кривой на фиг. 7.7, которая, как известно, равна 2p/Т. Мы приходим к результату
Это очень важный результат; перед нами общая теория поглощения света любой молекулярной или атомной системой. Хотя мы вначале считали, что состояние |I> обладает более высокой энергией, чем состояние |II>, но никакие наши рассуждения от этого не зависели. Уравнение (7.55) соблюдается и тогда, когда энергия состояния |I> ниже энергии состояния |II>; тогда Р (I®II) представляет собой вероятность перехода с поглощением энергии от падающей электромагнитной волны. Поглощение атомной системой света всегда предполагает, что имеется амплитуда для перехода в колеблющемся электрическом поле между состояниями, отличающимися на энергию E=hw0. В каждом отдельном случае она рассчитывается так же, как мы это проделали, и дает выражения наподобие (7.55). Поэтому мы подчеркнем следующие свойства этой формулы. Во-первых, вероятность пропорциональна Т. Иными словами, существует неизменная вероятность на единицу времени, что переход произойдет. Во-вторых, эта вероятность пропорциональна интенсивности света, падающего на систему. В-третьих, вероятность перехода пропорциональна m2, где, как вы помните, mx определяет энергетический сдвиг, вызываемый электрическим полем x. По этой именно причине mx появлялось и в уравнениях (7.38) и (7.39) в качестве коэффициента связи, ответственного за переход между стационарными состояниями |I> и |II>. Иными словами, для рассматривавшихся нами малых x член mx есть так называемое «возмущение» в матричном элементе гамильтониана, связывающем состояния |/> и |//>. В общем случае mx заменилось бы матричным элементом <II|H|I> (см. гл. 3, § 6).
В гл. 42, § 5 (вып. 4) мы говорили о связи между поглощением света, вынужденным испусканием и самопроизвольным испусканием в терминах введенных Эйнштейном коэффициентов А и В. Здесь наконец-то в наших руках появляется квантовомеханическая процедура для подсчета этих коэффициентов. То, что мы обозначили Р (I®II) для нашей аммиачной двухуровневой молекулы, в точности соответствует коэффициенту поглощения Bnmв эйнштейновской теории излучения. Из-за сложности молекулы аммиака — слишком трудной для расчета — нам пришлось взять матричный элемент <II|H|I> в виде mx и говорить, что m извлекается из опыта. Для более простых атомных систем величину mmn, отвечающую к произвольному переходу, можно подсчитать, исходя из определения
где Нmn — это матричный элемент гамильтониана, учитывающего влияние слабого электрического поля. Величина mmn, вычисленная таким способом, называется электрическим дипольным матричным элементом, Квантовомеханическая теория поглощения и испускания света сводится тем самым к расчету этих матричных элементов для тех или иных атомных систем.
Итак, изучение простых систем с двумя состояниями (двухуровневых) привело нас к пониманию общей проблемы поглощения и испускания света.
* Теперь мы опять будем писать | I> и | II> вместо |yI> и |yII>. Вы должны вспомнить, что настоящие состояния |yI> и |yII> суть энергетические базисные состояния, умноженные на соответствующий экспоненциальный множитель.
* Например, как легко убедиться, одно из допустимых решений имеет вид
* Очень жаль, но нам придется ввести новое обозначение. Раз буквы р и Е заняты у нас импульсом и энергией, то мы поостережемся опять обозначать ими дипольный момент и электрическое поле. Напомним, что в этом параграфе m означает электрический дипольный момент.
* В дальнейшем полезно (и читая, и произнося вслух) отличать арабские 1 и 2 и римские I и II. Мы считаем, что удобно для арабских, цифр резервировать названия «один» и «два», а I и II читать как «первый», «второй».
Глава 8 ДРУГИЕ СИСТЕМЫ С ДВУМЯ состояниями
§ 1. Молекулярный ион водорода
§ 2. Ядерные силы
§ 3. Молекула водорода
§ 4.Молекула бензола
§ 5. Красители
§ 6.Гамильтониан частицы со спином 1/2 в магнитном поле
§ 7.Вращающийся электрон в магнитном поле
§ 1. Молекулярный ион водорода
В предыдущей главе мы обсудили некоторые свойства молекулы аммиака в предположении, что это система о двух состояниях (или двухуровневая система). На самом деле, конечно, это не так — у нее есть множество состояний: вращения, колебания, перемещения и т. д., но в каждом из этих состояний движения следует говорить о паре внутренних состояний из-за того, что атом азота может быть переброшен с одной стороны плоскости трех атомов водорода на другую. Сейчас мы рассмотрим другие примеры систем, которые в том или ином приближении можно будет считать системами с двумя состояниями. Многое здесь будет приближенным, потому что всегда имеется множество других состояний, и в более точном анализе их следовало бы учитывать. Но в каждом из этих примеров мы окажемся в силах очень многое понять, рассуждая только о двух состояниях.
Раз мы будем иметь дело только с двухуровневыми системами, то нужный нам гамильтониан будет выглядеть так же, как и в предыдущей главе. Когда гамильтониан не зависит от времени, то известно, что имеются два стационарных состояния с определенными (и обычно разными) энергиями. В общем случае, однако, мы будем начинать наш анализ с выбора базисных состояний (не обязательно этих стационарных состояний), таких, которые, скажем, имеют другой простой физический смысл. Тогда стационарные состояния системы будут представлены линейной комбинацией этих базисных состояний.
Для удобства подытожим важнейшие уравнения, выведенные в гл. 7, Пусть первоначально в качестве базисных состояний были приняты |1> и |2>. Тогда любое состояние |y> представляется их линейной комбинацией:
Амплитуды Сi (под этим подразумеваются как C1так и С2) удовлетворяют двум линейным дифференциальным уравнениям
где и i, и j принимают значения 1 и 2.
Когда члены гамильтониана Hij не зависят от t, то два состояния с определенной энергией (стационарные), которые мы обозначим
обладают энергиями
Для каждого из этих состояний оба С имеют одинаковую зависимость от времени. Векторы состояний |I> и |II>, которые отвечают стационарным состояниям, связаны с нашими первоначальными базисными состояниями |1> и |2>формулами
Здесь а —комплексные постоянные, удовлетворяющие равенствам
Если H11 и H22 между собой равны, скажем оба равны Е0, а H12=H21=-А, то EI=E0+A, ЕII=Е0-А, и состояния | I> и |II> особенно просты:
Эти результаты мы хотим теперь использовать, чтобы рассмотреть ряд интересных примеров, взятых из химии и физики. Первый пример — это ион молекулы водорода. Положительно ионизированная молекула водорода состоит из двух протонов и одного электрона, как-то бегающего вокруг них. Каких состояний можно ожидать для этой системы, если расстояние между протонами велико? Ответ вполне ясен: электрон расположится вплотную к одному протону и образует атом водорода в его наинизшем состоянии, а другой протон останется одиночкой, положительным ионом. Значит, когда два протона удалены друг от друга, то можно себе наглядно представить одно физическое состояние, в котором электрон «придан» одному из протонов. Существует, естественно, и другое, симметричное первому состояние, в котором электрон находится возле второго протона, а ионом оказывается первый протон. Эту пару состояний мы и сделаем базисными, обозначив их |1> и |2>. Они показаны на фиг. 8.1.
Фиг. 8.1. Совокупность базисных состояний для двух протонов и электрона.
Конечно, на самом деле у электрона возле протона имеется множество состояний, потому что их комбинация может существовать в виде одного из возбуждённых состояний атома водорода. Но нас сейчас не интересует это разнообразие состояний, мы будем рассматривать лишь случай, когда атом водорода пребывает в наинизшем состоянии — своем основном состоянии,— и пренебрежем на время спином электрона. Мы просто предположим, что для всех наших состояний спин электрона направлен вверх по оси z.
Чтобы убрать электрон из атома водорода, требуется 13,6 эв энергии. Столько же энергии — очень много по нашим теперешним масштабам — понадобится и на то, чтобы электрон оказался на полпути между протонами (коль скоро сами протоны сильно удалены друг от друга). Так что по классическим понятиям электрону немыслимо перескочить от одного протона к другому. Однако в квантовой механике это возможно, хоть и не очень вероятно. Существует некая малая амплитуда того, что электрон уйдет от одного протона к другому. Тогда в первом приближении каждое из наших базисных состояний |1> и |2> будет иметь энергию Е0, равную просто сумме энергий атома водорода и протона. Матричные элементы Н11и H22 гамильтониана мы можем принять приближенно равными Е0. Другие матричные элементы Н12и Н21, представляющие собой амплитуды перехода электрона туда и обратно, мы опять запишем в виде -А.
Вы видите, что это та же игра, в какую мы играли в последних двух главах. Если пренебречь способностью электрона перескакивать туда и обратно, то два состояния будут иметь в точности одинаковую энергию. Эта энергия, однако, расщепляется на два энергетических уровня из-за того, что электрон может переходить туда и назад, и чем больше вероятность перехода, тем больше расщепление. Стало быть, два уровня энергии системы равны Е0+А и Е0-А, и состояния, у которых такие энергии, даются уравнениями (8.7).
Из нашего решения мы видим, что если протон и водородный ион как-то расположить близко один к другому, то электрон не останется подле одного протона, а будет перескакивать от протона к протону и обратно. Если вначале он был близ одного из протонов, то затем он начнет колебаться туда и назад между состояниями |1> и |2>, давая решение, меняющееся во времени. Чтобы получить решение, отвечающее самой низкой энергии (которое не меняется со временем), необходимо, чтобы вначале система обладала одинаковыми амплитудами пребывания электрона возле каждого из протонов. Кстати, вспомните, что электронов отнюдь не два; мы совсем не утверждаем, что вокруг каждого протона имеется электрон. Имеется только один электрон, и это он имеет одинаковую амплитуду (1/Ц2 по величине) быть в том или ином положении.
Дальше, для электрона, который находится близ одного протона, амплитуда А оказаться близ другого зависит от расстояния между протонами. Чем они ближе один к другому, тем больше амплитуда. Вы помните, что в гл. 5 мы говорили об амплитуде «проникновения» электрона «сквозь барьер», на что по классическим канонам он не способен. Здесь то же самое положение дел. Амплитуда того, что электрон переберется к другому протону, спадает с расстоянием примерно по экспоненте (для больших расстояний). Раз вероятность, а следовательно, и значение А при сближении протонов возрастают, то возрастает и расстояние между уровнями энергии. Если система находится в состоянии |I>, то энергия Е0+А с уменьшением расстояния растет так, что эти квантовомеханические эффекты приводят к силе отталкивания, стремящейся развести протоны. Если же система пребывает в состоянии |II>, то полная энергия при сближении протонов убывает; существует сила притяжения, подтягивающая протоны один к другому. Эти энергии меняются с расстоянием между протонами примерно так, как показано на фиг. 8.2.
Фиг. 8.2. Энергии двух стационарных состояний иона h+2 как функция расстояния между двумя протонами.
Тем самым у нас появляется квантовомеханическое объяснение силы связи, скрепляющей
ион H+2.
Однако мы позабыли об одной вещи. В дополнение к только что описанной силе имеется также электростатическая сила взаимного отталкивания двух протонов. Когда оба протона очень удалены друг от друга (как на фиг. 8.1), то «голый» протон видит перед собой только нейтральный атом, так что электростатической силой можно пренебречь. При очень тесных сближениях, однако, «голый» протон оказывается порой «внутри» электронного распределения, т. е. в среднем он ближе к протону, чем к электрону. Появляется некоторая добавочная электростатическая энергия, которая, конечно, положительна. Эта энергия — она тоже зависит от расстояния — должна быть включена в Е0. Значит, за Е0мы должны принять нечто похожее на штриховую кривую на фиг. 8.2; она быстро подымается на расстояниях, меньших, чем радиус атома водорода. Энергию переворота А надо вычесть и прибавить к этому Е0. Если это сделать, то энергии ЕIи ЕIIбудут меняться с межпротонным расстоянием D, как показано на фиг. 8.3.
Фиг. 8.3. Уровни энергии иона H+2 как функция межпротонного расстояния D (EH=13,6 эв).
[На рисунке мы воспроизвели результаты более детальных выкладок. Межпротонное расстояние дано в ангстремах (1Е=10-8 см), а избыток энергии над протоном плюс водородным ионом дается в единицах энергии связи атома водорода, так называемых «ридбергах» (13,6 эв).]Мы видим, что состояние |II> имеет точку минимума энергии — равновесную конфигурацию (условие наинизшей энергии) для иона Н+2 . Энергия в этой точке ниже, чем энергии отдельно протона и отдельно водородного иона, так что система связана. Отдельный электрон действует так, что скрепляет протоны. Химик назвал бы это «одноэлектронной связью».
Этот род химической связи часто также называют «квантовомеханическим резонансом» (по сходству с двумя связанными маятниками, о котором мы уже говорили). Но звучит это таинственнее, чем оно есть на самом деле; это только тогда «резонанс», когда базисные состояния с самого начала неудачно выбраны, как у нас и было! А если выбрать состояние |II>, вы сразу получите наинизшее энергетическое состояние — и все.
Можно и по-иному объяснить, отчего энергия этого состояния должна быть ниже, чем у протона плюс атома водорода. Представим себе электрон возле двух протонов, удаленных на определенное, но не очень большое расстояние. Вы помните, что электрон возле одиночного протона «размазан» из-за принципа неопределенности. Он ищет равновесия, пытаясь раздобыть энергию пониже (низкую кулоновскую потенциальную энергию) и не оказаться при этом сжатым в пространстве чересчур тесно, что привело бы к высокой кинетической энергии (из-за соотношения неопределенности DpDx»h). Если же протонов два, то будет больше места, где у электрона может быть низкая потенциальная энергия. Он может размазаться (снижая тем самым свою кинетическую энергию), не повышая при этом своей потенциальной энергии. В итоге его энергия ниже, чем в атоме водорода. Тогда почему же у другого состояния |I> энергия выше? Но заметьте, что это состояние есть разность состояний |1> и |2>. Вследствие симметрии |1> и |2> разность должна иметь нулевую амплитуду того, что электрон окажется на полпути между протонами. Это означает, что электрон немного сильнее ограничен в пространстве, что и приводит к большей энергии.
Следует сказать, что наше приближенное рассмотрение иона H+2 как двухуровневой системы рассыпается в прах, едва лишь протоны сблизятся до минимума энергии на кривой фиг. 8.3; тогда больше не получается хорошего значения истинной энергии связи. На малых удалениях энергии двух «состояний» на самом деле уже не равны Е0; требуется более тонкое квантовомеханическое рассмотрение.
Положим, мы теперь заинтересуемся, что случилось бы, если бы вместо двух протонов у нас были два разных объекта, скажем один протон и один положительный ион лития (причем обе частицы по-прежнему имеют по единичному положительному заряду). В этом случае два члена Н11и H22 в гамильтониане больше не совпадали бы; они были бы совершенно различны. Если бы оказалось, что разность (H11-H22) по абсолютной величине много больше А=-H12, то сила притяжения стала бы очень слабой. В этом можно убедиться следующим образом.
Если в (8.3) подставить H12H21=A2, то мы получим
Когда H11-H22 много больше А2, корень довольно точно равен
Тогда энергии обращаются в
Теперь они почти вплотную совпадают с энергиями H11 и H22 изолированных атомов и только чуть-чуть отличаются из-за наличия амплитуды перескока А.
Разность энергий (ЕI-ЕII) равна
Добавка к расстоянию между уровнями из-за переброса электрона уже не равна 2А; она составляет А /(Н11-Н22) — часть этой величины (что по предположению много меньше единицы). Кроме того, сама зависимость ЕI-ЕIIот расстояния между ядрами сейчас намного слабее, чем для иона Н+2: в нее тоже входит множитель А/(Н11-Н22).Можно поэтому понять, отчего связь несимметричных двуатомных молекул, как правило, очень слаба.
В нашей теории иона Н+2 мы открыли объяснение механизма, с помощью которого электрон, распределенный между двумя протонами, создает в итоге силу притяжения между ними даже тогда, когда они очень удалены друг от друга. Сила притяжения проистекает от уменьшения энергии системы, вызываемого тем, что у электрона есть возможность прыгать от одного протона к другому. При таких прыжках система переходит от конфигурации атом водорода — протон к конфигурации протон — атом водорода и обратно. Процесс символически можно записать так:
Сдвиг энергии, вызываемый этим процессом, пропорционален амплитуде А того, что электрон с энергией ─WH (его энергия связи в атоме водорода) может от одного протона перейти к другому.
При больших расстояниях R между протонами электростатическая потенциальная энергия электрона близка к нулю почти во всем том пространстве, которое он вынужден преодолеть, делая прыжок. Так что в этом пространстве электрон движется почти как свободная частица в пустом пространстве, но обладая при этом отрицательной энергией! В гл. 1 [уравнение (1.7)] мы видели, что амплитуда для частицы определенной энергии перейти с одного места на другое, удаленное на расстояние r, пропорциональна
где р — импульс, отвечающий заданной энергии. В теперешнем случае (применяется нерелятивистская формула) р определяется из выражения
А это значит, что р —число мнимое:
(другой знак перед корнем приводит к абсурду).
Стало быть, следует ожидать, что амплитуда А для иона
Н+2 будет меняться как
при больших расстояниях R между протонами. Сдвиг энергии, вызываемый электронной связью, пропорционален А;значит, существует сила, сближающая два протона, которая пропорциональна (при больших R) производной от (8.10) по R.
Наконец, для полноты следует заметить, что в одноэлектронной системе с двумя протонами есть еще один эффект, который тоже приводит к зависимости энергии от R. Мы пока им пренебрегали, поскольку он обычно не очень важен, за исключением как раз тех больших расстояний, на которых энергия обменного члена А убывает экспоненциально до очень малых величин. Новый эффект, о котором мы говорим,— это электростатическое притяжение протона к атому водорода, возникающее по той же причине, по какой любой заряженный предмет притягивает к себе незаряженный. «Голый» протон создает электрическое поле x(изменяющееся как 1/R2)возле нейтрального атома водорода. Атом становится поляризованным, приобретая наведенный дипольный момент m, пропорциональный x. Энергия диполя есть (mx,т. е. пропорциональна x2, или 1/R4. Значит, в выражении для энергии системы существует член, убывающий как четвертая степень расстояния (это поправка к e0). Эта энергия спадает с расстоянием медленнее, чем сдвиг А, даваемый формулой (8.10). На каких-то больших расстояниях R член с R4становится важнейшим, определяющим изменение энергии с R, и поэтому единственной оставшейся силой. Заметьте, что электростатический член для обоих базисных состояний имеет один знак (раз сила притягивает, то энергия отрицательна), а потому и для обоих стационарных состояний его знак один и тот же, в то время как член электронного обмена А для двух стационарных состояний дает разные знаки.
§ 2. Ядерные силы
Мы видели, что система, составленная из атома водорода и протона, вследствие обмена одним электроном обладает энергией взаимодействия, которая на больших расстояниях R меняется как
где a =. (Обычно говорят, что происходит обмен «виртуальным» электроном, когда, как в нашем случае, электрон вынужден перепрыгивать через ту область, где его энергия оказалась бы отрицательной. Конкретнее говоря, «виртуальный обмен» означает, что явление предполагает квантовомеханическую интерференцию между состоянием без обмена и состоянием с обменом.)
А теперь следует задать такой вопрос: не может ли быть, что и силы, действующие между другими частицами, имеют сходное происхождение? Что, к примеру, можно сказать о ядерной силе, действующей между нейтроном и протоном или между двумя протонами? Пытаясь объяснить природу ядерных сил, Юкава предположил, что сила, действующая между двумя нуклонами, вызывается сходным обменным эффектом, только в этом случае из-за виртуального обмена не электроном, а какой-то новой частицей, которую он назвал «мезон». Сегодня мы бы отождествили мезон Юкавы с p-мезоном (или «пионом»), возникающим в высокоэнергетических столкновениях протонов или других частиц.
Посмотрим для примера, какого рода силы возникнут от того, что протон и нейтрон обменяются положительным пионом (p+), имеющим массу mp. Как атом водорода Н0 может, отказавшись от электрона е-, превратиться в протон р+
Н0® р+ + е-, (8.12)
точно так же протон р+ может перейти в нейтрон n0, отказавшись от p+-мезона:
р+®n0+p+ . (8.13)
Значит, если у нас есть протон (в точке а) и нейтрон (в точке b), разделенные расстоянием R, то протон может стать нейтроном, испуская p+-мезон, который затем поглощается нейтроном в точке b, обращая его в протон. И имеется энергия взаимодействия системы из двух нуклонов и одного пиона, зависящая от амплитуды А пионного обмена, как это было с электронным обменом в ионе Н+2.
В процессе (8.12) энергия атома Н0 (если вычислять ее нерелятивистски, опуская энергию поля электрона WH) меньше энергии протона на величину mc2, так что кинетическая энергия электрона отрицательна — или импульс мнимый [см. уравнение (8.9)]. В ядерном процессе (8.13) массы протона и нейтрона почти равны, так что полная энергия p+-мезона окажется равной нулю. Соотношение между полной энергией Е и импульсом р пиона с массой mpтаково:
E2=р2с2+m2pc4.
раз Е равно нулю (или по крайней мере пренебрежимо мало
по сравнению с mp), то импульс опять выходит мнимый:
p=impc.
Повторяя знакомые нам уже рассуждения, с помощью которых мы вычисляли амплитуду того, что связанный электрон проникнет через барьер в пространстве между двумя протонами, мы получаем для ядерного случая амплитуду обмена А, которая — при больших R — будет вести себя как
Энергия взаимодействия пропорциональна А и, значит, меняется таким же образом. Мы получаем изменение энергии в форме так называемого потенциала Юкавы между двумя нуклонами. Кстати, ту же формулу мы получили раньше прямо из дифференциального уравнения для движения пиона в пустом пространстве [см. гл. 28 (вып. 6), уравнение (28.18)].
Следуя той же линии рассуждений, можно попытаться прикинуть взаимодействие двух протонов (или двух нейтронов), происходящее от обмена нейтральными пионами (p0). Основной процесс теперь таков:
р+®р++p0. (8.15)
Протон может испустить виртуальный p0, оставаясь после этого все еще протоном. Если протонов два, то протон № 1 может испустить виртуальный p0, который поглотится протоном № 2. В конце остается опять пара протонов. Это немного не то, что было в случае иона H+2. Тогда Н0 переходил после испускания электрона в другое состояние — в протон. Теперь же мы предполагаем, что протон может испускать p0, не меняя своего характера. Такие процессы и впрямь наблюдаются в высокоэнергетических столкновениях. Процесс аналогичен тому, как электрон, испуская фотон, остается все же электроном:
е®е+фотон. (8.16)
Мы не «видим» фотонов внутри электрона до того, как они испустятся, или после того, как они поглотятся, и их «испускание» не изменяет «природы» электрона.
Вернемся к нашей паре протонов. Между ними существует взаимодействие из-за наличия амплитуды А — амплитуды того, что один из протонов испускает нейтральный пион, который проскакивает (с мнимым импульсом) к другому протону и там поглощается. Амплитуда эта опять пропорциональна (8.14), но mp— теперь масса нейтрального пиона. Сходные рассуждения приводят к такому же взаимодействию между двумя нейтронами. А раз ядерные силы (в пренебрежении электрическими эффектами), действующие между нейтроном и протоном, между протоном и протоном, между нейтроном и нейтроном, одинаковы, то мы приходим к заключению, что массы заряженного и нейтрального пионов обязаны быть равны между собой. И экспериментально оказывается, что массы действительно очень близки друг к другу, а небольшая разница между ними — это примерно то, что и следует из поправок на собственную энергию [см. гл. 28 (вып. 6)].
Существуют и другие виды частиц, скажем .K-мезоны, которыми могут обмениваться два нуклона. Допустим также и одновременный обмен двумя пионами. Но у всех этих прочих обмениваемых «объектов» масса покоя mxвыше массы пиона mp, что приводит к членам в амплитуде обмена, изменяющимся как
Такие члены с ростом R отмирают быстрее, чем одномезонный член. Сегодня еще никто не знает, как вычислять эти члены с большей массой, но для достаточно высоких значений R выживает только однопионный член. И действительно, те опыты, в которых играет роль только взаимодействие на больших расстояниях, свидетельствуют, что энергия взаимодействия именно такова, как предсказывает теория однопионного обмена.
В классической теории электричества и магнетизма кулоновское электростатическое взаимодействие и излучение света ускоряемым зарядом тесно связаны — оба они вытекают из уравнений Максвелла. Мы видели, что в квантовой теории свет может быть представлен как квантовые возбуждения гармонических колебаний классического электромагнитного поля в ящике. С другой стороны, квантовая теория может быть построена при помощи описания света как частиц — фотонов, подчиняющихся статистике Бозе. В гл. 2, § 5, мы подчеркнули, что обе эти взаимоисключающие точки зрения всегда приводят к одинаковым предсказаниям. Может ли вторая точка зрения быть проведена последовательно и до конца, так чтобы в нее вошли все электромагнитные эффекты? В частности, если мы хотим описать электромагнитное поле полностью на языке бозе-частиц, т. е. фотонов, то чем будет вызвана сила Кулона?
С точки зрения «частиц» кулоновское взаимодействие между двумя электронами вытекает из обмена виртуальными фотонами. Один из электронов испускает фотон [как в реакции (8.16)], который переходит к другому электрону и там поглощается,— та же реакция идет в обратную сторону. Энергия взаимодействия снова дается формулой типа (8.14), но теперь mpзаменяется массой покоя фотона, которая равна нулю. Значит, виртуальный обмен фотоном приводит к энергии взаимодействия, которая меняется просто обратно пропорционально R — расстоянию между электронами — в точности, как нормальная кулоновская потенциальная энергия! В «частичной» (от слова частица) теории электромагнетизма процесс обмена виртуальным фотоном приводит ко всем явлениям электростатики.
§ 3. Молекула водорода
В качестве очередной системы с двумя состояниями рассмотрим нейтральную молекулу водорода Н2. В ней, естественно, труднее разобраться, потому что там имеются два электрона. Мы опять начнем с рассуждений о том, что происходит, когда оба протона достаточно удалены друг от друга. Но теперь к ним следует добавить еще два электрона. Чтобы удобнее было следить за ними, назовем их «электрон о» и «электрон 6». Здесь опять можно себе вообразить два мыслимых состояния. Одна возможность: «электрон а» размазан вокруг первого протона, а «электрон b» — вокруг второго (фиг. 8.4).
Фиг. 8.4. Совокупность базисных состояний для молекулы Н2.
Получаются попросту два атома водорода. Это состояние назовем |1>. Но есть и другая возможность: вокруг первого протона размазан «электрон b», а вокруг второго — «электрон а». Это состояние обозначим |2>. Из-за симметрии эти две возможности обязаны быть энергетически эквивалентными, но, как мы увидим, энергия системы не есть просто энергия двух атомов водорода.
Нужно заметить, что имеются многие другие возможности. Например, «электрон а» может находиться близ первого протона, а «электрон 6» — в другом состоянии вокруг того же протона. Мы не станем рассматривать такой случай, поскольку его энергия заведомо будет больше (из-за сильного кулоновского отталкивания между двумя электронами). Для большей точности, конечно, стоило бы учесть и такие состояния; но уже из рассмотрения одной только пары состояний, показанных на фиг. 8.4, мы узнаем самое главное о молекулярной связи. В этом приближении мы можем описать всякое состояние, задав амплитуду <1|j> быть в состоянии |1> и амплитуду <2|j> быть в состоянии |2>. Иными словами, вектор состояния |j> может быть записан в виде линейной комбинации
Для дальнейшего, как всегда, предположим, что имеется некоторая амплитуда А того, что электроны могут проходить через промежуточное пространство и обмениваться местами. Эта возможность обмена означает, что энергия системы, как мы наблюдали и в других системах с двумя состояниями, расщеплена. Как и у молекулярного иона водорода, расщепление очень мало, когда расстояние между протонами велико. А когда протоны сближаются, возрастает амплитуда переходов электронов туда-сюда, а вместе с ней растет и расщепление. Убывание энергии в нижнем состоянии означает, что имеется сила притяжения, сближающая атомы. И опять, когда протоны сблизятся особенно тесно, уровни энергии поднимутся вследствие кулоновского отталкивания. В итоге энергии двух стационарных состояний будут меняться с расстоянием так, как показано на фиг. 8.5.
Фиг. 8.5. Уровни анергии молекулы Н2 для различных межпротонных расстояний D (ЕH=13,в эв).
На расстоянии порядка 0,74 Е низший энергетический уровень достигает минимума; это и есть расстояние между протонами в настоящей молекуле водорода.
Но у вас уже, вероятно, появилось возражение. А как же быть с тем, что оба электрона — тождественные частицы? Мы их назвали «электрон а» и «электрон b», но на самом-то деле невозможно сказать, кто из них кто. И мы еще говорили в гл. 2, что если за счет обмена электронами (ферми-частицами) имеются два пути, по которым что-то может произойти, то две амплитуды будут интерферировать с отрицательным знаком. Это значит, что если у электронов переставить обозначающие их номера, то знак амплитуды должен перемениться. Однако мы только что пришли к выводу, что связанное состояние молекулы водорода имело бы вид (при t=0)
А согласно нашим правилам, перечисленным в гл. 2, такое состояние недопустимо. Если переставить номера электронов, то мы получим состояние
и знак выйдет тот же, а не обратный.
Эти рассуждения верны, но только тогда, когда спины обоих электронов одинаковы. Если у них обоих спины смотрят вверх (или вниз), то единственно допустимое состояние таково:
Для этого состояния перестановка электронов дает
что, как и положено, равно |I>. Значит, если сблизить два атома водорода так, чтобы их электроны вращались глядя в одну сторону, то они смогут перейти лишь в состояние |I>, но не в состояние |II>.Но заметьте теперь, что состояние |I> — это верхнее энергетическое состояние. Его кривая «энергия—расстояние» не имеет минимума. Два атома водорода всегда будут отталкиваться и не смогут образовать молекулу. Мы заключаем, что молекула водорода, в которой спины электронов параллельны, не способна существовать. И это на самом деле так.
С другой стороны, наше состояние |II>полностью симметрично по двум электронам. Действительно, если переименовать электроны, назвав первый а, а второй b, то мы снова получим в точности то же состояние. В гл. 2, § 7, мы видели, что если две ферми-частицы находятся в одном и том же состоянии, то спины их обязаны быть противоположными. Значит, у связанной молекулы водорода спин одного из электронов должен быть направлен вверх, а спин другого — вниз.
Весь рассказ о молекуле водорода на самом деле будет звучать еще более запутанно, если мы захотим включить в него спины протонов. Тогда уже будет нельзя считать молекулу системой с двумя состояниями. Она скорее должна походить на систему с восемью состояниями — для каждого из наших состояний |1> и |2> возможны четыре различные расстановки спинов так что, пренебрегая спинами, мы слегка упростили дело. Наши окончательные выводы, однако, все равно верны.
Мы нашли, что в низшем энергетическом состоянии молекулы Н2 — единственном связанном состоянии — спины двух электронов противоположны друг другу. Полный спиновый момент количества движения электронов равен нулю. Наоборот, два близких атома водорода с параллельными спинами (и, стало быть, с полным моментом количества движения h) должны находиться в высшем (несвязанном) энергетическом состоянии; атомы будут отталкиваться. Налицо интересная корреляция между спинами и энергиями. Она еще раз иллюстрирует то, о чем мы упоминали раньше: что выходит, будто у двух спинов существует энергия «взаимодействия», потому что случай параллельных спинов обладает большей энергией, чем случай спинов антипараллельных. В каком-то смысле можно говорить, что спины стремятся выстроиться в антипараллельное положение и стремясь к этому, обладают потенциалом к высвобождению энергии не из-за того, что там имеется большая магнитная сила, а из-за принципа запрета.
В § 1 мы видели, что связь двух различных ионов посредством одного электрона чаще всего оказывается весьма слабой. При двухэлектронной связи это не так. Представим, что два протона на фиг. 8.4 мы заменили любой парой ионов (с замкнутыми внутренними электронными оболочками и единичным ионным зарядом) и что энергии связи электрона в этих двух ионах различны. Энергии состояний |1> и |2>по-прежнему будут равны друг другу, потому что в каждом из этих состояний имеется по одному электрону на каждый ион. Поэтому у нас всегда будет расщепление, пропорциональное А. Двухэлектронная связь поистине вездесуща — это самая обычная валентная связь. Химическая связь, как правило, предполагает эту игру в «туда-сюда», в которую играют два электрона. Хотя пара атомов может быть связана только одним электроном, это случается сравнительно редко, потому что требует надлежащих условий.
Наконец, надо заметить, что если энергия притяжения электрона к одному ядру намного больше, чем к другому, то уже нельзя говорить, будто можно игнорировать другие мыслимые состояния. Пусть ядро а (это может быть и положительный ион) притягивает электрон намного сильнее, чем ядро b. Это сильное притяжение может более чем компенсировать взаимное отталкивание двух электронов. И если это так, то низшее энергетическое состояние может обладать большой амплитудой того, что оба электрона окажутся возле а (образуя отрицательный ион), и малой амплитудой того, что хотя бы один из них обнаружится возле b. Состояние выглядит как отрицательный ион рядом с положительным ионом. Именно это и случается в «ионных» молекулах наподобие NaCl. Вы видите, что мыслимы любые градации между ковалентной связью и ионной связью.
Теперь вы ясно видите, что многие химические факты на квантовомеханическом языке удается очень отчетливо понять.
§ 4. Молекула бензола
Для изображения сложных органических молекул химики изобрели изящные диаграммы. Мы хотим теперь поговорить об одной из самых интересных молекул — о молекуле бензола, диаграмма которой приведена на фиг. 8.6.
Фиг. 8.6. Молекула бензола С6Н6.
В нее входят по шести весьма симметрично расположенных атомов углерода и водорода. Каждая черточка на диаграмме представляет пару электронов с противоположными спинами, пляшущих танец ковалентной связи. Каждый атом водорода вводит в игру по одному электрону, а каждый атом углерода — по четыре, образуя в общей сложности систему из 30 участвующих в игре электронов. (В углероде ближе к ядру есть еще два электрона, образующих первую, или К, оболочку. Они не показаны, поскольку их связь столь тесна, что сколько-нибудь заметной важности для ковалентной связи они не представляют.) Итак, каждая черточка на рисунке представляет связь, или пару электронов, а двойные связи означают, что между чередующимися парами атомов углерода имеются по две пары электронов.
С молекулой бензола связана одна загадка. Можно подсчитать, какая энергия должна потребоваться на образование этого химического соединения, потому что химики измерили энергии различных соединений, включающих части кольца; к примеру, изучая этилен, они узнали энергию двойной связи и т. д. Поэтому мы можем подсчитать полную энергию, которую должна была бы иметь молекула бензола. Однако истинная энергия бензольного кольца намного меньше, чем получается при таком подсчете: кольцо связано куда крепче, чем полагается обычной системе «ненасыщенных двойных связей». Как правило, система двойных связей, не образующая подобного кольца, весьма легко поддается химическим атакам: ее энергия сравнительно высока, и, добавляя лишние атомы водорода, двойные связи удается легко разрывать. Не то у бензола — кольцо его почти нерушимо: сломать его нелегко. Иными словами, энергия бензола намного ниже, чем дает подсчет по картине двойных связей.
Имеется еще и другая загадка. Пусть мы заменили два смежных водорода атомами брома, образуя орто-дибромбензол. Это можно сделать двумя путями. Атомы брома могут быть на противоположных концах двойной связи (фиг. 8.7, а) или могут быть на противоположных концах одинарной связи (фиг. 8.7, б).
Фиг.8.7. Две возможности для орто-дибромбензола. Два атома брома могут разделяться либо одиночной связью, либо двойной.
Можно было бы подумать, что должны существовать две разные формы opmo-дибромбензола, но это не так. Есть только одно такое вещество.
Теперь мы собираемся разрешить эти загадки, и вы, может быть, уже догадались как: конечно, дело в том, что «основное состояние» бензольного кольца на самом деле является системой с двумя состояниями. Можно представить себе, что связи в бензоле могут быть расположены двояким образом, как показано на фиг. 8.8.
Фиг. 8.8. Совокупность базисных состояний для молекулы бензола.
Вы скажете: «Но ведь это одно и то же; у них должна быть одинаковая энергия». Конечно, должна быть. Именно поэтому их и надо анализировать как систему с двумя состояниями. Каждое состояние представляет другую конфигурацию всей совокупности электронов, и существует некоторая амплитуда А того, что все переплетение переключится с одного расположения на другое, есть какой-то шанс, что электроны смогут сменить фигуру в танце.
Как мы видели, эта вероятность переброса приводит к смешанному состоянию, энергия которого ниже, чем получилось бы, если бы мы рассчитали каждую из схем, представленных на фиг. 8.8, по отдельности. Вместо этого существуют два стационарных состояния: одно с энергией выше, другое — ниже ожидаемого значения. Значит, в действительности истинное нормальное состояние бензола (с наинизшей энергией) не есть какая-либо из возможностей, представленных на фиг. 8.8, а обладает амплитудой 1/Ц2 пребывания в каждом из нарисованных состояний. Это единственное состояние, которое и стоит принимать в расчет в химии бензола при нормальных температурах. Кстати, существует и верхнее состояние; мы вправе так говорить, потому что бензол обладает сильным поглощением света в ультрафиолетовой области с частотой w= (ЕI -EII)/h. Вспомните, что в аммиаке, где прыгающим вверх и вниз объектом являлась тройка протонов, расстояние между энергиями приходилось на микроволновую область. В бензоле таким объектом являются электроны, и, поскольку они намного легче, им и перескакивать туда-сюда тоже намного легче, отчего и коэффициент А становится куда больше. В итоге разница энергий намного больше — около 1,5 эв, а это энергия ультрафиолетового фотона.
Что же происходит, когда мы присоединяем бром? Тогда опять возникают две возможности с двумя разными электронными конфигурациями, показанные на фиг. 8.7. Отличие их в том, что те два базисных состояния, из которых мы исходим, обладают теперь слегка различными энергиями. В стационарное состояние с наинизшей энергией по-прежнему войдет линейная комбинация двух состояний, но с неравными амплитудами. Для состояния |1> амплитуда может стать равной, скажем, Ц2/3, для состояния |2> она будет Ц1/3 чтобы знать коэффициенты точно, нужна добавочная информация, но, во всяком случае, если уж энергии H11 и H22 не равны друг другу, то и амплитуды С1и С2не могут быть равны между собой. Это, естественно, означает, что одна из двух изображенных на рисунке возможностей более вероятна, чем другая, но все же электроны достаточно подвижны, чтобы и та, и другая обладали какой-то конечной амплитудой. У другого стационарного состояния
амплитуды другие (скажем, Ц1/3 и — Ц2/3), но оно лежит при более высокой энергии. Есть только одно наинизшее состояние, а не два, как можно было бы подумать, пользуясь наивной теорией закрепленных химических связей.
§ 5. Красители
Приведем еще один химический пример явления, связанного с двумя состояниями, но на этот раз на уровне крупных молекул. Касается это теории красителей. У многих красителей, а именно у большинства искусственных красителей, есть одна общая характеристика — они обладают своего рода симметрией. На фиг. 8.9 изображен ион одного из красителей — фуксина (он дает пурпурный цвет).
Фиг. 8.9. Пара базисных состояний для молекулы красителя фуксин.
В молекуле есть три кольцевые структуры, две из которых — бензольные кольца. Третья не совсем совпадает с бензольным кольцом, потому что внутри кольца в ней только две двойные связи. На рисунке показаны две в равной степени подходящие схемы, и мы догадываемся, что их энергии должны быть равны. Но имеется еще и амплитуда того, что все электроны смогут переброситься из одного состояния в другое, передвинув местоположение «незаполненного» кольца в другой конец. Когда электронов так много, то амплитуда переброса несколько ниже, чем у бензола, и различие в энергиях двух стационарных состояний не так велико. Но тем не менее все равно имеется обычная пара стационарных состояний |I> и |II>, представляющая собой сумму и разность двух базисных состояний, показанных на рисунке. Энергетический промежуток между |I>и |II> оказывается равным энергии фотона в оптической области. Если молекулу осветить, возникает очень сильное поглощение при некоторой частоте и молекула покажется ярко окрашенной. Вот почему она краситель! Другая интересная черта такой молекулы красителя — в двух изображенных базисных состояниях центры электрического заряда расположены в разных местах. В итоге молекула должна быть сильно подвержена действию внешнего электрического поля. Такой же эффект мы наблюдали в молекуле аммиака. Ясно, что его можно анализировать при помощи той же математики, если только известны числа Е0и А. Их. вообще говоря получают, накапливая опытные данные. Если проделать измерения со многими красителями, то часто можно догадаться, что произойдет с какой-то родственной молекулой красителя. Из-за сильного сдвига местоположения центра электрического заряда значение m в формуле (7.55) велико, и вещество обладает большой вероятностью поглощения света с характеристической частотой 2A/h. Значит, вещество не просто окрашено, а окрашено очень густо — малое количество вещества поглощает много света. Скорости переброса (и тем самым А) очень чувствительны ко всей структуре молекулы. Если изменить А, то изменится расщепление энергии и вместе с ним цвет красителя. Кроме того, молекулы не обязаны быть совершенно симметричными. Мы видели, что то же самое основное явление бывает и при небольших видоизменениях—даже когда имеется небольшая асимметрия. Небольшого изменения цвета можно добиваться введением в молекулы легких асимметрий. Так, другой важный краситель, малахитовая зелень, очень похож на фуксин, только у него две из имеющихся молекул водорода замещены на СН3. Цвет выходит другой, потому что А сдвинуто и скорость переброса электронов изменилась.
§ 6. Гамильтониан частицы со спином 1/2 в магнитном поле
Обратимся теперь еще к одной системе с двумя состояниями. На этот раз нашим объектом будет частица со спином 1/2. Кое-что из того, что мы намерены сказать, затрагивалось уже в предыдущих главах, но повторение поможет нам немного прояснить кое-какие темные места. Покоящийся электрон мы можем считать тоже системой с двумя состояниями. Хотя в этом параграфе мы будем толковать об «электроне», но то, что мы выясним, будет справедливо по отношению ко всякой частице со спином 1/2.
Предположим, что в качестве наших базисных состояний |1>и |2>мы выбрали состояния, в которых z-компонента спина электрона равна либо +h/2, либо -h/2. Эти состояния, конечно, те же самые состояния (+) и (-), с которыми мы встречались в прежних главах. Чтобы согласовать эти и прежние обозначения, спиновое состояние 1 у мы будем отмечать «плюсом», а спиновое состояние | 2 у — «минусом», причем «плюс» и «минус» относятся к моменту количества движения в направлении z.
Всякое мыслимое состояние |y>электрона можно описать уравнением (8.1), задав амплитуду С1того, что электрон находится в состоянии |1>, и амплитуду С2 того, что он находится в состоянии 2у. Для этого нам понадобится гамильтониан нашей системы с двумя состояниями — электрона в магнитном поле. Начнем с частного случая магнитного поля в направлении z.
Пусть вектор В имеет только z-компоненту Bz. Из определения двух базисных состояний (что их спины параллельны и антипараллельны В) мы знаем, что они уже являются стационарными состояниями — состояниями с определенной энергией в магнитном поле. Состояние |1> соответствует энергии, равной — mВz, а состояние |2> — энергии +mBz. В этом случае гамильтониан должен быть очень простым, поскольку на С1 — амплитуду оказаться в состоянии |1> С2 не влияет и наоборот:
В этом частном случае гамильтониан равен
Итак, мы знаем, какой вид имеет гамильтониан, когда магнитное поле направлено по z, и знаем еще энергии стационарных состояний.
А теперь пусть поле не направлено по z. Каков теперь гамильтониан? Как меняются матричные элементы, когда поле не направлено по z? Мы сделаем предположение, что для членов гамильтониана имеется своего рода принцип суперпозиции. Точнее, мы предположим, что если два магнитных поля налагаются одно на другое, то члены гамильтониана просто складываются: если нам известно Hijдля поля, состоящего из одной только компоненты Bz, и известно Нijдля одной только Вх, то Hij для поля с компонентами Bz, Bxполучится простым сложением. Это бесспорно верно, если рассматриваются только поля в направлении z: если удвоить Bz, то удвоятся и все Нij. Итак, давайте допустим, что Н линейно по полю В. Чтобы найти Hijдля какого угодно магнитного поля, больше ничего и не нужно.
Пусть у нас есть постоянное поле В. Мы бы могли провести нашу ось z в направлении поля и обнаружили бы два стационарных состояния с энергиями ±mB. Простой выбор другого направления осей не изменил бы физики дела. Наше описание стационарных состояний стало бы иным, но их энергии по-прежнему были бы ±mB, т. е.
Дальше все уже совсем легко. У нас есть формулы для энергий. Нам нужен гамильтониан, линейный по Вх, Вyи Bz, который даст именно такие энергии, если применить нашу общую формулу (8.3). Задача — найти гамильтониан. Прежде всего заметим, что энергия расщепляется симметрично и ее среднее значение есть нуль. Взглянув на (8.3), мы сразу же увидим, что для этого требуется
Н22=-H11.
(Заметьте, что это подтверждается тем, что нам уже известно при Вx=Вy=0; в этом случае Н11=-mBzи H22=mBz.) Если теперь приравнять энергии из (8.3) к тому, что нам известно из (8.19), то получится
(Мы использовали также тот факт, что Н21=Н*12, так что H12H21 может быть записано в виде |Н12|2.) Опять в частном случае поля в направлении z это даст
откуда | H12| в этом частном случае равно нулю, что означает, что в H12не может войти член с Вz. (Вы помните, что мы говорили о линейности всех членов по Вх, Вyи Bz.)
Итак, пока мы узнали, что в Н11и H22 входят члены с Вz, а в H12 и H21 — нет. Можно попробовать угадать формулы, которые будут удовлетворять уравнению (8.20), написав
H11=-mВz,
H22=mBz
и
Оказывается, что никак иначе этого сделать нельзя!
«Погодите,— скажете вы,— H12 по В не линейно. Из (8.21) следует, что H12=mЦ(В2x+В2y)». Не обязательно. Есть и другая возможность, которая уже линейна, а именно
Н12=m(Вx+iBy).
На самом деле таких возможностей не одна, в общем случае можно написать
где d — произвольная фаза.
Какой же знак и какую фазу мы обязаны взять? Оказывается, что можно выбрать любой знак и фазу тоже любую, а физические результаты от этого не изменятся. Так что выбор — это вопрос соглашения. Еще до нас кто-то решил ставить знак минус и брать еid=-1. Мы можем делать так же и написать
(Кстати, эти соглашения связаны и согласуются с тем произволом в выборе фаз, который мы использовали в гл. 4.) Полный гамильтониан для электрона в произвольном магнитном поле, следовательно, равен
уравнения для амплитуд С1 и С2 таковы:
Итак, мы открыли «уравнения движения спиновых состояний» электрона в магнитном поле. Мы угадали их, пользуясь некоторыми физическими аргументами, но истинная проверка всякого гамильтониана заключается в том, что он обязан давать предсказания, согласующиеся с экспериментом. Из всех сделанных проверок следует, что эти уравнения правильны. Более того, хотя все наши рассуждения относились к постоянному полю, написанный нами гамильтониан правилен и тогда, когда магнитные поля меняются со временем. Значит, мы теперь можем применять уравнения (8.23) для решения всевозможных интересных задач.
§ 7. Вращающийся электрон в магнитном поле
Пример первый: пусть сначала имеется постоянное поле в направлении z. Ему соответствуют два стационарных состояния с энергиями ±mBz. Добавим небольшое поле в направлении х. Тогда уравнения получатся такими же, как в нашей старой задаче о двух состояниях. Опять, в который раз, получается знакомый уже нам переброс, и уровни энергии немного расщепляются. Пусть, далее, x-компонента поля начнет меняться во времени, скажем, как coswt. Тогда уравнения станут такими, как для молекулы аммиака в колеблющемся электрическом поле (см. гл. 7). И тем же способом, что и прежде, вы можете рассчитать процесс во всех деталях. При этом вы увидите, что колеблющееся поле приводит к переходам от +z-состояния к —z-состоянию и обратно, если только горизонтальное поле колеблется с частотой, близкой к резонансной, w0=2mBz/h. Это приводит к квантовомеханической теории явлений магнитного резонанса, описанной нами в гл. 35 (вып. 7).
Можно еще сделать мазер, в котором используется система со спином 1/2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении +z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнитным моментом, вызовут переходы, которые будут снабжать полость энергией.
Рассмотрим теперь второй пример. Пусть у нас имеется магнитное поле В, направление которого характеризуется полярным углом 6 и азимутальным углом j (фиг. 8.10).
Фиг. 8.10. Направление В определяется полярным углом q и азимутальным углом j.
Допустим еще, что имеется электрон, спин которого направлен по полю. Чему равны амплитуды С1и С2для этого электрона? Иными словами, обозначая состояние электрона |y>, мы хотим написать
где C1и С2 равны
а |1> и |2>обозначают то же самое, что раньше обозначалось |+> и |-> (по отношению к выбранной нами оси z).
Ответ на этот вопрос также содержится в наших общих уравнениях для систем с двумя состояниями. Во-первых, мы знаем, что раз спин электрона параллелен В, то электрон находится в стационарном состоянии с энергией ЕI=-mB. Поэтому и c1 и С2 должны изменяться как
[см. уравнение (7.18)]; и их коэффициенты а1и а2 даются формулой (8.5):
Вдобавок a1 и а2 должны быть нормированы так, чтобы было |a|2 +|а2|2=1. Величины Н11и H12 мы можем взять из (8.22), используя равенства
Bz=Bcosq, Вх=Вsinqcosj, Ву=Вsinqsinj.
Тогда мы имеем
Кстати, скобка во втором уравнении есть просто, так что проще писать
Подставляя эти матричные элементы в (8.24) и сокращая на -mB, находим
Зная это отношение и зная условие нормировки, можно найти и а1, и а2. Сделать это нетрудно, но мы сократим путь, прибегнув к одному трюку. Известно, что
1-cosq=2sin2(q/2) и sinq=2sin(q/2)cos(q/2). Значит, (8.27) совпадает с
Один из ответов, следовательно, таков:
Он удовлетворяет и уравнению (8.28), и условию
Вы знаете, что умножение a1 и а2 на произвольный фазовый множитель ничего не меняет. Обычно формуле (8.29) предпочитают более симметричную запись, умножая на e'f'2. Принято писать так:
Это и есть ответ на наш вопрос. Числа а1и а2 — это амплитуды того, что электрон будет замечен спином вверх или вниз (по отношению к оси z), если известно, что его спин направлен вдоль оси (q,j). [Амплитуды C1и С2равны просто a1 и a2, умноженным на
Заметьте теперь занятную вещь. Напряженность В магнитного поля нигде в (8.30) не появляется. Тот же результат разумеется, получится в пределе, если поле В устремить к нулю Это означает, что мы дали общий ответ на вопрос, как представлять частицу, спин которой направлен вдоль произвольной оси. Амплитуды (8.30) — это проекционные амплитуды для частиц со спином 1/2, подобные проекционным амплитудам для частиц со спином 1, приведенным в гл. 3 [уравнения (3.38)]. Теперь мы сможем находить для фильтрованных пучков частиц со спином 1/2 амплитуды проникновения через тот или иной фильтр Штерна — Герлаха.
Пусть |+z> представляет состояние со спином, направленным по оси z вверх, а |-z> — состояние со спином вниз. Если | +z'> представляет состояние со спином, направленным вверх по оси z', образующей с осью z углы q и j, то в обозначениях гл. 3 мы имеем
Эти результаты эквивалентны тому, что мы нашли из чисто геометрических соображений в гл. 4 [уравнение (4.36)]. (Если вы в свое время решили пропустить гл. 4, то вот перед вами один из ее существенных результатов.)
Напоследок вернемся еще раз к тому примеру, о котором уже не раз говорилось. Рассмотрим такую задачу. Сперва имеется электрон с определенным образом направленным спином, затем на 25 минут включается магнитное поле в направлении z, а затем выключается. Каким окажется конечное состояние? Опять представим состояние в виде линейной комбинации |y>=|1>C1+|2>С2, Но в нашей задаче состояния с определенной энергией являются одновременно нашими базисными состояниями |1> и |2>, Значит, С1и С2 меняются только по фазе. Мы знаем, что
и
Мы сказали, что вначале у спина электрона было определенное направление. Это означает, что вначале С1и С2были двумя числами, определяемыми формулами (8.30). Переждав Т секунд, новые С1 и С2 мы получим из прежних умножением соответственно на и. Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол j, вычтя из него 2mBzT/h, и не трогать угол q.
Это значит, что к концу интервала времени Т состояние |y> будет представлять электрон, выстроенный в направлении, отличающемся от первоначального только поворотом вокруг оси z на угол Dj=2mBzT/h. Раз этот угол пропорционален Т, то можно говорить, что направление спина прецессирует вокруг оси z с угловой скоростью 2mBz/h. Этот результат мы уже получали раньше несколько раз, но не так полно и строго. Теперь мы получили полное и точное квантовомеханическое описание прецессии атомных магнитов.
Любопытно, что математические идеи, которые мы только что применили к электрону, вращающемуся в магнитном поле, применимы и для любой системы с двумя состояниями. Это означает, что, проведя математическую аналогию с вращающимся электроном, можно при помощи чисто геометрических рассуждений решить любую задачу для двухуровневой системы. Сперва вы сдвигаете энергию так, чтобы (H11+H22) было равно нулю (так что H11=-H22). И тогда любая задача о такой системе формально совпадет с задачей об электроне в магнитном поле. Вам нужно будет только отождествить —mBzс H11, а -m(Вх-iBy) с H12. И неважно, какая физика там была первоначально — молекула ли аммиака или что другое,— вы можете перевести ее на язык соответствующей задачи об электроне. Стало быть, если мы в состоянии решить в общем случае задачу об электроне, мы уже решили все задачи о двух состояниях.
А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью w(t), равной некоторой константе, умноженной на вектор В (а именно w=2mВ/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11).
Фиг. 8.11. Направление спина электрона в изменяющемся магнитном поле В (t) прецессирует с частoтой w(t) вокруг оси, параллельной В.
Если все время это делать, вы остановитесь на какой-то конечной, ориентации спиновой оси, и амплитуды С1и С2 получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.
Вы видите, что задача эта чисто геометрическая: надо заметить, где закончились все ваши вращения. Хотя сразу видно, что для этого требуется, но эту геометрическую задачу (отыскание окончательного итога вращений с переменным вектором угловой скорости) нелегко в общем случае решить явно. Во всяком случае, мы в принципе видим общее решение любой задачи для двух состояний. В следующей главе мы глубже исследуем математическую технику обращения с частицами спина 1/2 и, следовательно, обращения с системами, обладающими двумя состояниями, в общем случае.
* Мы принимаем энергию покоя m0c2 за «нуль» энергии и считаем магнитный момент m электрона отрицательным числом, поскольку он направлен против спина.
* Сказанное нами может вас слегка ввести в заблуждение. Поглощение ультрафиолетового света в принятой нами для бензола системе с двумя состояниями было бы очень слабым, потому что матричный элемент дипольного момента между двумя состояниями равен нулю. [Оба состояния электрически симметричны, и в нашей формуле (7.55) для вероятности перехода дипольный момент m равен нулю, и свет не поглощается.] Если бы других состояний не было, существование верхнего состояния пришлось бы доказывать иными путями. Однако более полная теория бензола, которая исходит из большего числа базисных состояний (обладающих, скажем, смежными двойными связями), показывает, что истинные стационарные состояния бензола слегка искажены по сравнению с найденными нами. В результате все же возникает дипольный момент, который и разрешает упомянутые в тексте переходы, приводящие к поглощению ультрафиолетового света.
* Мы немного упрощаем дело. Первоначально химики думали, что должны существовать четыре формы дибромбензола: две формы с атомами брома при соседних атомах углерода (орто-дибромбензол), третья форма с атомами брома при атомах углерода, идущих через один (.мета-дибромбензол), и четвертая форма с атомами брома, стоящими друг против друга (пара-дибромбензол). Однако отыскали они только три формы — существует лишь одна форма орто-молекулы.
* До тех пор, пока нет сильных магнитных полей, это предположение вполне удовлетворительно. Влияние магнитных полей на электрон мы обсудим в этой же главе позже, а очень слабые спиновые эффекты в атоме водорода — в гл. 10.
Глава 9 ЕЩЕ СИСТЕМЫ С ДВУМЯ СОСТОЯНИЯМИ
§ 1. Спиновые матрицы Паули
§ 2.Спиновые матрицы как операторы
§ З. Решение уравнений для двух состояний
§ 4. Состояния поляризации фотона
§ 5. Нейтральный K-мезон *
§ 6. Обобщение на системы с N состояниями
Повторить: гл. 33 (вып. 3) «Поляризация»
§ 1. Спиновые матрицы. Паули
Продолжаем обсуждение свойств двухуровневых систем. В конце предыдущей главы мы говорили о частице со спином l/2в магнитном поле. Мы описывали спиновое состояние, задавая амплитуду С1того, что z-компонента спинового момента количества движения равна +h/2, и амплитуду С2 того, что она равна -h/2. В предыдущих главах мы эти базисные состояния обозначали |+> и |->. Прибегнем опять к этим обозначениям, хотя, когда это будет удобнее, мы будем менять их на |1> и |2>. Мы видели в последней главе, что когда частица со спином 1/2 и с магнитным моментом m, находится в магнитном поле В=(Вx, Вy, Bz), то амплитуды С+(=C1)и С-(=С2) связаны следующими дифференциальными уравнениями:
Иначе говоря, матрица-гамильтониан Hijимеет вид
конечно, уравнения (9.1) совпадают с
где i и j принимают значения + и - (или 1 и 2).
Эта система с двумя состояниями — спин электрона — настолько важна, что очень полезно было бы найти для ее описания способ поаккуратнее и поизящнее. Мы сейчас сделаем небольшое математическое отступление, чтобы показать вам, как обычно пишутся уравнения системы с двумя состояниями. Это делается так: во-первых, заметьте, что каждый член гамильтониана пропорционален m, и некоторой компоненте В; поэтому (чисто формально) можно написать
Здесь нет какой-либо новой физики; эти уравнения просто означают, что коэффициенты— их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
Посмотрим, почему это так. Начнем с Bz. Раз Вz встречается только в H11 и H22, то все будет в порядке, если взять
Мы часто пишем матрицу Hijв виде таблички такого рода:
Для гамильтониана частицы со спином 1/2 в магнитном поле В—это все равно что
Точно так же и коэффициенты можно записать в виде матрицы
Расписывая коэффициенты при Вх, получаем, что элементы матрицы sхдолжны иметь вид
Или сокращенно:
Инаконец, глядя на By, получаем
или
Если так определить три матрицы сигма, то уравнения (9.1) и (9.4) совпадут. Чтоб оставить место для индексов i и j, мы отметили, какая а стоит при какой компоненте В, поставив индексы х, у, z сверху. Обычно, однако, i и j отбрасывают (их легко себе и так вообразить), а индексы х, у и z ставят внизу. Тогда (9.4) записывается так:
Матрицы сигма так важны (ими беспрерывно пользуются),
что мы выписали их в табл. 9.1. (Тот, кто собирается работать
в квантовой физике, обязан запомнить их.) Их еще называют
спиновыми матрицами Паули — по имени физика, который
их выдумал.
Таблица 9.1 · СПИНОВЫЕ МАТРИЦЫ ПАУЛИ
В таблицу мы включили еще одну матрицу 2X2, которая бывает нужна тогда, когда мы хотим рассматривать систему, о6a спиновых состояния которой имеют одинаковую энергию, или когда хотим перейти к другой нулевой энергии. В таких случаях к первому уравнению в (9.1) приходится добавлять E0С+ , а ко второму Е0С-. Это можно учесть, введя новое обозначение — единичную матрицу «1», или dij:
переписав (9.8) в виде
Обычно просто понимают без лишних оговорок, что любая константа наподобие Е0автоматически умножается на единичную матрицу, и тогда пишут просто
Одна из причин, отчего спиновые матрицы так полезны,— это что любая матрица 2x2 может быть выражена через них. Во всякой матрице стоят четыре числа, скажем
Ее всегда можно записать в виде линейной комбинации четырех матриц. Например,
Это можно делать по-всякому, но, в частности, можно сказать, что М состоит из какого-то количества sхплюс какое-то количество а и т. д., и написать
где «количества» a, b, g и d в общем случае могут быть комплексными числами.
Раз любая матрица 2X2 может быть выражена через единичную матрицу и матрицу сигма, то все, что может понадобиться для любой системы с двумя состояниями, у нас уже есть. Какой бы ни была система с двумя состояниями — молекула аммиака, краситель фуксин, что угодно,— гамильтоново уравнение может быть переписано в сигмах. Хотя в физическом случае электрона в магнитном поле сигмы кажутся имеющими геометрический смысл, но их можно считать и просто полезными матрицами, пригодными к употреблению во всякой системе с двумя состояниями.
Например, один из способов рассмотрения протона и нейтрона — это представлять их как одну и ту же частицу в любом из двух состояний. Мы говорим, что нуклон (протон или нейтрон) есть система с двумя состояниями, в данном случае состояниями по отношению к электрическому заряду. Если рассматривать нуклон таким образом, то состояние |1>может представлять протон, а |2> — нейтрон. Говорят, что у нуклона есть два состояния «изотопспина».
Поскольку мы будем применять матрицы сигма в качестве «арифметики» квантовой механики систем с двумя состояниями, то наскоро познакомимся с соглашениями матричной алгебры. Под «суммой» двух или большего числа матриц подразумевается как раз то, что имелось в виду в уравнении (9.4).
Вообще если мы «складываем» две матрицы А и В, то «сумма» С означает, что каждый ее элемент Cijдается формулой
Cij=Aij+Bij.
Каждый элемент С есть сумма элементов А и В, стоящих на тех же самых местах.
В гл. 3, § 6, мы уже сталкивались с представлением о матричном «произведении». Та же идея полезна и при обращении с матрицами сигма. В общем случае «произведение» двух матриц A и В (в этом именно порядке) определяется как матрица С с элементами
Это — сумма произведений элементов, взятых попарно из i-й строчки А и k-ro столбца В. Если матрицы расписаны в виде таблиц, как на фиг. 9.1, то можно указать удобную «систему» получения элементов матрицы-произведения.
Фиг. 9.1. Перемножение двух матриц.
Скажем, вы вычисляете С23. Вы двигаете левым указательным пальцем по второй строчке А, а правым — вниз по третьему столбцу В, перемножаете каждую пару чисел и складываете пары по мере движения. Мы попытались изобразить это на рисунке.
Для матриц 2X2 это выглядит особенно просто. Например, если sхумножается на sx, то выходит
т. е. просто единичная матрица. Или, для примера, подсчитаем еще
Взглянув на табл. 9.1, вы видите, что это просто матрица sx, умноженная на i. (Вспомните, что умножение матрицы на число означает умножение каждого элемента матрицы на число.) Попарные произведения сигм очень важны и выглядят они довольно забавно, так что мы их выписали в табл. 9.2. Вы сами можете подсчитать их, как мы сделали это с s2хи sхsy.
С матрицами о связан еще один очень интересный и важный момент. Можно, если угодно, представить себе, что три матрицы sх., syи sz подобны трем компонентам вектора; его иногда именуют «вектором сигма» и обозначают а. Это на самом деле «матричный вектор», или «векторная матрица». Это три разные матрицы, связанные каждая со своей осью х, у или z. С их помощью гамильтониан системы можно записать в красивом виде, пригодном для любой системы координат:
Таблица 9.2 · ПРОИЗВЕДЕНИЯ СПИНОВЫХ МАТРИЦ
Хотя мы записали эти три матрицы в представлении, в котором понятия «вверх» и «вниз» относятся к направлению z (так что sz выглядит особенно просто), но можно представить себе, как будут они выглядеть в любом другом представлении. И хотя это требует немалых выкладок, можно все же показать, что они изменяются как компоненты вектора. (Мы, впрочем, пока не будем заботиться о том, чтобы доказать это. Проверьте сами, если хотите.) Вы можете пользоваться о в различных системах координат, как если бы это был вектор.
Вы помните, что гамильтониан Н связан в квантовой механике с энергией. Он действительно в точности совпадает с энергией в том простом случае, когда состояний только одно. Даже в системе с двумя состояниями, какой является спин электрона, если записать гамильтониан в виде (9.13), он очень напоминает классическую формулу энергии магнита с магнитным моментом m в магнитном поле В. Классически это выглядит так:
где m — свойство объекта, а В — внешнее поле. Можно вообразить себе, что (9.14) обращается в (9.13), если классическую энергию заменяют гамильтонианом, а классическое m — матрицей (ms. Тогда после такой чисто формальной замены результат можно будет интерпретировать как матричное уравнение. Иногда утверждают, что каждой величине в классической физике соответствует в квантовой механике матрица. На самом деле правильнее было бы говорить, что матрица Гамильтона соответствует энергии и что у каждой величины, которая может быть определена через энергию, есть соответствующая матрица. Например, магнитный момент можно определить через энергию, сказав, что энергия во внешнем поле В есть —m·B. Это определяет вектор магнитного момента m. Затем мы смотрим на формулу для гамильтониана реального (квантового) объекта в магнитном поле и пытаемся угадать, какие матрицы соответствуют тем или иным величинам в классической формуле. С помощью этого трюка иногда у некоторых классических величин появляются их квантовые двойники.
Если хотите, попробуйте разобраться в том, как, в каком смысле классический вектор равен матрице ms; может быть, вы что-нибудь и откроете. Но не надо ломать над этим голову. Право же, не стоит: на самом-то деле они не равны. Квантовая механика — это совсем другой тип теории, другой тип представлений о мире. Иногда случается, что всплывают некоторые соответствия, но вряд ли они представляют собой нечто большее, нежели мнемонические средства — правила для запоминания.
Иначе говоря, вы запоминаете (9.14), когда учите классическую физику; затем если вы запомнили соответствие m®ms, то у вас есть повод вспомнить (9.13). Разумеется, природа знает квантовую механику, классическая же является всего лишь приближением, значит, нет ничего загадочного в том, что из-за классической механики выглядывают там и сям тени квантовомеханических законов, представляющих на самом деле их подоплеку. Восстановить реальный объект по тени прямым путем никак невозможно, но тень помогает нам вспомнить, как выглядел объект. Уравнение (9.13) — это истина, а уравнение (9.14) — ее тень. Мы сперва учим классическую механику и поэтому нам хочется выводить из нее квантовые формулы, но раз и навсегда установленной схемы для этого нет. Приходится каждый раз возвращаться обратно к реальному миру и открывать правильные квантовомеханические уравнения. И когда они оказываются похожими на что-то классическое, мы радуемся. Если эти предостережения покажутся вам надоедливыми, если, по-вашему, здесь изрекаются старые истины об отношении классической физики к квантовой, то прошу прощения: сработал условный рефлекс преподавателя, который привык втолковывать квантовую механику студентам, никогда прежде не слыхавшим о спиновых матрицах Паули. Мне всегда казалось, что они не теряют надежды, что квантовая механика как-то сможет быть выведена как логическое следствие классической механики, той самой, которую они старательно учили в прежние годы. (Может быть, они просто хотят обойтись без изучения чего-то нового.) Но, к счастью, вы выучили классическую формулу (9.14) всего несколько месяцев тому назад, да и то с оговорками, что она не совсем правильна, так что, может быть, вы не будете столь неохотно воспринимать необходимость рассматривать квантовую формулу (9.13) в качестве первичной истины.
§ 2. Спиновые матрицы как операторы
Раз уж мы занялись математическими обозначениями, то хотелось бы описать еще один способ записи, способ, часто употребляемый из-за своей краткости. Он прямо следует из обозначений, введенных в гл. 6. Если имеется система в состоянии |y|(t)>, изменяющемся во времени, то можно, как мы это делали в уравнении (6.31), написать амплитуду того, что система при t+Dt оказалась бы в состоянии |i>:
Матричный элемент <i|U(t, t+Dt) |j> — это амплитуда того, что базисное состояние |j> превратится в базисное состояние |i> за время Dt. Затем мы определяли Нijпри помощи
и показывали, что амплитуды Ci(t)=<i|y(t)> связаны дифференциальными уравнениями
Если амплитуды Ciзаписать явно, то это же уравнение будет выглядеть по-иному:
Далее, матричные элементы Hij — это тоже амплитуды, которые можно записывать в виде <i|H|j>; наше дифференциальное уравнение выглядит тогда так:
Мы видим, что —i/h <1|H|j> — это амплитуда того, что в физических условиях, описываемых матрицей Н, состояние |j> за время dt «генерирует» состояние |i>. (Все это неявно подразумевалось в рассуждениях гл. 6, § 4.)
Теперь, следуя идеям гл. 6, § 2, мы можем сократить в (9.17) общий «множитель» <i|, поскольку (9.17) справедливо при любом |i>, и записать это уравнение просто в виде
Или, сделав еще один шаг, убрать к тому же и j и написать
В гл. 6 мы указывали, что при такой записи Н в Н|j> или в Н|y> называется оператором. Отныне на операторы мы будем надевать маленькие шапочки (^), чтобы напоминать вам, что это оператор, а не число. Мы будем писать
. Хотя оба уравнения (9.18) и (9.19) означают в точности то же самое, что и (9.15) или (9.17), мы можем думать о них совершенно иначе. Например, уравнение, (9.18) можно было бы описывать так: «Производная по времени от вектора состояния |y> равняется тому, что получается от действия оператора Гамильтона Н на каждое базисное состояние, умноженному на амплитуду <j|y> того, что y окажется в состоянии j, и просуммированному по всем j». Или уравнение (9.19) можно описать так: «Производная по времени (умноженная на ih) от состояния |y> равняется тому, что вы получите, если подействуете гамильтонианом Н на вектор состояния |y>». Это просто сокращенный способ выражения того, что содержится в (9.17), но, как вы потом убедитесь, он может оказаться очень удобным.
Если хотите, идею «абстрагирования» можно продвинуть еще на шаг. Уравнение (9.19) справедливо для всякого состояния |y>. Кроме того, левая сторона ihd/dt — это тоже оператор; его действие: «продифференцируй по t и умножь на ih». Итак, (9.19) можно рассматривать как уравнение между операторами — операторное уравнение
Ih(d/dt)=
Оператор Гамильтона (с точностью до константы), действуя на любое состояние, приводит к тому же результату, что и d/dt. Помните, что это уравнение, как и (9.19), не есть утверждение о том, что оператор просто та же операция, что и d/dt. Эти уравнения — динамический закон природы (закон движения) для квантовой системы.
Только для того, чтобы попрактиковаться в этих представлениях, продемонстрируем вам другой вывод уравнения (9.18). Вы знаете, что любое состояние |y> можно записать через его проекции на какой-то базис [см. (6.8)]:
Как же меняется |y> во времени? Продифференцируем его:
Но базисные состояния |i> во времени неменяются (по крайней мере у нас они всегда были определенными, закрепленными состояниями), и только амплитуды <i|y>—это числа, которые могут меняться. Иначе говоря, (9.21) прекращается в
Но ведь d<i|y>/dt нам известно—это (9.16); получается, следовательно,
А это опять-таки уравнение (9.18).
Итак, на гамильтониан можно смотреть по-разному. Можно рассматривать совокупность коэффициентов Hijпросто как компанию чисел, можно говорить об «амплитудах» <i|Н|j>, можно представлять себе «матрицу» Hijи можно считать его
«оператором» H^. Все это одно и то же.
Вернемся теперь к нашей системе с двумя состояниями. Если уж мы записываем гамильтониан через матрицы сигма (с подходящими численными множителями, такими, как Вх и т. д.), то естественно рассматривать и sxij как амплитуду < i|sх|j>, или, для краткости, как оператор s^л. Если применить эту идею оператора, то уравнение движения состояния |y> в магнитном поле можно написать в виде
Желая «использовать» это уравнение, нам, естественно, приходится выражать |y> через базисные векторы (равносильно тому, что приходится находить компоненты пространственных векторов, когда задача доводится до числа). Так что обычно мы предпочитаем расписывать (9.23) в более раскрытом виде:
Сейчас вы увидите, чем красива идея оператора. Чтобы применять уравнение (9.24), нужно знать, что будет, когда операторы о подействуют на каждое базисное состояние. Напишем s^z|+>; это какой-то вектор |?>, но какой? Что ж, умножим его слева на <+| и получим
(пользуясь табл. 9.1). Итак, мы знаем, что
<+|?>=1. (9.25)
Теперь умножим s^z|+> слева на <-|. Получится
т, е.
Существует только один вектор состояния, удовлетворяющий и (9.25), и (9.26); это |+>. Мы, стало быть, открыли, что
Такого рода рассуждениями можно легко показать, что все свойства матриц сигма могут быть в операторных обозначениях описаны рядом правил, приведенных в табл. 9.3.
Таблица 9.3 · СВОЙСТВА ОПЕРАТОРА s^
Если у нас есть произведения матриц сигма, то они переходят в произведения операторов. Когда два оператора стоят рядом в виде произведения, то сперва приступает к операции тот оператор, который стоит правее. Скажем, под s^xs^y|+> надо понимать s^х(s^y|+>). Из табл. 9.3 получаем s^y|+>=i|-> так что
Числа (как, например, i) просто проходят сквозь операторы (операторы действуют только на векторы состояний); значит (9.28) перейдет в
Если сделать то же самое с s^xs^y|->, то получится
Если взглянуть на табл. 9.3, то видно, что s^хs^у, действуя на |+> или |->, даст в точности то же, что получается, если просто подействовать оператором s^zи умножить на — i. Поэтому можно сказать, что операция s^хs^yсовпадает с операцией is^z, и записать это утверждение в виде операторного уравнения
Убедитесь, что это уравнение совпадает с одним из наших матричных уравнений табл. 9.2. Итак, мы опять видим соответствие между матричной и операторной точкой зрения. Каждое из уравнений в. табл. 9.2 может поэтому рассматриваться и как
уравнение относительно операторов сигма. Можно проверить,
что они действительно следуют из табл. 9.3. Работая с этими
вещами, лучше не следить за тем, являются ли величины типа 0
или Н операторами или матрицами. Чем их ни считай, уравнения
: выйдут одни и те же, так что табл. 9.2 можно при желании относить то к операторам сигма, то к матрицам сигма.
§ 3. Решение уравнений для двух состояний
Теперь можно писать наше уравнение двух состояний в раз-jличных видах, например:
или вот так:
Оба они означают одно и то же. Для частицы со спином 1/2 в магнитном поле гамильтониан Н дается уравнением (9.8) или (9.13). I Если поле направлено по г, то, как мы уже много раз видели, решение заключается в том, что состояние |y>, каким бы оно ни было, прецессирует вокруг оси z (в точности, как если бы взять \ физическое тело и вращать его как целое вокруг оси z) с угловой
скоростью, вдвое большей, чем mB/h. Все это, конечно, относится и к магнитному полю, направленному под другим углом, ведь физика от системы координат не зависит. Если магнитное поле время от времени как-то сложно меняется, то такое положение пещей можно анализировать следующим образом. Пусть вначале спин был в направлении +z, а магнитное поле — в направлении х. Спин начал поворачиваться. Если выключить x-поле, поворот прекратится. Если теперь включить z-поле, спин начнет поворачиваться вокруг z и т. д. Значит, смотря по тому, как меняются поля во времени, вы можете представить себе, каким будет конечное состояние — по какой оси оно будет направлено. Затем можно отнести это состояние к первоначальным |+> и |-> по отношению к z, пользуясь проекционными формулами, полученными в гл. 8 (или в гл. 4). Если в конечном состоянии спин направлен по (q, j), то амплитуда того, что спин будет смотреть вверх, равна, а амплитуда того, что спин будет смотреть вниз, равна. Это решает любую задачу. Таково словесное описание решений дифференциальных уравнений.
Только что описанное решение достаточно общо для того. чтобы справиться с любой системой с двумя состояниями. Возьмем наш пример с молекулой аммиака, на которую действует электрическое поле. Если система описывается на языке состояний |I> и |II>, то уравнения выглядят так:
Вы скажете: «Нет, там, я помню, стояло еще E0». Неважно, мы просто сдвинули начало отсчета энергий, чтобы Е0стало равно нулю. (Это всегда можно сделать, изменив обе амплитуды в одно и то же число раз — в eiE0T/h; так можно избавиться от любой постоянной добавки к энергии.) Одинаковые уравнения обладают одинаковыми решениями, поэтому не стоит решать их вторично. Если взглянуть на эти уравнения и на (9.1), то их можно отождествить между собой следующим образом. Состояние |+> обозначим |I>, состояние |-> обозначим |Н>. Это вовсе не значит, что мы выстраиваем аммиак в пространстве в одну линию или что |+> и |-> как-то связаны с осью z. Это все делается чисто искусственно. Имеется искусственное пространство, которое можно было бы назвать, например, «модельным пространством молекулы аммиака» или еще как-нибудь иначе. Это просто трехмерная «диаграмма», и направление «вверх» означает пребывание молекулы в состоянии |I>, а направление «вниз» по фальшивой оси z означает пребывание молекулы в состоянии |II>. Тогда уравнения отождествляются следующим образом.
Прежде всего вы видите, что гамильтониан может быть записан через матрицы сигма:
Если сравнить это с (9.1), то mBzбудет соответствовать -А, а mВхбудет соответствовать -mx. В нашем «модельном» пространстве возникает, стало быть, постоянное поле В, направленное по оси z. Если есть, кроме этого, электрическое поле x, меняющееся со временем, то у поля В появится и пропорционально меняющаяся x-компонента. Таким образом, поведение электрона в магнитном поле с постоянной составляющей в направлении z и колеблющейся составляющей в направлении х математически во всем подобно и точно соответствует поведению молекулы аммиака в осциллирующем электрическом поле, К сожалению, у нас нет времени входить глубже в детали этого соответствия или разбираться в каких-либо технических деталях. Мы только хотели подчеркнуть, что можно сделать так, чтобы все системы с двумя состояниями были аналогичны объекту со спином 1/2, прецессирующему в магнитном поле.
§ 4. Состояния поляризации фотона
Есть множество других интересных для изучения систем с двумя состояниями, и первая, о которой мы бы хотели поговорить,— это фотон. Чтобы описать фотон, нужно сначала задать вектор его импульса. У свободного фотона импульс определяет и частоту, так что указывать особо частоту не придется. Но еще остается одно свойство, именуемое поляризацией. Представьте себе фотон, приходящий к вам с определенной монохроматической частотой (которую во всем нашем обсуждении мы будем считать постоянной, так что можно не говорить о множестве состояний импульса).Тогда существуют два направления поляризации. По классической теории свет обладает, например, либо горизонтально колеблющимся электрическим полем, либо вертикально колеблющимся электрическим полем; этот свет двух сортов называют x-поляризованным и y-поляризованным светом. У света может быть и какое-то иное направление поляризации, его можно создать суперпозицией полей в направлении x и в направлении у. Или, взяв х- и y-компоненты со сдвигом фаз в 90°, получить вращающееся электрическое поле — свет будет поляризован эллиптически. [Это краткое напоминание классической теории поляризованного света, которую мы изучали в гл. 33 (вып. 3).]
Пусть теперь у нас есть одиночный фотон, всего один. Уже нет электрического поля, которое можно было бы рассматривать прежним способом. Один-единственный фотон и ничего больше. по он тоже должен обладать аналогом классического явления поляризации. Значит, должны существовать по крайней мере два разных сорта фотонов. Сперва могло бы показаться, что их должно быть бесконечное множество, ведь, как бы то ни было, электрический вектор может быть направлен в любую сторону. Однако поляризацию фотона можно описать как систему с двумя состояниями. Фотон может быть либо в состоянии |х>, либо |в состоянии | у>. Под |х>подразумевается состояние поляризации каждого из фотонов в пучке света, который классически x-поляризован. А | у>означает состояние поляризации каждого из фотонов в y-поляризованном пучке. Эти |х>и |у>вы можете выбрать в качестве базисных состояний фотона с данным [направленным на вас импульсом—импульсом в направлении z.
Итак, существуют два базисных состояния |x> и |y>, и их вполне хватает, чтобы описать всякий фотон.
К примеру, если у нас есть поляроид, ось которого расположена так, чтобы пропускать свет, поляризованный в направлении, которое мы называем направлением х, и если мы направили туда фотон, который, как нам известно, находится в состоянии |у>, то он поглотится поляроидом. Если послать туда фотон, который, как нам известно, находится в состоянии |х>, он и выйдет в состоянии |x>. Когда мы берем кусок кальцита (исландского пшата), который расщепляет пучок поляризованного света на |x>-пучок и |y>-пучок, то этот кусок кальцита полностью аналогичен прибору Штерна — Герлаха, расщепляющему пучок атомов серебра на два состояния |+> и |->. Значит, все, что мы раньше делали с частицами и приборами Штерна — Герлаха, можно повторить со светом и кусками поляроида. А что можно сказать о свете, который отфильтрован куском поляроида, повернутым на угол 6? Другое ли это состояние? Да, действительно, это другое состояние. Обозначим ось поляроида х' , чтобы отличать ее от осей наших базисных состояний (фиг. 9.2).
Фиг. 9.2. Оси координат, перпендикулярные к вектору импульса фотона.
Выходящий наружу фотон будет в состоянии |х'>. Но всякое состояние может быть представлено в виде линейной комбинации базисных состояний, а формула для такой комбинации известна:
Иначе говоря, если фотон пройдет сквозь кусок поляроида, повернутого на угол q (по отношению к х), он все равно может быть разрешен на |x>- и |y>-пучки (например, куском кальцита). Или, если угодно, вы можете в своем воображении просто разбить его на х- и y-компоненты. Любым путем вы получите амплитуду cosq быть в |х>-состоянии и амплитуду sinq быть в |y>-состоянии.
Теперь поставим такой вопрос: пусть фотон поляризован в направлении х' куском поляроида, повернутого на угол q,
и пусть он попадет в другой поляроид, повернутый на угол нуль (фиг. 9.3).
Фиг. 9.3. Две поляроидные пластины с углом q между плоскостями поляризации.
Что тогда произойдет? С какой вероятностью он пройдет сквозь поляроид? Ответ: Пройдя первый поляроид, фотон наверняка оказывается в состоянии |х'>. Через второй поляроид он протиснется лишь в том случае, если будет в состоянии |x> (и поглотится им, оказавшись в состоянии |у>). Значит, мы спрашиваем, с какой вероятностью фотон окажется в состоянии |x>? Эту вероятность мы получим из квадрата модуля амплитуды <x|x'>, амплитуды того, что фотон в состоянии |х'>находится также и в состоянии |x>. Чему равно <x|x'>? Умножив (9.33) на <x|, получим
Но <x|y>=0; это следует из физики, так должно быть, если |х>и |у>суть базисные состояния, а <x|x>=l. И мы получаем
<x|x'>=cosq,
а вероятность равна cos2q. Например, если первый поляроид поставлен под углом 30°, то 3/4 времени фотон будет проходить через него, a 1/4времени будет нагревать поляроид, поглощаясь внутри него.
Посмотрим теперь, что в такой же ситуации происходит с точки зрения классической физики. Там мы имели бы пучок света, электрическое поле которого меняется тем или иным образом,— скажем «неполяризованный» пучок. После того как он прошел бы через первый поляроид, электрическое поле величины x начало бы колебаться в направлении х' ; мы бы начертили его в виде колеблющегося вектора с пиковым значением x0на диаграмме фиг, 9.4.
Фиг. 9.4. Классическая картина электрического вектора x.
Если бы затем свет достиг второго поляроида, то черен него прошла бы только x-компонента x0cosq электрического поля. Интенсивность была бы пропорциональна квадрату поля, т. е. x2cos2q. Значит, проходящая сквозь последний поляроид энергия была бы в cos2q слабее энергии, поступающей в него.
И классическая, и квантовая картины приводят к одинаковым результатам. Если бы вы бросили на второй поляроид 10 миллиардов фотонов, а средняя вероятность прохождения каждого из них была бы, скажем, 3/4, то следовало бы ожидать, что сквозь него пройдет 3/4 от 10 миллиардов. Равным образом и энергия, которую они унесли бы, составила бы 3/4 той энергии, которую вам хотелось протолкнуть через поляроид. Классическая теория ничего не говорит о статистике этих вещей, она попросту утверждает, что энергия, которая пройдет насквозь, в точности равна 3/4 той энергии, которая была пущена в поляроид. Это, конечно, немыслимо, если фотон только один. Не бывает 3/4 фотона. Либо он весь здесь, либо его вовсе нет. И квантовая механика говорит нам, что он бывает весь здесь 3/4 времени. Связь обеих теорий ясна.
А как же с другими сортами поляризации? Скажем, с правой круговой поляризацией? В классической теории компоненты х и у правой круговой поляризации были равны, но сдвинуты по фазе на 90°. В квантовой теории фотон, поляризованный по кругу вправо («правый»), обладает равными амплитудами быть |х>- и |у>-поляризованным, и эти амплитуды сдвинуты по фазе на 90°. Обозначая состояние «правого» фотона через |II>, а состояние «левого» фотона через |Л>, можно написать [см. гл. 33, § 1 (вып. 3)]
множитель 1/Ц2 поставлен, чтобы нормировать состояния. С помощью этих состояний можно подсчитывать любые эффекты, связанные с фильтрами или интерференцией, применяя законы квантовой теории. При желании можно также выбрать в качестве базисных состояний |П> и |Л> и все представлять через них. Надо только предварительно убедиться, что <П|Л>=0, а это можно сделать, взяв сопряженный вид первого уравнения [см. (6.13)] и перемножив их друг с другом. Можно раскладывать свет, пользуясь в качестве базиса и х-, и y-поляризациями, и х'-, и y'-поляризациями, а можно—и правой, и левой поляризациями.
Попробуйте (просто для упражнения) обратить наши формулы. Можно ли представить состояние |х> в виде линейной комбинации правого и левого? Да, вот ответ:
Доказательство: сложите и вычтите два уравнения в (9.34). От одного базиса к другому очень легко переходить.
Впрочем, одно замечание надо бы сделать. Если фотон поляризован по правому кругу, он не имеет никакого касательства к осям х и у. Если бы мы взглянули на него из системы координат, повернутой вокруг направления полета на какой-то угол, то свет по-прежнему был бы поляризован по кругу; то же с левой поляризацией. Право- и левополяризованный по кругу свет при любом таком повороте одинаков; определение не зависит от выбора направления х (если не считать того, что направление фотона задано). Великолепно, не так ли? Для определения не нужны никакие оси. Куда лучше, чем х и у!Но, с другой стороны, не чудо ли, что, складывая левое и правое, вы в состоянии узнать, где было направление x? Если «правое» и «левое» никак не зависят от х, как же получается, что мы можем сложить их и вновь получить x? На этот вопрос можно частью ответить, расписав состояние |П'>, представляющее фотон, правополяризованный в системе координат х', у'. В этой системе мы бы написали
Как же будет выглядеть такое состояние в системе х, у? Подставим | х'> из (9.33) и соответствующее |у'>; мы его не выписывали, но оно равно (-sinq)|x>+(cosq)|y>. Тогда
Первый множитель — это просто | П>, а второй е-iq; итог таков:
Состояния | П'> и | П> отличаются только фазовым множителем е-iq. Если подсчитать такую же вещь для | Л' >, мы получим
Теперь мы видим, что происходит. Сложив |П> и |Л>, мы получаем нечто отличное от того, что получилось бы при сложении |П'> и |Л'>. Скажем, x-поляризованный фотон есть [см. (9.35)] сумма |П> и |Л>, но y-поляризованный фотон — это сумма со сдвигом фазы первого на 90° назад, а второго — на 90° вперед. Это просто то же самое, что получилось бы из суммы |П> и |Л'> при определенном выборе угла 0=90°, и это правильно, В штрихованной системе x-поляризация — это то же самое, что y-поляризация в первоначальной системе. Значит, не совсем верно, что поляризованный по кругу фотон выглядит в любой системе осей одинаково. Его фаза (фазовое соотношение между право- и левополяризованными по кругу состояниями) запоминает направление х.
§ 5. Нейтральный К-мезон**
Теперь мы расскажем о двухуровневой системе из мира странных частиц — о системе, для которой квантовая механика приводит к поразительнейшим предсказаниям. Полное описание этой системы потребовало бы от нас таких знаний о странных частицах, каких у нас пока нет, поэтому, к сожалению, кое- какие углы нам придется срезать. Мы лишь вкратце успеем изложить историю того, как было сделано одно открытие, чтобы показать вам, какого типа рассуждения для этого потребовались. Началось это с открытия Гелл-Манном и Нишиджимой понятия странности и нового закона сохранения странности.
И вот когда Гелл-Манн и Пайс проанализировали следствия из этих новых представлений, то они пришли к предсказанию замечательнейшего явления, о котором мы и хотим повести речь.
Сперва, однако, нужно немного рассказать о «странности».
Начать нужно с того, что называется сильными взаимодействиями ядерных частиц. Существуют взаимодействия, которые ответственны за мощные ядерные силы, в отличие, например, от относительно более слабых электромагнитных взаимодействий. Взаимодействия «сильны» в том смысле, что если две частицы сойдутся так близко, чтобы быть способными взаимодействовать, то взаимодействуют они очень мощно и создают другие частицы очень легко. Ядерные частицы обладают еще так называемым «слабым взаимодействием», в результате которого происходят такие вещи, как бета-распад; но они всегда происходят очень медленно (по ядерным масштабам времени): слабые взаимодействия на много-много порядков величины слабее, чем сильные, и даже слабее, чем электромагнитные.
Когда при помощи больших ускорителей начали изучать сильные взаимодействия, все были поражены, увидев, что некоторые вещи, которые «должны были» произойти (ожидалось, что они произойдут), на самом деле не возникали. К примеру, в некоторых взаимодействиях не появлялась частица определенного сорта, хотя ожидалось, что она появится. Гелл-Манн и Нишиджима заметили, что многие из этих странных случаев можно было объяснить одним махом, изобретя новый закон сохранения: сохранение странности. Они предположили, что существует свойство нового типа, связываемое с каждой частицей,— число, названное ими «странностью»,— и что во всяком сильном взаимодействии «количество странности» сохраняется. Предположим, например, что отрицательный K-мезон высокой энергии, скажем с энергией во много Гэв, сталкивается с протоном. Из их взаимодействия могут произойти много других частиц: p-мезонов, K-мезонов, A-частиц, S-частиц,— любые из мезонов или барионов, перечисленных в табл. 2.2 (вып. 1). Оказалось, однако, что возникали только определенные комбинации, а другие — никогда.
Про некоторые законы сохранения было известно, что они обязаны соблюдаться. Во-первых, всегда сохранялись энергия и импульс. Полная энергия и импульс после события должны быть такими же, как и перед событием. Во-вторых, существует закон сохранения электрического заряда, утверждающий, что полный заряд выходящих частиц обязан равняться полному заряду, внесенному начальными частицами. В нашем примере столкновения К-ыезона. и протона действительно происходят такие реакции:
И никогда из-за несохранения заряда не идут реакции
Было также известно, что количество барионов сохраняется. Количество выходящих барионов должно быть равно количеству входящих. В этом законе античастица бариона считается за минус один барион. Это значит, что мы можем видеть — и видим — реакции
(где — это антипротон, несущий отрицательный заряд). Но мы никогда не увидим
(даже если энергия очень-очень большая), потому что число барионов здесь не сохранялось бы.
Эти законы, однако, не объясняют того странного факта, что нижеследующие реакции, которые с виду не особенно отличаются от кое-каких приведенных в (9.38) или (9.40), тоже никогда не наблюдались:
Объяснением служит сохранение странности. За каждой частицей следует число — ее странность S, и имеется закон, что в любом сильном взаимодействии полная странность на выходе должна равняться полной странности на входе. Протон и антипротон (), нейтрон и антинейтрон () и p-мезоны (p+ , p0, p-) — все имеют странность нуль; у К+- и K0-мезонов странность равна +1;у К-и (анти-К0), у L0- и S-частиц (2S+ , S0, S-) странность равна -1. Существует также частица со странностью -2 (-частица), а может быть, и другие, пока неизвестные. Перечень этих странностей приведен в табл. 9.4.
Таблица 9.4 · СТРАННОСТИ СИЛЬНО ВЗАИМОДЕЙСТВУЮЩИХ ЧАСТИЦ
Посмотрим, как действует сохранение странности в некоторых написанных реакциях. Если мы исходим из К-и протона, то их суммарная странность равна (-1)+0 =-1. Сохранение странности утверждает, что странности продуктов реакции после сложения тоже должны дать -1. Вы видите, что в реакциях (9.38) и (9.40) это действительно так. Но в реакциях (9.42) странность справа во всех случаях есть нуль. В них странность не сохраняется, и они не происходят. Почему? Это никому не известно. Никому не известно что-либо сверх того, что мы только что рассказали. Просто природа так действует — и все.
Давайте теперь взглянем на такую реакцию: p-попадает в протон. Вы можете, например, получить L0-частицу плюс нейтральный K-мезон — две нейтральные частицы. Какой же из нейтральных K-мезонов вы получите? Раз у L-частицы странность -1, а у p- и p+ странность нуль и поскольку перед нами быстрая реакция рождения, то странность измениться не должна. Вот K-частица и должна обладать странностью +1,—и быть поэтому К0. Реакция имеет вид
причем
(сохраняется).
Если бы здесь вместо К0стояло К°, то странность справа была бы -2, чего природа не позволит, ведь слева странность нуль.
С другой стороны, К° может возникать в других реакциях:
где
или
где
Вы можете подумать: «Не слишком ли много разговоров. Как узнать, это или K0? Выглядят-то они одинаково. Они античастицы друг друга, значит, массы их одинаковы, заряды у обеих равны нулю. Как вы их различите?» По реакциям, которые они вызывают. Например, -мезон может взаимодействовать с веществом, создавая L-частицу, скажем, так:
а K0-мезон не может. У К0 нет способа создать L-частицу, взаимодействуя с обычным веществом (протонами и нейтронами). Значит, экспериментальное отличие между К0- и -мезонами состояло бы в том, что один из них создает L-частицу, а другой— нет.
Одно из предсказаний теории странности тогда заключалось бы в следующем: если в опыте с пионами высокой энергии L-частица возникает вместе с нейтральным K-мезоном, тогда этот нейтральный K-мезон, попадая в другие массивы вещества, никогда не создаст L-частицы. Опыт мог бы протекать таким образом. Вы посылаете пучок p--мезонов в большую водородную пузырьковую камеру. След p- исчезает, но где-то в стороне появляется пара следов (протона и p- -мезона), указывающая на то, что распалась Λ-частица (фиг. 9.5). Тогда вы знаете, что где-то есть K0-мезон, который вам не виден.
Но вы можете представить, куда он направился, применяя сохранение импульса и энергии. (Он затем иногда раскрывает свое местоположение, распадаясь на пару заряженных частиц, как показано на фиг. 9.5, а.)
Когда К0-мезон летит в веществе, он может провзаимодействовать с одним из ядер водорода (протонов), создав при этом, быть может, еще какие-то частицы.
Предсказание теории странности состоит в том, что K0-мезон никогда не породит L-частицу в простой реакции, скажем, такого типа
хотя -мезон это может сделать. Иначе говоря, в пузырьковой камере -мезон мог бы вызвать событие, показанное на фиг. 9.5, б, где L0-частицу из-за распада можно заметить, а К0-мезон не смог бы. Это первая часть рассказа. Это и есть сохранение странности.
Странность, впрочем, сохраняется не совсем. Существуют очень медленные распады странных частиц — распады, происходящие за большое время — порядка 10-10 сек, в которых странность не сохраняется. Их называют «слабые» распады. Например, K0-мезон распадается на пару p-мезонов (+ и -) со временем жизни 10-10 сек. Именно так на самом деле впервые были замечены K-частицы. Обратите внимание, что распадная реакция
не сохраняет странности, так что «быстро», путем сильного взаимодействия, она идти не может. Может она идти только через слабый распадный процесс.
Далее, -мезон также распадается таким же путем (на p+ и p-) и тоже с таким же самым временем жизни:
Здесь опять идет слабый распад, потому что он не сохраняет странности. Существует принцип, по которому для всякой реакции всегда найдется соответствующая реакция, в которой «материя» заменяется «антиматерией» и наоборот. Раз— это античастица К0, она обязана распадаться на античастицы p+ и p- , но античастица p+есть p- . (Или, если вам угодно, наоборот. Оказывается, что для p-мезонов неважно, кого из них назовут «материей», их эта материя совсем не интересует.) Итак, как следствие слабых распадов К0- и -мезоны могут превращаться в одинаковые конечные продукты. Если «видеть» их по их распадам (как в пузырьковой камере), то выглядят они, как совершенно одинаковые частицы. Отличаются только их сильные взаимодействия.
Теперь наконец-то мы доросли до того, чтобы описать работу Гелл-Манна и Пайса. Во-первых, они отметили, что раз К0 и оба могут превращаться в два p-мезонов, то должна также существовать некоторая амплитуда того, что К0может превратиться в К0, и такая же амплитуда того, что превратится в К0. Реакцию можно записать так, как это делают химики:
Из существования таких реакций следует, что есть амплитуда, которую мы обозначим через, превращения К0в, обусловленная тем самым слабым взаимодействием, с которым связан распад на два p-мезона. Ясно, что есть и амплитуда обратного процесса. Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А:
И вот, сказали Гелл-Манн и Пайс, здесь возникает интересная ситуация. То, что люди назвали двумя разными состояниями мира (К0и), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2 л и т. д.; но поскольку наши физики интересовались главным образом связью К0 с, то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).
В соответствии с этим Гелл-Манн и Пайс анализировали нейтральную частицу как систему с двумя состояниями. Начали они с того, что выбрали состояния | К0> и | > за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |y> нейтрального K-мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды
Следующим шагом мы должны написать уравнение Гамильтона для такой системы с двумя состояниями. Если бы К0и не были бы связаны между собой, то уравнения выглядели бы просто
Однако есть еще амплитуда
перехода К0в ; поэтому в правую часть первого уравнения надо еще добавить слагаемое
Аналогичное слагаемое АС+ надо добавить и в уравнение, определяющее скорость изменения С _. Но это еще не все! Если уж мы учитываем двухпионный эффект, то надо учесть и то, что существует еще дополнительная амплитуда превращения К0 в самого себя по цепочке
Эта дополнительная амплитуда (обозначим ее)в точности равна амплитуде
, так как амплитуды перехода в пару p-мезонов или от пары p-мезонов в К0или одни и те же.
Если угодно, можно показать это и подробнее. Прежде всего напишем
Симметрия между материей и антиматерией требует, чтобы
а также
Отсюда
а также
очем мы уже говорили выше.
Итак, у нас есть две дополнительные амплитуды и
, обе равные А, которые надо вставить в уравнения Гамильтона. Первая приводит к слагаемому АС+в правой части уравнения для dC+/dt, а вторая — к слагаемому АС-в правой части уравнения для dC-/dt. Рассуждая именно так, Гелл-Манн и Пайс пришли к заключению, что уравнения Гамильтона для системы должны иметь вид
Теперь надо сделать поправку к сказанному в прежних главах: к тому, что две амплитуды, такие, как и , выражающие обратные друг к другу процессы, всегда комплексно сопряжены. Это было бы верно, если бы мы говорили о частицах, которые не распадаются. Но если частицы могут распадаться, а поэтому «пропадать», то амплитуды не обязательно комплексно сопряжены. Значит, равенство (9.44)
не означает, что наши амплитуды суть действительные числа. На самом деле они суть комплексные числа. Поэтому коэффициент А комплексный и его нельзя просто включить в энергию Е0.
Часто, возясь со спинами электронов и тому подобными вещами, наши герои знали: такие уравнения означают, что имеется другая пара базисных состояний с особенно простым поведением, которые также пригодны для представления системы .K-частиц. Они рассуждали так: «Возьмем теперь сумму и разность этих двух уравнений. Будем отсчитывать все энергии от Е0и возьмем для энергии и времени такие единицы, при которых h=1». (Так всегда поступают современные теоретики. Это не меняет, конечно, физики, но уравнения выглядят проще.) В результате они получили
откуда ясно, что комбинации амплитуд С++С-и С+-С-действуют друг от друга независимо (и отвечают стационарным состояниям, которые мы раньше изучали). Они заключили, что удобнее было бы для K-частиц употреблять другое представление, Они определили два состояния:
и сказали, что вместо того, чтобы думать о -мезонах, с равным успехом можно рассуждать на языке двух «частиц» (т. е. «состояний») К1и К2. (Они, конечно, соответствуют состояниям, которые мы обычно называли |I> и |II>. Мы не пользуемся нашими старыми обозначениями, потому что хотим следовать обозначениям самих авторов, тем, которые вы встретите на физических семинарах.)
Но Гелл-Манн и Пайс проделывали все это не для того, чтобы давать частицам новые названия; во всем этом имеется еще некоторая весьма странная физика. Пусть C1и С2 суть амплитуды того, что некоторое состояние |y> окажется либо k1-, либо K2-мезоном:
Из уравнений (9.49)
Тогда (9.48) превращается в
Их решения имеют вид
где С1(0) и С2(0) — амплитуды при t=0.
Эти уравнения говорят, что если нейтральный K-мезон при t=0 находится в состоянии |К1> [так что С1(0)=1 и
С2(0)=0], то амплитуды в момент t таковы:
Вспоминая, что А — комплексное число, удобно положить
(так как мнимая часть 2А оказывается отрицательной, мы пишем ее как минус ib). После такой подстановки С1(t) принимает вид
Вероятность обнаружить в момент t частицу К1равна квадрату модуля этой амплитуды, т. е. e-2bt. А из (9.52) следует, что вероятность обнаружить в любой момент состояние K2равна нулю. Это значит, что если вы создаете К -мезон в состоянии |К1>, то вероятность найти его в том же состоянии со временем экспоненциально падает, но вы никогда не увидите его в состоянии |К2>. Куда же он девается? Он распадается на два p-мезона со средним временем жизни t=1/2b, экспериментально равным 10-10 сек. Мы предусмотрели это, говоря, что А комплексное.
С другой стороны, (9.52) утверждают, что если создать .K-мезон целиком в состоянии К2, он останется в нем навсегда. На самом-то деле это не так. На опыте замечено, что он распадается на три p-мезона, но в 600 раз медленнее, чем при описанном нами двухпионном распаде. Значит, имеются какие-то другие малые члены, которыми мы в нашем приближении пренебрегли. Но до тех пор, пока мы рассматриваем только двухпионные распады, К2остается «навсегда».
Рассказ о Гелл-Манне и Пайсе близится к концу. Дальше они посмотрели, что будет, когда K-мезон образуется вместе с L0-частицей в сильном взаимодействии. Раз его странность должна быть +1, он обязан возникать в состоянии К0, Значит, при t=0 он не является ни К1, ни К2, а их смесью. Начальные условия таковы:
Но это означает [из (9.50)], что
а из (9.52) следует, что
Теперь вспомним, что K1 и К2суть линейные комбинации К0и К°. В (9.54) амплитуды были выбраны так, что при t=0 части,
из которых состоит, взаимно уничтожаются за счет интерференции, оставляя только состояние К0. Но состояние |К1> со временем меняется, а состояние |К2> — нет. После t=0 интерференция С1и С2 приведет к конечным амплитудам и для К0, и для.
Что же все это значит? Возвратимся назад и подумаем об опыте, показанном на фиг. 9.5. Там p--мезон образовал L0-частицу и K0-мезон, который летит без оглядки сквозь водород камеры. Когда он движется, существует ничтожный, но постоянный шанс, что он столкнется с ядром водорода. Раньше мы думали, что сохранение странности предохранит K-мезон от образования L0-частицы в таком взаимодействии. Теперь, однако, мы понимаем, что это не так. Потому что, хотя наш К-мезон вначале является К0-мезоном, неспособным к рождению L°-частицы, он не остается им навечно. Через мгновение появляется некоторая амплитуда того, что он перейдет в состояние. Значит, следует ожидать, что иногда мы увидим L0-частицу, образованную вдоль следа K-мезона. Вероятность такого происшествия дается амплитудой С-, которую можно [решая (9.50)] связать с С1и С2. Связь эта такова:
И когда K-частица движется, вероятность того, что она будет «действовать как», равна |С-|2, т. е.
Сложный и поразительный результат!
Это и есть замечательное предсказание Гелл-Манна и Пайса: когда возникает K0-мезон, то шанс, что он превратится в -мезон, продемонстрировав это возможностью создания L0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутренних механизмов K-частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально наблюдаемой скорости распада на два p-мезона (2b=1,1·1010 сек-1), но про a они ничего не смогли сказать.
Мы изобразили функцию (9.56) для двух значений a на фиг. 9.6.
Видно, что форма ее сильно зависит от отношения a и b. Наблюдать -мезон сперва нет никакой вероятности, но затем она появляется. Если значение a велико, вероятность сильно осциллирует; если оно мало, осцилляции невелики или вовсе отсутствуют, вероятность просто плавно возрастает до 1/4.
Как правило, K-мезоны движутся с постоянной скоростью, близкой к скорости света. Тогда кривые фиг. 9.6 также представляют вероятность наблюдения -мезона вдоль следа с типичными расстояниями порядка нескольких сантиметров. Теперь вы видите, отчего это предсказание так удивительно своеобразно. Вы создаете отдельную частицу, и она не просто распадается, а проделывает нечто совсем иное. Временами она распадается, а порой превращается в частицу другого сорта. Характеристическая вероятность этого эффекта по мере ее движения меняется очень странно. Ничего другого, похожего на это, в природе нет. И это удивительнейшее предсказание было сделано только на основе рассуждений об интерференции амплитуд.
Если и существует какое-то место, где есть шанс проверить главные принципы квантовой механики самым прямым образом — бывает ли суперпозиция амплитуд или не бывает,— то оно именно здесь. Несмотря на то что этот эффект был предсказан уже несколько лет тому назад, до сих пор достаточно ясного опытного определения еще не было. Имеются некоторые грубые результаты, указывающие, что значение a не равно нулю и что эффект действительно наблюдается: они свидетельствуют, что a по порядку величины равно b. И это все, что мы знаем из эксперимента. Было бы замечательно, если бы удалось точно проверить и посмотреть, действительно ли работает принцип суперпозиции в этом таинственном мире странных частиц — с неизвестными поводами для распадов и неизвестным поводом существования странности.
Анализ, который мы только что привели,— характерный пример того, как сегодня используется квантовая механика, чтобы разгадать странные частицы. Во всех сложных теориях, о которых вы, быть может, слышали, нет ничего сверх этого элементарного фокуса, использующего принципы суперпозиции и другие принципы квантовой механики того же уровня. Некоторые утверждают, что у них есть теории, с помощью которых можно подсчитать b и a или по крайней мере a при данном b. Но эти теории совершенно бесполезны. Например, теория, предсказывающая значение а при данном b, говорит, что a должно быть бесконечным. Система уравнений, из которой они исходят, включает два p-мезона и затем возвращается от двух p-мезонов обратно к K0-мезону и т. д. Если все выкладки проделать, то действительно возникает пара уравнений, похожих на те, что у нас получались, но, поскольку у двух p-мезонов имеется бесконечно много состояний, зависящих от их импульсов, интегрирование по всем возможностям приводит к a, равному бесконечности. А природное a не бесконечно. Значит, динамические теории неверны. На самом деле чрезвычайно поразительно, что единственные явления, которые могут быть в мире странных частиц предсказаны, вытекают из принципов квантовой механики на том уровне, на котором вы их сейчас изучаете.
§ 6. Обобщение на системы с N состояниями
Мы покончили с системами с двумя состояниями, рассказав все, что хотелось. В дальнейших главах мы перейдем к изучению систем с большим числом состояний. Расширение на системы с N состояниями идей, разработанных для двух состояний, проходит довольно просто. Это делается примерно так.
Если система обладает N различными состояниями, то всякое состояние |y(t)>можно представить как линейную комбинацию произвольной совокупности базисных состояний |t>, где i=l, 2, 3, . . ., N:
Коэффициенты Ci(t) — это амплитуды <i|y(t)>. Поведение амплитуд Сiво времени направляется уравнениями
где энергетическая матрица Hijописывает физику задачи. С виду она такая же, как и для двух состояний. Но только теперь и i, и j должны пробегать по всем N базисным состояниям, и энергетическая матрица Hij(или, если вам больше нравится, гамильтониан) — это теперь матрица NXN, состоящая из N2чисел. Как и прежде, Hij=Hji (до тех пор, пока частицы сохраняются) и диагональные элементы Hiiсуть вещественные числа.
Мы нашли общее решение для всех С в системе с двумя состояниями, когда энергетическая матрица постоянна (не зависит от t). Точно так же нетрудно решить и уравнение (9.58) для системы с N состояниями, когда Н не зависит от времени. Опять мы начинаем с того, что ищем возможное решение, в котором у всех амплитуд зависимость от времени одинакова. Мы пробуем
Если все эти Ciподставить в (9.58), то производные dCi(t)/dt превращаются просто в (-i/h)ECi. Сокращая повсюду на общую экспоненту, получаем
Эта система N линейных алгебраических уравнений для N неизвестных a1 а2, . . ., аn;решение у нее бывает только тогда, когда вам сильно повезет, когда определитель из коэффициентов при всех а равен нулю. Но не нужно чересчур умничать: можете просто начать их решать любым способом, и вы сразу увидите, что решить их удается лишь при некоторых значениях E. (Вспомните, что единственная величина, которая в этих уравнениях подлежит подгонке, это Е.)
Если, впрочем, вы хотите, чтобы все было по форме, перепишите (9.60) так:
Затем примените правило (если оно вам знакомо), что эти уравнения будут иметь решения лишь для тех значений Е, для которых
Каждый член в детерминанте — это просто Hijи только из диагональных отнято Е. Иначе говоря, (9.62) означает просто
Это, конечно, всего-навсего особый способ записывать алгебраические уравнения для Е, складывая вереницы членов, перемножаемых в определенном порядке. Эти произведения дадут все степени Е вплоть до EN.
Значит, у нас есть многочлен N-йстепени, который равняется нулю. У него, вообще говоря, есть N корней. (Нужно помнить, однако, что некоторые из них могут быть кратными корнями; это значит, что два или более корней могут быть равны друг другу.) Обозначим эти N корней так:
(пусть n обозначает n-е порядковое числительное, так что n принимает значения I,II, . . ., N). Некоторые из этих энергий могут быть между собой равны, скажем ЕII=ЕIII, но мы решили все же обозначать их разными именами.
Уравнения (9.60) или (9.61) имеют по одному решению для каждого значения Е [из (9.64)]. Если вы подставите любое из Е, скажем En, в (9.60) и найдете все аi, то получится ряд чисел аi, относящихся к энергии En . Этот ряд мы обозначим аi (n).
Если подставить эти аi (n) в (9.59), то получатся амплитуды Сi(n) того, что состояния с определенной энергией находятся в базисном состоянии |i>. Пусть |n> обозначает вектор состояния для состояния с определенной энергией при t=0. Тогда можно написать
где
Полное состояние с определенной энергией |yn(t)> можно тогда записать так:
или
Векторы состояний |n> описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от времени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.
Каждое из состояний |n> обладает тем свойством (в чем легко убедиться), что при действии на него оператором Гамильтона Н получится просто Еn , умноженное на то же состояние:
Значит, энергия Еn — это характеристическое число оператора Гамильтона Н^. Как мы видели, у гамильтониана в общем случае бывает несколько характеристических энергий. Физики обычно называют их «собственными значениями» матрицы Н. Для каждого собственного значения Н^, иными словами, для каждой энергии, существует состояние с определенной энергией, которое мы называли «стационарным». Состояния |n> обычно именуются «собственными состояниями Н^». Каждое собственное состояние отвечает определенному собственному значению Еn.
Далее, состояния |n> (их N штук) могут, вообще говоря, тоже быть выбраны в качестве базиса. Для этого все состояния должны быть ортогональны в том смысле, что для любой нары их, скажем |n> и |m),
<n|m>=0. (9.68)
Это выполнится автоматически, если все энергии различны. Кроме того, можно умножить все аi(n) на подходящие множители, чтобы все состояния были отнормированы: чтобы для всех n было
<n|n>=1. (9.69)
Когда оказывается, что (9.63) случайно имеет два (или больше) одинаковых корня с одной и той же энергией, то появляются небольшие усложнения. По-прежнему имеются две различные совокупности аi, отвечающие двум одинаковым энергиям, но состояния, которые они дают, не обязательно ортогональны. Пусть вы проделали нормальную процедуру и нашли два стационарных состояния с равными энергиями. Обозначим их |m>и |v>. Тогда они не обязательно окажутся ортогональными: если вам не повезло, то обнаружите, что
<m|v>№0.
Но зато всегда верно, что можно изготовить два новых состояния (обозначим их | m'> и |v'>) с теми же энергиями, но ортогональных друг другу:
<m'|v'>=0. (9.70)
Этого можно добиться, составив |m'> и |v'> из подходящих линейных комбинаций |m> и |v> с так подобранными коэффициентами, что (9.70) будет выполнено. Это всегда полезно делать, и мы будем вообще предполагать, что это уже проделано, так что можно будет считать наши собственноэнергетические состояния | n> все ортогональными.
Для интереса докажем, что когда два стационарных состояния обладают разными энергиями, то они действительно ортогональны. Для состояния |n> с энергией Еn
Это операторное уравнение на самом деле означает, что имеется соотношение между числами. Если заполнить недостающие части, то оно означает то же самое, что и
Проделав здесь комплексное сопряжение, получим
Теперь вспомним, что комплексно сопряженная амплитуда — это амплитуда обратного процесса, так что (9.73) можно переписать в виде
Поскольку это уравнение справедливо для всякого i, то его можно «сократить» до
Это уравнение называется сопряженным с (9.71).
Теперь легко доказать, что Еn— число вещественное. Умножим (9.71) на <n|. Получится
(с учетом, что <n|n>=1). Умножим теперь (9.75) справа на
|n>:
Сравнивая (9.76) с (9.77), видим, что
Еn=Еn*, (9.78)
а это означает, что En вещественно. Звездочку при Еnв (9.75) можно убрать.
Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть |n> и |m> — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния |m> и умножив его на |n>, получим
Но если (9.71) умножить на <m|, то будет
Раз левые части этих уравнений равны, то равны и правые:
Если Еm=Еn , то это равенство ни о чем не говорит. Но если энергии двух состояний |m> и |n> различны (Еm№Еn), то уравнение (9.79) говорит, что <m|n> должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Еnи Еmотличаются друг от друга.
* Такую интерференцию действительно наблюдали. Коэффициент a оказался равным — 0,96b. Отсюда можно было вычислить и разность масс К1- и K2-мезонов. Она оказалась равной около —0,35·10-5 эв. Это наименьшая разность масс двух частиц, известных физикам.— Прим. ред.
* Мы здесь упрощаем. Система 2p может иметь множество состояний, отвечающих различным импульсам p-мезонов, и в правой части >того равенства следовало бы поставить сумму по всем базисным состояниям p-мезонов. Но полный вывод все равно приводит к тем же результатам.
* Типичное время для сильного взаимодействия ближе к 10-23 сек.
* Если, конечно, он не создает еще двух К+ или других частиц с общей странностью +2. Можно считать, что здесь речь идет о реакциях, в которых не хватает энергии для возникновения этих добавочных странных частиц.
** Свободная L-частица медленно распадается путем слабого взаимодействия (так что странность не обязана при этом сохраняться). Продуктами распада могут быть либо р и p-, либо n и p0. Время жизни 2,2·10-10сек.
* Читайте: «.K-нуль с чертой».
** Среди новых частиц есть барион W- со странностью -3.—Прим. ред.
* Это похоже на то, что мы обнаружили (в гл. 4) для частиц со спином 1/2. когда поворачивали систему координат вокруг оси z; тогда мы получили фазовые множители exp (±ij/2). В действительности это в точности то же самое, что мы писали в гл. 3, § 7, для состояний |+> и |-> частицы со спином 1, и это не случайно. Фотон— это частица со спином 1, у которой, однако, нет «нуль»-состояния.
** Мы сознаем, что материал этого параграфа длиннее и труднее, чем это положено на нашем уровне знаний. Лучше пропустите его и переходите прямо к § 6. Но если у вас есть самолюбие и время, попозже вернитесь к нему опять. Это великолепнейший пример (взятый к тому же из последних работ по физике высоких энергий) того, что можно сотворить с помощью нашей формулировки квантовой механики двухуровневых систем. (Для русского издания параграф переделан проф. Сэндсом. — Прим. ред.)
* Параграф 5 при первом чтении книги можно пропустить. Он сложнее, чем положено в таких курах.
Глава 10 СВЕРХТОНКОЕ РАСЩЕПЛЕНИЕ В ВОДОРОДЕ
§ 1. Базисные состояния для системы двух частиц со спином 1/2
§2. Гамильтониан основного состояния водорода
§ 3. Уровни энергии
§ 4. Зеемановское расщепление
§ 5. Состояния в магнитном поле
§ 6.Проекционная матрица для спина 1
§ 1. Базисные состояния для системы двух частиц со спином 1/2
В этой главе мы займемся «сверхтонким расщеплением» водорода — интересным примером того, что мы уже в состоянии делать с помощью квантовой механики. Здесь у нас уже будут не два состояния, а больше. Поучительность этого примера в том, что он познакомит нас с методами квантовой механики, применяемыми в более сложных задачах. Сам по себе этот пример достаточно сложен, и как только вы поймете, как с ним справляться, вам сразу же станет ясно, как обобщить его на другие возможные задачи.
Как известно, атом водорода состоит из электрона и протона; электрон сидит неподалеку от протона и может существовать в одном из многих дискретных энергетических состояний, в каждом из которых его картина движения другая. Так, первое возбужденное состояние лежит на 3/4 ридберга, или на 10 эв, выше основного состояния. Но даже так называемое основное состояние водорода на самом деле не является отдельным состоянием с определенной энергией, ибо у электрона и у протона есть спины. Эти спины и ответственны за «сверхтонкую структуру» в уровнях энергии, которая расщепляет все уровни энергии на несколько почти одинаковых уровней.
Спин электрона может быть направлен либо вверх, либо вниз; у протона тоже его собственный спин может смотреть вверх или вниз. Поэтому на всякое динамическое состояние атома приходятся четыре возможных спиновых состояния. Иначе говоря, когда физик говорит об «основном состоянии» водорода, он на самом деле имеет в виду «четыре основных состояния», а не просто самое низкое из них. У четырех спиновых состояний энергия не совсем одинакова; имеются небольшие сдвиги по отношению к тому, что наблюдалось бы в отсутствие спинов. Эти сдвиги, однако, во много-много раз меньше, чем те 10 эв, которые лежат между основным состоянием и следующим более высоким состоянием.
В итоге энергия каждого динамического состояния расщеплена на ряд очень тесных уровней — это так называемое сверхтонкое расщепление.
Разности энергий четырех спиновых состояний — это и есть то, что мы хотим рассчитать в этой главе. Сверхтонкое расщепление вызывается взаимодействием магнитных моментов электрона и протона; оно приводит для каждого спинового состояния к слегка отличающимся магнитным энергиям. Эти сдвиги энергии составляют только около десятимиллионной части электрон-вольта, что действительно много меньше 10 эв!
Именно из-за столь большого промежутка основное состояние водорода мы вправе считать «четырехуровневой системой», не заботясь о том, что на самом-то деле при более высоких энергиях состояний куда больше. Мы намерены ограничиться здесь изучением сверхтонкой структуры только основного состояния атома водорода.
Для наших целей нам неважны различные детали расположения электрона и протона, потому что все они, так сказать, уже выработаны атомом, все они получились сами собой, когда атом попал в основное состояние. Достаточно знать только, что электрон и протон находятся невдалеке друг от друга, в каком-то определенном пространственном соотношении. Кроме того, у них могут быть всевозможные взаимные ориентации спинов. И мы хотим рассмотреть только спиновые эффекты.
Первый вопрос, на который нужно ответить: каковы базисные состояния для этой системы? Но вопрос этот поставлен неправильно. Такой вещи, как единственный базис, не существует, а всякая система базисных состояний, которую вы выберете, не будет единственной. Всегда можно составить новые системы из линейных комбинаций старой. Для базисных состояний всегда есть множество выборов и все они одинаково законны.
Значит, надо спрашивать: не «каков базис?», а «каким его можно выбрать?». И выбрать вы вправе какой угодно, лишь бы вам было удобно.
Обычно лучше всего начинать с базиса, который физически наиболее очевиден. Он не обязательно должен решать какую-то задачу или быть непосредственно важным в каком-то отношении, нет, он в общем должен только облегчать понимание того, что происходит.
Мы выбираем следующие базисные состояния:
Состояние 1. И у электрона, и у протона спины смотрят вверх.
Состояние 2. У электрона спин смотрит вверх, а у протона— вниз.
Состояние 3. У электрона спин смотрит вниз, а у протона —
вверх.
Состояние 4. И у электрона, и у протона спины смотрят
вниз.
Для краткой записи этих четырех состояний введем следующие обозначения:
Состояние 1: |+ +>; у электрона спин вверх, у протона спин вверх.
Состояние 2: | + ->; у электрона спин вверх,
у протона спин вниз.
Состояние 3: |- +>; у электрона спин вниз, у протона спин вверх.
Состояние 4: |- ->; у электрона спин вниз, у протона спин вниз. (10.1)
Помните, что первый знак плюс или минус относится к электрону, второй — к протону. Чтобы эти обозначения были у вас под рукой, они сведены на фиг. 10.1.
Фиг. 10.1. Совокупность базисных состояний
для основного состояния атома водорода.
Эти состояния мы обозначаем | + +>, | + ->> |- +>.
Временами будет удобнее обозначать эти состояния |1>, |2>, |3> и |4>.
Вы можете сказать: «Но частицы взаимодействуют, и, может быть, эти состояния вовсе не являются правильными базисными состояниями. Получается, будто вы рассматриваете обе частицы независимо». Да, действительно! Взаимодействие ставит перед нами вопрос: каков гамильтониан системы? Но вопрос о том, как описать систему, не касается взаимодействия. Что бы мы ни выбрали в качестве базиса, это никак не связано с тем, что случится после. Может оказаться, что атом не способен оставаться в одном из этих базисных состояний, даже если с него все и началось. Но это другой вопрос. Это вопрос о том, как со временем меняются амплитуды в выбранном (фиксированном) базисе. Выбирая базисные состояния, мы просто выбираем «единичные векторы» для нашего описания.
Раз уже мы коснулись этого, бросим взгляд на общую проблему отыскания совокупности базисных состояний, когда имеется не одна частица, а больше. Вы знаете базисные состояния для одной частицы. Электрон, например, полностью описывается в реальной жизни (не в наших упрощенных случаях, а в реальной жизни) заданием амплитуд пребывания в одном из следующих состояний:
| Электрон спином вверх с импульсом р> или
| Электрон спином вниз с импульсом р>.
В действительности существуют две бесконечные совокупности состояний, по одному на каждое значение р. Значит, сказать, что электронное состояние |y> описано полностью, можно лишь тогда, когда вы знаете все амплитуды
где + и - представляют компоненты момента количества движения вдоль какой-то оси, обычно оси z, a p — вектор импульса. Стало быть, для каждого мыслимого импульса должны быть две амплитуды (дважды бесконечная совокупность базисных состояний). Вот и все, что нужно для описания отдельной частицы.
Таким же образом могут быть написаны базисные состояния, когда частиц не одна, а больше. Например, если надо было бы рассмотреть электрон и протон в более сложном, чем у нас, случае, то базисные состояния могли бы быть следующими: Электрон с импульсом p1 движется спином вверх, а протон с импульсом р2 движется спином вниз. И так далее для других спиновых комбинаций. Если частиц больше двух, идея остается та же. Так что вы видите, что расписать возможные базисные состояния на самом деле очень легко. Вопрос только в том, каков гамильтониан.
Нам для изучения основного состояния водорода нет нужды применять полные совокупности базисных состояний для различных импульсов. Мы оговариваем и фиксируем определенные импульсные состояния протона и электрона, когда произносим слова «основное состояние». Детали конфигурации — амплитуды для всех импульсных базисных состояний — можно рассчитать, но это уже другая задача. А мы сейчас касаемся только влияния спина, так что ограничимся только четырьмя базисными состояниями (10.1). Очередной вопрос таков: каков гамильтониан для этой совокупности состояний?
§ 2. Гамильтониан основного состояния водорода
Через минуту вы это узнаете. Но прежде хочу вам напомнить одну вещь: всякое состояние всегда можно представить в виде линейной комбинации базисных состояний. Для любого состояния |y|> можно написать
Напомним, что полные скобки — это просто комплексные числа, так что их можно обозначить обычным образом через Сi, где i=l, 2, 3 или 4, и записать (10.2) в виде
Задание четверки амплитуд Сi полностью описывает спиновое состояние |y>. Если эта четверка меняется во времени (как это и будет на самом деле), то скорость изменения во времени дается оператором Н^. Задача в том, чтобы найти этот оператор H^ .
Не существует общего правила, как писать гамильтониан атомной системы, и отыскание правильной формулы требует большего искусства, чем отыскание системы базисных состояний. Мы вам смогли дать общее правило, как записывать систему базисных состояний для любой задачи, в которой есть протон и электрон, но описать общий гамильтониан такой комбинации на этом уровне слишком трудно. Вместо этого мы подведем вас к гамильтониану некоторыми эвристическими рассуждениями, и вам придется признать его .правильным, потому что результаты будут согласовываться с экспериментальными наблюдениями.
Вспомните, что в предыдущей главе мы смогли описать гамильтониан отдельной частицы со спином 1/2, применив сигма-матрицы или в точности эквивалентные им сигма-операторы. Свойства операторов сведены в табл. 10.1. Эти операторы, являющиеся просто удобным, кратким способом запоминания матричных элементов типа <+|sz|+> были полезны для описания поведения отдельной частицы со спином 1/2. Возникает вопрос, можно ли отыскать аналогичное средство для описания системы с двумя спинами. Да, и очень просто. Вот смотрите. Мы изобретем вещь, которую назовем «электрон-сигма» и которую будем представлять векторным оператором se с тремя компонентами sex, sey и sez. Дальше условимся, что когда одна из них действует
Таблица 10.1 · СВОЙСТВА СИГМА-ОПЕРАТОРОВ
на какое-то из наших четырех базисных состояний атома водорода, то она действует на один только спин электрона, причем гак, как если бы электрон был один, сам по себе. Пример: чему равно syе|-+>? Поскольку sy , действующее на электрон со спином вниз, дает -i, умноженное на состояние с электроном, у которого спин вверх, то
sey|-+>=-i|++>.
(Когда syе действует на комбинированное состояние, оно переворачивает электрон, не затрагивая протон, и умножает результат на -i.) Действуя на другие состояния, sеудаст
Напомним еще раз, что оператор sе действует только на первый спиновый символ, т. е. на спин электрона.
Теперь определим соответствующий оператор «протон-сигма» для спина протона. Три его компоненты spx, spy, spz, действуют так же, как и sе, но только на протонный спин. Например, если spxбудет действовать на каждое из четырех базисных состояний, то получится (опять с помощью табл. 10.1)
Как видите, ничего трудного. В общем случае могут встретиться вещи и посложнее. Например, произведение операторов seyspz. Когда имеется такое произведение, то сначала делается то, что хочет правый оператор, а потом — чего требует левый. Например,
Заметьте, что эти операторы с числами ничего не делают; мы использовали это, когда писали sex(-1)=(-1) sex . Мы говорим, что операторы «коммутируют» с числами или что числа «можно протащить» через оператор. Попрактикуйтесь и покажите, что произведение sехspz дает для четырех состояний следующий результат:
Если перебрать все допустимые операторы, каждый по разу, то всего может быть 16 возможностей. Да, шестнадцать, если включить еще «единичный оператор» 1. Во-первых, есть тройка sех, sеy, sеz, затем тройка spx, spy, spz, итого шесть. Кроме того, имеется девять произведений вида sехspy, итого 15. И еще единичный оператор, оставляющий все состояния нетронутыми. Вот и все шестнадцать!
Заметьте теперь, что для системы с четырьмя состояниями матрица Гамильтона должна представлять собой матрицу коэффициентов 4x4, в ней будет 16 чисел. Легко показать, что всякая матрица 4X4, и в частности матрица Гамильтона, может быть записана в виде линейной комбинации шестнадцати двойных спиновых матриц, соответствующих системе операторов, которые мы только что составили. Поэтому для взаимодействия между протоном и электроном, в которое входят только их спины, мы можем ожидать, что оператор Гамильтона может быть записан в виде линейной комбинации тех же 16 операторов. Вопрос только в том, как.
Но, во-первых, мы знаем, что взаимодействие не зависит от нашего выбора осей для системы координат. Если нет внешнего возмущения — чего-то вроде магнитного поля, выделяющего какое-то направление в пространстве,— то гамильтониан не может зависеть от нашего выбора направлений осей х, у и z. Это означает, что в гамильтониане не может быть таких членов, как sex сам по себе. Это выглядело бы нелепо, потому что кто-нибудь в другой системе координат пришел бы к другим результатам.
Единственно возможны только член с единичной матрицей, скажем постоянная а (умноженная на 1^), и некоторая комбинация сигм, которая не зависит от координат, некоторая «инвариантная» комбинация. Единственная скалярная инвариантная комбинация из двух векторов — это их скалярное произведение, имеющее для наших сигм вид
Этот оператор инвариантен по отношению к любому повороту системы координат. Итак, единственная возможность для гамильтониана с подходящей симметрией в пространстве — это постоянная, умноженная на единичную матрицу, плюс постоянная, умноженная на это скалярное произведение, т. е.
Это и есть наш гамильтониан. Это единственное, чему, исходя из симметрии в пространстве, он может равняться, пока нет внешнего поля. Постоянный член нам многого не сообщит; он просто зависит от уровня, который мы выбрали для отсчета энергий. С равным успехом можно было принять Е0=0.А второй член поведает нам обо всем, что нужно для того, чтобы найти расщепление уровней в водороде.
Если угодно, можно размышлять о гамильтониане иначе. Если поблизости друг от друга находятся два магнита с магнитными моментами mе и mр, то их взаимная энергия зависит, кроме всего прочего, и от mе·mр. А мы, как вы помните, выяснили, что та вещь, которую мы в классической физике называли mе, в квантовой механике выступает под именем mese. Подобным же образом, то, что в классической физике выглядит как mp, в квантовой механике обычно оказывается равным mрsр (где mр— магнитный момент протона, который почти в 1000 раз меньше mе и имеет обратный знак). Значит, (10.5) утверждает, что энергия взаимодействия подобна взаимодействию двух магнитов, но не до конца, потому что взаимодействие двух магнитов зависит от расстояния между ними. Но (10.5) может считаться (и на самом деле является) своего рода средним взаимодействием. Электрон как-то движется внутри атома, и .наш гамильтониан дает лишь среднюю энергию взаимодействия. В общем все это говорит о том, что для предписанного расположения электрона и протона в пространстве существует энергия, пропорциональная косинусу угла между двумя магнитными моментами (выражаясь классически). Такая классическая качественная картина может помочь вам понять, откуда все получается, но единственное что важно при этом то, что (10.5) — это правильная квантовомеханическая формула.
Порядок величины классического взаимодействия между двумя магнитами должен был бы даваться произведением двух магнитных моментов, деленным на куб расстояния между ними. Расстояние между электроном и протоном в атоме водорода, грубо говоря, равно половине атомного радиуса, т. е. 0,5 А. Поэтому можно примерно прикинуть, что постоянная А должна быть равна произведению магнитных моментов mе и mp, деленному на куб половины ангстрема. Такая пристрелка приводит к числам, попадающим как раз в нужный район. Но оказывается, что А можно подсчитать и аккуратней, стоит только разобраться в полной теории атома водорода, что нам пока не по силам. На самом деле А было подсчитано с точностью до 30 миллионных. Как видите, в отличие от постоянной переброса А молекулы аммиака, которую по теории невозможно хорошо подсчитать, наша постоянная А для водорода может быть рассчитана из более детальной теории. Но ничего не поделаешь, нам для наших теперешних целей придется считать А числом, которое может быть определено из опыта, и анализировать физику дела.
Взяв гамильтониан (10.5), можно подставить его в уравнение
и посмотреть, что делает спиновое взаимодействие с уровнями энергии. Для этого надо подсчитать шестнадцать матричных элементов Hij=<i|H|j>, отвечающих любой двойке из четырех базисных состояний (10.1).
Начнем с того, что подсчитаем, чему равно Н^ |j> для каждого из четырех базисных состояний. К примеру,
Пользуясь способом, описанным немного раньше (вспомните табл. 10.1, она очень облегчит дело), мы найдем, что каждая пара а делает с |+ +>· Ответ таков:
Значит, (10.7) превращается в
Таблица 10.2 · спиновые операторы ДЛЯ АТОМА ВОДОРОДА
А раз все наши четыре базисных состояния ортогональны, то это немедленно приводит к
Вспоминая, что <j|Н|i>=<.i|H|j>*, мы сразу сможем написать дифференциальное уравнение для амплитуды С1:
или
Вот и все! Только один член.
Чтобы теперь получить оставшиеся уравнения Гамильтона, мы должны терпеливо пройти через те же процедуры с H^, действующим на другие состояния. Во-первых, попрактикуйтесь в проверке того, что все произведения сигм в табл. 10.2 написаны правильно. Затем с их помощью получите
И тогда, умножая их все по порядку слева на все прочие векторы состояний, мы получаем следующую гамильтонову матрицу Hij:
Это, конечно, означает, что дифференциальные уравнения для четырех амплитуд Сi имеют вид
Но прежде чем перейти к их решению, трудно удержаться от того, чтобы не рассказать вам об одном умном правиле, которое вывел Дирак. Оно поможет вам ощутить, как много вы уже знаете, хотя нам в нашей работе оно и не понадобится. Из уравнений (10.9) и (10.12) мы имеем
«Взгляните, — сказал Дирак, — первое и последнее уравнения я могу записать также в виде
и тогда все они станут похожими. Теперь я придумаю новый оператор, который обозначу Рспин. обмен и который, по определению, будет обладать следующими свойствами:
Оператор этот, как видите, только обменивает направления спина у двух частиц. Тогда всю систему уравнений (10.15) я могу написать как одно простое операторное уравнение:
Это и есть формула Дирака. Оператор обмена спинами дает удобное правило для запоминания sе·sp . (Как видите, вы теперь уже все умеете делать. Для вас все двери открыты.)
§ 3. Уровни энергии
Теперь мы готовы к тому, чтобы вычислить уровни энергии основного состояния водорода, решая гамильтоновы уравнения (10.14). Мы хотим найти энергии стационарных состояний. Это значит, что мы должны отыскать те особые состояния |y>, для которых каждая из принадлежащих |y> амплитуд Ci=<i|y> обладает одной и той же зависимостью от времени, а именно е-wt. Тогда состояние будет обладать энергией E=hw. Значит, мы ищем совокупность амплитуд, для которых
где четверка коэффициентов аi не зависит от времени. Чтобы увидеть, можем ли мы получить эти амплитуды, подставим (10.17) в (10.14) и посмотрим, что из этого выйдет. Каждое ihdCi/dt в (10.14) перейдет в ECi. И после сокращения на общий экспоненциальный множитель каждое Сiпревратится в аi; получим
Это и нужно решить для отыскания a1, а2, а3и а4. Право, очень мило со стороны первого уравнения, что оно не зависит от остальных,— а это значит, что одно решение сразу видно. Если выбрать Е=А, то
a1=1, a2=a3=a4=0
даст решение. (Конечно, если принять все а равными нулю, то это тоже будет решение, но состояния оно не даст!) Будем считать наше первое решение состоянием | I>:
Его энергия
ЕI=А.
Все это немедленно дает ключ ко второму решению, получаемому из последнего уравнения в (10.18):
а1=а2=а3=0, а4=1, Е=А.
Это решение мы назовем состоянием |II>:
|//> = |4> = |-->,(10.20)
ЕII=А.
Дальше пойдет чуть труднее; оставшиеся два уравнения (10.18) переплетены одно с другим. Но мы все это уже делали. Сложив их, получим
Е(а2+ а3) = А(а2+ а3). (10.21)
Вычитая, будем иметь
Окидывая это взглядом и припоминая знакомый нам уже аммиак, мы видим, что здесь есть два решения:
Это смеси состояний |2> и |3>. Обозначая их |III> и |IV> и вставляя для правильной нормировки множитель 1/Ц2, имеем
ЕIII=А (10.24)
и
Мы нашли четверку стационарных состояний и их энергии. Заметьте, кстати, что наши четыре состояния ортогональны друг другу, так что их тоже можно при желании считать базисными состояниями. Задача наша полностью решена.
У трех состояний энергия равна А, а у последнего -ЗА. Среднее равно нулю, а это означает, что когда в (10.5) мы выбрали Е0=0, то тем самым мы решили отсчитывать все энергии от их среднего значения. Диаграмма уровней энергии основного состояния водорода будет выглядеть так, как на фиг. 10.2.
Фиг. 10.2. Диаграмма уровней энергии основного состояния атомарного водорода.
Различие в энергиях между состоянием |IV> и любым из остальных равно 4A. Атом, который случайно окажется в состояний |I>, может оттуда упасть в состояние |IV>и испустить свет: не оптический свет, потому что энергия очень мала, а микроволновой квант. Или, если осветить водородный газ микроволнами, мы заметим поглощение энергии, оттого что атомы в состоянии |IV>будут ее перехватывать и переходить в одно из высших состояний, но все это только на частоте w=4A/h. Эта частота была измерена экспериментально; наилучший результат, полученный сравнительно недавно, таков:
Ошибка составляет только три стомиллиардных! Вероятно, ни одна из фундаментальных физических величин не измерена лучше, чем эта; таково одно из наиболее выдающихся по точности измерений в физике. Теоретики были очень счастливы, когда им удалось вычислить энергию с точностью до 3·10-5; но к этому времени она была измерена с точностью до 2·10-11,т.е. в миллион раз точнее, чем в теории. Так что экспериментаторы идут далеко впереди теоретиков. В теории основного состояния атома водорода и вы, и мы находимся в одинаковом положении. Вы ведь тоже можете взять значение А из опыта — и всякому, в конце концов, приходится делать то же самое.
Вы, вероятно, уже слышали раньше о «21-с.м линии» водорода. Это и есть длина волны спектральной линии в 1420 Мгц между сверхтонкими состояниями. Излучение с такой длиной волны испускается или поглощается атомарным водородным газом в галактиках. Значит, с помощью радиотелескопов, настроенных на волны 21 см (или примерно на 1420 Мгц), можно наблюдать скорости и расположение сгущений атомарного водорода. Измеряя интенсивность, можно оценить его количество. Измеряя сдвиг в частоте, вызываемый эффектом Допплера, можно выяснить движение газа в галактике. Это одна из великих программ радиоастрономии. Так что мы с вами сейчас ведем речь о чем-то очень реальном, это вовсе не какая-то искусственная задача.
§ 4. Зеемановское расщепление
Хотя с задачей отыскания уровней энергии основного состояния водорода мы и справились, мы все же продолжим изучение этой интересной системы. Чтобы сказать о ней еще что-то, например чтобы подсчитать скорость, с какой атом водорода поглощает или испускает радиоволны длиной 21 см, надо знать, что с ним происходит, когда он возмущен. Нужно проделать то, что мы сделали с молекулой аммиака,— после того как мы нашли уровни энергии, мы отправились дальше и выяснили, что происходит, когда молекула находится в электрическом поле. И после этого нетрудно оказалось представить себе влияние электрического поля радиоволны. В случае атома водорода электрическое поле ничего с уровнями не делает, разве что сдвигает их все на некоторую постоянную величину, пропорциональную квадрату поля, а нам это неинтересно, потому что это не меняет разностей энергий. На сей раз важно уже магнитное поле. Значит, следующим шагом будет написать гамильтониан для более сложного случая, когда атом сидит во внешнем магнитном поле.
Каков же этот гамильтониан? Мы просто сообщим вам ответ, потому что никакого «доказательства» дать не можем, разве что сказать, что именно так устроен атом.
Гамильтониан имеет вид
Теперь он состоит из трех частей. Первый член А(sе·sр) представляет магнитное взаимодействие между электроном и протоном; оно такое же, как если бы магнитного поля не было. Влияние внешнего магнитного поля проявляется в остальных двух членах. Второй член (-mеsе·В) — это та энергия, которой электрон обладал бы в магнитном поле, если бы он там был один. Точно так же последний член (-mрsр·В) был бы энергией протона-одиночки. Согласно классической физике, энергия их обоих вместе была бы суммой их энергий; по квантовой механике это тоже правильно. Возникающая из-за наличия магнитного поля энергия взаимодействия равна просто сумме энергий взаимодействия электрона с магнитным полем и протона с тем же полем, выраженных через операторы сигма. В квантовой механике эти члены в действительности не являются энергиями, но обращение к классическим формулам для энергии помогает запоминать правила написания гамильтониана. Как бы. то ни было, (10.27) — это правильный гамильтониан.
Теперь нужно вернуться к началу и решать всю задачу сызнова. Но большая часть работы уже сделана, надо только добавить эффекты, вызываемые новыми членами. Примем, что магнитное поле В постоянно и направлено по z. Тогда к нашему старому гамильтонову оператору Н^ надо добавить два новых куска; обозначим их Н^':
Пользуясь табл. 10.1, мы сразу получаем
Смотрите, как удобно! Оператор Н', действуя на каждое состояние, дает просто число, умноженное на это же состояние. В матрице <i|H'|j> есть поэтому только диагональные элементы, и можно просто добавить коэффициенты из (10.28) к соответствующим диагональным членам в (10.13), так что гамильтоновы уравнения (10.14) обращаются в
Форма уравнений не изменилась, изменились только коэффициенты. И пока В не меняется со временем, можно все делать так же, как и раньше.
Подставляя
, мы получаем
К счастью, первое и четвертое уравнения по-прежнему не зависят от остальных, так что снова пойдет в ход та же техника. Одно решение — это состояние |I>, для которого
или
Другое решение
Для остальных двух уравнений потребуется больше работы, потому что коэффициенты при а2 и a3 уже не равны друг другу. Но зато они очень похожи на ту пару уравнений, которую мы писали для молекулы аммиака. Оглядываясь на уравнения (7.20) и (7.21), можно провести следующую аналогию (помните, что тамошние индексы 1 и 2 соответствуют здесь индексам 2 и 3):
Раньше энергии давались формулой (7.25), которая имела вид
Подставляя сюда (10.33), получаем для энергии
В гл. 7 мы привыкли называть эти энергии ЕIи ЕII, теперь мы их обозначим ЕIIIи EIV:
Итак, мы нашли энергии четырех стационарных состояний атома водорода в постоянном магнитном поле. Проверим наши выкладки, для чего устремим В к нулю и посмотрим, получатся ли те же энергии, что и в предыдущем параграфе. Вы видите, что вес в порядке. При В=0энергии ЕI, ЕIIи ЕIIIобращаются в +А, a EIV — в -ЗА. Даже наша нумерация состояний согласуется с прежней. Но когда мы включим магнитное поле, то каждая энергия начнет меняться по-своему. Посмотрим, как это происходит.
Во-первых, напомним, что у электрона mе отрицательно и почти в 1000 раз больше mр, которое положительно. Значит, и me+mp и me-mp оба отрицательны и почти равны друг другу. Обозначим их -m и -m':
(И m и m' положительны и по величине почти совпадают с mе, которое примерно равно одному магнетону Бора.) Наша четверка энергий тогда обратится в
Энергия ЕIвначале равна А и линейно растет с ростом В со скоростью m. Энергия ЕIIтоже вначале равна A, но с ростом В линейно убывает, наклон ее кривой равен -m. Изменение этих уровней с В показано на фиг. 10.3. На рисунке показаны также графики энергий ЕIIIи EIV . Их зависимость от В иная. При малых В они зависят от В квадратично; вначале наклон их равен нулю, а затем они начинают искривляться и при больших В приближаются к прямым с наклоном ±m', близким к наклону eiи ЕII
Сдвиг уровней энергии атома, вызываемый действием магнитного поля, называется эффектом Зеемана. Мы говорим, что кривые на фиг. 10.3 показывают зеемановское расщепление основного состояния водорода.
Фиг. 10.3. Уровни энергии основного состояния
водорода в магнитном поле В.
Кривые EIII и ЕIV приближаются к пунктирным прямым
А±m'В.
Когда магнитного поля нет, то просто получается одна спектральная линия от сверхтонкой структуры водорода. Переходы между состоянием |IV> и любым из остальных трех происходят с поглощением или испусканием фотона, частота которого равна 1420 Мгц:1/h, умноженной на разность энергий 44. Но когда атом находится в магнитном поле В, то линий получается гораздо больше. Могут происходить переходы между любыми двумя из четырех состояний. Значит, если мы имеем атомы во всех четырех состояниях, то энергия может поглощаться (или излучаться) в любом из шести переходов, показанных на фиг. 10.4 вертикальными стрелками.
Фиг. 10.4. Переходы между уровнями энергии основного состояния водорода в некотором магнитном поле В.
Многие из этих переходов можно наблюдать с помощью техники молекулярных пучков Раби, которую мы описывали в гл. 35, § 3 (вып.7).
Что же является причиной переходов? Они возникают, если наряду с сильным постоянным полем B приложить малое возмущающее магнитное поле, которое меняется во времени. То же самое мы наблюдали и при действии переменного электрического поля на молекулу аммиака. Только здесь виновник переходов — это магнитное поле, действующее на магнитные моменты. Но теоретические выкладки те же самые, что и в случае аммиака. Проще всего они получаются, если взять возмущающее магнитное поле, вращающееся в плоскости ху, хотя то же будет от любого осциллирующего горизонтального поля. Если вы вставите это возмущающее поле в качестве добавочного члена в гамильтониан, то получите решения, в которых амплитуды меняются во времени, как это было и с молекулой аммиака. Значит, вы сможете легко и аккуратно рассчитать вероятность перехода из одного состояния в другое. И обнаружите, что все это согласуется с опытом.
§ 5. Состояния в магнитном поле
Теперь займемся формой кривых на фиг. 10.3. Во-первых, если говорить о больших полях, то зависимость энергии от поля довольно интересна и легко объяснима. При достаточно больших В (а именно при mB/A>>1) в формулах (10.37) можно пренебречь единицей. Четверка энергий принимает вид
Это уравнения четырех прямых на фиг. 10.3. Эти формулы можно физически понять следующим образом. Природа стационарных состояний в нулевом поле полностью определяется взаимодействием двух магнитных моментов. Перемешивание базисных состояний | + -> и | - +> в стационарных состояниях |III>и |IV>вызвано этим взаимодействием. Однако вряд ли можно ожидать, что каждая из наших частиц (и протон, и электрон) в сильных внешних полях будет испытывать влияние поля другой частицы; каждая будет действовать так, как если бы во внешнем поле находилась она одна. Тогда (как мы уже много раз видели) спин электрона окажется направленным вдоль внешнего магнитного поля (по нему или против него).
Пусть спин электрона направлен вверх, т. е. вдоль поля; энергия его будет -meB. Протон при - этом может стоять по-разному. Если у него спин тоже направлен вверх, то его энергия -mpB. Их сумма равна -(mе+mр)B=mB. А это как раз и есть EI, и это очень приятно, потому что мы описываем состояние |+ +>=|I>. Есть еще небольшой дополнительный член А (теперь (mB>>A), представляющий энергию взаимодействия протона и электрона, когда их спины параллельны. (Мы с самого начала считали А положительным, потому что так должно было быть по теории, о которой шла речь; то же получается и на опыте.) Но спин протона может быть направлен и вниз. Тогда его энергия во внешнем ноле обратится в +mРB, а вместе с электроном их анергия будет -(me-mр) В=mВ. А энергия взаимодействия обращается в -А. Их сумма даст энергию ЕIII, в (10.38). Так что состояние |III>в сильных полях становится состоянием |+ ->.
Пусть теперь спин электрона направлен вниз. Его энергия во внешнем ноле равна meВ. Если и протон смотрит вниз, то их общая энергия равна {me+mp)В = -mВ плюс энергия взаимодействия А (спины-то теперь параллельны). Это приводит как раз к энергии ЕIIв (10.38) и соответствует состоянию |- ->=|II>, что очень мило. И наконец, если у электрона спин направлен вниз, а у протона — вверх, то мы получим энергию (me -mp)В-А (минус А потому, что спины противоположны), т. е. EIV. А состояние отвечает |- +>.
«Погодите минутку,— вероятно, скажете вы.— «Состояния | Ill>и |IV> — это не состояния | + — > и | — + >; они являются их смесями». Верно, но перемешивание здесь едва заметно. Действительно, при 5=0 они являются смесями, но мы пока не выясняли, что бывает при больших В. Когда мы для получения энергии стационарных состояний пользовались аналогией между (10.33) и формулами гл. 7, то заодно можно было оттуда взять и амплитуды. Они получатся из (7.23):
Отношение a2/a3 — это, конечно, на сей раз C2/C3Вставляя аналогичные величины из (10.33), получаем
или
где вместо Е надо взять подходящую энергию (либо ЕIII, либо EIV). Например, для состояния |III>имеем
Значит, при больших В у состояния | ///> С2>>С3;состояние почти полностью становится состоянием | 2>=|+ ->. Точно так же если в (10.39) подставить eiv, то получится, что (С2/С3)IV<<1; в сильных полях состояние | IV>обращается попросту в состояние |3>=|- +>. Вы видите, что коэффициенты в линейных комбинациях наших базисных состояний, составляющих стационарные состояния, сами зависят от В.
Состояние, которое мы именуем |III>, в очень слабых полях представляет собой смесь |+ -> и |- +> в пропорции 1:1, но в сильных полях целиком смещается к |+ ->. Точно так же и состояние |IV>, которое в слабых полях также является смесью |+ -> и |- +> в пропорции 1:1 (с обратным знаком), переходит в состояние | - + ), когда спины из-за сильного внешнего поля больше друг с другом не связаны.
Хотелось бы обратить ваше внимание, в частности, на то, что происходит в очень слабых магнитных полях. Имеется одна энергия (-3А), которая не изменяется при включении слабого магнитного поля. И имеется другая энергия (+А), которая при включении слабого магнитного поля расщепляется на три различных уровня энергии. В слабых полях энергии с ростом В меняются так, как показано на фиг. 10.5. Допустим, что у нас есть каким-то образом отобранное множество атомов водорода, у которых у всех энергия равна -3А. Если пропустить их через прибор Штерна — Герлаха (с не очень сильными полями), то мы найдем, что они просто проходят целиком насквозь. (Поскольку их энергия не зависит от В, то, согласно принципу виртуальной работы, градиент магнитного поля не создает никакой силы, которая бы ощущалась ими.) Пусть, с другой стороны, мы бы отобрали группку атомов с энергией +А и пропустили их через прибор Штерна — Герлаха, скажем через прибор S. (Опять поля в приборе не должны быть столь сильными, чтобы разрушить внутренность атома; подразумевается, что поля малы настолько, что энергии можно считать линейно зависящими от В.) Мы бы получили три пучка. На состояния |I> и |II> действуют противоположные силы, их энергии меняются по В линейно с наклоном ±m, так что силы сходны с силами, действующими на диполь, у которого mz=±m, а состояние |III> проходит насквозь. Мы опять возвращаемся к гл. 3. Атом водорода с энергией +А — это частица со спином 1. Это энергетическое состояние является «частицей», для которой j=1, и может быть описано (по отношению к некоторой системе осей в пространстве) в терминах базисных состояний |+S>, | 0S> и |-S>, которыми мы пользовались в гл. 3. С другой стороны, когда атом водорода имеет энергию -3А, он является частицей со спином нуль. (Напоминаем, что все сказанное, строго говоря, справедливо лишь для бесконечно малых магнитных полей.) Итак, состояния водорода в нулевом магнитном поле можно сгруппировать следующим образом:
В гл. 35 (вып. 7) мы говорили, что у всякой частицы компоненты момента количества движения вдоль любой оси могут принимать только определенные значения, всегда отличающиеся на h. Так, z-компонента момента количества движения Jzможет быть равна jh, (j-1)h, (j-2)h,..., (-j)h, где j — спин частицы (который может быть целым или полуцелым). Обыкновенно пишут
Jz=mh, (10.43)
где т стоит вместо любого из чисел j, j-1, j-2, . . .,-j (в свое время мы не сказали об этом). Вы поэтому часто встретите в книжках нумерацию четырех основных состояний при помощи так называемых квантовых чисел j и m [часто именуемых «квантовым числом полного момента количества движения» (j) и «магнитным квантовым числом» (m)]. Вместо наших символов состояний |I>, |II> и т. д. многие часто пишут состояния в виде |j, m>. Нашу табличку состояний для нулевого поля в (10.41) и (10.42) они бы изобразили в виде табл. 10.3. Здесь нет какой-либо новой физики, это просто вопрос обозначении.
Таблица 10.3 · СОСТОЯНИЯ АТОМА ВОДОРОДА В НУЛЕВОМ ПОЛЕ
§ 6. Проекционная матрица для спина 1
Теперь мы хотели бы применить наши знания об атоме водорода к одной специальной задаче. В гл. 3 мы говорили о том, что частица со спином 1, находящаяся в одном из базисных состояний (+, 0, -) по отношению к прибору Штерна — Герлаха с какой-то частной ориентацией (скажем, по отношению к прибору S), будет иметь определенную амплитуду пребывания в одном из трех состояний по отношению к прибору Т, ориентированному в пространстве по-другому. Имеются девять таких амплитуд <jT|iS>, которые вместе образуют проекционную матрицу. В гл. 3, § 7, мы без доказательства выписали элементы этой матрицы для различных ориентации Т по отношению к S. Теперь мы хотим показать вам один из способов их вывода.
В атоме водорода мы с вами отыскали систему со спином 1, составленную из двух частиц со спином 1/2. В гл. 4 мы уже научились преобразовывать амплитуды для спина 1/2. Эти знания можно применить к тому, чтобы получить преобразование для спина 1. Вот как это делается: имеется система (атом водорода с энергией +А) со спином 1. Пусть мы пропустили ее сквозь фильтр S Штерна — Герлаха так, что знаем теперь, что она находится в одном из базисных состояний по отношению к S, скажем в |+S). Какова амплитуда того, что она окажется в одном из базисных состояний, скажем |+T), по отношению к прибору Т? Если вы назовете систему координат прибора S системой х, у, z, то состояние |+S> — это то, что недавно называлось состоянием |+ +>. Но представьте, что какой-то ваш приятель провел свою ось z вдоль оси Т. Он свои состояния будет относить к некоторой системе х', у', z'. Его состояния «вверх» и «вниз» для электрона и протона отличались бы от ваших. Его состояние «плюс — плюс», которое можно записать | +'+'>, отмечая «штрихованность» системы, есть состояние |+Т> частицы со спином 1. А вас интересует <+T|+S>, что есть просто иной способ записи амплитуды <+'+' | + + >.
Амплитуду <+ '+' | + +> можно найти следующим образом. В вашей системе спин электрона из состояния | + +> направлен вверх. Это означает, что у него есть некоторая амплитуда <+'|+>e оказаться в системе вашего приятеля спином вверх и некоторая амплитуда <-' |+>е оказаться в этой системе спином вниз. Равным образом, протон в состоянии + + У имеет спин вверх в вашей системе и амплитуды <+'|+>р и <-'|+>p оказаться спином вверх или вниз в «штрихованной» системе. Поскольку мы говорим о двух разных частицах, то амплитуда того, что обе частицы вместе в его системе окажутся спинами вверх, равна произведению амплитуд
Мы поставили значки е и р под амплитудами <+'|+>, чтоб было ясно, что мы делаем. Но обе они — это просто амплитуды преобразований для частицы со спином 1/2, так что на самом деле — это одни и те же числа. Фактически — это те же амплитуды, которые мы в гл. 4 называли <+Т|+S> > и которые мы привели в табл. 4.1 и 4.2.
Но теперь, однако, нам угрожает путаница в обозначениях. Надо уметь различать амплитуду <+T|+S) для частицы со спином 1/2 от того, что мы также назвали <+T|+S>, но для спина 1—между ними нет ничего общего! Надеюсь, вас не очень собьет с толку, если мы на время введем иные обозначения амплитуд для спина 1/2, Они приведены в табл. 10.4. Для состояний частиц спина 1 мы по-прежнему будем прибегать к обозначениям | +S, | 0S> и |-S>.
Таблица 10.4 · АМПЛИТУДЫ для СПИНА 1/2
В наших новых обозначениях (10.44) просто превращается в
Это как раз амплитуда <+T|+S> для спина 1. Теперь давайте, например, предположим, что у вашего приятеля система координат, т. е. «штрихованный» прибор Т, повернута вокруг вашей оси z на угол j; тогда из табл. 4.2 получается
Значит, из (10.44) амплитуда для спина 1 окажется равной
Теперь вам понятно, как мы будем действовать дальше.
Но хорошо бы провести выкладки в общем случае для всех состояний. Если протон и электрон в нашей системе (системе S) оба смотрят вверх, то амплитуды того, что в другой системе (системе Т)они будут в одном из четырех возможных состояний,
равны
Затем мы можем записать состояние |+ +> в виде следующей линейной комбинации:
Но теперь мы замечаем, что |+ '+'> — это состояние |+Т>, что {| + '-'>+|-'+'>} — это как раз Ц2, умноженный на состояние |0T> [см. (10.41)], и что | - '-'> = |-Т>. Иными словами, (10.47) переписывается в виде
Точно так же легко показать, что
С |0S> дело обстоит чуть посложнее, потому что
Но каждое из состояний | + - > и | - +> можно выразить через «штрихованные» состояния и подставить в сумму:
Умножая сумму (10.50) и (10.51) на 1/Ц2, получаем
Отсюда следует
Теперь у нас есть все необходимые амплитуды. Коэффициенты в (10.48), (10.49) и (10.52) —это матричные элементы
<jТ|iS>. Сведем их в одну матрицу:
Мы выразили преобразование спина 1 через амплитуды а, b, с и d преобразования спина 1/2.
Если, например, система Т повернута по отношению к S на угол а вокруг оси у (см. фиг. 3.6, стр. 64), то амплитуды в табл. 10.4—это просто матричные элементы Ry (a) в табл. 4.2:
Подставив их в (10.53), получим формулы (3.38), которые приведены на стр. 80 без доказательства.
Но что же случилось с состоянием |IV)?! Это система со спином нуль; значит, у нее есть только одно состояние — оно во всех системах координат одно и то же. Можно проверить, что все так и выходит, если взять разность (10.50) и (10.51); получим
Но (ad-bc) — это определитель матрицы для спина 1/2, он просто равен единице. Получается
|IV'>=|IV> при любой относительной ориентации двух систем координат.
* Тем, кто перескочил через гл. 4, придется пропустить и этот параграф.
* Вспомните, что классически U= -m·B, так что энергия наименьшая, когда момент направлен по полю. Для положительно заряженных частиц магнитный момент параллелен спину, для отрицательных — наоборот. Значит, в (10.27) mр— число положительное, а (mе— отрицательное.
*Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963).
*В действительности состоянием является
но, как обычно, мы отождествим состояния с постоянными векторами, которые при t=0 совпадают с настоящими векторами.
* Этот оператор сейчас называют оператор обмена спинами.
* Для этих операторов, правда, оказывается, что от их порядка ничего не зависит.


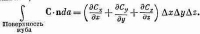

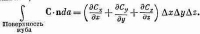

Комментарии к книге «8a. Квантовая механика I», Ричард Филлипс Фейнман
Всего 0 комментариев