7. Физика сплошных сред
Глава 30 ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
§ 1. Внутренняя геометрия кристаллов
§ 2. Химические связи в кристаллах
§ 3. Рост кристаллов
§ 4. Кристаллические решетки
§ 5. Симметрии в двух измерениях
§ 6. Симметрии в трех измерениях
§ 7. Прочность металлов
§ 8. Дислокации и рост кристаллов
§ 9. Модель кристалла по Брэггу и Наю
§ 1. Внутренняя геометрия кристаллов
Мы закончили изучение основных законов электричества и магнетизма и теперь можем заняться электромагнитными свойствами вещества. Начнем с изучения твердых тел, точнее кристаллов. Если атомы в веществе движутся не слишком активно, они сцепляются и располагаются в конфигурации с наименьшей возможной энергией. Если атомы где-то разместились так, что их расположения отвечают самой низкой энергии, то в другом месте атомы создадут такое же расположение. Поэтому в твердом веществе расположение атомов повторяется.
Иными словами, условия в кристалле таковы, что каждый атом окружен определенно расположенными другими атомами, и если посмотреть на атом такого же сорта в другом месте, где-нибудь подальше, то обнаружится, что окружение его и в новом месте точно такое же. Если вы выберете атом еще дальше, то еще раз найдете точно такие же условия. Порядок повторяется снова и снова и, конечно, во всех трех измерениях.
Представьте, что вам нужно создать рисунок на обоях или ткани или некий геометрический чертеж для плоской поверхности, в котором (как вы предполагаете) имеется элемент, повторяющийся непрерывно снова и снова, так что можно сделать эту поверхность настолько большой, насколько вам захочется. Это двумерный аналог задачи, которая решается в кристалле в трех измерениях. На фиг. 30.1,а показан общий характер рисунка обоев. Один элемент повторяется регулярно, и это может продолжаться бесконечно.
Фиг. 30.1. Повторяющийся рисунок обоев в двух намерениях.
Геометрические характеристики этого рисунка обоев, учитывающие только его свойства повторяемости и не касающиеся геометрии самого цветка или его художественных достоинств, показаны на фиг. 30.1,б. Если вы возьмете за отправную какую-то точку, то сможете найти соответствующую точку, сдвигаясь на расстояние а в направлении, указанном стрелкой 1. Вы можете попасть в соответствующую точку, также сдвинувшись на расстояние b в направлении, указанном другой стрелкой. Конечно, имеется еще много других направлений. Так, вы можете из точки a отправиться в точку b и достигнуть соответствующего положения, но такой шаг можно рассматривать как комбинацию шага в направлении 1 вслед за шагом в направлении 2. Одно из основных свойств ячейки состоит в том, что ее можно описывать двумя кратчайшими шагами к соседним эквивалентным расположениям. Под «эквивалентными» расположениями мы подразумеваем такие, что в каком бы из них вы ни находились, поглядев вокруг себя, вы увидите точно то же самое, что и в любом другом положении. Это фундаментальное свойство кристаллов. Единственное различие в том, что кристалл имеет трехмерное, а не двумерное расположение и, естественно, каждый элемент решетки представляет не цветы, а какие-то образования из атомов, например шести атомов водорода и двух атомов углерода, регулярно повторяющихся. Порядок расположения атомов в кристалле можно исследовать экспериментально с помощью дифракции рентгеновских лучей. Мы кратко упоминали об этом методе раньше и не будем добавлять здесь к сказанному чего-либо, а отметим лишь, что точное расположение атомов в пространстве установлено для большинства простых кристаллов, а также для многих довольно сложных кристаллов.
Внутреннее устройство кристалла проявляется по-разному. Во-первых, связующая сила атомов в определенных направлениях сильнее, чем в других направлениях. Это означает, что имеются определенные плоскости, по которым кристалл разбить легче, чем в других направлениях. Они называются плоскостями спайности. Если кристалл расколоть лезвием ножа, то скорее всего он расщепится именно вдоль такой плоскости. Во-вторых, внутренняя структура часто проявляется в форме кристалла.
Представьте себе, что кристалл образуется из раствора. В растворе плавают атомы, которые в конце концов пристраиваются, когда находят положение, отвечающее наименьшей энергии. (Все происходит так, как если бы обои были созданы из цветов, плавающих в разных направлениях до тех пор, пока случайно один из цветков не зацепился бы накрепко за определенную точку, за ним другой и т. д., пока постепенно не образовался узор.) Вы, вероятно, догадываетесь, что в одних направлениях кристалл будет расти быстрее, чем в других, создавая по мере роста некоторую геометрическую форму. Именно поэтому внешняя поверхность многих кристаллов носит на себе отпечаток внутреннего расположения атомов.
В качестве примера на фиг. 30.2,a показана типичная форма кристалла кварца, ячейка которого гексагональна. Если вы внимательно посмотрите на этот кристалл, то обнаружите, что его внешние грани образуют не слишком хороший шестиугольник, потому что не все стороны имеют одинаковую длину, а часто бывают даже совсем разными.
Фиг.30.2. Природный кристалл кварца (а), крупинки соли (б) и слюды (в).
Но в одном отношении этот шестиугольник вполне правильный: углы между гранями составляют в точности 120°. Ясное дело, размер той или иной грани случайно складывается в процессе роста, но в углах проявляется геометрия внутреннего устройства. Поэтому все кристаллы кварца имеют разную форму, но в то же время углы между соответствующими гранями всегда одни и те же.
Внутреннее геометрическое устройство кристалла хлористого натрия также легко понять из его внешней формы.
На фиг. 30.2, б показана типичная форма крупинки соли. Это опять не совершенный куб, но грани действительно перпендикулярны друг другу. Более сложный кристалл — это слюда, он имеет форму, изображенную на фиг 30.2, в. Этот кристалл в высшей степени анизотропен — он очень прочен в одном направлении (на рисунке — горизонтальном) и его трудно расколоть, а в другом направлении он легко расщепляется (в вертикальном). Обычно он используется для получения очень прочных, тонких листов. Слюда и кварц — примеры природных минералов, содержащих кремний. Третий минерал, содержащий кремний,— это асбест, обладающий тем интересным свойством, что его легко растянуть в двух направлениях, а в третьем он не поддается растягиванию. Создается впечатление, что он сделан из очень прочных нитей.
§ 2. Химические связи в кристаллах
Механические свойства кристаллов несомненно зависят от рода химических связей между атомами. Поражающая неодинаковая прочность слюды по разным направлениям зависит от характера межатомной связи в этих направлениях. Вам наверняка уже рассказывали на лекциях по химии о разных типах химических связей. Прежде всего бывают ионные связи, мы уже говорили о них, когда толковали о хлористом натрии. Грубо говоря, атомы натрия теряют по одному электрону и становятся положительными ионами; атомы хлора приобретают электрон и становятся отрицательными ионами. Положительные и отрицательные ионы располагаются в трехмерном шахматном порядке и удерживаются вместе электрическими силами.
Ковалентная связь (когда электроны принадлежат одновременно двум атомам) встречается чаще и обычно более прочна. Так, в алмазе атомы углерода связаны ковалентными связями с ближайшими соседями в четырех направлениях, поэтому-то кристалл такой твердый. Ковалентная связь имеется и в кристалле кварца между кремнием и кислородом, но там связь на самом деле только частично ковалентная. Поскольку там электроны распределяются неравномерно между двумя атомами, атомы частично заряжены и кристалл до некоторой степени ионный. Природа не так проста, как мы пытаемся ее представить: существуют всевозможные градации между ковалентной и ионной связями.
Кристалл сахара обладает другим типом связи. Он состоит из больших молекул, атомы которых сильно связаны ковалентной связью, так что молекула образует прочную структуру. Но так как сильные связи вполне насыщены, то между отдельными молекулами имеется относительно слабое притяжение. В таких молекулярных кристаллах молекулы сохраняют, так сказать, свою индивидуальность, и внутреннее устройство можно изобразить так, как на фиг. 30.3.
Фиг. 30.3. Решетка молекулярного кристалла.
Поскольку молекулы не очень крепко держатся друг за друга, то кристалл легко можно расколоть. Такого рода кристаллы резко отличаются от кристаллов типа алмаза, который есть не что иное, как одна гигантская молекула, не поддающаяся разлому без того, чтобы не нарушить сильные ковалентные связи.
Другим примером молекулярного кристалла может служить парафин.
Предельным случаем молекулярного кристалла являются вещества типа твердого аргона. Там притяжение между атомами незначительно — каждый атом представляет собой вполне насыщенную одноатомную «молекулу». Но при очень низких температурах тепловое движение настолько слабо, что крошечные межатомные силы могут заставить атомы расположиться в правильном порядке, подобно картофелинам, тесно набитым в кастрюле.
Металлы образуют совсем особый класс веществ. Там связь имеет совершенно другой характер. В металле связь возникает не между соседними атомами, а является свойством всего кристалла. Валентные электроны принадлежат не одному-двум атомам, а всему кристаллу в целом. Каждый атом вкладывает свой электрон в общий запас электронов, и положительные атомные ионы как бы плавают в океане отрицательных электронов. Электронный океан, подобно клею, удерживает ионы вместе.
Поскольку в металлах нет особых связей в каком-то определенном направлении, то там связь слабо зависит от направления. Однако металлы — это еще кристаллические тела, потому что полная энергия принимает наименьшее значение, когда ионы образуют упорядоченную систему, хотя энергия наиболее выгодного расположения обычно ненамного ниже других возможных расположений. В первом приближении атомы многих металлов подобны маленьким шарикам, упакованным с максимальной плотностью.
§ 3. Рост кристаллов
Попробуйте представить себе образование кристаллов на Земле в естественных условиях. В поверхностном слое Земли все сорта атомов перемешаны между собой. Вулканическая деятельность, ветер и вода постоянно их смешивают, и они то и дело взбалтываются и перемешиваются. Но, несмотря на это, каким-то чудом атомы кремния постепенно начинают отыскивать друг друга, а потом и атомы кислорода, чтобы образовать вместе кремнезем. К одним атомам поодиночке пристраиваются другие, образуя кристалл, и смесь разделяется. А где-нибудь по соседству атомы хлора и натрия находят друг друга и строят кристалл соли.
Как же получается, что кристалл, начав строиться, позволяет присоединяться к себе только определенному сорту атомов? Так происходит потому, что вся система в целом стремится к наименьшему возможному значению энергии. Растущий кристалл примет новый атом, если благодаря ему энергия станет наименьшей. Но откуда кристалл знает, что атом кремния (или кислорода), будучи поставлен в данное место, приведет к наименьшему значению энергии? Узнаёт он это методом проб и ошибок. В жидкости все атомы находятся в непрестанном движении. Каждый атом ударяется о соседние примерно 1013 раз в секунду. Если он ударяется о подходящее место в растущем кристалле, вероятность того, что он улетит обратно, будет несколько меньше там, где меньше энергия. Продолжая так пробовать миллионы лет, с частотой 1013 проб в секунду, атомы постепенно оседают на тех местах, где находят для себя положение с наименьшей энергией. В конце концов из них вырастают большие кристаллы.
§ 4. Кристаллические решетки
Расположение атомов в кристалле — кристаллическая решетка — может принимать множество геометрических форм. Мы опишем сначала простейшие решетки, характерные для большинства металлов и инертных газов в твердом состоянии. Это кубические решетки, которые могут быть двух видов: объемноцентрированная кубическая (фиг. 30.4, а) и гранецентрированная кубическая (фиг. 30.4, б).
Фиг. 30.4. Элементарная ячейка кубического кристалла, а — объемноцентрированная; б — гранецентрированная.
Конечно, на рисунках показан только один «куб» решетки; вы должны мысленно представить, что все это повторяется в трех измерениях до бесконечности. Для простоты на рисунке показаны только «центры» атомов. В настоящих кристаллах атомы скорее похожи на соприкасающиеся друг с другом шарики. Темные и светлые шарики на приведенных рисунках могут, вообще говоря, означать либо разные, либо одинаковые сорта атомов. Так, железо имеет объемноцентрированную кубическую решетку при низких температурах и гранецентрированную кубическую решетку при более высоких температурах. Физические свойства этих двух кристаллических форм совершенно различны.
Но как возникают такие формы? Представьте, что вы должны как можно плотнее упаковать атомы — шарики. Можно было бы начать со слоя, где шарики уложены в «гексагональной плотной упаковке», как показано на фиг. 30.5, а.
Фиг. 30.5. Устройство гексагональной решетки с плотной упаковкой.
Затем можно построить второй слой наподобие первого, но сместив его в горизонтальном направлении, как показано на фиг. 30.5, б. А потом можно наложить и третий слой. Вот тут — внимание! Третий слой можно наложить двумя разными способами. Если вы начнете класть третий слой, помещая атом в точку А на фиг. 30.5, б, то каждый атом в третьем слое окажется прямо над атомом первого нижнего слоя. Если же начать класть третий слой, помещая атом в точку В, то атомы третьего слоя будут расположены как раз над центрами треугольников, образованных тремя атомами нижнего слоя. Любая другая начальная точка эквивалентна А или В, так что существует только два способа размещения третьего слоя.
Если третий слой имеет атом в точке В, кристаллическая решетка будет гранецентрированной кубической, но видно это под некоторым углом. Забавно, что, начав с шестиугольников, можно прийти к кубической структуре. Но обратите внимание, что куб, рассматриваемый под определенным углом, имеет очертания шестиугольника. Например, фиг. 30.6 может изображать либо плоский шестиугольник, либо и куб в перспективе!
Если к фиг. 30.5, б добавляется третий слой, начиная с атома в точке А, то кубической структуры не возникает и у решетки будет только гексагональная симметрия. Ясно, что обе описанные нами возможности дают одинаковую плотную упаковку.
Некоторые металлы (например, серебро и медь) выбирают первую альтернативу — решетка у них гранецентрированная кубическая. Другие же (например, бериллий и магний) предпочитают вторую возможность и образуют гексагональные кристаллы. Очевидно, появление той или иной решетки не может зависеть только от способа упаковки маленьких шариков, но должно еще определяться и другими факторами. В частности, оказывается существенной небольшая угловая зависимость межатомных сил (или в случае металлов от энергии электронного океана).
Фиг. 30.6. Что это — шестиугольник или куб?
Все эти вещи вы несомненно узнаете из курса химии.
§ 5. Симметрии в двух измерениях
Теперь мне хотелось бы обсудить некоторые свойства кристаллов с точки зрения их внутренних симметрии. Основное свойство кристалла состоит в том, что если вы сдвинетесь от одного атома на один период решетки к соответствующему атому, то попадете в точно такое же окружение. Это фундаментальное утверждение. Но если бы вы сами были атомом, то могли бы заметить другое передвижение, которое привело бы вас в точно такое же окружение, т. е. в другую возможную «симметрию». На фиг. 30.7, а показан еще один возможный узор обоев (хотя вы, наверно, такого никогда не видали).
Фиг. 30.7. Узор обоев с высокой симметрией.
Предположим, что мы сравниваем окружения в точках А и В. Вы могли бы сперва подумать, что они одинаковы. Не совсем. Точки С и D эквивалентны А, но окружение В подобно А, только если все рядом обращать как будто в зеркале.
В этом узоре имеются еще и другие виды «эквивалентных» точек. Так, точки Е и F обладают «одинаковыми» окружениями, за тем исключением, что одно повернуто на 90° по отношению к другому. Узор особенный. Вращение на 90°, проделанное сколько угодно раз вокруг такой вершины, как A, снова дает тот же узор. Кристалл с такой структурой имел бы на поверхности прямые углы, но внутри он устроен сложнее, чем простой куб.
Теперь, когда мы описали ряд частных случаев, попытаемся вывести все возможные типы симметрии, какие может иметь кристалл. Прежде всего посмотрим, что получается в плоскости. Плоская решетка может быть определена с помощью двух так называемых основных векторов, которые идут от одной точки решетки к двум ближайшим эквивалентным точкам. Два вектора 1 и 2 суть основные векторы решетки на фиг. 30.1. Два вектора а и b на фиг. 30.7, а — основные векторы для изображенного там узора. Мы могли бы, конечно, с тем же успехом заменить а на -а или b на -b. Раз а и b одинаковы по величине и перпендикулярны друг другу, то вращение на 90° переводит а в b и b в а и снова дает ту же решетку.
Итак, мы видим, что существуют решетки, обладающие «четырехсторонней» симметрией. А раньше мы описали плотную упаковку, основанную на шестиугольнике и обладающую шестисторонней симметрией. Вращение набора кружков на фиг. 30.5, а на угол 60° вокруг центра любого шарика переводит рисунок сам в себя.
Какие виды вращательной симметрии существуют еще? Может ли быть, например, вращательная симметрия пятого или восьмого порядка? Легко понять, что они невозможны. Единственная симметрия, связанная с фигурой, имеющей более четырех сторон, есть симметрия шестого порядка. Прежде всего покажем, что симметрия более чем шестого порядка невозможна. Попытаемся вообразить решетку с двумя равными основными векторами, образующими угол менее 60° (фиг. 30.8, а).
Фиг. 30.8. Симметрия вращения выше шестого порядка невозможна (а); симметрия вращения пятого порядка невозможна (б).
Мы должны предположить, что точки В и С эквивалентны А и что а и b — наиболее короткие векторы, проведенные из А до эквивалентных соседей. Но это, безусловно, неверно, потому что расстояние между В и С короче, чем от любого из них до А. Должна существовать соседняя точка D, эквивалентная А, которая ближе к А, чем к В или С. Мы должны были бы выбрать b' в качестве одного из основных векторов. Поэтому угол между основными векторами должен быть равен 60° или еще больше. Октагональная симметрия невозможна.
А как быть с пятикратной симметрией? Если мы предположим, что основные векторы а и b имеют одинаковую длину и образуют угол 2p/5=72° (фиг. 30.8, б), то должна существовать эквивалентная точка решетки в D под 72° к линии АС. Но вектор b' от Е к D тогда короче b, и b уже не основной вектор. Пятикратной симметрии быть не может. Единственные возможности, не приводящие к подобным трудностям, это q=60, 90 или 120°. Очевидно, допустимы также нуль и 180°. Можно еще так выразить полученный нами результат: рисунок может не меняться при повороте на полный оборот (ничего не изменяется), полоборота, одну треть, одну четверть или одну шестую оборота. И этим исчерпываются все возможные вращательные симметрии на плоскости — всего их пять. Если 8=2p/n, то мы говорим об «n-кратной» симметрии, или симметрии n-го порядка. Мы говорим, что узор, для которого n равно 4 или 6, обладает более «высокой симметрией», чем узор с n, равным 1 или 2.
Вернемся к фиг. 30.7, а. Мы видим, что узор там обладает четырехкратной вращательной симметрией. На фиг. 30.7, б мы нарисовали другое расположение, которое обладает теми же свойствами симметрии, что и фиг. 30.7, а. Маленькие фигурки, похожие на запятые,— это асимметричные объекты, которые служат для определения симметрии изображения внутри каждого квадратика. Заметьте, что запятые в соседних квадратиках перевернуты попеременно, так что элементарная ячейка больше одного квадратика. Если бы запятых не было, рисунок по-прежнему обладал бы четырехкратной симметрией, но элементарная ячейка была бы меньше. Посмотрим внимательно на фиг. 30.7; мы обнаружим, что они обладают еще и другими типами симметрии. Так, отражение относительно каждой пунктирной линии R—R воспроизводит рисунок без изменений. Но это еще не все. У них есть еще один тип симметрии. Если отразить рисунок относительно линии y—y, а затем сдвинуть на один квадратик вправо (или влево), то снова получится первоначальный рисунок. Линия у—у называется линией скольжения.
Этим исчерпываются все типы симметрии в пространстве двух измерений. Есть еще одна пространственная операция симметрии, которая на плоскости эквивалентна вращению на 180°, однако в трехмерном пространстве она не сводится к этому вращению, а есть совсем другая операция. Я говорю об инверсии. Под инверсией мы подразумеваем такую операцию, когда любая точка, отвечающая вектору смещения из начала координат R (например, точка А на фиг. 30.9, б), переносится в точку —R.
Фиг. 30.9. Операция симметрии, называемая инверсией.
а — рисунок меняется; б — рисунок не меняется при преобразовании R ® -R;
в — в трех измерениях рисунок не симметричен после операции инверсии;
г — рисунок симметричен в трех измерениях.
Инверсия рисунка а на фиг. 30.9 дает новый рисунок, а инверсия рисунка б приводит к такому же рисунку. На двумерном узоре (вы можете это видеть) инверсия рисунка б в точке А эквивалентна повороту на 180° вокруг той же самой точки. Предположим, однако, что мы сделали узор на фиг. 30.9, б трехмерным, вообразив на маленьких шестерках и девятках «стрелочки», смотрящие из страницы кверху. В результате инверсии в трехмерном пространстве все стрелочки перевернутся и направятся вниз, так что узор не воспроизведется. Если мы обозначим острия и хвосты стрелок точками и крестиками, то сможем образовать трехмерный рисунок (фиг. 30.9, в), который несимметричен относительно инверсии, или же мы можем получить рисунок, который такой симметрией обладает (фиг. 30.9, г). Заметьте, что трехмерную инверсию нельзя получить никакой комбинацией вращений.
Если мы будем характеризовать «симметрию» рисунка (или решетки) разного рода операциями симметрии, которые мы только что описали, то окажется, что в двумерном случае существуют 17 различных форм узоров. Узор с наинизшей возможной симметрией мы изобразили на фиг. 30.1, а узор с одной из наивысших симметрии — на фиг. 30.7. Отыщите сами все 17 возможных форм рисунков.
Удивительно, как мало типов из этих 17 используется при изготовлении обоев и тканей! Всегда видишь одни и те же три или четыре основных типа. В чем здесь дело? Неужели так убога фантазия художников или, может быть, многие из возможных типов рисунков не будут радовать глаз?
§ 6. Симметрии в трех измерениях
До сих пор мы говорили только об узорах в двух измерениях. На самом же деле нас интересуют способы размещения атомов в трех измерениях. Прежде всего очевидно, что трехмерный кристалл имеет три основных вектора. Если же мы поинтересуемся возможными операциями симметрии в трех измерениях, то обнаружим, что существует 230 возможных типов симметрии! По некоторым соображениям, эти 230 типов можно разделить на семь классов, представленных на фиг. 30.10.
Фиг. 30.10. Семь классов кристаллической решетки.
Решетка с наименьшей симметрией называется триклинной. Ее элементарная ячейка представляет собой параллелепипед. Основные векторы все имеют разную длину и нет ни одной одинаковой пары углов между ними. И никакой вращательной или зеркальной симметрии здесь нет. Однако есть еще одна операция: при инверсии в узле элементарная ячейка может меняться, а может и не меняться. [Под инверсией в трех измерениях мы снова подразумеваем, что пространственное смещение R заменяется на -R, или, другими словами, точка с координатами (х, у, z) переходит в точку с координатами (-x,-y, -z). Поэтому симметрия триклинной решетки может быть только двух типов — с центром инверсии и без него.] Пока мы считали, что все векторы разные и расположены под произвольными углами. Если же все векторы одинаковы и углы между ними равны, то получается тригональная решетка, изображенная на рисунке. Ячейка такой решетки может иметь добавочную симметрию; она может еще и не меняться при вращении вокруг наибольшей телесной диагонали.
Если один из основных векторов, скажем с, направлен под прямым углом к двум остальным, то мы получаем моноклинную элементарную ячейку. Здесь возможна новая симметрия — вращение на 180° вокруг с. Гексагональная решетка — это частный случай, когда векторы а и b равны и угол между ними составляет 60°, так что вращение на 60, 120 или 180° вокруг вектора с приводит к той же самой решетке (для определенных внутренних типов симметрии).
Если все три основных вектора перпендикулярны друг другу, но не равны по длине, получается ромбическая ячейка. Фигура симметрична относительно вращений на 180° вокруг трех осей. Типы симметрии более высокого порядка возникают у тетрагональной ячейки, все углы которой прямые и два основных вектора равны. Наконец, имеется еще кубическая ячейка, самая симметричная из всех.
Основной смысл всего этого разговора о типах симметрии состоит в том, что внутренняя симметрия кристалла проявляется (иногда весьма тонким образом) в макроскопических физических свойствах кристалла. В гл. 31 мы увидим, например, что электрическая поляризуемость кристалла, вообще говоря, представляет собой тензор. Если описывать тензор в терминах эллипсоида поляризуемости, то мы должны доказать, что некоторые типы симметрии кристалла проявятся в этом эллипсоиде. Так, кубический кристалл симметричен по отношению к вращению на 90° вокруг любого из трех взаимно перпендикулярных направлений. Единственный эллипсоид с таким свойством,—очевидно, сфера. Кубический кристалл должен быть изотропным диэлектриком.
С другой стороны, тетрагональный кристалл обладает вращательной симметрией четвертого порядка. Две главные оси его эллипсоида должны быть равны, а третья должна быть параллельна оси кристалла. Аналогично, поскольку ромбический кристалл обладает вращательной симметрией второго порядка относительно трех перпендикулярных осей, его оси должны совпадать с осями эллипсоида поляризуемости. Точно так же одна из осей моноклинного кристалла должна быть параллельна одной из главных осей эллипсоида, хотя о других осях мы ничего сказать не можем. Триклинный кристалл не обладает вращательной симметрией, поэтому его эллипсоид может иметь любую ориентацию.
Как видите, мы можем с пользой провести время, придумывая всевозможные типы симметрии и связывая их со всевозможными физическими тензорами. Мы рассмотрели только тензор поляризуемости, здесь дело было простое, а для других тензоров, например для тензора упругости, рассуждать будет труднее. Существует раздел математики, называемый «теорией групп», который занимается такими вещами, но обычно можно сообразить все, что нужно, опираясь лишь на здравый смысл.
§ 7. Прочность металлов
Мы говорили, что металлы обычно имеют простую кубическую кристаллическую структуру; сейчас мы обсудим их механические свойства, которые зависят от этой структуры. Вообще говоря, металлы очень «мягкие», потому что один слой кристалла легко заставить скользить над другим. Вы, наверное, подумаете: «Ну, это дико — металлы ведь твердые». Нет, монокристалл металла легко деформируется.
Рассмотрим два слоя кристалла, подвергающихся действию силы сдвига (фиг. 30.11, а).
Фиг. 30.11. Сдвиг плоскостей кристалла.
Вероятно, вы сперва решите, что весь слой будет сопротивляться сдвигу, пока сила не станет достаточно велика, чтобы сдвинуть весь слой «над горбами» на одно место влево. Хотя скольжение по некоторой плоскости возможно, все происходит совсем не так. (Иначе, согласно вычислениям, получилось бы, что металл гораздо прочнее, чем он есть на самом деле.) В действительности же дело больше походит на то, что атомы перескакивают поочередно: сначала прыгает первый атом слева, затем следующий и т. д., как показано на фиг. 30.11, б. В результате пустое место между двумя атомами быстро путешествует направо и весь второй ряд сдвигается на одно межатомное расстояние. Скольжение происходит таким образом, что на перекатывание атома через горб поодиночке требуется гораздо меньше энергии, чем на поднятие всего ряда в целом. Как только сила возрастет до значения, достаточного для начала процесса, весь процесс протекает очень быстро.
Оказывается, что в реальном кристалле скольжение возникает поочередно: сначала в одной плоскости, затем заканчивается там и начинается в другом месте. Почему оно начинается и почему заканчивается — совершенно непонятно. В самом деле, очень странно, что последовательные области скольжения часто расположены довольно редко. На фиг. 30.12 представлена фотография очень маленького и тонкого кристалла меди, который был растянут.
Фиг. 30.12. Маленький кристалл меди после растяжения.
Вы можете заметить разные плоскости, в которых возникало скольжение.
Неожиданное соскальзывание отдельных кристаллических плоскостей легко заметить, если взять кусок оловянной проволоки, в которой содержатся большие кристаллы, и растягивать ее, держа близко к уху. Вы ясно различите звуки «тик-тик», когда плоскости защелкиваются в новых положениях, одна за другой.
Проблема «нехватки» атома в одном из рядов сложнее, чем может показаться при рассматривании фиг. 30.11.
Когда слоев больше, ситуация скорее походит на то, что изображено на фиг. 30.13.
Фиг. 30.13. Дислокация в кристалле.
Подобный дефект в кристалле называют дислокацией. Считается, что такие дислокации возникают при образовании кристалла или же в результате царапины или трещины на его поверхности. Раз возникнув, они довольно свободно могут проходить сквозь кристалл. Большие нарушения возникают из-за движения множества таких дислокаций.
Дислокации могут свободно передвигаться. Это значит, что для них требуется немного дополнительной энергии, если только весь остальной кристалл имеет совершенную решетку. Но они могут и «застыть», встретив какой-нибудь другой дефект в кристалле. Если для прохождения дефекта требуется много энергии, они остановятся. Это и есть тот механизм, который сообщает прочность несовершенным кристаллам металла. Кристаллы чистого железа совсем мягкие, но небольшая концентрация атомов примесей может вызвать достаточное количество дефектов, чтобы противостоять дислокациям. Как вы знаете, сталь, состоящая в основном из железа, очень тверда. Чтобы получить сталь, при плавке к железу примешивают немного углерода; при быстром охлаждении расплавленной массы углерод выделяется в виде маленьких зерен, образуя в решетке множество микроскопических нарушений. Дислокации уже не могут свободно передвигаться, и металл становится твердым.
Чистая медь очень мягкая, но ее можно «закалить» наклепом. Это делается отбиванием или сгибанием ее в одну и другую стороны. В таком случае образуется много различных дислокаций, которые взаимодействуют между собой и ограничивают подвижность друг друга. Быть может, вы видели фокус, когда берут кусочек «мягкой» меди и легко обвивают чье-нибудь запястье в виде браслета. В тот же момент медь становится закаленной и разогнуть ее становится очень трудно! «Закаленный» металл типа меди можно снова сделать мягким с помощью отжига при высокой температуре. Тепловое движение атомов «размораживает» дислокации и вновь создает отдельные большие кристаллы. О дислокациях можно рассказывать очень много. Так, до сих пор мы описывали только так называемые «дислокации скольжения» (краевые дислокации). Существует еще множество других видов, в частности винтовая дислокация, изображенная на фиг. 30.14.
Фиг. 30.14. Винтовая дислокация.
Такие дислокации часто играют важную роль в росте кристаллов.
§ 8. Дислокации и рост кристаллов
Одну из величайших загадок природы долгое время представлял процесс роста кристаллов. Мы уже описывали, как атом, многократно примериваясь, может определить, где ему лучше — в кристалле или снаружи. Но отсюда следует, что каждый атом должен найти положение с наименьшей энергией. Однако атом, попавший на новую поверхность, связан только одной-двумя связями с нижними атомами, и его энергия при этом не равна энергии того атома, который попал в угол, где он окружен атомами с трех сторон. Вообразим растущий кристалл как набор из кубиков (фиг. 30.15).
Фиг. 30.15. Схематическое представление роста кристалла.
Если мы поставим новый кубик, скажем, в положение А, он будет иметь только одного из тех шести соседей, какими он в конце концов будет окружен. А раз не хватает стольких связей, то и энергия его не будет очень низкой. Более выгодно положение В, где кристалл уже имеет половину своей доли связей. И действительно, кристаллы растут, присоединяя новые атомы к участкам типа В.
Но что произойдет, когда данный ряд завершится? Чтобы начать новый ряд, атом должен осесть, имея связь с двух сторон, а это опять же маловероятно. Даже если он осядет, что произойдет, когда весь слой будет завершен? Как мог бы начаться новый слой? Один из возможных ответов — кристалл предпочитает расти по дислокации, например по винтовой дислокации, вроде той, что показана на фиг. 30.14. По мере прибавления кубиков к этому кристаллу всегда остается место, где можно получить три связи. Следовательно, кристалл предпочитает расти с встроенной внутрь дислокацией. Иллюстрацию такого спирального роста представляет собой фотография монокристалла парафина (фиг. 30.16).
Фиг. 30.16. Кристалл парафина, выросший вокруг винтовой дислокации.
§ 9. Модель кристалла по Брэггу и Наю
Мы, разумеется, не можем увидеть, что происходит с отдельными атомами в кристалле. Как вы теперь понимаете, существует еще множество сложных явлений, которые трудно описать количественно. Лоуренс Брэгг и Дж. Най придумали модель металлического кристалла, которая удивительным образом моделирует множество явлений, возникающих, по-видимому, в реальном металле. Лучше всего прочесть эту работу самим; в ней описан и сам метод, и полученные с его помощью результаты [статья была напечатана в Proceedings of the Royal Society of London, 190, 474 (1947)] .
* В сокращенном виде она помещена в конце этого выпуска, — Прим. ред.
* Литература: Ch. Кittel, Introduction to Solid State Physics, 2nd ed., New York, 1956. (Имеется перевод: Ч.Киттель, Введение в физику твердого тела, Физматгиз, М., 1962.)
Глава 31 ТЕНЗОРЫ
§1. Тензор поляризуемости
§2. Преобразование компонент тензора
§3. Эллипсоид энергии
§4. Другие тензоры; тензор инерции
§5. Векторное произведение
§6. Тензор напряжений
§7. Тензоры высших рангов
§8. Четырехмерный тензор электромагнитного импульса
Повторить: гл. 11 (вып. 1)
«Векторы»; гл. 20 (вып. 2)
«Вращение в пространстве»
§ 1. Тензор поляризуемости
У физиков есть привычка брать простейший пример какого-то явления и называть его «физикой», а примеры посложнее отдавать на растерзание других наук, скажем прикладной математики, электротехники, химии или кристаллографии. Даже физика твердого тела для них только «полуфизика», ибо ее волнует слишком много специальных вопросов. По этой-то причине мы в наших лекциях откажемся от множества интересных вещей. Например, одно из важнейших свойств кристаллов и вообще большинства веществ — это то, что их электрическая поляризуемость различна в разных направлениях. Если вы в каком-либо направлении приложите электрическое поле, то атомные заряды слегка сдвинутся и возникнет дипольный момент; величина же этого момента зависит очень сильно от направления приложенного поля. А это, конечно, усложнение. Чтобы облегчить себе жизнь, физики начинают разговор со специального случая, когда поляризуемость во всех направлениях одинакова. А другие случаи мы предоставляем другим наукам. Поэтому для наших дальнейших рассмотрении нам совсем не понадобится то, о чем мы собираемся говорить в этой главе.
Математика тензоров особенно полезна для описания свойств веществ, которые изменяются с направлением, хотя это лишь один из примеров ее использования. Поскольку большинство из вас не собираются стать физиками, а намерены заниматься реальным миром, где зависимость от направления весьма сильная, то рано или поздно, но вам понадобится использовать тензор. Вот, чтобы у вас не было здесь пробела, я и собираюсь рассказать вам про тензоры, хотя и не очень подробно. Я хочу, чтобы ваше понимание физики было как можно более полным. Электродинамика, например, у нас вполне законченный курс; она столь же полна, как и любой курс электричества и магнетизма, даже институтский. А вот механика у нас не закончена, ибо, когда мы ее изучали, вы еще не были столь тверды в математике и мы не могли обсуждать такие разделы, как принцип наименьшего действия, лагранжианы, гамильтонианы и т. п., которые представляют наиболее элегантный способ описания механики. Однако полный свод законов механики, за исключением теории относительности, у нас все же есть. В той же степени, как электричество и магнетизм, у нас закончены многие разделы. Но вот квантовую механику мы так и не закончим; впрочем, нужно что-то оставить и на будущее! И все же, что такое тензор, вам все-таки следует знать уже сейчас.
В гл. 30 мы подчеркивали, что свойства кристаллического вещества в разных направлениях различны — мы говорим, что оно анизотропно. Изменение индуцированного дипольного момента с изменением направления приложенного электрического поля — это только один пример, но именно его мы и возьмем в качестве примера тензора. Будем считать, что для заданного направления электрического поля индуцированный дипольный момент единицы объема Р пропорционален напряженности прикладываемого поля Е. (Для многих веществ при не слишком больших Е это очень хорошее приближение.) Пусть константа пропорциональности будет α. Теперь мы хотим рассмотреть вещества, у которых а зависит от направления приложенного поля, например известный вам кристалл турмалина, дающий удвоенное изображение, когда вы смотрите через него.
Предположим, мы обнаружили, что для некоторого выбранного кристалла электрическое поле Е1; направленное по оси х, дает поляризацию Р1, направленную по той же оси, а одинаковое с ним по величине электрическое поле Е2, направленное по оси у, приводит к какой-то другой поляризации Р2, тоже направленной по оси у. А что получится, если электрическое поле приложить под углом 45°? Ну, поскольку оно будет просто суперпозицией двух полей, направленных вдоль осей х и y, то поляризация Р равна сумме векторов P1 и Р2, как это показано на фиг. 31.1, а.
Фиг. 31.1. Сложение векторов поляризации в анизотропном кристалле.
Поляризация уже не параллельна направлению электрического поля. Нетрудно понять, отчего так происходит. В кристалле есть заряды, которые легко сдвинуть вверх и вниз, но которые очень туго сдвигаются в стороны. Если же сила приложена под углом 45°, то эти заряды более охотно движутся вверх, чем в сторону. В результате такой асимметрии внутренних упругих сил перемещение идет не по направлению внешней силы. Разумеется, угол 45° ничем не выделен. То, что индуцированная поляризация не направлена по электрическому полю, справедливо и в общем случае. Перед этим нам просто «посчастливилось» выбрать такие оси х и у, для которых поляризация Р была направлена по полю Е. Если бы кристалл был повернут по отношению к осям координат, то электрическое поле Е2, направленное по оси y, вызвало бы поляризацию как по оси у, так и по оси х. Подобным же образом поляризация Р, вызванная полем, направленным вдоль оси х, тоже имела бы как х-, так и y-компоненты. Так что вместо фиг. 31.1, а мы получили бы нечто похожее на фиг. 31.1,6. Но несмотря на все это усложнение, величина поляризации Р для любого поля Е по-прежнему пропорциональна его величине.
Рассмотрим теперь общий случай произвольной ориентации кристалла по отношению к осям координат. Электрическое поле, направленное по оси х, дает поляризацию Р с компонентами по всем трем осям, поэтому мы можем написать
Рx =axxEx, Ру=aухЕх, Рz=azxЕx. (31.1)
Этим я хочу сказать лишь, что электрическое поле, направленное по оси х, создает поляризацию не только в этом направлении, оно приводит к трем компонентам поляризации Рх, Рyи Pz, каждая из которых пропорциональна Ех. Коэффициенты пропорциональности мы назвали aхх, aухи azx (первый значок говорит, о какой компоненте идет речь, а второй относится к направлению электрического поля).
Аналогично, для поля, направленного по оси у, мы можем написать
Рх=aхуЕy, Ру=aууЕу, Рz=aгуЕу, (31.2)
а для поля в z-направлении
Px=axzEz, Py=ayzEz Pz=azzEz. (31,3)
Дальше мы говорим, что поляризация линейно зависит от поля; поэтому если у нас есть электрическое поле Е с компонентами х и у, то x-компонента поляризации Р будет суммой двух Рх, определенных уравнениями (31.1) и (31.2), ну а если Е имеет составляющие по всем трем направлениям х, у и z, то составляющие поляризации Р должны быть суммой соответствующих слагаемых в уравнениях (31.1), (31.2) и (31.3). Другими словами, Р записывается в виде
Диэлектрические свойства кристалла, таким образом, полностью описываются девятью величинами (axx,, axy,,axz,ayz , ...), которые можно записать в виде символа aij. (Индексы i и j заменяют одну из трех букв: х, у или z.) Произвольное электрическое поле Е можно разложить на составляющие Еx, Еyи Еz. Зная их, можно воспользоваться коэффициентами aijи найти Рх, Рy и Pz, которые в совокупности дают полную поляризацию Р. Набор девяти коэффициентов aijназывается тензором — в данном примере тензором поляризуемости. Точно так же как три величины (Ех, Еу, Еz) «образуют вектор Е», и мы говорим, что девять величин (aхх, aху, ...)«образуют тензор aij».
§ 2. Преобразование компонент тензора
Вы знаете, что при замене старых осей координат новыми х', у' и z' компоненты вектора Ех', Еу', Ег'тоже оказываются другими. То же самое происходит и с компонентами Р, так что для разных систем координат коэффициенты aijоказываются различными. Однако вполне можно выяснить, как должны изменяться а при надлежащем изменении компонент Е и Р, ибо, если мы описываем то же самое электрическое поле, но в новой системе координат, мы должны получить ту же самую поляризацию Р. Для любой новой системы координат Px' будет линейной комбинацией Рх, Рy' , и Рz':
Рx’=аРх+bРу+сРz,
и аналогично для других компонент. Если вместо Рх, Рyи Рzподставить их выражения через Е согласно (31.4), то получится
Теперь напишите, как выражается Ех, Еyи Ezчерез Еx' , Еy'и Еz' , например,
Ex = a'Ex'+b'Ey'+c'Ez' ,
где числа а', b' и с' связаны с числами а, b и c, но не равны им. Таким образом, у вас получилось выражение Рх'через компоненты Ех', Еy'и Ez' , т. е. получились новые aij. Никаких хитростей здесь нет, хотя все это достаточно запутано.
Когда мы говорили о преобразовании осей, то считали, что положение самого кристалла фиксировано в пространстве. Если же вместе с осями поворачивать и кристалл, то a не изменяются. И обратно, если по отношению к осям изменять ориентацию кристалла, то получится новый набор коэффициентов а. Но если они известны для какой-то одной ориентации кристалла, то с помощью только что описанного преобразования их можно найти и для любой другой ориентации. Иначе говоря, диэлектрические свойства кристалла полностью описываются заданием компонент тензора поляризуемости aij. в любой произвольно выбранной системе координат. Точно так же как вектор скорости v = (vx, vy , vz) можно связать с частицей, зная, что три его компоненты при замене осей координат будут изменяться некоторым определенным образом, тензор поляризуемости aij, девять компонент которого при изменении системы осей координат преобразуются вполне определенным образом, можно связать с кристаллом.
Связь между Р и Е в уравнении (31.4) можно записать в более компактном виде:
где под значком i понимается какая-то из трех букв х, у или z, а суммирование ведется по j=x, у и z. Для работы с тензорами было придумано много специальных обозначений, но каждое из них удобно для ограниченного класса проблем. Одно из таких общих соглашений состоит в том, что можно не писать знака суммы (S) в уравнении (31.5), понимая при этом, что когда один и тот же индекс встречается дважды (в нашем случае j), то нужно просуммировать по всем значениям этого индекса. Однако, поскольку работать с тензорами нам придется немного, давайте не будем осложнять себе жизнь введением каких-то специальных обозначений или соглашений.
§ 3. Эллипсоид энергии
Потренируемся теперь в обращении с тензорами. Рассмотрим такой интересный вопрос: какая энергия требуется для поляризации кристалла (в дополнение к энергии электрического поля, которая, как известно, равна e0Е2/2 на единицу объема)? Представьте на минуту атомные заряды, которые должны быть перемещены. Работа, требуемая для перемещения одного такого заряда на расстояние dx, равна qExdx, а если таких зарядов в единице объема содержится N штук, то для перемещения их требуется работа qExNdx. Но qNdx равно изменению дипольного момента единицы объема dPx. Так что работа, затраченная на единицу объема, равна
ExdPx.
Складывая теперь работы всех трех компонент, найдем, какой должна быть работа в единице объема:
E·dP.
Но поскольку величина Р пропорциональна Е, то работа, затраченная на поляризацию единицы объема от 0 до Р, равна интегралу от E·dP. Обозначая ее через ир, можно написать
Теперь можно воспользоваться уравнением (31.5) и выразить Р через E. В результате получим
Плотность энергии ир — величина, не зависящая от выбора осей, т. е. скаляр. Таким образом, тензор обладает тем свойством, что, будучи просуммирован по одному индексу (с вектором), он дает новый вектор, а будучи просуммирован по обоим индексам (с двумя векторами), дает скаляр.
Тензор aijна самом деле нужно называть «тензором второго ранга», ибо у него два индекса. В этом смысле вектор, у которого всего один индекс, можно назвать «тензором первого ранга», а скаляр, у которого вообще нет индексов,— «тензором нулевого ранга». Итак, выходит, что электрическое поле Е будет тензором первого ранга, а плотность энергии up — тензором нулевого ранга. Эту идею можно распространить на тензоры с тремя и более индексами и определить тензоры, ранг которых выше двух.
Индексы нашего тензора поляризуемости могут принимать три различных значения, т. е. это трехмерный тензор. Математики рассматривают также тензоры размерности четыре, пять и больше. Кстати, четырехмерный тензор нам уже встречался при релятивистском описании электромагнитного поля (см. гл. 26, вып. 6) — это Fmv .
Тензор поляризуемости aijобладает одним интересным свойством: он симметричен, т. е. axy=ayx и т. п. для любой пары индексов. (Это свойство отражает физические качества реального кристалла, и вовсе не обязательно у любого тензора.) Вы можете самостоятельно доказать это, подсчитав изменения энергии кристалла по следующей схеме:
1) включите электрическое поле в направления оси х;
2) включите поле в направлении оси у;
3) выключите x-поле;
4) выключите y-поле.
Теперь кристалл вернулся к прежнему положению и полная работа, затраченная на поляризацию, должна быть нулем. Но для этого, как вы можете убедиться, axy должно быть равно а. Однако те же рассуждения можно провести и для axzи т. д. Таким образом, тензор поляризуемости симметричен.
Это означает также, что тензор поляризуемости можно найти простым измерением энергии, необходимой для поляризации кристалла в различных направлениях. Предположим, мы сначала взяли электрическое поле Е с компонентами х и у; тогда, согласно уравнению (31.7),
Если бы у нас была только одна компонента Ех, мы могли бы определить aхх, а с одной компонентой Еyможно определить ayy . Включив обе компоненты Ехи Еy, мы из-за присутствия члена (aху+aух) получим добавочную энергию, ну а поскольку axy и ayx равны, то этот член превращается в 2axy и может быть вычислен из добавочной энергии.
Выражение для энергии (31.8) имеет очень красивую геометрическую интерпретацию. Предположим, что нас интересует, какие поля Ехи Еyотвечают данной плотности энергии, скажем u0. Возникает чисто математическая задача решения уравнения
Это уравнение второй степени, так что, если мы отложим по осям величины Ехи Еy , решением этого уравнения будут все точки эллипса (фиг. 31.2).
Фиг. 31.2 Конец любого вектора E=(Ex, ev) , лежащего на этой кривой, дает одну и ту же анергию поляризации.
(Это должен быть именно эллипс, а не парабола и не гипербола — ведь энергия поля всегда положительна и конечна.) А само Е с компонентами Ехи Еyпредставляет вектор, идущий из начала координат до точки на эллипсе. Такой «энергетический эллипс» — хороший способ «увидеть» тензор поляризуемости.
Если теперь пустить в дело все три компоненты, то любой вектор Е, необходимый для создания единичной плотности энергии, задается точками, расположенными на эллипсоиде, подобно изображенному на фиг. 31.3. Форма этого эллипсоида постоянной энергии однозначно характеризует тензор поляризуемости.
Заметьте теперь, что эллипсоид имеет очень интересное свойство — его всегда можно описать простым заданием направления трех «главных осей» и диаметров эллипсоида по этим осям. Такими «главными осями» являются направления наименьшего и наибольшего диаметра и направление, перпендикулярное к ним. На фиг. 31.3 они обозначены буквами а, b и с.
Фиг. 31.3. Эллипсоид анергии для тензора поляризуемости.
По отношению к этим осям уравнение эллипсоида имеет особенно простую форму:
Итак, по отношению к главным осям у тензора поляризуемости останутся только три ненулевые компоненты aаа, abbи aсс. Другими словами, сколь бы ни был сложен кристалл, всегда можно выбрать оси так (они не обязательно будут осями самого кристалла), что у тензора поляризуемости останется только три компоненты. Уравнение (31.4) для таких осей становится особенно простым:
Ра =aааЕа, Рb =abbEb, Рс =aссЕс. (31.9)
Иначе говоря, электрическое поле, направленное по любой одной из главных осей, дает поляризацию, направленную по той же оси, но, разумеется, для различных осей коэффициенты будут разными.
Тензор часто записывается в виде таблицы из девяти коэффициентов, взятых в скобки:
Для главных же осей а, b и с в таблице остаются только диагональные члены, поэтому мы говорим, что тензор становится «диагональным», т. е.
Самое важное здесь то, что к такой форме подходящим выбором осей координат можно привести любой тензор поляризуемости (фактически любой симметричный тензор второго ранга какого угодно числа измерений).
Если все три элемента тензора поляризуемости в диагональной форме равны друг другу, т. е. если
то эллипсоид энергии превращается в сферу, поляризуемость во всех направлениях становится одинаковой, а материал изотропным. В тензорных обозначениях
где.dij—единичный тензор:
что, разумеется, означает
Тензор dijчасто называют также «символом Кронекера». Для забавы вы можете доказать, что тензор (31.14) после замены одной прямоугольной системы координат на другую будет иметь в точности ту же самую форму. Тензор поляризуемости типа (31.13) дает
т. е. получается наш старый результат для изотропного диэлектрика:
Р=aЕ.
Форму и ориентацию эллипсоида поляризуемости иногда можно связать со свойствами симметрии кристалла. В гл. 30 мы уже говорили, что трехмерная решетка имеет 230 различных возможных внутренних симметрии и что для многих целей их удобно разбить на 7 классов в соответствии с формой элементарной ячейки. Эллипсоид поляризуемости должен отражать геометрию внутренней симметрии кристалла. Например, триклинный кристалл имеет самую низкую симметрию; у него все три оси эллипсоида разные и направления их, вообще говоря, не совпадают с направлением осей кристалла. Более симметричный моноклинный кристалл обладает той особенностью, что его свойства не меняются при повороте кристалла на 180° относительно одной оси, поэтому тензор поляризуемости при таком повороте должен остаться тем же самым. Отсюда следует, что эллипсоид поляризуемости при повороте на 180° должен переходить сам в себя. Но такое может случиться только, когда одна из осей эллипсоида совпадет с направлением оси симметрии кристалла. В других же отношениях ориентация и размеры эллипсоида могут быть какими угодно.
Оси эллипсоида ромбического кристалла должны совпадать с кристаллическими осями, так как вращение такого кристалла на 180° вокруг любой оси повторяет ту же кристаллическую решетку. Если же взять тетрагональный кристалл, то эллипсоид тоже должен повторять его симметрию, т. е. два из его диаметров должны быть равны между собой. Наконец, для кубического кристалла равными должны быть все три диаметра эллипсоида — он превращается в сферу и поляризуемость кристалла одинакова во всех направлениях.
Существует очень серьезная игра, состоящая в выяснении всех возможных свойств тензоров для всех возможных симметрии кристалла. Она мудрено называется «теоретико-групповым анализом». Однако для простых случаев тензора поляризуемости увидеть, какова должна быть эта связь, относительно легко.
§ 4. Другие тензоры; тензор инерции
В физике есть еще немало других примеров тензоров. В металле, например, или каком-либо другом проводнике зачастую оказывается, что плотность тока j приблизительно пропорциональна электрическому полю Е, причем константа пропорциональности называется проводимостью s
j=sЕ.
Однако для кристалла соотношение между j и Е более сложно, проводимость в различных направлениях не одинакова. Она становится тензором, поэтому мы пишем
Другим примером физического тензора является момент инерции. В гл. 18 (вып. 2) мы видели, что момент количества движения L твердого тела, вращающегося относительно фиксированной оси, пропорционален угловой скорости w, и коэффициент пропорциональности I мы назвали моментом инерции:
L = Iw.
Момент инерции тела произвольной формы зависит от его ориентации относительно оси вращения. Моменты инерции прямоугольного бруска, например, относительно каждой из трех ортогональных осей будут разными. Но угловая скорость со и момент количества движения L — оба векторы. Для вращения относительно одной из осей симметрии они параллельны. Но если моменты инерции относительно каждой из трех главных осей различны, то направления to и L, вообще говоря, не совпадают (фиг. 31.4).
Фиг. 31.4. Момент количества движения L твердого предмета, вообще говоря, не параллелен вектору угловой скорости w.
Они связаны точно таким же образом, как Е и Р, т. е. мы должны писать:
Девять коэффициентов Iij называют тензором инерции. По аналогии с поляризацией кинетическая энергия для любого момента количества движения должна быть некоторой квадратичной формой компонент wx, wy и wz:
Мы можем снова воспользоваться этим выражением для определения эллипсоида инерции. Кроме того, снова можно воспользоваться энергетическими соображениями и показать, что этот тензор симметричен, т. е. Iij=Iji.
Тензор инерции твердого тела можно написать, если известна форма тела. Нам нужно только выписать полную кинетическую энергию всех частиц тела. Частица с массой m и скоростью v обладает кинетической энергией 1/2mv2, а полная кинетическая энергия равна просто сумме
S1/2mv2
по всем частицам тела. Но скорость v каждой частицы связана с угловой скоростью wтвердого тела. Предположим, что тело вращается относительно центра масс, который мы будем считать покоящимся. Если при этом r — положение частицы относительно центра масс, то ее скорость v задается выражением wXr. Поэтому полная кинетическая энергия равна
к. э.=S1/2m(wX г)2. (31.18)
Единственное, что нужно теперь сделать,— это переписать wXr через компоненты wх, wy , wz и координаты х, у, z, а затем сравнить результат с уравнением (31.17); приравнивая коэффициенты, найдем Iij. Проделывая всю эту алгебру, мы пишем:
Умножая это уравнение на m/2, суммируя по всем частицам и сравнивая с уравнением (31.17), мы видим, что Ixx, например, равно
Это и есть та формула для момента инерции тела относительно оси х, которую мы получали уже раньше (гл. 19, вып. 2).
Ну а поскольку r2 =x2+y2+z2, то эту же формулу можно написать в виде
Ixx=Sm(r2-x2). Выписав остальные члены тензора инерции, получим
Если хотите, его можно записать в «тензорных обозначениях»:
где через ri обозначены компоненты (х, у, z) вектора положения частицы, а 2 означает суммирование по всем частицам. Таким образом, момент инерции есть тензор второго ранга, элементы которого определяются свойствами тела и который связывает момент количества движения L с угловой скоростью w:
Для любого тела независимо от его формы можно найти эллипсоид энергии, а следовательно, и три главные оси. Относительно этих осей тензор будет диагональным, так что для любого объекта всегда есть три ортогональные оси, для которых момент количества движения и угловая скорость параллельны друг другу. Они называются главными осями инерции.
§ 5. Векторное произведение
Сами того не подозревая, вы пользуетесь тензором второго ранга уже начиная с гл. 20 (вып. 2). В самом деле, мы определили там «момент силы, действующий в плоскости», например txy, следующим образом:
txy=xFy-yFx.
Обобщая это определение на три измерения, можно написать
tij=riFj-rjFi. (31.22)
Как видите, величина tij — это тензор второго ранга. Один из способов убедиться в этом — свернуть tij с каким-то вектором, скажем с единичным вектором е, т. е. составить
Если эта величина окажется вектором, то tijдолжен преобразовываться как тензор — это просто наше определение тензора. Подставляя выражение для tij, получаем
Поскольку скалярные произведения, естественно, являются скалярами, то оба слагаемых в правой части — векторы, как и их разность. Так что tij-— действительно тензор.
Однако tijпринадлежит к особому сорту тензоров, он антисимметричен, т. е.
tij=-tji.
Поэтому у такого тензора есть только три разные и неравные нулю компоненты: txy, tyz и tzz. В гл. 20 (вып. 2) нам удалось показать, что эти три члена почти «по счастливой случайности» преобразуются подобно трем компонентам вектора; поэтому мы могли тогда определить вектор
t=(tx,. ty, tz) = (tyz, tzx, txy).
Я сказал «по случайности» потому, что это происходит только в трехмерном пространстве. Например, для четырех измерений антисимметричный тензор второго ранга имеет шесть различных ненулевых членов, и его, разумеется, нельзя заменить вектором, у которого компонент только четыре.
Точно так же как аксиальный вектор t==rXF является тензором, по тем же соображениям тензором будет и любое векторное произведение двух полярных векторов. К счастью, они тоже представимы в виде вектора (точнее, псевдовектора), что немного облегчает нам всю математику.
Вообще говоря, для любых двух векторов а и b девять величин aibjобразуют тензор (хотя для физических целей он не всегда может быть полезен). Таким образом, для вектора положения r величины rirjявляются тензором, а поскольку dij. тоже тензор, то мы видим, что правая часть (31.20) действительно является тензором. Подобным же образом тензором будет и (31.22), так как оба члена в правой части — тензоры.
§ 6. Тензор напряжений
Встречавшиеся до сих пор симметричные тензоры возникали как коэффициенты, связывающие один вектор с другим. Сейчас я познакомлю вас с тензором, имеющим совершенно другой физический смысл,— это тензор напряжений. Предположим, что на твердое тело действуют различные внешние силы. Мы говорим, что внутри тела возникают различные «напряжения», имея при этом в виду внутренние силы между смежными частями материала. Мы уже говорили немного о подобных напряжениях в двумерном случае, когда рассматривали поверхностное натяжение напряженной диафрагмы (см. гл. 12, § 3, вып. 5). А теперь вы увидите, что внутренние силы в материале трехмерного тела записываются в виде тензора.
Рассмотрим тело из какого-то упругого материала, например брусок из желе. Если мы разрежем этот брусок, то материал на каждой стороне разреза будет, вообще говоря, претерпевать перемещение под действием внутренних сил. До того как был сделан разрез, между двумя этими частями должны были действовать силы, которые удерживали обе части в едином куске; мы можем выразить напряжение через эти силы. Представьте себе, что мы смотрим на воображаемую плоскость, перпендикулярную оси х, подобную плоскости s на фиг. 31.5, и интересуемся силами, действующими на маленькой площадке Dy/Dz, расположенной в этой плоскости.
Фиг. 31.5. Материал, находящийся слева от плоскости s на площади Dy/Dz, действует на материал, находящийся справа, с силой DF1.
Материал, находящийся слева от площадки, действует на материал с правой стороны с силой DF1 (фиг. 31.5, б). Есть, конечно, и обратная реакция, т.е. на материал слева от поверхности действует сила —DF1. Если площадка достаточно мала, то мы ожидаем, что сила DF1 пропорциональна площади Dy/Dz.
Вы уже знакомы с одним видом напряжений — статическим давлением жидкости. Там сила была равна давлению, умноженному на площадь, и направлена под прямым углом к элементу поверхности. Для твердого тела, а также движущейся вязкой жидкости сила не обязательно перпендикулярна поверхности: помимо давления (положительного или отрицательного), появляется еще и сдвигающая сила. (Под «сдвигающей» силой мы подразумеваем тангенциальные компоненты сил, действующих на поверхности.) Для этого нужно учитывать все три компоненты силы. Заметьте еще, что если разрез мы сделаем по плоскости с какой-то другой ориентацией, то действующие на ней силы тоже будут другими. Полное описание внутренних напряжений требует применения тензоров.
Определим тензор напряжений следующим образом. Вообразите сначала разрез, перпендикулярный оси х, и разложите силу DF1, действующую на разрезе, на ее компоненты: DFx1, DFy1, DFz1 (фиг. 31.6).
Фиг. 31.6. Сила DF1, действующая на элементе площади DyDz, перпендикулярной оси х, разлагается на три компоненты: DFx1, DFу1 и DFz1.
Отношение этих сил к площади Dy/Dz мы назовем Sxx, Syxи Szx. Например,
Syx=DFу1/DyDz
Первый индекс у относится к направлению компоненты силы, а второй х — к направлению нормали к плоскости. Если угодно, площадь DyDz можно записать как Dах, имея в виду элемент площади, перпендикулярный оси х, т. е.
Syx=DFу1/Dах
А теперь представьте себе разрез, перпендикулярный оси у. Пусть на маленькую площадку DxDz действует сила DF2.
Разлагая снова эту силу на три компоненты, как показано на фиг. 31.7, мы определяем три компоненты напряжения Sxy, Syy, Szyкак силы, действующие на единичную площадь в этих трех направлениях.
Фиг. 31.7. Сила, действующая на элемент площади, перпендикулярной оси у, разлагается на три взаимно перпендикулярные компоненты.
Наконец, проведем воображаемый разрез, перпендикулярный оси z, и определим три компоненты Sxz, Syzи Szz. Таким образом, получается девять чисел:
Я хочу теперь показать, что этих девяти величин достаточно, чтобы полностью описать внутреннее напряженное состояние, и что Sij-—действительно тензор. Предположим, что мы хотим знать силу, действующую на поверхность, наклоненную под некоторым произвольным углом. Можно ли найти ее, исходя из Sij? Можно, и это делается следующим образом. Вообразите маленькую призму, одна грань N которой наклонна, а другие — параллельны осям координат. Если окажется, что грань N параллельна оси z, то получается картина, изображенная на фиг. 31.8.
Фиг. 31.8. Разложение на компоненты силы Fn, действующей на грани N (с единичной нормалью n).
(Это, конечно, частный случай, но он достаточно хорошо иллюстрирует общий метод.) Дальше, напряжения, действующие на эту призмочку, должны быть такими, чтобы она находилась в равновесии (по крайней мере в пределе бесконечно малого размера), так что действующая на нее полная сила должна быть равна нулю. Силы, действующие на грани, параллельные осям координат, известны нам непосредственно из тензора Sij. А их векторная сумма должна равняться силе, действующей на грань N, так что эту силу можно выразить через Sij.
Наше допущение, что поверхностные силы, действующие на малый объем, находятся в равновесии, предполагает отсутствие объемных сил, подобных силе тяжести или псевдосилам, которые тоже могут присутствовать, если наша система координат не инерциальна. Заметьте, однако, что такие объемные силы будут пропорциональны объему призмочки и поэтому пропорциональны Dx,Dy, Dz, тогда как поверхностные силы пропорциональны DxDy, DyDz и т. п. Итак, если размер призмочки взять достаточно малым, то объемные силы будут пренебрежимо малы по сравнению с поверхностными.
А теперь сложим силы, действующие на нашу призмочку. Возьмемся сначала за х-компоненту, которая состоит из пяти частей, по одной от каждой грани. Но если Dz достаточно мало, то силы от треугольных граней (перпендикулярные оси z) будут равны друг другу и противоположны по направлению, поэтому о них можно забыть. На основание призмы действует x-компонента силы, равная
DFx2=SxyDxDz,
а x-компонента силы, действующей на вертикальную прямоугольную грань, равна
DFx1=SхxDz.
Сумма этих двух сил должна быть равна x-компоненте силы, действующей извне на грань N. Обозначим через n единичный вектор нормали к грани N, а через Fn — действующую на нее силу, тогда получим
DFxn=SxxDyDz+SxyDxDz.
Составляющая напряжения по оси х (Sxn), действующего в этой плоскости, равна силе DFxn, деленной на площадь, т. е. DzЦ(Dx2+Dy2), или
Но, как видно из фиг. 31.8, отношение Dх/Ц(Dx2+Dy2) — это косинус угла q между n и осью у и может быть записан как пу, т. е. y-компонента вектора n. Аналогично, Dy/Ц(Dx2+Dy2) равно sinq=nх. Поэтому мы можем написать
Sxn=Sxxnx+Sxyny
рели теперь обобщить это на произвольный элемент поверхности, то мы получим
Sxn= Sxxnx+Sxyny+Sxznz,
или в еще более общей форме:
Так что мы действительно можем выразить силу, действующую на произвольную площадь, через элементы Sijи полностью описать внутреннее напряжение.
Уравнение (31.24) говорит, что тензор Sij связывает силу Sn с единичным вектором n точно так же, как aijсвязывает Р с Е. Но поскольку n и Sn — векторы, то компоненты Sijпри изменении осей координат должны преобразовываться как тензор. Так что Sijдействительно тензор.
Можно также доказать, что Sij симметричный тензор. Для этого нужно обратить внимание на силы действующие на маленький кубик материале. Возьмем кубик, грани которого параллельны осям координат, и посмотрим на его разрез (фиг. 31.9).
Фиг. 31.9. х- и у-компоненты сил, действующих на четыре грани маленького единичного кубика.
Если допустить что ребра куба равны единице, то х- и y-компоненты сил на гранях, перпендикулярных к осям х и у, должны быть такими, как показано на рисунке. Если взять достаточно маленький кубик, можно надеяться, что напряжение на его противоположных гранях будет отличаться ненамного, а поэтому компоненты сил должны быть равны и противоположны, как это показано на рисунке. Заметьте теперь, что на кубик не должен действовать никакой момент си иначе кубик начал бы вращаться. Но полный момент относительно центра равен произведению (Syx-Sxy) на единичную длину ребра куба, а поскольку полный момент равен нулю, то S должно быть равно Sxy, и тензор напряжений, таким образом, оказывается симметричным.
Благодаря этой симметрии тензора Sijего можно то; описывать эллипсоидом с тремя главными осями. Напряжение имеет особенно простой вид на площадках, нормальных к этим: осям: оно соответствует чистому сжатию или растяжению в направлении главных осей. Вдоль этих площадок нет никак сдвиговых сил, причем такие оси, для которых отсутствуют сдвиговые силы, можно выбрать для любого напряжения. Если эллипсоид превращается в сферу, то в любом направлении действуют только нормальные силы. Это соответствует гидростатическому давлению (положительному или отрицательном. Таким образом, для гидростатического давления тензор диагонален, причем все три компоненты его равны друг другу (фактически они просто равны давлению р). В этом случае мы можем написать
(31.25)
Вообще говоря, тензор напряжений в куске твердого тела, а также его эллипсоид изменяются от точки к точке, поэтому для описания всего куска мы должны задать каждую компоненту Sijкак функцию положения. Тензор напряжений, таким образом, является полем. Мы уже имели примеры скалярных полей, подобных температуре Т(х, у, z), и векторных полей, подобных Е(х, у, z), которые в каждой точке задавались тремя числами. А теперь перед нами пример тензорного поля, задаваемого в каждой точке пространства девятью числами, из которых для симметричного тензора Sijреально остается только шесть. Полное описание внутренних сил в произвольном твердом теле требует знания шести функций координат х, у и z.
§ 7. Тензоры высших рангов
Тензор напряжений Sijописывает внутренние силы в веществе. Если при этом материал упругий, то внутренние деформации удобно описывать с помощью другого тензора Tij— так называемого тензора деформаций. Для простого объекта, подобного бруску из металла, изменение длины DL, как вы знаете, приблизительно пропорционально силе, т. е. он подчиняется закону Гука
DL=gF.
Для произвольных деформаций упругого твердого тела тензор деформаций Tijсвязан с тензором напряжений Sijсистемой линейных уравнений
Вы знаете также, что потенциальная энергия пружины (или бруска) равна
а обобщением плотности упругой энергии для твердого тела будет выражение
Полное описание упругих свойств кристалла должно задаваться коэффициентами gijkl. Это знакомит нас с новым зверем — тензором четвертого ранга. Поскольку каждый из индексов может принимать одно из трех значений — х, у или z, то всего оказывается 34=81 коэффициент. Но различны из них на самом деле только 21. Во-первых, поскольку тензор Sij симметричен, у него остается только шесть различных величин, и поэтому в уравнении (31.27) нужны только 36 различных коэффициентов. Затем, не изменяя энергии, мы можем переставить Sijи Skl, так что gijkl должно быть симметрично при перестановке пары индексов ij и kl. Это уменьшает число коэффициентов до 21. Итак, чтобы описать упругие свойства кристалла низшей возможной симметрии, требуется 21 упругая постоянная! Разумеется, для кристаллов с более высокой симметрией число необходимых постоянных уменьшается. Так, кубический кристалл описывается всего тремя упругими постоянными, а для изотропного вещества хватит и двух.
В справедливости последнего утверждения можно убедиться следующим образом. В случае изотропного материала компоненты gijklне должны зависеть от поворота осей. Как это может быть? Ответ: они могут быть независимы, только когда выражаются через тензоры dij. Но существует лишь два возможных выражения, имеющих требуемую симметрию,— это dijdkl и dikdjl+dil+djk, так что gijkl должно быть их линейной комбинацией. Таким образом, для изотропного материала
gijkl =а(dijdkl) + b(dikdjl+dildjk);
следовательно, чтобы описать упругие свойства материала, требуются две постоянные: а и b. Я предоставляю вам самим доказать, что для кубического кристалла требуются три такие постоянные.
И еще один последний пример (на этот раз пример тензора третьего ранга) дает нам пьезоэлектрический эффект. При напряженном состоянии в кристалле возникает электрическое поле, пропорциональное тензору напряжений. Общий закон пропорциональности имеет вид
где ei— электрическое поле, a Pijk— пьезоэлектрические коэффициенты (пьезомодули), составляющие тензор. Можете ли вы сами доказать, что если у кристалла есть центр инверсии (т. е. если он инвариантен относительно замены х, у, z®-х,-y,-z), то все его пьезоэлектрические коэффициенты равны нулю.
§ 8. Четырехмерный тензор электромагнитного импульса
Все тензоры, с которыми мы сталкивались в этой главе, были связаны с трехмерным пространством; они определялись как величины, имеющие известные трансформационные свойства при пространственных поворотах. А вот в гл. 26 (вып. 6) мы имели возможность воспользоваться тензором в четырехмерном пространстве-времени: это был тензор электромагнитного поля Fmv. Компоненты такого четырехмерного тензора особым образом преобразуются при преобразованиях Лоренца. (Мы этого, правда, не делали, но могли бы рассматривать преобразования Лоренца как своего рода «вращение» в четырехмерном «пространстве», называемом пространством Минковского; тогда аналогия с тем, что мы рассматривали здесь, была бы ярче.)
В качестве последнего примера мы хотим рассмотреть другой тензор в четырех измерениях (t, x, y, z) теории относительности. Когда мы говорили о тензоре напряжений, то определяли Sijкак компоненту силы, действующую на единичную площадку. Но сила равна скорости изменения импульса со временем. Поэтому вместо того, чтобы говорить «Sxy — это х-компонента силы, действующей на единичную площадку, перпендикулярную оси у», мы с равным правом могли бы сказать: «Sxy — это скорость потока x-компоненты импульса через единичную площадку, перпендикулярную оси у». Другими словами, каждый член Sij представляет поток i-й компоненты импульса через единичную площадку, перпендикулярную оси j. Так обстоит дело с чисто пространственными компонентами, но они составляют только часть «большего» тензора Smvв четырехмерном пространстве m. и v=t, x, у, z), содержащего еще дополнительные компоненты Stx, S yt, Sttи т. п. Попытаемся теперь выяснить физический смысл этих дополнительных компонент.
Нам известно, что пространственные компоненты представляют поток импульса. Чтобы найти ключ к распространению этого понятия на «временное направление», обратимся к «потоку» другого рода — потоку электрического заряда. Скорость потока скалярной величины, подобной заряду (через единичную площадь, перпендикулярную потоку), является пространственным вектором — вектором плотности тока j. Мы видели, что временная компонента вектора потока — это плотность текущего вещества. Например, j можно скомбинировать с плотностью заряда jt=r и получить четырехвектор jm=(r, j), т. е. значок m у вектора jm принимает четыре значения: t, х, у, z. Это означает «плотность», «скорость потока в x-направлении», «скорость потока в y-направлении» и «скорость потока в z-направлении» скалярного заряда.
Теперь по аналогии с нашим утверждением о временной компоненте потока скалярной величины можно ожидать, что вместе c Sxx,Sxyи Sxz, описывающими поток x-компоненты импульса, должна быть и временная компонента Sxt, которая по идее должна бы описывать плотность того, что течет, т. е. Sxtдолжна быть плотностью х-компоненты импульса. Таким образом, мы можем расширить наш тензор по горизонтали, включив в него t-компоненты, и в нашем распоряжении оказываются:
Sxt— плотность x-компоненты импульса,
Sxx — поток z-компоненты импульса в направлении оси х,
Sxy — поток y-компоненты импульса в направлении оси у,
Sxz — поток z-компоненты импульса в направлении оси z.
Аналогичная вещь происходит и с y-компонентой; у нас есть три компоненты потока: Syx, Syyи Syz, к которым нужно добавить четвертый член:
Syt — плотность y-компоненты импульса,
а к трем компонентам Szx, Szyи Szzмы добавляем
Szt — плотность z-компоненты импульса.
В четырехмерном пространстве у импульса существует также и t-компонента, которой, как мы знаем, является энергия. Так что тензор Sijследует продолжить по вертикали с включением в него Stx, Styи Stz, причем
Stx — поток энергии в направлении оси х, Sty — поток энергии в направлении оси у, (31.28) Stz — поток энергии в направлении оси z,
т. е. Stx— это поток энергии в единицу времени через поверхность единичной площади, перпендикулярную оси х, и т. д. Наконец, чтобы пополнить наш тензор, нужна еще величина Stt, которая должна быть плотностью энергии. Итак, мы расширили наш трехмерный тензор напряжений до четырехмерного тензора энергии-импульса Smv. Индекс m может принимать четыре значения: t, х, у и z, которые означают «плотность», «поток через единичную площадь в направлении оси х», «поток через единичную площадь в направлении оси y» и «поток через единичную площадь в направлении оси z». Значок v тоже принимает четыре значения: t, х, у, z, которые говорят нам, что же именно течет: «энергия», x-компонента импульса», «y-компонента импульса» или же «z-компонента импульса».
В качестве примера рассмотрим этот тензор не в веществе, а в пустом пространстве с электромагнитным полем. Вы знаете, что поток энергии электромагнитного поля описывается вектором Пойнтинга S=e0c2EXВ. Так что х-, у- иz-компоненты вектора S с релятивистской точки зрения являются компонентами: Six, Stни Stzнашего тензора энергии-импульса. Симметрия тензора Sijпереносится и на временные компоненты, так что четырехмерный тензор Smv тоже симметричен:
Smv=Svm. . (31.29)
Другими словами, компоненты Sxt, Syt, Szt, которые представляют плотности х-, у- и z-компонент импульса, равны также х-, у- и z-компонентам вектора Пойнтинга S, или, как мы видели раньше из других соображений, вектора потока энергии.
Оставшиеся компоненты тензора электромагнитного напряжения Smvтоже можно выразить через электрическое и магнитное поля Е и В. Иначе говоря, для электромагнитного поля в пустом пространстве мы должны допустить существование тензора напряжений, или, выражаясь менее таинственно, потока импульса электромагнитного поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но тогда мы не входили в детали.
Тем из вас, кто хочет испытать свою удаль на четырехмерных тензорах, может понравиться выражение для тензора Smvчерез поля:
где суммирование по a и b проводится по всем их значениям (т. е. t, x, у и z), но, как обычно в теории относительности, для суммы S и символа d принимается специальное соглашение. В суммах слагаемые со значками х, у, z должны вычитаться, а dtt=+1, тогда как dxx.=dуу = dzz=-1 и dmv=0 для всех m№v (с=1). Сможете ли вы доказать, что эта формула приводит к плотности энергии Stt=(e0/2)(E2+B2) и вектору Пойнтинга e0ЕXВ? Можете ли вы показать, что в электростатическом поле, когда В=0, главная ось напряжения направлена по электрическому полю и вдоль направления поля возникает натяжение (e0/2)E2и равное ему давление в направлении, перпендикулярном направлению поля?
* Если не полагать с=1, как это делается здесь, то плотность энергии в принятых в книге единицах будет равна (e0/2)(E2+с2B2) или в единицах СИ 1/2[e0E2+(l/m0)B2]. — Прим. ред.
* Эту работу, затраченную на создание поляризации электрическим полем, не нужно путать с потенциальной энергией —p0*Е постоянного дипольного момента p0 в поле Е.
* Обычно для коэффициентов пропорциональности между Р и Е пользуются термином тензор восприимчивости, оставляя термин поляризуемость для величин, относящихся к одной частице. Прим. ред.
* В гл. 10, следуя общепринятому соглашению, мы писали Р=e0cЕ и величину c (хи) называли «восприимчивостью». Здесь же нам удобнее пользоваться одной буквой, так что вместо e0c мы будем писать a. Для изотропного диэлектрика a=(c-1)e0, где c — диэлектрическая проницаемость (см. гл. 10 §4 вып.5)
Глава 32 ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
§ 1. Поляризация вещества
§ 2. Уравнения Максвелла в диэлектрике
§ 3. Волны в диэлектрике
§ 4. Комплексный показатель преломления
§ 5. Показатель преломления смеси
§ 6. Волны в металлах
§ 7.Низкочастотное и высокочастотное приближение глубина скин-слоя и плазменная частота
Повторить: всё что в табл. 32.
§ 1. Поляризация вещества
Здесь я хочу обсудить явления преломления света, ну и, разумеется, его поглощение плотным веществом. Теорию показателя преломления мы уже рассматривали в гл. 31 (вып. 3), но тогда наши знания математики были весьма ограничены и мы остановились только на показателе преломления веществ с малой плотностью наподобие газов. Но физические принципы, приводящие к возникновению показателя преломления, мы там все же выяснили. Электрическое поле световой волны поляризует молекулы газа, создавая тем самым осциллирующие дипольные моменты, а ускорение осциллирующих зарядов приводит к излучению новых волн поля. Это новое поле, интерферируя со старым, изменяет его. Изменение поля эквивалентно тому, что происходит сдвиг фазы первоначальной волны. Из-за того что сдвиг фазы пропорционален толщине материала, эффект в целом оказывается эквивалентным изменению фазовой скорости света в материале. Прежде, когда рассматривалось это явление, мы пренебрегали усложнениями, возникающими от таких эффектов, как действие новой измененной волны на поле осциллирующего диполя. Мы предполагали, что силы, действующие на заряды атомов, определяются только падающей волной, тогда как на самом деле на осциллятор действует не только падающая волна, но и волны, излученные другими атомами. В то время нам еще было трудно учесть этот эффект, поэтому мы изучали только разреженные газы, где его можно считать несущественным.
Ну а теперь мы увидим, что эта задача с помощью дифференциальных уравнений решается совсем просто. Конечно, дифференциальные уравнения затуманивают физическую причину возникновения преломления (как результата интерференции вновь излученных волн с первоначальными), но зато они упрощают теорию плотного материала. В этой главе сойдется вместе многое из того, что мы делали уже раньше. Практически мы уже получили все, что нам потребуется, так что по-настоящему новых идей в этой главе будет сравнительно немного. Поскольку вам может понадобиться освежить в памяти то, с чем мы здесь столкнемся, то в табл. 32.1 приводится список уравнений, которые я собираюсь использовать вместе со ссылкой на те места, где их можно найти. Во многих случаях из-за нехватки времени я не смогу снова останавливаться на физических аргументах, а сразу же буду браться за уравнения.
Таблица 32.1 · ЧТО БУДЕТ ИСПОЛЬЗОВАНО В ЭТОЙ ГЛАВЕ
Начну с напоминания о механизме преломления в газе. Мы предполагаем, что в единице объема газа находится N частиц и каждая из них ведет себя как гармонический осциллятор. Мы пользуемся моделью атома или молекулы, к которой электрон привязан силой, пропорциональной его перемещению (как будто он удерживается пружинкой). Отметим, что такая модель атома с классической точки зрения незаконна, однако позднее будет показано, что правильная квантовомеханическая теория дает (в простейших случаях) эквивалентный результат. В наших прежних рассмотрениях мы не учитывали «тормозящей» силы в атомном осцилляторе, а сейчас это будет сделано. Такая сила соответствует сопротивлению при движении, т. е. она пропорциональна скорости электрона. Уравнением движения при этом будет
F=qeE =m(x+gx+w20x), (32.1)
где х — перемещение, параллельное направлению поля Е. (Осциллятор предполагается изотропным, т. е. восстанавливающая сила одинакова во всех направлениях. Кроме того, на время мы ограничимся линейно поляризованной волной, так что поле Е не меняет своего направления.) Если действующее на атом электрическое поле изменяется со временем синусоидально, то мы пишем.
E=E0eiwt. (32.2)
С той же самой частотой будет осциллировать и перемещение, поэтому можно считать
х=х0еiwt .
Подставляя х=iwx и х=-w2х, можно выразить х через Е:
А зная перемещение, можно вычислить ускорение х и найти ответственную за преломление излученную волну. Именно таким способом в гл. 31 (вып. 3) мы подсчитывали показатель преломления.
Теперь же мы пойдем другим путем. Индуцированный дипольный момент атома р равен qex, или в силу уравнения (32.3)
Так как р пропорционально Е, то мы пишем
р=e0a(w)Е, (32,5) где a — атомная поляризуемость:
Подобный же ответ для движения электронов в атоме дает и квантовая механика, но с учетом следующих особенностей. У атомов есть несколько собственных частот, каждая из которых имеет свою диссипативную постоянную g. Кроме того, каждая гармоника имеет еще свою эффективную «силу», выражаемую в виде произведения поляризуемости при данной частоте на постоянную связи f, которая, как ожидается, по порядку величины равна единице. Обозначая каждый из трех параметров w0, g и f для каждой из гармоник через wok, gk и fk и суммируя по всем гармоникам, мы вместо (32.6) получаем
Если число атомов в единице объема вещества равно N, то поляризация Р будет просто Np=e0NaE, т. е. пропорциональна Е:
Р=e0Na(w)Е. (32.8)
Другими словами, когда на материал действует синусоидальное электрическое поле, оно индуцирует пропорциональный себе дипольный момент, причем константа пропорциональности а, как мы уже отмечали, зависит от частоты. При очень больших частотах a мала: реакция материала слабая. А вот при низких частотах реакция может быть очень сильной. Константа пропорциональности, кроме того, еще оказывается комплексной, т. е. поляризация не следует точно за всеми изменениями электрического поля, а в какой-то степени может быть сдвинута по фазе. Во всяком случае, электрическое поле вызывает в материале поляризацию, пропорциональную его напряженности.
§ 2. Уравнения Максвелла в диэлектрике
Наличие в веществе поляризации означает, что там возникают поляризационные заряды и токи, которые необходимо учитывать в полных уравнениях Максвелла при нахождении полей. Сейчас мы собираемся решать уравнения Максвелла для случая, когда заряды и токи не равны нулю, но неявно определяются вектором поляризации. Нашим первым шагом должно быть явное нахождение плотности зарядов r и плотности тока j, усредненных по тому же самому малому объему, который имелся в виду при определении вектора Р. Потом необходимые нам значения r и j могут быть определены из поляризации. В гл. 10 (вып. 5) мы видели, что когда поляризация Р меняется от точки к точке, то возникает плотность зарядов:
rпол=-С·Р. (32.9)
В то время мы имели дело со статическими полями, но эта же формула справедлива и для переменных полей. Но когда Р изменяется со временем, заряды движутся, так что появляется поляризационный ток. Каждый из осциллирующих зарядов вносит в ток свой вклад, равный произведению его заряда qeна скорость v. Когда же таких зарядов в единице объема N штук, то они создают плотность тока j:
j=Nqev.
Ну а поскольку известно, что v=dx/dt, то j=Nqedx/dt, что как раз
равно dP/dt.Следовательно, при переменной поляризации возникает плотность тока
jпол=dP/dt (32.10)
Наша задача стала теперь простой и понятной. Мы пишем уравнения Максвелла с плотностями заряда и тока, определяемыми поляризацией Р посредством уравнений (32.9) и (32.10). (Предполагается, что других зарядов и токов в веществе нет.) Затем мы свяжем Р с Е формулой (32.5) и будем разрешать их относительно Е и В, отыскивая при этом волновое решение.
Но прежде чем приступить к решению, мне бы хотелось сделать одно замечание исторического характера. Первоначально Максвелл писал свои уравнения в форме, отличающейся от той, в которой они используются нами. И именно потому, что уравнения писались в другой форме в течение многих лет (да и сейчас многими пишутся так), я постараюсь объяснить вам разницу. В те дни механизм диэлектрической проницаемости не был понятен с ясностью и полнотой. Не была ясна ни природа атомов, ни существование поляризации в веществе. Поэтому тогда не понимали, что С·P дает дополнительный вклад в плотность заряда р. Были известны только заряды, не связанные в атомах (такие, как заряды, текущие по проводу или возникающие при трении).
Сегодня же мы предпочитаем обозначать через r полную плотность зарядов, включая в нее и заряды, связанные с индивидуальными атомами. Если назвать эту часть зарядов rпол, то можно написать
r=rпол+rдр,
где rдр— плотность зарядов, учтенная Максвеллом и относящаяся к другим зарядам, не связанным с определенными атомами. При этом мы бы написали
После подстановки rпол из (32.9) получаем
или
В плотность тока, фигурирующую в уравнениях Максвелла для СXB, вообще говоря, тоже вносится вклад от связанных атомных электронных токов. Поэтому мы можем написать
j=jпол+jдр,
причем уравнение Максвелла приобретает вид
Используя уравнение (32.10), получаем
Теперь вы видите, что если бы мы определили новый вектор D
D=e0E+P, (32.14)
то два уравнения поля приняли бы вид
С·D=rдр (32.15)
и
Это и есть та форма уравнений, которую использовал Максвелл для диэлектриков. А вот и остальные два уравнения:
СXЕ=-дB/дt
и
С·B=0,
которые в точности совпадают с нашими.
Перед Максвеллом и другими учеными того времени вставала проблема магнетиков (за них мы вскоре примемся). Они ничего не знали о циркулирующих токах, ответственных за атомный магнетизм и поэтому, в плотности тока утеряли еще одну часть. Вместо уравнения (32.16) они на самом деле писали
где Н отличается от e0с2В, так как последнее учитывает эффекты атомных токов. (При этом j' представляет то, что осталось от токов.) Таким образом, у Максвелла было четыре полевых вектора: Е, D, В и Н, причем в D и Н скрывалось то, на что он не обратил внимания,— процессы, происходящие внутри вещества. Уравнения, написанные в таком виде, вы встретите во многих местах.
Чтобы решить их, необходимо как-то связать D и Н с другими полями, поэтому зачастую писали
D =eE
и
В=mH. (32.18)
Однако эти связи верны лишь приближенно для некоторых веществ, и то лишь когда поля не изменяются слишком быстро со временем. (Для синусоидально изменяющихся полей зачастую можно писать уравнения таким способом, считая при этом e и m комплексными функциями частоты, но для произвольных изменений поля со временем это неверно.) На какие только ухищрения не пускаются ученые, чтобы решить уравнения! А мне кажется, что правильнее всего оставить уравнения записанными через фундаментальные величины, как мы понимаем их теперь, т. е. как раз то, что мы и проделали.
§ 3. Волны в диэлектрике
Теперь нам предстоит выяснить, какого сорта электромагнитные волны могут существовать в диэлектрическом веществе, где других зарядов, кроме тех, что связаны в атомах,
нет. Таким образом, мы возьмем r=-С·Р и j=дP/дt . При этом уравнения Максвелла примут такой вид:
Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:
СX(СXE)=-(д/дt)СXB.
Используя затем векторное тождество
СX(СXE) = С(С·E)-С2E и подставляя выражение для СXB из (32.19б), получаем
Используя уравнение (32.19а) для С·Е, находим
Таким образом, вместо волнового уравнения мы теперь получили, что даламбертиан Е равен двум членам, содержащим поляризацию Р.
Однако Р зависит от Е, поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем ограничиваться изотропными диэлектриками, т. е. Р всегда будет иметь то же направление, что и Е. Попробуем найти решение для волны, движущейся в направлении оси z. Электрическое поле при этом будет изменяться как еi(wt-kz). Предположим также, что волна поляризована в направлении оси х, т. е. что электрическое поле имеет только x-компоненту. Все это записывается следующим образом:
Ex=E0ei(wt-kz). (32.21)
Вы знаете, что любая функция от (z-vt) представляет волну, бегущую со скоростью v. Показатель экспоненты в выражении (32.21) можно переписать в виде
-ik[z-(w/k)t],
так что выражение (32.21) представляет волну, фазовая скорость которой равна
vфаз=w/k.
В гл. 31 (вып. 3) показатель преломления n определялся нами из формулы
vфаз=c/n.
С учетом этой формулы (32.21) приобретает вид
Ex=E0eiw(t-nz/c).
Таким образом, показатель n можно определить, если мы найдем ту величину k, которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим уравнениям поля, и затем воспользуемся соотношением
n=kc/w. (32.22)
В изотропном материале поляризация будет иметь только x-компоненту; кроме того, Р не изменяется с изменением координаты х, поэтому С·P=0 и мы сразу же избавляемся от первого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш диэлектрик «линейным», поэтому Рхбудет изменяться как еiwtи d2Px/dt2= -w2Px. Лапласиан же в уравнении (32.20) превращается просто в д2Ex/dz2=-k2Еx, так что в результате получаем
Теперь на минуту предположим, что раз Е изменяется синусоидально, то Р можно считать пропорциональной Е, как в уравнении (32.5). (Позднее мы вернемся к этому предположению и обсудим его.) Таким образом, пишем
Px=e0NaEx.
При этом Ехвыпадает из уравнения (32.23), и мы находим
k2=w2/c2(1+Na). (32.24)
Мы получили, что волна вида (32.21) с волновым числом k, задаваемым уравнением (32.24), будет удовлетворять уравнениям поля. Использование же выражения (32.22) для показателя n дает
n2 = l+Na. (32.25)
Сравним эту формулу с тем, что получилось у нас для показателя преломления газа (гл. 31, вып. 3). Там мы нашли уравнение (31.19), которое тогда имело вид
Формула (32.25) после подстановки w из (32.6) дает
Что здесь нового? Во-первых, появился новый член igw, возникший в результате учета поглощения энергии в осцилляторах. Во-вторых, слева вместо n теперь стоит n2и, кроме того, отсутствует дополнительный множитель 1/2. Но заметьте, что если значение N достаточно мало, так что n близок к единице (как это имеет место в газе), то выражение (32.27) говорит, что n2 равен единице плюс некое малое число, т. е. n2=1+e. При этом условии мы можем написать, что n=Ц(1+e)»l+e/2, и оба выражения оказываются эквивалентными. Таким образом, наш новый метод дает для газа тот же самый, найденный нами ранее результат.
Теперь можно надеяться, что выражение (32.27) должно давать показатель преломления и для плотных материалов. Но по некоторым причинам оно нуждается в модификации. Во-первых, при выводе этого уравнения предполагалось, что поляризованное поле, действующее на каждый из атомов,— это поле Ех. Однако такое предположение неверно, поскольку в плотном материале существуют и другие поля, создаваемые соседними атомами, которые могут быть сравнимы с Ех. Аналогичную задачу мы уже рассматривали при изучении статических полей в диэлектрике (см. гл. 11, вып. 5). Вы, вероятно, помните, что мы нашли поле, действующее на отдельный атом, представив его сидящим в сферической полости в окружающем диэлектрике. Поле в такой полости (мы назвали его локальным) увеличивается по сравнению со средним полем Е на величину Р/3e0. (Не забудьте, однако, что этот результат, строго говоря, справедлив только для изотропного материала, а также в случае кубического кристалла.)
Те же рассуждения верны и для электрического поля в волне, но до тех пор, пока длина ее много больше расстояния между атомами. При таком ограничении
Именно это локальное поле следует использовать вместо Е в (32.8), т. е. это выражение должно быть переписано следующим образом:
Р =e0NaЕлок. (32.29)
Подставляя теперь Елок из формулы (32.28), находим
или
Иными словами, Р для плотного материала все еще пропорциональна Е (для синусоидального поля). Однако константа пропорциональности будет уже e0/Na/[1-(Na/3)], а не e0Nallfa, как раньше. Таким образом, нам нужно поправить формулу (32.25):
Более удобно переписать это в виде
который алгебраически эквивалентен прежнему. Это и есть известная формула Клаузиуса — Моссотти.
В плотном материале возникает и другое усложнение. Поскольку атомы расположены слишком тесно, они сильно взаимодействуют друг с другом. Поэтому внутренние гармоники осцилляции изменяются. Собственные частоты атомных осцилляций размазываются этими взаимодействиями и обычно весьма сильно подавляются ими, а коэффициент трения становится очень большим. Таким образом, все w0 и g твердого вещества будут другими, чем для свободных атомов. С этой оговоркой мы все-таки можем представлять а, по крайней мере приближенно, уравнением (32.7), так что
Наконец, последнее усложнение. Если плотный материал представляет собой смесь нескольких компонент, то каждая из них дает свой вклад в поляризацию. Полная a будет суммой вкладов различных компонент смеси [за исключением неточности приближения локального поля в упорядоченных кристаллах, т. е. выражения (32.28) — эффекты, которые мы обсуждали при разборе сегнетоэлектриков]. Обозначая через njчисло атомов каждой компоненты в единице объема, мы должны заменить формулу (32.32) следующей:
где каждая aj будет определяться выражением типа (32.7). Выражение (32.34) завершает нашу теорию показателя преломления. Величина 3(n2-1)/(n2+2) задается комплексной функцией частоты, каковой является средняя атомная поляризуемость a(w). Точное вычисление a(w) (т. е. нахождение fk, gkи w0k) для плотного вещества — одна из труднейших задач квантовой механики. Это было сделано только для нескольких особенно простых веществ.
§ 4. Комплексный показатель преломления
Обсудим теперь следствия нашего результата (32.33). Прежде всего обратите внимание на то, что a — комплексное число, так что показатель преломления n тоже оказывается комплексным. Что это означает? Давайте возьмем и запишем n в виде вещественной и мнимой частей:
где nRи nj — вещественные функции w. Мы написали injс отрицательным знаком, так что njдля обычных оптических материалов будет положительной величиной. (Для обычных оптически неактивных материалов, которые не служат сами источниками света, как это происходит у лазеров, g—положительное число, а это делает мнимую часть n отрицательной.) Наша: плоская волна запишется теперь через n следующим образом:
Ех=Е0е-iw(t-nz/c).
Если подставить n в виде выражения (32.35), то мы получим
и с увеличением z она экспоненциально убывает. График напряженности электрического поля как функции от z в некоторый момент времени и для nI» nR/2p показан на фиг. 32.1.
Фиг. 32.1. График поля Ех в некоторый момент t при nI»nR2/p.
Мнимая часть показателя преломления из-за потерь энергии в атомных осцилляторах приводит к ослаблению волны. Интенсивность волны пропорциональна квадрату амплитуды, так что
Интенсивность ~е-2wnIz/c.
Часто это записывается как
Интенсивность ~е-bz,
где b=2wnI/с — коэффициент поглощения. Таким образом, в уравнении (32.33) содержится не только теория показателя преломления вещества, но и теория поглощения им света.
В тех материалах, которые мы обычно считаем прозрачными, величина c/wnI, имеющая размерность длины, оказывается гораздо больше толщины материала.
§ 5. Показатель преломления смеси
В нашей теории показателя преломления имеется еще одно предсказание, которое можно проверить экспериментально. Предположим, что мы рассматриваем смесь двух материалов. Показатель преломления смеси не будет средним двух показателей, а определяется через сумму двух поляризуемостей, как в уравнении (32.34). Если, скажем, мы интересуемся показателем преломления раствора сахара, то полная поляризуемость будет суммой поляризуемостей воды и сахара. Но каждая из них, разумеется, должна подсчитываться исходя из данных о числе молекул N данного сорта в единице объема. Другими словами, если в данном растворе содержится N1молекул воды, поляризуемость которой a1, и N2молекул сахарозы (C12H22O11), поляризуемость которой a2, то мы должны получить
Этой формулой можно воспользоваться для экспериментальной проверки нашей теории — измерения показателя для различных концентраций сахарозы в воде. Однако здесь мы должны сделать несколько допущений. Наша формула предполагает, что при растворении сахарозы никакой химической реакции не происходит и что возмущение индивидуальных осцилляторов при различных частотах отличается не слишком сильно. Поэтому наш результат, безусловно, будет только приближенным. Тем не менее давайте посмотрим, насколько он хорош.
Раствор сахара мы выбрали потому, что мы располагаем хорошими данными измерений показателя преломления и, кроме того, сахар представляет собой молекулярный кристалл и переходит в раствор без ионизации и других изменений химического состояния.
В первых трех столбцах табл. 32.2 приведены данные из указанного справочника. В столбце А дан процент сахарозы по весу, в столбце В приведена измеренная плотность в г/см3, а в столбце С даны измерения показателя преломления света с длиной волны 589,3 ммк. В качестве показателя чистого сахара мы взяли результаты измерений для кристалла сахара. Эти кристаллы не изотропны, так что показатель преломления в разных направлениях различен.
Таблица 32.2 в ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ РАСТВОРА САХАРА И СРАВНЕНИЕ С ПРЕДСКАЗАНИЕМ УРАВНЕНИЯ (32.37)
Справочник дает три величины:
n1=1,5376, n2=1,5651, n3=1,5705.
Мы взяли среднее.
Попытаемся теперь подсчитать n для каждой концентрации, но мы не знаем, какие нужно взять значения a1 и a2. Проверим теорию таким способом: будем предполагать, что поляризуемость воды (a1) при всех концентрациях одна и та же, и подсчитаем поляризуемость сахарозы, используя экспериментальную величину n и разрешая (32.37) относительно a2. Если теория верна, то мы для любой концентрации должны получить одно и то же значение a2.
Прежде всего нам нужно знать числа N1и N2; выразим их через число Авогадро N0. В качестве нашей единицы объема давайте возьмем один литр (1000 см3). Тогда отношение Ni/N0 равно весу одного литра, поделенному на грамм-молекулу. А вес литра равен произведению плотности (умноженной на 1000, чтобы получить граммы) на весовую долю либо сахарозы, либо воды. Таким путем получаем N2//N0и n1/n0, записанные в столбцах D и Е нашей таблицы. В столбце F мы подсчитали 3(n2-1)/(n2+2), исходя из экспериментальных значений n (столбец С). Для чистой воды 3(n2-1)/(n2+2) равно 0,617, что как раз будет N1a1. Затем мы можем заполнить остальную часть колонки G, поскольку для каждой строки отношение G/E должно быть одной и той же величиной, именно 0,617:55,5. Вычитая столбец G из столбца F, находим вклад N2a2, вносимый сахарозой, который записан в столбце Н. А затем, поделив эти данные на величину N2/N0 из столбца D, мы получаем величину N0a2, приведенную в столбце 1.
Из нашей теории мы ожидали, что все величины N0a2должны получиться одинаковыми. Они получились хотя и не точно равными, но довольно близкими друг к другу. Отсюда можно заключить, что наши идеи правильны. Более того, мы нашли, что поляризуемость молекул сахара, по-видимому, не зависит сильно от ее окружения: их поляризуемость приблизительно одна и та же как в разбавленном растворе, так и в кристалле.
§ 6. Волны в металлах
Теорию, которая в этой главе развивалась для твердых материалов, после очень небольшой модификации вполне можно применить и к хорошим проводникам типа металлов. На некоторые из электронов в металлах не действует сила, привязывающая их к какому-то частному атому; это так называемые «свободные» электроны, ответственные за проводимость. Там есть и другие электроны, которые связаны в атомах, и изложенная выше теория непосредственно приложима именно к ним. Однако их влияние обычно «забивается» эффектами электронов проводимости. Поэтому сейчас мы рассмотрим только эффекты
свободных электронов.
Если на электрон не действует никакая восстанавливающая сила, но сопротивление его движению все же остается, то уравнение движения электрона отличается от (32.1) только отсутствием члена w20х. Так что единственное, что нам нужно сделать,— это положить w20=0 во всей остальной части наших выводов. Но есть еще одно отличие. В диэлектриках мы должны различать среднее и локальное поля и вот почему: в изоляторе каждый из диполей занимает фиксированное положение по отношению к другим диполям. Но в металле из-за того, что электроны проводимости движутся и меняют свое место, поле, действующее на них, в среднем как раз равно среднему полю Е. Так что поправка, которую мы сделали к формуле (32.5), не годится, т. е. применение формулы (32.28) для электронов проводимости недопустимо. Следовательно, выражение для показателя преломления в металле должно выглядеть подобно выражению (32.27), в котором следует положить w0=0, именно:
Это только вклад от электронов проводимости, которые, как мы думаем, играют в металлах главную роль.
Но теперь мы даже знаем, какой нам взять величину g, ибо она связана с проводимостью металла. В гл. 43 (вып. 4) мы обсудили связь проводимости металлов с диффузией свободных электронов в кристалле. Электроны движутся по ломаному пути от одного соударения до другого, а между этими толчками они летят свободно, за исключением ускорения из-за какого-то среднего электрического поля (фиг. 32.2).
Фиг. 32.2. Движение свободного электрона.
Там же, в гл. 43 (вып. 4), мы нашли, что средняя скорость дрейфа равна просто произведению ускорения на среднее время между соударениями t. Ускорение равно qeE/m, так что
vдрейф=(qeE/m)t. (32.39)
В этой формуле поле Есчитается постоянным, так что скорость vдрейф тоже постоянна. Поскольку в среднем ускорение отсутствует, сила торможения равна приложенной силе. Мы определили g через силу торможения, равную gmv [см. (32.1)], или qeE, поэтому получается, что
g=1/t (32.40)
Несмотря на то что мы не можем с легкостью измерять непосредственно t, можно определять его, измеряя проводимость металла. Экспериментально обнаружено, что электрическое поле Е порождает в металлах ток с плотностью j, пропорциональной Е (для изотропного материала, конечно):
причем постоянная пропорциональности s называется проводимостью.
В точности то же самое мы ожидаем из выражения (32.39),
если положить
j=Nqevдрейф,
тогда
Таким образом, t, а следовательно, и g могут быть связаны с наблюдаемой электрической проводимостью. Используя (32.40] и (32.41), можно переписать нашу формулу (32.38) для показателя преломления в виде
где
Это и есть известная формула для показателя преломления в металлах.
§ 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
Наш результат для показателя преломления в металлах —формула (32.42) — предсказывает для распространения волн с разными частотами совершенно различные характеристики. Прежде всего давайте посмотрим, что получается при низких частотах. Если величина w достаточно мала, то (32.42) можно приближенно записать в виде
Возведением в квадрат можно проверить, что
таким образом, для низких частот
Вещественная и мнимая части n имеют одну и ту же величину. С такой большой мнимой частью n волны в металлах затухают очень быстро. В соответствии с выражением (32.36) амплитуда волны, идущей в направлении оси z, уменьшается как
Запишем это в виде
е-z/d, (32.47)
где d — это то расстояние, на котором амплитуда волны уменьшается в е=2,72 раза, т. е. приблизительно в 3 раза. Амплитуда такой волны, как функция от z, показана на фиг. 32.3.
Фиг. 32.3. Амплитуда поперечной электромагнитной волны в металле как функция расстояния.
Поскольку электромагнитные волны проникают в глубь металла только на это расстояние, величина d называется глубиной скин-слоя и определяется выражением
Но что все-таки мы понимаем под «низкими» частотами? Взглянув на уравнение (32.42), мы видим, что его можно приближенно заменить уравнением (32.44), только когда wt много меньше единицы и когда we0/s также много меньше единицы, т. е. наше низкочастотное приближение применимо при
w<<1/t
и
w<<s/e0. (32.49)
Давайте посмотрим, какие частоты соответствуют этому приближению для такого типичного металла, как медь. Для вычисления t воспользуемся уравнением (32.43), а для вычисления s/e0 — известными значениями s и e0. Справочник дает нам такие данные:
s=5,76·107 (ом·м)-1,
Атомный вес = 63,5 г,
Плотность = 8,9 г/см3,
Число Авогадро=6,02·1023.
Если мы предположим, что на каждый атом приходится по одному свободному электрону, то число электронов в кубическом метре будет равно
N=8,5·1028 м-3.
Используя далее
qe=1,6·10-19 кулон,
e0=8,85·10-12 ф/м,
m=9,11·10-31 кг,
получаем
t=2,4·10-14 сек,
1/t=4,l·1013 сек-1,
s/e0 = 6,5·1018 сек-1.
Таким образом, для частот, меньших чем приблизительно 1012 гц, медь будет иметь описанное нами «низкочастотное» поведение. (Это будут волны с длиной, большей 0,3 мм, т. е. очень короткие радиоволны!)
Для таких волн глубина скин-слоя равна
Для микроволн с частотой 10 000 Мгц (3-сантиметровые волны)
s=6,7·10-4 см,
т. е. волны проникают на очень малое расстояние.
Теперь вы видите, почему при изучении полостей (и волноводов) нам нужно беспокоиться только о полях внутри полости, а не о волнах в металле или вне полости. Кроме того, мы видим, почему серебрение или золочение полости уменьшает потери в ней. Ведь потери происходят благодаря токам, которые ощутимы только в тонком слое, равном глубине скин-слоя.
Рассмотрим теперь показатель преломления в металле типа меди при высоких частотах. Для очень высоких частот сот много больше единицы, и уравнение (32.42) очень хорошо аппроксимируется следующим:
Для высокочастотных волн показатель преломления в металлах становится чисто вещественным и меньшим единицы! Это следует также из выражения (32.38), если пренебречь диссипативным членом с 7, что может быть сделано при очень больших значениях w. Выражение (32.38) дает при этом
что, разумеется, эквивалентно уравнению (32.50). Раньше нам
уже встречалась величина (Nq2e/e0m)1/2, которую мы назвали
плазменной частотой (см. гл. 7, § 3, вып. 5);
Таким образом, (32.50) или (32.51) можно переписать в виде
Эта плазменная частота является своего рода «критической». Для w<wр показатель преломления металла имеет мнимую часть и происходит поглощение волн, но при w>>wp показатель становится вещественным, а металл — прозрачным. Вы знаете, конечно, что металлы в достаточной мере прозрачны для рентгеновских лучей. Но некоторые металлы прозрачны даже для ультрафиолета. В табл. 32.3 мы приводим для некоторых металлов экспериментально наблюдаемые длины волн, при которых эти металлы начинают становиться прозрачными. Во второй колонке дана вычисленная критическая длина волны lp =2pc/wp . Учитывая, что экспериментальная длина волны определена не очень хорошо, согласие с теорией следует признать замечательным.
Таблица 32.3 · длины волн, при которых МЕТАЛЛ СТАНОВИТСЯ ПРОЗРАЧНЫМ
Вас может удивить, почему плазменная частота wр должна иметь отношение к распространению волн в металлах. Плазменная частота появилась у нас в гл. 7 (вып. 5) как собственная частота колебаний плотности свободных электронов. (Электрическое расталкивание группы электронов и их инерция приводят к колебаниям плотности.) Продольные волны плазмы резонируют при частоте w. Но сейчас мы говорим о поперечных волнах, и мы уже нашли, что при частотах, меньших wр, происходит их поглощение. (Это очень интересное и отнюдь не случайное совпадение.)
Хотя мы все время говорили о распространении волн в металлах, вы одновременно, должно быть, почувствовали универсальность явлений физики: нет никакой разницы в том, находятся ли свободные электроны в металле, в плазме, в ионосфере Земли или в атмосфере звезд. Чтобы понять распространение радиоволн в ионосфере, можно воспользоваться тем же выражением, разумеется, при надлежащих значениях величин N и t. Теперь мы можем видеть, почему длинные радиоволны поглощаются или отражаются ионосферой, тогда как короткие свободно проходят через нее. (Поэтому для связи с искусственными спутниками Земли должны применяться короткие волны.)
Мы говорили о распространении предельных высоко- и низкочастотных волн в металлах. Для промежуточных же частот необходимо использовать «полновесное» уравнение (32.42). В общем случае показатель преломления будет иметь вещественную и мнимую части, и при распространении волн в металлах происходит их поглощение. Очень тонкие слои металла прозрачны даже для обычных оптических частот. В качестве примера приведем специальные защитные очки для рабочих, работающих около высокотемпературных печей. Эти очки изготавливаются напылением на стекло очень тонкого слоя золота; стекло это достаточно прозрачно для видимого света и на просвет выглядит как зеленое, но инфракрасные лучи сильно поглощает.
И, наконец, от читателя невозможно скрыть тот факт, что многие из этих формул в некотором отношении напоминают формулы для диэлектрической проницаемости c, рассмотренные в гл. 10 (вып. 5). Диэлектрической проницаемостью c измеряется реакция материала на статическое электрическое поле, т. е. когда w=0. Если вы посмотрите повнимательнее на определение n и c, то обнаружите, что c есть не что иное, как предел n2 при w®0. В самом деле, положив в уравнениях этой главы w=0 и n2=c, мы воспроизведем уравнения теории диэлектрической проницаемости гл. 11 (вып. 5).
* Или записав — i=е-ip/2; Ц-i=e-ip/4 = соsp/4- isinp/4, что приводит к тому же результату.
* Взяты из справочника «Handbook of Physics and Chemistry».
* Всюду в этой главе мы будем пользоваться обозначениями, принятыми в гл. 31 (вып. 3); пусть a — атомная поляризуемость, как это определено здесь. В предыдущей главе мы пользовались буквой a для обозначения объемной поляризуемости, т. е. отношения Р к Е. Но в обозначениях этой главы P=Nae0E [см. выражение (32.8)].
Глава 33 ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
§1. Отражение и преломление света
§2. Волны в плотных материалах
§3. Граничные условия
§4. Отраженная и преломленная волны
§5. Отражение от металлов
§6. Полное внутреннее отражение
Повторить: гл. 33 (вып. 3) « Поляризация »
§ 1. Отражение и преломление света
Предметом обсуждения в этой главе будет преломление и отражение света и электромагнитных волн вообще от поверхности. О законах отражения и преломления света мы говорили уже в вып. 3. Вот что мы там выяснили:
1. Угол отражения равен углу падения. Причем углы определяются, как это показано на фиг. 33.1:
Фиг. 33.1. Отражение и преломление волн на поверхности.
Направления распространения волн перпендикулярны их гребням.
qr=qi. (33.1)
2. Произведение nsinq одинаково как для падающего луча, так и для преломленного (закон Снелла):
n1sinq=n2sinqt. (33.2)
3. Интенсивность отраженного света зависит как от угла падения, так и от направления поляризации. Для вектора Е, перпендикулярного плоскости падения, коэффициент отражения R┴ равен
Для вектора Е, параллельного плоскости падения, коэффициент отражения R║ равен
4. Для перпендикулярно падающего луча (разумеется, при любой поляризации!)
(Мы использовали индекс i для обозначения величин в падающем луче, t — в преломленном, а r — в отраженном.)
Наши прежние рассуждения практически достаточно полны для обычной работы, но мы собираемся применить здесь другой способ. Вы хотите знать почему? Причина заключается в том, что раньше мы считали показатель преломления вещественным (т. е. что никакого поглощения в материале не происходит). Однако есть и другая причина: вам следует уметь обращаться с волнами на поверхности с точки зрения уравнений Максвелла. Ответы, конечно, получатся одинаковые, но теперь уже путем непосредственного решения волновой задачи, а не с помощью правдоподобных рассуждений.
Я хочу подчеркнуть, что амплитуда отраженной от поверхности волны не определяется такими свойствами материала, как показатель преломления. Она зависит от чисто «поверхностных свойств», которые, строго говоря, определяются тем, как обработана поверхность. Тонкий слой посторонней примеси на границе между двумя материалами с показателями n1 и n2 обычно изменяет отражение. (Имеются всяческие виды интерференции, примером которой могут служить разноцветные масляные пленки на воде. Подбором толщины можно свести амплитуду отражения данной частоты к нулю. Именно так и делаются просветленные линзы.) Формулы, которые мы получим, будут верны, только когда показатель преломления резко изменится на расстояниях, малых по сравнению с длиной волны. Длина волны света, например, составляет около 5000 Е, так, что под «гладкой» поверхностью мы понимаем поверхность, на которой условия изменяются всего на протяжении нескольких атомов (или на расстоянии нескольких ангстрем). Так что для света наши формулы будут работать только на хорошо отполированной поверхности. Вообще же если показатель преломления постепенно меняется на расстоянии нескольких длин волн, то отражение будет незначительным.
§ 2. Волны в плотных материалах
Прежде всего я напомню вам об удобном способе описания синусоидальных плоских волн, которым мы пользовались в гл. 36 (вып. 3). Любая компонента поля в волне (возьмем, например, Е) может быть записана в форме
E=E0ei(wt-k·r), (33.6)
где Е — амплитуда поля в точке г (относительно начала координат) в момент t. Вектор k указывает направление распространения волны, а его величина |k|=k=2pl равна волновому числу. Фазовая скорость волны vфаз=w/k для света в материале с показателем n будет равна c/n, поэтому
k=wn/c. (33.7)
Предположим, что вектор k направлен по оси z; тогда k·r будет просто хорошо знакомым нам kz. Для вектора k в любом другом направлении z следует заменить на rk — расстояние от начала в направлении вектора k, т. е. kz мы должны заменить на krk, что как раз равно k·r (фиг. 33.2).
Фиг. 33.2. Фаза волны в точке Р, распространяющейся в направлении k, равна (wt-k·r).
Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.
Разумеется, при этом мы должны помнить, что
k·r=kxx+kyy+k:zz,
где kx, kyи kz — компоненты вектора k по трем осям. Мы уже отмечали однажды, что на самом деле величины (w, kx, ky, kz) образуют четырехвектор и что его скалярное произведение на (t, x, у, z) является инвариантом. Таким образом, фаза волны есть инвариант и формулу (33.6) можно записать в виде
Однако сейчас нам такие хитрости не понадобятся.
Для синусоидального поля Е, подобного выражению (33.6), производная dE/дt — это то же самое, что и iwE, a дЕ/дх — то же, что и ikxE, и аналогично для остальных компонент. Вы видите, чем удобна форма (33.6): когда мы работаем с дифференциальными уравнениями, то дифференцирование заменяется простым умножением. Другое полезное качество состоит в том, что операция С=(д/дx), (д/ду), (д/дz) заменяется тремя умножениями (-ikx,-iky , -ikz). Но эти три множителя преобразуются как компоненты вектора k, так что оператор С заменяется умножением на
Правило остается справедливым для операции С в любой комбинации, будь то градиент, дивергенция или ротор. Например, z-компонента СXЕ равна
Если и Еуи Ехизменяются как e-ik·r, то мы получаем
-ikxEy+ikyEx,
что представляет, как вы видите, z-компоненту —ikXЕ.
Таким образом, мы получили очень полезный общий закон, что в любом случае, когда вам нужно взять градиент от вектора, который изменяется, как волна в трехмерном пространстве (а они в физике играют важную роль), эту операцию вы можете проделать быстро и почти без всяких раздумий, если вспомните, что оператор С эквивалентен умножению на —ik.
Например, уравнение Фарадея
СXЕ=дB/дt
превращается для волны в
— ikXЕ=-iwB. Оно говорит, что
В=kXE/w. (33.9)
Это соответствует результату, найденному ранее для волн в пустом пространстве, т. е. что вектор В в волне направлен под прямым углом к вектору Е и направлению распространения волны. (В пустом пространстве w/k=с.) Знак в уравнении (33.9) вы можете проверить, исходя из того, что k является направлением вектора Пойнтинга S=e0c2(EXВ).
Если вы примените то же самое правило к другим уравнениям Максвелла, то снова получите результаты последней главы, в частности
Но раз уже это известно нам, давайте не будем проделывать все сначала.
Если вы хотите поразвлечься, можете попытаться решить такую устрашающую задачу (в 1890 г. она предлагалась студентам на выпускных экзаменах): решите уравнения Максвелла для плоской волны в анизотропном кристалле, т. е. когда поляризация Р связана с электрическим полем Е через тензор поляризуемости. Конечно, в качестве ваших осей вы выберете главные оси тензора, так что связи при этом упростятся (тогда Рх=aaЕх, Ру=abЕу, a Pz=acEz), но направление волны и ее поляризация пусть останутся произвольными. Вы должны найти соотношение между Е и В и определить, как изменяется k с направлением распространения волны и ее поляризацией. После этого вам будет понятна оптика анизотропного кристалла. Лучше начать с более легкого случая дважды лучепреломляющего кристалла, подобного турмалину, для которого два коэффициента поляризуемости равны между собой (например, ab=ac), и попытаться понять, почему, когда мы смотрим через такой кристалл, мы видим два изображения. Если это вам удастся, тогда испытайте свои силы на более трудном случае, когда все три а различны. После этого вам уже будет ясен уровень ваших знаний — знаете ли вы столько же, сколько студент, заканчивавший университет в 1890 г. Но мы с вами в этой главе будем рассматривать только изотропные вещества.
Из опыта вам известно, что когда на границу раздела двух материалов, скажем воздуха и стекла или воды и бензина, попадает плоская волна, то возникают как отраженная, так и преломленная волны.
Предположим, что, кроме этого факта, нам больше ничего неизвестно, и посмотрим, что можно из него вывести. Выберем наши оси так, чтобы плоскость yz совпадала с поверхностью раздела, а плоскость ху была перпендикулярна фронту волны (фиг. 33.3).
Фиг. 33.3. Векторы, распространения k, k' и k" для падающей, отраженной и преломленной волн.
Электрический вектор в падающей волне может быть записан в виде
Поскольку вектор k перпендикулярен оси z, то
k·r=kxx+kyy. (33.12) Отраженную волну мы запишем как
так что ее частота равна w', волновое число k', а амплитуда Е'0. (Мы, конечно, знаем, что частота и величина вектора k в отраженной волне те же, что и в падающей волне, но не хотим предполагать даже это. Пусть это все получится само собой из математического аппарата.) Наконец, запишем преломленную волну:
Вы знаете, что одно из уравнений Максвелла дает соотношение (33.9), так что для каждой из волн
Кроме того, если показатели преломления двух сред мы обозначим через n1и n2, то из уравнения (33.10) получится
Поскольку отраженная волна находится в том же материале, то
в то время как для преломленной волны
§ 3. Граничные условия
Все что мы делали до сих пор, было описанием трех волн; теперь нам предстоит выразить параметры отраженной и преломленной волн через параметры падающей. Как это сделать?
Три описанные нами волны удовлетворяют уравнениям Максвелла в однородном материале, но, кроме того, уравнения Максвелла должны удовлетворяться и на границе между двумя материалами. Так что нам нужно сейчас посмотреть — что же происходит на самой границе. Мы найдем, что уравнения Максвелла требуют, чтобы три волны определенным образом согласовывались друг с другом.
Вот один из примеров того, что мы имеем в виду. Составляющая по оси у электрического поля Е должна быть одинакова по обеим сторонам границы. Это требуется законом Фарадея:
СXE=дB/дt, (33.19)
в чем нетрудно убедиться. Рассмотрим для этого маленькую петлю Г, которая с обеих сторон охватывает границу (фиг. 33.4).
Фиг. 33.4. Граничное условие Ey2=Ey1, полученное из равенства
Согласно уравнению (33.19), криволинейный интеграл от Е по петле Г равен скорости изменения потока В через эту петлю:
Вообразите теперь, что прямоугольник очень узок, так что он замыкается в бесконечно малой области. Если при этом поле В остается конечным (нет никаких причин ему быть бесконечным!), то поток через эту область будет равен нулю. Таким образом, контурный интеграл от Е должен быть нулем. Если y-компоненты поля на двух сторонах границы равны Еy1и Еy2, а длина прямоугольника равна l, то мы получаем
Ey1l-Ey2l=0
или
Еу1=Еу2, (33.20)
как мы и ожидали. Это условие дает нам одно соотношение между полями в трех волнах.
Процедура нахождения следствий уравнений Максвелла на границе называется «определением граничных условий». Обычно она заключается в нахождении стольких уравнений типа (33.20), сколько возможно, и выполняется она с помощью рассмотрении маленьких прямоугольников, подобных Г на фиг. 33.4, или маленьких гауссовых поверхностей, охватывающих границу с двух сторон. Хотя это совершенно правильный способ рассуждений, он создает впечатление, что в различных физических задачах с границами нужно обращаться по-разному.
Как, например, в задаче о тепловом потоке через поверхность определить температуру на обеих прилежащих к ней сторонах? Конечно, вы вправе утверждать, что тепло, притекающее к границе с одной стороны, должно быть равно теплу, утекающему от нее с другой. Обычно это возможно и, вообще говоря, очень полезно находить граничные условия из такого рода физических рассуждений. Однако могут встретиться случаи, когда при работе над какой-то проблемой вам известны лишь уравнения и вы не можете непосредственно увидеть, какие же физические аргументы можно использовать. Так что, хотя в данный момент мы заинтересованы только в электромагнитных явлениях, где можно привести физические аргументы, я хочу научить вас методу, который можно применить в любой задаче: общему методу нахождения непосредственно из дифференциальных уравнений того, что происходит на границе.
Начнем с выписывания всех уравнений Максвелла для диэлектрика, но на этот раз скрупулезно выписывая все компоненты:
Эти уравнения должны быть справедливы как в области 1 (слева от границы), так и в области 2 (справа от нее). Мы уже выписывали решения в областях 1 и 2. Они должны удовлетворяться и на самой границе, которую мы можем назвать областью 3. Хотя обычно мы считаем границу чем-то абсолютно резким, на самом деле таких границ не бывает. Физические свойства, правда, изменяются очень быстро, но все же не бесконечно быстро. Во всяком случае, мы можем считать, что между областями 1 и 2 изменение показателя преломления хотя и очень быстрое, но непрерывное. Это небольшое расстояние, на котором оно происходит, мы можем назвать областью 3. Подобный же переход в области 3 будут претерпевать и другие характеристики поля, такие, как Рхили Еyи т. п. Однако дифференциальные уравнения должны удовлетворяться; именно следуя за дифференциальными уравнениями в этой области, мы придем к необходимым «граничным условиям».
Предположим, например, что у нас есть граница между вакуумом (область 1) и стеклом (область 2). В вакууме нечему поляризоваться, так что P1=0. А поляризация в стекле пусть равна Р2. Между вакуумом и стеклом существует гладкий, но быстрый переход. Если мы проследим за какой-то компонентой Р, скажем Рх, то она может изменяться так, как это показано на фиг. 33.5, а.
Фиг. 33.5. Поля в переходной области 3 между двумя различными материалами в областях 1 и 2.
Предположим теперь, что мы взяли первое из наших уравнений — уравнение (33.21). В него входит производная от компонент Р по переменным х, у и z. Производные по у и r не очень интересны — в этих направлениях не происходит ничего замечательного. Но производная от Рхпо х в области 3 из-за быстрого изменения Рхбудет громадна. Производная дРх/дх, как показано на фиг. 33.5,б, имеет на границе очень резкий пик. Если вы представите, что граница сжимается до еще более тонкой области, пик вырастет еще больше. Если для интересующих нас волн граница действительно резкая, то величина дP/дx в области 3 будет больше, много больше любого вклада, который может получиться из-за изменения Рв стороне от границы, так что мы пренебрегаем любыми другими изменениями, за исключением происходящих на границе.
Но как теперь можно удовлетворить уравнению (33.21), если с правой стороны у нас возвышается огромный пик? Только если существует равный ему громадный пик с другой стороны. Что-то и с левой стороны должно быть большим. Единственная возможность — это дЕх/дх, поскольку изменения в направлениях у и z в тех волнах, о которых мы только что упомянули, дают лишь малый эффект. Таким образом, -e0(дЕх/дх) должно быть, как это показано на фиг. 33.5,в, точной копией дP/дx. Получается
Если это уравнение проинтегрировать по х по всей области 3, то мы придем к заключению, что
e0(Еx2-Еx1)=-(Рx2-Рx1). (33.25)
Другими словами, скачок e0Ехпри переходе от области 1 к области 2 должен быть равен скачку —Рх.
Уравнение (33.25) можно переписать в виде
e0Ex2+Рx2=e0Ex1+Рx1; (33.26)
оно гласит, что величина (e0Ex+Рx) имеет равные значения как в области 2, так и в области 1. В таких случаях люди говорят, что величина (e0Еx+Рх) непрерывна на границе. Таким образом, мы получили одно из наших граничных условий.
Хотя в качестве иллюстрации мы взяли случай, когда значение Р1 равно нулю, ибо в области 1 у нас был вакуум, ясно, что те же аргументы приложимы для любого материала в этих двух областях, так что уравнение (33.26) верно в общем случае. Давайте перейдем к остальным уравнениям Максвелла и посмотрим, что скажет нам каждое из них. Следующим мы возьмем уравнение (33.22а). У него нет производной по х, так что оно ничего нам не говорит. (Вспомните, что на границе сами поля не особенно велики. Только их производные по х могут стать столь огромными, что будут доминировать в уравнении.) Взглянем теперь на уравнение (33.22.б). Смотрите! Именно здесь у нас есть производная по х! С левой стороны имеется дEz/дx. Предположим, что эта производная громадна. Но минуточку терпения! С правой стороны нет ничего, способного потягаться с ней, поэтому Еz не может иметь скачка при переходе из области 1 к области 2. [Если бы это было так, то с левой стороны уравнения (33.22а) мы бы получили скачок, а с правой — его не было бы, и уравнение оказалось бы неверным.] Итак, мы получили новое условие:
Eя2=Eя1. (33.27)
После тех же самых рассуждений уравнение (33.22в) дает
Ey2=Ey1. (33.28)
Последний результат в точности совпадает с полученным с помощью контурного интеграла условием (33.20).
Перейдем к уравнению (33.23). Единственное, что может дать пик,— это дВх/дх. Но справа опять нет ничего, способного противостоять ему; в результате мы заключаем, что
Bx2=Bx1. (33.29)
И, наконец, последнее из уравнений Максвелла! Уравнение (33.24а) ничего не дает, ибо там нет производных по х. В уравнении (33.236) — одна производная: — с2(дВz/дх), но ей снова нечего противопоставить с другой стороны равенства, поэтому мы получаем
Bz1=Bz2. (33.30)
Совершенно аналогично второе уравнение, которое дает
By1=By2. (33.31)
Итак, последние три условия говорят нам, что В2=В1.
Хочу здесь подчеркнуть, что такой результат получен только потому, что по обеим сторонам границы мы взяли немагнитный материал, вернее, потому, что магнитным эффектом этих материалов мы можем пренебречь. Обычно это вполне допустимо для большинства материалов, за исключением ферромагнетиков. (Магнитные свойства материалов мы будем рассматривать в последующих главах.).
Наша программа привела нас к шести соотношениям между полями в областях 1 и 2. Все они выписаны в табл. 33.1. Их можно использовать для согласования волн в двух областях.
Таблица 33.1 · граничные условия на поверхности ДИЭЛЕКТРИКА
(Поверхность расположена в плоскости yz.)
Однако я хочу отметить, что идея, которую мы только что использовали, будет работать в любой физической ситуации, где у вас есть дифференциальные уравнения и требуется найти решение в области, пересекаемой резкой границей, по обе стороны которой некоторые из физических свойств различны. Для наших теперешних целей было бы легче получить те же самые уравнения с помощью рассуждений о потоках и циркуляциях на границе. (Проверьте, можно ли подобным путем получить те же самые результаты.) Однако теперь вы знаете метод, который будет хорош, даже когда вы попали в затруднительное положение и не видите простых физических соображений относительно того, что происходит на границе. Вы можете просто воспользоваться дифференциальными уравнениями.
§ 4. Отраженная и преломленная волны
Теперь мы готовы применить наши граничные условия к волнам, перечисленным в § 2, где мы получили:
Нами получены еще кое-какие сведения: вектор Е перпендикулярен для каждой волны вектору распространения k.
Полученный результат будет зависеть от направления вектора Е («поляризации») в падающей волне. Анализ сильно упростится, если мы рассмотрим отдельно случай, когда вектор Е параллелен «плоскости падения» (т. е. плоскости ху), и случай, когда он перпендикулярен к ней. Волна с любой другой поляризацией будет просто линейной комбинацией этих волн. Другими словами, отраженные и преломленные интенсивности для различных поляризаций будут разными и легче всего отобрать два простейших случая и отдельно рассмотреть их.
Я подробно проанализирую случай падающей волны, перпендикулярной к плоскости падения, а потом просто опишу вам, что получается в других случаях. Я немного жульничаю, рассматривая простейший пример, однако в обоих случаях принцип один и тот же. Итак, мы считаем, что вектор Еi имеет только z-компоненту, а поскольку все векторы Е смотрят в одном и том же направлении, векторный значок можно опустить.
Оба материала изотропны, поэтому вынужденные колебания зарядов в материале будут происходить в направлении оси z и у полей Е в преломленной и отраженной волнах тоже будет только одна z-компонента. Таким образом, для всех волн Ех и Еy , Рхи Рyравны нулю. Направления векторов Е и В в этих волнах показаны на фиг. 33.6.
Фиг. 33.6. Поляризации отраженной и преломленной волн, когда поле Е в падающей волне перпендикулярно к плоскости падения.
(Здесь мы изменили нашему первоначальному намерению все получить из уравнений. Этот результат также можно было бы получить из граничных условий, однако, используя физические аргументы, мы избежали больших алгебраических выкладок. Когда у вас будет свободное время, посмотрите, можно ли его действительно вывести из уравнений. Он, разумеется, согласуется с уравнениями; просто мы не доказали, что отсутствуют другие возможности.)
Теперь наши граничные условия [уравнения (33.26) — (33.31)] должны дать соотношения между компонентами Е и В в областях 1 и 2. В области 2 у нас есть только одна преломленная волна, а вот в области 1 — их две. Какую же из них нам взять? Поля в области 1 будут, разумеется, суперпозицией полей падающей и отраженной волн. (Поскольку каждое удовлетворяет уравнениям Максвелла, то им удовлетворяет и сумма.) Поэтому, когда мы используем граничные условия, нужно помнить, что
E1=Ei+Er, E2=Et
я аналогично для В.
Для поляризаций, которыми мы сейчас занимаемся, уравнения (33.26) и (33.28) не дают никакой новой информации, и только уравнение (33.27) поможет нам. Оно говорит, что на границе, т. е. при х=0:
Ei+Er=Et.
Таким образом, мы получаем уравнение
которое должно выполняться для любого t и любого у. Возьмем сначала y=0. Для этого значения уравнение (33.38) превращается в
согласно которому два осциллирующих члена равны третьему. Это может произойти, только когда частоты всех осцилляции одинаковы. (Невозможно, сложив три или какое-то другое число подобных членов с различными частотами, получить для любого момента времени в результате нуль.) Итак,
w"=w'=w, (33.39)
как это и было нам всегда известно, т. е. частоты преломленной и отраженной волн те же самые, что и падающей.
Если бы мы предположили это с самого начала, то несомненно избежали бы многих трудностей, но мне хотелось показать вам, что тот же самый результат можно получить и из уравнений. А вот когда перед вами будет стоять реальная задача, лучше всего пускать в оборот сразу все, что вы знаете. Это избавит вас от лишних хлопот.
По определению абсолютная величина k задается равенством k2=n2w2/с2, поэтому
А теперь обратимся к уравнению (33.38) для t=0. Используя снова те же рассуждения, что и прежде, но на сей раз основываясь на том, что уравнения должны быть справедливы при всех значениях у, мы получаем
k"y=k'y=ky. (33.41)
Из формулы (33.40) k'2=k2, так что
k'2x+k'2y =k2x+k2y. Комбинируя это с (33.41), находим
k'2x=k2x , или k'x=+kx. Знак плюс не имеет никакого смысла; он не дает нам никакой отраженной волны, а лишь другую падающую волну, и с самого начала мы говорили, что будем решать задачу с единственной падающей волной, так что
k'x=-kx. (33.42)
Два соотношения (33.41) и (33.42) говорят нам, что угол отражения равен углу падения, как это и ожидалось (см. фиг. 33.3). Итак, в отраженной волне
Для преломленной волны мы уже получали
Их можно решить и в результате получить
Предположим на мгновение, что n1и n2 — вещественные числа (т. е. что мнимая часть показателей очень мала). Тогда все k тоже будут вещественными и из фиг. 33.3 мы видим, что
ky/k =sinqi, ky/k"=sinqt. (33.46)
Но ввиду уравнения (33.44) мы получаем
n2sinqt=nisinqi;, (33.47)
т. е. уже известный нам закон Снелла для преломления. Если же показатель преломления не вещественный, то волновые числа оказываются комплексными и нам следует воспользоваться
(33.45). [Конечно, мы могли бы определить углы qi. и qt из
(33.46), и тогда закон Снелла (33.47) был бы верен и в общем случае. Однако при этом углы тоже стали бы комплексными числами и, следовательно, потеряли бы свою геометрическую интерпретацию как углы. Уж лучше описывать поведение волн соответствующими комплексными величинами kx или k"x..]
До сих пор мы не обнаружили ничего нового. Мы доставили себе только простенькое развлечение, выводя очевидные вещи из сложного математического механизма. А сейчас мы готовы найти амплитуды волн, которые нам еще не известны. Используя результаты для всех w и k, мы можем сократить экспоненциальный множитель в (33.38) и получить
е0+е'0=е"0. (33.48)
Но поскольку мы не знаем ни Е'0, ни Е"9, то необходимо еще одно соотношение. Нужно использовать еще одно граничное условие. Уравнения для Ехи Еyне помогут, ибо все Е имеют только одну z-компоненту. Так что мы должны воспользоваться условием на В. Попробуем взять (33.29):
Bx2 =Bx1. Согласно условиям (33.35)—(33.37),
Вспоминая, что w" =w'= w и k"y=k'y=ky, получаем
е0+е'0 =е"0.
Но это снова уравнение (33.48)! Мы напрасно потратили время и получили то, что уже давно нам известно.
Можно было бы обратиться к (33.30) Bz2=Вz1, но у вектора В отсутствует z-компонента! Осталось только одно условие — (33.31) Ву2=Ву1. Для наших трех волн
Подставляя вместо Ei,Erи Etволновые выражения при x=0 (ибо дело происходит на границе), мы получаем следующее граничное условие:
Учитывая равенство всех w и ky , снова приходим к условию kxE0 + k'xE'0=k"xE"0. (33.50)
Это дает нам уравнение для величины Е, отличное от (33.48). Получившиеся два уравнения можно решить относительно E'0 и Е"0. Вспоминая, что k’x=-kx, получаем
Вместе с (33.45) или (33.46) для k”xэти формулы дают нам все, что мы хотели узнать. Следствия полученного результата мы обсудим в следующем параграфе.
Если взять поляризованную волну с вектором Е, параллельным плоскости падения, то Е, как это видно из фиг. 33.7, будет иметь как x-, так и y-компоненту. Вся алгебра при этом будет менее хитрая, но более сложная. (Можно, правда, несколько уменьшить работу в этом случае, выражая все через магнитное поле, которое целиком направлено по оси z.)
Фиг. 33.7. Поляризации волн, когда поле Е в падающей волне параллельно плоскости падения.
При этом мы найдем
и
Давайте посмотрим, будет ли наш результат согласовываться с тем, что мы получали раньше. Выражение (33.3) мы вывели в вып. 3, когда находили отношение интенсивностей отраженной и падающей волн. Однако тогда мы рассматривали только вещественный показатель преломления. Для вещественного показателя (или вещественных k) можно записать:
kx=kcosqi=(wn1/c)cosqi,
k"x=k"cosqt=(wn2/c)cosqt.
Подставляя это в уравнение (33.51), получаем
что нисколько не похоже на уравнение (33.3). Если, однако, мы воспользуемся законом Снелла и избавимся от всех n, то сходство будет восстановлено. Подставляя n2=n1(sinqi/sinqt) и умножая числитель и знаменатель на sinqt, получаем
Обратите внимание, что в числителе и знаменателе стоят просто синусы (qi-qt) и (qi+qt), поэтому
Поскольку амплитуды E'0 и E0 измеряются в том же самом материале, интенсивности пропорциональны квадратам электрических полей и мы получаем тот же результат, что и раньше. Подобным же образом формула (33.53) тоже аналогична формуле (33.4).
Для волн, падающих перпендикулярно, qi=0 и qt=0. Формула (33.56) выглядит как 0/0, от чего нам пользы мало. Однако мы можем вернуться назад к формуле (33.55), согласно которой
Этот результат, естественно, применим для «любой» поляризации, поскольку для перпендикулярного луча нет никакой особой «плоскости падения».
§ 5. Отражение от металлов
Теперь мы можем использовать наши результаты для понимания интересного явления — отражения от металлов. Почему металлы блестят? В предыдущей главе мы видели, что показатель преломления металлов для некоторых частот имеет очень большую мнимую часть. Давайте посмотрим, какова будет интенсивность отраженной волны, когда свет падает из воздуха (с показателем n=1) на материал с n=- inI. При этом условии уравнение (33.55) дает (для нормального падения)
Для интенсивности отраженной волны нам нужны квадраты абсолютных величин Е'0и Е0:
или
Для материала с чисто мнимым показателем преломления получается стопроцентное отражение!
Металлы не отражают 100% света, но все же многие из них хорошо отражают видимый свет. Другими словами, мнимая часть их показателя очень велика. Однако мы видели, что большая мнимая часть показателя означает сильное поглощение. Итак, имеется общее правило: если какой-то материал оказывается очень хорошим поглотителем при какой-то частоте, то отражение волн от его поверхности очень велико и очень мало волн попадает внутрь. Этот эффект вы можете наблюдать на сильных красителях. Чистые кристаллы самых сильных красителей имеют «металлический» блеск. Вероятно, вы замечали, что на краях бутылки с фиолетовыми чернилами засохший краситель имеет золотистый металлический блеск, а засохшие красные чернила имеют иногда зеленоватый металлический оттенок. Красные чернила поглощают из проходящего света зеленые лучи, так что, если концентрация чернил очень велика, они будут давать сильное поверхностное отражение при частоте зеленого света.
Вы можете очень эффектно продемонстрировать это. Намажьте стеклянную пластинку красными чернилами и дайте им высохнуть. Если вы направите пучок белого света на обратную сторону пластинки (фиг. 33.8), то сможете наблюдать проходящий красный свет и отраженный зеленый свет.
Фиг. 33.8. Материал, который сильно поглощает свет с частотой w, отражает его с той же частотой.
§ 6. Полное внутреннее отражение
Если свет идет из материала, подобного стеклу, с вещественным показателем преломления n, большим единицы, в воздух с показателем n2, равным единице, то, согласно закону Снелла,
sinqt=nsinqi.
Угол qt преломленной волны становится равным 90° при угле падения qiравном некоторому «критическому углу» qc, определяемому равенством nsinqc= l. (33.59)
Что происходит при qi, большем, чем критический угол? Вы уже знаете, что здесь возникает полное внутреннее отражение. Но откуда оно все-таки берется?
Вернемся назад к уравнению (33.45), которое дает волновое число k"xдля преломленной волны. Из него получилось
Но так как ky=ksinqi, a k=wn/с, то
Если nsinqi больше единицы, то k"2х становится отрицательным, a k"x — чисто мнимым, скажем ±ik. Однако теперь вы знаете, что это значит! «Преломленная» волна при этом будет иметь вид [см. (33.34)]
т. е. с увеличением х амплитуда волны будет либо экспоненциально расти, либо падать, но сейчас, разумеется, нам нужен только отрицательный знак. При этом амплитуда волны справа от границы будет вести себя, как показано на фиг. 33.9.
Фиг. ЗЗ.9. Полное внутреннее отражение.
Обратите внимание, что k1по порядку величины равно а/с, т. е. l0 равна длине волны света в пустоте. Когда свет полностью отражается от внутренней поверхности стекло — воздух, то в воздухе возникают поля, но они не выходят за пределы расстояний, равных по порядку величины длине волны света.
Теперь нам ясно, как нужно отвечать на такой вопрос: если световая волна в стекле падает на поверхность под достаточно большим углом, то она полностью отражается; если же придвинуть к поверхности другой кусок стекла (так что «поверхность» фактически исчезает), то свет будет проходить. В какой точно момент происходит этот переход? Ведь наверняка должен существовать непрерывный переход от полного отражения к полному его отсутствию! Ответ, разумеется, состоит в том, что если прослойка воздуха настолько мала, что экспоненциальный «хвост» волны в воздухе имеет еще ощутимую величину во втором куске стекла, то он будет «трясти» электроны и порождать новую волну (фиг. 33.10).
Фиг. 33.10. Для очень маленькой щели внутреннее отражение не будет «полным», за щелью появляется прошедшая волна.
Некоторое количество света будет проходить через систему. (Конечно, наше решение неполно; нам следовало бы заново решить все уравнения для случая тонкого слоя воздуха между двумя областями стекла.)
Для обычного света этот эффект прохождения можно наблюдать, только если щель очень мала (порядка длины волны, т. е. 10-5 см), но для 3-сантиметровых волн он демонстрируется очень легко. Для таких волн экспоненциально затухающие поля распространяются на расстояние нескольких сантиметров.
Микроволновая аппаратура, с помощью которой демонстрируют этот эффект, изображена на фиг. 33.11.
Фиг. 33.11. Проникновение волн внутреннего отражения.
Волны из маленького передатчика 3-сантиметровых волн направляются на парафиновую призму, имеющую сечение в форме равнобедренного прямоугольного треугольника. Показатель преломления парафина для этих частот равен 1,50, поэтому критический угол будет 41,5°. Таким образом, волны полностью отражаются от поверхности, наклоненной под 45°, и принимаются детектором А (фиг.33.11, а). Если к первой призме плотно приложить вторую парафиновую призму (фиг. 33.11, б), то волны проходят прямо сквозь них и регистрируются детектором В. Если же между призмами оставить щель в несколько сантиметров (фиг.33.11, в), то мы получим как отраженную, так и проходящую волны. Поместив детектор В в нескольких сантиметрах от наклоненной под 45° поверхности призмы, можно увидеть и электрическое поле вблизи нее.
Глава 34 МАГНЕТИЗМ ВЕЩЕСТВА
§ 1. Диамагнетизм и парамагнетизм
§ 2. Магнитные моменты и момент количества движения
§ 3. Прецессия атомных магнитиков
§ 4. Диамагнетизм
§ 5. Теорема Лармора
§ 6. В классической физике нет ни диамагнетизма, ни парамaгнетизма
§7. Момент количества движения в квантовой механике
§ 8. Магнитная энергия атомов
Повторить: гл. 15 (вып. 6) «Векторный потенциал»
§ 1. Диамагнетизм и парамагнетизм
В этой главе я начну рассказывать о магнитных свойствах материалов. Материал, обладающий наиболее сильными магнитными свойствами, разумеется,— железо. Подобными же магнитными свойствами обладают еще такие элементы, как никель, кобальт и (при достаточно низких температурах, ниже 16° С) гадолиний и другие редкоземельные металлы, а также некоторые особые сплавы. Такой вид магнетизма называется ферромагнетизмом. Это достаточно сложное и удивительное явление, и ему мы посвятим специальную главу. Но и все обычные вещества тоже имеют некоторые магнитные свойства, хотя и не столь ярко выраженные, а много слабее — в тысячи и миллион раз меньше, чем эффекты в ферромагнитных материалах. Здесь мы собираемся описать обычный магнетизм, т. е. магнетизм неферромагнитных веществ.
Этот слабый магнетизм бывает двух сортов. Некоторые материалы притягиваются магнитным полем, другие же отталкиваются им. В отличие от электрического эффекта в веществе, который всегда приводит к притяжению диэлектриков, магнитный эффект имеет два знака. Наличие этих двух знаков легко продемонстрировать с помощью сильного электромагнита, один из полюсных наконечников которого заострен, а другой — плоский (фиг. 34.1).
Фиг. 34.1. Небольшой висмутовый цилиндр слабо отталкивается заостренным полюсом; кусочек алюминия будет притягиваться.
Магнитное поле у заостренного полюса намного сильнее, нежели у плоского. Если небольшой кусочек материала, подвешенный на длинной струне, поместить между полюсами такого магнита, то на него, вообще говоря, действует очень слабенькая сила. Действие этой силы можно обнаружить по незначительному смещению подвешенного кусочка материала при повороте магнита. Оказывается, что ферромагнитные материалы сильно притягиваются заостренным полюсом, а все остальные — очень слабо. А есть и такие, которые не притягиваются заостренным полюсом, а слабо отталкиваются.
Этот эффект легче всего наблюдать на маленьком цилиндре из висмута, который выталкивается, из области сильного поля. Вещества, которые отталкиваются, подобно висмуту, называются диамагнетиками. Висмут — один из сильнейших диамагнетиков, но даже и его магнитный эффект очень слаб. Диамагнетизм всегда очень слаб. Если между полюсами подвесить кусочек алюминия, то на него все же будет действовать слабенькая сила, но направленная в сторону заостренного полюса. Вещества, подобные алюминию, называются парамагнетиками. (В таких экспериментах при включении и выключении магнита из-за вихревых токов возникают силы, которые могут дать сильный толчок. Поэтому нужно быть очень внимательным и смотреть только на чистое перемещение после того, как подвешенный предмет успокоился.)
Сейчас я коротко опишу механизм этих двух эффектов. Прежде всего атомы многих веществ не имеют постоянных магнитных моментов, или, вернее, все магнитные моменты внутри каждого атома уравновешены так, что суммарный магнитный момент атома равен нулю. Спиновые и орбитальные моменты электронов сбалансированы так, что у каждого данного атома никакого среднего магнитного момента нет. Если при этих обстоятельствах вы включаете магнитное поле, то внутри атома по индукции генерируются слабые дополнительные токи.
В соответствии с законом Ленца эти токи действуют так, чтобы сопротивляться увеличивающемуся магнитному полю. Таким образом, наведенный магнитный момент атомов направлен противоположно магнитному полю. Это и есть механизм диамагнетизма.
Однако существуют такие вещества, атомы которых все же обладают магнитным моментом, т. е. электронные спины и орбиты которых имеют ненулевой полный циркулирующий ток. Таким образом, кроме диамагнитного эффекта (а он всегда присутствует), существует еще возможность «выстраивания» индивидуальных атомных моментов в одном направлении. Магнитные моменты в этом случае стараются выстроиться по направлению магнитного поля (точно так же, как постоянные диполи в диэлектрике выстраиваются в электрическом поле) и наведенный магнетизм стремится усилить магнитное поле. Это и есть парамагнитные вещества. Парамагнетизм, вообще говоря, довольно слаб, потому что выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стараются разрушить упорядочивание. Отсюда также следует, что парамагнетизм обычно чувствителен к температуре. (Исключение составляет парамагнетизм, обусловленный спинами электронов, ответственных за проводимость металлов. Но мы не будем обсуждать здесь это явление.) Для обычного парамагнетизма эффект тем сильнее, чем ниже температура. При низких температурах атомы выстраиваются в большей степени, поскольку разупорядочивание вследствие тепловых колебаний (соударений) будет меньше. Но, с другой стороны, диамагнетизм более или менее не зависит от температуры. У любого вещества с выстроенными магнитными моментами есть как диамагнитный, так и парамагнитный эффекты, причем парамагнитный эффект обычно доминирует.
В гл. 11 (вып. 5) мы описывали сегнетоэлектрические материалы, все электрические диполи которых выстраиваются в результате взаимного действия атомов друг на друга своими электрическими полями. Можно представить себе магнитный аналог сегнетоэлектричества, в котором все атомные моменты, действуя друг на друга, выстраивают сами себя. Если бы вы попытались вычислить, как это должно происходить, то обнаружили бы, что из-за того, что магнитные силы гораздо слабее электрических, тепловое движение должно расстраивать упорядочивание даже при столь низких температурах, как 10° К. Так что при комнатных температурах любое постоянное выстраивание магнитных моментов казалось бы невозможно.
Но, с другой стороны, именно это явление происходит в железе: там магнитные моменты все-таки выстраиваются. Между магнитными моментами различных атомов железа действуют эффективные силы, которые во много-много раз больше прямого магнитного взаимодействия. Это косвенный эффект, который можно объяснить только с помощью квантовой механики. Он примерно в десять тысяч раз сильнее прямого магнитного взаимодействия, и именно он выстраивает магнитные моменты в ферромагнитных материалах. Об этом особом взаимодействии мы будем говорить в дальнейшем.
Я попытался дать вам качественные объяснения диамагнетизма и парамагнетизма, однако хочу тут же внести поправку и сказать, что с точки зрения классической механики честным путем понять магнитные эффекты невозможно. Подобные магнитные эффекты — явления целиком квантовомеханические. Тем не менее привести некоторые «правдоподобные» классические рассуждения и дать вам представление о том, как здесь все происходит, все-таки небесполезно.
Попробуем встать на этот путь. Можно приводить разные физические аргументы и строить догадки о том, что происходит с веществом, однако все эти аргументы будут в той или иной степени «незаконными», так как в любом из магнитных явлений весьма существенную роль играет квантовая механика. С другой стороны, бывают такие системы, подобные плазме или скоплению множества свободных электронов, где электроны все же живут по законам классической механики. При таких обстоятельствах некоторые из теорем классического магнетизма будут очень полезны. Кроме того, классические рассуждения полезны еще и по историческим причинам: ведь пока люди еще не могли понять глубокий смысл и поведение магнитных материалов, они пользовались классическими аргументами. Так что классическая механика все же способна дать нам полезные сведения. И только если стремиться быть совсем честным, то надо отложить изучение магнетизма до тех пор, пока вы не пройдете квантовую механику.
А мне все-таки не хочется ждать так долго ради того, чтобы понять такую простую вещь, как диамагнетизм. Для целого ряда полуобъяснений происходящего можно ограничиться классической механикой, сознавая, однако, что наши доводы на самом деле нуждаются в квантовомеханическом подкреплении.
§ 2. Магнитные моменты и момент количества движения
Первая теорема, которую мы хотим доказать в классической механике, гласит: если электрон движется по круговой орбите (например, крутится вокруг ядра под действием центральных сил), то менаду магнитным моментом и моментом количества движения существует определенное соотношение. Обозначим через J момент количества движения, а через m — магнитный момент электрона на орбите. Величина момента количества движения равна произведению массы электрона на скорость и на радиус (фиг. 34.2). Он направлен перпендикулярно плоскости орбиты:
J=mvr. (34.1)
Фиг. 34.2. Для любой круговой орбиты магнитный момент m равен произведению q!2m на момент количества движения J.
(Хотя эта формула и нерелятивистская, но для атома она должна быть достаточно хороша, ибо у захваченного на орбиту электрона отношение v/c в общем случае равно по порядку величины е2/hc=1/137, или около 1%.)
Магнитный момент той же самой орбиты равен произведению тока на площадь (см. гл. 14, § 5, вып. 5). Ток равен положительному заряду, проходящему в единицу времени через любую точку на орбите, т. е. произведению заряда q на частоту вращения. А частота равна скорости, поделенной на периметр орбиты, так что
I=q(v/2pr). Так как площадь равна pr2, то магнитный момент будет
m=qvr/2 (34.2)
Он тоже направлен перпендикулярно плоскости орбиты. Таким образом, J и mимеют одинаковое направление:
m=(q/2m)J(орбиты). (34.3)
Их отношение не зависит ни от скорости, ни от радиуса. Для любой частицы, движущейся по круговой орбите, магнитный момент равен произведению q/2m на момент количества движения. Для электрона, заряд которого отрицателен (обозначим его через -qe),
m=-(qe/2m)J(для электрона на орбите). (34.4)
Вот что получается в классической физике, и совершенно удивительно, что то же самое справедливо и в квантовой механике. Это один из правильных выводов. Однако если развивать его дальше по пути классической физики, то вы натолкнетесь на такие места, где он даст неправильные ответы; разобраться же потом, какие результаты верны, а какие неверны, — целое дело. Уж лучше я сразу скажу, что в квантовой механике верно в общем случае. Прежде всего соотношение (34.4) остается верным для орбитального движения; однако это не единственное место, где мы встречаемся с магнетизмом. Электрон, кроме того, совершает еще вращение вокруг собственной оси (подобное вращению Земли вокруг ее оси), и в результате этого вращения у него возникает момент количества движения и магнитный момент. Но по чисто квантовомеханическим причинам (классическое объяснение этого совершенно отсутствует) отношение m к J для собственного вращения (спина) электрона в два раза больше, чем для орбитального движения крутящегося электрона:
m=-(qe/m)J (спин электрона). (34.5)
В любом атоме, вообще говоря, имеется несколько электронов, и его полный момент количества движения и полный магнитный момент представляют некоторую комбинацию спиновых и орбитальных моментов. И без каких-либо на то классических оснований в квантовой механике (для изолированного атома) направление магнитного момента всегда противоположно направлению момента количества движения. Отношение их не обязательно должно быть -qe/m или -qe/2m; оно расположено где-то между ними, ибо здесь «перемешиваются» вклады от спинов и орбит. Можно записать
'm=-g(qe/2m)J (34.6)
где множитель g характеризует состояние атома. Для чисто орбитальных моментов он равен единице, для чисто спиновых равен 2, а для сложной системы, подобной атому, он расположен где-то между ними. Конечно, пользы от этой формулы не очень много. Она только говорит, что магнитный момент параллелен моменту количества движения, но может иметь любую величину. Тем не менее форма уравнения (34.6) все же удобна, ибо величина g, называемая «фактором Ланде», есть безразмерная постоянная порядка единицы. Одна из задач квантовой механики — предсказание фактора g для разных атомных состояний. Быть может, вам интересно знать, что происходит в ядрах атомов. Протоны и нейтроны в ядре движутся по своего рода орбитам и в то же время, подобно электронам, имеют спин. Магнитный момент снова параллелен моменту количества движения. Только теперь порядок величины отношения магнитного момента к моменту количества движения для каждой из этих частиц будет таким, как можно было ожидать для протона, движущегося по кругу; при этом массу m в уравнении (34.3) нужно взять равной массе протона.
Поэтому для ядер обычно пишут (в скобках положительная величина)
m=g(qe/2mp)J (34.7)
где mp— масса протона, а постоянная g, называемая ядерным g-фактором,— число порядка единицы, которое должно определяться отдельно для каждого сорта ядер.
Другое важное отличие в случае ядер состоит в том, что g-фактор спинового магнитного момента протона не равен 2, как у электрона. Для протона g=2·(2,79). Крайне удивительно, что спиновый магнитный момент есть и у нейтрона и отношение этого магнитного момента к моменту количества движения равно 2·(-1,93). Другими словами, нейтрон в магнитном смысле не будет в точности «нейтральным». Он напоминает маленький магнитик и имеет такой же магнитный момент, как и вращающийся отрицательный заряд.
§ 3. Прецессия атомных магнитиков
Одно из следствий пропорциональности магнитного момента моменту количества движения заключается в том, что атомные магнитики, помещенные в магнитное поле, будут прецессироватъ. Обсудим это сначала с точки зрения классической физики. Пусть у нас имеется магнитный момент m, свободно висящий в однородном магнитном поле. Он испытывает действие момента силы t, равного mXB, пытающегося повернуть его в том же направлении, что и поле. Но атомный магнит — ведь это гироскоп, у него есть момент количества движения J. Поэтому момент силы от магнитного поля не вызовет поворота в направлении поля. Вместо этого магнит, как мы видели, когда говорили о гироскопе в гл. 20 (вып. 2), начнет првцессироватъ. Момент количества движения, а вместе с ним и магнитный момент прецессируют вокруг оси, параллельной магнитному полю. Скорость прецессии можно найти тем же методом, что и в гл. 20 (вып. 2).
Предположим, что за малый промежуток времени Dt момент количества движения меняется от J до J' (фиг. 34.3), оставаясь при этом всегда под одним и тем же углом q к направлению магнитного поля В.
Фиг. 34.3. Объект в моментом количества движения J и параллельным ему магнитным моментом m в магнитном поле В прецессирует с угловой скоростью wp,.
Обозначим через wp угловую скорость прецессии, так что за промежуток времени Dt угол прецессии будет равен wpDt. Из геометрии рисунка мы видим, что изменение момента количества движения за время Dt равно
DJ=(Jsinq)(wpDt), а скорость изменения момента количества движения
dJ/dt=wpJsinq (34.8)
что должно равняться моменту силы
t=mBsinq. (34.9)
Угловая скорость прецессии будет равна
Подставляя из уравнения (34.6) отношение m/J, мы видим, что для атомной системы
wp=g(qe/2m)B (34.11)
т. е. частота прецессии пропорциональна В. Полезно запомнить, что для атома (или электрона)
а для ядра
(Формулы для атомов и ядер различны только благодаря различным соглашениям относительно g в этих двух случаях.) Итак, в соответствии с классической теорией электронные орбиты и спины в атоме должны прецессировать в магнитном поле. Верно ли это и в квантовой механике? В сущности это верно, однако смысл «прецессии» здесь совсем иной. В квантовой механике нельзя говорить о направлении момента количества движения в том же смысле, как это делается классически; тем не менее аналогия здесь очень близкая, настолько близкая, что мы продолжаем пользоваться термином «прецессия». Мы еще обсудим это позднее, когда будем говорить о квантовомеханической точке зрения.
§ 4. Диамагнетизм
Рассмотрим теперь с классической точки зрения диамагнетизм. К этому можно подойти несколькими путями, но один из лучших такой. Предположим, что по соседству с атомом медленно включается магнитное поле. При изменении магнитного поля благодаря магнитной индукции будет генерироваться электрическое поле. По закону Фарадея контурный интеграл от Е по замкнутому контуру равен скорости изменения магнитного потока через этот контур. Предположим, что в качестве контура Г мы выбрали окружность радиусом r, центр которой совпадает с центром атома (фиг. 34.4).
Фиг. 34.4. Индуцированные электрические силы, действующие на электроны в атоме.
Среднее тангенциальное электрическое поле Е на этом контуре определяется выражением
т. е. возникает циркулирующее электрическое поле, напряженность которого равна
Индуцированное электрическое поле, действуя на атомный электрон, создает момент силы, равный -qeEr, который должен быть равен скорости изменения момента количества движения dJ/dt:
Интегрируя теперь по времени, начиная с нулевого поля, мы находим, что изменение момента количества движения из-за включения поля будет равно
Это и есть тот дополнительный момент количества движения, который сообщается электрону за время включения поля.
Такой добавочный момент количества движения приводит к добавочному магнитному моменту, который благодаря тому, что это орбитальное движение, равен просто произведению -qe/2m на момент количества движения. Наведенный диамагнитный момент
Знак минус (как можно убедиться непосредственно из закона Ленца) означает, что направление добавочного момента противоположно магнитному полю.
Мне бы хотелось написать выражение (34.16) несколько по-иному. Появившаяся у нас величина r2 представляет собой расстояние от оси, проходящей через атом и параллельной полю В, так что если поле В направлено по оси z, то оно равно x2+y2. Если мы рассмотрим сферически симметричные атомы (или усредним по атомам, естественные оси которых могут располагаться во всех направлениях), то среднее от z2+y2 равно 2/3 среднего квадрата истинного радиального расстояния от центра атома. Поэтому уравнение (34.16) обычно более удобно записывать в виде
Во всяком случае, мы нашли, что индуцированный атомный момент пропорционален магнитному полю В и противоположен ему по направлению. Это и есть диамагнетизм вещества. Именно этот магнитный эффект ответствен за малые силы, действующие на кусочек висмута в неоднородном магнитном поле.(Вы можете определить величину этой силы, воспользовавшись выражением для энергии наведенного момента в поле и результатами измерений изменения энергии при движении образца в область сильного поля или из нее.)
Но перед нами все еще стоит такая проблема: чему равен средний квадратичный радиус <r2>ср? Классическая механика не может дать нам ответа. Мы должны вернуться назад и, вооружившись квантовой механикой, начать все снова. Мы не можем знать, где именно находится электрон в атоме, а знаем лишь, что имеется вероятность его обнаружить в некотором месте. Если мы будем интерпретировать <r2>ср как среднее значение квадрата расстояния от центра для данной вероятности распределения, то диамагнитный момент, даваемый квантовой механикой, определяется тем же самым выражением (34.17). Оно, разумеется, дает нам момент одного электрона. Полный же момент будет суммой по всем электронам в атоме. Удивительно, что и классические рассуждения и квантовая механика дают тот же ответ, хотя, как мы увидим дальше, «классические» рассуждения, которые приводят к (34.17), на самом деле несостоятельны в рамках самой классической механики.
Такой же диамагнитный эффект будет наблюдаться даже у атомов с постоянным магнитным моментом. При этом система тоже будет прецессировать в магнитном поле. Во время прецессии атома в целом он набирает небольшую дополнительную угловую скорость, а подобное медленное вращение приводит к маленькому току, который дает поправку к магнитному моменту. Это тот же диамагнитный эффект, но поданный по-другому. Однако на самом деле, когда мы говорим о парамагнетизме, нам не нужно заботиться об этой добавке. Если мы сначала подсчитали диамагнитный эффект, как это было сделано здесь, нас не должен беспокоить небольшой дополнительный ток, происходящий из-за прецессии. Он уже включен нами в диамагнитный член.
§ 5. Теорема Лармора
Теперь уже из наших результатов можно сделать кое-какие заключения. Прежде всего в классической теории момент m всегда пропорционален J, причем для каждого вида атомов со своей константой пропорциональности. В классической теории у электрона нет никакого спина и константа пропорциональности всегда равна -qe/2m, иначе говоря, мы должны в (34.6) положить g=1. Отношение m к Jне зависело от внутреннего движения электронов. Таким образом, в соответствии с классической теорией все системы электронов должны были прецессировать с одной и той же угловой скоростью. (В квантовой механике это неверно.) Этот результат связан с одной теоремой классической механики, которую мне бы хотелось сейчас доказать. Предположим, что имеется группа электронов, которые удерживаются вместе притяжением к центральной точке, подобно электронам, притягиваемым ядром. Эти электроны будут также взаимодействовать друг с другом, и движение их, вообще говоря, довольно сложно. Пусть вы нашли их движение в отсутствие магнитного поля и хотите знать, каково будет движение в слабом магнитном поле. Теорема утверждает, что движение в слабом магнитном поле всегда будет таким же, как и движение без поля с добавочным вращением относительно оси поля с угловой скоростью wL=qeB/2m. (Это то же самое, что и wp при g=1.) Разумеется, возможных движений может быть много. Все дело в том, что каждому движению без магнитного поля соответствует движение в поле, которое состоит из первоначального движения плюс равномерное вращение. Это и есть теорема Лармора, а частота wL называется ларморовой частотой.
Мне бы хотелось показать вам, как можно доказать эту теорему, но детали доказательства я предоставлю вам самим.
Возьмем сначала электрон в центральном силовом поле. На него просто действует направленная к центру сила F(r). Если теперь включить однородное магнитное поле, то появится дополнительная сила qvXВ, так что полная сила будет равна
F(r)+qvXB. (34.18)
Посмотрим теперь на те же самые электроны из системы координат, вращающейся с угловой скоростью w относительно оси, проходящей через центр силы и параллельной полю В. Она уже не будет инерциальной системой, а посему нам нужно добавить надлежащие псевдосилы: центробежные силы и силы Кориолиса, о которых мы говорили в гл. 19 (вып. 2). Там мы обнаружили, что в системе отсчета, вращающейся с угловой скоростью w, действуют кажущиеся тангенциальные силы, пропорциональные vr— радиальной компоненте скорости:
Ft = -2mwvr. (34.19) Кроме того, там действует кажущаяся радиальная сила
Fr=mw2r+2mwvt, (34.20)
где vt — тангенциальная компонента скорости, измеряемая во вращающейся системе отсчета. (Радиальная компонента vrодна и та же как для вращающихся, так и для инерциальных систем.)
Теперь для достаточно малых угловых скоростей (т. е. когда (wr<<vt) первым (центробежным) слагаемым в уравнении (34.20) можно пренебречь по сравнению со вторым (кориолисовым). После этого уравнения (34.19) и (34.20) можно записать вместе как
F=-(2mwXv). (34.21)
Если же теперь скомбинировать вращение и магнитное поле, то мы должны к силе (34.18) добавить силу (34.21). Полная сила получится такой:
F(r)+qvXB+2mvXw. (34.22)
[В последнем слагаемом по сравнению с (34.21) мы переставили сомножители в векторном произведении и изменили знак.] Взглянув теперь на полученный результат, мы видим, что если
2mw=-qB,
то последние два члена сократятся, и единственной силой в движущейся системе будет сила F(r). Движение электрона будет таким же, как и в отсутствие магнитного поля, но добавится, разумеется, вращение. Мы доказали теорему Лармора для одного электрона. Поскольку при доказательстве мы предполагали со малым, то это означает, что теорема верна только для слабых магнитных полей. Единственно, что я прошу вас рассмотреть самостоятельно,— это случай многих электронов, взаимодействующих друг с другом в том же самом центральном поле. Докажите теорему для такого случая. Таким образом, каким бы сложным ни был атом, если его поле центральное,— теорема будет верна. Но это уже конец классической механики, ибо то, что система прецессирует таким образом, неверно. Частота прецессии wp в уравнении (34.11) только тогда равна wL., когда g=1.
§ 6. В классической физике пет ни диамагнетизма, ни парамагнетизма
Сейчас я хочу показать вам, что в соответствии с классической механикой не получается ни диамагнетизма, ни парамагнетизма. На первый взгляд это звучит дико — ведь только что мы доказали, что там есть и диамагнетизм, и парамагнетизм, и прецессирующие орбиты и т. п., а теперь собираемся доказывать, что все это ложь. Увы, так оно и есть! Я собираюсь доказать, что если достаточно долго следовать за классической механикой, то никаких магнитных эффектов не получится: они исчезнут все до единого. Если вы начнете с классических рассуждений, но вовремя остановитесь, то получите желаемый результат. И только законные и последовательные доказательства показывают, что никаких магнитных эффектов нет.
Вот одно из следствий классической механики. Если у вас есть какая-то заключенная в ящик система, скажем электронный или протонный газ или что-то в этом роде, не способная вращаться как нечто целое, то никакого магнитного эффекта возникнуть не может. Магнитный эффект может получиться лишь при наличии изолированной системы, удерживаемой от разлетания своими собственными силами подобно звезде, которая, будучи помещена в магнитное поле, может начать вращаться. Но если ваш кусок материала удерживается в одном положении и не может начать крутиться, то никакого магнитного эффекта не будет. Более точно мы понимаем под этим следующее: мы предполагаем, что при данной температуре существует только одно состояние теплового равновесия. Тогда теорема утверждает, что если вы включите магнитное поле и выждете, пока система не придет в тепловое равновесие, то никакого наведенного магнитного эффекта не появится — ни диамагнетизма, ни парамагнетизма. Доказательство: Согласно статистической механике, вероятность того, что система имеет заданное состояние движения, пропорциональна e-U/kT, где U — энергия этого движения. Но что такое энергия движения? Для частиц в постоянном магнитном поле она равна обычной потенциальной энергии плюс mv2/2 без какой бы то ни было добавки от магнитного поля. [Вы знаете, что сила, действующая со стороны электромагнитного поля, равна q(E+vXB), а мощность F·v будет просто qE·v, т. е. никакого влияния магнитного поля нет и в помине.] Итак, энергия системы независимо от того, находится ли она в магнитном поле или нет, всегда будет суммой только кинетической и потенциальной энергий. А поскольку вероятность любого движения зависит только от энергии, т. е. от скорости и положения, то для нее безразлично, включено ли магнитное поле или нет. Следовательно, на тепловое равновесие магнитное поле не оказывает никакого влияния. Если мы возьмем сначала одну систему, заключенную в первом ящике, а затем другую — во втором ящике, но на этот раз в магнитном поле, то вероятность какого-то определенного значения скорости в некоторой точке в первом ящике будет той же самой, что и во втором. Если в первом ящике отсутствуют средние циркулирующие токи (которых не должно быть, если система находится в равновесии со стационарными стенками), то там нет никакого магнитного момента. А поскольку все движения во втором ящике такие же, как и в первом, у него тоже нет никакого магнитного момента. Следовательно, если температура поддерживается постоянной, то после включения поля и восстановления теплового равновесия никакого наведенного магнитного момента в соответствии с классической механикой быть не должно. Удовлетворительное объяснение магнитных явлений можно получить только в квантовой механике.
К сожалению, я не уверен в вашем полном понимании квантовой механики, поэтому обсуждать эти вопросы здесь вряд ли уместно. Но, с другой стороны, не всегда следует начинать изучение чего-то с выписывания правил и применения их в различных обстоятельствах. Почти каждый предмет, с которым мы имели дело в нашем курсе, начинался по-разному. Для электродинамики, например, мы на первой же странице выписали уравнения Максвелла, а уж затем выводили из них все следствия. Это один способ. Однако сейчас я не собираюсь начать новую «первую страницу» выписыванием уравнений квантовой механики и получением следствий из них. Я просто расскажу вам о некоторых результатах квантовой механики до того еще, как вы узнали, откуда они берутся. Итак, за дело.
§ 7. Момент количества движения в квантовой механике
Я уже приводил вам соотношение между магнитным моментом и моментом количества движения. Очень хорошо. Но что означает магнитный момент и момент количества движения в Квантовой механике? Оказывается, что для полной уверенности в том, что они означают в квантовой механике, лучше определять вещи, подобные магнитному моменту, через другие понятия, такие, как энергия. Магнитный момент легко определить через энергию, ибо энергия магнитного момента в магнитном поле равна в классической теории—m·В. Следовательно, в квантовой механике необходимо принять следующее определение. Если мы вычисляем энергию системы в магнитном поле и видим, что она пропорциональна напряженности (для малых полей), то коэффициент пропорциональности мы будем называть магнитным моментом в направлении поля. (Нам сейчас в нашей работе не требуется особой элегантности и мы можем продолжать думать о магнитном моменте в обычном, т. е. в каком-то отношении классическом смысле.)
Теперь мне бы хотелось обсудить понятие момента количества движения в квантовой механике, или, вернее, характеристики того, что в квантовой механике называется моментом количества движения. Видите ли, при переходе к законам нового рода нельзя предполагать, что каждое слово будет в точности означать то же, что и раньше. Подумав, вы можете сказать: «Постойте, а ведь я знаю, что такое момент количества движения. Это штука, которую измеряет момент силы». Но что такое момент силы? В квантовой механике у нас должно быть новое определение старых величин. Поэтому законно было бы назвать ее каким-то другим именем, вроде «углоквантового момента», или чем-то в этом духе, и уж это был бы момент количества движения «по-квантовомеханически». Однако если в квантовой механике мы можем найти величину, которая, когда система становится достаточно большой, идентична нашему старому понятию момента количества движения, то никакой пользы от изобретения новых слов нет. Ее тоже можно называть моментом количества движения. В этом понимании та странная вещь, которую мы собираемся описать, и есть момент количества движения. Это характеристика, в которой мы для больших систем узнаем момент количества движения классической механики.
Прежде всего возьмем систему с сохраняющимся моментом количества движения наподобие атома в пустом пространстве. Такая система (подобно Земле, вращающейся вокруг собственной оси) может крутиться вокруг любой оси, какую бы нам ни вздумалось выбрать. Для данной величины спина возможно много различных «состояний» с одной и той же энергией, причем каждое из них соответствует какому-то направлению оси момента количества движения. Таким образом, в классической механике с данным моментом количества движения связано бесконечное число возможных состояний с одной и той же энергией.
Однако в квантовой механике, как оказывается, происходит несколько странных вещей. Во-первых, число состояний, в которых может находиться, такая система, ограниченно — их можно перечислить. Для маленькой системы это число довольно мало, но если система велика, конечное число становится очень и очень большим. Во-вторых, мы не можем описывать «состояния» заданием направления момента количества движения, а можем только задавать его компоненту в некотором направлении, скажем в направлении оси z. Классически объект с данным полным моментом количества движения J может в качестве z-компоненты иметь любую величину между -J и +J. Но в квантовой механике z-компонента момента количества движения может принимать только определенные дискретные значения. Любая данная система, в частности атом или ядро или что-то другое, с заданной энергией имеет характерное число j, а ее z-компонента момента количества движения может принимать только одно из значений:
Наибольшая величина z-компоненты равна произведению j на h, следующая на h меньше и т. д. до — jh. Число j называется «спином системы». (Некоторые называют его «квантовым числом полного момента количества движения», а мы будем называть его попросту «спином».)
Вас, вероятно, волнует, не будет ли все сказанное нами верно только для некоторой особой оси z? Это не так. Для системы со спином j компонента момента количества движения по любой оси может принимать только одно из значений (34.23). Хотя все это выглядит довольно невероятно, я еще раз прошу вас мне поверить. Позднее мы еще вернемся к этому пункту и обсудим его. Вам, наверно, будет приятно услышать, что z-компонента пробегает набор значений от некоторого числа до минус то же самое число, так что нам, к счастью, не приходится гадать, какое же направление оси z положительное. (Конечно, если бы я сказал, что он пробегает значения от +j до минус какое-то другое число, это было бы крайне подозрительно, ибо тогда мы были бы лишены возможности направить ось z в другую сторону.)
Но если z-компонента момента количества движения изменяется на целое число от +j до -j, то не должно ли само j тоже быть целым числом? Нет! Не совсем так, целым должно быть удвоенное j, т. е. 2j. Иначе говоря, целым должна быть лишь разность между +j и -j. Таким образом, спин j', вообще говоря, может быть либо целым, либо полуцелым в зависимости от того, будет ли 2/ нечетным или четным. Возьмем, к примеру, ядро типа лития, спин которого равен j=3/2. При этом момент количества движения относительно оси z принимает в единицах h одно из следующих значений:
Так что если ядро находится в пустом пространстве в отсутствие внешних полей, то у него имеются четыре возможных состояния, каждое с одной и той же энергией. Для системы со спином 2 z-компонента момента количества движения принимает в единицах h только следующие значения:
2; 1; 0; -1; -2.
Если вы подсчитаете, сколько возможно состояний для данного спина j, то их получится (2j+1). Другими словами, если вы скажете мне, какова энергия системы и ее спин j, то число состояний с этой же энергией в точности будет равно (2j+1), причем каждое из них соответствует одной из различных величин z-компоненты момента количества движения.
Мне хотелось бы прибавить еще один факт. Если вы случайно выберете некоторый атом с известным j и измерите его s-компоненту момента количества движения, то сможете получить какое-то одно из возможных значений, причем каждое из них равновероятно. Любое состояние может характеризоваться только одним из возможных значений, но каждое из них столь же хорошо, как и любое другое. Каждое из них имеет в мире один и тот же вес (мы предполагаем, что никакой предварительной «сортировки» не было).
Кстати, этот факт имеет простой классический аналог. Представьте, что тот же самый вопрос вас интересует с классической точки зрения: какова вероятность какого-то определенного значения z-компоненты момента количества движения, если из набора систем, имеющих один и тот же момент количества движения, вы наугад выбрали одну? Ответ: любое из значений от максимального до минимального равновероятно (в чем вы можете легко убедиться сами). Этот классический результат соответствует равной вероятности любой из (2j+1) возможностей в квантовой механике.
Из того, что у нас было до сих пор, можно получить другое интересное и в каком-то смысле удивительное заключение. В некоторых классических расчетах в окончательном результате появлялась величина, равная квадрату момента количества движения J, другими словами, J·J. И вот оказывается, что правильную квантовомеханическую формулу можно угадать с помощью классических вычислений и следующего простого правила: замените J2 = J·J на j(j+1)h2. Этим правилом часто пользуются, и обычно оно дает верный результат, однако не всегда. Чтобы показать вам, почему это правило может хорошо работать, я приведу следующее рассуждение.
Скалярное произведение J·J можно записать как
J·J=J2x+J2y+J2z
Поскольку это скаляр, то он должен оставаться одним и тем же для любой ориентации спина. Предположим, что мы случайно выбрали образец какой-либо атомной системы и произвели измерения либо величины J2x, либо J2y, либо J2z — среднее
значение любой из них должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества перед любым другим.) Следовательно, среднее значение J·J равно просто утроенной средней величине любой компоненты, скажем J2z :
<J·J>cp=3<J2z>.
Но поскольку J·J при любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной
J·J = 3<J2z>cp. (34.24)
Если же мы теперь скажем, что то же самое уравнение будет использоваться и в квантовой механике, то можем легко найти <J2z>ср. Нам просто нужно взять сумму (2j+1) возможных значений J2zи поделить ее на число всех значений:
Вот что получается для системы со спином 3/2:
Отсюда мы заключаем, что
На вашу долю остается доказать, что соотношение (34.25) вместе с (34.24) дает в результате
Хотя в рамках классической физики мы бы думали, что наибольшее возможное значение z-компоненты J равно просто абсолютной величине J, именно Ц(J·J), в квантовой механике максимальное значение Jzвсегда немного меньше его, ибо jh всегда меньше Ц[j(j+1)]h. Момент количества движения никогда не направлен «полностью вдоль оси z».
§ 8. Магнитная энергия атомов
Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):
где -qe—заряд, а m — масса электрона.
Атомные магнитики, будучи помещены во внешнее магнитное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в направлении поля. Мы знаем, что
Uмаг=-m·В. (34.28) Выбирая ось z вдоль направления поля В, получаем
Uмаг=mzВ. (34.29) А используя уравнение (34.27), находим
Согласно квантовой механике, величина Jzможет принимать только такие значения: jh, (j-1)h,...,- jh. Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии равна
Величину qeh/2m обычно называют «магнетоном Бора» и обозначают через mB:
Возможные значения магнитной энергии будут следующими:
где Jz/h принимает одно из следующих значений: j, (j-1), (j-2), ..., (-j+1), -j.
Другими словами, энергия атомной системы, помещенной в магнитное поле, изменяется на величину, пропорциональную полю и компоненте Jг. Мы говорим, что энергия атомной магнитной системы «расщепляется магнитным полем на 2j+1 уровня». Например, атомы со спином j=3/2, энергия которых вне магнитного поля равна U0, в магнитном поле будут иметь четыре возможных значения энергии. Эти энергии можно изобразить на диаграмме энергетических уровней наподобие фиг. 34.5.
Фиг. 34.5. Возможные магнитные энергии атомной системы со спином 3/2 в магнитном поле В.
Однако энергия каждого атома в данном поле В принимает только одно из четырех возможных значений. Именно это говорит квантовая механика о поведении атомной системы в магнитном поле.
Простейшая «атомная» система — отдельный электрон. Спин электрона равен J/2, поэтому у него возможны два состояния: Jz=h/2 и Jz=-h/2. Для спинового магнитного момента отдельного покоящегося электрона (у которого отсутствует орбитальное движение) g=2, так что магнитная энергия будет ±mBB. На фиг. 34.6 показаны возможные энергии электрона в магнитном поле.
Фиг. 34.6. Два возможных энергетических состояния электрона в магнитном поле В.
Грубо говоря, спин электрона направлен либо «вверх» (по магнитному полю), либо «вниз» (против поля).
У системы с более высоким спином число состояний тоже больше. Поэтому мы можем в зависимости от величины Jzговорить о спине, направленном «вверх» или «вниз» или под некоторым «углом».
Эти результаты квантовой механики мы будем использовать при обсуждении магнитных свойств материалов в следующей главе.
Глава 35 ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
§ 1. Квантованные магнитные состояния
§ 2. Опыт Штерна — Герлаха
§ 3. Метод молекулярных пучков Раби
§ 4. Парамагнетизм
§ 5. Охлаждение адиабатическим размагничиванием
§ 6. Ядерный магнитный резонанс
Повторить: гл. 1 (вып. 5) «Внутреннее устройство диэлектрика
§ 1. Квантованные магнитные состояния
В предыдущей главе мы говорили, что в квантовой механике момент количества движения системы не может иметь произвольного направления, а его компоненты вдоль данной оси могут принимать только определенные дискретные эквидистантные значения. Это поразительная, но характерная особенность квантовой механики. Вам может показаться, что еще слишком рано влезать в такие вещи, что надо подождать, пока вы хоть немного не привыкнете к ним и не будете готовы воспринимать подобные идеи. Но дело в том, что привыкнуть к ним вы никогда не сможете. Вы никогда не сможете легко их воспринимать. Это, пожалуй, самое сложное из всего, что я рассказывал вам до сих пор и, главное, нет способа описать это как-то более вразумительно и не так хитроумно и сложно по форме. Поведение вещества в малых масштабах, как я уже говорил много раз, отличается от всего того, к чему вы привыкли, и поистине весьма странно. Вы, конечно, согласитесь, что было бы неплохо попытаться поближе познакомиться с явлениями в малом масштабе, продолжая одновременно использовать классическую физику, и приобрести поначалу хоть какой-то опыт, пусть даже не понимая всего достаточно глубоко. Понимание этих вещей приходит очень медленно, если оно приходит вообще. Конечно, понемногу начинаешь чувствовать, что может и что не может произойти в данной квантовомеханической ситуации, а это, возможно, и называется «пониманием», но добиться приятного чувства «естественности» квантовомеханических правил здесь невозможно. Они-то, конечно, естественны, но с точки зрения нашего повседневного опыта на привычном уровне остаются очень уж необычными. Мне бы хотелось объяснить вам, что позиция, которую мы собираемся занять по отношению к этому правилу о дискретности значений момента количества движения, совершенно отлична от отношения ко многим другим вещам, о которых шла речь. Я даже не буду пытаться «объяснять» его, но должен хоть рассказать вам, что получается. Было бы нечестно с моей стороны, описывая магнитные свойства материалов, не указать, что классическое объяснение магнетизма, т. е. момента количества движения и магнитного момента, несостоятельно.
Одно из наиболее необычных следствий квантовой механики состоит в том, что момент количества движения вдоль любой оси всегда оказывается равным целой или полуцелой доле h, причем какую бы ось вы ни взяли, это всегда будет так. Парадоксальность здесь заключается в следующем любопытном факте: если вы возьмете любую другую ось, то окажется, что компоненты относительно этой оси тоже будут взяты из того же самого набора значений. Однако оставим рассуждения до того времени, когда у вас наберется достаточно опыта и вы сможете насладиться тем, как этот кажущийся парадокс в конце концов разрешится.
Сейчас просто примите на веру, что у каждой атомной системы есть число j, называемое спином системы (оно может быть либо целым, либо полуцелым), и что компоненты момента количества движения относительно любой данной оси всегда принимают одно из значений между +jh и -jh:
Мы упомянули также, что магнитный момент любой простой атомной системы имеет то же самое направление, что и ее момент количества движения. Это справедливо не только для атомов или ядер, но и для элементарных частиц. Каждая элементарная частица обладает характерной для нее величиной j и своим собственным магнитным моментом. (Для некоторых частиц обе они равны нулю.) Мы понимаем под «магнитным моментом системы», что ее энергия в направленном по оси z магнитном поле для слабых полей может быть записана как — mzВ. Мы должны условиться не брать слишком больших полей, ибо они будут возмущать внутренние движения системы и энергия не будет мерой магнитного момента, который система имела до включения магнитного поля. Но если поле достаточно слабо, то оно изменяет энергию на величину
DU=-mzB, (35.2)
с тем условием, что в этом выражении мы должны сделать подстановку
причем Jzравно одному из значений (35.1).
Предположим, что мы взяли систему со спином j=3/2 В отсутствие магнитного поля у системы было бы четыре различных возможных состояния, соответствующих различным значениям Jz с одной и той же энергией. Но в тот момент, когда мы включаем магнитное поле, появляется дополнительная энергия взаимодействия, которая разделяет эти состояния на четыре состояния, слабо различающиеся по энергии, или, как говорят, первоначальный энергетический уровень расщепился; на четыре новых уровня. Эти уровни определяются энергией, пропорциональной произведению В на h, и на 3/2, 1/2 , -1/2 или -3/2 в зависимости от величины Jг. Расщепление энергетических уровней в атомной системе со спинами 1/2, 1 и 3/2 показаны на фиг. 35.1.
(Вспомните, что для любого расположения электронов магнитный момент всегда направлен противоположно моменту количества движения.)
Обратите внимание, что «центр тяжести» энергетических уровней на фиг. 35.1 один и тот же как в присутствии магнитного поля, так и без него. Заметьте также, что все расстояния от одного уровня до следующего для данной частицы в данном магнитном поле равны между собой. Расстояние между уровнями для данного магнитного поля В мы будем записывать как hwp, что является просто определением wp . Воспользовавшись (35.2) и (35.3), получим
hwp=g(qe/2m)hB.
или
wp=g(qe/2m)B.(35.4)
Величина g(qe/2m) равна просто отношению магнитного момента к моменту количества движения и характеризует свойства частицы. Формула (35.4) в точности совпадает с формулой, полученной нами в гл. 34 для угловой скорости прецессии гироскопа с магнитным моментом (m и моментом количества движения J в магнитном поле.
§ 2. Опыт Штерна — Герлаха
Факт квантования момента количества движения — вещь настолько удивительная, что мы поговорим немного об ее истории. Ученый мир был буквально потрясен, когда было сделано это открытие (даже несмотря на то, что это ожидалось теоретически). Первыми экспериментально наблюдали этот факт Штерн и Герлах в 1922 г. Если хотите, опыт Штерна и Герлаха можно рассматривать как прямое подтверждение квантования момента количества движения. Штерн и Герлах поставили эксперимент по измерению магнитного момента отдельных атомов серебра. Испаряя серебро в горячей печи и пропуская пары серебра через систему маленьких отверстий, они получали пучок атомов серебра. Этот пучок направлялся между полюсными наконечниками специального магнита (фиг. 35.2).
Фиг. 35.2. Опыт Штерна и Герлаха.
Идея заключалась в следующем. Если магнитный момент атомов серебра равен m, то в магнитном поле В, направленном по оси z, они приобретут добавочную энергию -mzB. В классической теории mг равно произведению магнитного момента на косинус угла между моментом и магнитным полем, так что дополнительная энергия в поле была бы равна
DU=-mBcosq. (35.5)
Разумеется, когда атомы вылетают из печи, их магнитные моменты имеют любые направления, поэтому возможны все значения угла 0. Но если магнитное поле быстро изменяется с изменением z, т. е. если есть большой градиент, магнитная энергия с изменением положения тоже меняется, а поэтому на магнитные моменты действует сила, направление которой зависит от того, будет ли косинус положительным или отрицательным. Атомы при этом должны отклоняться вверх или вниз силой, пропорциональной производной магнитной энергии; из принципа виртуальной работы
Fz=-дU/дz=mcosq(дB/дz). (35.6)
Чтобы получить очень быстрое изменение магнитного поля, Штерн и Герлах сделали один из полюсных наконечников своего магнита очень острым. Пучок атомов серебра направлялся прямо вдоль этого острого края, так что на атомы в таком неоднородном поле должна была действовать вертикальная сила. Атомы серебра с горизонтально направленными магнитными моментами не чувствовали бы никакой силы и проходили бы через магнит без отклонения. На атомы, магнитный момент которых направлен в точности вертикально, действовала бы максимальная сила по направлению к острому краю магнита. А атомы с магнитным моментом, направленным вниз, чувствовали бы силу, тянущую их вниз. Следовательно, покинув магнит, атомы должны были «расползтись» в соответствии с вертикальными компонентами своих магнитных моментов. В классической теории возможны любые углы, так что после осаждения пучка на стеклянной пластинке следовало ожидать «размазывания» его по вертикальной линии. Высота линии при этом должна была быть пропорциональной величине магнитного момента. Однако когда Штерн и Герлах увидели, что получается на самом деле, то полное поражение классических понятий стало явным. На стеклянной пластинке они обнаружили два отдельных пятнышка. Пучок атомов серебра распался на два пучка.
Самое удивительное, что пучок атомов, спины которых, казалось бы, должны были быть направлены совершенно случайно, расщепился на два отдельных пучка. Откуда магнитный момент может знать, что ему полагается иметь определенные компоненты вдоль направления магнитного поля? Этот вопрос и послужил началом открытия квантования момента количества движения, и я не буду сейчас даже пытаться дать вам теоретическое объяснение, а просто призову вас поверить в результаты этого эксперимента так же, как физики тех дней были вынуждены их признать. То, что энергия атома в магнитном поле может принимать только какой-то набор дискретных значений,— экспериментальный факт. Для каждого из этих значений энергия пропорциональна напряженности поля. Так что в той области, где поле изменяется, принцип виртуальной работы говорит нам, что возможные магнитные силы, действующие на атомы, могут принимать только дискретные значения: для каждого состояния силы оказываются различными и пучок атомов расщепляется на небольшое число отдельных пучков. Измеряя отклонение пучка, можно найти величину магнитного момента.
§ 3. Метод молекулярных пучков Раби
Теперь мне бы хотелось описать улучшенную аппаратуру для измерения магнитных моментов, разработанную И. Раби и его сотрудниками. В экспериментах Штерна — Герлаха отклонение атомов было очень небольшим и измерения магнитных моментов не очень точными. А техника Раби позволяет добиться фантастической точности при измерении магнитных моментов. Метод основан на том факте, что в магнитном поле первоначальная энергия атомов расщепляется на конечное число энергетических уровней. Тот факт, что энергия атома может иметь только определенные дискретные значения, на самом деле не более удивителен, чем то, что атом вообще имеет дискретные энергетические уровни; об этом мы часто говорили в начале курса. Почему бы этого не могло происходить и с атомами в магнитном поле? Так именно все и происходит. Однако когда пытаются связать расщепление с идеей ориентированных магнитных моментов, то в квантовой механике появляются некоторые странные выводы.
Когда атом имеет два уровня, отличающихся по энергии на величину DU, это может вызвать переход с верхнего уровня на нижний с излучением кванта света
hw=DU, (35.7)
где w — частота.
То же самое может произойти и с атомами в магнитном поле. Но только разность энергий настолько мала, что частота ее соответствует не свету, а микроволнам или радиочастотам. Переход с нижнего энергетического уровня на верхний может также происходить с поглощением света или (в случае атомов в магнитном поле) микроволновой энергии. Итак, если у нас есть атом в магнитном поле, то, прикладывая дополнительное электромагнитное поле надлежащей частоты, мы можем вызвать переход из одного состояния в другое. Другими словами, если у нас есть атом в сильном магнитном поле и мы будем «щекотать» его слабым переменным электромагнитным полем, то имеется некоторая вероятность «выбить» его на другой уровень, когда частота поля близка к w, определяемой соотношением (35.7). Для атома в магнитном поле эта частота в точности равна частоте, названной нами wри зависящей от магнитного поля, согласно формуле (35.4). Если атом «щекотать» с другой частотой, то вероятность перехода станет очень мала. Таким образом, вероятность перехода при частоте wримеет резкий резонанс. Измеряя частоту этого резонанса в известном магнитном поле В, можно измерить величину g(q/2m), а следовательно, и g-фактор, причем с огромной точностью.
Интересно, что к такому же заключению можно прийти и с классической точки зрения. В соответствии с классической картиной, когда мы помещаем гироскоп, обладающий магнитным моментом m, и моментом количества движения 3, во внешнее магнитное поле, гироскоп начнет прецессировать вокруг оси, параллельной этому полю (фиг. 35.3).
Фиг. 35.3. Классическая прецессия атома с магнитным моментом m и моментом количества движения J,
Предположим, нас интересует, как можно изменить угол классического гироскопа по отношению к магнитному полю, т. е. по отношению к оси z? Магнитное поле создает момент силы относительно горизонтальной оси. На первый взгляд кажется, что такой момент силы старается выстроить магниты в направлении поля, но он вызывает только прецессию. Если же мы хотим изменить угол гироскопа по отношению к оси z, то должны приложить момент силы относительно оси z. Если мы приложим момент силы, действующий в том же направлении, что и прецессия, угол гироскопа изменится и это приведет к уменьшению компоненты J в направлении оси z. Угол между направлением J и осью z на фиг. 35.3 должен увеличиться. Если мы попытаемся воспрепятствовать прецессии, вектор J будет двигаться по направлению к вертикали.
Но каким образом к нашему прецессирующему атому можно приложить нужный момент силы? Ответ: с помощью слабого магнитного поля, направленного в сторону. На первый взгляд вам может показаться, что направление этого магнитного поля должно крутиться вместе с прецессией магнитного момента, так чтобы поле всегда было направлено к нему под прямым углом, как это показано на фиг. 35.4, а с помощью поля В'.
Фиг. 35.4. Угол прецессии атомного магнитика можно изменить двумя путями:
а — горизонтальным магнитным полем, направленным всегда под прямым углом к m; б—осциллирующим полем.
Такое поле работает очень хорошо, однако нисколько не хуже действует и переменное горизонтальное поле. Если у нас есть горизонтальное поле В', которое всегда направлено по оси х (в положительную или отрицательную сторону) и которое осциллирует с частотой wp, тогда через каждые полпериода действующая на магнитный момент пара сил переворачивается, так что получается суммарный эффект, который почти столь же эффективен, как и вращающееся магнитное поле. С точки зрения классической физики мы бы ожидали при этом изменения компоненты магнитного момента вдоль оси z, если у нас есть очень слабое магнитное поле, осциллирующее с частотой, в точности равной wp. Разумеется, по классической физике mг должно изменяться непрерывно, но в квантовой механике z-компонента магнитного момента не может быть непрерывной. Она должна неожиданно «прыгать» от одного значения до другого. Я сравнивал следствия классической и квантовой механики, чтобы дать вам понятие о том, что может происходить классически, и как это связано с тем, что происходит на самом деле в квантовой механике. Обратите внимание, между прочим, что в обоих случаях ожидаемая резонансная частота одна и та же.
Еще одно дополнительное замечание. Из того, что мы говорили о квантовой механике, не видно, почему переходы не могут происходить при частоте 2wр. Оказывается, что в классическом случае этому совершенно нет никакого аналога, но в квантовой механике такие переходы невозможны, по крайней мере в описанном нами способе вынужденных переходов. При горизонтальном осциллирующем магнитном поле вероятность того, что частота 2wp вызовет скачок сразу на два шага, равна нулю. Все переходы, будь то переход вверх или вниз, предпочитают происходить только при частоте wр.
Вот теперь мы готовы к описанию метода Раби. Здесь мы опишем только, как этот метод измерения магнитных моментов работает в случае частиц со спином 1/2. Схема аппаратуры показана на фиг. 35.5.
Фиг. 35.5. Схема установки Раби в опытах с молекулярными пучками.
Вы видите здесь печь, которая создает поток нейтральных атомов, летящих по прямому пути через три магнита. Магнит 1 — такой же, как и на фиг. 35.2, он создает поле; с большим, скажем положительным, градиентом dBz/dz. Если атомы обладают магнитным моментом, то они будут отклоняться вниз при Jz=+h/2 или вверх приJz =-h/2 (поскольку для электронов m направлен противоположно J). Если мы будем рассматривать только те атомы, которые могут проходить через щель S1, то, как это показано на фиг. 35.5, возможны две траектории. Чтобы попасть в щель, атомы с Jz=+h/2 должны лететь по кривой а, а атомы с Jz=-h/2 — по кривой b. Атомы, вылетающие из печи в другом направлении, вообще не попадут в щель.
Магнит 2 создает однородное поле. В этой области на атомы никакие силы не действуют, поэтому они просто пролетают через нее и попадают в магнит 3. Этот магнит представляет собой копию магнита 1, но с перевернутым полем, так что у него, dBz/dz имеет отрицательный знак. Атомы с Jz=+h/2 (будем говорить «со спином, направленным вверх»), которые в магните 1 отклонялись вниз, в магните 3 будут отклоняться вверх; они продолжат свой полет по траектории а и через щель S2попадут в детектор. Атомы с Jz=-h/2 («со спином, направленным вниз») в магнитах 1 и 3 тоже будут испытывать действие противоположных сил и полетят по траектории b, которая через щель S2тоже приведет их в детектор.
Детектор можно сделать разными способами в зависимости от измеряемых атомов. Так, для щелочных металлов, подобных натрию, детектором может служить тонкая раскаленная вольфрамовая нить, подсоединенная к чувствительному гальванометру. Атомы натрия, оседая на этой нити, испаряются в виде ионов Na+ и оставляют на ней электрон. Возникает ток, пропорциональный числу осевших в 1 сек атомов натрия.
В щели магнита 2 находится набор катушек, которые создают небольшое горизонтальное магнитное поле В'. Эти катушки питаются током, осциллирующим с переменной частотой w, так что между полюсами магнита 2 создается сильное вертикальное магнитное поле В0 и слабое осциллирующее горизонтальное магнитное поле В'.
Предположим теперь, что частота со осциллирующего поля подобрана равной wp — частоте «прецессии» атомов в поле В. Переменное поле вызовет у некоторых из пролетающих атомов переход от одного значения Jzк другому. Атомы, спины которых были первоначально направлены вверх (Jг=+h/2), могут перевернуться вниз (Jz=-h/2). Теперь магнитный момент этих атомов перевернут, так что в магните 3 они будут чувствовать силу, направленную вниз, и полетят по траектории а', как показано на фиг. 35.5. Теперь они уже не смогут пройти через щель S2 и попасть в детектор. Точно так же некоторые из атомов, спин которых был первоначально направлен вниз
(Jz=-h/2), перевернутся при прохождении через магнит 2 вверх (Jz=+h/2). После этого они полетят по траектории b' и не попадут в детектор.
Если частота осциллирующего поля В' значительно отличается от wp оно не сможет вызвать переворачивания спина и атомы по своим «невозмущенным» орбитам пройдут прямо к детектору. Итак, как видите, можно найти частоту «прецессии» атомов wp в поле В0, подбирая частоту со магнитного поля В', пока не получим уменьшения тока атомов, приходящих в детектор. Уменьшение тока будет происходить тогда, когда w попадет «в резонанс» с wp. График зависимости тока в детекторе от со может напоминать кривую, изображенную на фиг. 35.6.
Фиг. 35.6. Количество атомов в пучке при w=wp уменьшается.
Зная w , можно найти величину g для данного атома.
Такой резонансный эксперимент с атомными или, как их часто называют, «молекулярными» пучками представляет очень красивый и точный способ измерения магнитных свойств атомных объектов. Резонансную частоту wp можно определить с очень большой точностью, по сути дела значительно точнее, нежели мы способны измерить поле В0, необходимое при нахождении g.
§ 4. Парамагнетизм
Теперь мне бы хотелось описать явление парамагнетизма вещества. Предположим, имеется вещество, в составе которого имеются атомы, обладающие постоянным магнитным моментом, например кристаллы медного купороса. В этих кристаллах содержатся ионы меди, у которых электроны на внутренних оболочках имеют суммарный момент количества движения и магнитный момент, не равные нулю. Таким образом, ионы меди будут источником постоянного магнитного момента молекул купороса. Буквально несколько слов о том, какие атомы имеют постоянный магнитный момент, а какие — нет. Любой атом, у которого число электронов нечетно, подобно натрию, например, будет иметь магнитный момент. На незаполненной оболочке натрия имеется один электрон. Этот электрон и определяет спин и магнитный момент атома. Однако обычно при образовании соединения этот дополнительный электрон на внешней оболочке спаривается с другим электроном, направление спина которого в точности противоположно, так что все моменты количества движения и магнитные моменты валентных электронов в точности компенсируют друг друга. Вот почему молекулы, вообще говоря, не обладают магнитным моментом. Конечно, если у вас есть газ атомов натрия, то там такой компенсации не происходит. Точно так же если у вас есть то, что в химии называется «свободным радикалом», т. е. объект с нечетным числом валентных электронов, то связи оказываются неполностью насыщенными и появляется ненулевой момент количества движения.
У подавляющего большинства материалов полный магнитный момент появляется только тогда, когда там присутствуют атомы с незаполненной внутренней электронной оболочкой. Благодаря этому они могут иметь суммарный момент количества движения и магнитный момент. Такие атомы принадлежат к «переходным элементам» периодической таблицы Менделеева, например: хром, марганец, железо, никель, кобальт, палладий и платина — элементы как раз такого сорта. Кроме того, все редкоземельные элементы имеют незаполненную внутреннюю оболочку, а следовательно, и постоянные магнитные моменты. Правда, встречаются еще странные вещества (к числу их относятся жидкий кислород и окись азота), которые, оказывается, тоже обладают магнитным моментом, но объяснить причины этих странностей я предоставляю химикам.
Предположим теперь, что у нас есть ящик, наполненный молекулами или атомами с постоянным магнитным моментом, скажем газ, жидкость или кристалл. Нам хочется знать, что получится, если мы поместим его во внешнее магнитное поле. В отсутствие магнитного поля атомы сбиваются тепловым движением и их магнитные моменты распределяются по всем направлениям. Но когда действует магнитное поле, оно выстраивает эти маленькие магнитики, так что магнитных моментов, направленных по полю, становится больше, чем направленных против него. Материал «намагничивается».
Намагниченность М материала мы определяем как полный магнитный момент единицы объема, под которым мы понимаем векторную сумму всех атомных магнитных моментов единицы объема. Если среднее число атомов в единице объема равно N, а их средний момент равен <m>cp, то М можно записать как произведение N на средний магнитный момент:
м = n<m>cp. (35.8)
Это определение М аналогично определению электрической поляризации Р, данному в гл. 10 (вып. 5).
Классическая теория парамагнетизма, как вы уже убедились в гл. 10 (вып. 5), в точности аналогична теории диэлектрической проницаемости. Предполагается, что магнитный момент m каждого из атомов всегда имеет одну и ту же величину, но может быть направлен в любую сторону. Магнитная энергия в поле В равна -m·B=-mBcosq, где q — угол между моментом и полем. Согласно статистической физике, относительная вероятность угла равна e-энергия/kT так что угол 0° более вероятен, чем угол p. Следуя в точности по пути, проделанному нами в гл. 11, § 3 (вып. 5), мы обнаружим, что для слабых магнитных полей М направлена параллельно В и имеет величину
[См. выражение (11.20), вып. 5.] Эта приближенная формула верна, только когда отношение mB/kT много меньше единицы.
Мы нашли, что намагниченность, т. е. магнитный момент единицы объема, пропорциональна магнитному полю. Это явление и называется парамагнетизмом. Вы увидите, что эффект сильнее проявляется при низких температурах и слабее при высоких. При помещении вещества в магнитное поле возникающий в нем магнитный момент в случае слабых полей пропорционален величине поля. Отношение М к В (для слабых полей) называется магнитной восприимчивостью.
Рассмотрим теперь парамагнетизм с точки зрения квантовой механики. Обратимся сначала к атомам со спином 1/2. Если в отсутствие магнитного поля атомы обладают вполне определенной энергией, то в магнитном поле энергия изменится; возможны два значения энергии для разных значений Jz. Для Jz=+h/2
магнитное поле изменяет энергию на величину
(Для атомов сдвиг энергии DU положителен, ибо заряд электрона отрицателен.) Для Jг =-h/2 энергия изменяется на величину
Для сокращения записи обозначим
тогда
DU = ±m0В. (35.13)
Совершенно ясен и смысл m0; — m0равно z-компоненте магнитного момента для спина, направленного вверх, а + m0 равно z-компоненте магнитного момента в случае спина, направленного вниз.
Статистическая механика говорит нам, что вероятность нахождения атома в каком-то состоянии пропорциональна
g-(энергия состояния)/kT.
В отсутствие магнитного поля энергия обоих состояний одна и та же, поэтому в случае равновесия в магнитном поле вероятности пропорциональны
е-DU/kT, (35.14)
Число же атомов в единице объема со спином, направленным вверх, равно
а со спином, направленным вниз,
Постоянная а должна определяться из условия
Nвверх+Nвниз=N (35.17)
т.е. равна полному числу атомов в единице объема. Таким образом, мы получаем
Однако нас интересует средний магнитный момент в направлении оси z. Каждый атом со спином, направленным вверх, дает в этот момент вклад, равный -m0, а со спином, направленным вниз, + m0, так что средний момент будет
Тогда М — магнитный момент единицы объема — будет равен N<m>ср. Воспользовавшись выражениями (35.15)—(35.17), получим
Это и есть квантовомеханическая формула для М в случае атомов со спином j=1/2. К счастью, ее можно записать более коротко через гиперболический тангенс:
График зависимости М он В приведен на фиг. 35.7.
Фиг. 35.7. Изменение намагниченности парамагнетика при изменении напряженности магнитного поля В.
Когда поле В становится очень большим, гиперболический тангенс приближается к единице, а М — к своему предельному значению Nm0. Таким образом, при сильных полях происходит насыщение. Нетрудно понять, почему так получается — ведь при достаточно больших полях все магнитные моменты выстраиваются в одном и том же направлении. Другими словами, при насыщении все атомы находятся в состоянии со спинами, направленными вниз, и каждый из них дает вклад в магнитный момент, равный m0.
Обычно при комнатной температуре и полях, которые можно получить (порядка 10000 гс), отношение m0B/kT равно приблизительно 0,02. Чтобы наблюдать насыщение, необходимо спуститься до очень низких температур. Для комнатной и более высоких температур обычно можно thx заменить на x и написать
Точно так же, как и в классической теории, намагниченность М оказывается пропорциональной полю В. Даже формула оказывается той же самой, за исключением того, что в ней, по-видимому, где-то потерян множитель 1/3. Но нам еще нужно связать m0в квантовомеханической формуле с величиной m, которая появилась в классическом результате, в выражении (35.9).
В классической формуле у нас появилось m2=m·m — квадрат вектора магнитного момента, или
В предыдущей главе я уже говорил, что очень часто правильный ответ можно получить из классических вычислений с заменой J·J на j(j+1)h2. В нашем частном примере j=1/2, так что
j(j+1)h2=3/4h2.
Подставляя этот результат вместо J·J в (35.23), получаем
или, вводя величину m0, определенную соотношением (35.12), получаем
m·m=3m20.
Подставляя это вместо m2 в классическое выражение (35.9), мы действительно воспроизведем истинный квантовомеханический результат — формулу (35.22).
Квантовая теория парамагнетизма легко распространяется на атомы с любым спином j. При этом для намагниченности в слабом поле получим
где
представляет комбинацию постоянных с размерностью магнитного момента. Моменты большинства атомов приблизительно равны этой величине. Она называется магнетоном Бора. Спиновый магнитный момент электрона почти в точности равен
§ 5. Охлаждение адиабатическим размагничиванием
Парамагнетизм имеет одно весьма интересное применение. При очень низкой температуре и в сильном магнитном поле атомные магнитики выстраиваются. При этом с помощью процесса, называемого адиабатическим размагничиванием, можно получить самые низкие температуры. Возьмем какую-то парамагнитную соль, содержащую некоторое число редкоземельных атомов (например, аммиачный нитрат празеодима), и начнем охлаждать ее жидким гелием до 1—2° К в сильном магнитном поле. Тогда показатель mВ/kT будет больше единицы, скажем 2 или 3. Большинство спинов направлено вверх, и намагниченность почти достигает насыщения. Для облегчения давайте считать, что поле настолько велико, а температура так низка, что все атомы смотрят в одном направлении. Теплоизолируйте затем соль (удалив, например, жидкий гелий и создав вакуум) и выключите магнитное поле. При этом температура соли падает.
Если бы это поле вы выключили внезапно, то раскачивание и сотрясение атомов кристаллической решетки постепенно перепутало бы все спины. Некоторые из них остались бы направленными вверх, а другие повернулись бы вниз. Если никакого поля нет (и если не учитывать взаимодействия между атомными магнитами, которое привносит только небольшую ошибку), то на переворачивание магнитиков энергии не потребуется. Поэтому случайное распределение спинов установится без какого-либо изменения температуры.
Предположим, однако, что в то время как спины переворачиваются, магнитное поле еще не вполне исчезло. Тогда для переворачивания спинов против поля требуется некоторая работа, она должна затрачиваться на преодоление поля. Этот процесс отбирает энергию у теплового движения и понижает температуру. Таким образом, если сильное магнитное поле выключается не слишком быстро, температура соли будет уменьшаться. Размагничиваясь, она охлаждается. С точки зрения квантовой механики, когда поле сильно, все атомы находятся в наинизшем состоянии, так как слишком много шансов против того, чтобы они находились в высшем состоянии. Но как только напряженность поля понижается, тепловые флуктуации со все большей и большей вероятностью будут «выталкивать» атомы на высшее состояние, и когда это происходит, атом поглощает энергию DU=m0B. Таким образом, если магнитное поле выключается медленно, магнитные переходы могут отбирать энергию у тепловых колебаний кристалла, тем самым охлаждая его. Таким способом можно понизить температуру от нескольких градусов до температуры в несколько тысячных долей градуса от абсолютного нуля.
А если нам захочется охладить что-то еще сильнее? Оказывается, что здесь природа тоже была очень предусмотрительной. Я уже упоминал, что магнитные моменты есть и у атомных ядер. Наши формулы для парамагнетизма работают и в случае ядер, только надо иметь в виду, что моменты ядер приблизительно в тысячу раз меньше. (По порядку величины они равны qh/2mp, где mp — масса протона, так что они меньше в число раз, равное отношению масс протона и электрона.) Для таких магнитных моментов даже при температуре 2° К показатель mB/kT составляет всего несколько тысячных. Но если мы используем парамагнитное размагничивание и достигнем температуры нескольких тысячных градуса, то mB/kT становится порядка единицы; при столь низких температурах мы уже можем говорить о насыщении ядерного магнетизма. Это очень кстати, ибо теперь, воспользовавшись адиабатическим размагничиванием системы магнитных ядер, можно достичь еще более низких температур. Таким образом, в магнитном охлаждении возможны две стадии. Сначала мы используем диамагнитное размагничивание парамагнитных ионов и спускаемся до нескольких тысячных долей градуса. Затем мы применяем холодную парамагнитную соль для охлаждения некоторых материалов, обладающих сильным ядерным магнетизмом. И, наконец, когда мы выключаем магнитное поле, температура материалов доходит до миллионных долей градуса от абсолютного нуля, если, конечно, все было проделано достаточно тщательно.
§ 6. Ядерный магнитный резонанс
Я уже говорил, что атомный парамагнетизм очень слаб и что ядерный магнетизм в тысячу раз слабее его. Но все же с помощью явления, называемого «ядерным магнитным резонансом», наблюдать его относительно легко. Предположим, что мы взяли такое вещество, как вода, у которого все электронные спины в точности компенсируют друг друга, так что их полный магнитный момент равен нулю. У таких молекул все же останется очень-очень слабый магнитный момент благодаря наличию магнитного момента у ядер водорода. Предположим, что мы поместили небольшой образец воды в магнитное поле В. Поскольку спин протонов (входящих в атом водорода) равен 1/2, то у них возможны два энергетических состояния. Если вода находится в тепловом равновесии, то протонов в нижнем энергетическом состоянии, моменты которых направлены параллельно полю, будет немного больше. Поэтому каждая единица объема обладает очень маленьким магнитным моментом. А поскольку протонный момент составляет только одну тысячную долю атомного момента, то намагниченность, которая ведет себя как m2 [см. уравнение (35.22)], будет в миллион раз слабее обычной атомной парамагнитной намагниченности. (Вот почему мы должны выбирать материал, у которого отсутствует атомный парамагнетизм.) После того как мы подставим все величины, окажется, что разность между числом протонов со спином, направленным вверх, и спином, направленным вниз, составляет всего несколько единиц на 108, так что эффект и в самом деле очень мал! Однако его можно наблюдать следующим образом.
Предположим, что мы поместили ампулу с водой внутрь небольшой катушки, которая создает слабое горизонтальное осциллирующее магнитное поле. Если это поле осциллирует с частотой wp, то оно вызовет переходы между двумя энергетическими состояниями точно так же, как это было в опытах Раби, которые мы описывали в § 3. Когда протон «сваливается» с верхнего энергетического состояния на нижнее, он отдает энергию mzB, которая, как мы видели, равна hwp. Если же он переходит с нижнего состояния на верхнее, то будет отбирать энергию hwpу катушки. А поскольку в нижнем состоянии имеется немного больше протонов, чем в верхнем, то из катушки будет поглощаться энергия. И хотя эффект весьма мал, с помощью чувствительного электронного усилителя можно наблюдать даже столь малое поглощение энергии.
Как и в эксперименте Раби с молекулярными пучками, поглощение энергии будет заметно только тогда, когда осциллирующее поле находится в резонансе, т. е. когда
Часто удобнее искать резонанс, изменяя В и оставляя постоянной w. Очевидно, что поглощение энергии происходит, когда
Типичная установка, применяемая при изучении ядерного магнитного резонанса, показана на фиг. 35.8.
Фиг. 35.8. Схема аппаратуры для изучения ядерного магнитного резонанса.
Между полюсами большого электромагнита помещена небольшая катушка, питаемая высокочастотным генератором. Вокруг наконечников полюсов магнитов намотаны две вспомогательные катушки, питаемые током с частотой 60 гц, так что магнитное поле немного «колеблется» вокруг своего среднего значения. Для примера скажу вам, что ток главного магнита создает поле в 5000 гс, а вспомогательные катушки изменяют его на ±1 гс. Если генератор настроен на частоту 21,2 Мгц, то протонный резонанс будет происходить всякий раз, когда поле проходит через 5000 гс [используйте соотношение (34.13) для протона с величиной g=5,58].
Схема генератора устроена так, что дает на выход дополнительный сигнал, пропорциональный изменению мощности, поглощенной из генератора, а этот сигнал подается после усиления на вертикально отклоняющие пластины осциллографа. В горизонтальном направлении луч пробегает один раз за каждый период изменения дополнительного вспомогательного поля. (Впрочем, чаще горизонтальная развертка делается пропорциональной частоте вспомогательного поля.)
До того как внутрь высокочастотной катушки мы поместим ампулу с водой, мощность, отдаваемая генератором, имеет какую-то величину. (Она не изменяется с изменением магнитного поля.) Но как только внутрь катушки мы поместим небольшую ампулу с водой, на экране осциллографа появляется сигнал (см. фиг. 35.8). Мы непосредственно видим график мощности, поглощаемой протонами!
На практике трудно установить, когда основной магнит создает поле точно 5000 гс. Ток в главном магните обычно подбирают, изменяя его постепенно до тех пор, пока на экране не появится резонансный сигнал. Оказывается, на сегодняшний день это наиболее удобный способ точного измерения напряженности магнитного поля, Разумеется, кто-то должен был когда-то точно измерить магнитное поле и частоту и определить величину g для протона. Однако сейчас, после того как это уже сделано, протонную резонансную аппаратуру типа той, что изображена на рисунке, можно использовать как «протонный резонансный магнитометр».
Несколько слов о форме сигнала. Если бы мы очень медленно изменяли магнитное поле, то можно было бы ожидать, что мы увидим нормальную резонансную кривую. Поглощение энергии достигло бы максимума, когда частота генератора была бы в точности равна wp. Небольшое поглощение происходило бы, конечно, и при близлежащих частотах, так как не все протоны находятся в точности в одинаковом поле, а различные поля означают несколько отличные резонансные частоты.
Но так ли все это? Должны ли мы на самом деле видеть при резонансной частоте какой-то сигнал? Не следует ли ожидать, что высокочастотное поле выравнивает населенность обоих состояний, так что, за исключением первого момента, никакого сигнала не будет, когда вода помещается внутрь поля? Не совсем так, поскольку хотя мы и стараемся выровнять обе населенности, тепловое движение со своей стороны старается сохранить равновесные значения, присущие данной температуре Т. Если мы находимся точно в резонансе, то мощность, поглощенная ядрами, в точности равна мощности, теряемой на тепловое движение. Однако «тепловой контакт» между системой протонных магнитных моментов и атомным движением довольно слабый. Каждый протон относительно изолирован в центре электронного облака. Таким образом, чистая вода дает слишком слабый резонансный сигнал, чтобы его можно было заметить. Для увеличения поглощения необходимо улучшить «тепловой контакт». Это обычно делается путем добавления в воду небольшого количества окиси железа. Атомы железа — совсем как маленькие магнитики, и когда они прыгают туда и сюда в своем «тепловом танце», то создают слабенькое прыгающее магнитное поле, которое действует на протоны. Эти изменяющиеся доля «связывают» протонные магнитные моменты с атомными колебаниями и стремятся восстановить тепловое равновесие. Именно из-за этого взаимодействия протоны в состояниях с большой энергией теряют свою энергию и снова становятся способными к поглощению энергии генератора.
На практике же сигнал на выходе ядерной резонансной аппаратуры не похож на обычную резонансную кривую. Обычно это более сложный сигнал с осцилляциями, похожими на те, что изображены на фиг. 35.8. Такая форма сигнала обусловлена изменяющимися полями. Объяснять ее следовало бы с точки зрения квантовой механики, однако можно показать, что объяснение таких экспериментов при помощи представлений классической физики, как мы их использовали выше, тоже дает правильный ответ. С точки зрения классической физики мы бы сказали, что когда мы попадаем в резонанс, то синхронно начинаем раскачивать множество прецессирующих ядерных магнитиков. В результате мы их заставляем прецессировать все вместе. А вращаясь все вместе, эти маленькие магнитики создают в катушке индуцированную э.д.с. с частотой, равной wp . Но поскольку со временем магнитное поле увеличивается, то увеличивается и частота прецессии, поэтому наведенное напряжение вскоре приобретает частоту, большую, чем частота генератора. Так как при этом наведенная э.д.с. попеременно попадает то в фазу, то в противофазу с переменным внешним полем, «поглощенная» мощность становится попеременно то положительной, то отрицательной. Таким образом, на экране мы видим запись биений между частотой протона и частотой генератора. Из-за того что частоты не всех протонов в точности одинаковы (разные протоны находятся в нескольких различных полях), а возможно, и в результате возмущений, вносимых атомами железа, находящимися в воде, свободно прецессирующие моменты скоро выбиваются из фазы и сигналы биений исчезают.
Эти явления магнитного резонанса используются во многих методах как орудие выяснения новых свойств вещества — особенно в химии и в физике. Я не говорю уже о том, что число магнитных моментов ядра говорит нам кое-что и о его структуре. В химии многое можно узнать из структуры (или формы) резонансов. Благодаря магнитным полям, создаваемым близлежащими ядрами, точная частота ядерного резонанса для данного частного атома немного сдвигается; величина этого сдвига зависит от окружения, в котором он находится. Измерение этих сдвигов помогает определить, какой атом находится рядом с каким, и проливает свет на детали структуры молекул. Столь же важен и электронный спиновый резонанс свободных радикалов. Такие радикалы, обычно крайне неустойчивые, часто появляются на промежуточных этапах ряда химических реакций. Измерение электронного спинового резонанса служит очень чувствительным индикатором при обнаружении свободных радикалов и часто дает ключ к пониманию механизма некоторых химических реакций.
* Обычные пары натрия в основном моноатомны, хотя изредка там и встречаются молекулы Na2.
Глава 36 ФЕРРОМАГНЕТИЗМ
§ 1. Токи намагничивания
§ 2. Поле Н
§ 3. Кривая намагннчивання
§ 4. Индуктивность с железным сердечником
§ 5. Электромагниты
§ 6. Спонтанная намагниченность
Повторить: гл. 10 (вып. 5)«Диэлектрики»
гл. 17 (вып. 6) «Законы индукции»
§ 1. Токи намагничивания
В этой главе мы поговорим о некоторых материалах, в которых полный эффект магнитных моментов проявляется во много раз сильнее, чем в случае парамагнетизма или диамагнетизма. Это явление называется ферромагнетизмом. В парамагнитных и диамагнитных материалах при помещении их во внешнее магнитное поле возникает обычно настолько слабый наведенный индуцированный магнитный момент, что нам не приходится думать о добавочных магнитных полях, создаваемых этими магнитными моментами. Другое дело магнитные моменты ферромагнитных материалов, которые создаются приложенным магнитным полем. Они очень велики и оказывают существенное воздействие на сами поля. Эти индуцированные магнитные моменты так огромны, что они вносят главный вклад в наблюдаемые поля. Поэтому нам следует позаботиться о математической теории больших индуцированных магнитных моментов. Это, разумеется, чисто формальный вопрос. Физическая проблема состоит в том, почему магнитные моменты столь велики и как они «устроены». Но к этому вопросу мы подойдем немного позже.
Нахождение магнитных полей в ферромагнитных материалах несколько напоминает задачу о нахождении электрических полей в диэлектриках. Помните, сначала мы описывали внутренние свойства диэлектрика через векторное поле Р — дипольный момент единицы объема. Затем мы сообразили, что эффект этой поляризации эквивалентен плотности заряда rпол, определяемой дивергенцией Р;
rпол= -С·Р. (36.1)
Полный же заряд в любой ситуации можно записать в виде суммы этого поляризационного заряда и всех других зарядов, плотность которых мы обозначим через rдр. Тогда уравнения Максвелла, которые связывают дивергенцию Е с плотностью зарядов, примут вид:
или
Затем мы можем перебросить поляризационную часть заряда в левую сторону уравнения и получить
С· (e0Е+Р)=rдр. (36.2)
Этот новый закон говорит, что дивергенция величины (e0 Е+Р) равна плотности других зарядов.
Совместная запись Е и Р, как это сделано в уравнении (36.2), полезна, разумеется, только когда мы знаем какие-то соотношения между ними. Мы видели, что теория, связывающая наведенный электрический дипольный момент с полем,— вещь довольно сложная и ее на самом деле можно применять только в относительно простых случаях, но и то только как приближение. Я хочу напомнить вам об одном приближении.
Фиг. 36.1. Электрическое поле в полости в диэлектрике зависит от формы полости.
Чтобы найти наведенный дипольный момент атома внутри диэлектрика, необходимо знать электрическое поле, которое действует на отдельный атом. В свое время мы использовали приближение, пригодное во многих случаях; было предположено, что на атом действует поле, которое было бы в центре небольшой полости, оставшейся после удаления этого атома (считая, что дипольные моменты всех других соседних атомов при этом не изменяются). Вспомните также, что электрическое поле в полости внутри поляризованного диэлектрика зависит от формы этой полости. Эти результаты мы подытожили на фиг. 36.1. В тонкой дискообразной полости, перпендикулярной направлению поляризации, электрическое поле, как было показано с помощью закона Гаусса, имеет вид
Еполость=Едиэл+P/e0 (дискообразная полость). С другой стороны, используя равенство нулю ротора, мы нашли, что электрическое поле внутри и вне иглообразной полости одно и то же:
Еполость= Едиэл (иглообразная полость).
Наконец, мы обнаружили, что величина электрического поля внутри сферической полости лежит между этими двумя значениями:
Еполость=Едиэл+1/3P/e0 (сферическая полость). (36.3)
Это и было то поле, которым мы пользовались, рассуждая о том, что происходит с атомами внутри поляризованного диэлектрика.
Попробуем обсудить аналогичную задачу в случае магнетизма. Легче всего и короче просто сказать, что М — магнитный момент единицы объема (намагниченность) — в точности аналогичен Р — электрическому дипольному моменту единицы объема (поляризация) и что, следовательно, отрицательная дивергенция М эквивалентна «плотности магнитных зарядов» rm, что бы это ни означало. Но беда в том, что в физическом мире не существует такой штуки, как «магнитный заряд». Как мы знаем, дивергенция В всегда равна нулю. Это, однако, не помешает нам провести искусственную аналогию и написать
СM=-rm, (38.4)
но нужно понимать, что rm— величина чисто математическая. Затем мы можем все делать полностью аналогично электростатике и использовать все старые электростатические уравнения. К этому часто прибегают. Когда-то такая аналогия считалась даже правильной. Ученые верили, что rmпредставляет плотность «магнитных полюсов». Однако сейчас нам известно, что намагничивание материала происходит за счет токов, циркулирующих внутри атомов, т. е. либо вращения электронов, либо движения их в атоме. Следовательно, с физической точки зрения лучше описывать намагничивание только при помощи реальных атомных токов, а не вводить плотность каких-то мистических «магнитных зарядов». Эти токи иногда называются еще «амперовскими», ибо Ампер первый предположил, что магнетизм вещества происходит за счет циркуляции атомных токов.
Микроскопические плотности токов в намагниченном веществе, разумеется, очень сложны. Их величина зависит от местоположения в атоме: в некоторых местах они велики, в других — малы, в одной части они текут в одну сторону, а в другой — в противоположную (точно так же, как микроскопическое электрическое поле, которое внутри диэлектрика в высшей степени неоднородно). Однако во многих практических задачах нас интересуют только поля вне вещества или средние магнитные поля внутри него, причем под средним мы имеем в виду усреднение по очень многим атомам. В таких макроскопических задачах магнитное состояние вещества удобно описывать через намагниченность М — средний магнитный момент единицы объема. Я расскажу сейчас, как атомные токи в намагниченном веществе вырастают до макроскопических токов, которые связаны с М.
Разобьем плотность тока j, которая является реальным источником магнитных полей, на разные части; одна из них описывает циркулирующие токи атомных магнитиков, а остальные — другие возможные токи. Обычно удобнее делить токи на три части. В гл. 32 мы делали различие между токами, свободно текущими по проводникам, и токами, обусловленными движением связанных зарядов в диэлектрике то туда, то сюда. В гл. 32, §2, мы писали
j=jпол+ jдр,
причем величина jпол представляла токи от движения связанных зарядов в диэлектриках, a jдp — все другие токи. Пойдем дальше. Я хочу из jр выделить часть jмar, которая описывает усредненные токи внутри намагниченных материалов, и дополнительный член, который мы будем называть jnpов и который будет описывать все остальное. Он, вообще говоря, относится к токам в проводниках, но может описывать и другие токи, например токи зарядов, движущихся свободно через пустое пространство. Таким образом, полную плотность тока мы будем писать в виде
j =jпол+jмaг+jnpoв. (36.5)
Разумеется, именно этот ток входит в уравнение Максвелла с ротором В;
Теперь мы должны связать ток jмaг с величиной вектора намагниченности М. Чтобы вы представляли, к чему мы стремимся, скажу, что должен получиться такой результат:
jмaг=СXM. (36.7)
Если в магнитном материале нам всюду задан вектор намагниченности М, то плотность циркуляционного тока определяется ротором М. Посмотрим, можно ли понять, почему так происходит.
Сначала возьмем цилиндрический стержень, равномерно намагниченный параллельно его оси. Мы знаем, что физически такая равномерная намагниченность означает на самом деле однородную повсюду внутри материала плотность атомных циркулирующих токов. Попытаемся представить себе, как выглядят эти реальные токи в поперечном сечении стержня. Мы ожидаем увидеть токи, напоминающие изображенные на фиг.36.2.
Фиг.36.2. Схематическая диаграмма циркулирующих атомных токов в поперечном сечении железного стержня, намагниченного в направлении оси z.
Каждый атомный ток течет по кругу, образуя крохотную цепь, причем все циркулирующие токи текут в одном и том же направлении. Каким же тогда будет эффективный ток? В большей части стержня он, конечно, не дает вообще никакого эффекта, ибо рядом с каждым током есть другой ток, текущий в противоположном направлении. Если представить себе небольшую поверхность, показанную на фиг. 36.2 линией АВ, которая, однако, чуть-чуть толще отдельного атома, то полный ток через такую поверхность должен быть равен нулю. Внутри материала никакого тока нет. Однако обратите внимание, что на поверхности материала атомные токи не компенсируются соседними токами, текущими в другом направлении. Поэтому по поверхности все время в одном направлении вокруг стержня течет ток. Теперь вам понятно, почему я утверждал, что равномерно намагниченный стержень эквивалентен соленоиду с текущим по нему электрическим током.
Как же эта точка зрения согласуется с выражением (36.7)? Прежде всего намагниченность М внутри материала постоянна, так что все ее производные равны нулю. Это согласуется с нашей геометрической картиной. Однако М на поверхности на самом деле не постоянна, она постоянна вплоть до поверхности, а затем неожиданно падает до нуля. Таким образом, непосредственно на поверхности возникает громадный градиент, который в соответствии с выражением (36.7) даст огромную плотность тока. Предположим, что мы наблюдаем за тем, что происходит вблизи точки С на фиг. 36.2. Если выбрать направления осей х и у так, как это показано на фигуре, то намагниченность М будет направлена по оси z. Выписывая компоненты уравнения (36.7), мы получаем
Хотя производная dMz/dy в точке С равна нулю, производная dMz/dx будет большой и положительной. Выражение (36.7) говорит, что в отрицательном направлении оси у течет ток огромной плотности. Это согласуется с нашим представлением о поверхностном токе, текущем вокруг цилиндра.
Теперь мы можем найти плотность тока в более сложном случае, когда намагниченность в материале меняется от точки к точке. Качественно нетрудно понять, что если в двух соседних областях намагниченность различная, то полной компенсации циркулирующих токов не происходит, поэтому полный ток внутри материала не равен нулю. Именно этот эффект мы и хотим получить количественно.
Прежде всего вспомните, что в гл. 14, § 5 (вып. 5), мы выяснили, что циркулирующий ток I создает магнитный момент
m=IА, (36.9)
где А— площадь, ограниченная контуром тока (фиг. 36.3).
Фиг. 36.3. Дипольный момент m кон тура тока равен IA.
Рассмотрим маленький прямоугольный кубик внутри намагниченного материала (фиг. 36.4).
Фиг. 36.4. Небольшой намагниченный кубик эквивалентен циркулирующему поверхностному току.
Пусть кубик будет так мал, что намагниченность внутри него можно считать однородной. Если компонента намагниченности этого кубика в направлении оси z равна Мz, то полный эффект будет таким, как будто по вертикальным граням течет поверхностный ток. Величину этого тока мы можем найти из равенства (36.9). Полный магнитный момент кубика равен произведению намагниченности на объем:
m=Mz(abc),
откуда, вспоминая, что площадь равна ас, получаем
I=Мzb.
Другими словами, на каждой из вертикальных поверхностей величина тока на единицу длины по вертикали равна Мz.
Представьте теперь два таких маленьких кубика, расположенных рядом друг с другом (фиг. 36.5).
Фиг. 36.5. Если намагниченность двух соседних кубиков различна, то на их границе течет поверхностный ток.
Кубик 2 несколько смещен по отношению к кубику 1, поэтому его вертикальная компонента намагниченности будет немного другой, скажем Mz+DМz. Теперь полный ток на поверхности между этими двумя кубиками будет слагаться из двух частей. По кубику 1 в положительном направлении по оси у течет ток I1, а по кубику 2 в отрицательном направлении течет ток I2. Полный поверхностный ток в положительном направлении оси у будет равен сумме
I=I1-I2=Мzb-(Мz+DМz)b=-DMzb.
Величину DМгможно записать в виде произведения производной от Mzпо х на смещение кубика 2 относительно кубика 1, которое как раз равно а:
DMz=(дMz /дx)а. Тогда ток, текущий между двумя кубиками, будет равен
I=(-дMz/дx)ab.
Чтобы связать ток I со средней объемной плотностью тока j, необходимо понять, что этот ток на самом деле размазан по некоторой области поперечного сечения. Если мы вообразим, что такими маленькими кубиками заполнен весь объем материала, то за такое сечение (перпендикулярное оси х) может быть выбрана боковая грань одного из кубиков. Теперь вы видите, что площадь, связанная с током, как раз равна площади ab одной из фронтальных граней. В результате получаем
Наконец-то у нас начинает получаться ротор М.
Но в выражении для jyдолжно быть еще одно слагаемое, связанное с изменением x-компоненты намагниченности с изменением z. Этот вклад в j происходит от поверхности между двумя маленькими кубиками, поставленными друг на друга (фиг. 36.6).
Фиг. 36.6. Два кубика, расположенных один над другим, тоже могут давать вклад в jy.
Воспользовавшись только что проведенными рассуждениями, мы можем показать, что эта поверхность будет давать в величину jy вклад, равный dMx/dz. Только эти поверхности и будут давать вклад в y-компоненту тока, так что полная плотность тока в направлении оси у получается равной
Определяя токи на остальных гранях куба или используя тот факт, что направление оси z было выбрано совершенно произвольно, мы можем прийти к заключению, что вектор плотности тока действительно определяется выражением .
j=СXM.
Итак, если вы решили описывать магнитное состояние вещества через средний магнитный момент единицы объема М, то оказывается, что циркулирующие атомные токи эквивалентны средней плотности тока в веществе, определяемой выражением (36.7). Если же материал обладает вдобавок еще диэлектрическими свойствами, то в нем может возникнуть и поляризационный ток jпол=dP/dt. А если материал к тому же и проводник, то в нем может течь и ток проводимости jпров. Таким образом, полный ток можно записать как
J = Jпрoв+СXM+дP/дt; (36.10)
§ 2. Поле Н
Теперь можно подставить выражение для тока (36.10) в уравнение Максвелла. Мы получаем
Слагаемое с М можно перенести в левую часть:
Как мы уже отмечали в гл. 32, иногда удобно записывать (Е+Р/e0) как новое векторное поле D/e0. Точно так же удобно (В-М/e0с2) записывать в виде единого векторного поля. Такое поле мы обозначим через Н, т. е.
H=В-M/(e0c2). (36.12)
После этого уравнение (36.11) принимает вид
e0c2СXH=jnpов+дD/дt. (36.13)
Выглядит оно просто, но вся его сложность теперь скрыта в буквах D и Н.
Хочу предостеречь вас. Большинство людей, которые применяют систему СИ, пользуются другим определением Н. Называя свое поле через Н' (они, конечно, не пишут штриха), они определяют его как
Н'=e0с2В-М. (36.14)
(Кроме того, величину e0с2 они обычно записывают в виде l/m0, так что появляется еще одна постоянная, за которой все время нужно следить!) При таком определении уравнение (36.13) будет выглядеть еще проще:
СXH' = jnpoв+дD/дt. (36.15)
Но трудность здесь заключается в том, что такое определение, во-первых, не согласуется с определением, принятым теми, кто не пользуется системой СИ, и, во-вторых, поля Н' и В измеряются в различных единицах. Я думаю, что Н удобнее измерять в тех же единицах, что и В, а не в единицах М, как Н'. Но если вы собираетесь стать инженером и проектировать трансформаторы, магниты и т. п., то будьте внимательны. Вы столкнетесь со множеством книг, где в качестве определения Н используется уравнение (36.14), а не (36.12), а в других книгах, особенно в справочниках о магнитных материалах, связь между В и Н такая же, как и у нас. Нужно быть внимательным и понимать, какое где использовано соглашение.
Одна из примет, указывающих нам на соглашение,— это единицы измерения. Напомним, что в системе СИ величина В, а следовательно, и наше Н измеряются в единицах вб/м2 (1 вб/м2=10 000 гс). Магнитный же момент (т. е. произведение тока на площадь) в той же системе СИ измеряется в единицах а·м2. Тогда намагниченность М имеет размерность а/м. Размерность Н' та же, что и размерность М. Нетрудно видеть, что это согласуется с уравнением (36.15), поскольку у имеет размерность обратной длины.
Те, кто работает с электромагнитами, привыкли измерять поле Н (определенное как Н') в ампер-витках/метр, имея при этом в виду витки провода в обмотке. Но «виток» ведь фактически величина безразмерная, и она не должна вас смущать. Поскольку наше Н равно H'/e0c2, то, если вы пользуетесь системой СИ, Н (в вб/м) равно произведению 4p·10-7 на Н'(в а/м). Может быть, более удобно помнить, что Н (в гс) равно 0,0126 H' (в а/м).
Здесь есть еще одна ужасная вещь. Многие люди, использующие наше определение Н, решили назвать единицы измерения Н и В по-разному! И даже несмотря на одинаковую размерность, они называют единицу В гауссом, а единицу Н — эрстедом (конечно, в честь Гаусса и Эрстеда). Таким образом, во многих книгах вы найдете графики зависимости В в гауссах от Н в эрстедах. На самом деле это одна и та же единица, равная 10-4 единиц СИ. Эту неразбериху в магнитных единицах мы увековечили в табл. 36.1.
Таблица 36.1 · ЕДИНИЦЫ МАГНИТНЫХ ВЕЛИЧИН
§ 3. Кривая намагничивания
Рассмотрим теперь некоторые простые случаи, когда магнитное поле остается постоянным или изменения поля настолько медленны, что можно пренебречь dD/dt по сравнению с jnpoв. В этом случае поля подчиняются уравнениям
СXB=0, (36.16)
СXH=jпров/e0c2, (36.17)
H=B-M/e0c2. (36.18)
Предположим, что у нас есть железный тор с намотанной на него медной проволокой, как это показано на фиг. 36.7, а.
Фиг. 36.7. Железный тор, обмотанный витками изолированного провода (а), и его поперечное сечение (б). Показаны силовые линии.
Пусть по проводу течет ток I. Каково при этом магнитное поле? Оно будет сосредоточено главным образом внутри железа, причем там (см. фиг. 36.7, б) силовые линии должны быть круговыми. Вследствие постоянства потока В его дивергенция равна нулю, и уравнение (36.16) удовлетворяется автоматически. Запишем затем уравнение (36.17) в другой форме, проинтегрировав его по замкнутому контуру Г, показанному на фиг. 36.7, б. Из теоремы Стокса мы получаем
где интеграл от j берется по поверхности S, ограниченной контуром Г. Каждый виток обмотки пересекает эту поверхность один раз, поэтому каждый виток дает в интеграл вклад, равный I, а поскольку всего витков N штук, то интеграл будет равен NI. Из симметрии нашей задачи видно, что В одинаково на всем контуре Г, если, конечно, намагниченность, а следовательно, и поле Н тоже постоянны на контуре Г. Уравнение (36.19) при таких условиях принимает вид
где l—длина кривой Г. Таким образом,
Именно из-за того что в задачах подобного типа поле Н прямо пропорционально намагничивающему току, оно иногда называется намагничивающим.
Единственное, что нам теперь требуется,— это уравнение, связывающее Н с В. Однако такого уравнения просто не существует! У нас есть, конечно, уравнение (36.18), но от него мало проку, ибо в ферромагнитных материалах типа железа оно не дает прямой связи между М и В. Намагниченность М зависит от всей предыдущей истории данного образца железа, а не только от того, каково поле В в данный момент и как оно изменялось раньше.
Впрочем, еще не все потеряно. В некоторых простых случаях мы все же можем найти решение. Если взять ненамагниченное железо, скажем, отожженное при высокой температуре, то для такого простого тела, как тор, магнитная предыстория всего железа будет одной и той же. Затем из экспериментальных измерений мы можем кое-что сказать относительно М, а следовательно, и о связи между В и Н. Из уравнения (36.20) видно, что поле В внутри тора равно произведению некоторой постоянной на величину тока в обмотке I. А поле В можно измерить интегрированием по времени э.д.с. в намагничивающей обмотке, изображенной на рисунке (или в дополнительной обмотке, намотанной поверх нее). Эта э.д.с. равна скорости изменения потока В, так что интеграл от э.д.с. по времени равен произведению В на площадь поперечного сечения тора.
На фиг. 36.8 показано соотношение между В и Н, наблюдаемое в сердечнике из мягкого железа.
Фиг. 36.8. Типичная кривая намагничивания и петля гистерезиса мягкого железа.
Когда ток включается в первый раз, увеличение В с Н происходит по кривой а. Обратите внимание на различие масштабов по осям В и Н; вначале, чтобы получить большое В, необходимо относительно малое Н. Почему же в случае железа поле В намного больше, чем было бы без него? Да потому, что возникает большая намагниченность М, эквивалентная большому поверхностному току в железе, а поле определяется суммой этого тока и тока проводимости в обмотке. А почему намагниченность М оказывается такой большой, мы обсудим позднее.
При больших значениях Н кривая намагничивания «выравнивается». Мы говорим, что железо насыщается. В масштабах нашей фигуры кривая становится горизонтальной, на самом же деле намагниченность продолжает слабо расти: для больших полей В становится равным Н и намагниченность М уже не увеличивается. Кстати, если бы сердечник был сделан из немагнитного материала, то намагниченность М была бы равна нулю, а В было бы равно для всех полей Н.
Прежде всего заметим, что кривая а на фиг. 36.8, так называемая кривая намагничивания,— в высшей степени нелинейна. Впрочем, положение здесь гораздо сложнее. Если после достижения насыщения мы уменьшим ток в катушке и вернем Н снова к нулю, магнитное поле В будет падать по кривой b. Когда Н достигнет нуля, В еще не будет нулем. Даже после выключения намагничивающего тока магнитное поле в железе остается: железо становится постоянно намагниченным. Если теперь включить в катушке ток в обратном направлении, то кривая В—Н пойдет дальше по ветви b до тех пор, пока железо не намагнитится до насыщения в противоположном направлении. При дальнейшем уменьшении тока до нуля В пойдет по кривой с. Когда мы меняем ток от большой положительной до большой отрицательной величины, кривая В—Н будет идти вверх и вниз очень близко к ветвям b и c. Если же, однако, Н менять каким-то произвольным образом, то возникнут более сложные кривые, которые, вообще говоря, будут лежать между кривыми b и c. Кривая, полученная повторными изменениями полей, называется петлей гистерезиса.
Вы видите, что невозможно написать функциональное соотношение типа В=f(Н), так как В в любой момент зависит не только от Н в тот же момент, но и от всей предыстории материала. Естественно, что намагниченность и петли гистерезиса для разных веществ различны. Форма кривых критически зависит от химического состава материала, а также от деталей технологии его приготовления и последующей физической обработки. В следующей главе мы обсудим физическое объяснение некоторых из этих сложностей.
§ 4. Индуктивность с железным сердечником
Одно из наиболее важных применений магнитные материалы находят в электрических устройствах, например трансформаторах, электрических моторах и т. п. Объясняется это прежде всего тем, что с помощью железа можно контролировать поведение магнитного поля, а также при данном электрическом токе получать значительно большие поля. Например, типичное «тороидальное» индуктивное устройство во многом напоминает то, что изображено на фиг. 36.7. При большой индуктивности мы можем сделать устройство гораздо меньшего объема и затратить намного меньше меди, чем в эквивалентном устройстве с «воздушным сердечником». Поэтому при большой индуктивности мы добиваемся гораздо меньшего сопротивления обмотки, так что устройство более близко к «идеальному», особенно при низких частотах. Нетрудно качественно проследить, как работает такое устройство. Если в обмотке течет ток I, то создаваемое внутри поле Н, как это видно из уравнения (36.20), пропорционально току I. Напряжение V на выводах связано с магнитным полем В. Если пренебречь сопротивлением обмотки, то напряжение V будет пропорционально dB/dt. Индуктивность L, которая равна отношению V к dI/dt (см. гл. 17, § 7, вып. 6), зависит, таким образом, от связи между В и Н в железе. Поскольку В гораздо больше Н, то это во много раз увеличивает индуктивность, как будто малый ток в катушке, который обычно дает слабое магнитное поле, заставляет выстраиваться маленькие магнитики, сидящие в железе, и создает «магнитный» ток, который в огромное число раз больше внешнего тока в обмотке. Все происходит так, как будто в катушке возникает ток, намного больший, чем на самом деле. Когда мы меняем направление тока, все маленькие магнитики переворачиваются, внутренние токи потекут в другом направлении и наведенная э.д.с. получается гораздо больше, чем без железа. Если мы хотим вычислить индуктивность, то это можно сделать, вычисляя энергию наподобие того, как описано в гл. 17, § 8. Скорость, с которой энергия отдается источником тока, равна IV. Напряжение V равно площади поперечного сечения сердечника А, умноженной на N и на dB/dt. А согласно выражению (36.20), I=(e0c2l/N)H. Таким образом,
Интегрируя по времени, получаем
Заметьте, что 1А равно объему тора, поэтому плотность энергии и=U/(Объем магнитного материала), как мы показали, равна
Здесь выявляется одно интересное обстоятельство. Когда в обмотке течет переменный ток, то В в железе «ходит» по петле гистерезиса. А поскольку В — неоднозначная функция Я,
то интеграл ∫HdB по замкнутому циклу равен не нулю, а площади, заключенной внутри петли гистерезиса. Таким образом, за каждый цикл источник тока отдает некоторую энергию, равную площади петли гистерезиса. Это есть потери из электромагнитного цикла; энергия уходит на нагревание железа. Такие потери называются гистерезисными. Чтобы они были поменьше, петлю гистерезиса желательно сделать как можно уже. Один из способов уменьшить площадь петли — это максимально уменьшить поле в каждом цикле. Для меньших максимальных полей мы получаем гистерезисную кривую, подобную изображенной на фиг. 36.9.
Фиг. 36.9. Петля гистерезиса, не достигающая насыщения.
Кроме того, применяются особые материалы с очень узкой петлей. Чтобы получить это свойство, специально создано так называемое трансформаторное железо, которое представляет сплав железа с небольшой примесью кремния.
Когда петля гистерезиса очень мала, соотношение В и Н приближенно можно представлять в виде линейного уравнения. Обычно пишут
В=mН. (36.23)
Здесь постоянная m вовсе не магнитный момент, с которым мы встречались раньше. Она называется магнитной проницаемостью. (Иногда ее называют также относительной проницаемостью.) Типичная проницаемость обычных сортов железа равна нескольким тысячам. Однако существуют специальные сплавы, типа так называемого «супермаллоя», проницаемость которых может быть порядка миллиона.
Если в уравнении (36.21) мы воспользуемся приближением В=mН, то энергию индуктивности, имеющей форму тора, можно записать как
так что плотность энергии приближенно равна
Теперь мы можем выражение для энергии (36.24) положить равным энергии индуктивности LI2/2 и найти L. Получается
А воспользовавшись выражением (36.20) для отношения H/I, находим
Таким образом, индуктивность пропорциональна m. Если вам нужна индуктивность для таких устройств, как звуковые усилители, то желательно иметь материал, у которого связь между В и Н достаточно линейна. [Вы, должно быть, помните, что в гл. 50 (вып. 4) мы говорили о генерации гармоник в нелинейных системах.] Для таких задач уравнение (36.23) будет очень хорошим приближением. С другой стороны, если нужно генерировать гармоники, то используют индуктивности, ведущие себя в высшей степени нелинейно. При этом вы должны пользоваться сложной кривой Н—В и применять при вычислениях графические или численные методы.
В обычных «трансформаторах» на одном и том же торе, или сердечнике, из магнитного материала намотаны две катушки. (В больших трансформаторах сердечник для удобства делается прямоугольным.) При этом изменение тока в «первичной» обмотке вызывает изменение поля в сердечнике, которое индуцируется э.д.с. во «вторичной» обмотке. Поскольку поток через каждый виток обеих обмоток один и тот же, то величина отношения э.д.с. в этих двух обмотках такая же, как отношение числа витков в каждой из них. Напряжение, приложенное к первичной обмотке, преобразуется во вторичной в напряжение другой величины. А поскольку для создания требуемых изменений магнитного поля необходим определенный полный ток, то алгебраическая сумма токов в двух обмотках должна оставаться постоянной и равной требуемому «намагничивающему» току. При изменении напряжения изменяется и сила тока в обмотках, т. е. вместе с преобразованием напряжения происходит и преобразование тока.
§ 5. Электромагниты
Поговорим теперь о практической стороне дела, которая немного более сложна. Предположим, что мы имеем электромагнит стандартной формы, изображенный на фиг. 36.10.
Фиг. 36.10. Электромагнит.
Он состоит из С-образного железного ярма, на которое намотано много витков провода. Чему равно магнитное поле В в зазоре?
Если ширина зазора мала по сравнению со всеми другими размерами, то в качестве первого приближения мы можем считать, что линии В образуют замкнутые кривые так же, как это происходит и в обычном торе. Они выглядят примерно так, как показано на фиг. 36.11,а.
Фиг. 36.11. Поперечное сечение электромагнита.
Они стремятся вылезть из зазора, но если он узок, то эффект этот очень мал. Предположение о постоянстве потока В через любое поперечное сечение ярма будет довольно хорошим приближением. Если поперечное сечение ярма меняется равномерно и если мы пренебрежем любыми краевыми эффектами на зазоре или на углах, то можно говорить, что по всей окружности ярма В однородно.
Поле В в зазоре будет по величине тем же самым. Это следует из уравнений (36.16). Представьте себе замкнутую поверхность S (см. фиг. 36.11,б), одна грань которой находится в зазоре, а другая — в железе. Полный поток поля В через эту поверхность должен быть равен нулю. Обозначая через В1 величину поля в зазоре, а через B2 — величину поля в железе, мы видим, что
B1A1-В2А2=0,
а поскольку А1=А2, то отсюда следует, что В1=В2.
Посмотрим теперь на Н. Мы снова можем воспользоваться уравнением (36.19), взяв криволинейный интеграл по контуру Г (см. фиг. 36.11,6). Как и прежде, правая часть равна NI— произведению числа витков на ток. Однако теперь Н в железе и в воздухе будет различным. Обозначая через Н2поле в железе, а через l2 — Длину пути по окружности ярма, мы видим, что эта часть кривой дает вклад в интеграл H2l2. Если же поле в зазоре равно Н1, а ширина его l1, то вклад зазора оказывается равным H1l1. Таким образом, получаем
Но это еще не все. Нам известно еще, что намагниченность в воздушной щели пренебрежимо мала, так что B1=H1. А так как B1=B2, то уравнение (36.26) принимает вид
Остаются еще два неизвестных. Чтобы найти В2и H2, необходимо еще одно соотношение, которое связывает В с H в железе.
Если можно приближенно считать, что B2=mH2, то уравнение разрешается алгебраически. Рассмотрим более общий случай, для которого кривая намагничивания железа имеет вид, изображенный на фиг. 36.8. Единственное, что нам нужно,— это найти совместное решение этого функционального соотношения с уравнением (36.27). Его можно найти, строя зависимость (36.27) на одном графике с кривой намагничивания, как это сделано на фиг. 36.12. Точки, где эти кривые пересекутся, и будут нашими решениями.
Для данного тока I уравнение (36.27) описывается прямой линией, обозначенной I>0 на фиг. 36.12. Эта линия пересекает ось Н (B2=0) в точке H2=NI/e0c2l2и имеет наклон -l2/l1 Различные величины токов приводят просто к горизонтальному сдвигу этой линии. Из фиг. 36.12 мы видим, что при данном токе существует несколько различных решений, зависящих от того, каким образом вы получили их.
Фиг. 36.12. Определение поля в электромагните.
Если вы только что построили магнит и включили ток /, то поле B2 (которое равно B1) будет иметь величину, определяемую точкой а. Если вы сначала увеличили ток до очень большой величины, а затем понизили до I, то значение поля будет определяться точкой b. А если, увеличивая ток от большого отрицательного значения, вы дошли до /, то поле определяется точкой с. Поле в зазоре зависит от того, как вы поступали в прошлом.
Если ток в магните равен нулю, то соотношение между В2 и H2в уравнении (36.27) изображается кривой, обозначенной I=0 на фиг. 36.12. Здесь опять возможны различные решения. Если вы первоначально «насытили» железо, то в магните может сохраниться значительное остаточное поле, определяемое точкой d. Вы можете снять обмотку и получить постоянный магнит. Нетрудно понять, что для хорошего постоянного магнита необходим материал с широкой петлей гистерезиса. Такую очень широкую петлю имеют специальные сплавы, подобные Алнико V.
§ 6. Спонтанная намагниченность
Обратимся теперь к вопросу, почему в ферромагнитных материалах даже малые магнитные поля приводят к такой большой намагниченности. Намагниченность ферромагнитных материалов типа железа или никеля образуется благодаря магнитным моментам электронов одной из внутренних оболочек атома. Магнитный момент m каждого электрона равен произведению q/2m на g-фактор и момент количества движения J. Для отдельного электрона при отсутствии чисто орбитального движения g=2, а компонента J в любом направлении, скажем, в направлении оси z, равна ±h/2, так что компонента m в направлении оси z будет
mz=gh/2m=0,928·10-23 а/м2. (36.28)
В атоме железа вклад в ферромагнетизм фактически дают только два электрона, так что для упрощения рассуждений мы будем говорить об атоме никеля, который является ферромагнетиком, подобно железу, но имеет на той же внутренней оболочке только один «ферромагнитный» электрон. (Все рассуждения нетрудно затем распространить и на железо.)
Все дело в том, что точно так же, как и в описанных нами парамагнитных материалах, атомные магнитики в присутствии внешнего магнитного поля В стремятся выстроиться по полю, но их сбивает тепловое движение. В предыдущей главе мы выяснили, что равновесие между силами магнитного поля, старающимися выстроить атомные магнитики, и действием теплового движения, стремящегося их сбить, приводит к тому, что средний магнитный момент единицы объема в направлении В оказывается равным
где под Вамы подразумеваем поле, действующее на атом, а под kT — тепловую (больцмановскую) энергию. В теории парамагнетизма мы в качестве Ваиспользовали само поле В, пренебрегая при этом частью поля, действующего на каждый атом со стороны соседнего. Но в случае ферромагнетиков возникает усложнение. Мы уже не можем в качестве поля Ва, действующего на индивидуальный атом, брать среднее поле в железе. Вместо этого нам следует поступить так же, как это делалось в случае диэлектрика: нам нужно найти локальное поле, действующее на отдельный атом. При точном решении нам следовало бы сложить вклады всех полей от других атомов кристаллической решетки, действующих на рассматриваемый нами атом. Но подобно тому как мы поступали в случае диэлектрика, сделаем приближение, состоящее в том, что поле, действующее на атом, будет таким же, как и в маленькой сферической полости внутри материала (предполагая при этом, как и раньше, что моменты соседних атомов не изменяются из-за наличия полости).
Следуя рассуждениям гл. 11 (вып. 5), мы можем надеяться, что должна получиться формула
похожая на формулу (11.25). Но это будет неправильно. Однако мы все же можем использовать полученные там результаты, если тщательно сравним уравнения из гл. 11 с уравнениями ферромагнетизма, которые мы напишем сейчас. Сопоставим сначала соответствующие исходные уравнения. Для областей, в которых токи проводимости и заряды отсутствуют, мы имеем:
Эти два набора уравнений можно считать аналогичными, если мы чисто математически сопоставим
Это то же самое, что и
Другими словами, если уравнения ферромагнетизма записать как
то они будут похожи на уравнения электростатики.
В прошлом это чисто алгебраическое соответствие доставило нам некоторые неприятности. Многие начинали думать, что именно Н и есть магнитное поле. Но, как мы уже убедились, физически фундаментальными полями являются Е и В, а поле Н — понятие производное. Таким образом, хотя уравнения и аналогичны, физика их совершенно различна. Однако это не может заставить нас отказаться от принципа, что одинаковые уравнения имеют одинаковые решения.
Теперь можно воспользоваться нашими предыдущими результатами о полях внутри полости различной формы в диэлектриках, которые приведены на фиг. 36.1, для нахождения поля Н. Зная Н, можно определить и В. Например, поле Н внутри иглообразной полости, параллельной М (согласно результату, приведенному в § 1), будет тем же самым, что и поле Н внутри материала:
Но поскольку в нашей полости М равна нулю, то мы получаем
С другой стороны, для дискообразной полости, перпендикулярной М,
что в нашем случае превращается в
или в величинах В:
Наконец, для сферической полости аналогия с уравнением (36.3) дала бы
Результаты для магнитного поля, как видите, отличаются от тех, которые мы имели для электрического поля.
Конечно, их можно получить и более физически, непосредственно используя уравнения Максвелла. Например, уравнение (36.34) непосредственно следует из уравнения С·B=0. (Возьмите гауссову поверхность, которая наполовину находится в материале, а наполовину — вне его.) Подобным же образом вы можете получить уравнение (36.33), воспользовавшись контурным интегралом по пути, который туда идет по полости, а назад возвращается через материал. Физически поле в полости уменьшается благодаря поверхностным токам, определяемым как V X М. На вашу долю остается показать, что уравнение (36.35) можно получить, рассматривая эффекты поверхностных токов на границе сферической полости.
При нахождении равновесной намагниченности из уравнения (36.29) удобнее, оказывается, иметь дело с Н, поэтому мы пишем
В приближении сферической полости коэффициент Я следует взять равным 1/3, но, как вы увидите позже, нам придется пользоваться несколько другим его значением, а пока оставим его как подгоночный параметр. Кроме того, все поля мы возьмем в одном и том же направлении, чтобы нам не нужно было заботиться о направлении векторов. Если бы теперь мы подставили уравнение (36.36) в (36.29), то получили бы уравнение, которое связывает намагниченность М с намагничивающим полем Н:
Однако это уравнение невозможно решить точно, так что мы будем делать это графически.
Сформулируем задачу в более общей форме, записывая уравнение (36.29) в виде
где Мнас — намагниченность насыщения, т. е. Nm, a x — величина mBa/kT. Зависимость М/Мнасот х показана на фиг. 36.13 (кривая а).
Фиг. 36.13. Графическое решение уравнений (36.37) и (36.38),
Воспользовавшись еще уравнением (36.36) для Ва, можно записать х как функцию от М:
Эта формула определяет линейную зависимость между М/Мнас и х при любой величине Н. Прямая пересекается с осью х в точке x=mH/kT, и наклон ее равен e0с2kT/mlKMнас. Для любого частного значения Н это будет прямая, подобная прямой b на фиг. 36.13. Пересечение кривых а и о дает нам решение для М/Мнас. Итак, задача решена.
Посмотрим теперь, годны ли эти решения при различных обстоятельствах. Начнем с H=0. Здесь представляются две возможности, показанные кривыми b1и b2на фиг. 36.14.
Фиг. 36.14. Определение намагниченности при Н=0.
Обратите внимание, что наклон прямой (36.38) пропорционален абсолютной температуре Т. Таким образом, при высоких температурах получится прямая, подобная b1Решением будет только М/Мнас=0. Иначе говоря, когда намагничивающее поле Я равно нулю, намагниченность тоже равна нулю. При низких температурах мы получили бы линию типа b2 и стали возможны два решения для М/Мнас: одно М/Мнас=0, а другое М/Мнас порядка единицы. Оказывается, что только второе решение устойчиво, в чем можно убедиться, рассматривая малые вариации в окрестности указанных решений.
В соответствии с этим при достаточно низких температурах магнитные материалы должны намагничиваться спонтанно. Короче говоря, когда тепловое движение достаточно мало, то взаимодействие между атомными магнитиками заставляет их выстраиваться параллельно друг другу, получается постоянно намагниченный материал, аналогичный постоянно поляризованным сегнетоэлектрикам, о которых мы говорили в гл. 11 (вып. 5).
Если мы отправимся от высоких температур и начнем двигаться вниз, то при некой критической температуре, называемой температурой Кюри Тc, неожиданно проявляется ферромагнитное поведение. Эта температура соответствует на фиг. 36.14 линии b3, касательной к кривой а, наклон которой равен единице. Так что температура Кюри определяется из равенства
При желании уравнение (36.38) можно записать в более простом виде через Тc:
Что же получается для малых намагничивающих полей Н? Из фиг. 36.14 нетрудно понять, что получится, если нашу прямую линию сдвинуть немного направо. В случае низкой температуры точка пересечения немного сдвинется направо по слабо наклоненной части кривой а и изменения М будут сравнительно невелики. Однако в случае высокой температуры точка пересечения побежит по крутой части кривой а и изменения М станут относительно быстрыми. Эту часть кривой мы фактически можем приближенно заменить прямой линией а с единичным наклоном и написать
Теперь можно разрешить уравнение относительно М/Мнас:
Мы получаем закон, несколько напоминающий закон для парамагнетизма:
Отличие состоит, в частности, в том, что мы получили намагниченность как функцию Н, с учетом взаимодействия атомных магнитиков, однако главное то, что намагниченность обратно пропорциональна разности температур Т и Тс, а не просто абсолютной температуре Т. Пренебрежение взаимодействием между соседними атомами соответствует l=0, что, согласно уравнению (36.39), означает Тс=0. Результат при этом получится в точности таким же, как и в гл. 35.
Нашу теоретическую картину можно сверить с экспериментальными данными для никеля. На опыте обнаружено, что ферромагнитные свойства никеля исчезают, когда температура поднимается выше 631° К. Это значение можно сравнить со значением Тс, вычисленным из равенства (36.39). Вспоминая, что Mнас=mN, мы получаем
Из плотности и атомного веса никеля находим
N=9,1·1028м-3. А вычисление m, из уравнения (36.28) и подстановка l=1/3 дает
Tс=0,24°K.
Различие с экспериментом примерно в 2600 раз! Наша теория ферромагнетизма полностью провалилась!
Можно попытаться «подправить» нашу теорию, как это сделал Вейсс, предположив, что по каким-то неизвестным причинам К равно не 1/3, а (2600) ·1/3, т. е. около 900. Оказывается, что подобная величина получается и для других ферромагнитных материалов типа железа. Вернемся к уравнению (36.36) и попробуем понять, что это может означать? Мы видим, что большая величина Я означает, что Ва(локальное поле, действующее на атом) должно быть больше, много больше, чем мы думали. Фактически, записывая Н = В-M/e0c2, мы получили
В соответствии с нашей первоначальной идеей, когда мы принимали l=1/3, локальная намагниченность М уменьшает эффективное поле Вана величину — 2М/Зe0. Даже если бы наша модель сферической полости была не очень хороша, мы все равно ожидали бы некоторого уменьшения. Вместо того чтобы объяснить явление ферромагнетизма, мы вынуждены считать, что намагниченность увеличивает локальное поле в огромное число раз: в тысячу и даже больше. По-видимому, не существует какого-то разумного способа для создания действующего на атом поля такой ужасной величины, ни даже поля нужного знака! Ясно, что наша «магнитная» теория ферромагнетизма потерпела досадный провал. Мы вынуждены заключить, что в ферромагнетизме мы имеем дело с какими-то немагнитными взаимодействиями между вращающимися электронами соседних атомов. Это взаимодействие должно порождать у соседних спинов сильную тенденцию к выстраиванию в одном направлении. Мы увидим позднее, что это взаимодействие связано с квантовой механикой и принципом запрета Паули. И, наконец, посмотрим, что происходит при низких температурах, когда Т<Tс. Мы видели, что даже при Н=0 в этом случае должна существовать спонтанная намагниченность, определяемая пересечением кривых а и b2 на фиг. 36.14. Если мы, изменяя наклон линии b2, будем находить М для различных температур, то получим теоретическую кривую, показанную на фиг. 36.15.
Фиг. 36.15. Зависимость спонтанной намагниченности никеля от температуры.
Для всех ферромагнитных материалов, атомные моменты которых обусловлены одним электроном, эта кривая должна быть одной и той же. Для других материалов подобные кривые могут отличаться лишь немного.
В пределе, когда Т стремится к абсолютному нулю, М стремится к Mнac. При увеличении температуры намагниченность уменьшается, падая до нуля при температуре Кюри. Точками на фиг. 36.15 показаны экспериментальные данные для никеля. Они довольно хорошо ложатся на теоретическую кривую. Хотя мы и не понимаем лежащего в основе механизма, но общие свойства теории, по-видимому, все же правильны.
Но в нашей попытке понять ферромагнетизм есть еще одна неприятная несогласованность, которая должна нас заботить. Мы нашли, что выше некоторой температуры материал должен вести себя как парамагнитное вещество, намагниченность которого пропорциональна Н (или В), а ниже этой температуры должна возникать спонтанная намагниченность. Но при построении кривой намагничивания для железа мы этого как раз и не обнаружили. Железо становится постоянно намагниченным только после того, как мы его «намагнитим». А в соответствии с только что высказанными идеями оно должно намагничиваться само! Что же неверно? Оказывается, что если вы рассмотрите достаточно маленький кристалл железа или никеля, то увидите что он и впрямь полностью намагничен! А большой кусок железа состоит из массы таких маленьких областей, или «доменов», которые намагничены в различных направлениях, так что средняя намагниченность в большом масштабе оказывается равной нулю. Однако в каждом маленьком домене железо все же намагничивает само себя, причем М приблизительно равно Mнac. Как следствие этой доменной структуры свойства большого куска материала должны быть совершенно отличны от микроскопических, как это и оказывается на самом деле.
* В системе, которой пользуется здесь автор, В=Н+1/e0c2 М, но
D=e0E+P. В старой, доброй системе единиц писали В=m0Н=(1/e0c2)Н и
D=e0Е или В=(Н+4pМ) и D=Е+4pР. Надо быть очень внимательным, когда формулы для магнетиков пишутся по аналогии с формулами для диэлектриков (ср. § 6).— Прим. ред.
* Или, если хотите, ток I на каждой грани может быть поровну; распределен на кубиках с двух сторон.
* Если бы все «другие» заряды находились на проводниках, то rдр было бы тем же самым, что и rсвоб в гл. 10 (вып. 5).
Глава 37 МАГНИТНЫЕ МАТЕРИАЛЫ
§ 1.Сущность ферромагнетизма
§ 2.Термодинамические свойства
§ 3. Петля гистерезиса
§ 4.Ферромагнитные материалы
§ 5.Необычные магнитные материалы
§ 1. Сущность ферромагнетизма
В этой главе мы поговорим об особенностях и поведении ферромагнетиков и некоторых других необычных магнитных материалов. Но перед тем как приступить к этой теме, я сделаю маленький обзор некоторых вопросов общей теории магнитов, которые мы изучали в предыдущей главе.
Мы сначала представили себе «магнитные» токи, текущие внутри материала и порождающие магнетизм, а затем стали их описывать через объемную плотность токов jмar=СXM. Заметьте, что эти токи нереальные. Даже когда намагниченность вещества однородна, токи в нем на самом деле не исчезают полностью: круговые токи электрона в одном атоме и круговые токи электрона в другом атоме, перекрываясь, не дают в сумме точно нуль. Даже внутри каждого отдельного атома распределение магнетизма не очень гладкое. В атоме железа, например, намагниченность распределена более или менее по сферической поверхности не слишком близко к ядру, но и не слишком далеко от него. Таким образом, магнетизм в веществе — вещь довольно сложная в своих деталях и весьма нерегулярная. Но сейчас мы должны об этих сложностях забыть и рассматривать явление, пользуясь более грубой усредненной моделью. Только тогда становится верным утверждение о равенстве нулю среднего тока при М=0 в ограниченной внутренней области, большой по сравнению с размерами атома. Таким образом, под магнитным моментом единицы объема (намагниченностью) и под jмаг и т. п. на нашем теперешнем уровне рассмотрения мы понимаем среднее по областям, большим по сравнению с пространством, занимаемым отдельным атомом.
В предыдущей главе мы обнаружили, что ферромагнитные материалы обладают следующим интересным свойством: при температурах выше некоторой их магнитные свойства проявляются слабо и лишь ниже этой температуры они становятся сильными магнетиками. Этот факт легко продемонстрировать. Кусок никелевого провода при комнатной температуре притягивается магнитом. Но если мы его нагреем в пламени газовой горелки выше температуры Кюри, то он станет практически немагнитным и не будет притягиваться к магниту, даже если мы поднесем его совсем близко. Если же оставить его остывать возле магнита, то в тот момент, когда его температура упадет ниже критической, он внезапно снова притянется к магниту!
В общей теории магнетизма, которой мы пользуемся, предполагается, что за намагниченность ответствен спин электрона. Спин электрона равен 1/2 и сопровождается магнитным моментом, равным одному магнетону Бора: (m=mb=qeh/2m. Спин электрона может быть направлен либо вверх, либо вниз. Поскольку заряд электрона отрицателен, то магнитный момент его направлен вниз, когда спин направлен вверх, и направлен вверх, когда спин направлен вниз. В соответствии с нашим обычным соглашением магнитный момент электрона (А — число отрицательное. Мы нашли, что потенциальная энергия магнитного диполя в заданном приложенном поле В равна—m·B. Энергия вращающегося электрона зависит также и от расположения соседних спинов. Если в железе момент соседнего атома направлен вверх, то момент следующего атома имеет сильную тенденцию тоже направиться вверх. Именно это делает железо, кобальт и никель такими сильными магнетиками — все моменты атомов в них стремятся быть параллельными. И вот первый вопрос, который мы должны обсудить, — почему так происходит?
Вскоре после развития квантовой механики было замечено, что существуют чрезвычайно мощные кажущиеся силы (однако не магнитные и не другие известные силы), которые стараются выстроить спины соседних электронов противоположно один другому. Эти силы тесно связаны с силами химической валентности. В квантовой механике есть так называемый принцип запрета, который говорит, что два электрона не могут занимать в точности одно и то же состояние, т. е. они не могут находиться в тех же самых условиях в смысле положения и ориентации спина. Если два электрона находятся в одном и том же месте, то единственной возможностью им различаться будет только противоположное направление их спинов. Таким образом, если между атомами имеется область пространства, где скапливаются электроны(так происходит при химической связи), и если на сидящий уже там электрон нам захочется посадить другой, то единственный способ это сделать — направить спин второго электрона противоположно спину первого. Параллельность спинов противоречит принципу запрета, если, конечно, электроны расположены в одной точке. В результате пара близких друг к другу электронов с параллельными спинами обладает гораздо большей энергией, нежели пара электронов с противоположными спинами; в целом же эффект будет таким, как будто действует сила, старающаяся развернуть спины противоположно друг другу. Иногда такие «спин-вращающие» силы называются обменными, но это название только увеличивает таинственность, так что термин этот не слишком удачен. Стремление электронов иметь противоположные спины обязано просто принципу запрета. Но фактически это объясняет отсутствие магнетизма почти у всех веществ! Спины свободных электронов на окраине атомов стремятся уравновешиваться в противоположных направлениях. Проблема заключается в том, чтобы объяснить, почему же материалы, подобные железу, ведут себя совсем не так, как ожидается.
Предполагаемый эффект выстраивания мы учитывали добавлением в выражение для энергии подходящего слагаемого, приговаривая, что если соседние электронные магнитики дают среднюю намагниченность М, то магнитный момент электрона имеет сильную тенденцию смотреть в том же самом направлении, что и средняя намагниченность соседних атомов. Таким образом, для двух возможных ориентации спинов можно написать:
Когда стало ясно, что квантовая механика может объяснить нам огромные спин-ориентирующие силы, пусть даже с очевидно неправильным знаком, то было предложено, что ферромагнетизм возникает именно за счет этих сил, но что вследствие сложности железа и большого числа участвующих в игре электронов знак энергии электронов получается обратным. Как только это стало ясно, т. е. примерно с 1927 г., когда была понята квантовая механика, многие исследователи стали делать разные оценки, прикидки, полуподсчеты, стремясь получить теоретически величину К. Но все равно наиболее поздние вычисления энергии взаимодействия между двумя электронными спинами в железе, предполагавшие прямое взаимодействие между двумя электронами в соседних атомах, дали неправильный знак. Сейчас, описывая это явление, говорят, что за все как-то ответственна сложность ситуации и что есть надежда, что кому-то, кто сумеет проделать вычисления для более сложного случая, удастся получить правильный ответ!
Полагают, что направленный вверх спин одного из электронов внутренней оболочки, который ответствен за магнетизм, стремится заставить спины электронов проводимости, витающих вокруг него, повернуться в противоположную сторону. Можно надеяться, что это ему вполне удастся, ибо электроны проводимости движутся в той же самой области, что и «магнитные» электроны. А поскольку они движутся то туда, то сюда, то могут передать свой приказ перевернуться «вверх ногами» спинам электронов других атомов; таким образом, «магнитный» электрон заставляет электрон проводимости направить спин в противоположную сторону, а тот в свою очередь заставляет следующий «магнитный» электрон направить свой спин противоположно его спину. Это двойное взаимодействие эквивалентно взаимодействию, стремящемуся выстроить два «магнитных» электрона в одном направлении. Иными словами, тенденция соседних спинов быть параллельными есть результат действия промежуточной среды, которая в некотором смысле стремится быть противоположной им обоим. Этот механизм не требует, чтобы все электроны проводимости были повернуты «вверх ногами». Достаточно, чтобы они лишь слегка стремились повернуться вниз, и шансы «магнитных» электронов повернуться вверх перевесят. Как полагают те исследователи, которые работали с этими вещами, это и есть тот механизм, который ответствен за ферромагнетизм. Но должен отметить, что вплоть до сегодняшнего дня никто не может вычислить величину l материала, зная просто, что в периодической системе элементов этот материал стоит, скажем, под номером 26. Короче говоря, мы все еще не можем понять явление до конца.
Теперь же продолжим рассуждения о нашей теории, а потом вернемся снова назад и обсудим некоторые ошибки избранного нами пути. Если магнитный момент какого-то электрона направлен вверх, то его энергия частично обусловлена внешним полем, а частично связана с тенденцией спинов быть параллельными. Поскольку при параллельных спинах энергия меньше, то эффект получается таким же, как и от «внешнего эффективного поля». Но помните, что обязано это не истинным магнитным силам, а более сложному взаимодействию. Во всяком случае, в качестве выражений для энергии двух спиновых состояний «магнитного» электрона мы примем уравнения (37.1). Относительная вероятность этих двух состояний при температуре Т пропорциональна exp[-энергия/kT], что можно записать как е±х, где х=|m|(H+lM/e0с2)/kT. Если затем мы вычислим среднюю величину магнитного момента, то найдем (как и в предыдущей главе), что она равна
M=N |m|thx. (37.2)
Теперь я могу подсчитать внутреннюю энергию материала. Отметим, что энергия электрона в точности пропорциональна магнитному моменту, так что все равно, вычислять ли средний момент или среднюю энергию. Среднее значение энергии будет при этом
Но это не совсем верно. Выражение lM/e0c2 представляет взаимодействие всех возможных пар атомов, а мы должны помнить, что каждую пару следует учитывать только один раз. (Когда мы учитываем энергию одного электрона в поле остальных, а затем энергию второго электрона в поле остальных, то мы еще раз учитываем часть первой энергии.) Поэтому выражение взаимодействия мы должны разделить на 2 и наша формула для энергии приобретет вид
В предыдущей главе мы обнаружили одну очень интересную особенность: для каждого материала ниже определенной температуры существует такое решение уравнений, при котором магнитный момент не равен нулю даже в отсутствие внешнего намагничивающего поля. Если в уравнении (37.2) мы положим Н=0, то найдем
где Мнас=N|m| и Tc=|m|lMнас./ke0c2. Решив это уравнение (графически или каким-то другим способом), мы найдем, что отношение М/Мнаскак функция от T/Tcпредставляет кривую, названную на фиг. 37.1 «квантовая теория».
Фиг. 37.1. Зависимость спонтанной намагниченности (Н=0) ферромагнитных кристаллов от температуры.
Пунктирная кривая «Кобальт, Никель» — это полученная экспериментально кривая для кристаллов этих элементов. Теория и эксперимент находятся в разумном согласии. Там же представлены результаты классической теории, в которой вычисления проводились в предположении, что атомные магнитики могут иметь всевозможные ориентации в пространстве.
Можете убедиться, что это предположение приводит к предсказаниям, которые весьма далеки от экспериментальных данных.
Даже квантовая теория недостаточно хорошо описывает наблюдаемое поведение при высоких и низких температурах. Причина этого отклонения заключена в принятом нами довольно грубом приближении: мы предполагали, что энергия атома зависит лишь от средней намагниченности соседних с ним атомов. Другими словами, каждый атом со спином, направленным вверх, находящийся по соседству с данным атомом, из-за квантовомеханического эффекта выстраивания вносит свой вклад в энергию. А сколько таких атомов? В среднем это измеряется величиной намагниченности, но это только в среднем. Может оказаться, что для какого-то одного атома спины всех его соседей направлены вверх. Тогда его энергия будет выше средней. У другого же спины некоторых соседей направлены вверх, а некоторых — вниз, а среднее может быть нулем, и тогда никакого вклада в энергию вообще не будет и т. д. Из-за того что атомы в разных местах имеют различное окружение с различным числом направленных вверх и вниз спинов, нам следовало бы воспользоваться более сложным способом усреднения. Вместо того чтобы брать один атом, подверженный среднему влиянию, нам следовало бы взять каждый атом в его реальной обстановке, подсчитать его энергию, а затем найти среднюю энергию. Но как же все-таки определить, сколько соседей атомов направлено вверх, а сколько — вниз? Это как раз и нужно вычислить, но здесь мы сталкиваемся с очень сложной задачей внутренних корреляций,— задачей, которую никому еще не удавалось решить. Эта животрепещущая и интригующая проблема в течение многих лет волновала умы физиков; по этому вопросу писалось множество статей крупнейшими учеными, но и они не могли найти полного решения.
Оказывается, что при низких температурах, когда почти все атомные магниты направлены вверх и лишь некоторые направлены вниз, задача решается довольно легко; то же самое можно сказать и о высоких температурах, значительно превышающих температуру Кюри Тс, когда почти все они направлены совершенно случайно. Часто легко вычислить небольшие отклонения от некоторой простой идеализированной теории, и довольно ясно, почему такие отклонения имеются при низких температурах. Физически понятно, что по статистическим причинам намагниченность при высоких температурах должна исчезать. Но точное поведение вблизи точки Кюри никогда во всех подробностях не было установлено. Это очень интересная задача, над которой стоит потрудиться, если когда-нибудь вам вздумается взяться за еще не решенную проблему.
§ 2. Термодинамические свойства
В предыдущей главе мы заложили основу, необходимую для вычисления термодинамических свойств ферромагнитных материалов. Они, естественно, связаны с внутренней энергией кристалла, которая обусловлена взаимодействием между различными спинами и определяется формулой (37.3). Для нахождения энергии, связанной со спонтанной намагниченностью (ниже точки Кюри), мы можем в уравнении (37.3) положить Н=0 и, заметив, что thx=М/Мнас, найти, что средняя энергия пропорциональна М2:
Если мы теперь построим график зависимости намагниченности от температуры, то получим кривую, которая описывается отрицательным квадратом функции (37.1) и представлена на фиг. 37.2, а. Если бы мы измеряли удельную теплоемкость такого материала, то получили бы кривую (фиг. 37.2, б), которая представляет производную кривой, изображенной на фиг. 37.2, а.
Фиг. 37.2. Энергия в единице объема и удельная теплоемкость ферромагнитного материала.
С увеличением температуры эта кривая медленно растет, но затем при Т = Тснеожиданно падает до нуля. Резкое падение вызвано изменением наклона кривой магнитной энергии, и кривая ее производной попадает прямо в точку Кюри. Таким образом, совершенно без магнитных измерений, лишь наблюдая за термодинамическими свойствами, мы бы смогли установить, что внутри железа или никеля что-то происходит. Однако как из эксперимента, так и из улучшенной теории (с учетом внутренних флуктуации) следует, что эти простые кривые неправильны и что истинная картина на самом деле более сложна. Пик этих кривых поднят выше, а падение до нуля происходит несколько медленнее. Даже если температура достаточно велика, так что спины в среднем распределены совершенно случайно, все равно попадаются области с определенным значением намагниченности, и спины в этих областях продолжают давать небольшую дополнительную энергию взаимодействия, которая медленно уменьшается с ростом температуры и увеличением беспорядка. Так что реальная кривая выглядит так, как показано на фиг. 37.2, в. Одна из целей физики сегодняшнего дня — найти точное теоретическое описание удельной теплоемкости вблизи точки перехода Кюри — захватывающая проблема, не решенная до сих пор. Естественно, что эта проблема очень тесно связана с формой кривой намагничивания в той же самой области.
Опишем теперь некоторые эксперименты, отнюдь не термодинамического характера, которые показывают, что мы все же в каком-то смысле правы в нашей интерпретации магнетизма. Когда материал при достаточно низких температурах намагничен до насыщения, то М очень близка к Мнас, т. е. почти все спины, равно как и магнитные моменты, параллельны. Это можно проверить экспериментально. Предположим, что мы подвесили магнитную палочку на тонкой струне, а затем окружили ее катушкой, так что можем менять магнитное поле, не притрагиваясь к магниту и не прикладывая к нему никакого момента сил. Это очень трудный эксперимент, ибо магнитные силы столь велики, что любая нерегулярность, любой перекос или несовершенство в железе могут дать случайный момент. Однако такой эксперимент был выполнен со всей необходимой аккуратностью и роль случайных моментов была сведена до минимума. С помощью магнитного поля катушки, которая окружает палочку, мы сразу можем перевернуть все магнитные моменты. Когда мы это проделаем, то заодно «сверху вниз» перевернутся и все моменты количества движения, связанные со спином (фиг. 37.3).
Фиг. 37.3. При перемагничивании железного бруска он приобретает некоторую угловую скорость.
Но поскольку момент количества движения должен сохраняться, то, когда все спины перевернулись, момент количества движения палочки должен измениться в противоположную сторону. Весь магнит должен начать вращаться. Это произошло на самом деле. Когда опыт был проделан, то было обнаружено слабое вращение магнита. Мы можем измерить полный момент количества движения, переданный всему магниту, который просто равен произведению N на h и на изменение момента количества движения каждого спина. Оказалось, что измеренное этим способом отношение момента количества движения к магнитному с 10%-ной точностью совпадает с нашими вычислениями. На самом деле в наших вычислениях мы исходили из того, что атомный магнетизм целиком обязан электронным спинам, однако в большинстве материалов есть еще и орбитальное движение. Орбитальное движение связано с решеткой, но она дает в магнетизм вклад не более нескольких процентов. Действительно, если взять Mнас=Nm и для плотности железа взять значение 7,9, а для m—момент электрона, связанный с его спином, то для магнитного поля получим насыщение около 20 000 гс. Однако опыт показывает, что на самом деле оно имеет значение вблизи 21500 гс. Ошибка в 5 или 10% возникает как раз из-за того, что мы пренебрегли вкладами орбитальных моментов. Таким образом, небольшое расхождение с гиромагнитными измерениями совершенно понятно.
§ 3. Петля гистерезиса
Из нашего теоретического анализа мы заключили, что магнитные материалы ниже некоторой температуры должны становиться спонтанно намагниченными, так что все магнитики в них должны смотреть в одном и том же направлении. Однако для обычного куска ненамагниченного железа это, как мы знаем, неверно. Почему железо не намагничивается все целиком? С помощью фиг. 37.4 я могу объяснить вам это. Допустим, что все железо было бы одним большим кристаллом такой формы, как показано на фиг. 37.4, а, и этот кристалл целиком намагнитился бы в одном направлении.
Фиг. 37.4. Образование доменов в монокристалле железа.
При этом создалось бы значительное внешнее магнитное поле, содержащее в себе огромную энергию. Мы можем уменьшить эту энергию поля, если расположим атомы так, чтобы одна часть кубика была намагничена вверх, а другая — вниз, как показано на фиг. 37.4, б. При этом, разумеется, поле вне железа будет занимать меньший объем и будет нести в себе меньше энергии.
Постойте, постойте! В слое между двумя областями рядом с электронами со спином, направленным вверх, сидят электроны со спином, направленным вниз. Но ферромагнетизм появляется только в тех материалах, для которых энергия уменьшается, когда спины параллельны, а не противоположны. Так что вдоль пунктирной линии на фиг. 37.4, б возникает некоторая добавочная энергия. Эта энергия иногда называется энергией стенки. Область, имеющая только одно направление намагниченности, называется доменом. На каждой единице площади разделяющей поверхности между двумя доменами у стенки домена, с противоположных сторон которой у нас расположены атомы, чьи магнитные моменты направлены противоположно, сосредоточена энергия. Конечно, нельзя говорить строго, что на границе моменты двух соседних атомов в точности противоположны, природа-то сделала этот переход более постепенным. Но сейчас нам не стоит интересоваться такими тонкими деталями.
Главный же вопрос теперь заключается вот в чем: выгодны такие стенки или нет? Ответ на него зависит от размеров доменов. Предположим, что мы увеличили размеры так, что все стало вдвое больше. При этом объем внешнего пространства, заполненного магнитным полем данной силы, станет в восемь раз больше, а энергия магнитного поля, которая пропорциональна объему, тоже возрастет в восемь раз. Но площадь границы между двумя доменами, на которой сосредоточена энергия стенки, возрастет только в четыре раза. Следовательно, если кусок железа достаточно велик, ему выгодно расщепиться на некое число доменов. Вот почему лишь очень маленькие кристаллы могут состоять только из одного домена. Любой большой объект, размер которого больше приблизительно одной тысячной миллиметра, будет иметь по крайней мере одну междоменную стенку, а обычный «сантиметровый» объект расщепляется, как это показано на рисунке, на множество доменов. Расщепление на домены будет происходить до тех пор, пока энергия, необходимая на установление еще одной дополнительной стенки, не сравняется с уменьшением энергии магнитного поля вне кристалла.
Природа же нашла еще один способ понижения энергии. Полю нет никакой необходимости выходить наружу, если, как это показано на фиг. 37.4, г, взять маленькие треугольные области с направленной в сторону намагниченностью. При таком расположении, как на фиг. 37.4, г, внешнее поле полностью отсутствует, а площадь доменных стенок лишь незначительно больше.
Но это приводит к новой проблеме. Оказывается, что если намагнитить отдельный кристалл железа, то он изменяет свою длину в направлении намагничивания; так что «идеальный» куб с намагниченностью «вверх» уже не будет безупречным кубом. Его «вертикальный» размер будет отличаться от «горизонтального».Этот эффект называется магнитострикцией. В результате таких геометрических изменений небольшой треугольный кусочек, показанный на фиг. 37.4, г, не сможет больше, так сказать, «умещаться» в отведенном ему пространстве: в одном направлении кристалл становится слишком длинным, а в другом — слишком коротким. Фактически-то он, конечно, умещается, но только немного сплющивается, что приводит к некоторым механическим напряжениям. Отсюда возникает и дополнительная энергия. Полный баланс вкладов в энергию и определяет сложный вид расположения доменов в куске ненамагниченного железа.
А что получится, если мы приложим внешнее магнитное поле? В качестве простого примера рассмотрим кристалл, домены которого показаны на фиг. 37.4, д. Если мы приложим магнитное поле, направленное вверх, то как будет происходить намагничивание кристалла? Прежде всего средняя доменная стенка может передвинуться в сторону (направо) и уменьшить энергию. Она перемещается таким образом, чтобы область направления «вверх» стала больше области направления «вниз», Элементарных магнитиков, направленных по полю, становится больше, а это приводит к понижению энергии. Таким образом, в куске железа в слабых магнитных полях с самого начала намагничивания доменная стенка начнет двигаться и «съедать» области, намагниченные противоположно полю. По мере того как поле продолжает увеличиваться, весь кристалл постепенно превращается в один большой домен, в котором внешнее поле помогает сохранять направление «вверх». В сильном магнитном поле кристаллы намагничиваются в одну сторону как раз потому, что их энергия в приложенном поле уменьшается. Внешнее магнитное поле кристаллов теперь уже не так существенно.
А что если геометрия кристалла не так проста? Что если какая-то ось кристалла и его спонтанная намагниченность направлены в одну сторону, а мы прилагаем поле, направленное в другую, скажем под углом 45°? Можно думать, что домены повернутся так, чтобы их намагниченность стала параллельной полю, а затем они, как и прежде, смогут слиться в один домен. Но сделать это для железа нелегко, ибо энергия, необходимая для намагничивания кристалла, зависит от направления намагничивающего поля относительно кристаллической оси. Намагнитить железо в направлении, параллельном кристаллической оси, относительно легко, но для того чтобы намагнитить его в каком-то другом направлении, скажем под углом 45° к направлению оси, энергии требуется больше. Следовательно, если в таком направлении приложить магнитное поле, то сначала происходит рост доменов, намагниченных в одном из избранных направлений, близких к направлению приложенного поля, пока в эту сторону не будет направлена намагниченность всех областей. Затем при гораздо больших полях общая намагниченность постепенно поворачивается к направлению поля, как это показано на фиг. 37.5.
Фиг. 37.5. Намагничивающее поле Н, направленное под некоторым углом к кристаллической оси, постепенно изменяет направление намагниченности М, не изменяя ее величины.
На фиг. 37.6 показаны полученные из опыта кривые намагничивания монокристаллов железа.
Фиг. 37.6. График компоненты М, параллельной полю Н, при различных направлениях Н (по отношению к осям кристалла).
Чтобы вы поняли их, я предварительно должен объяснить кое-какие обозначения, используемые для описания направлений в кристалле. Существует много способов расслоения кристалла на плоскости, в которых расположены атомы.
Каждый из вас, кто в прошлом работал или бывал в саду или на винограднике, знаком с этим любопытным зрелищем. Посмотрев в одну сторону, вы видите линию деревьев, а если посмотрите в другую,— вам откроется совсем другой ряд и т. д. Так и в кристалле — там есть определенные семейства плоскостей, содержащие много атомов; у таких плоскостей есть важная особенность (для простоты рассмотрим кубический кристалл). Если мы отметим, где эти плоскости пересекаются с тремя осями координат, то окажется, что обратные величины расстояний трех точек пересечения от начала относятся как целые числа. Эти три целых числа и принимаются для обозначения плоскостей. На фиг. 37.7, а, например, показана плоскость, параллельная плоскости yz. Она называется плоскостью (100), так как обратные величины отрезков, отсекаемых этой плоскостью по осям у и z, равны нулю.
Фиг. 37.7. Способы обозначения кристаллических плоскостей.
Направление, перпендикулярное этой плоскости (в кубическом кристалле), задается тем же самым набором чисел, но записывается в квадратных скобках: [100]. Основную идею в случае кубического кристалла понять очень легко, ибо символ [100] обозначает вектор, который имеет единичную компоненту в направлении оси х и нулевые в направлениях осей у и. z. Комбинация [110] обозначает направление под 45° к осям x и y, как показано на фиг. 37.7, б, а [111] — направление диагонали куба (фиг. 37.7,в).
Вернемся теперь к фиг. 37.6. На ней мы видим кривые намагничивания монокристалла в различных направлениях. Прежде всего заметьте, что для очень слабых полей, столь слабых, что в нашем масштабе их трудно изобразить, намагниченность чрезвычайно быстро возрастает до весьма больших значений. Если приложить поле в направлении [100], т. е. в одном из направлений легкого намагничивания, то кривая идет вверх до еще большего значения, затем несколько закругляется и наступает насыщение. Происходит это потому, что домены, которые уже там есть, ликвидируются очень легко. Чтобы передвинуть доменные стенки и «проглотить» все «неправильные» домены, требуется совсем слабое поле. Монокристаллы железа обладают огромной проницаемостью (в магнитном смысле), гораздо большей, чем поликристаллическое железо. Совершенный кристалл намагничивается очень легко. Почему же его кривая все же закругляется? Почему она не идет прямо до насыщения? Точно не известно. Быть может, вам когда-нибудь удастся изучить это явление. Мы понимаем, почему при больших полях она плоская. Когда весь кубик становится единым доменом, то добавочное магнитное поле не может создать большей намагниченности, она уже равна Mнас— значит, спины всех электронов направлены вверх.
Что получится, если мы попытаемся повторить то же самое для направления [110], которое лежит в плоскости ху под углом 45° к оси х? Мы включаем небольшое поле, и намагниченность за счет роста домена резко увеличивается. Если затем мы продолжаем увеличивать поле, то выясняется, что для достижения насыщения поле должно быть довольно большим, ибо вектор намагниченности нужно повернуть в сторону от направления легкого намагничивания. Если это объяснение правильно, то при экстраполяции кривой [110] точка пересечения с вертикальной осью должна будет давать значение намагниченности, составляющее 1/Ц2от намагниченности насыщения. Оказывается, что так оно на самом деле и происходит. Это отношение очень-очень близко к 1/Ц2. Аналогично для направления [111], которое идет по диагонали куба, мы находим, как и ожидали, что при экстраполяции кривая пересекает вертикальную ось на расстоянии, составляющем 1/Ц2 от значения, соответствующего насыщению.
На фиг. 37.8 показано соответствующее поведение двух других ферромагнетиков: никеля и кобальта.
Фиг. 37.8. Кривые намагничивания для монокристаллов железа, никеля и кобальта.
Никель отличается от железа. Оказывается, что направлением легкого намагничивания у него будет направление [111]. Кобальт имеет гексагональную кристаллическую структуру; для этого случая система обозначений была изменена. Здесь в основании шестиугольника располагают три оси и еще одну ось, перпендикулярную к ним, так что здесь используется четыре числа. Направление [0001] — это направление гексагональной оси, а [1010]— направление, перпендикулярное к этой оси. Вы видите, что кристаллы различных металлов устроены по-разному.
Теперь мы рассмотрим такой поликристаллический материал, как обычный кусок железа. Внутри него содержится огромное множество маленьких кристалликов, кристаллические оси которых направлены во все стороны. Но это не то же самое, что домены. Вспомните, все домены были частью одного кристалла, а в куске железа, как видно из фиг. 37.9, содержится множество различных кристаллов с разной ориентацией.
Фиг. 37.9. Микроструктура ненамагниченного поликристаллического ферромагнитного материала.
Каждый кристаллик имеет направление легкого намагничивания и разбивается на домены, которые обычно спонтанно намагничены в атом направлении.
В каждом из этих кристаллов, вообще говоря, содержится несколько доменов. Когда к куску поликристаллического материала мы прилагаем слабое магнитное поле, доменные барьеры в кристалликах начинают смещаться, и домены, направление намагниченности которых совпадает с направлением легкого намагничивания, растут все больше и больше. До тех пор пока поле остается очень малым, этот рост обратим; если мы выключим поле, намагниченность снова вернется к нулю. Этот участок кривой намагничивания обозначен на фиг. 37.10 буквой а.
Для больших полей в области, обозначенной буквой b, все становится гораздо более сложным. В каждом маленьком кристалле материала встречаются напряжения и дислокации, там есть примеси, грязь и дефекты. И при всех полях, за исключением лишь очень слабых, стенки доменов при своем движении наталкиваются на них. Между доменной стенкой и дислокацией (или границей зерна или примесью) возникают взаимодействия. В результате, когда стенка наталкивается на препятствие, она как бы приклеивается и держится там, пока поле не достигнет определенной величины. Затем, когда поле несколько подрастет, стенка внезапно срывается. Таким образом, движение доменной стенки оказывается отнюдь не плавным, как в идеальном кристалле: она движется скачкообразно, то и дело останавливаясь на мгновение. Если бы мы рассмотрели кривую намагничивания в микроскопическом масштабе, то увидели бы нечто подобное изображенному на вставке фиг. 37.10.
Но самое важное заключается в том, что эти прыжки намагничивания могут вызвать потерю энергии. Прежде всего, когда стенка домена проскакивает наконец через препятствие, она очень быстро движется к следующему. Быстрое движение влечет за собой и быстрое изменение магнитного поля, которое в свою очередь создает в кристалле вихревые токи. Последние растрачивают энергию на нагревание металла. Другой эффект состоит в том, что, когда домен неожиданно изменяется, часть кристаллов из-за магнитострикции изменяет свои размеры. Каждый неожиданный сдвиг доменной стенки создает небольшую звуковую волну, которая тоже уносит энергию. Благодаря таким эффектам эта часть кривой намагничивания необратима: происходит потеря энергии. В этом и заключается причина гистерезисного эффекта, ибо движение скачками вперед — одно, а движение назад — уже другое и в оба конца затрачивается энергия. Это похоже на езду по ухабистой дороге.
В конечном счете при достаточно сильных полях, когда все доменные стенки сдвинуты и намагниченность каждого кристаллика направлена по ближайшей к полю оси легкого намагничивания, остаются еще некоторые кристаллики, у которых ось легкого намагничивания далека от направления внешнего магнитного поля. Чтобы повернуть эти магнитные моменты, требуется еще дополнительное поле. Таким образом, в сильных полях именно в области, обозначенной на фиг. 37.10 буквой с, намагниченность возрастает медленно, но гладко.
Фиг. 37.10. Кривая намагничивания поликристаллического железа.
Намагниченность не сразу достигает своего насыщения, ибо в этой последней части кривой происходит доворачивание атомных магнитиков в сильном поле. Таким образом, мы видим, почему кривая намагничивания поликристаллического материала обычно имеет вид, изображенный на фиг. 37.10: сначала она немного возрастает и это возрастание обратимо, затем возрастает быстро, но уже необратимо, а потом медленно загибается. Разумеется, между этими тремя областями никакого резкого перехода нет— они плавно переходят одна в другую.
Нетрудно убедиться в том, что процесс намагничивания в средней части кривой носит скачкообразный характер, что доменные стенки при сдвиге прыгают и даже щелкают. Для этого нам нужна только катушка со многими тысячами витков провода, связанная через усилитель с громкоговорителем (фиг. 37.11).
Фиг. 37.11. Скачкообразные изменения намагниченности листков кремнистой стали сопровождаются щелчками в громкоговорителе.
Если внутрь катушки поместить несколько листков кремнистой стали (такого же сорта, как и в трансформаторах) и медленно подносить к этой пачке постоянный магнит, то скачкообразные изменения намагниченности будут создавать в катушке импульсы э. д. с., которые в громкоговорителе будут слышны как отдельные щелчки. По мере приближения магнита к железу на вас обрушится целый град щелчков, напоминающий шум, создаваемый падающими друг на друга песчинками, высыпающимися из наклоненной жестянки. Это прыгают, покачиваются и щелкают доменные стенки по мере увеличения магнитного поля. Это явление называется эффектом Баркгаузена.
По мере приближения магнита к железным листикам шум некоторое время будет все возрастать, но когда магнит окажется совсем близко, шум начинает затихать. Почему? Да потому, что все доменные стенки передвинулись уже насколько возможно и теперь любое увеличение поля просто поворачивает векторы намагниченности в каждом из доменов, а это уже вполне плавный процесс.
Если вы теперь будете плавно отодвигать магнит так, чтобы вернуться назад по нижней петле гистерезиса, то все домены будут тоже стремиться вернуться назад в положение низшей энергии и вы снова услышите град щелчков. Обратите внимание, что если вы отодвинете магнит до какого-то определенного положения, а затем начнете немного двигать магнит взад и вперед, звук будет относительно слабым. Это снова напоминает поведение наклоненной жестянки с песком: когда песчинки «осели» на свое место, небольшой наклон жестянки уже не потревожит их. Небольшое изменение магнитного поля в железе неспособно заставить доменную стенку перескочить через «горб».
§ 4. Ферромагнитные материалы
Сейчас было бы хорошо рассказать о различных сортах магнитных материалов, применяемых в технике, и о некоторых проблемах, связанных с созданием магнитных материалов для разных целей. Прежде всего о самом термине «магнитные свойства железа», который часто приходится слышать. Он, строго говоря, не имеет смысла и способен ввести в заблуждение: «железо» как строго определенный материал не существует. Свойства железа существенно зависят от количества примесей, а также от способа его приготовления. Вы понимаете, что магнитные свойства будут зависеть от того, насколько легко движутся доменные стенки, именно это свойство будет определяющим, а совсем не то, как ведут себя отдельные атомы. Так что практически ферромагнетизм не является свойством атомов железа: это свойство куска железа в определенном состоянии. Железо, например, может находиться в двух различных кристаллических формах. Обычная форма имеет объемноцентрированную кубическую решетку, но может еще иметь и гранецентрированную решетку, которая, однако, стабильна только при температурах выше 1100°С. При этих температурах, разумеется, железо уже прошло точку Кюри. Однако, сплавляя с железом хром и никель (один из возможных составов содержит 18% хрома и 8% никеля), мы можем получить то, что называется нержавеющей сталью; хотя она и состоит главным образом из железа, но сохраняет гранецентрированную решетку даже при низких температурах. Благодаря своей кристаллической структуре этот материал обладает совершенно другими магнитными свойствами. Обычно нержавеющая сталь немагнитна в сколько-нибудь заметной степени, хотя есть сорта с другим составом сплава, которые в какой-то степени магнитны. Хотя такой сплав, как любое вещество, является магнетиком, он не ферромагнетик, как обычное железо, несмотря на то, что в основном он все же состоит из железа.
Существуют специальные материалы, которые были придуманы для получения особых магнитных свойств. О некоторых из них я хочу рассказать. Если нужно сделать постоянный магнит, то требуется найти материал с необычно широкой петлей гистерезиса, чтобы при выключении тока, когда мы спустимся к нулевому намагничивающему полю, намагниченность все же осталась большой. Для таких материалов границы доменов должны быть «заморожены» на месте как можно крепче. Одним из таких материалов является замечательный сплав АлникоV (51% Fe, 8% Аl, 14% Ni, 24% Со, 3% Cu). Довольно сложный состав этого сплава говорит о том кропотливом труде, который надо было затратить, чтоб создать хороший магнит. Сколько терпения потребовалось для того, чтобы, смешивая по-разному пять компонент, проверять разные составы их до тех пор, пока не был найден идеальный сплав! Когда АлникоV затвердевает, у него появляется «вторая фаза», которая, осаждаясь, образует множество маленьких зерен и вызывает очень большие внутренние напряжения. Движение доменных стенок в этом материале очень затруднено. А чтобы получить вдобавок нужное строение, Алнико V механически «обрабатывается» так, чтобы кристаллы выстраивались в форме продолговатых зерен в направлении будущей намагниченности. При этом намагниченность, естественно, стремится смотреть в нужном направлении и противостоять эффектам анизотропии. Более того, в процессе приготовления материал даже охлаждается во внешнем магнитном поле, так что зерна растут с правильной ориентацией кристаллов. Петля гистерезиса АлникоV приведена на фиг. 37.12.
Фиг. 37.12. Петля гистерезиса сплава АлникоV.
Видите, она в 500 раз шире петли гистерезиса мягкого железа, которую я вам показывал (см.фиг.36.8, стр.146). Обратимся теперь к другим сортам материалов. Для изготовления трансформаторов и моторов необходим материал, который был бы «мягким» в магнитном отношении, т. е. такой, намагниченность которого могла бы легко изменяться, так что даже очень малое приложенное поле приводило бы к очень большой намагниченности. Для этого нужны чистые, хорошо отожженные материалы с очень малым количеством дислокаций и примесей, так чтобы доменные стенки могли легко двигаться. Анизотропию желательно сделать как можно меньше. Тогда если даже зерна материала расположены под «неправильным» углом по отношению к полю, материал все равно будет легко намагничиваться. Мы говорили, что железо предпочитает намагничиваться в направлении [100], тогда как никель предпочитает направление [111], так что если мы будем в различных пропорциях смешивать железо и никель, то можно надеяться найти такую их пропорцию, когда сплав не будет иметь никакого предпочтительного направления, т. е. направления [100] и [111] будут эквивалентны. Оказывается, что это достигается при смешивании 70% никеля и 30% железа. Вдобавок (вероятно, по счастливой случайности, а быть может, по какой-то физической взаимосвязи между анизотропией и магнитострикционными эффектами) оказалось, что константы магнитострикции железа и никеля имеют противоположные знаки. Для сплава этих двух металлов магнитострикция исчезает при содержании никеля около 80%. Так что при содержании никеля где-то между 70 и 80% у нас получаются очень «мягкие» магнитные материалы — сплавы, которые очень легко намагничиваются. Они называются пермаллоями. Пермаллои используются в высококачественных трансформаторах (при низких уровнях сигналов), но совершенно не годятся для постоянных магнитов. Приготовлять пермаллои и работать с ними нужно очень осторожно. Магнитные свойства пермаллоя в корне меняются, если его деформировать выше предела его упругости, так что этот материал никоим образом нельзя сгибать. Иначе в результате возникновения дислокаций, поверхностей скольжения и других механических деформаций проницаемость его уменьшается и границы доменов уже будут двигаться не так легко. Впрочем, былую высокую проницаемость можно восстановить отжигом при высокой температуре.
Полезно для характеристики различных магнитных материалов оперировать какими-то числами. Двумя такими характеристиками являются значения В и Н в точках пересечения петли гистерезиса с осями координат (фиг. 37.12). Эти значения называются остаточным магнитным полем Вrи коэрцитивной силой Нс. В табл. 37.1 приведены эти характеристики для некоторых материалов.
§ 5. Необычные магнитные материалы
Здесь мне бы хотелось рассказать о некоторых более экзотических магнитных материалах. В периодической таблице есть немало элементов, имеющих незаполненные внутренние электронные оболочки, а следовательно, и атомные магнитные моменты. Так, сразу вслед за ферромагнитными элементами — железом, никелем и кобальтом — вы найдете хром и марганец. Почему же они не ферромагнитны? Ответ заключается в том, что в выражении (37.1) член с К для этих элементов имеет противоположный знак. В решетке хрома, например, направления магнитных моментов атомов чередуются друг за другом (фиг. 37.13, б).
Фиг. 37.13. Относительная ориентация электронных спинов в различных материалах:
а — ферромагнетик;, б — антиферромагнетик; в — феррит.
Так что со своей точки зрения хром все же «магнетик», но с точки зрения технических применений это не представляет интереса, так как не дает внешнего магнитного эффекта. Таким образом, хром — пример материала, в котором кванто-вомеханический эффект вызывает чередование направлений спинов. Такой материал называется антиферромагнетиком. Упорядочивание магнитных моментов в антиферромагнитных материалах зависит и от температуры. Ниже критической температуры все спины выстраиваются в чередующейся последовательности, но если материал нагрет выше определенной температуры, которая по-прежнему называется температурой Кюри, направления спинов внезапно становятся случайными. Этот резкий внутренний переход можно наблюдать на кривой удельной теплоемкости. Он проявляется еще в некоторых особых «магнитных» эффектах. Например, существование чередующихся спинов можно проверить по рассеянию нейтронов на кристалле хрома. Нейтрон сам по себе имеет спин (и магнитный момент), поэтому амплитуда его рассеяния различна в зависимости от того, параллелен ли его спин спину рассеивателя или противоположен. В результате нейтронная интерференционная картина для чередующихся спинов отлична от картины при случайном их распределении.
Существует еще один сорт веществ, у которых квантово-механический эффект приводит к чередующимся спинам электронов, но которые тем не менее являются ферромагнетиками, т. е. их кристаллы имеют постоянную результирующую намагниченность. Идея, лежащая в основе объяснения свойств таких материалов, иллюстрируется схемой на фиг. 37.14.
Фиг. 37.14. Кристаллическая структура минерала шпинель (MgOAl2O3).
Ионы Mg2+ занимают тетраэдрические места, и каждый из них окружен четырьмя ионами кислорода; ионы А13+ занимают октаэдрические места, и каждый окружен шестью ионами кислорода.
На схеме показана кристаллическая структура минерала, известного под названием шпинели (MgOAl2O3), который, как это показано, не является магнетиком. Этот минерал содержит два сорта металлических атомов — магний и алюминий. Если теперь заменить магний и алюминий магнитными элементами типа железа, т. е. вместо немагнитных атомов вставить магнитные, то получится преинтереснейший эффект. Давайте назовем один сорт атомов металла а, а другой сорт — b; необходимо рассмотреть разные комбинации сил! Существует взаимодействие а—b, которое старается направить спины атома а и атома b противоположно, ибо квантовая механика всегда требует, чтобы спины были противоположны (за исключением таинственных кристаллов железа, никеля и кобальта). Затем существует взаимодействие а—а, которое старается направить противоположно спины атомов а; кроме того, есть еще взаимодействие b—b,которое старается направить противоположно спины атомов b. Конечно, сделать все противоположным всему (а противоположно b и а противоположно а и b противоположно b) невозможно. По-видимому, благодаря удаленности атомов а и присутствию атомов кислорода (с достоверностью мы не знаем, почему) оказывается, что взаимодействие а—b сильнее взаимодействий а—а и b—b. Словом, природа в этом случае воспользовалась решением, в котором спины всех атомов b параллельны друг другу, а все атомы а тоже параллельны друг другу, но между собой эти две системы спинов противоположны. Такой распорядок благодаря более сильному взаимодействию а—b соответствует наинизшей энергии. В результате спины всех атомов а направлены вверх, а спины всех атомов b — вниз (может быть, конечно, и наоборот). Но если магнитные моменты атомов а и атомов b не равны друг другу, то создается картина, показанная на фиг. 37.13, в: материал может оказаться спонтанно намагниченным. При этом он будет ферромагнетиком, хотя и несколько слабее настоящего. Такие материалы называются ферритами. У них по очевидным причинам намагниченность насыщения не столь велика, как у железа, поэтому они полезны только при слабых магнитных полях. Но они обладают очень важным преимуществом — это изоляторы, т. е. ферриты являются ферромагнитными изоляторами. Вихревые токи, создаваемые в них высокочастотными полями, очень малы, поэтому ферриты можно использовать, скажем, в микроволновых системах. Микроволновые поля способны проникать внутрь таких непроводящих материалов, тогда как в проводниках типа железа этому препятствуют вихревые токи.
Существует еще один вид магнитных материалов, открытых совсем недавно,— это члены семейства со структурой ортосиликатов, называемых гранатами. Это тоже кристаллы, в решетке которых содержатся два сорта металлических атомов; здесь мы снова сталкиваемся с ситуацией, когда оба сорта атомов можно заменять почти по желанию. Среди множества интересующих нас составов есть один, который обладает ферромагнетизмом. В структуре граната он содержит атомы иттрия и железа и причина его ферромагнетизма весьма любопытна. Здесь снова по квантовой механике соседние спины противоположны, так что это опять замкнутая система спинов, в которой электронные спины ионов железа направлены в одну сторону, а электронные спины ионов иттрия — в противоположную. Но атомы иттрия очень сложны. В их магнитный момент большой вклад вносит орбитальное движение электронов. Вклад орбитального движения для иттрия противоположен вкладу спина, и, кроме того, он больше его. Таким образом, хотя квантовая механика, опираясь на свой принцип запрета, стремится направить спины ионов иттрия противоположно спинам ионов железа, результирующий магнитный момент иттрия в результате орбитального эффекта оказывается параллельным спинам ионов железа. И соединение работает как настоящий ферромагнетик.
Другой интересный пример ферромагнетизма дают некоторые редкоземельные элементы. Здесь мы встречаемся с еще большими странностями в расположении спинов. Эти металлы не ферромагнетики в том смысле, что все спины в них параллельны, и не антиферромагнетики в том смысле, что спины соседних атомов противоположны. В этих кристаллах все спины в одном слое параллельны и лежат в плоскости слоя. В следующем слое все спины снова параллельны друг другу, но смотрят уже в несколько ином направлении. В следующем слое они тоже направлены в другую сторону и т. д. В результате вектор локального намагничивания (в слоях) меняется по спирали: магнитные моменты последовательных слоев поворачиваются при движении вокруг линии, перпендикулярной слоям. Интересно попытаться проанализировать, что получается, когда к такой спирали прилагается поле, найти все скручивания и повороты, которые должны происходить со всеми этими атомными магнитиками. (Некоторые люди просто увлечены теориями подобных вещей!) В природе встречаются не только «плоские» спирали, но существуют еще случаи, когда направления магнитных моментов последовательных слоев образуют конус, так что у них есть не только спиральная компонента, но и однородная ферромагнитная компонента в том же направлении!
Магнитные свойства материалов на более высоком уровне, чем занимались мы с вами, очаровывают многих физиков. Прежде всего этим увлекаются люди практического склада, которые любят придумывать способы улучшать разные вещи; им нравится изобретать более совершенные и интересные магнитные материалы. Открытие таких материалов, как ферриты, или их применение немедленно привело в восторг тех, кто выискивает новые хитрые пути сделать вещи совершеннее. Но есть еще люди, которые находят очарование в той ужасной сложности, которую природа создает на основе лишь нескольких фундаментальных законов. На основе одной и той же общей идеи природа от ферромагнетизма железа и его доменов дошла до антиферромагнетизма хрома, магнетизма ферритов и гранатов, до спиральной структуры редкоземельных элементов и шагает все дальше и дальше. До чего же приятно экспериментально открывать все эти странные явления, упрятанные в подобных особых веществах! А физикам-теоретикам ферромагнетизм подарил целый ряд интереснейших еще не решенных красивых проблем. Одна из них: почему вообще существует ферромагнетизм? Другая — вывести статистику взаимодействующих спинов в идеальной решетке. Даже если пренебречь дополнительными усложнениями, эти проблемы до сих пор не поддаются полному пониманию. Причина, по которой они так интересны,— удивительная простота постановки задачи: в правильной решетке задано множество электронных спинов, взаимодействующих по такому-то и такому-то закону; что с ними в конце концов происходит? Поставить-то задачу было легко, а вот полному анализу она не поддавалась многие годы. И хотя для температур, не слишком близких к точке Кюри, она была проанализирована довольно тщательно, теория внезапного перехода в точке Кюри до сих пор еще ждет своего решения.
Наконец, задача о поведении систем атомных магнитиков: и ферромагнетизм, и парамагнетизм, и ядерный магнетизм — исключительно полезные вещи для студентов-физиков старших курсов. Внешним магнитным полем на систему спинов можно воздействовать и так и сяк, поэтому можно придумать множество фокусов с резонансами, процессами релаксации, спиновым эхом и другими эффектами. Эта задача служит прототипом многих сложных термодинамических систем, с тем преимуществом, что в парамагнитных материалах положение обычно гораздо проще и исследователи с удовольствием ставят здесь эксперименты и объясняют явления теоретически.
Мы заканчиваем наше изучение электричества и магнетизма. В гл. 1 (вып. 5) мы говорили о великом пути, пройденном со времен, когда древние греки наблюдали странное поведение янтаря и магнитного железняка. Но еще нигде в наших длинных и запутанных рассуждениях мы не объяснили, почему, когда мы натираем кусок янтаря, на нем возникает заряд, не объяснили мы и того, почему намагничен природный магнитный железняк! Вы можете возразить: «Нам просто не удалось получить правильного знака». Нет, дело обстоит гораздо хуже. Если бы мы все-таки получили правильный знак, по-прежнему остался бы вопрос: почему кусок магнитного железняка в земле оказался намагниченным? Конечно, существует магнитное поле Земли, но откуда взялось это магнитное поле Земли? Вот этого-то на самом деле никто и не знает, и приходится довольствоваться только некоторыми правдоподобными догадками. Так что, как видите, наша хваленая современная физика — сплошное надувательство: начали мы с магнитного железняка и янтаря, а закончили тем, что не понимаем достаточно хорошо ни того, ни другого. Зато в процессе изучения мы узнали огромное количество удивительных и очень полезных для практики вещей!
* Вас может удивить, каким образом спины, которые должны быть направлены либо «вверх», либо «вниз», могут также быть направлены «вбок»! Это, конечно, правильно, но мне, право, не хотелось бы останавливаться на этом вопросе сейчас. Мы просто встанем на классическую точку зрения, представив себе атомные магнитики в виде магнитных диполей, которые могут быть ориентированы и в боковом направлении. Чтобы понять, как в квантовой механике можно в одно и то же время квантовать как «вверх—вниз», так и «направо — налево», требуется поднакопить больше знаний.
* Вместо В мы записали это уравнение через H=B-M/e0c2, чтобы согласовать со сказанным в предыдущей главе. Если вам больше нравится, можете написать U=±|m|Ba=±|m|(В+l'M/e0с2), где l'=l-1. Это одно и то же.
Литература: Ch. Кittel, Introduction to Solid State Physics, 2nd ed., New York, 1956. (Имеется перевод: Ч. Киттель, Введение в физику твердого тела, Физматгиз, М., 1962.— Ред.)
Глава 38 УПРУГОСТЬ
§ 1.Закон Гука
§ 2.Однородная деформация
§ 3. Кручение стержня; волны сдвига
§ 4.Изгибание балки
§ 5.Продольный изгиб
Повторить: гл. 47 (вып. 4) «Звук, волновое уравнение»
§ 1. Закон Гука
Теория упругости занимается поведением таких тел, которые обладают свойством восстанавливать свой размер и форму после снятия деформирующих сил. В какой-то степени этими упругими свойствами обладают все твердые тела. Если бы у нас было время заниматься этим предметом подольше, то нам пришлось бы рассмотреть множество вопросов: поведение напряженных материалов, законы упругости и общая теория упругости, атомный механизм, определяющий упругие свойства, и, наконец, ограничения на законы упругости, когда силы становятся настолько велики, что возникает пластическое течение и разрушение. Детальное рассмотрение всех этих вопросов потребовало бы гораздо больше времени, чем мы располагаем, поэтому кое от чего нам придется отказаться. Например, мы не будем обсуждать вопросы пластичности и ограничений на законы упругости. (Этого мы коснемся только очень кратко, когда у нас речь пойдет о дислокациях в металлах.) Мы не сможем также обсудить механизм упругости, так что наше исследование не будет обладать той полнотой, к которой мы стремились в предыдущих главах. Основная цель лекции — познакомить вас с некоторыми способами обращения с такими практическими задачами, как, например, задача об изгибании бруска.
Если вы надавите на кусок материала, то материал «поддастся» — он деформируется. При достаточно малых силах относительное перемещение различных точек материала пропорционально силе. Такое поведение называется упругим. Мы будем говорить только о таком упругом поведении. Сначала мы выпишем фундаментальный закон упругости, а затем применим его к нескольким различным ситуациям.
Предположим, что мы взяли прямоугольный брусок длиной l, шириной w и высотой h (фиг. 38.1).
Фиг. 38.1. Растяжение бруска под действием однородной нагрузки.
Если мы потянем за его конец с силой F, то его длина увеличится на Dl. Во всех случаях мы будем предполагать, что изменение длины составляет малую долю от первоначальной. На самом деле материалы, подобные стали или дереву, разрушаются еще до того, как изменение длины достигнет нескольких процентов от первоначального значения. Опыты показывают, что для большого числа материалов при достаточно малых удлинениях сила пропорциональна удлинению
F~Dl. (38.1)
Это соотношение известно как закон Гука.
Удлинение бруска Dl зависит и от его длины. Это можно продемонстрировать следующими рассуждениями. Если мы скрепим вместе два одинаковых бруска конец к концу, то на каждый будет действовать одна и та же сила и каждый из них удлинится на Dl. Таким образом, удлинение бруска длиной 2l будет в два раза больше удлинения бруска того же поперечного сечения, но длиной l. Чтобы получить величину, полнее характеризующую сам материал и менее зависящую от формы образца, будем оперировать отношением Dl/l (удлинение к первоначальной длине). Это отношение пропорционально силе, но не зависит от l:
F~Dl/l(38.2)
Сила F зависит также от площади сечения бруска. Предположим, что мы поставили два бруска бок о бок. Тогда для данного удлинения Dl мы должны приложить силу F к каждому бруску, или для комбинации двух брусков требуется вдвое большая сила. При данной величине растяжения сила должна быть пропорциональна площади поперечного сечения бруска А. Чтобы получить закон, в котором коэффициент пропорциональности не зависит от размеров тела, мы для прямоугольного бруска будем писать закон Гука в виде
F=YA(Dl/l) (38.3)
Постоянная Y определяется только свойствами природы материала; ее называют модулем Юнга. (Обычно модуль Юнга обозначается буквой Е, но эту букву мы уже использовали для электрического поля, для энергии и для э. д. с., так что теперь лучше взять другую.)
Силу, действующую на единичной площади, называют напряжением, а удлинение участка, отнесенное к его длине, т. е. относительное удлинение называют деформацией. Уравнение (38.3) можно переписать следующим образом;
F/A =YXDl/l. (38.4)
Напряжение=(Модуль Юнга)X(Деформация).
При растяжении, подчиняющемуся закону Гука, возникает еще одно осложнение: если брусок материала растягивается в одном направлении, то под прямым углом к растяжению он сжимается. Уменьшение толщины пропорционально самой толщине w и еще отношению Dl/l. Относительное боковое сжатие одинаково как для ширины, так и для его высоты и обычно записывается в виде
где постоянная s характеризует новое свойство материала и называется отношением Пуассона. Это число положительное до знаку, по величине меньше 1/2. (То, что постоянная о в общем случае должна быть положительной, «разумно», но ниоткуда не следует, что она должна быть такой.)
Две константы Y и s полностью определяют упругие свойства однородного изотропного (т. е. некристаллического) материала. В кристаллическом материале растяжение и сокращение в разных направлениях может быть различным, поэтому и упругих постоянных может быть гораздо больше. Временно мы ограничим наши обсуждения однородными изотропными материалами, свойства которых могут быть описаны постоянными s и Y. Как обычно, существует множество способов описания свойств.
Некоторым, например, нравится описывать упругие свойства материалов другими постоянными. Но таких постоянных всегда берется две, и они могут быть связаны с нашими s и Y.
Последний общий закон, который нам нужен,— это принцип суперпозиции. Поскольку оба закона (38.4) и (38.5) линейны в отношении сил и перемещений, то принцип суперпозиция будет работать. Если при одном наборе сил вы получаете некоторое дополнительное перемещение, то результирующее перемещение будет суммой перемещений, которые бы получились при независимом действии этих наборов сил.
Теперь мы имеем все необходимые общие принципы: принцип суперпозиции и уравнения (38.4) и (38.5), т. е. все, что нужно для описания упругости. Впрочем, с таким же правом можно было заявить: у нас есть законы Ньютона, и это все, что нужно для механики. Или, задавшись уравнениями Максвелла, мы имеем все необходимое для описания электричества. Оно, конечно, так; из этих принципов вы действительно можете получить почти все, ибо ваши теперешние математические возможности позволяют вам продвинуться достаточно далеко. Но мы все же рассмотрим лишь некоторые специальные приложения.
§ 2. Однородная деформация
В качестве первого примера посмотрим, что происходит с прямоугольным бруском при однородном гидростатическом сжатии. Давайте поместим брусок в резервуар с водой. При этом возникнет сила, действующая на каждую грань бруска и пропорциональная его площади (фиг. 38.2).
Фиг. 38.2. Брусок под действием равномерного гидростатического давления.
Поскольку гидростатическое давление однородно, то напряжение (сила на единичную площадь) на каждой грани бруска будет одним и тем же. Прежде всего найдем изменение длины бруска. Его можно рассматривать как сумму изменений длин, которые происходили бы в трех независимых задачах, изображенных на фиг. 38.3.
Фиг. 38.3. Гидростатическое давление равно суперпозиции трех сжатий.
Задача 1. Если мы приложим к концам бруска давление р, то деформация сжатия будет отрицательна и равна p/Y:
Задача 2. Если мы надавим на горизонтальные грани бруска, то деформация по высоте будет равна -p/Y, а соответствующая деформация в боковом направлении будет +sp/Y. Мы получаем
Задача 3. Если мы приложим к сторонам бруска давление р, то деформация давления снова будет равна p/Y, но теперь нам нужно определить деформацию длины. Для этого боковую деформацию нужно умножить на -s. Боковая деформация равна
так что
Комбинируя результаты этих трех задач, т. е. записывая Dl как dl1+Dl2+Dl3, получаем
Задача, разумеется, симметрична во всех трех направлениях, поэтому
Интересно также найти изменение объема при гидростатическом давлении. Поскольку V=lwh, то для малых перемещений можно записать
Воспользовавшись (38.6) и (38.7), мы имеем
Имеются любители называть DV/V объемной деформацией и писать
Объемное напряжение р (гидростатическое давление) пропорционально вызванной им объемной деформации — снова закон Гука. Коэффициент К называется объемным модулем и связан с другими постоянными выражением
Поскольку коэффициент К представляет некоторый практический интерес, то во многих справочниках вместо Y и s приводятся У и К. Но если вам нужно знать а, то вы всегда можете получить это значение из формулы (38.9). Из этой формулы видно также, что коэффициент Пуассона s должен быть меньше 1/2. Если бы это было не так, то объемный модуль К был бы отрицательным и материал при увеличении давления расширялся бы. Это позволило бы добывать механическую энергию из любого кубика, т. е. это означало бы, что кубик находится в неустойчивом равновесии. Если бы он начал расширяться, то расширение продолжалось бы само по себе с высвобождением энергии.
Посмотрим, что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или скалывающим, напряжением мы подразумеваем такое воздействие, как показано на фиг. 38.4.
Фиг. 38.4. Однородный сдвиг.
В качестве предварительной задачи посмотрим, какова будет деформация кубика под действием сил, показанных на фиг. 38.5.
Фиг. 38.5. Действие сжимающих сил, давящих на вершину и основание, и равных им растягивающих сил с двух сторон.
Снова можно разделить эту задачу на две: вертикальное давление и горизонтальное растяжение. Обозначая через А площадь грани кубика, мы получаем для изменения горизонтальной длины
Изменение же высоты по вертикали равно просто тому же выражению с обратным знаком.
Предположим теперь, что мы имеем тот же самый кубик, и подвергнем его действию сдвиговых сил, показанных на фиг. 38.6, а.
Фиг. 38.6. Две пары сил сдвига (а) создают то же самое напряжение, что и сжимающие = растягивающие силы (б).
Заметим теперь, что все силы должны быть равными, ибо на тело не должен действовать никакой момент сил и оно должно находиться в равновесии. (Подобные силы должны действовать также и в случае, изображенном на фиг. 38.4, поскольку кубик находится в равновесии. Они обеспечиваются тем, что кубик «приклеен» к столу.) При таких условиях говорят, что кубик находится в состоянии чистого сдвига. Но обратите внимание, что если мы разрежем кубик плоскостями под углом 45°, скажем, вдоль диагонали А на фиг. 38.6, а, то полная сила, действующая в этой плоскости, нормальна к ней и равна Ц2G.Площадь, на которой действует эта сила, равна Ц2A;следовательно, напряжение, нормальное к этой плоскости, будет просто G/A. Точно так же если взять плоскость, наклоненную под углом 45° в другую сторону, т. е. по диагонали В, то мы увидим, что на ней действует нормальное сдавливающее напряжение, равное -G/A. Из этого ясно, что напряжение при «чистом сжатии» эквивалентно комбинации растягивающего и сжимающего напряжений, направленных под прямым углом друг к другу и под углом 45° к первоначальным граням кубика. Внутренние напряжения и деформации будут такими же, как и в большом кубике материала под действием сил, показанных на фиг. 38.6, б. Но эту задачу мы уже решили. Изменение длины диагонали задается уравнением (38.10):
(Одна диагональ сокращается, а другая удлиняется.)
Часто деформацию сдвига удобно описывать с помощью угла «искажения» кубика q, показанного на фиг. 38.7.
Фиг. 38.7. Напряжение сдвига q равно 2DD/D.
Из геометрии фигуры вы видите, что горизонтальный сдвиг б верхнего края равен Ц2DD, так что
Напряжение сдвига g определяется как отношение тангенциальной силы, действующей на грань, к площади грани g=G/A. Воспользовавшись уравнением (38.11), мы из (38.12) получаем
Или, если написать это в форме
Напряжение = ПостояннаяXДеформация
g=mq. (38.13)
Коэффициент пропорциональности m называется модулем сдвига (или иногда коэффициентом жесткости). Вот как он выражается через Y и s:
Кстати, модуль сдвига должен быть положительным, иначе мы бы могли получить энергию от самопроизвольного сдвига кубика. Из уравнения (38.14) очевидно, что постоянная а должна быть больше -1. Теперь мы знаем, что о заключена между -1 и 1/2, но на практике, однако, она всегда больше нуля. В качестве последнего примера состояний подобного типа, когда напряженность постоянна по всему материалу, давайте рассмотрим задачу о бруске, который растягивается и в то же время закреплен таким образом, что боковое сокращение невозможно. (Технически немного легче сжимать брусок и сдерживать бока его от «распирания», но в сущности — это та же самая задача.) Что при этом происходит? На брусок должны действовать боковые силы, которые препятствуют изменению его толщины,— силы, которых мы не знаем непосредственно, но которые следует вычислить. Эта задача того же самого сорта, что мы решали, но только с немного другой алгеброй. Представьте себе силы, действующие на все три стороны, как это показано на фиг. 38.8.
Фиг. 38.8. Растяжение без сокращения бокового размера.
Мы вычислим изменение размеров и подберем такие поперечные силы, чтобы ширина и высота оставались постоянными. Следуя обычным рассуждениям, мы получаем для трех напряжений
Но поскольку по условию Dlу и Dlz равны нулю, то уравнения (38.16) и (38.17) дают два соотношения, связывающие Fyи Fzс Fx. Совместно решая их, найдем
а подставляя (38.18) в (38.15), получаем
Это соотношение вы часто можете встретить «перевернутым» и с преобразованным квадратичным полиномом по s, т. е.
Когда вы удерживаете бока, модуль Юнга умножается на некоторую сложную функцию s. Из уравнения (38.19) можно сразу же увидеть, что множитель перед Y всегда больше единицы. Растянуть брусок, когда его бока удерживаются, гораздо труднее. Это означает также, что брусок становятся жестче, когда его боковые стороны закреплены, нежели когда они свободны.
§ 3. Кручение стержня; волны сдвига
Обратимся теперь к более сложному примеру, когда различные части материала напряжены по-разному. Рассмотрим скрученный стержень — скажем, приводной вал какой-то машины или подвеску из кварцевой нити, применяемую в точных приборах. Из опытов с маятником кручения вы, по-видимому, знаете, что момент сил, действующий на закручиваемый стержень, пропорционален углу, причем константа пропорциональности, очевидно, зависит от длины стержня, его радиуса и свойств материала. Но каким образом — вот в чем вопрос? Теперь мы в состоянии ответить на него: просто нужно немного разобраться в геометрии.
На фиг. 38.9, а показан цилиндрический стержень, обладающий длиной L и радиусом а, один из концов которого закручен на угол j по отношению к другому.
Фиг. 38.9. Кручение цилиндрического стержня (а), кручение цилиндрического слоя (б) и сдвиг любого маленького кусочка в слое (в).
Если мы хотим связать деформацию с тем, что уже известно, то стержень можно представить состоящим из множества цилиндрических оболочек и выяснить, что происходит в каждой из этих оболочек. Начнем с рассмотрения тонкого короткого цилиндра радиусом r(меньшего, чем в) и толщиной Dr, как показано на фиг. 38.9, б. Если теперь посмотреть на кусочек внутри этого цилиндра, который первоначально был маленьким квадратом, то можно заметить, что он превратился в параллелограмм. Каждый элемент цилиндра сдвигается, а угол сдвига q равен
q=rj/L.
Поэтому напряжение сдвига g в материале будет [из уравнения (38.13)]
Напряжение среза равно тангенциальной силе DF, действующей на конец квадратика, поделенной на его площадь Dl/Dr (см. фиг. 38.9, б):
g=DF/DlDr.
Сила DF, действующая на конец такого квадратика, создает относительно оси стержня момент сил Dt, равный
Dt=rDF=rgDlDr. (38.22)
Полный момент t равен сумме таких моментов по всему периметру цилиндра. Складывая достаточное число таких кусков так, чтобы все Dl составляли 2pr, находим, что полный момент сил для пустотелой трубы равен
гg(2pr)Dr. (38.23)
Или, используя уравнение (38.21),
Мы получили, что жесткость t/j пустотелой трубы по отношению к кручению пропорциональна кубу радиуса r и толщине Dr и обратно пропорциональна его длине L.
Теперь представьте себе, что стержень сделан из целой серии таких концентрических труб, каждая из которых закручена на угол j (хотя внутренние напряжения в каждой трубе различны). Полный момент равен сумме моментов, требуемых для скручивания каждой оболочки, так что для твердого стержня
где интеграл берется от 0 до а — радиуса стержня. После интегрирования получаем
Если закручивать стержень, то его момент оказывается пропорциональным углу и четвертой степени диаметра: стержень вдвое большего радиуса в шестнадцать раз жестче относительно кручения.
Прежде чем расстаться с кручением, рассмотрим применение теории к одной интересной задаче — волнам кручения. Возьмем длинный стержень и неожиданно закрутим один его конец; вдоль стержня, как показано на фиг. 38.10, а, пойдет волна кручения.
Фиг. 38.10. Волна кручения в стержне (а) и элемент объема стержня (б).
Это явление более интересно, нежели простое статическое скручивание. Посмотрим, можем ли мы понять, как это происходит.
Пусть z — расстояние от некоторой точки до основания стержня. Для статического закручивания момент сил на всем протяжении стержня один и тот же и пропорционален j/L — полному углу вращения на полную длину. Но в нашей задаче важна местная деформация кручения, которая, как вы сразу поймете, равна дj/дz. Если кручение вдоль стержня неравномерное, то уравнение (38.25) следует заменить таким:
Посмотрим теперь, что же происходит с элементом длины Dz, который показан в увеличенном масштабе на фиг. 38.10, б. На конце 1 маленького отрезка стержня действует момент t(z), а на конце 2— другой момент сил t(z+Dz). Если величина Dz достаточно мала, то можно воспользоваться разложением в ряд Тэйлора и, сохранив только два члена, написать
Полный момент сил Dt, действующий на маленький отрезок стержня между z и Dz, равен разности t(z) и
t(z+Dz),
или
Dt=(дt/дz)Dz.
Дифференцируя уравнение (38.26), получаем
Действие этого полного момента должно вызвать угловое ускорение отрезка стержня. Масса его равна
где r — плотность материала. В гл. 19 (вып. 2) мы нашли, что момент инерции кругового цилиндра равен mr2/2; обозначая момент инерции нашего отрезка через Dl, получаем
Закон Ньютона говорит нам, что момент силы равен произведению момента инерции на угловое ускорение, или
Собирая теперь все воедино, находим
или
Вы, должно быть, уже узнали, что это такое: это одномерное волновое уравнение. Мы получили, что волны кручения распространяются по стержню со скоростью
Чем плотнее стержень при одной и той же жесткости, тем медленнее движется волна, а чем он жестче, тем волна бежит быстрее. Скорость ее не зависит от диаметра стержня.
Волны кручения представляют частный случай волн сдвига. Волны сдвига в общем случае — это такие волны, при которых деформация не изменяет объема любой части материала. В волнах кручения мы сталкиваемся с особым распределением напряжений сдвига — они распределены по кругу. Но волны при любом распределении напряжений сдвига будут распространяться с одной и той же скоростью, которая определяется формулой (38.32). Сейсмологи, например, обнаружили, что такие волны сдвига распространяются и внутри Земли.
В мире упругих явлений возможен и другой сорт волн внутри твердого материала. Если вы толкнете что-нибудь, то можете возбудить «продольные» волны, так называемые волны «сжатия». Они подобны звуковым волнам в воздухе или в воде, т. е. перемещение вещества в них происходит в ту же сторону, что и распространение волны. (На поверхности упругого тела могут распространяться и другие типы волн, называемые «волнами Рэлея». Деформация в них ни продольная, ни поперечная. Однако у нас нет времени говорить о них подробно.)
Раз уж мы коснулись вопроса о волнах, то какова скорость волн чистого сжатия в большом твердом теле, подобном Земле? Я сказал в «большом», ибо скорость звука в массивном теле отлична от скорости, свойственной, скажем, тонкому стержню. Под массивным телом я подразумеваю тело, поперечные размеры которого много больше длины волны звука. Поэтому, нажимая на такой объект, можно обнаружить, что он не «раздается» в стороны — он может сжиматься только в одном направлении. К счастью, однако, мы уже разобрали специальный случай сжатия «сдавленного» упругого материала, а в гл. 47 (вып. 4) мы познакомились еще со скоростью звука в газе. Рассуждая так же, как и выше, вы можете убедиться, что скорость звука в твердом теле равна Ц(Y'/r), где Y' — «продольный модуль», т. е. давление, деленное на относительное изменение длины (для случая «сдавленного» стержня). Равно это просто отношению Dl/l к F/A, полученному нами в уравнении (38.20). Таким образом, скорость продольных волн определяется выражением
Поскольку значение s заключено между 0 и 1/2, то модуль сдвига m меньше модуля Юнга Y, a Y', кроме того, больше Y, так что
m<Y<Y'.
Это означает, что продольные волны распространяются быстрее, чем волны сдвига. Один из наиболее точных способов определения упругих постоянных вещества дает измерение плотности материала и скоростей двух сортов волн. Из этой информации можно получить как Y, так и s. Кстати, именно измеряя разность во времени прихода двух сортов волн от землетрясения, сейсмологи только по сигналам, принятым одной станцией, способны установить расстояние до эпицентра.
§ 4. Изгибание балки
Разберем теперь другой практический вопрос — изгибание балки, стержня или бруска. Чему равны силы, необходимые для изгибания балки произвольного поперечного сечения?
Мы определим эти силы для балки круглого сечения, но ответ будет пригоден для балки любой формы. Чтобы сберечь время, мы кое-где упростим дело, так что теория, которую мы разовьем, будет только приближенной. Наши результаты верны лишь при том условии, что радиус изгибания много больше толщины балки.
Представьте, что вы ухватились за оба конца прямой балки и согнули ее в виде кривой, похожей на ту, что изображена на фиг. 38.11.
Фиг. 38.11. Изогнутая балка.
Что же происходит внутри балки? Раз она искривлена, значит, материал на внутренней стороне сгиба сжат, а на внешней стороне растянут. Но имеется какая-то поверхность, более или менее параллельная оси балки, которая и не сжата, и не растянута. Называется она нейтральной поверхностью. По-видимому, эта поверхность проходит где-то «посредине» поперечного сечения. Можно показать (но я не буду этого здесь делать), что для небольшого изгиба простой балки нейтральная поверхность проходит через «центр тяжести» поперечного сечения. Но это справедливо только для «чистого» сгиба, т. е. когда балка не растягивается и не сжимается как целое.
При чистом сгибе тонкий поперечный отрезок балки возмущен (фиг. 38.12, а).
Фиг. 38.12. Маленький отрезок изогнутой балки (а) и поперечное сечение балки (б).
Материал под нейтральной поверхностью испытывает деформацию сжатия, которая пропорциональна расстоянию от нейтральной поверхности, а материал над ней растянут тоже пропорционально расстоянию от нейтральной поверхности. Таким образом, продольное удлинение Dl пропорционально высоте у. Константа пропорциональности равна просто длине l, деленной на радиус кривизны балки (см. фиг. 38.12):
Dl/l=y/R.
Так что напряжение, т. е. сила, действующая на единичную площадь в некоторой маленькой полоске вблизи у, тоже пропорциональна расстоянию от нейтральной поверхности
Теперь рассмотрим те силы, которые привели бы к подобной деформации. Силы, действующие на маленький отрезок, изображенный на фиг. 38.12, показаны на том же рисунке. Если мы возьмем любое поперечное сечение, то действующие на нем силы направлены в одну сторону выше нейтральной поверхности и в другую — ниже ее. Получается пара сил, которая создает «изгибающий момент», под которым мы понимаем момент силы относительно нейтральной линии. Интегрируя произведение силы на расстояние от нейтральной поверхности, можно вычислить полный момент на одной из граней отрезка фиг. 38.12:
Согласно (38.34), dF=Y(y/R)dA, так что
Но интеграл от y2dA можно назвать «моментом инерции» геометрического поперечного сечения относительно горизонтальной оси, проходящей через его «центр масс»; мы будем обозначать его через I, т. е.
Уравнение (38.36) дает нам соотношение между изгибающим моментом и кривизной балки 1/R. «Жесткость» балки пропорциональна Y и моменту инерции I. Другими словами, если вы хотите какую-то балку, скажем из алюминия, сделать как можно жестче, то вы должны как можно больше вещества поместить как можно дальше от оси, относительно которой берется момент инерции. Но этого нельзя доводить до предела, ибо тогда балка не будет искривляться так, как мы предположили: она согнется или скрутится и снова станет слабее. Вот почему каркасные балки делают в форме буквы I или Н (фиг. 38.13).
Фиг. 38.13. Двутавровая балка.
В качестве примера применения нашего уравнения (38.36) для балки вычислим отклонение консольной балки под действием сосредоточенной силы W, действующей на ее свободный конец (фиг. 38.14).
Фиг. 38.14. Консольная балка с нагрузкой на конце.
(Консольная балка закреплена одним концом, который вмурован в стенку.) Какая же тогда будет форма балки? Обозначим отклонение на расстоянии х от закрепленного конца через z; мы хотим найти z(x). Будем вычислять только малые отклонения. Как вы знаете из курса математики, кривизна 1/R любой кривой z(x) задается выражением
Нас интересуют только малые изгибы (обычная вещь в инженерных конструкциях), поэтому квадратом производной (dz/dx)2можно пренебречь по сравнению с единицей и считать
Нам нужно еще знать изгибающий момент . Он является функцией от х, так как в любом поперечном сечении он равен моменту относительно нейтральной оси. Весом самой балки пренебрежем и будем учитывать только силу W, действующую вниз на свободный ее конец. (Если хотите, можете сами учесть ее вес.) При этом изгибающий момент на расстоянии х равен
ибо это и есть момент сил относительно точки х, с которым действует груз W, т. е. груз, который должен поддерживать балку. Получаем
или
Это уравнение можно проинтегрировать без всяких фокусов и получить
воспользовавшись предварительно нашим предположением, что z(0)=0 и что dz/dx в точке x=0 тоже равно нулю. Это и есть граничные условия. А отклонение конца будет
т, е. отклонение возрастает пропорционально кубу длины балки. При выводе нашей приближенной теории мы предполагали, что при изгибании поперечное сечение бруска не изменяется. Когда толщина бруска мала по сравнению с радиусом кривизны, поперечное сечение изменяется очень мало и все отлично. Однако в общем случае этим эффектом пренебречь нельзя — согните пальцами канцелярскую резинку и вы сами убедитесь в этом. Если первоначально поперечное сечение было прямоугольным, то, согнув резинку, вы увидите, как она выпирает у основания (фиг. 38.15).
Фиг. 38.15. Согнутая резинка (а) и ее поперечное сечение (б).
Это получается потому, что, согласно отношению Пуассона, при сжатии основания материал «раздается» вбок. Резинку очень легко согнуть или растянуть, но она несколько напоминает жидкость в том отношении, что изменить ее объем очень трудно. Это и сказывается при сгибании резинки. Для несжимаемых материалов отношение Пуассона было бы точно равно 1/2, для резинки те оно близко к этому числу.
§ 5. Продольный изгиб
Теперь воспользуемся нашей теорией, чтобы понять, что происходит при продольном изгибе бруска, опоры или стержня. Рассмотрим то, что изображено на фиг. 38.16.
Фиг. 38.16. Продольно изогнутая балка.
Здесь стержень, обычно прямой, удерживается в согнутом виде двумя противоположными силами, давящими на его концы. Найдем форму стержня и величину сил, действующих на концы.
Пусть отклонение стержня от прямой линии между концами будет у(х), где х — расстояние от одного конца. Изгибающий момент в точке Р на рисунке равен силе F, умноженной на плечо, перпендикулярное направлению у:
Воспользовавшись выражением для момента (38.36), имеем
При малых отклонениях можно считать 1/R=-d2y/dx2(отрицательный знак выбран потому, что кривизна направлена вниз). Отсюда
т. е. появилось дифференциальное уравнение для синуса. Таким образом, для малых отклонений кривая такого продольно изогнутого стержня представляет синусоиду. «Длина волны» l. этой синусоиды в два раза больше расстояния L между концами. Если изгиб невелик, она просто равна удвоенной длине неизогнутого стержня. Таким образом, получается кривая
Беря вторую производную, находим
Сравнивая это с (38.45), видим, что сила равна
Для малого продольного изгиба сила не зависит от перемещения у!
Физически же получается вот что. Если сила F меньше определяемой уравнением (38.46), то никакого продольного изгиба не происходит. Но если она хоть немного больше этой силы, то балка внезапно и очень сильно согнется, т. е. под действием сил, превышающих критическую величину p2YI/L2(часто называемую «силой Эйлера»), балка будет «гнуться». Если на втором этаже здания разместить такой груз, что нагрузка на поддерживающие колонны превысит силу Эйлера, то здание рухнет. Другая область, где очень важны продольно изгибающие силы,— это космические ракеты. С одной стороны, ракета должна выдерживать свой вес на стартовой площадке и вынести напряжения во время ускорения, а с другой — очень важно свести вес всей конструкции до минимума, чтобы полезная нагрузка и полезная мощность двигателей были как можно больше.
Фактически превышение силы Эйлера вовсе не означает, что после этого балка полностью разрушится. Когда отклонение становится большим, сила благодаря члену (dz/dx)2в уравнении (38.38), которым мы пренебрегли, будет на самом деле больше вычисленной. Чтобы найти силы при большом продольном изгибании стержня, мы должны вернуться к точному уравнению (38.44), которое получалось до использования приближенной связи между R и y.
Уравнение (38.44) имеет довольно простые геометрические свойства. Решается оно немного сложнее, но зато гораздо интереснее. Вместо того чтобы описывать кривую через х и у, можно воспользоваться двумя новыми переменными:
S — расстоянием вдоль кривой и
q— наклоном касательной к кривой (фиг. 38.17.)
Фиг. 38.17. Координаты кривой продольно изогнутой балки S и q.
Тогда кривизна будет равна скорости изменения угла с расстоянием
Поэтому точное уравнение (38.44) можно записать в виде
После взятия производной этого уравнения по S и замены dy/dS на sinq получим
[Если углы q малы, то мы снова приходим к уравнению (38.45), стало быть здесь все в порядке.
Не знаю, можете ли вы еще удивляться, но уравнение (38.47) получилось в точности таким же, как и для колебаний маятника с большой амплитудой (разумеется, с заменой F/YI другой постоянной). Еще раньше, в гл. 9 (вып. 1), мы узнали, как находить решение такого уравнения численным методом. В ответе вы получите очаровательную кривую. На фиг. 38.18 показаны три кривые для разных значений постоянной F/YI.
* Кстати, точно такое же уравнение возникает и в других физических ситуациях: например, в мениске на поверхности жидкости, заключенной между двумя параллельными стенками, а поэтому можно воспользоваться тем же самым геометрическим рассмотрением.
* Решение его можно выразить также через особые функции, называемые «эллиптическими функциями Якоби», которые когда-то раз навсегда были вычислены и протабулированы.
* Это и есть момент инерции пластинки единичной плотности и с единичной площадью сечения
Глава 39 УПРУГИЕ МАТЕРИАЛЫ
§ 1. Тензор деформации
§ 2. Тензор упругости
§ З. Движения в упругом теле
§ 4. Неупругое поведение
§ 5. Вычисление упругих постоянных
§ 1. Тензор деформации
В предыдущей главе мы говорили о возмущениях упругих тел в простых случаях. В этой главе мы посмотрим, что может происходить внутри упругого материала в общем случае. Как описать условия напряжения и деформации в большом куске желе, скрученном и сжатом каким-то очень сложным образом? Для этого необходимо описать локальную деформацию в каждой точке упругого тела, а это можно сделать, задав в ней набор шести чисел — компонент симметричного тензора. Ранее (в гл. 31) мы говорили о тензоре напряжений, теперь же нам потребуется тензор деформации.
Предположим, что мы взяли недеформированный материал и, прикладывая напряжение, наблюдаем за движением маленького пятнышка примеси, попавшей внутрь. Пятнышко, которое вначале находилось в точке Р и имело положение г=(x, у, z), передвигается в новую точку Р', т. е. в положение r'=(х', у', z'), как это показано на фиг. 39.1.
Фиг. 39.1. Пятнышко примеси в материале из точки Р недеформированного кубика после деформации перемещается в точку Р'.
Мы будем обозначать через и вектор перемещения из точки Р в точку Р', т. е.
u = r'-r. (39.1)
Перемещение и зависит, конечно, от точки Р, из которой оно выходит так, что и есть векторная функция от г или от (х, у, z).
Сначала рассмотрим простейший случай, когда деформация по всему материалу постоянна, т. е. то, что называется однородной деформацией. Предположим, например, что мы взяли балку из какого-то материала и равномерно ее растянули. Иначе говоря, мы просто равномерно изменили ее размер в одном направлении, скажем в направлении оси х (фиг. 39.2).
Фиг. 39.2. Однородная деформация растяжения.
Перемещение uxпятнышка с координатой х пропорционально самому х.
Действительно,
Мы будем записывать uxследующим образом:
иx=еххх.
Разумеется, константа пропорциональности ехх— это то же, что наше старое отношение Dl/l. (Скоро вы увидите, почему нам потребовался двойной индекс.)
Если же деформация неоднородна, то связь между х и uxв материале будет изменяться от точки к точке. В таком общем случае мы определим еххкак своего рода локальную величину Dl/l, т. е.
Это число, которое теперь будет функцией х, у и z, описывает величину растяжения в направлении оси х по всему куску желе. Возможны, конечно, растяжения и в направлении осей у и z. Мы будем описывать их величинами
Кроме того, нам нужно описать деформации типа сдвигов. Вообразите, что в первоначально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3).
Фиг. 39.3. Однородная деформация сдвига.
При такой деформации перемещение в направлении х каждой частицы пропорционально ее координате у:
а перемещение в направлении у пропорционально х:
uy=(q/2)x. (39.5)
Таким образом, деформацию сдвигового типа можно описать с помощью
ux=exyy uу=eyxx,
где
Теперь вы сочтете, что при неоднородной деформации обобщенную деформацию сдвига можно описать, определив величины еxyи еyxследующим образом:
Однако здесь есть некая трудность. Предположим, что перемещения uхи uyимеют вид
Они напоминают уравнения (39.4) и (39.5), за исключением того, что при uyстоит обратный знак. При таком перемещении маленький кубик из желе претерпевает простой поворот на угол q/2 (фиг. 39.4).
Фиг. 39.4. Однородный поворот. Никаких деформаций нет.
Никакой деформации здесь вообще нет, а есть просто вращение в пространстве. При этом никакого возмущения материала не происходит, а относительное положение всех атомов совершенно не изменяется. Нужно как-то устроить так, чтобы чистое вращение не входило в наше определение деформации сдвига. Указанием может послужить то, что если дuy/дх и дux/ду равны и противоположны, никакого напряжения нет; этого можно добиться, определив
Для чистого вращения оба они равны нулю, но для чистого сдвига мы получаем, как и хотели, еху=еуx.
В наиболее общем случае возмущения, который наряду со сдвигом может включать растяжение или сжатие, мы будем определять состояние деформации заданием девяти чисел:
Они образуют компоненты тензора деформации. Поскольку тензор этот симметричен (согласно нашему определению, ехувсегда равно еух), то на самом деле различных чисел здесь только шесть. Вы помните (см. гл. 31) общее свойство всех тензоров — элементы его преобразуются при повороте подобно произведению компонент двух векторов. (Если А и В — векторы, то Сij=АiВj — тензор.) А каждое наше eijесть произведение (или сумма таких произведений) компонент вектора
u=(uх, uу, uz) и оператора С=(д/дx,д/дy,д/дz), который, как
мы знаем, преобразуется подобно вектору. Давайте вместо х, у и z писать x1, x2и x3, а вместо uх, uyи uгписать u1, u2 и u3; тогда общий вид элемента тензора eijбудет выглядеть так:
где индексы i и j могут принимать значения 1, 2 или 3.
Когда мы имеем дело с однородной деформацией, которая может включать как растяжения, так и сдвиги, то все eij — постоянные, и мы можем написать
uх=еххх+ехуy+ехzг. (39.9)
(Начало координат выбрано в точке, где и равно нулю.) В этих случаях тензор деформации eijдает соотношение между двумя векторами — вектором координаты r=(x, y, z) и вектором перемещения u=(uх, uу, uг).
Если же деформация неоднородна, то любой кусочек желе может быть как-то искажен и, кроме того, могут возникнуть местные повороты. Когда все возмущения малы, мы получаем
где wij, — антисимметричный тензор
описывающий поворот. Нам незачем беспокоиться о поворотах; займемся только деформацией, которая описывается симметричным тензором еij.
§ 2. Тензор упругости
Теперь, чтобы описать деформации, мы должны связать их с внутренними силами — с напряжениями в материале. Мы предполагаем, что закон Гука справедлив для любого кусочка материала, т. е. что напряжения всюду пропорциональны деформациям. В гл. 31 мы определили тензор напряжений Sijкак i-ю компоненту силы, действующей на единичной площадке, перпендикулярной оси j. Закон Гука говорит, что каждая компонента Sijлинейно связана с каждой компонентой напряжения. Но поскольку S и l содержат по девяти компонент, то всего для описания упругих свойств материала требуется 9X9=81 возможный коэффициент. Если материал однороден, то все эти коэффициенты будут постоянными. Мы обозначим их Cijklопределив посредством уравнения
где каждый значок i, j, k и l может принимать значения 1, 2 или 3. Поскольку коэффициенты Сijklсвязывают один тензор с другим, они тоже образуют тензор — на этот раз тензор четвертого ранга. Мы можем назвать его тензором упругости.
Предположим, что все Cijklизвестны и что к телу какой-то произвольной формы мы приложили сложные силы. При этом возникнут все сорта деформаций — тело как-то исказится. Каковы будут перемещения? Вы понимаете, что это довольно сложная задача. Если вам известны деформации, то из уравнения (39.12) можно найти напряжения, и наоборот. Но напряжения и деформации, которые возникли в любой точке, зависят от того, что происходит во всей остальной части материала.
Наиболее простой способ подступиться к такой задаче — это подумать об энергии. Когда сила F пропорциональна перемещению х, скажем F=kx, то работа, затраченная на любое перемещение х, равна kx2/2. Подобным же образом энергия w, запасенная в любой единице объема деформированного материала, оказывается равной
Полная же работа W, затраченная на деформацию всего тела, будет интегралом от w по всему его объему:
Следовательно, это и есть потенциальная энергия, запасенная во внутренних напряжениях материала. Когда тело находится в равновесии, эта внутренняя энергия должна быть минимальной. Таким образом, проблема определения деформаций в теле может быть решена нахождением таких перемещений и по всему телу, при которых W минимальна. В гл. 19 (вып. 6) я говорил вам о некоторых общих идеях вариационного исчисления, применяемого при решении задач на минимизацию подобного рода. Однако сейчас мы больше не будем вдаваться в подробности этой задачи.
Сейчас нас главным образом будет интересовать то, что можно сказать относительно общих свойств тензора упругости. Прежде всего ясно, что на самом деле в Cijklсодержится не 81 различный параметр. Поскольку Sijи eij— симметричные тензоры, каждый из которых включает только шесть различных элементов, то Cijklсостоит максимум из 36 различных компонент. Обычно же их гораздо меньше.
Рассмотрим специальный случай кубического кристалла. Плотность энергии w для него получается такой:
т. е. всего 81 слагаемое! Но кубический кристалл обладает определенными симметриями. В частности, если кристалл повернуть на 90°, то все его физические свойства останутся теми же. Например, у него должна быть одна и та же жесткость относительно растяжения как в направлении оси у, так и в направлении оси х. Следовательно, если мы переменим наши определения осей координат х и у в уравнении (39.15), то энергия не должна измениться. Поэтому для кубического кристалла
Cхххх=Суууу=Czzzz. (39.16)
Мы можем еще показать, что компоненты, наподобие Сххху, должны быть нулями. Кубический кристалл обладает тем свойством, что он симметричен при отражении относительно любой плоскости, перпендикулярной к одной из осей координат. Если мы заменим у на —y, то ничего не должно измениться. Но изменение у на -у меняет еxyна -еxy , так как перемещение в направлении +у будет теперь перемещением в направлении -у. Чтобы энергия при этом не менялась, Схххудолжно переходить в -СхххуНо отраженный кристалл будет тем же, что и прежде, поэтому Сххxyдолжно быть таким же, как и -Сххху. Это может произойти только тогда, когда оба они равны нулю.
Но вы можете сказать: «Рассуждая таким же образом, можно сделать и Cyyyy=0!» Это неверно. Ведь здесь у нас четыре игрека. Каждый у изменяет знак, а четыре минуса дают плюс. Если у встречается два или четыре раза, то такие компоненты не должны быть равны нулю. Нулю равны только те компоненты, у которых у встречается либо один, либо три раза. Таким образом, для кубического кристалла не равны нулю только те С, у которых один и тот же значок встречается четное число раз. (Рассуждения, которые мы провели для у, имеют силу и для х и для z.) Таким образом, выживают только компоненты типа Сххуу, Схуху, Схуухи т. д. Однако мы уже показали, что если изменить все х на у и наоборот (или все z на x и т. д.), то для кубического кристалла мы должны получить то же самое число. Это означает, что остаются всего три различные ненулевые возможности:
Плотность же энергии для кубического кристалла выглядит так:
У изотропного, т. е. некристаллического, материала симметрия еще выше. Числа С должны быть теми же самыми при любом выборе осей координат. При этом, как оказывается, существует другая связь между коэффициентами С:
Cхххх=Cххуу+Cхуху (39.19)
Это можно усмотреть из следующих общих рассуждений. Тензор напряжений Sijдолжен быть связан с eijспособом, который совершенно не зависит от направления осей координат, т. е. он должен быть связан только с помощью скалярных величин. «Это очень просто»,— скажете вы. «Единственный способ получить Sijиз eij — умножить последнее на скалярную постоянную. Получится как раз закон Гука: Sij=(Постоянная)Xеij». Однако это не совсем верно. Дополнительно здесь можно вставить единичный тензор dij, умноженный на некоторый скаляр, линейно связанный с еij. Единственный инвариант, который можно составить и который линеен по е,— это Sejj. (Он преобразуется подобно х2+y2+z2, а значит является скаляром.) Таким образом, наиболее общей формой уравнения, связывающего Sijс eijдля изотропного материала, будет
(Первая константа обычно записывается как 2m; при этом коэффициенту равен модулю сдвига, определенному нами в предыдущей главе.) Постоянные (m, и l называются упругими постоянными Лямэ. Сравнивая уравнения (39.20) с уравнением (39.12), вы видите, что
Таким образом, мы доказали, что уравнение (39.19) действительно правильное. Вы видите также, что упругие свойства изотропного материала, как уже говорилось в предыдущей главе, полностью задаются двумя постоянными.
Коэффициенты С могут быть выражены через любые две из упругих постоянных, которые использовались ранее, например через модуль Юнга Y и отношение Пуассона s. На вашу долю оставляю показать, что
§ 3. Движения в упругом теле
Мы подчеркивали, что в упругом теле, находящемся в равновесии, внутренние напряжения распределяются так, чтобы энергия была минимальной. Посмотрим теперь, что происходит, если внутренние силы не уравновешены. Возьмем маленький кусочек материала внутри некоторой поверхности А (фиг. 39.5).
Фиг. 39.5. Маленький элемент объема V, ограниченный поверхностью А,
Если этот кусочек находится в равновесии, то полная действующая на него сила Fдолжна быть равна нулю. Можно считать, что эта сила состоит из двух частей, одна из которых обусловлена «внешними» силами, подобными гравитации, действующими на расстоянии на вещество нашего кусочка и приводящими к величине силы на единицу объема fвнешн. Полная же внешняя сила Fвнешн равна интегралу от fвнешн по всему объему кусочка:
В равновесии эти силы балансируются полной силой Fвнутр, действующей по поверхности А со стороны окружающего материала. Когда же этот кусочек не находится в равновесии, а движется, сумма внутренних и внешних сил будет равна произведению массы на ускорение. При этом мы получаем
где r—плотность материала, а а — его ускорение. Теперь мы можем скомбинировать уравнения (39.23) и (39.24) и написать
Нашу запись можно упростить, положив
Тогда уравнение (39.25) запишется в виде
Величина, названная нами Fвнутр, связана с напряжениями в материале. Тензор напряжений Sijбыл определен нами в гл. 31 таким образом, что x-компонента силы dF, действующей на элемент поверхности da с нормалью n, задается выражением
Отсюда х-компонента силы Fвнутр, действующей на наш кусочек, равна интегралу от dFxпо всей поверхности. Подставляя это в x-компоненту уравнения (39.27), получаем
Оказалось, что поверхностный интеграл связан с интегралом по объему, а это напоминает нам нечто знакомое по главам об электричестве. Заметьте, что если не обращать внимания на первый значок х в каждом из S в левой части (39.29), то она выглядит в точности как интеграл от величины (S·n), т.е. нормальной компоненты вектора по поверхности. Она была бы равна потоку S через объем. А используя теорему Гаусса, поток можно было бы записать в виде объемного интеграла от дивергенции S. На самом деле все это справедливо независимо от того, есть ли у нас индекс х или нет. Это просто математическая теорема, которая доказывается интегрированием по частям. Другими словами, уравнение (39.29) можно превратить в
Теперь можно отбросить интегралы по объему и написать дифференциальное уравнение для любой компоненты f:
Оно говорит нам, как связана сила, действующая на единицу объема с тензором напряжения Sij.
Вот как работает эта теория внутренних движений твердого тела. Если первоначально нам известны перемещения, задаваемые, скажем, вектором и, то можно найти деформации eij. Из деформаций с помощью уравнения (39.12) можно получить напряжения. Затем с помощью уравнения (39.31) мы из напряжений можем найти плотности сил f. А зная f, мы из уравнения (39.26) получаем ускорение r в материале, которое подскажет нам, как изменятся перемещения. Собирая все это вместе, мы получаем ужасно сложные уравнения движения упругого твердого тела. Я просто напишу вам ответ для изотропного материала. Если вы воспользуетесь для Sijуравнением (39.20) и запишете eijв виде 1/2 (dui/dxj+duj]dxi), то окончательно получите векторное уравнение:
Вы можете очень просто убедиться в том, что уравнение должно иметь такую форму. Сила должна зависеть от второй производной — перемещения и. Но какие можно составить вторые производные и так, чтобы они были векторами? Одна из них С (С·u); это самый настоящий вектор. Есть еще только одна такая комбинация — это С2u. Так что наиболее общей формой силы будет
что как раз дает (39.32) с другим определением постоянных. Вас может удивить, почему у нас нет третьего слагаемого СXСXu, которое тоже вектор. Но вспомните, что СXСXu
в точности равно С2u-С(С·u), т. е. это линейная комбинация двух уже написанных слагаемых. Так что оно не добавит ничего нового. Мы еще раз доказали, что в изотропном материале есть только две упругие постоянные.
Для получения уравнения движения материала мы можем положить выражение (39.32) равным rд2u/дt2и, пренебрегая объемными силами типа силы тяжести, написать
Это уравнение выглядит похожим на волновое уравнение, с которым мы познакомились в электромагнетизме, за исключением одного добавленного слагаемого, которое усложняет дело. Для материалов, упругие свойства которых всюду одинаковы, мы можем увидеть, на что похоже общее решение. Вы, наверное, помните, что любое векторное поле может быть записано в виде суммы двух векторов, у одного из которых нулю равна дивергенция, а у другого — ротор. Другими словами, можно положить
где
Подставляя вместо u в уравнении (39.33) u1+u2, получаем
Взяв дивергенцию этого уравнения, мы можем исключить из него u1:
Поскольку операторы С2 и С могут быть переставлены, можно вынести оператор дивергенции и получить
А так как СXu2, по определению, равно нулю, то ротор выражения в фигурных скобках также будет нулем, так что выражение в скобках само по себе тождественно равно нулю и
Это векторное волновое уравнение для волн, движущихся со скоростью С2 = Ц(l+2m)/r. Поскольку ротор u2 есть нуль, то эти волны не связаны со сдвигом, а представляют просто волны сжатия наподобие звуковых, которые мы изучали в предыдущих главах и скорость которых как раз равна найденной нами для Спрод.
Подобным же образом, беря ротор уравнения (39.36), можно показать, что u1 удовлетворяет уравнению
Это снова векторное волновое уравнение для волн, распространяющихся со скоростью C2=Цm/r. Поскольку С·u1 равно нулю, то перемещение u1не приводит к изменению плотности; вектор u1 соответствует поперечным или сдвиговым волнам, которые встречались нам в предыдущей главе, а
C2=Cсдвиг.
Если мы хотим знать статические напряжения в изотропном материале, то в принципе их можно найти, решая уравнение (39.32) с f, равным нулю (или равным статическим объемным силам, обусловленным силой тяжести, такой, как rg) при определенных условиях, связанных с силами, действующими на поверхности нашего большого куска материала. Сделать это несколько сложнее, чем в соответствующих задачах электромагнетизма. Во-первых, это более трудно потому, что сами уравнения несколько сложнее, и, во-вторых, формы тех упругих тел, которыми мы обычно интересуемся, гораздо сложнее. На лекциях по электричеству мы часто интересовались решением уравнений Максвелла в областях сравнительно простой геометрической формы, таких, как цилиндр, сфера и т. д. В теории упругости, нам приходится заниматься объектами гораздо более сложной формы, например крюком подъемного крана, или коленчатым автомобильным валом, или ротором газовой турбины. Такие задачи иногда можно приближенно решить численным методом, воспользовавшись принципом минимальной энергии, о котором мы упомянули ранее. Другой способ — это воспользоваться моделями предметов и измерять внутренние напряжения экспериментально с помощью поляризованного света.
Метод этот состоит в следующем. Когда кусок упругого изотропного материала, например прозрачную пластмассу типа плексигласа, подвергают напряжению, в ней возникает двойное лучепреломление. Если пропускать через эту пластмассу поляризованный свет, то плоскость поляризации повернется на величину, связанную с напряжением. Измеряя угол плоскости поляризации, можно измерить напряжение. На фиг. 39.6 показан примерный вид этого устройства, а на фиг. 39.7 приведена фотография упругой модели сложной формы под напряжением.
Фиг. 39.6. Измерение внутренних напряжений с помощью поляризованного света.
Фиг. 39.7. Вид напряженной пластмассовой модели между двумя скрещенными поляроидами.
§ 4. Неупругое поведение
Во всем, что до сих пор говорилось, мы предполагали, что напряжение пропорционально деформации, а это вообще-то неверно. На фиг. 39.8 приведена типичная диаграмма напряжение — деформация упругого материала.
Фиг. 39.8. Типичная диаграмма напряжение — деформация для больших деформаций.
Для малых деформаций напряжение пропорционально деформации. Однако после некоторой точки зависимость напряжения от деформации начинает отклоняться от прямой линии. Для многих материалов, которые мы назовем «хрупкими», разрушение наступает, когда деформация несколько превысит ту точку, где кривая начинает загибаться. В общем же случае в диаграмме напряжение — деформация есть и другие усложнения. Например, когда вы деформируете предмет, существующие большие напряжения могут затем медленно уменьшиться со временем. Если вы достигнете высоких напряжений, однако ниже точки разрыва, а затем будете уменьшать деформацию, то напряжения будут возвращаться назад уже по другой кривой. Возникает небольшой гистерезисный эффект (наподобие того, что мы видели в связи между В и Н в магнитных материалах).
Напряжения, при которых происходит разрушение, сильно изменяются от материала к материалу. Некоторые материалы разрушаются при максимальном растягивающем напряжении. Другие же разрушаются при определенной величине напряжения сдвига. Скажем, мел гораздо слабее противостоит растяжению, тем сдвигу. Если вы потянете за концы палочки мела, то она сломается перпендикулярно направлению приложенной силы (фиг. 39.9, справа).
Фиг. 39.9. Сломанный кусочек мела:
Справа — растягиванием за "концы", слева — скручиванием.
Ведь мел — это только спрессованные частички, которые легко растаскиваются в стороны, поэтому он ломается перпендикулярно приложенной силе. А в отношении сдвига этот материал гораздо крепче, так как в этом случае частицы мешают друг другу. Вспомните теперь, что когда мы скручиваем стержень, то в любом его поперечном сечении возникают сдвиги. Мы показали, кроме того, что сдвиг эквивалентен комбинации растяжения и сжатия под углом 45°. По этой причине при скручивании кусочек мела разломится по сложной поверхности, которая расположена под углом 45° к образующим. На фиг. 39.9 (слева) приведена фотография куска мела, сломанного таким способом. Мел ломается там, где напряжения максимальны.
Есть и другие материалы, которые ведут себя очень странным и сложным образом. Чем сложнее материал, тем причудливей его поведение. Если мы возьмем лист сарана, скомкаем его и бросим на стол, то постепенно он расправится и примет свою первоначальную плоскую форму. На первый взгляд кажется соблазнительным считать, что здесь основную роль играет именно упругость. Но простой подсчет покажет, что она слишком слаба (на несколько порядков слабее), чтобы как-то влиять на этот эффект. Оказывается, что здесь соревнуются два механизма; «нечто» внутри материала «помнит» первоначальную форму и «пытается» вернуться к старому виду, а «нечто» другое «предпочитает» новую форму и сопротивляется возврату к старой.
Я не хочу вдаваться в подробности и описывать тот механизм, который играет роль в поведении скомканного листа сарана, но получить представление о том, как такие эффекты происходят, вы можете на следующей модели. Представьте себе материал, изготовленный из длинных гибких, но крепких нитей вперемешку с пустотелыми ячейками, заполненными вязкой жидкостью. Представьте также, что между каждой ячейкой и соседними с ней имеются узкие проходы, по которым жидкость может медленно проникать из одной ячейки в другую. Если мы скомкаем лист такого материала, то длинные нити деформируются, жидкость из одной ячейки будет выжиматься и переходить в другие ячейки, которые оказались растянутыми. Когда же мы отпускаем лист, то длинные нити будут стремиться вернуться к своей первоначальной форме. Однако, чтобы сделать это, они должны заставить жидкость возвратиться на свое прежнее место, что происходит довольно медленно из-за ее вязкости. Силы, которые мы прилагаем, комкая лист, гораздо больше сил, развиваемых нитями. Скомкать лист можно очень быстро, а вот вернуться к прежнему виду он сможет гораздо медленнее. Несомненно, что здесь основную роль играет комбинация больших, жестких молекул и более мелких, но более подвижных. Этот механизм согласуется также с тем фактом, что материал быстрее принимает свою первоначальную форму, если он нагрет, и медленнее в холодном состоянии: тепло увеличивает подвижность (уменьшает вязкость) мелких молекул.
Хотя мы обсуждали, как происходит нарушение закона Гука, но, по-видимому, наиболее удивительно все же не нарушение этого закона при больших деформациях, а его универсальность. Некоторое понятие о том, почему так происходит, вы можете получить, рассматривая энергию деформации материала. Утверждение о том, что напряжение пропорционально деформации, равносильно утверждению, что энергия деформации изменяется как квадрат напряжения. Предположим, что мы скрутили стержень на малый угол q. Если справедлив закон Гука, то энергия деформации должна быть пропорциональна квадрату q. Предположим, что энергия является некоторой произвольной функцией угла. Мы можем записать ее в виде разложения Тэйлора около нуля:
U(q)=U(0)+U'(0)q +1/2U’’(0)q2+1/6 U'''(q)q3+ -.. . (39.40)
Момент силы t представляет производную U по углу, поэтому
t(q)=U'(0)+U"(0) q+1/2U’’’(0)q2 + ... . (39.41)
Если теперь отсчитывать угол от положения равновесия, то первое слагаемое будет равно нулю. Таким образом, первое оставшееся слагаемое пропорционально q и при достаточно малых углах оно будет превосходить слагаемое с q2. [На самом деле, внутренне материалы в достаточной мере симметричны, так что t(q)=-t(-q); слагаемое с q2 оказывается нулем, а отклонение от линейности происходит только из-за слагаемого с q3. Однако нет причин, по которым это было бы верно для растяжения и сжатия.] Единственно, что мы не объяснили,— почему материалы обычно разрушаются вскоре после того, как становятся существенными члены высшего порядка.
§ 5. Вычисление упругих постоянных
Последний вопрос в теории упругости, который я разберу,— это попытка вычислить упругие постоянные материала, исходя из некоторых свойств атомов, составляющих этот материал. Мы рассмотрим простой случай ионного кубического кристалла типа хлористого натрия. Размер или форма деформированного кристалла изменяются. Такие изменения приводят к увеличению потенциальной энергии кристалла. Для вычисления изменения энергии деформации следует знать, куда идет каждый атом. Чтобы сделать полную энергию как можно меньше, атомы в решетке сложных кристаллов перегруппировываются весьма сложным образом. Это довольно сильно затрудняет вычисление энергии деформации. Но понять, что получается в случае простого кубического кристалла, все-таки можно. Возмущения внутри кристалла будут геометрически подобны возмущениям его внешних граней.
Упругие постоянные кубического кристалла можно вычислить следующим образом. Прежде всего мы предположим наличие некоего закона взаимодействия между каждой парой атомов в кристалле. Затем вычислим изменение внутренней энергии кристалла при отклонении от равновесной формы. Это даст нам соотношения между энергией и деформацией, которая квадратична по деформациям. Сравнивая энергию, полученную таким способом, с уравнением (39.13), можно идентифицировать коэффициенты при каждом слагаемом с упругими постоянными Cijkl.
В нашем примере мы будем предполагать следующий простой закон взаимодействия: между соседними атомами действуют центральные силы, имея в виду, что они действуют по линии, соединяющей два соседних атома. Мы ожидаем, что силы в ионных кристаллах должны быть именно такого типа, ибо в основе их лежит простое кулоновское взаимодействие. (При ковалентной связи силы обычно более сложны, ибо они приводят и к боковому давлению на соседние атомы; но нам все эти усложнения ни к чему.) Кроме того, мы собираемся учесть только силу взаимодействия каждого атома с ближайшим к нему и следующими поблизости соседями. Другими словами, мы будем делать приближение, в котором пренебрежем силами между далекими атомами. На фиг. 39.10,а показаны силы в плоскости ху, которые мы будем учитывать. Следует еще учесть соответствующие силы в плоскостях yz и zx.
Поскольку нас интересуют только упругие постоянные, которые описывают малые деформации, и, следовательно, в выражении для энергии нам нужны только слагаемые, квадратичные по деформациям, то можно считать, что силы между каждой парой атомов изменяются с перемещением линейно.
Фиг. 39.10. Принимаемые нами в расчет межатомные силы (а) и модель, в которой атомы связаны пружинками (б).
Поэтому для наглядности можно представлять, что каждая пара атомов соединена «линейной» пружинкой (фиг. 39.10, б). Все пружинки между атомами натрия и хлора должны иметь одну и ту же упругую постоянную, скажем k1. Пружинки между двумя атомами натрия и двумя атомами хлора могут иметь различные постоянные, но я хочу упростить наши рассуждения, и поэтому буду считать эти постоянные равными. Обозначим их через k2. (Позднее, когда мы посмотрим, как пойдут вычисления, вы сможете вернуться назад и сделать их разными.)
Предположим теперь, что кристалл возмущен однородной деформацией, описываемой тензором eij. В общем случае у него будут компоненты, содержащие х, у и z, но мы для большей наглядности рассмотрим только деформации с тремя компонентами: ехх, еxyи еyy . Если один из атомов выбрать в качестве начала координат, то перемещение любого другого атома задается уравнением типа (39.9):
Назовем атом с координатами х=у=0 «атомом 1», а номера его соседей показаны на фиг. 39.11.
Фиг,39.11. Перемещение ближайших и следующих поблизости соседей атома 1. (Масштаб сильно искажен.)
Обозначая постоянную решетки через а, мы получаем х- и y-компоненты перемещения ux, uy , выписанные в табл. 39.1.
Таблица 39.1 · КОМПОНЕНТЫ ПЕРЕМЕЩЕНИЯ ux, uу
Теперь можно вычислить энергию, запасенную в пружинках, которая равна произведению k2/2 на квадрат растяжения каждой пружинки. Так, энергия горизонтальной пружинки между атомами 1 и 2 будет равна
Заметьте, что с точностью до первого порядка y-перемещение атома 2 не изменяет длины пружинки между атомами 1 и 2. Однако, чтобы получить энергию деформации диагональной пружинки, той, что идет к атому 3, нам нужно вычислить изменение длины как из-за вертикального, так и из-за горизонтального перемещений. Для малых отклонений от начала координат куба изменение расстояния до атома 3 можно записать в виде суммы компонент uхи uv в диагональном направлении:
Воспользовавшись величинами uхи uy. можно получить выражение для энергии
Для полной энергии всех пружинок в плоскости ху нам нужна сумма восьми членов типа (39.43) и (39.44). Обозначая эту энергию через U0, получаем
Чтобы найти полную энергию всех пружинок, связанных с атомом 1, мы должны сделать некую добавку к уравнению (39.45). Хотя нам нужны только х- и y-компоненты деформации, вклад в них дает еще некоторая добавочная энергия, связанная с диагональными соседями вне плоскости ху. Эта добавочная энергия равна
Упругие постоянные связаны с плотностью энергии w уравнением (39.13). Энергия, которую мы вычислили, связана с одним атомом, точнее это удвоенная энергия, приходящаяся на один атом, ибо на каждый из двух атомов, соединенных пружинкой, должно приходиться по 1/2 ее энергии. Поскольку в единице объема находится 1/a3 атомов, то w и U0связаны соотношением
w=U0/2a3.
2а3
Чтобы найти упругие постоянные Cijkl, нужно только возвести в квадрат суммы в скобках в уравнении (39.45), прибавить (39.46) и сравнить коэффициенты при еijеklссоответствующими коэффициентами в уравнении (39.13). Например, собирая слагаемые с е2xxи е2yy , мы находим, что множитель при нем равен
поэтому
В остальных слагаемых нам встретится небольшое усложнение. Поскольку мы не можем отличить произведения еххеyyот еyyехх, то коэффициент при нем в выражении для энергии равен сумме двух членов в уравнении (39.13). Коэффициент при еххеyyв уравнении (39.45) равен 2k2, так что получаем
Однако из-за симметрии выражения для энергии при перестановке двух первых значений с двумя последними можно считать, что Скхуу=Суухх, поэтому
Таким же способом можно получить
Заметьте, наконец, что любой член, содержащий один раз значок х или у, равен нулю, как это было найдено ранее из соображений симметрии. Подытожим наши результаты:
Итак, оказалось, что мы способны связать макроскопические упругие постоянные с атомными свойствами, которые проявляются в постоянных k1 и k2. В нашем частном случае Cхуxу=Cххуу.Эти члены для кубического кристалла, как вы, вероятно, заметили из хода вычислений, оказываются всегда равными, какие бы силы мы ни принимали во внимание, но только при условии, что силы действуют вдоль линии, соединяющей каждую пару атомов, т. е. до тех пор, пока силы между атомами подобны пружинкам и не имеют боковой составляющей (которая несомненно существует при ковалентной связи).
Наши вычисления можно сравнить с экспериментальными измерениями упругих постоянных. В табл. 39.2 приведены наблюдаемые величины трех упругих коэффициентов для некоторых кубических кристаллов. Вы, вероятно, обратили внимание на то, что Сxxyy , вообще говоря, не равно Сxyxy . Причина заключается в том, что в металлах, подобных натрию и калию, межатомные силы не направлены по линии, соединяющей атомы, как предполагалось в нашей модели. Алмаз тоже не подчиняется этому закону, ибо силы в алмазе — это ковалентные силы, которые обладают особым свойством направленности: «пружинки» предпочитают связывать атомы, расположенные в вершинах тетраэдра. Такие ионные кристаллы, как фтористый литий или хлористый натрий и т. д., обладают почти всеми физическими свойствами, предположенными в нашей модели; согласно данным табл. 39.2, постоянные Сxxyyи Сxyxy у них почти равны.
Таблица 39.2 · упругие постоянные
КУБИЧЕСКИХ КРИСТАЛЛОВ
Только хлористое серебро почему-то не хочет подчиняться условию Сххуу=Cxyxy..
* В литературе вы часто столкнетесь с другими обозначениями. Так, многие пишут:
* Пластик с мудреным названием «поливинилиденхлорид», применяемый для обертки.— Прим. ред.
* Предположим на минуту, что полный угол сдвига q делится на две равные части, чтобы деформация была симметричной относительно осей x и y.
Литература: Ch. Kittel, Introduction to Solid State Physics, 2nd ed., New York, 1956. (Имеется перевод: Ч. Киттель, Введение в физику твердого тела, Физматгиз, М., 1962.)
Глава 40 ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
§ 1. Гидростатика
§ 2. Уравнение движения
§ 3. Стационарный поток; теорема Бернулли
§ 4. Циркуляция
§ 5. Вихревые линии
§ 1. Гидростатика
Кого не пленяет течение жидкости, кто не любуется течением воды! Все мы в детстве любили плескаться в ванне или возиться в грязных лужах. Став постарше, мы восхищались плавным течением реки, водопадами и водоворотами; мы любуемся ими, рядом с твердыми телами они кажутся нам почти одушевленными.
Предметом этой и следующей глав будет поведение жидкости, столь неожиданное и столь интересное. Попытки ребенка преградить путь маленькому ручейку, текущему по улице, и его удивление перед тем, как вода умудряется все же пробить себе дорогу, напоминает наши многолетние попытки понять механизм течения жидкости. Мы пытались мысленно преградить путь воды дамбой, т. е. получить законы и уравнения, которые описывают поток. Рассказу об этих попытках и посвящена настоящая глава. А в следующей главе мы опишем тот уникальный способ, с помощью которого вода прорывает дамбу и ускользает от нас, не дав нам понять ее.
Я предполагаю, что элементарные свойства воды вам уже известны. Основное свойство, которое отличает жидкость от твердого тела, заключается в том, что жидкость не способна сдерживать ни мгновение напряжения сдвига. Если к жидкости приложить напряжение сдвига, то она начинает двигаться. Густые жидкости, подобные меду, движутся менее легко, чем жидкости типа воды или воздуха. Мерой легкости, с которой жидкость течет, является ее вязкость. В этой главе мы рассмотрим такие случаи, когда эффектом вязкости можно пренебречь. А эффекты вязкости отложим до следующей главы.
Начнем с рассмотрения гидростатики, т. е. теории неподвижной жидкости. Если жидкость находится в покое, то на нее не действуют никакие сдвиговые силы (даже в вязкой жидкости). Поэтому закон гидростатики заключается в том, что напряжения внутри жидкости всегда нормальны к любой ее поверхности. Нормальная сила на единичную площадь называется давлением. Из того факта, что в неподвижной жидкости нет сдвигов, следует, что напряжение давления во всех направлениях одинаково (фиг. 40.1).
Фиг. 40.1. В неподвижной жидкости сила, действующая на единичную площадь любой поверхности, перпендикулярна этой поверхности и при любых ориентациях поверхности одна и та же.
Займитесь самостоятельно доказательством того, что если на любой плоскости в жидкости сдвиг отсутствует, то давление во всех направлениях должно быть одинаковым.
Давление в жидкости может изменяться от точки к точке. Так, в неподвижной жидкости на поверхности Земли давление будет изменяться с высотой из-за веса жидкости. Если плотность жидкости r считается постоянной и давление на некотором нулевом уровне обозначено через р0(фиг. 40.2), то давление на высоте h над этой точкой будет р=р0 -rgh, где g — сила тяжести единицы массы.
Фиг. 40.2. Давление в неподвижной жидкости.
Комбинация р+rgh в неподвижной жидкости остается постоянной. Вы знаете это соотношение, но теперь мы получим более общий результат, где наше соотношение будет лишь частным случаем. Возьмем маленький кубик воды. Какая сила действует на него в результате оказываемого давления? Поскольку давление в любом месте во всех направлениях одинаково, то полная сила, действующая на единицу объема, может быть обусловлена только изменением давления от точки к точке. Предположим, что давление изменяется в направлении оси х, и выберем направления других осей координат параллельно ребрам кубика. Давление на грань с координатой х дает силу pDy/Dz (фиг. 40.3), а давление на грань с координатой х+Dх дает силу—[р+(др/дх) Dх] DyDz, так что результирующая сила равна -(др/дх)DxDyzDz.
Фиг. 40.3. Полная сила давления, действующая на куб, составляет -Сp на единицу объема.
Если же мы учтем остальные пары граней куба, то нетрудно убедиться, что сила давления на единичный объем равна -Сp. Если вдобавок есть еще и другие силы, наподобие силы тяжести, то давление при равновесии должно компенсироваться ими.
Разберем случай, когда такие дополнительные силы можно описать потенциальной энергией, наподобие силы тяжести. Обозначим через j потенциальную энергию единицы массы. (Для притяжения, например, j просто равно gz.) Сила, действующая на единичную массу, задаётся через потенциал j выражением -Сj, а если плотность жидкости равна r, то на единицу объема будет действовать сила -rСj. В состоянии равновесия эта действующая на единичный объем сила в сумме с силой давления должна давать нуль:
-Сp-rСj=0. (40.1)
Это и есть уравнение гидростатики. В общем случае оно не имеет решения. Если плотность изменяется в пространстве каким-то произвольным образом, то нет возможности уравновесить все силы и жидкость не может находиться в состоянии статического равновесия. В ней возникнут разные конвекционные потоки. Это видно прямо из уравнения, ибо член с давлением представляет чистый градиент, тогда как второй член из-за плотности r не может быть им. И только когда величина r постоянна, потенциальный член становится чистым градиентом.
Решение уравнения в этом случае имеет вид
р+rj=const.
Другая возможность, допускающая состояние равновесия,— это когда r зависит только от р. Однако на этом мы расстанемся с гидростатикой, ибо она не так интересна, как движущаяся жидкость.
§ 2. Уравнение движения
Сначала обсудим движение жидкости с чисто абстрактной теоретической стороны, а затем рассмотрим некоторые частные примеры. Чтобы описать движение жидкости, мы должны задать в каждой точке ее некие свойства. Например, вода (будем называть жидкость просто «водой») в разных местах движется с различными скоростями. Следовательно, чтобы определить характер потока, мы должны в каждой точке и в любой момент времени задать три компоненты скорости. Если нам удастся найти уравнения, определяющие скорость, то мы будем знать, как в любой момент движется жидкость. Но скорость — не единственная характеристика жидкости, которая меняется от точки к точке. Только что мы изучали изменение давления от точки к точке. А есть еще и другие переменные. От точки к точке может меняться также плотность. Вдобавок жидкость может быть проводником и переносить электрический ток, плотность которого j изменяется от точки к точке как по величине, так и по направлению. От точки к точке может меняться температура, магнитное поле и т. д. Так что число полей, необходимых для полного описания ситуации, зависит от сложности задачи. Очень интересные явления возникают, когда доминирующую роль в определении поведения жидкости играют токи и магнетизм. Эта наука носит название магнитогидродинамика. В настоящее время ей уделяется очень большое внимание. Но мы не собираемся рассматривать эти весьма сложные случаи, ибо имеется немало менее сложных, но столь же интересных явлений, и даже этот более элементарный уровень будет достаточно труден.
Возьмем случай, когда нет ни магнитного поля, ни проводимости и нам, кроме того, не следует беспокоиться о температурах, ибо мы предположим, что температура в любой точке единственным образом определяется плотностью и давлением. Фактически мы уменьшим сложность нашей работы, допустив, что плотность постоянна, т. е. что жидкость существенно несжижаема. Другими словами, мы предполагаем, что изменения давлений настолько малы, что производимыми ими изменениями плотности можно пренебречь. Если бы это было не так, то в дополнение к явлениям, рассмотренным здесь, необходимо было бы учитывать и другие явления, скажем распространение звуковых или ударных волн. Распространение звуковых и ударных волн мы уже в какой-то степени изучали, так что при нашем рассмотрении гидродинамики мы изолируемся от этих явлений, допустив, что приближенно плотность r постоянная. Легко определить, когда такое предположение о постоянстве r будет хорошим. Если скорость потока гораздо меньше скорости звуковой волны, то нам не нужно заботиться об изменениях плотности. Тот факт, что вода ускользает от нас при попытке понять ее, не связан с этим приближением постоянной плотности. Усложнения, которые все-таки позволили ей остаться непонятой, мы обсудим в следующей главе.
Общую теорию жидкостей мы должны начать с уравнения состояния жидкости, связывающего давление и плотность; в нашем приближении оно имеет очень простой вид:
r=const.
Это и есть первое уравнение для наших переменных. Следующее соотношение выражает сохранение вещества. Когда вещество утекает из какой-то точки, то количество его в этой точке должно уменьшаться. Если скорость жидкости равна v, то масса, которая протекает за единичное время через единицу площади поверхности, равна нормальной к поверхности компоненте rv. Подобное соотношение у нас получалось уже в теории упругости. Из знакомства с электричеством мы знаем также, что дивергенция такой величины определяется скоростью уменьшения плотности. Также и здесь уравнение
выражает сохранение массы жидкости: это гидродинамическое уравнение непрерывности. В нашем приближении, т. е. в приближении несжимаемой жидкости, плотность r постоянна и уравнение непрерывности превращается просто в
(С·v)=0. (40.3)
Дивергенция скорости жидкости v, как и магнитного поля В, равна нулю. (Гидродинамические уравнения очень часто оказываются аналогичными уравнениям электродинамики; вот почему мы сначала изучали электродинамику. Некоторые предпочитают другой путь, считая, что сначала следует изучать гидродинамику, чтобы потом было легче понять электричество. На самом же деле электродинамика гораздо проще, чем гидродинамика.)
Следующее уравнение мы получим из закона Ньютона; оно говорит нам, как происходит изменение скорости в результате действия сил. Произведение массы элемента объема жидкости на ускорение должно быть равно силам, действующим на этот элемент. Выбирая в качестве элемента объема единичный объем и обозначая силу, действующую на единичный объем, через f, получаем
rX(Ускорение)=f.
Плотность сил можно записать в виде суммы трех слагаемых. Одно из них, силу давления на единицу объема — (Сp), мы уже рассматривали. Но есть еще действующие на расстоянии «внешние» силы, подобные тяжести или электричеству. Если эти силы консервативные с потенциалом, отнесенным к единице массы, равным j, то они приводят к плотности сил —r(Сj). (Если же внешние силы не консервативные, то мы вынуждены писать внешнюю силу, приходящуюся на единицу объема, как fвнешн.) Кроме нее, на единицу объема действует еще одна «внутренняя» сила, которая возникает из-за того, что в текущей жидкости могут действовать сдвиговые силы. Они называются силами вязкости, и мы будем обозначать их через fвязк. Тогда наше уравнение движения приобретает вид
rX(Ускорение)=-( Сp)-r(Сj)+fвязк. (40.4)
В этой главе мы будем предполагать, что наша вода «жидкая» в том смысле, что ее вязкость несущественна, так что слагаемое fвязк будет опускаться. Выбрасывая слагаемое с вязкостью, мы делаем приближение, которое описывает некое идеальное вещество, а не реальную воду. Об огромной разнице, возникающей в зависимости от того, оставляем ли мы слагаемое с вязкостью или нет, в свое время хорошо знал Джон фон Нейманн. Известно ему было и то, что во времена наибольшего расцвета гидродинамики, т. е. примерно до 1900 г., основные усилия были направлены на решение красивых математических задач в рамках именно этого приближения, которое ничего не имеет общего с реальными жидкостями. Поэтому теоретиков, которые занимались подобными веществами, он называл людьми, изучающими «сухую воду». Они отбрасывали важнейшее свойство жидкости. Именно потому, что в этой главе мы при наших вычислениях тоже этим свойством будем пренебрегать, я озаглавил ее «Течение «сухой» воды». А обсуждение настоящей, «мокрой» воды мы отложим до следующей главы.
Если мы отбросим fвязк, то в уравнении (40.4) все нам известно, за исключением выражения для ускорения. Может показаться, что формула для ускорения частиц жидкости должна быть очень простой, ибо очевидно, что если v — скорость частицы в некотором месте жидкости, то ускорение ее будет просто равно дv//дt. Но это совсем неверно, и по довольно хитрой причине. Производная дv/дt выражает изменение скорости v (х, у, z, t) в фиксированной точке пространства. А нам нужно знать, как изменяется скорость данной капельки жидкости. Представьте, что мы пометили одну капельку воды цветной краской и можем наблюдать за ней. За маленький интервал времени At эта капелька продвинется в другое положение. Если капелька движется по некоторому пути, изображенному на фиг. 40.4, то за промежуток Dt она из точки Р1переместится в точку Р2.
Фиг. 40.4. Ускорение частицы жидкости.
Фактически в направлении оси х она передвинется на расстояние vxDt, в направлении оси у — на расстояние vуDt, а в направлении оси z — на расстояние vzDt. Мы видим, что если v (х, у, z, t) — скорость частицы в момент t, то скорость той же самой частицы в момент t+Dt представляет величину v (х+Dx, у+Dy, z+Dz, t+Dt), причем
Dx=vxDt, Dy=vyDt и Dz=vzDt.
Из определения частных производных [вспомните уравнения гл. 2, вып. 5] мы с точностью до членов первого порядка получаем
Ускорение же Dv/Dt будет равно
Считая С вектором, это можно записать символически:
Обратите внимание, что, даже когда дv/дt=0, т. е. когда скорость в данной точке не изменяется, ускорение все же останется. Примером может служить вода, текущая с постоянной скоростью по кругу: она ускоряется даже тогда, когда скорость в данной точке не изменяется. Причина, разумеется, состоит в том, что скорость данной капельки воды, которая первоначально находилась в одной точке, моментом позднее будет иметь другое направление — это центростремительное ускорение.
Остальная часть нашей теории — чисто математическая: нахождение решения уравнения движения, полученного подстановкой ускорения (40.5) в (40.4), т. е.
где слагаемое с вязкостью уже выброшено. Воспользовавшись известным тождеством из векторного анализа, это уравнение можно переписать по-другому:
Если определить новое векторное поле Wкак ротор скорости v, т. е.
то векторное тождество можно записать так:
а наше уравнение движения (40.6) примет вид
Вы можете проверить эквивалентность уравнений (40.6) и (40.8), расписывая их по компонентам и сравнивая их, воспользовавшись при этом выражением (40.7).
Если Wвсюду равно нулю, то такой поток мы называем безвихревым (или потенциальным). В гл. 3, § 5 (вып. 5), мы уже определяли величину, называемую циркуляцией векторного поля. Циркуляция по любой замкнутой петле в жидкости равна криволинейному интегралу от скорости жидкости в данный момент времени вокруг этой петли:
Циркуляция на единицу площади для бесконечно малой петли по теореме Стокса будет тогда равна СXv. Таким образом, W представляет собой циркуляцию вокруг единичной площади (перпендикулярной направлению W). Кроме того, ясно, что если в любое место жидкости поместить маленькую соринку (именно соринку, а не бесконечно малую точку), то она будет вращаться с угловой скоростью W/2. Попытайтесь доказать это. Вы можете также попробовать доказать, что для ведра воды на вращающемся столике W равна удвоенной локальной угловой скорости воды.
Если нас интересует только поле скоростей, то из наших уравнений можно исключить давление. Взяв ротор обеих частей уравнения (40.8) и вспомнив, что r — величина постоянная, а ротор любого градиента равен нулю, а также использовав уравнение (40.3), находим
Это уравнение вместе с уравнениями
W=СXv (40.10)
и
С·v=0 (40.11)
полностью описывают поле скоростей v. На языке математики — если в некоторый момент мы знаем W, то мы знаем ротор вектора скорости и, кроме того, знаем, что его дивергенция равна нулю, так что в этих физических условиях у нас есть все необходимое для определения скорости v повсюду. (Все это в точности напоминает нам знакомые условия в магнетизме, где С·B=0 и СXB=j/e0c2.) Таким образом, данная величина W определяет v точно так же, как j определяет В. Затем из известного значения v уравнение (40.9) даст нам скорость изменения W, откуда мы можем получить новую W в следующий момент. Используя снова уравнение (40.10), найдем новое значение v и т. д. Теперь вы видите, как в эти уравнения входит весь механизм, необходимый для вычисления потока. Заметьте, однако, что эта процедура дает только скорости, а всю информацию о давлении мы потеряли.
Отметим особое следствие нашего уравнения. Если в какой-то момент времени t повсеместно W=0, то дW/дt тоже исчезает, так что W всюду останется равной нулю и в момент t +Dt. Отсюда следует, что поток все время остается безвихревым. Если вначале поток не вращался, то он так никогда и не начнет вращаться. При этом уравнения, которые мы должны решать, таковы:
С·v=0, СXv=0.
Они в точности напоминают уравнения электростатики или магнитостатики в пустом пространстве. Позднее мы вернемся к ним и рассмотрим некоторые частные задачи.
§ 3. Стационарный поток; теорема Бернулли
Вернемся к уравнениям движения (40.8), но ограничимся теперь приближением «стационарного» потока. Под стационарным потоком я подразумеваю поток, скорость которого в любом месте жидкости никогда не изменяется. Жидкость в любой точке постоянно заменяется новой жидкостью, движущейся в точности таким же образом. Картина скоростей всегда выглядит одинаково, т. е. v представляет статическое векторное поле. Как в магнитостатике мы рисовали силовые линии, так и здесь можно начертить линии, которые всегда касательны к скорости жидкости (фиг. 40.5).
Фиг. 40.5. Линии тока стационарного потока.
Эти линии называются «линиями тока». Для стационарного потока они действительно представляют реальные пути частиц жидкости. (В нестационарном потоке картина линий тока меняется со временем, однако в любой момент времени она не представляет пути частиц жидкости.)
Стационарность потока вовсе не означает, что ничего не происходит — частички жидкости движутся и изменяют свои скорости. Это означает только то, что дv/дt=0. Если теперь мы скалярно умножим уравнение движения на v, то слагаемое v·(WXv) выпадет и у нас останется только
Согласно этому уравнению, при малых перемещениях в направлении скорости жидкости величина внутри скобок не изменяется. В стационарном потоке все перемещения направлены вдоль линий тока; поэтому уравнение (40.12) говорит, что для всех точек вдоль линии тока
Это и есть теорема Бернулли. Постоянная, вообще говоря, для различных линий тока может быть разной; мы знаем только, что левая часть уравнения (40.13) постоянна всюду вдоль данной линии тока. Заметьте, кстати, что если стационарный поток безвихревой, т. е. если для него W=0, то уравнение движения (40.8) дает нам соотношение
так что
Оно в точности напоминает уравнение (40.13), за исключением того, что теперь постоянная во всей жидкости одна и та же. На самом деле теорема Бернулли не означает ничего большего, чем утверждение о сохранении энергии. Подобные теоремы о сохранении дают нам массу информации о потоке без детального решения уравнений. Теорема Бернулли настолько важна и настолько проста, что мне бы хотелось показать вам, как можно ее получить другим способом, отличным от тех формальных вычислений, которые мы только что провели. Представьте себе пучок линий тока, образующих трубку тока (фиг. 40.6, а).
Фиг. 40.6. Движение жидкости в трубке.
Поскольку стенки трубки образуются линиями тока, то жидкость через них не протекает. Обозначим площадь на одном конце трубки через A1, скорость жидкости через v1, плотность через r1 а потенциальную энергию через j1. Соответствующие величины на другом конце трубки мы обозначим через A2, v2, r2 и j2. После короткого интервала времени Dt жидкость на одном конце передвинется на расстояние v1Dt, а жидкость на другом конце — на расстояние v2Dt (см. фиг. 40.6, б). Сохранение массы требует, чтобы масса, которая вошла через A1была равна массе, которая
вышла через А2. Изменение масс в этих двух концах должно быть одинаково:
Таким образом, мы получаем равенство
Оно говорит нам, что при постоянном r скорость изменяется обратно пропорционально площади трубки тока.
Вычислим теперь работу, произведенную давлением в жидкости. Работа, произведенная над жидкостью, входящей со стороны сечения А1, равна р1A1v1АDt, а работа, произведенная в сечении А2, равна p2A2v2Dt. Следовательно, полная работа, произведенная над жидкостью, заключенной между A1 и А2, будет
что должно быть равно возрастанию энергии массы жидкости DM при прохождении от А1до А2. Другими словами,
где Е1 — энергия единицы массы жидкости в сечении А1, а Е2 — энергия единицы массы в сечении А2. Энергию единицы массы жидкости можно записать в виде
где 1/2v2 — кинетическая энергия единицы массы, j — потенциальная энергия, a U — дополнительный член, представляющий внутреннюю энергию единицы массы жидкости. Внутренняя энергия может соответствовать, например, тепловой энергии сжимаемой жидкости или химической энергии. Все эти величины могут изменяться от точки к точке. Воспользовавшись выражением для энергии в уравнении (40.16), получим
Но мы видели, что DМ=rDvDt, и получили
а это как раз приводит нас к результату Бернулли, где имеется дополнительный член, представляющий внутреннюю энергию. Если жидкость несжимаемая, то внутренняя энергия с обеих сторон одна и та же и мы снова убеждаемся в справедливости уравнения (40.14) вдоль любой линии тока.
Рассмотрим теперь некоторые простые примеры, в которых интеграл Бернулли позволяет нам сразу описать поток. Предположим, что из отверстия вблизи дна резервуара вытекает вода (фиг. 40.7).
Фиг. 40.7. Вытекание жидкости из резервуара.
Рассмотрим случай, когда скорость потока vвых в отверстии гораздо больше скорости потока вблизи поверхности воды в резервуаре; другими словами, предположим, что диаметр резервуара настолько велик, что падением уровня жидкости можно пренебречь. (Мы могли бы при желании проделать и более аккуратные вычисления.) Давление на поверхность воды в резервуаре равно р0(атмосферному давлению), т. е. такое же, как и давление на бока струи. Напишем теперь уравнение Бернулли для линии тока наподобие той, что показана на фиг. 40.7. В верхней части резервуара скорость v мы примем равной нулю; гравитационный потенциал j здесь выберем тоже равным нулю. В отверстии же скорость равна vвых а j =-gh, так что
или
Скорость получилась в точности равной скорости предмета, падающего с высоты h. В этом нет ничего удивительного —ведь в конечном счете вода на выходе получает свою кинетическую энергию из запаса потенциальной энергии воды, находящейся наверху резервуара. Однако не воображайте, что вы можете определить скорость убывания жидкости из резервуара, умножив эту скорость vвых на площадь отверстия. Скорости частиц жидкости в тот момент, когда струя вырывается из отверстия, не параллельны друг другу, а имеют компоненту, направленную к центру потока; струя сужается. Пройдя небольшое расстояние, струя перестает сжиматься, и скорости становятся параллельными. Таким образом, полный поток равен скорости, умноженной на площадь именно в том месте, где сжатие струи прекратилось. На самом деле, если у нас есть выходное отверстие просто в виде круглой дыры с острым краем, то сечение струи сокращается до 62% от площади отверстия. Уменьшение эффективной площади выходного отверстия для различных форм выходных труб разное, а его экспериментальное значение можно найти в таблице коэффициентов истечения.
Если выходная труба вдается в резервуар, как показано на фиг. 40.8, то можно весьма красиво доказать, что коэффициент истечения в точности равен 50%. Я лишь намекну вам, как проводится это доказательство.
Фиг. 40.8. Если выходная труба вставлена внутрь жидкости, то сокращение струи составляет половину площади отверстия.
Чтобы получить скорость, мы использовали закон сохранения энергии [см. уравнение (40.18)]. Можно еще рассмотреть закон сохранения импульса. Поскольку с выходящей струей должен утекать и импульс, то к поперечному сечению выходящей трубы должна быть приложена сила. Откуда же она берется? Сила эта должна происходить от давления на стенки. Но наше выходное отверстие мало и расположено далеко от стенок, поэтому скорость жидкости вблизи стенок резервуара будет очень мала. Следовательно, давление на каждую стенку, согласно (40.14), почти точно такое же, как статическое давление в покоящейся жидкости. При этом статическое давление на любую точку с одной стороны резервуара должно уравновешиваться равным давлением на противоположную стенку, за исключением точки на стороне, противоположной выходной трубе. Если теперь мы вычислим импульс, выталкиваемый со струей этим давлением, то сможем показать, что коэффициент истечения равен 1/2. Однако этот метод непригоден для отверстия, наподобие показанного на фиг. 40.7, ибо увеличение скорости около стенок вблизи области отверстия дает падение давления, которое невозможно вычислить.
Рассмотрим теперь другой пример — горизонтальную трубу с переменным поперечным сечением (фиг. 40.9), по которой от одного конца к другому течет вода.
Фиг. 40.9. Там, где скорость повышается, давление понижается.
Сохранение энергии, а именно формула Бернулли, говорит, что в суженной области, там, где скорость выше, давление ниже. Мы можем легко продемонстрировать этот эффект, измеряя давление в разных местах с различным сечением с помощью столбика воды, сообщающегося с потоком через достаточно малые отверстия, не возмущающие потока. При этом давление измеряется высотой вертикального столбика воды. И оно в узких местах действительно оказывается меньше, чем в широких. Если после сужения площадь сечения возвращается к своей прежней величине — той, что была до сокращения, то давление снова возрастает. Формула Бернулли предсказывает, что давление до сужения должно быть тем же, что и после него, однако на самом деле оно заметно меньше. Ошибка нашего предсказания кроется в том, что мы пренебрегли трением, вязкой силой, которая вызывает падение давления вдоль трубы. Однако, несмотря на это падение, давление в узком месте определенно меньше (из-за возрастания скорости), чем по обеим сторонам от него, как это предсказал Бернулли. Скорость v2 должна превышать скорость v1 чтобы через сужение могло пройти то же количество воды. Поэтому вода должна ускоряться, переходя из широкой части в узкую. Силы, которые приводят к этому ускорению, и есть перепад давления.
Этот результат можно проверить с помощью еще одного простого опыта. Представьте, что у нас есть резервуар с водой и выходной трубой, которая выбрасывает струю воды вверх (фиг. 40.10).
Фиг. 40.10. Доказательство того что v не равно Ц2gh,
Если бы скорость истечения была в точности равна Ц2gh, то выходящая вода должна была бы подняться вплоть до уровня воды в резервуаре. Однако на опыте она начинает падать несколько ниже его. Наше приближение оказывается очень грубым; вязкое трение, которое мы не учли в нашей формуле для сохранения энергии, приводит к потере энергии. Пытались ли вы когда-нибудь, дунув между двумя слипшимися листками бумаги, оторвать их друг от друга? Попытайтесь! Они сойдутся вновь. Причина, разумеется, состоит в том, что воздух между листами имеет большую скорость, нежели когда он выходит наружу. Поэтому давление между листами ниже атмосферного, и они вместо того, чтобы разлететься в разные стороны, соединятся.
§ 4. Циркуляция
В начале предыдущего параграфа мы видели, что если у нас есть безвихревая несжимаемая жидкость, то поток удовлетворяет следующим двум уравнениям:
С·v=0, СXv=0. (40.19)
Эти уравнения аналогичны уравнениям электростатики или магнитостатики в пустом пространстве. При отсутствии зарядов дивергенция электрического поля равна нулю, а ротор электростатического поля всегда равен нулю. Ротор магнитного поля равен нулю при отсутствии токов, а дивергенция магнитного поля всегда равна нулю. Следовательно, уравнения (40.19) имеют такие же решения, как и уравнения для Е в электростатике или уравнения для В в магнитостатике. Фактически в гл. 12, § 5 (вып. 5), мы уже решили задачу об обтекании сферы потоком в качестве электростатического аналога. Электростатическим аналогом является однородное электрическое поле плюс поле диполя, причем поле диполя подбирается таким, чтобы скорость потока, нормальная к поверхности сферы, была равна нулю. Задачу об обтекании цилиндра можно решить таким же способом, выбрав подходящее направление диполя относительно однородного потока. Эти решения справедливы в тех случаях, когда скорость жидкости на больших расстояниях постоянна как по величине, так и по направлению. Они изображены на фиг. 40.11,а.
Фиг. 40.11. Обтекание цилиндра идеальной жидкостью (а), циркуляция вокруг цилиндра (б) и cy перпозuция случаев а и б (в).
Задача об обтекании цилиндра имеет и другое решение, когда условия таковы, что поток на больших расстояниях движется по окружности вокруг цилиндра. Тогда поток будет круговым повсюду (фиг. 40.11,6). У такого потока есть циркуляция вокруг цилиндра, хотя СXv в жидкости остается нулем. Но как циркуляция может существовать без ротора?
У нас есть циркуляция вокруг цилиндра, ибо криволинейный интеграл от v по замкнутой петле, охватывающей цилиндр, не равен нулю. В то же время криволинейный интеграл от v по любому замкнутому пути, который не охватывает цилиндра, будет нулем. Аналогичные вещи встречались нам и раньше, когда мы определяли магнитное поле вокруг проводника. Ротор В был нулем вне провода, хотя криволинейный интеграл от В по пути, охватывающему провод, не исчезает. Поле скоростей в безвихревой циркуляции вокруг цилиндра в точности такое же, как и магнитное поле вокруг провода. Для кругового пути с центром, совпадающим с центром цилиндра, криволинейный интеграл от скорости равен
Для безвихревого потока интеграл не должен зависеть от r. Обозначим его через постоянную С и получим
где v — тангенциальная скорость, а r — расстояние от оси. Существует очень хороший способ демонстрации циркуляции жидкости в трубе. Вы берете прозрачный цилиндрический резервуар с трубкой в центре дна. Наполняете его водой, немного раскручиваете ее палочкой и вынимаете пробку из отводной трубы. И получаете тот красивый эффект, который показан на фиг. 40.12.
Фиг. 40.12. Вода с циркуляцией вытекает из резервуара.
(Подобное явление вы наверняка много раз видели в ванне!) Хотя вначале вы и создали некоторую угловую скорость w, она из-за вязкости вскоре затухает и поток становится безвихревым. Однако какая-то циркуляция вокруг трубки все же остается.
Из теории можно вычислить форму поверхности воды в цилиндре. По мере того как частицы движутся внутрь, они набирают скорость. Согласно уравнению (40.20), тангенциальная скорость увеличивается как 1/r — просто благодаря закону сохранения момента количества движения, как у фигуриста, прижавшего руки к телу. Радиальная скорость тоже возрастает как 1/r. Если пренебречь тангенциальным движением, то получится, что вода идет внутрь по радиусу к отверстию, а из уравнения С·v=0 следует, что радиальная скорость пропорциональна 1/r. Таким образом, полная скорость тоже возрастает как 1/г и вода идет по спирали Архимеда. Поверхность вода — воздух целиком находится под атмосферным давлением, так что, согласно уравнению (40.14), она должна обладать свойством
gz+1/2mv2=const.
Ио здесь v пропорционально 1/r, поэтому форма поверхности будет такой:
Обратите внимание на одну интересную особенность, которая наблюдается в случае несжимаемого безвихревого потока (в общем случае ее нет): если у нас есть какое-то одно решение и какое-то второе решение, то сумма их тоже будет решением. Это справедливо потому, что уравнения (40.19) — линейные. Полный же набор гидродинамических уравнений, т. е. уравнений (40.8) — (40.10), не линеен, а это уже совсем другое дело. Однако для безвихревого потока вокруг цилиндра мы можем сложить один поток (фиг. 40.11,а) и другой поток (фиг. 40.11,б) и получить новый вид потока (фиг. 40.11,в). Этот новый поток особенно интересен. Скорость потока на верхней стороне цилиндра оказывается больше, чем на нижней, так что когда на циркуляцию вокруг цилиндра налагается чистый горизонтальный поток, то возникнет действующая на цилиндр вертикальная сила; она называется подъемной силой. Разумеется, если циркуляция отсутствует, то в соответствии с нашей теорией «сухой» воды для любого тела суммарная сила обращается в нуль.
§ 5. Вихревые линии
Мы уже выписывали общие уравнения потока несжимаемой жидкости при наличии завихренности:
Физическое содержание этих уравнений было на словах описано Гельмгольцем в трех теоремах. Прежде всего представьте себе, что мы вместо линий потока нарисовали вихревые линии. Под вихревыми линиями мы подразумеваем линии поля, которые имеют направление вектора W, а плотность их в любой области пропорциональна величине W. Из уравнения (II) дивергенция W всегда равна нулю [вспомните гл.3,§ 7 (вып. 5): дивергенция ротора всегда нуль]. Таким образом, вихревые линии подобны линиям поля В: они нигде не кончаются и нигде не начинаются и всегда стремятся замкнуться. Формулу (III) Гельмгольц описал словами: вихревые линии движутся вместе с жидкостью. Это означает, что если бы вы пометили частички жидкости, расположенные на некоторой вихревой линии, например окрасив их чернилами, то в процессе движения жидкости и переноса этих частичек они всегда отмечали бы новое положение вихревой линии. Каким бы образом ни двигались атомы жидкости, вихревые линии движутся вместе с ними. Это один из способов описания законов. Он также содержит и метод решения любых задач. Задавшись первоначальным видом потока, скажем задав всюду v, вы можете вычислить W. Зная v, можно также сказать, где будут вихревые линии немного позднее: они движутся со скоростью v. А с новым значением W можно воспользоваться уравнениями (I) и (II) и найти новую величину v. (Точно как в задаче о нахождении поля В по данным токам.) Если нам задан вид потока в какой-то один момент, то в принципе мы можем вычислить его во все последующие моменты. Мы получаем общее решение невязкого потока.
Мне бы хотелось показать вам, как (по крайней мере частично) можно понять утверждение Гельмгольца, а следовательно, формулу (III). Фактически это просто закон сохранения момента импульса, примененный к жидкости. Представьте себе маленький жидкий цилиндр, ось которого параллельна вихревым линиям (фиг. 40.13,а).
Фиг. 40.13. Группа вихревых линий в момент t (а) и те же самые линии в более поздний момент t' (б).
Спустя некоторое время, тот же самый объем жидкости будет находиться где-то в другом месте. Вообще говоря, он будет иметь форму цилиндра с другим диаметром и находиться в другом месте. Он может еще иметь другую ориентацию (фиг. 40.13,б). Но если изменяется диаметр, то длина тоже должна измениться так, чтобы объем остался постоянным (поскольку мы считаем жидкость несжимаемой). Кроме того, поскольку вихревые линии связаны с веществом, их плотность увеличивается обратно пропорционально уменьшению площади поперечного сечения цилиндра. Произведение W на площадь цилиндра А будет оставаться постоянной, так что в соответствии с Гельмгольцем
Теперь обратите внимание, что при нулевой вязкости все силы на поверхности цилиндрического объема (или любого объема в этом веществе) перпендикулярны поверхности. Силы давления могут заставить его изменить форму, но без тангенциальных сил величина момента количества движения жидкости внутри измениться не может. Момент количества движения жидкости внутри маленького цилиндра равен произведению его момента инерции I на угловую скорость жидкости, которая пропорциональна завихренности W. Момент же инерции цилиндра пропорционален mr2. Поэтому из сохранения момента количества движения мы бы заключили, что
Но масса будет одной и той же (М1=М2), а площадь пропорциональна R2, так что мы снова получим просто уравнение (40.21). Утверждение Гельмгольца, которое эквивалентно формуле (III), есть просто следствие того факта, что в отсутствие вязкости момент количества движения элемента жидкости измениться не может.
Есть хороший способ продемонстрировать движущийся вихрь с помощью аппаратуры, показанной на фиг. 40.14.
Фиг. 40.14. Распространяющиеся вихревые кольца.
Это «барабан» диаметром и длиной около 60 см, состоящий из цилиндрической коробки с натянутым на ее открытое основание толстым резиновым листом. Барабан стоит на боку, а в центре его твердого дна вырезано отверстие диаметром около 8 см. Если резко ударить по резиновой диафрагме рукой, то из отверстия вылетает кольцевой вихрь. Хотя этот вихрь увидеть нельзя, можно смело утверждать, что он существует, так как он гасит пламя свечи, стоящей в 3—6 м от барабана. По запаздыванию этого эффекта вы можете сказать, что «нечто» распространяется с конечной скоростью. Лучше разглядеть то, что вылетает, можно, предварительно напустив в барабан дыму. Тогда вы увидите вихри в виде изумительно красивых колец «табачного дыма».
Кольца дыма (фиг. 40.15,а) — это просто баранка из вихревых линий.
Фиг. 40.15. Движущееся вихревое кольцо (я) и его поперечное сечение (б).
Поскольку W=СXv, то эти вихревые линия описывают также циркуляцию v (фиг. 40.15,б). Для того чтобы объяснить, почему кольцо движется вперед (т. е. в направлении, составляющем с направлением W правый винт), можно рассуждать так: скорость циркуляции увеличивается к внутренней поверхности кольца, причем скорость внутри кольца направлена вперед. Поскольку линии W переносятся вместе с жидкостью, то и они движутся вперед со скоростью v. (Конечно, большая скорость на внутренней части кольца ответственна за движение вперед вихревых линий на его внешней части.)
Здесь необходимо указать на одну серьезную трудность. Как мы уже отмечали, уравнение (40.90) говорит, что если первоначально завихренность W была равна нулю, то она всегда останется равной нулю. Этот результат — крушение теории «сухой» воды, ибо он означает, что если в какой-то момент значение W равно нулю, то оно всегда будет равно нулю, и ни при каких обстоятельствах создать завихренность нельзя. Однако в нашем простом опыте с барабаном мы могли породить вихревые кольца в воздухе, который до того находился в покое. (Ясно, что пока мы не ударили по барабану, внутри него v = 0 и W=0.) Все знают, что, загребая веслом, можно создать в воде вихри. Несомненно, для полного понимания поведения жидкости следует перейти к теории «мокрой» воды.
Другим неверным утверждением в теории «сухой» воды является предположение, которое мы делали при рассмотрении потока на границе между ним и поверхностью твердого предмета. Когда мы обсуждали обтекание потоком цилиндра (например, фиг. 40.11), то считали, что жидкость скользит по поверхности твердого тела. В нашей теории скорость на поверхности твердого тела могла иметь любое значение, зависящее от того, как началось движение, и мы не учитывали никакого «трения» между жидкостью и твердым телом. Однако то, что скорость реальной жидкости должна на поверхности твердого тела сходить на нуль,— экспериментальный факт. Следовательно, наши решения для цилиндра и с циркуляцией, и без нее неправильны, как и результат о создании вихря. О более правильных теориях я расскажу вам в следующей главе.
Глава 41 ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
§ 1.Вязкость
§ 2. Вязкий поток
§ 3.Число Рейнольдса
§ 4.Обтекание кругового цилиндра
§ 5. Предел нулевой вязкости
§ 6.Поток Куеттэ
§ 1. Вязкость
В предыдущей главе мы говорили о поведении воды, пренебрегая при этом эффектами вязкости. Теперь же мне хотелось бы обсудить, как вязкость влияет на течение жидкости. Рассмотрим реальное поведение жидкости. Я опишу качественно, как ведет себя жидкость в самых разных условиях, так чтобы вы получше прочувствовали эту науку. И хотя вы увидите сложные уравнения и услышите о трудных вещах, наша цель совсем не в том, чтобы изучить все тонкости. Цель этой главы скорее «общеобразовательная», просто я хочу дать вам некоторое понятие о том, как устроен мир. Однако здесь все же есть один пункт, который стоит того, чтобы его выучить: полезно знать простое определение вязкости. С него мы и начнем. Все же остальное предназначено для вашего удовольствия.
В предыдущей главе мы нашли, что законы движения жидкости содержатся в уравнении
В нашем приближении «сухой» воды мы отбрасывали последнее слагаемое, так что всеми эффектами вязкости мы пренебрегали. Кроме того, мы иногда делали еще дополнительное приближение, считая жидкость несжимаемой, и при этом получали дополнительное уравнение;
С·v=0.
Это приближение часто оказывается вполне приличным, особенно когда скорость потока много меньше скорости звука. Но в реальных жидкостях мы почти никогда не можем пренебречь внутренним трением, называемым нами вязкостью; большинство интересных вещей в поведении жидкости так или иначе связано именно с этим свойством. Так, мы узнали, что циркуляция «сухой» воды никогда не изменяется: если ее не было вначале, то она никогда и не появится. Но в то же время мы повседневно сталкиваемся с циркуляцией в жидкости. Так что нашу теорию надо подправить.
Начнем с важного экспериментального факта. Когда мы занимались потоком «сухой» воды, обтекающей какой-то предмет или текущей мимо него, т. е. так называемым «потенциальным потоком», у нас не было причин запретить воде иметь составляющую скорости, тангенциальную к поверхности предмета; только нормальная компонента должна была быть равна нулю. Мы не принимали во внимание возможность возникновения сил сдвига между жидкостью и твердым телом. А вот оказывается, хотя это далеко и не очевидно, что во всех случаях, где это было проверено экспериментально, скорость жидкости на поверхности твердого тела в точности равна нулю. Вы замечали, конечно, что лопасти вентилятора собирают на себя тонкий слой пыли, и это несмотря на то, что они вращаются в воздухе. Тот же эффект можно наблюдать даже в больших аэродинамических трубах. Почему же пыль не сдувается воздухом? Несмотря на то что лопасти вентилятора быстро вращаются в воздухе, скорость воздуха относительно них, измеренная непосредственно на их поверхности, равна нулю, так что поток воздуха не возмущает даже мельчайших пылинок. Мы должны модифицировать теорию так, чтобы она согласовалась с тем экспериментальным фактом, что во всех обычных жидкостях молекулы, находящиеся рядом с поверхностью, имеют нулевую скорость (относительно поверхности).
Сначала мы характеризовали жидкость так, что если приложить к ней напряжение сдвига, то, сколь бы мало оно ни было, жидкость «поддается» и течет. В статическом случае никаких напряжений сдвига нет. Однако, когда равновесия еще нет, в момент, когда вы давите на жидкость, силы сдвига вполне могут быть. Вязкость как раз и описывает эти силы, возникающие в движущейся жидкости. Чтобы измерить силы сдвига в процессе движения жидкости, рассмотрим такой эксперимент. Предположим, что имеются две плоские твердые пластины, между которыми находится вода (фиг. 41.1), причем одна из пластин неподвижна, тогда как другая движется параллельно ей с малой скоростью v0.
Фиг. 41.1. Увлечение жидкости между двумя параллельными пластинками.
Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отношению v0/d, где d — расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально v0/d:
Коэффициент пропорциональности h называется коэффициентом вязкости.
Если перед нами более сложный случай, то мы всегда можем рассмотреть в воде небольшой плоский прямоугольный объем, грани которого параллельны потоку (фиг. 41.2).
Фиг. 41.2. Напряжения сдвига в вязкой жидкости.
Силы в этом объеме определяются выражением
Далее, дvx/дy представляет скорость изменения деформаций сдвига, определенных нами в гл. 38, так что силы в жидкости пропорциональны скорости изменения деформаций сдвига.
В общем случае мы пишем
При равномерном вращении жидкости производная дuх/ду равна дvy/дx с обратным знаком, a Sxyбудет равна нулю, как это и требуется, ибо в равномерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проделывали в гл. 39 при определении еxy.) Разумеется, для Syzи Sгхтоже есть соответствующие выражения.
В качестве примера применения этих идей рассмотрим движение жидкости между двумя коаксиальными цилиндрами. Пусть радиус внутреннего цилиндра равен а, его скорость будет vа, а радиус внешнего цилиндра пусть будет b, а скорость равна vb(фиг. 41.3).
Фиг. 41.3. Поток жидкости между двумя концентрическими цилиндрами, вращающимися с разными угловыми скоростями.
Возникает вопрос, каково распределение скоростей между цилиндрами? Чтобы ответить на него, начнем с получения формулы для вязкого сдвига в жидкости на расстоянии r от оси. Из симметрии задачи можно предположить, что поток всегда тангенциален и что его величина зависит только от r; v=v(r). Если мы понаблюдаем за соринкой в воде, расположенной на расстоянии r от оси, то ее координаты как функции времени будут
x = rcoswt, у=rsinwt,
где w=v/r. При этом х- и y-компоненты скорости равны
vx=-rwsinwt =-wу и vy= rwcoswt=wх. (41.4)
Из формулы (41.3) получаем
Для точек с у=0 имеем дw/ду=0, а х(дw/дх) будет равно r(dw)/dr). Так что в этих точках
(Разумно думать, что величина S должна зависеть от дw/дr, когда w не изменяется с r, жидкость находится в состоянии равномерного вращения и напряжения в ней не возникают.) Вычисленное нами напряжение представляет собой тангенциальный сдвиг, одинаковый повсюду вокруг цилиндра. Мы можем получить момент сил, действующий на цилиндрической поверхности радиусом r, путем умножения напряжения сдвига на плечо импульса r и площадь 2prl:
Поскольку движение воды стационарно и угловое ускорение отсутствует, то полный момент, действующий на цилиндрическую поверхность воды между радиусами r и r+dr, должен быть нулем; иначе говоря, момент сил на расстоянии r должен уравновешиваться равным ему и противоположно направленным моментом сил на расстоянии r+dr, так что t не должно зависеть от r. Другими словами, r3(dw/dr) равно некоторой постоянной, скажем А, и
dw/dr=A/r3 (41.8)
Интегрируя, находим как w изменяется с r:
Постоянные А и В должны определяться из условия, что w=wa в точке r=a, a w=wb в точке r=b. Тогда находим
Таким образом, w как функция r нам известна, а стало быть, известно и v=wr.
Если же нам нужно определить момент сил, то его можно получить из выражений (41.7) и (41.8);
или
Он пропорционален относительной угловой скорости двух цилиндров. Имеется стандартный прибор для измерения коэффициентов вязкости, который устроен следующим образом: один из цилиндров (скажем, внешний) посажен на ось, но удерживается в неподвижном состоянии пружинным динамометром, который измеряет действующий на него момент сил, а внутренний цилиндр вращается с постоянной угловой скоростью. Коэффициент вязкости определяется при этом из формулы (41.11).
Из определения коэффициента вязкости вы видите, что h измеряется в ньютон·сек/м2. Для воды при 20° С
h=103 нъютон·сек/м2.
Часто удобнее бывает пользоваться удельной вязкостью, которая равна h, деленной на плотность r. При этом величины удельных вязкостей воды и воздуха сравнимы:
Вода при 20°С h/r=10-6м2/сек
Воздух при 20°С h/r=15·10-6м2/сек. , (41.12)
Обычно вязкость очень сильно зависит от температуры. Например, для воды непосредственно над точкой замерзания отношение h/r в 1,8 больше, чем при 20° С.
§ 2. Вязкий поток
Перейдем теперь к общей теории вязкого потока, по крайней мере настолько общей, насколько это и известно человеку. Вы уже понимаете, что компоненты сдвиговых напряжений сдвига пропорциональны пространственным производным от различных компонент скорости, таких, как dvx/dy или dvy/дх. Однако в общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от других производных скорости. Общее выражение имеет вид
где хi — какая-либо из координат х, у или z; vi — какая-либо з прямоугольных составляющих скорости. (Значок dij обозначает символ Кронекера, который равен единице при i=j и нулю при i№j.) Ко всем диагональным элементам Sijтензора напряжений прибавляется дополнительный член h'С·v. Если жидкость несжимаема, то С·v=0 и дополнительного члена не появляется, так что он действительно имеет отношение к внутренним силам при сжатии. Для описания жидкости, точно так же как и для описания однородного упругого тела, требуются две постоянные. Коэффициент h представляет «обычный» коэффициент вязкости, который мы уже учитывали. Он называется также первым коэффициентом вязкости, а новый коэффициент h' называется вторым коэффициентом вязкости.
Теперь нам предстоит найти вязкую силу fвязк, действующую на единицу объема, после чего мы сможем подставить ее в уравнение (41.1) и получить уравнение движения реальной жидкости. Сила, действующая на маленький кубический объем жидкости, представляет собой равнодействующую всех сил, действующих на все шесть граней. Взяв их по две сразу, мы получим разность, которая зависит от производных напряжений, и, следовательно, от вторых производных скоростей. Это приятный результат, ибо он приведет нас опять к векторному уравнению. Компонента вязкой силы, действующей на единицу объема в направлении оси хi, равна
Обычно зависимость коэффициентов вязкости от координат положения несущественна и ею можно пренебречь. Тогда вязкая сила на единицу объема содержит только вторые производные скорости. Мы видели в гл. 39, что наиболее общей формой вторых производных в векторном уравнении будет сумма Лапласиана (С·С)v = С2v и градиента дивергенции (С (С·v)). Выражение (41.14) представляет как раз такую сумму с коэффициентами h и (h+h'). Мы получаем
В случае несжимаемой жидкости С·v=0 и вязкая сила в единице объема будет просто равна hС2v. Это и все, чем обычно пользуются; однако если вам понадобится вычислить поглощение звука в жидкости, то вам потребуется и второй член. Теперь мы можем закончить вывод уравнения движения реальной жидкости. Подставляя (41.15) в уравнение (41.1), получаем
Уравнение получилось, конечно, сложное, но ничего не поделаешь, такова природа.
Если мы введем W=СXv, как делали это раньше, то наше уравнение можно записать в виде
Мы снова предполагаем, что единственными объемными силами являются консервативные силы типа сил тяжести. Чтобы понять смысл нового члена, давайте рассмотрим случай несжимаемой жидкости. Если мы возьмем ротор уравнения (41.16), то получим
Это напоминает (40.9) с той только разницей, что в правой части имеется еще одно слагаемое. Когда правая часть была равна нулю, то имелась теорема Гельмгольца о том, что вихри всегда движутся вместе с жидкостью. Теперь же в правой части появилось довольно сложное выражение, из которого, однако, не сразу же следуют физические выводы. Если бы мы пренебрегли членом СX(WXv), то получили бы диффузионное уравнение. Новый член означает, что вихри диффундируют в жидкости. При большом градиенте вихри расползаются в соседние области жидкости.
Именно поэтому утолщаются кольца табачного дыма. С этим же связано красивое явление, возникающее при прохождении кольца «чистого» вихря (т. е. «бездымного» кольца, созданного с помощью описанной в предыдущей главе аппаратуры) через облако дыма. Когда оно выходит из облака, к нему «прилипает» некое количество дыма и мы видим полую оболочку из дыма. Какое-то количество завихренности W диффундирует в окружающий дым, продолжая свое движение вперед вместе с вихрем.
§ 3. Число Рейнольдса
Посмотрим теперь, как изменяется течение жидкости из-за нового члена с вязкостью. Рассмотрим несколько подробнее две задачи. Первая — обтекание жидкостью цилиндра; эту задачу мы пытались решить в предыдущей главе, используя теорию невязкой жидкости. Оказывается, что сегодня возможно найти решение вязких уравнений только для некоторых специальных случаев. Так что кое-что из того, что я расскажу вам, основано на экспериментальных измерениях, считая, конечно, что экспериментальная модель удовлетворяла уравнению (41.17).
Математически задача состоит в следующем: мы хотим найти решение для потока несжимаемой вязкой жидкости вблизи длинного цилиндра диаметром D. Поток должен определяться уравнением (41.17) и
W=СXv (41.18)
с условием, что скорость на больших расстояниях равна некоторой постоянной V (параллельной оси х), а на поверхности цилиндра равна нулю. Так что
vя=vу=vz=0 (41.19)
при
x2+y2=D2/4.
Это полностью определяет математическую задачу.
Если вы вглядитесь в эти выражения, то увидите, что в задаче есть четыре различных параметра: h, r, D и V. Можно подумать, что нам придется иметь дело с целой серией решений для разных V, разных D и т. д. Вовсе нет. Все возможные различные решения соответствуют разным значениям одного параметра. Такова наиболее важная общая вещь, которую мы можем сказать о вязком потоке. А чтобы понять, почему это так, заметьте сначала, что вязкость и плотность появляются в виде отношения h/r, т. е. удельной вязкости. Это уменьшает число независимых параметров до трех. Предположим теперь, что все расстояния мы измеряем в единицах той единственной длины, которая появляется в задаче: диаметра цилиндра D, т. е. вместо х, у, z мы вводим новые переменные х', у', z', причем
x=x'D, y=y'D, z=z'D.
При этом параметр D из (41.19) исчезает. Точно так же если будем измерять все скорости в единицах V, т. е. если мы положим v=v'V, то избавимся от V, а v' на больших расстояниях будет просто равно единице. Поскольку мы фиксировали наши единицы длины и скорости, то единицей времени теперь должно быть D/V, так что мы должны сделать подстановку;
t=t'D/V. (41.20)
В наших новых переменных производные в уравнении (41.18) тоже изменятся: так, д/дх перейдет в (1/D)(д/дх') и т. д., так что уравнение (41.18) превратится в
А наше основное уравнение (41.17) перейдет в
Все постоянные при этом собираются в один множитель, который мы, следуя традиции, обозначим через:
Если теперь мы просто запомним, что все наши уравнения должны выписываться для величин, измеряемых в новых единицах, то все штрихи можно опустить. Тогда уравнения для потока примут вид
и
с условиями ,
v=0 , для
х2+у2 =1/4 (41.24)
и
vx=1, vy=vz=0
для
x2+y2+z2>>1.
Что все это значит? Если, например, мы решили задачу для потока с одной скоростью V1и некоторого цилиндра диаметром D1 а затем интересуемся обтеканием цилиндра другого диаметра D2другой жидкостью, то ноток будет одним и тем же при такой скорости V2, которая отвечает тому же самому числу Рейнольдса, т. е. когда
В любых случаях, когда числа Рейнольдса одинаковы, поток при выборе надлежащего масштаба х', у', z' и t' будет «выглядеть» одинаково. Это очень важное утверждение, ибо оно означает, что мы можем определить поведение потока воздуха при обтекании крыла самолета, не строя самого самолета и не испытывая его. Вместо этого мы можем сделать модель и провести измерения, используя скорость, которая дает то же самое число Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений над маленькой моделью самолета в аэродинамической трубе или результаты, полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В противном случае войдет новая величина — скорость звука. При этом различные модели будут действительно соответствовать друг другу только тогда, когда отношение V к скорости звука тоже приблизительно одинаково. Отношение скорости V к скорости звука называется числом Маха. Таким образом, для скоростей, близких к скорости звука или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха и число Рейнольдса в обеих ситуациях одинаковы.
§ 4. Обтекание кругового цилиндра
Вернемся теперь обратно к задаче об обтекании цилиндра медленным (почти несжимаемым) потоком. Я дам вам качественное описание потока реальной жидкости. О таком потоке нам необходимо знать множество вещей. Например, какая увлекающая сила действует на цилиндр? Сила, увлекающая цилиндр, показана на фиг. 41.4 как функция величины , которая пропорциональна скорости V, если все остальное фиксировано.
Фиг. 41.4. Коэффициент увлечения Сd кругового цилиндра как функция числа Рейнольдса.
Фактически на рисунке отложен коэффициент увлечения Сd — безразмерное число, равное отношению силы к 1/2rV2Dl (d — диаметр, l —длина цилиндра, а r —плотность жидкости):
Коэффициент увлечения изменяется довольно сложным образом, как бы намекая нам на то, что в потоке происходит нечто интересное и сложное. Свойства потока полезно описывать для различных областей изменения числа Рейнольдса. Прежде всего, когда число Рейнольдса очень мало, поток вполне стационарен, скорость в любой точке потока постоянна и он плавно обтекает цилиндр. Однако распределение линий потока не похоже на их распределение в потенциальном потоке. Они описывают решение несколько другого уравнения. Когда скорость очень мала или, что эквивалентно, вязкость очень велика, так что вещество по своей консистенции напоминает мед, можно отбросить инерционные члены и описать поток уравнением
Это уравнение впервые было решено Стоксом. Он также решил задачу для сферы. Когда маленькая сфера движется при малых числах Рейнольдса, то к ней приложена сила, равная 6phaV, где а — радиус сферы, a V — его скорость.
Это очень полезная формула: она говорит нам о скорости, с которой мельчайшие частички, которые приближенно можно считать шариками, движутся в жидкости под действием данной силы, как, например, в центрифуге, или при осаждении, или, наконец, в процессе диффузии. В области малых чисел Рейнольдса, т. е. при <1, линии v вокруг цилиндра имеют такой вид, как на фиг. 41.5.
Фиг. 41.5. Вязкий поток вблизи цилиндра (малая вязкость).
Если теперь мы увеличим скорость потока, так что число Рейнольдса станет несколько больше единицы, то увидим, что поток изменится.
Фиг. 41.6. Поток, обтекающий цилиндр, при различных числах Рейнольдса.
Как показано на фиг. 41.6, б, за сферой возникнут вихри. До сих пор неясно, существовали ли вихри и при малых числах Рейнольдса или же они возникли неожиданно при некотором определенном числе? Обычно считали, что циркуляция нарастает постепенно. Однако теперь думают, что скорее она проявляется неожиданно и возрастает с увеличением . Во всяком случае, поток в районе от =10 до =30 меняет свой характер. За цилиндром образуется пара вихрей.
Когда число Рейнольдса проходит через значения в районе 40, поток снова меняется. Характер движения претерпевает неожиданное и резкое изменение. Один из вихрей за цилиндром становится настолько длинным, что он отрывается и плывет вниз по течению вместе с жидкостью. При этом жидкость за цилиндром снова закручивается и возникает новый вихрь. Эти вихри поочередно отслаиваются то с одной, то с другой стороны, так что в какой-то момент поток выглядит приблизительно так, как показано на фиг. 41.6, в. Такой поток вихрей называется вихревой цепочкой Кармана. Она всегда появляется для чисел Рейнольдса >40. Фотография такого потока показана на фиг. 41.7.
Фиг. 41.7. Фотография цепочки вихрей в потоке за цилиндром.
Разница в режиме между двумя потоками, изображенными на фиг. 41.6, а, б или в, очень велика. На фиг. 41.6, а и б скорость постоянна, тогда как на фиг. 41,6, в скорость в любой точке изменяется со временем. Выше =40 стационарное решение отсутствует; граница перехода отмечена на фиг. 41.4 пунктирной линией. Для таких более высоких чисел поток изменяется со временем некоторым регулярным периодическим образом. Создаются вихри.
Можно представить себе физическую причину возникновения этих вихрей. Мы знаем, что на поверхности цилиндра скорость жидкости должна быть равна нулю, но при удалении от поверхности скорость быстро возрастает. Это большое местное изменение скорости жидкости и создает вихри. Когда скорость основного потока достаточно мала, у вихрей хватает времени, чтобы продиффундировать из тонкого слоя вблизи поверхности твердого тела, где они создаются, и «расплыться» на большую область. Эта физическая картина должна подготовить нас к следующему изменению природы потока, когда скорость основного потока или число увеличивается еще больше.
По мере возрастания скорости у вихря остается все меньше и меньше времени, чтобы «расплываться» на большую область жидкости. К тому моменту, когда число Рейнольдса достигнет нескольких тысяч, вихри начинают заполнять тонкую ленту (фиг. 41.6, г). В таком слое поток хаотичен и нерегулярен. Такая область называется пограничным слоем, и этот нерегулярный поток с увеличением пробивает себе путь все дальше и дальше вниз по течению. В области турбулентности скорости очень нерегулярны и «беспорядочны», вдобавок поток больше не двумерный — он крутится во всех трех измерениях. Кроме того, на турбулентное движение налагается еще регулярное переменное движение.
При дальнейшем увеличении числа Рейнольдса область турбулентности пробирается вперед, пока при потоке с , превышающим 105, не достигнет места, где линии тока огибают цилиндр. При этом поток будет похож на то, что показано на фиг. 41.6, д, и мы получаем так называемый «турбулентный след». Кроме того, происходят еще коренные изменения в силе увлечения — она, как видно из фиг. 41.4, сильно падает. При таких скоростях увлекающая сила с возрастанием скорости действительно уменьшается. По-видимому, здесь проявляется некоторое стремление к периодичности.
А что происходит при еще больших числах Рейнольдса? С дальнейшим увеличением скорости размер области турбулентности снова увеличивается и сила сопротивления возрастает. Последние эксперименты, которые дошли до области R=107 или несколько больше, показывают, что в турбулентной области появляется новая периодичность, быть может, потому, что вся область колеблется вперед и назад в общем движении, а может быть, из-за нового сорта вихрей, которые появляются вместе с нерегулярным «шумовым» движением. Детали его полностью еще не ясны, и они до сих пор изучаются экспериментально.
§ 5. Предел пулевой вязкости
Мне бы хотелось подчеркнуть, что ни один из описанных нами потоков ни в каком отношении не похож на решение уравнения потенциального потока, о котором говорилось в предыдущей главе. На первый взгляд это очень удивительно. Ведь R в конце концов пропорционально 1/h. Так что предел h®0 эквивалентен пределу R®Ґ. И если мы перейдем к пределу больших R в (41.23), то избавимся от правой части и получим как раз уравнения из предыдущей главы. Но все же трудно поверить, что сильно турбулентный поток с R=107 хоть в какой-то степени приближается к гладкому потоку, вычисленному из уравнений «сухой» воды. Как может случиться, что при R=Ґ поток, описываемый уравнением (41.23), дает решение, полностью отличное от решения, полученного при h=0, с которого мы начали? Ответ очень интересен. Обратите внимание, что в правой части (41.23) стоит произведение 1/R на вторую производную. Это наиболее высокая степень производной в уравнении: слева только первые производные. Получается так, что, хотя коэффициент 1/R становится малым, W в пространстве вблизи поверхности претерпевает очень быстрые изменения. Эти резкие изменения компенсируют малость коэффициента, и произведение с увеличением R не стремится к нулю. Поэтому, хотя коэффициент при С2W стремится к нулю, решения не приближаются к предельному случаю.
Вас может удивить: «Что же такое мелкомасштабная турбулентность и как она может поддерживать сама себя? Как завихренность, которая создается где-то на краях цилиндра, приводит к такому шуму позади него?». Ответ снова очень интересен. Завихренность имеет тенденцию к самоусилению. Если мы на минуту забудем о диффузии завихренности, которая обусловливает потери, то законы потока говорят (как мы уже видели), что линии вихря переносятся вместе с жидкостью со скоростью v. Представьте себе некоторое количество линий О, которые возмущаются и скручиваются очень сложной картиной скоростей потока v. Прежде простые линии спутаются и сожмутся. Величина завихренности будет возрастать, равно как и ее нерегулярности (положительные и отрицательные), которые, вообще говоря, тоже будут увеличиваться. Таким образом, завихренность в трех измерениях по мере перемешивания жидкости будет возрастать.
Вы можете также спросить: «Когда же в конце концов справедлива теория потенциального потока?» Прежде всего она удовлетворительна вне турбулентной области, куда проникновение завихренности из-за диффузии незначительно. Изготовляя специальные обтекаемые тела, мы стараемся сделать область турбулентности как можно меньше. Поток, обтекающий крылья самолета, которые имеют специальную рассчитанную форму,— почти настоящий потенциальный поток.
§ 6. Поток Куеттэ
Можно показать, что сложный и изменчивый характер потока мимо цилиндра не исключение и что такое разнообразие возможностей получается и в общем случае. В § 1 мы нашли решение для вязкой жидкости между двумя цилиндрами и можем сравнить эти результаты с тем, что получается на самом деле. Если мы возьмем два концентрических цилиндра и заполним пространство между ними маслом с добавленной в него мелкой алюминиевой пудрой, то поток можно легко наблюдать. Если начнем медленно вращать внешний цилиндр, то ничего неожиданного не произойдет (фиг. 41.8, а). Можно медленно вращать и внутренний цилиндр, все равно ничего потрясающего не будет. А вот если мы начнем очень быстро вращать внутренний цилиндр — случится нечто удивительное. Жидкость разобьется на горизонтальные полосы (фиг. 41.8, б). Если с подобной же скоростью мы будем вращать внешний, цилиндр, а внутренний оставим в покое, то никакого похожего эффекта не возникает. Как же получается, что не все равно, какой цилиндр вращать — внутренний или внешний. Ведь в конце концов вид потока, который мы нашли в § 1, зависел только от wb-wа. Ответ можно получить, взглянув на сечение цилиндра, изображенного на фиг. 41.9. Когда внутренние слои жидкости движутся быстрее, чем внешние, они стремятся двигаться наружу: центробежная сила становится больше удерживающего давления. Но весь слой целиком не может двигаться равномерно, так как на его пути стоят внешние слои. Поэтому они
разбиваются на клетки и циркулируют, как показано на фиг. 41.9, б.
Фиг. 41.9. Вот почему поток разбивается на полосы.
Это напоминает конвекционные токи в комнате, где на уровне пола имеется слой теплого воздуха. Когда внутренний цилиндр находится в покое, а внешний цилиндр вращается с большой скоростью, центробежные силы создают градиент давления, который удерживает все в равновесии
(фиг. 41.9, в),как теплый воздух, находящийся у нотолка.
Теперь ускорим внутренний цилиндр. Сначала число полос увеличится. Затем неожиданно полосы станут волнистыми (см. фиг. 41.8,в), и волны эти начнут обтекать цилиндр.
Фиг. 41.8. Виды потока жидкости между двумя прозрачными вращающимися цилиндрами.
Скорость этих волн легко измерить. При больших скоростях вращения она приближается к 1/3от скорости внутреннего цилиндра, а почему, никто не знает. Здесь есть над чем подумать. Простое число 1/3 и полное отсутствие объяснения! Вообще говоря, весь механизм образования волн тоже далеко не ясен, хотя мы имеем дело со стационарным ламинарным потоком.
Если теперь мы еще начнем вращать и внешний цилиндр, но в противоположную сторону, то картина потока начнет разбиваться. Волновые области начнут чередоваться со спокойными на вид областями, образуя спиральную картину (см. фиг. 41.8, г). Однако в этих «спокойных» областях, как можно заметить, поток на самом деле совсем не регулярен; он полностью турбулентен. Кроме того, в волновых областях начинает еще появляться нерегулярный турбулентный поток. Если цилиндры вращаются еще быстрее, то весь поток становится хаотическим турбулентным.
Этот простой эксперимент показал нам много интересных режимов потока, совершенно отличных один от другого и все же содержащихся в нашем простом уравнении при различных величинах одного-единственного параметра R. С помощью наших вращающихся цилиндров мы можем наблюдать многие эффекты, проявляющиеся в потоке, проходящем мимо цилиндра: во-первых, это стационарный поток, во-вторых, целый набор потоков, которые изменяются со временем, но регулярным гладким образом, и, наконец, поток становится полностью нерегулярным. Те же самые эффекты каждый из вас видел в столбике табачного дыма, струящегося от сигареты, когда воздух спокоен. Сначала этот столбик гладкий, затем он как-то скручивается, поток дыма начинает разрушаться, и, наконец, все заканчивается беспорядочными клубами.
Основное, что вам следует вынести из всего сказанного, заключается в том, что в одном простом наборе уравнений (41.23) скрывается огромное разнообразие поведений. Все это решения одного и того же уравнения при различных значениях R. У нас нет причин думать, что в этом уравнении мы потеряли какие-то слагаемые. Единственная трудность заключается в том, что нам сегодня не хватает математических знаний, чтобы проанализировать уравнение, за исключением очень малых чисел Рейнольдса, т. е. в случае очень вязкой жидкости. Написав уравнение, мы не отняли у потока жидкости ни его чарующей прелести, ни его таинственности, ни его поразительности.
Что ожидает нас в более сложных уравнениях, если даже в таком простом уравнении с одним-единственным параметром мы видим такое разнообразие возможностей! Вполне возможно, что основное уравнение, которое описывает завихрение туманностей, или образование вращений, или взрыв звезд и галактик, будет всего-навсего простым уравнением гидродинамики почти чистого водорода. Часто люди в каком-то неоправданном страхе перед физикой говорят, что невозможно написать уравнение жизни. А может быть, и можно. Очень возможно, что на самом деле мы уже располагаем достаточно хорошим приближением, когда пишем уравнение квантовой механики
Только что мы видели, как явления во всей их сложности легко и поразительно получаются из простых уравнений, которые описывают их. Не подозревая о возможностях простых уравнений, люди часто заключают, что для объяснения всей сложности мира требуется нечто данное от бога, а не просто уравнения.
Мы написали уравнения для течения воды. Но из нашего опыта у нас сложились какие-то понятия и приближения, пользуясь которыми, мы можем обсуждать разные решения — цепочку вихрей, турбулентный след, пограничный слой. Когда подобные уравнения встречаются нам в менее знакомой ситуации, где мы еще не можем экспериментировать, то мы пытаемся решать такие уравнения примитивным, извилистым и запутанным путем, стремясь определить, какие же качественные явления можно получить из него или какие новые качественные формы являются следствием этого уравнения. Наши уравнения для Солнца, например, представляющие его как водородный шар, описывают Солнце без солнечных пятен, без зернистой структуры его поверхности, без неровностей и короны. Тем не менее все это действительно находится в уравнениях, только у нас нет еще способа вытащить их оттуда.
Есть такие люди, которые будут очень расстроены, если на других планетах не будет найдено жизни. Я не принадлежу к их числу. И я никогда не смогу перестать удивляться и радоваться результатам межпланетных исследований, обнаруживающих бесконечное разнообразие и новизну явлений, порожденных одними и теми же самыми простыми принципами. Критерий науки — ее способность предсказывать. Могли бы вы предсказать бури, вулканы, океанские волны, зори и красочные закаты, если бы вы никогда не были на Земле?
Драгоценным сокровищем для нас будет все, что мы узнаем о происходящем на каждой из мертвых планет, каждого из десятка шаров, образовавшихся из того же самого облака пыли и подчиняющихся тем же самым законам физики, что и наша планета.
Грядущая великая эра пробуждения человеческого разума принесет с собой метод понимания качественного содержания уравнений. Сегодня еще мы не способны на это. Сегодня мы не можем увидеть в уравнениях потока воды такие вещи, как спиральное строение турбулентности, которую мы видим между вращающимися цилиндрами. Сегодня мы не можем сказать с уверенностью, содержит ли уравнение Шредингера и лягушек, и композиторов, и даже мораль или там ничего похожего и быть не может. Мы не можем сказать, требуется ли что-либо сверх уравнения, вроде каких-то богов, или нет. Поэтому каждый из нас может иметь на этот счет свое особое мнение.
* Большие частицы можно сдуть со стола, а мельчайшие— невозможно. Их верхушки не «высовываются» в поток.
** Можно представить себе и такой случай, когда это окажется неверным. Теоретически стекло есть тоже «жидкость», однако оно вполне может скользить по стальной поверхности. Так что и такая теория где-то должна погореть.

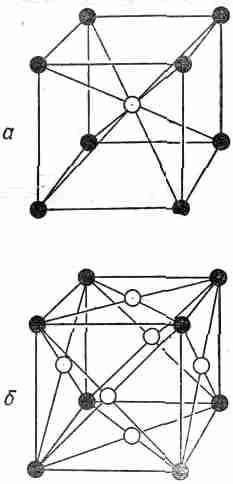



Комментарии к книге «7. Физика сплошных сред», Ричард Филлипс Фейнман
Всего 0 комментариев