5b. Электричество и магнетизм
Глава 10 ДИЭЛЕКТРИКИ
§1. Диэлектрическая проницаемость
§2. Вектор поляризации Р
§З. Поляризационные заряды
§4. Уравнения электростатики для диэлектриков
§5. Поля и силы в присутствии диэлектриков
§ 1. Диэлектрическая проницаемость
Сейчас мы разберем еще одно характерное свойство материи, возникающее под влиянием электрического поля. В одной из предыдущих глав мы рассмотрели поведение проводников, в которых заряды под влиянием электрического поля свободно текут в такие участки, что поле внутри проводника обращается в нуль. Теперь мы будем говорить об изоляторах, т. е. таких материалах, которые не проводят электричество. Сначала можно было бы подумать, что в них вообще ничего не происходит. Но Фарадей с помощью простого электроскопа и конденсатора, состоящего из двух параллельных пластин, обнаружил, что это не так. Его опыт показал, что если между пластинами поместить изолятор, то емкость такого конденсатора увеличится. Когда изолятор целиком заполняет пространство между пластинами, емкость возрастает в x раз, причем x зависит только от свойств изолирующего материала. Изолирующие материалы называют также диэлектриками; тогда множитель x характеризует свойства диэлектрика и называется диэлектрической проницаемостью. Диэлектрическая проницаемость вакуума, конечно, равна единице.
Наша задача теперь состоит в том, чтобы объяснить, почему вообще возникает электрический эффект, раз изоляторы фактически являются изоляторами и не проводят электричества. Начнем с экспериментального факта, что емкость увеличивается, и попытаемся разобраться, что же там может происходить. Рассмотрим плоский конденсатор, на проводящих пластинах которого имеются заряды, скажем, на верхней пластине отрицательные, а на нижней — положительные.
Фиг. 10.1. Плоский конденсатор с диэлектриком. Показаны линии паяя E.
Пусть расстояние между пластинами равно d, а площадь каждой пластины А. Как мы показали раньше, емкость равна
(10.1)
а заряд и потенциал конденсатора связаны соотношением
(10.2)
Далее, экспериментальный факт состоит в том, что если мы положим между пластинами кусок изолирующего материала, например стекла или плексигласа, то емкость возрастет. Это, разумеется, означает, что при том же заряде потенциал стал меньше. Но разность потенциалов есть интеграл от электрического поля, взятый поперек конденсатора; отсюда мы должны заключить, что электрическое поле внутри конденсатора стало меньше, хотя заряды пластин и не изменились.
Но как может это быть? Нам известна теорема Гаусса, которая утверждает, что полный поток электрического поля прямо связан с находящимся внутри объема электрическим зарядом. Рассмотрим входящую в теорему Гаусса поверхность S, изображенную пунктиром на фиг. 10.1. Поскольку электрическое поле в присутствии диэлектрика уменьшается, мы заключаем, что полный заряд внутри поверхности должен теперь быть меньше, чем до внесения изолятора. Остается сделать единственный вывод, что на поверхности диэлектрика должны находиться положительные заряды. Раз поле уменьшилось, но все же не обратилось в нуль, значит, этот положительный заряд меньше отрицательного заряда в проводнике. Итак, явление это можно объяснить, если мы поймем, почему на одной поверхности диэлектрика, помещенного в электрическое поле, индуцируется положительный заряд, а на другой — отрицательный.
Фиг. 10.2. Если поместить пластинку проводника внутрь плоского конденсатора, наведенные заряды обратят поле в проводнике в нуль.
Все было бы понятно, если бы речь шла о проводнике. Пусть у нас был бы, например, конденсатор, расстояние между пластинами которого равно d, и мы вставили бы между этими пластинами незаряженный проводник толщиной b (фиг. 10.2). Электрическое поле индуцирует положительный заряд на верхней поверхности и отрицательный заряд на нижней поверхности, так что в результате поле внутри проводника погашается. Во всех остальных местах поле такое же, какое было без проводника, поэтому оно равно поверхностной плотности зарядов, деленной на eо; но расстояние, по которому мы должны интегрировать, чтобы получить напряжение (разность потенциалов), стало меньше.
Напряжение равно
Окончательное выражение для емкости похоже на (10.1), где d нужно заменить разностью (d-b):
(10.3)
Емкость увеличилась в некоторое число раз, зависящее от b/d, доли объема, занятого проводником.
Отсюда мы получаем модель того, что происходит в диэлектриках: внутри материала имеется множество мелких проводящих слоев. Беда такой модели состоит в том, что в ней должна иметься выделенная ось — перпендикуляр ко всем слоям, а у большинства диэлектриков такой оси нет.
Фиг. 10.3. Модель диэлектрика; маленькие проводящие шарики, вставленные внутрь идеального изолятора.
Эту трудность, однако, можно устранить, предположив, что все изолирующие материалы содержат маленькие проводящие шарики, отделенные один от другой изолятором (фиг. 10.3). Появление диэлектрической проницаемости тогда объясняется действием зарядов, индуцируемых в каждом шарике. В этом и состоит одна из самых первых физических моделей диэлектриков, предложенная для объяснения явления, которое наблюдал Фарадей. Точнее, предполагалось, что каждый атом материала есть идеальный проводник, изолированный от остальных атомов. Диэлектрическая проницаемость x тогда должна была определяться долей того объема, который занимают проводящие шарики. Теперь, однако, пользуются другой моделью.
§ 2. Вектор поляризации Р
Продолжив наш анализ, мы обнаружим, что идея о проводящих и непроводящих участках не так уж существенна. Любой из маленьких шариков действует как диполь, момент которого создается внешним полем. Для понимания диэлектриков существенной является идея о том, что в материале возбуждается множество маленьких диполей. Почему они возбуждаются — то ли потому, что в материале есть проводящие шарики, то ли по каким-либо другим причинам — абсолютно несущественно.
Почему поле должно индуцировать дипольный момент у атома, хотя атом не является проводящим шариком? Мы обсудим этот вопрос гораздо подробнее в следующей главе, которая будет посвящена внутреннему механизму диэлектрических материалов. А сейчас мы дадим лишь один пример, только чтобы проиллюстрировать возможный механизм. Атом имеет ядро с положительным зарядом, окруженное отрицательными электронами. В электрическом поле ядро притягивается в одну сторону, а электроны в другую. Орбиты или плотности вероятности электронов (или какая-либо другая картина, используемая в квантовой механике) несколько искажаются (фиг. 10.4); центр тяжести отрицательных зарядов сместится и больше не будет совпадать с положительным зарядом ядра. Мы уже обсуждали такое распределение заряда. Если взглянуть на него издалека, то подобная нейтральная конфигурация в первом приближении эквивалентна маленькому диполю.
Если поле не чересчур велико, естественно считать величину индуцированного дипольного момента пропорциональной полю. Иначе говоря, небольшое поле сместит заряды чуть-чуть, а более сильное поле раздвинет их дальше — пропорционально величине поля, пока смещение не станет чересчур большим.
Фиг. 10.4. Распределение электронов атома в электрическом поле сдвигается относительно ядра.
До конца этой главы мы будем считать, что дипольный момент в точности пропорционален полю.
Предположим теперь, что в каждом атоме заряды q разделены промежутком d, так что qd есть дипольный момент одного атома. (Мы пишем d, потому что d уже использовано для обозначения расстояния между пластинами.) Если в единице объема имеется N атомов, то дипольный момент в единице объема равен Nqd. Этот дипольный момент в единице объема мы запишем в виде вектора Р. Нет необходимости подчеркивать, что он лежит в направлении всех отдельных дипольных моментов, т. е. в направлении смещения зарядов d:
(10.4)
Вообще говоря, Р будет меняться в диэлектрике от точки к точке. Но в каждой точке Р пропорционален электрическому полю Е. Константа пропорциональности, которая определяется тем, насколько легко можно сместить электрон, зависит от сорта атомов в материале.
О том, что действительно определяет поведение этой константы и степень ее постоянства для больших полей, а также о том, что происходит внутри разных материалов, мы поговорим позже. А пока мы просто предположим, что существует какой-то механизм, благодаря которому индуцируется дипольный момент, пропорциональный электрическому полю.
§ 3. Поляризационные заряды
Посмотрим теперь, что дает эта модель для конденсатора с диэлектриком. Рассмотрим сначала лист материала, в котором на единицу объема приходится дипольный момент Р. Получится ли в результате в среднем какая-нибудь плотность зарядов? Нет, если Р постоянен.
Если положительные и отрицательные заряды, смещенные относительно друг друга, имеют одну и ту же среднюю плотность, то сам факт их смещения не приводит к появлению суммарного заряда внутри объема. С другой стороны, если бы Р в одном месте был больше, а в другом меньше, то это означало бы, что в некоторые области попало больше зарядов, чем оттуда вышло; тогда мы бы могли получить объемную плотность заряда. В случае плоского конденсатора предположим, что Р — величина постоянная, поэтому достаточно будет только посмотреть, что происходит на поверхностях. На одной поверхности отрицательные заряды (электроны) эффективно выдвинулись на расстояние d, а на другой поверхности они сдвинулись внутрь, оставив положительные заряды снаружи на эффективном расстоянии d. Возникает, как показано на фиг. 10.5, поверхностная плотность зарядов, которую мы будем называть поляризационным зарядом.
Этот заряд можно подсчитать следующим образом. Если площадь пластинки равна А, то число электронов, которое окажется на поверхности, есть произведение А и N (числа электронов на единицу объема), а также смещения S, которое, как мы предполагаем, направлено перпендикулярно к поверхности. Полный заряд получится умножением на заряд электрона qe. Чтобы найти поверхностную плотность поляризационных зарядов, индуцируемую на поверхности, разделим на А. Величина поверхностной плотности зарядов равна
Но она равна как раз длине Р вектора поляризации Р [формула (10.4)]:
Фиг. 10.5. Диэлектрик в однородном поле. Положительные заряды сместились на расстояние d относительно отрицательных.
(10.5)
Поверхностная плотность зарядов равна поляризации внутри материала. Поверхностный заряд, конечно, на одной поверхности положителен, а на другой отрицателен.
Предположим теперь, что наша пластинка служит диэлектриком в плоском конденсаторе. Пластины конденсатора также имеют поверхностный заряд (который мы обозначим sсвоб, потому что заряды в проводнике могут двигаться «свободно» куда угодно). Конечно, это тот самый заряд, который мы сообщили конденсатору при его зарядке. Следует подчеркнуть, что sпол существует только благодаря sсвоб. Если, разрядив конденсатор, удалить sсвоб, то sпол также исчезнет, но он не стечет по проволоке, которой разряжают конденсатор, а уйдет назад внутрь материала, за счет релаксации поляризации в диэлектрике.
Теперь мы можем применить теорему Гаусса к поверхности S, изображенной на фиг. 10.1. Электрическое поле Е в диэлектрике равно полной поверхностной плотности зарядов, деленной на e0. Очевидно, что sпол и sсвоб имеют разные знаки, так что
(10.6)
Заметьте, что поле Е0между металлической пластиной и поверхностью диэлектрика больше поля Е; оно соответствует только sсвоб. Но нас здесь интересует поле внутри диэлектрика, которое занимает почти весь объем, если диэлектрик заполняет почти весь промежуток между пластинами. Используя формулу (10.5), можно написать
(10.7)
Из этого уравнения мы не можем определить электрическое поле, пока не узнаем, чему равно Р. Здесь мы, однако, предполагаем, что Р зависит от Е и, более того, пропорционально Е. Эта пропорциональность обычно записывается в виде
(10.8)
Постоянная c (греческое «хи») называется диэлектрической восприимчивостью диэлектрика.
Тогда выражение (10.7) приобретает вид
(10.9)
откуда мы получаем множитель 1/(1+c), показывающий, во сколько раз уменьшилось поле.
Фиг.10.6. Количество ааряда, прошедшее через элемент воображаемой поверхности в диэлектрике, пропорционально компоненте Р, нормальной к поверхности.
Напряжение между пластинами есть интеграл от электрического поля. Раз поле однородно, интеграл сводится просто к произведению Е и расстояния между пластинами d. Мы получаем
Полный заряд конденсатора есть sсвоб А, так что емкость, определяемая формулой (10.2), оказывается равной
(10.10)
Мы объяснили явление, наблюдавшееся на опыте. Если заполнить плоский конденсатор диэлектриком, емкость возрастает на множитель
(10.11)
который характеризует свойства данного материала. Наше объяснение останется, конечно, неполным, пока мы не объясним (а это мы сделаем позже), как возникает атомная поляризация.
Обратимся теперь к чуть более сложному случаю — когда поляризация Р не всюду одинакова. Мы уже говорили, что если поляризация непостоянна, то вообще может возникнуть объемная плотность заряда, потому что с одной стороны в маленький элемент объема может войти больше зарядов, чем выйдет с другой. Как определить, сколько зарядов теряется или приобретается в маленьком объеме?
Подсчитаем сначала, сколько зарядов проходит через воображаемую плоскость, когда материал поляризуется. Количество заряда, проходящее через поверхность, есть просто Р, умноженное на площадь поверхности, если поляризация направлена по нормали к поверхности. Разумеется, если поляризация касательна, к поверхности, то через нее не пройдет ни одного заряда.
Продолжая прежние рассуждения, легко понять, что количество заряда, прошедшее через любой элемент поверхности, пропорционально компоненте Р, перпендикулярной к поверхности. Сравним фиг. 10.6 и 10.5. Мы видим, что уравнение (10.5) в общем случае должно быть записано так:
(10.12)
Фиг. 10.7. Неоднородная поляризация Р может приводить к появлению результирующего заряда внутри диэлектрика.
Если мы имеем в виду воображаемый элемент поверхности внутри диэлектрика, то формула (10.12) дает заряд, который прошел через поверхность, но не приводит к результирующему поверхностному заряду, потому что возникают равные и противоположно направленные вклады от диэлектрика по обе стороны поверхности.
Однако смещение зарядов может привести к появлению объемной плотности зарядов. Полный заряд, выдвинутый из объема V за счет поляризации, есть интеграл от внешней нормальной составляющей Р по поверхности S, охватывающей объем (фиг. 10.7). Такой же излишек зарядов противоположного знака остается внутри. Обозначая суммарный заряд внутри F через DQпол, запишем
(10.13)
Мы можем отнести DQпол за счет объемного распределения заряда с плотностью rпол, так что
(10.14)
Комбинируя оба уравнения, получаем
(10.15)
Мы получили разновидность теоремы Гаусса, связывающую плотность заряда поляризованного материала с вектором поляризации Р. Мы видим, что она согласуется с результатом, полученным для поверхностного поляризационного заряда или же для диэлектрика в плоском конденсаторе. Уравнение (10.15) с гауссовой поверхностью S, изображенной на фиг. 10.1, дает в правой части интеграл по поверхности, равный РDA, а в левой части заряд внутри объема оказывается sпол DA, так что мы снова получаем s=Р.
Точно так же, как мы делали в случае закона Гаусса для электростатики, мы можем перейти в уравнении (10.15) к дифференциальной форме, пользуясь математической теоремой Гаусса:
Мы получаем
(10.16)
Если поляризация неоднородна, ее дивергенция определяет появляющуюся в материале результирующую плотность зарядов. Подчеркнем, что это совсем настоящая плотность зарядов; мы называем ее «поляризационным зарядом», только чтобы помнить, откуда она взялась.
§ 4. Уравнения электростатики для диэлектриков
Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид
(10.17)
где r — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить r на две части. Обозначим снова через rпол заряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем rсвоб. Обычно rсвоб означает заряд, сообщаемый проводникам или распределенный известным образом в пространстве. В этом случае уравнение (10.17) приобретает вид
или
(10.18)
Уравнение для ротора от Е, конечно, не меняется:
(10.19)
Подставляя Р из уравнения (10.8), получаем более простое уравнение:
(10.20)
Это и есть уравнения электростатики в присутствии диэлектриков. Они, конечно, не дают ничего нового, но имеют вид, более удобный для расчетов в тех случаях, когда rсвоб известно, а поляризация Р пропорциональна Е.
Заметьте, что мы не вытащили «константу» диэлектрической проницаемости x за знак дивергенции. Это потому, что она может не быть всюду одинаковой. Если она повсюду одинакова, то ее можно выделить в качестве множителя и уравнения станут в точности обычными уравнениями электростатики, где только rсвоб нужно поделить на x. В написанной нами форме уравнения годятся в общем случае, когда в разных местах поля расположены разные диэлектрики. В таких случаях решить уравнения иногда бывает очень трудно.
Здесь следует отметить один момент, имеющий историческое значение. На заре рождения электричества атомный механизм поляризации не был еще известен и о существовании rпол не знали. Заряд rсвоб считался равным всей плотности зарядов. Чтобы придать уравнениям Максвелла простой вид, вводили новый вектор D как линейную комбинацию Е и Р:
(10.21)
В результате уравнения (10.18) и (10.19) записывались в очень простом виде:
(10.22)
Можно ли их решить? Только когда задано третье уравнение, связывающее D и Е. Если справедливо уравнение (10.8), то эта связь есть
(10.23)
Последнее уравнение обычно записывается так:
(10.24)
где e — еще одна постоянная, описывающая диэлектрические свойства материалов. Она также называется «проницаемостью». (Теперь вы понимаете, почему в наших уравнениях появилось e0, это «проницаемость пустого пространства».) Очевидно.
(10.25)
Сейчас мы рассматриваем эти вещи уже с другой точки зрения, а именно что в вакууме всегда имеются самые простые уравнения, и если в каждом случае учесть все заряды, какова бы ни была причина их возникновения, то они всегда справедливы. Выделяя часть зарядов либо из соображений удобства, либо потому, что мы не хотим вникать в детали процесса, мы всегда можем при желании написать уравнения в любой удобной для нас форме.
Сделаем еще одно замечание. Уравнение D = eE представляет собой попытку описать свойства вещества. Но вещество исключительно сложно по своей природе, и подобное уравнение на самом деле неправильно. Так, если Е становится очень большим, D перестает быть пропорциональным Е. В некоторых веществах пропорциональность нарушается уже при достаточно слабых полях. Кроме того, «константа» пропорциональности может зависеть от того, насколько быстро Е меняется со временем. Следовательно, уравнение такого типа есть нечто вроде приближенного уравнения типа закона Гука. Оно не может быть глубоким, фундаментальным уравнением. С другой стороны, наши основные уравнения для Е (10.17) и (10.19) выражают наиболее полное и глубокое понимание электростатики.
§ 5. Поля и силы в присутствии диэлектриков
Мы докажем сейчас ряд довольно общих теорем электростатики для тех случаев, когда имеются диэлектрики. Мы уже видели, что емкость плоского конденсатора при заполнении его диэлектриком увеличивается в определенное число раз. Сейчас можно показать, что это верно для емкости любой формы, если вся область вокруг двух проводников заполнена однородным линейным диэлектриком. В отсутствие диэлектрика уравнения, которые требуется решить,
такие:
Когда имеется диэлектрик, первое из этих уравнений изменяется, и мы получаем
(10.26)
Далее, поскольку мы считаем и всюду одинаковой, последние два уравнения можно записать в виде
(10.27)
Следовательно, для хЕ получаются такие же уравнения, как для Е0, и тогда они имеют решение хЕ = Е0. Другими словами, поле всюду в х раз меньше, чем в отсутствие диэлектрика. Поскольку разность потенциалов есть линейный интеграл от поля, она уменьшится во столько же раз. А так как заряд на электродах конденсатора в обоих случаях тот же самый, то уравнение (10.2) говорит, что емкость в присутствии всюду однородного диэлектрика увеличивается в х раз.
Зададимся теперь вопросом, как взаимодействуют два заряженных проводника в диэлектрике. Рассмотрим жидкий диэлектрик, повсюду однородный. Мы уже видели раньше, что один из способов найти силу — это продифференцировать энергию по соответствующему расстоянию. Если заряды на проводниках равны и противоположны по знаку, то энергия U — QZ/2C, где С — их емкость. С помощью принципа виртуальной работы любая компонента силы получается некоторым дифференцированием; например,
(10.28)
Поскольку диэлектрик увеличивает емкость в х раз, все силы уменьшатся в такое же число раз.
Однако все это не так просто. Сказанное справедливо, только если диэлектрик жидкий. Любое перемещение проводников, окруженных твердым диэлектриком, изменяет условия механических напряжений в диэлектрике и его электрические свойства, а также несколько меняет механическую энергию диэлектрика. Движение проводников в жидкости не меняет свойств жидкости. Жидкость перетекает в другое место, но ее электрические свойства остаются неизменными.
Во многих старых книгах по электричеству изложение начинается с «основного» закона, по которому сила, действующая между двумя зарядами, есть
(10.29)
а эта точка зрения абсолютно неприемлема. Во-первых, это не всегда верно; это справедливо только в мире, заполненном жидкостью; во-вторых, так получается лишь для постоянного значения х, что для большинства реальных материалов выполняется приближенно.
Гораздо легче начинать со всегда справедливого (для неподвижных зарядов) закона Кулона для зарядов в вакууме.
Что же происходит с зарядами в твердом теле? На это трудно ответить, потому что даже не вполне ясно, о чем идет речь. Если вы вносите заряды внутрь твердого диэлектрика, то возникают всякого рода давления и напряжения. Вы не можете считать работу виртуальной, не включив сюда также механическую энергию, необходимую для сжатия тела, а отличить однозначным образом электрические силы от механических, возникающих за счет самого материала, вообще говоря, очень трудно. К счастью, никому на самом деле не бывает нужно знать ответ на предложенный вопрос. Иногда нужно знать величину натяжений, которые могут возникнуть в твердом теле, а это можно вычислить. Но результаты здесь оказываются гораздо сложнее, чем простой ответ, полученный нами для жидкостей.
Неожиданно сложной оказывается следующая проблема в теории диэлектриков: почему заряженное тело подбирает маленькие кусочки диэлектрика? Если вы в сухой день причесываетесь, то ваша расческа потом легко будет подбирать маленькие кусочки бумаги. Если вы не вдумались в этот вопрос, то, вероятно, сочтете, что на расческе заряды одного знака, а на бумаге противоположного. Но бумага ведь была сначала электрически нейтральной. У нее нет суммарного заряда, а она все же притягивается. Правда, иногда бумажки подскакивают к расческе, а затем отлетают, сразу же отталкиваясь от нее. Причина, конечно, заключается в том, что, коснувшись расчески, бумага сняла с нее немного отрицательных зарядов, а одноименные заряды отталкиваются. Но это все еще не дает ответа на первоначальный вопрос. Прежде всего, почему бумажки вообще притягиваются к расческе?
Ответ заключается в поляризации диэлектрика, помещенного в электрическое поле. Возникают поляризационные заряды обоих знаков, притягиваемые и отталкиваемые расческой. Однако в результате получается притяжение, потому что поле поблизости от расчески сильнее, чем вдали от нее, ведь расческа не бесконечна. Ее заряд локализован. Нейтральный кусочек бумаги не притянется ни к одной из параллельных пластин конденсатора. Изменение поля составляет существенную часть механизма притяжения.
Как показано на фиг. 10.8, диэлектрик всегда стремится из области слабого поля в область, где поле сильнее. В действительности можно показать, что сила, действующая на малые объекты, пропорциональна градиенту квадрата электрического поля. Почему она зависит от квадрата поля? Потому что индуцированные поляризационные заряды пропорциональны полям, а для данных зарядов силы пропорциональны полю. Однако, как мы уже указывали, результирующая сила возникает, только если квадрат поля меняется от точки к точке. Следовательно, сила пропорциональна градиенту квадрата поля. Константа пропорциональности включает помимо всего прочего еще диэлектрическую проницаемость данного тела и зависит также от размеров и формы тела.
Фиг. 10.8, На диэлектрик в неоднородном поле действует сила, направленная в сторону областей с большей напряженностью поля.
Фиг. 10.9. Сила, действующая на диэлектрик в плоском конденсаторе, может быть вычислена с помощью закона сохранения энергии.
Есть еще одна близкая задача, в которой сила, действующая на диэлектрик, может быть найдена точно. Если мы возьмем плоский конденсатор, в котором плитка диэлектрика задвинута лишь частично (фиг. 10.9), то возникнет сила, вдвигающая диэлектрик внутрь. Провести детальное исследование силы очень трудно; оно связано с неоднородностями поля вблизи концов диэлектрика и пластин. Однако если мы не интересуемся деталями, а просто используем закон сохранения энергии, то силу легко вычислить. Мы можем определить силу с помощью ранее выведенной формулы. Уравнение (10.28) эквивалентно
(10.30)
Нам осталось только найти, как меняется емкость в зависимости от положения плитки диэлектрика.
Пусть полная длина пластин есть L, ширина их равна W, расстояние между пластинами и толщина диэлектрика равна d, а расстояние, на которое вдвинут диэлектрик, есть х. Емкость есть отношение полного свободного заряда на пластинах к разности потенциалов между пластинами. Выше мы видели, что при данном потенциале V поверхностная плотность свободных зарядов равна
xe0V/d. Следовательно, полный заряд пластин равен
откуда мы находим емкость
(10.31)
С помощью (10.30) получаем
(10.32)
Но пользы от этого выражения не очень много, разве только вам понадобится определить силу именно в таких условиях. Мы хотели лишь показать, что можно подчас избежать страшных осложнений при определении сил, действующих на диэлектрики, если пользоваться энергией, как это было в настоящем случае.
В нашем изложении теории диэлектриков мы имели дело только с электрическими явлениями, принимая как факт, что поляризация вещества пропорциональна электрическому полю. Почему возникает такая пропорциональность — вопрос, представляющий, пожалуй, еще больший интерес для физики. Стоит нам понять механизм возникновения диэлектрической проницаемости с атомной точки зрения, как мы сможем использовать измерения диэлектрической проницаемости в изменяющихся условиях для получения подробных сведений о строении атомов и молекул. Эти вопросы будут частично изложены в следующей главе.
Глава 11 ВНУТРЕННЕЕ УСТРОЙСТВО ДИЭЛЕКТРИКОВ
§1. Молекулярные диполи
§2. Электронная поляризация
§3. Полярные молекулы; ориентационная поляризация
§4. Электрические поля в пустотах диэлектрика
§5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти
§6. Твердые диэлектрики
§7. Сегнетоэлектричество; титанат бария
Повторить: гл. 3 (вып. 3) «Как возникает показатель преломления», гл. 40 (вып. 4) «Принципы статистической механики »
§ 1. Молекулярные диполи
В этой главе мы поговорим о том, почему вещество бывает диэлектриком. В предыдущей главе мы указывали, что свойства электрических систем с диэлектриками можно было бы понять, предположив, что электрическое поле, действуя на диэлектрик, индуцирует в атомах дипольный момент. Именно, если электрическое поле Е индуцирует средний дипольный момент в единице объема Р, то диэлектрическая проницаемость х дается выражением
(11.1)
О применениях этого выражения мы уже говорили; сейчас же нам нужно обсудить механизм возникновения поляризации внутри материала под действием электрического поля. Начнем с самого простого примера — поляризации газов. Но даже в газах возникают сложности: существуют два типа газов. Молекулы некоторых газов, например кислорода, в каждой молекуле которого имеются два симметричных атома, лишены собственного дипольного момента. Зато молекулы других газов, вроде водяного пара (у которого атомы водорода и кислорода образуют несимметричную молекулу), обладают постоянным электрическим дипольным моментом. Как мы отмечали в гл. 6 и 7, в молекуле водяного пара атомы водорода в среднем имеют положительный заряд, а атом кислорода — отрицательный. Поскольку центры тяжести положительного и отрицательного зарядов не совпадают, то распределение всего заряда в молекуле обладает дипольным моментом.
Фиг. 11.1. Молекула кислорода с нулевым дипольным моментом (а) и молекула воды с постоянным дипольным моментом р0 (б).
Такая молекула называется полярной молекулой. А у кислорода вследствие симметрии молекулы центр тяжести и положительных, и отрицательных зарядов один и тот же, так что это неполярная молекула. Она, правда,
может стать диполем, если ее поместить в электрическое поле. Формы этих двух типов молекул нарисованы на фиг. 11.1.
§ 2. Электронная поляризация
Займемся сначала поляризацией неполярных молекул. Начнем с простейшего случая одноатомного газа (например, гелия). Когда атом такого газа находится в электрическом поле, электроны его тянутся в одну сторону, а ядро — в другую, как показано на рис. 10.4 (стр. 200). Хотя атомы имеют очень большую жесткость по отношению к электрическим силам, которые мы можем приложить к ним на опыте, центры зарядов чуть-чуть смещаются относительно друг друга и индуцируется дипольный момент. В слабых полях величина смещения, а следовательно, и дипольного момента пропорциональна напряженности электрического поля. Смещение электронного распределения, которое приводит к этому типу индуцированного дипольного момента, называется электронной поляризацией.
Мы уже обсуждали воздействие электрического поля на атом в гл. 31 (вып. 3), когда занимались теорией показателя преломления. Подумав немного, вы сообразите, что теперь нужно сделать то же, что и тогда. Только теперь нас заботят поля, не меняющиеся со временем, тогда как показатель преломления был связан с полями, зависящими от времени.
В гл. 31 (вып. 3) мы предполагали, что центр электронного заряда атома, помещенного в осциллирующее электрическое поле, подчиняется уравнению
(11.2)
Первый член — это произведение массы электрона на его ускорение, а второй — возвращающая сила; справа стоит сила, действующая со стороны внешнего электрического поля. Если электрическое поле меняется с частотой w, то уравнение (11.2)
допускает решение
(11.3)
имеющее резонанс при w=w0. Когда раньше мы нашли это решение, то интерпретировали w0 как частоту, при которой атом поглощает свет (она лежит либо в оптической, либо в ультрафиолетовой области, в зависимости от атома). Для нашей цели, однако, достаточно случая постоянных полей, т.е. w=0; поэтому мы можем пренебречь членом с ускорением в (11.2) и получаем смещение
(11.4)
Отсюда находим дипольный момент р одного атома
(11.5)
В таком подходе дипольный момент р действительно пропорционален электрическому полю. Обычно пишут
(11.6)
(Снова e0 вошло по историческим причинам.) Постоянная a называется поляризуемостью атома и имеет размерность L3. Это мера того, насколько легко индуцировать электрическим полем дипольный момент у атома. Сравнивая
(11.5) и (11.6), получаем, что в нашей простой теории
(11.7)
Если в единице объема содержится N атомов, то поляризация (дипольный момент единицы объема) дается формулой
(11.8)
Объединяя (11.1) и (11.8), получаем
(11.9)
или в силу (11.7)
(11.10)
С помощью уравнения (11.9) можно предсказать, что диэлектрическая проницаемость х различных газов должна зависеть от плотности газа и от резонансной частоты w0.
Наша формула, конечно, лишь очень грубое приближение, потому что в уравнении (11.2) мы воспользовались моделью, игнорирующей тонкости квантовой механики. Например, мы считали, что атом имеет только одну резонансную частоту, тогда как на самом деле их много. Чтобы по-настоящему вычислить поляризуемость атомов, нужно воспользоваться последовательной квантовомеханической теорией, однако и классический подход, изложенный выше, дает вполне разумную оценку.
Посмотрим, сможем ли мы получить правильный порядок величины диэлектрической проницаемости какого-нибудь вещества. Возьмем, к примеру, водород. Мы уже оценивали (вып. 4, гл. 38) энергию, необходимую для ионизации атома водорода, и получили приближенно
(11.11)
Для оценки собственной частоты w0 можно положить эту энергию равной ћw0— энергии атомного осциллятора с собственной частотой w0. Получаем
Пользуясь этой величиной в уравнении (11.7), находим электронную поляризуемость
(11.12)
Величина (h2/mez) есть радиус основной орбиты атома Бора (см. вып. 4, гл. 38), равный 0,528 А. При нормальном давлении и температуре (1 атм, 0°С) в газе на 1 см3приходится 2,69·1019 атомов, и уравнение (11.9) дает
c= 1+ (2,69·1019) 16p (0,528·10-8)3 = 1,00020. (11.13) Измеренная на опыте диэлектрическая проницаемость равна
cэксп = 1,00026.
Видите, наша теория почти правильна. Лучшего нельзя было и ожидать, потому что измерения проводились, конечно, с обычным водородом, обладающим двухатомными молекулами, а не одиночными атомами. Не следует удивляться тому, что поляризация атомов в молекуле не совсем такая, как поляризация отдельных атомов. На самом деле молекулярный эффект не столь велик. Точное квантовомеханическое вычисление величины a для атомов водорода дает результат, превышающий (11.12) примерно на 12% (вместо 16p получается 18p), поэтому он предсказывает для диэлектрической проницаемости значение, более близкое к наблюденному. Во всяком случае, совершенно очевидно, что наша модель диэлектрика вполне хороша.
Еще одна проверка нашей теории. Попробуем применить уравнение (11.12) к атомам с большей частотой возбуждения. Например, чтобы отобрать электрон у гелия, требуется 24,5 в, тогда как для ионизации водорода необходимы 13,5 в. Поэтому мы предположим, что частота поглощения w0 для гелия должна быть примерно в два раза больше, чем для водорода, а a должна быть меньше в четыре раза. Мы ожидаем, что
хгелнй»1,000050, а экспериментально получено
xгелий=1,000068,
так что наши грубые оценки показывают, что мы на верном пути. Итак, мы поняли диэлектрическую проницаемость неполярного газа, но только качественно, потому что пока мы еще не использовали правильную атомную теорию движения атомных электронов.
§ 3. Полярные молекулы; ориентационная поляризация
Теперь рассмотрим молекулу, обладающую постоянным дипольным моментом р0 , например молекулу воды. В отсутствие электрического поля отдельные диполи смотрят в разных направлениях, так что суммарный момент в единице объема равен нулю. Но если приложить электрическое поле, то сразу же происходят две вещи: во-первых, индуцируется добавочный дипольный момент из-за сил, действующих на электроны; эта часть приводит к той же самой электронной поляризуемости, которую мы нашли для неполярной молекулы. При очень точном исследовании этот эффект, конечно, нужно учитывать, но мы пока пренебрежем им. (Его всегда можно добавить в конце.) Во-вторых, электрическое поле стремится выстроить отдельные диполи, создавая результирующий момент в единице объема.
Фиг. 11.2. В газе полярных молекул отдельные моменты ориентированы случайным образом, средний момент в небольшом объеме равен нулю (а); под действием электрического поля в среднем возникает некоторое выстраивание молекул (б).
Если бы в газе выстроились все диполи, поляризация была бы очень большой, но этого не происходит. При обычных температурах и напряженностях поля столкновения молекул при их тепловом движении не позволяют им как следует выстроиться. Но некоторое выстраивание все же происходит, а отсюда и небольшая поляризация (фиг. 11.2). Возникающая поляризация может быть подсчитана методами статистической механики, описанными в гл. 40 (вып. 4).
Чтобы использовать этот метод, нужно знать энергию диполя в электрическом поле. Рассмотрим диполь с моментом р0 в электрическом поле (фиг. 11.3). Энергия положительного заряда равна qj (1), а энергия отрицательного есть —qj(2). Отсюда получаем энергию диполя
или
(11.14)
где q — угол между р0 и Е. Как и следовало ожидать, энергия становится меньше, когда диполи выстраиваются вдоль поля. Теперь с помощью методов статистической механики мы выясним, насколько сильно диполи выстраиваются. В гл. 40 (вып. 4) мы нашли, что в состоянии теплового равновесия относительное число молекул с потенциальной энергией U пропорционально
(11.15)
Фие. 11.3. Энергия диполя р0 в поле Е равна —р0·Е.
где U (х, у, z) — потенциальная энергия как функция положения. Оперируя теми же аргументами, можно сказать, что если потенциальная энергия как функция угла имеет вид (11.14), то число молекул под углом 0, приходящееся на единичный телесный угол, пропорционально ехр (— U/kT).
Полагая число молекул на единичный телесный угол, направленных под углом q, равным n(q), имеем
(11.16)
Для обычных температур и полей показатель экспоненты мал, и, разлагая экспоненту, можно воспользоваться приближенным выражением
(11.17)
Найдем n , проинтегрировав (11.17) по всем углам; результат должен быть равен N, т.е. числу молекул в единице объема. Среднее значение cos q при интегрировании по всем углам есть нуль, так что интеграл равен просто n0 , умноженному на полный телесный угол 4p. Получаем
(11.18)
Из (11.17) видно, что вдоль поля (cosq=1) будет ориентировано больше молекул, чем против поля (cosq = -1). Поэтому в любом малом объеме, содержащем много молекул, возникнет суммарный дипольный момент на единицу объема, т.е. поляризация Р. Чтобы вычислить Р, нужно знать векторную сумму всех молекулярных моментов в единице объема. Мы знаем, что результат будет направлен вдоль Е, поэтому нужно только просуммировать компоненты в этом направлении (компоненты, перпендикулярные Е, при суммировании дадут нуль):
Мы можем оценить сумму, проинтегрировав по угловому распределению. Телесный угол, отвечающий q, есть 2psin qdq; отсюда
(11.19)
Подставляя вместо n(q) его выражение из (11.17), имеем
что легко интегрируется и приводит к следующему результату:
(11.20)
Поляризация пропорциональна полю Е, поэтому диэлектрические свойства будут обычные. Кроме того, как мы и ожидаем, поляризация обратно пропорциональна температуре, потому что при более высоких температурах столкновения больше разрушают выстроенность. Эта зависимость вида 1/T называется законом Кюри. Квадрат постоянного момента р0появляется по следующей причине: в данном электрическом поле выстраивающая сила зависит от р0, а средний момент, возникающий при выстраивании, снова пропорционален р0. Средний индуцируемый момент пропорционален р02
Теперь посмотрим, насколько хорошо уравнение (11.20) согласуется с экспериментом. Возьмем водяной пар. Поскольку мы не знаем, чему равно р0, то не можем прямо вычислить и Р, но уравнение (11.20) предсказывает, что x-1 должна меняться обратно пропорционально температуре, и это нам следует проверить.
Из (11.20) получаем
(11.21)
так что x-1 должна меняться прямо пропорционально плотности N и обратно пропорционально абсолютной температуре. Диэлектрическая проницаемость была измерена при нескольких значениях давления и температуры, выбранных таким образом, чтобы число молекул в единице объема оставалось постоянным. (Заметим, что, если бы все измерения выполнялись при постоянном давлении, число молекул в единице объема уменьшалось бы линейно с повышением температуры, а х-1 изменялась бы как T-2, а не как T-1.)
Фиг. 11.4. Измеренные значения диэлектрической проницаемости водяного пара при нескольких температурах.
На фиг. 11.4 мы отложили измеренные значения к — 1 как функцию 1/T. Зависимость, предсказываемая формулой (11.21), выполняется хорошо.
Есть еще одна особенность диэлектрической проницаемости полярных молекул — ее изменение в зависимости от частоты внешнего поля. Благодаря тому что молекулы имеют момент инерции, тяжелым молекулам требуется определенное время, чтобы повернуться в направлении поля. Поэтому, если использовать частоты из верхней микроволновой зоны или из еще более высокой, полярный вклад в диэлектрическую проницаемость начинает спадать, так как молекулы не успевают следовать за полем. В противоположность этому электронная поляризуемость все еще остается неизменной вплоть до оптических частот, поскольку инерция
электронов меньше.
§ 4. Электрические поля в пустотах диэлектрика
Теперь мы переходим к интересному, но сложному вопросу о диэлектрической проницаемости плотных веществ. Возьмем, например, жидкий гелий, или жидкий аргон, или еще какое-нибудь неполярное вещество. Мы по-прежнему ожидаем, что у них есть электронная поляризуемость. Но в плотных средах значение Р может быть велико, поэтому в поле, действующее на отдельный атом, вклад будет давать поляризация атомов, находящихся по соседству. Возникает вопрос, чему равно электрическое поле, действующее на отдельный атом?
Фиг. 11.5. Поле внутри щели, вырезанной в диэлектрике, зависит от ее формы, и ориентации.
Вообразите, что между пластинами конденсатора находится жидкость. Если пластины заряжены, они создадут в жидкости электрическое поле. Но каждый атом имеет заряды, и полное поле Е есть сумма обоих этих вкладов. Это истинное электрическое поле в жидкости меняется очень-очень быстро от точки к точке. Оно чрезвычайно велико внутри атомов, особенно вблизи ядра, и сравнительно мало между атомами. Разность потенциалов между пластинами есть интеграл от этого полного поля. Если мы пренебрежем всеми быстрыми изменениями, то можем представить себе некое среднее электрическое поле Е, равное как раз V/d. (Именно это поле мы использовали в предыдущей главе.) Это поле мы должны себе представлять как среднее по пространству, содержащему много атомов.
Вы можете подумать, что «средний» атом в «среднем» положении почувствует именно это среднее поле. Но все не так просто, и в этом можно убедиться, представив, что в диэлектрике имеются отверстия разной формы. Предположим, что мы вырезали в поляризованном диэлектрике щель, ориентированную параллельно полю (фиг. 11.5, а). Поскольку мы знаем, что СXE = 0, то линейный интеграл от Е вдоль кривой Г, направленной так, как показано на фиг. 11.5, б, должен быть равен нулю. Поле внутри щели должно давать такой вклад, который в точности погасит вклад от поля вне щели. Поэтому поле E0 в центре длинной тонкой щели равно Е, т.е. среднему электрическому полю, найденному в диэлектрике.
Рассмотрим теперь другую щель, повернутую своей широкой стороной перпендикулярно Е (фиг. 11.5, в). В этом случае поле e0 в щели не совпадает с Е, потому что на стенках щели возникают поляризационные заряды. Применив закон Гаусса к поверхности S, изображенной на фиг. 11.5, г, мы находим, что поле Ей внутри щели дается выражением
(11.22)
где Е, как и раньше,— электрическое поле в диэлектрике. (Гауссова поверхность охватывает поверхностный поляризационный заряд sпол = Р.) Мы отмечали в гл. 10, что e0Е + Р часто обозначают через D, поэтому e0Е0 = D0равно величине D в диэлектрике.
В ранний период истории физики, когда считалось очень важным определять каждую величину прямым экспериментом, физики были очень довольны, обнаружив, что они могут определить то, что понимают под Е и D в диэлектрике, не ползая в промежутках между атомами. Среднее поле Е численно равно полю Е0, измеренному в щели, параллельной полю. А поле D могло быть измерено с помощью Е0, найденной в щели, перпендикулярной полю. Но никто эти поля никогда не измерял (таким способом, во всяком случае), так что это одна из многих бесплодных проблем.
В большинстве жидкостей, не слишком сложных по своему строению, каждый атом в среднем так окружен другими атомами, что можно с хорошей точностью считать его находящимся в сферической полости. И тогда мы спросим: «Чему равно поле в сферической полости?» Мы замечаем, что вырезание сферической дырки в однородном поляризованном диэлектрике равносильно отбрасыванию шарика из поляризованного материала, так что мы можем ответить на этот вопрос. (Мы должны представить себе, что поляризация была «заморожена» до того, как мы вырезали дырку.) Однако в силу принципа суперпозиции поле внутри диэлектрика, до того как оттуда был вынут шарик, есть сумма полей от всех зарядов вне объема шарика плюс полей от зарядов внутри поляризованного шарика.
Фиг. 11.6. Поле в любой точке А диэлектрика можно представить в виде суммы поля сферической дырки и поля сферического вкладыша.
Фиг. 11.7. Электрическое поле однородно поляризованного шарика.
Следовательно, если поле внутри однородного диэлектрика мы назовем Е, то можно записать
E=Eдырка+Eшарнк,
(11.23)
где Eдырка — поле в дырке, а Eшарик — поле в однородно поляризованном шарике (фиг. 11.6). Поле однородно поляризованного шарика показано на фиг. 11.7. Электрическое поле внутри шарика однородно и равно
(11.24)
С помощью (11.23) получаем
(11.25)
Поле в сферической полости больше среднего поляна величину Р/Зe0. (Сферическая дырка дает поле, находящееся на 1/3 пути от поля параллельной щели к полю перпендикулярной щели.)
§ 5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти
В жидкости мы ожидаем, что поле, поляризующее отдельный атом, скорее похоже на Едырка, чем просто на Е. Если взять Eдырка из (11.25) в качестве поляризующего поля, входящего в (11.6), то уравнение (11.8) приобретет вид
(11.26)
или
(11.27)
Вспоминая, что х-1 как раз равна Р/e0Е, получаем
(11.28)
что определяет диэлектрическую проницаемость жидкости и через атомную поляризуемость a. Это формула Клаузиуса — Моссотти.
Если Naочень мало, как, например, для газа (потому что там мала плотность N), то членом Na/3 можно пренебречь по сравнению с 1, и мы получаем наш старый результат — уравнение (11.9), т.е.
(11.29)
Давайте сравним уравнение (11.28) с некоторыми экспериментальными данными. Сначала стоит обратиться к газам, для которых из измерений x можно с помощью уравнения (11.29) найти значение а. Так, для дисульфида углерода при нулевой температуре по Цельсию диэлектрическая проницаемость равна 1,0029, так что Na= 0,0029. Плотность газа легко вычислить, а плотность жидкостей можно найти в справочниках. При 20°C плотность жидкого CS2 в 381 раз выше плотности газа при 0°С, Это значит, что N в 381 раз больше в жидкости, чем в газе, а отсюда (если сделать допущение, что исходная атомная поляризуемость дисульфида углерода не меняется при его конденсации в жидкое состояние) Naв жидкости в 381 раз больше 0,0029, или равно 1,11. Заметьте, что Na/З составляет почти 0,4. С помощью этих чисел мы предсказываем, что величина диэлектрической проницаемости равна 2,76, что достаточно хорошо согласуется с наблюденным значением 2,64.
В табл. 11.1 мы приводим ряд экспериментальных данных по разным веществам, а также значения диэлектрической проницаемости, вычисленной, как только что было описано, no формуле (11.28).
Согласие между опытом и теорией для аргона и кислорода даже лучше, чем для CS2, и не столь хорошее для четыреххлористого углерода. В целом результаты показывают, что уравнение (11.28) работает с хорошей точностью.
Наш вывод уравнения (11.28) справедлив только для электронной поляризации в жидкостях. Для полярных молекул вроде Н2O он неверен. Если провести такие же вычисления для воды, то для Na. получим значение 13,2, что означает, что диэлектрическая проницаемость этой жидкости отрицательна, тогда как опытное значение x равно 80. Дело здесь связано с неправильной трактовкой постоянных диполей, и Онзагер указал правильный способ решения. Мы не можем сейчас останавливаться на этом вопросе, но если он вас интересует, то подробно это обсуждается в книге Киттеля «Введение в физику твердого тела».
§ 6. Твердые диэлектрики
Обратимся теперь к твердым телам. Первый интересный факт относительно твердых тел заключается в том, что у них бывает постоянная поляризация, которая существует даже и без приложения внешнего электрического поля. Примеры можно найти у веществ типа воска, который содержит длинные молекулы с постоянным дипольным моментом. Если растопить немного воску и, пока он еще не затвердел, наложить на него сильное электрическое поле, чтобы дипольные моменты частично выстроились, то они останутся в таком положении и после того, как воск затвердеет. Твердое вещество будет обладать постоянной поляризацией, которая остается и в отсутствие поля. Такое вещество называется электретом.
На поверхности электрета расположены постоянные поляризационные заряды. Электрет представляет собой электрический аналог магнита, однако пользы от него гораздо меньше, потому что свободные заряды воздуха притягиваются к его поверхности и в конце концов нейтрализуют поляризационные заряды. Электрет «разряжается» и заметного внешнего поля не создает.
Постоянная внутренняя поляризация Р встречается и у некоторых кристаллических веществ. В таких кристаллах каждая элементарная ячейка решетки обладает одним и тем же постоянным дипольным моментом (фиг. 11.8). Все диполи направлены в одну сторону даже в отсутствие электрического поля. Многие сложные кристаллы обладают такой поляризацией; обычно мы этого не замечаем, потому что создаваемое ими внешнее поле, как и у электретов, разряжается.
Если, однако, внутренние диполъные моменты кристалла меняются, то внешнее поле становится заметным, потому что блуждающие заряды не успевают собраться и нейтрализовать поляризационные заряды. Если диэлектрик находится в конденсаторе, свободные заряды индуцируются на электродах. Моменты могут, например, измениться вследствие теплового расширения, если нагреть диэлектрик. Такой эффект называется пироэлектричеством. Аналогично, если менять напряжения в кристалле, скажем, сгибая его, то момент может снова немного измениться, и тогда обнаружится слабый электрический эффект, называемый пьезоэлектричеством.
Для кристаллов, не обладающих постоянным моментом, можно развить теорию диэлектрической проницаемости, куда включается электронная поляризуемость атомов. Делается это почти так же, как для жидкостей. Некоторые кристаллы имеют внутренние моменты, и вращение их также вносит вклад в x. В ионных кристаллах, таких, как NaCl, возникает также ионная поляризуемость. Кристалл состоит из положительных и отрицательных ионов, расположенных в шахматном порядке, и в электрическом поле положительные ионы тянутся в одну сторону, а отрицательные — в другую; возникает результирующее смещение положительных и отрицательных зарядов, а следовательно, и объемная поляризация. Мы могли бы оценить величину ионной поляризуемости, зная жесткость кристаллов соли, но мы не будем сейчас останавливаться на этом вопросе.
Фиг. 11.8. Сложная кристаллическая решетка может иметь постоянную внутреннюю поляризацию Р.
§ 7. Сегиетоэлектричество; титанат бария
Мы опишем здесь особый класс кристаллов, которые, можно сказать, почти случайно обладают «встроенным» постоянным электрическим моментом. Ситуация здесь настолько критична, что, если слегка увеличить температуру выше некоторой, кристалл этого класса совсем потеряет постоянный момент. С другой стороны, если структура кристалла близка к кубической, так что электрические моменты могут располагаться в разных направлениях, можно обнаружить большие изменения полного момента при изменении приложенного электрического поля. Все моменты перевертываются в направлении поля, и мы получаем большой эффект. Вещества, обладающие такого рода постоянным моментом, называются сегнетоэлектриками. Мы хотели бы объяснить механизм сегнетоэлектричества на частном примере какого-нибудь сегнетоэлектрического материала. Сегнетоэлектрические свойства могут возникать несколькими путями; однако мы разберем только один из них на примере таинственного титаната бария (BaТiO3). Это вещество обладает кристаллической решеткой, основная ячейка которого изображена на фиг. 11.9. Оказывается, что выше некоторой температуры (а именно 118°С) титанат бария — обычный диэлектрик с огромной диэлектрической проницаемостью, а ниже этой температуры он неожиданно приобретает постоянный момент.
При вычислении поляризации твердых тел мы должны сначала найти локальные поля в каждой элементарной ячейке. Причем для этого нужно ввести поля самой поляризации, как это делалось в случае жидкости. Но кристалл — не однородная жидкость, так что мы не можем взять в качестве локального поля то, что мы нашли в сферической дыре. Если мы сделаем это для кристалла, то окажется, что множитель 1/3 в уравнении (11.24) слегка изменится, но ненамного. (Для простого кубического кристалла он равен в точности 1/3.) Поэтому предположим в нашем предварительном обсуждении, что этот множитель для BaTi03 действительно равен 1/3.
Далее, когда мы писали уравнение (11.28), вам, наверное, было интересно знать, что случится, если Naстанет больше 3. На первый взгляд величина x должна бы стать отрицательной. Но такого наверняка не может быть. Посмотрим, что произойдет, если в каком-нибудь определенном кристалле постепенно увеличивать значение a.
Фиг. 11.9. Элементарная ячейка ВаТiO3.
Атомы в действительности заполняют большую часть пространства; показаны только положения их центров.
По мере роста a растет и поляризация, создавая большее локальное поле. Но увеличившееся локальное поле заполяризует атом еще больше, дополнительно усиливая само локальное поле. Если атомы достаточно «податливы», процесс продолжается; возникает своего рода обратная связь, приводящая к безудержному росту поляризации (если предположить, что поляризация каждого атома увеличивается пропорционально полю). Условие «разгона» возникает при Na = 3. Поляризация, конечно, не обращается в бесконечность, потому что при сильных полях пропорциональность между индуцированным моментом и электрическим полем нарушается, так что наши формулы становятся неправильными. А получается то, что в решетку, оказывается, «встроена» большая внутренняя самопроизвольная поляризация.
В случае ВаТiO3 вдобавок к электронной поляризации имеется довольно большая ионная поляризация, обусловленная, как предполагают, ионами титана, которые могут слегка сдвигаться внутри кубической решетки. Решетка сопротивляется большим смещениям, так что ион титана, переместившись на небольшое расстояние, затормаживается и останавливается. Но тогда у кристаллической решетки образуется постоянный дипольный момент.
У большинства сегнетоэлектрических кристаллов такая ситуация действительно возникает при всех достижимых температурах. Однако титанат бария представляет особый интерес: он так деликатно устроен, что при малейшем уменьшении Na момент «высвобождается». Поскольку N с повышением температуры уменьшается (вследствие теплового расширения), то можно изменять Na, меняя температуру. Ниже критической температуры момент сразу образуется, и тогда, накладывая внешнее поле, поляризацию легко повернуть и закрепить в нужном направлении.
Попробуем разобраться в происходящем более подробно. Назовем критической температуру Тс, при которой Na равно в точности 3. При увеличении температуры значение N немного уменьшается вследствие расширения решетки. Поскольку расширение мало, мы можем сказать, что вблизи критической температуры
(11.30)
где b — малая константа, того же порядка величины, что и коэффициент теплового расширения, т. е. около 10-5—10-6град-1. Подставляя это в выражение (11.28), получаем
Поскольку мы считаем величину b (Т -Тс) малой по сравнению с единицей,можно записать приближенно
(11.31)
Это, конечно, справедливо только для Т>Тс. Мы видим, что если температура чуть выше критической, то величина х огромна. Из-за того, что Na так близко к 3, возникает громадный эффект усиления и диэлектрическая проницаемость легко достигает величины от 50 000 до 100 000. Она тоже весьма чувствительна к температуре. При увеличении температуры диэлектрическая проницаемость уменьшается обратно пропорционально температуре, но в отличие от дипольного газа, где разность x-1 обратно пропорциональна абсолютной температуре, у сегнетоэлектриков она меняется обратно пропорционально разности между абсолютной и критической температурами (этот закон называется законом Кюри — Вейсса).
Что получается, когда мы понижаем температуру до критического значения? Если кристаллическая решетка состоит из элементарных ячеек вида, изображенного на фиг. 11.9, то, очевидно, можно выбрать цепочки ионов вдоль вертикальных линий. Одна из них состоит попеременно из ионов кислорода и титана. Имеются и другие цепочки, состоящие либо из ионов бария, либо из ионов кислорода, но расстояния между ионами вдоль таких линий оказываются больше. Используем простую модель, вообразив ряд ионных цепочек (фиг. 11.10, а). Вдоль цепочки, которую мы назовем главной, расстояние между ионами равно а, что составляет половину постоянной решетки; поперечное
расстояние между одинаковыми цепочками равно 2а.
Фиг. 11.10. Модели сегнетоалектрика.
а — антисегнетоэлектрик; б — нормальный сегнетовлектрик.
В промежутке имеются менее плотные цепочки, которые мы пока не будем рассматривать. Чтобы немного упростить наш анализ, предположим еще, что все ионы главной цепочки одинаковы. (Упрощение не очень значительное, потому что все важные эффекты еще останутся. Это просто одна из хитростей теоретической физики. Сначала решают видоизмененную задачу, потому что так в первый раз ее легче понять, а затем, разобравшись, как все происходит, вносят все усложнения.)
Попробуем теперь выяснить, что будет происходить в нашей модели. Предположим, что дипольный момент каждого иона равен р, и пусть мы хотим вычислить поле вблизи одного из ионов в цепочке. Мы должны найти сумму полей от всех остальных ионов. Сначала вычислим поле от диполей только в одной вертикальной цепочке; об остальных цепочках поговорим позже. Поле на расстоянии r от диполя в направлении вдоль его оси дается формулой
(11.32)
Для точки вблизи любого иона прочие диполи, расположенные на одинаковом расстоянии кверху и книзу от него, дают поля в одном и том же направлении, поэтому для всей цепочки получаем
(11.33)
Не представляет большого труда показать, что если бы наша модель была подобна кубическому кристаллу, т. е. если бы следующая идентичная линия проходила на расстоянии а, число 0,383 превратилось бы в 1/3 (~0,333). Другими словами, если бы соседние линии проходили на расстоянии а, они вносили бы в нашу сумму всего лишь —0,050. Однако следующая главная цепочка, которую мы рассмотрим, находится на расстоянии 2а, и, как вы помните из гл. 7, поле, создаваемое периодической структурой, спадает с расстоянием экспоненциально. Поэтому эти линии вносят в сумму гораздо меньше —0,050, и мы можем просто пренебречь всеми остальными цепочками.
Теперь нужно выяснить, какова должна быть поляризуемость а, чтобы привести в действие механизм разгона. Предположим, что индуцированный момент р каждого атома цепочки в соответствии с уравнением (11.6) пропорционален действующему на него полю. Поляризующее поле, действующее на атом, мы получаем из Eцепочка с помощью формулы (11.32). Итак, мы имеем два уравнения:
Имеются два решения: когда Е и р оба равны нулю и когда Е и р не равны нулю, но при условии, что
Таким образом, если a достигает величины a3/0,383, устанавливается постоянная поляризация, поддерживаемая своим собственным полем. Это критическое равенство должно достигаться для титаната бария как раз при температуре Тс. (Заметьте, что если бы поляризуемость a была больше критического значения для слабых полей, то она уменьшится при больших полях и в точке равновесия установится полученное нами равенство.)
Для ВаТiO3 промежуток a равен 2·10-8 см, поэтому мы должны ожидать значения a=21,8·10-24 см3. Мы можем сравнить эту величину с известными величинами поляризуемости отдельных атомов. Для кислорода a = 30,2·10-24 см3. (Мы на верном пути!) Но для титана a = 2,4·10-24см3. (Слишком мало.) В нашей модели нам, видимо, следует взять среднее. (Мы могли бы рассчитать снова цепочку для перемежающихся атомов, но результат был бы почти такой же.) Итак, aсредн = 16,3·10-24 см3, что недостаточно велико для установления постоянной поляризации.
Но подождите! Мы ведь до сих пор складывали только электронные поляризуемости. А есть еще и ионная поляризация, возникающая из-за смещения иона титана. Однако потребуется ионная поляризуемость величиной 9,2·10-24 см3.
(Более точное вычисление с учетом перемежающихся атомов показывает, что на самом деле требуется даже 11,9·10-24см3.) Чтобы понять свойства ВаТiO3, мы должны предположить, что возникает именно такая ионная поляризуемость.
Почему ион титана в титанате бария имеет столь большую ионную поляризуемость, неизвестно. Более того, непонятно, почему при меньших температурах он поляризуется одинаково хорошо и в направлении диагонали куба и в направлении диагонали грани. Если мы вычислим действительные размеры шариков на фиг. 11.9 и попробуем найти, достаточно ли свободно титан держится в коробке, образованной соседними атомами кислорода (а этого хотелось бы, потому что тогда его было бы легко сдвинуть), то получится совсем противоположный ответ. Он сидит очень плотно. Атомы бария держатся намного свободнее, но если считать, что это они движутся, то ничего не получится. Так что, как видите, вопрос совсем не ясен; остаются еще загадки, которые очень хотелось бы разгадать.
Возвращаясь к нашей простой модели (см. фиг. 11.10, а), мы видим, что поле от одной цепочки будет вызывать поляризацию соседней цепочки в противоположном направлении. Это значит, что, хотя каждая цепочка будет заморожена, постоянная поляризация в единице объема будет равна нулю! (Внешние электрические проявления тут не возникли бы, но можно было бы наблюдать определенные термодинамические эффекты.) Такие системы существуют и называются они антисегнетоэлектриками. Поэтому наше объяснение фактически относилось к антисегнетоэлектрикам. Однако в действительности титанат бария устроен очень похоже на то, что изображено на фиг. 11.10, б. Все кислородо-титановые цепочки поляризованы в одном направлении, потому что между ними помещаются промежуточные цепочки атомов. Хотя атомы в этих цепочках поляризованы не очень сильно и не очень тесно расположены, они все-таки будут немного поляризованы в направлении, антипараллельном кислородо-титановым цепочкам. Небольшие поля, создаваемые у следующей кислородо-титановой цепочки, заставят ее поляризоваться параллельно первой. Поэтому ВаТiO3 на самом деле сегнетоэлектрик, и произошло это благодаря атомам, находящимся в промежутке. Вы можете спросить: «А что же получается с прямым взаимодействием между двумя цепочками О — Ti?» Вспомним, однако, что прямое взаимодействие убывает с расстоянием экспоненциально; действие цепочки из сильных диполей на расстоянии 2а может быть меньше действия цепочки слабых диполей на расстоянии а.
На этом мы закончим довольно подробное изложение наших сегодняшних познаний о диэлектрических свойствах газов, жидкостей и твердых тел.
* Sānger, Steiger, Gachter, Helvetica Physica Acta, 5, 200 (1932).
Имеется перевод: Ч. Киттель, «Введение в физику твердого тела», М., 1962.— Прим. ред.
*По-английски сегнетоэлектричество называется ferroelectricity (ферроэлектричество); этот термин возник по аналогии с ферромагнетизмом: наличие спонтанного момента (электрического в сегнетоэлектриках, магнитного в ферромагнетиках), точки Кюри, гистерезиса и т. п. Однако физическая природа этих групп явлений совершенно различна.— Прим. ред.
Глава 12 ЭЛЕКТРОСТАТИЧЕСКИЕ АНАЛОГИИ
§1. Одинаковые уравнения— одинаковые решения
§2.Поток тепла; точечный источник вблизи бесконечной плоской границы
§3. Натянутая мембрана
§4. Диффузия нейтронов; сферически-симметричный источник в однородной среде
§5. Безвихревое течение жидкости; обтекание шара
§6. Освещение; равномерное освещение плоскости
§7. «Фундаментальное единство» природы
§ 1. Одинаковые уравнения — одинаковые решения
Вся информация о физическом мире, приобретенная со времени зарождения научного прогресса, поистине огромна, и кажется почти невероятным, чтобы кто-то овладел заметной частью ее. Но фактически физик вполне может постичь общие свойства физического мира, не становясь специалистом в какой-то узкой области. Тому есть три причины. Первая. Существуют великие принципы, применимые к любым явлениям, такие, как закон сохранения энергии и момента количества движения. Глубокое понимание этих принципов позволяет сразу постичь очень многие вещи. Вторая. Оказывается, что многие сложные явления, как, например, сжатие твердых тел, в основном обусловливаются электрическими и квантовомеханическими силами, так что, поняв основные законы электричества и квантовой механики, имеется возможность понять многие явления, возникающие в сложных условиях. Третья. Имеется замечательнейшее совпадение: Уравнения для самых разных физических условий часто имеют в точности одинаковый вид. Использованные символы, конечно, могут быть разными — вместо одной буквы стоит другая, но математическая форма уравнений одна и та же. Это значит, что, изучив одну область, мы сразу получаем множество прямых и точных сведений о решениях уравнений для другой области.
Мы закончили электростатику и скоро перейдем к изучению магнетизма и электродинамики. Но прежде хотелось бы показать, что, изучив электростатику, мы одновременно узнали о многих других явлениях. Мы увидим, что уравнения электростатики фигурируют и в ряде других областей физики. Путем прямого переноса решений (одинаковые математические уравнения должны, конечно, иметь одинаковые решения) можно решать задачи из других областей с той же легкостью (или с таким же трудом), как и в электростатике. Уравнения электростатики, как мы знаем, такие:
(12.1)
(12.2}
(Мы пишем уравнения электростатики в присутствии диэлектриков, чтобы учесть общий случай.) То же физическое содержание может быть выражено в другой математической форме:
(12.3)
(12.4)
И вот суть дела заключается в том, что существует множество физических проблем, для которых математические уравнения имеют точно такой же вид. Сюда входит потенциал (j), градиент которого, умноженный на скалярную функцию (x), имеет дивергенцию, равную другой скалярной функции (-r/e0).
Все, что нам известно из электростатики, можно немедленно перенести на другой объект, и наоборот. (Принцип, конечно, работает в обе стороны: если известны какие-то характеристики другого объекта, то можно использовать эти сведения в соответствующей задаче по электростатике.) Мы рассмотрим ряд примеров из разных областей, когда имеются уравнения такого вида.
§ 2. Поток тепла; точечный источник вблизи бесконечной плоской границы
Ранее мы уже обсуждали (гл. 3, § 4) поток тепла. Вообразите кусок какого-то материала, необязательно однородного (в разных местах может быть разное вещество), в котором температура меняется от точки к точке. Как следствие этих температурных изменений возникает поток тепла, который можно обозначить вектором h. Он представляет собой количество тепловой энергии, которое проходит в единицу времени через единичную площадку, перпендикулярную потоку. Дивергенция h есть скорость ухода тепла из данного места в расчете на единицу объема:
С·h = Скорость ухода тепла на единицу объема.
(Мы могли, конечно, записать уравнение в интегральном виде, как мы поступали в электродинамике с законом Гаусса, тогда оно выражало бы тот факт, что поток через поверхность равен скорости изменения тепловой энергии внутри материала. Мы не будем больше переводить уравнения из дифференциальной формы в интегральную и обратно, это делается точно так же, как в электростатике.)
Скорость, с которой тепло поглощается или рождается в разных местах, конечно, зависит от условий задачи. Предположим, например, что источник тепла находится внутри материала (возможно, радиоактивный источник или сопротивление, через которое пропускают ток). Обозначим через s тепловую энергию, производимую этим источником в единице объема за 1 сек. Кроме того, могут возникнуть потери (или, наоборот, дополнительное рождение) тепловой энергии за счет перехода в другие виды внутренней энергии в данном объеме. Если и — внутренняя энергия в единице объема, то —du/dt будет тоже играть роль «источника» тепловой энергии. Итак, имеем
(12.5)
Мы не собираемся здесь обсуждать полное уравнение, величины в котором изменяются со временем, потому что мы проводим аналогию с электростатикой, где ничто не зависит от времени. Мы рассмотрим только задачи с постоянным потоком тепла, в которых постоянные источники создают состояние равновесия. В таких случаях
(12.6)
Нужно иметь, конечно, еще одно уравнение, которое описывает, как поток течет в разных местах. Во многих веществах поток тепла примерно пропорционален скорости изменения температуры с положением: чем больше разность температур, тем больше поток тепла. Мы знаем, что вектор потока тепла пропорционален градиенту температуры. Константа пропорциональности К, зависящая от свойств материала, называется коэффициентом теплопроводности
(12.7)
Если свойства материала меняются от точки к точке, то К=К (х, у, z) и есть функция положения. [Уравнение (12.7) не столь фундаментально, как (12.5), выражающее сохранение тепловой энергии, потому что оно зависит от характерных свойств вещества.] Подставляя теперь уравнение (12.7) в (12.6), получаем
(12.8)
что в точности совпадает по форме с (12.4). Задачи с постоянным потоком тепла и задачи электростатики одинаковы. Вектор потока тепла h соответствует Е, а температура Т соответствует j.
Фиг. 12.1. Поток тепла в случае цилиндрической симметрии (а) и соответствующая задача из электричества (б).
Мы уже отмечали, что точечный тепловой источник создает поле температур, меняющееся, как 1/r, и поток тепла, меняющийся, как 1/r2. Это есть не более чем простой перенос утверждений электростатики, что точечный заряд дает потенциал, меняющийся, как 1/r, и электрическое поле, меняющееся, как 1/r2. Вообще мы можем решать статистические тепловые задачи с той же степенью легкости, как и задачи электростатики.
Рассмотрим простой пример. Пусть имеется цилиндр с радиусом а при температуре T1? поддерживающейся за счет генерации тепла в цилиндре. (Это может быть, скажем, проволока, по которой течет ток, или трубка с конденсацией пара внутри цилиндра.) Цилиндр покрыт концентрической обшивкой из изолирующего материала с теплопроводностью К. Пусть внешний радиус изоляции равен b, а в наружном пространстве поддерживается температура T2(фиг. 12. 1, а). Нам нужно определить скорость потери тепла проволокой или паропроводом (все равно чем), проходящим по центру цилиндра. Пусть полное количество тепла, теряемого на длине трубы L, равно G, его-то мы и хотим найти.
Как надо решать такую задачу? У нас есть дифференциальные уравнения, но поскольку они такие же, как в электростатике, то математическое решение их нам уже известно. Аналогичная задача электростатики относится к проводнику радиусом а при потенциале j1, отделенном от другого проводника радиусом b при потенциале j2, с концентрическим слоем диэлектрика между ними (фиг. 12.1, б). Далее, поскольку поток тепла h соответствует электрическому полю Е, то наша искомая величина G соответствует потоку электрического поля от единичной длины (другими словами, электрическому заряду на единице длины, деленному на e0). Мы решали электростатическую задачу с помощью закона Гаусса. Нашу задачу о потоке тепла будем решать таким же способом.
Из симметрии задачи мы видим, что h зависит только от расстояния до центра. Поэтому мы окружим трубку гауссовой поверхностью — цилиндром длиной L и радиусом r. С помощью закона Гаусса мы выводим, что поток тепла h, умноженный на площадь поверхности 2prL, должен быть равен полному количеству тепла, рождаемому внутри, т. е. тому, что мы назвали G:
(12.9)
Поток тепла пропорционален градиенту температуры
или в данном случае величина h равна
Вместе с (12.9) это дает
(12.10)
Интегрируя от r=а до r=b, получаем
(12.11)
Разрешая отнсительно G, находим
(12.12)
Этот результат в точности соответствует формуле для заряда цилиндрического конденсатора:
Задачи одинаковые и имеют одинаковые решения. Зная электростатику, мы тем самым знаем, сколько тепла теряет изолированная труба.
Рассмотрим еще один пример. Пусть мы хотим узнать поток тепла в окрестности точечного источника, расположенного неглубоко под поверхностью земли или же вблизи поверхности большого металлического предмета. В качестве локализованного источника тепла может быть и атомная бомба, которая взорвалась под землей и представляет собой мощный источник тепла, или же небольшой источник радиоактивности внутри железного блока — возможностей очень много.
Рассмотрим идеализированную задачу о точечном источнике тепла, мощность которого G, на расстоянии а под поверхностью бесконечной однородной среды с коэффициентом теплопроводности К. Теплопроводностью воздуха над поверхностью среды мы пренебрежем. Мы хотим определить распределение температуры на поверхности среды. Насколько горячо будет прямо над источником и в разных местах на поверхности?
Как же решить эту задачу? Она похожа на задачу по электростатике, в которой имеются два материала с разной диэлектрической проницаемостью x по обе стороны от разделяющей их границы. Здесь что-то есть! Возможно, это похоже на точечный заряд вблизи границы между диэлектриком и проводником или что-нибудь вроде этого. Посмотрим, что происходит вблизи границы. Физическое условие состоит в том, что нормальная составляющая h на поверхности равна нулю, поскольку мы предположили, что потока из блока нет. Мы должны задать вопрос: в какой электростатической задаче возникает условие, что нормальная компонента электрического поля Е (представляющая собой аналог h) равна нулю у поверхности? Нет такой!
Это один из тех случаев, к которым следует относиться с осторожностью. По физическим причинам могут быть определенные ограничения тех математических условий, которые возникают в каком-либо случае. Поэтому если мы проанализировали дифференциальное уравнение только для некоторых ограниченных примеров, то вполне можем упустить ряд решений, возникающих в других физических условиях. Например, нет материала, обладающего диэлектрической проницаемостью, равной нулю, а теплопроводность вакуума равна нулю. Поэтому нет электростатического аналога идеального теплоизолятора. Мы можем, однако, попытаться использовать те же методы. Попробуем вообразить, что произошло бы, если бы диэлектрическая проницаемость была равна нулю. (Разумеется, в реальных условиях диэлектрическая проницаемость никогда не обращается в нуль. Но может представиться случай, когда вещество имеет очень большую диэлектрическую проницаемость, так что диэлектрической проницаемостью воздуха вне среды можно пренебречь.)
Как же найти электрическое поле, у которого нет составляющей, перпендикулярной к поверхности? Иначе говоря, такое поле, которое всюду касательно к поверхности? Вы заметите, что эта задача обратна задаче о точечном заряде вблизи проводящей плоскости. Там нам нужно было поле, перпендикулярное
к поверхности, потому что проводник всюду находился при одном и том же значении потенциала.
В задаче об электрическом поле мы придумали решение, вообразив за проводящей плоскостью точечный заряд. Можно воспользоваться снова этой же идеей. Попытаемся выбрать такое «изображение» источника, которое автоматически обращало бы в нуль нормальную компоненту поля вблизи поверхности. Решение показано на фиг. 12.2. Электрическое изображение источника с тем же знаком и той же величины, находящееся на расстоянии а над поверхностью, дает поле, горизонтальное повсюду у поверхности. Нормальные компоненты от обоих источников взаимно уничтожаются.
Итак, наша задача о потоке тепла решена. Температура во всем пространстве одинакова по непосредственной аналогии с потенциалом от двух одинаковых точечных зарядов. Температура Т на расстоянии r от одного точечного источника G в бесконечной среде равна
(12.13)
(Это, конечно, полностью аналогично j= q/4pe0r.) Температура точечного источника и, кроме того, его изображения равна
(12.14)
Эта формула дает нам температуру всюду внутри блока. Несколько изотермических поверхностей приведено на фиг. 12.2.
Показаны также линии h, которые можно получить из выражения h =-КСТ.
В самом начале мы интересовались распределением температуры на поверхности. Для точки на поверхности находящейся на расстоянии р от оси, r1=r2=Ц (р2 + а2),
Фиг. 12.2. Поток тепла и изотерма у точечного источника тепла, расположенного на расстоянии а под поверхностью тела с хорошей теплопроводностью. Вне тела показано мнимое изображение источника.
следовательно,
(12.15)
Эта функция также изображена на фиг. 12.2. Естественно, что температура прямо над источником выше, чем вдали от него. Такого рода задачи часто приходится решать геофизикам. Теперь мы видим, что это те же самые задачи, которые мы решали в электричестве.
§ 3. Натянутая мембрана
Рассмотрим теперь совсем другую область физики, в которой тем не менее мы придем снова к точно таким же уравнениям. Возьмем тонкую резиновую пленку — мембрану, натянутую на большую горизонтальную раму (наподобие кожи на барабане). Нажмем на мембрану в одном месте вверх, а в другом — вниз (фиг. 12.3). Сможем ли мы описать форму поверхности? Покажем, как можно решить эту задачу, когда отклонения мембраны не очень велики.
В пленке действуют силы, потому что она натянута. Если сделать в каком-нибудь месте пленки небольшой разрез, то два края разреза разойдутся (фиг. 12.4). Следовательно, в пленке имеется поверхностное натяжение, аналогичное одномерному натяжению растянутой веревки. Определим величину поверхностного натяжения t как силу на единицу длины, которая как раз удержала бы вместе две стороны разреза (см. фиг. 12.4).
Предположим теперь, что мы смотрим на вертикальное поперечное сечение мембраны. Оно будет иметь вид некоторой кривой, похожей на изображенную на фиг. 12.5. Пусть и — вертикальное смещение мембраны от ее нормального положения, а х и у — координаты в горизонтальной плоскости
Фиг. 12.3. Тонкая резиновая пленка, натянутая на цилиндр (нечто вроде барабана).
Какой формы будет поверхность, если пленку приподнять в точке A и опустить в точке В?
Фиг. 12.4. Поверхностное натяжение t натянутой, резиновой пленки есть сила отнесенная к единице длины и направленная перпендикулярно линии разреза.
(Приведенное сечение параллельно оси х.)
Возьмем небольшой кусочек поверхности длиной Dx; и шириной Dу. На него действуют силы вследствие поверхностного натяжения вдоль каждого края. Сила на стороне 1 (см. фиг. 12.5) будет равна t1Dy и направлена по касательной к поверхности, т. е. под углом q1 к горизонтали. Вдоль стороны 2 сила будет равна t2Dy и направлена к поверхности под углом q2. (Подобные силы будут и на двух других сторонах кусочка, но мы пока забудем о них.) Результирующая сила от сторон 1 и 2, действующая на кусочек вверх, равна
Мы ограничимся рассмотрением малых искажений мембраны, т. е. малых изгибов и наклонов: тогда мы сможем заменить sinq на tgq и записать как дu/дx. Сила при этих условиях дается выражением
Величина в скобках может быть с тем же успехом записана (для малых Dx:) как
Фиг. 12.5. Поперечное сечение изогнутой пленки.
Тогда
Имеется и другой вклад в DF от сил на двух других сторонах; полный вклад, очевидно, равен
(12.16)
Искривления диафрагмы вызваны внешними силами. Пусть / означает направленную вверх силу на единичную площадку пленки (своего рода «давление»), возникающую от внешних сил. Если мембрана находится в равновесии (статический случай), то сила эта должна уравновешиваться только что вычисленной внутренней силой [уравнение (12.16)]. Иначе говоря,
Уравнение (12.16) тогда может быть записано в виде
(12.17)
где под знаком Смы теперь подразумеваем, конечно, двухмерный оператор градиента (д/дх, д/ду). У нас есть дифференциальное уравнение, связывающее u(х, у) с приложенными силами f(x, у) и поверхностным натяжением пленки t(x, у), которое, вообще говоря, может меняться от места к месту. (Деформации трехмерного упругого тела тоже подчиняются таким уравнениям, но мы ограничимся двухмерным случаем.) Нас будет интересовать только случай, когда натяжение t постоянно по всей пленке. Тогда вместо (12.17) мы можем записать
(12.18)
Снова мы получили такое же уравнение, как в электростатике! Но на сей раз оно относится к двум измерениям. Смещение u соответствует j, а f/t соответствует r/e0. Поэтому тот труд, который мы потратили на бесконечные заряженные плоскости, или параллельные провода большой длины, или заряженные цилиндры, пригодится для натянутой мембраны.
Предположим, мы подтягиваем мембрану в каких-то точках на определенную высоту, т. е. фиксируем величину и в ряде точек. В электрическом случае это аналогично заданию определенного потенциала в соответствующих местах. Например, мы можем устроить положительный «потенциал», если подопрем мембрану предметом, который имеет такое же сечение, как и соответствующий цилиндрический проводник. Если, скажем, мы подопрем мембрану круглым стержнем, поверхность примет форму, изображенную на фиг. 12.6.
Фиг. 12.6. Поперечное сечение натянутой резиновой пленки, подпертой круглым стержнем.
Функция u(х, у) та же, что и потенциал j(х, у) от очень длинного заряженного стержня.
Высота и имеет такой же вид, как электростатический потенциал j заряженного цилиндрического стержня. Она спадает, как ln(1/r). (Наклон поверхности, который соответствует электрическому полю Е, спадает, как 1/r.)
Натянутую резиновую пленку часто использовали для решения сложных электрических задач экспериментальным путем. Аналогия используется в обратную сторону! Для подъема мембраны на высоту, соответствующую потенциалам всего набора электродов, подставляют разные стержни и полоски. Затем измерения высоты дают электрический потенциал в электростатической задаче. Аналогия проводится даже еще дальше. Если на мембране поместить маленькие шарики, то их движение примерно схоже с движением электронов в соответствующем электрическом поле. Таким способом можно воочию проследить за движением «электронов» по их траекториям. Этот метод был использован для проектирования сложной системы многих фотоумножительных трубок (таких, например, какие используются в сцинтилляционном счетчике или для управления передними фарами в автомашине кадиллак). Метод используется и до сих пор, но его точность не очень велика. Для более точных расчетов лучше находить поле численным путем с помощью больших электронных вычислительных машин.
§ 4. Диффузия нейтронов; сферически-симметричный источник в однородной среде
Приведем еще один пример, дающий уравнение того же вида, но на сей раз относящееся к диффузии. В гл. 43 (вып. 4) мы рассмотрели диффузию ионов в однородном газе и диффузию одного газа сквозь другой. Теперь возьмем другой пример — диффузию нейтронов в материале типа графита. Мы выбрали графит (разновидность чистого углерода), потому что углерод не поглощает медленных нейтронов. Нейтроны путешествуют в нем свободно. Они проходят по прямой в среднем несколько сантиметров, прежде чем рассеются ядром и отклонятся в сторону. Так что если у нас есть большой кусок графита толщиной в несколько метров, то нейтроны, находившиеся сначала в одном месте, будут переходить в другие места.
Фиг. 12.7. Нейтроны рождаются однородно внутри сферы радиуса а в большом графитовом блоке и диффундируют наружу. Плотность нейтронов N получена как функция r, расстояния от центра источника.
Справа показана электростатическая аналогия: однородно заряженная сфера, причем N соответствует j, а J соответствует Е.
Мы опишем их усредненное поведение, т. е. их средний поток.
Пусть N(x, у, z)DV — число нейтронов в элементе объема DV в точке (х, у, г). Движение нейтронов приводит к тому, что одни покидают DV, а другие попадают в него. Если в одной области оказывается нейтронов больше, чем в соседней, то оттуда их будет переходить во вторую область больше, чем наоборот; в результате возникнет поток. Повторяя доказательства, приведенные в гл. 43 (вып. 4), можно описать поток вектором потока J. Его компонента Jxесть результирующее число нейтронов, проходящих в единицу времени через единичную площадку, перпендикулярную оси х. Мы получим тогда
(12.19)
где коэффициент диффузии D дается в терминах средней скорости v и средней длины свободного пробега l между столкновениями:
Векторное уравнение для J имеет вид
(12.20)
Скорость, с которой нейтроны проходят через некоторый элемент поверхности da, равна J·nda (где n, как обычно,— единичный вектор нормали). Результирующий поток из элемента объема тогда равен (пользуясь обычным гауссовым доказательством) С·JdV. Этот поток приводил бы к уменьшению числа нейтронов в DV, если нейтроны не генерируются внутри DV (с помощью какой-нибудь ядерной реакции). Если в объеме присутствуют источники, производящие S нейтронов в единицу времени в единице объема, то результирующий поток из DV будет равен [S-(dNIdt)]DV. Тогда получаем
(12.21)
Комбинируя (12.21) и (12.20), получаем уравнение диффузии нейтронов
(12.22)
В статическом случае, когда dN/dt=0, мы снова имеем уравнение (12.4)! Мы можем воспользоваться нашими знаниями в электростатике для решения задач по диффузии нейтронов. Давайте же решим какую-нибудь задачу. (Пожалуй, вы недоумеваете: зачем решать новую задачу, если мы уже решили все задачи в электростатике? На этот раз мы можем решить быстрее именно потому, что электростатические задачи действительно уже решены!)
Пусть имеется блок материала, в котором нейтроны (скажем, за счет деления урана) рождаются равномерно в сферической области радиусом а (фиг. 12.7). Мы хотели бы узнать, чему равна плотность нейтронов повсюду? Насколько однородна плотность нейтронов в области, где они рождаются? Чему равно отношение нейтронной плотности в центре к нейтронной плотности на поверхности области рождения? Ответы найти легко. Плотность нейтронов в источнике S0стоит вместо плотности зарядов r, поэтому наша задача такая же, как задача об однородно заряженной сфере. Найти N—все равно, что найти потенциал j. Мы уже нашли поля внутри и вне однородно заряженной сферы; для получения потенциала мы можем их проинтегрировать. Вне сферы потенциал равен Q/4pe0r, где полный заряд Q дается отношением 4pа3r/3. Следовательно,
(12.23)
Для внутренних точек вклад в поле дают только заряды Q(r), находящиеся внутри сферы радиусом r; Q(r) =4pг3r/3, следовательно,
(12.24)
Поле растет линейно с r. Интегрируя Е, получаем j:
На расстоянии радиуса а jвнешн должен совпадать с jвнутр) поэтому постоянная должна быть равна rа2/2e0. (Мы предполагаем, что потенциал j равен нулю на больших расстояниях от источника, а это для нейтронов будет отвечать обращению .N в нуль.) Следовательно,
(12.25)
Теперь мы сразу же найдем плотность нейтронов в нашей диффузионной задаче
(12.26)
и
(12.27)
На фиг. 12.7 представлена зависимость N от r.
Чему же теперь равно отношение плотности в центре к плотности на краю? В центре (r=0) оно пропорционально За2/2, а на краю (r=а) пропорционально 2а2/2; поэтому отношение плотностей равно 3/2. Однородный источник не дает однородной плотности нейтронов. Как видите, наши познания в электростатике дают хорошую затравку для изучения физики ядерных реакторов.
Диффузия играет большую роль во многих физических обстоятельствах. Движение ионов через жидкость или электронов через полупроводник подчиняется все тому же уравнению. Мы снова и снова приходим к одним и тем же уравнениям.
§ 5. Безвихревое течение жидкости; обтекание шара
Рассмотрим теперь пример, по существу, не такой уж хороший, потому что уравнения, которые мы будем использовать, на самом деле не описывают новый объект полностью, а отвечают лишь некоторым идеализированным условиям. Это задача о течении воды. Когда мы разбирали случай натянутой пленки, то наши уравнения представляли приближение, справедливое лишь для малых отклонений. При рассмотрении течения воды мы прибегнем к приближению другого рода; мы должны принять ограничения, которые, вообще говоря, к обычной воде неприменимы. Мы разберем только случай постоянного течения несжимаемой, невязкой, лишенной завихрений жидкости. Потом мы опишем течение, задав ему скорость v(r) как функцию положения г. Если движение постоянно (единственный случай, для которого имеется электростатическая аналогия), v не зависит от времени. Если r — плотность жидкости, то rv — масса жидкости, проходящая в единицу времени через единичную площадку. Из закона сохранения вещества дивергенция pv, вообще говоря, равна изменению со временем массы вещества в единице объема. Мы предположим, что процессы непрерывного рождения или уничтожения вещества отсутствуют. Сохранение вещества требует тогда, чтобы С·rv=0. (В правой части должно было бы стоять, вообще говоря, —dr/dt, но поскольку наша жидкость несжимаема, то r меняться не может.) Так как r повсюду одинаково, то его можно вынести, и наше уравнение запишется просто
С·v=0.
Чудесно! Снова получилась электростатика (без зарядов); уравнение совсем похоже на С·E=0. Ну не совсем! В электростатике не просто С·E=0. Есть два уравнения. Одно уравнение еще не дает нам всего; нужно дополнительное уравнение. Чтобы получилось совпадение с электростатикой, у нас rot от v должен был бы равняться нулю. Но для настоящих жидкостей это вообще не так. В большинстве их обычно возникают вихри. Следовательно, мы ограничиваемся случаем, когда циркуляция жидкости отсутствует. Такое течение часто называют безвихревым. Как бы то ни было, принимая наши предположения, можно представить себе течение жидкости, аналогичное электростатике. Итак, мы берем
С·v=0 (12.28)
и
СXv = 0. (12.29)
Мы хотим подчеркнуть, что условия, при которых течение жидкости подчиняется этим уравнениям, встречаются весьма нечасто, но все-таки бывают. Это должны быть случаи, когда поверхностным натяжением, сжимаемостью и вязкостью можно пренебречь и когда течение можно считать безвихревым. Эти условия выполняются столь редко для обычной воды, что математик Джон фон Нейман сказал по поводу тех, кто анализирует уравнения (12.28) и (12.29), что они изучают «сухую воду»!
| (Мы возвратимся к задаче о течении жидкости более подробно
в вып. 7, гл. 40 и 41.)
Поскольку СXv=0, то скорость «сухой воды» можно написать в виде градиента от некоторого потенциала
v=-Сj. (12.30)
Каков физический смысл y? Особо полезного смысла нет. Скорость можно записать в виде градиента потенциала просто потому, что течение безвихревое. По аналогии с электростатикой y называется потенциалом скоростей, но он не связан с потенциальной энергией так, как это получается для j. Поскольку дивергенция v равна нулю, то
(12.31)
Потенциал скоростей y подчиняется тому же дифференциальному уравнению, что и электростатический потенциал в пустом пространстве (r=0).
Давайте выберем какую-нибудь задачу о безвихревом течении и посмотрим, сможем ли мы решить ее изученными методами. Рассмотрим задачу о шаре, падающем в жидкости. Если он движется слишком медленно, то силы вязкости, которыми мы пренебрегали, будут существенны. Если он движется слишком быстро, то следом за ним будут идти маленькие вихри (турбулентность) и возникнет некоторая циркуляция воды. Но если шар движется и не чересчур быстро, и не чересчур медленно, то течение воды будет более или менее отвечать нашим предположениям, и мы сможем описать движение воды нашими простыми уравнениями.
Удобно описывать процесс в системе координат, скрепленной с шаром. В этой системе координат мы задаем вопрос: как течет вода около неподвижного шара, если на больших расстояниях течение однородно? Иначе говоря, если вдали от шара течение всюду одинаково? Течение вблизи шара будет иметь вид, показанный линиями потока на фиг. 12.8. Эти линии, всегда параллельные v, соответствуют линиям напряженностей электрического поля.
Фиг. 12.8. Поле скоростей безвихревого обтекания сферы жидкостью.
Мы хотим получить количественное описание поля скоростей, т. е. выражение для скорости в любой точке Р.
Можно найти скорость как градиент от y), поэтому сначала определим потенциал. Мы хотим найти потенциал, который удовлетворял бы всюду (12.31) при следующих двух условиях: 1) течение отсутствует в сферической области за поверхностью шара; 2) течение постоянно на больших расстояниях. Чтобы выполнялось первое ограничение, компонента v, перпендикулярная поверхности шара, должна обращаться в нуль. Это значит, что dy/dr=0 при r=а. Для выполнения второго ограничения нужно иметь dy/dz=v0всюду, где r>>а.Строго говоря, нет ни одной электростатической задачи, которая в точности соответствовала бы нашей задаче. Она фактически соответствует сфере с нулевой диэлектрической проницаемостью, помещенной в однородное электрическое поле. Если бы мы имели решение задачи для сферы с диэлектрической проницаемостью x, то, положив x=0, немедленно решили бы нашу задачу.
Мы раньше не разобрали такую электростатическую задачу во всех подробностях; давайте сделаем это сейчас. (Мы могли бы сразу решить задачу о жидкости с v и y, но будем пользоваться Е и j, потому что привыкли к ним.)
Задача ставится так: найти такое решение уравнения С2j=0, чтобы Е=-Сj равнялось постоянной, скажем Е0, для больших r и, кроме того, чтобы радиальная компонента Е была равна нулю при r=а. Иначе говоря,
(12.32)
Наша задача включает новый тип граничных условий — когда дj/дr постоянно, а не тот, когда потенциал j постоянен на поверхности. Это немножко другое условие. Получить ответ сразу нелегко. Прежде всего без шара j был бы равен —E0z.Тогда Е было бы направлено по z и имело бы всюду постоянную величину Е0. Мы уже исследовали случай диэлектрического шара, поляризация внутри которого однородна, и нашли, что поле внутри поляризованного шара однородно, а вне его оно совпадает с полем точечного диполя, расположенного в центре шара. Давайте напишем, что искомое решение есть суперпозиция однородного поля плюс поле диполя. Потенциал диполя (см. гл. 6) есть pz/4pe0r3. Итак, мы предполагаем, что
(12.33)
Поскольку поле диполя спадает, как 1/r3, то на больших расстояниях мы как раз имеем поле Е0. Наше предположение автоматически удовлетворяет сформулированному выше второму условию (стр. 249). Но что нам взять в качестве силы диполя p? Для ответа мы должны использовать другое условие [уравнение (12.32)]. Мы должны продифференцировать j по r, но, разумеется, это нужно сделать при постоянном угле q, поэтому удобнее выразить сначала j через r и q, а не через z и r. Поскольку z=rcosq, то
(12.34)
Радиальная составляющая Е есть
(12.35)
Она должна быть равна нулю при r=а для всех q. Это будет выполнено, если
(12.36)
Заметьте хорошенько, что если бы оба члена в уравнении (12.35) зависели бы от q по-разному, то мы не смогли бы выбрать р так, чтобы (12.35) обращалось в нуль при r=а для всех углов. Тот факт, что это получилось, означает, что мы были мудры, написав уравнение (12.33). Конечно, когда мы догадывались, мы заглядывали вперед; мы знали, что понадобится еще один член, который бы, во-первых, удовлетворял С2j=0 (любое действительное поле удовлетворяет этому), во-вторых, зависел от cosq и, в-третьих, спадал бы к нулю при больших r. Поле диполя — единственное, которое удовлетворяет всем трем требованиям.
С помощью (12.36) наш потенциал приобретает вид
(12.37)
Решение задачи о течении жидкости может быть записано просто:
(12.38)
Отсюда прямо находится v. Больше мы не будем заниматься этим вопросом.
§ 6. Освещение; равномерное освещение плоскости
В этом параграфе мы обратимся к совсем другой физической проблеме — мы ведь хотим показать большое разнообразие возможностей. На этот раз мы проделаем кое-что, что приведет нас к интегралу того же сорта, что мы нашли в электростатике.
Фиг. 12.9. Освещенность In поверхности равна энергии излучения, падающей в единицу времени на единичную площадку поверхности.
(Если перед нами стоит математическая задача, приводящая к некоторому интегралу, а интеграл этот уже знаком нам по другой задаче, то кое-что о его свойствах нам известно.) Возьмем пример из техники освещения. Пусть на расстоянии а над плоскостью имеется какой-то источник света. Как будет освещаться поверхность? Чему равна энергия излучения, падающая на единичную площадку поверхности за единицу времени (фиг. 12.9)? Мы предполагаем, что источник сферически-симметричный, так что свет излучается одинаково во всех направлениях. Тогда количество излученной энергии, проходящее через единичную площадку, перпендикулярную потоку света, меняется обратно пропорционально квадрату расстояния. Очевидно, что интенсивность света в направлении нормали дается такой же формулой, что и электрическое поле от точечного источника. Если световые лучи падают на поверхность под углом 6 к нормали, то /, энергия, падающая на единичную площадку поверхности, уменьшается в cos 9 раз, потому что та же энергия падает на площадь в I/cos 9 раз большую. Если мы назовем силу нашего источника S, тогда In, освещенность поверхности, равна
(12.39)
где er — единичный вектор в направлении от источника, а n — единичная нормаль к поверхности. Освещенность In соответствует нормальной компоненте электрического поля от точечного источника с зарядом 4pe0S. Учитывая это, мы видим, что для любого распределения источников света можно найти ответ, решая соответствующую задачу электростатики. Мы вычисляем вертикальную компоненту электрического поля на плоскости от распределения зарядов точно таким же образом, как для источников света.
Рассмотрим такой пример. Нам необходимо для какого-то эксперимента устроить так, чтобы стол освещался равномерно. Мы располагаем длинными трубками флуоресцентных ламп, излучающих равномерно по всей своей длине. Наш стол можно осветить, разместив флуоресцентные трубки правильными рядами на потолке, который находится на высоте z над столом. Чему должно быть равно наибольшее расстояние b от трубки до трубки, если мы хотим, чтобы поверхностное освещение было равномерным с точностью до одной тысячной? Ответ: 1) найдите электрическое поле от набора равномерно заряженных проводов с промежутком между ними, равным b; 2) подсчитайте вертикальную компоненту электрического поля; 3) определите, чему должно быть равно b, чтобы волнистость поля была не больше одной тысячной.
В гл. 7 мы видели, что электрическое поле от ряда заряженных проводов может быть представлено в виде суммы членов, каждый из которых дает синусоидальное изменение поля с периодом b/n, где n — целое число. Амплитуда любого из этих членов дается уравнением (7.44):
Нам нужно взять только случай n=1, раз мы хотим получить поле в точках, не слишком близких к проводам. Чтобы получить полное решение, нам еще нужно определить коэффициенты Аn, которые мы пока не нашли (хотя они находятся прямым вычислением). Поскольку нам нужно знать только A1то можно оценить его величину, считая ее равной средней величине поля. Экспоненциальный множитель тогда дает нам сразу относительную амплитуду изменений. Если мы хотим, чтобы этот множитель был равен 10-3, то b оказывается равным 0,91 z. Если промежуток между лампами сделать равным 3/4 расстояния до потолка, экспоненциальный множитель тогда будет равен 1/4000, и мы имеем фактор надежности 4, так что мы можем быть вполне уверены, что освещение будет постоянным с точностью до одной тысячной. (Точное вычисление показывает, что A1в действительности в два раза больше среднего поля, так что точный ответ будет b=0,8 z.)
Немного неожиданно, что для столь равномерного освещения допустимый промежуток между трубками оказался таким большим.
§ 7. «Фундаментальное единство» природы
В этой главе мы хотели показать, что, изучая электростатику, вы одновременно учитесь ориентироваться во многих вопросах физики и что, помня об этом, можно выучить почти всю физику за несколько лет.
Но в конце, естественно, напрашивается вопрос: почему уравнения для разных явлений столь похожи? Мы могли бы сказать: «В этом проявляется фундаментальное единство природы». Но что это значит? Что могло бы означать такое заявление? Это могло бы просто означать, что уравнения для разных явлений похожи; но тогда, конечно, мы не дали никакого объяснения. «Фундаментальное единство» могло бы означать, что все сделано из одного и того же материала, а потому подчиняется одним и тем же уравнениям. Звучит как неплохое объяснение, но давайте поразмыслим. Электростатический потенциал, диффузия нейтронов, поток тепла — неужели мы действительно имеем дело с одним и тем же материалом? Можем ли мы, в самом деле, представить себе, что электростатический потенциал физически идентичен температуре или плотности частиц? Наверняка j не совсем то же самое, что тепловая энергия частиц. Смещение мембраны явно не похоже на температуру. С какой же стати тогда здесь проявляется «фундаментальное единство»?
Более пристальный взгляд на физику разных вопросов показывает, что уравнения на самом деле не идентичны. Уравнение, найденное нами для диффузии нейтронов, всего лишь приближение, которое оказывается хорошим, если интересующее нас расстояние велико по сравнению с длиной свободного пробега. Если бы мы пригляделись повнимательнее, то увидели бы, как движутся отдельные нейтроны. Разумеется, движение одного нейтрона и гладкие изменения, которые мы получаем при решении дифференциального уравнения, вещи разные. Дифференциальное уравнение — это приближение, потому что мы сочли, что нейтроны гладко распределены в пространстве.
Может быть, в этом и состоит разгадка? Может быть, общее всем явлениям есть пространство, те рамки, в которые вложена физика? Пока все меняется в пространстве достаточно плавно, важными факторами, входящими в рассмотрение, будут скорости изменения величин в зависимости от положения в пространстве. Вот почему у нас всегда получается уравнение с градиентом. Производные должны появляться в виде градиента или дивергенции; законы физики не зависят от направления, поэтому они должны выражаться в виде векторов. Уравнения электростатики — это простейшие векторные уравнения, включающие только пространственные производные величин, которые можно вообще записать. Любая другая простая проблема— или упрощение сложной проблемы — должна быть похожа на электростатику. Общим для всех наших задач является то, что они связаны с пространством, и то, что мы имитируем по-настоящему сложные явления простым дифференциальным уравнением.
Отсюда возникает еще один интересный вопрос. А не справедливо ли это утверждение и для уравнений электростатики? Может быть, и они годятся только как сглаженная имитация на самом деле гораздо более сложного микромира? И реальный мир состоит из маленьких Х-онов, которые можно различить только на чрезвычайно малых расстояниях? А проводя наши измерения, мы всегда наблюдаем все в таком грубом масштабе, что не можем увидеть эти маленькие Х-оны, вот почему мы и приходим к дифференциальным уравнениям?
Наша современная наиболее полная теория электродинамики действительно обнаруживает трудности на очень малых расстояниях. Поэтому в принципе возможно, что эти уравнения представляют собой сглаженные версии чего-то: Они оказываются правильными на расстояниях вплоть до 10-14 см, но затем они начинают выглядеть неправильными. Возможно, что существует пока еще не открытый «механизм» и что детали внутреннего сложного устройства скрыты в уравнениях, имеющих гладкий вид, как это получается в «гладкой» диффузии нейтронов. Но никто еще не сумел сформулировать успешной теории, которая бы работала таким образом.
Как это ни странно, оказывается (по причинам, в которых мы еще не разобрались), что комбинация релятивизма и квантовой механики, насколько мы их знаем, по-видимому, запрещает придумывание уравнений, фундаментально отличных от уравнения (12.4) и в то же время свободных от противоречий. Заметьте: не из-за расхождений с экспериментом, а от внутренних противоречий. Таких, как, скажем, предсказание, что сумма вероятностей всех возможных исходов станет не равной единице или что энергии оказываются комплексными числами, или еще какой-нибудь чепухи. Никто еще не создал теории электричества, в которой С2j=-r/e0 понималось бы как сглаженное приближение к более глубокому механизму и которая не приводила бы, в конечном счете к какому-либо абсурду. Но надо сказать, что правильно также и то, что предположение о справедливости С2j=-r/e0 для любых как угодно малых расстояний тоже приводит к дикому абсурду (электрическая энергия электрона бесконечна) — абсурду, от которого никто еще не сумел избавиться.
* Поскольку мы говорим о некогерентных источниках, интенсивности, которых всегда складываются линейно, то электрические заряды в аналогичной задаче всегда будут иметь одинаковые знаки. Следует учесть, что наша аналогия применяется только к световой энергии, падающей на поверхность непрозрачной плоскости, поэтому мы должны включить в интеграл лишь источники, излучающие над поверхностью (конечно, не те, которые расположены под поверхностью!).
Глава 13 МАГНИТОСТАТИКА
§1.Магнитное поле
§2.Электрический ток; сохранение заряда
§З. Магнитная сила, действующая на ток
§4.Магнитное поле постоянных токов; закон Ампера
§5.Магнитное поле прямого провода и соленоида; атомные токи
§6.Относительность магнитных и электрических полей
§7.Преобразование токов и зарядов
§8.Суперпозиция; правило правой руки
Повторить: гл. 15 (вып. 2) «Специальная теория относительности»
§ 1. Магнитное поле
Сила, действующая на электрический заряд, зависит не только от того, где он находится, но и от того, с какой скоростью он движется. Каждая точка в пространстве характеризуется двумя векторными величинами, которые определяют силу, действующую на любой заряд. Во-первых, имеется электрическая сила, дающая ту часть силы, которая не зависит от движения заряда. Мы описываем ее с помощью электрического поля Е. Во-вторых, есть еще добавочная компонента силы, называемая магнитной силой, которая зависит от скорости заряда. Эта магнитная сила имеет удивительное свойство: в любой данной точке пространства, как направление, так и величина силы зависят от направления движения частицы; в каждый момент сила всегда перпендикулярна вектору скорости; кроме того, в любом месте сила всегда перпендикулярна определенному направлению в пространстве (фиг. 13.1), и, наконец, величина силы пропорциональна компоненте скорости, перпендикулярной этому выделенному направлению. Все эти свойства можно описать, если ввести вектор магнитного поля В, который определяет выделенное направление в пространстве и одновременно служит константой пропорциональности между силой и скоростью, и записать магнитную силу в виде qvXB. Полная электромагнитная сила, действующая на заряд, может тогда быть записана так:
F=q(E+vXB), (13.1)
Она называется силой Лоренца.
Фиг. 13.1. Зависящая от скорости компонента силы на движущийся заряд направлена перпендикулярно V и вектору В. Она пропорциональна также компоненте V, перпендикулярной В, т. е. vsinq.
Магнитную силу можно легко продемонстрировать, если поднести магнит вплотную к катодной трубке. Отклонение электронного луча указывает на то, что магнит возбуждает силы, действующие на электроны перпендикулярно направлению их движения (мы уже об этом говорили в вып. 1, гл. 12).
Единицей магнитного поля В, очевидно, является 1 ньютон-секунда, деленная на кулон-метр. Та же единица может быть написана как вольт-секунда на квадратный метр. Ее называют еще вебер на квадратный метр.
§ 2. Электрический ток; сохранение заряда
Подумаем теперь о том, почему магнитные силы действуют на провода, по которым течет электрический ток. Для этого определим, что понимается под плотностью тока. Электрический ток состоит из движущихся электронов или других зарядов, которые образуют результирующее течение, или поток. Мы можем представить поток зарядов вектором, определяющим количество зарядов, которое проходит в единицу времени через единичную площадку, перпендикулярную потоку (точь-в-точь как мы это делали, определяя поток тепла). Назовем эту величину плотностью тока и обозначим ее вектором j. Он направлен вдоль движения зарядов. Если взять маленькую площадку Da в данном месте материала, то количество зарядов, текущее через площадку в единицу времени, равно
j·nDa, (13.2)
где n — единичный вектор нормали к Dа.
Плотность тока связана со средней скоростью течения зарядов. Предположим, что имеется распределение зарядов, в среднем дрейфующих со скоростью v. Когда это распределение проходит через элемент поверхности Dа, то заряд Dq, проходящий через Dа за время Dt, равен заряду, содержащемуся в параллелепипеде с основанием Dа и высотой vDt (фиг. 13.2).
Фиг. 13.2. Если распределение зарядов с плотностью r движется со скоростью v, то количество заряда, проходящее в единицу времени через площадку Dа, есть rv·nDа.
Объем параллелепипеда есть произведение проекции Dа, перпендикулярной к v, на vDt, а умножая его на плотность зарядов r, получаем Dq. Таким образом,
Dq = rv·nDaDt.
Заряд, проходящий в единицу времени, тогда равен рv·nDа, откуда получаем
j = pv. (13.3)
Если распределение зарядов состоит из отдельных зарядов, скажем электронов с зарядом q, движущихся со средней скоростью v, то плотность тока равна
j = Nqv,(13.4)
где N — число зарядов в единице объема.
Полное количество заряда, проходящее в единицу времени через какую-то поверхность S, называется электрическим током I. Он равен интегралу от нормальной составляющей потока по всем элементам поверхности (фиг. 13.3):
Фиг. 13.3. Ток I через поверхность S равен ∫j·nda
Фиг. 13.4. Интеграл от j·n no замкнутой поверхности равен скорости изменения полного заряда Q внутри.
Ток I из замкнутой поверхности S представляет собой скорость, с которой заряды покидают объем V, окруженный поверхностью 5. Один из основных законов физики говорит, что электрический заряд неуничтожаем; он никогда не теряется и не создается. Электрические заряды могут перемещаться с места на место, но никогда не возникают из ничего. Мы говорим, что заряд сохраняется. Если из замкнутой поверхности возникает результирующий ток, то количество заряда внутри должно соответственно уменьшаться (фиг. 13.4). Поэтому мы можем записать закон сохранения заряда в таком виде:
(13.6)
Заряд внутри можно записать как объемный интеграл от плотности заряда
(13.7)
Применяя (13.6) к малому объему DV, можно учесть, что интеграл слева есть С·jDV. Заряд внутри равен rDV, поэтому сохранение заряда можно еще записать и так:
(13.8)
(опять теорема Гаусса из математики!).
§ 3. Магнитная сила, действующая на ток
Теперь мы достаточно подготовлены, чтобы определить силу, действующую на находящуюся в магнитном поле проволоку, по которой идет ток. Ток состоит из заряженных частиц, движущихся по проволоке со скоростью v. Каждый заряд чувствует поперечную силу F = qvXB (фиг. 13.5, а).
Фиг. 13.5. Магнитная сила на проволоку с током равна сумме сил на отдельные движущиеся заряды
Если в единичном объеме таких зарядов имеется N, то их число в малом объеме внутри проволоки DV равно NDV. Полная магнитная сила DV, действующая на объем DV, есть. сумма сил на отдельные заряды
Ho Nqv ведь как раз равно j, так что
(13.9)
(фиг. 13.5, б). Сила, действующая на единицу объема, равна JXB.
Если по проволоке с поперечным сечением А равномерно по сечению течет ток, то можно в качестве элемента объема взять цилиндр с основанием А и длиной DL. Тогда
DF = jXBDL. (13.10)
Теперь можно jA назвать вектором тока I в проволоке. (Его величина есть электрический ток в проволоке, а его направление совпадает с направлением проволоки.) Тогда
DF=IXBDL. (13.11)
Сила, действующая на единицу длины проволоки, есть IXB.
Это уравнение содержит важный результат — магнитная
сила, действующая на проволоку и возникающая от движения в ней зарядов, зависит только от полного тока, а не от величины заряда, переносимого каждой частицей (и даже не зависит от его знака!). Магнитная сила, действующая на проволоку вблизи магнита, легко обнаруживается по отклонению проволоки при включении тока, как было нами описано в гл. 1 (см. фиг. 1.6, стр. 20).
§ 4. Магнитное поле постоянного тока; закон Ампера
Мы видели, что на проволоку в магнитном поле, создаваемом, скажем, магнитом, действует сила. Из закона о том, что действие равно противодействию, можно ожидать, что, когда по проволоке протекает ток, возникает сила, действующая на источник магнитного поля, т. е. на магнит. Такие силы действительно существуют; в этом можно убедиться по отклонению стрелки компаса вблизи проволоки с током. Далее, мы знаем, что магниты испытывают действие сил со стороны других магнитов, а отсюда вытекает, что когда по проволоке течет ток, то он создает собственное магнитное поле. Значит, движущиеся заряды создают магнитное поле. Попытаемся понять законы, которым подчиняются такие магнитные поля. Вопрос ставится так: дан ток, какое магнитное поле он создаст? Ответ на этот вопрос был получен экспериментально тремя опытами и подтвержден блестящим теоретическим доказательством Ампера. Мы не будем останавливаться на этой интересной истории, а просто скажем, что большое число экспериментов наглядно показало справедливость уравнений Максвелла. Их мы и возьмем в качестве отправной точки. Опуская в уравнениях члены с производными по времени, мы получаем уравнения магнитостатики
(13.12)
и
(13.13)
Эти уравнения справедливы только при условии, что все плотности электрических зарядов и все токи постоянны, так что электрические и магнитные поля не меняются со временем — все поля «статические».
Можно тут заметить, что верить в существование статического магнитного поля довольно опасно, потому что вообще-то для получения магнитного поля нужны токи, а токи возникают только от движущихся зарядов. Следовательно, «магнитостатика» — только приближение.
Она связана с особым случаем динамики, когда движется большое число зарядов, которые можно приближенно описывать как постоянный поток зарядов. Только в этом случае можно говорить о плотности тока j, которая не меняется со временем. Более точно эту область следовало бы назвать изучением постоянных токов. Предполагая, что все поля постоянны, мы отбрасываем члены с dE/dt и dB/dt в полных уравнениях Максвелла [уравнения (2.41)] и получаем два написанных выше уравнения (13.12) и (13.13). Заметьте также, что поскольку дивергенция ротора любого вектора всегда нуль, то уравнение (13.13) требует, чтобы С·j=0. В силу уравнения (13.8) это верно, только если дr/дt=0. Но такое может быть, если Е не меняется со временем, следовательно, наши предположения внутренне согласованы.
Условие, что С·J= 0, означает, что у нас могут быть только заряды, текущие по замкнутым путям. Они могут, например, течь по проводам, образующим замкнутые петли, которые называются цепями. Цепи могут, конечно, содержать генераторы или батареи, поддерживающие ток зарядов. Но в них не должно быть конденсаторов, которые заряжаются или разряжаются. (Мы, конечно, расширим теорию, включив переменные поля, но сначала мы хотим взять более простой случай постоянных токов.)
Обратимся теперь к уравнениям (13.12) и (13.13) и посмотрим, что они означают. Первое говорит, что дивергенция В равна нулю. Сравнивая его с аналогичным уравнением электростатики, по которому С·Е=r/e0, можно заключить, что магнитного аналога электрического заряда не существует. Не бывает магнитных зарядов, из которых могли бы исходить линии В. Если говорить о «линиях» векторного поля В, то они нигде не начинаются и нигде не оканчиваются. Но тогда откуда же они берутся? Магнитные поля «появляются» в присутствии токов; ротор, взятый от них, пропорционален плотности тока. Когда есть токи, есть и линии магнитного поля, образующие петли вокруг токов. Поскольку линии В не имеют ни конца, ни начала, они часто возвращаются в исходную точку, образуя замкнутые петли. Но могут возникнуть и более сложные случаи, когда линии не представляют собой простых петель. Однако как бы они ни шли, они никогда не исходят из точек. Никаких магнитных зарядов никто никогда не находил, поэтому С·В=0. Это же утверждение справедливо не только для магнитостатики, но справедливо всегда — даже для динамических полей.
Связь между полем В и токами дается уравнением (13.13). Положение здесь совсем другое, в корне отличное от электростатики, где у нас было СXЕ = 0. Это уравнение означало, что линейный интеграл от Е по любому замкнутому пути равен нулю:
Фиг. 13.6. Контурный интеграл от тангенциальной составляющей В равен поверхностному интегралу от нормальной составляющей вектора
(СX B).
Мы получили этот результат с помощью теоремы Стокса, согласно которой интеграл по любому замкнутому пути от любого векторного поля равен поверхностному интегралу от нормальной компоненты ротора этого вектора (интеграл берется по дюбой поверхности, натянутой на данный контур). Применяя эту же теорему к вектору магнитного поля и используя обозначения, показанные на фиг. 13.6, получаем
(13.14)
Найдя rot В из уравнения (13.13), имеем
(13.15)
Интеграл от j по S, согласно (13.5), есть полный ток I через поверхность S. Поскольку для постоянных токов ток через S не зависит от формы S, если она ограничена кривой Г, то обычно говорят о «токе через замкнутую петлю Г». Мы имеем, таким образом, общий закон: циркуляция В по любой замкнутой кривой
равна току I сквозь петлю, деленному на e0с2:
(13.16)
Этот закон, называемый законом Ампера, играет такую же роль в магнитостатике, как закон Гаусса в электростатике. Один лишь закон Ампера не определяет В через токи; мы должны, вообще говоря, использовать также С·В=0. Но, как мы увидим в следующем параграфе, он может быть использован для нахождения поля в тех особых случаях, которые обладают некоторой простой симметрией.
§ 5. Магнитное поле прямого провода и соленоида; атомные токи
Можно показать, как пользоваться законом Ампера, определив магнитное поле вблизи провода. Зададим вопрос: чему равно поле вне длинного прямолинейного провода цилиндрического сечения? Мы сделаем одно предположение, может быть, не столь уж очевидное, но тем не менее правильное: линии поля В идут вокруг провода по окружности. Если мы сделаем такое предположение, то закон Ампера [уравнение (13.16)] говорит нам, какова величина поля. В силу симметрии задачи поле В имеет одинаковую величину во всех точках окружности, концентрической с проводом (фиг. 13.7). Тогда можно легко взять линейный интеграл от B·ds. Он равен просто величине В, умноженной на длину окружности. Если радиус окружности равен r, то
Полный ток через петлю есть просто ток I в проводе, поэтому
или
(13.17)
Напряженность магнитного доля спадает обратно пропорционально r, расстоянию от оси провода. При желании уравнение (13.17) можно записать в векторной форме. Вспоминая, что В направлено перпендикулярно как I, так и r, имеем
(13.18)
Фиг. 13.7. Магнитное поле вне длинного провода с током I.
Фиг. 13.8. Магнитное поле длинного соленоида.
Мы выделили множитель 1/4pe0с2, потому что он часто появляется. Стоит запомнить, что он равен в точности 10-7 (в системе единиц СИ), потому что уравнение вида (13.17) используется для определения единицы тока, ампера. На расстоянии 1 м ток в 1a создает магнитное поле, равное 2·10-7 вебер/м2.
Раз ток создает магнитное поле, то он будет действовать с некоторой силой на соседний провод, по которому также проходит ток. В гл. 1 мы описывали простой опыт, показывающий силы между двумя проводами, по которым течет ток. Если провода параллельны, то каждый из них перпендикулярен полю В другого провода; тогда провода будут отталкиваться или притягиваться друг к другу. Когда токи текут в одну сторону, провода притягиваются, когда токи противоположно направлены,— они отталкиваются.
Возьмем другой пример, который тоже можно проанализировать с помощью закона Ампера, если еще добавить кое-какие сведения о характере поля. Пусть имеется длинный провод, свернутый в тугую спираль, сечение которой показано на фиг. 13.8. Такая спираль называется соленоидом. На опыте мы наблюдаем, что когда длина соленоида очень велика по сравнению с диаметром, то поле вне его очень мало по сравнению с полем внутри. Используя только этот факт и закон Ампера, можно найти величину поля внутри.
Поскольку поле остается внутри (и имеет нулевую дивергенцию), его линии должны идти параллельно оси, как показано на фиг. 13.8. Если это так, то мы можем использовать закон Ампера для прямоугольной «кривой» Г на рисунке. Эта кривая проходит расстояние L внутри соленоида, где поле, скажем, равно В0, затем идет под прямым углом к полю и возвращается назад по внешней области, где полем можно пренебречь.
Фиг. 13.9. Магнитное поле вне соленоида.
Линейный интеграл от В вдоль этой кривой равен в точности B0L, и это должно равняться 1/e0с2, умноженному на полный ток внутри Г, т. е. на NI (где N — число витков соленоида на длине L). Мы имеем
Или же, вводя n — число витков на единицу длины соленоида (так что n=N/L), мы получаем
(13.19)
Что происходит с линиями В, когда они доходят до конца соленоида? По-видимому, они как-то расходятся и возвращаются в соленоид с другого конца (фиг. 13.9). В точности такое же поле наблюдается вне магнитной палочки. Ну а что же такое магнит? Наши уравнения говорят, что поле В возникает от присутствия токов. А мы знаем, что обычные железные бруски (не батареи и не генераторы) тоже создают магнитные поля. Вы могли бы ожидать, что в правой части (13.12) или (13.13) должны были бы быть другие члены, представляющие «плотность намагниченного железа» или какую-нибудь подобную величину. Но такого члена нет. Наша теория говорит, что магнитные эффекты железа возникают от каких-то внутренних токов, уже учтенных членом j.
Вещество устроено очень сложно, если рассматривать его с глубокой точки зрения; в этом мы уже убедились, когда пытались понять диэлектрики. Чтобы не прерывать нашего изложения, отложим подробное обсуждение внутреннего механизма магнитных материалов типа железа. Пока придется принять, что любой магнетизм возникает за счет токов и что в постоянном магните имеются постоянные внутренние токи. В случае железа эти токи создаются электронами, вращающимися вокруг собственных осей. Каждый электрон имеет такой спин, который соответствует крошечному циркулирующему току. Один электрон, конечно, не дает большого магнитного поля, но в обычном куске вещества содержатся миллиарды и миллиарды электронов. Обычно они вращаются любым образом, так что суммарный эффект исчезает. Удивительно то, что в немногих веществах, подобных железу, большая часть электронов крутится вокруг осей, направленных в одну сторону,— у железа два электрона из каждого атома принимают участие в этом совместном движении. В магните имеется большое число электронов, вращающихся в одном направлении, и, как мы увидим, их суммарный эффект эквивалентен току, циркулирующему по поверхности магнита. (Это очень похоже на то, что мы нашли в диэлектриках,— однородно поляризованный диэлектрик эквивалентен распределению зарядов на его поверхности.) Поэтому не случайно, что магнитная палочка эквивалентна соленоиду.
§ 6. Относительность магнитных и электрических полей
Когда мы сказали, что магнитная сила на заряд пропорциональна его скорости, вы, наверное, подумали: «Какой скорости? По отношению к какой системе отсчета?» Из определения В, данного в начале этой главы, на самом деле ясно, что этот вектор будет разным в зависимости от выбора системы отсчета, в которой мы определяем скорость зарядов. Но мы ничего не сказали о том, какая же система подходит для определения магнитного поля.
Оказывается, что годится любая инерциальная система. Мы увидим также, что магнетизм и электричество — не независимые вещи, они всегда должны быть взяты в совокупности как одно полное электромагнитное поле. Хотя в статическом случае уравнения Максвелла разделяются на две отдельные пары: одна пара для электричества и одна для магнетизма, без видимой связи между обоими полями, тем не менее в самой природе существует очень глубокая взаимосвязь между ними, возникающая из принципа относительности. Исторически принцип относительности был открыт после уравнений Максвелла. В действительности же именно изучение электричества и магнетизма привело Эйнштейна к открытию принципа относительности. Но посмотрим, что наше знание принципа относительности подскажет нам о магнитных силах, если предположить, что принцип относительности применим (а в действительности так оно и есть) к электромагнетизму.
Давайте подумаем, что произойдет с отрицательным зарядом, движущимся со скоростью v0параллельно проволоке, по которой течет ток (фиг. 13.10).
Фиг. 13.10. Взаимодействие проволоки с током и частицы с зарядом q,
рассматриваемое в двух системах координат.
а — в системе S покоится проволока; б — в системе S' покоится заряд.
Постараемся разобраться в происходящем, используя две системы отсчета: одну, связанную с проволокой, как на фиг. 13.10, а, а другую — с частицей, как на фиг. 13.10, б. Мы будем называть первую систему отсчета S, а вторую S'.
В системе S на частицу явно действует магнитная сила. Сила направлена к проволоке, поэтому, если заряду ничего не мешает, его траектория загнется в сторону проволоки. Но в системе S' магнитной силы на частицу быть не может, потому что скорость частицы равна нулю. Что же, следовательно, она так и будет стоять на месте? Увидим ли мы в разных системах разные вещи? Принцип относительности утверждает, что в системе S' мы увидели бы тоже, как частица приближается к проволоке. Мы должны попытаться понять, почему такое могло бы произойти.
Вернемся к нашему атомному описанию проволоки, по которой идет ток. В обычном проводнике, вроде меди, электрические токи возникают за счет движения части отрицательных электронов (называемых электронами проводимости), тогда как положительные ядерные заряды и остальные электроны остаются закрепленными внутри материал а. Пусть плотность электронов проводимости есть r, а их скорость в системе S есть v. Плотность неподвижных зарядов в системе S есть r+, что должно быть равно r- с обратным знаком, потому что мы берем незаряженную проволоку. Поэтому вне проволоки электрического поля нет, и сила на движущуюся частицу равна просто
F=qv0XB.
Используя результат, найденный нами в уравнении (13.18) для магнитного поля на расстоянии r от оси проволоки, мы заключаем, что сила, действующая на частицу, направлена к проволоке и равна по величине
С помощью уравнений (13.4) и (13.5) ток I может быть записан как r+vA, где А — площадь поперечного сечения проволоки. Тогда
(13.20)
Мы могли бы продолжить рассмотрение общего случая произвольных скоростей v и v0, но ничуть не хуже будет взять частный случай, когда скорость v0частицы совпадает со скоростью v электронов проводимости. Поэтому мы запишем v=v0 , и уравнение (13.20) приобретет вид
(13.21)
Теперь обратимся к тому, что происходит в системе S', где частица покоится и проволока бежит мимо нее (влево на фиг. 13.10, б) со скоростью v. Положительные заряды, движущиеся вместе с проволокой, создадут около частицы некоторое магнитное поле В'. Но частица теперь покоится, так что магнитная сила на нее не действует! Если и возникает какая-то сила, то она должна появиться за счет электрического поля. Выходит, что движущаяся проволока создает электрическое поле. Но она может это сделать, только если она кажется заряженной; должно получаться так, чтобы нейтральная проволока с током казалась заряженной, если ее привести в движение.
Нужно в этом разобраться. Попробуем вычислить плотность зарядов в проволоке в системе S', пользуясь тем, что мы знаем о ней в системе S. На первый взгляд можно было бы подумать, что плотности одинаковы, но из гл. 15 (вып. 2) мы знаем, что при переходе от одной системы к другой длины меняются, следовательно, объемы также изменятся. Поскольку плотности зарядов зависят от объема, занимаемого зарядами, плотности будут также меняться.
Прежде чем определить плотности зарядов в системе S', нужно знать, что происходит с электрическим зарядом группы электронов, когда заряды движутся. Мы знаем, что кажущаяся масса частицы приобретает множитель 1/Ц(1-v2/c2). Происходит ли что-нибудь подобное с ее зарядом? Нет! Заряды никогда не меняются независимо от того, движутся ли они или нет. Иначе мы не могли бы наблюдать на опыте сохранение полного заряда.
Возьмем кусок вещества, например проводника, и пусть он вначале незаряжен. Теперь нагреем его. Поскольку масса электронов иная, чем у протонов, скорости электронов и протонов изменятся по-разному. Если бы заряд частицы зависел от скорости частицы, которая его переносит, то в нагретом куске заряды электронов и протонов не были бы скомпенсированы. Кусок материала при нагревании становился бы заряженным.
Фиг. 13.11. Если распределение заряженных частиц имеет плотность зарядов р0, то с точки зрения системы, движущейся с относительной скоростью v, плотность зарядов будет равна r=r0/Ц (1 - v2/с2).
Мы видели раньше, что очень малое изменение заряда у каждого из электронов в куске привело бы к огромным электрическим полям. Ничего подобного никогда не наблюдалось.
Кроме того, можно заметить, что средняя скорость электронов в веществе зависит от его химического состава. Если бы заряд электрона менялся со скоростью, суммарный заряд в куске вещества изменялся бы в ходе химической реакции. Как и раньше, прямое вычисление показывает, что даже совсем малая зависимость заряда от скорости привела бы в простейших химических реакциях к огромным полям. Ничего похожего не наблюдалось, и мы приходим к выводу, что электрический заряд отдельной частицы не зависит от состояния движения или покоя.
Итак, заряд частицы q есть инвариантная скалярная величина, не зависящая от системы отсчета. Это означает, что в любой системе плотность зарядов у некоторого распределения электронов просто пропорциональна числу электронов в единице объема. Нам нужно только учесть тот факт, что объем может меняться из-за релятивистского сокращения расстояний.
Применим теперь эти идеи к нашей движущейся проволоке. Если взять проволоку длиной L0, в которой плотность неподвижных зарядов есть r0, то в ней будет содержаться полный заряд Q-r0L0A0. Если те же заряды движутся в другой системе со скоростью v, то они все будут находиться в куске материала
меньшей длины
(13.22)
но того же сечения A0, поскольку размеры в направлении, перпендикулярном движению, не меняются (фиг. 13.11).
Если через r обозначить плотность зарядов в системе, где они движутся, то полный заряд Q будет rLA0. Но это должно быть также равно r0L0А, потому что заряд в любой системе одинаков, следовательно, rL=r0L0, или с помощью (13.22)
(13.23)
Плотность зарядов движущейся совокупности зарядов меняется таким же образом, как и релятивистская масса частицы. Применим теперь этот результат к плотности положительных зарядов r+ в нашей проволоке. Эти заряды покоятся в системе S. Однако в системе S", где проволока движется со скоростью v, плотность положительных зарядов становится равной
(13.24)
Отрицательные заряды в системе S' покоятся, поэтому их плотность в этой системе есть «плотность покоя» r0. В уравнении (13.23) r0=r-, потому что их плотность зарядов равна r- , если проволока покоится, т. е. в системе S, где скорость отрицательных зарядов равна v. Тогда для электронов проводимости мы получаем
(13;25)
или
(13.26)
Теперь мы можем понять, почему в системе S' возникают электрические поля: потому что в этой системе в проволоке имеется результирующая плотность зарядов r', даваемая формулой
С помощью (13.24) и (13.26) имеем
Поскольку покоящаяся проволока нейтральна, r- = -r+, получаем
(13.27)
Наша движущаяся проволока заряжена положительно и должна создавать поле Е' в точке, где находится внешняя покоящаяся частица. Мы уже решали электростатическую задачу об однородно заряженном цилиндре. Электрическое поле на расстоянии r от оси цилиндра есть
(13.28)
Сила, действующая на отрицательно заряженную частицу, направлена к проволоке. Мы имеем силу, направленную одинаково в обеих системах; электрическая сила в системе S' направлена так же, как магнитная сила в системе S. Величина силы в системе S' равна
(13.29)
Сравнивая этот результат для F' с нашим результатом для F в уравнении (13.21), мы видим, что величины сил с точки зрения двух наблюдателей почти одинаковы. Точнее,
(13.30)
поэтому для малых скоростей, которые мы рассматриваем, обе силы одинаковы. Мы можем сказать, что по меньшей мере для малых скоростей магнетизм и электричество суть просто «две разные стороны одной и той же вещи».
Но оказывается, что все обстоит даже еще лучше, чем мы сказали. Если принять во внимание тот факт, что силы также преобразуются при переходе от одной системы к другой, то окажется, что оба способа наблюдения за происходящим дают на самом деле одинаковые физические результаты при любой скорости.
Чтобы это увидеть, можно, например, задать вопрос: какой поперечный импульс приобретет частица, на которую в течение некоторого времени действовала сила? Мы знаем из вып. 2, гл. 16, что поперечный импульс частицы должен быть один и тот же как в системе S, так ив системе S'. Обозначим поперечную координату у и сравним Dpyи Dpy’ . Используя релятивистски правильное уравнение движения F—dp/dt, мы ожидаем, что за время Dt наша частица приобретет поперечный импульс Dpyв системе S, даваемый выражением
(13.31)
В системе S' поперечный импульс будет равен
(13.32)
Фиг. 13.12. В системе S плотность зарядов есть нуль, а плотность тока равна j. Есть только магнитное поле. В системе S' плотность зарядов равна р', а плотность тока j'. Магнитное поле здесь равно В' и существует электрическое поле Е'.
Мы должны сравнивать Dpy и Dpy' , конечно, для соответствующих интервалов времени Dt и Dt'. В гл. 15 (вып. 2) мы видели, что интервалы времени, относящиеся к движущейся частице, кажутся длиннее интервалов в системе покоя частицы. Поскольку наша частица первоначально была в покое в системе S', то
мы ожидаем, что для малых Dt
(13.33)
и все получается великолепно. Согласно (13.31) и (13.32),
и если скомбинировать (13.30) и (13.33), то это отношение равно единице.
Вот и выходит, что мы получаем один и тот же результат, независимо от того, анализируем ли мы движение летящей рядом с проволокой частицы в системе покоя проволоки или в системе покоя частицы. В первом случае сила была чисто «магнитной», во втором — чисто «электрической». Оба способа наблюдения показаны на фиг. 13.12 (хотя во второй системе еще есть и магнитное поле В', оно не воздействует на неподвижную частицу).
Если бы мы выбрали еще одну систему координат, мы бы нашли некую другую смесь полей E и В. Электрические и магнитные силы составляют части одного физического явления— электромагнитного взаимодействия частиц. Разделение этого взаимодействия на электрическую и магнитную части в большой степени зависит от системы отсчета, в которой мы описываем взаимодействие. Но полное электромагнитное описание инвариантно; электричество и магнетизм, вместе взятые, согласуются с принципом относительности, открытым Эйнштейном.
Раз электрические и магнитные поля появляются в разных соотношениях при изменении системы отсчета, мы должны проявлять осторожность в обращении с полями Е и В. Если, например, мы говорим о «линиях» Е или В, то не нужно преувеличивать реальность их существования. Линии могут исчезнуть, если мы захотим увидеть их в другой системе координат. Например, в системе S' имеются линии электрического поля, однако мы не видим их «движущимися мимо нас со скоростью v в системе S1». В системе S линий электрического поля нет вообще! Поэтому бессмысленно говорить что-нибудь вроде: «Когда я двигаю магнит, он несет свое поле с собой, поэтому линии поля В тоже движутся». Нет никакого способа сделать вообще осмысленным понятие о «скорости движущихся линий поля».
Поля суть способ описания того, что происходит в некоторой точке пространства. В частности, Е и В говорят нам о силах, которые будут действовать на движущуюся частицу. Вопрос «чему равна сила, действующая на заряд со стороны движущегося магнитного поля?» не имеет сколько-нибудь точного содержания. Сила дается величинами Е и В в точке заряда, и формула (13.1) не изменится, если источник полей Е или В движется (изменятся в результате движения как раз значения Е и В). Наше математическое описание относится только к полям как функциям х, у, z и t, взятым в некоторой инерциалъной системе отсчета.
Позднее мы будем говорить о «волне электрического и магнитного полей, распространяющейся в пространстве», например о световой волне. Но это все равно, что говорить о волне, бегущей по веревке. Мы при этом не имеем в виду, что какая-нибудь часть веревки движется в направлении волны, а подразумеваем, что смещение веревки появляется сначала в одном месте, а затем в другом. Аналогично для электромагнитной волны — сама волна распространяется, а величина полей изменяется.
Так что в будущем, когда мы — или кто-нибудь еще — будем говорить о «движущемся» поле, вы должны понимать, что речь идет просто о коротком и удобном способе описания изменяющегося ноля в определенных условиях.
§ 7. Преобразование токов и зарядов
Вы, вероятно, были обеспокоены сделанным нами упрощением, когда мы взяли одну и ту же скорость v для частицы и электронов проводимости в проволоке. Можно было бы вернуться назад и снова проделать анализ с двумя разными скоростями, но легче просто заметить, что плотность заряда и тока являются компонентами четырехвектора (см. вып. 2, гл. 17).
Мы видели уже, что если r0 есть плотность зарядов в их системе покоя, то в системе, где они имеют скорость v, плотность равна
В этой системе их плотность тока есть
(13.34)
Далее, мы знаем, что энергия U и импульс частицы р, движущейся со скоростью v, даются выражениями
где m0 — ее масса покоя. Мы знаем также, что U и р образуют релятивистский четырехвектор. Поскольку r и j зависят от скорости v в точности, как U и р, то можно заключить, что r и j также компоненты релятивистского четырехвектора. Это свойство есть ключ к общему анализу поля проволоки, движущейся с любой скоростью, и мы могли бы его использовать, если бы захотели решить снова задачу со скоростью частицы v0, не равной скорости электронов проводимости.
Если нам нужно перевести r и j в систему координат, движущуюся со скоростью и в направлении х, то мы знаем, что они преобразуются в точности как t и (х, у, z); поэтому мы имеем (см. вып. 2, гл. 15)
(13.35)
С помощью этих уравнений можно связать заряды и токи в одной системе с зарядами и токами в другой. Взяв заряды и токи в какой-то системе, можно решить электромагнитную задачу в этой системе, пользуясь уравнениями Максвелла. Результат, который мы получим для движения частиц, будет одним и тем же, независимо от выбранной системы отсчета. Позже мы вернемся к релятивистским преобразованиям электромагнитных полей.
§ 8. Суперпозиция; правило правой руки
Мы закончим эту главу еще двумя замечаниями по вопросам магнитостатики. Первое: наши основные уравнения для магнитного поля
линейны до В и j. Это означает, что принцип суперпозиции (наложения) приложим и к магнитному полю. Поле, создаваемое двумя разными постоянными токами, есть сумма собственных полей от каждого тока, действующего по отдельности. Наше второе замечание относится к правилам правой руки, с которыми мы уже сталкивались (правило правой руки для магнитного поля, создаваемого током). Мы указывали также, что намагничивание железного магнита объясняется вращением электронов в материале. Направление магнитного поля вращающегося электрона связано с осью его вращения тем же самым правилом правой руки. Поскольку В определяется правилом определенной руки (с помощью либо векторного произведения, либо ротора), он называется аксиальным вектором. (Векторы, направление которых в пространстве не зависит от ссылок на левую или правую руку, называются полярными векторами. Например, смещение, скорость, сила и Е — полярные векторы.)
Физически наблюдаемые величины в электромагнетизме, однако, не связаны с правой или левой рукой. Из гл. 52 (вып. 4) мы знаем, что электромагнитные взаимодействия симметричны по отношению к отражению. При вычислении магнитных сил между двумя наборами токов результат всегда инвариантен по отношению к перемене рук. Наши уравнения, независимо от условия правой руки, приводят к конечному результату, что параллельные токи притягиваются, а противоположные — отталкиваются. (Попробуйте вычислить силу с помощью «правила левой руки».) Притяжение или отталкивание есть полярный вектор. Так получается потому, что при описании любого полного взаимодействия мы пользуемся правилом правой руки дважды — один раз, чтобы найти В из токов, а затем, чтобы найти силу, оказываемую полем В на второй ток. Два раза пользоваться правилом правой руки — все равно что два раза пользоваться правилом левой руки. Если бы мы условились перейти к системе левой руки, все наши поля В изменили бы знак, но все силы или (что, пожалуй, нагляднее) наблюдаемые ускорения объектов не изменились бы.
Хотя физики недавно, к своему удивлению, обнаружили, что не все законы природы всегда инвариантны по отношению к зеркальным отражениям, тем не менее законы электромагнетизма обладают этой фундаментальной симметрией.
* Или, короче,─ тесла. ─ прим. ред.
*Потом мы увидим, что такие предположения, вообще говоря, неправильны для электромагнитных сил!
*Это и есть магнитная проницаемость пустоты.
Глава 14 МАГНИТНОЕ ПОЛЕ В РАЗНЫХ СЛУЧАЯХ
§1.Векторный потенциал
§2.Векторный потенциал заданных токов
§3. Прямой провод
§4.Длинный соленоид
§5.Поле маленькой петли; магнитный диполь
§6. Векторный потенциал цепи
§7.3акон Био—Савара
§ 1, Векторный потенциал
В этой главе мы продолжим разговор о магнитостатике, т, е. о постоянных магнитных полях и постоянных токах. Магнитное поле и электрические токи связаны нашими основными уравнениями:
(14.1)
и
(14.2)
На этот раз нам нужно решить эти уравнения математически самым общим образом, а не ссылаться на какую-нибудь особую симметрию или на интуицию. В электростатике мы нашли прямой способ вычисления поля, когда известны положения всех электрических зарядов: скалярный потенциал j дается просто интегралом по зарядам, как в уравнении (4.25) на стр. 77. Если затем нужно знать электрическое поле, то его получают дифференцированием j. Мы покажем сейчас, что для нахождения поля В существует аналогичная процедура, если известна плотность тока j всех движущихся зарядов.
В электростатике, как мы видели (из-за того, что rot от Е везде равен нулю), всегда можно представить Е в виде градиента от скалярного поля j. А вот rot от В не везде равен нулю, поэтому представить его в виде градиента, вообще говоря, невозможно. Однако дивергенция В везде равна нулю, а это значит, что мы можем представить В в виде ротора от другого векторного поля. Ибо, как мы видели в гл. 2, § 8, дивергенция ротора всегда равна нулю. Следовательно, мы всегда можем выразить В через поле, которое мы обозначим А:
(14.3)
Или, расписывая компоненты:
(14.4)
Запись B=СXA гарантирует выполнение (14.1), потому что обязательно
Поле А называется векторным потенциалом.
Вспомним, что скалярный потенциал j оказывается не полностью определенным. Если мы нашли для некоторой задачи потенциал j, то всегда можно найти столь же хороший другой потенциал j', добавив постоянную:
Новый потенциал j' дает те же электрические поля, потому что градиент СС есть нуль; j' и j отвечают одной и той же картине.
Точно так же у нас может быть несколько векторных потенциалов А, приводящих к одним и тем же магнитным полям. Опять-таки, поскольку В получается из А дифференцированием, то прибавление к А константы не меняет физики дела. Но для А свобода больше. Мы можем добавить к А любое поле, которое есть градиент от некоторого скалярного поля, не меняя при этом физики. Это можно показать следующим образом. Пусть у нас есть А, которое в какой-то реальной задаче дает правильное поле В. Спрашивается, при каких условиях другой векторный потенциал А', будучи подставлен в (14.3), дает то же самое поле В. Значит, А и А' имеют одинаковый ротор
Поэтому
Но если ротор вектора есть нуль, то вектор должен быть градиентом некоторого скалярного поля, скажем y, так что А'-A=Сy. Это означает, что если А есть векторный потенциал, отвечающий данной задаче, то при любом y
(14.5)
также будет векторным потенциалом, в одинаковой степени удовлетворяющим данной задаче и приводящим к тому же полю В.
Обычно бывает удобно уменьшить «свободу» А, накладывая на него произвольно некоторое другое условие (почти таким же образом мы считали удобным — довольно часто — выбирать потенциал ср равным нулю на больших расстояниях). Мы можем, например, ограничить А, наложив на него такое условие, чтобы дивергенция А чему-нибудь равнялась. Мы всегда можем это сделать, не задевая В. Так получается потому, что, хотя А' и А имеют одинаковый ротор и дают одно и то же В, они вовсе не обязаны иметь одинаковую дивергенцию. В самом деле, С·A' = С·A+С2y, и, подбирая соответствующее y, можно придать С·A' любое значение.
Чему следует приравнять С·А? Выбор должен обеспечить наибольшее математическое удобство и зависит от нашей задачи. Для магнитостатики мы сделаем простой выбор
С·A = 0. (14.6)
(Потом, когда мы перейдем к электродинамике, мы изменим наш выбор.) Итак, наше полное определение А в данный момент есть СXA=B и С·А=0.
Чтобы привыкнуть к векторному потенциалу, посмотрим сначала, чему он равен для однородного магнитного поля В0. Выбирая ось z в направлении В0, мы должны иметь
(14.7)
Рассматривая эти уравнения, мы видим, что одно из возможных решений есть
Или с тем же успехом можно взять
Еще одно решение есть комбинация первых двух
Ясно, что для каждого поля В векторный потенциал А не единственный; существует много возможностей.
Фиг. 14.1. Однородное магнитное поле В, направленное по оси z, соответствует векторному потенциалу А (А=Вr'/2), который вращается вокруг оси z. т' — расстояние до оси z.
Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку x-компонента пропорциональна -y, а y-компонента пропорциональна -+x, то вектор А должен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r' (штрих означает, что это не вектор расстояния от начала). Кроме того, величина А пропорциональна Ц(x2+y2) и, следовательно, пропорциональна r'. Поэтому А (для однородного поля) может быть записано просто
(14.9)
Векторный потенциал А равен по величине Br' /2, и вращается вокруг оси z, как показано на фиг. 14.1. Если, например, поле В есть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.
Векторный потенциал однородного поля может быть получен и другим способом. Циркуляция А вдоль любой замкнутой петли Г может быть выражена через поверхностный интеграл от СXА с помощью теоремы Стокса [уравнение (3.38), стр. 63]
(14.10)
Но интеграл справа равен потоку В сквозь петлю, поэтому
(14.11)
Итак, циркуляция А вдоль всякой петли равна потоку В сквозь петлю. Если мы возьмем круглую петлю радиуса r' в плоскости, перпендикулярной однородному полю В, то поток будет в точности равен
Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией только от r', то циркуляция будет равна
Как и раньше, получаем
В только что разобранном примере мы вычисляем векторный потенциал из магнитного поля, обычно поступают наоборот. В сложных задачах всегда проще найти векторный потенциал, а затем уже из него найти магнитное поле. Сейчас мы покажем, как это можно сделать.
§ 2. Векторный потенциал заданных токов
Раз В определяется токами, значит, и А тоже. Мы хотим теперь выразить А через токи. Начнем с нашего основного уравнения (14.2):
откуда, конечно, следует
Это уравнение для магнитостатики; оно похоже на уравнение
(14.13)
для электростатики.
Наше уравнение (14.12) для векторного потенциала станет еще более похожим на уравнение для j, если переписать СX(СX А), используя векторное тождество [см. уравнение (2.58) стр. 44]
(14.14)
Поскольку мы выбрали С·А=0 (и теперь вы видите, почему), уравнение (14.12) приобретает вид
(14.15)
Фиг. 14.2. Векторный потенциал А в точке 1 определяется интегралом по элементам тока jdV во всех точках 2.
Это векторное уравнение, конечно, распадается на три уравнения
и каждое из этих уравнений математически идентично уравнению
(14.17)
Все, что мы узнали о нахождении потенциала для известного r, можно использовать для нахождения каждой компоненты А, когда известно j!
В гл. 4 мы видели, что общее решение уравнения электростатики (14.17) имеет вид
Тогда мы немедленно получаем общее решение для Аx:
(14.18)
и аналогично для Ауи Az. (Фиг. 14.2 напоминает вам о принятых нами обозначениях для r12 и dV2.) Мы можем объединить все три решения в векторной форме:
(14.19)
(Вы можете при желании проверить прямым дифференцированием компонент, что этот интеграл удовлетворяет С·А=0, поскольку С·j=0, а последнее, как мы видели, должно выполняться для постоянных токов.)
Мы имеем, таким образом, общий метод вычисления магнитного поля от постоянных токов. Принцип такой: x-компонента векторного потенциала, возникающая от плотности тока j, точно такая же, как электрический потенциал j, который был бы создан плотностью зарядов р, равной jx/c2, и аналогично для у- и z-компонент. (Этот принцип действует только для декартовых компонент. Например, «радиальная» компонента А не связана таким же образом с «радиальной» компонентой j.) Итак, из вектора плотности тока j можно найти А, пользуясь уравнениями (14.19), т. е. мы находим каждую компоненту А, решая три воображаемые электростатические задачи для распределений заряда r1=jx/с2, r2=jу/с2 и r3=jz/с2. Затем мы находим В, вычислив разные производные от А, входящие в ухА. Немного сложнее, чем в электростатике, но идея та же. Сейчас мы проиллюстрируем теорию, вычислив векторный потенциал в нескольких частных случаях.
§ 3. Прямой провод
В качестве первого примера снова вычислим поле прямого провода, которое мы находили в предыдущем параграфе, пользуясь уравнением (14.2) и соображениями симметрии. Возьмем длинный прямой провод радиуса а, по которому течет постоянный ток I. В отличие от заряда в проводнике в случае электростатики постоянный ток в проводе распределен равномерно по поперечному сечению провода. При таком выборе координат, как показано на фиг. 14.3, вектор плотности тока j имеет только z-компоненту. По величине она равна
(14.20)
внутри провода и нулю вне его.
Поскольку jхи jy оба равны нулю, то сразу же получим
Ах = 0, Ау = 0.
Чтобы получить Аг, можно использовать наше решение для электростатического потенциала j от провода с однородной плотностью заряда r=/г/с2.
Фиг. 14.3. Длинный цилиндрический провод с однородной плотностью тока j, направленный вдоль оси z.
Для точек вне бесконечного заряженного цилиндра электростатический потенциал равен
где r'=Ц(x2+y2), a l, — заряд на единицу длины pа2r. Следовательно, Агдолжно быть равно
для точек вне длинного провода с равномерно распределенным током. Поскольку pа2jz=I то можно также написать
(14.21)
Теперь можно найти В, пользуясь (14.4). Из шести производных от нуля отличны только две. Получаем
(14.22)
,(14.23)
Мы получаем тот же результат, что и раньше: В обходит провод по окружности и по величине равен
(14.24).
§ 4. Длинный соленоид
Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным пI на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток I, и пренебрегаем небольшими зазорами между витками.)
Точно так же, как мы выводили «поверхностную плотность заряда» а, определим здесь «поверхностную плотность тока» J, равную току на единице длины по поверхности соленоида (что, конечно, есть просто среднее j, умноженное на толщину тонкой намотки). Величина J здесь равна nI. Этот поверхностный ток (фиг. 14.4) имеет компоненты
Мы должны теперь найти А для такого распределения токов. Прежде всего найдем Ах в точках вне соленоида. Результат такой же, как электростатический потенциал вне цилиндра с поверхностным зарядом:
Фиг. 14.4. Длинный соленоид с поверхностной плотностью тока J.
где s0=-,//c2. Мы не решали случай такого распределения заряда, но делали нечто похожее. Это распределение заряда эквивалентно двум жестким цилиндрам, состоящим из зарядов, один из положительных, другой из отрицательных, с малым относительным смещением их осей в направлении у. Потенциал такой пары цилиндров пропорционален производной по у от потенциала одного однородно заряженного цилиндра. Мы, конечно, можем вычислить константу пропорциональности, но пока не будем возиться с этим.
Потенциал заряженного цилиндра пропорционален lnr'; потенциал пары тогда равен
Итак, мы знаем, что
(14.25)
где К — некоторая константа. Рассуждая точно так же, найдем
(14.26)
Хотя мы раньше говорили, что вне соленоида магнитного поля нет, теперь мы находим, что поле А существует и циркулирует вокруг оси z (см. фиг. 14.4). Возникает вопрос: равен ли нулю его ротор?
Очевидно, Вхи Вyравны нулю, а
Итак, магнитное поле вне очень длинного соленоида действительно равно нулю, хотя векторный потенциал нулю не равен.
Мы можем проверить наш результат, прибегнув к другим соображениям. Циркуляция векторного потенциала вокруг соленоида должна равняться потоку В внутри катушки [уравнение (14.11)]. Циркуляция равна А·2pr' или, поскольку А=К1r', она равна 2pК. Заметьте, что циркуляция не зависит от r'. Так и должно быть, если В вне соленоида отсутствует, потому что поток есть просто величина В внутри соленоида, умноженная на pа2. Он один и тот же для всех окружностей с радиусом r'>а. Раньше мы нашли, что поле внутри равно n//e0c2, поэтому мы можем определить константу К:
или
Итак, векторный потенциал снаружи имеет величину
(14.27)
и всегда перпендикулярен вектору r'.
Мы говорили о соленоидальной катушке из проволоки, но такое же поле мы могли бы создать, вращая длинный цилиндр с электростатическим зарядом на поверхности. Если у нас есть тонкий цилиндрический слой радиуса а с поверхностным зарядом s, то вращение цилиндра образует поверхностный ток J=sv, где v=sw — скорость поверхностного заряда. Внутри цилиндра тогда будет магнитное поле B=saw/e0с2.
Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5). Эта проволока движется в магнитном поле, так что сила vXB приведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Е зарядов не уравновесит силы vXB). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)!
Но вы, наверно, засомневаетесь: «А что, если я сам перейду,— скажете вы,— в систему координат вращающегося цилиндра? Там заряженный цилиндр покоится, а я знаю из электростатических уравнений, что внутри цилиндра никакого поля не будет, не будет и силы, толкающей заряды к центру. Поэтому здесь что-то не так?» Нет. Все правильно.
Фиг. 14.5.Вращающийся заряженный цилиндр создает внутри себя магнитное поле.
Короткая проволока, закрепленная вдоль радиуса, вращаясь вместе с цилиндром, приобретает на своих концах индуцированные заряды.
«Относительности вращения» не существует. Вращающаяся система — не инерциальная система, и законы физики в ней другие. Мы должны пользоваться уравнениями электромагнетизма только в инерциальных системах координат.
Было бы здорово, если бы смогли измерить абсолютное вращение Земли с помощью такого заряженного цилиндра, но эффект, к несчастью, настолько мал, что его невозможно наблюдать даже с помощью самых тонких современных приборов.
§ 5. Поле маленькой петли; магнитный диполь
Воспользуемся методом векторного потенциала, чтобы найти магнитное поле маленькой петли с током. Как обычно, под словом «маленькая» мы просто подразумеваем, что нас интересуют поля только на больших расстояниях по сравнению с размером петли. Как мы увидим, любая петелька представляет собой «магнитный диполь». Это значит, что она создает магнитное поле, подобное электрическому полю от электрического диполя.
Возьмем сначала прямоугольную петлю и выберем оси координат, как показано на фиг. 14.6. Токов в направлении z нет, поэтому Azравно нулю. Есть токи в направлении х по обеим сторонам прямоугольника, длина которых а. В каждой стороне плотность тока и ток однородны. Поэтому решение для Ахв точности подобно электростатическому потенциалу от двух заряженных палочек (фиг. 14.7). Поскольку палочки имеют противоположные заряды, их электрический потенциал на больших расстояниях есть как раз дипольный потенциал (см. гл. 6,
§ 5). В точке Р на фиг. 14.6 потенциал равен
(14.28)
где р — дипольный момент распределения зарядов. В данном случае дипольный момент равен полному заряду на одной палочке, умноженному на расстояние между ними:
(14.29)
Дипольный момент смотрит в отрицательном направлении y, поэтому косинус угла между R и р равен —ylR (где у — координата Р). Итак, мы имеем
Заменяя l на I/с2, сразу же получаем Ах:
(14.30)
С помощью тех же рассуждений:
(14.31)
Фиг. 14.7. Распределение jx в проволочной петле о током, изображенной на фиг. 14.6.
Фиг. 14.8. Векторный потенциал маленькой петли с током, расположенной в начале координат (в плоскости ху). Поле магнитного диполя.
Снова Аупропорционально х, а Ахпропорционально —y, так что векторный потенциал (на больших расстояниях) идет по кругу вокруг оси z, циркулируя таким же образом, как ток I в петле (фиг. 14.8).
Величина А пропорциональна Iab, т. е. току, умноженному на площадь петли. Это произведение называется магнитным дипольным моментом (или часто просто «магнитным моментом») петли. Мы обозначим его через m:
(14.32)
Векторный потенциал маленькой плоской петельки любой формы (круг, треугольник и т. п.) также дается уравнениями (14.30) и (14.31), если заменить Iab на
(14.33)
Мы предоставляем вам право это доказать.
Нашему уравнению можно придать векторную форму, если определить вектор m как нормаль к плоскости петли с положительным направлением, определяемым по правилу правой руки (см. фиг. 14.8). Тогда можно написать
(14.34)
Нам еще нужно найти В. Пользуясь (14.33) и (14.34), а также (14.4). получаем
(14.35)
(под многоточием мы подразумеваем m/4pe0с2),
Компоненты поля В ведут себя точно так же, как компоненты поля Е для диполя, ориентированного вдоль оси z [см. уравнения (6.14) и (6.15), а также фиг. 6.5, стр. 115]. Вот почему мы называем петлю магнитным диполем. Слово «диполь» в применении к магнитному полю немного запутывает, потому что нет отдельных магнитных «полюсов», соответствующих электрическим зарядам. Магнитное «дипольное поле» создается не двумя «зарядами», а элементарной петлей с током.
В общем-то довольно любопытно, что, начав с совсем разных законов, С·Е=r/e0 и СXВ=j/e0с2, можно прийти к полю одного и того же вида. Почему так получается? Потому что дипольные поля возникают, только когда мы находимся далеко от всех токов и зарядов. Тогда в большей части пространства уравнения для Е и В одинаковы: у обоих дивергенция и ротор равны нулю. Следовательно, они дают одни и те же решения. Однако источники, конфигурацию которых мы описываем с помощью дипольных моментов, физически совершенно различны. В одном случае это циркулирующий ток, а в другом — пара зарядов, один над, а другой под плоскостью петли для соответствующего поля.
§ 6. Векторный потенциал цепи
Нас часто интересует магнитное поле, создаваемое цепью проводов, в которой диаметр провода очень мал по сравнению с размерами всей системы. В таких случаях мы можем упростить уравнения для магнитного поля.
Для тонкого провода элемент объема можно записать в виде
dV = Sds,
где S — площадь поперечного сечения провода, a ds — элемент расстояния вдоль проволоки. В самом деле, поскольку вектор ds имеет то же направление, что и j (фиг. 14.9), и мы можем предположить, что j постоянно по любому данному сечению, то можно записать векторное уравнение
(14.37)
Фиг. 14.9. Для тонкой проволоки jdV то же самое, что и Ids.
Фиг. 14.10. Магнитное поле провода может быть получено интегрированием по всей цепи.
Ho jS — как раз то, что мы называем током I во всем проводе, так что наш интеграл для векторного потенциала (14.19) становится равным
(14.38)
(фиг. 14.10). (Мы предполагаем, что / одно и то же вдоль всего контура. Если есть несколько ответвлений с разными токами, то следует, конечно, брать соответствующий ток в каждой ветви.)
Как и раньше, можно найти поле с помощью (14.38) либо прямым интегрированием, либо решая соответствующую электростатическую задачу.
§ 7. Закон Био— Савара
В ходе изучения электростатики мы нашли, что электрическое поле известного распределения зарядов может быть получено сразу в виде интеграла [уравнение (4.16)]
Как мы видели, вычислить этот интеграл (а их на самом деле три, по одному на каждую компоненту) обычно бывает труднее, чем вычислить интеграл для потенциала и взять от него градиент.
Подобный интеграл связывает и магнитное поле с токами. Мы уже имеем интеграл для А [уравнение (14.19)]; мы можем получить интеграл и для В, если возьмем ротор от обеих частей:
А теперь мы должны быть осторожны. Оператор ротора означает взятие производных от А(1), т. е. он действует только на координаты (x1, y1, z1). Можно внести оператор СX под интеграл, если помнить, что он действует только на переменные со значком 1, которые появляются, конечно, только в
Мы получаем для x-компоненты В:
(14.41)
Величина в скобках есть просто x-компонента от
Такие же результаты получаются и для других компонент, и мы имеем
(14.42)
Интеграл дает В сразу через известные токи. Геометрия здесь точно такая же, какая изображена на фиг. 14.2.
Если токи текут только по тонким проводам, мы можем, как в предыдущем параграфе, немедленно взять интеграл поперек провода, заменив jdV на Ids, где ds — элемент длины провода. Тогда, пользуясь обозначениями фиг. 14.10, имеем
(14.43)
(Знак минус появляется потому, что мы изменили порядок векторного произведения.) Это уравнение для В называется законом Био — Савара в честь открывших его ученых. Он дает формулу для прямого вычисления магнитного поля, создаваемого проводами с током.
Вероятно, вы удивились: «Какой же прок от векторного потенциала, если мы можем сразу найти В в виде векторного интеграла? В конце концов А тоже определяется тремя интегралами!» Из-за векторного произведения интегралы для В обычно сложнее устроены, как это видно из уравнения (14.41). Кроме того, поскольку интегралы для А похожи на электростатические, то нам не надо их вычислять заново. Наконец, мы увидим, что в более трудных теоретических вопросах, таких, как теория относительности, в современном изложении законов механики, вроде принципа наименьшего действия, о котором будет рассказано позже, в квантовой механике, векторный потенциал играет важную роль.
*Наше определение все еще не полностью задает А. Чтобы задание было единственным, мы должны были бы лто-нибудь сказать о поведении поля А на какой-либо границе или на больших расстояниях. Иногда бывает удобно выбрать, например, поле, спадающее к нулю на больших расстояниях.

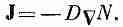




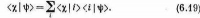
Комментарии к книге «5b. Электричество и магнетизм», Ричард Филлипс Фейнман
Всего 0 комментариев