4. Кинетика. Теплота. Звук
Глава 39 КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
§ 1. Свойства вещества
§ 2. Давление газа
§ 3. Сжимаемость излучения
§ 4. Температура и кинетическая энергия
§ 5. Закон идеального газа
§ 1. Свойства вещества
С этой главы мы начнем изучение новой темы, которая займет у нас довольно много времени. Мы начнем анализ свойств вещества с физической точки зрения. Зная, что вещество построено из большого числа атомов или каких-то других элементарных частей, взаимодействующих электрически и подчиняющихся законам механики, мы постараемся понять, почему скопления атомов ведут себя именно так, а не иначе.
Нечего и говорить, что это трудная задача. И будет лучше, если мы с самого начала подчеркнем, что это чрезвычайно трудная задача и что решать ее нам придется совсем иными способами, чем раньше. Когда мы изучали механику и оптику, то могли начинать с точных формулировок некоторых законов, например законов Ньютона или формулы для поля, порождаемого ускоренным зарядом. Узнав их, мы сразу же могли объяснить бездну всяких явлений, а потом эти законы становились для нас прочной основой, опираясь на которую, мы совершенствовались и в механике, и в оптике. Мы можем продолжать изучение и дальше, но мы не обнаружим при этом какую-то новую физику, мы просто будем решать старые задачи более точными математическими методами.
Такой способ непригоден для изучения свойств вещества. Мы можем сказать о свойствах вещества лишь самые простые вещи. Предмет этот слишком сложен, чтобы можно было начать с самых основных законов. Мы по-прежнему будем пользоваться законами механики и электричества. Но законы эти слишком далеки от тех свойств, которые мы собираемся изучать. От законов Ньютона до свойств вещества очень много шагов и каждый шаг очень труден. Сейчас мы сделаем несколько таких шагов, но мне хочется предупредить вас, что если в предыдущих главах мы анализировали явления более или менее строго, то теперь с каждым шагом мы все больше будем терять строгость. Свойства вещества мы сможем понять лишь весьма приближенно.
Происходит это по нескольким причинам. Во-первых, наш анализ не может быть полным потому, что для этого нужно глубокое знание теории вероятностей; мы ведь не собираемся следить за движением каждого атома, а хотим узнать о среднем числе атомов, движущихся в том или ином направлении, и прикинуть, к чему приведет разница в этих средних. Таким образом, теория вероятностей органически входит в нашу тему, а в математике мы еще не очень сильны и многого от нас не потребуешь.
Вторая и более серьезная причина — чисто физическая. Поведение атомов подчиняется законам не классической, а квантовой механики, и пока мы не изучим квантовую механику, нельзя серьезно говорить об изучении свойств вещества. Речь идет не просто о переходе от больших предметов к маленьким, например от автомобилей к биллиардным шарам, разница между законами классической и квантовой механики гораздо глубже и существенней, и многие объяснения, если исходить из классической механики, будут просто неверными. Так что многих вещей мы пока никак не в состоянии понять, однако мы будем подчеркивать каждый раз, когда объяснения приведут нас в тупик, чтобы по крайней мере хоть предупредить, где он находится. Для этого и говорилось о квантовой механике в предыдущих главах: надо было понять, в каких случаях отказывает механика классическая.
Почему же мы вообще изучаем свойства вещества? Не лучше ли было бы подождать с полгода или год, пока мы не подучим теорию вероятностей и квантовую механику, а потом уж и взяться за свойства вещества поосновательней? На это следует ответить, что трудные вещи лучше изучать не спеша! Сначала мы — плохо ли, хорошо ли — познакомимся с общими идеями, подумаем, что может произойти в тех или иных обстоятельствах, а потом, когда лучше узнаем основные законы, сформулируем все это поточнее.
Каждый, кто хочет всерьез анализировать свойства вещества, должен сначала написать основные уравнения и попытаться решить их. Но каждого, кто начинал с этого, ждала неудача. Успех приходил лишь к тем, кто подходил к делу как физик: у этих людей сначала не было ничего, кроме грубой идеи, а затем они находили верное приближение, соображая, что в этой трудной ситуации можно считать большим, а что малым.
Задачи в этой области столь сложны, что даже не очень четкая и половинчатая идея оправдывает затраченное на нее время, и можно то и дело возвращаться к одной и той же задаче, приближаясь понемногу к ее точному решению. Так мы и поступаем в нашем курсе.
И еще одна причина, по которой мы приступаем сейчас к изучению свойств веществ: нам уже приходилось встречать похожие идеи, например в химии. Некоторые из них известны нам со школы. Было бы интересно понять их с точки зрения физика.
Вот один из самых увлекательных примеров: известно, что равные объемы газов содержат при одинаковом давлении и температуре равное число молекул. Авогадро первым понял закон кратных отношений: из того, что в химической реакции между двумя газами объемы реагирующих газов относятся как целые числа, следует, что равные объемы содержат равное число атомов. Но почему в равных объемах содержится равное число атомов? Можно ли объяснить это, исходя из законов Ньютона? Для этого вам придется изучить эту главу. Мы еще будем впоследствии много говорить о давлениях, объемах, температуре и теплоте.
Мы обнаружим при этом, что многие соотношения между свойствами вещества можно понять, ни слова не говоря об атомах. Например, если какое-нибудь тело сжать, оно нагреется; если тело нагревать, оно начнет расширяться. Связь между этими явлениями можно понять, не изучая строения тела. Занимающаяся такими вещами наука называется термодинамикой. Конечно, глубокое понимание термодинамики возможно лишь после подробного изучения механизма, лежащего в основе того или иного процесса. Вот этим мы и займемся: мы примем с самого начала тот факт, что все вещества состоят из атомов, и постараемся понять свойства вещества и законы термодинамики.
Итак, начнем изучение свойств газов, исходя из законов Ньютона.
§ 2. Давление газа
Каждый знает, что газ оказывает давление. Но отчего? В этом надо разобраться как следует. Если бы наши уши были намного чувствительнее, чем они есть на самом деле, мы бы все время слышали страшный шум. Но природа позаботилась, чтобы наши уши не были столь восприимчивы, ведь они оказались бы для нас совершенно бесполезными — в них постоянно стоял бы дикий гул, похожий на шум от стартующей ракеты. Дело в том, что барабанные перепонки наших ушей соприкасаются с воздухом, а воздух состоит из великого множества беспорядочно движущихся молекул, которые, ударяясь о барабанные перепонки, создают такой шум, как будто сразу очень много барабанщиков отбивают беспорядочную дробь — бум, бум, бум... Однако мы не слышим этих звуков, потому что атомы очень малы, а уши наши недостаточно чувствительны. Беспорядочные удары молекул должны были бы собственно продавить барабанную перепонку, но ее непрестанно бомбардируют и с внутренней стороны, и в результате полная сила, действующая на перепонку, оказывается равной нулю. Если бы откачать воздух с одной стороны или хотя бы сделать разным его относительное количество с обеих сторон, то перепонка продавилась бы в ту или иную сторону, потому что бомбардировка с одной стороны оказалась бы гораздо сильнее. Мы иногда испытываем это неприятное ощущение, когда очень быстро поднимаемся в лифте или на самолете, а хуже всего, если мы еще при этом простужены (в этом случае распухшая слизистая оболочка закрывает каналы, соединяющие через носоглотку внутреннюю полость уха с внешним пространством, и таким образом оба давления не могут быстро уравняться.)
Чтобы проанализировать это явление количественно, предположим, что газ находится в ящике, одна стенка которого представляет собой поршень, способный перемещаться (фиг. 39.1).
Фиг. 39. 1. Атомы газа в ящике, в котором движется поршень без трения.
Найдем силу, с которой действуют на поршень находящиеся внутри ящика атомы. О поршень ударяются атомы, движущиеся внутри объема V со всевозможными скоростями. Предположим, что вне ящика ничего нет — сплошной вакуум. Что же произойдет? Если предоставить поршень самому себе и не придерживать его, то с каждым ударом молекулы он будет приобретать небольшой импульс и постепенно будет вытолкнут совсем из ящика. Чтобы удержать его в ящике, придется приложить силу F. Какова должна быть эта сила? Говоря о силе, мы будем относить ее к единице площади: если площадь поршня равна А, то действующая на него сила будет пропорциональна площади. Определим давление как величину, равную отношению приложенной к поршню силы к площади поршня:
P =F/A. (39.1)
Чтобы лучше понять, для чего это делается, подсчитаем бесконечно малую работу dW, которую надо затратить, чтобы протолкнуть поршень на бесконечно малое расстояние —dx (позднее это понадобится нам и для других целей); эта работа равна произведению силы на расстояние или, согласно (39.1), произведению давления, площади поршня и расстояния. Все это равно произведению давления на изменение объема, взятого с обратным знаком:
dW=F(-dx)=-PAdx=-PdV. (39.2)
(Произведение площади А на изменение высоты dx равно изменению объема.) Знак минус в этом выражении возникает из-за того, что при сжатии объем уменьшается; если принять это во внимание, то мы получим правильный результат: чтобы сжать газ, надо затратить работу.
Итак, с какой силой надо давить на поршень, чтобы уравновесить удары молекул? При каждом ударе поршню сообщается некий импульс. В каждую секунду поршень получает определенный импульс и начинает двигаться. Чтобы предотвратить это, приложенная нами сила за секунду должна сообщить поршню точно такой же импульс. Таким образом, сила равна импульсу, сообщенному поршню за 1 сек. Можно об этом сказать и иначе: если предоставить поршень самому себе, то он за счет бомбардировки наберет скорость и с каждым ударом будет подталкиваться и двигаться с ускорением. Быстрота изменения скорости поршня, или ускорение, пропорциональна действующей силе. Таким образом, сила, которую мы определили как произведение давления на площадь, равна импульсу, сообщенному поршню за 1 сек всеми молекулами внутри ящика.
Подсчитать импульс, передаваемый поршню за 1 сек, легко; мы сделаем это в два этапа: сначала определим импульс, переданный одним атомом при столкновении с поршнем, а потом умножим эту величину на число соударений атомов с поршнем за 1 сек. Сила и будет произведением этих двух величин.
Займемся теперь этими величинами: предположим сначала, что поршень — это идеальный «отражатель» атомов. Если это не так, то вся наша теория рухнет — поршень начнет нагреваться и произойдет много всяких событий, предсказать которые мы не в состоянии. Однако, когда снова установится равновесие, в результате окажется, что каждое столкновение будет эффективно упругим. В среднем энергия приходящих и уходящих частиц не изменяется. Таким образом, предположим, что газ находится в равновесии и поршень, будучи неподвижным, энергии не поглощает. В этом случае частица, подлетевшая к поршню с определенной скоростью, улетит от него с той же скоростью, причем масса частицы не изменится.
Если v есть скорость атома, a vx— составляющая скорости вдоль оси х, то импульс «к поршню» равен mvx, но раз частица «отражается», то импульс «от поршня» равен той же величине; значит, за одно соударение поршню сообщается импульс 2mvx.
Нужно теперь подсчитать число соударений атома за 1 сек; для этого можно взять любой промежуток времени dt, а потом разделить число соударений на dt. Много ли атомов попадает за это время в цель? Предположим, что в объеме V заключено N атомов, т. е. в каждом единичном объеме имеется n= N/V атомов. Теперь заметим, что за время t достигнут поршня не все частицы, движущиеся к поршню с заданной скоростью, а только те, которые оказались достаточно близко от него. Если частицы были очень далеко, то, хотя они и стремятся к поршню, к сроку они не успеют. Таким образом, за время t о поршень ударятся лишь те частицы, которые в начальный момент были не дальше чем на расстоянии vxt от него. Следовательно, число соударений за время t равно числу атомов, находящихся на расстоянии, не превышающем vxt, а поскольку площадь поршня равна А, то атомы, которые со временем попадут в цель, занимают объем Avxt. А число атомов, попавших в цель, равно произведению объема на число атомов в единичном объеме nvxAt. Но нас, конечно, интересует не число соударений за время t, а мы хотим знать число соударений за 1 сек, поэтому мы делим на t и получаем nvxA. (Время t может быть взято очень малым, для красоты можно писать dt и затем дифференцировать, но это все одно и то же.)
Итак, мы нашли, что сила равна
F=nvxA·2mvx. (39.3)
Обратите внимание, что если фиксировать плотность частиц, то сила оказывается пропорциональной площади! После этого давление найти очень просто:
P=-2nmv2x. (39.4)
Теперь надо исправить кое-какие неточности: прежде всего не все молекулы имеют одну и ту же скорость и не все они движутся в одном направлении, так что нам приходится иметь дело с разными v2x! Каждая молекула, ударяясь о поршень, вносит свой вклад, поэтому надо взять среднее по всем молекулам. Сделав это, мы получим
P=nm<v2x>. (39.5)
А не забыли ли мы множитель 2? Нет, потому что лишь половина атомов движется к поршню. Другие летят в противоположную сторону, а усредняя по v2x, мы усредняем как по положительным, так и по отрицательным составляющим vx.
Если просто усреднить по v2x, получится вдвое больший результат. Среднее v2x для положительных vxравно половине среднего v2x для всех vx.
Но атомы прыгают в ящике как хотят, и поэтому ясно, что x-направление» для них ничем не отличается от любого другого; они движутся куда угодно: вправо — влево, вверх — вниз, взад — вперед. Поэтому <v2x> (средний квадрат скорости движения в одном направлении) равен среднему квадрату скорости в любом другом направлении
<v2x>=<v2y>=<v2z>. (39.6)
Используем это обстоятельство для небольшого математического трюка и обнаружим, что каждый из членов в (39.6) равен их сумме, деленной на три, а сумма — это квадрат величины скорости:
<v2x>=1/3<v2x+v2y+v2z>=<v2>/3. (39.7)
Это очень хорошо, потому что теперь уже не надо заботиться о координатных осях, и формулу для давления можно записать в виде
P=2/3n(mv2/2). (39.8)
Мы выделили множитель <mv2/2>, потому что это кинетическая энергия движения молекулы как целого. Итак, мы нашли
PV=N2/3(mv2/2). (39.9)
Если мы будем знать скорость молекул, то очень быстро подсчитаем давление.
В качестве простого примера можно описать такие газы, как гелий, пары ртути или калия при достаточно высокой температуре или аргон; это одноатомные газы, для которых можно считать, что их атомы не имеют внутренних степеней свободы. Если нам попадется сложная молекула, то в ней могут быть всевозможные внутренние движения, всякого рода колебания и т. д. Мы предполагаем, что можно не принимать их в расчет; но можно ли это делать — вопрос сложный и мы к нему вернемся; в действительности для нашего случая это окажется допустимым. Итак, предположим, что внутреннее движение атомов можно не рассматривать, и поэтому кинетическая энергия движения молекулы как целого восполняет всю энергию. Для одноатомного газа кинетическая энергия — действительно полная энергия. Будем обозначать полную энергию буквой U (иногда ее называют полной внутренней энергией, как-будто у газа может быть какая-то внешняя энергия), т. е. всю энергию всех молекул газа или любого другого объекта.
В случае одноатомного газа мы предположим, что полная энергия U равна произведению числа атомов на среднюю кинетическую энергию каждого из них, потому что мы пренебрегли возможным возбуждением атомов или какими-то внутриатомными движениями. Тогда
PV=2/3U. (39.10)
Немного задержимся и ответим на такой вопрос: предположим, что мы медленно сжимаем газ; каким должно быть давление, чтобы сжать газ до заданного объема? Определить это легко, так как давление есть энергия, деленная на объем. Но когда газ сжимается, производится работа и поэтому энергия газа U возрастает. Процесс сжатия описывается неким дифференциальным уравнением. В начальный момент газ занимает определенный объем и обладает определенной энергией, поэтому нам известно и давление. Как только мы начинаем сжимать газ, энергия U возрастает, объем V уменьшается, а как изменяется давление, нам еще предстоит узнать.
Итак, нам предстоит решить дифференциальное уравнение. Сейчас мы это сделаем. Однако подчеркнем сначала, что, сжимая газ, мы предполагаем, что вся работа уходит на увеличение энергии атомов газа. Вы спросите: «А необходимо ли на этом останавливаться? Куда же еще она может уйти?» Но оказывается, что затраченная работа может уйти и в другое место. Энергия может «вытечь» из ящика сквозь стенки: горячие (т. е. очень быстрые) атомы при бомбардировке будут нагревать стенки ящика и энергия выйдет наружу. Но мы предполагаем, что в нашем случае этого не происходит.
Сделаем небольшое обобщение, хотя и в этом случае мы будем рассматривать лишь очень частный случай: запишем вместо PV=2/3U
PV = (g-1)U. (39.11)
Энергия U умножается на (g-1) для удобства, потому что в дальнейшем нам придется иметь дело с газами, для которых множитель перед U равен не 2/3, а какому-то другому числу. Чтобы можно было описывать и такие случаи, запишем этот множитель так, как его обозначают почти сто лет. Тогда в нашем случае одноатомного газа, такого, как гелий, g=5/з, потому что 5/3-1=2/з.
Мы уже говорили, что совершаемая при сжатии газа работа равна -PdV. Сжатие, при котором тепло не поглощается и не выделяется, называется адиабатическим сжатием; это слово образовано из трех греческих слов: а(не)+dia(сквозь)+bainein(проходить). (Слово адиабатический употребляется в физике в разных смыслах, так что не всегда можно понять, что между ними общего.) При адиабатическом сжатии вся затраченная работа уходит на изменение внутренней энергии. Вот в этом и смысл, что нет потерь энергии и, значит, PdV=-dU. Но поскольку U=PV/g-1, то можно записать
dU=(PdV+VdP)/(g-1). (39.12)
Итак, PdV =-(PdV+VdP)/ (g-1) или, приводя подобные члены, получаем gPdV=-VdP, или
gdv/v+dp/p=0, (39.1З)
Если мы примем, что g постоянна, а это так в случае одноатомных газов, то уравнение интегрируется и мы получаем glnV+lnP=lnC, где С — постоянная интегрирования. Переходя к степеням, мы получаем такой закон:
PVg=C (постоянная). (39.14)
Иначе говоря, если выполнены условия адиабатичности, т. е. потерь энергии нет и газ при сжатии нагревается, то в случае одноатомного газа произведение объема на давление в степени 5/3 есть величина постоянная! Этот результат мы получили чисто теоретически, но опыт показывает, что и в действительности все происходит именно так.
§ 3. Сжимаемость излучения
Приведем еще один пример из кинетической теории газов; он не особенно интересует химиков, но очень важен для астрономов. Внутри нагретого до высокой температуры ящика имеется огромное число фотонов. (В качестве такого ящика надо взять очень горячую звезду. Солнце недостаточно горячо для этих целей. В звезде, правда, слишком много атомов, но если ее температура очень высока, то атомами можно пренебречь и считать, что внутренность звезды целиком заполнена фотонами.) Вспомним теперь, что фотон обладает импульсом р. (При изучении кинетической теории газов мы всегда будем испытывать страшные неудобства: р — это давление, но р — еще и импульс; v — это объем, но это и скорость одновременно, а. Т — это и температура, и кинетическая энергия, и время, и момент силы; тут нужен глаз да глаз.) Сейчас буква р — это импульс, вектор. Поступим так же, как и в предыдущем параграфе, за удары фотонов о стенку ответственна x-составляющая импульса, а удвоенная x-составляющая импульса — это импульс, полученный стенкой после каждого удара. Итак, вместо 2mvxпишем 2рх, а при вычислении числа столкновений нужно по-прежнему подставлять vx; проделав все это, формулу (39.4) для давления мы уже записываем в виде
P=2npxvx. (39.15)
После усреднения мы получим произведение nна среднее значение pxvx(вспомните, что мы говорили о множителе 2), а после того как на помощь будут призваны два других измерения, мы найдем
PV=N<p·v>/3. (39.16)
о
Эта формула почти совпадает с (39.9), потому что импульс равен mv, просто это более общая формула, вот и все. Произведение давления на объем равно произведению полного числа атомов на среднее значение 1/3(p·v).
Чему равно p·v для фотонов? Импульс и скорость направлены одинаково, а скорость равна скорости света, поэтому интересующее нас произведение — это импульс фотона, умноженный на скорость света. Произведение импульса фотона на скорость света — это энергия фотона: Е=рс. Мы имеем дело с энергией каждого фотона и должны умножить среднюю энергию фотона на число фотонов. Получается одна треть полной энергии:
PV=Ui3 (в случае фотонного газа). (39.17)
Для фотонов, следовательно, поскольку впереди стоит 1/3, множитель (g-1) в (39.11) равен l/4, т. е. g= 4/3, значит, излучение в ящике подчиняется закону
РV4/3=С. (39.18)
Таким образом, мы знаем сжимаемость излучения! Можно использовать эту формулу при анализе вклада излучения в давление внутри звезды, подсчитать давление и оценить, как оно изменяется при сжатии звезды. Просто удивительно, как много мы уже умеем!
§ 4. Температура и кинетическая энергия
До сих пор мы не имели дела с температурой; мы сознательно избегали разговоров на эту тему. Мы знаем, что если сжимать газ, энергия молекул возрастает, и мы обычно говорим, что газ при этом нагревается. Теперь надо понять, какое это имеет отношение к температуре. Нам известно, что такое адиабатическое сжатие, а как поставить опыт, чтобы можно было сказать, что он был проведен при постоянной температуре? Если взять два одинаковых ящика с газом, приставить их один к другому и подержать так довольно долго, то даже если вначале эти ящики обладали тем, что мы назвали различной температурой, то в конце концов температуры их станут одинаковыми. Что это означает? Только то, что ящики достигли того состояния, которого они в конце концов достигли бы, если бы их надолго предоставили самим себе! Состояние, в котором температуры двух тел равны — это как раз то окончательное состояние, которого достигают после длительного соприкосновения друг с другом.
Давайте посмотрим, что случится, если ящик разделен на две части движущимся поршнем и каждое отделение заполнено разным газом, как это показано на фиг. 39.2 (для простоты предположим, что имеются два одноатомных газа, скажем, гелий и неон).
Фиг.39. 2. Атомы двух разных одноатомных газов, разделенных подвижным поршнем.
В отделении 1 атомы массы m1движутся со скоростью v1, а в единице объема их насчитывается n1 штук, в отделении 2 эти числа соответственно равны m2, v2 и n2. При каких же условиях достигается равновесие?
Разумеется, бомбардировка слева заставляет поршень двигаться вправо и сжимает газ во втором отделении, затем то же самое происходит справа и поршень ходит так взад и вперед, пока давление с обеих сторон не сравняется, и тогда поршень остановится. Мы можем устроить так, чтобы давление с обеих сторон было одинаковым, для этого нужно, чтобы внутренние энергии, приходящиеся на единичный объем, были одинаковыми или чтобы произведения числа частиц nв единице объема на среднюю кинетическую энергию было одинаковым в обоих отделениях. Сейчас мы попытаемся доказать, что при равновесии должны быть одинаковы и отдельные сомножители. Пока мы знаем только, что равны между собой произведения чисел частиц в единичных объемах на средние кинетические энергии
это следует из условия равенства давлений и из (39.8). Нам предстоит установить, что по мере постепенного приближения к равновесию, когда температуры газов сравниваются, выполняется не только это условие, а происходит и еще кое-что.
Чтобы было яснее, предположим, что нужное давление слева в ящике достигается за счет очень большой плотности, но малых скоростей. При больших nи малых v можно получить то же самое давление, что и при малых nи больших v. Атомы, если они плотно упакованы, могут двигаться медленно, или атомов может быть совсем немного, но ударяют они о поршень с большей силой. Установится ли равновесие навсегда? Сначала кажется, что поршень никуда не сдвинется и так будет всегда, но если продумать все еще раз, то станет ясно, что мы упустили одну очень важную вещь. Дело в том, что давление на поршень вовсе не равномерное, поршень-то раскачивается точно так же, как барабанная перепонка, о которой мы говорили в начале главы, ведь каждый новый удар не похож на предыдущий. Получается не постоянное равномерное давление, а скорее нечто вроде барабанной дроби — давление непрерывно меняется, и наш поршень как бы постоянно дрожит. Предположим, что атомы правого отделения ударяют о поршень более или менее равномерно, а слева атомов меньше, и удары их редки, но очень энергичны. Тогда поршень то и дело будет получать очень сильный импульс слева и отходить вправо, в сторону более медленных атомов, причем скорость этих атомов будет возрастать. (При столкновении с поршнем каждый атом приобретает или теряет энергию в зависимости от того, в какую сторону движется поршень в момент столкновения.) После нескольких столкновений поршень качнется, потом еще, еще и еще..., газ в правом отделении будет время от времени встряхиваться, а это приведет к увеличению энергии его атомов, и движение их ускорится. Так будет продолжаться до тех пор, пока не уравновесятся качания поршня. А равновесие установится тогда, когда скорость поршня станет такой, что он будет отбирать у атомов энергию так же быстро, как и отдавать. Итак, поршень движется с какой-то средней скоростью, и нам предстоит найти ее. Если нам это удастся, мы подойдем к решению задачи поближе, потому что атомы должны подогнать свои скорости так, чтобы каждый газ получал через поршень ровно столько энергии, сколько теряет.
Очень трудно рассчитать движение поршня во всех деталях; хотя все это очень легко понять, оказывается, что проанализировать это несколько труднее. Прежде чем приступить к такому анализу, решим другую задачу: пусть ящик заполнен молекулами двух сортов с массами m1и m2, скоростями v1и v2 и т. д.; теперь молекулы смогут познакомиться поближе. Если сначала все молекулы № 2 покоятся, то долго это продолжаться не может, потому что о них будут ударять молекулы № 1 и сообщать им какую-то скорость. Если молекулы № 2 могут двигаться значительно быстрее, чем молекулы № 1, то все равно рано или поздно им придется отдать часть своей энергии более медленным молекулам. Таким образом, если ящик заполнен смесью двух газов, то проблема состоит в определении относительной скорости молекул обоих сортов.
Это тоже очень трудная задача, но мы все-таки решим ее. Сначала нам придется решить «подзадачу» (опять это один из тех случаев, когда, независимо от того как решается задача, окончательный результат запоминается легко, а вывод требует большого искусства). Предположим, что перед нами две сталкивающиеся молекулы, обладающие разными массами; во избежание осложнений мы наблюдаем за столкновением из системы их центра масс (ц. м.), откуда легче уследить за ударом молекул. По законам столкновений, выведенным из законов сохранения импульса и энергии, после столкновения молекулы могут двигаться только так, что каждая сохраняет величину своей первоначальной скорости, и изменить они могут только направление движения. Типичное столкновение выглядит так, как его изобразили на фиг. 39.3.
Фиг. 39. 3. Столкновение двух неодинаковых молекул, если смотреть из системы центра масс.
Предположим на минутку, что мы наблюдаем столкновения, системы центра масс которых покоятся. Кроме того, надо предположить, что все молекулы движутся горизонтально. Конечно, после первого же столкновения часть молекул будет двигаться уже под каким-то углом к исходному направлению. Иначе говоря, если вначале все молекулы двигались горизонтально, то спустя некоторое время мы обнаружим уже вертикально движущиеся молекулы. После ряда других столкновений они снова изменят направление и повернутся еще на какой-то угол. Таким образом, если кому-нибудь и удастся сначала навести порядок среди молекул, то все равно они очень скоро разбредутся по разным направлениям и с каждым разом будут все больше и больше распыляться. К чему же это в конце концов приведет? Ответ: Любая пара молекул будет двигаться в произвольно выбранном направлении столь же охотно, как и в любом другом. После этого дальнейшие столкновения уже не смогут изменить распределения молекул.
Что имеется в виду, когда говорят о равновероятном движении в любом направлении? Конечно, нельзя говорить о вероятности движения вдоль заданной прямой — прямая слишком тонка, чтобы к ней можно было относить вероятность, а следует взять единицу «чего-нибудь». Идея заключается в том, что через заданный участок сферы с центром в точке столкновения проходит столько же молекул, сколько через любой другой участок сферы. В результате столкновений молекулы распределяются по направлениям так, что любым двум равным по площади участкам сферы будут соответствовать равные вероятности (т. е. одинаковое число прошедших через эти участки молекул).
Между прочим, если мы будем сравнивать первоначальное направление и направление, образующее с ним какой-то угол 0, то интересно, что элементарная площадь на сфере единичного радиуса равна произведению 2p на sinqdq, или, что то же самое, на дифференциал cosq. Это означает, что косинус угла 9 между двумя направлениями с равной вероятностью принимает любое значение между -1 и +1.
Теперь нам надо вспомнить о том, что имеется на самом деле; ведь у нас нет столкновений в системе центра масс, а сталкиваются два атома с произвольными векторными скоростями v1 и v2. Что происходит с ними? Мы поступим так: снова перейдем к системе центра масс, только теперь она движется с «усредненной по массам» скоростью vц.м.=(m1v1+m2v2)/(m1+m2). Если следить за столкновением из системы центра масс, то оно будет выглядеть так, как это изображено на фиг. 39.3, только надо подумать об относительной скорости столкновения w. Относительная скорость равна v1-v2. Дело, следовательно, обстоит так: движется система центра масс, а в системе центра масс молекулы сближаются с относительной скоростью w; столкнувшись, они движутся по новым направлениям. Пока все это происходит, центр масс все время движется с одной и той же скоростью без изменений.
Ну и что же получится в конце концов? Из предыдущих рассуждений делаем следующий вывод: при равновесии все направления, w равновероятны относительно направления движения центра масс. Это означает, что в конце концов не будет никакой корреляции между направлением относительной скорости и движением центра масс. Если бы даже такая корреляция существовала вначале, то столкновения ее бы разрушили и она в конце концов исчезла бы полностью. Поэтому среднее значение косинуса угла между w и vц.м. равно нулю. Это значит, что
<w·vц.м.>=0. (39.19)
Скалярное произведение w·vц.м. легко выразить через v1 и v2:
Займемся сначала v1·v2; чему равно среднее v1·v2? Иначе говоря, чему равно среднее проекции скорости одной молекулы на направление скорости другой молекулы? Ясно, что вероятности движения молекулы как в одну сторону, так и в противоположную одинаковы. Среднее значение скорости v2 в любом направлении равно нулю. Поэтому и в направлении v1 среднее значение v2 тоже равно нулю. Итак, среднее значение v1·v2 равно нулю! Следовательно, мы пришли к выводу, что среднее т1v21должно быть равно т2v22. Это значит, что средние кинетические энергии обеих молекул должны быть равны:
1/2m1v21=1/2m2v22. (39.21)
Если газ состоит из атомов двух сортов, то можно показать (и мы даже считаем, что нам удалось это сделать), что средние кинетические энергии атомов каждого сорта равны, когда газ находится в состоянии равновесия. Это означает, что тяжелые атомы движутся медленнее, чем легкие; это легко проверить, поставив эксперимент с «атомами» различных масс в воздушном желобе.
Теперь сделаем следующий шаг и покажем, что если в ящике имеются два газа, разделенные перегородкой, то по мере достижения равновесия средние кинетические энергии атомов разных газов будут одинаковы, хотя атомы и заключены в разные ящики. Рассуждение можно построить по-разному. Например, можно представить, что в перегородке проделана маленькая дырочка (фиг. 39.4), так что молекулы одного газа проходят сквозь нее, а молекулы второго слишком велики и не пролезают.
Фиг. 39. 4. Два газа в ящике, разделенном полупроницаемой перегородкой.
Когда установится равновесие, то в том отделении, где находится смесь газов, средние кинетические энергии молекул каждого сорта сравняются. Но ведь в числе проникших сквозь дырочку молекул есть и такие, которые не потеряли при этом энергии, поэтому средняя кинетическая энергия молекул чистого газа должна быть равна средней кинетической энергии молекул смеси. Это не очень удовлетворительное доказательство, потому что ведь могло и не быть такой дырочки, сквозь которую пройдут молекулы одного газа и не смогут пройти молекулы другого.
Давайте вернемся к задаче о поршне. Можно показать, что кинетическая энергия поршня тоже должна быть равна 1/2m2v22. Фактически кинетическая энергия поршня связана только с его горизонтальным движением. Пренебрегая возможным движением поршня вверх и вниз, мы найдем, что горизонтальному движению соответствует кинетическая энергия 1/2m2v22x. Но точно так же, исходя из равновесия на другой стороне, можно показать, что кинетическая энергия поршня должна быть равна 1/2т1v21x. Хотя мы повторяем предыдущее рассуждение, возникают некоторые дополнительные трудности в связи с тем, что в результате столкновений средние кинетические энергии поршня и молекулы газа сравниваются, потому что поршень находится не внутри газа, а смещен в одну сторону.
Если вас не удовлетворит и это доказательство, то можно придумать искусственный пример, когда равновесие обеспечивается устройством, по которому молекулы каждого газа бьют с обеих сторон. Предположим, что сквозь поршень проходит короткий стержень, на концах которого насажено по шару. Стержень может двигаться сквозь поршень без трения. По каждому из шаров со всех сторон бьют молекулы одного сорта. Пусть масса нашего устройства равна m, а массы молекул газа, как и раньше, равны m1и m2. В результате столкновений с молекулами первого сорта кинетическая энергия тела массы mравна среднему значению 1/2 mtv21(мы уже доказали это). Точно так же, столкновения с молекулами второго сорта заставляют тело иметь кинетическую энергию, равную среднему значению 1/2mzv22. Если газы находятся в тепловом равновесии, то кинетические энергии обоих шаров должны быть равны. Таким образом, результат, доказанный для случая смеси газов, можно немедленно обобщить на случай двух разных газов при одинаковой температуре.
Итак, если два газа имеют одинаковую температуру, то средние кинетические энергии молекул этих газов в системе центра масс равны.
Средняя кинетическая энергия молекул — это свойство только «температуры». А будучи свойством «температуры», а не газа, она может служить определением температуры. Средняя кинетическая энергия молекулы, таким образом, есть некоторая функция температуры. Но кто нам подскажет, по какой шкале отсчитывать температуру? Мы можем сами определить шкалу температуры так, что средняя энергия будет пропорциональна температуре. Лучше всего для этого назвать «температурой» саму среднюю энергию. Это была бы самая простая функция, но, к несчастью, эту шкалу уже выбрали иначе и вместо того, чтобы назвать энергию молекулы просто «температурой», используют постоянный множитель, связывающий среднюю энергию молекулы и градус абсолютной температуры, или градус Кельвина. Этот множитель: k=1,38·10-23 дж на каждый градус Кельвина. Таким образом, если абсолютная температура газа равна Т, то средняя кинетическая энергия молекулы равна 3/2kT (множитель 3/2 введен только для удобства, благодаря чему исчезнут множители в других формулах).
Заметим, что кинетическая энергия, связанная с составляющей движения в любом направлении, равна только 1/2kТ. Три независимых направления движения доводят ее до 3/2kT.
§ 5. Закон идеального газа
Теперь можно подставить наше определение температуры в уравнение (39.9) и найти закон зависимости давления газа от температуры: произведение давления на объем равно произведению полного числа атомов на универсальную постоянную k и температуру:
PV=NkT. (39.22)
Следовательно, при одинаковых температуре, давлении и объеме число атомов строго определено — это тоже универсальная постоянная! Таким образом, из законов Ньютона следует, что в равных объемах любых газов при одинаковых температуре и давлении содержится равное число молекул. Вот какой неожиданный вывод!
На практике, когда имеешь дело с молекулами, приходится оперировать большими числами, поэтому химики произвольно выбрали число, очень большое число, и придумали ему специальное название. Они назвали его моль. Моль — это очень искусственное число. Почему химики не приняли за единицу 1024, чтобы вышло круглое число,— это вопрос исторический.
Случилось так, что они для удобства выбрали стандартное число N0=6,02·1023 объектов и назвали это число молем объектов. После этого, вместо того чтобы измерять число молекул в штуках, они измеряют их в молях. Можно написать число молей (выражая их через N0) и умножить его на число атомов в моле, потом умножить на kT, а затем, если захотим, выделить произведение числа атомов в моле на k, тогда получится молярное значение k; для этой величины выделим особую букву R. Молярное значение k равно 8,317 дж: R=N0k=8,317дж/молъ·°К-1. Таким образом мы нашли газовый закон, выраженный в виде произведения числа молей (его обозначают буквой N) на RT, или в виде произведения числа атомов на kT:
PV=NRT. (39.23)
Смысл тот же самый, только единицы измерения разные. В качестве единицы мы используем 1, а химики используют 6·1023!
Сделаем еще одно замечание по поводу газового закона; оно касается вещей более сложных, чем одноатомные молекулы. Пока мы имели дело только с движением одноатомного газа в центре масс. А что если при этом учесть действие сил? Рассмотрим сначала случай, когда поршень удерживается горизонтально расположенной пружинкой, на которую действует сила. Взаимная встряска атомов и поршня в каждый данный момент, конечно, не зависит от положения поршня. Условия равновесия остаются прежними. Независимо от того, где находится поршень, от него требуется только, чтобы скорость его движения была такой, чтобы он получал от молекул столько же энергии, сколько отдавал им. Наличие пружинки не меняет дела. Скорость, с которой движется поршень, в среднем та же. Таким образом, наша теорема о том, что средняя кинетическая энергия в одном направлении равна 1/2kT, справедлива независимо от того, есть силы или их нет.
Рассмотрим, например, двухатомную молекулу, составленную из атомов с массами mАи mB. Нам удалось доказать, что движение в центре масс части А и части В таково, что <1/2mAv2A>=<1/2mBv2B> = 3/2kT. Но как это может быть, если отдельные части связаны друг с другом? Хотя они и связаны между собой, но обмен энергией при взаимных вращениях, изменении расстояния и соударениях с другими молекулами зависит только от того, как быстро они движутся. Только этим определяется обмен энергией при соударениях. Сила в каждый отдельный момент не имеет никакого значения. Следовательно, даже если между отдельными частями молекулы действуют силы, верен тот же принцип.
Докажем, наконец, что газовый закон справедлив и в том случае, когда внутреннее движение не учитывается. До сих пор нам не надо было включать внутреннее движение. Мы просто рассматривали одноатомный газ. Но теперь мы покажем, что скорость центра масс любого объекта, который можно рассматривать как тело массы М, равна
1/2Mv2ц..м.=3/2kT. (39.24)
Иначе говоря, можно рассматривать как отдельные части, так и всю молекулу в целом! Посмотрим, почему это можно делать: масса двухатомной молекулы равна М=mА+mB, а скорость центра масс равна vц.м. =(mAvA+mBvB)/M. Нам нужно теперь определить <v2ц.м.>. Если возвести в квадрат vц.м., то получится
Умножив это на 1I2M и усреднив, получим
[Мы воспользовались тем, что (mA+mB)/М=1.] А чему равно <vA·vB>? (Хорошо бы, чтобы это было равно нулю!) Чтобы найти это среднее, используем наше предположение, что относительная скорость w=vA-vb не предпочитает какое-то одно определенное направление остальным, т. е. средняя составляющая вдоль любого направления равна нулю. Мы предполагаем, следовательно, что
<w·vц.м.>=0.
Но что такое w·vц.м.? Это скалярное произведение, равное
Далее, поскольку <,mAv2A>= <mBv2B>, то первый и последний члены взаимно уничтожаются, и мы получаем
(mB-mA)<vA·vB>=0.
Итак, если mА№mB, то <va·vв>=0, а это означает, что жесткому движению всей молекулы, рассматриваемой как одна частица массы М, соответствует средняя кинетическая энергия, равная 3/2kT.
Одновременно мы доказали, что средняя кинетическая энергия внутреннего движения двухатомной молекулы, если не учитывать движения центра масс, равна 3/2kT! Ведь полная кинетическая энергия отдельных частей молекулы равна 1/2mAv2A+1/2mBv2B, а среднее ее значение — это 3/2kT+3/2kT, или 3kT. Кинетическая энергия движения центра масс равна 3/2kT, так что средняя кинетическая энергия вращательного и колебательного движений двух атомов внутри молекулы — это разность этих величин, 3/zkT.
Теорема о средней энергии центра масс — это весьма общая теорема: для каждого объекта, рассматриваемого как единое целое, независимо от того, действуют на этот объект силы или нет, средняя кинетическая энергия каждого независимого движения равна 1l2kT. Эти «независимые направления движения» иногда называют степенями свободы системы. Число степеней свободы молекулы, составленной из rатомов, равно 3r, потому что для определения положения каждого атома нужны три координаты. Полную кинетическую энергию молекулы можно представить либо как сумму кинетических энергий отдельных атомов, либо как сумму кинетической энергии движения Центра масс и кинетической энергии внутренних движений. Последнюю иногда можно представить как сумму кинетической энергии вращений и кинетической энергии колебаний, но это можно сделать только приближенно. Наша теорема, если применить ее к r-атомной молекуле, гласит, что средняя кинетическая энергия молекулы равна 3/2rkT дж, из которых 3/2kT — кинетическая энергия движения молекулы как целого, а остаток 3/2(r-1)kT — это внутренняя кинетическая энергия вращений и колебаний.
* Стоградусная шкала— это шкала Кельвина, в которой за нуль принята температура 273,16°, так что T=273,16+стоградусная температура.
** То, что химики называют молекулярным весом, есть не что иное, как масса моля молекул в граммах. Моль определяется так, что масса моля атомов изотопа углерода 12 (ядра которого состоят из 6 протонов и 6 нейтронов) равна в точности 12 г.
* Этот аргумент, который приводил еще Максвелл, несколько коварен. Хотя окончательный вывод и справедлив, но он не следует непосредственно из соображений симметрии, которыми мы пользовались раньше. Ведь перейдя к движущейся через газ системе отсчета, мы можем обнаружить искаженное распределение скоростей. Мы не смогли найти простого доказательства этого результата.
Глава 40 ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
§ 1. Экспоненциальная атмосфера
§ 2. Закон Больцмана
§ 3. Испарение жидкости
§ 4. Распределение молекул по скоростям
§ 5. Удельные теплоемкости газов
§ 6. Поражение классической физики
§ 1. Экспоненциальная атмосфера
Мы уже изучали некоторые свойства большого числа сталкивающихся атомов. Наука, которая занимается этим, называется кинетической теорией, и она описывает свойства вещества, рассматривая, как сталкиваются атомы. Мы утверждаем, что все свойства вещества в целом можно объяснить, рассматривая движение отдельных его частей.
Пока мы ограничимся случаем теплового равновесия, т. е. всего лишь подклассом всех явлений природы. Законы механики, применяемые в условиях теплового равновесия, получили название статистической механики, и в этой главе вы немного познакомитесь с некоторыми основными теоремами этой науки.
Одна теорема статистической механики вам уже известна. Согласно этой теореме, для любого движения при абсолютной температуре Т средняя кинетическая энергия каждого независимого движения (каждой степени свободы) равна 1/2kT. После этого нам становится кое-что известно о среднем квадрате скорости атомов. Теперь нам необходимо узнать чуть побольше о координатах атомов, чтобы выяснить, много ли их находится при тепловом равновесии в той или иной точке пространства, а также немного подробнее изучить распределение атомов по скоростям. Хотя мы знаем, чему равен средний квадрат скорости, мы все же не можем ответить на вопрос, сколько атомов обладают скоростью, в три раза большей, чем корень из среднего квадрата скорости, или скоростью, равной одной четверти корня из среднего квадрата скорости. А вдруг все атомы имеют одинаковую скорость?
Итак, вот два вопроса, на которые мы попытаемся дать ответ: 1) Как атомы располагаются в пространстве, когда на них действуют силы? 2) Каково распределение атомов по скоростям?
Заметим, что это два совершенно независимых вопроса и что распределение по скоростям всегда одинаково. Этого можно было ожидать после того, как мы выяснили, что средняя кинетическая энергия степени свободы всегда равна 1/2kT, независимо от того, какие силы действуют на молекулы. Распределение по скоростям молекул не зависит от сил, потому что силы не влияют на частоту столкновений.
Давайте начнем с примера распределения молекул в атмосфере, подобной той, в которой мы живем, но без ветра или других каких-либо возмущений.
Предположим, что мы имеем дело с довольно высоким столбом газа, находящегося в тепловом равновесии (не так, как в настоящей атмосфере; в ней, как известно, по мере подъема вверх становится холоднее). Укажем здесь, что нарушение равновесия в случае разницы температур на разных высотах можно продемонстрировать, поместив в столб газа металлический стержень так, что его концы соприкасаются с маленькими шариками (фиг. 40.1).
Фиг. 40. 1. Равновесие в атмосфере с постоянной температурой.
Давление на высоте h должно превосходить давление на высоте h+dh на вес заключенного между этими уровнями газа. Стержень и шарики выравнивают температуру.
Нижние шарики, получая от молекул газа энергию l/2kT, передают ее через стержень верхним шарикам и встряхивают их; верхние шарики в свою очередь будут встряхивать соприкасающиеся с ними наверху молекулы. В конце концов, конечно, температура на разных высотах гравитационного поля станет одинаковой.
Нам предстоит найти закон, по которому происходит разрежение атмосферы по мере подъема вверх, когда температура на всех высотах одинакова. Если N — полное число молекул в объеме V газа с давлением Р, то PV=NkT, или Р=nkT, где n — число молекул в единичном объеме. Иначе говоря, если известно число молекул в единичном объеме, то известно и давление, и наоборот: давление и плотность пропорциональны друг другу, ведь температура в нашем случае постоянна. Но давление не может быть постоянным: с уменьшением высоты оно должно возрастать, потому что нижнему слою приходится, так сказать, выдерживать вес всех расположенных сверху атомов. Теперь можно определить, как давление меняется с высотой. Если на высоте h выделить площадку единичной площади, то на эту площадку снизу будет действовать сила, равная давлению Р. Если бы не было силы тяжести, то на площадку на высоте h+dh действовала бы сверху вниз точно такая же сила. Но в нашем случае это не так: действующая снизу сила должна превосходить силу, действующую сверху, на величину, равную весу газа, заключенного между слоями h и h+dh. На каждую молекулу действует сила тяжести mg, где g — ускорение силы тяжести. В интересующем нас слое находится ndh молекул. Это приводит к такому дифференциальному уравнению: Ph+dh-Ph=dP=-mgndh. Поскольку Р=nkT, а Т—постоянная, то можно избавиться или от Р, или от n. Исключим из уравнений Р; тогда получим
Это дифференциальное уравнение говорит нам, как убывает плотность по мере увеличения высоты.
Мы располагаем теперь дифференциальным уравнением для плотности частиц n, которая меняется с высотой, но меняется так, что производная плотности пропорциональна себе самой. Функция, производная которой пропорциональна себе самой,— это экспоненциальная функция и, значит, решение дифференциального уравнения имеет вид
n=n0e-mgh/kT. (40.1)
Здесь постоянная интегрирования n0— плотность на высоте h=0 (которую можно задать произвольно); с высотой плотность экспоненциально убывает.
Заметим, что если имеется несколько сортов молекул с разными массами, то число их убывает по разным экспонентам. Число более тяжелых молекул убывает с высотой быстрее, чем число легких молекул. Поэтому можно ожидать, что раз кислород тяжелее азота, то по мере подъема вверх относительное содержание азота в атмосфере (смеси азота и кислорода) будет возрастать. В нашей атмосфере, во всяком случае на доступных высотах, этого фактически не происходит, ибо вследствие воздушных возмущений газы вновь перемешиваются.
Ведь это же не изотермическая атмосфера. Тем не менее на больших высотах преобладают очень легкие газы, например водород, так как молекулы легких газов способны забраться на такую высоту, где все остальные экспоненты уже вымрут (фиг. 40.2).
Фиг. 40.2. Нормированная плотность как функция высоты в гравитационном поле Земли для кислорода и водорода при постоянной температуре.
§ 2. Закон Болъцмаиа
Отметим здесь тот факт, что числитель показателя экспоненты в равенстве (40.1) — это потенциальная энергия, атома. Поэтому можно в нашем случае сформулировать закон следующим образом: плотность в каждой точке пропорциональна
e-п.э./kT
где п.э. — потенциальная энергия отдельного атома.
Возможно, что это случайность и этот закон справедлив только в частном случае однородного гравитационного поля. Однако можно показать, что это весьма общее утверждение. Предположим, что на молекулы газа действуют какие-то иные, не гравитационные, силы. Например, молекулы обладают электрическим зарядом, а тогда они реагируют на электрическое поле или на другой заряд, притягивающий их. А может быть, в результате взаимного притяжения атомов друг к другу или к стенкам, или к какому-нибудь твердому телу, или еще к чему-то существуют какие-то силы притяжения, которые зависят от взаимного расположения молекул и действуют на все молекулы. Предположим теперь для простоты, что все молекулы одинаковы и что сила действует на каждую отдельиую молекулу, так что полная сила, действующая на произвольно выделяемую часть газа, равна просто произведению числа молекул на силу, действующую на одну молекулу. Дело совсем упростится, если выбрать систему координат так, что сила F будет действовать вдоль оси х.
Так же, как и раньше, рассечем газ двумя параллельными плоскостями, промежуток между которыми равен dx. Тогда сила, действующая на каждый атом, умноженная на число атомов в 1 см3(обобщение прежнего nmg) и умноженная на dx, должна сбалансировать изменение давления: Fndx=dP=kTdn. Или, придав этому закону другую форму, которая пригодится позднее, запишем:
F=(kTd/dx)lnn (40.2)
Теперь заметим, что —Fdx — это работа, которую надо совершить для переноса молекулы из х в х+dx, и если сила F произошла из потенциала, т. е. работу можно описывать с помощью потенциальной энергии, то нужную нам величину можно считать изменением потенциальной энергии (п. э.). Отрицательное изменение потенциальной энергии — это произведенная работа Fdx, так что d(lnn)=-d(п. э.)/kT, или после интегрирования
n=(постоянная) е-п.э/kT. (40.3)
Таким образом, то, что нам удалось заметить в частном случае, справедливо вообще. (А что если F не происходит из потенциала? Тогда (40.2) просто-напросто не имеет решения. В этом случае, после того как какой-нибудь атом опишет замкнутый путь, вдоль которого полная работа не равна нулю, энергия либо прибавится, либо убавится и равновесие никогда не установится. Температурное равновесие невозможно, если внешние силы, действующие на газ, не консервативны.) Уравнение (40.3) известно под названием закона Болъцмана. Это еще один из принципов статистической механики: вероятность найти молекулу в заданной точке заданной пространственной конфигурации изменяется экспоненциально, причем показатель экспоненты состоит из потенциальной энергии в заданной пространственной конфигурации, взятой с обратным знаком и деленной на kT.
Таким образом, мы знаем кое-что о распределении молекул. Предположим, что в нашем распоряжении имеется плавающий в жидкости положительный ион; он притягивает окружающие его отрицательные ионы. Много ли их окажется на разных расстояниях от положительного иона? Если нам известно, как зависит от расстояния потенциальная энергия, то отношение чисел ионов на разных расстояниях определяется полученным нами законом. Этому закону можно найти еще много других применений.
§ 3. Испарение жидкости
В менее элементарной статистической механике пытаются решить следующую важную задачу. Предположим, что имеется совокупность притягивающихся друг к другу молекул и сила между любыми двумя молекулами, скажем i-й и j-й, зависит только от расстояния между ними rijи может быть представлена в виде производной от потенциальной энергии V(rij). На фиг. 40.3 показан возможный вид такой функции.
Фиг. 40. 3. Кривая потенциальной энергии для двух молекул. Потенциальная энергия зависит только от расстояний.
Если r>r0, то при сближении молекул энергия уменьшается, поэтому молекулы притягиваются; если же молекулы сближаются еще теснее, энергия очень резко возрастает, значит, на малых расстояниях молекулы сильно отталкиваются. Таково в общих чертах поведение молекул.
Предположим теперь, что мы заполнили этими молекулами какой-то ящик и хотим знать, как они там уместятся в среднем. На это даст ответ выражение ехр(-п. э./kT). В этом случае полная потенциальная энергия, если предположить, что молекулы взаимодействуют только попарно, равна сумме всех парных энергий (в более сложных случаях могут встретиться и тройные силы, но электрические силы, например, парные). Поэтому вероятность того, что молекулы образуют конфигурацию, характеризуемую заданными комбинациями расстояний rij, пропорциональна
Если температура очень высока, так что kT>>|V(r0)|, то экспонента почти всюду мала, и вероятность найти молекулу в том или ином месте почти не зависит от расстояния до других молекул, Рассмотрим случай двух молекул; в этом случае ехр (—п.э./kT) будет вероятностью найти молекулы на расстоянии rдруг от друга. Ясно, что вероятность максимальна тогда, когда потенциал наиболее отрицателен, а когда потенциал стремится к бесконечности, вероятность почти равна нулю (это происходит на очень малых расстояниях). Это означает, что у атомов газа нет шансов столкнуться друг с другом, уж очень сильно они отталкиваются. Но очень велики шансы найти эти молекулы (если отнести вероятность к единичному объему) вблизи точки r0. Здесь вероятность больше, чем в других точках, но насколько больше — это зависит от температуры. Если температура очень велика по сравнению с разностью энергий в точках r=r0и r=Ґ, то экспонента всегда почти равна единице. Это случай, когда средняя кинетическая энергия (она порядка kT) значительно превосходит потенциальную энергию. Силы тогда мало что значат. Но с падением температуры вероятность найти молекулы на расстоянии, близком к r0, резко возрастает по сравнению с вероятностью найти молекулы в любом другом месте; и в самом деле, если kT много меньше |V(r0)|, то около r0экспонента имеет довольно большой положительный показатель. Другими словами, при заданном объеме молекулы предпочитают быть на расстоянии минимальной энергии, а не очень далеко друг от друга. По мере падения температуры атомы сближаются, сбиваются в кучу, объединяются в жидкости, в твердые тела и молекулы, а если их подогреть, то они испаряются.
Если бывает необходимо точно описать, как происходит испарение, или вообще уточнить, как молекулы ведут себя в данных обстоятельствах, то поступать следует так. Прежде всего нужно как можно точнее узнать закон взаимодействия молекул V(r). Как это сделать — безразлично: можно вычислить потенциал с помощью квантовой механики или установить закон взаимодействия экспериментально. Но если даже закон взаимодействия молекул известен, нужно все же учесть, что дело идет о миллионах молекул и нам еще придется хватить горя при изучении функции ехр(—SVij/kT). Все же удивительно, что функция так проста и все как будто ясно, поскольку известен точный потенциал взаимодействия, а дело это оказывается невероятно сложным: трудность заключается в ужасающе большом числе переменных.
Но вопрос захватывающе интересен. Это один из примеров того, что называют «задачей многих тел», и он содержит много поистине увлекательных вещей. Одна-единственная формула, которую мы получим, решив задачу, должна содержать все детали, например переход газа в твердое состояние или возможные кристаллические строения твердого тела. Многие пытались ее сосчитать, но математические трудности уж очень велики, и дело не в трудности вывода общего закона, а просто в том, чтобы справиться с огромным числом переменных.
Вот и все, что касается распределения частиц в пространстве. На этом, собственно, и кончается классическая статистическая механика, ибо если нам известны силы, то в принципе мы можем найти пространственное распределение, а распределение скоростей находится сразу на все случаи жизни, оно не будет меняться от случая к случаю. Основная задача состоит в получении более конкретной информации из нашего формального решения: это и является основным занятием классической статистической механики.
§ 4. Распределение молекул по скоростям
Обсудим теперь распределение молекул по скоростям, потому что интересно, а иногда и полезно знать, какая часть молекул движется с той или иной скоростью. Чтобы выяснить это, можно использовать те знания, которые мы приобрели, когда изучали распределение газа в атмосфере. Мы считаем газ идеальным; мы предполагали это, пренебрегая взаимным притяжением атомов при расчете потенциальной энергии. В наш первый пример мы включили лишь потенциальную энергию силы тяжести. Если бы между атомами существовали взаимные силы, то нам, конечно, пришлось бы написать что-нибудь более сложное. Но мы по-прежнему будем предполагать, что между атомами никаких сил нет, и на момент даже забудем о столкновениях; потом мы попытаемся найти этому оправдание. Мы видим, что на высоте h находится гораздо меньше молекул, чем на высоте 0 (фиг. 40.4); согласно формуле (40.1), число их экспоненциально убывает с высотой.
Фиг. 40.4. Высоты h достигают только те молекулы, скорость которых на высоте h=0 достаточно велика.
Но почему же на большей высоте меньше молекул? Разве не все молекулы, живущие на высоте 0, появляются на высоте h? Нет! Потому что на высоте 0 есть молекулы, движущиеся слишком медленно, и они не способны взобраться на потенциальную гору до высоты h. Вот и ключ к решению задачи о распределении молекул по скоростям; ведь, зная равенство (40.1), мы знаем число молекул, скорость которых слишком мала для достижения высоты h. Их ровно столько, чтобы создать нужное падение плотности при увеличении h.
Давайте сформулируем все поточнее: подсчитаем, сколько молекул проходит снизу вверх через плоскость h=0 (называя заданный уровень нулевой высотой, мы вовсе не считаем, что здесь пол, просто это удобнее нам для начала отсчета, и на отрицательной высоте может находиться газ). Эти молекулы газа движутся во всех направлениях, и некоторые из них проходят через нашу плоскость; таким образом, в любой момент сквозь плоскость снизу вверх проходит известное число молекул в секунду с заданной скоростью. Затем отметим следующее: если через uобозначить скорость, необходимую для того, чтобы подняться на высоту h (кинетическая энергия mu2/2=mgh), то число молекул в секунду, поднимающихся с нижней плоскости строго вверх и имеющих составляющую скорости, большую чем u, в точности равно числу молекул, пересекающих верхнюю плоскость с любой вертикальной составляющей скорости. Те молекулы, вертикальная скорость которых не превышает и, не
достигают верхней плоскости. Таким образом,
Но число молекул, пересекающих h с любой скоростью, большей нуля, меньше числа молекул, пересекающих нижний уровень с любой скоростью, большей нуля, хотя бы потому, что внизу больше атомов. Вот и все, что нам нужно. Мы уже знаем, что распределение молекул по скоростям на всех высотах одинаково, ведь мы уже выяснили, что температура во всей атмосфере одинакова. Но поскольку распределение скоростей всюду одинаково и число атомов, пересекающих нижний уровень, больше, то ясно, что отношение n>0(h) (числа атомов, пересекающих высоту h с положительной скоростью) и n>0(0) (числа атомов, пересекающих с положительной скоростью высоту 0) равно отношению плотностей на этих высотах, т. е. ехр(—mgh/kT). Но n>0(h)=h>u(0), поэтому
поскольку 1/2mu2=mgh. Теперь скажем это своими словами: число молекул, пересекающих за 1 сек единичную площадь
на высоте 0 с вертикальной составляющей скорости, превышающей и, равно произведению числа молекул, пересекающих эту площадку со скоростью, большей нуля, на ехр(-mu2/2kT).
Это верно не только для произвольной высоты 0, но и для любой другой высоты, поэтому распределение по скоростям одинаково повсюду! (Окончательный результат не включает высоты h, она появляется только в промежуточных рассуждениях.) Это общая теорема о распределении по скоростям. В ней утверждается, что если в столбе газа просверлить крохотную дырочку, ну совсем малюсенькую, так что столкновения там будут редки и длина пробега молекул между столкновениями будет много больше диаметра дырочки, то молекулы будут вылетать из нее с разными скоростями, но доля частиц, вылетающих со скоростью, превышающей и, равна ехр(-mu2/2kT).
Теперь вернемся к вопросу о том, можно ли пренебрегать столкновениями. Почему это не имеет значения? Мы могли бы повторить все наши доводы, используя не конечную высоту h, а бесконечно малую высоту h, столь малую, что для столкновений между высотами 0 и h было бы слишком мало места. Но это не обязательно: наши доводы, очевидно, основаны лишь на анализе значений энергий и на сохранении энергии; при столкновениях же происходит обмен энергиями среди молекул. Но нам довольно безразлично, следим ли мы за одной и той же молекулой, раз происходит лишь обмен энергиями с другой молекулой. И получается, что если мы даже сделаем это достаточно тщательно (а такую работу тщательно проделать, конечно, труднее), то результат будет тот же.
Интересно, что найденное нами распределение по скоростям имеет вид
n>u~e-к.э./kT. (40.4)
Этот способ описания распределения по скоростям —когда подсчитывается число молекул, проходящих через выделенную площадку с заданной минимальной z-составляющей скорости,— отнюдь не самый удобный. Например, чаще хотят знать, сколько молекул в заданном объеме газа движется, имея z-составляющую скорости между двумя заданными значениями, а это, конечно, из (40.4) сразу не получишь. Поэтому придадим нашей формуле удобную форму, хотя то, что мы получили, — это весьма общий результат. Заметим, что невозможно утверждать, что любая молекула в точности обладает той или иной наперед заданной скоростью; ни одна из них не движется со скоростью, в точности равной 1,7962899173 м/сек. Итак, чтобы придать нашему утверждению какой-то смысл, мы должны спросить, сколько молекул можно найти в заданном интервале скоростей. Нам придется говорить о том, как часто встречаются скорости в интервале между 1,796 и 1,797 и т. п. Выражаясь математически, пусть f(u)du будет долей всех молекул, чьи скорости заключены в промежутке u и u+du, или, что то же самое (если du бесконечно мало), долей всех молекул, имеющих скорость и с точностью до du. На фиг. 40.5 представлена возможная форма функции f(u), а заштрихованная часть ширины du и средней высоты f(u) — это доля молекул f(u)du. Таким образом, отношение площади заштрихованного участка ко всей площади под кривой равно относительному числу молекул со скоростью и внутри отрезка du.
Фиг. 40.5. Функция, распределения скоростей.
Заштрихованная площадь равна f(u)du — это относительное число частиц, скорости которых заключены внутри отрезка du около точки u.
Если определить f(u) так, что относительное число молекул будет просто равно площади заштрихованного участка, то полная площадь под кривой — это все 100% молекул, т. е.
Теперь остается только найти это распределение, сравнив его с результатом доказанной ранее теоремы. Сначала надо выяснить, как выразить через f(u) число молекул, проходящих за 1 сек через заданную площадку со скоростью, превышающей u?
Это число не равно интегралу (хотя это первое, что приходит в голову), ведь нас интересует число молекул, проходящих через площадку за секунду. Более быстрые молекулы будут пересекать площадку, так сказать, чаще, чем более медленные, поэтому, чтобы найти число проходящих молекул, надо умножить плотность молекул на скорость. (Мы уже обсуждали это в предыдущей главе, когда подсчитывали число столкновений.)
Полное число молекул, проходящих через поверхность за время t, равно числу молекул, способных достигнуть поверхности, а это молекулы, проходящие к поверхности с расстояния ut. Таким образом, число молекул, достигающих площадки, определяется не просто числом молекул, движущихся с данной скоростью, а равно этому числу, отнесенному к единице объема, и умноженному на расстояние, которое они пройдут, прежде чем достигнут площадки, сквозь которую они, по-видимому, должны пройти, а это расстояние пропорционально и. Значит, нам предстоит вычислить интеграл от произведения и на f(u)du, взятый от и до бесконечности, причем мы уже знаем, что этот интеграл обязательно должен быть пропорционален ехр(-mu2/2kT), а постоянную пропорциональности еще надо определить:
Если теперь продифференцировать интеграл по и, то мы получим подынтегральное выражение (со знаком минус, потому что и — это нижний предел интегрирования), а дифференцируя правую часть равенства, мы получим произведение и на экспоненту (и на некоторую постоянную). Сократим в обеих частях и, и тогда
Мы оставили в обеих частях равенства du, чтобы помнить, что это распределение; оно говорит нам об относительном числе молекул, имеющих скорость между u и u+du.
Постоянная С должна определиться из условия равенства интеграла единице в согласии с уравнением (40.5). Можно доказать, что
Используя это обстоятельство, легко найти С=Ц(m/2pkT).
Поскольку скорость и импульс пропорциональны, можно утверждать, что распределение молекул по импульсам, отнесенное к единице импульсной шкалы, также пропорционально ехр(-к.э./kT). Оказывается, что эта теорема верна также в теории относительности, если только формулировать ее в терминах импульсов, тогда как в терминах скоростей это уже не так; поэтому сформулируем все в терминах импульсов:
f(p)dp=ce-к.э./kTdp. (40.8)
Это значит, что мы установили, что вероятности, определяемые энергиями разного происхождения (и кинетической и потенциальной), в обоих случаях выражаются одинаково: ехр(-энергия/kT); таким образом, наша замечательная теорема приобрела форму, весьма удобную для запоминания.
Однако пока мы говорили только о «вертикальном» распределении скоростей. Но мы можем спросить, какова вероятность того, что молекула движется в другую сторону? Конечно, эти распределения связаны друг с другом и можно получить полное распределение, исходя из какого-то одного, ведь полное распределение зависит только от квадрата величины скорости, а не от ее z-составляющей. Распределение по скоростям не должно зависеть от направления и определяться только функцией u2 — вероятностью величины скорости. Нам известно распределение z-составляющей, и мы хотим получить отсюда распределение других составляющих. В результате полное распределение по-прежнему пропорционально ехр(-к.э./kT), только теперь кинетическая энергия состоит из трех частей: mv2x/2, mv2y/2 и mv2z/2, суммируемых в показателе экспоненты. А можно записать это и в виде произведения:
f(vx,, vy, vz) dvx dvy dvz~
Вы можете убедиться в том, что эта формула верна, ибо, во-первых, распределение зависит только от v2 и, во-вторых, вероятности данных vгполучаются после интегрирования по всем vxи vyи это должно привести к (40.7). Но обоим этим требованиям удовлетворяет только функция (40.9).
§ 5. Удельные теплоемкости газов
Посмотрим теперь, как можно проверить теорию и оценить, насколько хороша классическая теория газов. Мы уже говорили, что если U—внутренняя энергия N молекул, то формула pV=NkT=(g-1)U иногда и для некоторых газов может оказаться правильной. Мы знаем, что для одноатомного газа правая часть равна 2/3 кинетической энергии движения центров масс атомов. В случае одноатомного газа кинетическая энергия равна внутренней энергии, поэтому g-1 == 2/з.
Но предположим, что мы столкнулись с более сложной молекулой, которая может вращаться и колебаться, и предположим (в классической механике это так), что энергии внутренних движений также пропорциональны kT. Поэтому при заданной температуре молекула, кроме кинетической энергии kT, имеет внутреннюю энергию колебания и вращения. Тогда полная энергия U включает не только кинетическую энергию, но и вращательную энергию и мы получаем другие значения у. Наилучший способ измерения g — это измерение удельной теплоемкости, характеризующей изменение энергии при изменении температуры. К этому способу мы еще вернемся, а пока предположим, что нам удалось экспериментально определить g с помощью кривой PVg , соответствующей адиабатическому сжатию.
Попробуем вычислить g для ряда частных случаев. Прежде всего для одноатомных газов полная энергия U есть не что иное, как кинетическая энергия, и в этом случае, как мы уже знаем, g равно 5/3. В качестве примера двухатомных газов рассмотрим кислород, водород, пары иода и т. д. и предположим, что двухатомный газ можно представить как собрание пар атомов, между которыми действуют силы, похожие на те, что изображены на фиг. 40.3. Можно также предположить, и оказывается, что это вполне законно, что при температурах; обычных для диатомных газов, пары атомов стремятся удалиться друг от друга на расстояние r0 (расстояние минимума потенциальной энергии). Если бы это было не так, и вероятность не очень сильно зависела от удаления от равновесной конфигурации, то мы обнаружили бы, что кислород есть смесь сравнимых количеств O2 и одиночных атомов кислорода. А мы знаем, что в кислороде присутствует очень мало одиночных атомов кислорода, а это означает, что глубина потенциальной ямы значительно больше kT, и это как раз мы и предполагали. Но раз атомы, составляющие молекулу, прочно закреплены на расстоянии r0, то нам понадобится лишь часть потенциальной кривой вблизи минимума, которую в этом случае можно приближенно заменить параболой. Параболический потенциал соответствует гармоническому осциллятору, и, в самом деле, отличной моделью молекулы кислорода могут служить два соединенных пружинкой атома.
Но чему же равна полная энергия молекулы при температуре Т? Мы знаем, что кинетическая энергия каждого из атомов равна 3/2 kT, так что кинетическая энергия обоих атомов равна 3/2kT +3/2kT. Можно распределить эту энергию иначе: тогда те же самые 3/2 плюс 3/2 будут выглядеть как кинетическая энергия центра масс (3/2), кинетическая энергия вращения (2/2) и кинетическая энергия колебаний (1/2). Известно, что на долю кинетической энергии колебаний приходится 1/2, потому что это одномерное движение, а каждой степени свободы соответствует l/2kT. Обращаясь к вращениям, мы можем выделить две оси вращения, что соответствует двум независимым движениям. Мы представляем себе атомы в виде точек, которые не могут вращаться вокруг соединяющей их линии. Но на всякий случай запомним о таком предположении, потому что если мы упремся где-то в тупик, то, может быть, здесь обнаружится корень зла. Нас должен интересовать еще и другой вопрос: чему равна потенциальная энергия колебаний, велика ли она? Средняя потенциальная энергия гармонического осциллятора равна средней кинетической энергии, т.е. также l/2kT. Полная энергия молекулы U = 7/2kT, или kT=2/7U на атом. Это означает, что g равно 9/7, а не 5/3, т. е. g=1,286. Можно сравнить эти числа с действительно измеренными значениями g, приведенными в табл. 40.1. Взгляните сначала на гелий; это одноатомный газ, и значение g очень близко к 5/3; отклонение от этого значения, вероятно, есть просто следствие экспериментальных неточностей, хотя при столь низких температурах между атомами могут появиться силы взаимодействия. Криптон и аргон — еще два одноатомных газа — также дают согласующиеся значения в пределах ошибки эксперимента.
Таблица 40.1 · ИЗМЕРЕННЫЕ ЗНАЧЕНИЯ g ДЛЯ РАЗЛИЧНЫХ ГАЗОВ
Перейдем к двухатомным газам. Тут же обнаружится, что значение gдля водорода, равное 1,404, не согласуется с теоретическим значением 1,286. Очень близкое значение дает и кислород, 1,399, но с теоретическим это снова не согласуется. Для йодистого водорода g равно просто 1,40. Начинает казаться, что мы нашли общий закон: для двухатомных молекул gравно 1,40. Но нет, поглядите дальше. Для брома мы получаем 1,32, а для иода 1,30. Поскольку 1,30 довольно близко к 1,286, то можно считать, что экспериментальное значение gдля иода согласуется с теоретическим, а кислород представляет собой исключение. Это уже неприятно. То, что верно для одной молекулы, неверно для другой, и нам, по-видимому, надо проявить хитроумие, чтобы объяснить это.
Давайте рассмотрим еще более сложные молекулы, состоящие из большого числа частей, например С2Н6 — этан. Молекула атома состоит из восьми разных атомов, и все они качаются и вращаются в самых разных комбинациях, так что полная величина внутренней энергии должна складываться из огромного числа kT, по крайней мере 12kT только для одной кинетической энергии, поэтому g-1 должно быть очень близко к нулю, a g почти в точности равно единице. И действительно, значение g для этана меньше, чем в предыдущих случаях, но 1,22— не так
уж мало, во всяком случае, больше l1/12, чему должно быть
равно g, если учесть только кинетическую энергию. Этого вообще нельзя понять!
Ну а дальше совсем плохо, ибо двухатомную молекулу нельзя рассматривать как абсолютно жесткую, даже в пределе. Даже если связь между атомами так сильна, что они не могут и пошевелиться, все равно нужно считать, что они колеблются. Колебательная энергия всегда равна kT, поскольку она не зависит от силы связи. Но если представить себе двухатомную молекулу абсолютно жесткой, остановить колебания и выбросить эту степень свободы, то мы получим U=5/2 kT и g=1,40 для двухатомных газов. Казалось бы, это подходит и для Н2, и для O2. Но вопрос по-прежнему остается открытым, потому что g и для кислорода, и для водорода зависит от температуры! На фиг. 40.6 показаны результаты нескольких измерений. Для Н2 значение g изменяется от 1,6 при
-185°С до 1,3 при 2000°С. В случае водорода изменения g еще больше, но и в случае кислорода g явно стремится возрасти при падении температуры.
Фиг. 40.6. Экспериментальные значения g как функция температуры для водорода и кислорода.
Классическая теория предсказывает не зависящее от температуры значение g=1,286.
§ 6. Поражение классической физики
Итак, приходится сказать, что мы натолкнулись на трудности. Можно соединить атомы не пружинкой, а чем-нибудь другим, но оказывается, что это только увеличит значение g. Если пустить в ход другие виды энергии, то вопреки фактам g очень приблизится к единице. Все известное нам из классической теоретической физики только ухудшает положение. Нам известно, например, что каждый атом содержит электроны, и атомные спектры обязаны своим существованием внутренним движениям электронов; каждый электрон должен иметь по крайней мере l/2kT кинетической энергии и еще кое-что из потенциальной, а когда все это складывается, то g становится еще меньше. Просто смешно. И явно что-то не так.
Первая замечательная работа по динамической теории газов была сделана Максвеллом в 1859 г. Исходя из идей, с которыми мы только что познакомились, он сумел точно объяснить очень много известных явлений, таких, как закон Бойля, теорию диффузии, вязкость газов и другие вещи, о которых мы еще будем говорить в следующей главе. Подводя итог всем этим великим достижениям, он писал: «Наконец, установив необходимое соотношение между поступательным и вращательным движением несферических частиц (он имел в виду теорему о l/2kT), мы доказали, что в системе из таких частиц не может выполняться известное соотношение между двумя теплоемкостями». Он говорит здесь о g (позднее мы увидим, что эта величина связана с двумя разными способами измерения удельной теплоемкости) и замечает, что никто не в состоянии дать верного ответа.
В прочитанной десять лет спустя лекции он сказал: «Я должен изложить Вам то, что я считаю наибольшей трудностью, стоящей перед молекулярной теорией». Это было первое указание на ложность законов классической физики, первое предчувствие того, что существует нечто, необъясненное с самого начала, ибо опыту противоречила строго доказанная теорема.
Примерно в 1890 г. Джинс заговорил вновь об этой загадке. Часто приходится слышать, что физики конца девятнадцатого столетия были уверены в том, что им известны все существенные законы природы и дело стоит лишь за тем, чтобы получить нужные числа с максимальным числом десятичных знаков. Кто-то это сказал, а остальные повторяют. Но если покопаться в физических журналах тех лет, то станет ясно, что почти каждый из них в чем-нибудь да сомневался. Джинс говорил об этой проблеме как о загадочном явлении, из которого как будто бы следует, что по мере падения температуры некоторые виды движения «замерзают».
Если бы мы могли предположить, что колебаний при низких температурах нет и возникают они только при высоких температурах, то можно было бы представить существование такого газа, у которого при очень низкой температуре колебательного движения нет совсем, так что g=1,40, а при высоких температурах возникают колебания и, следовательно, g убывает. То же самое можно предположить и о вращениях. Если бы можно было избавиться от вращений, скажем, «заморозить» их, понизив достаточно температуру, то стало бы понятно, почему при низких температурах для водорода g приближается к 1,66. Но как же понять все это? Конечно, оставаясь в рамках классической механики, «замерзающих» движений нельзя объяснить. Все стало на свои места лишь после открытия квантовой механики.
Мы сформулируем без доказательства основные результаты статистической механики, построенной на основе квантовой механики. Напомним, что, согласно квантовой механике, связанная потенциалом система, например осциллятор, имеет дискретный набор уровней энергии, т. е. состояний с различной энергией. Возникает вопрос: как модифицировать статистическую механику, чтобы привести ее в согласие с квантовой механикой? Обратите внимание на интересную деталь: хотя большинство задач квантовой механики сложнее соответствующих задач классической физики, проблемы статистической механики решаются с помощью квантовой теории много проще!
Простенький результат классической механики, что n= n0ехр(-энергия/kT), становится в квантовой теории весьма важной теоремой: если набор молекулярных состояний характеризуется энергиями Е0, Е1, e2, ..., Еi, ..., то в случае теплового равновесия вероятность найти молекулу в состоянии с энергией Еiпропорциональна ехр(-Ei/kT). Так определяется вероятность пребывания в различных состояниях. Иначе говоря, относительный шанс — вероятность нахождения в состоянии Е1по сравнению с вероятностью нахождения в состоянии Е0равен
это, конечно, то же самое, что и
потому что Р1=n1/N, а Р0=n0/N. Таким образом, состояния с большей энергией менее вероятны, чем состояние с меньшей энергией. Отношение числа атомов в верхнем состоянии к числу атомов в нижнем состоянии равно е в степени (разность энергий, деленная на kT,с обратным знаком) — очень простая теорема.
Обратим внимание на то, что уровни энергии гармонического осциллятора отстоят друг от друга на равных расстояниях. Припишем низшему уровню энергию Е0=0 (на самом деле эта энергия немного отличается от нуля, но сдвиг всех уровней на одну и ту же величину не имеет значения), тогда энергия следующего уровня E1=hw, затем следует 2hw, 3hw) и т. д.
А теперь посмотрим, что из этого получится. Предположим, что мы изучаем колебания двухатомной молекулы, которую можно сейчас считать гармоническим осциллятором. Каковы относительные шансы найти молекулу в состоянии Е1, а не в состоянии Е0? Ответ: Отношение шанса найти молекулу в состоянии Е1 к шансу найти эту молекулу в состоянии Е0равно ехр(-hw/kT}. Предположим, что kT много меньше hw, т. е. мы находимся в области низких температур. Тогда вероятность обнаружить состояние e1чрезвычайно мала. Практически все молекулы находятся в состоянии Е0. Если изменить температуру, но по-прежнему поддерживать ее очень малой, то шанс найти молекулу в состоянии Е1=hwпо-прежнему бесконечно мал — энергия осциллятора все еще почти равна нулю; она не изменяется с температурой, пока температура остается много меньше hw. Все осцилляторы находятся в низшем состоянии, их движение эффективно «заморожено», и они не дают вклада в теплоемкость. С помощью данных табл. 40.1 можно установить, что при 100°С, а это равно 373˚К (абсолютной температуры), kT много меньше колебательной энергии молекул кислорода и водорода, но сравнимо с колебательной энергией иода. Причина такой разницы в том, что атомы иода гораздо тяжелее атомов водорода и, хотя силы, действующие менаду атомами иода и водорода, сравнимы, молекула иода столь тяжела, что собственная частота ее колебаний чрезвычайно мала по сравнению с собственной частотой водорода. При комнатной температуре kT таково, что hwводорода больше kT, а hw иода — меньше. Поэтому классическую колебательную энергию можно обнаружить только у иода.
Если увеличивать температуру газа, начав с очень малых значений Т, когда почти все молекулы находятся в их низшем состоянии, то появляется ощутимая вероятность найти молекулу во втором состоянии, затем в следующем за ним и т. д. Когда много состояний получают заметную вероятность, газ ведет себя более или менее так, как того требует классическая физика, ведь в этом случае систему квантовых состояний трудно отличить от непрерывного распределения энергии, и система может обладать почти любой энергией. Таким образом, при повышении температуры мы снова попадаем в область классической физики, как это видно из фиг. 40.6. Аналогично можно показать, что точно так же квантуются и вращательные состояния атомов, но эти состояния размещены так тесно, что обычно kT больше расстояния между уровнями. В этом случае возбуждено сразу много уровней и вращательная кинетическая энергия системы ведет себя классически. Лишь водород при комнатных температурах ведет себя иначе.
Это первый случай, когда из сравнения с экспериментом обнаружилось, что с классической физикой что-то неблагополучно, мы искали способы уладить все трудности в квантовой механике тем самым путем, каким это происходило на самом деле. Прошло примерно лет 30 или 40, пока не была обнаружена еще одна трудность, и снова в статистической механике, но на этот раз в механике фотонного газа. Новая задача была решена Планком в первые годы нашего столетия.
* Чтобы вычислить этот интеграл, положим
Тогда
а это двойной интеграл в xy-плоскости. Но его можно вычислить и в полярных координатах:
Глава 41 БРОУНОВСКОЕ ДВИЖЕНИЕ
§ 1. Равнораспределение энергии
§ 2. Тепловое равновесие излучения
§ 3. Равномерное распределение и квантовый осциллятор
§ 4. Случайные блуждания
§ 1. Равнораспределение энергии
Броуновское движение открыл в 1827 г. ботаник Роберт Броун. Изучая жизнь под микроскопом, он заметил, что мельчайшие частицы цветочной пыльцы пляшут в его поле зрения; в то же время он был достаточно сведущ, чтобы понимать, что перед ним не живые существа, а просто плавающие в воде соринки. Чтобы окончательно доказать, что это не живые существа, Броун разыскал обломок кварца, внутри которого была заполненная водой полость. Вода попала туда много миллионов лет назад, но и в такой воде соринки все продолжали свою пляску. Казалось, что очень мелкие частицы пляшут непрерывно. Позднее было доказано, что это один из эффектов молекулярного движения и понять его качественно можно, представив себе, что мы откуда-то издалека следим за игрой в пушбол. Мы знаем, что под большим мячом движется толпа людей и каждый толкает мяч, куда хочет. Мы не видим отдельных игроков, потому что поле очень далеко от нас, но мяч мы видим и замечаем, что перемещается он очень беспорядочно. Мы уже знаем из разобранных в предыдущих главах теорем, что средняя кинетическая энергия взвешенной в газе или жидкости маленькой частицы равна 3/2kT, даже если эта частица гораздо тяжелее молекул газа. Если она очень тяжела, то и движется она сравнительно медленно, но на самом деле оказывается, что скорость частицы не так уж мала. Конечно, заметить движение частицы не очень легко, потому что средняя кинетическая энергия 3/2kT соответствует скорости около 1 мм/сек, если диаметр частицы равен 1 —2 мк. Такое движение трудно заметить даже под микроскопом, потому что частица постоянно меняет направление своего движения и пойти в какую-нибудь определенную сторону не желает. В конце главы мы посмотрим, далеко ли она может уйти. Этот вопрос впервые был разрешен Эйнштейном в начале нашего столетия.
Между прочим, когда говорят, что средняя кинетическая энергия частицы равна 3/2 kT, то требуют, чтобы этот результат был выведен из кинетической теории, т. е. из законов Ньютона. Мы уже можем получать разные удивительные вещи с помощью кинетической теории, самое интересное — что удается получить так много из столь малого. Конечно, мы не хотим сказать, что законы Ньютона — это «малое», они на самом деле дают все необходимое для решения задачи, просто нам пришлось потрудиться совсем немного. Как же нам удалось так много получить? Просто мы постоянно исходили из очень важного предположения, что если заданная система находится при некоторой температуре в тепловом равновесии, то при той же температуре она будет в равновесии с чем угодно. Скажем, нам хочется посмотреть, как движется частица, если она сталкивается с водой.
Для этого представим, что, кроме воды и частицы, есть еще и газ, состоящий из частиц еще одного сорта —маленьких дробинок, которые, как мы предполагаем, с водой не взаимодействуют и только сильно ударяют по нашей частице. Предположим, что частица ощетинилась острыми шипами и все дробинки наталкиваются на них. Об этом воображаемом газе из дробинок при температуре Т нам известно все — это идеальный газ. Вода — дело сложное, а идеальный газ — он попроще. И вот наша частица находится в равновесии с газом из дробинок. Следовательно, среднее движение частицы должно быть таким, каким ему следует быть вследствие столкновений с атомами, потому что если бы частица двигалась относительно воды с большей скоростью, чем положено, то дробинки, отняв у частицы часть ее энергии, нагрелись бы больше, чем вода. Но ведь мы начали с равных температур и предполагаем, что если равновесие однажды наступило, то оно таким и останется; не может вдруг одна часть системы нагреться, а другая остыть.
Фиг. 41.1. Чувствительный зеркальный гальванометр и образец записи шкалы как функция времени.
Пучок света из источника L отражается от маленького зеркальца на шкале.
Это предположение справедливо и его можно доказать, используя законы механики, но доказательство очень сложно и понять его можно, только хорошо зная механику. С помощью квантовой механики доказать это гораздо легче, чем с помощью классической. Впервые эту теорему доказал Больцман, а мы, приняв, что она верна, можем утверждать, что если частица сталкивается с воображаемыми дробинками, то ее энергия равна 3/2kT. Но этой же самой энергией она должна обладать, если мы удалим дробинки и оставим частицу наедине с водой при такой же температуре. Это странная, но правильная цепь рассуждений.
Кроме движения коллоидных частиц, на которых и было впервые открыто броуновское движение, имеется еще целый ряд других явлений, и не только в лабораторных, но и в других условиях, позволяющих обнаружить броуновское движение. Если бы мы смогли соорудить чрезвычайно тонкое измерительное устройство, скажем, крохотное зеркальце, прикрепленное к тонкой кварцевой нити очень чувствительного баллистического гальванометра (фиг. 41.1), то зеркальце не стояло бы на месте, а непрерывно плясало бы, поэтому если бы мы осветили это зеркальце лучом света и проследили за отраженным пятном, то потеряли бы надежду создать совершенный измерительный инструмент, так как зеркальце все время пляшет. Почему? Потому что средняя кинетическая энергия вращения зеркальца равна ll2kT.
Чему равен средний квадратичный угол качаний зеркальца? Предположим, что мы определили период собственных колебаний зеркальца, стукнув слегка по одной его стороне и наблюдая, как долго будет оно качаться взад и вперед, и пусть нам также известен момент инерции /. Формулу для кинетической энергии вращения мы знаем, это равенство (19.8): Т =1/2Iw2. А потенциальная энергия пропорциональна квадрату угла отклонения, т. е. V = l/2aq2. Но если мы знаем период колебаний t0и можем вычислить собственную частоту w0= 2p/t0, то можно и потенциальную энергию записать в виде V=1/2/Iw20q2. Мы знаем, что средняя кинетическая энергия равна l/2 kT', но поскольку перед нами гармонический осциллятор, то средняя потенциальная энергия также равна 1/2kT. Следовательно,
Таким образом мы можем рассчитать колебания зеркальца гальванометра и тем самым найти предел точности нашего инструмента. Если нам нужно уменьшить колебания, то следует охладить зеркальце. Но здесь возникает интересный вопрос — в каком месте его охладить? Все зависит от того, откуда оно получает больше «пинков». Если в колебаниях повинна кварцевая нить, то охлаждать нужно ее верхний конец, если же зеркальце находится в газовой среде и раскачивается в основном за счет соударений с молекулами газа, то лучше охладить газ. Итак, практически, если известно, почему происходит затухание колебаний, то оказывается, что имеется всегда какой-то источник флуктуации; к этому вопросу мы еще вернемся.
Те же флуктуации работают, и довольно удивительным образом, в электрических цепях. Предположим, что мы построили очень чувствительный, точный усилитель для какой-нибудь определенной частоты и к его входу подключили резонансную цепь (фиг. 41.2), настроенную на эту же частоту, наподобие радиоприемника, только получше.
Фиг. 41,2. Резонансная цепь с большим Q.
а — реальная цепь при температуре T; б — искусственная цепь с идеальным (бесшумным) сопротивлением и «генератором шума».
Предположим, что мы захотели как можно точнее изучить флуктуации, для этого мы сняли напряжение, скажем, с индуктивности и подали его на усилитель. Конечно, во всякой цепи такого рода имеются некоторые потери. Это не идеальная резонансная цепь, но все же очень хорошая цепь, и обладает она малым сопротивлением (на схеме сопротивление показано, надо только помнить, что оно очень мало). А теперь мы хотим узнать, как велики флуктуации падения напряжения на индуктивности? Ответ: Нам известно, что «кинетическая энергия», запасенная катушкой резонансной цепи, равна 1/2LI2(см. гл. 25). Поэтому среднее значение 1/2 LI2равно 1/2kT, это дает нам среднее квадратичное значение тока, а отсюда можно определить и среднее квадратичное значение напряжения. Если мы хотим знать падение напряжения на индуктивности, нам пригодится формула , тогда средний квадрат модуля падения напряжения на индуктивности равен <V2L> = L2w20<I2>, a полагая 1/2L<I2> = 1/2kT, получаем
<V2L>=Lw20kT. ... (41.2)
Итак, теперь мы можем рассчитать контур и предсказать, каким в нем будет так называемый шум Джонсона, т. е. шум, связанный с тепловыми флуктуациями!
Но откуда же эти флуктуации берутся? А все из-за сопротивления, точнее говоря, в результате пляски электронов в сопротивлении. Ведь они находятся в тепловом равновесии с остальным материалом сопротивления, а это приводит к флуктуациям плотности электронов. Таким образом они порождают крошечные электрические поля, управляющие резонансной цепью.
Инженеры-электрики объясняют все это иначе. Физически источником шумов служит сопротивление. Однако можно заменить реальную цепь с честным сопротивлением, вызывающим шумы, фиктивной цепью, содержащей маленький генератор, который якобы порождает шумы, а сопротивление теперь будет идеальным — оно уже не шумит. Все шумы теперь исходят от фиктивного генератора. Итак, если нам известны характеристики шума, порождаемого сопротивлением, и у нас для этого имеется подходящая формула, то можно рассчитать, как цепь реагирует на этот шум. Следовательно, нам нужна формула для шумовых флуктуации. Сопротивление одинаково хорошо порождает шумы всех частот, поскольку оно само отнюдь не резонатор. Резонансная цепь, конечно, «слышит» лишь часть этого шума вблизи определенной частоты, а в сопротивлении заключено много и других частот. Силу генератора можно описать таким образом: выделяемая на сопротивлении средняя мощность, если оно непосредственно соединено с генератором шума, равна <E2>/R, где Е — снимаемое с генератора напряжение. Но теперь мы хотим знать подробнее о распределении мощности по частотам. Каждой определенной частоте соответствует очень малая мощность. Пусть P(w)dw — мощность, которую генератор посылает сопротивлению в интервале частот dw. Тогда можно доказать (мы докажем это для другого случая, но математика и там и тут одинакова), что выделяемая мощность равна
P(w)dw=2/pkTdw(41.3) я, таким образом, не зависит от сопротивления.
§ 2. Тепловое равновесие излучения
Мы приступаем к обсуждению более сложной и интересной теоремы, суть которой состоит в следующем. Предположим, что унас имеется заряженный осциллятор, вроде того, о котором мы говорили, когда речь шла о свете. Пусть это будет электрон, колеблющийся в атоме вверх и вниз. А раз он колеблется, то излучает свет. Предположим теперь, что этот осциллятор попал в сильно разреженный газ, состоящий из других атомов, и время от времени эти атомы с ним сталкиваются. Когда в конце концов наступит равновесие, осциллятор приобретает такую энергию, что кинетическая энергия колебаний будет равна l/2kT, а поскольку это гармонический осциллятор, то полная энергия движения станет равной kT.
Это, конечно, неверно, потому что осциллятор несет электрический заряд, а поскольку он обладает энергией kТ, то, качаясь вверх и вниз, он излучает свет. Поэтому невозможно получить равновесие только самого вещества без того, чтобы заряды не излучали свет, а когда свет излучается, утекает энергия, осциллятор со временем растрачивает энергию kT, а окружающий газ, сталкивающийся с осциллятором, постепенно остывает. Именно таким образом остывает за ночь натопленная с вечера печка, выпуская все тепло на воздух. Прыгающие в ее кирпичах атомы заряжены и непрерывно излучают, а в результате этого излучения танец атомов постепенно замедляется.
Но если заключить все атомы и осцилляторы в ящик, так чтобы свет не смог уйти в бесконечность, тепловое равновесие может наступить. Мы можем поместить газ в ящик, в стенках которого есть и другие излучатели, испускающие свет внутрь ящика, а еще лучше соорудить ящик с зеркальными стенками. Этот пример поможет лучше понять, что произойдет. Итак, мы предполагаем, что все излучение от осциллятора остается внутри ящика. Осциллятор и в этом случае начинает излучать, но довольно скоро он все же соберет свое значение kT кинетической энергии. Происходит это потому, что сам осциллятор будет освещаться, так сказать, собственным светом, отраженным от стенок ящика. Вскоре в ящике будет много света и, хотя осциллятор продолжает излучать, часть света будет возвращаться и возмещать осциллятору потерянную им энергию.
А теперь подсчитаем, насколько должен быть освещен ящик при температуре Т, чтобы рассеяние света на осцилляторе обеспечивало его как раз такой энергией, какая нужна для поддержания излучения. Пусть атомов в ящике совсем немного и находятся они далеко друг от друга, так что наш осциллятор идеальный, не имеющий иного трения, кроме радиационного. Теперь заметим, что при тепловом равновесии осциллятор делает сразу два дела. Во-первых, он излучает, и мы можем подсчитать энергию излучения. Во-вторых, он в возмещение получает точно такое же количество энергии в результате рассеяния на нем света. Поскольку энергия ниоткуда больше притечь не может, то эффективное излучение — это как раз та часть «общего света», которая рассеялась на осцилляторе.
Таким образом, прежде всего мы вычисляем энергию, излучаемую в 1 сек осциллятором с заданной энергией. (Мы позаимствуем для этого в гл. 32, посвященной радиационному трению, несколько равенств и не будем здесь приводить их выводы.) Отношение энергии, излученной за радиан, к энергии осциллятора называется 1/Q [см. уравнение (32.8)] : 1/Q= (dW/dt)/( w0W. Используя величину у (постоянную затухания), можно записать это в виде 1/Q=g/w0, где w0— собственная частота осциллятора, если g очень мала, a Q очень велико. Излученная за 1 сек энергия равна
Излученная за 1 сек энергия просто равна произведению g на энергию осциллятора. Средняя энергия нашего осциллятора равна kT, поэтому произведение g на kT — это среднее значение излученной за 1 сек энергии:
<dW/dt>=gkT. (41.5)
Теперь нам нужно только узнать, что такое g. Эту величину легко найти из уравнения (32.12):
где r0= e2/mc2— классический радиус электрона, и мы положили Я = 2pс/w0.
Окончательный результат для средней скорости излучения света вблизи частоты w0 таков:
Теперь надо выяснить, сильно ли должен быть освещен осциллятор. Освещение должно быть таким, чтобы поглощенная осциллятором энергия (и впоследствии рассеянная) была в точности равна предыдущей величине. Иначе говоря, излученный свет — это свет, рассеянный при освещении осциллятором в полости. Итак, нам остается рассчитать, сколько света рассеивается осциллятором, если на него падает какая-то — неизвестная — доза излучения. Пусть I(w)dw— энергия света частоты w в интервале частот dw(ведь у нас нет света точно заданной частоты; излучение распределено по спектру). Таким образом, I(w) — это спектральное распределение, которое нам надо найти. Это тот цвет огня, который мы увидим внутри печи при температуре Т, если откроем дверцу и заглянем внутрь.
Сколько же все-таки света поглотится? Мы уже определяли количество излучения, поглощаемого из заданного падающего пучка света, и выразили его через эффективное сечение. Это соответствует тому, как если бы мы предполагали, что весь свет, падающий на площадку определенной площади, поглощается. Таким образом, полная переизлученная (рассеянная) интенсивность равна произведению интенсивности падающего света I(w)dw на эффективное сечение а.
Мы вывели формулу для эффективного сечения [см. уравнение (31.19)1, не включающую затухания. Нетрудно повторить этот вывод снова и учесть трение, которым мы тогда пренебрегли. Если это сделать, то, вычисляя эффективное сечение по прежнему образцу, мы получим
Пойдем дальше; ssкак функция частоты имеет более или менее заметную величину только для w около собственной частоты w0. (Вспомним, что для излучающего осциллятора Q — порядка 108.) Когда со равна w0, осциллятор рассеивает очень сильно, а при других значениях w он почти не рассеивает совсем. Поэтому можно заменить w на w0, а w2-w20 на 2w0(w-w0); тогда
Теперь почти вся кривая загнана в область около w=w0. (Фактически мы не должны делать никаких приближений, но легче иметь дело с интегралом, в котором подынтегральное выражение несколько проще.) Если умножить интенсивность в данном интервале частот на эффективное сечение рассеяния, то получится энергия, рассеянная в интервале dw. Полная рассеянная энергия — это интеграл по всем w. Таким образом,
Теперь мы положим dWs/dt=3gkT. Но почему здесь стоит 3? Потому что в гл. 32 мы предполагали, что свет поляризован так, что может раскачивать осциллятор. Если бы мы использовали осциллятор, способный раскачиваться только в одном направлении, а свет был бы, скажем, поляризован неверно, то он не рассеивался бы совсем. Поэтому мы должны либо усреднить эффективное сечение рассеяния на осцилляторе, способном раскачиваться только в одном направлении, по всем направлениям падающих пучков и поляризации света в пучке, либо, что легче сделать, представить себе, что наш осциллятор послушно следует за полем, каким бы оно ни было там, где он находится. Такой осциллятор, который одинаково легко раскачивается в любом из трех направлений, имеет среднюю энергию 3kT, потому что у него 3 степени свободы. А раз 3 степени свободы, то надо писать 3gkT.
Займемся теперь интегралом. Предположим, что неизвестное спектральное распределение света I(w) — это плавная кривая, которая в той узкой области частот, где ss имеет острый максимум, меняется не слишком сильно (фиг. 41.3).
Фиг. 41.3. Сомножители подынтегрального выражения (41.10).
Пик — это резонансная кривая 1/[(w-w0)2+(g2/4)]. Множитель I(w) можно с хорошим приближением заменить на I(w0).
Тогда сколько-нибудь существенный вклад в интеграл дают только частоты, близкие к w0 и отстоящие от нее на очень малую величину g. Поэтому, хотя I(w) неизвестная и, может быть, сложная функция, важно только ее поведение около w=w0 и можно заменить плавную кривую еще более ровной — «постоянной» — всюду одной высоты. Иначе говоря, мы просто вынесем I(w) из-под знака интеграла и назовем это I(w0). Вынесем за интеграл и остальные постоянные и тогда получим
Интеграл берется от 0 до Ґ, но 0 отстоит так далеко от w0, что кривая за это время идет почти вдоль оси абсцисс, поэтому заменим 0 на -Ґ, разница небольшая, а интеграл взять легче.
Интеграл вида ∫dx/(x2+а2) приводит к арктангенсу. Если
взглянуть в справочник, то мы увидим, что он равен я/а. Итак, для нашего случая это 2p/g. После небольших манипуляций мы получаем
Затем мы подставим сюда формулу (41.6) для у (мы уже не будем стараться писать w0; раз это верно для любой w0, то можно назвать ее просто w), и формула для I(w) примет вид
I(w)=w2kT/p2c2. (41.13)
Она и определяет распределение света в горячей печке. Это так называемое излучение абсолютно черного тела. Черного потому, что, если заглянуть в топку печки при абсолютном нуле, она будет черной.
Формула (41.13) задает распределение энергии излучения внутри ящика при температуре Т согласно классической теории. Отметим сначала замечательную особенность этого выражения. Заряд осциллятора, масса осциллятора, все частные его свойства выпали из формулы; ведь если мы достигли равновесия с одним осциллятором, мы должны позаботиться о равновесии и с любым другим осциллятором другой массы, иначе будут неприятности. Таким образом, это важный способ проверки нашей теоремы о том, что равновесие зависит только от температуры, а не от того, что приводит к равновесию. Теперь можно начертить кривую I(w) (фиг. 41.4).
Фиг. 41.4. Распределение интенсивности излучения черного тела при двух температурах.
Сплошные кривые — согласно классической теории; пунктирные — настоящее распределение, 1— paдuo ; 2 — инфракрасное; 3 — видимое; 4 — ультрафиолетовое; 5 — рентгеновские лучи.
Она покажет нам, какова освещенность при разных частотах.
В выражение для интенсивности в ящике на единицу частоты входит, как видно, квадрат частоты; это значит, что если взять ящик при любой температуре, то в нем обнаружится бездна рентгеновских лучей!
Мы знаем, конечно, что это неверно. Когда мы открываем печку и заглядываем в нее, мы не портим глаз рентгеновскими лучами. Дальше — хуже, полная, энергия, ящика, полная интенсивность, просуммированная по всем частотам, должна быть площадью под этой уходящей в бесконечность кривой. Итак, здесь что-то совсем неверно в самой основе.
Это значит, что классическая теория совершенно непригодна для правильного описания распределения излучения черного тела, так же как и для описания теплоемкостей газов. Физики ходили вокруг этого вывода, рассматривали его с различных точек зрения и не нашли выхода. Это предсказание классической физики. Уравнение (41.13) называется законом Рэлея, предсказано оно классической физикой и до очевидности абсурдно.
§ 3. Равномерное распределение и квантовый осциллятор
Только что отмеченная трудность — это еще одна сторона проблемы непрерывности в классической физике, она началась с непорядка в теплоемкостях газов, а потом эта проблема сконцентрировалась на распределении света в черном теле. Конечно, пока теоретики обсуждали эти вещи, производились еще и измерения настоящих кривых. И было установлено, что правильная кривая выглядит так, как пунктирные кривые на фиг. 41.4. Никаких рентгеновских лучей там нет. Если понижать температуру, то кривые приближаются, к оси абсцисс примерно так, как того требует классическая теория, но и при низкой температуре опытные кривые тоже в конце обрываются.
Таким образом, начало кривой распределения правильно описывает опыт, а ее высокочастотный конец сбивается с верного пути. Почему же так? Когда Джеймс Джинс размышлял о теплоемкостях газов, он заметил, что движение, совершаемое с большой частотой, «замерзает» при понижении температуры. Значит осциллятор не может обладать средней энергией kT, если температура слишком мала или если частота колебаний слишком велика. А теперь вспомним, как мы выводили (41.13). Все зависело от энергии осциллятора при тепловом равновесии. Когда мы подставляли kT в (41.5), это было то же kT, что и в (41.13), т. е. средняя энергия гармонического осциллятора частоты w при температуре Т. Классическая физика говорит, что она равна kT, а эксперимент отвечает: Нет! При очень низких температурах или при очень высоких частотах это не так. Таким образом, кривая падает по той же причине, что и теплоемкости газов. Кривую черного тела изучать легче, чем теплоемкости газов, где много сложностей, и мы сконцентрируем внимание на определении правильной кривой излучения черного тела, потому что эта кривая будет той кривой, которая расскажет нам, как средняя энергия гармонического осциллятора при любой его частоте зависит от температуры.
За изучение этой кривой взялся Планк. Сначала он нашел чисто эмпирический ответ, сравнивая опытную кривую с известными функциями, которые лучше всего эту кривую подгоняли. Таким образом, он получил эмпирическую формулу для средней энергии гармонического осциллятора как функцию температуры. Иначе говоря, он заменил kT правильной формулой, а потом нашел простой вывод этой формулы, правда, при очень странном предположении. Это предположение состоит в том, что гармонический осциллятор может поглотить за один прием только энергию hw. После этого нельзя и подумать, что осциллятор может обладать любой энергией. Конечно, это было началом конца классической физики.
Сейчас мы выведем первую правильную формулу квантовой механики. Предположим, что дозволенные уровни энергии гармонического осциллятора лежат на равном расстоянии hw0 друг от друга, поэтому осциллятор может обладать только одной из этих энергий (фиг. 41.5).
Фиг. 41.5, Уровни энергии гармонического осциллятора.
Отстоят друг от друга но равных расстояниям En=nhw.
Аргументы Планка выглядят немного сложнее наших, ведь это было самым началом квантовой механики, и ему приходилось кое-что доказывать. Ну, а мы просто примем как факт (который Планк и установил), что вероятность того, что занят уровень энергии Е, равна Р(Е)=aехр(-E/kT). Исходя из этого, мы получим правильный результат.
Предположим, что у нас есть много осцилляторов и каждый колеблется с частотой w0. Некоторые из них находятся в низшем квантовом состоянии, другие забрались на уровень выше и т. д. Нам нужно знать среднюю энергию этих осцилляторов. Чтобы найти ее, давайте вычислим полную энергию всех осцилляторов и поделим результат на их число. Тогда мы получим среднюю энергию на осциллятор при тепловом равновесии, а это то же самое, что и энергия при равновесии с излучением черного тела, и ее надо подставить в уравнение. (41.13) вместо kT.
Пусть N0 — число осцилляторов в основном состоянии (состоянии с наименьшей энергией), N1— число осцилляторов в состоянии Е1, n2— число осцилляторов в состоянии E2и т. д. Согласно гипотезе (которую мы не доказали), классические выражения для вероятности ехр(-п. э./kT) или ехр(-к. э./kT) заменяются в квантовой механике на ехр(-DE/kT), где DE — разность энергий, Можно утверждать, что число осцилляторов в первом состоянии N1равно произведению числа молекул в основном состоянии N0на ехр(-hw/kT). Аналогично, n2(число молекул во втором состоянии) равно N2=N0exp(-2hw/kT). Чтобы упростить алгебру, введем х=ехр(-hw/kT). Тогда все выглядит очень просто:
N1=N0x, N2=N0x2 ..., Nn=N0xn.
Сначала найдем полную энергию всех осцилляторов. Если осциллятор находится в основном состоянии, его энергия нуль. Если он находится в первом состоянии, то его энергия равна hw0, а таких осцилляторов N1. Значит, в этом состоянии запасена энергия N1hw, или hwN0x. Энергия осциллятора во втором состоянии 2hw0, а осцилляторов N2, поэтому мы получаем такую энергию: N22hw=2hw0N0x2 и т. д. Сложив все это, найдем полную энергию Eполн=N0hw (0+х+2х2+Зx3+...). А сколько всего осцилляторов? В основном состоянии, конечно, N0, в первом состоянии Nlи т. д.; снова все сложим и получим Nвcе=N0(1+x+x2+x3+...). Поэтому средняя энергия равна
Читателям представляется возможность позабавиться этими суммами и получить от этого удовольствие. Когда вы покончите с суммированием и подставите в окончательный результат значение х, то получите, если не ошиблись
Эта формула была не только самой первой формулой, но и самой первой мыслью квантовой механики, и она явилась великолепным ответом на все недоумения предшествующих десятилетий. Максвелл уже понимал, что что-то неверно, но вопрос был в том, что же правильно? Здесь содержится количественный ответ — что же надо взять вместо kT. Выражение для энергии, конечно, стремится к kT при w®0 или при Т®Ґ. Попробуйте это доказать — здесь надо поступить так, как этому учит математика.
Выражение для средней энергии содержит знаменитый обрезающий множитель, который предвидел Джине, и если использовать его вместо kT в (41.13), то мы получим распределение света в черном ящике:
Итак, мы видим, что при больших w кривая резко идет вниз; хотя в числителе стоит w3, знаменатель содержит е в чрезвычайно высокой степени; на кривой нет никакого намека на подъем, и там, где мы того не ждем, не появляется ни ультрафиолетовых, ни рентгеновских лучей!
Может возникнуть недовольство в связи с тем, что при выводе (41.16) мы пользовались квантовой теорией для уровней энергии гармонического осциллятора, а при определении эффективного сечения ssмы оставались верны классической теории. Но квантовая теория взаимодействия света с гармоническим осциллятором приводит точно к тем же результатам, что и классическая. Это обстоятельство оправдывает то время, которое мы затратили на изучение показателя преломления и рассеяние света, основанное на представлении об атоме как о маленьком осцилляторе, — квантовые формулы получаются точно такими же.
Теперь вернемся к шумам Джонсона в сопротивлении. Мы уже отмечали, что теория мощности шума, по существу, — та же самая, классическая теория излучения черного тела. На самом деле, как мы уже говорили, сопротивление в цепи — это не настоящее сопротивление, а похоже скорее на антенну (антенна ведь тоже похожа на сопротивление, она излучает энергию). Это радиационное сопротивление, и легко подсчитать излучаемую им мощность. Эта мощность равна той мощности, которую антенна получает от окружающего ее света, и мы должны прийти к тому же самому распределению с точностью до одного, двух множителей. Мы можем предположить, что сопротивление — это генератор с неизвестным спектром мощности Р(w). Найти распределение поможет то обстоятельство, что этот генератор, включенный в резонансную цепь произвольной частоты (как на фиг. 41.2, б), порождает на индуктивности падение напряжения, определяемое равенством
(41.2). Это приведет нас к тому же интегралу, что и (41.10), а продолжая работать тем же методом, мы получим уравнение
(41.3). Для низких температур kT в (41.3), конечно, надо заменить выражением (41.15). Две теории (излучения черного тела и шумов Джонсона) физически тесно связаны, так как мы можем связать резонансную цепь с антенной, тогда сопротивление R будет радиационным сопротивлением в чистом виде. Поскольку (41.2) не зависит от физических свойств сопротивления, генератор G для настоящего сопротивления и для радиационного сопротивления будет одинаковым. А что же будет источником генерируемой мощности Р(w), если сопротивление R — теперь просто-напросто идеальная антенна, находящаяся в равновесии с ее окружением при температуре Т? Это излучение в пространстве при температуре Т, которое обрушивается на антенну в качестве «принятого сигнала» и служит эффективным генератором. Следовательно, двигаясь от (41.13) к (41.3), можно найти прямое соответствие между P'(w) и I(w).
Объяснение явлений, о которых мы сейчас говорим (так называемый шум Джонсона, распределение Планка и теория броуновского движения, о которой мы собираемся говорить),— это достижения первого десятилетия нашего века. Узнав об этом и заглянув в историю, вернемся к броуновскому движению.
§ 4. Случайные блуждания
Попробуем понять, насколько меняется положение танцующей частицы за время, во много раз большее, чем промежуток между двумя ударами. Посмотрим на маленькую частицу, которая вовлеклась в броуновское движение и пляшет под непрерывно и беспорядочно сыплющимися на нее ударами молекул воды. Вопрос: Далеко ли отойдет частица от первоначального положения, когда истечет заданное время? Эту задачу решили Эйнштейн и Смолуховский. Представим себе, что мы разделили выделенное нам время на малые промежутки, скажем, по одной сотой доле секунды, так что после первой сотой доли секунды частица оказалась в одном месте, в течение второй сотой секунды она продвинулась еще, в конце следующей сотой секунды — еще и т. д. При той скорости бомбардировки, которой подвергается частица, одна сотая секунды — огромное время.
Читатель легко может проверить, что число столкновений, которые испытывает одна плавающая в воде молекула, порядка 1014 в секунду, так что на одну сотую долю секунды приходится примерно 1012 столкновений, а это очень много! Естественно, что по прошествии одной сотой доли секунды частица не «помнит», что с ней было до этого. Иначе говоря, все столкновения случайны, так что каждый последующий «шаг» частицы совершенно не зависит от предыдущего. Это напоминает знаменитую задачу о пьяном моряке, который выходит из бара и делает несколько шагов, но плохо держится на ногах, и каждый шаг делает куда-то в сторону, случайно (фиг. 41.6).
Фиг. 41.6. Зигзагообразный путь из 36 случайных шагов длиной L.
Как далеко расположена точка S36 от В? В среднем на 6L.
Так где же окажется наш матрос спустя некоторое время? Конечно, мы этого не знаем! И предсказать это невозможно. Все, что можно сказать, — это то, что он где-то наверняка находится, но это совершенно неопределенно. Ну хорошо, а далеко ли он все-таки уйдет? Каково будет то среднее расстояние от бара, на котором окажется матрос? На этот вопрос мы уже ответили, потому что мы однажды уже обсуждали суперпозицию света от огромного числа различных источников с различными фазами, а это значит, что мы складывали огромное число стрелок, направленных по произвольным направлениям (см. гл. 32) Тогда мы обнаружили, что средний квадрат расстояния от одного конца цепи беспорядочных шагов до другого (т. е. интенсивность света) равен сумме интенсивностей отдельных источников. Совершенно аналогично, используя ту же математику, можно немедленно показать, что если RN— векторное расстояние от начала через N шагов, то средний квадрат расстояния от начала пропорционален числу шагов N.
Это значит, что <R2N>=NL2, где L — длина каждого шага. Поскольку число шагов пропорционально выделенному нам условиями задачи времени, то средний квадрат расстояния пропорционален времени:
<R2>=at. (41.17)
Это не означает, что среднее расстояние пропорционально времени. Если бы среднее расстояние было пропорционально времени, то частица двигалась бы с вполне определенной постоянной скоростью. Матрос, несомненно, идет вперед, но движение его таково, что квадрат среднего расстояния пропорционален времени. Это и есть характерная особенность случайных блужданий.
Мы легко докажем, что каждый шаг увеличивает квадрат расстояния в среднем на L2. Если записать RN=RN-1+L, то окажется, что R2N равно
RN·RN=R2N=R2N-I +2RN-1·L+L2,
а усредняя по многим попыткам, получим <R2N>=<R2N-1>+L2, потому что <RN-1·L>=0. Таким образом, по индукции
R2N=NL2 (41.18)
Теперь хорошо бы вычислить коэффициент a в уравнении (41.17); для этого нужно еще кое-что добавить. Предположим, что если к частице приложена сила (она не имеет никакого отношения к броуновскому движению, просто мы подыскиваем выражение для импульса), то частица будет противодействовать силе следующим образом. Прежде всего должна проявиться инерция. Пусть m— коэффициент инерции, эффективная масса частицы (не обязательно настоящая масса настоящей частицы, потому что если протаскивать частицу сквозь воду, то движется и вода). Поэтому если мы рассматриваем движение в одном направлении, то нужно обзавестись с одной стороны слагаемым m(d2x/dt2). Далее подчеркнем, что, если мы толкаем частицу равномерно, она должна тормозиться жидкостью с силой, пропорциональной скорости. Кроме инерции жидкости, существует еще сопротивление течению, вызванное вязкостью и сложным строением жидкости. Для возникновения флуктуации абсолютно необходимо существование необратимых потерь, нечто вроде сопротивления. Пока таких потерь нет, нет способа получить kT'. Причина флуктуации тесно связана с такими потерями. Мы еще обсудим, каков механизм такого трения, мы поговорим о силах, пропорциональных скорости, и выясним, откуда они берутся. А пока давайте просто предположим, что такое сопротивление существует. Тогда формула для движения под действием внешней силы, если она толкает частицу самым обычным способом, выглядит
так:
Величину m можно определить экспериментально. Например, мы можем изучить падение капли под действием силы тяжести. Тогда известно, что сила равна mg, а m — это mg, деленное на окончательно установившуюся скорость падения капли. Или можно поместить каплю в центрифугу и следить за скоростью осаждения. А если она заряжена, то можно приложить электрическое поле. Таким образом, m— это измеряемая величина, а не какая-нибудь искусственная вещь, и ее значение известно для коллоидных частиц многих типов.
Применим эту формулу также в том случае, когда сила не внешняя, а равна беспорядочным силам броуновского движения. Попробуем определить средний квадрат пройденного телом пути. Будем рассматривать расстояния не в трех, а в одном измерении и определим среднее значение х2, чтобы подготовить себя к решению задачи. (Разумеется, среднее значение х2равно среднему y2 и среднему r2, поэтому средний квадрат расстояния будет втрое больше того, что мы получим.)
Конечно, x-составляющая беспорядочной силы так же беспорядочна, как и остальные компоненты. Чему же равна скорость изменения x2? Она равна (d/dt)(x2)=2x(dx/dt), поэтому скорость изменения среднего x2? можно найти, усреднив произведение скорости на координату. Покажем, что это постоянная величина, т. е. средний квадрат радиуса возрастает пропорционально времени, и найдем скорость возрастания. Если умножить уравнение (41.19) на х, то получим mx(d2x/dt2)+ mx(dx/dt)=xFx. Нас интересует среднее по времени x(dx/dt), поэтому усредним по времени все уравнение целиком и изучим все три слагаемых. Что можно сказать о произведении х на силу? Хоть частица и добралась до точки х, последующие толчки могут быть направлены в любом направлении по отношению к х, ведь случайная сила полностью случайна и ей нет дела, откуда частица начала двигаться. Если кордината х положительна, у средней силы нет никаких оснований направиться в этом же направлении. Для нее оно столь же вероятно, как и любое другое. Случайные силы не могут отправить частицу в определенном направлении. Поэтому среднее произведения х на Fхравно нулю. С другой стороны, слагаемому mx(d2x/dt2) можно, немного повозившись, придать вид
Мы разбили первоначальное слагаемое на два и должны усреднить их оба. Посмотрим, чему же равно произведение х на скорость. Это произведение не изменяется со временем, потому что, когда частица попадает в заданную точку, она уже не помнит, где она была раньше, и характеризующие такие ситуации величины не должны зависеть от времени. Поэтому среднее значение этой величины равно нулю. У нас осталось лишь mv2, а об этой величине нам кое-что известно: среднее значение mv2/2 равно 1/2 kT. Следовательно, мы установили,
что
влечет за собой
или
Это значит, что средний квадрат радиус-вектора частицы <R2> к моменту t равен
<R2>=2kTt/m. (41.21)
Таким образом, мы и в самом деле можем выяснить, как далеко уйдут частицы! Сначала нужно изучить реакцию частицы на постоянную силу, выяснить скорость дрейфа частицы под действием известной силы (чтобы определить m), а тогда мы сможем узнать, далеко ли расползутся беспорядочно движущиеся частицы. Полученное нами уравнение имеет большую историческую ценность, потому что на нем основан один из первых способов определения постоянной k. Ведь в конце концов можно измерить величину m, и время, определить расстояние, на которое удалится частица, и получить средние значения. Почему так важно определить точное значение k? Потому что по закону PV=RT для моля можно измерить R, которое равно произведению числа атомов в моле на k. Моль когда-то определялся как столько-то граммов кислорода 16 (теперь для этой цели используют углерод), поэтому числа атомов в моле сначала не знали. Это, конечно, интересный и важный вопрос. Каковы размеры атомов? Много ли их? Таким образом, одно из самых ранних определений числа атомов свелось к определению того, далеко ли уйдут мельчайшие соринки, пока мы будем терпеливо разглядывать их в микроскоп в течение строго определенного времени. После этого можно было найти и постоянную Больцмана k, и число Авогадро N0, потому что R к этому времени было уже измерено.
Глава 42 ПРИМЕНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ
§ 1. Испарение
§ 2. Термоионная эмиссия
§ 3. Тепловая ионизация
§ 4. Химическая кинетика
§ 5. Законы излучения Эйнштейна
§ 1. Испарение
Эта глава посвящена дальнейшим применениям кинетической теории. В предыдущей главе мы подчеркнули один из выводов этой теории, что средняя кинетическая энергия каждой степени свободы молекулы или любого другого объекта равна 1/2 kT. Сейчас центральным пунктом нашего изложения будет утверждение о том, что отнесенная к единице объема вероятность обнаружить частицу в том или ином месте пропорциональна ехр(-п.э./kT). (Это утверждение мы используем в ряде задач.)
Явления, которые мы собираемся изучить, довольно сложны: испарение жидкости, вылет электронов с поверхности металла или химическая реакция, в которой участвует много атомов. В таких случаях кинетическая теория не дает простых и точных предписаний, ситуация слишком сложна для этого. Поэтому выводы этой главы, за исключением особо оговоренных, весьма неточны. Мы только подчеркнем, что, исходя из кинетической теории, можно более или менее хорошо понять эти явления. Но гораздо более точное представление о них дают термодинамические аргументы или некоторые измерения отдельных критических величин.
Однако полезно знать, хотя бы очень приблизительно, почему то, что происходит, происходит именно так. Тогда, натолкнувшись на явление, которое содержит в себе нечто, чего мы еще не видели, или то, что проанализировать мы еще не собрались, мы, может быть, сможем более или менее точно сказать, что произошло. Такой анализ будет в высшей степени неточным, но в общих чертах верным — верным по сути, но чуть-чуть упрощенным, скажем, в некоторых тонких деталях.
Разберем первый пример — испарение жидкости. Предположим, что большой ящик при заданной температуре заполнен жидкостью и паром поровну. Будем считать, что средние расстояния между молекулами пара довольно велики, а вот в жидкости они упакованы плотно. Задача состоит в том, чтобы определить число молекул, находящихся в газовой фазе, по сравнению с числом молекул, находящихся в жидкости. Какова плотность пара при заданной температуре и как она зависит от температуры?
Пусть n — число молекул пара в единице объема. Это число, естественно, меняется с температурой. С притоком тепла испарение увеличивается. Добавим еще одну величину 1/Va, равную числу атомов в единице объема, содержащихся в жидкости; мы предполагаем, что в жидкости каждой молекуле отведен вполне определенный объем, поэтому чем больше в жидкости молекул, тем больший объем они занимают. Если Va — объем, отведенный одной молекуле, то число молекул в единичном объеме равно единичному объему, деленному на объем, занимаемый молекулой. Далее, предположим, что между молекулами действуют силы притяжения, удерживающие их внутри жидкости. Иначе нельзя понять, почему происходит конденсация. Итак, предположим, что имеется сила притяжения и существует энергия связи молекулы в жидкости, которая теряется при переходе молекул в пар. Это наводит на мысль, что для перевода какой-нибудь молекулы из жидкости в пар, нужно совершить работу W. Существует определенная разность W между энергией молекулы в жидкости и ее энергией в паре, потому что для переноса молекул в пар мы должны оторвать ее от всех молекул, к которым она притягивается.
Теперь обратимся к общему принципу, по которому отношение числа атомов в единице объема в разных областях равно n2/n1=ехр[-(Е2-E1/kT)]. Значит, n —число молекул в единичном объеме пара, деленное на 1/Va(число молекул в единичном объеме жидкости), равно
nVa=e-w/kT. (42.1)
Таково общее правило. Это очень похоже на равновесную атмосферу в ноле тяжести, когда низшие слои газа плотнее верхних, потому что для подъема молекулы на высоту h нужна энергия mgh. В жидкости молекулы размещены плотнее, чем в газе, так как их заставляет 'потесниться энергия «подъема» W, и отношение плотностей равно
ехр(-W/kT).
Это как раз то, что мы хотели вывести — плотность пара изменяется как е в некоторой степени. Показателем служит взятая со знаком минус похожая на энергию величина, деленная на kT. Множители перед экспонентой не особенно интересны, потому что в большинстве случаев плотность пара гораздо меньше плотности жидкости. При этих обстоятельствах, когда мы далеки от критической точки, где плотности почти одинаковы, соотношение плотностей, при котором nмного меньше l/Ve, обеспечивается тем, что W много больше kT. Поэтому формулы типа (42.1) интересны только тогда, когда W действительно гораздо больше kT; в этом случае е возводится в громадную отрицательную степень и если немного изменить Т, то изменится слегка и громадная степень, а это изменение повлечет за собой такие изменения экспоненты, которые будут гораздо важнее возможных изменений предэкспоненциальных множителей. Но отчего бы изменяться таким множителям, как l/Va? Да оттого, что наше описание приблизительно. Ведь в действительности каждая молекула не имеет определенного объема; при изменении температуры объем Vане остается постоянным — жидкости сжимаются и расширяются. Есть еще и другие мелочи вроде этой, так что действительная ситуация гораздо сложнее. Почти всюду стоят медленно изменяющиеся с температурой множители. В действительности само W медленно изменяется с температурой, потому что при разных температурах молекулам отведены разные объемы, и притяжение должно быть разным, и т. д. Итак, можно прийти к выводу, что поскольку у нас получилась формула, в которой все неизвестным образом изменяется с температурой, то на самом деле формулы никакой и нет. Но если мы знаем, что показатель у экспоненты W/kT заведомо велик, то можно убедиться, что наибольшие изменения кривой плотности пара как функции температуры обусловлены экспоненциальным множителем. Поэтому если мы будем считать W постоянной величиной, а коэффициент 1/Va — почти постоянной, то это будет хорошим приближением вдоль небольшого интервала нашей кривой. Иначе говоря, основные изменения определяются видом функции ехр(-W/kT),
Выходит, что в природе есть много, очень много процессов, для которых характерно взятие энергии взаймы; основным свойством таких процессов является экспоненциальная температурная зависимость: е возводится в отношение взятой с отрицательным знаком энергии к kT. Это полезный факт, но только в тех случаях, когда энергия велика по сравнению с kT, поскольку главная часть изменений с температурой определяется изменением kT, а не величиной постоянных и других сомножителей.
Давайте рассмотрим сейчас немного подробнее другой способ получения почти аналогичного результата для испарения. Чтобы получить (42.1), мы просто применили всегда справедливое при равновесии правило, но мало что поняли в существе явления. Поэтому невредно попытаться посмотреть детальнее, как происходит испарение. Можно описать его примерно так: молекулы пара непрерывно бомбардируют поверхность жидкости; при ударе они могут либо отскочить от поверхности, либо пробить ее. Что случается чаще, нам неизвестно, может быть, отношение этих исходов равно 50 к 50, а может быть и 10 к 90. Предположим, что поверхность пробивается всегда, потом мы посмотрим, к чему приводит предположение о более прочной поверхности. Тогда в каждый момент будет иметься определенное число атомов, сконденсировавшихся на поверхности жидкости. Число сконденсировавшихся молекул (число молекул, прошедших через площадку единичной площади) равно числу молекул в единице объема n, умноженному на скорость v. Эта скорость молекул связана с температурой; ведь известно, что в среднем 1/2mv2 равно 3/2 kT. Поэтому v —какая-то средняя скорость. Конечно, нужно еще проинтегрировать по углам и сделать всякого рода усреднения, но результат прямо пропорционален корню из среднего квадрата скорости. Таким образом,
Nc=nv, (42.2)
т. е. числу молекул, достигших единичной площадки и сконденсировавшихся.
Но атомы жидкости непрерывно пляшут, и время от времени отдельные атомы выскакивают наружу. Теперь нам нужно выяснить, часто ли это происходит. При равновесии число молекул, выскочивших за 1 сек из жидкости, равно числу молекул, поступивших за это же время на ее поверхность.
Ну, а много ли молекул выскакивает? Чтобы выскочить наружу, молекула должна как-то умудриться приобрести некоторую добавочную энергию, которая окажется больше, чем энергия ее соседок. И этот избыток энергии должен быть довольно большим, ведь наша молекула очень сильно притягивается к остальным молекулам жидкости. Обычно ей так и не удается преодолеть этого сильного притяжения, но иногда при столкновениях на ее долю выпадает излишек энергии. Шансы получить необходимую в нашем случае избыточную энергию W невелики, если W>>kT. Действительно, вероятность того, что атом приобретает энергию, большую чем W, равна ехр(-W/kT). Это общий принцип кинетической теории: шансы призанять энергию W сверх средней энергии равны е, возведенному в степень, показатель которой равен отношению W к kT со знаком минус. Предположим, что некоторым молекулам удалось получить эту энергию. Теперь можно установить, сколько молекул покидает поверхность жидкости за 1 сек. Конечно, получение молекулой нужной энергии еще не означает, что испарение обеспечено. Ведь эта молекула может находиться слишком глубоко в жидкости, а если она даже и находится у поверхности, то может двигаться не туда. Число молекул, покидающих единичную площадку за 1 сек, — это примерно число молекул на единице площади вблизи поверхности, деленное на время, которое требуется молекуле для побега, и умноженное на вероятность ехр(-W/kT) готовности молекул к побегу, в том смысле, что они уже получили достаточное количество энергии.
Предположим, что каждая молекула на поверхности жидкости занимает определенную площадку площади А. Тогда число молекул на единице поверхности жидкости равно 1/А. А много ли молекуле нужно времени, чтобы совершить свой побег? Если молекулы движутся с определенной средней скоростью v и должны пройти расстояние, равное, скажем, диаметру молекулы D (толщине наружного слоя), то время, нужное для преодоления этого расстояния, и есть время побега, если только молекула обладает достаточной энергией. Это время равно D/v. Таким образом, число испаряющихся молекул приблизительно равно
Заметим, что произведение площади каждой молекулы на толщину слоя приблизительно равно объему Va, отведенному каждой молекуле. Итак, для получения равновесия мы должны иметь Nc=Ne, или
Можно выкинуть из этого равенства скорости, потому что они равны; если даже специально отметить, что одна из них — скорость молекулы пара, а другая — скорость испаряющейся молекулы, — все равно они одинаковы, ведь мы знаем, что средняя кинетическая энергия обеих молекул (в одном направлении) равна 1/2kT. Но можно сказать: «Нет! Нет! Ведь испаряются только особо быстрые молекулы. Только они приобрели достаточный избыток энергии». Не совсем так, потому что в тот момент, когда эти молекулы выскакивают из жидкости, они теряют этот избыток, преодолевая потенциальную энергию. Поэтому при подходе к поверхности они уже движутся с замедленной скоростью v! Точно так же обстояло дело с распределением молекулярных скоростей в атмосфере — в нижних слоях молекулы были определенным образом распределены по энергиям. Те из них, которые достигали более высоких слоев, распределялись по энергиям точно так же, потому что медленные молекулы вверх совсем не поднимались, а быстрые, поднявшись, двигались медленнее. Испаряющиеся молекулы распределены по скоростям так же, как молекулы, движущиеся в глубине жидкости — поистине поразительный факт. Во всяком случае, нет смысла пытаться столь строго обсуждать нашу формулу, потому что в ней есть и другие неточности; например, мы рассматривали вероятность отражения молекул от поверхности, а не их конденсации и т. д. Мы имеем дело лишь с грубым описанием скорости испарения и конденсации и видим, естественно, что плотность пара nизменяется так же, как и раньше, но теперь мы понимаем этот процесс много лучше, а раньше писали почти произвольную формулу.
Более глубокое понимание позволит нам выяснить еще кое-что. Например, предположим, что мы откачиваем пар, причем так быстро, что пар удаляется практически с той же быстротой, с какой образуется (если наш насос очень хороший, а испарение происходит медленно). С какой скоростью будет происходить испарение, если температура жидкости Т будет поддерживаться постоянной? Предположим, что мы экспериментально уже измерили равновесную плотность пара и нам известно, сколько молекул в единице объема может быть в равновесии с жидкостью при заданной температуре. Теперь мы хотим узнать скорость испарения жидкости. Хотя мы ограничились лишь грубым анализом испарения, он все же дал нам сведения о числе прибывающих молекул пара, правда, с точностью до неизвестного коэффициента отражения. Поэтому мы можем использовать то обстоятельство, что при равновесии число покидающих пар молекул равно числу прибывающих молекул. Правда, пар откачивается и молекулы могут только покидать жидкость, но если оставить пар в покое, то установится равновесная плотность, при которой число прибывающих в жидкость молекул равно числу испаряющихся. Следовательно, легко видеть, что в этом случае число молекул, покидающих поверхность жидкости за 1 сек, равно произведению неизвестного коэффициента отражения R на число молекул, которые ежесекундно возвращались бы в жидкость, если бы пар не откачивался, потому что именно это число входит в уравнение баланса для испарения при равновесии:
Ne=nvR=(vR/Va)e-W/kT(42.5)
Конечно, легче подсчитать число молекул, переходящих из пара в жидкость, потому что в этом случае не надо ничего предполагать о силах, как это приходилось делать при подсчете числа покидающих жидкость молекул. Проще изменить путь рассуждений.
§ 2. Термоиониая эмиссия
Можно привести еще один пример часто встречающегося процесса, столь похожего на испарение жидкости, что его даже не придется анализировать отдельно. В сущности, это та же самая задача. В любой радиолампе есть источник электронов — вольфрамовая нить накаливания и положительно заряженная пластинка, притягивающая электроны. Оторвавшийся с поверхности вольфрама электрон немедленно улетает к пластинке. Это — «идеальный» насос, который непрерывно «откачивает» электроны. Возникает вопрос: сколько электронов ежесекундно покидает вольфрамовую проволоку и как их число зависит от температуры? Решение задачи дается той же формулой (42.5), потому что электроны, находящиеся в куске металла, притягиваются ионами или атомами металла. Они, грубо говоря, притягиваются металлом. Чтобы оторвать электрон от металла, надо сообщить ему определенное количество энергии, т. е. затратить для этого работу. Эта работа для разных металлов различна. Фактически она изменяется даже в зависимости от вида поверхности у одного и того же металла, но в целом она составляет несколько электронвольт,—величину, вообще типичную для энергии химических реакций. При этом полезно вспомнить, что разность потенциалов химических элементов, например батареи для магниевой вспышки, которая порождается химическими реакциями, порядка 1 в.
Как определить число электронов, покидающих металл за 1 сек? Очень трудно перечислить все, что может повлиять на выход электрона: легче решить задачу по-другому. Представим, что мы не удаляем вылетевшие электроны, а электроны образуют нечто вроде газа и могут вернуться в металл. В этом случае существует вполне определенная равновесная плотность электронов, которая определяется такой же формулой, как (42.1), где Va, грубо говоря, — объем, отведенный в металле одному электрону, a W=qej (j —так называемая работа выхода, или разность потенциалов, необходимая для того, чтобы вырвать электрон с поверхности металла). Эта формула подскажет нам, сколько электронов должно находиться в окружающем пространстве и проникать в металл, чтобы скомпенсировать потерю тех электронов, которые покинули металл. Теперь легко подсчитать, сколько электронов уйдет из металла, если мы будем непрерывно откачивать их, потому что число ушедших электронов в точности равно числу электронов, которые должны были бы вернуться в металл, если существовал электронный «пар», плотность которого определяется формулой (42.1). Иначе говоря, электрический ток через единичную площадку равен произведению заряда электрона на число электронов, проходящих за 1 сек через площадку единичной площади; последнее равно произведению числа электронов в единичном объеме на скорость: поэтому, как мы уже много раз видели,
Мы знаем, что 1 эв соответствует kT при температуре, достигающей 11 600 град. Нить накаливания радиолампы работает примерно при температуре 1100 град, поэтому экспоненциальный множитель равен примерно е-10; когда мы слегка изменяем температуру, экспоненциальный множитель изменяется очень сильно. Это опять основное свойство формул, содержащих ехр(-qej/kT). Предэкспоненциальный множитель на самом деле совершенно неверен; оказывается, что поведение электронов в металле правильно описывает квантовая, а не классическая механика, но правильный множитель лишь немного отличается от нашего. Фактически до сих пор никто еще не смог точно вычислить этот множитель, хотя многие при расчетах пользовались квантовыми формулами высшего класса. Основная задача состоит в том, чтобы выяснить, не меняется ли W хотя бы медленно с температурой? Если да, то медленно изменяющуюся с температурой величину W нельзя отделить от предэкспоненциальных коэффициентов. Если, например, W зависит от температуры линейно, так что W= W0+akT, то
Такая линейная зависимость W от температуры эквивалентна измененной «постоянной». Попытка точного вычисления пред-экспоненциального множителя очень трудна и обычно бесплодна.
§ 3. Тепловая ионизация
Перейдем теперь к еще одному применению все той же идеи. Теперь речь пойдет об ионизации. Предположим, что газ состоит из великого множества атомов, которые обычно нейтральны, но если газ нагреть, то атомы могут оказаться ионизованными. Нам нужно знать, сколько существует ионов при тех или иных обстоятельствах, т. е. при заданной плотности атомов в единичном объеме и при определенной температуре. Снова придется представить себе ящик, в котором находится N атомов, содержащих в себе электроны. (Если электрон покидает атом, то атому присваивается наименование ион, а если атом нейтрален, то говорят просто—атом.) Таким образом, предположим, что в заданный момент в единичном объеме число нейтральных атомов равно nа, число ионов равно ni, а число электронов равно nе. Нужно определить, как связаны эти три числа между собой?
Прежде всего эти числа подчиняются двум условиям или связям. Например, можно как угодно менять различные условия, температуру и т. д., но сумма na+niвсегда останется одной и той же, потому что это просто-напросто N — число атомных ядер в ящике. Если в единице объема число ядер сохраняется постоянным, а изменяется, скажем, температура, то, хотя в результате ионизации некоторые атомы превращаются в ионы, общее число атомов и ионов не изменяется. Значит, ne+ni.=N. Другое условие вытекает из того, что если газ в целом электрически нейтрален (и если мы пренебрегаем двойной или тройной ионизацией), то число ионов всегда равно числу электронов, или nе=ni. Эти дополнительные условия просто выражают сохранение заряда и сохранение атомов.
Эти равенства верны, и мы в конце концов всегда используем их при решении реальных задач. Но нам нужно получить другое соотношение между этими величинами. Сделать это можно так. Обратимся снова к идее о том, что для отрыва электрона от атома требуется какое-то количество энергии, которую мы будем называть энергией ионизации и обозначать буквой W (чтобы новые формулы выглядели так же, как и раньше). Итак, W равна энергии, потребной для того, чтобы оторвать электрон от атома и получить ион. Мы снова убеждаемся, что число свободных электронов в единичном объеме «пара» равно произведению числа электронов в единичном объеме, связанных в атомах, на е в степени минус разность энергий связанного и свободного электронов, деленная на kT. Опять основное уравнение. Но как это записать? Число свободных электронов в единичном объеме, конечно, ne, потому что определение nе. Ну, а что можно сказать о числе связанных в атоме электронов в единичном объеме? Общее число мест, отданных электронам, равно nа+ni;, и мы предположим, что когда все электроны связаны, то каждому отводится некоторый объем Va. Таким образом, полный атомный объем, занимаемый связанными электронами, равен (na+ni)Va, и нашу формулу теперь можно записать в виде
Но формула эта неверна. Мы упустили из вида одно существенное обстоятельство: когда один электрон попал в атом, другой электрон уже не может проникнуть в этот же объем! Иначе говоря, не все объемы из числа возможных доступны электрону, который раздумывает, куда бы ему отправиться — в пар или в конденсированное состояние. Здесь возникают непредвиденные осложнения, в силу которых электрон не может подойти близко к тому месту, где уже находится другой электрон — они отталкиваются. По этой причине мы должны считать только ту часть объема, в которой электрон может разместиться. Ведь те объемы, которые уже заняты, нельзя причислять к числу возможных, и только те объемы, которые предоставлены ионам, можно рассматривать как места, вакантные для электронов. Тогда, учтя это
обстоятельство, мы найдем, что более точная формула записывается в виде
Эту формулу называют уравнением ионизации, или уравнением Саха. Теперь посмотрим, можем ли мы качественно понять, почему получается формула, подобная этой, если следить за кинетикой процесса.
Прежде всего время от времени, когда электрон сталкивается с ионом, они объединяются в атом. Точно так же время от времени атом испытывает столкновение и разваливается на ион и электрон. Скорости обоих процессов должны быть равны. А долго ли электрону и иону искать друг друга? Встречи, конечно, учащаются, если возрастает число электронов в единичном объеме. К этому же приводит и увеличение числа ионов в единичном объеме. Следовательно, полная скорость рекомбинации пропорциональна произведению числа электронов на число ионов. Далее, полная скорость ионизации в результате столкновений должна линейно зависеть от числа способных к ионизации атомов. Таким образом, скорости обоих процессов сбалансируются тогда, когда установится определенное соотношение между произведением neniи числом атомов na. Тот факт, что это соотношение выражается особой формулой, куда входит энергия ионизации W, дает, конечно, несколько большую информацию, но мы можем легко сообразить, что такая формула обязательно должна содержать концентрации электронов, ионов и атомов в комбинации neni/na, которая приводит к постоянной, не зависящей больше от чисел n, а только от температуры, атомных размеров и других постоянных.
Заметим также, что поскольку уравнение содержит числа в единичном объеме и если мы поставим два опыта с одним и тем же полным числом N атомов и ионов, т. е. со строго определенным числом ядер, но заключим их в ящики разных объемов, то числа nбудут меньше для больших ящиков. Однако отношение neni/na должно оставаться постоянным, поэтому полное число электронов и ионов должно быть больше в большем ящике. Чтобы убедиться в этом, предположим, что в ящик объема V помещено N ядер и их f-я часть ионизована. Тогда ne=fN/V=niи na=(1-f)N/V. В этом случае наше уравнение принимает вид
Иначе говоря, если мы берем все меньшую и меньшую плотность атомов или непрерывно увеличиваем объем ящика, относительное число электронов и ионов должно возрасти. То, что ионизация может быть вызвана просто «расширением», при котором плотность уменьшается, объясняет нам, почему при очень малых плотностях (какие встречаются в холодном межзвездном пространстве) много ионов, хотя это трудно понять, учитывая имеющуюся в нашем распоряжении энергию. Энергия во много-много раз больше kT, но ионы все равно есть. Почему же ионы могут существовать лишь при условии, что вокруг них имеется много места, тогда как при увеличении плотности они стремятся исчезнуть? Ответ: Все дело в атомах. Время от времени свет или другой атом, или ион, или еще что-то, что поддерживает тепловое равновесие, разрушает атомы. Очень редко, потому что для этого требуются огромные количества избыточной энергии, электрон отрывается и происходит превращение атома в ион. Если пространства огромны, то электрон слоняется очень долго, быть может много лет и ничего не встречает. Но однажды он находит ион, и тогда они объединяются в атом. Скорость, с которой электроны покидают атомы, очень мала. Но если объем огромен, то сбежавший электрон так долго ищет ион, с которым он мог бы рекомбинировать, что вероятность рекомбинации совсем ничтожна; поэтому, несмотря на то, что для ионизации нужны большие излишки энергии, число электронов может быть вполне ощутимым.
§ 4. Химическая кинетика.
При химических реакциях происходит нечто похожее на «ионизацию». Например, два вещества А к В комбинируют в основном веществе АВ; тогда, подумав немного, мы можем АВ назвать атомом (В — то, что мы называем электроном, а А — то, что мы называем ионом). После такой замены, как и раньше, можно написать уравнение равновесия
Эта формула, конечно, неточна, потому что «постоянная» с зависит от того, в каком объеме позволено объединяться А и В и т. п., но, обратясь к термодинамическим аргументам, можно придать смысл величине W в экспоненциальном множителе, и тогда окажется, что она тесно связана с энергией, необходимой для реакции.
Попробуем понять эту формулу как результат столкновений, приблизительно так же, как мы постигали формулу испарения, подсчитывая электроны, вырывающиеся в пространство, и те, которые возвращаются назад за единицу времени. Предположим, что при столкновениях А и В иногда образуют соединение АВ. И предположим еще, что АВ — это сложная молекула, которая участвует в общей пляске и по которой ударяют другие молекулы, причем время от времени она получает энергию, достаточную для того, чтобы взорваться и снова развалиться на части А и В.
Заметим, что в химических реакциях дело обстоит так, что если сближающиеся атомы имеют слишком малую энергию, то, хотя этой энергии и достаточно для реакции
А+В®АВ, факт соударения атомов А и В еще не обязательно означает начало реакции. Обычно требуется, чтобы соударение было более «жестким», «мягкого» соударения между А и В может оказаться недостаточно для начала реакции, даже если в процессе освобождается достаточное для реакции количество энергии. Предположим, что общей чертой химических реакций является требование, по которому для объединения А и В в АВ недостаточно простого соударения, а нужно, чтобы они столкнулись, имея определенное количество энергии. Эта энергия называется энергией активации, т. е. энергия, нужная для «активации» реакции. Пусть А*— тот избыток энергии, который необходим, чтобы столкновения могли вызвать реакцию. Тогда скорость Rf, с которой А и В порождают АВ, должна содержать произведение числа атомов А и B, умноженное на скорость, с которой отдельный атом ударяется о некоторую площадку величиной sab, и на величину ехр(-A*/kT) (вероятность того, что атомы обладают достаточной энергией):
Rf =nAnBvsABe-A*/kT. (42.10)
Теперь надо найти скорость обратного процесса Rr. Есть некоторая вероятность, что А и В снова разойдутся. Чтобы разойтись, им недостаточно энергии W, которая обеспечит их раздельное существование. Но раз молекулам нелегко соединиться, должен существовать некий барьер, через который А и В должны перевалить, чтобы разлететься. Они должны запастись не только нужной для их существования энергией, но и взять кое-что про запас. Получается что-то вроде подъема на холм перед спуском в долину; сначала приходится вскарабкаться на высоту, потом спуститься, и только после этого разойтись (фиг. 42.1).
Фиг. 42.1. Соотношение энергий в реакции А+В®АВ.
Таким образом, скорость перехода АВ в А и В пропорциональна произведению nАВ — начальному числу молекул АВ на
ехр[-(W+A*)/kT]:
Rr=c'nABe-(W+A*)/kT). (42.11)
Постоянная с' складывается из объема атомов и частоты столкновений; ее можно получить, как и в случае испарения,
перемножая площадь и толщину слоя, но сейчас мы этого делать не будем. Сейчас нас больше интересует тот факт, что, когда эти скорости равны, их отношение равно единице. Это говорит о том, что, как и раньше, (nаnв/nав)=cехр(-W/kT), где с содержит сечения, скорости и другие множители, не зависящие от чисел п. Интересно, что скорость реакции по-прежнему изменяется как ехр(-const/kT), хотя эта постоянная уже не имеет никакого отношения к той, с которой мы встречались в задаче о концентрациях; энергия активации А* сильно отличается от энергии W. Энергия W регулирует пропорции А, В и АВ, при которых устанавливается равновесие, но если нам захочется узнать, быстро ли А+В переходит в АВ, то это уже к равновесию отношения не имеет, и появляется уже другая энергия, энергия активации, которая с помощью экспоненты управляет скоростью реакции.
Кроме того, A* не является фундаментальной постоянной, как W. Предположим, что реакция происходит на поверхности стены, или на какой-нибудь другой поверхности, тогда А и В могут растечься по ней так, что объединение в А В будет для них более легким делом. Иначе говоря, сквозь гору можно прорыть «туннель» или срыть вершину горы. В силу сохранения энергии, по какому бы пути мы ни шли, результат будет один: из А и В получится АВ, так что разность энергий W не зависит от пути, по которому идет реакция, однако энергия активации А* очень сильно зависит от этого пути. Вот почему скорости химических реакций столь чувствительны к внешним условиям. Можно изменить скорость реакции, изменив поверхность, с которой соприкасаются реактивы, можно изготовить «набор бочонков» и подбирать с его помощью любые скорости, если они зависят от свойств поверхности. Можно внести в среду, в которой происходит реакция, третий предмет; это также может сильно изменить скорость реакции, такие вещества при незначительном изменении А* иногда чрезвычайно влияют на скорость реакции; их называют катализаторами. Реакции может практически не быть совсем, потому что А* слишком велика для заданной температуры, но если добавить это специальное вещество — катализатор, то реакция протекает очень быстро, потому что А* уменьшается.
Между прочим, эта реакция А плюс В, дающая АВ, доставляет немало волнений. Ведь невозможно сохранить сразу и энергию, и импульс, пытаясь подогнать два предмета друг к другу, чтобы сделать из них один более устойчивый. Следовательно, необходим по крайней мере третий предмет С и реальная реакция выглядит гораздо сложнее. Скорость прямого процесса должна содержать произведение nAnBnC, и можно подумать, что наша формула становится неверной, но это не так! Если мы начнем искать скорость развала АВ, то выясним, что этой молекуле еще надо столкнуться с С, поэтому скорость обратной реакции пропорциональна nABnCи из формулы для равновесных концентраций nCвыпадает. Правильность закона равновесия (42.9), который мы написали прежде всего, абсолютно гарантирована независимо от любого возможного механизма реакции!
§ 5. Законы излучения Эйнштейна
Обратимся теперь к интересной задаче, похожей на только что описанную и связанную с законом излучения черного тела. В предыдущей главе мы разбирали вывод закона распределения излучения в полости по способу Планка, рассматривая излучение осциллятора. Осциллятор обладает определенной средней энергией, а раз он осциллирует, то должен и излучать и накачивать излучение в полость, пока она не заполнится как раз таким количеством излучения, которое нужно для поддержания равновесия между излучением и поглощением. Рассуждая таким образом, мы нашли, что интенсивность излучения частоты w задается формулой
Этот вывод содержит предположение, что генерирующий излучение осциллятор обладает определенными уровнями энергии, отстоящими друг от друга на равном расстоянии. Мы не говорили о том, что свет состоит из фотонов или чего-то вроде этого. Мы даже не задавали вопроса, каким способом при переходе атома с одного уровня энергии на другой переносится единичная энергия hw в виде света. Первоначальная идея Планка состояла в том, что вещество квантовано, а свет — нет: осциллятор не может получать любую энергию, а должен принимать ее порциями. Вызывает еще беспокойство то, что способ вывода — полуклассический. Мы вычислили скорость излучения осциллятора, исходя из законов классической физики, а потом забыли об этом и сказали: «Нет, этот осциллятор имеет много уровней энергии». Но для последовательно строгого вывода этой чисто квантовой формулы пришлось пройти длинный путь, завершившийся в 1927 г. созданием квантовой механики. А тем временем Эйнштейн попытался заменить точку зрения Планка, что квантованы только материальные осцилляторы, идеей о том, что свет в действительности состоит из фотонов и его следует в определенном смысле понимать как газ из частиц с энергией hw. Далее, Бор обратил внимание на то, что любая система атомов имеет уровни энергии, но расстояния между ними не обязательно постоянны, как у осцилляторов Планка. Поэтому возникла необходимость пересмотреть вывод или хотя бы более точно исследовать закон излучения, исходя из более последовательной квантовомеханической точки зрения.
Эйнштейн предположил, что окончательная формула Планка правильна и использовал ее для получения новой, ранее неизвестной информации о взаимодействии излучения с веществом. Он рассуждал так: надо рассмотреть любые два из возможных уровней энергии атома, скажем, m-й и n-й уровни (фиг. 42.2).
Фиг. 42.2. Переход между двумя уровнями энергии атома.
Затем Эйнштейн предположил, что, когда атом освещается светом подходящей частоты, он может поглотить фотон, перейдя из состояния n в состояние m, и вероятность такого перехода за 1 сек пропорциональна интенсивности освещающего атом света и еще зависит от того, какие уровни мы возьмем.
Назовем постоянную пропорциональности Bnm, чтобы помнить, что это не универсальная постоянная природы и зависит она от того, какую пару уровней мы выберем: некоторые уровни возбудить легко, а другие возбуждаются с большим трудом. Теперь надо найти формулу, описывающую скорость перехода из т в п. Эйнштейн предположил, что она складывается из двух частей. Даже если внешнего излучения нет, существует вероятность того, что атом, излучив фотон, перейдет из возбужденного состояния в состояние с меньшей энергией. Это так называемое спонтанное излучение.
Это предположение аналогично идее о том, что даже классический осциллятор, обладая определенной энергией, не может ее сохранить; излучение неизбежно вызывает потерю энергии. Таким образом, по аналогии со спонтанным излучением классических систем существует определенная вероятность Amn(она опять зависит от уровней), с которой атом переходит из состояния m в состояние n, и эта вероятность не зависит от того, освещается атом светом или нет. Но Эйнштейн пошел еще дальше и, сравнив с классической физикой и используя другие аргументы, пришел к заключению, что излучение зависит от наличия света вокруг. Когда атом освещается светом подходящей частоты, то вероятность излучения фотона возрастает пропорционально интенсивности света с постоянной пропорциональности Bmn. Если бы нам удалось выяснить, что этот коэффициент равен нулю, то мы уличили бы Эйнштейна в ошибке. Но, конечно, мы увидим, что он был прав.
Итак, Эйнштейн предположил, что существует три сорта процессов: поглощение, пропорциональное интенсивности света, излучение, пропорциональное интенсивности света (его называют индуцированным излучением, или вынужденным излучением), и спонтанное излучение, не зависящее от интенсивности света.
Предположим теперь, что при температуре Т установилось равновесие, и в состоянии n находится некоторое количество атомов Nn, а в состоянии m — некоторое количество атомов Nm. Тогда полное число атомов, переходящих из n в m, равно произведению числа атомов в состоянии n на скорость перехода одного атома из состояния n в состояние m. Таким образом, мы получили формулу для числа атомов, переходящих за 1 сек из n в m:
Rn®m= NnBnmI(w). (42.13)
Число атомов, переходящих из m в n, получается точно таким же способом: надо умножить число атомов в состоянии m на скорость перехода одного атома. На этот раз получаемое выражение выглядит так:
Rm®n=Nm[Amn+BmnI(w)]. (42.14)
Теперь предположим, что при тепловом равновесии число атомов, поднимающихся на верхний уровень, должно быть равно числу атомов, спускающихся вниз. Это по крайней мере один из способов удержать число атомов на каждом уровне постоянным. Следовательно, при равновесии мы считаем обе скорости равными. Но у нас в запасе есть еще кое-какая информация: мы знаем, насколько велико Nmпо сравнению с Nn; отношение этих чисел равно ехр[—(Em-En)/kT]. После этого Эйнштейн предположил, что частота света, который вовлекается в игру при переходах из m в n, соответствует разности энергий, так что во всех наших формулах Еm-Еn=hw. Итак,
Nm=Nne-hw/kT. (42.15)
Таким образом, если приравнять две скорости: NnBmnI(w) =Nm[Amn+BmnI(w)] и поделить на Nm, то мы получим BnmI(w)еhw/kT=Аnп+BmnI(w). (42.16) Из этого выражения можно найти I(w). Это просто:
Но Планк уже сказал нам, что формула должна иметь вид (42.12). Следовательно, мы можем сделать кое-какие выводы: прежде всего Bmnдолжно быть равно Bnm, потому что иначе ехр(hw/kT)-1 не получить. Таким образом, Эйнштейн открыл некоторые соотношения, прямого вывода которых он не знал, например, что вероятности вынужденного излучения и поглощения должны быть равны. Это интересно. Кроме того, чтобы (42.17) и (42.12) согласовались,
Amn/Bmn должно быть равно hw3/p2c2. (42.18)
Значит, если известна, скажем, скорость поглощения для заданного уровня, то можно получить скорость спонтанного излучения и скорость вынужденного излучения или какую-нибудь комбинацию этих величин.
Больше этого на основании столь общих предположений ни Эйнштейн, ни вообще кто-либо получить не сможет. Чтобы действительно вычислить абсолютную скорость спонтанного излучения или вообще любую скорость специфически атомного перехода, нужно знать все скрытые механизмы атома. Этому учит так называемая квантовая электродинамика, открытая лишь одиннадцать лет спустя. А Эйнштейн предсказал все это в 1916 г.
Возможность вынужденного излучения в наши дни нашла интересное применение. Если есть свет, то он стремится вызвать переход сверху вниз. Тогда этот переход может увеличить энергию света на hw, если найдутся такие атомы, у которых занят верхний уровень. Можно разработать нетепловой метод приготовления газа, в котором число состояний m гораздо больше числа состояний n. Газ будет очень далек от равновесия, и формулу ехр(-hw/kT), верную для равновесия, к нему применить нельзя. Можно добиться даже, чтобы число занятых верхних состояний было очень большим, тогда как число атомов в нижнем состоянии практически будет равно нулю. Тогда свет с частотой, соответствующей разности энергий Em-Еn, будет поглощаться очень слабо, потому что атомов, находящихся в состоянии n и способных поглотить его, очень мало. С другой стороны, когда газ из таких атомов освещен, то свет вызывает излучение из верхнего состояния! Таким образом, если в верхнем состоянии находится много атомов, то начинается что-то вроде цепной реакции, когда атомы вдруг начинают излучать; более того, они вынуждены излучать и все разом проваливаются в нижнее состояние. Так работает лазер, а если излучаются инфракрасные волны, то их источник называют мазером.
Чтобы загнать атомы в состояние m, прибегают к разным ухищрениям. Может существовать более высокий уровень, на который атомы можно поднять сильным пучком света высокой частоты. С этого высокого уровня атомы падают вниз, испуская самые различные фотоны, пока не соберутся на уровне т. Если атомы стремятся задержаться на уровне m, не излучая фотонов, то этот уровень называют метастабильным. А потом атомы разом спрыгивают с уровня m, сопровождая прыжок вынужденным излучением. Еще одна техническая деталь — если поместить нашу систему в обычный ящик, то она может спонтанно излучать во многих направлениях, что наносит ущерб вынужденному излучению. Но можно усилить эффект вынуждения и увеличить его значение, поставив у каждой стенки ящика почти полностью отражающие зеркала; тогда излученный свет получает шанс вызвать дополнительное излучение, следующее отражение добавит еще один такой шанс, а потом еще, еще и еще. Хотя зеркала отражают почти весь свет, существует небольшая вероятность прохождения части света сквозь зеркало и выхода наружу. В конце концов весь свет, подчиняясь закону сохранения энергии, выйдет наружу в виде тонкого, сильного пучка. Так и получают мощные пучки света в лазерах
Фиг. 42.3. При возбуждении голубым светом атом поднимается на высший уровень h и, быстро испустив фотон, сваливается с него на уровень m.
Когда число атомов в состоянии m становится достаточно большим, возникает действие лазера.
* Это не только способ удержать число атомов на каждом уровне постоянным, но и действительный путь, который избирает природа. При тепловом равновесии каждый процесс должен уравновеситься противоположным процессом, это так называемый принцип детального равновесия.
Глава 43 ДИФФУЗИЯ
§ 1. Столкновения молекул
§ 2. Средняя длина свободного пробега
§ 3. Скорость дрейфа
§ 4. Ионная проводимость
§ 5. Молекулярная диффузия
§ 6. Теплопроводность
§ 1. Столкновения молекул
До сих пор мы изучали движение молекул только при тепловом равновесии. А теперь нужно обсудить, как движутся молекулы газа, когда он близок к равновесию, но еще не достиг его полностью. Если газ слишком неравновесен, все становится чрезвычайно сложным и разобраться в том, что там происходит, очень трудно, а вот если отклонения от равновесия незначительны, то задачи решаются легко. Однако, чтобы рассмотреть, что происходит в таком газе, надо снова вернуться к кинетической теории. Статистическая механика и термодинамика пригодны, когда имеется равновесие, а чтобы проанализировать то, что происходит при отклонении от равновесия, приходится, так сказать, перебирать атом за атомом.
В качестве простого примера неравновесной задачи рассмотрим диффузию ионов в газе. Предположим, что в газе содержится немного ионов — электрически заряженных молекул. Если к газу приложить электрическое поле, то на каждый ион будет действовать сила, отличающаяся от сил, действующих на нейтральные молекулы. Если бы других молекул не было, то ион двигался бы с постоянным ускорением, пока не наткнулся бы на стенку ящика. Но наличие других молекул меняет дело: скорость иона возрастает лишь до тех пор, пока он не ударится о молекулу и не потеряет своего импульса. После этого он снова начинает ускоряться, но вновь теряет импульс. В результате ион вынужден двигаться по ломаному пути, хотя все же в конце концов он движется в направлении электрического поля.
Мы замечаем, таким образом, что ион «дрейфует» со средней скоростью, пропорциональной электрическому полю; чем сильнее поле, тем быстрее движется ион. Конечно, пока существует поле и пока ион продолжает двигаться, не может быть и речи о тепловом равновесии. Система стремится прийти к равновесию, но для этого нужно, чтобы все ионы приклеились к стенке ящика. С помощью кинетической теории возможно вычислить скорость дрейфа ионов.
Наших математических познаний еще недостаточно, чтобы точно вычислить все, что произойдет, но мы можем получить приближенное решение, которое правильно передаст все существенные особенности явления. Мы можем определить зависимость эффекта от давления, температуры и т. п., но не в наших силах вычислить точно все коэффициенты, стоящие перед этими сомножителями. Поэтому не будем мучить себя заботой о точных значениях таких коэффициентов. Получить их можно только после очень тонкого математического анализа.
Прежде чем рассуждать о том, что происходит в отсутствие равновесия, посмотрим повнимательнее на равновесный газ. Необходимо, например, знать среднее время между двумя последовательными столкновениями молекулы.
Каждая молекула непрерывно сталкивается с другими молекулами. Происходят все эти столкновения, конечно, случайно. Если выбрать какую-нибудь молекулу, то за достаточно долгое время Т она получит определенное число N ударов. Если увеличить промежуток времени вдвое, то и число ударов возрастет вдвое. Таким образом, число столкновений пропорционально времени Т. Это можно выразить следующим образом:
N=T/t (43.1)
Мы записали постоянную пропорциональности в виде 1/t, где t имеет размерность времени. Постоянная t — это среднее время между столкновениями. Предположим для примера, что за час происходит 60 столкновений; тогда t равно одной минуте. Мы будем говорить, что t (одна минута) это среднее время между столкновениями.
Часто нам придется искать ответ на такой вопрос: Какова вероятность того, что молекула испытает столкновение в течение малого промежутка времени dt? Мы догадываемся, что эта вероятность равна dt/t. Попытаемся, однако, привести более убедительные аргументы. Предположим, что в нашем распоряжении имеется очень большое число N молекул. Сколько молекул из этого числа столкнется в течение интервала времени dt? Если молекулы находятся в равновесном состоянии, то ничего не будет меняться в среднем со временем. Таким образом, N молекул, пробывших в ящике в течение интервала dt, испытают столько же соударений, сколько одна молекула за время Ndt. Число соударений одной молекулы за большое время Ndt известно — это Ndt/t. А если число соударений между N молекулами за время dt равно Ndtlt, то вероятность удара для одной молекулы равна 1/N части этой величины, или (1/N)(Ndt/t)=dt/t (как мы и говорили с самого начала). Таким образом, относительное число молекул, сталкивающихся за время dt, грубо говоря, равно dt/t. Если, например, t равно одной минуте, то за секунду столкнется 1/60 часть всех молекул.
Это означает, конечно, что если в данный момент 1/60 часть молекул подошла достаточно близко к тем, с кем они должны столкнуться, то их столкновение произойдет в течение следующей минуты.
Когда мы говорим, что t (среднее время между столкновениями) равно одной минуте, то мы вовсе не считаем, что все столкновения разделены в точности минутными интервалами. Частица, столкнувшись, совсем не выжидает потом еще минуту, чтобы нанести следующий удар. Промежутки между последовательными столкновениями весьма различны. В дальнейшем, правда, нам это не понадобится, но можно задать такой вопрос: А чему все же равно время между столкновениями? Мы уже знаем, что в приведенном выше примере среднее время равно одной минуте, но нам, быть может, нужно знать, какова вероятность того, что молекула не столкнется ни с кем в течение двух минут?
Ответим на более общий вопрос: Какова вероятность того, что молекула не испытает ни одного столкновения за время t? Начнем в какой-то произвольный момент времени, который мы назовем t=0, следить за определенной молекулой. Какова вероятность того, что до момента встречи ее с другой молекулой пройдет время t? Чтобы вычислить вероятность, посмотрим, что случится со всеми N0молекулами, находящимися в ящике. Пока мы ждем в течение времени t, некоторые молекулы испытают столкновения. Пусть N(t) — число молекул, не испытавших столкновений за время t. Мы можем определить N(t), ибо нам известно, как это число меняется со временем. Это число N(t), естественно, меньше общего числа молекул N0. Если мы знаем, что за время t избежать столкновений удалось N(t) молекулам, то N(t+dt) (число молекул, которым удалось сделать это за время t+dt) меньше N(t) на число молекул, все-таки столкнувшихся за время dt. Мы уже раньше научились определять число молекул, которым не удалось избежать столкновений за время dt, с помощью среднего времени т: dN=N(t)dt/t. Мы получаем уравнение
N(t+dt)=N(t)-N(t)dt/t. (43.2)
Величину, стоящую в левой части уравнения, N(t+dt), можно в согласии с общими правилами дифференциального исчисления записать в виде N(t)+(dN/dt)(dt). Сделав эту подстановку, мы приведем уравнение (43.2) к виду
Число молекул, выбывших из игры за промежуток dt, пропорционально числу наличных молекул и обратно пропорционально среднему времени жизни t. Уравнение (43.3) легко проинтегрировать, если переписать его в виде
Поскольку в каждой части стоит полный дифференциал, то интеграл уравнения таков:
lnN(t)=-t/t+ постоянная, (43.5)
или, что то же самое,
N(t)=(постоянная)е-t/t. (43.6)
Мы знаем, что постоянная должна быть равна N0— полному числу молекул, потому что в начальный момент t=0 все молекулы ждут «следующего» удара. Мы можем записать наш результат в виде
N(t)=N0e-t/t. (43.7)
Если мы хотим определить вероятность P(t) того, что молекула не испытает столкновений, нужно величину N(t) поделить на N0; тогда получим
P(t)=е-t/t. (43.8)
Вот наш результат: вероятность того, что какая-то молекула сможет прожить время t, не столкнувшись, равна ехр(-t/t), где t — среднее время между столкновениями. Вероятность эта начинается с 1 (очевидности) при t=0 и уменьшается по мере того, как t становится все больше и больше. Вероятность того, что молекула избежит столкновений за время t, равна е-1=0,37... Шансов выдержать дольше, чем среднее время между столкновениями, меньше половины. В этом нет ничего странного, потому что существует достаточно много молекул, которые избегают столкновений значительно дольше среднего времени между столкновениями, так что среднее время между столкновениями по-прежнему равно t,
Первоначально мы определили t как среднее время между столкновениями. Сформулированный в виде уравнения (43.7) результат говорит нам, что среднее время, отсчитываемое от произвольно взятого момента до следующего столкновения, также равно т. Этот несколько удивительный факт можно продемонстрировать следующим образом. Число молекул, которые испытают их следующее столкновение в промежутке dt, отсчитанного от времени t после произвольно взятого начального времени, равно N(t)dt/t. Их «промежуток времени до следующего столкновения» равен, конечно, t. «Среднее время до следующего столкновения» получается обычным образом:
Среднее время до следующего столкновения=
Используя полученное из (43.7) число N(t) и вычисляя интеграл, найдем, что t — это среднее время, отсчитанное от любого момента до следующего столкновения.
§ 2. Средняя длина свободного пробега
Есть еще возможность описать столкновения молекул, не вводя для этого времени между столкновениями. Можно определить, далеко ли успеет уйти частица между столкновениями. Если мы знаем, что среднее время между столкновениями равно t, а средняя скорость молекул равна v, то очевидно, что среднее расстояние между столкновениями, которое мы обозначим буквой l, равно произведению t и v;. Это расстояние между столкновениями обычно называют длиной свободного пробега:
Длина свободного пробега l=tv. (43.9)
В этой главе мы не будем уточнять, какого рода среднее мы имеем в виду в каждом случае. Существующие разные средние — среднее, корень из среднего квадрата и т. д.— приблизительно равны и отличаются только множителями, близкими к единице. Поскольку для получения правильных множителей необходим подробный анализ, нам нет смысла очень уж стараться уточнять, какое именно среднее используется в том или ином случае. Мы хотим еще предупредить читателей, что используемые для обозначения физических величин алгебраические символы (например, l для длины свободного пробега) не являются общепринятыми просто потому, что об этом никто еще специально не договаривался.
Вероятность того, что молекула испытает столкновение, пройдя расстояние dx, равна dx/l, как вероятность столкновения за короткий промежуток времени dt равна dt/t. Призвав на помощь те же аргументы, что и раньше, читатель сможет показать, что вероятность того, что молекула пройдет по крайней мере расстояние х, прежде чем испытает следующее столкновение, равна е-х/l.
Среднее расстояние, которое молекула проходит между столкновениями (длина свободного пробега l), зависит от количества молекул, ее окружающих, и от того, какого «размера» эти молекулы, т. е. от того, насколько уязвимую мишень представляют они собой. «Размеры» мишени при столкновениях обычно описывают при помощи «эффективного сечения столкновений»; эта же идея используется и в ядерной физике или в задачах о рассеянии света.
Рассмотрим движущуюся частицу, которая проходит расстояние dx внутри газа, содержащего n0рассеивателей (молекул) в единичном объеме (фиг. 43.1).
Фиг. 43,1. Эффективное сечение столкновения.
На каждой площадке единичной площади, перпендикулярной к направлению движения выбранной нами частицы, имеется n0dx молекул. Если каждая может быть представлена эффективной площадью столкновения, или, как обычно говорят, «эффективным сечением столкновения» sс, то полная площадь, покрываемая рассеивателями, равна scn0dx.
Под «эффективным сечением столкновения» понимается площадь, в которую должен попасть центр частицы, если она должна столкнуться с заданной молекулой. Если молекулы выглядят как маленькие шарики (классическая картина), то следует ожидать, что sс=p(r1+r2)2, где r1и r2— радиусы двух сталкивающихся молекул. Вероятность того, что наша частица столкнется с какой-нибудь молекулой, равна отношению площади, покрываемой рассеивающими молекулами, к полной площади, принятой нами за единицу. Таким образом, вероятность столкновения на пути dx равна sсn0dx:
Вероятность столкновения на пути dx =sn0 dx. (43.10)
Мы уже отметили раньше, что вероятность столкновения на пути dx может быть записана в терминах длины свободного пробега l как dx/l. Сравнивая это с (43.10), можно связать длину свободного пробега с эффективным сечением столкновения:
1/l= scn0. (43.11)
Это равенство легче запомнить, если записать его так:
sсn0l = 1. (43.12)
Эта формула говорит, что если частица проходит путь I внутрь рассеивателя, в котором молекулы могут как раз покрыть всю площадь, то в среднем происходит одно столкновение. В цилиндре высотой l, поставленном на основание единичной площади, содержится n0l рассеивателей; если каждый из них занимает площадь sс, то полная площадь, покрытая ими, равна n0lsc, а это как раз единичая площадь. Конечно, молекулы не покрывают всей площади целиком, потому что часть молекул прячется за соседние молекулы. Поэтому некоторые молекулы пройдут между столкновениями большее, чем l, расстояние. Ведь это только в среднем молекулам между столкновениями дается ровно столько времени, чтобы они смогли пройти расстояние l. Измеряя длину свободного пробега l, можно определить эффективное сечение рассеяния scи сравнить этот результат с расчетами, основанными на детальной теории строения атомов. Но это уже совсем другая тема! А пока вернемся к проблеме неравновесных состояний.
§ 3. Скорость дрейфа
Мы хотим описать поведение одной или нескольких молекул, которые чем-то отличаются от огромного большинства остальных молекул газа. Будем называть «большинство» молекул молекулами «фона», а отличающиеся от них молекулы получат название «особых» молекул, или (для краткости) S-молекул. Молекула может быть особой по целому ряду причин: она может быть, скажем, тяжелее молекул фона. Может она отличаться от них также химическим составом. А, может быть, особые молекулы несут электрический заряд — тогда это будет ион на фоне нейтральных молекул. Из-за необычности масс или зарядов на S-молекулы действуют силы, отличающиеся от сил между молекулами фона. Изучая поведение S-молекул, можно понять основные эффекты, которые вступают в игру во многих разнообразных явлениях. Перечислим некоторые из них: диффузия газов, электрический ток в батарее, осаждение, разделение при помощи центрифуги и т. д.
Начнем с изучения основного процесса: на S-молекулу в газе из молекул фона действуют какая-то особая сила F (это может быть сила тяжести или электрическая сила) и, кроме того, более обычные силы, обусловленные столкновениями с молекулами фона. Нас интересует общий характер поведения S-молекулы. Детальное описание ее поведения — это непрерывные стремительные удары и следующие одно за другим столкновения с другими молекулами. Но если проследить внимательно, то станет ясно, что молекула неуклонно движется по направлению силы F. Мы говорим, что дрейф накладывается на беспорядочное движение. Но нам хотелось бы знать, как зависит скорость дрейфа от силы F.
Если в какой-то произвольный момент времени начать наблюдать за S-молекулой, то можно надеяться, что попали мы как раз где-то между двумя столкновениями. Это время молекула употребит на то, чтобы в дополнение к скорости, оставшейся у нее после всех столкновений, увеличить составляющую скорости вдоль силы F. Немного погодя (в среднем через время t) она снова испытает столкновение и начнет двигаться по новому отрезку своей траектории. Стартовая скорость, конечно, будет другой, а ускорение от силы F останется неизменным.
Чтобы упростить сейчас дело, предположим, что после каждого столкновения наша S-молекула выходит на совершенно «свободный» старт. Это значит, что у нее не осталось никаких воспоминаний о прежних ускорениях под действием силы F. Такое предположение было бы разумным, если бы наша S-молекула была намного легче молекул фона, но это, конечно, не так. Позднее мы обсудим более разумное предположение.
А пока предположим, что все направления скорости S-молекулы после каждого столкновения равновероятны. Стартовая скорость имеет любое направление и не может дать никакого вклада в результирующее движение, поэтому мы не будем принимать во внимание начальную скорость после каждого столкновения. Но, кроме случайного движения, каждая S-молекула в любой момент имеет дополнительную скорость в направлении силы F, которая увеличивается со времени последнего столкновения. Чему равно среднее значение этой части скорости? Оно равно произведению ускорения F/m (где т — масса S-молекулы) на среднее время, прошедшее с момента последнего столкновения. Но среднее время, протекшее после последнего столкновения, должно быть равно среднему времени перед следующим столкновением, которое мы уже обозначили буквой t. Средняя скорость, порождаемая силой F,— это как раз скорость дрейфа; таким образом, мы пришли к соотношению
Vдр=Ft/m. (43.13)
Это наше основное соотношение, главное во всей главе. При нахождении t могут появиться всякого рода усложнения, но основной процесс определяется уравнением (43.13).
Обратите внимание, что скорость дрейфа пропорциональна силе. К сожалению, о названии для постоянной пропорциональности еще не договорились. Коэффициент перед силой каждого сорта имеет свое название. В задачах, связанных с электричеством, силу можно представить как произведение заряда на электрическое поле: F=qE; в этом случае постоянную пропорциональности между скоростью и электрическим полем Е называют «подвижностью». Несмотря на возможные недоразумения, мы будем применять термин подвижность для отношения скорости дрейфа к силе любого сорта. Будем писать
vдр=mF (43.14) и называть m, подвижностью. Из уравнения (43.13) следует
m=t/m. (43.15)
Подвижность пропорциональна среднему времени между столкновениями (редкие столкновения слабо тормозят S-молекулу) и обратно пропорциональна массе (чем больше инерция, тем медленнее набирается скорость между столкновениями).
Чтобы получить правильный численный коэффициент в уравнении (43.13) (а у нас он верен), нужна известная осторожность. Во избежание недоразумений нужно помнить, что мы используем коварные аргументы, и употреблять их можно только после осторожного и детального изучения. Чтобы показать, какие бывают трудности, хотя по виду вроде все благополучно, мы снова вернемся к тем аргументам, которые привели к выводу уравнения (43.13), но эти аргументы, которые выглядят вполне убедительно, приведут теперь к неверному результату (к сожалению, такого рода рассуждения можно найти во многих учебниках!).
Можно рассуждать так: среднее время между столкновениями равно т. После столкновения частица, начав двигаться со случайной скоростью, набирает перед следующим столкновением дополнительную скорость, которая равна произведению времени на ускорение. Поскольку до следующего столкновения пройдет время t, то частица наберет скорость (F/m)t. В момент столкновения эта скорость равна нулю. Поэтому средняя скорость между двумя столкновениями равна половине окончательной скорости, а средняя скорость дрейфа равна 1/2Ft/m. (Неверно!) Этот вывод неверен, а уравнение (43.13) правильно, хотя, казалось бы, в обоих случаях мы рассуждали одинаково убедительно. Во второй результат вкралась довольно коварная ошибка: при его выводе мы фактически предположили, что все столкновения отстоят друг от друга на время t. На самом деле некоторые из них наступают раньше, а другие позже этого времени. Более короткие времена встречаются чаще, но их вклад в скорость дрейфа невелика, потому что слишком мала в этом случае вероятность «реального подталкивания вперед». Если принять во внимание существование распределения свободного времени между столкновениями, то мы увидим, что множителю 1/2, полученному во втором случае, неоткуда взяться. Ошибка произошла из-за того, что мы, обманувшись простотой аргументов, попытались слишком просто связать среднюю скорость со средней конечной скоростью. Связь между ними не столь уж проста, поэтому лучше подчеркнуть, что нам нужна средняя скорость сама по себе. В первом случае мы с самого начала искали среднюю скорость и нашли ее верное значение! Быть может, теперь вам понятно, почему мы не пытались найти точного значения всех численных коэффициентов в наших элементарных уравнениях?
Вернемся к нашему предположению о том, что каждое столкновение полностью стирает из памяти молекулы все о былом ее движении и что после каждого столкновения для молекулы начинается новый старт. Предположим, что наша S-молекула — это тяжелый объект на фоне более легких молекул. Тогда уже недостаточно одного столкновения, чтобы отобрать у S-молекулы ее направленный «вперед» импульс. Только несколько последовательных столкновений вносят в ее движение «беспорядок». Итак, вместо нашего первоначального рассуждения предположим теперь, что после каждого столкновения (в среднем через время т) S-молекула теряет определенную часть своего импульса. Мы не будем исследовать детально, к чему приведет такое предположение. Ясно, что это эквивалентно замене времени t (среднего времени между столкновениями) другим, более длинным t, соответствующим среднему «времени забывания», т. е. среднему времени, за которое S-молекула забудет о том, что у нее когда-то был импульс, направленный вперед. Если понимать tтак, то можно использовать нашу формулу (43.15) для случаев, не столь простых, как первоначальный.
§ 4. Нонная проводимость
Применим наши результаты к частному случаю. Предположим, что в сосуде, заполненном газом, содержатся также ионы — атомы или молекулы с избыточным электрическим зарядом. Схематически это выглядит так, как на фиг. 43.2.
Фиг. 43.2. Электрический ток в ионизованном газе.
Если две противоположные стенки сосуда сделаны из металлических пластин, то их можно подсоединить к полюсам батареи и создать таким образом в газе электрическое поле.
Электрическое поле будет с некоторой силой воздействовать на ионы, и они начнут свой дрейф к одной из пластин. В результате возникнет электрический ток, и газ со своими ионами будет работать как сопротивление. Выразив через скорость дрейфа ионный поток, можно рассчитать величину сопротивления. Больше всего нас интересует зависимость ионного потока от приложенной к пластинам разности потенциалов V.
В нашем случае сосуд — это прямоугольный ящик, длина которого b, а площадь поперечного сечения А (см. фиг. 43.2). Если к пластинам приложена разность потенциалов V, то электрическое поле Е между пластинами равно V/b. (Электрический потенциал — это работа, совершаемая при переносе единичного заряда от одной пластины к другой. Сила, действующая на единичный заряд, равна Е. Если значение Е одинаково всюду между пластинами, что можно с достаточным основанием предположить в нашем случае, то затраченная на единичный заряд работа равна Eb, т. е. V=Eb.) В нашем случае на ионы действует сила qЕ, где q — заряд иона. Скорость дрейфа иона равна произведению силы на m:
vдр=mF=mq=mqV/b. (43.16)
Электрический ток I равен потоку заряда за 1 сек. Электрический ток через одну из пластин равен, таким образом, полному заряду ионов, достигающих пластины за 1 сек. Если ионы движутся к пластине со скоростью vдр, то за время Т пластины достигнут те ионы, которые находились не дальше, чем на расстоянии vдрT от нее. Если в единичном объеме содержится ni. ионов, то за время Т на пластине высадится niAvдрT ионов.
Каждый ион несет заряд q, поэтому
Собранный за время Т заряд=qniAvдрT. (43.17)
Ток / — это отношение собранного за время Т заряда к времени Т:
I=qniAvдр. (43.18)
Подставляя сюда скорость дрейфа vдр из (43.16), получаем
I=mq2ni(A/B)V. (43.19)
Мы выяснили, что ток пропорционален разности потенциалов, это и есть закон Ома, а сопротивление R равно обратной постоянной пропорциональности:
1/R=mq2ni(A/B). (43.20)
Мы нашли связь сопротивления со свойствами молекул niq и m, которое в свою очередь зависит от t и m. Если мы при помощи атомных измерений определим niи q, то, измеряя R, можно определить m, а потом и t.
§ 5. Молекулярная диффузия
Перейдем к другой задаче, для которой нам придется несколько изменить метод анализа, — к задаче о диффузии. Предположим, что мы взяли ящик, заполненный газом, находящимся в тепловом равновесии, а потом в любое место внутри ящика вспрыснули небольшое количество другого газа. Назовем первоначальный газ газом «фона», а новый газ — «особым» газом. Особый газ начинает распространяться по всему ящику, но распространение это замедляется наличием молекул фона. Явление такого замедленного распространения называется диффузией. Диффузия в основном определяется столкновениями молекул особого газа с молекулами фона. После многих столкновений особые молекулы более или менее равномерно распределятся по всему ящику. Важно не спутать диффузию газа с переносом больших количеств вещества в результате конвекционных токов. Обычно смешение двух газов происходит именно в результате комбинации конвекции и диффузии. Сейчас нас интересует только такое перемешивание, которое не сопровождается «порывами ветра». Газ распространяется только благодаря молекулярному движению, т. е. происходит диффузия. Давайте выясним, быстро ли происходит диффузия.
Итак, мы приступаем к вычислению общего потока молекул особого газа, порождаемого молекулярным движением. Общий поток не равен нулю только тогда, когда распределение молекул отличается от равновесного, иначе усреднение молекулярного движения сводит общий поток к нулю. Рассмотрим сначала поток в направлении оси х. Чтобы определить, чему этот поток равен, мы должны вообразить площадку, перпендикулярную к оси, и подсчитать число молекул, пересекающих эту площадку. Чтобы определить общий поток, мы должны считать положительными те молекулы, которые движутся в направлении положительных x, и вычесть из этого числа те молекулы, которые движутся в противоположном направлении. Как мы неоднократно убеждались, число молекул, пересекающих площадку в течение времени DT, равно числу молекул, находящихся к началу интервала DT внутри объема, заключенного между нашей площадкой и площадкой, расположенной от нее на расстоянии vDT. (Заметим, что здесь v — настоящая скорость молекулы, а отнюдь не скорость дрейфа.)
Мы упростим наши выкладки, если возьмем площадку единичной площади. Тогда число особых молекул, пересекающих площадку слева направо (справа от площадки лежат положительные x-направления), равно n_vDT, где n_ — число особых молекул в единичном объеме слева от площадки (с точностью до множителя ~1/6, но мы такими множителями пренебрежем!). Аналогично, число особых молекул, движущихся справа налево, равно n+vDT, где n+ — плотность особых молекул справа от площадки. Если мы обозначим молекулярный поток буквой J, под которой мы будем понимать общий поток молекул через единичную площадку за единицу времени, то получим
или
J=(n--n+)v. (43.22)
А что понимать под n-и n+? Когда мы говорим «плотность слева от площадки», то как далеко налево? Мы должны измерить плотность в том месте, откуда молекула отправляется в свой «свободный полет», потому что число стартующих молекул определяется числом молекул, находящихся в этом месте. Таким образом, n-— это плотность молекул на расстоянии длины свободного пробега l слева от нашей воображаемой площадки, а n+ — плотность молекул на расстоянии длины свободного пробега справа от нее.
Распределение особых молекул в ящике удобно описывать с помощью непрерывной функции х, у и z, которую мы обозначим na. Под na(х, у, z) нужно понимать плотность особых молекул в маленьком объеме вокруг точки (х, у, z). Тогда
разность (n+-n-) можно представить в виде
(n+-n-)=(dna/dx)Dx=(dna/dx) ·2l (43.23)
Подставляя этот результат в (43.22) и пренебрегая множителем 2, получаем
Jx=lv(dna/dx) (43.24)
Мы выяснили, что поток особых молекул пропорционален производной плотности, или, как иногда говорят, «градиенту плотности».
Ясно, что мы сделали несколько грубых приближений. Не говоря уже о том, что мы постоянно забывали о множителях, мы использовали v, когда нужно было ставить vx, а разместив объемы, содержащие молекулы n+и n-, на концах перпендикуляров к площадке, взяли перпендикуляры длиной l. Между тем для тех молекул, которые движутся не перпендикулярно к поверхности, l соответствует длине наклонного пути. Можно исправить эти недоделки; более тщательный анализ показал бы, что правую часть уравнения (43.24) нужно умножить на 1/3. Итак, более правильный ответ выглядит следующим образом:
Аналогичные уравнения можно написать для токов вдоль y- иz-направлений.
С помощью макроскопических наблюдений можно измерить ток Jхи градиент плотности dna/dx. Их отношение, найденное экспериментально, называется «коэффициентом диффузии» D, Это значит, что
Мы смогли показать, что ожидаемое значение коэффициента D для газа равно
Пока мы изучили в этой главе два разных процесса: подвижность (дрейф молекул под действием «внешней» силы) и диффузию (разбегание молекул, определяемое только внутренними силами, случайными столкновениями). Однако эти процессы связаны друг с другом, потому что в основе обоих явлений лежит тепловое движение, и оба раза в расчетах появлялась длина свободного пробега l.
Если в уравнение (43.25) подставить l=vt и t=mm, то получится
Ho mv2 зависит только от температуры. Мы еще помним, что
1/2mv2=3/2kT, (43.29)
так что
Jx=-mkT(dna/dx). (43.30)
Таким образом, D, коэффициент диффузии, равен произведению kT на m, коэффициент подвижности:
D=mkT. (43.31)
Оказывается, что (43.31) — это точное соотношение между коэффициентами. Хотя мы исходили из очень грубых предположений, не нужно к нему добавлять никаких дополнительных множителей. Можно показать, что (43.31) в самом деле всегда удовлетворяется точно. Это верно даже в очень сложных случаях (например, для случая взвешенных в жидкости мелких частиц), когда наши простые вычисления явно отказываются служить.
Чтобы показать, что (43.31) верно в самых общих случаях, мы выведем его иначе, используя только основные принципы статистической механики. Представьте себе, что почему-то существует градиент «особых» молекул и возник ток диффузии, пропорциональный, согласно (43.26), градиенту плотности. Тогда мы создадим в направлении оси х силовое поле так, что на каждую особую молекулу будет действовать сила F. По определению подвижности m скорость дрейфа дается соотношением
vдр=mF. (43.32)
Используя обычные аргументы, можно найти ток дрейфа, (общее число молекул, пересекающих единичную площадку за единицу времени):
Jдр=nаvдр. (43.33)
или
Jдр=namF. (43.34)
А теперь можно так распорядиться силой F, что ток дрейфа, вызываемый силой F, скомпенсирует диффузию, тогда полный ток особых молекул будет равен нулю. В этом случае мы имеем
Jх+Jдр=0,
или
D(dna/dx)=namF. (43.35)
В этом случае «компенсации» существует постоянный (во времени) градиент плотности, равный
dna/dx=namF/D. (43.36)
Теперь уже легко соображать дальше! Ведь мы добились равновесия, и можем теперь применять наши равновесные законы статистической механики. По этим законам вероятность найти молекулу около точки х пропорциональна ехр (-U/kT), где U — потенциальная энергия. Если говорить о плотности молекул nа, то это значит:
nа=n0e-UkT. (43.37) Дифференцируя (43.37) по х, получаем
или
В нашем случае сила F направлена вдоль оси х и потенциальная энергия U равна -Fx, a-dU/dx=F. Уравнение (43.39) принимает вид
[Это в точности уравнение (40.2), из которого мы и вывели ехр(-U/kT); круг замкнулся.] Сравнивая (43.40) и (43.36), мы получаем уравнение (43.31). Мы показали, что в уравнении (43.31), которое выражает ток диффузии через подвижность, все коэффициенты правильны, а само уравнение правильно всегда. Подвижность и диффузия тесно связаны. Эту связь открыл Эйнштейн.
§ 6. Теплопроводность
Методы кинетической теории, которую мы так успешно применяли, позволяют также рассчитать и теплопроводность газа. Если газ в верхней части ящика горячее, чем внизу, то тепло перетечет сверху вниз. (Мы предполагаем, что теплее верхняя часть ящика, потому что в противном случае возникнут поднимающиеся вверх конвекционные токи, а этот случай уже не имеет отношения к теплопроводности.) Перенос тепла от горячего газа к холодному вызывается диффузией «горячих» молекул (т. е. молекул с большой энергией) вниз и диффузией «холодных» молекул вверх. Чтобы вычислить поток тепловой энергии, мы должны узнать сначала об энергии, переносимой через выделенную площадку сверху вниз (ее переносят движущиеся вниз молекулы), потом об энергии, переносимой через эту же площадку снизу вверх (за это уже отвечают молекулы, поднимающиеся вверх). Разность этих потоков энергии даст нам полный поток энергии сверху вниз.
Теплопроводность c определяется как отношение скорости переноса тепловой энергии через единичную площадку к градиенту температуры:
Поскольку ход вычислений теплопроводности очень похож на вычисление потока заряженных частиц в ионизованном газе, то мы предлагаем читателю в виде упражнения доказать, что
при этом (g-1)kT —средняя энергия молекулы при температуре Т.
Если вспомнить о соотношении nlsc=1, то теплопроводность можно записать в виде
Мы получили поистине удивительный результат. Известно, что средняя скорость молекул газа зависит от температуры и не зависит от плотности. Можно думать, что sсзависит только от размеров молекул. Таким образом, наш очень простой вывод сводится к тому, что теплопроводность c (а следовательно, и скорость потока тепла в каждом частном случае) не зависит от плотности газа! Изменение числа «носителей» энергии при изменениях плотности в точности компенсируется изменением расстояния, которое пробегает «носитель» между столкновениями.
А теперь можно спросить: Действительно ли поток тепла всегда не зависит от плотности газа? Ну а если плотность стремится к нулю и в ящике совсем не остается газа? Конечно, нет! Формула (43.43), как и другие формулы этой главы, выведена в предположении, что средняя длина свободного пробега между столкновениями гораздо меньше любых размеров ящика. Если плотность газа столь мала, что молекула имеет неплохие шансы пробежаться от одной стенки ящика к другой, ни разу не столкнувшись, то все вычисления этой главы рухнут. В этих случаях следует вернуться к кинетической теории и заново все детально рассчитать.
Глава 44 ЗАКОНЫ ТЕРМОДИНАМИКИ
§ 1. Тепловые машины; первый закон
§ 2. Второй закон
§ 3. Обратимые машины
§ 4. Коэффициент полезного действия идеальной машины
§ 5. Термодинамическая температура
§ 6. Энтропия
§ 1. Тепловые машины; первый закон
До сих пор мы рассматривали свойства вещества с атомной точки зрения, причем мы пытались, хотя бы в общих чертах, понять, что произойдет, если принять, что вещество состоит из атомов, подчиняющихся тем или иным законам. Однако вещество обладает и такими свойствами, которые можно понять, не изучая подробно его строения. Поисками соотношений между различными свойствами вещества, не углубляясь в изучение внутреннего его строения, занимается термодинамика. Исторически термодинамика стала наукой еще до того, как более или менее точно узнали о внутреннем строении вещества.
Приведем пример: согласно кинетической теории, давление газа вызывается молекулярной бомбардировкой, и нам известно, что при нагревании газа бомбардировка усиливается и давление должно повыситься. И наоборот, если внутрь ящика с газом вдвигается поршень, преодолевающий сопротивление бомбардирующих его молекул, то энергия этих молекул возрастает, а соответственно повышается и температура. Итак, повышая температуру внутри заданного объема, мы увеличиваем давление. Если же мы сжимаем газ, то повышается его температура. Используя кинетическую теорию, можно найти количественные соотношения между этими двумя эффектами, однако каждому понятно, что между давлением и температурой обязательно должна существовать некоторая связь, не зависящая от деталей столкновений.
Рассмотрим еще один пример. Многим, наверное, известно интересное свойство резины — если растянуть ее, она нагреется. Если вы зажмете губами резиновую полоску и, потянув рукой, растянете ее, то отчетливо почувствуете, что она нагрелась. Это нагревание обратимо, т. е. если вы, продолжая держать полоску губами, быстро отпустите ее, то возникнет столь же отчетливое ощущение холода. Это означает, что при растяжении резина нагревается, а при ослаблении натяжения она охлаждается. Наш инстинкт может нам подсказать, что нагретая резина тянет лучше: если растяжение нагревает резину, то нагревание заставит ее сжаться. Действительно, если поднести к растягиваемой грузиком резиновой полоске газовую горелку, то мы заметим, что полоска резко сократится (фиг. 44.1).
Фиг. 44. 1. Нагретая резина.
Таким образом, при нагревании натяжение в резине возрастет, и это вполне согласуется с тем, что при уменьшении натяжения она остывает.
Скрытые в резине механизмы, управляющие этими эффектами, очень сложны. Мы опишем их с молекулярной точки зрения, хотя главная задача этой главы — научиться понимать связь между такими эффектами независимо от молекулярной модели. Тем не менее, именно исходя из молекулярной модели, мы можем показать, что оба эти явления тесно связаны. Поведение резины можно объяснить так. Представьте себе, что резина, по существу, огромный клубок, состоящий из очень длинных молекул, что-то вроде «молекулярных макарон», но с небольшим дополнительным усложнением: между этими молекулярными цепочками имеются соединительные цепочки. Таким образом, моделью куска резины могут служить слипшиеся во время варки макароны, образующие огромный ком. Когда мы растягиваем такой клубок, некоторые молекулярные цепи стремятся вытянуться в линию вдоль направления растяжения. В то же время все цепи участвуют в тепловом движении и непрерывно сталкиваются друг с другом. Поэтому такая цепь, когда ее растягивают, не остается в натянутом виде, так как об нее ударяют со всех сторон другие цепи и другие молекулы, и она будет вынуждена запутаться снова. Поэтому истинная причина того, почему резина все время стремится сократиться, заключается в следующем: при растяжении цепи действительно вытягиваются вдоль одной линии, но тепловые движения цепей стремятся запутать их снова и сократить их длину. Поэтому если растянуть цепи и увеличить температуру, то усилится и бомбардировка цепей, что приведет к увеличению натяжения. Этим объясняется способность нагретой резины поднять более тяжелый груз. Если растянутую в течение некоторого времени резину отпустить, то каждая цепь становится мягче, ударяющиеся о расслабленные цепи молекулы теряют энергию, и температура падает.
Итак, мы видели, как кинетическая теория устанавливает связь между сокращением при нагревании и остыванием при расслаблении, но было бы чересчур сложно пытаться вывести методами кинетической теории точные соотношения между этими эффектами. Нам пришлось бы для этого выяснить, сколько столкновений происходит ежесекундно и как выглядят молекулярные цепи. И вообще всех трудностей просто не перечислить. Детали механизма столь сложны, что кинетическая теория не в состоянии описать в точности все происходящее. Однако можно вывести некоторые соотношения между этими эффектами, практически ничего не зная о внутреннем механизме!
Вся термодинамика сводится примерно к таким рассуждениям: раз резина при высокой температуре «сильнее», чем при низкой, то с помощью тепла можно совершать самые разнообразные работы, скажем подымать грузы и передвигать их на новое место. И действительно, мы уже убедились, что нагретая резина способна поднимать тяжести. С изучения возможности использования тепла для совершения работы и начинается термодинамика. Можно ли построить машину, в которой используются тепловые свойства резины? Да, только выглядеть она будет глуповато. Для этого можно немного усовершенствовать велосипедное колесо, вставив туда резиновые спицы (фиг. 44.2).
Фиг. 44.2. Тепловая машина с резиновыми спицами.
Если с помощью двух ламп накаливания нагреть резину на одной стороне колеса, то она станет «сильнее», чем не нагретая резина на другой стороне. Центр тяжести колеса сдвинется и отойдет от точки опоры. Колесо повернется. После поворота холодные резиновые спицы пододвинутся поближе к теплу, а нагретые уступят им свое теплое место и остынут. И колесо будет медленно вращаться, пока будут гореть лампы. Коэффициент полезного действия такой машины чрезвычайно мал. Для вращения колеса едва хватает содержащейся в двух лампах мощности около 400 вт, а способно оно поднять лишь блоху! Однако тут же возникает интересный вопрос: нельзя ли более эффективно перевести тепло в работу?
Собственно говоря, термодинамика ведет свое начало с работ знаменитого инженера Сади Карно, который желал построить наилучшую и наиболее экономичную машину. Это один из немногих замечательных случаев, когда инженер заложил основы физической теории. На память приходит еще один пример, но уже сравнительно недавний — это анализ теории информации, сделанный Клодом Шенноном. Кстати, эти вопросы тесно связаны.
В паровой машине тепло используется для кипячения воды. Образующийся пар, расширяясь, толкает поршень, а поршень крутит маховик. Итак, пар вытолкнул поршень до отказа — что дальше? Эта порция пара свою работу выполнила, однако самое неразумное было бы закончить цикл выпуском пара в атмосферу, тогда к паровому котлу придется вновь подводить воду. Дешевле, а значит, и эффективнее отводить пар в другой сосуд, где он будет конденсироваться холодной водой, и образующуюся при этом воду можно будет снова вернуть в паровой котел, обеспечив непрерывную циркуляцию. Таким образом, паровая машина поглощает тепло и превращает его в работу. А может быть, лучше залить котел спиртом? Какими свойствами должно обладать вещество, чтобы обеспечить наилучшую работу машины? Этот вопрос задавал себе Карно и, размышляя таким образом, как мы уже сказали, попутно открыл соотношение очень общего типа.
Все результаты термодинамики содержатся в нескольких предельно простых утверждениях, называемых законами термодинамики. Во времена Карно первый закон термодинамики — закон сохранения энергии —был еще не известен. Однако аргументы были сформулированы Карно так точно, что они оказались правильными, хотя первый закон тогда не был еще открыт! Немного позже Клаузиус привел более простой вывод, который понять оказалось легче, чем очень тонкие рассуждения Карно. Но Клаузиус исходил из предположения, что сохраняется не полная энергия, а теплота; так считала в то время калорическая теория, которая впоследствии была вообще отвергнута как неверная. Поэтому часто говорят, что аргументы Карно были ложными. На самом же деле логика Карно безукоризненна. Неверно только упрощенное толкование этих аргументов Клаузиусом, а именно с ним все обычно знакомятся.
Так случилось, что так называемый второй закон термодинамики был открыт Карно раньше первого закона! Было бы очень интересно привести здесь аргументы Карно, не опирающиеся на первый закон. Но придется отказаться от этого, потому что мы изучаем физику, а не историю. С самого начала будем пользоваться первым законом, хотя многое можно было бы сделать и без него.
Сначала сформулируем первый закон, закон сохранения энергии: если нам дана система и мы подводим к ней тепло и производим над ней какую-то работу, то приращение энергии системы равно подведенному теплу и затраченной работе. Мы запишем все это так: к системе подводится тепло Q и над ней производится работа W, тогда энергия системы U возрастает; эту энергию иногда называют внутренней энергией. Связаны эти величины следующим соотношением:
Изменение U=Q+W. (44.1)
Изменение U можно получить, добавляя небольшое количество тепла DQ и небольшую работу DW:
DU=DQ+DW. (44.2)
Это — дифференциальная форма того же закона. Все это мы уже хорошо знаем из предыдущей главы.
§ 2. Второй закон
А что такое второй закон термодинамики? Мы знаем, что если при работе приходится преодолевать трение, то потерянная работа равна выделившемуся теплу. Если мы преодолеваем трение в комнате при температуре Т и делаем это достаточно медленно, то температура в комнате изменится ненамного. Мы превращаем работу в тепло при постоянной температуре. Ну, а можно ли поступить наоборот? Сумеем ли мы каким-то способом превратить тепло в работу при постоянной температуре? Второй закон термодинамики утверждает, что это невозможно. Было бы очень хорошо научиться превращать тепло в работу, изменив лишь направление процесса, похожего на трение. Если исходить только из закона сохранения энергии, можно считать, что тепловая энергия, например колебательная энергия молекул, способна служить удобным источником полезной энергии. Но Карно утверждал, что при постоянной температуре тепловую энергию нельзя извлечь из ее источника. Иначе говоря, если бы весь мир имел повсюду одинаковую температуру, то оказалось бы невозможным превратить тепловую энергию в работу. Хотя процессы, при которых работа переходит в тепло, могут идти при постоянной температуре, невозможно обратить их и вернуть работу обратно. Если говорить точно, Карно утверждал, что при постоянной температуре нельзя извлечь тепло из его источника и превратить в работу, не производя больше никаких изменений в заданной нам системе или в окружающем пространстве.
Последняя фаза очень важна. Предположим, что в запаянном контейнере находится сжатый воздух при постоянной температуре; мы позволили ему расшириться. Такое устройство может совершать работу; оно может привести в движение пневматический молоток. При расширении, например, воздух чуть-чуть охлаждается, но если в нашем распоряжении очень большое море, огромный тепловой резервуар, то мы снова сможем нагреть его. Итак, мы взяли из моря (резервуара) тепло и произвели работу при помощи сжатого воздуха. Однако Карно не ошибся. Ведь мы не сумели оставить все в системе без изменения. Чтобы сжать снова воздух, которому мы позволили расшириться, нам понадобится произвести дополнительную работу. Покончив с этим, мы обнаружим, что не только не смогли заставить систему работать при заданной температуре Т, но еще и сами вложили некую работу. Мы должны говорить только о таких случаях, когда полный результат всего процесса сводится к изъятию тепла и превращению его в работу, точно так же, как при преодолении трения конечный результат есть превращение работы в тепло. Если процесс сводится к движению по окружности, то систему можно вернуть точно в исходное положение, но конечным результатом этого процесса будет переход в тепло затраченной на преодоление трения работы. А можно ли обратить этот процесс? Повернуть, скажем, какую-нибудь ручку, чтобы все повернулось вспять, трение производило полезную работу, а моря остыли? Карно сказал, что этого не может быть. Давайте и мы предположим, что это невозможно.
Если бы это стало вдруг возможным, то это означало бы, что, помимо многих других полезных вещей, мы смогли бы, например, без всяких затрат отнять тепло у холодного тела и отдать его горячему. Между тем каждый знает, что тепло переходит от горячего тела к холодному.
Если мы просто приложим нагретое тело к холодному и больше ничего делать не будем, то, насколько известно, горячее тело никогда не станет горячее, а холодное — холоднее! Но если бы мы смогли произвести работу, отобрав тепло, скажем, у океана или от чего-нибудь еще, не изменив его температуры, то эту работу можно было бы, призвав на помощь трение, снова превратить в тепло, но уже при другой температуре. Например, второе плечо нашей воображаемой машины может тереться обо что-то, что и так уже нагрелось. Полный результат процесса в этом случае сводится к охлаждению «холодного» тела, в нашем случае океана, и нагреванию горячих трущихся частей машины. Гипотезу Карно, второй закон термодинамики, иногда формулируют так: тепло не может перетечь само собой от холодного тела к горячему. Но мы только что убедились в эквивалентности этих утверждений. Повторим их снова. Первое: нельзя осуществить процесс, единственным результатом которого является превращение тепла в работу при постоянной температуре. Второе: тепло не может перетечь само собой от холодного тела к горячему. Мы будем чаще пользоваться первой формулировкой.
Анализ работы тепловой машины, проделанный Карно, весьма похож на то, что мы делали в гл. 4 (вып. 1), когда изучали подъемные машины и рассуждали о законе сохранения энергии. Более того, приведенные там аргументы подсказаны аргументами Карно о работе тепловых машин. Поэтому некоторые рассуждения в этой главе покажутся вам уже знакомыми.
Предположим, что «котел» построенной нами тепловой машины поддерживается при температуре Т1. За счет отнятого у котла тепла Q1пар совершил работу W и выделил в «конденсоре» тепло Q2[температура конденсора равна Т2(фиг. 44.3)].
Фиг. 44.3. Схема тепловой машины.
Карно не уточнил, чему равно это тепло, потому что не знал первого закона и не предполагал, что Q2равно Q1потому что не верил этому. Многие считали, что Q1и Q2одинаковы, так предписывала калорическая теория. Но Карно этого не предполагал, в этом одна из тонкостей его аргументов. Если же использовать первый закон, то мы найдем, что выделенное тепло Q2равно теплу Q1за вычетом совершенной работы:
Q2=Q1-W. (44.3)
(Если бы наш процесс был циклическим и сконденсированная вода поступала бы снова в котел, то после каждого цикла при заданном количестве участвующей в цикле воды поглощалось бы тепло Q1и производилась бы работа W.)
А теперь построим другую машину и посмотрим, не сможем ли мы совершить большую работу при том же количестве тепла, выделяемого при температуре T1. В конденсоре будет поддерживаться та же температура Т2. Мы используем то же тепло Q1 из котла и попытаемся совершать большую работу, чем та, которая была произведена старой паровой машиной. Для этого, быть может, придется использовать другую жидкость, скажем спирт.
§ 3. Обратимые машины
Давайте разберемся в наших машинах получше. Одно из свойств всех машин нам уже известно. Если в машине есть трение, то неизбежны потери энергии. Наилучшей машиной была бы машина вообще без трения. Предположим, что мы имеем дело с теми же идеальными машинами, что и при изучении закона сохранения энергии, т. е. машинами, которым совсем не надо преодолевать трения.
А теперь обсудим аналог движения без трения — «лишенный трения» перенос тепла. Если мы приложим горячее тело к телу, обладающему более низкой температурой, то возникнет тепловой поток. Тепло течет от горячего тела к холодному, и, чтобы довернуть поток вспять, нужно слегка изменить температуру какого-нибудь одного тела. Но машина, лишенная трения, будет под действием сколь угодно малой силы послушно двигаться туда, куда ей приказывают, а когда сила будет действовать в другую сторону, охотно последует за ней. Аналогом машины без трения может служить устройство, в котором бесконечно малые изменения температуры могут повернуть тепловой поток вспять. Если разность температур конечна, то это невозможно. Но если тепло течет между двумя телами практически при одинаковой температуре и достаточно бесконечно малого изменения температуры, чтобы поток повернул в любом направлении, то поток считается обратимым (фиг. 44.4).
Фиг. 44.4. Обратимый перенос тепла.
Если нагреть слегка левую половину тела, тепло потечет вправо; если чуть-чуть охладить левую половину, тепло устремится влево. Итак, оказалось, что идеальной машиной является так называемая обратимая машина, в которой любой процесс обратим в том смысле, что малейшие изменения условий работы могут заставить машину работать в обратном направлении. Это означает, что машина не должна ни в каком месте иметь трения; в такой машине не должно быть также места, где тепло резервуара или пар котла прямо соприкасались бы с какими-то более холодными или более горячими частями.
Займемся идеальной машиной, в которой обратимы все процессы. Чтобы показать, что создание такой машины в принципе возможно, мы просто приведем пример рабочего цикла, причем нас не интересует возможность его практической реализации, достаточно того, что с точки зрения Карно он обратим.
Предположим, что в цилиндре, оборудованном поршнем без трения, имеется газ. Это не обязательно идеальный газ. Содержимое цилиндра вообще не обязано быть газом. Но для определенности будем считать, что в цилиндре идеальный газ. Предположим еще, что имеются две тепловые подушки Т1 и Т2— два очень больших тела, поддерживаемых при определенных температурах T1и Т2(фиг. 44.5).
Фиг. 44.5. Шаги цикла Карно.
а — шаг 1. Изотермическое расширения при t1, поглощается тепло Q1; 6 — шаг 2. Адиабатическое расширение; температура падает от T1, до Т2; в —шаг 3. Изотермическое сжатие при Т2; выделяется тепло Q2; г —шаг 4. Адиабатическое сжатие; температура поднимается от Т2, до T1.
Будем считать, что Т1больше Т2. Для начала нагреем газ и, положив цилиндр на подушку T1, позволим газу расшириться. Пусть по мере притока тепла в газ поршень очень медленно выдвигается из цилиндра. Тогда можно поручиться, что температура газа не будет сильно отклоняться от Т1. Если выдернуть поршень очень быстро, температура в цилиндре может упасть значительно ниже Т1и процесс уже нельзя будет считать полностью обратимым. Если же мы будем медленно вытаскивать поршень, температура газа останется близкой к температуре Т1. С другой стороны, если поршень медленно вдвигать обратно в цилиндр, температура станет лишь чуть-чуть повыше температуры Т1и тепло потечет вспять. Вы видите, что такое изотермическое (при постоянной температуре) расширение может быть обратимым процессом, если только производить его медленно и осторожно.
Чтобы лучше понять, что происходит, нарисуем кривую зависимости давления газа от его объема (фиг. 44.6).
Фиг. 44.6. Цикл Карно.
Когда газ расширяется, его давление падает. Кривая 1 показывает, как изменяются объем и давление, если в цилиндре поддерживается постоянная температура Т1. Для идеального газа эта кривая описывается уравнением PV=NkT1. Во время изотермического расширения по мере увеличения объема давление падает, пока мы не остановимся в точке b. За это время газ заберет из резервуара тепло Q1, ведь мы уже знаем, что если бы газ расширялся, не соприкасаясь с резервуаром, он бы остыл. Итак, мы закончили расширение в точке b. Давайте теперь: снимем цилиндр с резервуара и продолжим расширение.
Но теперь теплу уже неоткуда взяться. И снова мы медленно выдвигаем поршень, так что нет причины, почему бы процесс мог быть необратимым. Конечно, мы опять предполагаем, что трения нет. Газ продолжает расширяться, и температура падает, потому что связь с источниками тепла прервана.
Будем расширять газ так, чтобы расширение описывалось кривой 2 до тех пор, пока мы не достигнем точки с, где температура упадет до T2. Такое расширение без притока тепла называется адиабатическим. Мы уже знаем, что в случае идеального газа кривая 2 имеет вид PVg=const, где g — постоянная, большая единицы; поэтому адиабатическая кривая падает круче изотермической. Если температура газа в цилиндре
достигла Т2, то, положив цилиндр на вторую тепловую подушку, мы не рискуем вызвать температурных изменений.
Теперь можно медленно сжать газ, продвигаясь по кривой 3, причем цилиндр соприкасается с резервуаром при температуре t2(см. фиг. 44.5, шаг 2). Поскольку цилиндр соприкасается с резервуаром, его температура не может повыситься, но газу придется отдать резервуару тепло Q2при температуре T2. Продвинувшись по кривой 3 до точки d, мы снова снимем цилиндр с тепловой подушки при температуре Т2и продолжаем сжимать газ. На этот раз мы не станем отбирать у газа тепло. При этом поднимется температура, а давление пойдет по кривой 4. Если мы тщательно проделаем все этапы, то вернемся к исходной точке а при температуре Т1 иможем повторить цикл. По этой диаграмме судя, газ совершил полный цикл, отняв за это время тепло Q1при температуре T1и отдав тепло Q2 нри температуре T2. Этот цикл обратим, и поэтому мы можем шаг за шагом проделать весь путь в обратном направлении. Мы могли бы пойти назад, а не вперед, могли бы начать движение из точки а при температуре T1, двигаться по кривой 4, затем поглотить тепло Q2 при температуре T2 (для этого надо все время выдвигать поршень) и т. д., пока цикл не будет завершен. Если мы совершали цикл в одном направлении, то заставили газ работать, если же нам захотелось повернуть назад, то придется поработать самим.
Между прочим, легко сосчитать полную работу. Полная работа, совершаемая при расширении, равна произведению давления на изменение объема: ∫PdV. На нашей диаграмме мы откладывали Р вертикально, а V горизонтально. Если обозначать вертикальное расстояние буквой у, а горизонтальное буквой х, то мы получим интеграл ∫ydx, а это — площадь под кривой. Таким образом, площадь под каждой из пронумерованных кривых измеряет работу, совершенную либо газом, либо нами за соответствующий этап цикла. Легко понять, что чистый выход работы равен площади внутри кривых. Раз уж мы привели пример одной обратимой машины, то можно предположить, что возможно существование и других таких же устройств. Пусть обратимая машина А забирает Q1 при T1совершает работу W и возвращает какое-то количество тепла при температуре Т2. Предположим, что у нас есть еще одна машина В — творение рук человека, уже сконструированная, а может быть, еще и не изобретенная. Можно взять паровую машину, колесо с резиновыми спицами — словом, что угодно. Мы даже не интересуемся, обратима ли эта машина. Важно только, чтобы она забирала тепло Qlпри температуре Т1и возвращала часть этого тепла при более низкой температуре Т2. Предположим, что машина В совершает некую работу W'. Теперь покажем, что W' не может быть больше W; нет такой машины, которая работала бы лучше, чем обратимая. Но почему? Предположим, что W' больше W. Тогда мы можем забрать тепло Q1при температуре Т1и отдать его машине В. Эта машина совершит работу W' и отдаст какое-то количество тепла (неважно какое) резервуару с температурой Т2. После этого мы можем распорядиться какой-то частью работы W', которую мы считаем больше W. Прибережем пока часть работы W, а остаток W'-W употребим с пользой для себя (фиг. 44.7).
Фиг. 44.7. Машина В заставляет работать обратимую машину А в обратном направлении.
Обладая работой W, можно запустить машину А в обратном направлении, ведь это — обратимая машина. При этом она поглотит какое-то количество тепла из резервуара с температурой Т2, но зато вернет тепло Q1резервуару при температуре Т1. Каков чистый результат этого двойного цикла? Мы вернули все к исходному состоянию и совершили дополнительную работу W'-W. Дело свелось к тому, что мы извлекли энергию из резервуара с температурой Т2! Тепло Q1, взятое из резервуара с температурой T1 , было аккуратно возвращено. Раз это тепло все равно возвращается, то в качестве резервуара с температурой Т1можно взять что-нибудь поменьше океана и заключить это устройство внутрь составной машины А+В. Чистым результатом цикла такой машины будет изъятие из резервуара при температуре Т2тепла W'-W и превращение его в работу. Но извлечение полезной работы из резервуара при неизменной температуре без других изменений запрещается постулатом Карно. Этого нельзя сделать. Таким образом, не существует таких машин, которые извлекли бы некоторое количество тепла из резервуара при температуре Т1, возвратили бы какую-то его часть при температуре Т2и совершили большую работу, чем обратимая машина, работающая при тех же самых температурных условиях.
Предположим теперь, что машина В тоже обратима. Тогда, конечно, не только W' не больше W, но и W не больше W'. Чтобы доказать это, надо просто обратить предыдущие аргументы. Итак, если обе машины обратимы, то они должны производить одинаковую работу, и мы пришли к блестящему выводу Карно: если машина обратима, то безразлично, как она умудряется превращать тепло в работу. Произведенная машиной работа, если только машина поглощает определенное количество тепла при температуре Т1и возвращает какую-то его часть при температуре Т2, не зависит от устройства машины. Так уж устроен мир, и от частных свойств машины это не зависит.
Если бы мы нашли закон, определяющий работу, совершаемую при изъятии тепла Q1при температуре Т1и возвращении части этого тепла при температуре T2, то эта величина была бы универсальной постоянной, не зависящей от свойств вещества. Конечно, если нам известны свойства какого-нибудь вещества, мы можем вычислить интересующую нас величину. После этого мы будем вправе заявить, что все остальные вещества, если с их помощью построить обратимую машину, произведут точно такую же работу. Такова основная идея, ключ, с помощью которого мы можем найти последующие соотношения. Например, мы хотим узнать, насколько резина сжимается при нагревании и насколько она остывает, когда мы позволяем ей сжаться. Предположим, что мы взяли резину в качестве рабочего вещества обратимой машины и совершили обратимый цикл. Чистый результат, полная произведенная работа,— это универсальная функция, великая функция, не зависящая от свойств вещества. Таким образом, мы убеждаемся, что есть нечто, ограничивающее в известном роде разнообразие свойств вещества. Мы не можем сделать эти свойства какими захотим, не можем изобрести вещество, которое, будучи использованным в тепловой машине, произвело бы за обратимый цикл работу больше допустимой. Этот принцип, это ограничение,— единственное реальное правило, которое можно вывести из термодинамики.
§ 4. Коэффициент полезного действия идеальной машины
А сейчас попробуем найти закон, определяющий работу W как функцию Q1, Т1и Т2. Ясно, что W пропорционально Q1, ибо если две обратимые машины работают в параллель, то такая сдвоенная машина тоже будет обратимой машиной. Если каждая из этих машин поглощает тепло Q1, то обе сразу поглощают 2Q1, а работа, которую они совершают, равна 2 W и т. д. Поэтому пропорциональность W затраченному теплу Q1 вполне естественна.
После этого сделаем еще один важный шаг к универсальному закону. В качестве рабочего вещества машины можно взять одно вещество с хорошо известными нам свойствами. Воспользуемся этим и выберем идеальный газ. Можно и не делать этого, а вывести интересующее нас правило чисто логически, совсем не используя для этого какого-то вещества. Это одно из самых блестящих теоретических доказательств в физике, но пока мы используем менее абстрактный и более простой метод прямого вычисления.
Нам нужно лишь получить формулы для Q1и Q2 (ведь W=Q1-Q2) — тепла, которым машина обменивается с резервуарами во время изотермического расширения и сжатия. Для примера вычислим Q1— тепло, полученное от резервуара при температуре T1 во время изотермического расширения (кривая 1 на фиг. 44.6) от точки а, где давление равно pa, объем Va, температура Т1, до точки b, где давление равно рb, объем Vb, а температура та же самая T1. Энергия каждой молекулы идеального газа зависит только от температуры, а поскольку в точках а и b одинаковы и температура, и число молекул, то и внутренняя энергия тоже одинакова. Энергия U не изменяется; полная работа газа в период расширения
W=ab∫pdV
а
совершается за счет энергии Q1 , полученной из резервуара. Во время расширения pV=NkT1или
p-NkT1/V; значит,
т. е.
Q1=NkT1ln(Vb/Va).
Вот то тепло, которое взято из резервуара при температуре Т1. Точно так же можно вычислить и тепло, отданное при сжатии (кривая 3 на фиг. 44.6) резервуару при температуре T2:
Q2=NkT2ln(Vc/Vd). (44.5)
Чтобы закончить анализ, нужно еще найти соотношение между Vc/Vdи Vb/Va. Для этого взглянем сначала на кривую 2, которая описывает адиабатическое расширение от b до c. В это время pVgостается постоянным. Поскольку pV=NkT, то формулу для адиабатического расширения в конечных точках пути можно записать в виде (pV)Vg-1=const, или TVg-1=const, т. е.
T1Vbg-1=T2Vcg-1. (44.6)
Так как кривая 4 описывает адиабатическое сжатие от d до а, то
Т1Vag-1=T2Vdg-1. (44.6а)
Если поделить эти равенства одно на другое, то мы выясним, что отношения Vb/Vaи Vc/Vdравны, поэтому равны и логарифмы в (44.4) и (44.5). Значит,
Q1/T1=Q2/T2. (44.7)
Это и есть то соотношение, которое мы искали. Хотя оно доказано для машины с идеальным газом, мы уже знаем, что оно справедливо для любой обратимой машины.
А теперь посмотрим, как можно вывести этот универсальный закон на основании только логических аргументов, не интересуясь частными свойствами веществ. Предположим, что у нас есть три машины и три температуры Т1, Т2и Т3. Одна машина поглощает тепло Q1при температуре T1, производит работу W13и отдает тепло Q3при температуре T3(фиг. 44.8).
Фиг. 44.8. Спаренные машины 1 и 2 эквивалентны машине 3.
Другая машина работает при перепаде температур t2и Т3. Предположим, что эта машина устроена так, что она поглощает то же тепло Q3при температуре Т3и отдает тепло Q2. Тогда нам придется затратить работу W32, ведь мы заставили машину работать в обратном направлении. Цикл первой машины заключается в поглощении тепла Q1 и выделении тепла Q3при температуре Т3. Вторая машина в это время забирает из резервуара то же самое тепло Q3при температуре T3и отдает его в резервуар с температурой Т2. Таким образом, чистый результат цикла этих спаренных машин состоит в изъятии тепла Qlпри температуре Т1и выделении тепла Q2 при температуре T2. Эти машины эквивалентны третьей, которая поглощает тепло Qlпри температуре Т1, совершает работу W12и выделяет тепло Q2 при температуре Т2. Действительно, исходя из первого закона, можно сразу же показать, что W12=W13-W32:
W13-W32=(Q1-Q3)=(Q2-Q3)=Q1-Q2=W12 . (44.8)
Теперь можно получить закон, связывающий коэффициенты полезного действия машин. Ведь ясно, что между эффективностями машин, работающих при перепаде температур Т2-T3, t2-Т3и Т1-Т2, должны существовать определенные соотношения.
Сформулируем пояснее наши аргументы. Мы убедились, что всегда можем связать тепло, поглощенное при температуре T1 и тепло, выделенное при температуре T2, определив тепло, выделенное при какой-то другой температуре T3. Это значит, что мы можем описать все свойства машины, если введем стандартную температуру и будем анализировать все процессы с помощью именно такой стандартной температуры. Иначе говоря, если мы знаем коэффициент полезного действия машины, работающей между температурой Т и какой-то стандартной температурой, то сможем вычислить коэффициент полезного действия машины, работающей при любом перепаде температур. Ведь мы рассматриваем только обратимые машины, поэтому ничто не мешает нам спуститься от начальной температуры к стандартной, а потом снова вернуться к конечной температуре. Примем температуру в один градус за стандартную. Для обозначения выделяемого при стандартной температуре тепла используем особый символ Qs. Это значит, что если машина поглощает при температуре Т тепло Q, то при температуре в один градус она выделяет тепло QS. Если какая-то машина, поглощая тепло Q1 при T1, выделяет тепло QS при температуре в один градус, а другая машина, поглотив тепло Q2 при Т2, выделяет то же самое тепло QS при температуре в один градус, то машина, поглощающая Q1 при Т1 , должна при температуре Т2 выделять тепло Q2. Мы уже доказали это, рассмотрев три машины, работающие при трех температурах. Таким образом, для полного описания работы машин нам остается узнать совсем немного. Мы должны выяснить, сколько тепла Q1должна поглотить машина при температуре T1 , чтобы выделить при единичной температуре тепло QS. Конечно, между теплом Q и температурой Т существует зависимость. Легко понять, что тепло должно возрастать при возрастании температуры, ведь мы знаем, что если заставить работать машину в обратном направлении, то при более высокой температуре она отдает тепло. Легко также понять, что тепло Q1 должно быть пропорционально QS. Таким образом, наш великий закон выглядит примерно так: Каждому количеству тепла QS, выделенного при температуре в один градус, соответствует количество тепла, поглощенного машиной при температуре Т, равное QS, умноженному на некоторую возрастающую функцию Q температуры:
Q=QSf(T). (44.9)
§ 5. Термодинамическая температура
Пока мы не будем делать попыток выразить эту возрастающую функцию в терминах делений знакомого нам ртутного градусника, а взамен определим новую температурную шкалу. Когда-то «температура» определялась столь же произвольно. Мерой температуры служили метки, нанесенные на равных расстояниях на стенках трубочки, в которой при нагревании расширялась вода. Потом решили измерить температуру ртутным термометром и обнаружили, что градусные расстояния уже не одинаковы. Сейчас мы можем дать определение температуры, не зависящее от каких-либо частных свойств вещества. Для этого мы используем функцию f(T), которая не зависит ни от одного устройства, потому что эффективность обратимых машин не зависит от их рабочего вещества. Поскольку найденная нами функция возрастает с температурой, то мы можем считать, что она сама по себе измеряет температуру, начиная со стандартной температуры в один градус. Для этого надо только договориться, что
Q=QST, (44.10)
а
QS=S·1°. (44.11)
Это означает, что теперь мы можем найти температуру тела, определив количество тепла, которое поглощается обратимой машиной, работающей в интервале между температурой тела и температурой в один градус (фиг. 44.9)
Фиг. 44.9. Абсолютная термодинамическая температура.
Если машина забирает из котла в семь раз больше тепла, нежели поступает в одноградусный конденсор, то температура котла равна семи градусам и т. д. Таким образом, измеряя количество тепла, поглощаемого при разных температурах, мы определяем температуру. Полученная таким образом температура называется абсолютной термодинамической температурой и не зависит от свойств вещества. Теперь мы будем пользоваться исключительно этим определением температуры.
Теперь нам ясно, что если у нас имеются две машины, из коих одна работает при перепаде температур Т1и один градус, а другая — T2 и один градус, и обе они выделяют при единичной температуре одинаковое количество тепла, то поглощаемое ими тепло должно удовлетворять соотношению
Q1/T1=S=Q2/T2. (44.12)
Но это означает, что если какая-нибудь обратимая машина поглощает тепло q1при температуре Т1, а выделяет тепло Q2 при температуре Т2, то отношение Q1к T1 равно отношению Q2 к T2. Это справедливо для любой обратимой машины. Все, что будет дальше, содержится в этом соотношении: это центр термодинамической науки.
Но если это все, что есть в термодинамике, то почему же ее считают такой трудной наукой? А попробуйте описать поведение какого-нибудь вещества, если вам даже заранее известно, что масса вещества все время постоянна. В этом случае состояние вещества в любой момент времени определяется его температурой и объемом. Если известны температура и объем вещества, а также зависимость давления от объема и температуры, то можно узнать и внутреннюю энергию. Но кто-нибудь скажет: «А я хочу поступить иначе. Дайте мне температуру и давление и я скажу вам, каков объем. Я могу считать объем функцией температуры и давления и искать зависимость внутренней энергии именно от этих переменных». Трудности термодинамики связаны именно с тем, что каждый может подойти к задаче с того конца, с какого вздумает. Нужно только сесть и выбрать определенные переменные, а потом уж твердо стоять на своем, и все станет легко и просто.
Сейчас приступим к выводам. В механике мы подошли ко всем нужным нам результатам, исходя из центра механического мира F=ma. Такую же роль в термодинамике сыграет только что найденный нами принцип. Но какие выводы можно сделать, исходя из этого принципа?
Ну начнем. Сначала скомбинируем закон сохранения энергии и закон, связывающий Q1и Q2, чтобы найти коэффициент полезного действия обратимой машины. Первый закон говорит, что W=Q1-Q2. Согласно нашему новому принципу,
Q2=(T2/T1)Q1. Поэтому работа равна
W=Q1(l-T2/T1) =Q1(T1-T2)/T1. (44.13)
Это соотношение характеризует эффективность машины, т. е. количество работы, произведенное при заданной затрате тепла. Коэффициент полезного действия пропорционален перепаду температур, при котором работает машина, деленному на более высокую температуру:
К.п.д. =W/Q1=(T1-T2)/T1. (44.14)
Коэффициент полезного действия не может быть больше единицы, а абсолютная температура не может быть меньше нуля, абсолютного нуля. Таким образом, раз t2должна быть положительной, то коэффициент полезного действия всегда меньше единицы. Это наш первый вывод.
§ 6. Энтропия
Уравнение (44.7) или (44.12) может быть истолковано особо. При работе обратимых машин Q1/T1=Q2/T2, и тепло Q1при температуре Т1«эквивалентно» теплу Q2при температуре T2; ведь если поглощается Q1то всегда выделяется тепло Q2. Если теперь придумать для Q/T особое название, то можно сказать, что при обратимых процессах поглощается столько же Q/T, сколько и выделяется. Иначе говоря, Q/T не убывает и не прибывает. Эта величина Q/T называется энтропией, и мы говорим, что «за обратимый цикл изменение энтропии равно нулю». Если T=1°, то энтропия равна Q/1°; мы уже снабдили энтропию особым символом S=QS/1°. Энтропия повсюду обозначается буквой S, а численно она равна теплу (которое мы обозначили буквой QS), выделяемому в одноградусном резервуаре (энтропия не равна просто теплу, это тепло, деленное на температуру, и измеряется она в джоулях на градус).
Интересно, что, кроме давления, которое зависит от температуры и объема, и внутренней энергии (функции все тех же объема и температуры), мы нашли еще величину — энтропию вещества, которая тоже является функцией состояния. Постараемся объяснить, как вычислять энтропию и что мы понимаем под словами «функция состояния». Проследим за поведением системы в разных условиях. Мы уже умеем создавать разные условия экспериментально, например можно заставить систему расширяться адиабатически или изотермически. (Между прочим, машина не обязательно должна иметь только два резервуара, может быть и три, и четыре различные температуры, и машина будет обмениваться теплом с каждым из резервуаров.) Мы можем прогуляться по всей диаграмме pV, переходя от одного состояния к другому. Иначе говоря, можно перевести газ из состояния а в какое-нибудь другое состояние b и потребовать, чтобы переход из а в b был обратимым. Теперь предположим, что вдоль пути из а в b поставлены маленькие резервуары с разными температурами. Тогда каждый короткий шажок будет сопровождаться изъятием из вещества тепла dQ и передачей его в резервуар при температуре, соответствующей данной точке пути. Давайте свяжем все эти резервуары с помощью обратимых тепловых машин с одним резервуаром единичной температуры. После того как мы закончим перевод вещества из состояния а в состояние b, мы вернем все резервуары в их первоначальное состояние. Обратимая машина вернет каждую дольку тепла dQ, изъятого из вещества при температуре Т, и каждый раз при единичной температуре будет выделяться энтропия dS, равная
dS=dQ/T. (44.15)
Подсчитаем полное количество выделенной энтропии. Разность энтропии, или энтропия, нужная для перехода из а в b в результате какого-нибудь обратимого изменения, это — полная энтропия, т. е. энтропия, взятая из маленьких резервуаров и выделенная при единичной температуре:
Вопрос заключается в том, зависит ли разность энтропии от пути в плоскости pV? Из а b ведет много дорог. Вспомним, что в цикле Карно мы могли перейти из точки а в точку с (см. фиг. 44.6) двумя способами. Можно было расширить газ сначала изотермически, а потом адиабатически, а можно было начать с адиабатического расширения и окончить изотермическим. Итак, мы должны выяснить, меняется ли энтропия при изменении пути из а в b (фиг. 44.10).
Фиг. 44.10. Изменение энтропии при обратимом переходе.
Она не должна измениться, потому что если мы совершим полный цикл, выйдя из а в b по одному пути и возвратясь по другому, то это путешествие будет эквивалентно полному циклу обратимой машины. При таком цикле никакого тепла не передается одноградусному резервуару.
Поскольку мы не имеем права взять тепло из одноградусного резервуара, то при каждом путешествии из а в b приходится обходиться одним и тем же количеством энтропии. Это количество не зависит от пути, существенны только конечные точки. Таким образом, можно говорить о некоторой функции, которую мы назвали энтропией вещества. Эта функция зависит только от состояния вещества, т. е. только от объема и температуры.
Можно найти функцию S(V, Т). Мы подсчитаем изменение энтропии при обратимых изменениях вещества, следя за теплом, выделяемым в одноградусном резервуаре. Но это изменение можно выразить еще в терминах тепла dQ, изымаемого у вещества при температуре Т:
DS=∫dQ/T. (44.17)
Полное изменение энтропии равно разности энтропии в конечной и начальной точках пути:
Это выражение не определяет энтропию полностью. Пока известна лишь разность энтропии в двух разных состояниях. Определить энтропию абсолютно можно только после того, как мы сумеем вычислить энтропию одного какого-нибудь состояния.
Очень долго считалось, что абсолютная энтропия — это вообще ничего не значащее понятие. Но в конце концов Нернст высказал утверждение, названное им тепловой теоремой (иногда его называют третьим законом термодинамики). Смысл ее очень прост. Сейчас мы сообщим эту теорему, не объясняя, почему она верна. Постулат Нернста утверждает просто, что энтропия всякого тела при абсолютном нуле равна нулю. Тёперь мы знаем, при каких Т и V (при T=0) энтропия равна нулю, и сможем вычислить энтропию в любой другой точке.
Чтобы проиллюстрировать эту идею, давайте вычислим энтропию идеального газа. При изотермическом (а следовательно, обратимом) расширении ∫dQ/Tравен просто Q/T, потому
что Т постоянная. Таким образом, согласно (44.4), изменение энтропии равно
S(Va,T)-S(Vb,T)=Nkln(Va/Vb),
так что S(V,T)=NklnV плюс функция одной только температуры. А как S зависит от T? Мы уже знаем, что при адиабатическом расширении теплообмена нет. Таким образом, энтропия остается постоянной, хотя объем V изменяется, заставляя изменяться Т (чтобы сохранить равенство TVg-1=const). Ясно ли вам после этого, что
где а — постоянная, не зависящая ни от V, ни от Т? [Постоянная а называется химической постоянной. Она зависит от свойств газа, и ее можно определить экспериментально в соответствии с теоремой Нернста. Для этого надо измерить тепло, выделяемое газом при его охлаждении и конденсации до превращения его при 0° в твердое тело (гелий и при этой температуре остается
жидким). Потом надо найти интеграл ∫dQ/T. Можно найти а и
теоретически; для этого понадобятся постоянная Планка и квантовая механика, но в нашем курсе этого мы не будем касаться.]
Отметим некоторые свойства энтропии. Сначала вспомним, что на участке обратимого цикла между точками а и b энтропия меняется на Sb-Sa(фиг. 44.11).
Фиг. 44.11. Изменение энтропии за полный обратимый цикл. Полное изменение энтропии равно нулю.
Вспомним еще, что по мере продвижения вдоль этого пути энтропия (тепло, выделяемое при единичной температуре) возрастает в согласии с правилом dS=dQ/T, где dQ — тепло, изъятое из вещества при температуре Т.
Мы уже знаем, что после обратимого цикла полная энтропия всего, что включается в процесс, не изменяется. Ведь тепло Q1, поглощенное при T1, и тепло Q2, выделенное при Т2, вносят в энтропию равные по величине, но противоположные по знаку вклады. Поэтому чистое изменение энтропии равно нулю. Таким образом, при обратимом цикле энтропия всех участников цикла, включая резервуары, не изменяется. Это правило как будто похоже на закон сохранения энергии, но это не так. Оно применимо только к обратимым циклам. Если перейти к необратимым циклам, то закона сохранения энтропии уже не существует.
Приведем два примера. Для начала предположим, что какая-то машина с трением производит необратимую работу, выделяя тепло Q при температуре Т. Энтропия возрастет на Q/Т. Тепло Q равно затраченной работе, и когда мы производим какую-то работу с помощью трения о какой-то предмет, температура которого равна Т, то энтропия возрастает на величину W/Т.
Другой пример необратимости: если приложить друг к другу два предмета с разными температурами, скажем Т1и Т2, то от одного предмета к другому перетечет некоторое количество тепла. Предположим, например, что мы бросили в холодную воду горячий камень. Насколько изменяется энтропия камня, если он отдает воде тепло DQ при температуре T1? Она уменьшается на A DQ/T1. А как изменяется энтропия воды? Она возрастет на DQ/T2. Тепло, конечно, может перетечь только от более высокой температуры Т1к более низкой Т2. Поэтому если T1 больше Т2, то DQ положительно. Таким образом, изменение энтропии положительно и равно разности двух дробей:
DS=DQ/T2-DQ/T1. (44.19)
Итак, справедлива следующая теорема: в любом необратимом процессе энтропия всего на свете возрастает. Только обратимые процессы могут удержать энтропию на одном уровне. А поскольку абсолютно необратимых процессов не существует, то энтропия всегда понемногу растет. Обратимые процессы — это идеализированные процессы с минимальным приростом энтропии.
К сожалению, нам не придется углубиться в область термодинамики. Наша цель лишь проиллюстрировать основные идеи этой науки и объяснить причины, по которым возможно основываться на этих аргументах. Но в нашем курсе мы не будем часто прибегать к термодинамике. Термодинамикой широко пользуются в технике и в химии. Поэтому с термодинамикой вы практически познакомитесь в курсе химии или технических наук. Ну а дублировать нет смысла, и мы ограничимся лишь некоторым обзором природы теории и не будем вдаваться в детали для специальных ее применений.
Два закона термодинамики часто формулируют так:
Первый закон: Энергия Вселенной всегда постоянна. Второй закон: Энтропия Вселенной всегда возрастает.
Это не слишком хорошая формулировка второго закона. В ней ничего не говорится, например, о том, что энтропия не изменяется после обратимого цикла и не уточняется само понятие энтропии. Просто это легко запоминаемая форма обоих законов, но из нее нелегко понять, о чем собственно идет речь.
Все законы, о которых сейчас шла речь, мы собрали в табл. 44.1. А в следующей главе мы используем эту сводку законов, чтобы найти соотношение между теплом, выделяемым резиной при растяжении, и дополнительным натяжением резины при ее нагревании.
Таблица 44. 1 · ЗАКОНЫ ТЕРМОДИНАМИКИ
* Раньше мы определяли температурную шкалу иначе. Мы утверждали, что средняя кинетическая энергия молекулы идеального газа пропорциональна температуре или, согласно закону идеального газа, что pV пропорционально Т. Эквивалентно ли это новому определению? Да. Ведь окончательный результат (44.7), выведенный из закона идеального газа, совпадает с приведенным здесь результатом. Мы еще поговорим об этом в следующей главе.
Глава 45 ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ
§ 1. Внутренняя энергия
§ 2. Применения
§ 3. Уравнение Клаузиуса –Клайперона
§ 1. Внутренняя энергия
Когда приходится использовать термодинамику для дела, то оказывается, что она очень трудный и сложный предмет. В этой книге, однако, мы не будем залезать в самые дебри. Эта область особенно интересна для химиков и инженеров, и тем, кому захочется получше познакомиться с ней, следует обратиться к физической химии или инженерной термодинамике. Есть еще ряд хороших справочных книг, в которых эта тема обсуждается более подробно.
Термодинамика сложна потому, что каждое явление она позволяет описывать многими способами. Если нам нужно описать поведение газа, то мы можем исходить из того, что его давление зависит от температуры и объема, а можно предположить, что объем зависит от давления и температуры. То же самое и с внутренней энергией U: можно сказать, что она определяется температурой и объемом, стоит только выбрать именно эти переменные, но можно говорить о зависимости от температуры и давления или от давления и объема и т. д. В предыдущей главе мы познакомились с другой функцией температуры и объема, называемой энтропией S. И теперь ничто не помешает нам построить другие функции этих переменных. Например, функция U-TS тоже зависит от температуры и объема. Таким образом, нам приходится иметь дело с большим количеством разных величин, зависящих от разнообразных комбинаций переменных.
Чтобы упростить понимание этой главы, договоримся с самого начала выбрать в качестве независимых переменных температуру и объем. Химики используют для этого температуру и давление, потому что их легче измерять и контролировать в химических реакциях. Но мы используем повсюду в этой главе температуру и объем и изменим этому только в одном месте, чтобы посмотреть, как совершается переход к химическим переменным.
Итак, сначала рассмотрим только одну систему независимых переменных — температуру и объем. Затем нас будут интересовать только две функции этих переменных: внутренняя энергия и давление. Все другие термодинамические функции можно получить с помощью этих двух, но не обязательно это делать именно сейчас. Даже после таких ограничений термодинамика останется еще трудным предметом, но все же уже не столь невозможным для понимания!
Сначала немного займемся математикой. Если величина есть функция от двух переменных, то дифференцировать ее придется осторожнее, чем мы это делали раньше, имея дело с одной переменной. Что мы понимаем под производной давления по температуре? Изменение давления, сопровождающее изменение температуры, разумеется, зависит от того, что случилось с объемом, пока менялась температура. Прежде чем понятие производной по температуре обретет ясный смысл, надо сказать что-то определенное об изменении объема. Например, можно спросить, какова скорость изменения Р относительно Т при постоянном объеме. Тогда отношение изменений обеих этих величин, по существу, обычная производная, которой привыкли присваивать символ dP/dT. Мы обычно используем особый символ дР/дТ, он напоминает нам, что Р зависит, кроме Т, еще и от переменной V, и эта переменная не изменяется. Чтобы подчеркнуть тот факт, что V не изменяется, мы не только используем символ д, но еще пометим индексом остающуюся постоянной переменную (дР/дТ)у. Конечно, поскольку имеются только две независимые переменные, то это обозначение излишне, но оно, быть может, поможет нам легче пройти сквозь термодинамические дебри частных производных.
Предположим, что функция f(x, у) зависит от двух независимых переменных х и у. Под символом (дf/дх)умы понимаем самую обычную производную, получаемую общепринятым способом, если у постоянна:
Аналогично определяется и
Например, если f(x, у)=х2+ух, то (df/dx)y=2x+y, а (дfду)х=х. Мы можем распространить это на старшие производные:
д2f/дy2или д2f/дудх.
Последний случай означает, что сначала f продифференцировано по х, считая у постоянным, а затем результат продифференцирован по у, но теперь постоянным стало х. Порядок дифференцирования не имеет значения:
д2fldxdy=д2f/дyдx.
Нам придется подсчитывать изменение Df, происходящее с f(x, у), если х переходит в х+Dх, а у переходит в y+Dy. Будем предполагать, что Dx и Dy бесконечно малы:
Последнее уравнение и есть основное соотношение, связывающее приращение Df с Dx и Dy.
Посмотрим, как используется это соотношение; для этого вычислим изменение внутренней энергии U(Т,V), если температура Т переходит в Т+DT, а объем V переходит в V+DV. Используем формулу (45.1) и запишем
В предыдущей главе мы нашли другое выражение для изменения внутренней энергии DU; тогда к подводимому газу прибавлялось тепло DQ:
DU==DQ-РDV. (45.3)
Сравнив (45.2) и (45.3), можно было бы подумать, что P=(дU/дV)T, но это не так. Чтобы получить верный результат, сначала предположим, что газ получает тепло DQ, причем объем его не изменяется, так что DV=0. Если DV=0, то уравнение (45.3) говорит нам, что DU=DQ, а уравнение (45.2) утверждает, что DU=(дU/дT)VDT, поэтому (дU/дT)v=DQ/DT. Отношение DQ/DT—количество тепла, которое нужно подвести к телу, чтобы изменить его температуру на один градус, удерживая объем постоянным,— называется удельной теплоемкостью при постоянном объеме и обозначается символом CV, Таким образом, мы
показали, что
Теперь снова подведем к газу тепло DQ, но на этот раз договоримся, что температура газа останется постоянной, а объему мы позволим измениться на DV. В этом случае анализ сложнее, но мы можем вычислить DU, используя аргументы Карно, для чего нам придется снова призвать на помощь цикл Карно из предыдущей главы.
Диаграмма давление — объем для цикла Карно изображена на фиг. 45.1. Мы уже показали, что полная работа, совершаемая газом при обратимом цикле, равна DQ(DT/T), где DQ — тепло, подводимое к газу при температуре Т во время изотермического расширения от V до V+DV, а Т—DТ — это конечная температура, которой достигает газ при адиабатическом расширении на втором этапе цикла. Сейчас мы покажем, что эта работа равна, кроме того, заштрихованной площади на фиг. 45.1. Работа газа
во всех случаях жизни равна ∫PdV; она положительна, если
газ расширяется, и отрицательна, когда он сжимается. Если вычертить зависимость Р от V, то изменения Р и V изобразятся кривой, в каждой точке которой определенному значению Р соответствует определенное значение V. Работа, произведенная газом, пока его объем изменяется от одного значения до другого
(интеграл ∫PdV),— это площадь под кривой, соединяющей начальное и конечное значения V. Применим эту идею к циклу Карно и убедимся, что если обойти цикл, помня о знаке совершенной газом работы, то чистая работа газа будет равна заштрихованной на фиг. 45.1 площади.
Фиг. 45.1. Диаграмма Р — V для цикла Карно.
Кривые, помеченные Т и Т—DТ,— изотермы; крутые кривые между ними — адиабаты. Когда газ изотермически расширяется при температуре Т, он получает тепло DQ и увеличивает свой объем на DV; DР—изменение давления при постоянном объеме, температура в это время падает с Т до Т—DT.
А теперь вычислим эту площадь чисто геометрически. Цикл, который был использован для получения фиг. 45.1, отличается от цикла, описанного в предыдущей главе тем, что теперь DQ и DT бесконечно малы. Наши адиабаты и изотермы очень близки друг к другу, поэтому фигура, описанная жирными линиями на фиг. 45.1, приближается к параллелограмму, когда приращения DQ и DТ стремятся к нулю. Площадь этого параллелограмма в точности равна DVDP (где DV — изменение объема, когда к газу подводится энергия DQ при постоянной температуре, а DР — изменение давления при изменении температуры на DT и постоянном объеме). Легко показать, что заштрихованная площадь на фиг. 45.1 равна площади, ограниченной пунктиром на фиг. 45.2. А эту фигуру легко превратить в прямоугольник со сторонами DР и DV, для чего нужно лишь вырезать из нее треугольники и сложить их немного иначе.
Соберем все наши выводы вместе.
Выражение (45.5) содержит в себе суть результатов, следующих из аргументов Карно. Всю термодинамику можно вывести из (45.5) и первого закона, содержащегося в уравнении (45.3). Выражение (45.5)— это, в сущности, второй закон, хотя впервые Карно сформулировал его несколько иначе, поскольку не пользовался нашим определением температуры.
А теперь можно приступить к вычислению (дUlдV)T. Насколько изменится внутренняя энергия U, если объем изменится на DV? Во-первых, внутренняя энергия U меняется за счет подводимого тепла и, во-вторых, за счет совершаемой работы. Подводимое тепло, согласно (45.5), равно
DQ=(dP/дT)VDV,
а совершаемая над веществом работа равна —PDV. Поэтому изменение DU складывается из двух кусков
Поделив обе стороны на DV, мы найдем скорость изменения U относительно V при постоянной Т
В нашей термодинамике, где есть только две переменные, Т и V, и только две функции, Р и U, уравнения (45.3) и (45.7) — это основные уравнения, из которых можно вывести все последующие результаты.
§ 2. Применения
Теперь обсудим смысл уравнения (45.7) и посмотрим, почему оно дает ответ на поставленные в предыдущей главе вопросы. Мы занимались рассмотрением такой задачи: в кинетической теории ясно, что рост температуры приводит к увеличению давления, потому что усиливается бомбардировка поршня атомами. Те же физические причины приводят к тому, что при выталкивании поршня от газа отбирается тепло, и чтобы удержать температуру постоянной, надо позаботиться о подводе тепла. При расширении газ остывает, а при нагревании его давление возрастает. Между этими явлениями должна существовать какая-то связь, и она полностью определяется уравнением (45.7). Если мы удерживаем объем постоянным и поднимаем температуру, давление растет со скоростью (дР/дТ)V. Вот мы и нашли эту связь: если увеличить объем и не подвести какого-то количества тепла для поддержания температуры, то газ остынет, а величина (дU/дV)Tподскажет нам, сколько именно надо подбавить тепла. Уравнение (45.7) выражает фундаментальную связь между этими двумя эффектами. Именно это мы обещали найти, отправляясь на поиски законов термодинамики. Не зная внутреннего строения газа и лишь веря, что построить вечный двигатель второго рода выше наших сил, мы смогли вывести соотношение между количеством тепла, необходимого для поддержания постоянной температуры при расширении газа, и изменением давления газа при нагревании!
Получив от газа все, что нужно, рассмотрим другой случай— резину. Растянув резиновую полоску, мы обнаружили, что ее температура возросла, а нагревание заставило ее сжаться. Какое уравнение дает в случае резины тот же результат, что и уравнение (45.3) для газа? Сначала все идет, как и раньше: когда к резине подводится тепло DQ, внутренняя энергия изменяется на DU и производится какая-то работа. Только теперь эта работа равна —FDL вместо PDV, где F — это приложенная к резине сила, a L — длина резиновой полоски. Сила F зависит от температуры и длины резиновой полоски. Заменив в (45.3) PDV на —FDL, получим
DU=DQ+FDL. (45.8)
Сравнивая (45.3) и (45.8), мы убедимся, что уравнение для резины получилось сразу после замены одних букв другими. Если заменить V на L, а Р на —F, то все аргументы цикла Карно окажутся применимыми и к резине. Можно тотчас же, скажем, вывести, что нужное для растяжения на DL тепло DQ определяется уравнением, аналогичным (45.5): DQ=—Т(дF/дТ)LDL. Это уравнение говорит нам, насколько увеличится сила, если длина резиновой полоски при нагревании останется постоянной. Надо только узнать, сколько тепла требуется для поддержания постоянной температуры при небольшом растяжении полоски. Итак, мы видим, что и к резине, и к газу применимы одни и те же уравнения. Можно даже писать DU=DQ+ADB, где А и В — самые разные величины, сила и длина, давление и объем и т. д. Если интересует поведение газа, нужно заменить A и В на Р и V.
Для примера рассмотрим разность электрических потенциалов, или электродвижущую силу (э. д. с.) батареи Е, и заряд DZ, прошедший через батарею. Мы знаем, что работа, производимая обратимой электрической батареей, например аккумулятором, равна EDZ. (Поскольку мы не включили в рассмотрение член PDV, то придется потребовать, чтобы объем оставался постоянным.) Посмотрим, что скажет о работе батареи термодинамика. Если заменить Р на Е, а V на Z, то вместо уравнения (45.6) получится
Это уравнение говорит нам, что при путешествии заряда DZ по батарее меняется внутренняя энергия U. Но почему DU/DZ — это не просто э. д. с. батареи E? Дело в том, что в реальных обстоятельствах движение зарядов внутри батареи вызывает выделение тепла. Внутренняя анергия батареи изменяется, во-первых, за счет работы, производимой батареей во внешней цепи, и, во-вторых, за счет нагревания батареи. Интересно, что вторую часть изменения внутренней энергии опять-таки можно подсчитать, следя, как меняется э. д. с. батареи при изменении температуры. Между прочим, когда заряды текут по батарее, там происходят химические реакции, и уравнение (45.9) указывает на отличный способ измерения необходимой для реакции энергии. Для этого нам нужно лишь сделать батарею, работающую на этой реакции, и сначала просто измерить э. д. с., а потом проследить, как меняется э. д. с. с температурой, если ни один заряд не выпускается из батареи!
Мы предположили, что объем батареи можно поддерживать постоянным, только поэтому мы позволили себе пренебречь членом PDV и считать, что работа батареи равна EDZ. Но оказывается, что поддерживать объем постоянным технически очень трудно. Гораздо легче держать батарею под постоянным атмосферным давлением. Вот почему химики не любят только что написанных нами уравнений: они предпочитают уравнения, которые были бы связаны с постоянным давлением. Мы с самого начала этой главы за независимые переменные приняли V и Т. Химикам больше нравятся Р и Т, поэтому посмотрим теперь, как преобразуются наши выводы при переходе к химической системе переменных. Постарайтесь при этом не ошибиться, потому что мы как-никак сменили детали и перешли от Т и V к Т и Р.
Начнем с (45.3), где DU=DQ-PDV; член PDV можно заменить на EDZ или даже на АDВ. Если бы нам удалось как-нибудь заменить PDV на VDP, тогда V и Р поменялись бы ролями и химики остались бы довольны. Тот, кто сообразителен, заметит, что дифференциал произведения PV равен d(PV)=PdV+VdP. Добавив это равенство к (45.3), он получит
Чтобы все наши последующие выводы походили на выводы из уравнения (45.3), давайте будем считать U+PV какой-то новой функцией, назовем ее энтальпией Н, и напишем в таком виде: DH=DQ+VDP.
Вот теперь мы готовы перевести все наши рассуждения на химический язык, надо только помнить, что U®H, Р®V, V®P. Химики считают, что вся термодинамика содержится не в уравнении (45.7), а в уравнении
Выяснив, как происходит переход к химическим переменным Т и Р, вернемся к нашим старым переменным. Теперь и уже до конца главы нашими независимыми переменными будут Т и V. Сейчас давайте применим полученные результаты к некоторым физическим процессам. Сначала рассмотрим идеальный газ. Из кинетической теории известно, что внутренняя энергия газа зависит только от характера движения молекул и от их числа. Внутренняя энергия зависит только от Т, а к V она безразлична. Если изменять V при постоянной Т, то U не изменится. Значит, (dU/dV)T=0, и уравнение (45.7) говорит нам, что для идеального газа
Т(дP/дT)V-Р =0. (45.10)
Уравнение (45.10) — это дифференциальное уравнение, и оно кое-что расскажет нам о Р. Мы расправимся с частной производной так: поскольку частная производная вычислена при постоянном V, можно заменить частную производную обычной, только надо помнить, что все это делается «при постоянном V». Уравнение (45.10) тогда принимает вид
Т=DP/DT-P=0 (при постоянном V), (45.11)
интегрирование не составит для нас труда, и мы получим lnP=lnТ+const (при постоянном V),
P=constXT (при постоянном V). (45.12)
Мы знаем, что давление идеального газа равно
Р=RT/V. (45.13)
Это соотношение совместимо с (45.12), потому что R и V — постоянные. Но зачем же мы мучились, решая эти уравнения? Ведь результат-то был уже известен. Потому что мы пользовались двумя независимыми определениями температуры! Однажды мы предположили, что кинетическая энергия молекул пропорциональна температуре. Это предположение привело нас к температурной шкале, которую мы назвали шкалой идеального газа. Температура Т в уравнении (45.13) отсчитывается по газовой шкале. Мы называли отсчитанную по газовой шкале температуру кинетической температурой. Потом мы определили температуру иначе, и это определение вообще не нуждалось ни в каком веществе. Исходя из второго закона, мы определили то, что можно назвать «абсолютной термодинамической температурой» Т; она появляется в уравнении (45.12). Здесь мы только доказали, что давление идеального газа (идеальный газ для нас нечто, чья внутренняя энергия не зависит от объема) пропорционально абсолютной термодинамической температуре. Мы, кроме того, знаем, что давление пропорционально температуре, измеренной по газовой шкале. Таким образом, можно заключить, что кинетическая температура пропорциональна «абсолютной термодинамической температуре». Это, конечно, означает, что если бы мы были благоразумны, то показания обеих шкал могли бы всегда жить в согласии. В конце концов эти шкалы можно выбрать так, что они совпадут; постоянную пропорциональности можно положить равной единице. Очень долго люди сами себе создавали трудности, но наконец превратили две шкалы в одну!
§ 3. Уравнение Клаузиуса— Клайперона
Испарение жидкости — это еще одна область, в которой можно применить наши результаты. Предположим, что мы вдвигаем поршень в цилиндр с каким-то веществом.
Естественно задать себе вопрос: как зависит давление от объема, если температура остается постоянной? Иначе говоря, мы хотим начертить изотермические линии на диаграмме Р—V. Вещество в цилиндре — это далеко не идеальный газ, с которым мы имели дело; теперь это жидкость или пар, а может быть, и то и другое вместе. Если сжать вещество достаточно сильно, то оно начнет превращаться в жидкость. Если мы будем увеличивать давление, объем изменится очень мало, а наши изотермы при уменьшении объема пойдут резко вверх, как это показано в левой части фиг. 45.3.
Фиг. 45.3. Изотермы конденсирующегося пара.
Пар сжимается в цилиндре. Слева — все вещество превратилось в жидкость; справа — вся жидкость испарилась; в середине — в цилиндре сосуществуют жидкость и пар.
Если увеличивать объем, выдвигая поршень из цилиндра, давление будет падать, пока мы не достигнем точки кипения жидкости и в цилиндре появится пар. Дальнейшее вытягивание поршня приведет к более сильному испарению. Когда цилиндр заполнен частично паром, а частично жидкостью, то между ними устанавливается равновесие — жидкость испаряется, пар конденсируется, и скорости этих процессов равны. Если предоставить пару больший объем, то, чтобы удержать прежнее давление, понадобится больше пара. Поэтому, хоть жидкость все испаряется, давление остается прежним. Вдоль плоской части кривой на фиг. 45.3 давление не изменяется, это давление называется давлением пара при температуре Т. Если объем все увеличивается, наступит момент, когда запасы жидкости иссякнут. В такой ситуации давление падает при увеличении объема, ведь теперь мы имеем дело с обычным газом; это изображено в правой части диаграммы Р—V. Нижняя кривая на фиг. 45.3— это изотермическая кривая при более низкой температуре Т—DT. Давление жидкости в этом случае немного меньше, потому что с ростом температуры жидкости расширяются (не все жидкости, вода около точки замерзания поступает наоборот), а давление пара при уменьшении температуры, конечно, падает.
Из двух изотерм можно снова построить цикл, соединив концы их плоских участков (скажем, адиабатами), как это показано на фиг. 45.4. Небольшая зазубрина в нижнем правом углу фигуры несущественна, и мы просто забудем о ней. Используем аргументы Карно, которые показывают, как связано тепло, подведенное к жидкости для превращения ее в пар, с работой, совершаемой веществом при обходе цикла. Пусть L—это тепло, необходимое для испарения жидкости в цилиндре. Вспомним, как мы рассуждали при выводе уравнения (45.5), и немедленно скажем, что L(DT/T) равно работе, совершенной веществом. Как и раньше, работа вещества равна площади, заключенной внутри цикла. Эта площадь приблизительно равна DP(VG—VL), где DР — разность давлений пара при температурах Т и Т—DT, VG — объем газа, a VL—объем жидкости. Оба объема надо измерять при давлении, равном давлению пара.
Сравнивая два выражения для работы, мы получаем L(DT/T)= DP(VG-VL), или
Уравнение (45.14) связывает скорость изменения давления пара с температурой и количеством тепла, необходимым для испарения жидкости. Хотя вывел его Карно, называется оно уравнением Клаузиуса — Клайперона.
Сравним уравнение (45.14) с результатом, следующим из кинетической теории. Обычно VG гораздо больше VL. Поэтому VG-VL»VG=RT/P на моль. Если еще предположить, что L — не зависящая от температуры постоянная (хотя это не очень хорошее приближение), то мы получим dP/8T=L/(RT2P). Вот решение этого дифференциального уравнения:
P=const·e-L/RT. (45.15)
Надо выяснить, в каких отношениях находится это выражение с полученной ранее с помощью кинетической теории зависимостью давления от температуры. Кинетическая теория говорит, хотя и очень неопределенно, что число молекул пара над жидкостью примерно равно
где UG—UL— разность отнесенных к молю внутренних энергий газа и жидкости. Термодинамическое уравнение (45.15) и кинетическое уравнение (45.16) очень похожи, потому что давление равно nkT, но все-таки это разные уравнения. Однако их можно сделать одинаковыми, если заменить старое предположение L=const предположением о том, что L—UG=const. Если предположить, что L—UG — не зависящая от температуры постоянная, то соображения, из которых ранее следовало (45.15), приведут теперь к уравнению (45.16).
Это сравнение показывает преимущества и недостатки термодинамики по сравнению с кинетической теорией. Прежде всего полученное термодинамически уравнение (45.14) — это точное соотношение, а (45.16) — всего-навсего приближение. Ведь нам пришлось предположить, что U приблизительно постоянна и что наша модель верна. Во-вторых, нам, быть может, никогда не удастся понять до конца, как газ переходит в жидкость, и все-таки уравнение (45.14) правильно, а (45.16)— это только приближение. В-третьих, хотя мы говорили о превращении газа в жидкость, наши аргументы верны для любого перехода из одного состояния в другое. Например, переход твердое тело — жидкость описывается кривыми, очень похожими на кривые фиг. 45.3 и 45.4.
Фиг. 45.4. Диаграмма Р — V для цикла Карно с конденсирующимся в цилиндре паром.
Слева — все вещество переходит в жидкость. Чтобы полностью испарить ее при температуре Т, нужно добавить тепла L. При падении температуры от Т до Т—DT пар расширяется адиабатически.
Вводя скрытую теплоту плавления М/моль, мы получим формулу, аналогичную уравнению (45.14): (дPпл/дT)V=M/[T(VL-VS)]. Мы можем не знать ничего о кинетической теории процесса плавления, а все же получить правильное уравнение. Однако если мы узнаем кинетическую теорию, то сразу же получим большое преимущество. Уравнение (45.14) — это всего лишь дифференциальное уравнение, и мы еще совершенно не умеем находить постоянные интегрирования. В кинетической теории можно вычислить и эти постоянные, надо только придумать хорошую модель, описывающую все явление полностью. Итак, в каждой теории есть и хорошее, и плохое. Если познания наши слабы, а картина сложна, то термодинамические соотношения оказываются самым мощным средством. Когда же картина упрощается настолько, что можно ее проанализировать теоретически, то лучше сначала попробовать выжать из этого анализа как можно больше.
Еще один пример: излучение черного тела. Мы уже говорили об ящике, содержащем излучение и ничего больше, и уже толковали о равновесии между излучением и осциллятором.
Мы выяснили также, что когда фотоны ударяются о стенки ящика, они создают давление Р. Мы вывели формулу PV=U/3, где U — полная энергия фотонов, а V — объем ящика. Если подставить U=3РV в основное уравнение (45.7),то обнаружится, что
Поскольку объем ящика не изменяется, можно заменить (дP/дT)Vна dP/dT и получить обыкновенное дифференциальное уравнение. Оно легко интегрируется и дает lnP=4lnT+const, или Р=const·T4. Давление излучения изменяется как четвертая степень температуры, поэтому заключенная в излучении энергия U/V=P/3 тоже меняется как T4. Обычно пишут так: U/V=(4s/с)T4, где с — скорость света, а s— другая постоянная. Термодинамика сама по себе ничего не скажет нам об этой постоянной. Это хороший пример и ее могущества, и ее бессилия. Знать, что U/V изменяется как T4, — это уже большое дело, но узнать, чему именно равно U/V при той или иной температуре, можно, только разобравшись в деталях полной теории. У нас есть теория излучения черного тела и сейчас мы вычислим а.
Пусть I(w)dw — распределение интенсивности, иначе говоря, поток энергии через 1 м2за 1 сек в интервале частот между w и w+dw:
Распределение плотности энергии =
поэтому
U/V=Полная плотность энергии,
(Плотность энергии между w и w+dw),
Мы уже успели узнать, что
Подставляя выражение для I (w) в наше уравнение для U/V, получаем
Если сделать замену переменных x=hw/kT, то это выражение примет вид
Этот интеграл — просто-напросто какое-то число, и мы можем найти его приближенно. Для этого надо лишь вычертить подынтегральную кривую и подсчитать площадь под ней. Она приблизительно равна 6,5. Математики могут вычислить наш интеграл точно, он равен p4/15. Сравнивая это выражение с записанным ранее U/V=(4s/с)T4, мы найдем s:
Много ли энергии утечет за 1 сек из дырки единичной площади, проделанной в стенке ящика? Чтобы найти поток энергии, умножим плотность энергии U/V на с. Еще нужно умножить на 1/4; эта четверть набегает вот по каким причинам. Во-первых, l/2появляется из-за того, что мы вычисляем только вырвавшуюся наружу энергию, и, во-вторых, если поток подходит к дырке не под прямым углом, то вырваться ему труднее; это уменьшение эффективности учитывается умножением на косинус угла с нормалью. Среднее значение косинуса равно 1/2. Теперь понятно, почему мы писали U/V=(4s/c)T4: так проще выразить поток энергии сквозь маленькую дырку; если отнести поток к единичной площади, то он равен просто sT4.
* Поскольку (ex-1)-1 =е-x+е-2x +..., то интеграл равен
Но, поэтому, дифференцируя три раза по n, мы получаем
, так что интеграл равен 6 (1+1/16+1/81+...), и несколько первых членов ряда дают уже хорошее приближение. В гл. 50 мы сможем показать, что сумма обратных четвертых степеней целых чисел равна p5/90.

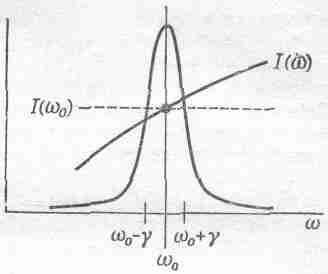

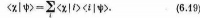
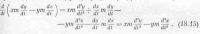


Комментарии к книге «4. Кинетика. Теплота. Звук», Ричард Филлипс Фейнман
Всего 0 комментариев