Алеку и Софии.
Предисловие
Если на пороге двадцатого столетия ещё и оставались сомнения, то в двадцать первом вывод был предрешён — в вопросах познания истинной природы реальности наш повседневный опыт вводит нас в заблуждение. Если вдуматься, это не так уж странно. Когда наши дальние предки охотились в саванне и собирали лесные дары, умение рассчитывать квантовое поведение электрона или определять космологическую роль чёрных дыр вряд ли могло быть подспорьем в выживании вида. Однако увеличившийся размер мозга действительно стал преимуществом, и за ростом наших интеллектуальных способностей открылись и новые возможности для более глубокого исследования окружающего мира. Одни представители вида создали инструменты, расширяющие сферу восприятия наших органов чувств, другие овладели методом систематического выявления и описания закономерностей — математикой. Вооружённые этим арсеналом, мы стали заглядывать за границы повседневного опыта.
То, что мы при этом обнаружили, потребовало масштабных перемен в нашей картине космоса. Путём интуитивных озарений в понимании физических явлений и строгих математических рассуждений, вдохновляемые экспериментами и подтверждающими наблюдениями, мы выяснили, что поведение пространства, времени, материи и энергии может разительно отличаться от всего, с чем мы непосредственно сталкивались. Теперь же, вдумчиво анализируя эти открытия и связанные с ними находки, мы приближаемся к тому, что может вызвать новый переворот в нашем понимании реальности, — мы допускаем возможность, что наша Вселенная — не единственная. В книге «Скрытая реальность» исследуется это предположение.
Работая над этой книгой, я исходил из того, что её читатели могут не иметь специальной подготовки в области физики или математики. Как и в предыдущих своих книгах, вместо формул я прибегаю к помощи метафор и аналогий, перемежающихся историческими отступлениями, чтобы в общедоступной форме рассказать о некоторых весьма странных и удивительных (если их правильность подтвердится) положениях современной физики. Многие из представленных здесь идей потребуют от читателя готовности отбросить привычный образ мышления и посмотреть на реальность с весьма необычной стороны. Но путь нам будут освещать научные достижения, так что путешествие будет ясным и захватывающим. Я придирчиво отобрал самые впечатляющие идеи на пути, ведущем от повседневного к неизведанному.
В этой книге, в отличие от предыдущих, нет вводных глав, где систематически излагались бы предварительные сведения по специальной и общей теории относительности и квантовой механике. Вместо этого я ввожу элементы этих теорий по мере необходимости; если я вижу, что в том или ином месте книга потеряет самодостаточность без подробного технического изложения, я предупреждаю об этом более подготовленных читателей и отмечаю те разделы, которые они могут пропустить без опасений. А вот последние страницы различных глав, наоборот, ведут к углублённому рассмотрению материала, который может оказаться сложным для некоторых читателей. Когда мы переходим к таким разделам, я предлагаю менее искушённым читателям краткое резюме и возможность перескочить вперёд, не потеряв при этом из виду целостную картину. Вместе с тем я хотел бы призвать всех читателей попытаться вникнуть в материал этих разделов настолько глубоко, насколько позволит любопытство и терпение. Несмотря на всё сказанное выше, этот материал предназначен для широкой аудитории, и единственным предварительным требованием для его освоения по-прежнему является лишь наличие у читателя упорства.
Примечания с этой точки зрения составлены иначе. Читатель-новичок может полностью пропустить их; читатель, обладающий более серьёзной подготовкой, найдёт в примечаниях дальнейшее развитие высказанных идей или те пояснения, которые я счёл важными, но слишком громоздкими для включения в основной текст книги. Многие из примечаний предполагают наличие у читателя специального образования в области математики или физики.
В процессе написания этой книги многие мои друзья, коллеги, члены моей семьи прочли отдельные главы или всю книгу целиком и поделились со мной своим мнением и критическими замечаниями, из которых я извлёк немало пользы. Мне хотелось бы особо отметить Дэвида Альберта, Кена Винберга, Риту Грин, Саймона Джудса, Трейси Дэй, Ричарда Истера, Дэниела Кабата, Дэвида Кагана, Пола Кайзера, Рафаэля Каспера, Хуана Малдасену, Катинку Мэтсон, Малика Париха, Маркуса Пёсселя и Майкла Поповица.
Работа с Марти Эшером, моим редактором в издательстве «Knopf», неизменно доставляет мне удовольствие. Благодарю Эндрю Карлсона, профессионально опекавшего мою книгу на заключительных этапах подготовки к печати. Прекрасные иллюстрации, созданные Джейсоном Северсом, сделали книгу гораздо более доступной, и я благодарен ему как за талант, так и за терпение. С удовольствием благодарю также моих литературных агентов — Катанку Мэтсон и Джона Брокмана.
В ходе многочисленных бесед с коллегами я оттачивал свой подход к материалу, изложенному в этой книге. Кроме тех, кого я уже упомянул, хочу особо поблагодарить Роберта Бранденбергера, Рафаэля Буссо, Эрика Вайнберга, Кумруна Вафу, Фредерика Денефа, Жака Дистлера, Майкла Дугласа, Лоуренса Краусса, Жанну Левин, Барри Лоевера, Андрея Линде, Сета Ллойда, Сола Перлмуттера, Леонарда Сасскинда, Пола Стейнхарда, Эндрю Строминджера, Генри Тая, Макса Тегмарка, Дэвида Уолласа, Лама Ху, Стива Шенкера, Юргена Шмидхубера и Шин-Туна Яу.
Свою первую научно-популярную книгу — «Элегантная Вселенная» — я начал писать летом 1996 года. На протяжении последующих пятнадцати лет у меня была возможность наслаждаться новыми неожиданными и плодотворными связями между областью моих технических исследований и вопросами, которые я поднимал в своих книгах. Я благодарен моим студентам и коллегам из Колумбийского университета за ту живую и творческую исследовательскую обстановку, которую они создали, Министерству энергетики — за финансирование моих научных изысканий, а также недавно нас покинувшему Пентти Коури — за щедрую поддержку исследовательского центра при Колумбийском университете — Института теории струн, космологии и астрофизики.
Наконец, спасибо Трейси, Алеку и Софии: благодаря им эта Вселенная стала лучшей из всех возможных!
Глава 1. Границы реальности О параллельных мирах
Если бы, когда я был ребёнком, в моей комнате было лишь одно зеркало, мои детские мечты были бы, вероятно, совсем другими. Но зеркал было два. И каждое утро, когда я открывал шкаф, чтобы достать одежду, зеркало в дверце шкафа оказывалось напротив зеркала на стене, порождая бесконечную череду отражений всего, что попадало в пространство между зеркалами. Это было чарующее зрелище. Я восхищённо наблюдал за картинами, заполнявшими параллельные зеркальные плоскости и уходившими вглубь, насколько хватало взгляда. Казалось, что все отражения двигаются в такт, — но я понимал, что причиной тому является ограниченность человеческих органов чувств: с довольно юных лет я знал о том, что скорость распространения света конечна. А потому мысленным взором я видел, как свет путешествует взад-вперёд — туда, обратно и снова туда. Бесшумное эхо от кивка головы, от взмаха руки носилось между зеркалами, поочерёдно отражавшими образы. Порой я воображал, что одно из моих далёких отражений дерзко отказывается встать на место и ломает строгий ряд, творя новую реальность, которая формирует все следующие за ней. А когда на уроке в школе вдруг наступало затишье, я иногда задумывался о том луче света, который покинул меня этим утром и до сих пор скачет между зеркалами, и мысленно присоединялся к одному из своих отражений, входя в воображаемый параллельный мир, созданный светом и оживлённый моей фантазией.
Конечно, отражения сами по себе не стоят особого упоминания. Но полёты детской фантазии в воображаемых параллельных реальностях перекликаются с одной научной темой, звучащей всё громче и громче, — с идеей о том, что за пределами известного нам мира могут существовать другие миры. Эта книга представляет собой исследование такой возможности — вдумчивую экскурсию в теорию параллельных вселенных.
Вселенная и вселенные
Когда-то слово «вселенная» означало «всё сущее». Абсолютно всё. Всё и всякую всячину вокруг нас. Упоминание о более чем одной вселенной, более чем одном «всём» выглядело бы терминологическим противоречием. Однако постепенно исследователи в своих теоретических изысканиях понемногу уточняли интерпретацию слова «вселенная». Значение этого слова стало зависеть от контекста. Иногда «вселенной» по-прежнему называли всё. Иногда под этим понимали только ту часть всего, до которой кто-либо вроде вас или меня может так или иначе добраться. А иногда это понятие применяют, чтобы обозначить самостоятельные области реальности, которые частично или полностью, временно или навсегда недоступны для нас; в таком значении это слово низводит нашу Вселенную до положения одной из широкого (возможно, бесконечно широкого) набора других.
Лишённое своего господствующего положения, слово «вселенная» открыло путь другим терминам, охватывающим то более обширное полотно, на котором можно разместить картину всей полноты реальности. Параллельные миры, или параллельные вселенные, или множественные миры, или альтернативные вселенные, или метаверс, мегаверс либо мультиверс, мультивселенные — всё это синонимы в ряду тех слов, с помощью которых люди стремятся охватить не только нашу Вселенную, а весь спектр других вселенных, возможно, существующих за пределами известного.
Вы можете заметить, что эти термины несколько расплывчаты. Из чего в точности составлен мир, или Вселенная? По какому критерию мы можем отличить разные области одной вселенной от самостоятельных вселенных? Возможно, в один прекрасный день наше понимание того, что такое множественные вселенные, станет достаточно полным, чтобы мы смогли дать точные ответы на эти вопросы. Пока же мы не станем сражаться с абстрактными определениями, а используем подход, который с успехом применил судья Поттер Стюарт, — когда Верховный суд США бился над выработкой стандарта для определения порнографии, Стюарт провозгласил: «Если я её увижу, то сразу узнаю».
В конечном итоге вопрос о том, назвать ли ту или иную область реальности параллельной вселенной, — исключительно лингвистический. Действительно важный вопрос, который является средоточием проблемы, звучит так: существуют ли такие области, которые бросают вызов устоявшимся взглядам и заставляют нас предположить, что то, что мы до сих пор считали всей Вселенной, — лишь составная часть значительно большей, гораздо более странной и по большей части скрытой от нас реальности.
Разнообразие параллельных вселенных
Поразительный факт (послуживший одним из толчков к написанию этой книги) состоит в том, что многие из магистральных разработок в фундаментальной теоретической физике — в релятивистской физике, квантовой физике, космологии, теории объединения, вычислительной физике — приводят к размышлениям о той или иной разновидности параллельных вселенных. Маршрут нашего повествования в последующих главах проходит через девять вариаций на тему мультивселенной. В каждой из них наша Вселенная предстаёт как часть неожиданно более масштабного целого, но сложность этого целого и природа составляющих его вселенных весьма отличаются от главы к главе. В одних картинах параллельные вселенные разделены колоссальными расстояниями или промежутками времени; в других они ведут призрачное существование в считанных миллиметрах от нас; в третьих же сама попытка говорить об их местоположении наивна и лишена всякого смысла. Подобное многообразие возможностей обнаруживается и в тех законах, которые управляют этими параллельными вселенными. Где-то эти законы — такие же, как в нашей Вселенной; в других вселенных они выглядят иначе, но имеют похожую родословную; в третьих они по форме и структуре не похожи ни на что из того, с чем нам доводилось иметь дело прежде. Попытки представить себе, насколько разнообразной и необъятной может быть реальность, заставляют чувствовать одновременно и восторг, и покорность перед её величием.
Первые ранние научные вылазки в параллельные миры начались в 1950-х годах. Их предприняли исследователи, ломавшие голову над некоторыми вопросами квантовой механики — теории, призванной объяснить те явления, которые происходят на микроскопическом уровне — в царстве атомов и субатомных частиц. Квантовая механика сокрушила прежний каркас физики — классическую механику, — установив, что научные предсказания являются с неизбежностью вероятностными. Мы можем предсказать шансы одного исхода событий, мы можем предсказать шансы другого, но мы, вообще говоря, не можем с уверенностью сказать, какой из них действительно произойдёт. Этот хорошо известный отход от многовековых наработок научной мысли сам по себе поразителен. Но есть ещё более изумительный аспект квантовой теории, на который обращают мало внимания. После десятилетий пристального изучения квантовой механики, имея в распоряжении богатейший набор данных, накопленных за это время и подтверждающих её вероятностные предсказания, никто не в состоянии объяснить, почему в каждой конкретной ситуации в действительности случается только один из многих возможных исходов. Когда мы ставим эксперименты, когда мы исследуем наш мир, мы все сходимся в том, что имеем дело с единственной вполне определённой реальностью. Однако спустя более столетия после квантовой революции среди учёных-физиков нет согласия относительно того, как этот основополагающий факт согласуется с математической формулировкой квантовой теории.
С течением времени этот существенный пробел в нашем понимании породил множество творческих гипотез, но самая поразительная возникла одной из первых. Возможно, утверждает эта гипотеза, привычное представление о наличии одного и только одного исхода у любого эксперимента — в корне неверно. Математика, лежащая в основе квантовой механики, допускает (по крайней мере под некоторым углом зрения), что случаются все возможные исходы, но каждый из них обитает в собственной отдельной вселенной. Если квантовые расчёты предсказывают, что частица может находиться тут, а может — там, то в одной вселенной она находится тут, а в другой находится там. И в каждой такой вселенной есть копия вас, которая наблюдает за тем или иным исходом, полагая — ошибочно, — что окружающая её реальность единственна. Если вы задумаетесь о том, что квантовая механика стоит за всеми физическими процессами, от слияния атомов на Солнце до электрических перестрелок между нейронами, что составляет основу мышления, вам станет очевидно, как далеко могут завести нас следствия этой гипотезы. Она говорит нам, что нехоженых тропинок не бывает. Но каждая такая тропинка — каждая реальность — спрятана от всех остальных.
В последние десятилетия этот интригующий подход к квантовой механике, опирающийся на множественность миров, дразнит воображение. Однако исследования показали, что в качестве каркаса теории он слишком хрупок и противоречив (мы обсудим это в главе 8); поэтому даже сегодня, после более чем полувека проверок, это допущение остаётся спорным. Одни специалисты по квантовой теории утверждают, что его корректность уже доказана, тогда как другие столь же уверенно заявляют, что математические подпорки под этой гипотезой не стыкуются друг с другом.
Несмотря на столь неопределённое положение в науке, эта ранняя версия гипотезы о параллельных вселенных перекликается с идеями о затерянной земле или альтернативной истории, которые проникли в литературу, телесериалы, фильмы и которые продолжают творчески переосмыслять и в наши дни. (Среди моих любимых с детства произведений на эту тему — «Волшебник страны Оз», «Эта прекрасная жизнь», эпизод «Город на краю вечности» из сериала «Звёздный путь», рассказ Борхеса «Сад расходящихся тропок» и, из более позднего, «Осторожно, двери закрываются» и «Беги, Лола, беги».) Благодаря этим и многим другим творениям массовой культуры тема параллельных реальностей стала частью духа нашего времени и обрела притягательность для широкой публики. Однако квантовая механика — лишь один из многочисленных путей, на которых в современной физике возникает понятие параллельных вселенных. И этот путь мы будем обсуждать даже не в первую очередь.
В главе 2 мы изберём другой подход к теме параллельных вселенных — возможно, наиболее простой из всех. Мы увидим, что если пространство бесконечно — идея, которая находится в согласии со всеми наблюдениями и является частью той космологической модели, которую предпочитают многие физики и астрономы, — то где-то там обязаны существовать области, где копия меня, и копия вас, и копии всего вокруг нас наслаждаются альтернативной версией той реальности, с которой имеем дело мы. В главе 3 мы заберёмся глубже в космологические вопросы: инфляционная теория — подход, в котором ранние моменты существования связаны с колоссальным взрывом молниеносно расширяющегося пространства, — порождает собственную версию параллельных миров. Если инфляционный сценарий верен (а об этом свидетельствуют самые тщательные астрономические наблюдения), то взрыв, создавший нашу область пространства, мог быть не единственным. Инфляционное расширение в отдалённых областях прямо сейчас может порождать вселенную за вселенной и делать это вечно. Более того, каждая такая дочерняя вселенная сама бесконечно расширяется в пространстве и содержит бесконечное число параллельных миров, о которых говорится в главе 2.
В главе 4 наш маршрут свернёт к теории струн. После беглого ознакомления с основами я расскажу о нынешнем состоянии этого подхода к объединению всех законов природы. Опираясь на этот обзор, в главах 5 и 6 мы рассмотрим последние достижения теории струн, из которых следуют три новых вида параллельных вселенных. Первый возникает из сценария мира на бране, в котором наша Вселенная — один из по-видимому многочисленных «листов», парящих в многомерном пространстве, наподобие ломтя грандиозной космической буханки хлеба.{1} Если нам повезёт, то в не столь отдалённом будущем этот подход сможет пройти проверку на Большом адронном коллайдере в Женеве (Швейцария). Параллельные вселенные второго вида возникают, когда миры на бранах сталкиваются друг с другом, уничтожая всё своё содержимое и приводя к новому горячему большому взрыву — как тому началу, которое породило каждого из них. Подобно хлопкам двух огромных ладоней, это может происходить снова и снова: браны могут соударяться, отскакивать друг от друга, притягиваться силами тяготения и снова сталкиваться — циклический процесс, порождающий вселенные, параллельные не в пространстве, а во времени. Третий сценарий — это сценарий «ландшафта» в теории струн, в основе которого лежит колоссальное разнообразие форм и размеров дополнительных пространственных измерений, требуемых теорией. Мы увидим, что струнный ландшафт, будучи объединённым с идеей инфляционной мультивселенной, подразумевает наличие безграничного набора вселенных, реализующих все возможные формы дополнительных измерений.
В главе 6 мы сосредоточимся на том, как все эти соображения проливают свет на самые удивительные результаты наблюдений последнего столетия: похоже, что пространство равномерно заполнено рассеянной энергией, которая может оказаться вариацией на тему известной космологической постоянной Эйнштейна. Это наблюдение послужило отправной точкой для многих актуальных изысканий в области параллельных вселенных и стало причиной одной из самых горячих дискуссий за последние десятилетия — дискуссии о том, какими должны быть приемлемые научные объяснения. Глава 7 развивает эту тему, поднимая более общий вопрос: можно ли вообще рассматривать размышления о вселенных за пределами нашей как область науки? Можем ли мы проверить эти идеи? Продвигаемся ли мы вперёд, привлекая эти идеи для решения стоящих перед нами выдающихся проблем, — или просто заметаем эти проблемы под ковёр, удобный своей космической недоступностью? Я стремился к тому, чтобы изложить как есть основные доводы противоборствующих позиций, подчеркнув при этом мою собственную точку зрения: при определённых условиях параллельные вселенные несомненно попадают в сферу компетенции науки.
Квантовая механика с её вариантом параллельных вселенных в форме множественных миров является предметом обсуждения в главе 8. Я кратко напомню основные положения квантовой механики, а затем сосредоточусь на самой трудной проблеме теории: как получить чётко определённые результаты от теории, базовая парадигма которой допускает сосуществование несовместимых реальностей в аморфном (хотя и математически точно описанном) вероятностном тумане. Я бережно проведу вас через рассуждения, которые в поисках ответа на этот вопрос приводят нас к идее разместить квантовую реальность в её собственном изобилии параллельных миров.
Глава 9 погружает нас в квантовую реальность ещё глубже, рассказывая о том, что, на мой взгляд, является самым странным вариантом идеи параллельных вселенных. Речь идёт о предложении, которое исподволь вызревало в ходе теоретического изучения квантовых свойств чёрных дыр в течение последних тридцати лет. Эта работа достигла кульминации в последнее десятилетие, когда теория струн дала ошеломительный результат, из которого следует удивительный вывод: весь наш опыт — не что иное как голографическая проекция процессов, происходящих на некоторой очень далёкой поверхности, окружающей нас. Вы можете ущипнуть себя, и ваши ощущения будут при этом реальными, но они отразят собой параллельный процесс, который имеет место в другой, далёкой реальности.
Наконец, в главе 10 на сцену выходит ещё более причудливая возможность — искусственные вселенные. Первым пунктом нашей повестки дня будет вопрос о том, позволяют ли нам законы физики создавать новые вселенные. Затем мы обратим свой взгляд на вселенные, создаваемые не физическим путём, а программным — на такие вселенные, которые мог бы смоделировать некий сверхмощный компьютер, — и поразмыслим над тем, уверены ли мы, что не являемся обитателями созданной кем-то или чем-то имитации. Это приведёт нас к самому необузданному предположению о параллельных вселенных, выдвинутому философским сообществом: каждый возможный вариант вселенной реализован где-то внутри того, что с уверенностью можно назвать величайшей из мультивселенных. Это обсуждение естественным образом упирается в вопрос о роли математики в распутывании научных загадок и, в конечном итоге, о нашей способности или неспособности достичь глубочайшего понимания природы реальности.
Космический порядок
Обсуждение параллельных вселенных в большой степени умозрительно. Нет никаких экспериментов или наблюдений, свидетельствующих о том, что какой-либо из вариантов этой идеи реализуется в природе. Поэтому при написании этой книги я не ставил перед собой задачу убедить вас, что мы — часть мультивселенной. Я не убеждён (и, вообще говоря, никто не обязан быть убеждённым) ни в чём, что не подкреплено надёжными данными. В то же время я нахожу одновременно занятным и интригующим тот факт, что многие направления развития физики, если следовать по ним достаточно далеко, упираются в ту или иную вариацию на тему параллельных вселенных. Не то чтобы физики стояли наготове с мультиверсными сетями, отлавливая любую проходящую мимо теорию, которую можно с грехом пополам втиснуть в парадигму параллельных вселенных. Вовсе нет: все гипотезы о параллельных вселенных, которые мы принимаем всерьёз, пришли к нам непрошеными гостями из математических выкладок тех теорий, которые разрабатывались для объяснения вполне традиционных данных и наблюдений.
Моё намерение, таким образом, состоит в том, чтобы ясно и сжато описать те интеллектуальные шаги и цепочки теоретических озарений, которые вынудили физиков с разных точек зрения рассматривать возможность того, что наша Вселенная — лишь одна из многих. Я хочу, чтобы вы увидели, как эта поразительная возможность возникает не в безудержных фантазиях вроде моих детских отражательных иллюзий, а в современных научных исследованиях. Я хочу показать, как некоторые сбивающие с толку результаты наблюдений могут стать совершенно понятными в контексте той или иной конструкции параллельных вселенных; вместе с тем я опишу не решённые до сих пор критические вопросы, которые удерживают нас от того, чтобы в полной мере принять такие объяснения. Моя цель состоит в том, чтобы к последней странице этой книги ваша точка зрения на возможное, ваше представление о том, в какой степени границы реальности могут быть однажды полностью пересмотрены благодаря уже идущим научным исследованиям, стали более насыщенными и яркими.
Некоторых людей пугает одно лишь упоминание о параллельных мирах; им кажется, что если мы вдруг окажемся частью мультивселенной, наше значение и наше место в космосе станут ничтожными. У меня иной взгляд на вещи. Я не нахожу особой доблести в том, чтобы измерять нашу значимость относительной плотностью. Скорее радость быть человеком, восторг от занятий научной деятельностью возникают благодаря нашей способности применять аналитическое мышление, чтобы охватить безбрежные пространства, проникнуть во внешние и внутренние области реальности и — если подтвердятся какие-то из идей, изложенных в этой книге, — возможно, даже выйти за границы нашей Вселенной. На мой взгляд, именно то, что мы, затерянные посреди чернильно-чёрной тишины холодного и равнодушного космоса, обладаем таким глубоким пониманием, и есть знак нашего присутствия, отражённый необъятными просторами реальности.
Глава 2. Бесконечные двойники Лоскутная мультивселенная
Если бы вы отправились в космос, забираясь всё глубже и глубже, что бы вы обнаружили — что пространство тянется бесконечно или же где-то внезапно заканчивается? Или, может быть, вы описали бы круг и вернулись в начальную точку, подобно сэру Фрэнсису Дрейку, совершившему кругосветное плавание? Обе эти возможности — космос бесконечно протяжённый и космос громадный, но конечный — находятся в согласии со всеми нашими наблюдениями, и ведущие учёные на протяжении последних десятилетий энергично исследовали каждую из них. Однако несмотря на столь пристальное изучение, если Вселенная бесконечна, то из этого следует один захватывающий вывод, который был обойдён должным вниманием.
Где-то в отдалённом уголке бесконечного космоса есть галактика, которая выглядит в точности как Млечный Путь, в которой есть солнечная система, как две капли воды похожая на нашу, с планетой, которая является вылитой копией Земли, на которой стоит дом, неотличимый от вашего, в котором живёт кто-то, абсолютно похожий на вас, и он прямо сейчас читает точно такую же книгу и представляет себе вас, затерянного где-то в далёкой галактике и только что добравшегося до конца этой фразы. И такая копия не одна. В бесконечной Вселенной их бесконечно много. В каких-то ваш двойник сейчас читает это предложение вместе с вами. В других он перескочил вперёд или же отложил книгу, чтобы подкрепиться. Ещё где-то жизнь у него сложилась далеко не так удачно, и вы вряд ли захотели бы встретиться с ним в тёмном переулке.
И вы никогда не встретитесь. Эти копии обитают в настолько далёких друг от друга областях, что даже у луча света, начавшего своё путешествие в момент Большого взрыва, не хватило бы времени пересечь разделяющее их пространство. Но даже не имея возможности наблюдать эти далёкие области, мы понимаем: из ключевых физических принципов вытекает, что бесконечно большой космос является вместилищем для бесконечного числа параллельных миров — какие-то из них идентичны нашему, какие-то отличаются, а какие-то вовсе на него не похожи.
На пути к этим параллельным мирам мы должны сначала в общих чертах выстроить каркас космологии — научной теории о происхождении и эволюции космоса как целого.
Приступим.
Отец Большого взрыва
«Ваши математические выкладки корректны, но ваши физические выводы чудовищны». Сольвеевский конгресс по физике 1927 года был в самом разгаре, когда этими словами Альберт Эйнштейн встретил сообщение бельгийца Жоржа Леметра о том, что уравнения общей теории относительности, которые Эйнштейн опубликовал десятилетием раньше, влекут за собой драматическую перекройку истории творения. Согласно вычислениям Леметра, начало Вселенной положила крошечная пылинка немыслимой плотности («первородный атом», как он её назвал), которая на протяжении долгого времени разрасталась, чтобы превратиться в наблюдаемый нами космос.
На фоне десятков именитых физиков, которые, вместе с Эйнштейном, собрались на неделю в брюссельском отеле «Метрополь» для интенсивных дебатов о квантовой теории, Леметр был довольно необычной фигурой. К 1923 году он не только закончил работу над докторской диссертацией, но также завершил своё обучение в семинарии Сен-Ромбо и был посвящён в духовный сан ордена иезуитов. Во время перерыва между выступлениями Леметр, в пасторском воротнике, подошёл к человеку, чьи уравнения, как он считал, были основой новой научной теории происхождения космоса. Эйнштейн знал о теории Леметра, несколькими месяцами раньше прочёл его статью на эту тему и не смог найти никакого изъяна в его манипуляциях с уравнениями общей теории относительности. На самом деле Леметр был не первым, кто показал Эйнштейну этот результат. В 1921 году русский математик и метеоролог Александр Фридман нашёл класс решений уравнений Эйнштейна, описывающий вселенную, растущую благодаря расширению пространства. Вначале Эйнштейн отверг эти решения, считая их ошибочными. Позже он признал, что был не прав, и взял свои слова назад. Однако он не желал быть заложником математиков и попытался исправить свои уравнения, руководствуясь интуитивным представлением о том, каким должен быть космос, и опираясь на свою глубоко укоренившуюся веру в то, что вселенная вечна и на больших масштабах статична и неизменна. Вселенная, — убеждал Леметра Эйнштейн, — не расширяется и никогда не расширялась.
Шестью годами позже на семинаре в обсерватории Маунт-Вильсон Эйнштейн внимательно выслушал, как Леметр излагает более подробный вариант своей теории о том, что Вселенная началась с первичной вспышки, а галактики были тлеющими углями этой вспышки в разливающемся море пространства. Когда семинар подошёл к концу, Эйнштейн встал и объявил, что теория Леметра — это «самое прекрасное и убедительное объяснение творения», которое ему когда-либо доводилось слышать.{2} Самый знаменитый физик склонился к тому, чтобы изменить своё мнение о самой интригующей тайне. Хотя широкой публике имя Леметра ни о чём не говорит, среди учёных он известен как отец Большого взрыва.
Общая теория относительности
Космологические теории, разработанные Фридманом и Леметром, опираются на работу Эйнштейна, отправленную в немецкий журнал «Annalen der Physik» 25 ноября 1915 года. Эта статья подводила итог примерно десятилетней математической одиссеи, а представленному в ней результату — общей теории относительности — суждено было стать наиболее целостным научным достижением Эйнштейна, влекущим за собой чрезвычайно глубокие следствия. В своей теории Эйнштейн задействовал элегантный геометрический язык, чтобы переосмыслить наши представления о гравитации. Если вы уже знакомы с основными положениями этой теории и её космологическими следствиями, можете спокойно пропустить три следующих раздела. Если же вам нужно освежить в памяти основные моменты, давайте вместе пойдём дальше.
Эйнштейн начал работу над общей теорией относительности примерно в 1907 году — в то время, когда большинство учёных считали, что гравитация давным-давно получила объяснение в трудах Исаака Ньютона. Во всём мире студентов год за годом учили, что в конце XVII века Ньютон сформулировал так называемый закон всемирного тяготения, который стал первым математическим описанием этой наиболее известной силы природы. Закон Ньютона настолько точен, что инженеры НАСА до сих пор используют его при расчёте траекторий космических кораблей, а астрономы с его помощью предсказывают поведение комет, звёзд и даже целых галактик.{3}
Эта поразительная эффективность тем более стоит упоминания, что, как осознал в начале XX века Эйнштейн, ньютоновский закон тяготения содержит глубокий изъян. Обманчиво наивный вопрос, который задал себе Эйнштейн, обнажает это со всей очевидностью: как действует гравитация? Каким образом, к примеру, Солнце сквозь 150 миллионов километров практически пустого пространства дотягивается до Земли, чтобы повлиять на её движение? Они не связаны друг с другом никакой верёвкой, их не соединяет никакая цепь — так посредством чего распространяется гравитационное влияние?
Публикуя в 1687 году свои «Математические начала натуральной философии», Ньютон отдавал себе отчёт в важности этого вопроса, но признавал, что закон всемирного тяготения обходит его тревожным молчанием. Ньютон был уверен, что должно быть нечто, передающее гравитационное воздействие от места к месту, но не мог определённо сказать, что это. В «Началах» он иронично оставил этот вопрос «на усмотрение читателя» — и на протяжении более чем двух столетий те, кто читал эти бросающие вызов слова, просто продолжали чтение дальше. Эйнштейн не смог так поступить.
Добрую половину десятилетия Эйнштейн был занят поисками механизма, лежащего в основе тяготения; в 1915 году он предложил ответ. Хотя этот ответ опирался на изощрённую математику и требовал невиданных в истории физики концептуальных пируэтов, ему был присущ тот же дух простоты, что и исходному вопросу. Посредством какого процесса гравитация распространяет своё влияние в пустом пространстве? Кажется, что пустота пустого пространства оставляет нас с пустыми руками. Однако на самом деле в пустом пространстве всё же кое-что есть: само пространство. Это подтолкнуло Эйнштейна к мысли о том, что пространство как таковое может быть посредником, передающим гравитационные силы.
Идея состоит в следующем. Представьте себе мраморный шарик, который катится по большому металлическому столу. Поскольку поверхность стола плоская, шарик будет катиться по прямой линии. Но если стол будет внезапно охвачен огнём, который заставит его вздуваться и изгибаться, траектория шарика изменится, потому что его будет направлять скрученная и вздыбившаяся поверхность стола. Эйнштейн утверждал, что сходную идею можно применить к структуре пространства. Совершенно пустое пространство напоминает плоский стол — оно позволяет объектам беспрепятственно двигаться по прямой. Но присутствие массивных тел влияет на форму пространства, подобно тому как жар пламени влияет на поверхность стола. Солнце, например, создаёт поблизости от себя изгиб, похожий на пузырь, вздувшийся на раскалённом столе. И так же как искривлённая поверхность стола заставляет шарик двигаться по кривой, искривлённая форма пространства вокруг Солнца ведёт Землю и другие планеты по их орбитам.
В этом кратком описании опущены некоторые существенные детали. Искривляется не только пространство, но и время (это называется кривизной пространства-времени); сила притяжения Земли помогает столу влиять на шарик, поскольку прижимает его к поверхности стола (Эйнштейн отстаивал идею, что искривлениям в пространстве и времени не нужен помощник, потому что они сами и есть гравитация); пространство трёхмерно, и когда оно искривляется, то становится искривлённым со всех сторон вокруг объекта, а не только «под» ним, как в аналогии со столом. Тем не менее метафора искривлённого стола отражает суть того, что предложил Эйнштейн. До Эйнштейна гравитация была таинственной силой, которая каким-то образом передаётся через пространство от одного тела к другому. После Эйнштейна под гравитацией стали понимать искажения окружающего пространства, создаваемые одним объектом и направляющие движение других. В соответствии с этой идеей вы здесь и сейчас прижаты к полу, потому что ваше тело стремится соскользнуть в пространственное (на самом деле пространственно-временное) углубление, созданное Землёй.[1]
Эйнштейн потратил годы на то, чтобы оформить эту идею в виде строгого математического каркаса, и возникшие в результате полевые уравнения Эйнштейна — ядро его общей теории относительности — рассказывают нам, как в точности искривляются пространство и время в присутствии заданного количества материи (более точно — материи и энергии; в соответствии с эйнштейновской формулой E = mc2, где E — это энергия, а m — масса, эти две величины взаимозаменяемы).{4} С той же точностью эта теория описывает, как такая кривизна пространства-времени повлияет на движение чего угодно — звезды, планеты, кометы, самого луча света, — движущегося через него; это позволяет физикам делать детальные предсказания о движении космических объектов.
Свидетельства, подтверждающие общую теорию относительности, не заставили себя ждать. Астрономам давно было известно, что движение Меркурия по орбите вокруг Солнца несколько отклоняется от предсказаний ньютоновской математики. В 1915 году Эйнштейн применил свои уравнения для того, чтобы заново рассчитать траекторию Меркурия, и смог объяснить расхождения; как он сказал позже своему коллеге Адриану Фоккеру, этот момент был настолько волнующим, что он несколько часов не мог унять сердцебиение. Затем в 1919 году астрономические наблюдения, организованные Артуром Эддингтоном и его коллегами, показали, что свет далёких звёзд, по дороге к Земле проходящий вблизи Солнца, следует по кривой в точном соответствии с предсказаниями общей теории относительности.{5} Вместе с этим подтверждением (и заголовком на первой полосе «Нью-Йорк Таймс», гласившим: «ВЕСЬ СВЕТ В НЕБЕСАХ ИСКРИВЛЯЕТСЯ — УЧЁНЫЙ МИР ВЗБУДОРАЖЕН») к Эйнштейну пришла всемирная известность — в нём увидели нового мирового научного гения и прямого наследника Исаака Ньютона.
Однако самые впечатляющие проверки общей теории относительности были ещё впереди. В 1970-х годах эксперименты с часами на основе водородного мазера (мазеры подобны лазерам, но действуют в микроволновой части спектра) подтвердили предсказанное теорией искривление пространства-времени вблизи Земли с отклонением не более чем на 1/15 000. В 2003 году для детального изучения траектории радиоволн, проходящих вблизи Солнца, был использован космический аппарат «Кассини-Гюйгенс»; собранные данные соответствуют картине искривления пространства-времени, предсказанной общей теорией относительности, с отклонением не более 1/50 000. А сейчас, как и должно происходить с теорией, достигшей истинной зрелости, доказательства общей теории относительности многие из нас держат буквально в руках: счётчики времени спутников системы глобального позиционирования, к услугам которой вы обращаетесь с помощью своих смартфонов, регулярно делают поправку на кривизну пространства-времени на своей орбите вокруг Земли. Если бы они это не учитывали, указанные ими значения пространственного положения довольно быстро стали бы неточными. То, что в 1916 году было набором абстрактных уравнений, предложенных Эйнштейном в качестве нового описания пространства, времени и гравитации, сегодня привычно используется устройством, которое помещается у вас в кармане.
Вселенная и чашка чая
Эйнштейн вдохнул жизнь в пространство-время. Он бросил вызов тысячелетней интуиции, основанной на повседневном опыте и считавшей пространство и время лишь неизменной декорацией спектакля. Кто бы мог вообразить, что пространство-время способно скручиваться и изгибаться, становясь невидимым балетмейстером космического движения? Эйнштейн представил себе этот революционный танец, а наблюдения подтвердили его правоту. Но вскоре он сам был сбит с толку старыми, хотя и безосновательными предубеждениями.
В течение года после публикации своей общей теории относительности Эйнштейн изучал её применение к самому масштабному объекту — космосу в целом. Может показаться, что это ошеломительная задача, однако искусство теоретической физики состоит в упрощении ужасающе сложных вещей таким образом, чтобы сделать их поддающимися анализу, сохранив при этом важные физические черты. Это искусство игнорирования. Посредством так называемого космологического принципа Эйнштейн выстроил упрощённый теоретический каркас, который лёг в основу теоретической космологии как науки и искусства.
Космологический принцип состоит в утверждении, что вселенная, рассматриваемая на больших масштабах, предстанет перед наблюдателем однородной. Представьте себе чашку с чаем. На микроскопическом уровне чай в значительной степени неоднороден: здесь молекулы H2O, тут немного пустого пространства, там чуть-чуть молекул полифенола и танина, ещё пустое пространство и так далее. Но на макроскопическом уровне, доступном невооружённому глазу, мы увидим однородный красно-коричневый напиток. Эйнштейн был убеждён в том, что Вселенная в этом смысле напоминает чашку чая. Те отклонения, которые мы видим, — Земля здесь, потом немного пустого пространства, Луна там, ещё немного пространства, за ним Венера, Меркурий, ещё клочки пустоты, а дальше Солнце, — всё это мелкомасштабные неоднородности. Он предположил, что в космологических масштабах этими отклонениями можно пренебречь, потому что, как и ваш чай, в среднем они образуют нечто однородное.
Во времена Эйнштейна свидетельства в поддержку космологического принципа были в лучшем случае призрачными (а вопрос о других галактиках ещё даже не стоял), но им руководило мощное интуитивное чувство, говорившее, что в космосе нет какого-либо особого выделенного места. Он ощущал, что в среднем любая область вселенной должна быть равноправной с другими и иметь в значительной степени идентичные общие физические свойства. За прошедшие годы астрономические наблюдения дали нам большое количество данных, подтверждающих космологический принцип — но только если рассматривать пространство в масштабах по крайней мере сотен миллионов световых лет (это примерно тысячекратная длина Млечного Пути). Если вы возьмёте коробку, каждая сторона которой имеет длину сто миллионов световых лет, и бросите её где-нибудь тут, возьмёте другую такую же коробку и оставите её где-нибудь там (скажем, в миллиарде световых лет отсюда), а затем измерите средние значения общих физических характеристик внутри каждой коробки — среднее число галактик, среднее количество материи, среднюю температуру и так далее, — вы увидите, что эти коробки трудно отличить друг от друга. Короче говоря, если вы видели один кусок космоса размером сто миллионов световых лет, то вы видели их все.
Такая однородность критически необходима, чтобы можно было применить уравнения общей теории относительности к вселенной в целом. Чтобы понять, почему это так, вообразите прекрасный, ровный, гладкий пляж и представьте себе, что я прошу вас описать его свойство в малом масштабе — то есть по сути свойства каждой-каждой песчинки. Вы воспротивитесь: задача слишком объёмна. Но если я попрошу описать только общие черты пляжа (такие, как средний вес песка на кубический метр, средняя отражательная способность поверхности в расчёте на квадратный метр и тому подобное), задача станет реально выполнимой. И выполнимой её делает именно однородность пляжа. Измерьте средний вес, температуру, отражательную способность песка где-нибудь в одном месте — и готово. Измерения в других местах дадут по существу такие же результаты. То же верно и для однородной вселенной. Описать каждую планету, звезду и галактику — задача безнадёжная, но дать усреднённое описание свойств однородного космоса — цель несравнимо более простая, и с появлением общей теории относительности она стала вполне достижимой.
Вот каким образом это происходит. Содержимое большого объёма пространства в целом характеризуется тем, как много «всякой всячины» содержит этот объём; более точно, речь идёт о плотности материи, а ещё точнее — о плотности материи и энергии в этом объёме. Уравнения общей теории относительности описывают, как эта плотность меняется с течением времени. Однако без привлечения космологического принципа эти уравнения безнадёжно сложны для анализа. Их десять, а поскольку каждое из них хитроумно связано с другими, то вместе они образуют весьма тугой математический гордиев узел. К счастью, Эйнштейн обнаружил, что в приложении к однородной вселенной математическая задача упрощается: набор из десяти уравнений становится избыточным и сводится по сути дела к одному уравнению. Космологический принцип позволяет разрубить гордиев узел, устранив математическую сложность и сведя анализ распределения материи и энергии в космосе к решению единственного уравнения (вы найдёте его в примечаниях).{6}
Не столь удачной, на взгляд Эйнштейна, оказалась другая находка: при изучении этого уравнения он обнаружил нечто неожиданное и для него неприемлемое. Среди учёных и философов того времени преобладала точка зрения, согласно которой в крупном масштабе вселенная не только однородна, но и неизменна. Подобно тому как быстрое движение молекул в вашем чае, будучи усреднённым, формирует жидкость, которая выглядит статичной, перемещения астрономических тел (такие как вращение планет по орбите вокруг Солнца и движение самого Солнца вокруг ядра галактики) при усреднении дают нам картину в целом неизменного космоса. Эйнштейн, который был приверженцем такого взгляда на космос, испытал ужас, когда обнаружил, что эта картина не стыкуется с уравнениями общей теории относительности. Математика указывала на то, что плотность материи и энергии не может оставаться неизменной с течением времени. Она либо растёт, либо уменьшается, но не может быть постоянной.
Хотя математические выкладки, ведущие к такому заключению, являются довольно изощрёнными, стоящая за ними физическая картина весьма проста. Представьте себе траекторию бейсбольного меча, летящего с основной базы к центру поля. Сперва он взмывает вверх, затем замедляется, достигает высшей точки и, наконец, летит вниз. Мяч не парит в воздухе, как воздушный шар, потому что гравитация, будучи силой притяжения и действуя в одном направлении, притягивает мяч к земной поверхности. Статическая ситуация — как ничья в перетягивании каната — требует действия равных и противоположно направленных сил, которые сводят друг друга на нет. В случае воздушного шара сила, направленная вверх и противодействующая силе притяжения, порождается давлением воздуха (воздушный шар наполнен гелием, который легче воздуха); на бейсбольный мяч над землёй не действует никакая сила, противоположная гравитации (на движущийся мяч воздействует сопротивление воздуха, но в статической ситуации оно не играет никакой роли), и потому мяч не может сохранять своё положение.
Эйнштейн обнаружил, что вселенная ведёт себя скорее как мяч, а не как воздушный шар. Поскольку нет никакой внешней силы, противодействующей гравитации, общая теория относительности показывает, что вселенная не может быть статичной. Ткань пространства или растягивается, или сжимается, но не может оставаться неизменной. Область пространства, которая сегодня имеет размер сто миллионов световых лет, завтра будет другого размера. Она или вырастет, и тогда плотность материи в ней станет ниже (то есть материя будет более свободно распределена по большему объёму), или сократится, и тогда плотность материи возрастёт (материя будет более тесно размещена в меньшем объёме).{7}
Эйнштейн был обескуражен. Согласно формулам общей теории относительности, вселенная в больших масштабах оказалась меняющейся, поскольку изменчивой была самая её основа — пространство. Картина вечного и статичного космоса, которую ожидал увидеть Эйнштейн, отсутствовала. Он, заложивший основы космологии как науки, был глубоко расстроен тем, куда привела его математика.
Гравитационная декларация
Часто говорят, что Эйнштейн пал духом — якобы он вернулся к своим записям и в отчаянии принялся корёжить уравнения общей теории относительности, пытаясь привести их в согласие с идеей однородной и неизменной вселенной. Это правда лишь отчасти. Эйнштейн действительно изменил свои уравнения так, чтобы они подкрепили его убеждённость в статичности космоса, однако эти изменения были минимальными и совершенно здравыми.
Чтобы получить представление о его математических шагах, вспомните, как выглядит бланк вашей налоговой декларации. Есть строки, в которые вы вписываете какие-то числа, а есть строки, остающиеся пустыми. С математической точки зрения незаполненная строка означает, что денежная сумма равна нулю, но психологически она подразумевает нечто большее. Она говорит о том, что вы проигнорировали эту строку, поскольку решили, что она не имеет отношения к вашей финансовой ситуации.
Если формулы общей теории относительности оформить наподобие налоговой декларации, получится бланк из трёх строк. Одна строка будет описывать геометрию пространства-времени — его искривления и скрученности, которые являются воплощением гравитации. Вторая строка будет описывать распределение материи в пространстве, то есть источник гравитации — причину появления этих искривлений и скрученностей. В итоге десятилетних напряжённых исследований Эйнштейн сформулировал математическое описание этих двух характеристик и тем самым с величайшим тщанием заполнил две строки нашего бланка. Однако полная бухгалтерия общей теории относительности требует наличия третьей строки — строки, которая опирается абсолютно на тот же математический фундамент, что и первые две, но имеет более тонкий физический смысл. Когда пространство и время, прежде лишь снабжавшие нас языком для описания того, где и когда происходят те или иные события, благодаря общей теория относительности стали активными участниками космического действа, они превратились в физические сущности с собственными важными свойствами. Третья строка налогового бланка общей теории относительности измеряет одно из этих свойств пространства-времени, имеющее отношение к гравитации, — количество энергии, «зашитой» в саму ткань пространства. Точно так же как каждый кубический метр воды содержит в себе определённое количество энергии, характеризуемое температурой воды, каждый кубический метр пространства содержит в себе определённое количество энергии, характеризуемое числом из третьей строки. В своей статье, излагающей общую теорию относительности, Эйнштейн не рассматривал эту строку. С математической точки зрения это то же самое, что поставить там нуль, но, как и в случае незаполненной строки в налоговой декларации, похоже, он просто проигнорировал её.
Когда выяснилось, что общая теория относительности несовместима со статической картиной вселенной, Эйнштейн вернулся к математическим выкладкам и на этот раз обратил более пристальное внимание на третью строку. Он осознал, что нет никаких наблюдений и экспериментальных данных, которые оправдывали бы её обнуление, и увидел, что у этой строки есть весьма примечательный физический смысл.
Если вместо нуля поставить в третью строку положительное число, снабдив пространственную ткань однородной постоянной энергией, то (по причинам, которые я объясню в следующей главе) каждая область пространства будет отталкиваться от всех остальных, порождая то, что большинство физиков считали невозможным, — отталкивающую гравитацию. Более того, Эйнштейн обнаружил, что если тщательно подобрать число, размещённое в третьей строке, отталкивающая гравитационная сила, возникающая во всём космическом пространстве, будет точно уравновешивать притягивающую гравитационную силу, которую порождает материя, наполняющая пространство, и тем самым вернёт к жизни статичную модель вселенной. Вселенная станет неизменной — подобно парящему в небе воздушному шару, который не поднимается и не падает.
Эту величину, вставленную в третью строку, Эйнштейн назвал космологическим членом, или космологической постоянной; этот шаг позволил ему вздохнуть с облегчением — по крайней мере отчасти. Если бы космологическая постоянная для вселенной имела подходящее значение — то есть если бы пространство обладало правильным количеством собственной энергии, — его теория гравитации оказалась бы в согласии с преобладавшим в то время убеждением о неизменности вселенной на больших расстояниях. Он не мог объяснить, почему пространство должно заключать в себе именно то количество энергии, которое нужно, чтобы обеспечить равновесие, но ему по крайней мере удалось показать, что общая теория относительности, дополненная космологической постоянной нужной величины, приводит к той картине космоса, в которую верил он сам и которую ожидали увидеть другие.[2]
Первородный атом
Леметр, подошедший к Эйнштейну на Сольвеевском конгрессе 1927 года в Брюсселе, выпадал из этой картины: из его результата следовало, что общая теория относительности стала лоном новой космологической парадигмы, согласно которой пространство расширяется. Эйнштейн не так давно одолел математику в схватке за статичную вселенную, отмёл сходные заявления Фридмана, и теперь у него попросту не было достаточного запаса терпения, чтобы ещё раз возвращаться к идее о расширяющемся космосе. Он поставил Леметру в вину слепое следование математическим выкладкам и готовность принять «чудовищные физические выводы», очевидно являвшиеся абсурдом.
Упрёк со стороны столь уважаемой фигуры стал для Леметра серьёзным ударом — но ненадолго. В 1929 году, используя крупнейший в мире на тот момент телескоп в обсерватории Маунт-Вилсон, американский астроном Эдвин Хаббл получил убедительные свидетельства в пользу того, что все далёкие галактики двигаются прочь от Млечного Пути. Фотоны, которые изучал Хаббл, проделали долгий путь к Земле, неся с собой ясное сообщение: вселенная не статична — она расширяется. Фундамент, который Эйнштейн подвёл под космологическую постоянную, обрушился. Модель Большого взрыва, описывавшая космос, который начал расширяться из чрезвычайно плотного состояния и продолжает делать это по сей день, обрела широкую известность как научный сценария творения.[3]
Леметр и Фридман были реабилитированы. Фридман снискал репутацию учёного, который первым исследовал решения, описывающие расширяющуюся вселенную, а Леметр стал известен как исследователь, который независимо получил эти решения и выстроил на их основе ясные космологические сценарии. Их работа была признана триумфом математического подхода к изучению космоса. Эйнштейна, напротив, оставили досадовать на то, что он вообще решил взяться за третью строку налогового бланка общей теории относительности. Если бы над ним не довлело ничем не подкреплённое убеждение в статичности вселенной, он бы не ввёл в свои уравнения космологическую постоянную и сумел бы предсказать расширение вселенной за десять с лишним лет до того, как его обнаружили экспериментально.
Однако история космологической постоянной была далека от завершения.
Модели и данные
В космологической модели Большого взрыва есть один момент, который представляется весьма существенным. Эта модель даёт нам не один космологический сценарий, а целый их набор; все они подразумевают расширение вселенной, но отличаются общей формой пространства и, в числе прочего, расходятся в ответе на вопрос о том, является ли всё пространство в целом конечным или же бесконечным. Поскольку последнее различие оказывается жизненно важным для размышлений о параллельных мирах, я опишу имеющиеся возможности подробнее.
Космологический принцип — предполагаемая однородность космоса — налагает ограничения на геометрию пространства, поскольку большинство геометрических форм недостаточно однородны, чтобы подойти под эти требования: они вспучиваются в одном месте, уплощаются в другом и скручиваются в третьем. Однако из космологического принципа не следует единственность формы трёх измерений нашего пространства — он лишь проводит жёсткий отбор среди кандидатов, ограничивая имеющиеся возможности. Наглядно представить возможные варианты — непростая задача даже для профессионала, однако нам поможет тот факт, что ситуация в двух измерениях, которую мы можем изобразить без труда, является математически точным аналогом трёхмерной картины.
Для начала рассмотрим с этой целью идеально круглый бильярдный шар. Его поверхность двумерна (положение точки на его поверхности, как и на поверхности Земли, мы можем задать двумя фрагментами данных — скажем, широтой и долготой, — а именно это мы и подразумеваем, когда говорим, что форма двумерна) и совершенно однородна в том смысле, что любое место на ней неотличимо от остальных. Математики называют поверхность бильярдного шара двумерной сферой и говорят, что она имеет постоянную положительную кривизну. «Положительность» здесь означает, грубо говоря, что ваше отражение в сферическом зеркале будет выглядеть раздувшимся наружу, а «постоянность» — что любая сторона сферы будет одинаково искажать отражение.
Теперь представим себе идеально гладкий стол. Поверхность стола, как и поверхность бильярдного шара, однородна (или почти однородна). Если бы вы были муравьём, гуляющим по столу, вашему взору открывался бы один и тот же вид, где бы вы ни находились — при условии, что это далеко от края стола. Впрочем, восстановить полную однородность не так уж трудно: мы просто должны вообразить стол без краёв. Сделать это можно двумя путями. Представьте себе стол, который бесконечно тянется влево, вправо, вперёд и назад. Это не совсем обычный стол — его поверхность бесконечна, — но упасть с него нельзя, а значит, мы достигли поставленной цели — убрали края. Альтернативный вариант — поверхность, имитирующая старую компьютерную игру: когда мистер Пакман исчезает за левым краем, он немедленно появляется у правого края; когда он уходит за край экрана снизу, он тут же возникает сверху. Ни один обычный стол не обладает таким свойством, но это вполне осязаемая геометрическая фигура, называемая двумерным тором. В примечаниях я обсуждаю эту фигуру более полно,{8} здесь же стоит подчеркнуть только две её характеристики: подобно бесконечному столу, экран компьютерной игры однороден и не имеет краёв. Границы являются кажущимися: мистер Пакман может пересечь их и при этом остаться в игре.
Математики говорят, что бесконечный стол и экран компьютерной игры — это поверхности постоянной нулевой кривизны. Слово «нулевая» говорит о том, что и зеркальный стол, и зеркальный компьютерный экран отразят вас без искажений, а слово «постоянная», как и прежде, означает, что ваше отражение будет выглядеть одинаково вне зависимости от того, напротив какой точки поверхности вы встанете. Разница между этими двумя формами проявляется только в глобальной перспективе. Если вы отправитесь в поездку по бесконечному столу, сохраняя постоянное направление, вы не вернётесь домой никогда; на экране компьютерной игры вы можете объехать всю фигуру и вернуться в пункт отправления, ни разу не повернув руль.
Наконец, ломтик картофельных чипсов «Принглс», если его бесконечно продолжить во все стороны (это несколько труднее изобразить), даёт представление об ещё одной однородной фигуре, про которую математики говорят, что она имеет постоянную отрицательную кривизну. Это означает, что ваше отражение в любой точке зеркальной чипсины будет выглядеть сжатым внутрь.
К счастью, эти описания двумерных однородных фигур без усилий расширяются на интересующий нас случай трёхмерного космического пространства. Положительная, отрицательная или нулевая кривизна — однородное раздувание, однородное сжатие или отсутствие искажений — с тем же успехом характеризуют трёхмерные однородные формы. В действительности нам повезло дважды, поскольку хотя трёхмерные формы очень трудно изобразить (представляя себе форму, наше сознание помещает её в некое окружение — аэроплан в пространстве, планета в пространстве, — но когда дело доходит до пространства, нет никакого окружения, в котором содержалось бы само пространство), трёхмерные однородные формы являются столь точными математическими аналогами своих двумерных родственников, что мы ничего не потеряем, когда станем делать то же, что делает большинство физиков, — мысленно использовать двумерные примеры.
В приведённой ниже таблице я перечислил возможные варианты формы пространства, подчеркнув, что одни из них имеют конечную протяжённость (сфера, экран компьютерной игры), а другие — бесконечную (бесконечный стол и бесконечная чипсина). Таблица 2.1 не является полной. Существуют другие возможные формы, которые носят загадочные названия вроде бинарного тетраэдрального пространства и додекаэдрального пространства Пуанкаре, также имеющие однородную кривизну; я не включил их сюда, поскольку их сложнее наглядно изобразить с помощью повседневных предметов. Они могут быть построены, если подходящим образом нарезать и скомпоновать уже знакомые пространства из нашего списка, так что табл. 2.1 в действительности даёт вполне представительную выборку. Однако все эти подробности второстепенны для нашего ключевого вывода: требование однородности космоса, отражённое в формулировке космологического принципа, существенным образом ограничивает набор возможных форм вселенной. Одни из этих форм имеют бесконечную пространственную протяжённость, другие — нет.{9}
Таблица 2.1. Возможные варианты формы космического пространства, которые находятся в согласии с космологическим принципом — допущением о том, что любое положение во вселенной эквивалентно любому другому
Форма Кривизна Протяжённость Сфера Положительная Конечная Поверхность стола Нулевая («плоская») Бесконечная Экран компьютерной игры Нулевая («плоская») Конечная Ломтик чипсов «Принглс» Отрицательная БесконечнаяНаша Вселенная
Расширение пространства, обнаруженное математическим путём Леметром и Фридманом, применимо к любой вселенной, имеющей одну из вышеперечисленных форм. В случае положительной кривизны можно воспользоваться двумерной аналогией и представить себе, как растягивается поверхность воздушного шарика по мере того, как его надувают воздухом. Для нулевой кривизны подходит образ плоского резинового коврика, который равномерно тянут во всех направлениях. В случае отрицательной кривизны вообразите растягиваемую резиновую чипсину. Если галактики представить себе как равномерно разбросанные блёстки на любой из этих поверхностей, расширение пространства приведёт к тому, что отдельные блёстки-галактики будут отодвигаться друг от друга — в точности как в той картине разбегания галактик, которую наблюдал Хаббл в 1929 году.
Это убедительная космологическая заготовка, но для её полного завершения и определения надо выяснить, какая из описанных форм соответствует нашей Вселенной. Мы можем определить форму знакомых нам объектов — бублика, бейсбольного мяча, куска льда, — взяв их в руки и повертев так и сяк. Проблема в том, что сделать то же самое со вселенной мы не в состоянии, поэтому определять её форму мы вынуждены косвенными методами. Уравнения общей теории относительности подсказывают нам математическую стратегию. Они говорят, что кривизна пространства сводится к единственной наблюдаемой величине — к пространственной плотности материи (более точно — материи и энергии). Если материи много, тяготение заставляет пространство сворачиваться на себя, порождая сферическую форму. Если материи мало, пространство чувствует себя свободно и разворачивается подобно ломтику чипсов «Принглс». А если пространство содержит некое точно определённое количество материи, то его кривизна равна нулю.[4]
Уравнения общей теории относительности также приводят к точному численному критерию, разделяющему данные три возможности. Математические выкладки показывают, что «определённое количество материи» — так называемая критическая плотность, составляет на сегодняшний день примерно 2 × 10−29 грамма на кубический сантиметр, что соответствует примерно шести атомам водорода в одном кубическом метре, или, в более привычных образах, — одной дождевой капле в объёме, равном объёму земного шара.[5] Если оглядеться вокруг, легко может показаться, что плотность вещества во вселенной превышает критическую, но такой вывод будет поспешным. При вычислении критической плотности исходят из того, что вещество равномерно распределено в пространстве. Поэтому надо представить, что атомы, из которых состоят Земля, Луна, Солнце и всё остальное, равномерно распределены по космосу. Тогда весь вопрос сводится к тому, будет ли каждый кубический метр весить больше или меньше шести атомов водорода.
В силу важности космологических следствий, связанных со средней плотностью материи во вселенной, астрономы в течение десятилетий пытались измерить её величину. Метод измерений, которым они пользовались, идейно прост. С помощью мощных телескопов астрономы тщательно обследовали большие области пространства и суммировали массы всех видимых звёзд, а также массу остального материала, наличие которого они могли предполагать, изучая движение звёзд и галактик. До недавнего времени все проведённые наблюдения указывали на то, что величина средней плотности не очень велика, примерно 27 процентов от критической плотности, что соответствует двум атомам водорода на кубический метр. В свою очередь, это означало бы, что вселенная имеет отрицательную кривизну.
Однако позже, в конце 90-х годов прошлого столетия, произошло нечто экстраординарное. На основе некоторых великолепных наблюдений, которые будут рассмотрены в главе 6, и их анализа астрономы осознали, что из подсчёта постоянно упускался некоторый существенный вклад: диффузная энергия, которая, по-видимому, равномерным образом распределена во всём пространстве. Эти данные потрясли всех. Энергия, наполняющая пространство? Звучит как космологическая постоянная, которую, как мы видели, восемьдесят лет назад ввёл Эйнштейн, и от которой, как хорошо известно, он позже сам отказался. Возродили ли современные наблюдения космологическую постоянную?
До сих пор у нас нет полной уверенности на этот счёт. Даже сейчас, спустя десятилетие после первоначальных наблюдений, астрономам всё ещё предстоит выяснить, является ли такая однородная энергия неизменной, или её величина в заданной области пространства изменяется со временем. Космологическая постоянная, как следует из самого её названия (и как следует из математической сути, так как это единственное фиксированное число в гравитационной налоговой декларации), должна быть неизменной. Для описания общего случая, если энергия может изменяться, а также чтобы подчеркнуть факт отсутствия у данной энергии излучения (это объясняет, почему её не могли обнаружить так долго), астрономы ввели новый термин: тёмная энергия. При этом прилагательное «тёмный» не менее хорошо характеризует и наше текущее понимание. Никто не в силах объяснить происхождение тёмной энергии, её фундаментальный состав или свойства — эти вопросы активно исследуются в настоящее время, и мы вернёмся к ним в последующих главах.
Несмотря на многие нерешённые вопросы, детальные наблюдения на орбитальном телескопе «Хаббл» и в наземных обсерваториях позволили определиться с количеством тёмной энергии, заполняющей пространство в настоящее время. Полученное значение отличается от когда-то предложенного Эйнштейном (он постулировал значение, приводящее к статичной вселенной, а наша Вселенная расширяется). Удивительно не это, а то, что согласно этим измерениям тёмная энергия в пространстве составляет примерно 73 процента от критической плотности. Добавив их к уже измеренным астрономами 27 процентам, мы получим ровно 100 процентов критической плотности, что и есть то самое определённое количество энергии и материи, приводящее ко вселенной с нулевой пространственной кривизной.
Итак, современные данные говорят в пользу постоянно расширяющейся вселенной, форма которой похожа на трёхмерный вариант бесконечной поверхности стола или конечный экран игровой приставки.
Реальность в бесконечной Вселенной
Как было отмечено в самом начале этой главы, нам неизвестно, конечна или бесконечна наша Вселенная. В предыдущих разделах обсуждался случай, когда обе эти возможности естественным образом возникают из теоретических конструкций, и тот или иной выбор никак не противоречит самым точным астрофизическим измерениям и наблюдениям. И как же тогда экспериментально установить, какая из этих возможностей верна?
Это трудный вопрос. Если пространство конечно, то свет от звёзд и галактик циркулировал бы по всему космосу, многократно отражаясь, прежде чем попасть в наши телескопы. Подобно бесконечным изображениям, возникающим при отражении луча света между параллельными зеркалами, зацикленный свет приводил бы к повторяющимся изображениям звёзд и галактик. Астрономы искали подобные повторяющиеся изображения, но пока ничего не обнаружили. Само по себе это не доказывает бесконечность пространства, но показывает следующее: если оно конечно, то может быть настолько большим, что у света попросту было недостаточно времени пройти больше одного круга по космическому гоночному треку. И в этом кроется вызов всей наблюдательной астрономии! Даже если вселенная конечна, то чем она больше, тем лучше маскируется под бесконечную.
Для некоторых космологических вопросов, таких как возраст вселенной, различие между этими двумя возможностями не играет никакой роли. Конечен ли космос или бесконечен, в ранние периоды его существования галактики располагались плотнее друг к другу и поэтому вселенная была более плотной, горячей и более экстремальной. Из данных современных наблюдений о скорости расширения и теоретического анализа того, как эта скорость меняется со временем, мы можем оценить время, прошедшее с того момента, — которое можно назвать началом, — когда всё, что мы сейчас видим, возникло из одной фантастически плотной крупицы. И неважно, конечна вселенная или бесконечна, современные расчёты относят этот момент на 13,7 миллиардов лет назад.
Однако для других вопросов конечность-бесконечность вселенной имеет значение. Например, в конечном случае, рассматривая космос во всё более ранние моменты времени, мы должны представлять пространство всё более и более сжатым. И хотя математика перестаёт работать в начальный, нулевой момент времени, тем не менее, будет правильно представлять пространство при приближении к начальному моменту как всё уменьшающееся ядрышко. А вот в бесконечном случае такое описание неверно: если пространство действительно бесконечно, то оно было и будет таким всегда. При сжатии содержимое пространства сдавливается, приводя к увеличению плотности вещества, но общий размер всё равно остаётся бесконечным. Действительно, если мы сожмём поверхность бесконечного стола в 2 раза, то что мы получим? Половину бесконечности, которая по-прежнему бесконечна. Сожмём в 1 миллион раз и что получим? По-прежнему бесконечность. Чем ближе в бесконечной Вселенной мы подходим к начальному моменту времени, тем плотнее она становится в каждой точке, всё равно оставаясь бескрайней.
И хотя наблюдения не дают ответа на вопрос о конечности-бесконечности вселенной, для себя я выяснил, что физики и космологи склонны считать, — если их настойчиво спрашивать, — что наша Вселенная бесконечна. Думаю, что до некоторой степени такая точка зрения возникла исторически, ведь в течение десятилетий конечному плоскому пространству (как плоский экран для видеоигр) не уделялось достаточно внимания, в основном из-за его математической сложности. Возможно, что данная точка зрения также отражает общий подход, будто различие между бесконечной и конечной-но-очень большой вселенной является космологическим вопросом, представляющим исключительно академический интерес. В конце концов, если пространство настолько огромно, что нам в любом случае будет доступна лишь малая его часть, стоит ли беспокоиться о том, простирается ли оно бесконечно или конечно за пределами того, что мы можем видеть?
Я думаю, что стоит. Вопрос о конечности или бесконечности пространства имеет фундаментальное значение для самой природы реальности. В нём вся суть этой главы. А теперь давайте представим, что космос бесконечен, и выясним, к чему это приводит. Недолго думая, мы обнаружим, что живём в одном из бесконечного множества параллельных миров.
Бесконечное пространство и лоскутное одеяло
Давайте забудем ненадолго о бесконечных просторах вселенной и начнём с простой, вполне себе земной ситуации. Представьте, что ваша подруга Имельда, идя на поводу у своей страсти к обновлению гардероба, приобрела пятьсот роскошных платьев и тысячу пар обуви от-кутюр. Если каждый день она будет надевать одно платье и одну пару обуви, то в какой-то момент все возможные комбинации будут исчерпаны, и ей придётся повторить наряд. Легко оценить, когда это произойдёт. Из пяти сотен платьев и одной тысячи пар обуви можно составить 500 000 различных комбинаций. Пятьсот тысяч дней — это примерно 1400 лет, и, поэтому, если Имельда проживёт достаточно долго, то её можно будет увидеть в том наряде, который она когда-то уже надевала. Если Имельда, дай бог ей крепкого здоровья, снова и снова будет перебирать наряды, то она обязательно наденет каждый из них бесконечное число раз. Бесконечное число появлений Имельды в конечном числе нарядов приводит к бесконечным повторениям.
Развивая эту же тему, представим что Рэнди, опытный крупье, последовательно перетасовал невообразимое количество карточных колод и аккуратно разложил стопками, одну за другой. Отличается ли порядок карт в каждой перетасованной колоде или же они должны повторяться? Ответ зависит от количества колод. Пятьдесят две карты в колоде могут быть расположены 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 284 000 000 000 000 различными способами (52 способа расположения первой карты умножить на 51 способ расположения второй карты, умножить на 50 способов расположения следующей карты, и так далее). Если количество колод, которые перетасовывает Рэнди, превышает число возможных раскладов карт внутри колоды, то тогда расклады в части колод совпадут. Если бы Рэнди перетасовывал бесконечное количество карт, то одинаковые расклады карт внутри колод обязательно бы повторялись бесконечное число раз. Так же как с Имельдой и её нарядами, бесконечное число событий при конечном числе возможных сочетаний приводит к тому, что различные расклады бесконечно повторяются.
Это базовое понятие очень важно для космологии бесконечной вселенной. Следующие два ключевых шага демонстрируют, почему это так.
Большая часть бесконечной вселенной находится за пределами видимого, даже если использовать самые мощные телескопы. Несмотря на то, что свет распространяется невероятно быстро, если объект достаточно удалён, то испущенный им свет — даже если это произошло сразу после Большого взрыва — просто не успеет долететь до нас. Так как возраст нашей Вселенной примерно 13,7 миллиарда лет, то можно подумать, что в эту категорию попадает всё, что находится далее чем 13,7 миллиардов световых лет. Такой интуитивный вывод в целом правильный, но надо учитывать, что расширение пространства увеличивает расстояние между объектами, один из которых испустил свет давным-давно, а другой только что этот свет поглотил; поэтому максимальное расстояние, на которое мы можем заглянуть, на самом деле больше — примерно 41 миллиард световых лет.[6] Точная цифра не имеет особого значения. Важно то, что области вселенной, находящиеся на определённом расстоянии от нас, недоступны нашим наблюдениям. Подобно кораблям, ушедшим за горизонт и потому невидимым с берега, объекты в пространстве, слишком удалённые, чтобы быть доступными для наблюдения, находятся, как говорят астрономы, за пределами нашего космического горизонта.
Точно так же свет, испущенный нами, ещё не достиг тех удалённых областей космоса, поэтому и мы находимся за пределами их космического горизонта. Причём космический горизонт — это единственное, что очерчивает доступное и недоступное нашему взору. Из специальной теории относительности Эйнштейна мы знаем, что никакой сигнал, возмущение или информация, вообще ничего не может распространяться быстрее света. Это означает, что области вселенной, расположенные настолько далеко друг от друга, что свет не успел дойти от одной области к другой, никак не взаимодействовали и развивались совершенно независимо друг от друга.
Воспользовавшись двумерной аналогией, мы можем сравнить пространство в некий момент времени с гигантским лоскутным одеялом (с круглыми лоскутками), каждый лоскут которого представляет отдельный космический горизонт. Некто, расположенный в центре лоскута, мог провзаимодействовать со всем, что находится внутри этого лоскутка, но с соседними лоскутками не было никакого контакта, потому что они находятся слишком далеко (см. рис. 2.1а). Точки вблизи границы двух лоскутков расположены ближе друг к другу, нежели соответствующие центры, и поэтому могли бы провзаимодействовать. Но если рассмотреть, например, лоскутки, расположенные через строку и через столбец в космическом одеяле, то ясно, что все точки, расположенные в разных лоскутках настолько далеки друг от друга, что никакое перекрёстное взаимодействие не имеет места (см. рис. 2.1б). Та же самая идея работает и в трёх измерениях, когда космические горизонты — лоскутки на космическом одеяле — имеют сферическую форму. Причём справедлив тот же вывод: достаточно отдалённые лоскутки находятся за пределами сферы влияния каждого и, поэтому, это независимые миры.
Рис. 2.1. а) Так как скорость света конечна, наблюдатель в центре лоскутка (называемом космическим горизонтом наблюдателя) может провзаимодействовать только с тем, что находится в том же самом лоскутке; б) Достаточно удалённые космические горизонты слишком далеко отстоят друг от друга, чтобы как-то взаимодействовать, и поэтому развиваются совершенно независимо.
Если пространство огромно, но имеет конечный размер, его можно разделить на большое, но всё же конечное число независимых лоскутков. Если же пространство бесконечно, то и число независимых лоскутков тоже бесконечно. Именно вторая возможность представляется наиболее захватывающей, и сейчас мы увидим, почему так происходит. В любом таком лоскутке частицы вещества (более точно, вещества и энергии всех видов) могут быть собраны лишь в конечное число различных конфигураций. Те же самые рассуждения, которые мы отрепетировали на Имельде и Рэнди, приводят нас к выводу, что условия существования в бесконечном разнообразии лоскутков — в областях вселенной, наподобие той, в которой мы живём, но распределённых в безграничном космосе — обязательно должны повторяться.
Конечность возможностей
Представьте душную летнюю ночь и жужжащую муху, которая назойливо кружит над вашей кроватью. Уже были попытки прихлопнуть вредное насекомое мухобойкой или уморить зловонным спреем. Ничего не помогает. В отчаянии вы пытаетесь убедить муху улететь. «Ведь это большая спальня», — уговариваете вы муху. «Здесь столько разных мест, где можно полетать. Нет никакой особой причины жужжать именно над моим ухом». «Неужжжели? — хитро парирует муха. — И сколько же их?».
В классической вселенной правильным ответом будет «бесконечно много». Как только вы скажете это мухе, она (а точнее её центр масс) может перелететь на 3 метра влево, либо на 2,5 метра вправо, а может быть на 2,236 метра наверх или на 1,195829 метра вниз, или… ну вы поняли идею. Так как положение мухи меняется непрерывно, то число мест, где она может оказаться, — бесконечно. На самом деле, как только вы станете объяснять это мухе, то сразу же поймёте, что не только положение бесконечно разнообразно характеризует муху, но и скорость. В какой-то момент муха может быть здесь и лететь направо со скоростью один километр в час или налево, со скоростью полкилометра в час. Может лететь вверх со скоростью в четверть километра в час или вниз — со скоростью 0,349283 километра в час, и так далее. И хотя скорость мухи ограничена некоторыми факторами (включая конечный запас энергии, — чем быстрее муха летит, тем больше энергии тратит), она может изменяться непрерывно, что приводит к ещё одному бесконечному выбору возможностей.
Но муху вы не убедили. «Я согласна с тобой, если речь идёт о смещении на сантиметр или полсантиметра, или даже на четверть сантиметра, — отвечает муха. — Но когда ты говоришь о положениях в пространстве, разделённых расстояниями в одну десятитысячную или в одну миллионную сантиметра, то я там просто не умещусь! Пусть для какого-нибудь умника это разные положения, но мой жизненный опыт подсказывает, что нет никакой разницы между быть здесь и быть на одну миллиардную сантиметра слева отсюда. Я не чувствую такую крошечную разницу и поэтому не могу считать их разными положениями. То же самое происходит и со скоростями. Я могу отличить скорость один километр в час от скорости в два раза меньше. Но разница между 0,25 километров в час и 0,249999999 километров в час? Я тебя умоляю! Только очень мудрая муха может утверждать, что видит разницу. Но на самом деле никто из нас не способен на такое. Что до меня — эти скорости одинаковые. Так что доступное разнообразие вариантов гораздо у́же, чем ты описываешь».
Муха подняла важный вопрос. Вообще говоря, количество положений мухи, как и количество возможных скоростей — бесконечно. Но на практике есть предел того, насколько точно можно ощутить разницу скоростей и положений, прежде чем она пропадёт окончательно. Это будет верно, даже если оснастить муху самым лучшим оборудованием. Всегда существует предел малости измеряемого приращения скорости или положения. И неважно, насколько малы эти минимальные приращения; если они отличны от нуля, они радикально сужают область возможных значений измерений.
Например, если наименьшее приращение, которое можно измерить, составляет сотую долю сантиметра, то в каждом сантиметре содержится не бесконечное число возможных измеряемых положений, а всего лишь сотня. Таким образом, в каждом кубическом сантиметре содержится 1003 = 1 000 000 различных положений, а в спальне средних размеров их будет около 100 триллионов. Трудно сказать, впечатлит ли муху такой спектр предложений, и оставит ли она вас в покое. Вывод, однако, состоит в том, что всё, кроме измерений с абсолютным разрешением, уменьшает число возможностей от бесконечного до конечного.
Вы можете возразить, что неспособность различать кратчайшие пространственные расстояния или фиксировать мельчайшую разницу между скоростями является всего лишь технологическим ограничением. Прогресс не стоит на месте, точность оборудования растёт, так что число заметно разных положений и скоростей, доступных хорошо финансируемой мухе, тоже будет увеличиваться. Здесь, однако, я должен обратиться к основам квантовой теории. В соответствии с квантовой механикой есть вполне определённый смысл в том, что существует фундаментальный предел точности, с которой могут быть проведены измерения, и такой предел в принципе не может быть преодолён, никогда, как бы далеко не продвинулся технологический прогресс. Данный предел возникает из основного принципа квантовой механики, принципа неопределённости.
Принцип неопределённости утверждает, что какие бы измерительные приборы или способы измерений вы не использовали, за увеличение разрешения при измерении одной величины неизбежно приходится платить — падает точность измерения некоторой дополнительной к ней величины. Одним из главных примеров проявлений принципа неопределённости является то, что чем точнее вы измеряете положение объекта, тем менее точно вы может измерить его скорость, и наоборот.
Для классической физики, той физики, которая во многом соответствует нашим интуитивным представлениям об устройстве этого мира, данное ограничение абсолютно чуждо. Однако как некую грубую аналогию, представьте себе процесс фотографирования той ехидной мухи. Если скорость затвора высока, получится контрастное изображение, на котором будет запечатлено положение мухи в тот момент, когда вы сделали снимок. Но из-за того, что это моментальный снимок, муха на нём неподвижна, и он не содержит никакой информации о её скорости. При уменьшении скорости затвора получится расплывчатый снимок, содержащий некоторую информацию о движении, однако именно из-за этой расплывчатости на снимке не будет точных данных о положении мухи. Невозможно сделать снимок, содержащий информацию и о точном положении, и о точной скорости мухи.
С помощью математического аппарата квантовой механики Вернер Гейзенберг определил точный предел того, насколько неточным должно быть с необходимостью совместное измерение положения и скорости. Эта неизбежная неточность и есть то, что физики называют квантово-механической неопределённостью. Существует особенно полезный для наших целей способ представить этот результат. Так же как для получения контрастной фотографии необходима высокая скорость затвора, соотношение Гейзенберга показывает, что для проведения более точного измерения положения объекта требуется зонд с большей энергией. Включите ваш прикроватный светильник, и этот зонд — рассеянный, слабый свет — позволит вам разглядеть глаза и лапки у мухи; а если посветить на муху высокоэнергичными фотонами, такими как рентгеновские лучи (только не переусердствуйте, иначе можно поджарить муху), то большее разрешение позволит разглядеть мышцы, приводящие в движение мушиные крылья. При этом абсолютное разрешение, согласно Гейзенбергу, требует бесконечных затрат энергии. А это недостижимо.
Итак, самый главный вывод мы уже сделали. Из классической физики со всей очевидностью следует, что абсолютное разрешение не достижимо на практике. Квантовая механика идёт дальше и утверждает, что абсолютное разрешение не достижимо в принципе. Если вы представляете, что скорость и положение объекта, будь то муха или электрон, одновременно изменяются на достаточно малые значения, то согласно квантовой механике вы представляете нечто, не имеющее смысла. Изменения, слишком малые чтобы их измерить, даже в принципе, не являются изменениями вообще.{10}
С помощью тех же рассуждений, что мы использовали в доквантовом анализе мухи, можно видеть, что ограничение на разрешение уменьшает от бесконечного до конечного число различных значений положения и скорости объекта. И поскольку ограниченное разрешение, вытекающее из квантовой механики, вплетено в саму ткань физических законов, уменьшение числа возможностей до конечного неизбежно и неопровержимо.
Космическая многократность
Но хватит о назойливых мухах. Давайте теперь рассмотрим достаточно большую область пространства. Пусть её размер сопоставим с размером современного космического горизонта — сферы радиусом 41 миллиард световых лет. То есть рассмотрим область размером с лоскут космического одеяла. Давайте поместим туда не одну единственную муху, а много частиц материи и квантов излучения. Теперь вопрос: сколько есть способов для различной компоновки частиц?
Так же как в конструкторе «Лего»: чем больше кубиков у вас есть (чем больше вещества и излучения вы втиснули в область пространства) — тем больше число возможных компоновок. Но вы не можете втиснуть бесконечное количество кубиков. У частиц есть энергия, поэтому чем больше частиц, тем больше энергии. Если в области пространства слишком много энергии, она схлопнется под собственным весом, и возникнет чёрная дыра.[7] Если после образования чёрной дыры попытаться втиснуть в эту область ещё больше материи и энергии, то граница чёрной дыры (её горизонт событий) расширится, охватив ещё больше пространства. Таким образом, существует предел того, сколько материи и энергии может находиться в области пространства заданного размера. Для области пространства, сопоставимой по размерам с современным космическим горизонтом, этот предел невероятно велик (примерно 1056 грамм). Однако величина предела не играет главной роли. Главное, что этот предел существует.
Количество энергии внутри космического горизонта конечно, поэтому число частиц тоже конечно, будь то электроны, протоны, нейтроны, нейтрино, мюоны, фотоны или любые другие известные или ещё не обнаруженные виды в сообществе элементарных частиц. Конечность энергии внутри космического горизонта также приводит к тому, что каждая из этих частиц, подобно надоедливой мухе в вашей спальне, обладает конечным числом разных возможных положений и скоростей. В целом, то, что существует конечное число частиц, каждая из которых может иметь конечное множество различных положений и скоростей, означает, что внутри любого космического горизонта доступно лишь конечное число различных компоновок частиц. (В главе 8 мы познакомимся с более тонким языком квантовой механики, когда говорят не о положениях частиц и их скоростях как таковых, а о квантовом состоянии этих частиц. Тогда мы будем говорить, что есть лишь конечное число наблюдаемых квантовых состояний частиц в данном космическом лоскутке.) Действительно, небольшое вычисление, которое любознательный читатель найдёт в примечаниях, показывает, что число различных конфигураций частиц внутри космического горизонта составляет примерно 1010122 (единица с 10122 нулями). Это огромное, но всё же конечное число.{11}
Ограниченность числа комбинаций разных платьев и туфель гарантирует, что спустя достаточное количество выходов в свет наряды Имельды начнут повторяться. Ограниченность числа различных карточных раскладов гарантирует, что если у Рэнди будет достаточно колод, то однажды итог очередного тасования карт обязательно повторит один из предыдущих. Рассуждая аналогично, мы придём к такому выводу: ограниченное количество компоновок частиц гарантирует, что при достаточном числе лоскутков в космическом одеяле, то есть при достаточном числе космических горизонтов, компоновки частиц, сравниваемые по-лоскутно, обязаны где-то повториться. Даже если бы вы могли выступить в роли космического дизайнера и попытались бы сделать так, чтобы каждый лоскуток отличался по дизайну от всех предыдущих, то в достаточно большом пространстве у вас закончатся свежие идеи, и вы будете вынуждены повторить вариант одного из предыдущих дизайнов.
В бесконечно большой вселенной многократность повторений вообще зашкаливает. Существует бесконечно много лоскутков на бесконечных просторах пространства, поэтому, при конечном наборе разных компоновок частиц, компоновки в лоскутках обязаны повторяться бесконечное число раз.
Как раз то, что нам нужно.
Ничего кроме физики
Анализируя следствия этого утверждения, я должен сразу сказать, куда клоню. Я считаю, что физическая система полностью определяется тем, как скомпонованы частицы, из которых она состоит. Скажите мне, какие возможные конфигурации допустимы для частиц, составляющих нашу планету, Солнце, галактику и всё остальное, и вы совершенно отчётливо опишите окружающую действительность. Такой редукционистский подход достаточно распространён среди физиков, но тем не менее, конечно же, есть люди, думающие иначе. Особенно, когда речь заходит о феномене жизни. Есть мнение, что должен существовать некий существенно нефизический аспект (дух, душа, жизненная сила, энергия ци и так далее), который одушевляет физический объект. Хотя я не исключаю такую возможность, но никогда не встречал какого-либо подтверждения этому. Наиболее осмысленная позиция для меня состоит в том, что физические и ментальные свойства кого-либо — это не более чем проявление способа организации частиц, составляющих чьё-либо тело. Задайте возможные конфигурации, и вы определите всё на свете.{12}
Придерживаясь такой точки зрения, можно сделать вывод, что если известные нам конфигурации частиц повторяются в другом лоскутке — в другом космическом горизонте, — то этот лоскуток будет во всём похож на наш. Это означает, что если вселенная простирается бесконечно, то вы не одиноки в своей реакции (какой бы она не была) на эту точку зрения об окружающей действительности. В глубине космоса существует множество ваших точных копий, ведущих и чувствующих себя точно так же как вы. И не существует никакого способа сказать, какая из них — это действительно вы. Все копии физически и, следовательно, ментально тождественны.
Можно даже оценить расстояние до ближайшей копии. Если конфигурации частиц случайно распределены от лоскутка к лоскутку (такое допущение согласуется с уточнённой космологической теорией, с которой мы познакомимся в следующей главе), то можно ожидать, что условия в нашем лоскутке будут повторяться столь же часто как и в любом другом. В каждой коллекции из 1010122 космических лоскутков будет, как мы ожидаем, в среднем один лоскуток, в точности похожий на наш.
То есть в каждой области пространства размером примерно 1010122 метров в поперечнике должен находиться один лоскуток, повторяющий наш, в котором находитесь вы, Земля, галактика и всё остальное, что населяет наш космический лоскуток.
Если умерить амбиции и не искать точную копию всего космического горизонта, а удовлетворится точной копией области протяжённостью в несколько световых лет с центром, где наше Солнце, то желаемого будет достичь гораздо проще: в среднем, в каждой области размером примерно 1010100 метров в поперечнике вы обнаружите одну такую копию. Приближённые копии найти ещё проще. Более того, есть только один способ найти точную копию данной области, и множество способов найти почти точную копию. Если бы вы посетили эти приближённые копии, то обнаружили бы, что некоторые из них практически неотличимы от нашей, а отличия других варьируются от очевидного до смешного и шокирующего. Любое когда-либо принятое вами решение равносильно какой-то частной конфигурации частиц. Если вы повернули налево, ваши частицы расположились одним образом, если вы повернули направо, то частицы расположились другим образом. Если вы сказали да, частицы вашего мозга, губ и голосовых связок дали одну конфигурацию; если вы сказали нет, — то другую конфигурацию. И поэтому каждое ваше действие, каждый сделанный выбор и каждая отклонённая возможность будут проиграны в том или ином лоскутке. В каком-то из них станут реальностью ваши самые худшие страхи о себе, вашей семье и жизни на земле. В других осуществятся ваши самые дикие фантазии. А в других похожие, но всё-таки отличные конфигурации частиц приведут к совершенно неузнаваемой среде обитания. А в большинстве лоскутков среди всего многообразия частиц будут отсутствовать некоторые, в высшей степени особые конфигурации, которые мы называем живыми организмами, так что эти лоскутки будут безжизненными, или, по крайней мере, лишёнными жизни в привычном нам виде.
Размер космических лоскутков, изображённых на рис. 2.1б, со временем будет увеличиваться. По прошествии времени свет будет проникать всё дальше и дальше, так что каждый из космических лоскутков будет расти. В конце концов космические горизонты пересекутся. И когда это произойдёт, области пространства больше не будут рассматриваться как отдельные и изолированные друг от друга, параллельные перестанут быть параллельными, они сольются. Тем не менее полученный нами ранее результат будет по-прежнему справедлив. Нарисуем новую решётку космических лоскутков, размер которых определяется расстоянием, которое прошёл свет с момента Большого взрыва и по настоящее время. Лоскутки увеличатся, поэтому на картинке, подобной рис. 2.1б, центры лоскутков отодвинутся дальше друг от друга. Однако в бесконечном пространстве найдётся предостаточно места для учёта такой поправки.{13}
Таким образом, мы пришли к общему удивительному заключению. Для большинства из нас реалии бесконечного космоса не соответствуют нашим ожиданиям. В каждый момент времени в пространстве существует бесконечное множество отдельных миров, объединение которых я буду называть лоскутной мультивселенной, где наша Вселенная всего лишь одна из многих. Осмысливая эту бесконечную коллекцию отдельных миров, мы обнаруживаем, что конфигурации частиц обязательно повторяются бесконечное число раз. Таким образом, реальность в любой наперёд заданной вселенной, включая нашу, воспроизводится в бесконечном числе других вселенных этой лоскутной мультивселенной.{14}
И как это понимать?
Вывод, к которому мы пришли, может показаться настолько ошеломляющим, что возникнет желание вернуть всё на круги своя. Вы можете возразить, что причудливое устройство описанного выше мира, все эти бесконечные копии всего и всех, есть просто свидетельство ошибочности одного или нескольких допущений, что привели нас сюда.
Может ли предположение о том, что космос наполнен частицами, быть неправильным? А вдруг за пределами нашего космического горизонта находится огромная пустыня, в которой нет ничего кроме пустоты. Такое может случиться, однако теоретические измышления, необходимые для обоснования такой возможности, совершенно неубедительны. Самые осмысленные космологические теории, с которыми мы ниже познакомимся, даже близко не допускают подобного результата.
Могут ли сами физические законы быть другими за пределами нашего космического горизонта, что лишит нас возможности сколь-нибудь надёжно теоретизировать об удалённых мирах? Опять же такое возможно. Но как станет видно в следующей главе, недавно был найден убедительный аргумент, почему, несмотря на то, что законы могут быть другими, эти изменения не в силах изменить наши выводы относительно лоскутной мультивселенной.
Может ли пространственная протяжённость вселенной быть конечной? Да, может. Это определённо возможно. Если пространство конечно, но достаточно большое, то где-то там всё равно могли бы существовать какие-нибудь интересные лоскутки. Однако в довольно маленькой конечной вселенной запросто может не хватить места для размещения сколько-нибудь значительного количества разных лоскутков, не говоря уж о копиях нашей собственной Вселенной. Поэтому конечность вселенной наиболее убедительным образом противоречит существованию лоскутной мультивселенной.
Однако физики в последние несколько десятилетий в попытке применить теорию Большого взрыва к самому начальному моменту времени — и достичь более глубокого понимания происхождения Вселенной и природы первичного атома Леметра — развили подход, который называется инфляционной космологией. В рамках инфляционного подхода доводы в пользу бесконечно большого космоса не только приобрели серьёзные наблюдательные и теоретические подтверждения, но и, как мы увидим в следующей главе, привели к почти неизбежному выводу.
Более того, инфляция выводит на первый план другой, ещё более экзотический вид параллельных миров.
Глава 3. Вечность и бесконечность Инфляционная мультивселенная
В середине XX века впервые было осознано, что если потушить Солнце и удалить все другие звёзды из Млечного Пути и даже размести по сторонам более удалённые галактики, то окружающее пространство всё равно не будет чёрным. Для человеческого глаза оно по-прежнему будет чёрным, но если бы мы могли видеть в микроволновой части спектра, то куда бы мы не посмотрели, повсюду будет однородное свечение. Где его начало? В начале! Физики замечательным образом обнаружили всепроникающее море микроволнового излучения, заполняющее пространство, — дошедший до наших дней отголосок рождения Вселенной. История этого достижения является очередной демонстрацией феноменального успеха теории Большого взрыва, но одновременно с этим вскрывает один из фундаментальных недостатков теории и создаёт площадку для последующего ключевого, после новаторских работ Леметра и Фридмана, прорыва в космологии — инфляционной космологии.
Инфляционная космология видоизменяет теорию Большого взрыва, дополняя её интенсивной вспышкой невероятно быстрого расширения в течение первых мгновений жизни Вселенной. Мы увидим, что такая модификация оказывается существенной для объяснения некоторых свойств реликтового излучения, которые иначе объяснить не удаётся. И более того, инфляционная космология играет ключевую роль в нашем повествовании, потому что в течение последних нескольких десятилетий учёные постепенно осознали, что наиболее убедительные варианты теории приводят к огромному количеству параллельных вселенных, коренным образом изменяя характер реальности.
Следы жаркого начала
Георгий Гамов, советский физик, иммигрировавший в США, за два метра ростом, известен благодаря своим открытиям в квантовой и ядерной физике в начале XX века. У него была непростая судьба, но он был жизнерадостный и находчивый (в 1932 году он и его жена хотели сбежать из Советского Союза за границу, пытаясь переплыть Чёрное море на байдарке с запасом шоколада и коньяка; когда плохая погода заставила беглецов вернуться на берег, Гамов заговорил зубы представителям властей, рассказав им историю про неудавшийся научный эксперимент в открытом море). В 1940-х годах, успешно перебравшись за железный занавес (по суше, без особых запасов шоколада) и обосновавшись в университете Вашингтона в Сент-Луисе, Гамов занялся космологией. Исследования, проведённые им при содействии своего феноменально талантливого аспиранта Ральфа Альфера, прояснили и оживили картину первых мгновений жизни Вселенной, по сравнению с ранними работами Фридмана (который был учителем Гамова в бытность его в Ленинграде) и Леметра. С учётом небольших современных дополнений картина, нарисованная Гамовым и Альфером, выглядела следующим образом.
Сразу после рождения, будучи невероятно горячей и плотной, Вселенная пребывала в угаре активной деятельности. Пространство быстро расширялось и остывало, что приводило к образованию частиц из первичной плазмы. В течение первых трёх минут температура быстро падала, однако оставалась достаточно высокой, чтобы Вселенная была похожа на космическую ядерную печь, где образовывались простейшие атомные ядра: водород, гелий, небольшие количества лития. По прошествию ещё нескольких минут температура упала до 108 градусов по Кельвину, что примерно в 10 000 раз выше температуры поверхности Солнца. Несмотря на то, что согласно привычным стандартам такая температура крайне высока, её уже не хватает для дальнейшего поддержания ядерных процессов, и, начиная с этого момента, интенсивность движения частиц сильно падает. Последующие миллиарды лет почти ничего не происходило, пространство просто продолжало расширяться, а плазма частиц продолжала остывать.
Затем, примерно 370 000 лет спустя, когда Вселенная остыла приблизительно до 3000 K, что составляет примерно половину от температуры поверхности Солнца, однообразие космических будней было кардинальным образом нарушено. На тот момент пространство было заполнено плазмой электрически заряженных частиц, в основном протонов и электронов. Поскольку электрически заряженные частицы обладают характерной особенностью отбрасывать частицы света — фотоны, то первичная плазма была непрозрачной; фотоны, непрестанно отталкиваемые электронами и протонами, давали рассеянное свечение, похожее на свет фар автомобиля в плотном тумане. Но как только температура опустилась ниже 3000 K, быстрые электроны и ядра замедлились и стали объединяться в атомы; электроны, захваченные атомными ядрами, сели на орбиты. В этом состояло главное изменение. Так как заряды протонов и электронов равны по величине, но противоположны друг другу, образуемые ими атомы электрически нейтральны. А поскольку фотоны проходят через вещество, состоящее из электрически нейтральных компонент, не хуже, чем вода через сито, образование атомов привело к тому, что космический туман рассеялся, и световое эхо Большого взрыва вырвалось наружу. С тех самых пор первичные фотоны пронизывают всё пространство.
Всё так, но важно сделать одно предостережение. Хотя электрически заряженные частицы больше не отбрасывают фотоны то туда, то сюда, частицы света оказались подвержены другому важному воздействию. При расширении пространства содержимое становится более разреженным и остывает, в том числе и фотоны. Однако, в отличие от частиц материи, фотоны не замедляются при остывании; являясь частицами света, они всегда летят со световой скоростью. Вместо этого при остывании колебательные частоты фотонов уменьшаются, что приводит к изменению цвета. Фиолетовые фотоны становятся голубыми, затем зелёными, жёлтыми, красными, после чего становятся инфракрасными (как те, что видны в приборе ночного видения), затем микроволновыми (как те, что разогревают пищу в микроволновой печи) и, наконец, становятся радиоволнами.
Гамов впервые понял, а Альфер и его соавтор Роберт Герман тщательным образом проделали вычисления, что если теория Большого взрыва верна, то пространство должно быть повсеместно наполнено остаточными фотонами с момента рождения Вселенной, разлетающимися во всех возможных направлениях. Колебательные частоты остаточных фотонов определяются тем, насколько Вселенная расширилась за последние миллиарды лет с момента их высвобождения. Подробные математические вычисления показали, что фотоны должны были остыть почти до абсолютного нуля и иметь частоты в микроволновой части спектра. По этой причине они называются космическим микроволновым фоновым (реликтовым) излучением[8].
Не так давно я перечитывал статьи Гамова, Альфера и Германа конца 1940-х годов, в которых были анонсированы и объяснены эти выводы. Эти статьи являются жемчужинами теоретической физики. Техническая сторона дела вряд ли требует подготовки выше уровня знаний первокурсников, в то время как получаемые результаты — выдающиеся. Авторы пришли к выводу, что мы целиком и полностью окружены реликтовыми фотонами, завещанными нам с момента бурного рождения Вселенной.
Теперь можно только удивляться, почему эти статьи остались незамеченными. Это произошло в основном потому, что они были написаны в тот период, когда в науке доминировали квантовая и ядерная физика. Космологии ещё предстояло стать точной наукой, и поэтому физическое сообщество было менее восприимчиво к тому, что, как казалось, лежало на периферии теоретической мысли. Не в последнюю очередь судьба этих статей объясняется необычным шутливым стилем самого Гамова (как-то раз он изменил авторство одной из статей, написанной совместно с Альфером, и включил туда своего друга, будущего нобелевского лауреата Ганса Бете, только для того, чтобы в заголовке стояло Альфер, Бете, Гамов, что звучало как первые три буквы греческого алфавита), это привело к тому, что некоторые физики воспринимали его не так серьёзно, как он того заслуживал. Как они не старались, Гамов, Альфер и Герман так и не смогли заинтересовать кого-либо в своих результатах, не говоря уж о том, чтобы убедить астрономов направить значительные усилия на поиск предсказанного ими реликтового излучения. Статьи были быстро забыты.
В самом начале 1960-х годов, ничего не зная о более ранних работах, принстонские физики Роберт Дикке и Джим Пиблс, путём похожих рассуждений, пришли к такому же выводу: Большой взрыв должен был привести к вездесущему фоновому излучению, наполняющему пространство.{15} Однако, в отличие от группы Гамова, Дикке был известным экспериментатором, и ему не надо было никого убеждать начать экспериментальные поиски. Этим он мог заняться и сам. Вместе со своими студентами Давидом Вилкинсоном и Питером Роллом Дикке разработал экспериментальную схему обнаружения реликтовых фотонов, оставшихся после Большого взрыва. Но прежде чем принстонские учёные приступили к осуществлению своих планов, прозвучал один из наиболее знаменитых телефонных звонков в истории науки.
Пока Дикке и Пиблс занимались вычислениями, физики Арно Пензиас и Роберт Вильсон из лаборатории Белла, расположенной менее чем в пятидесяти километрах от Принстона, боролись с радиоантенной (по случайному совпадению антенна была построена по проекту Дикке, разработанному им в 1940-х годах). Как они не бились с настройками, но приёмник антенны издавал постоянный и неустранимый шипящий фоновый шум. Пензиас и Вильсон были убеждены, что что-то не так с оборудованием. Но затем произошла цепочка случайных событий. Всё началось с доклада Пиблса в феврале 1965 года в университете Джона Хопкинса, на котором присутствовал радиоастроном Кеннет Тернер из института Карнеги. После семинара Тернер рассказал об этом своему коллеге из Массачусетского технологического института Бернарду Берку, который, как оказалось, был знаком с Пензиасом из лаборатории Белла. Услышав о принстонских исследованиях, группа лаборатории Белла осознала, что приёмник шипел не просто так: антенна принимала реликтовое излучение. Пензиас и Вильсон позвонили Дикке, и он сразу подтвердил, что они действительно случайно напали на отзвук Большого взрыва.
Обе группы учёных договорились опубликовать статьи одновременно в престижном «Астрофизическом журнале». Принстонская группа обсуждала выдвинутую ими теорию космологического происхождения фонового излучения, а группа лаборатории Белла сообщала, очень кратко, без какого-либо упоминания космологии, об обнаружении однородного микроволнового излучения, пронизывающего пространство. Ни одна из статей не упоминала ранние работы Гамова, Альфера и Германа. За открытие реликтового излучения Пензиас и Вильсон получили в 1978 году Нобелевскую премию по физике.
Гамов, Альфер и Герман были подавлены и в течение многих лет отчаянно боролись за признание своих работ. Лишь со временем и с большим запозданием физическое сообщество признало их ключевую роль в этом монументальном открытии.
Поразительная однородность древних фотонов
За десятилетия с момента первого наблюдения реликтовое излучение превратилось в основной инструмент космологических исследований. Причина этого проста. В большинстве областей науки исследователи многое дали бы за то, чтобы хоть ненадолго заглянуть в прошлое. Вместо этого они, как правило, вынуждены собирать по частям картину далёкого прошлого, основываясь лишь на обнаруженных останках — расколотых окаменелостях, рассыпающихся пергаментах или мумифицированном прахе. Космология является одной из наук, в которой мы можем стать по-настоящему свидетелями давно минувших событий. Свет от звёзд, которые мы видим невооружённым взглядом, это фотоны, летящие к нам в течение нескольких лет или нескольких тысяч лет. Свет от более удалённых объектов, попадающий в объективы мощных телескопов, летел значительно дольше, иногда миллиарды лет. Когда вы видите этот древний свет, то попадаете, буквально говоря, в древние времена. Те первобытные события происходили далеко отсюда, но выявленная однородность Вселенной на больших масштабах решительно свидетельствует в пользу, что то, что происходило там, происходило, в среднем, и здесь. Смотря вверх, мы смотрим в прошлое.
Благодаря реликтовым фотонам мы можем максимально использовать эту возможность. И неважно, как далеко могут продвинуться технологии; реликтовые фотоны — это самое древнее из всего, что можно увидеть, просто потому, что их старшие собратья не смогли пробиться сквозь непрозрачную плазму, заполнявшую Вселенную в более ранние эпохи. Изучая реликтовые фотоны, мы имеем возможность увидеть, как всё было устроено примерно 14 миллиардов лет назад.
Вычисления показывают, что в настоящее время примерно 400 миллионов реликтовых фотонов пролетают сквозь каждый кубический метр пространства. И хотя невооружённым глазом они не видны, их можно увидеть с помощью старого телевизора. Примерно 1 процент помех на экране отключённого от кабеля телевизора, настроенного на станцию, прекратившую вещание, вызван приёмом фотонов, оставшихся от Большого взрыва. А ведь это забавная мысль! Те же самые волны, передающие старые комедии, несут в себе свидетельства древнейшей драмы, произошедшей во Вселенной, которой было всего лишь несколько сотен тысяч лет от роду.
Оправдавшееся предсказание теории Большого взрыва о том, что пространство заполнено реликтовым излучением, стало триумфом. Всего лишь за триста лет научная мысль и технический прогресс человечества прошли путь от разглядывания неба через примитивные телескопы и бросания шаров с «падающих» башен до постижения физических процессов, произошедших в первые мгновения жизни Вселенной. Однако дальнейший анализ данных выявил проблему. Более точные измерения температуры излучения, проделанные, конечно же, не с помощью старого телевизора, а на самом передовом астрономическом оборудовании, показали, что излучение однородно — абсолютно однородно — в пространстве. Неважно, куда вы направите ваш приёмник, температура излучения будет 2,725 градуса выше абсолютного нуля. И задача в том, чтобы объяснить эту фантастическую однородность.
Могу представить, что, вспомнив идеи из главы 2 (и мои комментарии четырьмя абзацами выше), вы скажете: «Ну, это не более чем проявление космологического принципа: никакая точка во Вселенной никак не выделена по сравнению с любой другой точкой, поэтому температура реликтового излучения везде должна быть одинаковой». Весьма справедливый комментарий. Однако вспомните, что космологический принцип был упрощающим допущением, которое физики, включая Эйнштейна, ввели для математического анализа эволюции Вселенной. Так как реликтовое излучение действительно однородно в пространстве, его обнаружение является убедительным аргументом в пользу космологического принципа, что укрепляет нашу уверенность в полученных на его основе выводах. Однако удивительная однородность излучения проливает яркий свет и на сам космологический принцип. Каким бы разумным ни казался космологический принцип, что за механизм лежит за подтверждаемой наблюдениями однородностью Вселенной?
Быстрее скорости света
Всем нам знакомо неприятное ощущение, когда, подав кому-нибудь руку, мы обнаруживаем, что рука тёплая и влажная (что не так плохо) или холодная и липкая (определённо хуже). Однако если задержать руку на какое-то время, то окажется, что небольшая разница в температуре быстро исчезает. При контакте двух предметов тепло передаётся от горячего к холодному, и это продолжается до тех пор, пока их температуры не сравняются. Такое происходит повсеместно. Именно поэтому кофе, забытый на столе, в конце концов остывает до комнатной температуры.
Похожие рассуждения, по-видимому, объясняют однородность реликтового излучения. Точно так же как при рукопожатии и в случае забытого кофе однородность отражает, по-видимому, знакомое всем свойство окружающей среды выравнивать температуру. Единственное новшество состоит в том, что процесс выравнивания должен происходить на космических масштабах.
Однако в рамках теории Большого взрыва такое объяснение не проходит.
Для выравнивания температуры разных предметов существенным условием является взаимный контакт. Он может быть непосредственным, как при рукопожатии, либо по меньшей мере через обмен информацией, вследствие чего условия в разных местах становятся скоррелированными. Только посредством такого взаимного воздействия можно достичь общей среды. Термос, например, устроен так, чтобы избежать подобного взаимодействия и, препятствуя достижению однородности, сохранить разницу температур.
Это простое наблюдение указывает на трудности наивного объяснения однородности космической температуры. Рассмотрим две точки пространства, расположенные на очень большом расстоянии друг от друга: одна — справа от нас, так далеко в ночном небе, что первый испущенный ею луч света только что достиг нас, а вторая — столь же далеко, но слева от нас. Ясно, что они никогда не могли взаимодействовать друг с другом. И хотя мы можем видеть обе точки, расстояние, которое осталось преодолеть свету одной из них, чтобы достичь другую, огромно. Таким образом, воображаемым наблюдателям, находящимся в удалённых друг от друга правой и левой точках, только предстоит ещё увидеть друг друга, а поскольку скорость света является верхним пределом быстроты перемещения, то все взаимодействия для них ещё впереди. На языке предыдущей главы можно сказать, что каждый из них находится за пределами космического горизонта другого.
Вот мы и пришли к загадке. Вы бы сильно удивились, если бы узнали, что жители этих удалённых друг от друга мест говорят на одном языке, а их библиотеки заполнены одинаковыми книгами. Как может возникнуть общее наследие, если не было никакого контакта? Вы также должны удивиться, узнав, что без какого-либо явного контакта температура этих разделённых большим расстоянием областей одинакова с точностью, превышающей четыре знака после запятой.
Много лет назад, впервые столкнувшись с этой задачей, я действительно удивился. Однако, немного подумав, я уже удивился самой задаче. Как могли два предмета, когда-то находившиеся рядом друг с другом — а мы верим, что всё в наблюдаемой части Вселенной в момент Большого взрыва находилось рядом друг с другом, — отдалиться настолько быстро, что свету, испущенному одним из них, не хватит времени, чтобы достичь другого? Скорость света предельна для всего в космосе, поэтому как можно разнести предметы на такое расстояние, что даже свет не успевает его преодолеть?
Ответ на это вопрос выдвигает на передний план то, чему часто уделяют незаслуженно мало внимания. Предел скорости, устанавливаемый светом, относится исключительно к движению объектов сквозь пространство. Однако галактики удаляются друг от друга не потому, что они движутся в пространстве — у них нет реактивных двигателей, — а потому, что само пространство расширяется и галактики лишь увлекаются общим потоком.[9] Смысл в том, что теория относительности не накладывает никаких ограничений на скорость расширения пространства, и поэтому нет никаких ограничений на скорость разбегания галактик, увлекаемых общим расширением. Скорость разбегания галактик может быть выше любой скорости, включая скорость света.
Действительно, математический аппарат общей теории относительности показывает, что в самые ранние моменты Вселенной пространство может расширяться так быстро, что области будут удалятся друг от друга быстрее скорости света. В результате возможность оказывать друг на друга какое-либо влияние исчезает. Однако трудность теперь в том, чтобы объяснить, как практически одинаковые температуры возникли в независимых областях космоса: вопрос, который космологи назвали проблемой горизонта.
Расширяя горизонты
В 1979 году Алану Гуту (в ту пору сотруднику Стэнфордского линейного ускорителя) пришла идея, которая, подвергшись критическому осмыслению Андреем Линде (на тот момент сотрудником Физического института им. Лебедева в Москве), Полом Стейнхардом и Андреасом Альбрехтом (профессорско-студенческий дуэт из университета Пенсильвании), решает, по общему признанию, проблему горизонта. Это решение — инфляционная космология — основывается на тонких свойствах общей теории относительности Эйнштейна, которые я скоро объясню подробно, но основные черты можно сформулировать уже сейчас.
Проблема горизонта портит стандартную теорию Большого взрыва, потому что области пространства отдаляются слишком быстро для установления теплового равновесия. Инфляционная теория решает эту проблему, уменьшая скорость разделения областей пространства в начальные моменты времени и обеспечивая таким образом достаточно времени для выравнивания температуры. Затем из теории следует, что после завершения такого «космического рукопожатия» наступает непродолжительный период чрезвычайно быстрого и постоянно ускоряющегося расширения, названного инфляционным расширением, которое более чем достаточно компенсирует вялый старт и быстро разносит разные участки неба на огромные расстояния. Наблюдаемые нами однородные условия больше не являются загадкой, так как общая температура установилась до того, как разные области пространства были быстро разнесены.{16} В общих чертах, в этом и состоит суть идеи инфляционной теории.[10]
Однако следует иметь в виду, что не физики определяют, как расширяется Вселенная. Насколько мы можем судить из наиболее точных наблюдений, это делают уравнения общей теории относительности Эйнштейна. Таким образом, перспективность инфляционного сценария зависит от того, возникает ли предложенная модификация стандартной модели Большого взрыва из уравнений Эйнштейна. На первый взгляд это не так очевидно.
Например, я совершенно уверен, что будь у нас возможность встретиться с Ньютоном и объяснить ему в течение пяти минут основные положения общей теории относительности, не забыв про искривлённость пространства и расширяющуюся Вселенную, то он расценил бы наш последующий рассказ про инфляцию как абсурдный. Ньютон бы твёрдо настаивал, что независимо от вычурной математики и новомодного эйнштейновского языка, гравитация является силой притяжения. Стукнув кулаком по столу, он заявил бы, что гравитация притягивает предметы, снижая скорость любого космического разбегания. Расширение, которое начинается вяло, а затем резко ускоряется на каком-то коротком отрезке времени, могло бы решить проблему горизонта, но это фикция. Ньютон настаивал бы на том, что космическое расширение должно замедлиться со временем, подобно тому как гравитационное притяжение уменьшает скорость подброшенного вверх бейсбольного мяча. Конечно, если расширение полностью прекратится и начнётся космическое сжатие, то скорость схлопывания может постепенно возрастать, ровно так же как скорость мяча может расти по мере того, как он летит обратно вниз. Но скорость пространственного расширения не может увеличиваться.
Ньютон ошибается, но вы не вправе винить его. Ведь у вас было мало времени для подробного обзора общей теории относительности. Не поймите меня неправильно. Понятно, что, имея пять минут (одну из которых вы потратили на объяснение того, что такое бейсбол), вы сосредоточились на искривлённом пространстве-времени как источнике гравитации. Ньютон сам настаивал на том, что механизм распространения гравитации неизвестен, и он всегда считал это зияющей дырой в своей собственной теории. Поэтому естественно, что вы хотели продемонстрировать ему решение этого вопроса Эйнштейном. Однако эйнштейновская теория гравитации — это не просто латание дыр в ньютоновской физике. Гравитация общей теории относительности отличается по самой сути от гравитации ньютоновской физики; и есть одно свойство, которое следует особо отметить для нашего изложения.
В ньютоновской теории гравитация обусловлена лишь массой предмета. Чем больше масса, тем сильнее гравитационное притяжение предмета. В эйнштейновской теории гравитация обусловлена массой предмета (и его энергией), а также его давлением. Взвесьте запечатанный пакет с картофельными чипсами. Теперь сожмите пакет, чтобы воздух, находящийся внутри него, оказался под высоким давлением, и затем снова взвесьте его. Согласно Ньютону, вес не изменится, потому что масса не изменилась. Согласно Эйнштейну, сжатый пакет будет весить немножко больше, потому что, хотя масса осталась прежней, давление увеличилось.{17} При обычных обстоятельствах подобный эффект увеличения веса исчезающе мал, поэтому мы не обращаем на него никакого внимания. Однако из общей теории относительности и подтверждающих её экспериментов со всей очевидностью следует, что давление даёт вклад в гравитацию.
Это отклонение от ньютоновской теории крайне важно. Давление воздуха, будь это воздух в пакете с картофельными чипсами, надутом шаре или в комнате, где вы сейчас читаете эту книгу, положительно, и это означает, что воздух давит наружу. В общей теории относительности положительное давление, как и положительная масса, даёт положительный вклад в гравитацию, что приводит в увеличению веса. Однако, хотя масса всегда положительна, давление в некоторых ситуациях может быть отрицательным. Представьте себе растянутую резинку. Вместо того, чтобы толкать наружу, растянутые молекулы тянут вовнутрь, приводя к тому, что в физике называется отрицательным давлением (или упругостью). И точно так же как из общей теории относительности следует, что положительное давление приводит к гравитационному притяжению, эта теория утверждает, что отрицательное давление приводит к противоположному — гравитационному отталкиванию.
Гравитационное отталкивание?
Это поставило бы Ньютона в тупик. Для него гравитация была исключительно силой притяжения. Однако нас это не должно смущать: мы и раньше сталкивались с этим странным пунктом в договоре между общей теорией относительности и гравитацией. Помните, как в предыдущей главе мы обсуждали космологическую постоянную Эйнштейна? Я говорил, что при наполнении пространства однородной энергией космологическая постоянная приводит к гравитационному отталкиванию. Однако тогда я не стал объяснять, почему так происходит. Теперь я могу это сделать. Космологическая постоянная не только наполняет пространство однородной энергией, величина которой определяется значением самой константы (число в третьей строчке гравитационной декларации), но также приводит к появлению в пространстве однородного отрицательного давления (скоро увидим, почему). И когда, как в примерах выше, дело доходит до гравитации, отрицательное давление играет роль, противоположную положительной массе и положительному давлению. Так возникает гравитационное отталкивание.[11]
Гравитационное отталкивание возникло в работах Эйнштейна лишь однажды, и то с ошибочной целью. Он предлагал получить статичную вселенную путём тонкой подстройки значения отрицательного давления во всём пространстве, так чтобы возникшее гравитационное отталкивание точно компенсировало гравитационное притяжение обычного вещества во вселенной. Как мы видели, впоследствии он отказался от этого предложения. Шестьдесят лет спустя создатели инфляционной теории предложили вариант гравитационного отталкивания, который отличался от эйнштейновской версии, как финал восьмой симфонии Малера от звука камертона. Вместо умеренного и равномерного расширения, которое может стабилизировать вселенную, инфляционная теория порождает гигантскую волну гравитационного отталкивания, невероятно короткую и ураганно-мощную. До этого события, однако, есть достаточно времени, чтобы у разных областей пространства выровнялась температура, после чего они разносятся на волне на гигантские расстояния и занимают наблюдаемое сейчас положение на небе.
В этом месте Ньютон снова неодобрительно посмотрел бы на вас. Будучи скептиком, он нашёл бы другой пробел в вашем объяснении. Разобравшись в тонкостях общей теории относительности, почитав один из стандартных учебников, он согласился бы с тем странным фактом, что гравитация в принципе может быть отталкивающей. Но, спросил бы он, к чему весь этот разговор об отрицательном давлении, заполняющем пространство? Одно дело — использовать натяжение растянутой резинки в качестве иллюстрации отрицательного давления. Но совсем другое дело — доказывать, что миллиарды лет назад, примерно в момент Большого взрыва, пространство было мгновенно заполнено огромным и однородным отрицательным давлением. Что за процесс может обеспечить подобное мгновенное и при этом повсеместное распространение отрицательного давления?
В ответе на этот вопрос проявилось гениальное прозрение первооткрывателей инфляции. Было показано, что отрицательное давление, необходимое для создания антигравитационной волны, естественным образом возникает из нового механизма, составляющие которого известны как квантовые поля. Для нашего повествования детали этого явления очень важны, потому что способ инфляционного расширения играет ключевую роль в сценарии параллельных миров, к которому оно приводит.
Квантовые поля
Во времена Ньютона цель физики состояла в изучении движения обычных предметов — камней, пушечных ядер, планет — и полученные им уравнения прекрасно служили этой цели. Законы движения Ньютона — это математический способ выразить движение реальных тел, если их толкнуть, потянуть или бросить. В течение более чем столетия данный подход давал прекрасные результаты. Однако в начале XIX века английский учёный Майкл Фарадей ввёл в обиход трудное для понимания, но эффективное понятие поля.
Возьмите мощный магнит и разместите его в сантиметре от канцелярской скрепки. Вы знаете, что произойдёт. Скрепка подпрыгнет вверх и прилипнет к поверхности магнита. Этот опыт настолько распространён, настолько хорошо известен, что легко проглядеть, насколько он невероятен. Магнит заставляет двигаться канцелярскую скрепку, даже не прикоснувшись к ней. Как такое возможно? Каким образом передаётся влияние магнита на скрепку без какого-либо контакта? Эти и другие вопросы привели Фарадея к постулату, что хотя магнит в буквальном смысле слова не касается скрепки, он производит нечто, что касается. Это нечто было названо Фарадеем магнитным полем.
Поля, порождённые магнитом, нельзя увидеть, нельзя услышать, ни одно из наших чувств восприятия не настроено на них. Однако это всего лишь физиологические ограничения. Так же как от пламени идёт тепло, так и от магнита исходит магнитное поле. Находясь за пределами физической границы твёрдого магнита, магнитное поле является некоей «дымкой» или «эссенцией», которая наполняет пространство и действует по распоряжению магнита.
Кроме магнитных есть и другие поля. Заряженные частицы порождают другой тип — электрические поля, подобные тем, из-за которых можно получить удар током, прикоснувшись к металлической ручке двери комнаты, устланной шерстяными коврами. Эксперименты Фарадея совершенно неожиданно показали, что электрические и магнитные поля внутренне связаны: было обнаружено, что изменение электрического поля порождает магнитное и наоборот. В середине XIX века Джеймс Клерк Максвелл подвёл мощный математический фундамент под эти эксперименты, описав электрические и магнитные поля в виде чисел, приписанных каждой точке пространства, причём значения этих чисел характеризуют способность поля оказывать влияние в данной точке. В точках пространства, где численные значения магнитных полей велики, например в томографической камере, металлические предметы будут испытывать сильное отталкивание или притяжение. В точках пространства, где велики численные значения электрических полей, например внутри грозового облака, могут происходить сильные электрические разряды, такие как молнии.
Максвелл вывел уравнения, впоследствии названные в его честь, которые описывают изменение силы электрических и магнитных полей в пространстве от точки к точке и от одного момента времени к другому. Именно эти уравнения описывают море электрических и магнитных полей — так называемые электромагнитные волны, окружающие нас со всех сторон. Включите сотовый телефон, радио или беспроводной компьютер, и получаемые сигналы будут лишь крохотной крупицей из электромагнитного потока, молчаливо обтекающего нас каждую секунду. А более всего потрясает то, что и видимый свет, согласно уравнениям Максвелла, является электромагнитной волной, такой, которую научились воспринимать в процессе эволюции наши глаза.
Во второй половине XX столетия физики присоединили концепцию поля к быстро развивающемуся пониманию микромира, основанному на квантовой механике. В итоге квантовая теория поля стала математическим аппаратом для создания самых точных теорий материи и сил в природе. С её помощью физики установили, что помимо электрических и магнитных полей существует целый набор других полей, таких как сильные и слабые ядерные поля, электронные, кварковые, и нейтринные поля. Поле, которое является теоретическим фундаментом инфляционной космологии[12], называется полем инфлатона. Однако на настоящий момент его статус остаётся совершенно гипотетическим.
Квантовые поля и инфляция
Поля обладают энергией. Интуитивно мы знакомы с этим, потому что поля участвуют в процессах, требующих затрат энергии, как, например, вызванное полями движение предметов (как в случае с канцелярской скрепкой). В количественном отношении уравнения квантовой теории поля показывают, как при заданном численном значении поля в заданной области пространства вычислить содержащееся в нём количество энергии. Как правило, чем больше значение поля, тем больше количество энергии. Значение поля может изменяться от точки к точке, но если поле является постоянным, то есть везде имеет одинаковое значение, энергия также будет одинаковой в каждой точке пространства. Важное наблюдение Гута состояло в том, что такие однородные конфигурации поля наполняют пространство не только однородной энергией, но также и однородным отрицательным давлением. Таким способом он обнаружил физический механизм возникновения гравитационного отталкивания.
Чтобы увидеть, почему однородное поле приводит к отрицательному давлению, представьте сначала более привычную ситуацию с участием положительного давления: открытие бутылки шампанского. По мере того как вы медленно вытаскиваете пробку, вы ощущаете положительное давление газа в бутылке, которое выталкивает её наружу. Вы можете легко непосредственно убедиться, что на такое движение пробки наружу тратится лишь малая часть энергии шампанского. Вы видели дымок около бутылочного горлышка сразу после открытия бутылки? Он образуется, потому что энергия, истраченная шампанским при выталкивании пробки, приводит к уменьшению температуры, что заставляет конденсироваться окружающий водяной пар аналогично тому, как конденсируется выдыхаемый воздух в морозный день.
Теперь представьте, что шампанское заменили чем-нибудь менее праздничным, но более поучительным — полем, значение которого однородно во всей бутылке. На этот раз открытие пробки даст совершенно другой эффект. Пока пробка выходит наружу, внутри бутылки возникает небольшой дополнительный объём, куда может проникнуть поле. Так как энергия однородного поля одинакова во всех точках, то чем больший объём заполняется полем, тем бо́льшая полная энергия содержится в бутылке. Что означает, что, в отличие от шампанского, при вынимании пробки энергия добавляется в бутылку.
Как такое может быть? Откуда берётся энергия? Давайте представим, что произойдёт, если содержимое бутылки, вместо того чтобы выталкивать пробку наружу, начнёт тянуть её внутрь. Тогда для открытия бутылки нужно будет тянуть пробку на себя, то есть приложить усилия, которые в свою очередь передадут энергию ваших мышц содержимому бутылки. Таким образом, чтобы объяснить увеличение энергии бутылки, мы должны предположить, что в отличие от шампанского, выталкивающего пробку наружу, однородное поле засасывает её внутрь. Вот что мы имеем в виду, когда говорим, что однородное поле приводит к отрицательному, а не положительному давлению.
Хотя и не существует официанта, открывающего бутылку с космосом, условие остаётся в силе: если есть поле — гипотетическое поле инфлатона — однородное во всей области пространства, то оно заполнит эту область не только энергией, но и создаст в ней отрицательное давление. И, как теперь понятно, такое отрицательное давление создаёт гравитационное отталкивание, которое приводит к безостановочному расширению пространства. Когда Гут подставил в уравнения Эйнштейна предполагаемые значения энергии инфлатона и давления, согласованные с экстремальными условиями ранней Вселенной, то вычисления показали, что возникающее гравитационное отталкивание должно быть колоссальным. Оно на несколько порядков сильнее, чем гравитационное отталкивание, рассмотренное Эйнштейном годами ранее, когда он возился с космологической постоянной, и приводит к фееричному пространственному расширению. Уже одно это захватывало дух. Но Гут осознал, что имеется ещё один неотъемлемый бонус.
Такое же рассуждение, объясняющее, почему однородное поле обладает отрицательным давлением, применимо также и к космологической постоянной. (Если в бутылке находится пустое пространство с космологической постоянной, то при медленном вытаскивании пробки возникает дополнительное пространство, которое даёт дополнительный вклад в энергию. Единственный источник этой энергии находится в ваших мышцах, напряжение которых направлено против втягивающего отрицательного давления, создаваемого космологической постоянной.) Как и в случае с однородным полем, однородное отрицательное давление космологической постоянной приводит к гравитационному отталкиванию. Однако здесь важна не аналогия сама по себе, а то, как космологическая постоянная отличается от однородного поля.
Космологическая постоянная — это всего лишь константа, фиксированное число из третьей строчки гравитационной декларации, которая порождает сегодня ровно такое же гравитационное отталкивание, как и миллиарды лет назад. В противоположность этому значение поля может изменяться и, вообще говоря, изменяется. При включении микроволновой печи находящееся внутри неё электромагнитное поле изменяется; при включении томографа электромагнитное поле внутри камеры изменяется. Гут осознал, что инфляционное поле, заполняющее пространство, ведёт себя похожим образом — включается для инфляции и затем выключается, — что позволяет гравитационному отталкиванию действовать лишь в короткий промежуток времени. Это важно. Наблюдения показывают, что если взрывоподобное расширение пространства вообще имело место, то оно должно было произойти миллиарды лет назад и резко оборваться, после чего началось размеренное расширение, о котором свидетельствуют точные астрономические измерения. Итак, исключительно важное свойство инфляционной гипотезы состоит в том, что эпоха мощного гравитационного отталкивания была временной.
Механизм включения и последующего выключения инфляционного взрыва основывается на физических построениях, изначально предложенных Гутом и впоследствии существенно переработанных Линде, Альбрехтом и Стейнхардом. Чтобы понять суть их предложений, представьте себе шар, а ещё лучше представьте Колобка, неуверенно сидящего на вершине холма. Физик сказал бы, что благодаря своему положению Колобок обладает энергией. Точнее, он обладает потенциальной энергией, и это означает, что эта сдерживаемая энергия готова вот-вот вырваться наружу, и проще всего это произойдёт, когда Колобок свалится вниз, и потенциальная энергия превратится в энергию движения (кинетическую энергию). Опыт подтверждает, а физические законы делают точным утверждение о типичности такой ситуации. Система, наполненная потенциальной энергией, воспользуется любой возможностью высвободить её. Иными словами, если что-нибудь может упасть, оно падает.
Энергия, переносимая полем с ненулевым значением, также является потенциальной: она может высвободиться, что в случае с Колобком не привело ни к чему хорошему. Подобно тому как рост потенциальной энергии Колобка, по мере того как он забирается на гору, определяется формой склона — при движении с небольшим уклоном его потенциальная энергия изменяется минимально, а на крутых склонах, где надо карабкаться вверх, она резко возрастает, — потенциальная энергия поля имеет аналогичную форму, которая называется кривой потенциальной энергии. Такая кривая определяет изменения потенциальной энергии поля при изменении его значения (рис. 3.1).
Рис. 3.1. Энергия поля инфлатона (вертикальная ось) при заданном значении поля (горизонтальная ось)
Вслед за пионерами инфляции давайте представим, что в самые ранние моменты космоса пространство было равномерно заполнено полем инфлатона, значение которого соответствует самой высокой точке на кривой потенциальной энергии. Прислушаемся к их мнению и представим, что кривая потенциальной энергии выпрямляется и приобретает вид ровного плато (рис. 3.1), позволяя инфлатону задержаться на самой вершине. Что произойдёт дальше при таких гипотетических условиях?
Произойдут два события, и оба очень важны. Пока инфлатон находится на плато, он наполняет пространство большой потенциальной энергией и отрицательным давлением, приводя к взрывоподобному инфляционному расширению. Но подобно тому как потенциальная энергия Колобка высвобождается при скатывании с горы, так и инфлатон высвобождает потенциальную энергию во всё пространство, скатываясь к более низким значениям. И по мере уменьшения значения инфлатона его энергия и отрицательное давление рассеиваются, что приводит к завершению взрывоподобного расширения. Не менее важно, что высвободившаяся полем инфлатона энергия не теряется, а подобно остывающему пару, конденсирующемуся в капли воды, энергия инфляции конденсируется в однородную среду частиц, заполняющих пространство. Такой двухступенчатый процесс — короткое, но быстрое расширение, за которым следует преобразование энергии в частицы, — приводит к огромному однородному пространству, заполненному сырьём для будущих звёзд и галактик.
Подробности этого процесса зависят от факторов, которые ни теория, ни эксперимент пока не могут определить (начальное значение поля инфлатона, точная форма наклона кривой потенциальной энергии и так далее){18}, но типичные модели, возникающие в математических выкладках, говорят о том, что энергия инфлатона скатывается по наклону за кратчайшие доли секунды, порядка 10−35. И кроме того, за этот короткий промежуток времени пространство расширяется в колоссальное число раз, возможно в 1030, если не более. Эти числа настолько велики, что их сложно с чем-то сравнивать. Они говорят, что область пространства размером с горошину расширяется до размеров, превышающих наблюдаемую часть Вселенной, за время настолько малое, что одно моргание глазом превышает его в миллион миллиардов миллиардов миллиардов раз.
Хотя представить себе такой масштаб очень трудно, важно то, что область пространства, породившая наблюдаемую часть Вселенной, была настолько мала, что в ней легко могла установиться одинаковая температура, прежде чем молниеносный взрыв расширил её до космических масштабов. Инфляционное расширение и миллиарды лет последующей космологической эволюции значительно понизили температуру, но однородность пространства в ранние времена определила однородность в настоящую эпоху. Это решает загадку возникновения однородных условий во Вселенной. При инфляции однородная температура во всём пространстве неизбежна.{19}
Вечная инфляция
В течение почти трёх десятилетий с момента открытия инфляция является основным инструментом космологических исследований. Но для получения точного вида всей исследовательской панорамы следует помнить, что инфляция — это способ осмысления космологии, а не какая-то конкретная теория. Исследования показали, что существует множество способов для воплощения инфляции; отличаются лишь детали, такие как число полей инфлатона, обеспечивающих отрицательное давление, конкретные кривые потенциальной энергии различных полей и так далее. К счастью, разнообразные реализации инфляции имеют общие черты, и поэтому можно сделать определённые выводы, даже не имея окончательной версии теории.
Среди разных сценариев инфляции есть один, изначально выдвинутый Александром Виленкиным[13] из университета Тафтса и впоследствии разработанный другими исследователями, прежде всего Линде; он имеет первостепенную важность. Фактически именно поэтому я потратил первую половину этой главы, объясняя инфляционный сценарий.
Во многих вариантах инфляционной теории взрывоподобное пространственное расширение не является единомоментным событием. Наоборот, процесс, благодаря которому образовалась наша область Вселенной — быстрое расширение пространства и следующее за ним более обычное, более спокойное расширение, сопровождающееся рождением частиц, — может неоднократно повторяться в толще космоса. Если представить космос в целом, он будет изобиловать бесчисленным множеством далеко разбросанных областей, каждая из которых несёт след произошедшего инфляционного расширения. Наш мир, который мы издавна привыкли считать единственной вселенной, является одним из множества таких областей, парящих в неизмеримо большем пространстве. Если в других областях есть разумные существа, они бы также уверенно считали, что их вселенная единственна. Таким образом, инфляционная космология приводит нас к очередной вариации на тему параллельных миров.
Для понимания того, как возникает такая инфляционная мультивселенная, в мою аналогию с Колобком следует добавить два усложняющих обстоятельства.
Первое: образ Колобка, сидящего высоко на вершине холма, отражает поле инфлатона, обладающее значительной потенциальной энергией и отрицательным давлением и находящееся в неустойчивом равновесии. Но если Колобок сидит на вершине одного холма, поле инфлатона обладает значением в каждой точке пространства. В основу теории закладывается изначальное равенство значений поля инфлатона во всех точках исходной области. Поэтому чтобы более адекватно представить инфляционный сценарий, нам бы потребовалось вообразить нечто довольно странное: многочисленных клонов Колобка, забравшихся на многочисленные, близко расположенные, тождественные вершины гор во всём пространстве.
Второе: до сих пор мы почти никак не затрагивали квантовый аспект квантовой теории поля. Поле инфлатона, как и всё остальное в нашей квантовой вселенной, подвержено квантовой неопределённости. Это означает, что его значение будет испытывать случайные флуктуации, мгновенно немножко возрастая здесь и убывая немножко там. В обычной жизни квантовые флуктуации слишком малы, чтобы их заметить. Однако вычисления показывают, что чем больше энергия инфлатона, тем больше его флуктуации, возникающие из-за квантовой неопределённости. Поскольку энергия инфлатона во время инфляционного расширения крайне высока, то квантовые флуктуации в ранней Вселенной должны быть большими и доминирующими.{20}
Таким образом, следует представлять не просто целый отряд Колобков, забравшихся высоко на одинаковые горные вершины; также следует вообразить, что происходят случайные подземные толчки — тут сильнее, там слабее, а вот там очень сильно. Тогда можно понять, что произойдёт. Разные клоны Колобков будут удерживаться на своих горных вершинах в течение разного времени. Где-то сильное землетрясение свалит большинство Колобков вниз; где-то толчки будут не очень сильными, и им удастся свалить только часть Колобков; а где-то Колобки начали сваливаться вниз, но сильный толчок их может закинуть обратно на вершину. Через некоторое время вся местность поделится случайным образом на области (что похоже на то, как Соединённые Штаты разделены на отдельные штаты): в каких-то из них ни один из Колобков не удержался наверху, а в остальных Колобки спокойно сидят на своих вершинах.
Случайность квантовых флуктуаций приводит к похожему выводу для поля инфлатона. Исходно инфлатон находится на самом верху кривой потенциальной энергии в каждой точке некоторой области пространства. Затем квантовые флуктуации действуют как подземные толчки. По этой причине, как показано на рис. 3.2, пространство быстро разделяется на области: в некоторых квантовые флуктуации заставляют поле скатиться по кривой вниз, а в других оно остаётся наверху.
Рис. 3.2. Различные области пространства, где инфлатон уже скатился по склону (тёмно-серые), либо где он удерживается наверху (светло-серые)
Пока дела идут неплохо. Но теперь следите внимательнее, именно здесь начинается различие между Колобками и космологией. Поле, находящееся на вершине кривой потенциальной энергии, воздействует на окружение значительно сильнее, чем сидящие на вершинах Колобки. Вспоминая нашу присказку — что однородная энергия поля и отрицательное давление приводят к гравитационному отталкиванию, — мы понимаем, что область, заполненная полем инфлатона, расширяется с фантастической скоростью. Это означает, что эволюция поля инфлатона управляется двумя противоположными процессами. Квантовые флуктуации, стремящиеся сбросить поле с верхнего положения, уменьшают область пространства, заполненного большой энергией. Инфляционное расширение путём быстрого увеличения тех областей, где поле удерживается в верхнем положении, увеличивает объём пространства, заполненного большой энергией.
Какой из процессов возобладает?
В абсолютном большинстве предложенных вариантов инфляционной космологии увеличение происходит по-меньшей мере так же быстро, как уменьшение. Причина в том, что поле инфлатона, которое можно слишком быстро сбросить со своей вершины, как правило, создаёт очень небольшое инфляционное расширение для решения проблемы горизонта; таким образом, в космологически успешных вариантах инфляции увеличение превалирует над уменьшением, и поэтому полный объём пространства, в котором энергия поля велика, увеличивается со временем. Принимая, что подобные полевые конфигурации приводят к дальнейшему инфляционному расширению, мы видим, что однажды начавшись, инфляция не заканчивается никогда.
Это похоже на вирусную эпидемию, где для устранения угрозы необходимо уничтожить вирус быстрее, чем он сможет воспроизвести себя. Инфляционный вирус «воспроизводит» себя — большое значение поля порождает быстрое пространственное расширение и таким образом наполняет большую область с таким же большим значением поля — и это происходит быстрее, чем противоположный процесс успевает погасить этот эффект. Инфляционный вирус весьма успешно сопротивляется уничтожению.{21}
Космос и швейцарский сыр
Все эти идеи совместно показывают, что инфляционная космология значительно обновляет наше представление о реальном пространстве, что можно вообразить с помощью простой аналогии. Представьте вселенную в виде гигантского куска швейцарского сыра, в котором дырки соответствуют областям, где величина поля инфлатона мала, а в остальных местах, наоборот, велика. То есть дырки — это области, подобные нашей Вселенной, прошедшие стадию супербыстрого расширения, в процессе чего энергия поля инфлатона преобразовалась в частицы, которые со временем формируют галактики, звёзды и планеты. Перефразируя предыдущие результаты, в космическом сыре возникает всё больше и больше дырок, потому что квантовые процессы понижают величину поля инфлатона в случайном наборе местоположений. В то же время «сырно-заполненные» области без дырок растягиваются ещё больше, потому что в них происходит инфляционное расширение, подстёгиваемое большим значением поля инфлатона. Оба процесса совместно приводят к тому, что кусок космического сыра постоянно расширяется и в нём образуется всё большее количество дырок, из которых вырастают дочерние вселенные. На более стандартном языке космологии каждая дырка называется пузырьком-вселенной (или ячейкой-вселенной).[14] Каждая из них является полостью, образовавшейся в результате супербыстрого расширения пространства (рис. 3.3).
Рис. 3.3. Инфляционная мультивселенная возникает при непрерывном образовании пузырьков — дочерних вселенных — в постоянно расширяющемся пространственном окружении, заполненном полем инфлатона большой величины
Не позволяйте наглядному, но уменьшительному названию «пузырёк-вселенная» ввести вас в заблуждение. Наша вселенная огромна. То что она может быть образованием, вложенным в ещё бо́льшую космическую структуру — один пузырёк в огромном куске космического сыра, — лишь подтверждает фантастически огромные размеры, в рамках инфляционной парадигмы, космоса в целом. То же самое справедливо и для других пузырьков. Каждый из них — это вселенная, подобная нашей — настоящая, огромная, постоянно расширяющаяся.
Существуют варианты инфляционной теории, в которых инфлатон не вечен. Подбирая различные параметры теории, такие как число полей инфлатона и кривые потенциальной энергии, умные теоретики могут сделать так, чтобы инфлатон повсеместно скатился из верхнего положения. Но подобные идеи — скорее исключение. Как правило, инфляционные модели приводят к невообразимо огромному числу дочерних вселенных, находящихся в вечно расширяющемся пространстве. И поэтому если инфляционная теория верна, и если согласно множеству теоретических исследований её физически значимая реализация приводит к вечной инфляции, то существование инфляционной мультивселенной является неизбежным следствием.
Поворачивая перспективу
В 1980-х годах, когда Виленкин осознал вечный характер инфляционного расширения и сопутствующих параллельных вселенных, он пришёл в сильное возбуждение и поехал к Алану Гуту в Массачусетский технологический институт, чтобы рассказать ему об этом. Где-то в середине рассказа голова Гута склонилась — он уснул. В принципе, это не является плохим знаком; вообще-то, хорошо известно, что Гут начинает клевать носом во время семинаров — например, во время моих выступлений он несколько раз закрывал глаза, — но затем он просыпается и задаёт удивительно проницательный вопрос. Однако физическое сообщество проявило не больше энтузиазма, чем Гут; поэтому Виленкин отложил эту идею и стал работать над другими проектам.
Сегодня отношение к вечной инфляции очень разное. Когда Виленкин впервые задумался об инфляционной мультивселенной, прямых подтверждений в пользу самой инфляционной теории было не так и много. Поэтому те немногие, кто хоть как-то заинтересовался, считали, что идеи об инфляционном расширении, порождающем огромное множество параллельных Вселенных, являются спекуляцией на спекуляции. Но в последующие годы количество наблюдательных данных в пользу инфляции значительно увеличилось, в основном, благодаря точным измерениям реликтового излучения.
Хотя наблюдаемая однородность реликтового излучения является одной из основных мотиваций развития инфляционной теории, первые сторонники теории понимали, что быстрое пространственное расширение не сможет обеспечить абсолютную однородность излучения. Наоборот, они утверждали, что квантово-механические флуктуации, растянутые инфляционным расширением, нарушают однородность, создавая миниатюрные температурные колебания, подобные мельчайшей ряби на ровной поверхности пруда. Этот блистательный результат оказал огромное влияние на последующее развитие.[15] Рассмотрим всё поподробнее.
Квантовая неопределённость приводит к флуктуациям поля инфлатона. Действительно, если инфляционная теория верна, то взрывоподобное инфляционное расширение здесь закончилось, потому что большая и удачливая квантовая флуктуация почти 14 миллиардов лет назад сбросила инфлатон с верхней точки в нашей части вселенной. Но это ещё не конец истории. Пока инфлатон в нашем пузырьке-вселенной скатывается вниз к точке завершения инфляции, его значения по прежнему подвержены квантовым флуктуациям. Флуктуации, в свою очередь, могут изменить величину инфлатона на чуть выше здесь и чуть ниже там, подобно волнистой поверхности покрывала, брошенного поверх кровати. Это приводит к небольшим изменениям в энергии, которой инфлатон наполняет пространство. Как правило, такие квантовые изменения настолько малы и происходят на таких микроскопических расстояниях, что на космических масштабах ими можно спокойно пренебречь. Однако инфляционное расширение — это никак не обычный процесс.
Расширение пространства происходит настолько быстро, даже на выходе из инфляционного режима, что всё микроскопическое растягивается настолько, что становится макроскопическим. Подобно надписи, сделанной крохотными буковками на воздушном шаре, которая начинает проявляться, по мере того как воздух растягивает поверхность шара, влияние квантовых флуктуаций становится видимым, когда инфляционное расширение растягивает космическую ткань. В частности, небольшие отклонения в энергии, вызванные квантовыми флуктуациями, переходят в температурные отклонения, которые отпечатываются на реликтовом излучении. Вычисления показывают, что температурные отклонения нельзя назвать уж очень большими, но они могут достигать примерно одной тысячной доли градуса. Если температура в одной области составляет 2,725 K, то в близлежащих областях в результате растянутых квантовых флуктуаций температура может быть чуть ниже, скажем, 2,7245 K, или чуть выше — 2,7255 K.
Поиск таких температурных колебаний стал предметом скрупулёзных астрономических наблюдений. В конце концов они были обнаружены. В точном согласии с предсказаниями теории они составляют примерно тысячную долю градуса (рис. 3.4). Но больше всего впечатляет то, что картина расположения температурных отклонений на небе точно соответствует теоретическим предсказаниям. На рис. 3.5 сопоставлены теоретические предсказания колебаний температуры — как функция расстояния между областями (в угловых размерах между соответствующими прямыми, проведёнными с Земли) с наблюдательными данными. Согласие результатов просто потрясающее.
Рис. 3.4. В инфляционной космологии гигантское пространственное расширение растягивает микроскопические квантовые флуктуации до макроскопических размеров, что приводит к наблюдаемым температурным колебаниям реликтового излучения (более тёмные пятнышки чуть холоднее более светлых)
Рис. 3.5. Диаграмма температурных колебаний реликтового излучения. Температурные колебания отложены по вертикальной оси; расстояние между двумя областями (в угловых размерах между соответствующими прямыми, проведёнными с Земли — бо́льшие углы правее, меньшие углы левее) отложено на горизонтальной оси.{22} Теоретические предсказания нанесены сплошной линией; экспериментальные данные представлены кружочками
Нобелевская премия по физике 2006 года за обнаружение этих температурных колебаний была присуждена Джорджу Смуту и Джону Мазеру, которые в начале 1990-х годов возглавляли исследовательскую группу проекта COBE[16] из более чем тысячи сотрудников. За прошедшее десятилетие всё новые и более точные измерения подтверждают данные на рис. 3.5 и приводят к более точному согласию с предсказанными значениями температурных колебаний.
Эти исследования стали венцом захватывающей истории открытий, начавшихся с гипотез Эйнштейна, Леметра и Фридмана, стремительно продвинутых вперёд вычислениями Гамова, Альфера и Германа, усиленных идеями Дикке и Пиблса, подтверждёнными затем в наблюдениях Пензиаса и Вильсона, и теперь достигших кульминации благодаря скрупулёзной работе армии астрономов, физиков и инженеров, чьи совместные усилия привели к обнаружению невероятно слабого космического автографа, оставленного миллиарды лет назад.
На качественном уровне можно сказать, что мы все должны быть благодарны пятнышкам на рис. 3.4. Когда инфляция в нашем пузырьке-вселенной подходила к концу, области с несколько большей энергией (или массой, как следует из формулы E = mc2) создавали чуть более сильное гравитационное притяжение, притягивая больше частиц из близлежащих окрестностей и становясь, таким образом, больше. Большое скопление частиц в свою очередь создавало ещё более сильное гравитационное притяжение, притягивая ещё больше вещества и ещё больше увеличиваясь в размерах. С течением времени этот эффект снежного кома привёл к образованию целых глыб вещества и энергии, которые за миллиарды лет стали галактиками и звёздами. Таким способом инфляционная теория устанавливает замечательную связь между самыми большими и самыми маленькими структурами космоса. Само существование галактик, звёзд, планет и жизни как таковой возникает из микроскопической квантовой неопределённости, усиленной инфляционным расширением.
Теоретические умозаключения, лежащие в основе инфляции, не являются бесспорными: в конце концов, инфлатон является гипотетическим полем, существование которого всё ещё нужно доказать; кривая потенциальной энергии была постулирована теоретически, а не обнаружена экспериментально; инфлатон обязан каким-то образом начать свою эволюцию в заданной области пространства с самого верха кривой потенциальной энергии, и так далее. Несмотря на это, даже если какие-то детали теории не совсем верны, согласие между теорией и экспериментом убедило многих, что инфляционный сценарий правильно отражает фундаментальные представления о космической эволюции. Поскольку в большинстве сценариев инфляция является вечной и приводит к постоянно растущему числу дочерних вселенных, то такое объединение теории и эксперимента является пусть косвенным, но убедительным аргументом в пользу существования ещё одной версии параллельных миров.
Встречаем инфляционную мультивселенную
В лоскутной мультивселенной нет резкого раздела между одной параллельной вселенной и другой. Они все являются частями единственного пространства, качественные характеристики которого не сильно меняются от области к области. Сюрприз поджидает нас при более детальном рассмотрении. Большинство из нас никак не ожидают, что миры повторяются; мы не готовы регулярно сталкиваться со своими клонами, клонами друзей и близких. Но если бы мы могли углубиться в космос достаточно далеко, то обнаружили бы именно это.
В инфляционной мультивселенной есть резкий раздел между вселенными. Они являются дырками в космическом сыре, отделёнными друг от друга «сырно-заполненными» областями, в которых значение поля инфлатона остаётся большим. Поскольку «сырно-заполненные» промежуточные области до сих пор испытывают инфляционное расширение, дочерние вселенные, выросшие из пузырьков, быстро удаляются друг от друга со скоростью разбегания, пропорциональной объёму расширившегося пространства между ними. Чем дальше они удаляются, тем выше скорость расширения: в итоге удалённые пузырьки-вселенные разлетаются быстрее, чем скорость света. Даже при неограниченных технологиях и длительности жизни нет никакого способа преодолеть подобный раздел. Более того, нет никакого способа послать хотя бы сигнал.
И всё же мы можем вообразить путешествие к одной или многим дочерним вселенным. Что бы мы обнаружили во время такого путешествия? Поскольку каждая дочерняя вселенная возникает в результате одного и того же процесса — инфлатон скатывается с верхней точки, в результате чего область выходит из инфляционного режима, — все они управляются одной физической теорией, и поэтому подчиняются одному своду физических законов. Но так же как поведение однояйцевых близнецов может в корне отличаться в зависимости от окружения, так и тождественные законы при разных условиях могут проявлять себя огромным количеством способов.
Например, вообразите некую дочернюю вселенную, которая выглядит почти как наша, вся в галактиках, содержащих звёзды и планеты, однако с одним существенным отличием. Эту вселенную пронизывает магнитное поле, в тысячи раз более сильное, чем создаваемое в новейших магнитно-резонансных томографах, но нет такого оператора, который смог бы его отключить. Это мощное поле будет воздействовать на поведение многих вещей. Не только предметы с большим содержанием железа будут следовать привычке плыть по линиям поля, изменятся сами фундаментальные свойства частиц, атомов и молекул. Достаточно сильное магнитное поле настолько разрушительно для клеточных образований, что жизнь в привычном нам виде будет невозможна.
Физические законы одинаковы как внутри магнитно-резонансных томографов, так и снаружи, поэтому фундаментальные физические законы в намагниченной вселенной будут ровно такими же, как у нас. Различия в экспериментальных результатах и наблюдаемых свойствах будут полностью обусловлены внешними условиями — сильным магнитным полем. Талантливые учёные в намагниченной вселенной моментально выделят этот внешний фактор и придут к открытию таких же математических законов, как у нас.
В течение последних сорока лет исследователи разработали модель аналогичного сценария прямо здесь, в нашей с вами Вселенной. Самая известная теория в фундаментальной физике — Стандартная модель физики частиц — постулирует, что мы помещены в экзотический туман, название которому поле Хиггса (в честь английского физика Питера Хиггса, который, опираясь на работы Роберта Брута, Франсуа Энглера, Джеральда Гуральника, Карла Хагена и Тома Киббла, впервые сформулировал эту идею в 1960-х годах). Поле Хиггса и магнитное поле невидимы, и поэтому могут заполнять пространство без прямого указания на своё присутствие. Однако согласно современной теории частиц поле Хиггса маскируется более тщательно. При движении частиц сквозь однородное, заполняющее всё пространство поле Хиггса они не ускоряются, не замедляются, не следуют по каким-то особым траекториям, как в присутствии сильного магнитного поля. Из теории следует, что воздействие на частицы со стороны поля Хиггса более тонкое и глубокое.
При движении сквозь поле Хиггса фундаментальные частицы приобретают и поддерживают массу, о наличии которой говорят эксперименты. Согласно этой идее, когда вы толкаете электрон или кварк, пытаясь изменить его скорость, ощущаемое вами сопротивление возникает благодаря «трению» частицы о патокообразное поле Хиггса. Именно это сопротивление мы называем массой частицы. Если в заданной области пространства вы выключите поле Хиггса, то частицы в ней внезапно станут безмассовыми. А если в другой области пространства удвоите значение поля Хиггса, частицы в ней внезапно удвоят свои массы.[17]
Подобное антропогенное вмешательство гипотетично, потому что энергия, необходимая для существенного изменения величины поля Хиггса даже в малой области пространства, сильно превышает доступную нам энергию. (Другая причина гипотетичности такого вмешательства в том, что существование поля Хиггса до сих пор не доказано. Теоретики усердно предсказывают, что высокоэнергетичные столкновения между протонами на Большом адронном коллайдере смогут отколоть кусочек поля Хиггса — частицу Хиггса — и её можно будет обнаружить в ближайшие годы.) Однако во многих вариантах инфляционной космологии поле Хиггса в разных дочерних вселенных естественно обладает разными значениями.
Подобно полю инфлатона, полю Хиггса соответствует кривая, которая показывает, каким количеством энергии оно обладает при разных значениях. Существенное различие с кривой потенциальной энергии поля инфлатона лишь в том, что поле Хиггса, как правило, находится не в точке ноль (рис. 3.1), а скатывается в одну из ям (рис. 3.6а). Представьте теперь начальную стадию в двух дочерних вселенных, выросших из пузырьков, одна из которых наша. В обеих разогретых вселенных бурный ажиотаж приводит к тому, что величина поля Хиггса начинает безудержно колебаться. Поскольку каждая вселенная расширяется и остывает, поле Хиггса успокаивается и его значение скатывается в одну из ям (рис. 3.6а). В нашей вселенной величина поля Хиггса оказывается, например, в левой яме, что приводит к известным экспериментально наблюдаемым свойствам частиц. Но в другой вселенной движение поля Хиггса может привести к тому, что он окажется в правой яме. Если такое произойдёт, то свойства этой вселенной будут значительно отличаться от свойств нашей вселенной. И хотя основополагающие законы в обеих вселенных будут одинаковыми, массы и другие свойства частиц будут отличаться.
Рис. 3.6. а) Кривая потенциальной энергии поля Хиггса с двумя ямами. Известные свойства нашей вселенной обусловлены полем, расположенным в левой яме; однако в другой вселенной поле располагается в правой яме, что соответствует другим физическим свойствам;
Рис. 3.6. б) Пример поверхности потенциальной энергии в теории с двумя полями Хиггса
Даже небольшая разница в свойствах частиц приводит к серьёзным последствиям. Если масса электрона в другой дочерней вселенной в несколько раз больше, чем у нас здесь, электроны и протоны будут стремиться объединяться в нейтроны, препятствуя тем самым обильному образованию водорода. Фундаментальные взаимодействия — электромагнетизм, ядерное взаимодействие и (как мы считаем) гравитация — также переносятся частицами. Изменение свойств этих частиц коренным образом изменит свойства взаимодействий. Например, чем тяжелее частица, тем медленнее она движется и тем короче расстояние, на котором действует соответствующая сила. Образование и устойчивость атомов в нашей вселенной основано на свойствах электромагнитных и ядерных взаимодействий. Если существенно изменить эти взаимодействия, атомы развалятся или, что более вероятно, вообще не смогут образоваться. Таким образом, ощутимое изменение свойств частиц приведёт к нарушению самых фундаментальных процессов, обеспечивающих привычные свойства нашей вселенной.
На рис. 3.6а показан самый простой случай, когда имеется всего одна разновидность поля Хиггса. Однако физики-теоретики исследовали более сложные сценарии с участием нескольких полей Хиггса (мы скоро увидим, что такие возможности обязательно возникают в теории струн), что даёт ещё больший набор различных дочерних вселенных. Пример с двумя полями Хиггса показан на рис. 3.6б. Как и прежде, различные ямы соответствуют значениям полей Хиггса, где могут находиться те или иные дочерние вселенные, выросшие из пузырьков.
Вселенные, заполненные полями Хиггса с непривычными значениями, будут сильно отличаться от нашей (рис. 3.7). Поэтому путешествие сквозь инфляционную мультивселенную может оказаться опасной затеей. Сомнительно, чтобы вам захотелось непременно посетить большинство вселенных, ведь условия там могут оказаться несовместимы с биологическими процессами, критичными для жизнедеятельности; что придаёт новый смысл высказыванию, что дома лучше. В инфляционной мультивселенной наша Вселенная может вполне оказаться райским островком в огромном, но в основном не пригодном для жизни космическом архипелаге.
Рис. 3.7. Поскольку поля Хиггса могут обладать разными значениями в разных дочерних вселенных, вселенные в сценарии инфляционной мультивселенной могут иметь разные физические свойства, хотя все они и подчиняются одним и тем же физическим законам
Вселенные в ореховой скорлупе
Различия между лоскутной мультивселенной и инфляционной мультивселенной настолько фундаментальны, что они могут показаться никак не связанными друг с другом. Лоскутная мультивселенная возникает в случае бесконечного пространства, а инфляционная мультивселенная обусловлена вечным инфляционным расширением. И всё же между ними существует глубокая и удивительная связь, которая смыкает идеи из двух предыдущих глав: параллельные Вселенные, возникающие благодаря инфляции, порождают Вселенные из лоскутной мультивселенной. Важную роль в этом процессе играет время.
Среди многих странностей, вскрытых теорией Эйнштейна, наиболее трудно для понимания то, что время течёт. И хотя повседневный опыт убеждает нас в объективности понятия течения времени, теория относительности доказывает, что это всего лишь артефакт жизни в условиях малой гравитации и на малых скоростях. На околосветовых скоростях и в сильных гравитационных полях привычная универсальная концепция времени быстро испаряется. Если вы мчитесь мимо меня, то события, одновременные с моей точки зрения, для вас будут происходить в разные моменты времени. Если вы зависли где-то вблизи чёрной дыры, один час на ваших часах для меня будет длиться бесконечно долго. Никакого гипноза или фокусов. Течение времени зависит от условий, в которых находится наблюдатель, — траектории его движения и действующей на него гравитации.[18]
Применительно ко всей вселенной или к нашему инфляционному пузырьку это немедленно порождает вопрос: как такое податливое, зависящее от обстоятельств время согласуется с понятием абсолютного космологического времени? Мы уверенно говорим о «возрасте» нашей Вселенной, но если галактики быстро движутся относительно друг друга со скоростями, которые зависят от расстояния между ними, — разве тогда относительность течения времени не становится кошмарной проблемой для любого воображаемого вселенского хранителя времени? Более точно, когда мы говорим, что нашей Вселенной «14 миллиардов лет», используем ли мы для измерения этого промежутка времени какие-то конкретные часы?
Да, используем. Тщательное изучение этого космического времени вскрывает прямую связь между параллельными вселенными в инфляционной и лоскутной моделях вселенных.
Любой используемый нами метод измерения времени подразумевает учёт изменений, происходящих в какой-то конкретной физической системе. С помощью обычных настенных часов мы проверяем изменения в положении стрелок. С помощью Солнца мы проверяем изменения в его положении на небе. С помощью изотопа углерода C14 мы проверяем его процентное содержание в исходном образце, где происходит радиоактивный распад с выделением азота. Исторический опыт и общая договорённость привели нас к использованию орбитального вращения Земли и вращения вокруг своей оси в качестве физических реперных точек, что приводит к стандартным понятиям «дня» и «ночи». Но когда мы размышляем о космических масштабах, то существует другой, более полезный метод измерения времени.
Мы видели, что инфляционное расширение приводит к огромным областям с однородными в среднем свойствами. Измерьте температуру, давление и среднюю плотность вещества в двух больших, но удалённых областях одной дочерней вселенной, и результаты совпадут. Они могут изменяться во времени, но однородность на больших масштабах гарантирует, что, в среднем, изменение здесь такое же, как изменение там. Важный наглядный пример — это обусловленное постоянным расширением пространства уменьшение плотности массы в нашем пузырьке-вселенной, происходящее в течение нашей многомиллиардной истории. Однако, поскольку уменьшение происходит однородно, то однородность на больших расстояниях в нашем пузырьке-вселенной не нарушилась.
Это важно, потому что подобно тому, как устойчиво уменьшающееся количество изотопа углерода C14 в органическом мире даёт способ измерения времени на Земле, постоянно уменьшающаяся плотность массы даёт способ измерения времени во Вселенной. Поскольку уменьшение плотности происходит однородно, плотность массы как маркер течения времени обеспечивает наш пузырёк-вселенную единым стандартом. Если каждый из нас аккуратно установит время на своих часах в соответствии со средней плотностью массы (перенастройка обязательно понадобится после путешествия к чёрной дыре, либо после путешествий с околосветовыми скоростями), то все часы во Вселенной будут синхронизированы. Когда мы говорим о возрасте Вселенной, то есть о возрасте нашего пузырька, то речь идёт о времени, измеренном по таким воображаемым космическим синхронизированным часам. Единое космическое время осмысленно, только если оно измерено по таким часам.
Такой же вывод справедлив для раннего пузырька-вселенной, но с одной оговоркой. Обычное вещество ещё не сформировалось, поэтому нельзя говорить о средней плотности массы в пространстве. Наоборот, поле инфлатона наполняет нашу Вселенную энергией, которая вскоре будет преобразована в привычные частицы. Это следует учитывать, и установить свои часы согласно плотности энергии поля инфлатона.
Теперь вспомним, что энергия инфлатона задаётся его значением, что отражается кривой потенциальной энергии. Таким образом, чтобы определить время в заданной точке в нашем пузырьке-вселенной, мы должны определить в этой точке значение инфлатона. Затем, подобно тому как два дерева имеют одинаковый возраст, если у них одинаковое количество колец, а два образца ледникового отложения имеют одинаковый возраст, если процентное содержание изотопа углерода в них совпадает, — две точки пространства находятся в том же времени, если значения поля инфлатона в этих точках одинаковы. Таким способом мы устанавливаем и синхронизируем часы в нашем пузырьке-вселенной.
Причина, по которой я всё это обсуждаю, в том, что в приложении к космическому швейцарскому сыру инфляционной мультивселенной из этих размышлений следует вывод, который резко противоречит здравому смыслу. Подобно Гамлету, восклицавшему: «О боже, я бы мог замкнуться в ореховой скорлупе и считать себя царём бесконечного пространства»[19], — каждая из дочерних вселенных, выросших из пузырьков, обладает конечной пространственной протяжённостью, если на неё смотреть снаружи, но бесконечной, если смотреть изнутри. Осознание этого факта бесподобно. Именно бесконечное пространство необходимо для лоскутных параллельных вселенных. Поэтому теперь мы можем ввести лоскутную мультивселенную в инфляционный сценарий.
Крайнее несоответствие между внутренней и внешней перспективами возникает из-за того, что представления о времени внутреннего и внешнего наблюдателей совершенно не совпадают. Хотя это совсем не очевидно, но сейчас мы увидим, что то, что внешнему наблюдателю кажется бесконечным временем, для внутреннего наблюдателя в каждый данный момент времени кажется бесконечным пространством.[20]
Пространство в дочерней вселенной
Чтобы понять, как такое может быть, представьте себе некую молодую даму по имени Трикси, которая, путешествуя вместе с быстро расширяющейся областью пространства, заполненного инфлатоном, наблюдает образование из находящегося поблизости пузырька дочерней вселенной. Направив свой инфлатонный детектор на растущий пузырёк, она сможет напрямую зафиксировать изменение значения поля инфлатона. И хотя эта область — дырка в космическом сыре — трёхмерна, проще измерить поле вдоль какой-нибудь одномерной линии поперечного сечения по диаметру, и если Трикси так поступит, то получит данные, приведённые на рис. 3.8а. Строчки показывают значение инфлатона, измеренного последовательно во времени (чем выше, тем позже по времени) с точки зрения Трикси. Из рисунка очевидно, что Трикси видит пузырёк постоянно растущим (более светлые области на рисунке соответствуют меньшим значениям инфлатона).
Рис. 3.8а. По строкам указана величина инфлатона в определённый момент времени с точки зрения внешнего наблюдателя. Чем выше строка, тем более позднему моменту она соответствует. Столбцы соответствуют положению в пространстве. Пузырёк — это такая область пространства, в которой инфляция закончилась из-за уменьшения значения инфлатона. Всё более и более светлые клетки соответствуют величине инфлатона внутри пузырька. С точки зрения внешнего наблюдателя пузырёк всё время увеличивается
Теперь представим, что некий джентльмен Нортон тоже изучает тот же пузырёк, но только изнутри. Он упорно трудится, проводя точные астрономические наблюдения с помощью своего инфлатонного детектора. В отличие от Трикси, Нортон калибрует время по значению инфлатона. Эти рассуждения играют ключевую роль для понимания искомого вывода, поэтому постарайтесь в них вникнуть до конца. Итак, представьте, что все в нашем пузырьке-вселенной носят часы, измеряющие и показывающие значение инфлатона. Когда Нортон устраивает вечеринку, он приглашает гостей прийти к нему домой, когда инфлатонные часы покажут 60. Поскольку все часы установлены одинаково согласно единому стандарту — значению поля инфлатона, — вечеринка начнётся без заминки. Все придут в один и тот же момент времени, потому что у всех одно представление о синхронности.
В такой ситуации Нортону будет несложно определить размер пузырька-вселенной в любой заданный момент его шкалы времени. На самом деле всё просто, как в детских раскрасках, когда части рисунка обозначены цифрами, указывающими, каким цветом это нужно сделать. Соединяя все точки с одинаковым численным значением поля инфлатона, Нортон очертит всю область пузырька в какой-то определённый момент времени. Его времени. Времени внутреннего наблюдателя.
Результаты Нортона показаны на рис. 3.8б. Каждая линия соединяющая точки с одинаковыми значениями поля инфлатона отображает пространство в данный момент времени. Из рисунка явно следует, что каждая линия тянется бесконечно, и это означает, что размер пузырька-вселенной с точки зрения его населения бесконечен. Таким образом, бесконечное время снаружи, которое для Трикси представляется в виде бесконечного числа строк на рис. 3.8, оказывается в каждый момент времени безграничным пространством для внутреннего наблюдателя такого как Нортон.
Рис. 3.8б. Та же самая информация, что и на рис. 3.8а, видится иначе наблюдателю внутри пузырька. Совпадающие значения инфлатона соответствуют одинаковым моментам времени, поэтому нарисованные линии проходят через те точки пространства, которые существуют в один и тот же момент времени. Меньшие значения инфлатона соответствуют более поздним моментам. Заметим, что линии можно продолжить бесконечно далеко, так что с точки зрения внутреннего наблюдателя пространство бесконечно
Это очень серьёзное достижение. В главе 2 мы выяснили, что существование лоскутной мультивселенной зависит от того, бесконечен или нет размер пространства, а теперь оказывается, что это совсем не обязательно. Каждый пузырёк в инфляционной вселенной имеет конечный пространственный размер, если смотреть снаружи, и бесконечный размер, если смотреть изнутри. Таким образом, если инфляционная мультивселенная реальна, то население пузырька — мы — живёт не только в инфляционной, но также в лоскутной мультивселенной.{23}
Когда я впервые узнал о лоскутной и инфляционной мультивселенных, именно инфляционный сценарий представлялся мне наиболее правдоподобным. Инфляционная космология дала ответы на ряд давних вопросов и сделала предсказания, хорошо согласующиеся с наблюдениями. Как мы видели выше, инфляция по своей природе является процессом, который никогда не останавливается; она порождает и порождает пузырьки-вселенные, в одном из которых мы с вами живём. В свою очередь идея лоскутной мультивселенной, вступающая в полную силу, когда пространство не просто большое, а бесконечное (у вас может появиться клон в большой вселенной, а может и нет, но он обязательно появиться в бесконечной вселенной), может и не реализоваться: в конце концов может оказаться, что размер вселенной конечен. Но теперь мы видим, что пузырьки-вселенные, возникающие при вечной инфляции с точки зрения находящихся внутри них наблюдателей, являются пространственно бесконечными. Инфляционные параллельные вселенные порождают лоскутные вселенные.
Самая лучшая из имеющихся космологических теорий для объяснения большинства имеющихся космологических данных приводит нас к мысли о том, что мы населяем лишь одну из обширных инфляционных систем параллельных вселенных, в каждой из которых сокрыто своё многообразие параллельных лоскутных вселенных. Космос, каким он представляется в самых передовых исследованиях, содержит не только параллельные вселенные, но и вселенные, параллельные параллельным. Это наводит на мысль, что реальность не просто обширна — она невообразимо обширна.
Глава 4. Объединяя законы природы На пути к теории струн
Современная космология, от Большого взрыва до инфляции, ведёт своё начало из одного научного ядра: общей теории относительности Эйнштейна. В новой теории гравитации Эйнштейн отбросил общепринятое представление о жёстком и неизменном пространстве и времени; перед наукой предстал динамичный космос. Открытия такого масштаба крайне редки. Но Эйнштейн мечтал о покорении ещё более высоких вершин. С накопленным к 1920-м годам математическим арсеналом и геометрической интуицией он приступил к развитию единой теории поля.
Под единой теорией поля Эйнштейн подразумевал некую схему, которая позволит вплести все силы природы в единый и самосогласованный математический ковёр. Вместо одного набора законов для одних физических явлений и другого набора для других, Эйнштейн хотел свести все известные законы под единый свод. Но десятилетия напряжённой работы Эйнштейна в направлении объединения не оказали в то время значительного влияния — цель была великой, но для неё не пришло ещё время. Позднее другие исследователи подхватили знамя единой теории, широко шагая вперёд. Наиболее успешная схема объединения получила название теория струн.
В моих предыдущих книгах «Элегантная Вселенная» и «Ткань космоса» рассказывалось об истории возникновения теории струн и её основных свойствах. За годы, прошедшие с момента появления этих книг, состояние и общий статус теории привлекли внимание широкой общественности, что совершенно естественно. Несмотря на все успехи теории струн, от неё ждут определённых предсказаний, экспериментальная оценка которых даст ответ на вопрос о правильности или неправильности теории. Так как три новых типа мультивселенных (которые мы обсудим в главах 5 и 6) возникают в теории струн, сейчас важно обсудить текущий статус теории и возможности для её экспериментальной проверки и согласования с наблюдательными данными. Это и будет содержанием текущей главы.
Краткая история объединения
Когда Эйнштейн размышлял об объединении, науке были известны две силы: гравитация, описываемая его собственными уравнениями, и электромагнетизм, описываемый уравнениями Максвелла. Эйнштейн предполагал объединить две теории в единую математическую конструкцию, которая сочленила бы действие всех сил в природе. Эйнштейн был преисполнен надежд о своей единой теории. Работы Максвелла по объединению в XIX столетии совершенно справедливо рассматривались им как образцовый вклад в копилку человеческой мысли. До Максвелла электричество, текущее по проводам, притяжение, вызываемое детским магнитиком, и свет, идущий от Солнца к Земле, считались тремя разными, никак не связанными друг с другом явлениями. Максвелл осознал, что на самом деле они составляют сплетённое воедино научное триединство. Электрические токи порождают магнитные поля; магниты, перемещающиеся рядом с проводами, порождают в них электрические токи; а волнообразные возмущения, бегущие сквозь электрические и магнитные поля, порождают свет. Эйнштейн ожидал, что его собственная работа приведёт к продвижению программы объединения Максвелла и станет следующим и, возможно, финальным шагом на пути к единому описанию законов природы — такому описанию, в котором будут объединены электромагнетизм и гравитация.
Цель была весьма амбициозна, и Эйнштейн отнёсся к ней очень серьёзно. У него была уникальная способность полностью отдаваться задаче, которую он перед собой поставил, и последние тридцать лет своей жизни он полностью посвятил проблеме объединения. Его личный секретарь Хелен Дукас была рядом с ним в принстонском госпитале в предпоследний день его жизни, 17 апреля 1955 года. Она вспоминает, как прикованный к постели Эйнштейн почувствовал себя лучше и сразу же попросил принести черновики с уравнениями, в которых он писал и писал математические символы в безуспешной надежде, что единая теория поля выкристаллизуется. Настало утро, но Эйнштейн не проснулся. Его последние вычисления не пролили больше света на вопрос объединения.{24}
Немногие современники Эйнштейна разделяли его страсть к поискам объединения. С середины 1920-х до середины 1960-х годов физики, руководствуясь квантовой механикой, делали успехи в раскрытии тайны атома и использовании его скрытой мощи. Возник мощный очевидный соблазн подсмотреть, из чего устроена материя. И хотя многие соглашались, что единая теория была достойной целью, но в эру, когда теоретики и экспериментаторы рука об руку работали над открытием законов микромира, интерес к ней ослабевал. С уходом Эйнштейна работа над единой теорией практически прекратилась.
Вся глубина его неудачи была осознана, когда в последующих исследованиях выяснилось, что объединение осуществлялось в слишком узких рамках. Эйнштейн не только принижал роль квантовой физики (он полагал, что единая теория вытеснит квантовую механику, и поэтому нет никакой надобности закладывать её в основы теории), но в его работе не учитывались два дополнительных взаимодействия, обнаруженные экспериментально: сильное ядерное взаимодействие и слабое ядерное взаимодействие. Первое из них является тем сильным клеем, который не позволяет распасться атомному ядру, а второе, помимо прочего, ответственно за радиоактивный распад. Единая теория должна объединять не две силы, а четыре; мечта Эйнштейна стала ещё более призрачной.
В конце 1960-х и в начале 1970-х годов пошла обратная волна. Физики осознали, что методы квантовой теории поля, успешно применённые в электромагнетизме, также хорошо описывают слабое и сильное ядерные взаимодействия. Таким образом, все три негравитационные силы описываются на одном математическом языке. Более того, при подробном исследовании этих квантовых теорий поля — в основном в работах Шелдона Глэшоу, Стивена Вайнберга и Абдуса Салама, отмеченных Нобелевской премией, а также в последующих работах Глэшоу и его гарвардского коллеги Говарда Джорджи — обнаружились взаимосвязи, указывающие на возможное единство электромагнитных, слабых и сильных взаимодействий. Руководствуясь идеей Эйнштейна почти полувековой давности, эти теоретики доказали, что три на первый взгляд различные силы могут на самом деле быть проявлением единой, монолитной силы природы.{25}
Всё это явилось впечатляющим продвижением к единой теории, однако на таком обнадёживающем фоне возникла досадная проблема. Когда учёные применили методы квантовой теории к четвёртой силе в природе — гравитации, оказалась, что математика просто не работает. Вычисления, вовлекающие квантовую механику и общерелятивистское описание гравитационного поля по Эйнштейну, привели к странным результатам, равносильным математической галиматье. Как бы успешно не работали общая теория относительности и квантовая механика на своих естественных масштабах, на больших и малых расстояниях, бессмысленный результат, полученный при попытке их объединения, означал глубокую трещину в понимании законов природы. Являясь изначально лишь эстетическим устремлением, объединение стало логической необходимостью.
В середине 1980-х годов произошёл следующей ключевой скачок. Новая теория, теория суперструн, завладела умами физиков по всему миру. Она смягчила разногласия между общей теорией относительности и квантовой механикой и дала надежду, что гравитация может быть встроена в объединённый квантово-механический каркас. Наступила эра суперструнного объединения. Исследования шли с огромной скоростью, и тысячи журнальных страниц быстро заполнились вычислениями, прояснившими разные аспекты нового подхода и создавшими фундамент для его последовательной формулировки. Была развита впечатляющая и изощрённая математическая структура, но многое в теории суперструн (для краткости, теории струн) оставалось неясным.{26}
Позже, начиная с середины 1990-х годов, попытки теоретиков распутать эти загадки неожиданно привели теорию струн к сюжету с мультивселенными. Учёным давно было известно, что математические методы, применяемые при анализе теории струн, используют множество приближений, а потому их можно усовершенствовать. Когда была сделана часть уточнений, учёные осознали, что соответствующий математический аппарат ясно указывает, что наша Вселенная является, возможно, частью некоторой мультивселенной. На самом деле, из математики теории струн следует не одна мультивселенная, а несколько различных типов мультивселенных, частью которых мы можем быть.
Для полного осознания этих захватывающих и дискуссионных идей и для понимания их роли в неослабевающем поиске законов космоса, следует отступить на шаг назад и оценить для начала статус теории струн.
Ещё раз о квантовых полях
Давайте начнём с более внимательного рассмотрения традиционной квантовой тории поля, оказавшейся столь успешной. Это послужит подготовкой к обсуждению струнного объединения, а также поможет выявить ключевые взаимосвязи между этими двумя подходами к формулировке законов природы.
В главе 3 обсуждалось, что классическая физика описывает поле как нечто типа тумана, который пронизывает область пространства и может переносить возмущения в виде ряби и колебаний. Если бы Максвелл описывал свет, например, освещающий в данный момент этот текст, он бы с восторгом рассказывал об электромагнитных волнах, которые исходят от солнца или от настольной лампы и колеблются в пространстве, направляясь к этой странице. Он стал бы математически описывать движение волн с помощью чисел, изображающих силу поля и направление поля в каждой точке пространства. Колеблющееся поле соответствует колеблющимся числам: численное значение поля в каждой заданной точке периодически увеличивается и уменьшается.
Вовлечение в квантовую механику понятия поля приводит к квантовой теории поля, обладающей двумя существенно новыми свойствами. Мы встречались с ними ранее, но стоит напомнить. Во-первых, квантовая неопределённость заставляет значение поля в каждой точке случайно колебаться — вспомните флуктуирующее поле инфлатона в инфляционной космологии. Во-вторых, подобно воде, состоящей из молекул H2O, квантово-механическое поле состоит из бесконечно малых частиц, известных как кванты поля. Кванты электромагнитного поля — это фотоны, и поэтому квантовая физика изменяет классическое описание вашей настольной лампы, данное Максвеллом, — теперь лампа излучает устойчивый поток из 100 миллиардов миллиардов фотонов в секунду.
Десятилетия дальнейших исследований установили, что эти свойства квантовой механики, применённые к полям, являются совершенно общими. Каждое поле подвержено квантовым флуктуациям. Каждое поле сопоставляется какому-то виду частиц. Электроны — это кванты электронного поля. Кварки — это кванты кваркового поля. В качестве (очень) приближённого наглядного образа физики иногда думают о частицах как об узлах или плотных крупицах соответствующего поля. Но как бы вы не представляли частицы, в рамках квантовой теории поля они математически описываются как крохотные крапинки или точки, не имеющие пространственного размера и внутренней структуры.{27}
Наша вера в квантовую теорию поля обусловлена одним существенным фактом: ни один эксперимент не противоречит её предсказаниям. Наоборот, данные подтверждают, что уравнения квантовой теории поля описывают поведение частиц с изумительной точностью. Наиболее впечатляющим примером является квантовая теория поля электромагнитных сил, квантовая электродинамика. С её помощью физики провели подробные вычисления магнитных свойств электрона. Работа достаточно трудоёмкая, и точные результаты потребовали десятилетий вычислений. Но это того стоило. Полученные результаты совпадают с реальными измерениями с точностью до десяти знаков после запятой, что является совершенно невообразимым согласием теории и эксперимента.
После такого успеха можно ожидать, что квантовая теория поля является математическим фундаментом для понимания всех сил в природе. Многие известные физики разделяли такую точку зрения. В результате упорного труда многих из них к концу 1970-х было установлено, что слабое и сильное ядерные взаимодействия действительно прекрасно описываются квантовой теорией поля. Оба взаимодействия аккуратно описаны в терминах полей — сильные и слабые поля, — распространяющихся и взаимодействующих согласно математическим правилам квантовой теории поля.
Однако, как указывалось выше в историческом обзоре, многие из упомянутых физиков быстро пришли к выводу, что ситуация с четвёртым взаимодействием в природе — гравитацией, гораздо тоньше. Как только уравнения общей теории относительности объединяются с уравнениями квантовой теории, математика начинает бунтовать. Совместное использование уравнений для вычисления квантовой вероятности некоторых физических процессов — таких как вероятность того, что два электрона оттолкнуться друг от друга, притом что они электромагнитно притягиваются и гравитационно отталкиваются, — как правило, приводит к ответу бесконечность. И хотя некоторые вещи во Вселенной и могут быть бесконечными, например протяжённость пространства и количество заполняющего его вещества, но вероятности бесконечными быть не могут. По определению, значение вероятности должно находиться между 0 и 1 (между 0 и 100, если считать в процентах). Бесконечная вероятность совсем не означает, что нечто скорее всего произойдёт, или определённо случится; скорее наоборот — это бессмыслица, как говорить об одиннадцатом яйце в десятке. Бесконечная вероятность шлёт очевидный математический намёк: совместное использование уравнений бессмысленно.
Физики выяснили, что проблема коренится в дрожании и флуктуациях из-за квантовой неопределённости. Математические методы квантовой теории поля были разработаны для анализа флуктуаций сильных, слабых и электромагнитных полей, но, при их применении к гравитационному полю — полю, которое определяет кривизну пространства-времени, — оказалось, что они бесполезны. Возникли разные математические противоречия, такие как бесконечные вероятности.
Чтобы понять, почему так происходит, представьте, что вы владелец старого дома в Сан-Франциско. Если кто-то из ваших жильцов устраивает слишком бурные вечеринки, вам, наверное, придётся поднапрячься, чтобы привести жильцов в чувство, но вы точно можете не беспокоиться, что пирушка нарушит устойчивость самого здания. Однако, если начнётся землетрясение, вы столкнётесь с более серьёзной проблемой. Флуктуации трёх негравитационных полей — полей, что населяют здание пространства-времени, — подобны неутомимым участникам вечеринок. Целое поколение физиков боролось с квантовыми флуктуациями, и к началу 1970-х годов были развиты математические методы, адекватно описывающие квантовые свойства негравитационных полей. Однако флуктуации гравитационного поля качественно другие. Они больше похожи на землетрясение. Поскольку гравитационное поле вплетено в саму ткань пространства-времени, квантовые флуктуации сотрясают всю его структуру вдоль и поперёк. Математические методы, используемые для анализа таких всеобъемлющих квантовых флуктуаций, перестают работать.{28}
В течение многих лет физики смотрели сквозь пальцы на эту проблему, потому что она возникает только при весьма экстремальных условиях. Гравитация вступает в игру, когда объекты очень массивны, а квантовая механика — когда их размер очень мал. Редко бывает, чтобы предмет был одновременно и массивный, и малым, так что для его описания необходимо привлекать как квантовую механику, так и общую теорию относительности. Однако подобные ситуации возникают. Когда гравитация и квантовая механика применяются для описания или Большого взрыва или чёрных дыр, то есть когда действительно огромная масса вещества сжимается до небольших размеров, математические методы перестают работать в самый критический момент анализа, оставляя без ответа вопросы, касающиеся того, как Вселенная родилась и как она, возможно, умрёт в центре чёрной дыры.
Более того — и это действительно впечатляюще, — отвлекаясь от озвученных примеров чёрных дыр и Большого взрыва, можно вычислить, насколько массивным и малым должна быть физическая система, для того чтобы и гравитация, и квантовая механика играли существенную роль. Ответ такой — масса, примерно в 109 раз превышающая массу протона, так называемая масса Планка, сжатая до фантастически малого объёма примерно 10−99 кубического сантиметра (грубо говоря, это сфера с радиусом 10−33 сантиметра с так называемой планковской длиной, как показано на рис. 4.1).{29} Таким образом, расстояние, на котором квантовая гравитация вступает в права, в миллион миллиардов раз меньшее расстояния, достижимого на самых мощных в мире ускорителях. Такая огромная неисследованная территория легко может быть населена новыми полями и их частицами — и кто знает, чем ещё. В целях объединения гравитации и квантовой механики потребуется совершить множество переходов, сталкиваясь с известным и неизвестным на всей этой гигантской территории, которая по большей части остаётся экспериментально недоступной. Такая задача весьма амбициозна и многие учёные были убеждены, что она нерешаема.
Рис. 4.1. Планковская длина, на которой сходятся гравитация и квантовая механика, примерно в 100 миллиардов миллиардов раз меньше, чем любая область, когда-либо исследованная экспериментально. На схеме каждое большое деление соответствует уменьшению размера в 1000 раз; благодаря этому данная схема целиком умещается на одной странице, что, однако, визуально снижает масштабность этого огромного диапазона. Для лучшего понимания укажем, что если увеличить атом до размеров наблюдаемой Вселенной, то планковская длина будет равна размерам обычного дерева
Поэтому вы можете представить то удивление и недоверие, когда в середине 1980-х годов в физическом сообществе поползли слухи, что в направлении объединения произошёл серьёзный теоретический прорыв в рамках подхода, названного теорией струн.
Теория струн
Хотя теория струн имеет репутацию сложной теории, её основная идея очень проста. Мы видели, что стандартная точка зрения, до теории струн, состояла в том, что фундаментальные составляющие являются точечными частицами — точками без внутренней структуры, — которые описываются уравнениями квантовой теории поля. С каждым типом частиц связан свой тип поля. Теория струн бросает вызов такому представлению, утверждая, что частицы не являются точечными. Вместо этого в теории струн предлагается рассматривать их как крошечные, струноподобные вибрирующие нити, как на рис. 4.2. Приглядитесь поближе к любой частице, которая раньше считалась элементарной, и вы увидите, как того требует теория, крохотную вибрирующую струнку. Загляните поглубже в электрон и вы обнаружите струну, загляните поглубже в кварк и вы опять обнаружите струну.
Рис. 4.2. Согласно струнному объяснению устройства природы, на планковских расстояниях фундаментальные составляющие материи имеют вид струноподобных нитей. Однако из-за ограниченности разрешающей способности нашего оборудования мы видим эти струны как точки
При более детальном рассмотрении, говорит теория, вы увидите, что струны в частицах разного типа неразличимы — лейтмотив всей теории струн, — но вибрируют они по-разному. Электрон менее массивен чем кварк, и согласно теории струн это означает, что струна электрона вибрирует менее энергично, чем струна кварка (очередное проявление эквивалентности энергии и массы, воплощённое в уравнении E = mc2). Электрон также обладает электрическим зарядом, величина которого превышает величину заряда кварка, и эта разница объясняется другими, более тонкими, различиями в струнном вибрационном поведении каждого из них. Различные свойства частиц объясняются разным вибрационным поведением нитей в теории струн, подобно тому как разные вибрации гитарных струн порождают звучание разных музыкальных нот.
На самой деле, теория побуждает нас думать, что вибрирующие струны не просто порождают свойства частицы-хозяина, а что они и есть сама частица. По причине бесконечно малого размера струны, порядка планковской длины — 10−33 сантиметра, даже самые точные современные эксперименты не могут подтвердить или опровергнуть протяжённую структуру струны. Большой адронный коллайдер, на котором частицы сталкиваются друг с другом при энергиях, превышающих в 10 триллионов раз энергию покоящегося протона, может добраться до расстояний примерно 10−19 сантиметра; это миллионная от миллиардной доли толщины волоса, но всё же оно слишком велико, на много порядков больше планковских расстояний. Поэтому струны выглядят как точки, даже если их изучать на самых мощных в мире ускорителях частиц, подобно тому как Земля выглядит как точка, если на неё смотреть с Плутона. Тем не менее, согласно теории струн, частицы являются струнами.
В этом, в двух словах, и заключается теория струн.
Струны, точки и квантовая гравитация
У теории струн есть много других существенных свойств, и её развитие значительно расширило то схематическое описание, которое я изложил. В этой главе (а также в главах 5, 6 и 9) мы познакомимся с некоторыми наиболее важными достижениями, но сейчас я хотел бы подчеркнуть три особо важных момента.
Во-первых, когда учёные физики предлагают модель описания природы с помощью квантовой теории поля, они также выбирают поля, которые войдут в теорию. Этот выбор диктуется экспериментальными ограничениями (каждый известный тип частиц определяет отбор соответствующего поля), а также теоретическими предпосылками (гипотетические частицы и их поля, такие как инфлатон и поле Хиггса, вводятся для изучения открытых и спорных вопросов). Главным примером является Стандартная модель. Рассматриваемая как венец достижений физики частиц XX столетия благодаря своей способности правильно описывать огромное количество данных, собранных на ускорителях частиц по всему миру, Стандартная модель является квантовой теорией поля, в которой присутствуют пятьдесят семь различных квантовых полей (это поля, соответствующие электрону, нейтрино, фотону и различным типам кварков — u-кварку, d-кварку, c-кварку и так далее). Стандартная модель, безусловно, крайне успешна, но многие физики полагают, что по-настоящему фундаментальное понимание не требует такого разношёрстного набора ингредиентов.
Впечатляющее свойство теории струн состоит в том, что частицы определяются самой теорией: разные типы частиц соответствуют разному вибрационному поведению струны. И поскольку вибрационное поведение задаёт свойства соответствующей частицы, то если мы поймём теорию настолько хорошо, что определим все типы вибрационного поведения, мы сможем объяснить все свойства всех частиц. Тогда потенциал и перспективы теории струн заключаются в том, чтобы превзойти квантовую теорию поля путём получения всех свойств частиц математически. Это не только объединит всё на свете под зонтиком вибрирующих струн, а также покажет, что будущие «сюрпризы» — как, например, открытие неизвестных пока типов частиц — встроены в теорию струн с самого начала и в принципе будут доступны при достаточно упорных вычислениях. Теория струн строится не последовательными приближениями к полному описанию природы. Она предлагает полное описание с самого начала.
Во-вторых, среди возможных вибраций струны есть одна, обладающая всеми нужными свойствами для того, чтобы быть квантовой частицей гравитационного поля. Хотя дострунные попытки свести воедино гравитацию и квантовую механику оказались неудачными, исследования выявили свойства, которыми будет обладать гипотетическая частица — получившая название гравитон, — соответствующая квантовому гравитационному полю. Было показано, что гравитон должен быть безмассовым, не иметь заряда и обладать квантово-механическим свойством, известным как спин-2. (Грубо говоря, гравитон должен вращаться как волчок, причём в два раза быстрее, чем фотон.){30} Замечательно, что первые струнные теоретики — Джон Шварц, Джоэл Шерк и, независимо от них, Тамиаки Йонея — обнаружили, что в списке струнных вибраций присутствует именно такая вибрация, свойства которой соответствуют гравитону. В точности соответствуют. Когда в середине 1980-х годов были выдвинуты убедительные доводы в пользу того, что теория струн является математически согласованной квантово-механической теорией (в основном благодаря работам Шварца и его соавтора Майкла Грина), присутствие гравитонов означало, что теория струн является давно искомой квантовой теорией гравитации. Этот пункт в списке достижений теории струн наиболее важен, именно поэтому она так быстро воспарила к вершинам мировой научной известности.[21]{31}
В-третьих, как бы ни была радикальна теория струн, она идёт по проторённому пути, известному в истории физики. Обычно, новые и успешные теории не игнорируют предыдущие достижения. Наоборот, успешные теории, как правило, включают в себя добытые ранее знания, тем самым значительно расширяя область физических явлений, которые можно аккуратно описать. Специальная теория относительности расширяет наше понимание мира высоких скоростей; общая теория относительности идёт дальше и учитывает большие массы (там, где действуют сильные гравитационные поля); квантовая механика и квантовая теория поля вводят нас в мир малых расстояний. Понятия, привлекаемые этими теориями, и предсказываемые ими свойства не похожи ни на что известное ранее. Более того, если применять эти теории в привычных рамках доступных нам скоростей, размеров и масс, они сведутся к описаниям, открытым до XX столетия — к классической механике Ньютона и классическим полям Фарадея, Максвелла и других.
Возможно, теория струн является следующим и окончательным шагом на этом пути. В единых рамках она описывает области, подвластные релятивизму и квантам. Более того, важно то, что в теории струн это происходит таким образом, что охватываются все открытия, сделанные ранее. Может показаться, что теория, основанная на вибрирующих нитях, не имеет ничего общего с картиной гравитации как искривлённого пространства-времени, диктуемой общей теорией относительности. Тем не менее, применив теорию струн в ситуации, когда гравитация существенна, а квантовая механика нет (например, для массивного объекта большого размера, такого как Солнце), вы получите уравнения Эйнштейна. Вибрирующие нити и точечные частицы тоже мало похожи. Однако, применив теорию струн в ситуации, когда существенна квантовая механика, а гравитация нет (например, для небольших наборов медленно вибрирующих и движущихся с большой скоростью струн, или для сильно растянутых струн; энергия таких струн мала, что эквивалентно малости массы — поэтому гравитацией можно пренебречь), вы увидите, что математика теории струн трансформируется в математику квантовой теории поля.
На рис. 4.3 показаны логические связи между основными теориями, развитыми со времён Ньютона. Теория струн могла бы претендовать на существенный отрыв от своих предшественников и отступить от нарисованной схемы. Замечательно, что этого не происходит. Теория струн достаточно революционна для преодоления барьеров физики двадцатого столетия. При этом она достаточно консервативна, чтобы прошедшие три столетия открытий смогли уютно разместиться в её математическом аппарате.
Рис. 4.3. Взаимосвязи между основными теоретическими достижениями в физике. С исторической точки зрения, новые и успешные теории расширяют границы нашего понимания (более высокие скорости, бо́льшие массы, меньшие расстояния) и сводятся к предыдущим теориям в менее экстремальных физических условиях. Теория струн следует именно такому пути прогресса — расширяет границы понимания, и при определённых условиях сводится к общей теории относительности и квантовой теории поля
Пространственные измерения
Теперь обсудим кое-что необычное. Переход от точек к нитям — лишь часть нового подхода, предлагаемого теорией струн. В первые годы исследований по теории струн физики столкнулись с фатальными математическими изъянами (названными квантовыми аномалиями), влекущими за собой такие неприемлемые процессы, как спонтанное возникновение или исчезновение энергии. Как правило, когда подобные проблемы возникают в обсуждаемой теории, физики реагируют очень остро и быстро. От такой теории отказываются. Действительно, в 1970-х многие думали, что с теорией струн так и надо поступить. Но некоторые исследователи упорно придерживались другой точки зрения.
В результате сложных исследований было выяснено, что проблемные свойства тесно связаны с числом пространственных измерений. Вычисления показали, что если бы у Вселенной было не три привычных измерения, а больше — дополнительные измерения помимо обычных вправо/влево, вперёд/назад и вверх/вниз, — то уравнения теории струн стали бы непротиворечивыми. Точнее, в уравнениях теории струн нет изъянов во вселенной с девятью пространственными измерениями и одним временным, что в совокупности составляет десять измерений.
Было бы здорово объяснить, как это происходит, не вдаваясь в технические подробности. Однако я не умею этого делать, и никогда не встречал кого-нибудь, кто умел. Я предпринял такую попытку в «Элегантной Вселенной», но описал только самым общим образом, как число измерений влияет на струнные вибрации, и не объяснил, откуда возникает выделенное значение десять. Так что здесь дам некую техническую наводку. В теории струн есть одно уравнение, в котором присутствует вклад вида (D − 10) умножить на (проблему), где D — это число пространственно-временных измерений, а проблема — это некое математическое выражение, приводящее к проблемному физическому явлению, подобному ранее упомянутому нарушению закона сохранения энергии. Я не могу предложить никакого интуитивного, нетехнического объяснения, почему уравнение имеет именно этот вид. Но в вычислениях возникает именно оно. Простое, но ключевое наблюдение состоит в том, что если число измерений равно десяти, а не четырём, как можно было бы ожидать, вклад в уравнение становится 0 умножить на проблему. Поскольку умножение на ноль всегда даёт ноль, во вселенной с десятью пространственно-временными измерениями проблема исчезает. Таково математическое объяснение. Именно поэтому физики, занимающиеся теорией струн, рассматривают вселенную, в которой более четырёх пространственно-временных измерений.
Но даже если вы всем умом стремитесь идти по пути, благословлённому математикой, если об идее дополнительных измерений вы слышите в первый раз, то такая гипотеза может показаться довольно странной. Пространственные измерения так просто не теряются, ведь это не ключи от машины или один из ваших любимых носков. Если бы во Вселенной, помимо высоты, ширины и длины существовало что-то ещё, то это обязательно кто-нибудь заметил бы. Хотя и не обязательно. В начале XX столетия в нескольких пророческих статьях немецкого математика Теодора Калуцы и шведского физика Оскара Клейна было высказано предположение о существовании измерений, легко ускользающих от обнаружения. Они предсказывали, что в отличие от привычных пространственных измерений, простирающихся на большие или даже бесконечные расстояния, могут существовать дополнительные измерения, настолько малые и скрученные, что их очень трудно увидеть.
Возьмите обычную трубочку для коктейлей. А теперь вообразите, что она необычайно длина, что при той же ширине она по высоте равна Эмпайр-стейт-билдинг. Поверхность этой трубочки (как и любой другой) имеет два измерения. Длинное вертикальное измерение и короткое круговое измерение, накрученное вокруг трубочки. Теперь представьте, что вы смотрите на эту трубочку с другого берега реки Гудзон (рис. 4.4а). Трубочка очень тонкая, она выглядит как вертикальная линия, тянущаяся от земли до неба. Остроты зрения недостаточно, чтобы разглядеть маленькое круговое измерение с такого расстояния, хотя оно есть в каждой точке вдоль всего длинного вертикального измерения. Можно прийти к неправильному выводу, что поверхность трубочки имеет одно измерение, а не два.[22]
Рис. 4.4. а) Поверхность высокой трубочки имеет два измерения; длинное вертикальное измерение легко увидеть, а малое круговое измерение обнаружить труднее;
б) Гигантский ковёр имеет три измерения; протяжённые измерения с севера на юг и с запада на восток легко увидеть, а невысокий ворс ковра обнаружить труднее
Или представьте другую визуальную аналогию — огромный ковёр, покрывающий солончаки штата Юта. С высоты птичьего полёта ковёр выглядит как ровная поверхность с двумя измерениями, тянущимися с севера на юг и с запада на восток. Но если спуститься на землю и рассмотреть ковёр вблизи, можно увидеть, что его поверхность покрыта плотным ворсом: крохотные нитяные петельки протянуты в каждой точке ровной основы ковра. У ковра есть два больших, легко видимых измерения (с севера на юг и с запада на восток), но также одно малое измерение (петельки из ниток), которые труднее обнаружить (рис. 4.4б).
Из предложения Калуцы — Клейна следует, что похожее различие между одними измерениями, большими и легко видимыми, и другими, малыми и слабо различимыми, может иметь место и для структуры самого пространства. Причина, по которой мы всё знаем о привычных трёх пространственных измерениях, может быть в том, что их протяжённость, подобно вертикальной размерности трубочки или географическим измерениям ковра, велики (может даже бесконечны). Однако, если дополнительное пространственное измерение скручено подобно круговому измерению трубочки или ковра и имеет чрезвычайно малый размер — в миллионы или даже в миллиарды раз меньше, чем размер атома, — оно совершенно равноправно обычным нескрученным измерениям и при этом остаётся невидимым даже для самого мощного современного увеличивающего оборудования. Такое измерение действительно может легко потеряться. Так начиналась теория Калуцы — Клейна, гипотеза о том, что наша Вселенная имеет больше трёх пространственных измерений (рис. 4.5).
Рис. 4.5. Теория Калуцы — Клейна постулирует существование крошечных дополнительных пространственных измерений, прикреплённых к каждой точке обычных больших трёх пространственных измерений. Если бы можно было значительно увеличить структуру пространства, гипотетические дополнительные измерения стали бы видимыми. (Дополнительные измерения прикреплены для пущей ясности только к узловым точкам, изображённым на иллюстрации.)
Из вышесказанного следует, что предложение о «дополнительных» измерениях хоть и непривычно, но всё же не является абсурдом. Неплохое начало, но сразу же возникает вопрос: если вернуться в 1920-е годы, откуда вообще возникла такая экзотическая идея? Калуца заинтересовался этим, потому что вскоре после публикации Эйнштейном общей теории относительности ему на ум пришла одна идея. Он обнаружил, что одним росчерком пера, в прямом смысле слова, он может модифицировать уравнения Эйнштейна и применить их ко вселенной с одним дополнительным пространственным измерением. Результат изучения модифицированных уравнений оказался настолько захватывающим, что, как вспоминает его сын, Калуца повёл себя непривычным для него образом: отбросив обычную сдержанность, он ударил обеими руками по столу, вскочил на ноги и запел арию из «Женитьбы Фигаро».{32} Среди модифицированных уравнений Калуца обнаружил уравнения, уже применённые Эйнштейном для описания гравитации в трёх пространственных и одном временном измерениях. Но поскольку новая формулировка включала одно дополнительное пространственное измерение, Калуца обнаружил дополнительное уравнение. О, чудо! Получив это уравнение, Калуца распознал в нём уравнение электромагнитного поля, обнаруженное Максвеллом полувеком ранее.
Как показал Калуца, во вселенной с одним дополнительным пространственным измерением гравитация и электромагнетизм могут быть описаны единым образом как пространственно-временные искривления, рябь. Но гравитация рябит в привычных трёх пространственных измерениях, а электромагнетизм — в четвёртом. Огромной проблемой для гипотезы Калуцы стало объяснение того, почему мы не видим четвёртое пространственное измерение. Именно тогда Калуца предложил описанное выше решение: дополнительные измерения, если они достаточно малы, могут ускользать от фиксации нашими органами чувств и оборудованием.
В 1919 году, узнав о гипотезе объединения в дополнительных измерениях, Эйнштейн засомневался. Он был впечатлён подходом, который позволил продвинуть вперёд его мечту, но его беспокоила неординарность самого метода. После двухгодичных размышлений, задержав при этом выход в печать статьи Калуцы, Эйнштейн наконец-то принял эту идею и мгновенно стал одним из самым рьяных поклонников дополнительных пространственных измерений. В своих собственных поисках единой теории Эйнштейн постоянно возвращался к этой теме.
Несмотря на благословение самого Эйнштейна, последующие исследования показали, что программа Калуцы — Клейна сталкивается с некоторыми препятствиями, самым трудным из которых является невозможность встроить детальные свойства частиц материи, таких как электрон, в математическую структуру. В течение двух десятилетий предлагались и отвергались искусные способы обойти эту проблему, наравне с всевозможными обобщениями и модификациями исходного предложения Калуцы — Клейна, однако поскольку не было предложено ни одного подхода, свободного от этих недостатков, то к середине 1940-х годов идея объединения через дополнительные измерения практически была забыта.
Спустя тридцать лет возникла теория струн. Математический аппарат теории струн не просто разрешал существование во Вселенной дополнительных измерений, он требовал их присутствия. Таким образом, в теории струн возник новый, готовый к использованию формализм для привлечения программы Калуцы — Клейна. На вопрос «если теория струн является долгожданной искомой единой теорией, тогда почему мы не видим требуемые дополнительные измерения?» до нас эхом, сквозь десятилетия, доносится ответ теории Калуцы — Клейна, что эти измерения находятся вокруг нас, но слишком малы, чтобы их увидеть. Теория струн возродила программу Калуцы — Клейна, и к середине 1980-х годов учёные во всём мире воодушевлённо полагали, что это только вопрос времени — самого близкого времени, как говорили наиболее рьяные сторонники, — когда теория струн приведёт к полному описанию всей материи и взаимодействий.
Большие надежды
В первые годы теории струн развитие происходило настолько быстро, что уследить за всеми новостями было практически невозможно. Во многом похожая атмосфера царила в 1920-х годах, когда перед учёными распахнул свои двери мир квантовых явлений. При таком возбуждении понятно, что некоторые теоретики заговорили о скорой революции в решении основных проблем фундаментальной физики: слиянии гравитации и квантовой механики, объединении всех сил в природе, объяснении свойств материи, определении числа пространственных измерений, прояснении сингулярностей чёрных дыр, выяснении происхождения Вселенной. Но более умудрённые физики полагали, что такие надежды преждевременны. Теория струн настолько насыщена, обширна и математически трудна, что спустя почти три десятилетия после первой эйфории современные учёные одолели лишь часть исследовательского пути. С учётом того, что мир квантовой гравитации в сотни миллиардов миллиардов раз меньше чем всё, что мы сегодня можем экспериментально измерить, дорога будет длинная, даже по самым скромным оценкам.
В какой её части мы находимся? В конце главы я кратко опишу самые современные достижения в некоторых ключевых областях (оставляя в стороне вопрос о параллельных вселенных, что будет более подробно рассмотрено в последующих главах), дам оценку успехам и нерешённым проблемам.
Теория струн и свойства частиц
Один из самых основных вопросов всей физики стоит так: почему частицы, которые наблюдаются в природе, являются именно такими, а не какими-нибудь другими? Например, почему электрон обладает именно такой массой, а u-кварк имеет именно такой электрический заряд? Интерес к этим вопросам не просто академический, он отражает очень важный факт, что упоминался ранее. Если бы у частиц были другие свойства — например, будь электрон чуть тяжелее или легче, или электростатическое отталкивание между электронами сильнее или слабее, — ядерные процессы, питающие звёзды, подобные нашему Солнцу, были бы нарушены. Вселенная без звёзд была бы совсем другой.[23] Очевидно, что без солнечного света и тепла не возникла бы сложная цепочка событий, приведшая к возникновению жизни на Земле.
Поэтому возникает фундаментальный вопрос: как с помощью ручки, бумаги и, возможно, компьютера, а также руководствуясь нашим пониманием законов природы, вычислить свойства частиц и получить результаты, которые согласуются с экспериментальными данными. Если нам удастся ответить на этот вопрос, это станет одним из самых важных шагов на пути к пониманию того, почему Вселенная такая как она есть.
В рамках квантовой теории поля ответа на этот вопрос нет и не может быть. В квантовой теории поля измеренные свойства частиц выступают в качестве исходных данных — на их основе строится и определяется сама теория, — поэтому теория успешно работает с широким спектром значений масс и зарядов.[24] Если вообразить мир, где масса электрона или его заряд будут меньше или больше, чем в нашем, то квантовая теория поля опишет явления в таком мире, не моргнув глазом; для этого всего лишь надо будет подстроить значения параметров в уравнениях теории.
Сможет ли теория струн справиться с этим лучше?
Одна из самых красивых черт струнной теории (то, что более всего меня поразило, когда я приступил к её изучению) состоит в том, что свойства частиц определяются размером и формой дополнительных измерений. Поскольку струны очень малы, они вибрируют не только в трёх привычных больших измерениях, но и в малых, свёрнутых измерениях. Подобно тому как поток воздуха, проходящий сквозь духовой инструмент, приобретает колебательное движение, характер которого определяется геометрической формой инструмента, колебания струн в струнной теории определяются формой скрученных измерений. Вспоминая, что вибрационное поведение струн определяет свойства частиц, такие как массу и электрический заряд, мы видим, что эти свойства диктуются геометрией дополнительных измерений.
Поэтому если достоверно известно, как выглядят дополнительные измерения в теории струн, то можно легко предсказать любые свойства вибрирующих струн и, следовательно, все свойства элементарных частиц, порождённых колебаниями струны. Трудность, как и раньше, в том, что никто не знает, какова точная геометрическая форма дополнительных измерений. Уравнения теории струн накладывают математические ограничения на геометрию дополнительных измерений и требуют, чтобы они принадлежали частному классу так называемых пространств Калаби — Яу (на математическом жаргоне многообразия Калаби — Яу), названных в честь математиков Эудженио Калаби и Шин-Туна Яу, которые изучали их свойства задолго до осознания важности их роли в теории струн (рис. 4.6). Проблема в том, что нет какой-то одной, выделенной формы Калаби — Яу. Наоборот, подобно музыкальным инструментам, эти пространства имеют разные размеры и контуры. И так же как разные музыкальные инструменты издают разные звуки — дополнительные измерения, различающиеся по размерам и по форме (а также по другим параметрам, с которыми мы встретимся в следующей главе), порождают разные вибрации струн и, следовательно, разные наборы свойств частиц. Отсутствие однозначной спецификации для дополнительных измерений является главным камнем преткновения, который не позволяет струнным теоретикам делать конкретные предсказания.
Рис. 4.6. Крупный план пространственной структуры в теории струн, где показан пример дополнительных измерений, закрученных в одно из пространств Калаби — Яу. Подобно набивке на основе ковра, пространство Калаби — Яу прикреплено в каждой точке трёх привычных больших измерений (представленных двумерной решёткой), однако для простоты восприятия эти пространства размещены только в узлах решётки
Когда я начал заниматься теорией струн в середине 1980-х годов, было известно небольшое количество пространств Калаби — Яу, поэтому можно было надеяться проанализировать каждое из них и соотнести с известной физикой. Моя диссертация стала одним из самых первых шагов в этом направлении. Спустя несколько лет, когда я стал постдоком (под руководством того самого Яу из Калаби — Яу), число пространств Калаби — Яу возросло до нескольких тысяч, что стало серьёзной задачей для обстоятельного изучения — но ведь для этого и существуют студенты! Время шло и число страниц в каталоге пространств Калаби — Яу только увеличивалось; как будет видно в главе 5, теперь их больше чем песчинок на пляже. На всех пляжах вместе взятых. Даже представить невозможно. И речи быть не может о том, чтобы математически рассмотреть каждое на роль дополнительных измерений. Поэтому струнные теоретики продолжают поиск математической подсказки, которая позволит выделить из всех возможных пространств Калаби — Яу то самое, единственное. Пока это никому не удалось.
Поэтому теория струн пока не реализовала свои возможности по объяснению свойств фундаментальных частиц. В этом отношении теория струн до сих пор не имеет особых преимуществ перед квантовой теорией поля.{33}
Однако, следует помнить, что слава теории струн в первую очередь основана на том, что она может решить центральную дилемму теоретической физики XX столетия — непримиримость общей теории относительности и квантовой механики. В рамках теории струн общая теория относительности и квантовая механика наконец-то гармонично соединяются. Именно в этом состоит самое важное преимущество теории струн, позволяющее обойти основную преграду, препятствующую применению стандартных методов квантовой теории поля. Если бы мы обладали лучшим пониманием математического аппарата теории струн и могли бы однозначно выбрать форму дополнительных измерений, ту, которая приведёт к объяснению наблюдаемых свойств частиц, это был бы феноменальный триумф. Однако нет никакой гарантии, что теория струн сможет с этим справиться. Более того, нет никакой необходимости требовать этого от неё. Квантовая теория поля заслуженно считается в высшей степени успешной теорией, хотя она не может объяснить фундаментальные свойства частиц. Если теория струн тоже не сможет это объяснить, но при этом ключевым образом продвинется намного дальше квантовой теории поля, включив в себя гравитацию, то только это уже будет монументальным достижением.
Действительно, в главе 6 мы увидим, что в космосе, заполненном параллельными мирами — как следует из некоторых современных версий теории струн, — было бы совершенно неправильно думать, будто математический анализ выявит единственную форму дополнительных измерений. Наоборот, подобно тому как множество различных форм ДНК приводят к разнообразию жизни на Земле, огромное разнообразие форм дополнительных измерений может приводить к множеству вселенных, населяющих струнную мультивселенную.
Теория струн и эксперимент
Если типичная струна имеет крохотный размер, как на рис. 4.2, то для обнаружения её протяжённой структуры — той самой характеристики, которая отличает её от частицы — потребуется ускоритель в миллионы миллиардов раз мощнее, чем Большой адронный коллайдер. При современных технологиях такой ускоритель будет примерно с галактику и будет потреблять каждую секунду столько энергии, сколько потратит весь мир за тысячелетие. Предполагая, что выдающийся технологический прорыв не предвидится, такая ситуация означает, что на сравнительно малых энергиях, достижимых на имеющихся ускорителях, струны неотличимы от точечных частиц. Такова экспериментальная версия упомянутого ранее теоретического факта: на низких энергиях теория струн сводится к квантовой теории поля. Таким образом, даже если теория струн и является правильной фундаментальной теорией, в широком диапазоне доступных экспериментов она будет проявляться как квантовая теория поля.
Это уже хорошо. Хотя квантовая теория поля не может объединить общую теорию относительности и квантовую механику, не может предсказать фундаментальные свойства частиц в природе, но она умеет объяснять великое множество экспериментальных данных. Измеренные на эксперименте свойства частиц берутся в качестве исходных данных (это определяет состав полей и кривые энергии), после чего с помощью математического аппарата теории предсказывается поведение этих частиц в других экспериментах, в основном на ускорителях. Получаемые результаты в высшей степени достоверны; именно по этой причине поколения учёных, занимающихся физикой частиц, используют квантовую теорию поля в качестве основного метода.
Выбор полей и кривых энергий в квантовой теории поля равносилен выбору формы дополнительных измерений в теории струн. Одна из проблем в теории струн состоит в том, что математика, которая связывает свойства частиц (таких как массы и заряды) с формой дополнительных измерений, в высшей степени нетривиальна. Поэтому работа в обратном направлении очень трудна — использование экспериментальных данных для определения конкретной формы дополнительных измерений, аналогично тому как такие данные определяют состав полей и кривых энергий в квантовой теории поля. Возможно, что однажды удача улыбнётся теоретикам и они смогут из экспериментальных данных определить форму дополнительных измерений в теории струн, но пока этого не произошло.
Поэтому в обозримом будущем наиболее обещающим способом связи теории струн с экспериментальными данными будут предсказания, которые, конечно, можно объяснить с помощью более традиционных методов, но для которых гораздо более естественное и убедительное объяснение возникает из теории струн. Конечно, можно теоретизировать насчёт того, что я печатаю этот текст пальцами ног, но гораздо более естественная и убедительная гипотеза — и я оцениваю её как правильную, — что я всё-таки печатаю пальцами рук. Аналогичные рассуждения применительно к экспериментам, собранным в табл. 4.1, вполне могут служить косвенными подтверждениями правильности теории струн.
Таблица 4.1. Эксперименты и наблюдения, способные установить связь между экспериментальными данными и теорией струн
Эксперимент/наблюдения Объяснение Суперсимметрия В теории суперструн приставка «супер» отсылает к суперсимметрии — математической конструкции с чёткими следствиями: у каждой известной частицы должен иметься партнёр с такими же электрическими и сильными ядерными свойствами. Теоретики полагают, что эти частицы до сих пор не были обнаружены, потому что они тяжелее, чем их известные партнёры, и находятся вне досягаемости современных ускорителей. Энергии Большого адронного коллайдера может хватить для их рождения, поэтому многие считают, что мы, возможно, находимся на пороге открытия суперсимметричного характера природы. Дополнительные измерения и гравитация Поскольку пространство является средой для гравитации, увеличение числа измерений расширяет область действия гравитации. Подобно постепенному растворению капли чернил в стакане с водой, сила гравитации размывается при распространении сквозь дополнительные измерения — что, возможно, объясняет слабость гравитационного взаимодействия (когда вы поднимаете чашку с кофе, сила ваших мышц преодолевает гравитационное притяжение всей Земли). Если нам удастся измерить силу гравитации на расстояниях, меньших чем размер дополнительных измерений, это позволит ухватить её прежде, чем она растворится во всём пространстве, и, следовательно, есть шанс обнаружить более сильное притяжение. На сегодняшний день, измерения на расстояниях примерно в один микрон (10−6 метра) не обнаружили никаких отклонений от предсказаний, сделанных для мира с тремя пространственными измерениями. Наличие отклонений при уменьшении расстояния даст убедительное доказательство существования дополнительных измерений. Дополнительные измерения и потеря энергии Если дополнительные измерения существуют, но их размер меньше микрона, то они недоступны для экспериментов, напрямую измеряющих силу гравитации. Однако Большой адронный коллайдер предлагает другие способы их обнаружения. Осколки, возникающие при лобовых столкновениях быстрых протонов, могут выпасть из привычных трёх больших измерений и оказаться в других измерениях (где по причинам, которые мы рассмотрим позже, эти осколки, возможно, станут частицами гравитации, или гравитонами). В таком процессе осколки уносят с собой энергию, в результате чего наши детекторы после столкновения должны зафиксировать потерю энергии. Такая потеря энергии может убедительно свидетельствовать в пользу существования дополнительных измерений. Дополнительные измерения и чёрные мини-дыры Обычно считается, что чёрные дыры — это остатки массивных звёзд, истративших своё ядерное топливо и схлопнувшихся под собственным весом, однако это слишком упрощённый подход. При достаточном сжатии стать чёрной дырой может всё, что угодно. Более того, если есть дополнительные измерения, то гравитация усиливается при действии на малых расстояниях, поэтому создать чёрную дыру будет легче, так как сильное гравитационное поле приводит к тому, что для создания того же самого гравитационного притяжения необходимо меньшее давление. Даже если столкнуть всего два протона на скоростях, достижимых на Большом адронном коллайдере, то можно накачать достаточно малый объём пространства таким количеством энергии, что запустится механизм образования чёрных дыр. Возникнет лишь слабое подобие чёрной дыры, но оно будет безошибочно узнаваемо. Математический анализ, основанный на работах Стивена Хокинга, показывает, что крошечные чёрные дыры быстро распадаются на более лёгкие частицы, следы которых могут быть обнаружены детекторами коллайдера. Гравитационные волны Хотя размер струны очень мал, но если найдётся способ как-то её ухватить, её можно растянуть до больших размеров. Для этого потребуется приложить силу более чем 1020 тонн, но растяжение струны — это всего лишь вопрос приложения достаточной энергии. Теоретики обнаружили экзотические ситуации, когда энергия подобного растяжения рождается в астрофизических процессах, порождающих длинные струны, растянутые в пространстве. Их можно обнаружить, даже несмотря на очень большую отдалённость. Вычисления показывают, что при колебании длинной струны в пространстве-времени порождаются гравитационные волны — весьма специального характера, поэтому они могут дать ясный наблюдательный знак. В течение следующих нескольких десятилетий, если не раньше, высокочувствительные детекторы, расположенные на Земле и, при условии достаточного финансирования, на орбите, могут обнаружить эти волны. Реликтовое излучение Реликтовое излучение уже продемонстрировало свои возможности в тестировании квантовой физики: экспериментально зафиксированные температурные колебания реликтового излучения возникают из квантовых флуктуаций, растянутых при пространственном расширении. (Вспомните пример со словами, написанными крохотными буквами на поверхности воздушного шарика, которые проявляются по мере надувания шарика.) Расширение пространства при инфляции так велико, что даже небольшие следы, оставленные струнами, могут растянуться настолько, чтобы их можно было обнаружить — возможно, это сделает спутник «Планк» Европейского космического агентства. Успех или неудача зависит от деталей поведения струн в ранней Вселенной — что за сообщение было оставлено струнами на поверхности раздувающегося вселенского шарика. Есть много разных идей и вычислений. Теоретики ждут, что скажут наблюдательные данные.Возможные эксперименты ранжируются от экспериментов по физике частиц на Большом адронном коллайдере (поиск суперсимметричных частиц и указаний на дополнительные измерения) до настольных экспериментов (измерение силы гравитационного притяжения на расстояниях одной миллионной доли метра и даже меньше) и астрономических наблюдений (поиск определённых типов гравитационных волн и малых температурных колебаний реликтового излучения). В табл. 4.1 объясняются разные подходы, но общая оценка легко прослеживается. Положительный исход любого из этих экспериментов может быть объяснён без привлечения теории струн. Например, хотя математическое описание суперсимметрии (см. первую строчку в табл. 4.1) изначально было открыто в теоретических исследованиях по теории струн, с тех пор оно также используется в неструнных теоретических моделях. Таким образом, открытие суперсимметричных частиц станет подтверждением теории струн, но не бесспорным доказательством. Аналогично, хотя дополнительные пространственные измерения естественным образом возникают в теории струн, они также возникают и в неструнных моделях (мы помним, что Калуца, предлагая свою идею, совсем не думал о теории струн). Поэтому самой благоприятной следует рассматривать такую ситуацию, где будет получен ряд положительных результатов из тех, что приведены в табл. 4.1, которые подтвердят правильность теории в разных её проявлениях. И как в примере с печатью текста пальцами ног, неструнные объяснения окажутся надуманными перед лицом целого набора положительных результатов.
Отрицательные результаты экспериментов гораздо менее полезны. Провал в поисках суперсимметричных частиц может означать, что они не существуют или что они слишком тяжёлые, чтобы быть обнаруженными даже на Большом адронном коллайдере; провал в поисках свидетельств существования дополнительных измерений может означать, что они не существуют или что они слишком малы, чтобы быть доступными нашим технологиям; провал в поисках микроскопических чёрных дыр может означать, что гравитация не становится сильнее на малых расстояниях, или что наши ускорители недостаточно мощные для более глубокого проникновения в микромир; провал в поисках струнных проявлений в наблюдениях гравитационных волн или реликтового излучения может означать неправильность теории струн, или что эти проявления слишком малы, чтобы быть измеренным на современном оборудовании.
На сегодняшний день наиболее вероятно, что даже самые многообещающие положительные результаты экспериментов не смогут определённо подтвердить правоту теории струн, а отрицательные результаты, скорее всего, не смогут её опровергнуть.{34} При этом надо не ошибиться. Если мы обнаружим доказательства существования дополнительных измерений, суперсимметрии, чёрных мини-дыр или любого из других возможных проявлений теории струн, это станет важной вехой в поиске единой теории. Это придаст нам уверенность, что избранная нами математическая дорога ведёт в правильном направлении.
Теория струн, сингулярности и чёрные дыры
В большинстве ситуаций квантовая механика и гравитация успешно игнорируют друг друга, при этом первая применяется к малым объектам, таким как молекулы и атомы, а вторая к большим объектам, соразмерным звёздам и галактикам. Однако обе теории вынуждены встречаться в мирах, известных как сингулярности. Сингулярность — это любая физическая ситуация, реальная или гипотетическая, которая настолько экстремальна (огромные массы, малый размер, гигантская кривизна пространства, проколы или разрывы в самой пространственно-временной структуре), что квантовая механика и общая теория относительности ведут себя неадекватно, выдавая результаты, сродни сообщению об ошибке на экране калькулятора при попытке разделить на ноль.
Цель любой квантовой теории гравитации состоит в том, чтобы свести воедино квантовую механику и гравитацию таким образом, чтобы сингулярности исчезли. Разработанный математический аппарат должен быть непротиворечив даже в момент Большого взрыва или в центре чёрной дыры[25] и давать разумное описание ситуаций, которые в течение длительного времени ставили исследователей в тупик. Именно в этом направлении теория струн достигла своих самых впечатляющих успехов, уменьшив список сингулярностей.
В середине 1980-х годов группа исследователей, состоящая из Ланса Диксона, Джеффа Харви, Кумруна Вафы и Эдварда Виттена, пришла к выводу, что некоторые проколы в ткани пространства (называемые сингулярностями орбифолда), которые доставляли много хлопот уравнениям Эйнштейна, прекрасно ведут себя в теории струн. Ключ к успеху состоял в том, что струна в отличие от точечной частицы не может свалиться в такой прокол. Поскольку струна — это протяжённый объект, она может удариться о прокол, может обмотаться вокруг него либо воткнуться в него, но подобного рода умеренные взаимодействия совершенно не портят уравнения теории струн. Это важно не потому, что такие изъяны в пространстве действительно имеют место — может, да, а может, и нет, — а потому, что именно таких свойств мы хотим от квантовой теории гравитации: способности работать осмысленно в ситуации, когда по отдельности отказывают как общая теория относительности, так и квантовая механика.
В 1990-х годах в нашей работе с Полом Аспинволлом и Дэвидом Моррисоном, а также независимо Эдвардом Виттеном было установлено, что более сильные сингулярности (известные как флоп-сингулярности), возникающие при сжатии сферической области пространства до бесконечно малого размера, тоже описываются теорией струн. Интуиция подсказывает, что струна при движении может накрутиться на такую сжатую область пространства, подобно обручу на мыльный пузырь, создавая нечто вроде кругового ограждения. Вычисления показывают, что такой «струнный щит» сводит на нет любые потенциально разрушительные последствия и гарантирует, что уравнения теории струн остаются непротиворечивыми — никаких ошибок типа «1 разделить на 0», — даже когда отказывают уравнения общей теории относительности.
За прошедшие годы исследователи показали, что множество других, более сложных сингулярностей (с названиями конифолд, ориентифолд, энханкон и так далее) также полностью контролируются теорией струн. Таким образом, имеется растущий список ситуаций, в которых Эйнштейн, Бор, Гейзенберг, Уилер и Фейнман воскликнули бы: «Мы просто не понимаем, что происходит!», но теория струн даёт полный и непротиворечивый ответ.
Достигнут значительный прогресс. Но остаётся проблема устранения с помощью теории струн сингулярностей чёрных дыр и Большого взрыва, более суровых, чем рассмотренные ранее. Идя к этой цели, теоретики приложили немало усилий, и они добились значительных успехов. Но если подытожить, то впереди ещё долгий путь, прежде чем наиболее трудные и важные сингулярности будут полностью осознаны.
Тем не менее одно важное открытие пролило свет на теорию чёрных дыр. В 1970-х годах в работах Якоба Бекенштейна и Стивена Хокинга было установлено, что чёрные дыры обладают определённой степенью беспорядка, известной как энтропия (см. главу 9). Подобно тому как беспорядок, царящий в ящике для носков, отражает множество способов их случайного расположения, так и беспорядок внутри чёрной дыры, согласно фундаментальным физическим законам, свидетельствует о множестве вариантов случайного размещения её внутренностей. Однако даже после долгих усилий физикам не удалось достаточно хорошо разобраться в том, как устроены внутренности чёрных дыр, не говоря уж о том, чтобы проанализировать возможные способы их размещения. Струнные теоретики Эндрю Строминджер и Кумрун Вафа вырвались из этого тупика. Смешав фундаментальные ингредиенты теории струн (с некоторыми из них мы встретимся в главе 5), они построили математическую модель беспорядка чёрной дыры, достаточно простую и понятную, чтобы извлечь из неё численное значение энтропии. Полученный результат в точности совпал с ответом Бекенштейна и Хокинга. Хотя осталось много открытых вопросов (например, точная идентификация составляющих чёрной дыры), эта работа стала первым надёжным квантово-механическим анализом беспорядка чёрной дыры.[26]
Замечательный прогресс в изучении сингулярности чёрной дыры и её энтропии привёл физическую общественность к обоснованной убеждённости, что со временем оставшиеся трудности, связанные с чёрными дырами и Большим взрывом, будут преодолены.
Теория струн и математика
Сравнение с экспериментальными или наблюдательными данными является единственным способом определить, правильно ли теория струн описывает природу. Но эта цель оказалась труднодостижимой. Несмотря на все успехи теории струн, она остаётся исключительно математической конструкцией. Но было бы неправильным считать теорию струн простым потребителем математических идей. Наоборот, некоторые важные струнные достижения являются вкладом в развитие математики.
Как известно, работая над созданием общей теории относительности, Эйнштейн перерыл всю математическую литературу, пытаясь найти строгий язык описания искривлённых пространств. Более ранние математические достижения таких математиков, как Карл Фридрих Гаусс, Бернхард Риман и Николай Лобачевский, подвели под общую теорию относительности крепкий фундамент. В некотором смысле, сейчас теория струн помогает выплатить интеллектуальный долг Эйнштейна, подталкивая развитие новых математических направлений. Тому есть много примеров, но я приведу лишь один, который целиком отражает суть струнных открытий в математике.
В общей теории относительности выстроена прочная связь между геометрией пространства-времени и наблюдаемой физикой. Уравнения Эйнштейна, дополненные распределением материи и энергии в некоторой заданной области, определяют конечную форму пространства-времени. Различные физические условия (то есть различные конфигурации масс и энергии) приводят к различной форме пространства-времени; разные виды пространства-времени соответствуют физически различным условиям. Хотите узнать, каково это — падать в чёрную дыру? Проведите вычисления на основе пространственно-временной геометрии, открытой Карлом Шварцшильдом при изучении сферических решений уравнений Эйнштейна. А что если чёрная дыра быстро вращается? Тогда вычисляйте с помощью геометрии, открытой в 1963 году новозеландским математиком Роем Керром. Геометрия и физика в общей теории относительности подобны инь и ян.
Теория струн резко меняет подобное заключение, утверждая, что могут быть различные формы пространства-времени, приводящие, тем не менее, к физически неотличимым описаниям реальности.
Это можно осмыслить следующим образом. Начиная с античных времён и до эры современной математики, геометрические пространства рассматриваются как набор точек. Например, мячик для пинг-понга состоит из точек, составляющих его поверхность. До теории струн базовые конституэнты вещества также считались точками, точечными частицами, и такая общность основных ингредиентов говорила о согласованности между геометрией и физикой. Однако в теории струн основным объектом является не точка. Это струна. Отсюда следует, что с теорией струн должен быть связан новый тип геометрии, основанный не на точках, а на петлях. Эта новая геометрия получила название струнной геометрии.
Чтобы ощутить струнную геометрию, вообразите струну, которая движется в геометрическом пространстве. Заметим, что зачастую струна может вести себя как точечная частица, невинно скользя туда-сюда, сталкиваясь со стенками, взбираясь на горки и опускаясь в долины, и так далее. Но в определённых ситуациях струна способна на нечто новое. Представьте, что пространство (либо его часть) имеет форму цилиндра. Струна может навиться вокруг него, подобно резиновому колечку, натянутому на банку с газировкой, — такая конфигурация в принципе невозможна для точечной частицы. Такие «намотанные» струны и их «ненамотанные» коллеги прощупывают геометрическое пространство разными способами. Если цилиндр станет толще, то намотанная на него струна ответит растяжением, а ненамотанная струна, скользящая по его поверхности, ничего не заметит. Следовательно, намотанные и ненамотанные струны по-разному чувствуют проявления формы пространства, в котором они движутся.
Это наблюдение крайне интересно, потому что приводит к поразительному и совершенно неожиданному выводу. Струнные теоретики обнаружили специальные пары геометрических форм пространства, проявляющие совершенно разные свойства, когда их прощупывают с помощью ненамотанных струн. Они также проявляют совершенно разные свойства при их тестировании намотанными струнами. При этом — тут наступает кульминационный момент — при тестировании струнами обоих типов, намотанными и ненамотанными, эти пространства становятся неразличимы. То, что намотанные струны видят в одном пространстве, ненамотанные видят в другом, и наоборот, что приводит к одинаковой коллективной картине, составленной на основе полной физики теории струн.
Такие парные формы являются мощным математическим инструментом. Если в общей теории относительности вы интересуетесь тем или иным свойством, то следует выполнить математические расчёты, привлекая то единственное геометрическое пространство, возникающего в изучаемой системе. Но в теории струн существование пар физически эквивалентных геометрических форм означает, что у вас появился выбор: проводить вычисления можно с помощью любой формы. Совсем удивительно, что при гарантированно одинаковых ответах для любой формы математические выкладки по пути к ответу могут быть совершенно разными. Во многих ситуациях крайне трудные математические вычисления для одной геометрической формы становятся более чем простыми для другой. При этом понятно, что любой математический аппарат, позволяющий упростить сложные математические расчёты, имеет огромную ценность.
В течение многих лет физики и математики достаточно продуктивно пользовались этим словариком по переводу сложного в простое для продвижения вперёд в решении ряда важных математических проблем. Одна такая задача, которую я особенно люблю, посвящена подсчёту числа сфер, которые можно упаковать (некоторым специальным математическим способом) в заданное пространство Калаби — Яу. В течение долгого времени математики интересовались этим вопросом, но вычисления во всех случаях, кроме простейших, были непреодолимыми. Возьмите пространство Калаби — Яу, показанное на рис. 4.6. Если упаковывать сферу в это пространство, она может много раз намотаться на часть пространства Калаби — Яу, подобно тому как лассо может много раз намотаться на пивную бочку. Итак, сколько существует способов упаковать сферу в данное пространство, если сфера наматывается, скажем, пять раз? Услышав такой вопрос, математик должен кашлянуть, бросить мельком взгляд на свои ботинки и быстро удалиться, сославшись на неотложную встречу. Теория струн сгладила остроту вопроса. Переводя вычисления со сложного на простое пространство из пары Калаби — Яу, струнные теоретики получили ответы, которые огорошили математиков. Каково число пятикратно намотанных сфер, упакованных в пространство Калаби — Яу на рис. 4.6? 229 305 888 887 625. А если сфера намотана десять раз? 704 288 164 978 454 686 113 488 249 750. Двадцать раз? 53 126 882 649 923 577 113 917 814 483 472 714 066 922 267 923 866 451 936 000 000. Эти числа стали предвестниками целого спектра результатов, открывших новую главу в математике.{35}
Итак, независимо от того, правильно теория струн описывает физическую Вселенную или нет, она уже проявила себя в качестве мощного инструмента исследований вселенной математической.
Современный статус теории струн
Информация из предыдущих четырёх глав собрана в табл. 4.2, которая является своеобразным отчётом о состоянии теории струн. Также она включает некоторые дополнительные данные, на которых я подробно не останавливался. Эта картина описывает теорию в её развитии, которая уже добилась ошеломляющих результатов, но до сих пор лишена самого важного: экспериментального подтверждения. Она так и будет оставаться умозрительной до тех пор, пока не будет установлена убедительная связь с экспериментом или наблюдениями. Поиск такой связи является важнейшей задачей. Однако заметим, что такая ситуация характерна не только для теории струн. Любая попытка объединить гравитацию и квантовую механику выводит в область, находящуюся далеко за пределами современных возможностей экспериментальных исследований. Это неизбежно, когда ставятся такие в высшей степени амбициозные цели. Расширение границ фундаментальных знаний в поиске ответов на самые глубокие вопросы, занимающие умы человечества последние несколько тысячелетий, является выдающимся проектом, который вряд ли удастся быстро осилить. Скорее всего, не хватит даже десятилетий.
Таблица 4.2. Краткий отчёт о состоянии теории струн
Цель Цель необходима? Статус Объединение гравитации и квантовой механики ДА. Основная цель состоит в объединении общей теории относительности и квантовой механики. ОТЛИЧНО. Многочисленные вычисления и идеи подтверждают успешное объединение общей теории относительности и квантовой механики.[27] Объединение всех сил НЕТ. Объединение гравитации и квантовой механики не требует дальнейшего объединения с другими силами в природе. ОТЛИЧНО. Хоть такой необходимости нет, полная единая теория в течение долгого времени была целью физических исследований. Теория струн достигает этой цели, описывая все силы единым образом — их кванты являются проявлением определённых типов вибраций струн. Учёт ключевых достижений предыдущих теорий НЕТ. В принципе, новая успешная теория не обязана быть похожей на успешные теории прошлого. ОТЛИЧНО. Хотя прогресс не обязательно должен быть поступательным, история говорит, что обычно это именно так: как правило, старые успешные теории вытекают в предельном случае из новых успешных теорий. Теория струн включает ключевые достижения предыдущих физических теорий. Объяснение свойств частиц НЕТ. Достойная цель, достижение которой объяснит многое — но этого не требуется от успешной теории квантовой гравитации. НЕОПРЕДЕЛЁН; НЕТ ПРЕДСКАЗАНИЙ. Теория струн превосходит в этом смысле квантовую теорию поля и предлагает способ объяснения свойств частиц. Однако пока этот потенциал остаётся нераскрытым: разнообразие возможных различных форм дополнительных измерений означает разнообразие возможных наборов свойств частиц. Пока нет способа выделить из множества форм какую-то одну. Экспериментальное подтверждение теории ДА. Это единственный способ определить, правильно ли теория описывает природу. НЕОПРЕДЕЛЁН; НЕТ ПРЕДСКАЗАНИЙ. Наиболее важный критерий; на данный момент теория струн не прошла подобную проверку. Оптимисты надеются, что эксперименты на Большом адронном коллайдере и наблюдения на спутниковых телескопах смогут приблизить теорию струн к экспериментальной проверке. Но нет никакой гарантии, что современные технологии достаточно мощны для достижения этой цели. Устранение сингулярностей ДА. Квантовая теория гравитации должна уметь осмысленно описывать сингулярности, возникающие в ситуациях, которые могут хотя бы в принципе реализоваться физически. ОТЛИЧНО. Огромный прогресс; были устранены многие типы сингулярностей. Но сингулярности типа чёрных дыр и Большого взрыва ещё не поддаются теории струн. Объяснение энтропии чёрных дыр ДА. Именно в вопросе об энтропии чёрных дыр общая теория относительности и квантовая механика стыкуются ключевым образом. ОТЛИЧНО. Теория струн явным образом вычислила и подтвердила формулу для энтропии, предложенную в 1970-х годах. Вклад в математику НЕТ. Теории, правильно описывающие природу, не обязаны приводить к математическим открытиям. ОТЛИЧНО. Хотя математические открытия не являются необходимыми для подтверждения теории струн, её развитие привело к значительным достижениям, что продемонстрировало мощь математического фундамента теории.Оценивая текущей статус теории струн, многие струнные теоретики считают, что следующий важный шаг состоит в том, чтобы придать уравнениям теории наиболее полный и точный вид. Большая часть исследований на протяжении первых двух десятилетий развития теории до середины 1990-х годов была выполнена с помощью приближённых уравнений, ибо многие полагали, что так можно выявить общие свойства теории. Однако приближённые уравнения оказались слишком грубы, чтобы дать точные предсказания. Последние открытия, к которым мы сейчас перейдём, вывели понимание на уровень, намного превосходящий тот, что был достигнут приближёнными методами. Хотя определённые предсказания сделать сложно, открылись новые перспективы. Они опираются на достижения в области удивительных возможных приложений теории, к которым относятся и новые типы параллельных миров.
Глава 5. Вселенные по соседству в других измерениях Брана и циклические мультивселенные
Однажды, много лет назад я сидел поздно вечером в своём офисе в Корнелльском университете, придумывая на утро экзаменационные задачи для первокурсников. Это была группа отличников, и я решил разнообразить экзамен, добавив в список задач одну посложнее. Однако было поздно, я проголодался, поэтому вместо того чтобы аккуратно подобрать сложную задачку, я взял стандартную, с которой большинство из них уже встречались, быстро изменил некоторые условия, внёс её в экзаменационные билеты и направился домой. (Опуская подробности, в задаче рассматривалось движение лестницы, прислонённой к стене, которая скользит, а потом теряет опору и падает. Я изменил стандартные условия, добавив, что плотность лестницы изменяется по длине.) На следующее утро, во время экзамена, я стал решать задачи и обнаружил, что это скромное изменение условий сделало простую задачу трудно решаемой. Решение исходной задачи вполне уместилось бы на полстраницы. А решение этой заняло все шесть. У меня крупный почерк. Но смысл вам ясен.
Этот небольшой эпизод отражает правило, нежели исключение. Задачи из учебников подобраны очень специально, чтобы их можно было полностью решить разумными усилиями за разумное время. Однако чуть-чуть измените условия, и они быстро станут либо очень сложными, либо вообще не решаемыми. Иными словами, задачи из учебника быстро становятся такими же сложными, как задачи описания реального мира.
Но факт остаётся фактом: подавляющее большинство явлений, от движения планет до взаимодействия частиц, слишком сложно для точного математического описания. Физик-теоретик должен понять, какими усложнениями в данном контексте можно пренебречь, создав при этом доступную математическую модель явления, в которой учтены все существенные детали. Рассчитывая орбиту Земли, следует учитывать только притяжение Солнца; конечно, лучше учесть ещё и притяжение Луны, но тогда математическая сложность резко возрастает. (В XIX столетии французский математик Шарль-Эжен Делоне опубликовал 900-страничную книгу, в которой подробно рассматривался гравитационный танец Солнца, Земли и Луны.) Если попытаться продвинуться дальше и полностью учесть влияние движения остальных планет, то анализ становится необозримым. К счастью, во многих приложениях можно спокойно пренебрегать всем кроме влияния Солнца, так как эффект от воздействия других тел в Солнечной системе на орбиту Земли весьма незначителен. Подобные приближения лишь подтверждают высказывание, что искусство физики лежит в умении отмести несущественное.
Физикам, много работающим с вычислениями, хорошо известно, что приближения — это не только мощный способ достижения прогресса, в них таится и определённая опасность. Минимальные усложнения при ответе на один вопрос неожиданно могут привести к весьма существенным последствиям при ответе на другой. Одна дождевая капля вряд ли сможет повлиять на вес валуна. Но если этот валун еле держится на самом краю отвесного склона, то вполне вероятно, что дождевая капля приведёт к его скатыванию, что послужит толчком для схода лавины. Приближение, не учитывающее эту дождевую каплю, приведёт к потере существенного эффекта.
В середине 1990-х годов струнные теоретики натолкнулись на подобную дождевую каплю. Они обнаружили, что различные математические приближения, широко используемые в анализе теории струн, упускают из виду некоторое важное физическое явление. Развив и применив более точные математические методы, струнные теоретики наконец-то смогли выйти за рамки этих приближений; когда это произошло, в центр внимания попали неожиданные свойства теории. Среди них оказались новые типы параллельных вселенных; кажется, что у одного из них довольно высокие шансы быть обнаруженным экспериментально.
Выход за рамки приближений
Каждая из ведущих дисциплин теоретической физики — таких как классическая механика, электромагнетизм, квантовая механика и общая теория относительности — определена некоторым основным уравнением или набором уравнений. (Для нас не важен вид этих уравнений, однако некоторые из них я привёл в примечаниях в конце книги.){36} Проблема в том, что кроме простейших случаев эти уравнения крайне сложно решить. Поэтому физики, следуя заведённому обычаю, пользуются упрощениями — например, не учитывают притяжение Плутона или считают Солнце шаром, — это упрощает вычисления и вселяет надежду получить приближённое решение основного уравнения.
Довольно долго исследования в теории струн сталкивались с ещё бо́льшими трудностями. Даже нахождение основного уравнения оказалось настолько трудным, что физики смогли написать его лишь приближённо. Даже приближённые уравнения были столь сложными, что для нахождения решений пришлось пользоваться упрощающими приближениями, что стало приближённым исследованием приближений. Однако в течение 1990-х годов ситуация кардинальным образом улучшилась. Достижения струнных теоретиков показали, как выйти за рамки использования приближений.
Чтобы понять суть этих открытий, представьте, что некий азартный парень Ральф решил поучаствовать в двух последовательных раундах еженедельной всемирной лотереи, и для этого он с гордостью подсчитал шансы на выигрыш. Он сообщил своей подруге Элис, что если в каждом раунде у него есть один шанс на миллиард, то за два раунда его шанс возрастёт до двух на миллиард, 0,000000002. Элис усмехнулась: «Ну, что-то типа того». «Что значит типа того? — обиделся Ральф, — это именно так!» «Ну, — сказала она, — ты переоцениваешь. Если ты выиграешь первый раунд, то участие во втором раунде твои шансы не поднимет, ведь ты уже выиграл. Если же ты выиграешь два раза подряд, то денег у тебя, конечно, прибавится, но поскольку тебя интересует шанс выиграть сам по себе, то выигрыш во втором раунде после выигрыша в первом уже не будет иметь значения. Поэтому чтобы получить точный ответ, надо вычесть шанс выиграть в обоих раундах, а это 1 на миллиард умножить на 1 на миллиард, или 0,000000000000000001. В итоге получится 0,000000001999999999. Вопросы есть, Ральф?»
Если не отвлекаться на самоуверенность Элис, то её метод демонстрирует то, что физики называют теорией возмущений. В вычислениях, как правило, легче осуществить первый шаг, который содержит только самые очевидные вклады — отправная точка рассуждений Ральфа — затем делается второй шаг, включающий более тонкие детали, изменяя, или «возмущая» ответ на первом шаге, как в рассуждениях Элис. Этот подход может быть легко обобщён. Если бы Ральф решил поиграть в следующие десять еженедельных лотерей, то его шанс на выигрыш на первом шаге составил бы примерно 10 на миллиард, 0,00000001. Но так же как в предыдущем примере, это приближение не может правильно описать многократные выигрыши. Второй шаг Элис правильно описывает случаи, когда Ральф выигрывает два раза подряд — скажем, в первом и втором раундах, или во втором и третьем, или третьем и четвёртом. Эти поправки, как ранее указала Элис, пропорциональны 1 на миллиард умножить на 1 на миллиард. Есть ещё более крошечный шанс, что Ральф выиграет три раза подряд; на третьем шаге возникающая поправка пропорциональна 1 на миллиард, троекратно умноженной на себя, то есть 0,000000000000000000000000001. На четвёртом шаге происходит то же самое, но шанс выиграть подряд четыре раунда становится ещё меньше, и так далее. Каждый новый вклад меньше предыдущего, поэтому в определённый момент Элис сочтёт ответ достаточно точным и на этом остановится.
Вычисления в физике, а также во многих других областях науки, часто происходят аналогичным образом. Если вас интересует вероятность того, что две частицы, летящие навстречу друг другу в Большом адронном коллайдере, столкнутся друг с другом, то на первом шаге представьте, что они сталкиваются и отлетают друг от друга рикошетом (слово «сталкиваются» не означает, что они напрямую соприкасаются, наоборот, это означает, что единственная «пуля»-переносчик взаимодействия, такая как фотон, вылетает из одной частицы и поглощается другой частицей). На втором шаге учитывается возможность того, что эти частицы столкнутся дважды (между ними выстрелят два фотона); на третьем шаге возникающая поправка даёт вклад в предыдущие два и учитывает возможность трёхкратного столкновения частиц; и так далее (рис. 5.1). Как и в лотерее, теория возмущений работает хорошо, если вероятность взаимодействий частиц возрастающей кратности — подобно шансу выигрыша в каждом последующем раунде лотереи — резко падает.
Рис. 5.1. Две частицы (изображённые двумя сплошными линиями слева на каждой диаграмме) взаимодействуют, выстреливая друг в друга разными «пулями» («пули» — это такие частицы-переносчики взаимодействия, изображённые волнистыми линиями), после чего рикошетят вперёд (две сплошные линии справа). Каждая диаграмма даёт вклад в общую вероятность столкновения частиц друг с другом. Вклады с бо́льшим числом пуль становятся всё меньше
В лотерее спад определяется каждым следующим выигрышем, умноженным на фактор один на миллиард; в физическом примере он определяется каждым следующим столкновением с численным множителем, который называется константой связи, значение которой отражает вероятность того, что одна частица испустит «пулю»-переносчика взаимодействия, а вторая частица поглотит её. Для частиц, участвующих в электромагнитных взаимодействиях, например электронов, экспериментально измерено, что константа связи фотонных пуль равна примерно 0,0073.{37} Для нейтрино, участвующих в слабом взаимодействии, константа связи равна примерно 10−6. Для кварков, из которых состоят протоны, которые мчатся в Большом адронном коллайдере и участвуют в сильном ядерном взаимодействии, константа связи равна примерно 1. Эти числа не так малы, как число 0,000000001 из лотереи, но если многократно умножать 0,0073 на себя, то результат быстро станет исчезающее мал. После одной итерации это примерно 0,0000533, после второй итерации это примерно 0,000000389. Поэтому у теоретиков редко возникают проблемы при подсчёте числа многократных столкновений электронов. Вычисления с многократными столкновениями крайне сложны, а конечный ответ настолько мал, что можно остановиться на нескольких испущенных фотонах и всё равно получить очень точный ответ.
Даже не сомневайтесь, физики очень хотят иметь точные результаты. Однако большинство вычислений слишком сложны, поэтому теория возмущений — это лучший инструмент из тех, что у нас есть. К счастью, при достаточно малых константах связи приближённые вычисления могут приводить к предсказаниям, которые хорошо согласуются с экспериментом.
Похожий способ вычислений по теории возмущений долгое время являлся основой струнных исследований. В теории струн имеется некоторое число, которое называется струнной константой связи (струнная константа, для краткости), определяющая вероятность столкновения двух струн. Если теория окажется правильной, то однажды струнная константа может быть измерена, подобно перечисленным выше константам связи. Но так как такие измерения в настоящий момент совершенно гипотетичны, величина струнной константы остаётся абсолютно неизвестной. В течение последних нескольких десятилетий, не имея каких-либо указаний из эксперимента, струнные теоретики сделали ключевое допущение, что струнная константа мала. До некоторой степени это похоже на поиск потерянных ключей под фонарём, потому что малая струнная константа позволяет физикам с помощью теории возмущений пролить яркий свет на вычисления. Поскольку до теории струн в большинстве успешных теорий константа связи была действительно мала, то продолжая аналогию с фонарём, можно сказать, что ключи часто лежали именно там, где светло. Так или иначе, допущение малости константы связи позволило провести огромное количество математических вычислений, которые не только прояснили базовые процессы взаимодействия струн, но также дали много информации о фундаментальных уравнениях теории.
Если струнная константа действительно мала, то приближённые вычисления достаточно точно отразят физическую суть теории струн. Но что, если она не мала? В отличие от лотереи и сталкивающихся электронов, большая струнная константа означает, что последовательные уточнения к приближению на первом шаге приведут к растущим вкладам, поэтому не будет никаких оснований прекратить вычисления на определённом этапе. Тысячи вычислений, проделанных на основе теории возмущений, станут бессмысленными; годы исследований окажутся потраченными зря. Вдобавок, даже с умеренно малой константой связи всё равно надо заботиться о правомерности сделанных приближений, по крайней мере при определённых условиях, дабы не пропустить тонких, но важных физических эффектов, как с каплей дождя, падающей на валун.
В начале 1990-х мало что можно было ответить на эти неудобные вопросы. Но ко второй половине десятилетия молчание сменилось шумным восторгом открытий. Учёные обнаружили новые математические методы, способные перехитрить приближения по теории возмущений, призвав на помощь то, что получило название дуальность.
Дуальность
В 1980-х годах теоретики осознали, что есть не одна теория струн, а пять разных её вариантов с заковыристыми именами тип I, тип IIA, тип IIB, O-гетеротическая, E-гетеротическая. Я не упоминал об этом усложнении до сих пор, потому что все пять теорий, несмотря на различия в технических деталях, имеют одинаковые общие свойства — вибрирующие струны и дополнительные пространственные измерения, — которые были нами рассмотрены. Однако мы дошли до того момента, когда все пять вариантов теории струн выходят на передний план.
В течение многих лет физики использовали методы теории возмущений для анализа каждой из пяти теорий струн. При изучении теории струн типа I считалось, что её константа связи мала, поэтому физики пользовались многошаговой процедурой, похожей на анализ лотереи Ральфом и Элис. Такая же процедура использовалась при изучении O-гетеротической теории или любой другой теории струн. Однако за пределами ограниченной области малых струнных констант учёные лишь пожимали плечами, полагая, что используемый ими математический аппарат недостаточно силён для получения надёжных результатов.
Так было до весны 1995 года, когда Эдвард Виттен потряс струнное сообщество серией изумительных результатов. Опираясь на результаты таких учёных, как Джо Польчински, Майкл Дафф, Поль Таунсенд, Крис Халл, Джон Шварц, Ашок Сен и многих других, Виттен привёл убедительное доказательство того, что теперь струнные теоретики могут свободно выйти за рамки малых констант связи. Ключевая идея была простая и сильная. Виттен доказал, что при увеличении константы связи в одной из формулировок теории струн, теория замечательным образом постепенно трансформируется в нечто хорошо узнаваемое: в другую формулировку теории струн, в которой константа связи уменьшается. Например, когда константа связи в теории типа I велика, она переходит в O-гетеротическую теорию струн с малой константой связи. Это означает, что пять теорий струн не такие уж и разные. При ограниченном рассмотрении — при малых константах связи — каждая из них отличается от остальных, но при снятии этого ограничения каждая из теорий струн переходит в другие.
Недавно я натолкнулся на замечательную картинку, на которой при близком рассмотрении можно разглядеть Альберта Эйнштейна; отодвинув картинку чуть дальше ничего определённого не видно; а при взгляде издалека возникает изображение Мэрилин Монро (рис. 5.2). Если вы смотрите на изображения, проявляющиеся только в крайних фокусах, есть все основания считать, что это две разные картинки. Но анализируя картинку на промежуточных расстояниях, вы неожиданно обнаруживаете, что портреты Эйнштейна и Монро являются частью единого изображения. Точно так же рассмотрение двух теорий струн в крайнем положении, когда струнная константа каждой мала, приводит к заключению, что они столь же разные как Альберт и Мэрилин. Остановившись на этом, как в течение многих лет делали струнные теоретики, можно прийти к выводу, что изучаются две разные теории. Но если рассматривать теории при промежуточных значениях констант связи, то обнаружится, что подобно Эйнштейну, превращающемуся в Монро, одна теория постепенно переходит в другую.
Рис. 5.2. Если смотреть с близкого расстояния, на картинке виден Альберт Эйнштейн. Если смотреть издалека, появляется Мэрилин Монро. (Автор изображения Од Олива из Массачусетского технологического института)
Превращение Эйнштейна в Монро — не более чем курьёз. Переход от одной теории струн к другой теории струн — это уже настоящая трансформация. Она означает, что если нельзя провести вычисления в одной теории струн по теории возмущений, потому что её константа связи слишком велика, то эти вычисления могут быть легко проделаны на языке другой формулировки теории струн, где применима теория возмущений в силу малости константы связи. Такой переход между кажущимися разными теориями называется в физике дуальностью. Она стала одной из самых распространённых тематик в современных исследованиях по теории струн. Описывая одну и ту же физическую ситуацию двумя разными математическими способами, дуальность удваивает наш вычислительный арсенал. Безнадёжно трудные вычисления с одной стороны становятся вполне осуществимыми с другой стороны.[28]
Разобравшись в деталях, Виттен и другие исследователи показали, что все пять теорий струн связаны друг с другом целой сетью таких дуальностей.{38} В сплетении теорий и дуальностей, названном M-теорией (скоро увидим, почему), объединяются успехи всех пяти формулировок, сшитых вместе посредством дуальных взаимосвязей, что приводит к более глубокому пониманию каждой из них. Одним из открытий, особенно важным для наших целей, оказалось то, что в теории струн есть не только струны.
Браны
Начиная изучать теорию струн, я задавался тем же самым вопросом, который спустя много лет стали задавать мне самому: почему струны такие особенные? Почему надо рассматривать фундаментальные объекты, у которых есть только длина? В конце концов, теория сама требует, чтобы арена, где играют её актёры — пространственная Вселенная, — имела девять измерений, так почему не рассматривать объекты, имеющие форму двумерных листов или трёхмерных шариков, или их многомерные аналоги? Ответ на эти вопросы я узнал, когда был студентом в 1980-х. Потом мне часто приходилось объяснять его в своих лекциях в середине 1990-х годов. Ответ состоит в том, что математика, описывающая фундаментальные составляющие с более чем одним пространственным измерением, приводит к неустранимым противоречиям (таким как квантовые процессы с отрицательными вероятностями, а это математически бессмысленный результат). Но когда эти математические рассуждения проводятся для струн, все противоречия компенсируют друг друга и возникает самосогласованное описание.[29]{39} Струны, определённо, чем-то выделены.
По крайней мере так казалось.
Вооружившись новыми вычислительными методами, физики стали анализировать уравнения теории струн более аккуратно и получили ряд неожиданных результатов. Один из самых удивительных результатов состоял в том, что причина, по которой струны казались выделенными, довольно шаткая. Теоретики догадались, что математические проблемы, возникающие при изучении многомерных ингредиентов, подобных диску или шарику, были всего лишь последствиями использования приближённых методов. Вооружившись более точными методами, небольшая группа теоретиков выяснила, что под математическим покровом теории струн действительно скрываются структуры с разным числом пространственных измерений.{40} Техника теории возмущений слишком груба, чтобы обнаружить эти ингредиенты, но новые методы смогли это сделать. К концу 1990-х годов стало совершенно очевидно, что теория струн это не просто теория, описывающая струны.
Были обнаружены объекты, по форме похожие на летающую тарелку или ковёр-самолёт, с двумя пространственными измерениями: мембраны (одно из значений буквы M в M-теории), которые также называют два-бранами. Но это ещё не всё. Также были обнаружены объекты с тремя пространственными измерениями, так называемые три-браны; объекты с четырьмя пространственными измерениями — четыре-браны, и так далее вплоть до девять-бран. Математически было установлено, что все эти структуры, подобно струнам, могут вибрировать и извиваться; поэтому в этом контексте струну лучше всего рассматривать как один-брану — лишь одну из многих сущностей в неожиданно длинном списке фундаментальных кирпичиков теории струн.
С этим связано открытие, поразившее всех, кто провёл лучшие годы своей профессиональной жизни, занимаясь теорией струн. Оказалось, что количество пространственных измерений на самом деле вовсе не девять. Оно равно десяти. И если добавить временно́е измерение, получится точно одиннадцать пространственно-временных измерений. Как такое может быть? Мы же помним, как говорили «(D − 10) умножить на проблему» в главе 4, откуда был сделан вывод о необходимых десяти пространственно-временных измерениях теории струн. Однако, опять-таки, математические выкладки, приведшие к этому уравнению, были основаны на теории возмущений с малой струнной константой. А это приближение (сюрприз!) не учитывало одно измерение. Как показал Виттен, причина состояла в том, что величина струнной константы напрямую контролирует размер десятого пространственного измерения. Полагая константу связи малой, исследователи невольно делали малым и это пространственное измерение, слишком малым — настолько, что оно стало невидимым для самой математической структуры теории. Более точные методы исправили это упущение, что привело к появлению M-теоретико-струнной вселенной с десятью пространственными измерениями и одним временны́м, что в совокупности составляет одиннадцать пространственно-временных измерений.
Я хорошо помню наивно-изумлённые взгляды участников международной струнной конференции, проводимой в университете Южной Калифорнии в 1995 году, на которой Виттен впервые анонсировал часть результатов, совокупность которых теперь называется второй струнной революцией.[30] Именно браны выступают на авансцену в истории с мультивселенными. Благодаря им исследователи обнаружили ещё одно множество параллельных вселенных.
Браны и параллельные миры
Как правило, принято считать, что струны очень малы и именно это свойство становится большим препятствием для проверки теории. Однако в главе 4 было замечено, что струны не обязательно малы. Длина струны определяется её энергией. Энергии, сопоставляемые массам электронов, кварков, и других известных частиц настолько малы, что соответствующие струны имеют действительно крошечный размер. Но если в струну впрыснуть достаточно энергии, то можно очень сильно её растянуть. В земных условиях нет никаких возможностей осуществить подобное, но в принципе это не более чем технологическое ограничение. Если теория струн верна, технологически развитая цивилизация сможет растянуть струну настолько сильно, насколько она пожелает. Длинные струны могут возникать в природных космологических явлениях; например, струны могут намотаться на часть пространства, а потом сильно растянуться в процессе космологического расширения. Одна из возможных экспериментальных проверок (табл. 4.1) состоит в поиске гравитационных волн, испущенных длинными струнами, которые вибрируют в глубине космоса.
Подобно струнам, многомерные браны также могут быть большими. Отсюда возникает совершенно новый способ описания космоса в рамках теории струн. Чтобы понять, что я имею в виду, нарисуем сначала длинную струну, такую же длинную как электрические провода, тянущиеся за горизонт. Затем нарисуем большую два-брану, похожую на огромную скатерть или гигантский флаг с безграничной поверхностью. Такой рисунок легко себе представить, так как он вписывается в рамки привычных трёх измерений.
Если три-брана очень велика, возможно даже бесконечно большая, ситуация меняется. Три-брана такого типа полностью заполнит пространство, в котором мы живём, подобно воде, заполняющей аквариум. Такая вездесущность предполагает, что вместо того, чтобы считать три-брану объектом, расположенным в обычных трёх измерениях, следует рассматривать её как основу самого пространства. Подобно рыбам в воде, мы живём в заполняющей собой всё пространство три-бране. Пространство, по крайней мере то пространство, в котором мы непосредственно живём, может оказаться гораздо более осязаемым, нежели принято представлять. Пространство предстанет как вещь, объект, сущность — три-брана. Когда мы бежим или идём, живём и дышим, мы движемся внутри три-браны. Струнные теоретики называют это сценарием мира на бране.
Именно в этот момент в теории струн возникают параллельные вселенные.
Я сосредоточился на взаимосвязи между три-бранами и тремя пространственными измерениями, потому что хотел провести аналогию с повседневным опытом. Но в теории струн пространственных измерений больше трёх. В многомерном пространстве есть достаточно места для размещения не только одной три-браны. Допустим для начала, что имеются две огромные три-браны. Возможно, вам это нелегко представить. Мне, по крайней мере, — непросто. В процессе эволюции мы научились распознавать объекты, сулящие удачу или несущие опасность, которые находятся непосредственно внутри трёхмерного пространства. Следовательно, хотя мы можем легко нарисовать два любых трёхмерных объекта, расположенных в некоторой области пространства, мало кто сможет вообразить сосуществующие, но отделённые друг от друга трёхмерные сущности, каждая из которых полностью заполняет собой трёхмерное пространство. Поэтому для наглядности обсуждения сценария мира на бране давайте откажемся от одного пространственного измерения и будем представлять жизнь на гигантской два-бране. Для определённости будем думать о два-бране как о гигантском, сверхтонком ломтике хлеба.[31]
Чтобы в полной мере воспользоваться этой метафорой, представим, что на ломтике хлеба присутствует всё, что мы привыкли называть Вселенной — туманность Ориона, Конская голова, Крабовидная туманность; весь Млечный Путь; другие галактики — Андромеда, Сомбреро, Водоворот; и так далее — всё, что есть внутри нашего трёхмерного пространства, сколь угодно далеко друг от друга (рис. 5.3а). Чтобы представить вторую три-брану, нужно нарисовать ещё один огромный ломтик. Где именно? Расположите его рядом с нашим ломтиком, только чуть сдвиньте его в сторону в направлении дополнительных измерений (рис. 5.3б). Столь же легко представить три или четыре, или большее число три-бран. Нужно лишь добавить ломтиков космического батона. Хотя аналогия с батоном хорошо описывает расположенные стопкой браны, легко представить более общие возможности. Браны могут иметь любую ориентацию, быть других размерностей, бо́льших или меньших, и все они могут быть рассмотрены аналогичным образом.
Рис. 5.3. а) В сценарии мира на бране традиционно понимаемый нами космос оказывается трёхмерной браной. Для простоты мы отбрасываем одно измерение и изображаем мир на бране с двумя пространственными измерениями; брана может тянуться бесконечно далеко, поэтому представлена лишь конечная её часть; б) Многомерное пространство теории струн вмещает в себя много параллельных миров на бране
Во всём наборе бран будут действовать одинаковые, фундаментальные физические законы, потому что все они возникают из одной M-теории/теории струн. Так же как в случае с дочерними вселенными в инфляционной мультивселенной, физические свойства браны могут существенно меняться в зависимости от дополнительных условий, таких как значения полей, пронизывающих брану, или число её пространственных измерений. Некоторые миры на бране могут оказаться очень похожими на наш мир, с галактиками, звёздами и планетами, а некоторые могут сильно отличаться. На одной или нескольких таких бранах могут проживать разумные существа, которые подобно нам однажды решат, что их ломтик — их часть пространства — является всем космосом. Теперь мы понимаем, что в рамках бранного сценария в теории струн такая точка зрения слишком узкая. В бранном сценарии наша Вселенная лишь одна из многих, населяющих бранную мультивселенную.
Как только идея бранной мультивселенной возникла в струнном сообществе, немедленно возник вопрос. Если гигантские браны существуют по соседству, целые параллельные вселенные висят где-то рядом подобно ржаным ломтикам, удобно расположившимся по соседству, то почему мы не видим их?
Цепкие браны и гравитационные щупальца
Струны бывают двух видов: в виде петель и отрезков нитей. До сих пор мы не делали различий, потому что это несущественно для понимания большинства общих свойств теории. Но для миров на бране это различие между петлями и отрезками нитей становится решающим, и следующий простой вопрос объясняет, почему. Могут ли струны улететь с браны? Ответ: петли могут, отрезки нитей нет.
Знаменитый струнный теоретик Джо Польчински впервые осознал, что всё определяется поведением концов струнной нити. Уравнения, убедившие физиков, что браны являются частью струнной теории, также показали, что между струнами и бранами есть особенно тесная связь. Брана — это единственное место для концов струнных отрезков (рис. 5.4). Математические выкладки показывают, что открепить концы струнных отрезков от поверхности браны попросту невозможно, это всё равно, что пытаться уменьшить число π или увеличить квадратный корень из 2. С физической точки зрения такая ситуация сродни попытке удалить северный или южный полюс магнита. Сделать такое просто невозможно. Струнные нити могут свободно двигаться внутри и сквозь брану, играючи скользя туда и сюда, но покинуть её они не могут.
Рис. 5.4. Браны — это единственное место, где могут быть расположены концы отрезков струнных нитей
Если это не просто интересная математика, и мы действительно живём на бране, то прямо сейчас вы ощущаете, как наша брана мёртвой хваткой держит концы струнных отрезков. Попробуйте спрыгнуть с нашей три-браны. Попытайтесь ещё, сильнее. Подозреваю, что вы никуда не исчезли. Струны в бранном мире, из которых состоите вы и вся остальная привычная материя, — это отрезки нитей. Покинуть брану нельзя, хотя можно прыгать вверх и вниз, кидать бейсбольный мяч и посылать звуковые волны, совершенно беспрепятственно со стороны браны. Если вы попробуете спрыгнуть, то концы ваших струнных отрезков наглухо притянут вас к бране. Наш мир — это такой дрейфующий плот в многомерном океане, но мы не можем его покинуть, не можем вырваться и исследовать космос за его пределами.
То же самое происходит с частицами-переносчиками трёх негравитационных взаимодействий. Можно показать, что они тоже составлены из струнных отрезков. Самые важные среди них фотоны — переносчики электромагнитного взаимодействия. Таким образом, видимый свет потоком фотонов может свободно распространяться внутри нашей браны от этого текста до ваших глаз или от галактики Андромеды до Вильсоновской обсерватории, но всё равно не сможет вырваться за её пределы. Вполне возможно, что другой мир на бране находится в нескольких миллиметрах от нас, но свет не может преодолеть этот промежуток, и поэтому мы никогда не получим ни малейшего намёка на его существование.
Единственное взаимодействие, которое отличается в этом отношении — это гравитация. В главе 4 мы отметили особое свойство гравитона — спин-2, превышающий в два раза спин частиц, составленных из струнных отрезков (как фотоны), являющихся переносчиками негравитационных взаимодействий. Тот факт, что спин гравитона в два раза превышает спин отдельного струнного отрезка, означает, что гравитон можно представить в виде двух таких отрезков, причём концы одного слипаются с концами другого и возникает петля. Поскольку у петель нет концов, они не могут быть захвачены бранами. Поэтому гравитоны могут покинуть одну брану и попасть на другую. Тогда в сценарии мира на бране только с помощью гравитации можно прощупать то, что находится за пределами нашего трёхмерного пространства.
Такая идея играет ключевую роль для некоторых возможных тестов теории струн (глава 4, табл. 4.1). В 1980–1990-х годах, до появления концепции бран, физики полагали, что дополнительные измерения в теории струн имеют приблизительно планковский размер (примерно 10−33 сантиметра), естественный масштаб для теории, описывающей гравитацию и квантовую механику. Но сценарий мира на бране заставляет нас думать шире. Поскольку лишь гравитация, слабейшее из всех взаимодействий, может вырваться за пределы привычного трёхмерного пространства, дополнительные измерения вполне могут иметь достаточно большой размер и всё равно оставаться невидимыми. По крайней мере пока.
Если дополнительные измерения существуют и их размер значительно больше, чем считалось прежде — возможно в миллиард миллиардов миллиардов раз больше (примерно 10−4 сантиметра), — есть шанс их обнаружить в экспериментах по измерению силы гравитации (табл. 4.1, вторая строка). Когда объекты испытывают взаимное гравитационное притяжение, они обмениваются потоками гравитонов; гравитоны — это невидимые переносчики гравитации. Чем больше гравитонов летает между объектами, тем сильнее взаимное гравитационное притяжение. Когда часть гравитонов утекает с поверхности нашей браны и попадает в дополнительные измерения, гравитационное притяжение между объектами ослабевает, оно оказывается разбавленным. Чем больше дополнительные измерения, тем сильнее разбавление, тем слабее притяжение. Экспериментаторы считают, что путём точного измерения гравитационного притяжения между двумя объектами, сближенными на расстояние меньшее чем размер дополнительных измерений, можно перехватить гравитоны прежде, чем они утекут с нашей браны; если это так, то экспериментально измеренная сила гравитации должна пропорционально возрастать. Таким образом, хотя эти рассуждения и не упоминались в главе 4, данный способ открытия дополнительных измерений основан на сценарии мира на бране.
Более скромное увеличение размера дополнительных измерений, примерно до 10−8 сантиметра, может потенциально привести к их обнаружению на Большом адронном коллайдере. Осколки столкновений протонов на высоких энергиях могут быть выброшены в дополнительные измерения, что приведёт к очевидной утечке энергии в нашем пространстве, которую можно обнаружить (табл. 4.1, третья строка). Такой эксперимент тоже основывается на сценарии мира на бране. Данные, свидетельствующие об утечке энергии, можно объяснить, если постулировать существование нашей Вселенной на бране и опираться на то, что осколки, способные вырваться с нашей браны — гравитоны, — уносят энергию с собой.
Образование чёрных мини-дыр — это ещё один побочный продукт сценария мира на бране (табл. 4.1, четвёртая строка). Вероятность возникновения чёрных мини-дыр в протон-протонных столкновениях на Большом адронном коллайдере существует только в случае, когда сила гравитационного притяжения растёт при уменьшении расстояний. Как и ранее, именно сценарий мира на бране делает это возможным.
Озвученные выше подробности проливают новый свет на эти три эксперимента. Их целью является не только поиск таких экзотических структур как дополнительные измерения пространства и крошечные чёрные дыры, они также пытаются выяснить, живём мы на бране или нет. В свою очередь, помимо подтверждения сценария мира на бране в теории струн, положительный итог экспериментов станет косвенным свидетельством существования других вселенных за пределами нашей. Если удастся установить, что мы живём на бране, не останется никаких математических оснований считать, что наша Вселенная единственна.
Время, циклы и мультивселенная
Несмотря на различия в деталях, рассмотренные ранее мультивселенные имеют одну общую, характерную для всех черту. В лоскутной, инфляционной и бранной мультивселенных другие вселенные расположены «где-то там» в пространстве. Для лоскутной мультивселенной «где-то там» означает далеко в обычном смысле этого слова; для инфляционной мультивселенной это значит находиться вне нашего пузырька-вселенной, в быстро расширяющемся промежуточном пространстве; для вселенной на бране это значит находиться, может быть, на небольшом расстоянии, но разделённом другим измерением. Доказательства в поддержку сценария мира на бране приведут нас к рассмотрению существенно иного множества вселенных, в котором в полную силу задействованы возможности не пространственных, а временного измерения.{41}
Ещё со времён Эйнштейна мы знаем, что пространство и время могут искривляться, растягиваться и сворачиваться. Но обычно мы не представляем, что вся Вселенная смещается то туда, то сюда. Что значит для пространства сдвинуться на десять метров «вправо» или «влево»? Замечательная головоломка, которая становится заурядной при рассмотрении в сценарии мира на бране. Подобно частицам и струнам, браны могут двигаться в том пространстве, в котором они живут. Поэтому если наблюдаемая Вселенная — это три-брана, то мы сами тоже движемся внутри многомерного пространства.[32]
Если мы живём на бране, которая движется, и поблизости есть другие браны, что произойдёт, если мы столкнёмся с одной из них? Хотя детально этот процесс до конца не изучен, можно со всей определённостью сказать, что столкновение двух бран — столкновение двух вселенных — будет катастрофичным. Простейшая возможность — это когда две параллельные три-браны приближаются друг к другу всё ближе и ближе, пока наконец-то не столкнутся лоб в лоб, подобно двум музыкальным тарелкам. Невероятная энергия, запасённая в их относительном движении, приведёт к бурному выплеску частиц и излучения, уничтожающему любые организованные структуры, находящиеся во вселенных на бранах.
Группа исследователей, в которую входят Пол Стейнхард, Нил Тьюрок, Берт Оврут и Джастин Хури, видят в таком катаклизме не только конец всего, но и начало. Разгорячённая, плотная среда, в которой беспорядочно летают частицы, сильно напоминает условия сразу после Большого взрыва. Возможно, что после столкновения двух бран, когда уничтожаются любые структуры, возникшие за всю историю развития каждой из них — галактики, планеты, люди, — возникает площадка для рождения нового космоса. Действительно, три-брана, заполненная горячей плазмой из частиц и излучения, ведёт себя так, как обычное трёхмерное пространство: она расширяется. В течение этого процесса всё остывает, позволяя частицам соединяться друг с другом, что впоследствии приведёт к следующему поколению звёзд и галактик. Кто-то даже предложил, что подходящим именем для такого перерождения вселенных будет большой хлопок.
Хотя это название вполне выразительно, слово «хлопок» не отражает ключевого свойства столкновения бран. Стейнхард и его коллеги показали, что после столкновения браны не слипаются, а отскакивают. Взаимное гравитационное притяжение бран постепенно замедляет их относительное движение; в итоге они отдаляются на максимальное расстояние, после чего заново начинают сближаться. По мере того как браны сближаются, их скорости возрастают, происходит столкновение, и благодаря следующей за ним огненной буре условия на каждой бране опять возвращаются к начальным, что приводит к новой эпохе космологической эволюции. Суть этой космологической теории в том, что миры циклически повторяются во времени, что приводит к новому множеству параллельных вселенных, циклической мультивселенной.
Если мы живём на бране в циклической мультивселенной, остальные вселенные-участники (помимо партнёра нашей браны, с которым мы периодически сталкиваемся) находятся в нашем прошлом и будущем. Стейнхард и его соавторы провели оценку временно́го масштаба полного цикла космического танго столкновений — рождения, эволюции и смерти — и сошлись на времени примерно в триллион лет. В этом сценарии Вселенная в привычном нам виде является лишь самой последней во временно́м ряду вселенных, часть из которых могли содержать разумную жизнь и порождённую ей культуру, но давным-давно угасли. В своё время все достижения человечества, а также принадлежащие другим жизненным формам во Вселенной, так же исчезнут.
Прошлое и будущее циклических вселенных
Хотя теория мира на бране является наиболее разработанным направлением циклической космологии, у идеи цикличности весьма длительная история. Вращение Земли, приводящее к смене дня и ночи, и её движение по орбите, влекущее предсказуемую смену времён года, явились основой для идей цикличности, возникших во многих культурах в попытке объяснить космос. Одна из самых древних донаучных космологий — индуизм, рассматривает Вселенную как сложноподчинённый комплекс космологических циклов внутри циклов, продолжительность которых, согласно разным интерпретациям, от миллионов до триллионов лет. Западные мыслители, начиная от философа-досократика Гераклита и римского государственного деятеля Цицерона, развивали различные циклические космологические теории. Концепция гибнущей в огне и вновь рождающейся из пепла Вселенной была очень популярна среди тех, кто размышлял над высокими материями о происхождении космоса. С распространением христианства понятие о возникновении мира как об уникальном одновременном акте постепенно взяло верх, но и циклические теории время от времени привлекали внимание.
В эпоху современного научного знания интерес к циклическим моделям возобновился с развитием общей теории относительности. Александр Фридман в популярной книге, вышедшей в СССР в 1923 году, отмечал, что некоторые из найденных им космологических решений гравитационных уравнений Эйнштейна могут быть осмыслены как осциллирующая вселенная, которая расширяется, достигает максимального размера, затем сжимается, схлопывается в «точку», после чего опять начинает расширяться.{42} В 1931 году Эйнштейн, отказавшись к тому моменту от идеи статичной вселенной, также исследовал возможность осциллирующей вселенной. Но самой обстоятельной была серия статей, опубликованных в период с 1931 по 1934 год Ричардом Толманом из Калифорнийского технологического института. Толман провёл подробное математическое исследование циклических космологических моделей, что дало начало целому потоку работ в этом направлении — иногда пересыхавшему до тонкого ручейка, иногда становившемуся бурной рекой, — который не прекращается по сей день.
Частично привлекательность циклической космологии состоит в том, что ей очевидно удаётся избегать сложного вопроса о происхождении Вселенной. Если Вселенная переходит из цикла в цикл, и если циклы никогда не прекращались (и, возможно, никогда не прекратятся), то вопрос о том, как всё началось, теряет свою актуальность. Каждый цикл имеет своё начало, но в циклической теории этому имеется конкретная физическая причина — окончание предыдущего цикла. Если спросить о начале всех циклов Вселенной, то ответ будет, что такого начала просто нет, потому что циклы повторяются бесконечно.
Поэтому в фигуральном смысле циклические модели являются перепевом присказки «и волки сыты, и овцы целы». Если вернуться назад, в первые годы научной космологии, то мы увидим, что в теории стационарной вселенной был свой собственный обходной манёвр, чтобы избежать ответа на вопрос о происхождении космоса. Утверждалось, что, несмотря на постоянное расширение Вселенной, у этого процесса не было начала: при расширении Вселенной постоянно возникает новая материя, заполняющая дополнительное пространство, что гарантирует постоянство условий во всём космосе навечно. Однако теория стационарной вселенной противоречит астрономическим наблюдениям, прямо указывающим на ранние эпохи, условия в которых заметно отличались от современных. Самыми критическими оказались наблюдения, показавшие, что ранняя космологическая фаза была далека от стационарности и равновесия, вместо этого она была хаотичной и неустойчивой. Большой взрыв разрушает мечту о стационарной вселенной, поэтому вопрос о происхождении космоса выходит на первый план. Именно тут циклическая космология является убедительной альтернативой. Каждый цикл может включать Большой взрыв как часть прошлого, что нисколько не противоречит астрономическим наблюдениям. Однако, описывая бесконечное число циклов, теории не требуется предъявить начало всех начал. Таким образом, циклическая космология вобрала в себя наиболее привлекательные свойства теории стационарной вселенной и теории Большого взрыва.
Позже, в 1950-х годах, голландский физик Герман Занстра привлёк внимание к противоречию в циклических моделях, которое неявно присутствовало в работах Толмана двадцатью годами ранее. Занстра показал, что циклу нашей Вселенной не могло предшествовать бесконечное число циклов. Проблема кроется во втором законе термодинамики. Этот закон, более подробно обсуждаемый в главе 9, говорит, что беспорядок — энтропия — возрастает со временем. Мы наблюдаем это каждый день. Прибранная утром кухня к вечеру требует новой уборки; то же самое происходит с бельём в платяном шкафу, на письменном столе и в комнате для отдыха. В этих каждодневных ситуациях возрастание энтропии — лишь досадная мелочь, но в циклической космологии оно имеет решающее значение. Толман тоже понимал, что из уравнений общей теории относительности вытекает связь между энтропией Вселенной и продолжительностью данного цикла. Чем больше энтропия, тем больше неупорядоченных частиц сдавливаются при схлопывании Вселенной; это приводит к более мощному последующему взрыву, пространство расширяется сильнее, и поэтому цикл длится дольше. Если оглянуться назад, то окажется, что благодаря второму закону термодинамики более ранние циклы обладали меньшей энтропией (из второго закона термодинамики следует, что энтропия возрастает по направлению в будущее, а по направлению в прошлое обязательно убывает)[33], и поэтому каждый предыдущий цикл был короче. Проведя соответствующие математические вычисления, Занстра показал, что в достаточно удалённом прошлом циклы настолько укорачивались, что должны были прекратиться. Иными словами, у последовательности циклов должно было быть начало.
Стейнхард и компания утверждают, что их новая версия циклической космологии избегает этой ловушки. В рамках их подхода циклы возникают не из-за того, что Вселенная расширяется, сжимается и снова расширяется, а потому что пространство, разделяющее миры на бранах, расширяется, сжимается и вновь расширяется. Сами по себе браны постоянно расширяются — этот процесс происходит во всех циклах. Как того требует второй закон термодинамики, энтропия возрастает от одного цикла к другому, но из-за расширения бран энтропия распределяется по постоянно растущему пространственному объёму. Полная энтропия возрастает, но её плотность уменьшается. К концу каждого цикла энтропия настолько разбавляется, что её плотность практически обнуляется, то есть происходит полный возврат к начальному состоянию. И поэтому, в отличие от теории Толмана и Занстры, циклы могут продолжаться бесконечно в направлении как будущего, так и прошлого. У бранной циклической мультивселенной нет необходимости иметь начало во времени.[34]
Такое обхождение со старой головоломкой о начале всех начал, безусловно является большим успехом циклической мультивселенной. Однако, как подчёркивают сторонники теории, циклическая мультивселенная не только решает космологические головоломки — она даёт особое предсказание, которое сможет отличить её от широко признанной инфляционной модели. В инфляционной космологии взрывоподобное расширение ранней Вселенной настолько сильно воздействует на пространственную структуру, что возникают сильные гравитационные волны. Такие волны должны были оставить след в реликтовом излучении и сейчас ведётся их поиск на высокочувствительном астрономическом оборудовании. Столкновение же бран сопровождается сильной кратковременной бурей, но без эффектного инфляционного расширения пространства, поэтому любые возникшие гравитационные волны скорее всего будут слишком слабы и быстро затухнут. Поэтому обнаружение гравитационных волн станет серьёзным свидетельством против циклической мультивселенной. С другой стороны, отсутствие любых наблюдательных данных о существовании таких гравитационных волн создаст серьёзные трудности большинству инфляционных моделей, и сделает циклический подход более привлекательным.
Идея циклической вселенной широко известна в физическом сообществе, но принимается с большим скептицизмом. Наблюдения могут изменить эту ситуацию. Если на Большом адронном коллайдере удастся получить доказательства существования миров на бране и если не будут обнаружены гравитационные волны, идущие из эпохи ранней Вселенной, то популярность циклической мультивселенной может значительно возрасти.
Внутри потока
Математическое осознание того, что в теории струн есть не только струны, но также и браны, оказало огромное влияние на исследования в этой области. Бранный сценарий и сопутствующие ему мультивселенные составляют направление исследований, которое потенциально может привести к значительному пересмотру наших представлений о реальности. Без точных математических методов, разработанных за последние полтора десятка лет, значительная часть этих открытий осталась бы за пределами наших возможностей. Однако основная проблема, которую физики надеялись решить с помощью точных методов, — выбор единственной формы пространства дополнительных измерений из многих кандидатов, выявленных теоретическими исследованиями, — пока остаётся нерешённой. Мы по-прежнему далеки от её решения. На самом деле, новые методы только усугубили проблему. Было открыто огромное количество новых видов пространств дополнительных измерений, что привело к невероятному увеличению числа возможных кандидатов, а понимание того, как выбрать одно единственное пространство, не продвинулось ни на йоту.
Ключевым для этих исследований явилось наличие у бран важной характеристики — потока. Подобно электрону, порождающему электрическое поле — электрический «туман», заполняющий пространство вокруг него, или подобно магниту, порождающему магнитное поле — магнитный «туман», заполняющий пространство вокруг него, брана порождает бранное поле — бранный «туман», заполняющий пространство вокруг неё (рис. 5.5). Когда в 1800-х годах Фарадей проводил первые эксперименты с электрическими и магнитными полями, для измерения напряжённости поля он использовал плотность силовых линий поля, расположенных на заданном расстоянии от источника, и эту величину он назвал потоком поля. С тех пор этот термин прочно вошёл в обиход. Напряжённость поля браны тоже измеряется порождаемым ей потоком.
Рис. 5.5. а) Электрический поток, порождённый электроном; б) Магнитный поток, порождённый магнитным стержнем; в) Бранный поток, порождённый браной
Струнные теоретики, среди которых Рафаэль Буссо, Польчински, Стивен Гиддингс, Шамит Качру и многие другие, осознали, что для полного описания дополнительных измерений теории струн требуется не только определить их форму и размер — то, чем исследователи в этой области, включая меня, занимались в 1980–1990-х годах, — но также определить пронизывающие их потоки созданных бранами полей. Позвольте мне чуть более подробно остановиться на этом.
Со времён появления первых математических работ по дополнительным измерениям теории струн исследователям было известно, что пространства Калаби — Яу, как правило, содержат много пустых полостей, подобно пространству внутри мяча, внутри бублика или внутри фигурки из дутого стекла. Так продолжалось до тех пор, пока в самом начале нового тысячелетия теоретики не осознали, что пустые полости могут чем-нибудь заполняться. Они могут быть обёрнуты теми или иными бранами и пронизаны создаваемыми ими потоками полей (рис. 5.6). В более ранних исследованиях (кратко сформулированных, например, в «Элегантной Вселенной») по большей части рассматривались только «голые» пространства Калаби — Яу, для которых подобного рода украшения отсутствуют. Когда учёные осознали, что на пространства Калаби — Яу могут быть «навешены» дополнительные свойства, они обнаружили гигантский набор модифицированных пространств дополнительных измерений.
Рис. 5.6. В теории струн браны могут наматываться на часть дополнительных измерений, эти измерения могут быть пронизаны потоками созданных бранами полей — в результате получаются «одетые» пространства Калаби — Яу. (На рисунке представлена упрощённая версия пространства Калаби — Яу, «бублик с тремя дырками». Схематично показаны намотанные браны и линии потока в виде жгутов, намотанных на определённые части пространства)
Даже грубый подсчёт даёт представление о масштабе. Рассмотрим поток. Так же как в квантовой механике устанавливается, что число фотонов и электронов всегда целое — может быть 3 фотона и 7 электронов, но не 1,2 фотона или 6,4 электрона, — точно так же квантовая механика доказывает, что силовые линии потока собираются в целочисленные пучки. Они могут пронизывать охватывающую поверхность один раз, два раза, три раза и так далее. В принципе, помимо требования целочисленности, других ограничений не существует. На практике, когда количество линий в потоке велико, он стремится исказить пространство Калаби — Яу, что делает использованные ранее математические методы неточными. Во избежание попадания в этот математический омут учёные, как правило, рассматривают потоки с количеством линий не более 10, а часто и того меньше.{43}
Это означает, что если данное пространство Калаби — Яу содержит одну пустую полость, то её можно одеть потоком десятью разными способами, что приведёт к десяти новым пространствам дополнительных измерений. Если данное пространство Калаби — Яу имеет две такие полости, то имеем 10 × 10 = 100 различных способов одеть поток на пространство (10 возможных потоков на первую полость и 10 на вторую); если три пустые полости — имеем 103 различных способов одеть поток на пространство, и так далее. Насколько большим может быть это число? Некоторые пространства Калаби — Яу имеют порядка пятисот пустых полостей. Рассуждая аналогично, получаем, что число различных форм пространств дополнительных измерений будет порядка 10500.
Таким образом, вместо того чтобы просеять кандидатов и отобрать из них несколько выделенных пространств дополнительных измерений, точные математические методы открыли целый рог изобилия новых возможностей. Совершенно неожиданно выяснилось, что число возможных нарядов пространств Калаби — Яу значительно превышает число частиц в наблюдаемой части Вселенной. Для некоторых струнных теоретиков такой вывод стал большим разочарованием. Как подчёркивалось в предыдущей главе, не имея какого-нибудь способа выбрать точный вид дополнительных измерений — который, как мы теперь знаем, дополнен также выбором одетого на пространство потока, — математический аппарат теории струн лишается своей предсказательной силы. Так много надежд возлагалось на математические методы, которые могут работать вне рамок теории возмущений. Теперь же, когда некоторые из этих методов были реализованы, проблема фиксации формы пространства дополнительных измерений только усугубилась. После этого некоторые струнные теоретики совсем приуныли.
Другие, более жизнерадостные, верят, что сдаваться ещё рано. Однажды — возможно совсем скоро, а может и нет — будет найден недостающий принцип, определяющий вид дополнительных измерений, включая конкретный поток, в котором будет щеголять та или иная форма.
Иные теоретики придерживаются ещё более радикальной точки зрения. Возможно, говорят они, за десятилетиями бесплодных попыток установить точную форму пространства дополнительных измерений стоит некий смысл. Возможно, совершенно вызывающе продолжают эти радикалы, необходимо рассматривать все возможные формы и потоки, возникающие в математическом аппарате теории струн. Возможно, настаивают они, причина, по которой математика наполнена этими возможностями, в том, что они все реальны, каждая из форм задаёт дополнительные измерения в своей отдельной вселенной. И может быть, усмиряя необузданный полёт фантазии наблюдательными фактами, именно это и необходимо для рассмотрения самого трудного, по всей видимости, вопроса — космологической постоянной.
Глава 6. Новые мысли о старой константе Ландшафтная мультивселенная
Разница между 0 и 0,000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 может показаться не такой уж большой. И это именно так при любых обычных измерениях. Однако есть всё усиливающееся подозрение, что эта крошечная разница может оказаться ответственной за кардинальный сдвиг в том, как мы представляем ландшафт окружающей действительности.
Крошечное число, указанное выше, впервые было измерено в 1998 году двумя группами астрономов, которые проводили тщательные наблюдения взрывающихся звёзд в удалённых галактиках. С тех пор эти данные были подтверждены множеством других исследований. Что это за число, почему вокруг него такая шумиха? Это не что иное, как то, что было указано в третьей строке гравитационной декларации — космологическая постоянная Эйнштейна, определяющая количество невидимой тёмной энергии, которой пропитана ткань пространства.
Так как этот результат продолжает подтверждаться в тщательных исследованиях, физики вынуждены признать, что наблюдения и выводы, сделанные в предшествующие десятилетия и убедившие многих в том, что космологическая постоянная равна 0, должны быть отвергнуты. Теоретики начали спешно выяснять, где же они ошибались. Но ошибались не все. Годами ранее высказывались идеи, что ненулевая космологическая постоянна будет однажды обнаружена. В чём состояло ключевое предположение? В том, что мы живём в одной из многих вселенных. Многих вселенных.
Возвращение космологической постоянной
Напомню, что космологическая постоянная, если она существует, наполняет пространство невидимой энергией — тёмной энергией, — знаковым свойством которой является гравитационное отталкивание. Эйнштейн увлёкся этой идеей в 1917 году, считая, что порождаемая космологической постоянной антигравитация сбалансирует гравитационное притяжение обычной материи во Вселенной и таким образом приведёт к картине космоса, который не будет ни сжиматься, ни расширяться.[35]
Часто говорят, что когда Эйнштейн узнал о наблюдениях Хаббла 1929 года, обнаруживших расширение пространства, то назвал космологическую постоянную своей «величайшей ошибкой». Георгий Гамов вспоминал разговор, в котором Эйнштейн сказал об этом, но, учитывая склонность Гамова к литературным гиперболам, есть сомнения в надёжности этих воспоминаний.{44} Но совершенно точно, что Эйнштейн выбросил космологическую постоянную из своих уравнений после того, как наблюдения показали, что его вера в статичную вселенную безосновательна. Спустя много лет он заметил, что если бы «хаббловское расширение было обнаружено в момент создания общей теории относительности, то космологическая постоянная никогда не была бы введена».{45} Но «задний ум» не всегда крепок; иногда он может затуманить исходную идею. В 1917 году в письме, написанном физику Виллему де Ситтеру, Эйнштейн высказался более подробно:
В любом случае остаётся один вопрос. Общая теория относительности позволяет включить космологическую постоянную в полевые уравнения. Однажды наши настоящие знания об устройстве неподвижного звёздного неба, явные движения неподвижных звёзд и положение спектральных линий в зависимости от расстояния, возможно, станут достаточными для эмпирического разрешения вопроса о том, равна нулю или нет космологическая постоянная. Убеждённость — мощная пружина, но ненадёжный судья.{46}
Восемьдесят лет спустя космологический проект «Supernova cosmology», возглавляемый Солом Перлмуттером, и поисковая группа «High-Z Supernova», возглавляемая Брайаном Шмидтом, пошла именно по такому пути. Они аккуратно изучили плотность спектральных линий — свет, испущенный удалёнными звёздами, — и, как предсказывал Эйнштейн, смогли на основе опытных данных изучить задачу, чему равна космологическая постоянная.
К удивлению многих они обнаружили, что нулю она не равна.
Космическая судьба
Когда астрономы приступили к работе, ни одна из исследовательских групп не ставила своей целью измерить космологическую постоянную. Фокус был направлен на измерение другого космологического свойства — скорости замедления расширения пространства. Обычное гравитационное притяжение притягивает объекты друг к другу всё ближе и ближе, поэтому скорость расширения падает. Точная величина темпа замедления играет ключевую роль в предсказании того, как будет выглядеть Вселенная в далёком будущем. Сильное замедление означает, что в какой-то момент расширение прекратится, после чего пойдёт обратный процесс и начнётся период пространственного сжатия. В результате непрекращающегося сжатия произойдёт Большой хлопок — явление, обратное Большому взрыву, — или возможно отскок, как в циклических моделях, рассмотренных в предыдущей главе. Если замедление небольшое, то развязка будет совсем другая. Подобно мячу, который на большой скорости может преодолеть притяжение Земли и полететь дальше, при достаточно высокой скорости пространственного расширения и достаточно малом темпе замедления пространство может расширяться вечно. Измеряя космическое замедление, вышеназванные исследовательские группы пытались определить окончательную судьбу космоса.
Подход каждой группы был прост: измерить насколько быстро пространство расширялось в некоторые моменты в прошлом и, сравнив эти скорости, определить темп замедления расширения в течение всей истории развития Вселенной. Отлично! Но как это сделать? Подобно многим вопросам в астрономии, всё свелось к тщательному наблюдению света. Галактики подобны сигнальным огням маяков, чьё движение отражает пространственное расширение. Если бы мы могли определить насколько быстро галактики удалялись от нас в тот давний момент, когда они излучили свет, что сейчас дошёл до нас, мы смогли бы определить, как быстро расширялось пространство в различные моменты в прошлом. Сравнивая эти скорости, можно было бы узнать темп космического замедления. В этом и состоит главная идея.
Для проработки всех подробностей необходимо решить два основных вопроса. Как на основе современных наблюдений за удалёнными галактиками можно определить расстояния до них, и как мы можем измерить скорость их движения? Начнём с расстояния.
Расстояние и яркость
Одной из самых старых и важных проблем в астрономии является определение расстояний до небесных объектов. Метод параллакса — один из самых первых способов определения расстояния, можно объяснить даже пятилетнему ребёнку. Дети обычно (моментально) приходят в восторг, когда, смотря на какой-нибудь предмет, поочерёдно закрывая то один, то другой глаз, обнаруживают, что предмет начинает прыгать с место на место. Если вам уже не пять, попробуйте так поэкспериментировать с этой книгой, сфокусировав взгляд на какой-нибудь угол. Прыжки происходят потому, что наши глаза расположены на некотором расстоянии друг от друга, а следовательно, смотрят на предмет под разными углами. Для предметов, расположенных далеко, сдвиг менее заметен, потому что разница в углах уменьшается. Это простое наблюдение можно описать количественно, установив точную связь между разницей в угле между лучами зрения обоих глаз — параллаксом — и расстоянием до объекта, на который вы смотрите. Однако не беспокойтесь о деталях — ваша зрительная система делает это автоматически. Именно поэтому вы видите мир в 3D.[36]
Когда вы смотрите на звёзды в ночном небе, параллакс слишком мал, чтобы его заметить; ваши глаза расположены слишком близко друг к другу, чтобы возникла значительная разница в угле. Однако есть хитроумный способ преодолеть данное затруднение: нужно измерять положение звезды в два приёма, с периодом в шесть месяцев, заменив тем самым взаимное расположение ваших глаз двумя положениями Земли в пространстве. Большее расстояние между точками наблюдения увеличивает параллакс; он по-прежнему мал, но в некоторых случаях достаточно велик, чтобы его измерить. В самом начале XIX столетия среди учёных была напряжённая конкуренция, кто первый измерит такой звёздный параллакс; в 1838 году немецкий астроном и математик Фридрих Бессель заслужил лавры победителя, успешно измерив параллакс звезды под названием 61 Лебедя в созвездии Лебедя. Угловая разница оказалась равной 0,000084 градуса, что соответствует расстоянию до звезды в 10 световых лет.
С тех пор метод постоянно улучшался и теперь применяется на спутниках, которые могут измерять гораздо меньшие углы параллакса, чем в наблюдениях Бесселя. Эти достижения позволили проводить точные измерения расстояний до звёзд, если они не превышают несколько тысяч световых лет. Однако если сильно выйти за эти рамки, разница в углах опять становится слишком маленькой и метод перестаёт работать.
Другой подход, который может измерять гораздо бо́льшие расстояния на небе, основан на ещё более простой идее: чем дальше вы отодвигаете светящийся объект, будь это автомобильные фары или яркая звезда, тем больше излучённый свет рассеивается по пути своего движения к нам, и поэтому тускнеет. Сравнивая видимую яркость объекта (то, насколько ярок свет при наблюдении с Земли) с собственной яркостью (то, насколько ярок свет при наблюдении с близкого расстояния), можно найти расстояние до объекта.
Но здесь возникает отнюдь не малое препятствие, как определить собственную яркость астрофизических объектов. Звезда тусклая, потому что находится очень далеко или потому что сама по себе не очень яркая? Это объясняет, почему столь долгим оказался поиск астрономических объектов, которые были бы достаточно распространены в космосе, и собственную яркость которых можно было бы достоверно определить без необходимости находиться рядом. Если бы удалось найти такие стандартные свечи, то была бы найдена единая мера определения расстояний. Разница в яркости одной стандартной свечи по отношению к другой напрямую дала бы нам информацию о расстоянии между ними.
В течение всего столетия с попеременным успехом предлагалось и применялось множество разных стандартных свечей. В последнее время наиболее плодотворным оказался метод, использующий звёздные вспышки, называемые сверхновыми типа Ia. Сверхновая Ia возникает, когда белый карлик вытягивает вещество из своего близкого компаньона, как правило, красного гиганта, вокруг которого он вращается. Из хорошо развитых физических методов изучения звёздных структур следует, что если белый карлик вытянет достаточное количество вещества (так что его масса возрастёт примерно до 1,4 масс Солнца), то он больше не сможет поддерживать свой вес. Раздутый карлик коллапсирует, и происходит настолько мощный взрыв, что порождённая вспышка света сопоставима со светом около 100 миллиардов звёзд в окружающей его галактике.
Такие сверхновые звёзды являются идеальными стандартными свечами. Взрыв настолько мощный, что его можно видеть с фантастически больших расстояний. Важно, что поскольку вспышки являются результатом одного и того же физического процесса — увеличение массы карлика примерно до 1,4 масс Солнца и последующий взрыв, — то образовавшиеся сверхновые имеют примерно одинаковые собственные светимости. Однако проблема в использовании сверхновых типа Ia состоит в том, что в средней галактике такие вспышки происходят раз в несколько столетий: как нам поймать их в процессе взрыва? Обе группы, космологический проект «Supernova cosmology» и поисковая группа «High-Z Supernova», взялись за решение этого вопроса способом, похожим на эпидемиологические исследования: точная информация об однотипных относительно редких событиях может быть получена, если изучать достаточно большую популяцию. Поэтому на помощь пришли телескопы, снабжённые широкоформатными детекторами, способными одновременно анализировать тысячи галактик. Тогда исследователи смогли установить местоположение дюжины сверхновых типа Ia, которые в дальнейшем можно более детально изучать с помощью обычных телескопов. Основываясь на их яркости, учёные смогли определить расстояния до дюжины галактик, удалённых на миллиарды световых лет, — и таким образом завершить первый шаг в решении поставленной задачи.
И всё-таки, что за расстояние?
Прежде чем перейти к следующему шагу — определению скорости расширения Вселенной в момент взрыва каждой из сверхновых, стоит вкратце остановиться на одном затруднительном моменте. Когда мы говорим о расстояниях на таких фантастически огромных масштабах, причём в контексте постоянно расширяющейся Вселенной, возникает вопрос, какое именно расстояние измеряют астрономы? Это расстояние между теми положениями, которые мы и наблюдаемая галактика занимали миллиарды лет назад, когда галактика испустила свет, наблюдаемый нами теперь? Или это расстояние между нашим настоящим положением и положением галактики миллиарды лет назад, когда она испустила свет, наблюдаемый нами теперь? Либо это расстояние между нашим настоящим положением и настоящим положением галактики?
Я сейчас хочу предложить вам самый полезный, на мой взгляд, способ размышления об этом и о множестве других запутанных космологических вопросов.
Допустим, вы хотите знать кратчайшие расстояния между тремя городами, Нью-Йорком, Лос-Анджелесом и Остином, поэтому вы берёте карту Соединённых Штатов и измеряете по ней расстояния между городами. Вы обнаружите, что Нью-Йорк находится в 39 сантиметрах от Лос-Анджелеса; Лос-Анджелес находится в 19 сантиметрах от Остина; и Остин расположен в 24 сантиметрах от Нью-Йорка. Затем вы пересчитываете результаты замеров в километры с помощью легенды карты, на которой указано отношение пересчёта: 1 сантиметр = 100 километров — это позволяет выяснить, что данные три города расположены на расстоянии, соответственно, 3900 километров, 1900 километров и 2400 километров друг от друга.
Теперь представьте, что поверхность Земли равномерно раздулась и все расстояния удвоились. Это весьма радикальная трансформация, но и в этом случае ваша карта Соединённых Штатов останется абсолютно пригодной, если вы сделаете одно важное изменение. Понадобится изменить легенду карты так, чтобы отношение пересчёта теперь имело вид: 1 сантиметр = 200 километров. Тогда 39 сантиметров, 19 сантиметров и 24 сантиметра станут теперь соответствовать 7800 километрам, 3800 километрам и 4800 километрам по территории растянутых Соединённых Штатов. Если раздувание Земли продолжится, то статичная, неизменная карта будет оставаться пригодной, если постоянно поправлять её легенду, нужным образом меняя отношение пересчёта в каждый момент: 1 сантиметр = 200 километров в полдень; 1 сантиметр = 300 километров в два часа дня; 1 сантиметр = 400 километров в четыре часа дня — для адекватного отражения процесса удаления двух точек при расширении поверхности.
Такое сравнение с раздувающейся Землёй весьма полезно, потому что аналогичные рассмотрения применимы к расширяющемуся космосу. Сами по себе галактики остаются на месте. Но подобно городам на раздувающейся поверхности Земли, они удаляются друг от друга, потому что субстанция, в которую они погружены, — само пространство — растягивается в разные стороны. Это означает, что если бы космический картограф отметил положения галактик миллиарды лет назад, то такая карта была бы и сегодня так же справедлива, как и тогда.[37] Но подобно легенде карты расширяющейся Земли легенда космической карты также должна обновляться, чтобы отношение пересчёта от расстояний на карте до расстояний в реальности оставалось точным. Космологическое отношение пересчёта называется масштабным фактором Вселенной; в расширяющейся Вселенной масштабный фактор увеличивается со временем.
Всякий раз, когда вы думаете о расширяющейся Вселенной, всегда представляйте неизменную космическую карту. Представьте, будто это обычная карта, лежащая на столе, а космическое расширение постоянно подправляет её легенду. Немножко потренировавшись, вы убедитесь, что такой способ помогает преодолевать концептуальные барьеры.
Рассмотрим для примера свет, идущий от взрыва сверхновой в удалённой галактике Ноа. Сравнивая видимую яркость сверхновой с её собственной яркостью, мы определяем уменьшение интенсивности света с момента излучения (рис. 6.1а) до момента поглощения (рис. 6.1в), возникающее из-за рассеяния во время путешествия на огромной сфере (показанной в виде окружности на рис. 6.1 г). Измерив это уменьшение, можно определить размер сферы — площадь её поверхности, — а затем, вспомнив школьную геометрию, можно легко найти её радиус. Радиус сферы полностью совпадает с траекторией движения светового луча, поэтому длина радиуса равна расстоянию, пройденному лучом. А теперь вопрос, из-за которого и написан этот раздел: какому из трёх возможных расстояний соответствуют эти измерения, если вообще они чему-нибудь соответствуют?
Рис. 6.1. а) По мере приближения к нам свет от удалённой сверхновой рассеивается (мы находимся в галактике в правом нижнем углу карты); б) Пока свет путешествует, Вселенная расширяется, что отражено в легенде космической карты; в) Пока свет дойдёт до нас, он рассеется и его интенсивность упадёт; г) Сравнивая видимую яркость сверхновой с её собственной яркостью, мы измеряем площадь поверхности сферы, по которой свет рассеялся (показана в виде окружности) и, следовательно, находим её радиус. Радиус сферы отражает траекторию светового луча. Его длина — это расстояние между нами и галактикой, где находится сверхновая. Это и есть именно та величина, которую определяют в наблюдениях
Пока свет путешествует, пространство по-прежнему расширяется. Но единственное изменение на статичной космической карте состоит в регулярном обновлении масштабного фактора, записанного в легенде. Поскольку мы только что увидели свет от сверхновой, так как он только что завершил своё путешествие, мы должны воспользоваться тем масштабным фактором, который именно сейчас написан на легенде космической карты, и пересчитать расстояние — траекторию от нас до сверхновой (рис. 6.1, г) — в расстояние, пройденное световым лучом в реальном мире. Из этой процедуры ясно следует, что полученный результат является расстоянием в данный момент между нами и текущим положением галактики Ноа — то есть третий из предложенных вариантов ответа.
Также отметим, что вследствие непрерывного расширения Вселенной, более ранние сегменты траектории фотона ещё долго будут продолжать расширяться после того, как фотон пролетел. Если запечатлеть на фотографии путь фотона, то получится линия, длина которой будет увеличиваться по мере расширения пространства. Применив масштабный фактор в момент приёма фотона ко всему путешествию фотона, мы увидим, что третий ответ полностью учитывает всё произошедшее расширение. Это правильное объяснение, потому что степень уменьшения интенсивности света зависит от размера сферы, на которой в данный момент рассеивается свет, — а это сфера, радиус которой равен длине траектории светового луча в данный момент, с учётом всего расширения post factum.{47}
Таким образом, сравнивая собственную и видимую яркости сверхновой, мы определяем расстояние в данный момент между нами и галактикой, в которой она находится. Именно эти расстояния и измеряли две группы исследователей.{48}
Цвета космологии
Но довольно про измерение расстояний до далёких галактик и сияющих сверхновых типа Ia. Теперь выясним, как можно определить скорость расширения Вселенной в те давние времена, когда вспыхивали эти космические маяки. Оказывается, что физика этих процессов не намного сложнее физики свечения неоновых ламп.
Неоновые лампы светят красным цветом, потому что когда ток пропускают сквозь заполняющий их газ, электроны на орбитах атомов неона моментально переходят в возбуждённое состояние. Затем, после того как атомы неона успокоятся, электроны спускаются обратно на свои обычные орбиты, высвобождая при этом лишнюю энергию в виде излучения фотонов. Цвет фотонов — их длина волны — определяется переносимой ими энергией. Ключевое открытие, совершённое квантовой механикой ещё в первые десятилетия XX столетия, состоит в том, что атомы данного химического элемента обладают индивидуальными наборами возможных переходов электронов с орбиты на орбиту; это определяет индивидуальную цветовую гамму испущенных фотонов. Так, для атомов неона определяющим цветом является красный (точнее, красновато-оранжевый), это даёт характерный цвет неоновых огней. Другие элементы — гелий, кислород, хлор и так далее — обладают похожим поведением, отличаясь друг от друга главным образом длиной волны испущенных фотонов. Неоноподобные огни других цветов будут заполнены скорее всего или ртутью (голубой цвет), или гелием (золотой цвет), либо сделаны из стеклянных трубок, покрытых разными веществами, чаще всего фосфором, атомы которых могут излучать свет с другими длинами волн.
Наблюдательная астрономия в значительной мере основана на аналогичных рассуждениях. С помощью телескопов астрономы собирают свет от удалённых объектов и по его цвету — длине волны анализируемого света — могут определить химический состав источника света. Впервые это было осуществлено при солнечном затмении 1868 года, когда французский астроном Пьер Жансен и, независимо от него, английский астроном Джозеф Норман Локьер, изучали свет от солнечной короны, когда солнечный диск был закрыт луной. Они обнаружили странное яркое излучение с длиной волны, которое нельзя было воспроизвести в лаборатории с помощью известных веществ. Это привело к смелому — и правильному — предложению, что свет был испущен неким новым, ранее неизвестным элементом. Неизвестным элементом оказался гелий, в названии которого отражён тот факт, что это вещество было открыто сначала на Солнце, а потом на Земле. Это открытие убедительно показало, что подобно тому как любого из нас можно однозначно идентифицировать по отпечаткам пальцев, различные атомы однозначно определяются длинами волн излучаемого (и поглощаемого) ими света.
В последующие десятилетия астрономы, изучающие длины волн света, приходящего от всё более и более удалённых астрофизических источников, столкнулись с необычным свойством. Хотя набор длин волн наблюдаемого света был похож на тот, что получался в лабораторных экспериментах с хорошо известными атомами типа водорода и гелия, они оказались несколько длиннее. От одного удалённого источника длина волны могла быть на 3 процента больше, от другого источника на 12 процентов больше, от третьего — на 21 процент. Астрономы назвали это явление красным смещением, потому что увеличение длины волны, по крайней мере в видимой части спектра, соответствует покраснению.
Дать название явлению уже полдела, но в чём причина растяжения длины волны? Ответ нам хорошо известен. Как ясно показали наблюдения Весто Слайфера и Эдвина Хаббла, Вселенная расширяется. Упоминавшаяся ранее модель неизменной карты как раз подходит для интуитивного объяснения.
Давайте нарисуем световую волну, бегущую к нам из галактики Ноа. Отмечая на нашей неизменной карте путь, проходимый волной, мы увидим равномерную последовательность гребней волны, непреклонно движущихся как волновой поезд в наш телескоп. Одинаковость волн может побудить нас думать, что длина волны света в момент излучения (расстояние между двумя последовательными гребнями) будет той же самой, что и в момент приёма. Но самое интересное наступает тогда, когда мы подключаем легенду карты для пересчёта расстояний на карте в действительные расстояния. Поскольку Вселенная расширяется, отношение пересчёта в момент окончания пути больше, нежели в самом начале. Из этого следует, что хотя длина световой волны, измеряемая по карте, остаётся неизменной, при пересчёте в реальные длины она увеличивается. Когда свет достигает нашего телескопа, его длина волны больше, чем в момент излучения. Словно длина волны — это стежки на эластичной ткани. Если ткань растянуть, то стежки тоже растянутся. Аналогично, расширение пространства влечёт за собой растяжение световых волн.
Можно дать количественные оценки. Если длина волны увеличена на 3 процента, то в настоящий момент Вселенная на 3 процента больше, чем в момент испускания света; если длина волны больше на 21 процент, то Вселенная расширилась на 21 процент с того момента, когда свет начал своё путешествие. Таким образом, измерение красного смещения содержит информацию о размере Вселенной в момент испускания света, который сейчас до нас дошёл, по сравнению с размером Вселенной в настоящее время.[38] Следующий очевидный шаг состоит в том, чтобы выстроить последовательность измерений красных смещений для нахождения изменения расширения Вселенной во времени.
Засечка на стене в детской комнате отмечает рост ребёнка в определённый момент времени. Последовательность засечек задаёт рост ребёнка при соответствующих датах. Имея достаточно много засечек, можно определить, как быстро рос ребёнок в разные моменты времени. Рывок в девять, более спокойный период до одиннадцати, затем опять рывок в тринадцать, и так далее. Когда астрономы измеряют красное смещение сверхновых типа Ia, они делают аналогичные «засечки» для пространства. Во многом подобно засечкам роста ребёнка, последовательность красных смещений различных сверхновых типа Ia позволяет нам вычислять, как менялась скорость расширения Вселенной в разные периоды в прошлом. Имея такие данные, астрономы могут определить темп замедления расширения пространства. Именно такой подход был разработан упоминавшимися выше исследовательскими группами.
Для его осуществления осталось сделать последний шаг — найти метод датировать такие засечки. Астрономы должны были определить, когда был испущен свет той или иной сверхновой. Это несложная задача. Поскольку разница между видимой и собственной яркостями сверхновой задаёт расстояние и скорость света нам известна, можно непосредственно вычислить, когда именно свет был испущен сверхновой. Это правильные рассуждения, но важно не упустить из виду одну существенную деталь, связанную с рассмотренным выше растяжением траектории светового луча.
Когда свет распространяется в расширяющейся Вселенной, он покрывает заданное расстояние не только потому, что обладает собственной скоростью распространения в пространстве, но и частично благодаря расширению самого пространства. Можно провести аналогию с движущейся дорожкой в аэропорту. На дорожке можно уехать дальше, не увеличивая при этом свою собственную скорость, потому что движение самой дорожки дополняет ваше перемещение. Точно так же свет от удалённой сверхновой доходит дальше, без увеличения собственной скорости, потому что расширяющееся пространство способствует его движению. Для точного определения момента излучения дошедшего до нас света необходимо учесть оба вклада в проходимое им расстояние. Математические выкладки довольно хитроумные (если вы заинтересовались, загляните в примечания), но на сегодняшний день мы их ясно понимаем.{49}
Учитывая эти тонкости, а также многие другие теоретические и наблюдательные данные, обе исследовательские группы смогли определить масштабный фактор Вселенной в различные моменты в прошлом. Таким образом, была найдена последовательность засечек, задающих контур Вселенной, и исследователи смогли определить, как менялась скорость расширения при развитии космоса.
Космическое ускорение
Проверив и многократно перепроверив всё самым тщательным образом, обе группы опубликовали свои результаты. Противоположно тому, что ожидалось, на протяжении последних 7 миллиардов лет расширение пространства не замедлялось. Оно ускорялось.
Результаты этой новаторской работы и последующих наблюдений, которые лишь закрепили полученные выводы, представлены на рис. 6.2. Наблюдения показали, что более 7 миллиардов лет назад масштабный фактор действительно вёл себя, как ожидалось: его рост постепенно замедлялся. Если бы так продолжалось, кривая на рисунке постепенно стала бы горизонтальной или даже начала опускаться. Однако, как было выяснено, примерно 7 миллиардов лет назад произошло нечто экстраординарное. Кривая стала подниматься, что ознаменовало рост масштабного фактора. Расширение пространства начало ускоряться и Вселенная переключилась на более высокую передачу.
Рис. 6.2. Зависимость масштабного фактора Вселенной от времени. Космическое расширение замедлялось до примерно 7 миллиардов лет назад, а затем начало ускоряться
Космическая плотность зависит от формы кривой на рисунке. При ускоренном расширении пространство будет бесконечно расширяться, разводя удалённые галактики всё дальше и всё быстрее. Через сто миллиардов лет любая галактика, не находящаяся сейчас в нашей окрестности (в гравитационном кластере, состоящем примерно из дюжины галактик, называемом нашей «местной группой»), выйдет за пределы нашего космического горизонта и перестанет быть видимой для нас. Если у астрономов будущего не будет под рукой записей, оставленных для них в более ранние эпохи, их космологические теории будут создаваться в попытке объяснить изолированную вселенную с небольшим числом галактик, одиноко плывущую в море неподвижного мрака. Мы живём в особенную эпоху. Ускоренное расширение лишит нас знания, дарованного Вселенной.
Далее мы увидим, что ограничения на возможности будущих астрономов ещё более поражают, когда мы пониманием, сколь огромно космическое пространства, как это установило наше поколение, стремясь объяснить ускоренное расширение.
Космологическая постоянная
Если бы вы увидели, что скорость мяча, подброшенного вверх, вдруг начала увеличиваться, вы бы решили, что есть что-то, что толкает его прочь от земной поверхности. Точно так же исследователи сверхновых пришли к выводу, что для неожиданного ускорения космической экспансии требуется нечто, что толкает наружу, нечто преодолевающее гравитационное притяжение. Как мы теперь хорошо знаем, именно так можно описать работу космологической постоянной, а порождаемое ею гравитационное отталкивание является идеальным кандидатом. Таким образом, наблюдения за сверхновыми вернули космологическую постоянную обратно под свет софитов, и не потому что «убеждённость — плохой судья», как писал Эйнштейн в своём письме десятилетиями ранее, а по причине упрямой силы фактов.
Полученные данные также позволили исследователям определить численное значение космологической постоянной — количество тёмной энергии, заполняющей пространство. Выразив полученный результат через массовый эквивалент, как это принято среди физиков (используя формулу E = mc2 в менее привычном виде m = E/c2), исследователи показали, что данные, полученные из наблюдения сверхновых, приводят к значению космологической постоянной менее 10−29 грамма на кубический сантиметр.{50} Отталкивающая сила такой маленькой космологической постоянной в течение первых 7 миллиардов лет была подавлена притяжением обычного вещества и энергии, в согласии с наблюдательными данными. Но расширение пространства растворило, снизило плотность обычного вещества и энергии, что в конце концов позволило космологической постоянной взять верх. Напомним, что космологическая постоянная не подвержена растворению; гравитационное отталкивание, порождённое космологической постоянной, является внутренним свойством пространства — каждый кубический метр пространства даёт одинаковый вклад в отталкивающую силу, определяемый величиной космологической постоянной. Поэтому чем больше пространства находится между любыми двумя объектами благодаря космическому расширению, тем сильнее сила, отталкивающая их в разные стороны. Примерно 7 миллиардов лет гравитационное отталкивание, порождённое космологической постоянной, начало превалировать; с этого момента Вселенная расширяется с ускорением, так как описывает кривая на рис. 6.2.
Для соответствия с принятыми соглашениями мне следует выразить величину космологической постоянной в удобных единицах, наиболее часто используемых в физике. Согласитесь, странно просить продавца взвесить 1015 пикограмм картофеля (разумнее попросить 1 килограмм, в эквивалентных и более адекватных единицах меры), и ваш друг удивится, если вы попросите его подождать вас 109 наносекунд (лучше сказать, что вы будете через 1 секунду, в эквивалентных, но более удобных единицах времени). Для физиков столь же странно измерять энергию космологической постоянной в граммах на кубический сантиметр. По причинам, которые скоро прояснятся, естественным выбором будет выражение величины космологической постоянной в виде множителя от так называемой планковской массы (примерно 10−5 грамма), делённой на планковскую длину в кубе (куб с ребром примерно 10−33 сантиметра, что даёт для объёма примерно 10−99 кубического сантиметра). Измеренная в таких единицах величина космологической постоянной составляет примерно 10−123, крохотное число, приведённое в самом начале этой главы.{51}
Можно ли доверять такому результату? За годы, прошедшие с момента первых измерений, были получены ещё более убедительные данные, подтверждающие ускоренное расширение. Более того, новые экспериментальные данные (направленные, например, на анализ детальных свойств реликтового излучения; см. книгу «Ткань космоса», глава 14) прекрасно согласуются с данными по сверхновым. Если и есть место для манёвра, то оно может быть связано только с самим объяснением ускоренного расширения. Принимая, что общая теория относительности является математическим описанием гравитационного взаимодействия, единственной возможностью действительно является антигравитация, порождённая космологической постоянной. Другие возможные объяснения можно получить, если изменить эту картину, включив в неё дополнительные экзотические квантовые поля (которые, подобно тому что мы видели в инфляционной космологии, могут в определённые периоды космической эволюции маскироваться под космологическую постоянную){52}, либо изменить уравнения общей теории относительности (чтобы гравитационное притяжение убывало с расстоянием сильнее, чем это следует из механики Ньютона или теории Эйнштейна, позволяя таким образом удалённым областям разлетаться быстрее и не требуя присутствия космологической постоянной). Однако на сегодняшний день простейшее и наиболее убедительное объяснение наблюдаемому ускоренному расширению состоит в том, что космологическая постоянна отлична от нуля, а потому пространство заполнено тёмной энергией.
Для многих исследователей открытие ненулевой космологической постоянной стало самым удивительным наблюдательным результатом, о котором они когда-либо слышали.
Объяснение нуля
Когда я впервые столкнулся с данными по сверхновым, предполагающими ненулевое значение космологической постоянной, моя реакция была типичной для многих физиков. «Этого просто не может быть!» Большинство (но не все) теоретиков давно пришли к выводу, что значение космологической постоянной равно нулю. Такая точка зрения изначально возникла из истории про «самую большую ошибку Эйнштейна», но со временем возникло множество убедительных аргументов в её поддержку. Самый сильный основан на принципе квантовой неопределённости.
В силу квантовой неопределённости и сопутствующих флуктуаций, присущих всем квантовым полям, даже в пустом пространстве происходит неистовая микроскопическая активность. Подобно атомам, сталкивающимся со стенками сосуда, или детям, прыгающим по детской площадке, квантовые флуктуации обладают определённой энергией. Однако, в отличие от атомов и детей, квантовые флуктуации повсеместны и неизбежны. Нельзя объявить, что некоторая область пространства закрыта и отправить все квантовые флуктуации домой; энергия, присущая квантовым флуктуациям, пронизывает всё пространство и не может быть удалена. Поскольку космологическая постоянная есть не что иное, как энергия, пронизывающая пространство, то квантовые флуктуации являются именно тем микроскопическим механизмом, который порождает космологическую постоянную. Осознание этого факта имеет первостепенное значение. Вспомните, когда Эйнштейн ввёл понятие космологической постоянной, он сделал это абстрактно — не уточняя, чем она может быть на самом деле, откуда она может появиться и какое иметь происхождение. Установление связи с квантовыми флуктуациями сделало неизбежным возникновение космологической постоянной: если бы Эйнштейн её не придумал, то кто-нибудь другой, знакомый с квантовой физикой, обязательно бы сделал это. Как только мы принимаем во внимание квантовую механику, мы сталкиваемся с энергией полей, однородно распределённой в пространстве, что напрямую приводит нас к понятию космологической постоянной.
Вопрос только в численном значении. Сколько энергии содержится в вездесущих квантовых дрожаниях? Когда теоретики проделали соответствующие вычисления, получившийся ответ оказался довольно нелепым: в любом объёме пространства должно присутствовать бесконечное количество энергии. Чтобы понять почему, представьте квантовые дрожания поля внутри пустой коробки произвольного размера. На рис. 6.3 показаны примерные профили квантовых флуктуаций. Каждая флуктуация даёт вклад в энергию поля (чем короче длина волны, тем быстрее скорость флуктуации, следовательно, выше энергия). Поскольку существует бесконечно много возможных волновых профилей, у каждого из которых длина волны меньше, чем у предыдущего, то полная энергия квантовых флуктуаций бесконечна.[39]
Рис. 6.3. Существует бесконечно много волновых профилей в любом конечном объёме, следовательно, бесконечно много различных квантовых дрожаний. Это приводит к проблемному выводу о бесконечности энергии
И хотя совершенно очевидно, что такой вывод неприемлем, учёные не особо из-за этого переживали, потому что распознали в этой ситуации отражение хорошо известной проблемы, которую мы обсуждали ранее: противоречие между гравитацией и квантовой механикой. Всем было известно, что нельзя доверять выводам квантовой теории поля на супермалых расстояниях. Квантовые дрожания с длиной волны порядка планковской длины, 10−33 сантиметра и меньше, имеют энергию (эквивалентно, массу по формуле m = E/c2) настолько большую, что начинает играть роль гравитационное взаимодействие. Для адекватного описания квантовых флуктуаций необходимо иметь теорию, совмещающую общую теорию относительности и квантовую механику. Идейно это приводит к теории струн или к любой другой квантовой теории, включающей гравитацию. Но немедленный и более прагматичный ответ состоял в том, чтобы просто пренебречь всеми квантовыми флуктуациями на расстояниях меньше планковской длины. Если этого не сделать, то наши вычисления, очевидно, выйдут за пределы применимости квантовой теории поля. Ожидалось, что когда-нибудь мы поймём теорию струн или квантовую гравитацию настолько хорошо, что сможем проводить вычисления с учётом квантовых флуктуаций, но пока в качестве временной меры предлагалось поместить самые быстрые флуктуации на математический карантин. Смысл этой директивы прозрачен: если проигнорировать флуктуации с длиной волны короче, чем планковская длина, их останется лишь конечное число, поэтому энергия в пустом пространстве будет тоже конечной.
Это уже прогресс. По меньшей мере такой трюк отодвигает проблему под ответственность будущих открытий, которые, постучим по столу, смогут приручить супермалые длины волн квантовых флуктуаций. Но даже при таком отсечении для энергии конечных квантовых флуктуаций всё равно получился гигантский ответ, примерно 1094 грамм на кубический сантиметр. Это намного больше, чем все звёзды во всех известных галактиках, сжатые до размера напёрстка. Рассматривая бесконечно малый кубик с ребром, равным планковской длине, приходим к выводу, что эта колоссальная плотность составляет 10−5 грамма на куб планковской длины, или 1 планковская масса на планковский объём (именно поэтому такие единицы измерений как килограммы для картофеля и секунды для ожидания являются естественным и разумным выбором). Космологическая постоянная такой величины приведёт к невообразимо быстрому взрыву, так что всё, начиная с галактик и кончая отдельными атомами, просто разорвёт в клочья. С количественной стороны астрономические наблюдения установили жёсткий предел на то, как велика может быть космологическая постоянная, если она вообще существует, а теоретические результаты превысили этот предел на умопомрачительный множитель, больше чем на сотни порядков величины. Хотя большая энергия, заполняющая пространство, лучше, чем бесконечная, физики осознали отчаянную необходимость радикально уменьшить результат своих вычислений.
Именно здесь предвзятость теоретиков выходит на первый план. Предположим на мгновение, что космологическая постоянная не просто мала. Пусть она равна нулю. Ноль — это любимое число всех теоретиков, потому что имеется верный и испытанный способ его возникновения в вычислениях — симметрия. Например, представим, что Арчи был отправлен на курсы повышения квалификации и в качестве домашнего задания должен сложить первые десять чисел, возведённых в шестьдесят третью степень, 163 + 263 + 363 + 463 + 563 + 663 + 763 + 863 + 963 + 1063 и затем сложить полученный результат с суммой первых десяти отрицательных чисел, возведённых в шестьдесят третью степень, (−1)63 + (−2)63 +(−3)63 + (−4)63 + (−5)63 + (−6)63 + (−7)63 + (−8)63 + (−9)63 + (−10)63. Что получится в итоге? В тот момент, когда он кропотливо вычисляет, отчаиваясь всё сильнее и сильнее, умножая и затем складывая вместе числа, у которых более полусотни знаков, вмешивается Эдита. Она говорит: «Воспользуйся симметрией, Арчи». «Что?» — не понимает он. Эдита имеет в виду, что для каждого слагаемого в первой сумме имеется симметричный партнёр во второй сумме: 163 и (−1)63 в сумме дают ноль (отрицательное число, возведённое в нечётную степень, остаётся отрицательным), 263 и (−2)63 в сумме дают ноль, и так далее. Симметрия между двумя выражениями приводит к полному взаимному сокращению, как будто два ребёнка одинакового веса сидят на противоположных сторонах качелей. Без каких-либо вычислений Эдита находит, что ответ равен нулю.
Многие физики полагают — правильнее было бы сказать, надеются, — что некое подобное полное сокращение, обусловленное ещё не открытой симметрией физических законов, исправит вычисление энергии квантовых флуктуаций. Было высказано предположение, что когда наше понимание физики выйдет на новый уровень, будет выявлен некоторый огромный, пока неизвестный вклад, который скомпенсирует огромную энергию квантовых флуктуаций. Можно сказать, что это почти единственная стратегия, придуманная физиками, чтобы укротить неконтролируемые результаты грубых вычислений. Именно поэтому многие теоретики пришли к выводу, что космологическая постоянная обязана быть равной нулю.
В суперсимметричных моделях возникает конкретный пример того, как можно осуществить этот сценарий. Вспомним из главы 4 (табл. 4.1), что суперсимметрия приводит к парам частиц и, следовательно, парам полей: электрон составляет пару частице, названной суперсимметричным электроном, или сэлектроном, для краткости; кварки и скварки; нейтрино и снейтрино и так далее. На данный момент все такие «счастицы» являются гипотетичными, но эксперименты на Большом адронном коллайдере могут изменить ситуацию в течение ближайших нескольких лет. Так или иначе, при математическом анализе квантовых флуктуаций, связанных с каждой парой полей, всплывает один интригующий факт. Для каждой флуктуации первого поля имеется соответствующая флуктуация его партнёра с такой же формой, но противоположным знаком, точно так же как в домашнем задании Арчи. Так же как в том примере, при сложении все такие вклады пара за парой сокращаются, и окончательный ответ оказывается равным нулю.[40]
Подвох, и достаточно серьёзный, в том, что полное сокращение происходит тогда, когда оба партнёра имеют не только одинаковые электрические и ядерные заряды (что так и есть), но и одинаковые массы. Но экспериментальные данные исключают такую возможность. Даже если в природе и есть суперсимметрия, из наблюдений следует, что она не может быть реализована в самой полной форме. Пока не открытые частицы (сэлектроны, скварки, снейтрино и тому подобное) должны быть значительно тяжелее своих известных партнёров — только так можно объяснить, почему они до сих пор не были обнаружены в экспериментах на ускорителях. При разных массах частиц симметрия нарушается, баланс разбалансирован, сокращения неполные; итоговое значение опять огромно.
В течение многих лет было выдвинуто множество подобных принципов и механизмов сокращения, но ни один из них не достиг цели доказать теоретически равенство нулю космологической постоянной. Но даже в этой ситуации большинство исследователей воспринимали данный факт просто как отражение неполноты нашего понимания физики, а не как ключ к тому, что наша вера в равенство нулю космологической постоянной была ошибочна.
Одним из физиков, отвергающим ортодоксальный взгляд на проблему, был нобелевский лауреат Стивен Вайнберг.[41] В статье, опубликованной в 1987 году, более чем за десять лет до революционных данных по сверхновым, Вайнберг предложил альтернативный теоретический подход, приведший к радикально иному результату: малой, но не равной нулю космологической постоянной. При вычислениях Вайнберг исходил из идеи, относящейся к разряду тех, что делят физическое сообщество на два лагеря, — идеи, одними почитаемой, а другими отторгаемой, идеи, которую одни называют глубокой, а другие считают глупостью. Её официальное, хоть и обманчивое название — антропный принцип.
Космологическая антропность
Гелиоцентрическая модель солнечной системы Николая Коперника как ничто лучше доказывает, что мы, люди, отнюдь не центр Вселенной. Современные открытия упрочили этот урок, да ещё как! Теперь мы понимаем, что открытие Коперника всего лишь одно из череды доказательств, опровергающих столь долго лелеянные нами представления об особом статусе человечества: мы живём не в центре Солнечной системы, не в центре Галактики, не в центре Вселенной, мы даже не сделаны из тёмной материи, составляющей бо́льшую часть массы во Вселенной. Такое космическое понижение в статусе, от примы до статиста, является примером того, что учёные называют теперь принципом Коперника: в полной системе бытия всё указывает на то, что людям не предназначена сколь-нибудь особая роль.
Почти пятьсот лет спустя после работы Коперника на юбилейной конференции в Кракове один из докладов — представленный австралийским физиком Брэндоном Картером — вдруг заманчиво предложил неожиданный пересмотр принципа Коперника. Картер предположил, что излишняя приверженность коперниковским взглядам может, при определённых условиях, лишить исследователей возможности достичь прогресса. Да, соглашался Картер, человечество находится отнюдь не во главе устройства бытия. Но всё же, продолжал он, поддерживая похожие высказывания таких учёных, как Альфред Рассел Уоллес, Абрагам Зелманов и Роберт Дикке, есть сцена, на которой мы действительно играем совершенно исключительную роль — наши собственные наблюдения. Сколь бы далеко не отодвинул нас Коперник и его заветы, мы первые в списке, когда речь идёт о сборе и анализе данных, формирующих основу наших представлений о природе. И в силу такого неизбежного положения мы обязаны принимать во внимание то, что в статистике называется систематической ошибкой отбора.
Это простая идея, которая широко применяется. Если вы изучаете популяцию форели, но собираете данные лишь в пустыне Сахара, то вся полученная информация будет искажена неправильным фокусом на недружественной для форели среде обитания. Если вы изучаете интерес общества к опере, но проводите опрос только среди подписчиков журнала «Не могу жить без оперы», то результаты будут неточны, потому что опрашиваемые не являются типичными представителями населения в целом. Если вы проводите опрос в группе беженцев, перенёсших невероятные трудности во время переселения, то можете прийти к выводу, что эта этническая группа одна из самых жизнестойких на планете. Однако, когда вы узнаете тот удручающий факт, что те, с кем вы говорили, составляют лишь 1 процент от всех, кто был вынужден бежать из своей страны, то поймёте, что ваш вывод далёк от истины, потому что только феноменально сильные люди пережили такую миграцию.
Рассмотрение таких ошибок крайне важно для получения осмысленных результатов и во избежание напрасных усилий для объяснения выводов, сделанных на основе нерепрезентативных данных. Почему форель вымерла? В чём причина лихорадочного интереса к опере в обществе? Почему эта этническая группа настолько вынослива? Необъективные наблюдения могут заставить вас пуститься в бессмысленные поиски объяснений несуществующих вещей.
В большинстве случаев ошибки подобного рода легко определяются и устраняются. Но есть ошибки не столь очевидные, которые легко можно проглядеть. Это то, насколько ограничения на место и время, где и когда мы можем жить, имеют огромное влияние на то, что мы можем видеть. Если нам не удаётся адекватно воспринять последствия подобных ограничений на наши наблюдения, то тогда, подобно описанным выше примерам, мы можем прийти к совершенно неправильным выводам, в том числе к таким, которые могут побудить нас к бесплодным попыткам объяснить смысл дырки от бублика.
Представьте, например, что вы намереваетесь выяснить (подобно великому учёному Иоганну Кеплеру), почему Земля расположена в 150 миллионах километров от Солнца. Вы хотите найти нечто, оставаясь исключительно в рамках физических законов, что даст объяснение этому факту. Долгие годы вы упорно трудитесь, но не в силах найти убедительное объяснение. Имеет ли смысл продолжать? Если вы задумаетесь о потраченных усилиях и учтёте систематическую ошибку отбора, то быстро сообразите, что гоняетесь за тенью.
Законы гравитации Ньютона и Эйнштейна позволяют планетам двигаться вокруг Солнца по орбитам произвольного радиуса. Если бы вы могли передвинуть Землю на любое другое расстояние от Солнца и затем запустить заново с правильной скоростью (её просто вычислить с помощью основных физических законов), то она также легко будет вращаться по новой орбите. Единственное, что важно в положении Земли на расстоянии в 150 миллионов километров от Солнца — это температурный режим, благоприятствующий нашему присутствию здесь. Если Земля будет расположена гораздо ближе или дальше от Солнца, температура будет значительно выше или ниже, что приведёт к исчезновению важнейшей части, существенной для нашей формы жизни — жидкой воды. Это отражает встроенную систематическую ошибку. Сам факт того, что это мы измеряем расстояние от нашей планеты до Солнца, гарантирует, что полученный результат должен попасть в ограниченный диапазон значений, совместимых с самим нашим существованием. Иначе нас бы здесь не было, и некому было бы размышлять над расстоянием от Земли до Солнца.
Если бы Земля была единственной планетой в Солнечной системе или единственной планетой во Вселенной, то вы всё же могли бы чувствовать себя обязанным продолжить исследования. Хорошо, сказали бы вы, я понимаю, что моё собственное существование привязано к определённому расстоянию от Земли до Солнца, но это лишь усиливает необходимость объяснить, почему так получилось, что Земля расположена в таком удобном, привлекательном с точки зрения жизни месте? Является ли это всего лишь удачным совпадением? И есть ли более глубокое объяснение этому факту?
Но Земля не единственная планета во Вселенной и даже в Солнечной системе. Есть много других. Это заставляет посмотреть на вещи под иным углом. Чтобы понять, что я имею в виду, представьте, что вы зашли в обувной магазин. Вы почему-то считаете, будто в этом обувном магазине есть обувь только одного размера. Представляете, как вы обрадуетесь, когда продавец принесёт вам пару ботинок, идеально вам подходящих. «Из всех возможных размеров обуви, — подумаете вы, — удивительно, что этот размер оказался именно моим. Является ли это всего лишь счастливым совпадением? И есть ли более глубокое объяснение этому факту?» Но вопрос отпадёт, как только вы узнаете, что магазин продаёт обувь всех размеров. Похожая ситуация имеет место во Вселенной со многими планетами, расположенными на разных расстояниях от своих звёзд. Так же как нет ничего удивительного в том, что среди всех размеров обуви в магазине нашёлся по крайней мере один подошедший вам, так же нет ничего удивительного, что среди всех планет во всех солнечных системах во всех галактиках есть, по крайней мере, одна, расположенная на правильном расстоянии от звезды, что даёт климат, благоприятствующий нашей форме жизни. Конечно, мы с вами живём на одной из таких планет. Мы просто не сможем развиваться и жить на других планетах.
Поэтому нет никакой фундаментальной причины, почему Земля находится на расстоянии в 150 миллионов километров от Солнца. Определённое значение орбитального расстояния планеты от звезды обусловлено набором исторических случайностей, неисчислимых тонкостей в свойствах вращающегося газового облака, из которого образовывается та или иная солнечная система; это событие зависит от множества обстоятельств, не имеющих фундаментального объяснения. Действительно, такие астрофизические процессы привели к образованию планет во всём космосе, вращающихся вокруг своих звёзд на разных расстояниях. Мы живём на одной из них, расположенной на расстоянии в 150 миллионов километров от нашего Солнца, потому что именно на такой планете может развиваться наша форма жизни. Неспособность учесть эту систематическую ошибку отбора приведёт нас к поиску более глубокого ответа. Но это мартышкин труд.
Статья Картера подчёркивала важность принятия во внимание подобной систематической ошибки, учёт которой был назван им антропным принципом (неудачное название, потому что эта идея в равной степени применима к любой форме разумной жизни, которая проводит и анализирует наблюдения, а не только к человечеству). Никто не стал возражать против этой части рассуждений Картера. Дискуссионной оказалась часть, где он предположил, что антропный принцип может быть распространён не просто на отдельные объекты во Вселенной, например орбитальные расстояния планет, но и на всю Вселенную в целом.
Чтобы это могло значить?
Представьте, что вы размышляете над некоторым фундаментальным свойством Вселенной, скажем, массой электрона, 0,00054 (в долях от массы протона), или над силой электромагнитного поля, 0,0073 (в терминах его константы связи), или над главной нашей целью в этой главе — величиной космологической постоянной, 1,38 × 10−123 (выраженной в планковских единицах). Вы намерены объяснить, почему эти константы имеют именно такие значения. Пытаетесь снова и снова, но остаётесь с пустыми руками. Сделайте шаг назад, говорит Картер. Возможно, что причина ваших неудач такая же, как при объяснении расстояния от Земли до Солнца: фундаментального объяснения просто не существует. Подобно существованию множества планет на разных расстояниях, среди которых есть и планета, населённая нами, потому что её орбита приводит к благоприятным условиям для жизни, возможно, существует много вселенных с разными значениями «констант», а мы с необходимостью находимся во Вселенной, в которой эти значения благоприятствуют нашему существованию.
При таком образе мысли спрашивать, почему константы имеют такие значения, какие они имеют, неправильно. Нет никакого закона, определяющего их значения; они могут варьироваться, и действительно варьируются, внутри мультивселенной. Наша внутренняя систематическая ошибка отбора гарантирует, что мы находимся в той части мультивселенной, в которой привычные нам значения констант таковы просто потому, что мы не можем существовать в частях мультивселенной с другими значениями констант.
Отметим, что в случае, когда наша Вселенная единственная, подобные рассуждения теряют смысл, и вы по-прежнему можете задаваться вопросами насчёт «счастливого совпадения» или «глубокого понимания». Подобно тому как убедительное объяснение наличия в обувном магазине именно вашего размера требует, чтобы полки в магазине были плотно набиты обувью разных размеров, подобно тому как убедительное объяснение существования планеты, расположенной на биологически благоприятном расстоянии от звезды требует, чтобы существовало много планет, вращающихся вокруг своих звёзд на разных расстояниях, точно так же убедительное объяснение значений фундаментальных констант в природе требует огромного выбора вселенных, наделённых разными значениями констант. Только тогда — в рамках концепции мультивселенной — антропный принцип способен развеять ореол загадочности.[42]
Тогда очевидно, что ваша готовность принять антропный принцип зависит от того, насколько сильно вы верите в следующие три существенные предположения: (1) наша Вселенная — это часть мультивселенной; (2) в разных вселенных мультивселенной константы находятся в широком диапазоне возможных значений; (3) жизнь в известной нам форме невозможна при почти всех отклонениях от наблюдаемых значений констант.
В 1970-х году, когда Картер выдвинул эти идеи, на обсуждение концепции параллельных вселенных было наложено табу. Да и сейчас есть достаточно причин для скептицизма. Но мы видели в предыдущих главах, что хотя выбор того или иного конкретного вида мультивселенной остаётся сугубо умозрительным, есть причины серьёзно отнестись к такому новому взгляду на окружающую нас действительность. Это доводы в пользу предположения (1). Многие учёные сейчас им следуют. Что касается предположения (2), мы видели, что, например, в инфляционной мультивселенной и мультивселенной на бране значения фундаментальных констант природы действительно могут варьироваться от вселенной к вселенной. Далее в этой главе мы остановимся на этом вопросе более подробно.
Но как насчёт предположения (3), о взаимосвязи жизни с определёнными значениями констант?
Жизнь, галактики и фундаментальные числа природы
Даже небольшие отклонения от настоящих значений большинства фундаментальных констант в природе сделают жизнь в привычном нам виде невозможной. Увеличьте гравитационную постоянную, звёзды начнут сгорать быстрее и жизнь на близлежащих планетах не будет успевать развиваться. Уменьшите её, и галактики распадутся на части. Усильте электромагнитное взаимодействие, и атомы водорода будут отталкиваться друг от друга слишком сильно, чтобы образовывать устойчивые соединения, и это лишит звёзды необходимого топлива.{53} Но как быть с космологической постоянной? Зависит ли существование жизни от её значения? Именно этот вопрос поднял Стивен Вайнберг в своей статье 1987 года.
Понимая, что зарождение жизни является сложным процессом, о котором мы мало что понимаем, Вайнберг решил, что безнадёжно пытаться выяснять, каким образом то или иное значение космологической постоянной напрямую влияет на мириады явлений, вдыхающих жизнь в мёртвую материю. Однако Вайнберг не отступил от цели, а нашёл хитроумного посредника для задачи о зарождении жизни — зарождение галактик. Без галактик, рассуждал он, образование звёзд и планет станет сомнительным и не оставит никакого шанса на зарождение жизни. Такой подход к проблеме не только в высшей степени разумен, но ещё и полезен: он переносит акцент на рассмотрение того, как разные значения космологической постоянной влияют на процесс образования галактик, а эту задачу можно уже попытаться решить.
Суть физического процесса элементарна. Хотя точные детали образования галактик являются отдельной областью активных исследований, в общих чертах процесс напоминает эффект снежного кома в астрономических масштабах. Как только где-то возникает сгусток вещества, то в силу своей повышенной плотности он оказывает большее гравитационное притяжение на находящуюся поблизости материю, в результате чего ком ещё больше увеличивается. Этот процесс всё нарастает и нарастает, и наконец образуется разогретая масса пыли и газа, из которой появляются звёзды и планеты. Идея Вайнберга состояла в том, что если космологическая постоянная будет иметь достаточно большое значение, то она прервёт такой комообразующий процесс. Порождаемое космологической константой гравитационное отталкивание может оказаться достаточно сильным, чтобы прервать процесс зарождения галактик на начальной стадии образования кома, когда он ещё мал и хрупок, так что составляющее его вещество разлетится прежде, чем ком успеет укрупниться, притягивая окружающее вещество.
Вайнберг сделал математические расчёты и обнаружил, что если значение космологической постоянной в несколько сотен раз превысит современную космологическую плотность вещества — несколько протонов на кубический метр, — то процесс образования галактик нарушится. (Вайнберг также рассмотрел случай отрицательной космологической постоянной. Возникающие при этом ограничение ещё сильнее, потому что отрицательное значение приводит к росту гравитационного притяжения и заставляет всю Вселенную схлопнуться прежде, чем звёзды успеют зажечься.) Если теперь представить, что мы являемся частью мультивселенной, в которой значения космологической постоянной изменяются в широком диапазоне от вселенной к вселенной, так же как изменяются и расстояния от планет до их звёзд от одной солнечной системы до другой солнечной системы, — то единственные вселенные, в которых возможны галактики, и, следовательно, единственные вселенные, в которых мы можем жить, это те, где космологическая постоянная принимает значения, не превышающие предел Вайнберга, что составляет примерно 10−121 в планковских единицах.
На фоне многолетних безуспешных попыток работа Вайнберга стала первой, где были получены теоретические значения для космологической постоянной, не превышающие до абсурдной степени ограничений, накладываемых наблюдательной астрономией. При этом она не противоречила широко распространённому в то время убеждению, что космологическая постоянная равна нулю. Сам Вайнберг не остановился на этом и сделал шаг вперёд, придав этому результату следующую интерпретацию. Он предложил, что мы находимся во вселенной, в которой космологическая постоянная мала настолько, насколько необходимо, чтобы мы смогли существовать, но не значительно меньше. Значительно меньшая константа, рассуждал он, потребует объяснения, выходящего за рамки простого утверждения о согласованности с нашим существованием. Именно такого объяснения, которое всё это время доблестно искала наша физика, но не нашла. Это позволило Вайнбергу предположить, что однажды с помощью более точных измерений будет установлено, что космологическая постоянная не равна нулю, а имеет значение, близкое или пограничное с вычисленным им пределом. Как мы видели, спустя десять лет после появления работы Вайнберга, наблюдения в рамках проекта «Supernova cosmology» и поисковой группы «High-Z Supernova» подтвердили это пророческое предсказание.
Для полного осознания всей нестандартности этого подхода к объяснению давней проблемы рассмотрим более подробно ход рассуждений Вайнберга. Он полагал, что в мультивселенной должно быть так много вселенных, что обязательно должна найтись по крайней мере одна вселенная с наблюдаемым значением космологической постоянной. Но какой должна быть мультивселенная, чтобы это произошло наверняка или с высокой степенью вероятности?
Для ответа на этот вопрос рассмотрим сперва аналогичную проблему, но с более простыми и понятными числами. Представьте, что вы работаете на известного кинопродюсера Харви В. Айнштейна, который попросил вас провести кастинг на исполнителя главной роли в его новом фильме «Криминальное диво». «Какого роста нужен актёр?» — спрашиваете вы. «Без понятия. Выше метра, ниже двух. Но ты должен быть уверен, что какой бы рост я не выбрал, у тебя должен быть подходящий кандидат». Вы только открыли рот, чтобы поправить вашего босса, сказав, что в силу квантовой неопределённости на самом деле нет никакой необходимости иметь исполнителей любого роста, но, вспомнив, что стало с надоедливой говорящей мухой, вы решили, что лучше промолчать.
Теперь вы стоите перед выбором. Сколько актёров нужно привести на просмотр? Вы думаете так: если В. измеряет рост с точностью до сантиметра, то в диапазоне от одного до двух метров есть сто разных вариантов. Поэтому необходимо иметь по крайней мере сто актёров. Но так как некоторые актёры могут оказаться одинакового роста, и тогда какой-то рост не будет представлен, то лучше собрать больше сотни. Чтобы подстраховаться, возможно, следует позвонить нескольким сотням актёров. Это много, но меньше, чем понадобится, если И. начнёт измерять рост с точностью до миллиметра. В этом случае в пределах от одного метра до двух есть тысяча разных вариантов, поэтому будет надёжнее собрать несколько тысяч актёров.
Похожие рассуждения применимы и для вселенных с разными космологическими постоянными. Предположим, что все вселенные в мультивселенной обладают космологическими константами со значениями между нулём и единицей (в обычных планковских единицах); при меньших значениях вселенные будут схлопываться, а при больших значениях применимость наших математических методов будет под вопросом, и понимание ситуации, соответственно, тоже. Итак, подобно актёрам, чья разница в росте варьируется от 0 до 1 (в метрах), космологические постоянные вселенных варьируются от 0 до 1 (в планковских единицах). Если думать о точности измерений, то аналогом того, как В. изменяет рост с помощью сантиметровой или миллиметровой линейки, будет погрешность, с которой мы можем измерить космологическую постоянную. Погрешность современных измерений составляет примерно 10−124 (в планковских единицах). В будущем, точность измерений конечно же возрастёт, но как мы увидим, это вряд ли повлияет на наши выводы. Тогда подобно тому, как в диапазоне в один метр имеется 102 различных возможных отметок для роста, разделённых между собой интервалом по меньшей мере в 10−2 метра (1 сантиметр) и 103 различных возможных отметок для роста с интервалом по меньшей мере в 10−3 метра (1 миллиметр), существует 10124 различных значений космологической постоянной с интервалом 10−124 в диапазоне значений от 0 до 1.
Чтобы гарантировать реализацию каждого возможного значения космологической постоянной, необходимо иметь мультивселенную, в которой по-меньшей мере 10124 разных вселенных. Но как и в ситуации с актёрами необходимо учитывать возможные повторения — вселенные с одинаковыми значениями космологической постоянной. Чтобы каждое значение космологической постоянной наверняка было реализовано, следует располагать мультивселенной с числом вселенных, гораздо большим, чем 10124, например в миллион раз бо́льшим, что даст красивую цифру 10130. Я так непринуждённо жонглирую этими числами, потому что они настолько велики, что точное значение вряд ли является важным. Ни один из известных примеров чего-либо, будь то число клеток в человеческом теле (1013), число секунд, прошедших с момента Большого взрыва (1018), число фотонов в наблюдаемой части Вселенной (1088), даже близко не похоже на воображаемое число вселенных. Подводя итог, можно сказать, что подход Вайнберга для объяснения значения космологической постоянной применим, только когда мы являемся частью мультивселенной, содержащей огромное число различных вселенных; их космологические постоянные должны принимать примерно 10124 различных значений. Только в случае такого гигантского количества вселенных существует вероятность, что среди них найдётся одна с нашим значением космологической постоянной.
Здесь возникает вопрос, есть ли теоретические модели, которые естественным образом приводят к такому захватывающему изобилию вселенных с разными космологическими постоянными?{54}
От недостатка к достоинству
Да, есть. Мы уже встречались с такой моделью в предыдущей главе. Подсчёт различных возможных форм дополнительных измерений в теории струн, с учётом пронизывающих их потоков, дал примерно 10500. Это намного больше, чем 10124. Даже умножив 10124 на несколько сот порядков величины, всё равно 10500 будет значительно больше. Вычтем 10124 из 10500, потом ещё раз, и ещё, и так миллиард раз подряд, и всё равно это будет почти незаметно. В результате получится примерно всё то же 10500.
Важно, что космологическая постоянная действительно варьируется от одной такой вселенной к другой. Подобно тому как магнитный поток несёт энергию (и может двигать предметы), потоки внутри дырок в пространствах Калаби — Яу обладают энергией, величина которой очень чувствительна к геометрическим особенностям данного пространства. Если имеются два разных пространства Калаби — Яу с разными потоками, проходящими сквозь разные дырки, то их энергии, как правило, будут отличаться. Поскольку заданное пространство Калаби — Яу прикреплено к каждой точке трёх обычных измерений пространства, подобно петелькам ворса, прикреплённого к большому основанию ковра, энергия, содержащаяся в данном пространстве, будет равномерно заполнять три больших измерения, подобно тому как смачивание индивидуальных волокон в ворсе ковра приведёт к утяжелению всего ковра. Таким образом, какое бы из 10500 различных одетых пространств Калаби — Яу не определяло геометрию дополнительных измерений, энергия, которой оно обладает, даст вклад в космологическую постоянную. Результаты, полученные Рафаэлем Буссо и Джо Польчински, дают количественную оценку этой ситуации. Они показали, что различные космологические постоянные, к которым приводят приблизительно 10500 различных возможных пространств дополнительных измерений, равномерно распределены по широкому диапазону значений.
Как по заказу! Наличие 10500 отметок, распределённых в диапазоне от 0 до 1, гарантирует, что найдётся очень много со значениями, лежащими совсем рядом с теми значениями космологической постоянной, которые астрономы измеряют последние десяток лет. Возможно, что найти точные примеры среди 10500 вариантов не получится, потому что даже самые быстрые современные компьютеры тратят одну секунду на анализ каждой формы дополнительных измерений, так что через миллиард лет будут рассмотрены лишь какие-то жалкие 1023 примеров. Однако это сильные доводы в пользу того, что они существуют.
Конечно, набор из 10500 разных форм дополнительных измерений очень далёк от той единственной вселенной, о которой мы мечтали в теории струн. Тем, кто верит в мечту Эйнштейна о единой теории поля, описывающей единственную вселенную — нашу, — эти рассуждения причиняют сильный дискомфорт. Однако анализ вопроса о космологической постоянной представляет ситуацию в ином свете. Вместо того чтобы отчаиваться из-за того, что, по всей видимости, единственной вселенной не получится, нам следует радоваться: благодаря теории струн самая невероятная часть из объяснения Вайнбергом малости значения космологической постоянной — требование наличия огромного количества разных вселенных, значительно превышающего 10124 — неожиданно становится правдоподобной.
Заключительный шаг. Резюме
Похоже, что разные части этой захватывающей истории начинают стыковаться воедино. Однако в рассуждениях всё ещё остаётся некоторая брешь. Одно дело, когда из теории струн возникает огромное число различных вселенных. Но совсем другое дело — требовать, чтобы теория струн гарантировано обеспечивала, чтобы все возможные возникающие вселенные действительно существовали где-то там, являясь параллельными мирами внутри гигантской мультивселенной. Наиболее образно эту ситуацию охарактеризовал Леонард Сасскинд, вдохновлённый новаторской работой Шамита Качру, Ренаты Каллош, Андрея Линде и Сандипа Триведи, — если в ткань теории вплести вечную инфляцию, то брешь может затянуться.{55}
Я сейчас объясню этот заключительный шаг, но если вы уже устали и жаждете финала истории, то это можно сделать в трёх предложениях. Инфляционная мультивселенная — постоянно расширяющийся, похожий на швейцарский сыр, космос — содержит огромное, постоянно увеличивающееся число дочерних вселенных. Идея в том, что если объединить инфляционную космологию с теорией струн, то процесс вечной инфляции орошает 10500 возможных форм дополнительных измерений, возникающих в теории струн, привитых на пузырьки-вселенные, что даёт космологический способ реализации всех возможностей. Согласно этой логике, мы живём в пузырьке с такими дополнительными измерениями, такой космологической постоянной и всем остальным, которые благоприятствуют нашей форме жизни и согласуются с наблюдениями.
В оставшейся части главы я изложу это более подробно, поэтому если вам не терпится поскорее продвинуться дальше, спокойно переходите к последнему разделу.
Струнный ландшафт
Давайте вспомним аналогию, которую я использовал в главе 3 для объяснения инфляционной космологии. Вершины гор соответствовали наивысшим значениям энергии поля инфлатона в пространстве, а процесс скатывания вниз и достижение положения равновесия в низшей точке у подножия горы соответствовали тому, как инфлатон отдаёт свою энергию, которая при этом процессе преобразуется в частицы вещества и излучение.
А теперь рассмотрим заново три положения из этой аналогии уже с учётом полученных знаний. Во-первых, мы узнали, что инфлатон не единственный источник энергии, способной заполнять пространство; свои вклады дают также квантовые флуктуации всех других полей — электромагнитного, ядерного и так далее. Поэтому в используемой нами аналогии высота горы будет соответствовать совместной энергии от всех источников, однородно заполняющей всё пространство.
Во-вторых, в исходной аналогии высота подножия горы, куда в итоге скатывается инфлатон, считалась «уровнем моря», нулевой высотой, что означало, что инфлатон отдал всю свою энергию (и давление). Но после пересмотра высота подножия горы должна соответствовать совместной энергии от всех источников, заполняющей пространство, после завершения процесса инфляции. Тем самым мы получаем другой способ взглянуть на космологическую постоянную пузырька-вселенной. Таким образом, загадка объяснения нашей космологической постоянной переформулируется в загадку объяснения высоты подножия горы — почему она так близко к уровню моря, но не совпадает с ним?
В-третьих, исходно рассматривался простейший горный рельеф, когда вершина гладко переходит в основание горы, куда в итоге попадает инфлатон (см. рис. 3.1). Затем были учтены другие составляющие (поля Хиггса), эволюция которых и окончательные положения равновесия будут влиять на физические свойства и проявление пузырьков-вселенных (см. рис. 3.5). В теории струн диапазон возможных вселенных становится ещё богаче. Форма дополнительных измерений определяет физические свойства внутри конкретного пузырька-вселенной, поэтому возможные «положения равновесия», показанные как долины на рис. 3.6б, теперь будут соответствовать возможным формам дополнительных измерений. Чтобы разместить 10500 возможных форм для дополнительных измерений горный пейзаж должен быть с размахом дополнен долинами, террасами, обнажениями пород, подобно тому как показано на рис. 6.4. Любое место в горном рельефе, куда может скатиться шарик, соответствует некоторой форме дополнительных измерений; высота этого места определяет космологическую постоянную соответствующего пузырька-вселенной. На рис. 6.4 показано то, что называется струнным ландшафтом.
Рис. 6.4. Струнный ландшафт можно схематично рассматривать в виде горного рельефа, в котором разные долины соответствуют разным формам дополнительных измерений, а высота определяет величину космологической постоянной
Теперь, с учётом более тонкого понимания нашей аналогии с горным рельефом, или ландшафтом, рассмотрим как квантовые процессы влияют на форму дополнительных измерений. Мы увидим, что квантовая механика озаряет наш горный ландшафт.
Квантовое туннелирование в ландшафте
Рисунок 6.4, безусловно, схематичный (каждое из полей Хиггса на рис. 3.6 отложено в своих собственных осях; аналогично каждый из приблизительно 500 различных потоков поля, которые могут пронизывать формы Калаби — Яу, также должен быть отложен в отдельных осях — однако нарисовать горный рельеф в 500-мерном пространстве довольно затруднительно), однако этот рисунок правильно отражает тот факт, что вселенные с разными формами дополнительных измерений являются частями единого рельефа.{56} И если учесть квантовые эффекты, воспользовавшись результатами, полученными легендарным физиком Сиднеем Коулменом в соавторстве с Фрэнком де Луччией, то взаимосвязи между разными вселенными приведут к удивительным превращениям.
Ключевым физическим процессом при рассмотрении квантовых эффектов в мультивселенной является квантовое туннелирование. Представьте частицу, например электрон, налетающую на твёрдый барьер, пусть это будет стальная плита толщиной в три метра. Классическая физика говорит, что электрон не сможет пройти сквозь барьер. Отличительная черта квантовой механики состоит в том, что неумолимый классический вердикт «не сможет пройти», часто преобразуется в более мягкое квантовое утверждение «есть малая, но не равная нулю вероятность, что сможет». Причина в том, что квантовые флуктуации частицы позволяют ей время от времени неожиданно материализоваться на другой стороне непроницаемого барьера. Момент, когда такое квантовое туннелирование происходит, совершенно случаен; самое большее, что мы можем сделать, — это предсказать вероятность того, что это случиться в тот или иной временно́й интервал. Однако математические расчёты показывают, что если подождать достаточно долго, туннелирование произойдёт сквозь любой барьер. И оно действительно происходит. Если бы это не происходило, то Солнце не смогло бы светить: для сближения ядер водорода на расстояние, достаточное для начала ядерного синтеза, они должны протуннелировать сквозь барьер электромагнитного отталкивания протонов.
Коулмен и де Луччия, а затем и многие их последователи, отмасштабировали квантовое туннелирование от одной частицы до целой вселенной, перед которой также встаёт «непреодолимый» барьер, отделяющий текущую конфигурацию вселенной от другой возможной конфигурации. Чтобы качественно понять полученный ими результат, представьте себе две вселенные, одинаковые во всём кроме некоторого поля, равномерно заполняющего каждую из них, энергия которого выше в одной и ниже в другой. Если барьера нет, более высокое значение поля скатится до более низкого, подобно скатывающемуся с холма шарику при обсуждении инфляционной космологии. Но что произойдёт, если кривая энергии поля имеет «горный выступ», отделяющий данное значение от искомого, как показано на рис. 6.5? Коулмен и де Луччия обнаружили, что как и в случае одной частицы, вселенная поведёт себя запрещённым в классической физике образом: она может просочиться — квантово протуннелировать — сквозь барьер и оказаться в конфигурации с меньшей энергией.
Рис. 6.5. Пример кривой энергии поля с двумя значениями — двумя выемками, или долинами, — где поле естественно достигает положения равновесия. Вселенная, заполненная полем с более высоким значением, может квантово протуннелировать во вселенную с меньшим значением. В этом процессе небольшая, случайным образом расположенная область пространства в исходной вселенной приобретает меньшее значение поля; затем эта область расширяется, с трансформацией постоянно расширяющегося пространства от большей энергии к меньшей
Но поскольку мы обсуждаем вселенную, а не одну частицу, процесс туннелирования оказывается более сложным. Коулмен и де Луччия показали, что речь не идёт о том, что значение поля во всём пространстве туннелирует одновременно сквозь барьер. Наоборот, «затравочное» туннелирование порождает небольшой, случайно расположенный пузырёк, наполненный полем с меньшей энергией. Этот пузырёк растёт, подобно воннегутовскому льду-девять, постоянно расширяя область пространства, в которую поле протуннелировало к меньшей энергии.
Эти идеи можно непосредственно применить к струнному ландшафту. Представьте, что вселенная обладает какой-то определённой формой дополнительных измерений, которая соответствует левой долине на рис. 6.6а. Поскольку эта долина расположена высоко, космологическая постоянная в трёх привычных пространственных измерениях имеет большое значение — что приводит к большому гравитационному отталкиванию, — поэтому в пространстве происходит быстрое инфляционное расширение. Такая расширяющаяся вселенная со своими дополнительными измерениями показана на рис. 6.6б слева. Затем в некотором случайном месте, в случайный момент времени крохотная область пространства туннелирует сквозь промежуточный горный хребет в долину в правой части на рис. 6.6а. Не то чтобы крошечная область пространства двигалась (что бы это не значило), но меняется форма дополнительных измерений (геометрия, размер, потоки) в этой области. Дополнительные измерения в этой крошечной области трансформируются и приобретают форму, соответствующую правой долине на рис. 6.6а. Как показано на рис. 6.6б справа, эта новая дочерняя вселенная расположена внутри исходной.
Рис. 6.6. а) Квантовое туннелирование в струнном ландшафте; б) Туннелирование порождает небольшую область пространства, внутри которой произошло изменение формы дополнительных измерений (небольшой тёмный пузырёк)
Новая вселенная быстро расширяется и по мере расширения продолжает преобразовывать свои дополнительные измерения. Поскольку космологическая постоянная в новой вселенной уменьшилась — соответствующая ей высота ландшафта ниже исходной, — она испытывает меньшее гравитационное отталкивание, поэтому она будет расширяться не так быстро, как исходная. Таким образом, имеется дочерняя расширяющаяся вселенная с новой формой дополнительных измерений, расположенная внутри более быстро расширяющегося пузырька исходной вселенной с исходной формой дополнительных измерений.{57}
Процесс может повториться. Дальнейшее туннелирование в других местах внутри не только исходной вселенной, но и внутри новой вселенной, приведёт к появлению дополнительных расширяющихся пузырьков, что в свою очередь породит области с совсем другими формами дополнительных измерений (рис. 6.7). И так всё пространство будет заполнено пузырьками внутри пузырьков, расположенных, в свою очередь, внутри других пузырьков — в каждом будет происходит инфляционное расширение, каждому будет присуща своя форма дополнительных измерений и в каждом значение космологической постоянной будет меньше, чем у большего пузырька, внутри которого он образовался.
Рис. 6.7. Процесс туннелирования может повторяться, порождая обширную и сложную последовательность расширяющихся дочерних вселенных, вырастающих из пузырьков, каждая со своей формой дополнительных измерений
В итоге возникает более затейливый вариант мультивселенной в виде швейцарского сыра, рассмотренной нами при обсуждении вечной инфляции. Там было два типа областей: «сырно-заполненные» области, в которых происходит инфляционное расширение, и «дырки», в которых его нет. Такая мультивселенная напрямую соответствует упрощённому ландшафту с одной единственной горой, основание которой находится на уровне моря. Более богатый струнный ландшафт с его разнообразием вершин и долин, соответствующих разным значениям космологической постоянной, приводит к многообразию различных областей (рис. 6.7) — пузырькам внутри пузырьков, которые расположены внутри других пузырьков, подобно матрёшкам, каждая из которых раскрашена своим мастером. В итоге непрекращающиеся квантовые туннелирования сквозь гористый струнный ландшафт реализуют каждую возможную форму дополнительных измерений в том или ином пузырьке-вселенной. Это ландшафтная мультивселенная.
Именно ландшафтная мультивселенная необходима для того, чтобы принять идею Вайнберга, объясняющую значения космологической постоянной. Из наших рассуждений следует, что струнный ландшафт гарантирует, что в принципе существуют возможные формы дополнительных измерений, для которых грубая оценка для значения космологической постоянной попадает в диапазон наблюдаемых значений: в струнном ландшафте есть долины, чья крошечная высота перекликается с крошечным, но не нулевым значением космологической постоянной, которое получается из наблюдения сверхновых. Если струнный ландшафт соединить с вечной инфляцией, оживают все возможные формы дополнительных измерений, включая формы с очень малым значением космологической постоянной. Где-то внутри огромной и запутанной последовательности пузырьков, составляющих ландшафтную мультивселенную, есть вселенные со значением космологической постоянной, равным приблизительно 10−123, крохотному числу, приведённому в самом начале этой главы. Следуя этой логике рассуждений, оно соответствует тому из пузырьков, в котором мы живём.
А что с остальной физикой?
Космологическая постоянная является всего лишь одной из характеристик населяемой нами Вселенной. Эта задача находится, пожалуй, в ряду самых непонятных, потому что малость измеренного значения никак не вяжется с оценками, даваемыми устоявшимися теориями. Такое тотальное расхождение привлекает к космологической постоянной особое внимание, поэтому поиск идей, пусть даже экзотических, но способных объяснить малость космологической постоянной, является самой насущной задачей. Сторонники представленных выше идей утверждают, что струнная мультивселенная и есть именно то, что надо.
Но что делать с остальными свойствами нашей Вселенной — тремя типами существующих нейтрино, определённой массой электрона, величиной слабого ядерного взаимодействия и тому подобным? И хотя мы можем по крайней мере мечтать, что нам удастся вычислить эти фундаментальные константы, этого пока никому не удалось. Вы можете поинтересоваться, готовы ли эти числа к своему объяснению с помощью идеи мультивселенной? Оказалось, что физики, занимающиеся струнным ландшафтом, действительно обнаружили, что эти числа, подобно значению космологической постоянной, также изменяются от места к месту, и поэтому — если следовать нашему настоящему пониманию теории струн — они определены не однозначно. Это приводит к новому взгляду на проблему, весьма отличному от того, который преобладал в начале исследований. А именно мы видим, что попытка вычислить свойства фундаментальных частиц, так же как и попытка объяснить расстояние между Землёй и Солнцем, лишена, скорее всего, всякого смысла. Как и орбиты планет, некоторые (или все) свойства фундаментальных частиц будут меняться от одной вселенной к другой.
Чтобы такие рассуждения могли считаться осмысленными, мы должны по крайней мере знать, что найдутся пузырьки-вселенные с правильным значением космологической постоянной, и кроме того, что среди них будет хотя бы один пузырёк, в котором свойства взаимодействий и частиц согласуются с измерениями, полученными в нашей Вселенной. Необходимо знать наверняка, что наша Вселенная со всеми своими свойствами находится где-то внутри ландшафта. Это является целью очень активной области исследований, получившей название струнное моделестроение. Её программа состоит в математическом изучении струнного ландшафта и возможных форм дополнительных измерений с целью поиска вселенных, наиболее близко напоминающих нашу. Эта невероятно трудная задача, потому что ландшафт огромен и очень запутан, что препятствует исчерпывающему систематическому изучению. Продвижение в этом направлении требует выдающихся вычислительных способностей, а также интуитивного понимания, какие составляющие должны входить в искомую комбинацию — форма дополнительных измерений, их размер, потоки поля, пронизывающие дырки, наличие различных бран и так далее. Подобные исследования находятся на стыке строгой науки, искусства и проницательности. На сегодняшний день никому не удалось найти пример, точно воспроизводящий свойства нашей Вселенной. Однако, имея 10500 возможностей, ожидающих своего изучения, легко согласиться, что где-то внутри ландшафта есть место и для нашей Вселенной.
А это наука?
В этой главе мы совершили логический поворот. До сего момента мы рассматривали возможные сценарии для реальности, опирающиеся на достижения фундаментальной физики и космологические исследования. Я прихожу в восторг от мысли, что где-то в глубине космоса существуют, возможно, копии нашей Земли, или что наша Вселенная — это лишь один из многих пузырьков в инфляционном космосе, или что мы живём в одном из многих миров на бране, как на ломте гигантского космического хлеба. Такие идеи, безусловно, будоражат ум.
Однако в ландшафтной мультивселенной параллельные миры возникают совсем иным образом. Ландшафтная мультивселенная — это не просто более широкий взгляд на то, что может происходить где-то там. Наоборот, целый массив параллельных вселенных — миров, находящихся за рамками наших способностей видеть, изучать, как-то влиять, посещать сейчас, а возможно и никогда, нужен самым непосредственным образом для того, чтобы объяснить данные наблюдений, полученные нами здесь, в этом мире.
А это ставит перед нами очень важный вопрос: является ли это наукой?
Глава 7. Наука и мультивселенная О выводах, объяснениях и предсказаниях
Когда Дэвид Гросс, один из нобелевских лауреатов 2004 года по физике, яростно критикует струнную ландшафтную мультивселенную, он вполне мог бы процитировать речь Уинстона Черчилля, произнесённую им 29 октября 1941 года: «Никогда не уступайте… никогда, никогда, никогда — ни в чём, ни в большом, ни в малом, ни в великом, ни в мелочах — не уступайте никогда». Когда Пол Стейнхард, профессор Принстонского университета, соавтор современной инфляционной космологии, говорит о своём неприятии ландшафтной мультивселенной, он не столь патетичен, но будьте уверены, что в какой-то момент вы услышите не самое лицеприятное сравнение теории с религией. Мартин Риз, удостоенный звания Королевского астронома Великобритании, рассматривает мультивселенную как естественный шаг в нашем понимании всего сущего. Леонард Сасскинд утверждает, что те, кто игнорируют возможность того, что мы являемся частью некоей мультивселенной, просто не могут переварить богатство этой идеи. Я привёл лишь несколько примеров. Есть ещё много других — и яростных скептиков, и ревностных поклонников, по обе стороны баррикад, и своё мнение они часто облекают не в столь красивые формы.
Я занимаюсь теорией струн почти четверть века, но мне никогда прежде не доводилось встречать такого накала эмоций и резкости высказываемых мнений, как при обсуждении струнного ландшафта и возникающей из него мультивселенной. И совершенно ясно, почему это происходит, — многие рассматривают эту дискуссию как сражение за научный дух как таковой.
Научный дух
Хотя ландшафтная мультивселенная и стала катализатором, в спорах оказались затронуты вопросы, центральные для всех теоретических подходов, включающих понятие мультивселенной. Допустимо ли с научной точки зрения говорить о мультивселенной, о понятии, вовлекающем миры, недостижимые не только на практике, но во многих случаях даже в принципе? Является ли понятие мультивселенной проверяемым или фальсифицируемым? Сможет ли привлечение понятия мультивселенной помочь в объяснении того, что иными способами объяснить не удаётся?
Противники мультивселенной считают, что ответ на все эти вопросы отрицательный, однако её сторонники считают, что всё дело в непривычном взгляде на вещи. Непроверяемые и нефальсифицируемые гипотезы, содержащие в себе скрытые миры за границами достижимости, отстоят, как кажется, слишком далеко от того, что большинство из нас хотело бы называть наукой. Именно тут проскакивает искра, распаляющая страсти. Сторонники мультивселенной на это возражают, что хотя способ, которым мультивселенные могут проявить себя в наблюдениях, будет скорее всего сильно отличаться от привычного — будет не столь явным, опосредованным, и фортуна должна сильно к нам благоволить, чтобы такая связь была выявлена в будущих экспериментах, — нельзя сказать, что в разумных гипотезах подобные связи исключены на фундаментальном уровне. Если судить непредвзято, такой способ рассуждений даёт более широкий взгляд на возможности наших теорий и наблюдений и на способ проверки наших идей.
Критика понятия мультивселенной также зависит от понимания сути науки. Общие рассуждения обычно основаны на том, что наука является поиском закономерностей в нашей Вселенной, объяснением того, как эти закономерности отражают и подтверждают фундаментальные законы природы, а также проверкой предполагаемых законов путём формулировки предсказаний, которые можно проверить или опровергнуть экспериментальным путём или в наблюдениях. Но сколь бы разумным не было такое определение, оно обходит стороной тот факт, что настоящий научный процесс гораздо менее упорядочен и что постановка правильных вопросов зачастую так же важна как получение и проверка предлагаемых ответов. Было бы странно думать, что все вопросы живут себе спокойненько где-то в изначальной реальности и роль науки состоит в том, чтобы вытаскивать их на свет божий один за другим. Наоборот, сегодняшние вопросы зачастую обусловлены вчерашними достижениями. Как правило, прорывы в понимании дают ответы на часть вопросов, но одновременно приводят ко многим другим, о которых раньше и подумать было нельзя. При оценке любой идеи, включая теории с мультивселенными, необходимо принимать во внимание не только её способность выявлять скрытые истины, но также её влияние на задачи, к которым мы намереваемся подступиться. То есть влияние на саму научную деятельность. Далее станет ясно, что теории с мультивселенными обладают способностью пролить новый свет на некоторые важнейшие вопросы, над которыми учёные бьются в течение десятилетий. Эта перспектива даёт силы одним и приводит в ярость других.
Очертив арену действий, давайте приступим к систематическому анализу проверяемости, правильности и полезности теорий, где наша Вселенная является лишь одной из многих.
Доступные мультивселенные
Тяжело достичь согласия по всем этим вопросам, отчасти потому, что концепция мультивселенной не является монолитной. Мы рассмотрели уже пять различных версий — лоскутную, инфляционную, бранную, циклическую и ландшафтную, — в последующих главах нам встретятся ещё четыре. По вполне понятным причинам считается, что общее определение мультивселенной не поддаётся проверке. Обычные рассуждения, как правило, сводятся к тому, что мы конечно можем анализировать вселенные, отличные от нашей, но поскольку у нас есть доступ только к нашей, то с тем же успехом можно обсуждать приведения или домовых. Действительно, это центральная проблема, к которой мы вскоре вернёмся, но сперва заметим, что есть некоторые мультивселенные, которые действительно допускают взаимодействие между вселенными — членами мультивселенной. Мы видели, что в мультивселенной на бране струнные петельки могут свободно перемещаться с одной браны на другую. В инфляционной вселенной пузырьки могут взаимодействовать ещё более непосредственным образом.
Напомним, что в инфляционной мультивселенной пространство между двумя дочерними вселенными, вырастающими из пузырьков, заполнено полем инфлатона, чья энергия и отрицательное давление остаются большими, поэтому в промежуточном пространстве происходит инфляционное расширение. Это расширение отдаляет пузырьки друг от друга. Однако если скорость расширения самих пузырьков превышает скорость расширения пространства, пузырьки будут сталкиваться. Учитывая, что инфляционное расширение кумулятивно — чем больше расширяющегося пространства между пузырьками, тем быстрее они удаляются друг от друга, — приходим к интересному выводу. Если пузырьки действительно находятся близко друг к другу, промежуточного пространства между ними мало, то скорость разбегания окажется меньше скорости собственного расширения. Тогда пузырьки лягут на курс столкновения.
Эти рассуждения подкрепляются математическими расчётами. В инфляционной мультивселенной вселенные могут сталкиваться. Более того, ряд исследовательских групп (включая Джауме Гарригу, Алана Гута и Александра Виленкина; Бена Фрайфогеля, Мэтью Клебана, Альберто Николиса и Криса Сигурдсона; а также Энтони Эквайра и Мэтью Джонсона) установили, что хотя при некоторых столкновениях внутренняя структура пузырьков-вселенных может сильно разрушиться — что не очень приятно для его возможных обитателей, подобных нам с вами, — возможны и более мягкие соударения, без каких-либо катастрофических последствий, но дающие при этом наблюдаемые эффекты. Вычисления показывают, что если произойдёт такое мелкое ДТП с участием другой вселенной, то возникнут ударные волны, распространяющиеся в пространстве и изменяющие картину холодных и горячих областей в реликтовом излучении.{58} Учёные внимательно изучают возможные следы от такого столкновения и закладывают основу для наблюдений, которые однажды смогут доказать, что наша Вселенная столкнулась с другой вселенной, получив тем самым указания на существование других вселенных.
Однако сколь бы заманчивой не казалась такая возможность, что если ни один эксперимент по поиску свидетельств взаимодействия или столкновения с другой вселенной не окажется успешным? По здравому рассуждению, как тогда поддерживать идею мультивселенной, если мы не можем обнаружить каких-либо экспериментальных или наблюдательных доказательств существования других вселенных?
I. Наука и недоступность: Оправданно ли с научной точки зрения рассматривать ненаблюдаемые вселенные?
Каждый теоретический подход имеет свою архитектуру, куда входят основные составляющие теории и математические уравнения, которые их описывают. Архитектура не только задаёт теорию, но также указывает на то, какие вопросы могут быть заданы в рамках этой теории. Архитектура Исаака Ньютона была вполне осязаемой. В его уравнения входили положения и скорости объектов, с которыми мы непосредственно сталкиваемся в повседневной жизни или которые можем легко наблюдать, будь то горы и шары или Солнце и Луна. Великое множество наблюдений подтвердили предсказания теории Ньютона, что убедило нас в том, что соответствующие уравнения действительно описывают движение привычных объектов. Джеймс Клерк Максвелл и его архитектура привели к новому уровню абстракции. Колебания электрических и магнитных полей не относятся к тому роду вещей, которые наши органы чувств могут ощущать непосредственно. Хотя мы видим «свет» — электромагнитные колебания с длиной волны в том диапазоне, который воспринимает наш глаз, — наше зрение не может напрямую отследить колеблющиеся поля, постулируемые в теории Максвелла. Но несмотря на это, мы можем построить хитроумные приборы, измеряющие эти вибрации, которые совместно с множеством подтверждённых теоретический предсказаний дадут исчерпывающее доказательство того, что мы погружены в вибрирующий океан электромагнитных волн.
Фундаментальная наука в XX столетии всё больше и больше стала руководствоваться недоступными критериями. Пространство и время в своём спаянном единстве являются каркасом для специальной теории относительности. Наделённые затем Эйнштейном способностью к трансформации, они стали тем пластичным фоном, на котором развиваются события, описываемые общей теорией относительности. Я знаю, как тикают часы, и я могу измерить расстояния с помощью линейки, однако я никогда не смогу прикоснуться к пространству-времени, подобно тому как я касаюсь подлокотников своего кресла. Я ощущаю проявления гравитации, но если вы заставите меня ответить на вопрос, ощущаю ли я напрямую, что нахожусь в искривлённом пространстве-времени, я окажусь в ситуации как с теорией Максвелла. Я убеждён в правильности специальной и общей теорий относительности не потому, что непосредственно ощущаю их основные положения, а потому, что если следовать их подходу, то математические вычисления приведут к проверяемым на опыте предсказаниям. И эти предсказания оказываются в высшей степени точны.
Квантовая механика выводит подобного рода недоступность на новый уровень. Центральное понятие квантовой механики — это волны вероятности, удовлетворяющие уравнению, открытому в середине 1920-х годов Эрвином Шрёдингером. Хотя эти волны являются определяющим понятием для квантовой механики, в главе 8 мы увидим, что архитектура квантовой физики говорит о том, что они абсолютно ненаблюдаемы. Волны вероятности позволяют предсказать, где та или иная частица может находиться, но сами они находятся за кулисами повседневной реальности.{59} Однако, поскольку полученные предсказания очень хорошо подтверждаются на эксперименте, поколения учёных приняли эту странную ситуацию: в теории определяется радикально новая и необходимая конструкция, которая согласно самой теории является ненаблюдаемой.
Эти примеры объединяет та общая идея, что успешность теории может быть использована для оправдания постфактум её базисной архитектуры, даже в том случае, когда архитектура находится за рамками наших возможностей для её непосредственного восприятия. Это настолько вошло в обиход физиков-теоретиков, что они без малейших колебаний используют язык и ставят вопросы, в которых содержатся понятия совсем не такие осязаемые, как предметы обычного обихода, а некоторые и подавно находятся за пределами нашего чувственного опыта.[43]
Если продвинуться дальше и использовать архитектуру теории для изучения предсказываемых ею явлений, возникнут и другие типы недоступности. Чёрные дыры возникают как следствие математических вычислений в общей теории относительности, и астрономические наблюдения дают достаточно оснований считать, что они не только существуют, но при этом являются совершенно рядовым явлением. Однако внутренность чёрной дыры весьма экзотична. Согласно уравнениям Эйнштейна, край чёрной дыры, её горизонт событий, — это поверхность невозвращения. Её можно пересечь, но вернуться обратно невозможно. Мы, живущие снаружи горизонта событий, никогда не узнаем, что находится внутри, не только в силу практических ограничений, но как следствие самих законов общей теории относительности. И всё же имеется полное согласие в том, что область внутри горизонта событий чёрной дыры вполне реальна.
Применение общей теории относительности к космологическим вопросам даёт ещё более экстремальные примеры недоступности. Если вы не возражаете против путешествия в один конец, то внутренность чёрной дыры вполне подходит для этой цели. Однако миры за пределами нашего космического горизонта недостижимы, даже если бы мы могли путешествовать с околосветовыми скоростями. В ускоряющейся вселенной, такой как наша, это становится особенно очевидным. При данном измеренном значении космологического ускорения (в предположении, что оно неизменно) любой объект, отстоящий от нас на расстоянии, превышающем 20 миллиардов световых лет, будет всегда находиться вне нашего поля зрения, у нас никогда не будет возможности посетить его, измерить или как-то повлиять на него. Дальше этого расстояния пространство всегда будет отступать от нас настолько быстро, что любая попытка сократить дистанцию будет так же бесплодна, как стремление байдарочника плыть против потока, более быстрого, чем он может грести.
Объекты, всегда находившиеся за пределами нашего космического горизонта, никогда не наблюдались нами и никогда не будут наблюдаться; и наоборот, они никогда не видели нас и никогда не увидят. Объекты, которые в течение некоторого времени в прошлом находились внутри нашего космического горизонта, но были вытянуты за его пределы пространственным расширением, — это объекты, которые однажды прошли перед нашими глазами и исчезли навсегда. Но я думаю, мы согласны с тем, что такие объекты так же реальны, как ощущаемые нами вещи, и также реальны населяемые ими миры. Было бы довольно странно утверждать, что галактика, попавшая однажды в наше поле зрения, но впоследствии исчезнувшая с космического горизонта, ушла в несуществующий мир, который в силу своей перманентной недоступности должен быть стёрт с карты реальности. Даже если мы не можем наблюдать или воздействовать на такие миры, а они на нас, они вполне вписываются в нашу картину того, что существует.{60}
Эти примеры со всей очевидностью демонстрируют, что науке не чужды теории, в которые включены недоступные элементы, от основных ингредиентов до выводимых следствий. Наше принятие такого рода недоступности основано на нашей уверенности в теории. Когда квантовая механика вводит волны вероятности, её впечатляющая способность описывать такие измеряемые явления как движение атомов и субатомных частиц заставляет нас принять ту эфемерную реальность, которую она постулирует. Когда общая теория относительности предсказывает существование мест, недоступных для наблюдения, её феноменальный успех в описании тех явлений, которые можно наблюдать, таких как движение планет и траектория света, заставляет нас серьёзно отнестись к этим предсказаниям.
Поэтому для укрепления нашей веры в ту или иную теорию не надо требовать проверяемости всех её свойств; вполне достаточно разнообразного ассортимента подтверждённых предсказаний. Примерно столетие назад наука приняла, что теория может иметь скрытые и недоступные элементы — при условии, что при этом из неё также следуют интересные, новые и проверяемые предсказания для множества наблюдаемых явлений.
Это наводит на мысль, что можно подвести убедительный базис под теорию мультивселенной, даже если мы не сможем получить какого-либо прямого доказательства существования других вселенных, отличных от нашей. Если экспериментальные и наблюдательные данные говорят в пользу теории и побуждают вас принять её, если эта теория зиждется на математических структурах, которые не оставляют места для произвольного манёвра, то вы должны принять её целиком. Если эта теория приводит к существованию других вселенных, значит эту реальность следует принять на борт, как того требует теория.
Поэтому, в принципе, — и будьте уверены, я очень принципиален в этом вопросе — то, что теория допускает существования недоступных вселенных, не выводит само по себе теорию за научные рамки. Я разверну это утверждение: представим, что в один прекрасный момент мы получим убедительные экспериментальные и наблюдательные свидетельства в пользу теории струн. Например, в будущем на ускорителе мы сможем зафиксировать ряд струнных вибраций и отпечаток дополнительных измерений, а астрономические наблюдения выявят струнные черты у реликтового излучения и обнаружат следы длинных растянутых струн, вибрирующих в пространстве. Далее предположим, что наше понимание теории струн существенно улучшится и мы выясним, что эта теория абсолютно, точно и неоспоримо приводит к ландшафтной мультивселенной. Теория, опирающаяся на сильную экспериментальную и наблюдательную поддержку, внутренняя структура которой требует существования мультивселенной, приведёт нас к неумолимому заключению, что пришла пора «уступить», не взирая ни на какие призывы к обратному.[44]
Поэтому, возвращаясь к вопросу, вынесенному в заголовок этого раздела, я подчеркну, что имеются все основания для рассмотрения идеи мультивселенной в подходящем научном контексте; более того, если мы этого не сделаем, то проявим неоправданную ненаучную предубеждённость.
II. Наука и недоступность: Довольно о принципах; что же происходит на практике?
Скептик правильно заметит, что одно дело — рассматривать принципиальный вопрос о том, как можно обосновать ту или иную теорию с мультивселенной, и совсем другое дело — оценить, может ли какой-либо из описанных нами вариантов мультивселенной привести к экспериментальному подтверждению теорий, совершенно определённо предсказывающих существование других вселенных. Сделаем попытку это оценить.
Лоскутная мультивселенная возникает из-за бесконечности пространства. Эта возможность прямо соответствует общей теории относительности. Загвоздка лишь в том, что общая теория относительности допускает бесконечность пространства, но вовсе этого не требует. Поэтому, хотя общая теория относительности и является подходящей основой, сценарий лоскутной мультивселенной остаётся умозрительным. Конечно, бесконечность пространства напрямую следует из вечной инфляции — напомним, что каждый пузырёк видится изнутри бесконечно большим, — но в этом подходе у лоскутной мультивселенной нет определённой опоры, так как основная гипотеза, вечная инфляция, остаётся недоказанной.
Аналогичные доводы применимы и в случае инфляционной мультивселенной, также возникающей благодаря вечной инфляции. Астрономические наблюдения за последние десять лет укрепили веру физической общественности в инфляционную космологию, но не дали никаких подтверждений тому, что инфляционное расширение является вечным. Теоретические исследования показывают, что хотя многие варианты теории приводят к вечной инфляции и возникновению пузырьков одного за другим, есть и другие варианты, характеризующиеся одним единственным раздувающимся пространством.
Бранная, циклическая и ландшафтная мультивселенные основаны на теории струн, поэтому они страдают от множества неопределённостей. Сколь бы ни были они поразительны и структурно богаты, как и сама теория струн, однако отсутствие проверяемых предсказаний и, как следствие, невозможность соотнесения с наблюдениями и экспериментами переводят эти теории в область научных спекуляций. Более того, так как многие вопросы теории всё ещё находятся на первоначальной стадии разработки, то неясно, какие из них будут играть важную роль в будущем. Останутся ли браны — основа для бранной и циклической мультивселенных — на передних позициях? Сохранится ли богатый выбор форм пространств дополнительных измерений — основа ландшафтной мультивселенной, или наконец будет найден математический принцип, отбирающий одну определённую форму? Мы просто не знаем.
В принципе, мы могли бы, наверное, подобрать убедительный довод в пользу теории с мультивселенной, который мало или никак не связан с предсказаниями других вселенных, но для рассмотренных нами мультивселенных сценариев этот способ не подойдёт. По крайней мере, пока не подошёл. Чтобы оценить каждый из них, нам придётся напрямую разбираться с теми предсказаниями, что они дают для мультивселенной.
Можем ли мы это? Может ли включение в теорию других вселенных привести к проверяемым предсказаниям, даже если эти вселенные находятся за пределами досягаемости экспериментов и наблюдений? Давайте рассматривать этот ключевой вопрос шаг за шагом, следуя от «принципов» к «практике», как было оглашено выше.
I. Предсказания в мультивселенной: Если вселенные, составляющие мультивселенную, недоступны, могут ли они давать осмысленный вклад в предсказания?
Те учёные, которые не принимают теорию мультивселенной, смотрят на эту деятельность как на признание поражения, на полное отступление от великой цели постижения того, почему Вселенная, какой мы её наблюдаем, обладает именно такими свойствами. Я могу понять такие чувства, потому что я был среди тех, кто в течение десятилетий пытался материализовать обещания, даваемые теорией струн, и вычислить все фундаментальные наблюдаемые свойства Вселенной, включая значения всех констант в природе. Если допустить, что мы являемся частью мультивселенной, в которой некоторые, а может быть и все константы изменяются от одной вселенной к другой, то следует признать, что подобная цель является ошибочной. Если фундаментальные законы разрешают, скажем, константе связи электромагнитного взаимодействия принимать в мультивселенной самые разные значения, то сама задача вычисления определённого значения константы связи столь же бессмысленна, как попросить пианиста подобрать какую-то одну ноту.
Здесь возникает вопрос: если характеристики могут варьироваться, означает ли это, что мы теряем способность предсказать (или объяснить) значения, присущие именно нашей Вселенной. Не обязательно. Даже если мультивселенная исключает единственность, всё равно можно сохранить в какой-то мере предсказательную силу. Правда, теперь это становится делом статистики.
Поговорим для наглядности о собаках. Они все разные по весу. Есть очень маленькие собаки, например чихуахуа, весящие пару килограммов; есть очень крупные собаки, такие как английский мастиф, вес которых может зашкаливать за 100 килограммов. Если бы я попросил вас предсказать вес собаки, которая вам встретится на улице, то, возможно, наилучшим выходом для вас было бы назвать любое число в указанном выше диапазоне. Однако, обладая чуть большей информацией, вы смогли бы назвать вес точнее. Если вам предоставят данные по собакам, живущим в вашем районе, например, сколько человек держат ту или иную породу, каким весом обладает та или иная порода, и даже скажут, сколько ежедневных прогулок необходимо собакам каждой породы, вы сможете более точно оценить вес собаки, которая наиболее вероятно вам встретится на улице.
Вряд ли это будет точным предсказанием; как правило, в статистике такого не происходит. Однако, опираясь на данные о распределении собак, вы сможете дать гораздо более точный ответ, чем просто назвать произвольное число с потолка. Если распределение собак в вашем районе имеет некую конкретную специфику, например, 80 процентов собак составляют лабрадоры, средний вес которых 27 килограмм, а остальные 20 процентов приходятся на породы от шотландского терьера до пуделей, средний вес которых составляет 13 килограмм, то вы с большой точностью попадёте в точку, назвав вес в диапазоне от 25 до 30 килограмм. Конечно же, вам может встретиться пушистый ши-тцу, но это маловероятно. Если распределение ещё более скошено, ваши предсказания могут стать точнее. Если 95 процентов собак вокруг вас — это лабрадоры весом 27 килограмм, то можно уверенно предсказать, что вам встретится именно лабрадор.
Аналогичный статистический подход можно применить к мультивселенной. Представьте, что вы изучаете теорию мультивселенной, в которой свойства различных вселенных находятся в широком диапазоне — различные значения констант взаимодействий, свойств частиц, космологических постоянных и так далее. Также представьте, что космологический процесс образования этих вселенных (как, например, образование пузырьков в ландшафтной мультивселенной) достаточно хорошо понят, поэтому мы можем вычислить распределение вселенных с различными свойствами по всей мультивселенной. Наличие такой информации вполне может привести к значимым открытиям.
Для наглядности предположим, что вычисления дают особенно простое распределение: некоторые физические свойства широко варьируются от вселенной к вселенной, а другие остаются неизменными. Например, представим, что вычисления говорят, что должен быть некий набор частиц, общих для всех вселенных в мультивселенной, массы и заряды которых одинаковы в каждой из вселенных. Подобное распределение приводит к совершенно однозначным предсказаниям. Если эксперименты, проведённые в нашей выделенной Вселенной, не обнаружат предсказанного набора частиц, то соответствующая теория, мультивселенная и всё остальное должны быть отброшены. Таким образом, если мы знаем распределение, то гипотеза мультивселенной становится фальсифицируемой. Наоборот, если в наших экспериментах предсказанные частицы будут обнаружены, это укрепит нашу в веру в правильность выбранной теории.{61}
В качестве другого примера представьте мультивселенную, космологическая постоянная в которой варьируется в огромном диапазоне значений, но крайне неоднородно (рис. 7.1). На графике представлена доля вселенных внутри мультивселенной (вертикальная ось) с заданным значением космологической постоянной (горизонтальная ось). Если мы — часть такой мультивселенной, то загадка космологической постоянной имеет принципиально другой характер. Большинство вселенных в таком сценарии обладают космологической постоянной, значение которой близко к измеренному значению в нашей Вселенной; поэтому, хотя диапазон возможных значений огромен, скошенное распределение означает, что наблюдаемое нами значение ничем не примечательно. В такой мультивселенной удивляться тому, что космологическая постоянная в нашей Вселенной имеет значение 10−123, следует не больше, чем встрече с лабрадором весом в 27 килограмм. Каждое из этих событий наиболее вероятно при подходящем распределении.
Рис. 7.1. Распределение космологической постоянной в гипотетической мультивселенной, показывающее, как очень скошенное распределение позволяет объяснить загадочные наблюдательные данные
Теперь рассмотрим другую ситуацию. Представим, что в некоторой теории мультивселенной значения космологической постоянной варьируются в широком диапазоне, но в отличие от предыдущего примера варьируются однородно; количество вселенных с заданным значением космологической постоянной сравнимо с количеством вселенных с любым другим значением. Допустим также, что при тщательном математическом анализе теории выяснилось неожиданное свойство такого распределения: оказалось, что во вселенных со значением космологической постоянной в наблюдаемом нами диапазоне, всегда существуют частицы, массы которых, скажем, в 5000 раз превосходят массу протона — они слишком тяжёлые, чтобы их можно было наблюдать на ускорителях XX века, однако их масса вполне вписывается в диапазон ускорителей XXI века. В силу такой тесной связи между этими двумя физическими свойствами эта теория мультивселенной также является фальсифицируемой. Если у нас не получится обнаружить предсказанные тяжёлые частицы, то гипотеза будет отброшена; а открытие таких частиц наоборот усилит нашу убеждённость в её правильности.
Я хочу подчеркнуть, что эти сценарии умозрительны. Я привёл их в качестве примера, потому что они прекрасно демонстрируют возможности для научной идеи и её проверки в рамках концепции мультивселенной. Ранее я высказывал мнение, что если теория мультивселенной приводит к проверяемым свойствам помимо предсказания существования других вселенных, тогда, в принципе, возможно найти в её поддержку весомые аргументы, даже если другие вселенные недоступны. Примеры, приведённые выше, служат тому подтверждением. Для таких типов мультивселенных ответ на искомый вопрос будет безоговорочно положительным.
Важно, что такие «предсказуемые мультивселенные» не собраны как попало из составляющих вселенных. Наоборот, предсказательная сила обусловлена характерной математической структурой мультивселенной: физические свойства распределены между составляющими вселенными либо с большим перекосом, асимметрично, либо очень коррелированным образом.
Как такое может быть? Если абстрагироваться от красивого «в принципе», имеет ли это место на самом деле в рассмотренных нами ранее мультивселенных?
II. Предсказания в мультивселенной: Довольно о принципах; что же происходит на практике?
Распределение собак в данном районе зависит от ряда условий, например: от культурного слоя, финансовых возможностей и просто обычной случайности. В силу этих сложностей чтобы сделать верный статистический прогноз, лучше всего обратиться за нужными данными в местный клуб собаководов, избежав тем самым размышлений, откуда взялось именно такое распределение собак. К сожалению, никто не ведёт перепись населения мультивселенных, поэтому такая возможность оказывается недоступной. Мы вынуждены опираться на наши теоретические идеи о том, как может возникнуть данная мультивселенная с тем или иным распределением составляющих её вселенных.
Ландшафтная мультивселенная, основанная на вечной инфляции и теории струн, вполне подходит для подобных исследований. В этом сценарии двумя генераторами новых вселенных являются инфляционное расширение и квантовое туннелирование. Напомним, как это происходит: вселенная в процессе инфляции, соответствующая той или иной долине в струнном ландшафте, квантово туннелирует сквозь одну из ближайших гор и оказывается в другой долине. Из первой вселенной — с определённым набором свойств, таких как константы взаимодействий, характеристики частиц, значение космологической постоянной и так далее — возникает расширяющийся пузырёк новой вселенной (см. рис. 6.7) с новым набором физических свойств, после чего процесс продолжается.
Подобные туннелирования, являясь квантовыми процессами, обладают вероятностным характером. Нельзя предсказать, где и когда они произойдут. Но можно предсказать вероятность того, что туннелирование произойдёт в любом заданном интервале времени и в любом заданном направлении — вероятность этого зависит от конкретных свойств струнного ландшафта, таких как высоты различных вершин и долин (то есть значения соответствующих космологических постоянных). Более вероятные туннелирования происходят чаще, что находит отражение в возникающем распределении вселенных. Поэтому стратегия должна быть следующей: с помощью математического аппарата инфляционной космологии и теории струн попытаться вычислить распределение вселенных с различными физическими свойствами внутри ландшафтной мультивселенной.
Загвоздка в том, что до сих пор это никому не удавалось сделать. Струнный ландшафт в том виде, как мы его сейчас понимаем, обладает необъятным количеством вершин и долин, поэтому вычислить свойства возникающей мультивселенной является невероятно трудной математической задачей. Пионерские работы космологов и струнных теоретиков значительно расширили наше понимание, однако следует признать, что исследования в этой области всё ещё находятся на начальном уровне.{62}
Чтобы продвинуться дальше, сторонники мультивселенной предлагают добавить в анализ ещё один важный компонент. Это учёт эффекта отбора, о котором говорилось в предыдущей главе — антропного принципа.
III. Предсказания в мультивселенной: Антропный принцип
Многие вселенные в заданной мультивселенной обречены на безжизненность. Как мы видели, причина в том, что при отклонении значений фундаментальных параметров от наблюдаемых значений разрушаются условия, благоприятствующие возникновению жизни.[45] Сам факт нашего существования означает, что мы никогда не сможем оказаться в любой из таких безжизненных областей, и поэтому нечего дальше объяснять, почему мы не видим свойственную им комбинацию параметров. Если есть некий вариант мультивселенной, из которого гарантированно следует существование единственной вселенной с благоприятными условиями для возникновения жизни, то нам повезло. Мы сможем математически вывести свойства такой вселенной. Если они отличаются от измеряемых свойств нашей Вселенной, то этот вариант мультивселенной будет отброшен. Если же полученные свойства согласуются с нашими, это станет впечатляющим подтверждением антропного подхода, а также приведёт к неимоверному расширению существующей картины мира.
В более правдоподобном случае, когда вселенная с благоприятными условиями для возникновения жизни не является единственной, ряд теоретиков (таких как Стивен Вайнберг, Андрей Линде, Александр Виленкин, Джордж Эфстатиу и многие другие) ратуют за расширенный статистический подход. Вместо вычисления относительного соотношения разных вселенных в рамках мультивселенной, они предлагают вычислить число их обитателей — физики обычно называют их наблюдателями, — которые могли бы оказаться в той или иной вселенной. В некоторых вселенных условия вряд ли совместимы с жизнью, поэтому наблюдателей там будет немного, подобно случайному кактусу в безжизненной пустыне; вселенные с более благоприятными условиями будут изобиловать наблюдателями. Идея в том, что подобно тому как на основе данных по переписи собак можно предсказать, какая собака нам встретится сегодня, на основе данных по переписи наблюдателей можно предсказывать свойства, которые типичный житель мультивселенной — например, вы и я, согласно логике этого подхода, — ожидает увидеть.
Конкретный пример был проанализирован в 1997 году Вайнбергом и его соавторами Хьюго Мартелом и Полем Шапиро. Рассмотрев мультивселенную с космологической постоянной, варьирующейся от одной вселенной к другой, они вычислили, насколько возможной будет жизнь в каждой из них. Эта трудная задача поддалась решению при помощи трюка, предложенного Вайнбергом (см. главу 6): вместо жизни как таковой надо рассматривать образование галактик. Чем больше галактик, тем больше планетарных систем и, следовательно, согласно исходному предположению, бо́льшая вероятность жизни, например, разумной жизни. Тогда, как выяснил в 1987 году Вайнберг, даже совсем крошечная космологическая постоянная порождает достаточное гравитационное отталкивание, способное нарушить образование галактик, поэтому имеет смысл рассматривать лишь те области мультивселенной, в которых космологическая постоянная достаточно мала. Отрицательная космологическая постоянная соответствует вселенным, которые схлопываются прежде, чем успевают образоваться галактики, поэтому подобными областями мультивселенной также можно пренебречь. Таким образом, антропный принцип фокусирует наше внимание на части мультивселенной с очень узким диапазоном значений космологической постоянной; как обсуждалось в главе 6, вычисления показывают, что если в заданной вселенной имеются галактики, то её космологическая постоянная не должна превосходить приблизительно двухсоткратную критическую плотность (что эквивалентно по массе примерно 10−27 грамма на кубический сантиметр пространства, или что составляет примерно 10−121 в планковских единицах).[46]
Для вселенных, космологическая постоянная которых находится в этих пределах, Вайнберг, Мартел и Шапиро провели более подробные вычисления. Они выяснили, какая доля материи в каждой такой вселенной будет слипаться в сгустки в течение космологической эволюции, что является ключевым шагом на пути образования галактик. Они обнаружили, что если значение космологической постоянной находится очень близко к верхней границе допустимого диапазона, будет образовываться сравнительно немного сгустков материи, потому что отталкивающее действие космологической постоянной будет проявляться подобно сильному ветру, разгоняющему сгустки пыли. Если же значение космологической постоянной находится вблизи нижней границы допустимого диапазона, то есть нуля, то может возникнуть значительное количество сгустков материи, потому что разрушительное влияние космологической постоянной минимизировано. Это означает, что с высокой долей вероятности вы окажетесь во вселенной, космологическая постоянная которой почти равна нулю, так как подобные вселенные содержат большое количество галактик, а потому, следуя логике этого подхода, велик шанс возникновения жизни. Есть совсем небольшая вероятность оказаться во вселенной с космологической постоянной вблизи верхней границы допустимого диапазона значений, что составляет примерно 10−121, ибо такие вселенные населены небольшим количеством галактик. И существует некая скромная вероятность того, что вы окажетесь во вселенной с промежуточной космологической постоянной между двумя крайними значениями.
Используя количественные данные этих результатов, Вайнберг и его соавторы рассчитали космический аналог встречи с 27-килограммовым лабрадором во время обычной прогулки по району, то есть они вычислили значение космологической постоянной, каким оно видится среднестатистическому наблюдателю мультивселенной. И каким был ответ? Чуть больше найденного в измерениях по сверхновым, но примерно того же порядка. Они оценили, что примерно от 1 из 10 до 1 из 20 обитателей мультивселенной будут ощущать примерно то же, что и мы, измеряя при этом значение космологической постоянной в их вселенных, равное 10−123.
И хотя нам бы хотелось видеть более высокий процент, полученный результат всё равно впечатляет. До этих вычислений несоответствие между теорией и экспериментом составляло примерно 120 порядков величины, что, несомненно, указывало на громадный провал в наших знаниях. Однако подход Вайнберга и его соавторов продемонстрировал, что оказаться во вселенной с космологической постоянной, значение которой сопоставимо с измеряемым нами, не более удивительно, грубо говоря, чем натолкнуться на ши-тцу в районе, где преобладают лабрадоры. Иными словами, совсем не удивительно. Мы можем утверждать, что в рамках мультивселенного подхода то значение космологической постоянной, что мы наблюдаем, никак нельзя рассматривать как свидетельство нашего глубокого непонимания, а это громадный шаг вперёд.
Однако более детальный анализ выявил интересные тонкости, которые некоторые склонны рассматривать как слабое место этого результата. Ради простоты Вайнберг и его соавторы полагали, что в мультивселенной только значение космологической постоянной варьируется от вселенной ко вселенной; другие физические параметры считались фиксированными. Макс Тегмарк и Мартин Риз заметили, что если рассмотреть вариации не только значений космологической постоянной, но и, скажем, вариации размера исходных квантовых флуктуаций от вселенной ко вселенной, то конечный ответ будет другим. Напомним, что такие флуктуации являются первичными зёрнышками, из которых возникнут галактики: крохотные квантовые колебания, растянутые инфляцией, приводят к случайному набору областей, плотность вещества в которых чуть выше или чуть ниже среднего значения. Области с высокой плотностью сильнее притягивают материю по соседству, поэтому растут ещё быстрее, превращаясь в конце концов в галактики. Тегмарк и Риз указали, что первичные зёрнышки вещества легче противостоят гравитационному отталкиванию, порождаемому космологической постоянной, подобно тому как большая куча листьев лучше противостоит напорам ветра. Таким образом, мультивселенная, в которой варьируются как размеры первичных зёрнышек, так и значения космологической постоянной, будет содержать вселенные, в которых большие значения космологической постоянной окажутся скомпенсированы большим размером первичных зёрнышек; такая комбинация будет совместима с образованием галактик и, следовательно, — с жизнью как таковой. В мультивселенной такого сорта типичный наблюдатель увидит увеличенное значение космологической постоянной, что в свою очередь приводит к уменьшению — скорее всего, резкому — доли наблюдателей, которые обнаружат, что их космологическая постоянная так же мала, как наша собственная.
Преданные сторонники мультивселенной ссылаются на результат, полученный Вайнбергом и его соавторами, как на большой успех антропного принципа. А противники парируют результатами, полученными Тегмарком и Ризом и принижающими весомость антропных доводов. На самом деле, споры пока преждевременны. Это всё в высшей степени предварительные и пробные вычисления, которые в лучшем случае дают повод задуматься над самим антропным принципом. При определённых ограничениях из них следует, что антропный подход позволяет уложиться в диапазон измеряемых значений космологической постоянной; но стоит немножко ослабить эти ограничения, и вычисления мгновенно приводят к существенному росту диапазона допустимых значений. Такая чувствительность означает, что для более подробных вычислений в теории с мультивселенной потребуется более точное понимание характеристик составляющих вселенных и того, как они варьируются, что должно в конце концов привести к замене произвольных допущений чёткими теоретическими указаниями. Всё это очень важно для того, чтобы теория мультивселенной позволяла сделать определённые предсказания.
Учёные упорно трудятся над достижением этой цели, однако им предстоит ещё много чего преодолеть.{63}
IV. Предсказания в мультивселенной: Что ещё нужно?
Какие ещё препятствия нам предстоит преодолеть, прежде чем мы сможем получить точные предсказания из данной теории мультивселенной? Начнём с трёх самых главных.
Во-первых, как мы наглядно видели в рассмотренном выше примере, анализируемая модель мультивселенной должна давать возможность определить те физические свойства, которые варьируются от одной вселенной к другой, и для этих свойств мы должны уметь вычислять их статистическое распределение. Существенным здесь является понимание космологического механизма, благодаря которому мультивселенная населяется вселенными (такому как образование дочерних вселенных в модели ландшафтной мультивселенной). Именно этот механизм определяет, насколько один тип вселенных превалирует над другим, и, следовательно, именно он задаёт статистическое распределение физических свойств. Если повезёт, то получаемые распределения во всей мультивселенной, либо среди тех вселенных, в которых возможна жизнь, будут достаточно скошены, так что мы сможем извлечь определённые предсказания.
Во-вторых, если мы действительно опираемся на антропный принцип, то следует учесть то основное предположение, что мы, человечество, являемся самым заурядным видом. Жизнь может оказаться редким явлением для мультивселенной; а разумная жизнь ещё более редким. Но согласно антропному принципу, среди всех разумных существ мы настолько типичны, что то, что мы наблюдаем, должно представлять собой средние значения среди всех возможных значений, наблюдаемых любыми другими разумными существами, населяющими мультивселенную. (Александр Виленкин назвал это принципом заурядности.) Если распределение физических свойств среди вселенных, где возможна жизнь, известно, такие средние можно вычислить. Однако, как правило, в этом вопросе нет ясности. Если впоследствии учёные покажут, что наши наблюдения попадают в диапазон вычисленных средних для некоторой частной мультивселенной, то уверенность в нашей типичности — а также в гипотезе мультивселенной — заметно укрепится. Эго было бы здорово! Но если наши наблюдения не попадут в диапазон средних значений, тогда это может свидетельствовать об ошибочности гипотезы мультивселенной или же может означать, что человечество не заурядный вид, а какой-то особенный. Даже на территории, на 99 процентов населённой лабрадорами, всё равно можно натолкнуться на какого-нибудь добермана, нетипичную собаку для этого места. В этой ситуации будет совсем непросто определить, является ли гипотеза мультивселенной ошибочной, или же она верна, но наша Вселенная почему-то оказалась совсем нетипичной.{64}
Прогресс в этом направлении потребует, по всей видимости, более глубокого понимания механизма возникновения жизни в данной мультивселенной; подобные знания могли бы по крайней мере прояснить, насколько типичной была до сих пор наша эволюция. Это, конечно, очень важная задача. На данный момент, в большинстве антропных рассуждений этот вопрос полностью игнорируется под прикрытием идеи Вайнберга, что число разумных форм жизни в данной вселенной пропорционально числу содержащихся в ней галактик. Насколько мы понимаем, для разумной формы жизни необходима тёплая планета, для чего требуется звезда, входящая в какую-нибудь галактику, поэтому есть основания считать идею Вайнберга вполне убедительной. Но поскольку наши знания весьма рудиментарны, даже в вопросе собственной эволюции, это предположение не более чем гипотеза. Чтобы вычисления стали более точными, необходимо лучше понимать происхождение и развитие разумных форм жизни.
Мы подошли к третьему препятствию. На первый взгляд, его просто объяснить, но оно гораздо сложнее, чем кажется. Речь идёт о разделении бесконечности.
Разделение бесконечности
Чтобы сформулировать проблему, вернёмся к примеру с нашими собаками. Допустим, вы живёте в районе, в котором 3 лабрадора и одна такса. Закрывая глаза на усложнения типа частоты выгула собак, заключаем, что вероятность встретить лабрадора в 3 раза выше. Тот же вывод справедлив, если вокруг 300 лабрадоров и 100 такс; 3000 лабрадоров и 1000 такс; 3 миллиона лабрадоров и 1 миллион такс и так далее. Но что, если оба этих числа бесконечно большие? Как сравнить бесконечное число такс с троекратно бесконечным числом лабрадоров? Звучит как детский вопрос, ставящий в тупик родителей. Но это на самом деле серьёзный вопрос. Правда ли, что троекратная бесконечность больше обычной бесконечности? Если да, она больше именно в 3 раза?
Как известно, сравнение бесконечно больших чисел является исключительно хитроумной задачей. Для собак на Земле такой проблемы, конечно же, не возникает, потому что их численность конечна. Но для вселенных, входящих в какую-то определённую мультивселенную, эта проблема стоит весьма реально. Возьмём, например, инфляционную мультивселенную. Рассматривая весь кусок швейцарского сыра с точки зрения воображаемого внешнего наблюдателя, можно увидеть, что кусок продолжает увеличиваться и безостановочно порождает новые вселенные. Именно это подразумевается под термином «вечная» в «вечной инфляция». Кроме того, мы видели, что с точки зрения внутреннего наблюдателя каждая отдельная дочерняя вселенная тоже имеет бесконечное число разделённых между собой областей, что приводит к лоскутной вселенной. Пытаясь сделать те или иные предсказания, мы с неизбежностью сталкиваемся с бесконечностью вселенных.
Для понимания математической стороны вопроса представьте, что вы выиграли в телевизионной викторине и вам достался необычный приз: бесконечный набор конвертов, в первом из которых лежит 1 доллар, во втором 2 доллара, в третьем 3 доллара и так далее. Как обычно, под аплодисменты зала ведущий предлагает вам сделать выбор. Либо вы берёте ваш приз, как он есть, либо содержание каждого конверта можно удвоить. На первый взгляд вам очевидно, что второй вариант гораздо выигрышней. «В каждом конверте будет в 2 раза больше денег, чем раньше» — думаете вы, — «поэтому будет правильным выбрать именно второй вариант». Действительно, если число конвертов конечно, то такое решение было бы правильным. Обменять 5 конвертов с 1, 2, 3, 4 и 5 долларами на конверты с 2, 4, 6, 8 и 10 долларами будет более чем разумно. Однако, немного подумав, вы начнёте сомневаться, потому что поймёте, что в бесконечном случае всё не так очевидно. «Если выбрать второй вариант», — думаете вы, — «у меня останутся конверты с 2, 4, 6 и так далее долларами, то есть со всеми чётными числами. Но сейчас в конвертах находятся доллары, пробегающие весь ряд целых чисел, как чётных, так и нечётных. Поэтому если выбрать второй вариант, то из полной суммы денег будут отобраны все конверты с нечётным количеством долларов. Как-то непохоже, что это будет правильным решением». Вы начинаете лихорадочно соображать. Если сравнивать поконвертно, то второй вариант весьма привлекателен. А если сравнивать наборы конвертов, то не очень.
Дилемма, с которой вы столкнулись, иллюстрирует тип математических ловушек, которые так затрудняют сравнение бесконечных наборов. Зрители в зале начинают нервничать, вам пора уже сделать выбор, а ваша оценка того или иного выбора зависит от того, как вы сравниваете два результата.
Аналогичная неоднозначность возникает и при сравнении самих основ таких наборов: числа элементов в каждом из них. Пример с телевизионной викториной также хорошо иллюстрирует эту сторону вопроса. Чего больше: всех чётных чисел или всех целых чисел? Большинство людей ответят, что больше целых чисел, потому что чётные числа составляют лишь половину от общего количества. Однако опыт викторины позволяет более аккуратно подойти к этому вопросу. Представьте, что вы выбираете второй вариант — получить все чётные суммы долларов. В этом случае вам не придётся откладывать в сторону часть конвертов или требовать новые, так как ведущий просто удвоит сумму денег в каждом из них. Таким образом, заключаете вы, число конвертов, необходимых для размещения всех нечётных и всех целых сумм долларов является тем же самым, и, следовательно, заполнение каждой категории чисел равно между собой (табл. 7.1). И это странно. Сравнивая одним методом — рассматривая чётные числа как подмножество всех целых чисел, — вы делаете вывод, что целых чисел больше. Применяя другой метод — подсчитывая, сколько надо конвертов для размещения каждого вида чисел, — вы делаете вывод, что множество целых чисел и множество чётных чисел имеют одинаковое заполнение.
Таблица 7.1. Каждое целое число спарено с чётным числом, и наоборот, откуда возникает предположение, что их количества совпадают
Таблица 7.2. Каждое целое число спарено с дважды чётным числом, в результате чего остаётся бесконечный набор чётных чисел без пары. Отсюда возникает предположение, что чётных чисел больше, чем целых
Можно даже убедить себя, что чётных чисел больше чем целых. Представьте, что в качестве альтернативного варианта на викторине предлагается учетверить деньги в каждом конверте так, что в первом окажется 4, во втором 8, в третьем 12 долларов и так далее. Так как число конвертов опять не изменилось, возникает предположение, что количество целых чисел из первого варианта равно количеству чисел кратных 4 из второго варианта (табл. 7.2). Однако такое составление пар, когда каждое целое число сопоставляется числу кратному 4, даёт бесконечный набор чётных чисел, оставшихся без пары — 2, 6, 10 и так далее, — что наводит на мысль, что чётных чисел больше чем целых.
С одной стороны, количество чётных чисел меньше чем целых. С другой стороны, эти количества равны друг другу. С третьей стороны, чётных чисел больше чем целых. И выходит, что нет какого-то одного правильного вывода. Абсолютного ответа на вопрос, какой из этих бесконечных наборов больше, попросту не существует. Получаемый вами результат зависит от способа сравнения.{65}
Здесь возникает головоломка для теорий с мультивселенными. Как определить, что тот или иной тип вселенных имеет больше галактик и более расположен к возникновению жизни, если число рассматриваемых вселенных бесконечно? Мы столкнёмся с точно такими же двусмысленностями, как были описаны выше, если физические соображения не продиктуют, что взять за основу при определении способа сравнения. Теоретики сформулировали несколько способов сравнения, аналогичных составлению пар в приведённых выше таблицах, которые возникают в той или иной физической модели, — однако определённой процедуры, с которой согласны все, пока не разработано. Разные подходы приводят к разным результатам, подобно примерам с бесконечными наборами чисел. Согласно одному способу сравнения, преимущество имеют вселенные с одним набором свойств; согласно другому способу — другие.
Такой произвол сильно влияет на определение типичных или средних свойств в данной мультивселенной. Физики называют это проблемой измерения. Смысл этого математического термина вполне отражён в его названии. Необходимо иметь способ измерения размеров различных бесконечных наборов вселенных. Именно эта информация необходима для того, чтобы делать предсказания. Именно эта информация необходима, чтобы разобраться, насколько вероятнее, что мы находимся во вселенной одного типа, а не другого. Пока не будет найден фундаментальный принцип для сравнения бесконечных наборов вселенных, мы не сможем математически предсказывать результаты наблюдений и экспериментов, проводимых типичными обитателями мультивселенной, то есть нами. Поэтому нам не удастся избежать решения проблемы измерения.
Что ещё волнует скептиков
Я посвятил проблеме измерений отдельный раздел, не только потому что она является огромным препятствием на пути получения предсказаний, но также потому, что из неё вытекают другие проблемные следствия. В главе 3 было объяснено, почему инфляционная теория стала de facto космологической парадигмой. Крайне высокий темп расширения в течение первых мгновений жизни нашей Вселенной привёл к тому, что области, удалённые друг от друга в настоящем, могли быть связаны друг с другом в прошлом, что объясняет общую температуру, обнаруженную в современных экспериментах; быстрое расширение сглаживает также любую пространственную кривизну, что придаёт пространству плоскую форму, которая согласуется с наблюдениями; наконец, такое расширение превращает квантовые флуктуации в мельчайшие температурные колебания по всему пространству, которые наблюдаются в реликтовом излучении и которые важны для образования галактик. Эти достижения неоспоримы.{66} Однако если инфляция продолжается вечно, это может свести успехи на нет.
Когда в игру вступают квантовые процессы, лучшее, что можно сделать, — это предсказать вероятность одного результата относительно другого. Физики-экспериментаторы, понимая всю важность этого, вновь и вновь проводят эксперименты, набирая целую гору данных для статистической обработки. Когда квантовая механика предсказывает, что один результат в 10 раз вероятнее другого, полученные данные должны очень точно отражать это соотношение. Вычисления реликтового излучения, соответствие которого наблюдательным данным является наиболее убедительным аргументом в пользу инфляционной теории, основываются на квантовых флуктуациях, и поэтому тоже имеют вероятностный характер. Однако в отличие от лабораторных экспериментов эти вычисления нельзя проверить, запуская Большой взрыв снова и снова. Тогда как их интерпретировать?
Если в результате теоретического анализа получается, что, скажем, с вероятностью 99 процентов данные по реликтовому излучению имеют один вид, а не другой, и если более вероятный результат согласуется с нашими наблюдениями, то такие данные рассматриваются как серьёзный аргумент в пользу теории. Логика в том, что если некоторый набор вселенных возник на основе одних и тех же физических законов, то теория утверждает, что примерно 99 процентов таких вселенных будут похожи на то, что мы наблюдаем, а 1 процент будет иметь значительные отклонения.
Теперь если бы в инфляционной мультивселенной имелся конечный набор вселенных, то можно было бы прямо утверждать, что число нетипичных вселенных, в которых квантовые процессы привели бы к данным, не соответствующим ожидаемым, останется относительно малым. Однако, когда набор вселенных бесконечен, как в инфляционной мультивселенной, интерпретация чисел становится значительно более трудной задачей. Что такое 99 процентов от бесконечности? Бесконечность. А что такое 1 процент от бесконечности? Тоже бесконечность. Какая из них больше? От нас требуется сравнить два бесконечных набора. А как мы видели, даже когда кажется, что один набор больше другого, ответ зависит от используемого нами метода сравнения.
Тогда скептик делает вывод, что при вечной инфляции становятся условными сами предсказания, на которых зиждется наша уверенность в теории. Любой возможный результат, допустимый квантовыми вычислениями, каким бы маловероятным он ни был — 0,1 процента квантовой вероятности, 0,0001 процента квантовой вероятности или 0,0000000001 процента квантовой вероятности, — будет реализован в бесконечном числе вселенных просто потому, что любое из этих чисел, умноженное на бесконечность, равно бесконечности. Без фундаментального предписания того, как сравнивать бесконечные наборы, мы скорее всего не сможем сказать, что один набор вселенных больше другого, а потому он является наиболее вероятным типом наблюдаемых вселенных — мы теряем способность делать определённые предсказания.
Оптимист делает вывод, что замечательное согласие квантовых вычислений в инфляционной космологии с имеющимися данными (рис. 3.5) должно отражать какую-то глубокую истину. При конечном наборе вселенных и наблюдателей глубокая истина состоит в том, что вселенные, в которых данные отклоняются от квантовых предсказаний — те, которые составляют 0,1 процента квантовой вероятности, или 0,0001 процента квантовой вероятности, или 0,0000000001 процент квантовой вероятности, — встречаются действительно редко, и именно поэтому типичные обитатели мультивселенной, как мы с вами, не попадают ни в одну из них. При бесконечном наборе вселенных, заключает оптимист, глубокая истина должна быть в том, что аномальные вселенные встречаются опять-таки редко, однако нам ещё предстоит выяснить, как это происходит. Ожидается, что однажды мы найдём меру, определённый способ, который позволит сравнивать различные бесконечные наборы вселенных, и при этом доля вселенных, возникающих благодаря редким квантовым отклонениям, будет мала по сравнению с теми, квантовая вероятность которых более велика. Достижение этой цели остаётся колоссально трудной задачей, но большинство исследователей в этой области убеждены, что согласие теоретических выводов и полученных данных, представленное на рис. 3.5, означает, что когда-нибудь мы добьёмся успеха.{67}
Нерешённые вопросы и мультивселенные: Могут ли мультивселенные давать предсказания, которые нельзя получить другими способами?
Вы, безусловно, заметили, что даже в самых оптимистичных планах предполагается, что предсказания на основе мультивселенного подхода будут иметь другой характер, отличный от того, что мы традиционно ожидаем от физики. Прецессия перигелия Меркурия, магнитный дипольный момент электрона, энергия, выделяемая при расщеплении ядра урана на барий и криптон, — всё это примеры предсказаний. Они основаны на тщательных математических вычислениях, опирающихся на цельную физическую теорию, и дают в конце точные, проверяемые числа. Эти числа были подтверждены экспериментально. Например, вычисления дают, что магнитный момент электрона равен 2,0023193043628; измерения показывают, что он равен 2,0023193043622. С точностью до малых ошибок, присущих и первым и вторым, эксперимент таким образом подтверждает теорию с точностью 1 к 10 миллиардам.
В той ситуации, где мы сейчас находимся, кажется, что предсказания теории мультивселенной никогда не достигнут такого стандарта точности. Возможно, что в наиболее продвинутых сценариях мы сможем характеризовать как «весьма вероятные» предсказания того, что космологическая постоянная, или величина электромагнитного взаимодействия, или масса u-кварка будут лежать в некотором диапазоне значений. Но чтобы это улучшить, нам должно очень сильно повезти. Кроме решения проблемы измерения необходимо построить убедительный вариант теории мультивселенной с очень скошенными распределениями (например, чтобы с вероятностью 99,9999 процента наблюдатель оказался во вселенной с наблюдаемым значением космологической постоянной) или с удивительно тонкими корреляциями (например, что существование электрона возможно только во вселенных с космологической постоянной равной 10−123). Если теория мультивселенной не обладает такими правильными свойствами, то точность, всегда отличавшая физику от других дисциплин, будет потеряна. Есть много физиков, которые не готовы заплатить такую цену.
Довольно долго я тоже придерживался такой позиции, но затем моя точка зрения начала меняться. Как любой другой физик, я предпочитаю конкретные, точные и недвусмысленные предсказания. Но я, как и многие другие, пришёл к пониманию, что не все фундаментальные свойства Вселенной подходят для точных математических предсказаний; по крайней мере вполне логично допустить, что могут существовать свойства, не укладывающиеся в рамки точных предсказаний. С середины 1980-х годов, когда я был студентом, изучающим теорию струн, было широко распространено мнение, что эта теория однажды объяснит значения масс частиц, константы взаимодействий, число пространственных измерений и вообще любое фундаментальное физическое свойство. Я по-прежнему надеюсь, что эта цель будет достигнута. Однако я признаю, что чрезмерно требовать от уравнений теории так извернуться, чтобы выдать число типа массы электрона (0,000000000000000000000091095 в единицах планковской массы) или массы t-кварка (0,0000000000000000632 в единицах планковской массы). Когда же наступает очередь космологической постоянной, задача вырастает до исполинских масштабов. Вычисления, которые после многих страниц выкладок и мегаватт, затраченных на компьютерное моделирование, выдадут то самое заветное число, с которого начиналась глава 6, — не то чтобы в принципе были невозможны, но здесь может дать сбой даже самый оптимистичный оптимизм. Увы, теория струн сегодня ни чуть не ближе к вычислению любого из этих чисел, чем когда я был студентом. Однако это не значит, что теория струн или другая, ещё не известная теория, однажды не достигнет этого. Возможно, что оптимистам следует быть более изобретательными. Но в рамках сегодняшней физики имеет смысл поискать новые подходы. Именно этим занимается теория с мультивселенными.
В рамках хорошо разработанного подхода с мультивселенными можно чётко выделить те физические свойства, которые следует рассматривать с точки зрения, отличной от стандартной: это те свойства, которые изменяются от одной вселенной к другой. В этом сила данного подхода. В теории с мультивселенными можно иметь точный контроль над тем, какие нерешённые загадки, характерные для некоторой частной вселенной, сохранятся в мультивселенном контексте, а какие нет.
Космологическая постоянная являет собой первый пример. Если её значение варьируется в рамках данной мультивселенной, причём во вполне определённом интервале, тогда то, что когда-то было загадкой, — её значение — теперь становится весьма прозаичным. Подобно тому как в обувном магазине с налаженными поставками товара всегда найдутся ботинки вашего размера, так и необъятная мультивселенная заведомо будет содержать вселенные с измеренным нами значением космологической постоянной. Задача, над которой доблестно бились поколения учёных, легко может быть разрешена с помощью идеи мультивселенной. Мультивселенная показала, что этот вопрос, кажущийся столь глубоким и столь непонятным, возникает из-за ошибочного допущения, что космологическая постоянная имеет единственное значение. Именно в этом смысле теория мультивселенной может обладать значительной предсказательной силой и иметь потенциальную возможность оказать неоценимое влияние на ход научных исследований.
С подобными рассуждениями нужно обходиться очень аккуратно. Что если Ньютон, увидев упавшее яблоко, решил бы, что мы являемся частью мультивселенной, в которой яблоки в одних вселенных падают вниз, в других вверх, поэтому падающее яблоко лишь указывает на то, в какой именно вселенной мы находимся, и не стоит предпринимать никакие дальнейшие исследования? Или он бы пришёл к выводу, что в каждой вселенной какие-то яблоки падают вниз, а какие-то вверх, и причина, согласно которой мы видим только падающие вниз яблоки, — это всего лишь вопрос нашего окружения, то есть все падающие вверх яблоки в нашей Вселенной уже упали вверх, поэтому давно оказались где-то в глубинах космоса? Это, конечно же, глупый пример — никогда не существовало причины, в том числе теоретической, так думать — но вопрос сам по себе серьёзный. Привлекая мультивселенную, наука может ослабить стимул решать конкретные задачи, даже если некоторые из этих задач ждут своего решения в рамках стандартного подхода, без мультивселенной. Вместо того чтобы упорно трудиться и расширять своё понимание, можно попасть под обаяние мультивселенной и преждевременно забросить привычные методы исследований.
Здесь кроется потенциальная угроза, которая объясняет, почему некоторые учёные содрогаются при упоминании мультивселенных рассуждений. Именно поэтому концепция мультивселенной, если её воспринимать всерьёз, должна быть строго обоснована с помощью теоретических результатов, она должна чётко характеризовать вселенные, из которых она состоит. Анализ должен быть аккуратными и методичным. Однако отворачиваться от мультивселенной только потому, что она могла бы завести в тупик, также рискованно. Если мы так поступим, мы закроем глаза на реальность.
Глава 8. Множественные миры квантовой механики Квантовая мультивселенная
Квантовая реальность
Статус теорий с параллельными вселенными, которые были рассмотрены выше, находится под большим вопросом. Бесконечное пространство, вечная инфляция, миры на бранах, циклическая космология, струнный ландшафт — эти захватывающие идеи возникли из ряда научных открытий. Но каждая из них остаётся гипотетичной, как и породившие их мультивселенные. Хотя многие физики с готовностью высказывают своё мнение «за» или «против» разных схем мультивселенных, большинство признают, что только будущие открытия — теоретические, экспериментальные и наблюдательные — определят, какие из этих идей останутся в науке.
Идея мультивселенной, к рассмотрению которой мы сейчас перейдём, возникает из квантовой механики. У неё особый статус. Многие физики уже определились с окончательным вердиктом по поводу этой мультивселенной. Но особенность в том, что их вердикты не совпадают. Различия проистекают из глубокой и до сих пор нерешённой проблемы перехода от вероятностной интерпретации квантовой механики к определённости повседневной реальности.
В 1954 году, почти тридцать лет спустя после формулировки квантовой теории такими светилами науки, как Нильс Бор, Вернер Гейзенберг и Эрвин Шрёдингер, никому неизвестный студент Принстонского университета по имени Хью Эверетт III придумал поразительную интерпретацию. Анализируя проблему, над которой Бор, мэтр квантовой механики, безуспешно корпел и никак не мог решить, он показал, что для правильного понимания квантовой механики может потребоваться огромное количество параллельных вселенных. Теория Эверетта стала одной из первых математических конструкций, из которой следовало, что мы можем являться частью некоторой мультивселенной.
У теории Эверетта, которая позже будет названа многомировой интерпретацией квантовой механики, весьма извилистая судьба. Изложив математические следствия, вытекающие из его гипотезы, в январе 1956 года Эверетт послал рукопись своей докторской диссертации Джону Уилеру, своему научному руководителю. Уилер, один из наиболее выдающихся мыслителей в физике двадцатого столетия, был очень впечатлён. В мае того же года он посетил Копенгаген и обсудил с Бором идеи Эверетта. Однако Бор воспринял их весьма прохладно. Бор и его коллеги потратили годы, разрабатывая и уточняя своё видение квантовой механики. Для них поднятые Эвереттом вопросы и чудной способ ответа не представляли особой ценности.
Уилер относился к Бору с очень большим уважением и поэтому предпринял меры, чтобы учесть мнение старшего коллеги. После критической оценки Бора Уилер отложил защиту диссертации Эверетта и предложил значительно её переработать. Эверетт должен был убрать части с откровенной критикой подхода Бора и подчеркнуть, что его результаты лишь проясняют и расширяют стандартную формулировку квантовой теории. Эверетт сопротивлялся, но так как он уже принял предложение о работе в министерстве обороны (где он вскоре начнёт играть важную закулисную роль в политике по ядерным вооружениям, проводимой администрацией Кеннеди и Эйзенхауэра), а для работы в министерстве требовалась учёная степень, то он, скрепя сердце, согласился. В марте 1957 года Эверетт подготовил значительно урезанную версию своей диссертации; в апреле она была утверждена в Принстоне, как удовлетворяющая всем условиям, а в июле опубликована в журнале «Reviews of Modern Physics».{68} Но поскольку подход Эверетта к квантовой механике уже был раскритикован Бором и компанией, а более широкое видение проблемы, ясно изложенное в исходной версии диссертации, было заглушено, статья осталась незамеченной.{69}
Десять лет спустя знаменитый физик Брайс ДеВитт вытащил работы Эверетта из забвения. Вдохновлённый результатами своего студента Нила Грахама, развившего математические идеи Эверетта, ДеВитт стал активным сторонником переосмысления квантовой теории, предложенного Эвереттом. Помимо публикации нескольких технических статей, благодаря которым достижения Эверетта были представлены небольшой, но влиятельной группе специалистов, в 1970 году ДеВитт написал обзор для журнала «Physics Today», предназначенный для более широкой научной аудитории. В отличие от статьи 1957 года, в которой Эверетт уклонился от обсуждения других миров, ДеВитт, наоборот, сделал на этом акцент, назвав с необыкновенной искренностью «шоком» вывод Эверетта о том, что мы являемся частью огромного «мультимира». Статья получила значительный отклик в физическом сообществе, ставшем более восприимчивым к экспериментам с ортодоксальной квантовой идеологией, и привела к непрекращающимся по сей день спорам об устройстве природы, когда, как мы верим, правят бал квантовые законы.
Итак, перейдём к обсуждению.
Переворот в понимании, произошедший примерно между 1900 и 1930 годами, привёл к безжалостному удару по нашей интуиции, здравому смыслу и всем известным законам, которые новое авангардное поколение учёных стало называть «классической физикой» — термином, отражающим авторитет и уважение к картине реальности — почтенной, определённой, удовлетворительной и обладающей предсказательной силой. Скажите мне, что происходит сейчас, и я, воспользовавшись законами классической физики, предскажу, что будет в любой последующий момент времени или что было в любой предшествующий момент времени. Такие особенности, как хаос (технически говоря, когда небольшие изменения в текущем состоянии могут привести к огромным ошибкам в предсказаниях) и сложность уравнений, представляют собой проблему для практических применений почти всегда, кроме простых ситуаций, но сами по себе законы непоколебимы и мёртвой хваткой держат как прошлое, так и будущее.
Квантовая революция потребовала от нас отказаться от классической точки зрения, потому что новые результаты ясно продемонстрировали её неправильность. Классические законы прекрасно подходят для описания и предсказания движения больших объектов, таких как Земля или Луна, или повседневных объектов, например, камней или мячей. Но при переходе в микромир молекул, атомов и субатомных частиц законы классической физики перестают работать. Наперекор самой сути классических рассуждений, если вы проведёте одинаковые эксперименты с участием одинаковых частиц, одинаково подготовленных, то, как правило, вы не получите одинаковые результаты.
Представьте, например, что у вас есть 100 одинаковых коробок, и в каждой находится по одному электрону, каждый из которых создан согласно одной и той же лабораторной инструкции. Спустя ровно 10 минут вы и ваши 99 коллег измеряете положения каждого из 100 электронов. В отличие от того, что подумали бы в этом случае Ньютон, Максвелл и даже юный Эйнштейн — возможно, даже жизнью поручились бы за ожидаемый ответ, — 100 измерений не приведут к одному и тому же результату. На самом деле, на первый взгляд полученные результаты будут выглядеть случайными, ведь часть электронов окажется вблизи нижнего левого угла передней части коробки, часть — вблизи верхнего правого угла задней части коробки, какие-то из электронов будут где-то в середине коробки, и так далее.
Принципы и закономерности, благодаря которым физика является строгой и предсказательной дисциплиной, проявятся, только если вы будете снова и снова проводить этот эксперимент со 100 электронами. Проделав это, вы обнаружите следующее. В первой серии из 100 измерений 27 процентов электронов окажутся вблизи нижнего левого угла, 48 процентов вблизи верхнего правого угла и 25 процентов где-то в середине. Вторая серия измерений даст примерно такое же распределение. Аналогично с третьей серией, четвёртой и всеми последующими. Закономерность распределения не видна в отдельно взятом измерении; вы не сможете предсказать, где окажется отдельно взятый электрон. Наоборот, закономерность проявляется в статистическом распределении результатов многих измерений. Она состоит в определённой вероятности обнаружить электрон в том или ином положении.
Впечатляющее достижение основателей квантовой механики состояло в развитии математического формализма, в котором отсутствовали абсолютные предсказания, характерные для классической физики, а вместо них появились вероятности. С помощью уравнения, опубликованного Шрёдингером в 1926 году (эквивалентное, но менее удобное уравнение было получено в 1925 году Гейзенбергом), физики умеют задавать начальное состояние вещей, а затем вычислять вероятность того, что они окажутся в одном состоянии или в другом в любой последующий момент времени.
Но не думайте, что всё так элементарно, как в простом примере с электроном. Квантовая механика применима не только к электронам, но и ко всем типам частиц, и предсказывает не только их положения, но также скорости, угловые моменты, энергии, а также поведение в разных ситуациях, от потока нейтрино, пронизывающих в данный момент ваше тело, до бурных атомных реакций в оболочках далёких звёзд. В таком широком диапазоне явлений вероятностные предсказания квантовой механики согласуются с экспериментальными данными. Всегда. В течение более чем восьмидесяти лет с того момента, как была сформулирована квантовая механика, не появилось ни одного проверяемого эксперимента или астрофизического наблюдения, результаты которых расходились бы с квантово-механическими предсказаниями.
Для целого поколения физиков столкнуться с таким радикальным отходом от интуитивных представлений, основанных на тысячелетнем коллективном опыте, и при этом переосмыслить окружающую нас реальность в рамках совершенно нового подхода, основанного на вероятностях, несомненно явилось поистине великим интеллектуальным достижением. Однако была одна неудобная мелочь, что досаждала квантовой механике с самого момента её возникновения — та самая мелочь, которая проложила путь в мир параллельных вселенных. Для её понимания нам понадобится чуть более подробно познакомится с квантовым формализмом.
Головоломка с альтернативами
В апреле 1925 года во время одного эксперимента в лаборатории Белла, проводимого двумя американскими физиками, Клинтоном Дэвиссоном и Лестером Джермером, стеклянная трубка с раскалённым кусочком никеля внутри неожиданно взорвалась. Дэвиссон и Джермер потратили много дней, облучая образец никеля потоками электронов с целью изучения атомных свойств металлов, и выход из строя оборудования был очень некстати, хотя такие помехи вполне привычны для экспериментатора. Убирая стеклянные осколки, Дэвиссон и Джермер заметили, что во время взрыва кусочек никеля потускнел. Ничего страшного, конечно же. Для восстановления образца его надо было прокалить, чтобы испарились загрязняющие вещества, после чего можно было начинать заново. Так они и поступили. То, что они решили очистить старый образец, а не взять новый, стало счастливой случайностью. Когда они направили пучок электронов на очищенный образец, полученные результаты разительно отличались от того, что они ожидали. К 1927 году стало понятно, что Дэвиссон и Джермер установили важнейшее свойство квантовой теории. Спустя десять лет это открытие было удостоено Нобелевской премии.
Хотя эксперимент Дэвиссона и Джермера был проведён так давно (до появления звукового кино и до начала Великой депрессии в США), он по-прежнему широко применяется для иллюстрации основных идей квантовой теории. Эксперимент объясняется следующим образом. Когда Дэвиссон и Джермер накалили загрязнённый образец, в никеле образовались довольно крупные кристаллы. Поэтому поверхность образца никеля перестала быть однородной, и электронный пучок стал рассеиваться на неоднородностях, порождённых местонахождением больших никелевых кристаллов. Чтобы прояснить самые существенные физические закономерности этого явления, рассмотрим упрощённую версию этого эксперимента, изображённую на рис. 8.1. Пучок электронов падает на пластинку с двумя узкими щелями. Электроны, прошедшие сквозь одну или другую щель, подобны электронам, рассеивающимся на одном кристалле никеля или на соседнем. С помощью этой модели Дэвиссон и Джермер осуществили первый вариант того, что теперь называется экспериментом с двумя щелями.
Рис. 8.1. Суть эксперимента Дэвиссона и Джермера можно передать в опыте «с двумя щелями», где электронами облучают пластинку с двумя узкими щелями. В эксперименте Дэвиссона и Джермера два потока электронов возникают при рассеянии электронов на двух соседних кристаллах никеля; в эксперименте с двумя щелями два аналогичных потока порождаются электронами, прошедшими сквозь соседние щели
Чтобы понять этот потрясающий результатом, представьте, что одна из щелей закрыта, а прошедшие электроны фиксируются поочерёдно на экране детектора. После облучения большим количеством электронов экран детектора будет выглядеть как на рис. 8.2а или 8.2б. Разумный человек, не знакомый с квантовыми рассуждениями, ожидал бы, что картинка, которая появится, когда открыты обе щели, будет простым объединением этих двух результатов. Поразительно, но такого не происходит! Вместо этого Дэвиссон и Джермер обнаружили то, что примерно показано на рис. 8.2в. Возникающая картинка состояла из светлых и тёмных полос, указывающих на места попадания или непопадания электронов.
Рис. 8.2. а) Открыта только левая щель; б) Открыта только правая щель; в) Открыты обе щели
Этот результат отличается от ожидаемого самым странным образом. Тёмные полосы соответствуют местам обильного попадания электронов, когда открыта только правая или только левая щель (яркие области на рис. 8.2а и 8.2б), но они, оказывается, исчезают, когда открыты две щели. Таким образом, наличие левой щели изменяет возможные места попадания электронов, прошедших через правую щель, и наоборот. Это совершенно сбивает с толку. Для таких крохотных частиц, как электрон, расстояние между щелями огромно. Поэтому когда электрон проходит сквозь одну из щелей, то каким образом наличие или отсутствие другой щели может привести к хоть какому-то эффекту, не говоря уже о наблюдаемой поразительной картинке? Это похоже на то, как если бы вы в течение многих лет успешно заходили в здание, где работаете, через одну дверь, а когда руководство, наконец, решило сделать ещё один вход с другой стороны здания, то вы не смогли бы попасть в свой кабинет!
Как это понять? Эксперимент с двумя щелями неизбежно приводит к заключению, которое трудно осознать. Независимо от того, через какую щель прошёл электрон, он каким-то образом «знает» о существовании другой щели. Есть что-то, связанное с электроном, или сопоставляемое с ним, или являющееся его частью, на что влияют сразу две щели.
Что бы это могло быть?
Квантовые волны
Как можно объяснить, что электрон, проходящий сквозь одну щель, «знает» о другой? В качестве подсказки рассмотрим более подробно картинку, показанную на рис. 8.2в. Эта картинка с чередующимися полосами по типу «светлая — темноватая — тёмная» хорошо знакома любому физику. Она говорит нам — нет, она кричит — волны! Если вы когда-нибудь бросали в воду два камешка и потом наблюдали, как возникающие волны разбегаются и накладываются друг на друга, вы поймёте, что я имею в виду. Там, где гребень одной волны накладывается на гребень другой, результирующая волна высока; там, где впадина одной волны совпадает со впадиной другой волны, также впадина и у результирующей волны; но самое главное происходит, когда гребень одной волны пересекается со впадиной другой волны — тогда волны гасят друг друга и поверхность воды остаётся гладкой. Всё это проиллюстрировано на рис. 8.3. Если бы мы положили экран детектора на картинку, на которой отражён уровень волнения в каждой точке — чем сильнее волнение, тем ярче, — то результат предстал бы на экране в виде чередующихся ярких и тёмных областей. Там, где волны усиливают друг друга, что приводит к повышению уровня воды, находятся яркие области; тёмные области соответствуют самому низкому уровню воды там, где волны гасят друг друга. Физики говорят, что накладывающиеся волны интерферируют друг с другом, и называют чередование тёмных и светлых полос интерференционной картиной.
Рис. 8.3. Когда две волны на поверхности воды накладываются, они «интерферируют», образуя чередование областей с бо́льшим и меньшим волнением, что называется интерференционной картиной
Сходство с рис. 8.2в совершенно очевидно, поэтому глядя на данные по рассеянию электронов, мы начинаем думать о волнах. Хорошо. Это уже кое-что. Но детали происходящего по-прежнему остаются неясными. Что за волны? Откуда они? И как они связаны с частицами, такими как электроны?
Следующую подсказку даёт эксперимент, о котором я упомянул вначале. Собранные данные о движении частиц показывают, что полученные закономерности носят исключительно статистический характер. Проведя точно такие же измерения над идентично приготовленными частицами, мы увидим, что частицы, вообще говоря, окажутся в других местах; однако проведя большое количество таких измерений, мы обнаружим, что частицы в среднем обладают одинаковой вероятностью оказаться в любом заданном месте. В 1926 году немецкий физик Макс Борн, собрав воедино эти две подсказки, выдвинул неожиданную идею, которая спустя почти три десятилетия привела его к Нобелевской премии. Итак, есть экспериментальное подтверждение, что волны здесь как-то при чём. Есть экспериментальное подтверждение, что и вероятность здесь как-то при чём. Возможно, предположил Борн, волна, связанная с частицей, является волной вероятности.
Это была поразительно оригинальная идея. Суть в том, что анализируя движение частицы, не стоит представлять её как камешек, летящий отсюда туда. Наоборот, следует думать о ней как о волне, бегущей отсюда туда. Там, где значения волны велики, у её гребней или впадин, обнаружить частицу наиболее вероятно. Там, где значения малы, обнаружить частицу маловероятно. В тех местах, где значения равны нулю, частица оказаться не может. По мере того, как волна катится вперёд, значения меняются, возрастая в одних местах и уменьшаясь в других. Поскольку мы интерпретируем осциллирующие значения как осциллирующие вероятности, такая волна по праву называется волной вероятности.
Для уточнения картины рассмотрим, как это объясняет данные эксперимента с двумя щелями. Квантовая механика говорит нам, что движение электрона по направлению к пластинке на рис. 8.2в следует считать бегущей волной, как на рис. 8.4. Когда волна падает на пластинку, из щелей выходят два фрагмента волны, которые движутся далее по направлению к экрану детектора. А дальше происходит очень важное явление. Подобно перекрывающимся волнам на поверхности воды, волны вероятности, выходящие из двух щелей, перекрываются и интерферируют, приводя к картине, как на рис. 8.3. Распределение больших и малых значений отражает, согласно квантовой механике, распределение больших и малых вероятностей для положений, в которых может оказаться электрон. Электроны, испущенные друг за другом, дают суммарную картину попаданий, которая согласуется с такой вероятностной картинкой. Большинство электронов попадает туда, где вероятность велика, совсем немного оказывается там, где она мала, и ни одного электрона в тех местах, где вероятность равна нулю. В итоге возникают тёмные и светлые полосы, показанные на рис. 8.2в.{70}
Рис. 8.4. Описание движения электрона с помощью бегущей волны вероятности объясняет загадочный интерференционный узор в эксперименте с двумя щелями
Именно так квантовая теория объясняет полученные данные. То, что каждый электрон действительно «знает» о двух щелях, становится при таком описании явным, поскольку волна вероятности каждого электрона проходит сквозь обе щели. Именно объединение двух таких парциальных волн определяет вероятность того, куда попадёт электрон. Именно поэтому само наличие второй щели влияет на конечный результат.
Не так быстро!
Мы рассмотрели детально электроны, однако похожие эксперименты подтвердили, что такое же вероятностно-волновое описание справедливо для всех элементарных объектов в природе. Фотоны, нейтрино, кварки — любые фундаментальные частицы — все они описываются волнами вероятности. Но прежде чем праздновать победу, следует разрешить три неотложных вопроса. Два из них не вызывают затруднений. А один — весьма крепкий орешек. Именно последний вопрос рассматривал Эверетт в 1950-х годах, что привело его к квантовой версии параллельных миров.
Во-первых, если квантовая теория верна и мир развивается вероятностно, тогда почему невероятностный подход Ньютона так хорошо предсказывает движение тел, от бейсбольных мячей до планет и звёзд? Ответ на этот вопрос такой: волны вероятности для крупных объектов, как правило (но не всегда, как мы скоро убедимся), имеют очень специальный вид. Как показано на рис. 8.5а, у них очень узкий профиль, что означает огромную вероятность — чуть менее 100 процентов, — что объект будет находиться в точке самого пика волны, и совершенно ничтожную вероятность, чуть более 0 процентов, что он окажется где-то в другом месте.{71} Более того, квантовые законы показывают, что пики таких узких волн движутся по траекториям, которые возникают из уравнений Ньютона. Поэтому квантовая теория лишь минимально уточняет ньютоновские законы, задающие точную траекторию бейсбольного мяча, говоря, что существует почти 100-процентная вероятность падения мяча в место, вычисленное на основе уравнений Ньютона, и почти 0-процентная вероятность того, что он упадёт в другое место.
На самом деле, слова «чуть менее» и «почти» характеризуют физику не с лучшей стороны. Возможность отклонения движения макроскопического тела от предсказываемого ньютоновскими законами настолько фантастически мала, что если бы вы вели астрономические наблюдения в течение последних нескольких миллиардов лет, то с подавляющей долей вероятности ничего подобного бы не обнаружили. Однако, согласно квантовой механике, чем меньше объект, тем, как правило, более размазана его волна вероятности. Например, типичная волна электрона может выглядеть так, как показано на рис. 8.5б, когда есть несколько местоположений, где частица может находиться с существенной вероятностью, — что совершенно чуждо ньютоновской концепции мира. Поэтому именно в микромире вероятностная природа реальности выходит на первый план.
Рис. 8.5. а) Волна вероятности макроскопического объекта, как правило, имеет очень узкий пик; б) Волна вероятности микроскопического объекта, например частицы, как правило, широко размазана
Во-вторых, можем ли мы видеть волны вероятности, составляющие основу квантовой механики? Существует ли какой-нибудь прямой способ пощупать этот непривычный вероятностный туман, как тот, что изображён на рис. 8.5б, когда единственная частица имеет шанс оказаться во множестве положений? Нет. Из стандартного описания квантовой механики, развитого Бором и его группой и названного в их честь копенгагенской интерпретацией, следует, что если вы захотите увидеть волну вероятности, то сам акт наблюдения разрушит ваши планы. Когда вы смотрите на волну вероятности электрона, то слово «смотрите» означает «измеряете его положение», электрон моментально реагирует на это и занимает какое-то выделенное положение. Соответственно, его волна вероятности поднимается в этом месте до 100 процентов, а во всех остальных коллапсирует до 0 процентов (рис. 8.6). Отвернитесь от него, и пикообразный вид волны вероятности электрона быстро расплывётся, извещая о том, что снова имеется шанс обнаружить электрон во множестве мест. Снова посмотрите на электрон, его волна заново схлопнется, перераспределяясь из множества возможных положений в какое-то одно определённое место. Вкратце говоря, каждый раз, когда вы пытаетесь взглянуть на вероятностный туман, он рассеивается — схлопывается, коллапсирует — и замещается привычной реальностью. Экран детектора на рис. 8.2в демонстрирует как раз это явление: он измеряет падающую волну вероятности электрона, и таким образом немедленно заставляет её схлопнуться. Детектор заставляет электрон отказаться от множества допустимых мест его попадания и определиться с каким-нибудь конкретным местом, которое впоследствии станет крохотной точкой на экране.
Рис. 8.6. Согласно копенгагенскому описанию квантовой механики, при измерении или наблюдении волны вероятности частицы она мгновенно коллапсирует везде, кроме одной точки. Из всего множества возможных местоположений остаётся одно выделенное положение
Я вполне пойму, если такое объяснение заставит вас покачать головой. Спору нет, квантовая догма звучит как шарлатанство. Действительно, предлагается теория, утверждающая совершенно поразительную картину реальности, основанную на волнах вероятностей, после чего буквально сразу заявляющая, что увидеть эти волны нельзя. Представьте, что некая барышня говорит, будто она блондинка, но если кто-то взглянет на неё, то она немедленно становится рыжей. Почему физики согласились с теорией, которая помимо того, что странная, ещё и выглядит откровенно ненадёжной?
К счастью, несмотря на все свои странности и скрытые свойства, квантовая механика является проверяемой теорией. Согласно копенгагенской интерпретации, чем выше волна вероятности в какой-то выделенной точке, тем больше шанс, что при схлопывании волны её единственный оставшийся пик — то есть сам электрон — будет расположен именно там. Такое утверждение обладает предсказательной силой. Проводите какой-нибудь эксперимент снова и снова, подсчитайте, как часто вы обнаруживаете частицы в тех или иных местах, и оцените, согласуются ли наблюдаемые частоты появления частиц с вероятностями, которые задаёт волна вероятности. Если волна в 2,784 раза выше здесь чем там, то будете ли вы в 2,784 раза чаще обнаруживать частицы здесь, чем там? Подобные предсказания оказались невероятно успешными. Какой бы лукавой не выглядела квантовая идея, ей трудно противостоять, когда она показывает такие феноменальные результаты.
Трудно, но не невозможно.
Это приводит нас к третьему и самому трудному вопросу. Коллапс волн вероятности при измерении (рис. 8.6) является ключевым моментом в копенгагенской интерпретации квантовой теории. Совокупность успешных предсказаний и выдающаяся способность Бора убеждать заставили большинство физиков принять копенгагенскую интерпретацию. Однако немного поразмыслив, можно быстро выявить одно неудобное свойство. Уравнение Шрёдингера, математический мотор квантовой механики, определяет изменение формы волны вероятности со временем. Дайте мне исходную форму волны, например, такую как на рис. 8.5б, и я смогу с помощью уравнения Шрёдингера нарисовать, как она будет выглядеть через минуту, час или в любой другой момент времени. Однако из прямого анализа этого уравнения следует, что показанная на рис. 8.6 эволюция — мгновенное схлопывание волны во всех точках, кроме одной, напоминающее замешкавшегося прихожанина в огромном соборе, который остался одиноко стоять во время службы, в то время как все остальные уже опустились на колени — по всей видимости не может быть описана уравнением Шрёдингера. Несомненно, волны могут иметь пикообразный вид, и вскоре мы начнём широко использовать такие волны. Однако способом, предлагаемым Копенгагенской школой, волна вероятности не может приобрести пикообразный вид. Используемый математический аппарат просто-напросто не допускает подобного. (Мы скоро увидим, почему это происходит.)
Бор предложил некий способ, довольно неуклюжий, задвинуть проблему: следует использовать уравнение Шрёдингера и найти волны вероятности, когда не происходит никакого наблюдения или измерения. Но при наблюдении, продолжает Бор, уравнение Шрёдингера следует отодвинуть в сторонку и объявить, что наблюдение заставило волну схлопнуться.
Однако такое предписание не только нескладное, произвольное и не имеет математического обоснования, оно даже не является понятным. Например, в нём отсутствует точное определение того, что значит «посмотреть» или «измерить». Необходимо ли участие человека? Или, как однажды спросил Эйнштейн, хватит беглого взгляда мыши? Как насчёт использования компьютера или воздействия вирусами или бактериями? Могут ли эти «измерения» заставить схлопнуться волну вероятности? Бор заявлял, что есть существенная разница между микромиром, то есть атомами и элементарными частицами, для которых применимо уравнение Шрёдингера, и макромиром, в котором находятся экспериментаторы со своим оборудованием, для которых уравнение Шрёдингера не применимо. Однако он так и не сказал, в чём именно эта разница. В действительности, он не мог бы этого сказать. С каждым годом экспериментаторы подтверждают правильность уравнения Шрёдингера без каких-либо модификаций для постоянно увеличивающихся наборов частиц, и есть все основания полагать, что оно справедливо для изрядного числа частиц, составляющих нас и всё, что угодно. Подобно наводнению, когда уровень воды медленно растёт, затапливая сначала фундамент дома, потом комнаты, грозя затопить второй этаж, математический аппарат квантовой механики постепенно выходит за пределы атомных расстояний, успешно осваивая всё большие масштабы.
Таким образом, мы подходим к следующему способу осмысления этой проблемы. Мы с вами, наши компьютеры, бактерии и вирусы и всё материальное на этом свете состоит из атомов и молекул, которые сами сложены из частиц типа электронов и кварков. Уравнение Шрёдингера выполняется для электронов и кварков, и есть все основания считать, что оно верно и для более сложноустроенных тел, независимо от общего числа составляющих их частиц. Это означает, что уравнение Шрёдингера будет продолжать быть верным и при измерении. Помимо всего прочего, измерение — это всего лишь какой-то набор частиц (человек, прибор, компьютер…), вступающий в контакт с другим набором (измеряемая частица или частицы). В этом случае, если математическая сторона уравнения Шрёдингера остаётся при этом непротиворечивой, рассуждения Бора наталкиваются на проблему. Уравнение Шрёдингера не позволяет волнам схлопнуться. Таким образом, существенный элемент копенгагенской интерпретации оказывается под сомнением.
Итак, третий вопрос таков: если проведённые выше рассуждения верны и волны вероятности не схлопываются, то как перейти от совокупности возможных результатов до проведения измерения к единственному результату после измерения? Или, если сформулировать вопрос более широко, что происходит с волной вероятности во время измерения, что позволяет проявиться привычной, определённой и единственной реальности?
Эверетт изучил этот вопрос в своей принстонской докторской диссертации и пришёл к неожиданному выводу.
Линейность и неудовлетворённость
Чтобы понять, как Эверетт пришёл к своему открытию, следует иметь чуть большее представление об уравнении Шрёдингера. Я уже подчёркивал, что уравнение не позволяет волнам вероятности внезапно схлопываться. Но почему? И что оно позволяет? Давайте попробуем понять, как уравнение Шрёдингера управляет волной вероятности по мере её распространения во времени.
Это совсем несложно, потому что уравнение Шрёдингера относится к одному из самых простых классов математических уравнений, характеризующихся свойством линейности — математическим олицетворением того, что целое есть сумма своих частей. Чтобы понять, что это значит, представим, что график на рис. 8.7а — это некоторая волна вероятности электрона ровно в полдень (для большей наглядности я буду использовать волну вероятности, зависящую от положения на прямой, изображённой горизонтальной линией, однако это не умаляет общности обсуждаемых идей). С помощью уравнения Шрёдингера можно следить за распространением этой волны вперёд во времени и узнать, какова будет её форма, скажем, в час дня (рис. 8.7б. Теперь отметим следующее. Как показано на рис. 8.8а, исходную форму волны можно разложить на два более простых кусочка; если объединить две волны на рисунке, складывая их значения точка за точкой, можно восстановить исходную форму волны. Линейность уравнения Шрёдингера означает, что его можно применять отдельно для каждого кусочка на рис. 8.8а, определяя вид каждого фрагмента волны в час дня, и затем, объединяя результаты, согласно рис. 8.8б, можно будет получить полный ответ, показанный на рис. 8.7б. В разложении на два фрагмента нет ничего сакрального; исходную волну можно разложить на любое число составляющих, рассмотреть каждую отдельно, затем объединить полученные результаты для получения окончательной формы волны.
Рис. 8.7. а) Изначальная форма волны вероятности эволюционирует согласно уравнению Шрёдингера, переходя в другую форму (б) в последующий момент времени
Рис. 8.8. а) Исходную волну вероятности можно разложить в набор из двух волн с более простыми формами; б) Распространение исходной волны вероятности можно воспроизвести, если отдельно рассмотреть эволюцию более простых волн и затем объединить полученные результаты
Это может выглядеть как технический нюанс, но линейность является невероятно мощным математическим свойством. Она позволяет претворять в жизнь крайне важную стратегию «разделяй и властвуй». Если исходная форма волны сложна, её легко можно разделить на более простые фрагменты и проанализировать каждый по отдельности. В итоге все полученные результаты складываются вместе. На самом деле, при анализе эксперимента с двойной щелью (рис. 8.4) мы уже встречались с одним важным применением линейности. Задача определения распространения волны вероятности электрона была разбита на несколько этапов: сперва мы заметили, как фрагмент волны проходит сквозь левую щель, затем сквозь правую щель, после чего мы сложили две получившиеся волны. Именно так мы обнаружили знаменитую интерференционную картину. Посмотрев на исписанную формулами доску в кабинете у специалиста по квантовой физике, вы узнаете именно этот подход.
Однако линейность не только контролирует квантовые вычисления; она также порождает трудности теории при объяснении того, что происходит во время измерения. Лучше всего это можно понять, применяя линейность к самому акту измерения.
Представьте, что теперь вы экспериментатор и с большой ностальгией вспоминаете ваше детство в Нью-Йорке, поэтому, занимаясь измерением положений электронов, вы впрыскиваете их в миниатюрную настольную модель города. Вы начинаете эксперимент с одного электрона, волна вероятности которого имеет особенно простую форму — в виде прекрасного пика, как на рис. 8.9, что указывает на почти 100-процентную вероятность, что в данный момент электрон находится на углу тридцать четвёртой улицы и Бродвея. (Не беспокойтесь о том, как у электрона оказалась именно такая форма волны вероятности, воспринимайте её так, как есть.[47]) Если как раз в этот момент вы измеряете положение электрона с помощью очень хорошего детектора, то полученный результат будет очень точным, и на мониторе детектора должно появиться «Угол тридцать четвёртой улицы и Бродвея». Действительно, если провести такой эксперимент, то результат будет именно таким (рис. 8.9).
Рис. 8.9. Волна вероятности электрона в определённый момент имеет пик на углу Тридцать четвёртой улицы и Бродвея. Измерение положения электрона в тот момент подтверждает, что электрон находится там, где у волны имеется пик
Я думаю, будет очень сложно разобраться в том, как уравнение Шрёдингера вплетает волну вероятности этого электрона в волну вероятности около триллиона триллионов атомов, из которых состоит детектор, побуждая всю эту гигантскую совокупность каким-то образом организоваться и выдать на монитор «Угол тридцать четвёртой улицы и Бродвея», и кто бы не построил этот детектор, он задал нам трудную задачку. Детектор устроен так, что при взаимодействии с таким электроном на мониторе появляется сообщение о единственном определённом положении, в котором в данный момент времени находится электрон. Если бы в такой ситуации детектор выдал что-нибудь другое, то его следовало бы заменить на новый, работающий как положено. Конечно, на пересечении Тридцать четвёртой улицы и Бродвея нет ничего особенного, ну кроме разве магазина «Macy’s»; если провести такой же эксперимент с волной вероятности электрона, имеющей пик в планетарии Хейден рядом с восемьдесят первой улицей и Сентрал Парк Вест авеню или в офисе Билла Клинтона на 125-й улице рядом с Ленокс авеню, монитор детектора отобразит названия именно этих мест.
Теперь давайте рассмотрим чуть более сложный профиль волны (рис. 8.10). Эта волна вероятности указывает на то, что в данный момент времени есть два места возможного нахождения электрона — Земляничные поля (мемориал Джона Леннона в Центральном парке) и мемориал Гранта в Риверсайд парке. (Сегодня у электрона мрачное настроение.) Если мы измеряем положение электрона, но не следуем Бору и, придерживаясь наиболее точных экспериментов, предполагаем, что уравнение Шрёдингера продолжает быть применимым — к электрону и частицам, из которых состоит детектор, вообще ко всему, — то что тогда возникнет на мониторе детектора? Ключ к ответу в линейности. Нам известно, что происходит при измерении отдельных волн с одним пиком. Уравнение Шрёдингера заставляет монитор детектора сообщить нам положение пика (рис. 8.9). Тогда из линейности следует, что для нахождения ответа для волны с двумя пиками следует объединить результаты измерений каждого пика в отдельности.
Рис. 8.10. Волна вероятности электрона имеет пик в двух местах. Линейность уравнения Шрёдингера говорит, что измерение положения электрона приведёт к смешению двух положений
Именно здесь возникают некоторые странности. На первый взгляд, совокупный результат подразумевает, что монитор детектора должен одновременно зарегистрировать положения двух пиков. Как на рис. 8.10, слова «Земляничные поля» и «мемориал Гранта» должны вспыхнуть одновременно, накладываясь друг на другом, как на экране зависшего компьютера. Уравнение Шрёдингера также описывает, как волны вероятности фотонов, испущенных монитором детектора, спутываются с волнами частиц, из которых состоят палочки и колбочки в сетчатке вашего глаза, и затем распространяются по нейронам, порождая зрительный образ того, что вы видите. В предположении неограниченной гегемонии уравнения Шрёдингера, линейность применима и здесь, поэтому не только монитор детектора покажет сразу оба положения электрона, но также ваше сознание окажется в ступоре, полагая, что электрон одновременно находится в двух местах.
Для более сложных волновых профилей путаница становится ещё больше. От волны с четырьмя пиками голова ещё больше идёт кругом. С шестью ещё хуже. Заметим, что если продолжать добавлять волновые пики различной высоты в разных местах на модели Манхэттена, их совместная форма опишет обычный, спокойно меняющийся волновой профиль, как схематично изображено на рис. 8.11. Свойство линейности по-прежнему выполняется, и это означает, что итоговая надпись на мониторе, а также окончательное состояние вашего сознания и ментальный образ определяются объединением результатов, полученных от каждого пика в отдельности. Детектор должен одновременно регистрировать положения всех пиков без исключения — каждой точки Манхэттена, — приводя ваше сознание в полнейшее замешательство, не имея никакой возможности выделить единственное определённое положение электрона.{72}
Рис. 8.11. Общая волна вероятности является объединением многих волн с одним пиком, каждая из которых соответствует возможному положению электрона
Безусловно, такое положение дел никак не согласуется с нашим опытом. Никакой нормально работающий детектор при проведении измерения не выведет конфликтующих друг с другом результатов. Ни у одного нормального человека, выполняющего это измерение, не возникает в голове головокружительной смеси одновременных, но в это же время разных, результатов.
Теперь вы понимаете привлекательность идеи Бора. Примите таблетку от головокружения, посоветовал бы он. Согласно Бору, мы не видим противоречивых показаний детектора, потому что они не происходят. По его мнению, мы пришли к неправильному заключению, потому что переоценили применимость уравнения Шрёдингера для больших объектов — для лабораторного оборудования, на котором производятся измерения, и учёных, фиксирующих результаты. Хотя уравнение Шрёдингера и его свойство линейности говорят, что надо объединять результаты различных возможных исходов (и тогда ничего не схлопывается), Бор говорит, что это неверно, потому что акт измерения задвигает уравнение Шрёдингера за штору. Вместо этого, заявляет Бор, акт измерения заставляет все пики на рис. 8.10 или 8.11, кроме одного, сколлапсировать в ноль; вероятность выживания какого-то одного конкретного пика пропорциональна его высоте. Этот единственный оставшийся пик задаёт единственное показание детектора, а также распознаётся вашим сознанием как единственный результат. С головокружением справились.
Но для Эверетта, а позже для ДеВитта, цена за такую идею Бора была слишком высока. Уравнение Шрёдингера было придумано для описания частиц. Всех частиц. Так почему же оно каким-то образом не применимо к частным конфигурациям частиц — тем, из которых состоит экспериментальное оборудование, и тем, из которых состоят те, кто снимает с него показания? Это просто бессмысленно. Поэтому Эверетт предложил не отказываться от уравнения Шрёдингера так быстро. Наоборот, он предложил проанализировать, куда нас приведёт уравнение Шрёдингера, отталкиваясь от принципиально другой точки зрения.
Множественность миров
Однако мы сразу окажемся в затруднительном положении, если попытаемся думать, будто измерительный прибор или сознание человека способны одновременно воспринимать разные реальности. Такие мысли заводят в тупик. У нас могут быть противоречивые мнения о том или о сём, мы можем испытывать смешанные эмоции о разных людях, но когда речь заходит о фактах, образующих окружающую действительность, всё, что мы знаем, свидетельствует в пользу однозначного и объективного описания. Всё, что нам известно, говорит о том, что один прибор и одно измерение дадут один результат; а один результат и один ум приведут к одному умственному заключению.
Идея Эверетта была в том, что уравнение Шрёдингера, математическая основа квантовой механики, согласуется с таким опытом. А причина кажущейся неоднозначности в показаниях детектора и умственных заключениях коренится в способе нашего анализа этих математических вычислений — то есть в том, как мы объединяем результаты измерений, показанных на рис. 8.10 и рис. 8.11. Давайте остановимся на нём подробнее.
Если вы измеряете волну с единственным пиком, как на рис. 8.9, детектор регистрирует местоположение пика. Если пик находится в Земляничных полях, то детектор покажет это место; если вы посмотрите на полученный результат, ваше сознание зафиксирует это место и у вас отложится эта информация. Если пик находится в мемориале Гранта, то детектор покажет это место; если вы посмотрите на полученный результат, ваше сознание зафиксирует это место и у вас отложится эта информация. При измерении волны с двойным пиком (рис. 8.10), уравнение Шрёдингера требует объединить два только что полученных результата. Но, говорит Эверетт, будьте при этом внимательны и бдительны. Комбинированный результат не состоит в том, что детектор и сознание каждый одновременно зафиксирует два положения. Так думать неверно.
Наоборот, рассуждая буквально и последовательно, мы получаем комбинированный результат в таком виде: детектор и сознание фиксируют Земляничные поля и детектор и сознание фиксируют мемориал Гранта. Что бы это значило? Сначала я опишу ответ лишь в общих чертах, а подробности объясню позднее. Чтобы соответствовать идее Эверетта, детектор, вы и всё остальное обязано расщепиться при измерении, образуя две копии детектора, две копии вас и две копии всего остального, а единственное различие между копиями будет в том, что одна копия детектора и одна копия вас зафиксируют Земляничные поля, а другая копия детектора и другая копия вас зафиксируют мемориал Гранта. Как показано на рис. 8.12, это означает, что теперь имеется две параллельные реальности, два параллельных мира. Для каждой копии вас, находящейся в каждом из миров, проводимое измерение и умственное заключение относительно полученного результата представляется точным и единственным, что соответствует привычному течению жизни. Конечно же, особенность в том, что вас теперь двое.
Рис. 8.12. В картине Эверетта, если волна вероятности частицы имеет два пика, то измерение приводит к двум результатам. В одном мире частица находится в первом положении; в другом мире частица находится во втором положении
Для наглядности я рассмотрел измерение положения единственной частицы, волна вероятности которой особенно проста. Однако идея Эверетта применима в более широком контексте. При измерении положения частицы, волна вероятности которой имеет произвольное число пиков, например, пять пиков, будет пять параллельных реальностей, отличающихся друг от друга только разными местоположениями частиц, регистрируемыми детекторами в каждой реальности и сознанием каждого из вас в каждой реальности. Если один из этих пятикратных вас займётся измерением положения другой частицы, волна которой имеет семь пиков, то вы и тот мир снова расщепятся ещё на семь миров, по одному на каждый возможный результат. Если провести измерения волны, как на рис. 8.11, которую можно разбить на огромное количество близко расположенных пиков, то в результате возникнет огромное количество параллельных реальностей, в каждой из которых каждое возможное положение частицы будет зафиксировано детектором и прочитано вашей копией. В подходе Эверетта каждое квантово-механически вероятное событие, то есть такое, вероятность которого отлична от нуля, находит свою реализацию в своём отдельном мире. Это и есть множество миров в многомировом подходе к квантовой механике.
Если вернуться к терминологии предыдущих глав, такое множество миров следует описать как мультивселенную, составленную из множества вселенных. Она будет шестой по счёту. Я буду называть её квантовой мультивселенной.
История о двух историях
Описывая, как квантовая механика может порождать множественные реальности, я использовал глагол «расщепляться». Его использовал Эверетт. Также поступал и ДеВитт. Однако я признаю, что в данном контексте этот глагол может сбивать с толку, и я колебался, стоит ли его использовать. Но всё-таки поддался искушению. В своё оправдание скажу, что иногда более эффективно взять кувалду, чтобы пробить дыру в барьере, стоящем между нами и необычной гипотезой об устройстве реальности, после чего заделать рванные края, чем аккуратно вырезать безупречное окошко, сквозь которое открывается новая перспектива. Я решил воспользоваться такой кувалдой, и теперь в этом и следующем разделах будет произведён необходимый ремонт. Некоторые идеи чуть более сложны, чем те, с которыми мы уже познакомились, и цепочка изложений чуть более длинна, чем раньше, но я призываю вас набраться терпения. Мне приходилось сталкиваться с тем, что зачастую у людей, которые что-то слышали о многомировом подходе или даже как-то с ним знакомы, было впечатление, что он основан на крайне экстравагантных умозрительных построениях. Но ничего подобного. Как я объясню позднее, многомировой подход является, в некотором смысле, наиболее консервативным способом осмысления квантовой физики, и важно понять, почему это так.
Важно понять, что физикам всегда приходится рассказывать истории с двух сторон. Одна сторона история — математическая — о том, как вселенная развивается согласно данной теории. Другая история — физическая, которая переводит абстрактные математические термины на экспериментальный язык. Вторая история описывает то, как математическая эволюция видится таким наблюдателям, как мы с вами, и, в более общем смысле, что математические символы теории говорят нам о природе реальности.{73} Во времена Ньютона эти две истории в общем и целом были идентичны, как я отмечал в главе 7, когда говорил о непосредственности и осязаемости ньютоновской «архитектуры». Каждый математический символ в уравнениях Ньютона имеет прямой и очевидный физический аналог. Символ x? О, это положение мяча. Символ υ? Скорость мяча. Однако когда мы переходим к квантовой механике, перевод математических символов в наблюдаемые явления окружающего нас мира оказывается не столь простым. Более того, используемый язык и понятия, необходимые для двух историй, становятся столь отличными, что вам требуется хорошо разобраться с каждой. Однако важно разделять, что есть что: какие идеи и описания привлекаются как часть фундаментальной математической структуры теории, а какие используются для установления связи с человеческим опытом.
Давайте послушаем эти две истории в случае многомирового подхода к квантовой механике. Вот первая из них.
Математический аппарат многомирового подхода, в отличие от копенгагенского, ясен, прозрачен и неизменен. Уравнение Шрёдингера определяет распространение во времени волн вероятности и никогда не задвигается за штору; оно всегда при деле. Уравнение Шрёдингера направляет форму волн вероятности, заставляя их с течением времени смещаться, видоизменяться и колебаться. Определяем ли мы волну вероятности частицы или совокупности частиц или рассматриваем различные ансамбли частиц, составляющие вас или ваше измерительное оборудование, уравнение Шрёдингера берёт исходную форму волны вероятности в качестве начальных данных и подобно графической программе, управляющей замысловатой экранной заставкой, выдаёт волновой профиль в любой последующий момент времени. Согласно этому подходу, именно так развивается вселенная. На этом всё. Конец истории. Точнее, конец первой истории.
Отметим, что при изложении первой истории я не использовал ни слово «расщепляться», ни понятия «множество миров», «параллельные вселенные» или «квантовая мультивселенная». Многомировой подход не нуждается в этих гипотезах. Они не играют никакой роли в фундаментальной математической структуре теории. Но, как мы сейчас увидим, эти идеи будут призваны во второй истории, когда, следуя Эверетту и его последователям, расширившим его пионерские результаты, мы изучаем, как математика объясняет нам то, что мы наблюдаем и измеряем.
Давайте начнём с простого — или настолько простого, насколько получится. Допустим, мы измеряем положение электрона, волна вероятности которого имеет один пик (рис. 8.9). (Опять-таки, не беспокойтесь о том, почему у электрона именно такая форма волны вероятности — воспринимайте это как данность.) Как я уже говорил, нам не под силу детально изложить первую историю даже такого простого измерительного процесса. Для этого потребовалось бы с помощью уравнения Шрёдингера определить, как волна вероятности, описывающая положения огромного количества частиц, составляющих вас и ваш измерительный прибор, объединяется с волной вероятности электрона и как это объединение эволюционирует во времени. Мои студенты, многие из которых весьма способные, очень часто не могут решить уравнение Шрёдингера даже для одной частицы. Вы и детектор состоите примерно из 1027 частиц. Решить математически уравнение Шрёдингера для такого большого количества составляющих практически нереально. Однако мы качественно представляем результирующую картину. При измерении положения электрона массы частиц приходят в движение. Примерно 1027 частиц монитора детектора, подобно танцорам в хорошо поставленном шоу, спешат занять свои места, чтобы разом высветить «Угол тридцать четвёртой улицы и Бродвея», а примерно такое же количество частиц в моих глазах и голове делают всё необходимое для создания чёткого восприятия сообщаемого результата. Уравнение Шрёдингера, каким бы неподъёмным ни был точный анализ для столь огромного количества частиц, описывает именно такое перемещение.
Представить наглядно это преобразование на уровне волны вероятности также невозможно. На рис. 8.9 и других ему подобных я использовал сетку из двух координатных осей, ведущих с севера на юг и с востока на запад, чтобы обозначить возможные положения одной частицы на модели Манхэттена. Значения волны вероятности в каждом положении соответствовали высоте волны. Это уже является упрощением, потому что я не использовал третью ось, положение частицы по вертикали (где находится частица — на втором этаже «Macy’s» или на пятом). Я не мог использовать вертикальную ось, потому что иначе не осталось бы осей для отображения высоты волны. Таковы ограничения нашего головного мозга и зрительной системы, которые в результате эволюции воспринимают только три пространственных измерения. Для правильного изображения волны вероятности приблизительно 1027 частиц нам потребуется ввести по три оси для каждой, чтобы математически описать каждое возможное положение, которое может занять каждая из частиц.[48] Добавление даже одной вертикальной оси на рис. 8.9 затруднит его восприятие; добавление ещё миллиарда миллиардов лишает картину вообще какого-либо смысла.
Однако очень важно иметь наглядный образ всех ключевых идей; поэтому давайте попытаемся, понимая, что результат будет далёк от совершенства. При описании волны вероятности частиц, из которых состоите вы и ваш детектор, я буду придерживаться варианта с двумя осями на плоскости, но при этом использовать непривычную интерпретацию этих осей. Грубо говоря, я буду считать, что каждая ось представляет собой огромный пучок осей, плотно сгруппированных между собой, которые символически изображают возможные положения такого же огромного количества частиц. Таким образом, волна, изображённая с помощью таких осей-пучков, будет описывать вероятности местоположений огромного набора частиц. Чтобы подчеркнуть разницу между одночастичной и многочастичной ситуациями, волна вероятности многочастичного набора будет иметь светящийся контур (рис. 8.13).
Рис. 8.13. Схематичное изображение комбинированной волны вероятности для всех частиц, составляющих вас и детектор
Одночастичная и многочастичная иллюстрации имеют некоторые общие свойства. Подобно волне с одним пиком (рис. 8.6), которая задаёт резко скошенную вероятность (почти 100 процентов в области пика и почти 0 процентов во всех остальных местах), остроконечная волна (рис. 8.13) также обозначает сильно скошенную вероятность. Но следует проявить осторожность, потому что понимание, основанное на одночастичной модели, может сыграть с вами злую шутку. Например, глядя на рис. 8.6 естественно думать, что рис. 8.13 соответствует частицам, которые все скопились в одном месте. Однако это не так. Остроконечный вид волны на рис. 8.13 символизирует, что начальное состояние каждой из частиц, составляющих вас, и каждой из частиц, из которых составлен ваш детектор, является обычным, знакомым состоянием, когда положение определяется с почти 100-процентной вероятностью. Однако не все частицы находятся в одном месте. Частицы из которых состоят ваши рука, плечо и голова почти наверняка сгруппированы там, где находятся ваши рука, плечо или голова; частицы, составляющие ваш измерительный прибор, почти наверняка сгруппированы там, где находится ваш прибор. Остроконечный волновой профиль на рис. 8.13 означает, что каждая из этих частиц имеет очень малый шанс быть обнаруженной где-либо в другом месте.
Если теперь выполнить измерение, показанное на рис. 8.14, то многочастичная волна вероятности (для частиц, из которых состоите вы и ваш детектор) из-за взаимодействия с электроном начнёт распространяться (как схематически показано на рис. 8.14а). Все вовлечённые в этот процесс частицы всё ещё находятся вблизи определённых положений (внутри вас, внутри детектора), поэтому волна на рис. 8.14а сохраняет остроконечный профиль. Но происходит массовое перераспределение частиц, которое приводит к фразе «Земляничные поля» на мониторе детектора, а также в вашей голове (рис. 8.14б). Рис. 8.14а иллюстрирует математическое преобразование, определяемое уравнением Шрёдингера, соответствующее истории первого типа. Рис. 8.14б иллюстрирует физическое описание данной математической эволюции, что соответствует истории второго типа. Аналогично, если осуществить эксперимент, показанный на рис. 8.15, то произойдёт аналогичное смещение (рис. 8.15а). Данное смещение соответствует массовому перераспределению частиц, которое приводит к фразе «Мемориал Гранта» на мониторе детектора и порождает в вашей голове соответствующий образ (рис. 8.15б).
Рис. 8.14а. Схематическая иллюстрация эволюции комбинированной волны вероятности всех частиц, составляющих вас и ваш детектор, определяемой уравнением Шрёдингера, при измерении положения электрона. Волна вероятности самого электрона имеет пик на Земляничных полях
Рис. 8.14б. Соответствующая физическая (экспериментальная) история
Рис. 8.15а. Тот же самый тип математической эволюции, как и на рис. 8.14а, но волна вероятности электрона имеет пик на мемориале Гранта
Рис. 8.15б. Соответствующая физическая (экспериментальная) история
Теперь воспользуемся линейностью и соединим два результата воедино. При измерении положения электрона, волна вероятности которого имеет два пика, волна вероятности частиц, из которых состоите вы и детектор, смешивается с волной электрона, что приводит к эволюции, показанной на рис. 8.16а — объединённой эволюции, изображённой на рис. 8.14а и 8.15а. Пока что это не более чем иллюстрированная и прокомментированная версия квантовой истории первого типа. Мы стартуем от волны вероятности с заданной формой, далее она эволюционирует во времени как предписывает уравнение Шрёдингера, и в результате возникает волна вероятности с новой формой. Давайте, опуская подробности, изложим эту математическую историю не количественным, а качественным языком истории второго типа.
Рис. 8.16а. Схематическая иллюстрация эволюции комбинированной волны вероятности всех частиц, составляющих вас и ваш детектор, определяемой уравнением Шрёдингера, при измерении положения электрона, волна вероятности которого имеет два пика
С физической точки зрения, каждый пик на рис 8.16а соответствует конфигурации огромного числа частиц, возникающей в детекторе, на мониторе которого высвечивается определённая информация, воспринимаемая вашим сознанием. Левому пику соответствует «Земляничные поля», а правому «Мемориал Гранта». Кроме этого различия, нет ничего, что отличало бы один пик от другого. Я подчёркиваю это, потому что важно понимать, что ни один из них не является более реальным, чем другой. Ничего, кроме информации на мониторе детектора и вашего прочтения этой информации, не отличает два пика многочастичной волны вероятности.
Это означает, что наша история второго типа, как показано на рис. 8.16б, вовлекает две реальности.
Рис. 8.16б. Соответствующая физическая (экспериментальная) история
На самом деле, фокусировка на детекторе и на вашем сознании является ещё одним упрощением. Можно было бы добавить частицы, из которых состоит лаборатория и всё, что в ней находится, а также частицы, из которых состоит Земля, Солнце и всё остальное, и все рассуждения остались бы прежними, буквально дословными. Единственное различие в том, что светящийся профиль волны вероятности на рис. 8.16а теперь будет также содержать информацию о всех таких частицах. Но поскольку обсуждаемое нами измерение не оказывает на самом деле на них влияния, их роль совершенно вторична. Однако будет полезно учесть эти частицы, потому что нашу историю второго типа можно расширить и включить не только вашу копию, колдующую над детектором, который проводит измерение, но также копии вашей лаборатории, всего остального на Земле, вращающейся по орбите вокруг Солнца, и так далее. Это означает, что каждый пик в истории второго типа соответствует тому, что мы традиционно назвали бы настоящей вселенной. В одной такой вселенной на мониторе детектора вы видите «Земляничные поля», в другой — «Мемориал Гранта».
Если исходная волна вероятности электрона имеет, скажем, четыре пика, или пять, или сто, или любое другое число, произойдёт то же самое: волновая эволюция приведёт к четырём, или пяти, или сотне, или к любому другому числу вселенных. В самом общем случае, как на рис. 8.11, размазанная волна имеет пик в каждой точке, и поэтому волновая эволюция приводит к огромному набору вселенных, по одной на каждое возможное положение.{74}
Однако, как было указано, единственное, что происходит в любом из этих сценариев, заключается в том, что волна вероятности подставляется в уравнение Шрёдингера, далее в работу включается математика, и на выходе получается волна с изменённым профилем. Нет никакого «клонирующего механизма». Нет никакого «расщепляющего механизма». Именно поэтому я сказал ранее, что такие слова могут запутать читателя. Нет ничего кроме вероятностно-волнового «механизма», который управляется сухими математическими законами квантовой механики. Когда результирующая волна принимает конкретный профиль, например, показанный на рис. 8.16а, мы пересказываем математическую историю на языке второго типа, и делается вывод, что каждому пику соответствует учёное разумное существо, находящееся в обычной вселенной, уверенно наблюдающее один и только один определённый результат в заданном эксперименте (рис. 8.16б). Если бы существовал способ опросить всех этих учёных существ, то оказалось бы, что каждый из них — это точная копия других. Единственная разница будет в том, что все они будут наблюдать разные определённые результаты.
А поскольку Бор и Копенгагенская школа доказывали, что только одна из этих вселенных существует (потому что акт измерения, который, по их утверждению, не описывается уравнением Шрёдингера, приведёт к коллапсу всех остальных вселенных), и поскольку первый шаг в попытке выйти за рамки концепции Бора и расширить применимость уравнения Шрёдингера ко всем частицам, включая те, из которых состоит экспериментальное оборудование и головной мозг, привёл к невероятной путанице (потому что данное устройство или мозг, должны, по-видимому, воспринять все возможные результаты одновременно), Эверетт пришёл к выводу, что более внимательная трактовка уравнения Шрёдингера может дать нечто другое: обширную реальность, состоящую из постоянно растущего числа вселенных.
Препринт статьи Эверетта 1957 года был разослан ряду физиков по всему миру до публикации основной статьи. По настоянию Уилера изложение было настолько урезано, что многие, кто читал его, не были уверены, действительно ли Эверетт считает, что все вселенные в его математическом подходе реальны. Эверетт узнал об этой неясности и решил разъяснить ситуацию. В «примечаниях при корректуре», которые он, по-видимому, написал прямо перед публикацией и, скорее всего, не уведомляя об этом Уилера, Эверетт чётко выразил свою позицию относительно природы разных квантово-механических результатов: «С точки зрения теории, все… являются “настоящими”, ни одна из них не более “реальна”, чем все остальные».{75}
Когда возникает альтернативная вселенная?
Помимо слов «расщеплять» и «клонировать», которые мы довольно вольготно использовали при изложении историй второго типа, мы также употребляли взаимозаменяемым образом такие серьёзные термины, как «мир» и «вселенная». Есть ли какие-то чёткие указания, когда уместно использовать эти термины, а когда нет? Когда мы рассматриваем волну вероятности одного электрона с двумя (или более) пиками, мы не говорим о двух (или более) мирах. Мы подразумеваем один мир — наш — в котором содержится электрон с неоднозначным положением. Однако, применяя подход Эверетта, когда мы измеряем или наблюдаем этот электрон, мы говорим на языке множественных миров. В чём тогда различие между измеренной и неизмеренной частицей, что приводит к столь разительно отличающимся описаниям?
На ум быстро приходит такой ответ: для одного изолированного электрона нет надобности излагать историю второго типа, потому что без измерений или наблюдений нет никакой связи с человеческим опытом, который требует своего описания. Всё, что нужно, — это история первого типа о волне вероятности, распространяющейся согласно уравнению Шрёдингера. Без истории второго типа нет никакой возможности привлечь многократные реальности. Хотя такое объяснение разумно, имеет смысл покопаться поглубже и проанализировать специальные свойства квантовых волн, проявляющиеся в задачах со многими частицами.
Проще всего ухватить основную идею на примере эксперимента с двумя щелями (рис. 8.2 и рис. 8.4). Напомним, что волна вероятности падает на пластину, затем два волновых фрагмента, прошедшие сквозь щели, распространяются дальше и достигают экрана. Вдохновившись обсуждением многомирового подхода, мы можем поддаться соблазну представить две бегущие волны как две раздельные реальности. В одной из них электрон проскакивает сквозь левую щель, а в другой — через правую щель. Но вы быстро сообразите, что наложение этих двух предположительно «разных реальностей» существенно влияет на результат эксперимента; именно перекрывание двух волн приводит к интерференционной картине. Поэтому рассматривать две волновые траектории как существующие в двух разных вселенных не имеет никакого особого смысла и не даёт никакой дополнительной пищи для ума.
Однако если изменить условия эксперимента, расположив позади каждой из щелей детектор, который будет записывать, прошёл электрон сквозь неё или нет, то ситуация изменится коренным образом. Поскольку теперь привлечено макроскопическое оборудование, две различные траектории электрона порождают изменения в огромном количестве частиц — это огромное количество частиц участвует в появлении надписи «электрон прошёл сквозь левую щель» или «электрон прошёл сквозь правую щель». По этой причине соответствующие волны вероятности для каждой возможности становятся настолько несопоставимыми, что у них не оказывается практически никакой возможности как-то влиять друг на друга. Как показано на рис. 8.16а, различия в миллиардах миллиардов составляющих детектор частиц приводят к тому, что волны, соответствующие двум возможным результатам, расходятся друг с другом, практически не перекрываясь. А без перекрытия эти волны не могут участвовать ни в одном из характерных интерференционных явлений квантовой физики. Действительно, когда установлены детекторы, электроны перестают давать полосатый узор как на рис. 8.2в; наоборот, получается обычное объединение результатов, показанных на рис. 8.2а и рис. 8.2б. Физики в таком случае говорят, что волны вероятности декогерируют (более подробно вы можете прочитать об этом, например, в главе 7 книги «Ткань космоса»).
Суть тогда в том, что как только возникает декогерентность, две волны для каждого результата начинают распространяться независимо — они не смешиваются, — поэтому каждая из них может быть названа своим собственным миром или вселенной. В рассматриваемом случае в одной такой вселенной электрон проходит сквозь левую щель, и детектор это подтверждает; в другой вселенной электрон проходит сквозь правую щель, и детектор это подтверждает.
В этом и только в этом смысле есть некоторое перекликание с концепцией Бора. Согласно многомировому подходу, крупные тела, составленные из многих частиц, действительно отличаются от малых тел, составленных из одной или горстки частиц. Крупные тела не стоят особняком от математического аппарата квантовой механики, как думал Бор, но их волны вероятности могут обладать достаточными вариациями, вследствие чего их способность к интерференции становится ничтожной. И как только две и более волны перестают влиять друг на друга, они становятся невидимы друг для друга; каждая «думает», что другие исчезли. Итак, в то время как Бор просто декларировал, что акт измерения отметает все результаты, кроме одного, в многомировом подходе, дополненном декогерентностью, гарантируется, что в каждой вселенной всё оказывается так, как будто все остальные результаты исчезли. То есть в каждой вселенной всё выглядит так, как если бы волна вероятности схлопнулась, оставив лишь один пик. Однако по сравнению с копенгагенским подходом это «как если бы» приводит к совершенно другой картине устройства реальности. В многомировом подходе реализуются все возможные результаты, не только какой-то один.
Неопределённость на переднем крае
Может показаться, что на этом можно было бы и заканчивать главу. Мы видели, как сама математическая структура квантовой механики берёт нас под белы рученьки и подводит к новой концепции параллельных вселенных. Однако это ещё не конец истории. На последующих страницах я объясню, почему многомировое описание квантовой физики остаётся спорным; мы увидим, что неприятие данного подхода основано не просто на нежелании вникнуть в принципиально новую точку зрения на окружающую реальность. Но если вы, читатель, уже насытились и вам не терпится перейти к следующей главе, приведём короткое резюме.
В повседневной жизни мы сталкиваемся с вероятностью, когда видим, что в результате есть несколько возможных вариантов, но по той или иной причине не можем понять, какой из них на самом деле произойдёт. Иногда у нас имеется достаточно информации, чтобы понять, какой из результатов скорее всего произойдёт, и тогда вероятность является тем инструментом, который позволяет дать этому количественную оценку. Наша уверенность в вероятностном подходе возрастает, когда мы обнаруживаем, что результаты, которые считают вероятными, происходят часто, а маловероятные происходят редко. Проблема, стоящая перед многомировым подходом, состоит в том, что необходимо придать смысл вероятности — квантово-механическим вероятностным предсказаниям — в совершенно другом контексте, когда считается, что могут произойти все возможные результаты. Эту дилемму легко сформулировать: как можно говорить о том, что какие-то результаты вероятны, а другие маловероятны, если они все имеют место?
В последующих разделах я остановлюсь на этом более подробно и рассмотрю различные попытки решения. Хочу предупредить: мы сейчас обсуждаем вопросы, которые находятся на самом переднем крае науки, поэтому мнения о том, где мы сейчас находимся, сильно расходятся.
Вероятная проблема
Критика многомирового подхода часто сводится к тому, что этот подход слишком причудлив, чтобы быть правильным. История физики учит нас, что успешные теории просты и элегантны; они объясняют экспериментальные данные на основе минимального количества допущений и приводят к точному пониманию. Теория, в которой вселенные сыплются как из рога изобилия, далека от этого идеала.
Сторонники многомирового подхода справедливо говорят, что при оценке сложности научной теории не следует сосредотачиваться на её следствиях. Значение имеют лишь её фундаментальные свойства. В многомировом подходе считается, что всего одно уравнение — уравнение Шрёдингера — управляет распространением всех волн вероятности, так что по простоте формулировки и экономности допущений с этим подходом трудно соревноваться. Копенгагенский подход никак не проще. Он тоже основан на уравнении Шрёдингера, но при этом содержит туманное, плохо определённое предписание, когда уравнение Шрёдингера не следует применять, и ещё менее понятное описание, касающееся процесса схлопывания волны вероятности, который, как предполагается, имеет место быть. То, что многомировой подход приводит к исключительно богатой картине реальности, говорит о неблагонадёжности теории не более, чем разнообразие жизни на Земле говорит против дарвиновского естественного отбора. Механизмы, фундаментально простые по своей сути, могут привести к сложным заключениям.
Тем не менее, хотя отсюда следует, что бритва Оккама недостаточно остра, чтобы отсечь многомировой подход, переизбыток вселенных действительно приводит к потенциальному затруднению. Ранее я говорил, что физики, применяя какую-нибудь теорию, должны излагать её в двух ипостасях — описывать эволюцию мира с математической стороны, а затем интерпретировать полученные математические результаты с позиции нашего опыта. Но на самом деле есть ещё и третья сторона, связанная с первыми двумя, и физики должны её рассмотреть. Для квантовой механики эта третья сторона выглядит следующим образом: наша уверенность в квантовой механике идёт от её феноменального успеха в объяснении экспериментальных данных. Если физик-теоретик, используя квантовую механику, вычисляет, что при повторении некоторого эксперимента один результат будет возникать, скажем, в 9,62 раза чаще, чем другой, то именно это физик-экспериментатор будет устойчиво наблюдать в своих экспериментах. Перевернув эту фразу, можно сказать, что если эксперимент разойдётся с квантово-механическими предсказаниями, то экспериментаторы придут к выводу, что теория не верна. На самом деле, будучи аккуратными исследователями, они сделают более осторожное заключение. Экспериментаторы скажут, что сомневаются в правильности квантовой механики, но при этом отметят, что их результаты не отвергают эту теорию полностью. Даже для монетки идеальной формы, если её подбросить 1000 раз, может не получиться ожидаемой 50-процентной вероятности выпадения орла или решки. Но чем больше отклонение, тем больше оснований подозревать, что форма монетки отнюдь не идеальна; чем больше экспериментальные отклонения от предсказаний квантовой механикой, тем сильнее экспериментаторы будут подозревать, что теория ошибочна.
То, что уверенность в квантовой механике можно поколебать на основе полученных результатов, является важным моментом. Для любой предложенной научной теории, которая была подходящим образом развита и понята, мы должны быть в состоянии сказать, хотя бы в принципе, что если при осуществлении такого и такого эксперимента мы не получаем такого и такого результата, наша вера в эту теорию должна ослабнуть. И чем сильнее наблюдения отклоняются от предсказаний, тем меньше должно быть доверия такой теории.
Одно из затруднений с многомировым подходом и причина, по которой он остаётся спорным, состоят в том, что он способен лишить нас этих способов оценки уровня доверия к квантовой механике. И вот почему. При подбрасывании монетки я знаю, что с вероятностью 50 процентов выпадет решка и с вероятностью 50 процентов выпадет орёл. Но это заключение основывается на привычном допущении, что подбрасывание монетки даёт единственный результат. Если в одном мире выпадает орёл, а в другом решка, и более того, если есть копия меня в каждом мире, смотрящая на тот или иной результат, то какой тогда смысл у обычной вероятности? В одном мире будет некто, кто выглядит точно как я, обладает всей моей памятью и искренне утверждает, что он — это я, который видит, что выпала решка; а также будет другой, также уверенный что он — это я, который видит, что выпал орёл. Так как выпадают оба результата — есть Брайан Грин, видящий решку, и Брайан Грин, видящий орла, — то привычной вероятности того, что Брайан Грин с равным успехом увидит орла или решку, теперь, по-видимому, не останется.
То же самое можно сказать и про электрон, волна вероятности которого сосредоточена вблизи Земляничных полей и мемориала Гранта (рис. 8.16б). Традиционные квантовые рассуждения говорят, что у вас, экспериментатора, есть 50-процентая вероятность обнаружить электрон в одном из двух мест. Но в рамках многомирового подхода имеют место оба результата. Есть вы, который обнаружит электрон в Земляничных полях, и другой вы, который обнаружит его в мемориале Гранта. Поэтому как понимать традиционные вероятностные предсказания, которые в этом случае говорят, что с равной вероятностью вы обнаружите электрон в одном месте или в другом?
Естественная реакция многих людей, когда они в первый раз сталкиваются с этим вопросом, состоит в том, что они думают, что среди различных ваших копий в многомировом подходе есть какая-то одна, более реальная, чем все остальные. Даже если каждый из вас в любом из миров выглядит одинаково и имеет одинаковые воспоминания, люди будут думать, что только один из вас это действительно вы. И, продолжая эту линию рассуждения, это именно тот вы, который наблюдает один и только один результат, соответствующий вероятностным предсказаниям. Мне нравится подобный ответ. Много лет назад, когда я впервые узнал об этих идеях, я тоже так отвечал. Но эти рассуждения не имеют ничего общего с многомировым подходом. Ему свойственен минималистский стиль. Распространение волн вероятности непосредственно управляется уравнением Шрёдингера. И ничем более. Чтобы представить, что одна из ваших копий это «настоящий» вы, нужно проговорить что-нибудь в духе Копенгагенской школы. Схлопывание волны в копенгагенском подходе — это грубый способ сделать один и только один результат реальным. Если в многомировом подходе вы представите, что лишь одна ваша копия это действительно вы, то получится, что вы делаете то же самое, только менее заметно. Такие действия сведут на нет саму причину появления многомирового подхода. Он возник из попытки Эверетта исправить недочёты Копенгагенской школы, и план состоял в том, чтобы не привлекать ничего, кроме проверенного на опыте уравнения Шрёдингера.
Осознание этого выставляет многомировой подход совсем в другом свете. Наша уверенность в квантовой механике основана на экспериментальном подтверждении её вероятностных предсказаний. Однако в многомировом подходе трудно видеть, какую вообще роль играет вероятность. Тогда как можно говорить о третьей стороне вопроса, которая должна заложить основу нашей уверенности в многомировом подходе? Вот это действительно незадача.
Если подумать, то совсем не удивительно, что мы упёрлись в эту стену. В многомировом подходе нет ничего вероятностного. Распространение волны, её исходный и конечный профиль совершенно и полностью детерминировано описываются уравнением Шрёдингера. Никакой игры в кости; никакой крутящейся рулетки. В противоположность этому, в копенгагенском подходе вероятность возникает посредством туманно определённого схлопывания волны, вызванного измерением (напомним, чем больше высота волны в данной точке, тем больше вероятность того, что в результате схлопывания частица окажется именно там). Именно это является одним из ключевых моментов копенгагенской интерпретации, где начинается «игра в кости». Но так как многомировой подход отказывается от схлопывания, он отказывается от традиционной точки вхождения для вероятности.
Итак, есть ли в многомировом подходе место для вероятности?
Вероятность и множественность миров
Определённо можно сказать, что Эверетт считал ответ на этот вопрос положительным. Основная часть чернового варианта его диссертации 1956 года, а также урезанная версия 1957 года была посвящена объяснению того, как инкорпорировать вероятность в многомировой подход. Но дебаты не прекращаются и спустя полвека. Среди физиков и философов, потративших всю жизнь в поисках ответа на этот вопрос, имеется широкий диапазон мнений насчёт того, где и как встречаются множественность миров и вероятность. Некоторые из них утверждают, что проблема нерешаема, поэтому от многомирового подхода следует отказаться. Другие считают, что вероятность, или по крайней мере нечто, что можно назвать вероятностью, действительно присутствует в этом подходе.
Исходный анализ Эверетта является хорошим примером возникающих трудностей. В повседневном опыте мы пользуемся вероятностью, потому что наши знания, как правило, неполны. Если, подбросив монетку, мы имеем достаточно сведений (точный размер монетки, её вес, то, как она была подброшена), то результат можно предсказать. Но поскольку обычно мы лишены такой информации, приходится обращаться к вероятности. Аналогичные рассуждения справедливы для прогнозирования погоды, лотереи и многих других привычных ситуаций, в которых вероятность играет роль: мы прибегаем к вероятностной оценке того или иного исхода только потому, что наши знания ограничены. Эверетт считал, что вероятность находит дорогу в многомировую интерпретацию, потому что присутствует аналогичная неизвестность, но она имеет совершенно иную природу. У населения миров есть доступ только к своему единственному миру; они никак не контактируют с другими мирами. Эверетт считал, что вероятность возникает благодаря этой ограниченности.
Чтобы понять, как это происходит, оставим ненадолго квантовую механику и рассмотрим несовершенную, но очень полезную аналогию. Представьте, что инопланетяне с планеты Закстар преуспели в строительстве клонирующей машины, способной делать копии вас, меня и кого угодно. Если вы зайдёте в клонирующую машину, то вас выйдет двое, и вы оба будете абсолютно уверены, что именно вы это настоящий вы, и оба будете правы. Закстарианцам нравится ставить перед менее разумными формами жизни экзистенциальные вопросы, поэтому они прилетели на Землю и сделали вам следующее предложение. Сегодня вечером, когда вы пойдёте спать, вас аккуратно переместят в клонирующую машину; через пять минут будут созданы две ваши копии. Когда один из вас проснётся, его жизнь будет течь в привычном русле — но вдобавок вам будет гарантировано исполнение любого желания. Когда же проснётся другой из вас, его жизнь превратится в кошмар; вы будете перемещены в пыточную камеру на Закстаре и никогда не вернётесь обратно. Кроме того, вашему счастливому клону не будет позволено пожелать освобождения. Примете такое предложение?
Ответ большинства людей — нет. Поскольку каждый клон — это действительно настоящий вы, в случае принятия такого предложения вам будет гарантировано, что кто-то из вас, проснувшись, будет обречён на пожизненные муки. Несомненно, будет и другой из вас, который, проснувшись, вернётся к привычной жизни, получив исполнение всех желаний, но для вас, оказавшегося на Закстаре, останутся только пытки. Цена этого слишком велика.
Понимая, что вы вряд ли согласитесь, закстарианцы поднимают ставки. Всё то же самое, но теперь они сделают миллион плюс одну копию вас. Миллион ваших копий просыпается у себя дома, имея возможность исполнения любого желания; но кто-то один попадает в закстарианскую камеру пыток. Согласны? В этот момент вы начинаете сомневаться. «Эх, — думаете вы, — шанс проснуться в своей постели и иметь всё, что захочешь, а не закончить свои дни на Закстаре, очень велик!»
Это последнее рассуждение особенно существенно для многомирового подхода. Если вы начинаете думать о вероятности, потому что представили, что лишь один из миллиона и одного вашего клона — это «настоящий» вы, то вы не полностью осознали суть этого сценария. Каждая копия и есть вы. Один из вас со 100-процентной определённостью проснётся в невыносимом будущем. Если именно поэтому вы начали думать в терминах вероятностей, то об этом следует забыть. Однако для того чтобы думать о вероятности, есть более тонкий способ. Представьте, что вы согласились с предложением закстарианцев и теперь размышляете о том, как это будет — проснуться завтра утром. Завернувшись в тёплое одеяло, только-только осознавая себя, но ещё не открывая глаз, вы вспоминаете предложение закстарианцев. На первый взгляд оно покажется почти реальным ночным кошмаром, но ощущая тяжёлые удары сердца, вы понимаете, что всё реально — что миллион и одна ваша копия сейчас просыпается, причём один из вас просыпается в закстарианской камере, а для всех остальных исполняются любые желания. «Каковы шансы, — нервно спрашиваете вы себя, — что открыв глаза, я окажусь на Закстаре?»
До клонирования не было смысла говорить о том, вероятно или маловероятно то, что вы окажетесь в закстарианской тюрьме — совершенно определённо будет «тот вы», кто точно окажется там, поэтому как такое может быть маловероятным? Но после клонирования ситуация видится иной. Каждый клон ощущает себя как настоящий вы; каждый из них это действительно настоящий вы. Но каждая копия всё равно является отдельной и самостоятельной личностью, которая может интересоваться своим будущим. Каждый из миллиона и одного клона может задаться вопросом, какова вероятность того, что он окажется на Закстаре. Поскольку каждый из них знает, что только один из миллиона и одного проснётся не там, где хочет, то каждый уже подсчитал, что шансы оказаться этим несчастным очень малы. При пробуждении миллион обнаружит, что их радостные ожидания сбылись, и только один поймёт, что нет. Так что хотя в закстарианском сценарии нет ничего неопределённого, ничего вероятностного, ничего случайного — опять же никаких бросаний игральных костей и крутящихся рулеток, — кажется, что вероятность всё-таки появляется. Это происходит в силу субъективного незнания каждым клоном в отдельности того, что именно с ним произойдёт.
Отсюда возникает способ ввести вероятности в многомировую интерпретацию. До того, как поставить эксперимент, вы есть ваше доклонированное существо. Вы оцениваете все возможные результаты, допустимые квантовой механикой, и знаете, что есть 100-процентная вероятность, что ваша копия увидит каждую из них. Пока нет ничего случайного. Затем вы проводите эксперимент. В этот момент, так же как в закстарианском сценарии, возникает понятие вероятности. Каждая ваша копия является независимым разумным существом, способным поинтересоваться, в каком мире ей достанется жить — то есть вероятностью того, что когда результаты эксперимента будут проявлены, она увидит тот или иной определённый результат. Вероятность возникает посредством субъективного опыта каждого клона.
Подход Эверетта, который он охарактеризовал как «объективно детерминированный» с вероятностью, «возникающей на субъективном уровне», согласуется с описанной выше картиной. Эверетт был очень воодушевлён таким ходом мыслей. Он отмечал в черновике своей диссертации 1956 года, что предлагаемый подход перекидывает мостик между позицией Эйнштейна (который, как известно, считал, что фундаментальная физическая теория не должна содержать вероятности) и позицией Бора (который был совершенно доволен своей квантовой механикой). Согласно Эверетту, многомировой подход сочетает в себе обе эти позиции и различие между ними зависит только от угла зрения. Точка зрения Эйнштейна опирается на математический аппарат, в котором единая волна вероятности всех частиц непреклонно распространяется согласно уравнению Шрёдингера, и случай здесь не играет никакой роли.[49] Мне нравится представлять Эйнштейна, парящего высоко над множеством миров многомирового подхода и наблюдающего, как уравнение Шрёдингера полностью определяет развёртывание всей панорамы, заключающего с удовлетворением, что даже если квантовая механика верна, всё равно Бог не играет в кости. А Бор со своей точки зрения видит, как обитатель одного из миров, не менее счастливый, с помощью вероятностей объясняет с невероятной точностью доступные ему наблюдения.
Это замечательное зрелище — Эйнштейн и Бор, достигшие согласия по поводу квантовой механики. Но есть досадные мелочи, которые за более чем половину столетия убедили многих, что победу праздновать рано. Те, кто изучил диссертацию Эверетта, в целом согласны, что хотя его подход совершенно ясен — это детерминированная теория, которая, тем не менее, для её обитателей видится вероятностной, — он не смог убедительно показать, как этого достичь. Например, в духе изложения главы 7, Эверетт пытался определить, что «типичный» обитатель одного из множества миров будет наблюдать в любом наперёд заданном эксперименте. Но (в отличие от главы 7, где изложение было сфокусировано на другом) в многомировом подходе те обитатели, с которыми мы должны вести дискуссию, все являются одной и той же личностью; если вы экспериментатор, то все они — это вы, и все они коллективно видят весь набор разных результатов. И тогда возникает вопрос: «типичный» вы — это кто?
Вдохновившись закстарианском сценарием, естественным предложением будет подсчитать число вас, которые видят заданный результат; тогда то, что видит большинство из вас, будет считаться «типичным». Или, более количественно, определим, что вероятность некоторого результата пропорциональна числу тех из вас, кто его наблюдает. Для простых примеров это работает: на рис. 8.16 мы видим, как один из вас наблюдает один из результатов эксперимента, поэтому вы ставите 50:50, что произойдёт один или другой результат. Это уже хорошо; обычное квантово-механическое предсказание также даёт 50:50, потому что высота волны вероятности в каждом из двух положений одинакова.
Однако рассмотрим более общую ситуацию, когда высота волны вероятности в разных точках различается (рис. 8.17). Если волна на Земляничных полях в сто раз больше, чем на мемориале Гранта, то квантовая механика предсказывает, что в сто раз вероятнее вы обнаружите электрон на Земляничных полях. Но в многомировом подходе при проведении измерения вы всё равно получите одного из вас, наблюдающего Земляничные поля, и другого, наблюдающего мемориал Гранта; таким образом, вероятность, основанная на подсчёте числа ваших клонов, остаётся равной 50:50 — неправильный ответ. Причина расхождения очевидна. Число ваших клонов, которые наблюдают тот или иной результат, определяется числом пиков волны вероятности. Однако квантово-механические вероятности определяются другим — не только числом пиков, но и их относительной высотой. И именно эти предсказания — квантово-механические предсказания — получили убедительное экспериментальное подтверждение.
Рис. 8.17. Общая волна вероятности, описывающая вас и ваш детектор, встречается с волной вероятности с многочисленными пиками разной величины
Эверетт разработал математический аппарат, который предназначался для объяснения этой нестыковки; впоследствии он был значительно доработан многими другими исследователями.{76} В общих чертах идея такова, что при вычислении вероятности наблюдения того или иного результата следует придавать всё уменьшающийся вес вселенным со всё уменьшающейся высотой волны, как символически показано на рис. 8.18. Но такой рецепт выглядит неубедительно. К тому же он неоднозначен. Является ли вселенная, в которой электрон находится на Земляничных полях, в каком-то смысле в сто раз более настоящей, или в сто раз более вероятной, или в сто раз более существенной, чем та, в которой электрон находится в мемориале Гранта? Такие рассуждения определённо подорвут веру в то, что каждый мир так же реален, как и все остальные.
Рис. 8.18а. Схематическое изображение эволюции, определяемой уравнением Шрёдингера, общей волны вероятности всех частиц, составляющих вас и ваш детектор, при измерении положения электрона. Волна вероятности самого электрона имеет пики в двух местах, но разной высоты
Рис. 8.18б. Некоторые полагают, что в многомировом подходе разная высота волны означает, что некоторые миры менее настоящие или менее существенные, чем другие. Как бы то ни было, существуют разные точки зрения насчёт того, что бы это значило
Спустя более чем пятьдесят лет, в течение которых выдающиеся учёные пересматривали, перепроверяли и развивали рассуждения Эверетта, многие согласятся, что проблема остаётся. Однако столь соблазнительно думать, что существует математически простой, предельно аскетичный и глубоко революционный многомировой подход, который даёт вероятностные предсказания, составляющие основу нашей веры в квантовую теорию. Благодаря этому возникло многих других идей насчёт совмещения вероятности с многомировой интерпретацией, которые выходят за рамки рассуждений закстарианского типа.{77}
Ведущей группой учёных из Оксфорда, среди которых был Дэвид Дойч, Саймон Саундерс, Дэвид Уоллес и Хилари Гривс, была выдвинута выдающаяся гипотеза. Они разработали хитроумный способ рассуждения, основанный на, казалось бы, глупом вопросе. Если вы игрок и верите в многомировой подход, то какова оптимальная стратегия заключения пари в квантово-механических экспериментах? Их ответ, подтверждённый математически, таков, что вы должны играть по правилам подхода Бора. Высчитывая максимальное увеличение дохода, эти авторы рассуждают таким образом, который поверг бы Бора в шок — они рассматривают среднее по многим обитателям мультивселенной, считающих, что они — это вы. Но даже при этом их вывод таков, что числа, которые Бор и все остальные вслед за ним вычисляли и называли вероятностями, являются теми самыми числами, которые должны подсказать вам, какие ставки делать. То есть даже если квантовая теория является полностью детерминированной, эти числа следует рассматривать, как если бы они были вероятностями.
Некоторые исследователи уверены, что этим программа Эверетта завершается. А некоторые — нет.
Отсутствие согласия по важнейшему вопросу — как трактовать вероятности в многомировом подходе — отнюдь не является неожиданным. Проводимые исследования в высшей степени сложны технически, и затрагиваемая тема — вероятность — весьма коварна даже при обычном применении, за рамками квантовой теории. Все согласятся, что при бросании игральной кости есть 1 шанс из 6, что выпадет тройка, поэтому мы предсказываем, что через, например, 1200 бросаний тройка выпадет примерно 200 раз. Но так как очень даже возможно и, на самом деле, очень вероятно, что число выпадений тройки отклонится от 200, то какой тогда смысл мы вкладываем в наше предсказание? Мы хотим сказать, что очень вероятно, что в 1/6 части выпадений будет тройка, однако, произнеся такие слова, мы определили вероятность выпадения тройки, привлекая понятие вероятности. Мы ходим по кругу. Эта ситуация лишь отчасти демонстрирует то, насколько концептуально размыта постановка обсуждаемых вопросов, даже если отвлечься от их внутренней математической сложности. А если добавить сюда многомировую идею, что понятие «вы» больше не относится к одной личности, то немудрено, что учёные тут же обнаружат миллион причин для спора. Я почти уверен, что однажды наступит полная ясность, но не сейчас, и, возможно, пройдёт ещё какое-то время.
Предсказание и понимание
Несмотря на все противоречия, сама по себе квантовая механика является не менее успешной, как и любая другая теория в истории физических идей. Как мы видели, причина этого в том, что для определённых типов экспериментов, которые можно поставить в лаборатории, а также для многих наблюдений астрофизических процессов, у нас есть «квантовый алгоритм», выдающий проверяемые предсказания. С помощью уравнения Шрёдингера вычислите эволюцию рассматриваемой волны вероятности и воспользуйтесь полученными результатами — различными высотами волны — для предсказания вероятности возникновения того или иного исхода. Что касается самих предсказаний, то почему этот алгоритм работает — схлопывается ли волна при измерении, реализуется ли каждая возможность в своей собственной вселенной, идёт ли при этом ещё какой-нибудь процесс — это совершенно вторично.
Некоторые физики утверждают, что даже называя этот вопрос вторичным, мы придаём ему больше веса, чем он заслуживает. По их мнению, роль физики состоит исключительно в том, чтобы делать предсказания, и если разные подходы не влияют на конечный ответ, то почему нас должно волновать, какой из них на самом деле правильный? Я приведу три причины.
Во-первых, кроме предсказаний физические теории должны быть математически непротиворечивы. Усилия Копенгагенской школы заслуживают только похвалы, но их метод не соответствует приведённому выше стандарту: в критический момент наблюдения метод прячется в кусты.{78} Такая брешь в подходе весьма существенна. Многомировой метод нацелен на преодоление этого недочёта.
Во-вторых, в некоторых ситуациях предсказания многомирового подхода дают отличный от предсказаний Копенгагенской школы результат. В копенгагенском подходе процесс схлопывания приведёт к пересмотру картинки на рис. 8.16а — будет один пик вместо двух. Так что если вы сможете заставить две волны, изображённые на этом рисунке, соответствующие макроскопически различным ситуациям, интерферировать, порождая узор, как на рис. 8.2в, это будет свидетельствовать о том, что копенгагенское схлопывание волны не произошло. Как обсуждалось ранее, по причине декогерентности достичь этого невероятно сложно, но, по крайней мере, теоретически копенгагенский и многомировой подходы приводят к различным предсказаниям.{79} Это важный и принципиальный момент. Копенгагенский и многомировой подходы часто считаются разными «интерпретациями» квантовой механики. Так говорить неправильно. Если два подхода могут привести к различным предсказаниям, то вы не можете называть их всего лишь интерпретациями. Конечно, вы можете. И многие так делают. Но эта терминология неверна.
В-третьих, физика — это не только способ делать предсказания. Если однажды мы найдём чёрный ящик, всегда аккуратно предсказывающий результаты наших экспериментов по физике частиц, а также астрономических наблюдений, то существование этого ящика не приведёт к окончанию исследований в этих областях. Есть разница между продуцированием и пониманием предсказаний. Прелесть физики, смысл её существования в том, что она предлагает понимание того, почему вещи во Вселенной ведут себя так, а не иначе. Способность предсказывать является существенной частью мощи физической науки, но сама её суть исчезнет, если она не приведёт нас к глубокому пониманию скрытой реальности, лежащей за нашими наблюдениями. И если многомировой подход верен, то насколько захватывающая реальность откроется благодаря нашему неистребимому стремлению к истолкованию предсказаний.
Я не жду, что на моём веку мы достигнем теоретического или экспериментального консенсуса относительно того, какой из вариантов реальности — одна вселенная, мультивселенная, или что-то совсем другое — реализуется в квантовой механике. Но я не сомневаюсь, что будущие поколения, оглянувшись назад, сочтут нашу работу в двадцатом и двадцать первом столетиях превосходным фундаментом для картины, которая, в конце концов, проявится.
Глава 9. Чёрные дыры и голограммы Голографическая мультивселенная
Платон говорил, что наши взгляды на мир сродни взглядам древних предков, наблюдающих за пляшущими тенями на скудно освещённых стенах пещеры. Он утверждал, что наши ощущения — это не более чем слабое отражение гораздо более богатой реальности, проблёскивающей за пределами досягаемости. Похоже, что два тысячелетия спустя пещера Платона может стать чем-то бо́льшим, чем просто метафорой. Переворачивая с ног на голову его рассуждения, может оказаться, что реальный мир — а не просто его тень — живёт на удалённой граничной поверхности, в то время как всё, что мы видим в трёх привычных пространственных измерениях, это проекция происходящего где-то там далеко. Можно сказать, что реальность похожа на голограмму. Или, на самом деле, на голографическое кино.
Являясь, возможно, наиболее странной реализацией идеи о параллельных мирах, голографический принцип предполагает, что всё, что мы ощущаем, может быть полностью эквивалентным образом описано в виде нечто, происходящего на тонкой и удалённой поверхности. Он утверждает, что если было бы возможно понять законы, управляющие физикой на этой удалённой поверхности, и то, как происходящие там явления связаны с нашим опытом здесь, мы смогли бы полностью разобраться в окружающей действительности. Версия мира теней Платона — параллельное, но совершенно непривычное воплощение повседневных явлений — станет реальностью.
Для анализа этой весьма своеобразной возможности требуются глубокие и обширные знания — из общей теории относительности, теории чёрных дыр, термодинамики, квантовой механики, а также самые современные исследования по теории струн. Нитью, объединяющей эти несхожие области, является природа информации в квантовой вселенной.
Информация
Джон Уилер помимо способности находить и взращивать очень талантливых молодых учёных (помимо Хью Эверетта, его студентами были Ричард Фейнман, Кип Торн и, как мы вскоре увидим, Якоб Бекенштейн) обладал необъяснимой способностью ставить вопросы, изучение которых может изменить наши фундаментальные представления об устройстве природы. Однажды во время ланча в Принстоне в 1998 году я спросил его, что по его мнению будет доминантной темой в физике в последующие десятилетия. Он наклонил голову, как уже не раз делал в тот день, будто его стареющий скелет устал поддерживать такой могучий интеллект. Однако, теперь пауза затянулась, что заставило меня сомневаться, хочет ли он отвечать на мой вопрос или вообще забыл о нём. Но затем он медленно поднял свой взгляд на меня и промолвил одно единственное слово: «Информация».
Я не удивился. В течение некоторого времени он придерживался совершенно отличной точки зрения на физические законы по сравнению с тем, чему молодых физиков обучают в стандартных университетских курсах. Традиционно физика рассматривает объекты — планеты, камни, атомы, частицы, поля — и изучает силы, влияющие на их поведение и управляющие их взаимодействиями. Уилер полагал, что объекты — вещество и излучение — следует рассматривать как вторичные, как носителей более абстрактной и более фундаментальной сущности: информации. Уилер не утверждал, что вещество и излучение являются в том или ином смысле эфемерными; он считал, что их следует рассматривать как материальные проявления чего-то более фундаментального. Он считал, что информация — то, где частица находится, каков её спин, положителен её заряд или отрицателен, и так далее — образует цельное ядро в сердце реальности. То, что такая информация реализуется в реальных частицах, занимающих реальные положения, имеющие определённые спины и заряды, чем-то похоже на то, как рисунок архитектора воплощается в построенном небоскрёбе. Фундаментальная информация отражена в рисунке. Небоскрёб — это всего лишь реализация заложенной в проекте архитектора информации.
С этой точки зрения нашу вселенную можно рассматривать как информационный процессор. Он берёт информацию, касающуюся устройства вещей сейчас, и порождает информацию, характеризующую устройство вещей в следующем сейчас, и в последующем сейчас. Наши чувства улавливают этот процесс, замечая изменения окружающей среды во времени. Но окружающая среда сама является производной; она возникает из фундаментального ингредиента, информации, и развивается согласно фундаментальным правилам, законом природы.
Я не знаю, будет ли такая информационно-теоретическая установка доминировать в физике, как считал Уилер. Однако недавно, во многом благодаря работам физиков Герарда т’Хоофта и Леонарда Сасскинда, в сознании учёных произошёл сдвиг, вызванный изучением нетривиальных вопросов, касающихся поведения информации в одном особенном экзотическом контексте: в чёрных дырах.
Чёрные дыры
В течение года после публикации общей теории относительности немецкий астроном Карл Шварцшильд нашёл первое точное решение уравнений Эйнштейна, которое определяет форму пространства и времени в окрестности массивного сферического объекта, подобного звезде или планете. Замечательно не только то, что Шварцшильд нашёл своё решение, занимаясь вычислением траекторий артиллерийских снарядов на русском фронте во время Первой мировой войны, но также то, что он обыграл самого мастера игры — к тому моменту Эйнштейн нашёл лишь приближённые решения уравнений общей теории относительности. Эйнштейн был очень впечатлён и огласил достижения Шварцшильда, представив его работу перед Прусской академией наук; но даже он не смог увидеть то, что станет самым важным звеном наследия Шварцшильда.
Решение Шварцшильда показывает, что обычные тела, такие как Солнце и Земля, не сильно искривляют пространство, порождая очень мягкое давление на пространственно-временной батут, который в их отсутствие оставался бы плоским. Это хорошо соответствовало приближённым решениям Эйнштейна, которые ему удалось найти ранее. Но Шварцшильд смог выйти за рамки приближений. Его точное решение обладало поразительным свойством: если достаточное количество массы сжать до объёма небольшого шара, то возникнет гравитационная пропасть. Пространственно-временная кривизна станет настолько экстремальной, что всё, что отважится оказаться слишком близко, будет захвачено в ловушку. Поскольку это «всё» включает свет, такие области потемнеют и станут чёрными, что явилось причиной исходного термина «чёрные звёзды». Экстремальное искривление заставит замереть на краю звезды даже время: отсюда возник другой термин — «замёрзшие звёзды». Спустя полвека Уилер, который столь же хорошо умел рекламировать вещи, как и заниматься физикой, сделал популярными такие звёзды как среди научной общественности, так и у любителей науки, дав им более запоминающееся имя: «чёрные дыры». Название прижилось.
Когда Эйнштейн прочёл статью Шварцшильда, он согласился с математическими выкладками применительно к обычным звёздам и планетам. Однако выкладки насчёт того, что теперь называется чёрными дырами, Эйнштейн воспринял с улыбкой. В те времена даже Эйнштейну было трудно полностью разобраться в сложной математической структуре общей теории относительности. И хотя до появления современного понимания чёрных дыр оставалось несколько десятилетий, интенсивное сворачивание пространства и времени, уже в то время с очевидностью следовавшее из уравнений, было, по мнению Эйнштейна, слишком радикальным, чтобы быть правдой. Так же как спустя несколько лет он будет сопротивляться идее космического расширения, Эйнштейн отказывался верить, что такая экстремальная конфигурация вещества является чем-то бо́льшим, чем вышедшими из-под контроля математическими манипуляциями, хоть и вытекающими из его собственных уравнений.{80}
Когда вы видите числа, которые возникают из уравнений, и вы можете легко прийти к такому же выводу. Чтобы звезда с массой Солнца стала чёрной дырой, она должна сжаться до шара размером приблизительно три километра в поперечнике; тело с массой Земли станет чёрной дырой, только если сожмётся до шарика диаметром в один сантиметр. Идея о существовании таких экстремальных конфигураций вещества кажется просто смехотворной. Всё же за прошедшие десятилетия астрономы собрали многочисленные наблюдательные данные, свидетельства относительно того, что чёрные дыры существуют и их много. Широко признано, что в центре огромного количества галактик может находиться чёрная дыра; считается, что наша собственная галактика Млечный Путь вращается вокруг чёрной дыры, масса которой примерно равняется трём миллионам масс Солнца. Есть даже шанс, как обсуждалось в главе 4, что на Большом адронном коллайдере можно сгенерировать крошечные чёрные дыры посредством «утрамбовывания» массы (и энергии) протонов, сталкивающихся на очень высоких энергиях, в такой крохотный объём, что можно снова применить результаты Шварцшильда, хоть и на микроскопических расстояниях. Являясь выдающейся демонстрацией способности математики высветить самые тёмные уголки нашей Вселенной, чёрные дыры стали центром внимания современной физики.
Помимо того, что чёрные дыры — это находка для наблюдательной астрономии, они также стали богатым источником вдохновения в теоретических исследованиях, создавая математический плацдарм, на котором физики могут апробировать применимость своих идей, изучая с помощью бумаги и ручки одно из самых экстремальных явлений природы. Именно так получилось, когда в начале 1970-х годов Уилер осознал, что если почтенный Второй закон термодинамики — на протяжении примерно столетия являющийся указующим перстом для понимания взаимосвязи между энергией, работой и теплом — рассматривать применительно к окрестности чёрной дыры, то похоже, что он перестаёт работать. Свежий взгляд на этот вопрос Якоба Бекенштейна, студента Уилера, пришёл на выручку, посеяв при этом семена возникшего впоследствии голографического принципа.
Второй закон
Афоризм «лучше меньше, да лучше» имеет много форм. «Убрать всё лишнее». «Нужны только факты и ничего кроме фактов». «Меньше знаешь, крепче спишь». «Справок не даём!» Эти крылатые выражения настолько часто встречаются потому, что ежедневно, ежесекундно на нас сваливаются тонны информации. К счастью, в большинстве случаев наше восприятие отбрасывает ненужные подробности, оставляя лишь то, что действительно имеет значение. Если я нахожусь в саванне и вижу льва, меня не волнуют детали движения фотонов, отражающихся от его шкуры. Слишком много информации! Я хочу знать всего лишь некоторые общие свойства, те самые, которые воспринимают наши глаза и передают в мозг для обработки. Движется ли лев на меня? Он припал к земле и крадётся? Дайте мне посекундное описание движения каждого фотона, и, несомненно, я буду знать всё досконально. Но понимания от этого не прибавится. Действительно, меньше значительно лучше.
Аналогичные рассуждения играют центральную роль в теоретической физике. Иногда мы хотим знать каждую микроскопическую деталь системы, которую изучаем. В определённых местах вдоль 27-километрового туннеля Большого адронного коллайдера, в котором сталкиваются частицы, физики поместили громадные детекторы, способные отследить с невероятной точностью траектории порождаемых осколков частиц. Эти данные существенны для понимания фундаментальных законов физики частиц; они настолько подробные, что годичные наблюдения заполнят стопку DVD-дисков, в пятьдесят раз превышающую Эмпайр-стейт-билдинг. Подобно импровизированной встрече со львом, в физике есть другие ситуации, когда такой уровень подробности лишь затуманивает, а не проясняет. В разделе физики девятнадцатого столетия, называемом термодинамикой, или, в более современном варианте, статистической механикой, рассматриваются как раз такие системы. Паровой двигатель, технологическая инновация, положившая начало термодинамике — как и индустриальной революции — является прекрасной иллюстрацией.
Основу парового двигателя составляет бак с водяным паром, который расширяется при нагревании, двигая поршень вперёд, и сжимается при остывании, возвращая поршень в исходное положение, после чего он готов вновь выдвинуться вперёд. В конце девятнадцатого столетия и в начале двадцатого физики разработали молекулярное обоснование устройства материи, которое, помимо всего прочего, привело к микроскопическому описанию работы пара. При нагревании скорость молекул H2O возрастает и убыстряются их удары о дно поршня. Чем более они разогреты, тем быстрее движутся и сильнее ударяют. Простое, но крайне важное для термодинамики наблюдение состоит в том, что для понимания давления пара не требуется знание подробностей того, какие именно молекулы имеют ту или иную скорость и где именно они ударили по дну поршня. Со списком миллиарда миллиардов траекторий молекул я буду выглядеть таким же озадаченным, как со списком отражающихся от львиной шкуры фотонов. Чтобы представить давление на поршень, мне надо знать только среднее количество молекул, которые ударяют о дно поршня за данный временной интервал, и среднюю скорость в момент столкновения. Эти данные достаточно приближённые, но полезна именно такая урезанная информация.
При разработке математических методов систематического пожертвования подробностями в пользу более общего понимания физики изобрели широкий диапазон методов и развили ряд глубоких понятий. Одно из таких понятий, с которым мы кратко познакомились в предыдущих главах — это энтропия. Энтропия изначально была введена в середине девятнадцатого столетия для количественного описания рассеяния энергии в двигателях внутреннего сгорания, но современная точка зрения, введённая Людвигом Больцманом в 1870-х годах, такова, что энтропия является характеристикой того, насколько тонко упорядочена — или нет — данная система, для того чтобы иметь такой вид, какой она имеет.
Чтобы прочувствовать это, представьте сценку, в которой некий парень, Феликс, в ярости кричит, что в их дом проникли воры. «У нас всё переворошили!» — в гневе говорит он своему другу Оскару. Оскар отмахивается — он знает, что у Феликса бывают приступы подозрительности. Чтобы успокоить Феликса, Оскар распахивает дверь в свою комнату, где валяется разбросанная повсюду одежда, остатки пиццы и пустые банки из-под пива. «Выглядит как обычно», — рявкает он. Феликс не обращает на это внимания. «Конечно же, она выглядит как обычно — свинарник и после вторжения остаётся свинарником. Но взгляни на мою комнату!» И он открывает свою дверь. «Всё переворошили…» — хмыкает Оскар. — «Да она чище, чем неразбавленный виски!» «Да, чище. Но вторжение не осталось незамеченным. Смотри, вот баночки с витаминами — теперь они не выстроены в порядке уменьшения размера баночек. А сборник сочинений Шекспира? Не в алфавитном порядке! А ящик для носков? Посмотри на это — чёрные носки вперемешку с синими! Я тебе говорю, у нас всё переворошили. Это совершенно очевидно!»
Если не обращать внимания на истерику Феликса, данная ситуация подчёркивает простой, но существенный момент. Если что-то находится в большом беспорядке, как комната Оскара, то при большом количестве всяких разных перестановок содержащихся в нём составных частей общий вид остаётся прежним. Соберите двадцать шесть мятых рубашек, валяющихся на кровати, на полу, в гардеробе, и снова разбросайте их повсюду, разбросайте заново сорок две пустые банки из-под пива — и квартира всё равно будет выглядеть по-прежнему. Но когда что-то очень сильно упорядочено, как квартира Феликса, даже небольшая перемена становится заметной.
Это различие лежит в основе математического определения энтропии, данного Больцманом. Возьмите любую систему и подсчитайте число способов, которыми её компоненты могут быть переставлены, сохраняя при этом общий макроскопический вид.[50] Если есть большое число таких перестановок, то энтропия высока: система находится в сильном беспорядке. Если число таких перестановок мало, энтропия низкая: система высоко упорядочена (или, эквивалентно, имеет малый беспорядок).
В качестве более привычного примера рассмотрим контейнер с паром и куб изо льда. Будем рассматривать только их совокупные макроскопические свойства, которые можно наблюдать или измерять, не зная при этом детального состояния составляющих их молекул. Если опустить и вынуть руку из пара, то вы перемешаете между собой миллиарды молекул H2O, но при этом пар будет выглядеть столь же однородным, как и ранее. Но измените случайным образом положения и скорости многих молекул в куске льда, и результат вы увидите незамедлительно — кристаллическая структура льда будет разрушена. Появятся трещины и сколы. Пар, со случайно летающими по контейнеру молекулами H2O, обладает высокой степенью беспорядка; лёд, молекулы H2O которого расположены регулярным образом в кристаллической решётке, высоко упорядочен. Энтропия пара высока (много перестановок не приведут к изменению его вида); энтропия льда низкая (только небольшое количество перестановок не приведёт к изменению его вида).
Оценивая чувствительность макроскопического облика системы к её микроскопическому устройству, энтропия является естественным понятием в математическом формализме, который описывает совокупные физические свойства системы. Второй закон термодинамики развивает эту мысль количественным образом. Он устанавливает, что со временем полная энтропия системы будет возрастать.[51] Чтобы понять, почему так происходит, достаточно самых элементарных представлений о вероятности и статистике. По определению, конфигурация с высокой энтропией может реализоваться посредством большего числа микроскопических перестановок, чем конфигурация с меньшей энтропией. По мере эволюции системы она с огромной долей вероятности оказывается в состоянии с высокой энтропией, потому что, попросту говоря, таких состояний больше, чем остальных. Значительно больше. При выпекании хлеба вы чувствуете его запах по всему дому, потому что существует на триллионы больше конфигураций молекул, вылетающих из хлеба, таких, что они заполняют однородно весь дом, распространяя аромат свежевыпеченного хлеба, чем конфигураций, в которых молекулы плотно собираются в углу кухни. Случайные движения разогретых молекул почти наверняка будут направлены так, что молекулы сформируют одну из многочисленных распределённых по всему дому конфигураций, а не образуют одну из немногих скучкованных в углу конфигураций. Таким образом, набор молекул переходит от низкой энтропии к высокой, и в этом состоит действие Второго закона.
Эта идея универсальна. Бьющееся стекло, гаснущая свеча, расплывающиеся чернила, распространяющийся запах духов: это разные процессы, но их статистическое рассмотрение одинаково. В каждом из них порядок переходит в беспорядок, и это происходит потому, что есть масса способов создать беспорядок. Красота такого анализа — понимание этого вызвало моё самое восторженное «Вот это да!» в процессе моего физического образования — состоит в том, что не теряясь в микроскопических деталях, у нас есть ведущий принцип для объяснения, почему огромное количество явлений происходят так, а не иначе.
Следует отметить, что будучи по своей природе статистическим, Второй закон не утверждает, что энтропия не может уменьшиться, однако такое событие крайне маловероятно. Молекулы только что добавленного в чашку кофе молока могут, в результате своих случайных движений, объединиться в плавающую статуэтку Санта Клауса. Но не дождётесь. Плавающий Санта из молока имеет очень низкую энтропию. Если переместить несколько миллиардов молекул, вы увидите, что у Санты пропала голова или рука, или он растёкся в абстрактный белый завиток. По сравнению с этим конфигурация, в которой молекулы молока однородно распределены по чашке, имеет значительно более высокую энтропию: огромное число перегруппировок по-прежнему выглядит как обычный кофе с молоком. Тогда, с огромной долей вероятности добавленное в ваш чёрный кофе молоко придаст ему однородный коричневатый оттенок, в котором трудно будет разглядеть очертания Санты. Аналогичные рассуждения справедливы для огромного количества переходов от высокой к низкой энтропии, так что кажется, что Второй закон несокрушим.
Второй закон и чёрные дыры
Вернёмся теперь к взглядам Уилера на чёрные дыры. В начале 1970-х годов Уилер заметил, что когда чёрные дыры выплывают на сцену, Второй закон начинает сдавать свои позиции. По-видимому, наличие близлежащей чёрной дыры даёт готовый и надёжный способ уменьшить общую энтропию. Поместите в чёрную дыру любую изучаемую вами систему — битое стекло, потухшую свечку, расплывшиеся чернила. Так как ничего не может покинуть её пределы, беспорядок в системе окажется, по-видимому, навсегда исчезнувшим. Возможно, что такой подход несовершенен, но кажется, он легко понизит энтропию, окажись у вас под рукой чёрная дыра. Многие посчитали, что Второй закон столкнулся с достойным соперником.
Но студента Бекенштейна это не убедило. Возможно, предложил Бекенштейн, энтропия не пропадает в чёрной дыре, а просто каким-то образом в неё трансформируется. Кроме того, никто не утверждал, что поглощая пыль и звёзды, чёрные дыры приводят к нарушению Первого закона термодинамики, сохранению энергии. Наоборот, уравнения Эйнштейна показывают, что при поглощении вещества чёрная дыра становится больше и тяжелее. Энергия может перераспределиться, часть из неё упадёт в чёрную дыру, а часть останется снаружи, но общее количество сохранится. Может быть, предложил Бекенштейн, эта же идея применима и к энтропии. Часть энтропии остаётся снаружи чёрной дыры, а другая часть падает внутрь, но ничего не исчезает бесследно.
Это звучит разумно, но эксперты идею не одобрили. Найденное Шварцшильдом решение и последующие разработки говорят, по всей видимости, о том, что чёрные дыры — это последнее слово в стане порядка. Каким бы перемешанным и неупорядоченным не было падающее внутрь вещество и излучение, оно сжимается в бесконечно малый объём в центре чёрной дыры: чёрная дыра — это окончательный этап в упорядоченном сжатии мусора. По правде говоря, никто не знает, что происходит во время такого мощного сжатия, потому что экстремальная кривизна и плотность делают уравнения Эйнштейна непригодными; однако совсем не кажется, что в центре чёрной дыры может быть какой-то беспорядок. А за пределами своего центра чёрная дыра — просто пустая область пространства-времени, простирающаяся до границы невозврата — горизонта событий (рис. 9.1): Нет никаких снующих туда-сюда молекул и атомов, поэтому перегруппировываться нечему; кажется, что чёрная дыра вообще лишена энтропии.
Рис. 9.1. Чёрная дыра вмещает область пространства-времени, окружённую поверхностью невозврата — горизонтом событий
В 1970-х годах такая точка зрения была подкреплена так называемыми теоремами об отсутствии волос, которые на математическом языке утверждают, что чёрным дырам (подобно лысым фантомасам) недостаёт отличительных характеристик. Согласно этим теоремам любые две чёрные дыры, обладающие одинаковыми массами, зарядами и угловыми моментами (скоростью вращения), неразличимы. В отсутствие характерных отличительных черт — у фантомасов также нет чёлок, усов или дрэдов — чёрные дыры не имеют различий, в которых могла быть запасена энтропия.
Это был вполне убедительный аргумент сам по себе, но затем появилось ещё более убийственное рассуждение, которое, как казалось, полностью сводило на нет идею Бекенштейна. Согласно основным положениям термодинамики между температурой и энтропией есть тесная связь. Температура — это мера усреднённого движения составных частей данного объекта: компоненты разогретых объектов движутся быстро, компоненты холодных объектов движутся медленно. Энтропия является мерой возможных перегруппировок этих компонентов, которые с макроскопической точки зрения останутся незамеченными. Таким образом, как энтропия, так и температура зависят от совокупных свойств рассматриваемого объекта; они идут рука об руку. Если рассмотреть вопрос математически, то станет ясно, что если Бекенштейн прав и чёрные дыры обладают энтропией, то у них должна быть температура.{81} Именно это и вызвало тревогу. Любой объект с ненулевой температурой должен излучать. Горячий уголь излучает видимый свет; люди, как правило, излучают в инфракрасном диапазоне. Если чёрная дыра обладает ненулевой температурой, то сами законы термодинамики, которые Бекенштейн хотел сохранить, говорят, что она тоже должна излучать. Но это вопиющим образом противоречит принятому пониманию, что ничего не может вырваться из гравитационной хватки чёрной дыры. Почти все решили, что Бекенштейн ошибается. У чёрных дыр нет температуры. У них нет энтропии. Чёрные дыры — это сточная воронка для энтропии. В присутствии чёрных дыр нарушается Второй закон термодинамики.
Несмотря на многочисленные аргументы против, в пользу Бекенштейна говорил один замечательный результат. В 1971 году Стивен Хокинг осознал, что чёрные дыры подчиняются занятному правилу. Если имеется набор чёрных дыр разных размеров и масс, и при этом некоторые размеренно вальсируют по орбитам, другие подкрепляются веществом и излучением, а остальные сталкиваются друг с другом, то полная площадь поверхности всех чёрных дыр со временем возрастает. Под «площадью поверхности» Хокинг подразумевал площадь горизонта событий каждой чёрной дыры. В физике есть много результатов насчёт того, что какие-то величины не изменяются во времени (закон сохранения энергии и импульса, сохранение заряда и так далее), но также имеется небольшое число соотношений, которые диктуют рост величин. Поэтому естественно рассмотреть возможную связь между результатом Хокинга и Вторым законом. Если считать, что каким-то образом площадь поверхности чёрной дыры является мерой её энтропии, то возрастание площади полной поверхности может рассматриваться как рост полной энтропии.
Это была очень привлекательная аналогия, но никто не счёл её убедительной. Почти все считали, что сходство теоремы Хокинга о площади со Вторым законом не более чем случайность. Это положение сохранялось до того момента, пока несколько лет спустя Хокинг не сделал одно из самых важных вычислений в современной теоретической физике.
Излучение Хокинга
Поскольку квантовая механика не играет никакой роли в общей теории относительности Эйнштейна, решение Шварцшильда для чёрных дыр основывается исключительно на классической физике. Однако надлежащее рассмотрение вещества и излучения — таких частиц, как фотоны, нейтрино и электроны, которые могут переносить массу, энергию и энтропию из одного места в другое — требует привлечения квантовой механики. Чтобы в полной мере оценить природу чёрных дыр и разобраться, как они взаимодействуют с веществом и излучением, необходимо продлить решение Шварцшильда в квантовую область. Это нелегко. Несмотря на достижения теории струн (а также других подходов, которых мы не коснулись, таких как петлевая квантовая гравитация, твисторы, теория топосов), мы по-прежнему находимся на начальном уровне в наших попытках совместить квантовую физику и теорию гравитации. А в далёких 1970-х было ещё меньше теоретических оснований для понимания того, как квантовая механика может влиять на гравитацию.
Однако были физики, которые работали в этом направлении и которым удалось добиться частичного объединения квантовой механики и общей теории относительности, рассмотрев распространение квантовых полей (квантовая часть) в фиксированной, но искривлённой пространственно-временной среде (гравитационная часть). Как было указано в главе 4, полное объединение должно, как минимум, содержать рассмотрение не только квантовых флуктуаций полей на пространстве-времени, но также квантовых флуктуаций самого пространства-времени. Простоты ради это усложнение не учитывалось в первых работах. Хокинг воспользовался частичным объединением и рассмотрел, как квантовые поля будут вести себя в очень особой области пространства-времени — в окрестности чёрной дыры. То, что он обнаружил, поразило физиков до глубины души.
Хорошо известное свойство квантовых полей в обычном, пустом, неискривлённом пространстве-времени состоит в том, что из-за квантовых флуктуаций парам частиц, например электрону и его античастице, позитрону, позволяется мгновенно возникнуть из ничего, немножко пожить, после чего столкнуться друг с другом, и в результате взаимно аннигилировать. Этот процесс, квантовое рождение пары, интенсивно изучался как теоретически, так и экспериментально, и был разобран со всех сторон.
Новой характеристикой квантового рождения пары является то, что если один партнёр имеет положительную энергию, то из закона сохранения энергии следует, что другой партнёр должен обладать тем же количеством отрицательной энергии — понятие, которое не имеет смысла в классической вселенной.[52] Однако, благодаря принципу неопределённости имеется своеобразная лазейка, позволяющая частицам иметь отрицательную энергию, при условии, что возникнув, они не сильно долго будут злоупотреблять гостеприимством. Если частица существует лишь мимолётно, то квантовая неопределённость говорит, что никакому эксперименту не хватит времени, даже в принципе, определить знак её энергии. Именно такова основная причина, почему пара частиц обречена квантовыми законами на быструю аннигиляцию. Поэтому при квантовых флуктуациях пары частиц беспрестанно рождаются и аннигилируют, рождаются и аннигилируют, на фоне неизбежной непрекращающейся игры квантовой неопределённости в пространстве, которое иначе оставалось бы пустым.
Хокинг заново рассмотрел вездесущие квантовые флуктуации, но не в пустом пространстве, а вблизи горизонта событий чёрной дыры. Он обнаружил, что часто всё выглядит как обычно. Пары частиц образуются случайным образом; быстро находят друг друга; после чего аннигилируют. Но время от времени происходит нечто новое. Если частицы образуются достаточно близко к краю чёрной дыры, то одну из них может затянуть внутрь, а другая улетит в пространство. В отсутствии чёрной дыры такого никогда не происходит, потому что, если частицы не аннигилируют друг с другом, то частица с отрицательной энергией сможет пробиться сквозь защитную рябь квантовой неопределённости. Хокинг осознал, что столь радикальное закручивание пространства и времени чёрной дырой может привести к тому, что частицы, обладающие отрицательной энергией с точки зрения наблюдателя снаружи чёрной дыры, окажутся частицами с положительной энергией для несчастного наблюдателя внутри неё. Таким образом, чёрная дыра предоставляет частицам с отрицательной энергией надёжное убежище, поэтому нужда в квантовой маскировке отпадает. Возникшие частицы могут избежать взаимной аннигиляции и заявить о своей независимой жизни.{82}
Частицы с положительной энергией летят наружу от горизонта событий, поэтому издалека они выглядят как некое излучение, получившее название излучение Хокинга. Частицы с отрицательной энергией поглощаются чёрной дырой, поэтому их нельзя непосредственно наблюдать, однако их можно обнаружить косвенным способом. Подобно тому как масса чёрной дыры растёт при поглощении всего, что обладает положительной энергией, она также уменьшается при поглощении всего, что имеет отрицательную энергию. Эти два процесса в совокупности делают чёрную дыру похожей на кусок горящего угля: чёрная дыра беспрестанно излучает направленный наружу поток излучения по мере того как её масса уменьшается.[53] То есть, если добавить квантовую механику, то чёрные дыры перестают быть абсолютно чёрными. Открытие Хокинга было как гром среди ясного неба.
Однако это вовсе не означает, что типичная чёрная дыра нагрета до красного свечения. По мере того как поток частицы летит от чёрной дыры, он должен преодолевать невероятное сопротивление со стороны её гравитационного притяжения. На это частицы тратят свою энергию и поэтому значительно остывают. Хокинг вычислил, что наблюдатель, находящийся достаточно далеко от чёрной дыры, обнаружит, что температура остаточного «утомлённого» излучения обратно пропорциональна массе чёрной дыры. Огромная чёрная дыра, подобная находящейся в центре нашей Галактики, имеет температуру менее триллионной доли градуса выше абсолютного нуля. Чёрная дыра с массой Солнца будет иметь температуру меньше чем миллионная доля градуса, даже меньше, чем температура в 2,7 градуса реликтового излучения, оставшегося после Большого взрыва. Чтобы температура чёрной дыры была достаточно высока, чтобы приготовить барбекю для всей семьи, её масса должна быть примерно в десять тысяч раз больше массы Земли, а это экстраординарно малая величина в космических масштабах.
Однако само значение температуры чёрной дыры не столь важно. Хотя излучение, идущее от удалённых астрофизических чёрных дыр, не сможет осветить ночное небо, тот факт, что они действительно имеют температуру, что они действительно излучают, означает, что эксперты поспешили отбросить гипотезу Бекенштейна о том, что чёрные дыры действительно обладают энтропией. Хокинг великолепно справился с этой задачей. Его теоретические вычисления, определяющие температуру данной чёрной дыры и испускаемого ею излучения, дали все необходимые данные для определения количества энтропии, которую, согласно стандартным законам термодинамики, должна иметь чёрная дыра. Полученный ответ оказался пропорционален площади поверхности чёрной дыры, как и предполагал Бекенштейн.
Итак, к концу 1974 года Второй закон вновь стал законом. Открытия Бекенштейна и Хокинга выявили, что в любой ситуации полная энтропия возрастает, если при этом учитывать не только энтропию обычного вещества и излучения, но также и находящуюся внутри чёрных дыр и определяемую площадью их полной поверхности. Вместо того чтобы быть стоком для энтропии и приводить к нарушению Второго закона, чёрные дыры играют активную роль в исполнении этого закона во вселенной с постоянно увеличивающимся беспорядком.
Это заключение вызвало долгожданное облегчение. Для многих физиков Второй закон, основанный на казалось бы неоспоримых статистических рассуждениях, стал священным как практически никакой другой в науке. Его воскрешение означало, что с этим миром опять всё в порядке. Но со временем появилась небольшая, но первостепенно важная запись в бухгалтерской книге энтропии, которая показала, что вопрос о справедливости Второго закона не является самым приоритетным. Эта честь досталась задаче о месте хранения энтропии, задаче, важность которой станет очевидной, когда мы выявим глубокую связь между энтропией и центральной темой этой главы — информацией.
Энтропия и скрытая информация
До настоящего момента энтропия образно описывалась как мера беспорядка, и более количественно, как число перегруппировок компонент системы, не меняющих её совокупных макроскопических свойств. Выше это прозвучало неявно, но теперь можно сказать определённо, что энтропию можно осмыслить как измерение информационного разрыва между теми данными, которые у нас есть (общими макроскопическими свойствами), и теми данными, которых нет (конкретным устройством системы на микроскопическом уровне). Энтропия является мерой дополнительной информации, скрытой в деталях микроскопического устройства системы, которые, будь к ним доступ, позволили бы выделить эту микроуровневую конфигурацию системы на фоне всех макропроявлений.
В качестве иллюстрации представим, что Оскар навёл порядок в своей комнате, но не хватило времени убрать серебряные доллары, выигранные им в покер на прошлой неделе — тысяча монет так и осталась лежать разбросанной по полу. Даже если Оскар соберёт их потом в кучку, его взгляду предстанет хаотичный набор монет, часть из которых лежит вверх решкой, а часть вверх орлом. Если случайным образом поменять орлы на решки, а решки на орлы, то Оскар ничего не заметит — это свидетельствует о том, что тысяча собранных в кучку серебряных долларов обладает высокой энтропией. Этот пример настолько простой, что энтропию можно явно подсчитать. Для двух монет имеются четыре возможные конфигурации: (орёл, орёл), (орёл, решка), (решка, орёл), и (решка, решка) — две возможности для первого доллара умножаются на две для второго. Для трёх монет есть восемь возможных конфигураций — (орёл, орёл, орёл), (орёл, орёл, решка), (орёл, решка, орёл), (решка, орёл, орёл), (орёл, решка, решка), (решка, орёл, решка), (решка, решка, орёл), (решка, решка, решка) — возникающих из двух возможностей для первой монеты, помноженных на две для второй и помноженных на две для третьей. Для тысячи монет число возможностей вычисляется аналогично: множитель 2 для каждой монеты, и получаем число 21000, равное 10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376. Подавляющее большинство конфигураций орёл-решка не будут обладать особыми свойствами, поэтому они никак не будут выделены среди прочих. Однако некоторые будут выделены, если, скажем, все 1000 монет будут лежать кверху орлом или решкой, или если 999 монет будут лежать кверху орлом, или 999 кверху решкой. Но число таких необычных конфигураций настолько мало по сравнению с гигантским числом всех возможностей, что исключив их из подсчёта, вы вряд ли обнаружите какую-то разницу.[54]
Из нашей предыдущих обсуждений следует, что число 21000 задаёт энтропию монет. Для определённых целей этот вывод вполне достаточен. Однако для установления более глубокой связи между энтропией и информацией необходимо уточнить картину, описанную выше. Энтропия системы связана с числом неразличимых перегруппировок её компонентов, но, строго говоря, не равна ему. Эта взаимосвязь выражается с помощью математической операции, называемой логарифмом; не пугайтесь, если логарифм навевает дурные воспоминания о школьных уроках математики. В нашем примере с монетами это просто означает, что в качестве энтропии надо взять показатель полученного нами числа конфигураций, то есть энтропия определяется как 1000, а не 21000.
Преимущество использования логарифма в том, что он позволяет работать с более обозримыми числами, но есть и более важная причина. Представьте, что я спрашиваю вас, сколько информации вам понадобится для описания одной частной конфигурации орёл-решка в наборе из 1000 монет. Простейший ответ состоит в составлении списка — орёл, орёл, решка, орёл, решка, решка…, который описывает расположение каждой из 1000 монет. Конечно же, отвечу я, это даст мне полную информацию об этой конфигурации, но вопрос состоял не в этом. Я спрашивал, сколько информации содержится в этом списке.
Тут вы начнёте раздумывать. Чем на самом деле является информация и для чего она нужна? Вы даёте прямой и простой ответ. Информация отвечает на вопросы. Годы исследований по физике, математике и компьютерным технологиям сделали этот ответ точным. Эти исследования установили, что наиболее полезная мера содержания информации — это число различных «да или нет» вопросов, на которые у этой информации есть ответ. В примере с монетами есть 1000 таких вопросов: орёл у первого доллара? Да. Орёл для второго доллара? Да. Орёл для третьего доллара? Нет. Орёл для четвёртого доллара? Нет. И так далее. Элемент данных, который может содержать ответ на «да или нет» вопрос, называется битом — привычный для компьютерного века термин, являющийся сокращением от английского выражения binary digit, двоичный символ, означающий 0 или 1, о котором можно думать как о численном представлении ответов да или нет. Таким образом, конфигурации орёл-решка из 1000 монет содержат 1000 бит информации. Эквивалентным образом, если вы встанете на макроскопическую точку зрения Оскара и сосредоточитесь только на случайном расположении всех монет в целом, не обращая внимания на «микроскопические» детали орёл или решка, то информация, «скрытая» в этих монетах, составляет 1000 бит.
Отметим, что значение энтропии и количество скрытой информации равны. И это не случайно. Число возможных выпадений орёл-решка равно числу возможных ответов на 1000 вопросов — (да, да, нет, нет, да…) или (да, нет, да, да, нет…) или (нет, да, нет, нет, нет…) и так далее, а именно 21000. При определении энтропии как логарифма числа таких конфигураций — 1000 в нашем случае — энтропия равна числу «да или нет» вопросов для любой из таких последовательностей ответов.
Мы рассмотрели частный пример с 1000 монетами, но установленная связь между энтропией и информацией имеет совершенно общий характер. Микроскопические детали любой системы содержат информацию, которая скрыта только при рассмотрении макроскопических, совокупных свойств. Например, вы знаете температуру, давление и объём контейнера с паром, но известно ли вам, ударялась ли молекула H2O о верхний правый угол этого контейнера? А может быть другая молекула только что ударилась о нижний левый край? Так же как с разбросанными монетами, энтропия системы равна числу «да или нет» вопросов, ответы на которые содержатся в её микроскопическом состоянии, и поэтому энтропия является мерой, скрытой в системе информации.[55]
Энтропия, скрытая информация и чёрные дыры
Каким образом данное выше определение энтропии и его взаимосвязь со скрытой информацией применяется к чёрным дырам? Когда Хокинг разработал детальное квантово-механическое обоснование, связывающее энтропию чёрной дыры с площадью её горизонта событий, он не только дал количественное описание исходного утверждения Бекенштейна, но также создал алгоритм для его вычисления. Возьмите горизонт событий чёрной дыры, говорит Хокинг, и разбейте его на решётку, в которой сторона каждой клетки равна одной планковской длине (10−33 сантиметра). Хокинг математически доказал, что энтропия чёрной дыры равна числу таких клеток, которым покрывается весь горизонт событий — иными словами, это площадь поверхности чёрной дыры, измеренная в планковских единицах (клетки площадью 10−66 квадратного сантиметра). На языке скрытой информации всё выглядит так, как будто каждая клетка тайным образом несёт один бит, 0 или 1, что даёт ответ на один «да или нет» вопрос, описывающий какую-то характеристику чёрной дыры на микроскопическом уровне (рис. 9.2).[56]
Рис. 9.2. Стивен Хокинг математически показал, что энтропия чёрной дыры равна числу клеток планковского размера, необходимых для покрытия её горизонта событий. Как будто каждая клетка несёт один бит, базовую единицу информации
Общая теория относительности Эйнштейна, а также теоремы об отсутствии волос у чёрных дыр, не учитывают квантово-механические эффекты и поэтому полностью теряют эту информацию. Задайте массу чёрной дыры, её заряд и угловой момент, говорит общая теория относительности, и вы однозначным образом определите чёрную дыру. Однако Бекенштейн и Хокинг утверждают, что это не так. Они установили, что должно существовать много разных чёрных дыр с одинаковыми макроскопическими свойствами, которые, тем не менее, отличаются на микроскопическом уровне. Как и в более привычных примерах — про монеты на полу или пар в контейнере — энтропия чёрных дыр отражает информацию, скрытую в более мелких деталях.
Не менее неординарные, чем сами чёрные дыры, эти открытия установили, что в вопросе об энтропии чёрные дыры ничем не отличаются от всего остального. Однако полученные результаты привели к новым вопросам. Хотя Бекенштейн и Хокинг говорят нам, сколько информации скрыто в чёрной дыре, нам ничего не известно о том, что это за информация. Неизвестно, на какие специфические «да или нет» вопросы отвечает эта информация, не установлен состав микроскопических компонент, которые эта информация предназначена описывать. Математический анализ точно определил величину информации данной чёрной дыры, ничего не сообщив о природе этой информации.{83}
Эти вопросы до сих пор ставят в тупик. Но есть и другая загадка, которая видится ещё более важной: почему количество информации определяется площадью поверхности чёрной дыры? Если бы вы спросили меня, сколько информации содержится в библиотеке Конгресса, я стал бы говорить о доступном пространстве внутри здания библиотеки. Потребовалось бы знать вместимость залов библиотеки, необходимых для размещения полок, картотек, микрофишей, фотографий и документов. То же самое справедливо для информации внутри моей головы, объём которой, по-видимому, привязан к объёму головного мозга, доступному пространству для нейронных связей. То же самое имеет место для информации в контейнере с паром, которая содержится в свойствах заполняющих контейнер частиц. Однако удивительно, что применительно к чёрным дырам способность для хранения информации определяется, согласно Бекенштейну и Хокингу, не объёмом, а площадью поверхности.
До появления этих результатов физики считали, что поскольку планковская длина (10−33 сантиметра) является, по-видимому, наименьшей длиной, для которой понятие «расстояния» всё ещё имеет смысл, то наименьшим осмысленным объёмом будет крошечный кубик, грани которого имеют планковскую длину (объём кубика равен 10−99 кубического сантиметра). Разумная гипотеза, которой придерживались многие, была такова, что независимо от будущих технологических прорывов наименьший объём может хранить не более одной наименьшей единицы информации — одного бита. Поэтому ожидалось, что максимальное количество информации, которое может содержаться в данной области пространства, равно числу планковских кубиков, способных поместиться внутри этой области. Поэтому присутствие планковской длины в результате Хокинга не было неожиданным. Удивительно то, что хранилище информации чёрной дыры определяется не заполняющим её объём числом планковских кубиков, а числом покрывающих поверхность чёрной дыры планковских клеток.
Так впервые возникло указание на голографию — вместимость информационного хранилища определяется площадью граничной поверхности, а не объёмом находящегося внутри неё пространства. Через три десятилетия из этого указания прорастёт потрясающе новый взгляд на законы физики.
Где находится скрытая информация чёрной дыры
Планковская шахматная доска с нулями и единицами, разбросанными по поверхности горизонта событий (рис. 9.2), является символической иллюстрацией результата Хокинга о количестве информации, хранящейся внутри чёрной дыры. Однако можем ли мы буквально воспринимать этот рисунок? Если математика говорит, что информационный запас чёрной дыры измеряется площадью её поверхности, то является ли это просто средством численного подсчёта, или же это означает, что поверхность чёрной дыры и есть место фактического хранения информации?
Этот глубокий вопрос десятилетиями изучался самыми знаменитыми физиками.[57] Ответ на него в сильной степени зависит от того, смотрите вы на чёрную дыру снаружи или изнутри — если снаружи, то есть веская причина полагать, что информация действительно находится на горизонте.
Любому, кто знаком с подробностями описания чёрных дыр в общей теории относительности, данное замечание покажется весьма странным. Общая теория относительности со всей ясностью говорит, что при падении сквозь горизонт событий чёрной дыры ничего особенного не происходит — нет никакой материальной поверхности, никаких указателей, никаких сигнальных огней — ничего, что каким бы то ни было образом отметило пересечение вами границы невозврата. Это следствие одного из самых простых, но, тем не менее, самых важных достижений Эйнштейна. Эйнштейн осознал, что когда вы (или любой объект) находитесь в состоянии свободного падения, вы становитесь невесомым; спрыгните с высокого трамплина, и весы, привязанные к вашим ногам, будут падать с вами, показывая ноль. По сути, вы избавляетесь от гравитации, позволив ей действовать в полную силу. Из этого Эйнштейн делает немедленный вывод. Основываясь на ваших ощущениях в непосредственно окружающей вас среде, вы не сможете отличить свободного падения на массивный объект от свободного парения в глубинах пустого пространства: в обеих ситуациях вы абсолютно невесомы. Конечно, если вы откроете глаза и увидите, скажем, быстро приближающуюся поверхность земли, лучшим решением будет побыстрее дёрнуть за кольцо парашюта. Но если вы оказались заключённым в маленькую капсулу без окон, вы никак не сможете отличить свободное падение от свободного плавания.{84}
В первые годы двадцатого столетия Эйнштейн ухватился за эту простую, но глубокую взаимосвязь между движением и гравитацией; спустя десять лет работы он оформил её в виде общей теории относительности. Мы используем эту взаимосвязь более скромным образом. Предположим, что вы находитесь в этой капсуле и свободно падаете не на Землю, а в чёрную дыру. Ровно такие же рассуждения говорят, что ваши чувства не смогут отличить падение от плавания в пустом пространстве. Это означает, что не будет происходить ничего особого или необычного, пока вы свободно падаете сквозь горизонт чёрной дыры. В конце концов, вы ударитесь о центр чёрной дыры, свободное падение прекратится и здесь ваши чувства, несомненно, это зафиксируют. Причём мало не покажется. Но до этого момента вам будет казаться, что вы бесцельно блуждаете в мрачных глубинах космоса.
Этот сюжет придаёт энтропии чёрной дыры ещё больше загадочности. Если при пересечении горизонта чёрной дыры вы ничего не обнаруживаете, ничего отличающего горизонт от внешнего пространства, то как он может хранить информацию? Ответ, к которому тяготеют учёные в течение последнего десятилетия, перекликается с темой дуальности, уже встречавшейся нам в предыдущих главах. Напомним, что дуальность возникает в ситуациях, где есть взаимодополнительные точки зрения, кажущиеся совершенно разными, но при этом внутреннее скованные единой физической цепью. Изображение Альберта и Мэрилин на рис. 5.2, является хорошей наглядной аналогией; математические примеры возникают из зеркальных форм дополнительных измерений в теории струн (глава 4) и на первый взгляд различных, но дуальных теорий струн (глава 5). В последние годы, следуя Сасскинду, исследователи осознали, что чёрные дыры являются другим примером того, когда дополнительные и при этом совершенно разные точки зрения приводят к фундаментальным открытиям.
Одна существенная точка зрения принадлежит вам, свободно падающему в чёрную дыру. Другая принадлежит удалённому наблюдателю, следящему за вашим путешествием в телескоп. Замечательно то, что по мере того как вы, как ни в чём не бывало, пересекаете горизонт чёрной дыры, удалённый наблюдатель видит совершенно иную последовательность событий. Всё дело в излучении Хокинга.[58] Когда удалённый наблюдатель измеряет температуру излучения Хокинга, он обнаруживает, что она очень мала, пусть 10−13 K, и это говорит о том, что чёрная дыра по размеру примерно равна чёрной дыре в центре нашей Галактики. Однако удалённый наблюдатель знает, что излучение холодное лишь потому, что идущие к нему от горизонта фотоны истратили много своей энергии, отчаянно преодолевая гравитационное притяжение чёрной дыры; как мы говорили ранее, фотоны устали. Наблюдатель приходит к выводу, что при вашем приближении к горизонту чёрной дыры вы будете встречать всё более свежие фотоны, которые только начали своё путешествие и пока остаются более энергичными и горячими. Действительно, наблюдатель видит, как вы, подойдя на волосок от горизонту, облучаетесь всё более и более интенсивным излучением Хокинга, до тех пор пока от вас не останутся лишь обугленные останки.
К счастью, ваши ощущения гораздо более приятные. Вы не видите, не ощущаете и вообще никак не знаете о существовании этого горячего излучения. Опять же, поскольку состояние свободного падения нейтрализует действие гравитации,{85} ваши ощущения неотличимы от плавания в пустом пространстве. Мы знаем наверняка, что перемещаясь в пустом пространстве, нельзя вот так вдруг вспыхнуть. Поэтому с вашей точки зрения вы удачно проходите сквозь горизонт и (менее удачно) сваливаетесь в сингулярность чёрной дыры, а с точки зрения удалённого наблюдателя вы сгораете в пылающей короне, окружающей горизонт.
Какая из этих двух точек зрения правильная? Сасскинд и другие утверждают, что обе. Безо всяких сомнений, это трудно совместить с обычной логикой — логикой, согласно который вы либо живой, либо нет. Но это не обычная ситуация. Даже больше, эти две столь разные точки зрения никогда нельзя будет сопоставить. Вы не сможете выбраться из чёрной дыры и доказать удалённому наблюдателю, что живы. И, как оказывается, удалённый наблюдатель не может прыгнуть в чёрную дыру и озадачить вас утверждением, что вас больше нет. Когда я сказал, что удалённый наблюдатель «видит», как вы сгораете под воздействием излучения Хокинга, это было упрощением. Удалённый наблюдатель, внимательно изучая дошедшее до него уставшее излучение, может восстановить историю вашей гибели в огне. Но требуется время, чтобы эта информация достигла его. Математические расчёты показывают, что к тому моменту, когда он сможет сделать вывод, что вы сгорели, у него не останется достаточно времени прыгнуть в чёрную дыру и поймать вас прежде, чем вас поглотит сингулярность. Точки зрения могут быть разными, но у физики есть встроенный предохранитель против парадоксов.
Что насчёт информации? С вашей точки зрения вся информация, хранящаяся в вашем теле и голове, и в вашем ноутбуке, проходит вместе с вами сквозь горизонт чёрной дыры. С точки зрения удалённого наблюдателя вся переносимая вами информация поглощается слоем излучения, непрерывно клубящимся вблизи горизонта. Биты, содержащиеся в вашем теле, голове и ноутбуке, могут сохраниться, но при этом совершенно перемешаются после отчаянного столкновения и смешения с обжигающе горячим горизонтом. Поэтому для удалённого наблюдателя горизонт событий является реальным местом, населённым реальными вещами, физическими носителями информации, схематично изображённой в виде шахматной доски (рис. 9.2).
Вывод такой, что удалённый наблюдатель — мы — заключает, что энтропия чёрной дыры определяется площадью её горизонта, потому что горизонт является местом её хранения. Такое утверждение видится совершенно разумным. Однако не забывайте, насколько неожиданным является то, что объём чёрной дыры не является хранилищем информации. Мы сейчас увидим, что полученный результат не просто отражает одно из особых свойств чёрных дыр. Чёрные дыры говорят нам не просто о том, как чёрные дыры хранят информацию. Они информируют нас о хранении информации в произвольном контексте. Отсюда начинается прямая дорога к голографическому принципу.
За пределами чёрных дыр
Рассмотрим произвольный объект или набор объектов — набор библиотек Конгресса, все компьютеры корпорации Google, архивы ЦРУ, — расположенных в некоторой области пространства. Представим для простоты, что эта область окружена воображаемой сферой (рис. 9.3а). Теперь допустим, что полная масса объектов по сравнению с заполняемым ими объёмом настолько заурядна, что её даже близко не хватит для образования чёрной дыры. Такова постановка задачи. А теперь важный вопрос: какое максимальное количество информации может храниться в этой области пространства?
Рис. 9.3. а) Набор объектов, хранящих информацию и расположенных внутри чётко очерченной области пространства; б) Расширение информационной ёмкости данной области; в) Когда количество вещества превосходит некоторую пороговую величину (её можно вычислить, исходя из общей теории относительности){86}, данная область становится чёрной дырой
Ответ дают Второй закон и чёрные дыры, ставшие неожиданными партнёрами в этом вопросе. Представьте, что в область пространства добавляют вещество с целью увеличения её информационной ёмкости. Например, вы можете принести в корпорацию Google чипы с большим объёмом памяти или увесистые жёсткие диски; а в библиотеку Конгресса можно принести книги или электронные читалки. Поскольку даже сырое вещество несёт информацию — молекулы пара находятся здесь или там, они движутся со скоростью такой или сякой, — вы забиваете каждый уголок данной области пространства любой материей, какая только попадётся под руку. Пока не будет достигнута критическая отметка. В какой-то момент данная область станет настолько плотно набитой всякой всячиной, что если добавить ещё одно маленькое зёрнышко, то пространство внутри начнёт темнеть и превращаться в чёрную дыру. Когда такое случится, игра закончится. Размер чёрной дыры определяется её массой, поэтому при попытке увеличить её информационную ёмкость путём добавления большего количества вещества чёрная дыра начнёт увеличиваться в размере. Поскольку мы хотим рассмотреть информацию, которая может содержаться в данном фиксированном объёме пространства, такая ситуация выйдет за рамки поставленной задачи. Нельзя увеличить информационную ёмкость чёрной дыры, не заставив её при этом расти.{87}
Следующие два наблюдения выводят нас на финишную прямую. Второй закон гарантирует, что энтропия возрастает в течение всего процесса, поэтому информация, скрытая внутри жёстких дисков, электронных читалок, старомодных бумажных книг и во всём остальном, что вы поместили в данную область пространства, меньше, чем информация, скрытая в чёрной дыре. Результаты Бекенштейна и Хокинга гласят, что скрытая информация чёрной дыры задаётся площадью её горизонта событий. Более того, поскольку вы работали очень аккуратно, так чтобы не выйти за исходную область пространства, то горизонт событий чёрной дыры совпадает с границей данной области и энтропия чёрной дыры равна площади окружающей эту область поверхности. Таким образом, мы получаем важный результат: количество информации внутри некоторой области пространства, хранящейся в любых объектах любой формы, всегда меньше площади окружающей эту область поверхности (измеренной в планковских единицах).
Вот к такому выводу мы пришли. Отметим, что хотя чёрные дыры играют главную роль в этих рассуждениях, весь анализ применим к любой области пространства, независимо от того, есть там чёрная дыра или нет. Если максимизировать информационную ёмкость данной области, то возникнет чёрная дыра, но если не превышать лимит добавляемого вещества, чёрная дыра не сформируется.
Поспешу добавить, что предел информационной ёмкости не должен нас заботить с практической точки зрения. Если сравнивать с современными рудиментарными накопителями, то потенциальная информационная ёмкость поверхности пространственной области просто чудовищна. Стопка из пяти стандартных терабайтных жёстких дисков легко умещается внутри сферы радиуса 50 сантиметров, поверхность которой покрывается 1070 планковскими клетками. Таким образом, информационная ёмкость этой поверхности составляет примерно 1070 бит, что равно миллиарду триллионов триллионов триллионов триллионов терабайтов, и поэтому несоизмеримо превышает всё, что вы можете купить. В Силиконовой долине подобные теоретические ограничения никого особо сильно не беспокоят.
Всё же, если задумываться об устройстве Вселенной, ограничения информационной ёмкости говорят о многом. Представьте любую область пространства, например, комнату, в которой я пишу эту книгу, или комнату, в который вы читаете её. Примите точку зрения Уилера и представьте, что всё происходящее в этой области сводится к некоторым информационным процессам — информация об устройстве окружающей среды в данный момент трансформируется посредством физических законов в информацию об устройстве окружающей среды через секунду, минуту или через час. Поскольку наблюдаемые нами физические процессы, а также процессы, которые нами управляют, по всей видимости, происходят внутри данной области, то естественно ожидать, что переносимая этими процессами информация также находится внутри этой области. Но только что полученные результаты предлагают альтернативный взгляд. Обнаруженная связь между информацией и площадью поверхности чёрной дыры выходит далеко за рамки простого численного расчёта; есть конкретный смысл, в котором информация хранится на поверхности чёрной дыры. Сасскинд и т’Хоофт указали, что данное рассуждение имеет совершенно общий характер: поскольку информация, необходимая для описания физических явлений внутри любой заданной области пространства, может быть полностью представлена данными на окружающей её поверхности, то существует причина думать, что эта поверхность и является тем местом, где происходят фундаментальные физические процессы. Как предлагают эти смелые учёные, привычная нам трёхмерная реальность связана голографической проекцией с удалёнными двумерными физическими процессами.
Если эти рассуждения верны, тогда существуют физические процессы, происходящие на некоторой удалённой поверхности, которые, подобно тянущему за ниточки кукловоду, управляют процессами, происходящими в моей голове и моих руках, в тот самый момент, когда я печатаю эти слова на моём компьютере. Наш опыт здесь и удалённая реальность там образуют крепкую связку параллельных миров. Явления в этих двух мирах — я буду называть их голографическими параллельными вселенными — настолько полно связаны друг с другом, что происходящие в каждом из них эволюции будут так же крепко связаны, как я и моя тень.
Мелким шрифтом
То, что привычная нам реальность может быть отражением, а может быть даже порождением явлений, происходящих на далёкой поверхности меньшей размерности, является одним из самых неожиданных открытий во всей теоретической физике. Как можно быть уверенным в справедливости голографического принципа? Мы оказались на территории, лежащей в самой глубине теоретической физики, и опираемся почти целиком на разработки, которые не были проверены экспериментально, поэтому конечно же есть основания для скептицизма. Есть много причин сбиться с курса. Действительно ли чёрные дыры обладают ненулевой температурой и энтропией, и если так, согласуются ли эти значения с теоретическими предсказаниями? Действительно ли информационная ёмкость некоторой области пространства определяется количеством информации, которая может быть размещена на окружающей её поверхности? И для такой поверхности является ли один бит на одну планковскую клетку пределом на самом деле? Мы думаем, что ответ на каждый из этих вопросов положительный, потому что есть непротиворечивая, совместимая и аккуратно выстроенная теоретическая система, с которой такие выводы прекрасно согласуются. Но поскольку ни одна из этих идей не ложилась под экспериментальный скальпель, вполне возможно (хотя, на мой взгляд, совершенно невероятно), что будущие открытия убедят нас, что один или более из этих существенных промежуточных шагов являются неверными. Тогда, возможно, придётся отказаться от голографической идеи.
Другой важный момент состоит в том, что в наших рассуждениях речь шла об области пространства, об окружающей её поверхности, и о заполняющей их информации. Однако, поскольку акцент был сделан на энтропию и Второй закон — каждый из которых касается в первую очередь величины информации в данном контексте — мы пропустили детали того, как эта информация хранится или физически реализуется. Когда мы говорим об информации, которая находится на сфере, окружающей некоторую область пространства, то что это на самом деле означает? Как информация проявляет себя? Какую форму она приобретает? До какой степени мы можем развить подробный словарь по переводу явлений, происходящих на границе, в явления, происходящие в объёме?
Физикам ещё предстоит создать общую схему рассмотрения этих вопросов. Считая, что как гравитация, так и квантовая механика играют центральную роль в подобных рассуждениях, можно было бы ожидать, что возможная модель для теоретических исследований данных вопросов появится в теории струн. Однако, когда т’Хоофт сформулировал голографический принцип, он стал сомневаться, что теория струн поможет в развитии этой области, заметив, что «на планковских расстояниях природа гораздо более безумна, чем могут себе представить струнные теоретики».{88} Менее чем десятилетие спустя струнная теория доказала, что т’Хоофт ошибался, но его идеи верны. В эпохальной статье одного молодого теоретика было показано, что теория струн приводит к подробной реализации голографического принципа.
Теория струн и голография
Когда в 1998 году на ежегодной международной конференции по теории струн в университете Калифорнии в Санта-Барбаре объявили мой доклад, я, выходя к доске, сделал нечто, чего никогда ранее не делал, и подозреваю, больше никогда не сделаю. Я повернулся к аудитории, положил правую руку на левое плечо, затем левую руку на правое плечо, после чего опустил по очереди обе руки на задние карманы брюк, подпрыгнул, развернулся к доске и под сопровождающий меня смех зала сделал три оставшихся шага до трибуны, где и начал свой доклад. Аудитория поняла шутку. Накануне вечером на банкете участники конференции праздновали с песнями и танцами — только так, как могут физики, — выдающийся результат аргентинского струнного теоретика Хуана Малдасены. Мы придумали слова что-то типа:
Чёрные дыры были большой мистикой, а теперь мы с помощью D-бран считаем D-энтропию,и распевали их на мотив «Макарены», известного танцевального хита начала 1990-х годов. Мы выражали восторг сильнее, чем участники национального съезда демократов приветствовали Эла Гора, и наша песня ничем не уступала оригинальному исполнению «Лос дель Рио» по накалу страстей. На конференции я был один из немногих, доклад которых не был посвящён открытию Малдасены, поэтому, выйдя к доске на следующий день, я решил предварить свой доклад персональным танцем одобрения.
Сейчас, спустя десять лет, многие согласятся, что ни одно достижение в теории струн не было настолько существенным и важным. Одним из следствий результата Малдасены, имеющим прямое отношение к нашим рассуждениям, было то, что в некотором модельном варианте результат Малдасены явно выражал голографический принцип, давая первый математический пример голографических параллельных вселенных. Для этого Малдасена рассмотрел теорию струн во вселенной, которая отличается по форме от нашей Вселенной, но которую было легче анализировать для поставленных целей. Математически отличие состояло в том, что у вселенной была граница — непроницаемая поверхность, полностью охватывающая внутренность пространства. Сосредоточившись на граничной поверхности, Малдасена убедительно доказал, что всё, происходящее внутри этой особой вселенной, является отражением действующих на границе законов и процессов.
И хотя метод Малдасены не применим, скорее всего, напрямую ко вселенной с нашей формой, этот результат имел решающее значение, потому что благодаря этому появился прямой математический способ количественного анализа идей, касающихся голографических вселенных. Результаты таких исследований привлекли внимание большого количества физиков, которые раньше относились к голографическому принципу с подозрением, и таким образом вызвали шквал исследований, которые привели к тысячам статей и значительно углубили наше понимание. Самое захватывающее, что теперь есть основание думать, что связь между этими теоретическими открытиями и физикой в нашей Вселенной может быть установлена. Через несколько лет эта связь вполне может привести к экспериментальной проверке голографических идей.
Оставшаяся часть этого и следующего раздела будет посвящена объяснению того, как Малдасена пришёл к этому открытию; эта часть изложения самая трудная. Я начну с краткого резюме в виде шпаргалки, но если вы почувствуете, что уже насытились деталями, можете без зазрения совести перейти к последнему разделу.
Идея Малдасены состояла в использовании новой версии дуальности, которую мы обсуждали в главе 5. Напомним, что там мы рассматривали вселенные на бране, представимые в виде нарезанных ломтей хлеба. Малдасена рассмотрел с двух дополнительных точек зрения свойства плотной стопки трёхмерных бран (рис. 9.4). С одной, «внутренней» точки зрения, рассматриваются струны, которые движутся, вибрируют и извиваются вдоль этих бран. С другой, «внешней», точки зрения рассматривается, какое гравитационное воздействие браны оказывают на своё непосредственное окружение, подобно тому как Солнце и Земля влияют на своё окружение. Малдасена показал, что обе точки зрения описывают одну и ту же физическую ситуацию, но с разных сторон. Внутренняя точка зрения рассматривает движение струн на стопке бран, а внешняя точка зрения рассматривает движение струн в области искривлённого пространства, ограниченного стопкой бран. Приравнивая обе точки зрения, Малдасена обнаружил явную связь между физикой внутри области с физикой на границе области — была найдена подробная реализация голографии. В этом состоит основная идея.
Рис. 9.4. Набор близко расположенных три-бран, к которым прикреплены концы открытых струн, а замкнутые струны двигаются внутри «балка»
А если добавить красок, то ситуация описывается следующим образом.
Рассмотрим, говорит Малдасена, стопку из три-бран, настолько близко расположенных друг к другу, что они выглядят как монолитная плита (рис. 9.4), и изучим поведение движущихся в этой среде струн. Вспомним, что есть два типа струн — открытые, как кусочки ниточек, и замкнутые, как колечки. Вспомним также, что концы открытых струн могут скользить по бранам, но не могут отрываться от них, а замкнутые струны не имеют концов и поэтому могут свободно перемещаться по всему пространству. На теоретико-струнном жаргоне мы говорим, что открытые струны прикреплены к бранами, а замкнутые струны могут двигаться по всему объёму пространства (или в «балке»).
Сначала Малдасена математически проанализировал струны с низкой энергией — то есть струны, вибрирующие относительно медленно. И вот почему: сила гравитации между двумя любыми объектами пропорциональна массе каждого объекта; это же справедливо для гравитационного притяжения между любыми двумя струнами. Струны с низкой энергией обладают малой массой и поэтому практически не реагируют на гравитационное притяжение. Таким образом, сфокусировавшись на низкоэнергетических струнах, Малдасена пренебрёг влиянием гравитации. Это стало существенным упрощением. В главе 5 мы видели, что в теории струн гравитационное взаимодействие переносится замкнутыми струнами. Поэтому пренебречь силой гравитации эквивалентно пренебречь влиянием замкнутых струн на всё, с чем они могут встретиться, — в особенности, с живущими на стопке из бран ниточками открытых струн. Таким образом, добившись, что два типа струн, открытые и замкнутые, не оказывают влияния друг на друга, Малдасена добился того, что их можно анализировать по отдельности.
Затем Малдасена изменил точку зрения и стал анализировать ту же самую ситуацию под другим углом. Вместо того чтобы считать три-браны вместилищем для движения открытых струн, он рассмотрел три-брану как самостоятельный объект, у которого есть присущая ему масса и который, таким образом, искривляет вокруг себя пространство и время. Малдасене повезло, потому что к тому времени другими физиками были уже получены результаты, где были заложены основы для такого альтернативного рассмотрения. В этих работах было установлено, что при увеличении числа бран в стопке их коллективное гравитационное поле возрастает. В конце концов плита из бран ведёт себя подобно чёрной дыре, но не обычной, а бранообразной, поэтому такая стопка была названа чёрной браной. Как и в случае чёрных дыр, если приблизиться слишком близко к чёрной бране, то вырваться оттуда не получится. И так же как в случае чёрных дыр, если наблюдать издалека за приближением какого-нибудь объекта к чёрной бране, то дошедший до вас свет будет точно так же измотан борьбой с гравитационным притяжением чёрной браны. Это приведёт к тому, что объект будет выглядеть замедляющимся и теряющим энергию.[59]
В этом контексте Малдасена вновь сосредоточился на низкоэнергетических свойствах вселенной, в которой содержится такая чёрная плита. Во многом аналогично тому, как он действовал в первом подходе, он осознал, что в низкоэнергетической физике присутствуют две составляющие, которые можно анализировать независимо друг от друга. Первая — это медленно вибрирующие замкнутые струны, движущиеся в балке пространства, которые являются очевидными переносчиками низкой энергии. Вторая составляющая возникает благодаря присутствию чёрной браны. Представьте теперь, что вы находитесь далеко от чёрной браны и в вашем распоряжении имеется вибрирующая замкнутая струна, энергия которой может быть произвольно большой. Затем представьте, что струна опускается на горизонт событий, а вы наблюдаете за ней с безопасного расстояния. Как говорилось ранее, чёрная брана будет понижать энергию струны; свет, доходящий до вас, будет изображать струну как в замедленном кино. Таким образом, вторыми низкоэнергетическими переносчиками являются любые вибрирующие струны, которые находятся достаточно близко к горизонту событий чёрной браны.
Наконец, Малдасена сравнил оба подхода. Он заметил, что, поскольку они описывают одну и ту же стопку бран, только с разных точек зрения, они обязаны совпадать. Каждое описание вовлекает низкоэнергетические замкнутые струны, движущиеся в балке пространства, поэтому в этой части совпадение очевидно. Однако согласованность должна быть и в остальных частях каждого описания.
Удивительно, но именно так и происходит!
Оставшийся кусок первого описания состоит из низкоэнергетических открытых струн, движущихся на три-бранах. Вспомним из главы 4, что низкоэнергетические струны хорошо описываются квантовой теорией поля точечных частиц, именно то, что нам здесь требуется. Этот тип квантовой теории поля привлекает ряд хитроумных математических построений (чего стоит только одно название — конформно-инвариантная суперсимметричная квантовая калибровочная теория поля), но нам важны две её характеристики, которые можно достаточно легко понять. Во-первых, отсутствие замкнутых струн гарантирует отсутствие гравитационного поля. Во-вторых, поскольку струны движутся только на плотно упакованных в стопку бранах, квантовая теория поля живёт в трёх пространственных измерениях (что в совокупности с одним временным измерением даёт четыре пространственно-временных измерения).
Что касается второго описания, то оставшийся кусок состоит из произвольно вибрирующих замкнутых струн, которые, однако, оказались достаточно близко к горизонту событий чёрной браны, а потому кажутся вялыми — то есть как будто они обладают низкой энергией. Такие струны, хотя и ограниченные близостью к чёрной бране, по-прежнему вибрируют и движутся сквозь девять пространственных измерений (что в совокупности с одним временным измерением даёт десять пространственно-временных измерений). Поскольку этот сектор построен из замкнутых струн, в нём присутствует гравитационное взаимодействие.
Однако сколь бы разными не казались два подхода, они описывают одну физическую ситуацию и поэтому должны быть согласованы. Это приводит к совершенно невероятному заключению. Квантовая теория поля (определённого вида) точечных частиц без гравитации в четырёх пространственно-временных измерениях (первая точка зрения) описывает такую же физику, что и теория струн с гравитацией, где струны движутся внутри определённой области десятимерного пространства-времени. Звучит так же странно, как… даже не знаю что — сколько я не пытался, я не смог найти две менее похожие вещи в реальном мире, чем эти две теории. Однако Малдасена доверился математике в обсуждавшемся выше смысле и, сделав такой вывод, попал в самую точку.
Исключительная неожиданность этого результата — и смелость утверждения — не умаляется тем фактом, что он моментально находит своё место в цепочке рассуждений, приведённых выше в этой главе. Как схематично показано на рис. 9.5, гравитация чёрной плиты из бран искривляет окрестность рассматриваемой области в форму десятимерного пространства-времени (детали вторичны, но искривлённое пространство-время называется пятимерным анти-де ситтеровское пространством на пятимерную сферу); причём плита из чёрных бран является границей этого пространства. Поэтому результат Малдасены состоит в том, что теория струн в балке этого пространства-времени идентична квантовой теории поля, живущей на его границе.{89}
Рис. 9.5. Схематическая иллюстрация дуальности между теорией струн внутри некоторого пространства-времени и квантовой теорией поля на его границе
Так возникает голография.
Малдасена построил самосогласованную математическую лабораторию, в которой, помимо всего прочего, физики могли исследовать конкретные детали голографической реализации физических законов. В течение нескольких месяцев появились две статьи, одна из них принадлежала Эдварду Виттену, а вторая была написана совместно Стивеном Габсером, Игорем Клебановым и Александром Поляковым, которые вывели результат Малдасены на новый уровень понимания. В них был создан точный математический словарь для перевода с одной теории на другую: если задан физический процесс на границе браны, то словарь говорит, как он будет выглядеть в балке внутри объёма и наоборот. С помощью этого словаря в умозрительной вселенной голографический принцип становится точным и определённым. На границе вселенной информация закодирована в квантовых полях. После математического перевода она предстаёт как струнный сюжет, разворачивающийся внутри объёма.
Математический словарь сам по себе подчёркивает голографическую аналогию. Обычная голограмма не похожа на трёхмерный объект, который она порождает. На её поверхности видны лишь линии, дуги, завитки, вытравленные на пластиковой пластинке. Однако сложное преобразование, выполняемое при прохождении лазерного луча сквозь пластинку, переводит эти отметины в узнаваемое трёхмерное изображение. Это означает, что пластиковая голограмма и трёхмерное изображение содержат одинаковые данные, даже если информация в одной из них нераспознаваема с точки зрения другой. Аналогичным образом, при анализе квантовой теории поля на границе вселенной Малдасены не видно, что у неё есть явные сходства с теорией струн, живущей в балке. Если физику показать две теории и умолчать о связи, которую мы только что выяснили, то скорее всего он сделает вывод, что они независимы. Тем не менее математический словарь, связывающий обе теории — и работающий как лазер в обычных голограммах, — со всей определённостью говорит, что всё, происходящее в одной теории, имеет своё воплощение в другой. А само изучение этого словаря выявляет, что подобно обычным голограммам, информация в каждой из этих теорий оказывается зашифрованной при переводе на другой язык.
В качестве особенно впечатляющего примера рассмотрим задачу, которую исследовал Виттен: как будет выглядеть обычная чёрная дыра, находящаяся внутри вселенной Малдасены, с точки зрения теории на границе. Напомним, что теория на границе не содержит гравитации, и потому чёрная дыра трансформируется в нечто совсем не похожее. Виттен показал, что подобно тому как за устрашающим видом волшебника Изумрудного города скрывался обыкновенный человек, так и ненасытная чёрная дыра является голографической проекцией чего-то совершенно обычного — разгорячённого газа частиц в теории на границе (рис. 9.6). Подобно настоящей голограмме и порождаемому ею изображению, две теории — чёрная дыра внутри и разогретая квантовая теория поля на границе — ничем друг на друга не похожи, но при этом они несут одинаковую информацию.[60]
Рис. 9.6. Голографическая эквивалентность применительно к чёрной дыре в «балке» пространства-времени приводит к разогретому газу частиц и излучения на границе рассматриваемой области
В притче Платона о пещере наши чувства воспринимают лишь плоскую, усечённую версию истинной, более богатой реальности. Плоский мир Малдасены совсем другой. Далёкий от какого-либо усечения, он представляет события во всей полноте. Это совершенно другая история, отличная от того, к чему мы привыкли. Но этот плоский мир может вполне оказаться первичным.
Параллельные вселенные или параллельная математика?
Результат Малдасены и многие другие достижения, сделанные за прошедшие годы, воспринимаются как гипотезы. Поскольку математическая структура теории невероятно сложна, нахождение окончательных и безупречных аргументов является трудной задачей. Однако голографические идеи с успехом прошли строгие математические проверки, попав в мейнстрим физических исследований, направленных на поиск глубинных основ законов природы.
Один из факторов, вносящий свою лепту в сложность доказательства того, что граничный и объёмный миры — это разные замаскированные версии одной и той же физики, подчёркивает значительность этого результата, если он, конечно, справедлив. В главе 5 я говорил, что в большинстве случаев физики используют приближённые методы, и описал методы теории возмущений (вспомните пример с лотереей Ральфа и Элис). Я также подчеркнул, что такие методы приводят к правильным результатам только в случае, когда константа связи мала. При сравнении квантовой теории поля на границе и теории струн в балке Малдасена осознал, что когда константа связи одной теории мала, константа связи другой теории велика, и наоборот. Естественная проверка и возможный способ доказательства того, что две теории скрыто идентичны друг другу, сводится к проведению независимых вычислений в каждой теории и последующему сравнению. Однако это трудно сделать, потому что когда приближённые методы работают в одной теории, то они становятся неприменимыми в другой.{90}
Но если вы принимаете более абстрактные доводы Малдасены из предыдущего раздела, то, что было пертурбативным злом, становится вычислительной добродетелью. По аналогии со струнными дуальностями из главы 5, словарь, устанавливающий соответствия между границей и балком, переводит устрашающие вычисления, отягощённые большой константой связи в одном подходе, в простые вычисления с малой константой связи в другом подходе. В последние годы этот эффект был умело использован для получения результатов, которые могут быть экспериментально проверены.
На релятивистском коллайдере тяжёлых ионов (RHIC) в Брукхэйвене, Нью-Йорк, ядра золота сталкиваются друг с другом на почти околосветовых скоростях. Поскольку ядра содержат много протонов и нейтронов, в столкновениях рождаются многочисленные частицы, температура которых может в 200 000 раз превышать температуру поверхности Солнца. Это достаточно горячо для того, чтобы из протонов и нейтронов образовалась жидкость из кварков и связывающих их глюонов. Физики потратили много усилий, чтобы понять, как устроена эта жидкая фаза, получившая название кварк-глюонная плазма, потому что считается, что именно в этом состоянии находилось вещество вскоре после Большого взрыва.
Сложность в том, что константа связи в этой квантовой теории поля (квантовой хромодинамике), описывающей горячий суп из кварков и глюонов, имеет большое значение, что ставит под сомнение применимость методов теории возмущения. Для преодоления этого препятствия были развиты многие изощрённые методы, но некоторые теоретические результаты по-прежнему не согласуются с экспериментальными данными. Например, при течении любой жидкости — будь то вода, патока или кварк-глюонная плазма — каждый слой жидкости оказывает тормозящее воздействие на слои сверху и снизу. Такое тормозящее воздействие известно как сдвиговая вязкость. В экспериментах на RHIC были проведены измерения сдвиговой вязкости кварк-глюонной плазмы, и полученные результаты оказались гораздо меньше, чем аналитические предсказания, сделанные с помощью пертурбативных методов квантовой теории поля.
Возможный способ преодолеть эту трудность заключается в следующем. Когда я вводил голографический принцип, я принял ту точку зрения, что всё, происходящее с нами внутри пространства-времени, является с помощью какого-то неожиданного трюка отражением процессов, которые происходят на удалённой граничной поверхности. Давайте обратим эту точку зрения. Представим, что наша Вселенная, или, более точно, кварки и глюоны в нашей Вселенной живут на границе, и потому эксперименты RHIC ставятся именно там. Теперь привлечём гипотезу Малдасены. Его результат показывает, что RHIC-эксперименты (описываемые квантовой теорией поля) имеют альтернативное математическое описание в терминах движущихся в объёме (или балке) струн. Детали происходящего сложны, но следствия такой перефразировки не заставляют себя долго ждать: трудные вычисления на границе (с большой константой связи) превращаются в более лёгкие вычисления в объёме (с малой константой связи).{91}
Павел Ковтун, Андрей Старинец и Дам Сон провели такие вычисления и получили результат, который оказался впечатляюще близок к экспериментальным данным. Эта пионерская работа вдохновила целую армию теоретиков провести множество струнных расчётов в попытке установить связь с наблюдениями на RHIC, что оживило взаимодействие между теорией и экспериментом — к чему долго стремились струнные теоретики.
Следует заметить, что граничная теория не может полностью воспроизводить нашу Вселенную, поскольку, например, она не содержит гравитации. Но это не препятствует установлению связи с данными на RHIC, потому что в проводимых экспериментах массы частиц настолько малы (даже при движении на околосветовых скоростях), что гравитационное притяжение не играет никакой практической роли. Однако это подчёркивает, что в таких приложениях теория струн не выступает как «теория всего»; наоборот, теория струн предоставляет новые вычислительные инструменты для преодоления препятствий, затрудняющих применение более традиционных методов. С консервативной точки зрения, рассмотрение кварков и глюонов с помощью многомерной теории струн может рассматриваться как некий мощный математический трюк. При менее консервативном подходе можно считать, что высокоразмерное струнное описание является, в некотором смысле, физически реальным, но этот смысл ещё предстоит установить.
Независимо от того, консервативна точка зрения или нет, возникающее слияние математических результатов и экспериментальных наблюдений в высшей степени впечатляет. Я не сторонник преувеличивать, но считаю эти достижения самыми выдающимися за последние десятилетия. Математические выкладки, описывающие движение струн внутри десятимерного пространства-времени, дают нам информацию о кварках и глюонах, живущих в четырёхмерном пространстве-времени, — и эта информация, рождённая на кончике пера, подкрепляется, как нам видится, экспериментами.
Кода: будущее теории струн
Научные достижения, рассмотренные нами в этой главе, далеко выходят за рамки теории струн. Мы начали с идеи Уилера, что нашу Вселенную следует анализировать в терминах информации, потом мы увидели, что энтропия есть мера скрытой информации, затем мы поняли, что второй закон термодинамики мирно уживается с чёрными дырами, после чего осознали, что чёрные дыры хранят энтропию на поверхности горизонта, а также максимизируют количество информации, способной находиться в заданной области пространства-времени, — мы прошли извилистый путь сквозь многие десятилетия и познакомились с набором нетривиальных результатов. Этот процесс был наполнен замечательными открытиями и привёл нас к новой объединяющей идее — голографическому принципу. Этот принцип, как мы видели, предполагает, что наблюдаемые нами явления являются отражением происходящего на тонкой удалённой ограничивающей поверхности. Заглядывая в будущее, я ожидаю, что голографический принцип останется путеводной звездой для физиков в XXI столетии.
То что теория струн охватывает голографический принцип и даёт конкретные примеры голографических параллельных миров, демонстрирует, как сочетание передовых идей приводит к получению новых ярких результатов. То что эти примеры задали основу для явных вычислений, часть из которых могут быть сопоставлены с экспериментальными данными, является важным шагом на пути установления связи с окружающей нас реальностью. Однако внутри самой теории струн имеется более общий контекст, в рамках которого следует рассматривать эти результаты.
На протяжении почти тридцати лет после открытия теории струн физикам не хватало полного математического определения теории. В самом начале струнные теоретики выдвинули важные идеи о вибрирующих струнах и дополнительных измерениях, но даже спустя десятилетия активных разработок математические основания теории остаются приближёнными и, следовательно, неполными. Открытие Малдасены является выдающимся достижением на этом пути. Модели квантовой теории поля, которые, согласно Малдасене, живут на границе, активно изучались физиками с середины XX века и относятся к категории теорий элементарных частиц, хорошо понятых с математической точки зрения. Туда не входит гравитация и это большой плюс, поскольку мы видели, что непосредственная попытка совместить общую теорию относительности и квантовую теорию поля подобна разведению костра на пороховой фабрике. Теперь мы понимаем, что эта математически дружелюбная, негравитационная теория поля голографически порождает теорию струн — теорию с гравитацией. Живя по своим законам на границе вселенной специальной формы (рис. 9.5), эта квантовая теория поля охватывает все физические свойства, процессы и взаимодействия движущихся в объёме струн, и эта связь явно устанавливается с помощью словаря, переводящего явления из одной теории на язык другой. Поскольку у нас есть твёрдое математическое определение граничной квантовой теории, то его можно использовать как математическое определение теории струн, по крайней мере для струн, движущихся внутри этого пространства-времени. Таким образом, голографические параллельные вселенные могут стать чем-то бо́льшим, нежели просто следствием фундаментальных законов; они могут стать частью самого определения фундаментальных законов.{92}
Когда я знакомил вас с теорией струн в главе 4, я отметил, что она является достойным претендентом на роль новой теории, которая объясняет фундаментальные законы природы, но при этом не отрицает предыдущие теории. Результаты, которые мы только что видели, поднимают это замечание на совершенно другой уровень. Теория струн не просто сводится к квантовой теории поля при определённых обстоятельствах. Гипотеза Малдасены говорит, что теория струн и квантовая теория поля являются эквивалентными подходами, но выраженными на разных языках. Переход между ними достаточно сложен и именно поэтому прошло более сорока лет, прежде чем эта взаимосвязь была обнаружена. Но если результаты Малдасены полностью верны, как на то указывают доступные нам данные, то теория струн и квантовая теория поля вполне могут оказаться двумя сторонами одной медали.
Физики упорно трудятся над обобщением этих идей, с тем чтобы их можно было применить к вселенным любой формы; если теория струн верна, то в них будет содержаться и наша Вселенная. Но даже при настоящих ограничениях, тот факт, что появилась надёжная формулировка теории, над которой мы работали много лет, является существенной основой для будущего прогресса. Этого вполне достаточно, чтобы вдохновить многих физиков петь и танцевать.
Глава 10. Вселенные, компьютеры и математическая реальность Смоделированные мультивселенные и окончательная мультивселенная
Теории параллельных вселенных, рассмотренные в предыдущих главах, были основаны на математических законах, разработанных физиками в стремлении понять глубочайшие принципы устройства природы. Степень нашей веры в тот или иной свод законов весьма разнится — квантовая механика рассматривается как установленный факт; инфляционная космология имеет наблюдательную поддержку; теория струн в значительной степени умозрительна — в той же степени это верно и для типа и логической необходимости параллельных миров, ассоциированных с каждым из них. Но общий принцип ясен. Каждый раз, когда мы передаём управление математическому аппарату основных физических законов, мы вновь и вновь оказываемся в некоторой версии параллельных миров.
Теперь давайте пойдём другим путём. Что произойдёт, если мы возьмём управление в свои руки? Можем ли мы, люди, руководить космической эволюцией и по собственной воле создать вселенную, параллельную нашей собственной? Если вы, подобно мне, верите, что поведение живых существ определяется законами природы, то это можно считать не другим путём, а всего лишь сужением перспективы, когда действие физических законов рассматривается сквозь призму человеческого опыта. Такой способ мышления быстро приводит к болезненным вопросам, подобным стародавнему спору о детерминизме и свободе воли, и это не тот путь, котором я собираюсь пойти. Вопрос в другом: с тем же ощущением желания и контроля, что вы чувствуете, когда выбираете продукты или фильм, можете ли вы создать вселенную?
Вопрос звучит парадоксально. Так оно и есть. Должен вас предупредить, что задавая подобные вопросы, мы ступаем на почву ещё более зыбкую, чем прежде, и, если вспомнить, где мы уже прошли, это говорит о многом. Но позволим себе увлечься и посмотрим, куда мы придём. Итак, я очерчу дорогу, по которой мы последуем. Когда я рассуждаю о рождении вселенной, меня больше интересуют возможности, предоставляемые физическими законами, чем практические ограничения. Поэтому когда я говорю, что «вы» создаёте вселенную, то на самом деле я имею в виду вас, или ваших далёких потомков, или, возможно, армию таких потомков спустя тысячелетия. Эти настоящие или будущие люди также будут подчиняться законам физики, но при этом я буду считать, что в их распоряжении окажутся сколь угодно развитые технологии. Я также буду рассматривать рождение вселенных двух разных типов. Вселенные первого типа — это обычные вселенные, которые заключают в себе пространство и которые заполнены различными формами вещества и энергии. Вселенные второго типа не столь осязаемы: это виртуальные компьютерные вселенные. Данное обсуждение естественным образом установит связь с мультивселенными третьего типа. Эта разновидность вселенных не является следствием целенаправленных размышлений об образовании вселенных, а скорее здесь поднимается вопрос о том, «реальна» ли математика или она является порождением нашего разума.
Породить вселенную
Несмотря на то, что состав вселенной нам до конца неясен и есть много вопросов по поводу тёмной энергии или окончательного набора фундаментальных корпускулярных ингредиентов, учёные уверены, что если взвесить всё находящееся внутри нашего космического горизонта, то получится примерно 10 миллиардов миллиардов миллиардов миллиардов миллиардов миллиардов грамм. Если содержимое будет весить значительно больше или меньше, то его гравитационное влияние на реликтовое излучение приведёт к тому, что пятна на рис. 3.4, будут больше или меньше, что войдёт в противоречие с современными измерениям их угловых размеров. Однако точный вес наблюдаемой вселенной вторичен; достаточно того, что он огромен. Настолько огромен, что мысль о нас, человеческих существах, создающих другой такой мир, видится крайне бессмысленной.
Опираясь на космологию Большого взрыва в качестве модели образования вселенной, мы не видим, как преодолеть эту трудность. В стандартной теории Большого взрыва наблюдаемая вселенная во всё более ранние времена имела всё меньший размер, но колоссальные значения вещества и энергии, которые мы теперь измеряем, присутствовали всегда; они были просто сжаты в меньшем объёме. Если вы хотите иметь вселенную подобную той, что мы сегодня наблюдаем, для начала необходимо обзавестись исходным материалом, масса и энергия которого совпадает с наблюдаемыми значениями. В теории Большого взрыва наличие такого исходного материала никак не объясняется, а рассматривается как данность.{93}
Если кратко, то согласно инструкции по порождению вселенной типа нашей, следующей из теории Большого взрыва, требуется собрать гигантское количество массы и сжать её до фантастически малого размера. Однако, достигнув этого (что практически невозможно), мы столкнёмся с другой проблемой. Как инициировать взрыв? Данное затруднение становится ещё более серьёзным, если вспомнить, что Большой взрыв — это не взрыв, происходящий в статичной области пространства; Большой взрыв — это расширение пространства как такового.
Если бы теория Большого взрыва была вершиной космологической мысли, то научное изучение образования вселенной на этом бы и остановилось. Но это не так. Мы видели, что теория Большого взрыва дала дорогу более убедительной теории — инфляционной космологии, а инфляция предлагает стратегию дальнейшего развития. Мощный выброс расширяющегося пространства — характерная черта теории — задаёт взрыв в Большом взрыве, и действительно большой; согласно инфляционной теории, антигравитационная тяга приводит в движение расширение пространства. Столь же важным, как мы сейчас увидим, является то, что при инфляции огромное количество материи может возникнуть из очень скромных зёрнышек.
Вспомним из главы 3, что в инфляционном подходе вселенная, подобная нашей — дырка в космическом швейцарском сыре — образуется, когда значение инфлатона скатывается вниз по кривой потенциальной энергии, выплеснув феноменальную волну в окрестности нашего пузырька. При падении значения инфлатона содержащаяся в нём энергия трансформируется в газ частиц, равномерно заполняющий наш пузырёк-вселенную. Именно так образуется наблюдаемая материя. Налицо определённый прогресс в понимании, но возникает следующий вопрос: где источник энергии инфлатона?
Причина в гравитации. Вспомните, что инфляционное расширение очень похоже на репликацию вируса: поле инфлатона с большим значением заставляет расширяться область пространства, в которой он находится, при этом возникает всё более расширяющийся объём, который, в свою очередь, также заполняется полем инфлатона с большим значением. Поскольку однородное поле инфлатона приводит к постоянной энергии на единицу объёма, то чем больше заполняемый объём, тем больше энергии он содержит. Сила, подгоняющая расширение, — это отталкивающая гравитация, и поэтому гравитация является источником постоянно увеличивающейся энергии в данной области пространства.
Таким образом, можно считать, что инфляционная космология создаёт устойчивый энергетический поток от гравитационного поля к полю инфлатона. Такое объяснение может выглядеть как очередной уход от ответа на вопрос, откуда сама гравитация берёт свою энергию. Однако ситуация гораздо лучше. Гравитация отличается от других сил, потому что там, где имеется гравитация, там фактически неисчерпаемый резервуар энергии. Это известная идея, но выраженная на непривычном языке. Когда вы прыгаете с обрыва, ваша кинетическая энергия — энергия вашего движения — увеличивается. Гравитация — сила, заставляющая вас падать, — служит источником энергии. В любой реальной ситуации вы упадёте на землю, но в принципе можно падать бесконечно долго, кувыркаясь вниз по нескончаемой кроличьей норе, а кинетическая энергия будет постоянно расти. Причина, по которой гравитация служит источником такой неограниченной энергии, в том, что, подобно министерству финансов США, она не боится брать в долг. Во время падения ваша кинетическая энергия положительна и растёт, а гравитация компенсирует её своей растущей отрицательной энергией. Интуитивно вы понимаете, что гравитационная энергия отрицательна, потому что для того, чтобы выбраться из кроличьей норы, необходимо приложить положительную энергию — отталкиваться ногами, подтягиваться на руках; именно так вы отдаёте энергетический долг, который взяла гравитация.{94}
Вывод по сути состоит в том, что во время быстрого расширения области пространства, заполненной инфлатоном, последний берёт энергию у неисчерпаемого гравитационного источника, что также приводит к быстрому увеличению энергии, содержащейся в данной области. Поскольку поле инфлатона поставляет энергию, которая затем перейдёт в обычную материю, инфляционная космология — в отличие от модели Большого взрыва — не нуждается в исходном материале для последующего образования планет, звёзд и галактик. Гравитация играет роль богатого покровителя материи во вселенной.
Единственное, в чём нуждается инфляционная космология, это независимый запас энергии для образования исходного инфляционного зёрнышка — маленькой сферической крупицы пространства, заполненной полем инфлатона с большим значением, которое запускает инфляционное расширение. Если обратиться к числам, то уравнения показывают, что такая крупица должна иметь всего примерно 10−26 сантиметра в поперечнике и быть заполнена полем инфлатона, энергия которого, при пересчёте на массу, будет весить менее 10 грамм.{95} Такое крохотное зёрнышко испытает молниеносное эффектное расширение, вырастая до размеров, превышающих наблюдаемую вселенную, и накапливая при этом постоянно увеличивающуюся энергию. Полная энергия инфлатона быстро превысит значение, необходимое для образования всех звёзд во всех наблюдаемых галактиках. Поэтому, если динамикой вселенной управляет инфляция, то начальное условие, невыполнимое в модели Большого взрыва — наличие исходной массы, превышающей 1055 грамм, сжатой в бесконечно малую крупинку — подвергается радикальному пересмотру. Соберите 10 грамм поля инфлатона и сожмите их в комочек примерно 10−26 сантиметра в поперечнике. Такой комочек вполне может уместиться в кошельке.
Тем не менее и здесь перед нами встают острые вопросы. Начать с того, что инфлатон остаётся чисто гипотетическим полем. Космологи свободно вводят поле инфлатона в уравнения, однако, в отличие от электронов и кварков, у нас пока нет никаких доказательств существования поля инфлатона. Даже если инфлатон существует, и даже если однажды мы разработаем способ управлять им так же, как электромагнитным полем, то плотность необходимого инфлатонного зёрнышка будет огромной: примерно в 1067 раз больше плотности атомного ядра. Хотя это зёрнышко будет весить меньше горсти попкорна, необходимая сила сжатия в триллионы и триллионы раз превышает наши настоящие возможности.
Но это относится скорее к технологической проблеме, которую высокоразвитая цивилизация, как мы думаем, однажды сможет решить. Поэтому, если наши далёкие потомки смогут обуздать поле инфлатона и построить уникальный компрессор, способный создавать такие плотные крупинки, получим ли мы статус создателей вселенных? Если мы задумаем такое восхождение на Олимп, не следует ли нам озаботиться тем, что в случае искусственного рождения новых инфляционных миров наш собственный уголок пространства будет поглощён расширяющимся космосом? Алан Гут и его соавторы проанализировали эти вопросы в ряде статей и обнаружили как хорошие новости, так и плохие. Начнём с последнего вопроса, для которого новости хорошие.
Гут, совместно со Стивеном Блау и Эдуардо Генделманом, показал, что не стоит беспокоиться насчёт искусственности инфляционного расширения, пронзительно взрывающего нашу окружающую среду. Причина в давлении. Если инфляционное зёрнышко создадут в лаборатории, то оно будет наполнено полем инфлатона с характерной положительной энергией и иметь отрицательное давление, но при этом будет окружено обычным пространством, в котором значение поля инфлатона и его давление равно (или почти равно) нулю.
Обычно мы не обращаем особого внимания на ноль, но в данном случае весь смысл именно в нём. Нулевое давление больше отрицательного, поэтому давление снаружи зёрнышка будет больше давления внутри. Поэтому на зёрнышко будет давить внешняя сила, подобно давлению на барабанные перепонки во время глубоководного погружения. Разница в давлении достаточно существенна, чтобы не дать зёрнышку расшириться во внешнее пространство.
Однако это не помешает инфлатону стремиться к расширению. Если надувать воздушный шарик, но при этом крепко зажимать его руками, то резиновая поверхность шарика начнёт вылезать между пальцами. Инфлатонное зёрнышко может вести себя похожим образом. Оно может породить новый расширяющийся мир, отделяющийся от исходного пространства, как показано на примере небольшой растущей сферы, см. рис. 10.1. Вычисления показывают, что как только новый мир достигает критического размера, его связь с родительским пространством рвётся (крайнее справа изображение на рис. 10.1) и рождается независимая инфляционная вселенная.
Рис. 10.1. Из-за большего давления окружающей среды инфляционное зёрнышко вынуждено расшириться с образованием нового пространства. Пузырёк-вселенная растёт, затем отщепляется от исходной вселенной и становится отдельным, расширяющимся пространством. Для наблюдателя из окружающей среды этот процесс выглядит как образование чёрной дыры
Каким бы увлекательным ни был этот процесс — искусственное образование новой вселенной, — взгляд из лаборатории не оправдывает потраченных на это усилий. Хорошо, что инфляционный пузырёк не поглотит лабораторию и всё окружающее пространство, но обратная сторона медали такова, что практически невозможно будет доказать сам факт рождения. Новая расширяющаяся вселенная, которая затем отделится от нашей, — это вселенная, которую мы не можем наблюдать. Действительно, после отпочкования новой вселенной, единственным напоминанием о ней будет глубокая гравитационная яма (крайнее справа изображение на рис. 10.1), которая в нашей вселенной будет выглядеть как чёрная дыра. Поскольку мы не можем заглянуть внутрь чёрной дыры, то нет никакой уверенности в успешности нашего эксперимента; не имея доступа к новой вселенной, мы не сможем подтвердить её рождение с помощью наблюдений.
Физические законы стоят на нашей защите, но цена безопасности — отлучение нас от плодов нашего труда. Это хорошие новости.
Перейдём теперь к плохим новостям. Честолюбивых создателей вселенных отрезвит результат, полученный Гутом и его коллегой из Массачусетского технологического института Эдвардом Фархи. Проведённые ими аккуратные математические вычисления показали, что в последовательности картинок на рис. 10.1 пропущен один шаг. Вспомним ситуацию с воздушным шариком — если в него дунуть сильно в самом начале, то затем его надуть гораздо проще; аналогичным образом Гут и Фархи обнаружили, что зарождающаяся вселенная на рис. 10.1 для запуска инфляционного расширения требует сильного толчка в самом начале. Настолько сильного, что существует лишь единственная сущность, способная на такое — белая дыра. Белая дыра — противоположность чёрной дыры — это гипотетический объект, который фонтанирует веществом, а не поглощает его. Для этого нужны настолько экстремальные условия, что известные математические методы перестают работать (также как в случае с центром чёрной дыры); достаточно сказать, что никто не ожидает создания белых дыр в лаборатории. Никогда. Гут и Фархи обнаружили фундаментальный изъян в работах по созданию вселенных.
Ряд исследовательских групп предложили возможные способы для преодоления обнаруженной проблемы. Гут и Фархи совместно с Джемалом Гувеном выяснили, что если инфляционное зёрнышко образуется с помощью процесса квантового туннелирования (аналогичного тому, что обсуждалось в контексте ландшафтной вселенной), сингулярности белой дыры можно избежать; однако вероятность квантового туннелирования настолько ничтожна, что нет никакого шанса, что оно произойдёт за какое-нибудь разумное время. Группа японских физиков, куда входили Нобуюки Сакаи, Кен-ичи Накао, Хидеки Ишихара и Макото Кобаяши, показала, что магнитный монополь — гипотетическая частица, у которой есть только один полюс обычного магнита, либо северный, либо южный — может послужить катализатором инфляционного расширения без сингулярностей; но за почти сорок лет интенсивных поисков никому не удалось обнаружить хотя бы одну такую частицу.[61]
На сегодняшний день ситуация такова, что дверь в мир создания новых вселенных приоткрыта, но лишь на чуть-чуть. Учитывая, что процесс создания в значительной мере основан на гипотетических элементах, будущие исследования могут захлопнуть эту дверь навсегда. Но если этого не случится — или, возможно, если последующие исследования предъявят веские доводы в пользу возможности создания вселенных — останется ли ещё мотивация для занятия этим? Зачем создавать вселенную, если нет возможности её увидеть или взаимодействовать с ней, или даже узнать наверняка, что она получилась? Андрей Линде, знаменитый не только благодаря своим достижениям в космологии, но и своим чувством юмора, заметил, что соблазн сыграть роль Бога просто невозможно будет преодолеть.
Я не знаю, как это будет. Безусловно, было бы полным восторгом обладать таким всеобъемлющим пониманием законов природы, что можно было бы заново проиграть самые важные события. Однако я подозреваю, что к тому времени, когда можно будет серьёзно рассматривать создание вселенной — если такое время вообще когда-нибудь наступит — наши научные и технологические достижения приведут ко многим другим красивым открытиям, результаты которых можно будет не только вообразить, но по-настоящему экспериментально проверить, так что создание ускользающих вселенных станет гораздо менее интересным.
Интерес к подобного рода занятиям был бы гораздо сильнее, если бы мы поняли, как сотворить вселенную, которую можно наблюдать или вступать с ней в контакт. Для «реальной» вселенной, в обычном смысле вселенной, составленной из стандартных ингредиентов в виде пространства и времени, материи и энергии, у нас нет какой-либо стратегии подобных действий, что согласуется с нашим настоящим пониманием законов физики.
Но что если отложить в сторонку реальные вселенные и задуматься о вселенных виртуальных?
Субстанция мышления
Пару лет назад я заболел таким сильным гриппом и так температурил, что у меня начались галлюцинации, гораздо более реальные, чем обычный ночной кошмар. В одной из них я оказался в группе людей, сидящих в пустой комнате в отеле, и у меня начались галлюцинации внутри моей собственной галлюцинации. Я был абсолютно уверен, что прошли дни и недели до того момента, как я вернулся обратно в исходную галлюцинацию, в которой я с удивлением узнал, что прошло совсем немного времени. Каждый раз, когда я чувствовал, что уплываю обратно, в ту комнату, я начинал отчаянно сопротивляться, потому что из предыдущего опыта знал, что там всё будет восприниматься по-настоящему, и я буду не в состоянии понять, что всё вокруг обман, до тех пор, пока не вернусь в исходную галлюцинацию, где снова с ужасом осознаю, что то, что казалось реальностью, было иллюзией. Периодически, когда температура падала, я возвращался в обычное состояние и понимал, что все эти перемещения происходили в моём бурлящем разуме.
Обычно я не обращаю внимания на болезни и температуру. Но этот случай придал осязаемости тому, что обычно я воспринимал весьма отвлечённо. Наше понимание реальности более тонкое, чем диктуется нашим повседневным опытом. Измените чуть-чуть обычную деятельность мозга, и фундамент реальности может неожиданно сдвинуться; хотя внешний мир останется прежним, изменится наше восприятие. Возникает классический философский вопрос. Поскольку весь наш опыт фильтруется и анализируется нашим мозгом, как можно быть уверенным, что мы действительно воспринимаем мир таким, какой он есть? Философы любят задавать этот вопрос в следующем виде: откуда вам знать, что вы читаете это предложение, а не плаваете в каком-нибудь контейнере на удалённой планете, а инопланетные учёные не стимулируют ваш мозг, дабы ваши мысли и переживания казались вам настоящими?
Такие вопросы являются центральными в эпистемологии — философском течении, изучающем из чего состоит знание, то, как мы его приобретаем, и почему мы уверены, что мы что-то знаем. Массовая культура познакомила широкую аудиторию с этими академическими изысканиями в таких фильмах, как «Матрица», «Тринадцатый этаж» и «Ванильное небо», облекая их в развлекательную форму и заставляя задуматься над ними. Итак, если говорить по-простому, вопрос таков: откуда нам знать, что мы не в Матрице?
В сухом остатке можно сказать, что нельзя знать этого наверняка. Вы воспринимаете мир с помощью органов чувств, стимулирующих ваш мозг теми способами, чувствительность к интерпретации которых выработалась у вашей нервной системы в процессе эволюции. Если происходит искусственная стимуляция мозга, причём возникающие электрические импульсы в точности такие же, как при поглощении пиццы, чтении этого предложения или прыжках с парашютом, то восприятие будет неотличимо от реального. Наш опыт определяется происходящими в головном мозге процессами, а не тем, что инициирует эти процессы.
Если сделать ещё один шаг вперёд, то можно вообще отказаться от неудобного биологического материала. Может ли так оказаться, что все ваши мысли и переживания являются не более чем симуляцией, которая с выгодой для себя использует программное обеспечение и сложноорганизованные электрические схемы для имитации обычных функций мозга? Уверены ли вы в реальности плоти, крови и физического мира, когда весь ваш опыт — это всего лишь набор электрических импульсов, бегущих внутри гиперсложного суперкомпьютера?
Непосредственная проблема, связанная с рассмотрением таких сценариев, в том, что они легко приводят к нарастающему недоверию, которое заканчивается полным крахом сознания; мы перестаём чему-нибудь верить, даже в нашу способность к дедуктивным рассуждениям. Моя первая реакция на подобного рода утверждения состоит в просьбе оценить, насколько мощным должен быть компьютер, чтобы возникла возможность смоделировать деятельность человеческого мозга. Но если я действительно являюсь частью такого компьютерного моделирования или симуляции, то почему я должен верить тому, что написано в учебниках по нейробиологии? Эти книги тоже будут результатом моделирования, написанные смоделированными биологами, открытия которых могут определяться программой, которая осуществляет это компьютерное моделирование, и таким образом могут просто не иметь отношения к работе «настоящего» головного мозга. Само понятие «настоящий мозг» может быть компьютерным артефактом. Если вы не можете доверять вашей базе знаний, то реальность быстро теряет очертания.
Мы ещё вернёмся к этим вопросам, но я не хочу, чтобы они поглотили всё наше внимание — по крайней мере, не сейчас. Поэтому давайте пока бросим якорь. Представьте, что вы состоите из реальной плоти и крови, и я тоже, и всё, что вы и я считаем реальным в привычном смысле этого слова, является реальным. С учётом этого давайте порассуждаем о компьютерах и возможностях мозга. Какова, приблизительно, скорость обработки информации человеческим мозгом, и как она соотносится с компьютерными возможностями?
Даже если мы сумели не завязнуть в скептической трясине, такой вопрос очень труден. Деятельность головного мозга является, в основном, неисследованной территорией. Чтобы хоть немножко представить, как всё устроено, пусть даже приблизительно, приведём некоторые числа. Сетчатка человеческого глаза, тонкая пластинка, состоящая из 100 миллионов нейронов, размером меньше десятицентовой монетки, с толщиной в несколько листков бумаги, является одним из самых изученных нейронных кластеров. Специалист по робототехнике Ханс Моравец провёл оценку и выяснил, что для того, чтобы смоделированная на компьютере сетчатка выступала на равных с человеческой, она должна выполнять примерно миллиард операций в секунду. Чтобы экстраполировать объём сетчатки до объёма всего человеческого мозга, необходимо использовать множитель 100 000; Моравец предположил, что для эффективного моделирования мозга потребуется соответствующее увеличение компьютерной мощности, что составляет примерно 100 миллионов миллионов (1014) операций в секунду.{96} Независимые оценки, основанные на числе синапсов в нейронной сети мозга и их стандартной производительности, приводят к скорости, на несколько порядков превышающей результат Моравеца, примерно 1017 операций в секунду. Хотя трудно достичь большей точности, это даёт представление о характеристиках системы. Скорость моего компьютера составляет примерно миллиард операций в секунду; самые быстрые современные компьютеры могут достигать скорости примерно 1015 операций в секунду (несомненно, на момент выхода настоящей книги эта статистика уже устарела). Можно сказать, что сто миллионов ноутбуков или сто суперкомпьютеров приближаются по производительности к человеческому мозгу.
Подобные сравнения конечно же наивны: тайны человеческого мозга разнообразны, и его скорость лишь одна из главных характеристик его активности. Но практически любой согласится, что однажды мы достигнем таких компьютерных мощностей, которые сравняются и, вполне вероятно, значительно превысят мощности, данные нам от природы. Футуристы заявляют, что такие технологические скачки так сильно изменят наш мир и всё, к чему мы привыкли, что мы даже не можем это себе представить. Привлекая аналогию с явлениями, находящимися за пределами наших самых развитых физических теорий, они называют этот воображаемый барьер сингулярностью. В одном прогнозе вчерне утверждается, что преодоление компьютерами мощности человеческого мозга полностью сотрёт границу между людьми и технологиями. Некоторые верят, что мир быстро заполнится думающими и чувствующими машинами, и те из нас, кто по старинке использует старомодные биологические процессы, в плановом порядке перепишут содержание мозгов на резервные жёсткие диски, для безопасного хранения личностей и их знаний in silico в течение неограниченного срока.
Такая перспектива вполне может оказаться преувеличением. Никто не спорит о применении компьютерных мощностей, однако нам с очевидностью неизвестно, станем ли мы когда-нибудь направлять такие мощности для радикального слияния человеческого мозга и машины. Этот вопрос современен по форме, но корни его уходят в глубокую древность; человек тысячелетиями думал над тем, как он думает. Как так происходит, что внешний мир порождает наши внутренние эмоции? Вы также воспринимаете цвет, как и я? Как насчёт вашего восприятия звука и прикосновений? Чем именно является голос, который мы слышим внутри головы, этот поток внутренней речи, которым мы говорим с сознательным собой? Возникает ли он только лишь из физических процессов? Или сознание возникает в слое реальности, который выходит за пределы физического мира? Проницательные мыслители на протяжении многих веков, Платон и Аристотель, Гоббс и Декарт, Юм и Кант, Кьеркегор и Ницше, Джемс и Фрейд, Витгенштейн и Тьюринг, и многие другие, пытались выявить (или развенчать) процессы, которые оживляют мозг и создают исключительную внутреннюю жизнь, доступную посредством самоанализа.
Было разработано много великих теорий о работе человеческого мозга, которые различаются в большом и малом. Мы не собираемся углубляться в них, но с целью понимания того, куда они привели, упомянем некоторые из них: теория дуализма и её разные многочисленные варианты утверждают, что в человеческом мозге обязательно имеется принципиально нефизическая составляющая. Физикалистические теории мышления, которых тоже великое множество, отрицают подобное; наоборот, акцент ставится на то, что за каждым уникальным, субъективным опытом стоит некоторое уникальное состояние мозга. Теории функционализма идут дальше в этом направлении, предполагая, что настоящее значение для мозга имеют процессы и функции — схемы и связи между ними, — а не особенности физической среды, в которой эти процессы происходят.
Физикалисты в основном согласятся, что если вы исправно реплицируете мой мозг тем или иным способом — молекула за молекулой, атом за атомом, — конечный продукт будет действительно думать и чувствовать так же, как я. Функционалисты в основном согласятся, что если вы сосредоточитесь на структурах более высокого уровня — реплицируя все нейронные связи в моём мозгу, сохраняя при этом все мозговые процессы и изменяя только физический субстрат, в котором они происходят, — то итог будет таким же. Дуалисты же, в свою очередь, не согласятся ни с теми, ни с другими.
Очевидно, что возможность искусственных ощущений основывается на точке зрения функционализма. Центральное предположение этого подхода состоит в том, что разумная мысль не накладывается на мозг, а сама является ощущением, порождаемым информационным процессом определённого типа. Происходит ли это в биологической массе весом в полтора килограмма или внутри электрических схем компьютера, не является принципиальным. Такое предположение может оказаться неверным. Возможно, для того чтобы какой-то пучок связей осмыслил себя, ему требуется наличие субстрата из извилистого влажного вещества. Возможно, если разумная мысль призвана одушевить неодушевлённое, то нужны настоящие физические молекулы, из которых состоит мозг, а не только процессы и связи между этими молекулами. Возможно, идущие в компьютерах информационные процессы всегда будут отличаться некоторым существенным образом от активности мозга, что не позволит наделить компьютеры ощущениями. Возможно, разумная мысль является фундаментально нефизической, как того требуют различные религии, и поэтому всегда будет находиться за пределами технологических инноваций.
С появлением всё более сложных технологий эти вопросы стали острее, а путь к ответу на них более осязаемым. Ряд исследовательских групп уже предприняли начальные шаги в направлении компьютерного моделирования биологического мозга на компьютере. Например, проект «Blue Brain», совместное предприятие IBM и федерального политехнического института в Лозанне, Швейцария, посвящён моделированию деятельности мозга на самом быстром суперкомпьютере IBM, который носит имя Blue Gene. Этот суперкомпьютер является наиболее мощной версией Deep Blue, компьютера, который обыграл в 1997 году чемпиона мира по шахматам Гарри Каспарова. Нельзя сказать, что проект «Blue Brain» чем-то отличается от описанных выше сценариев. Основываясь на подробнейшем анатомическом изучении реального мозга, исследователи получают более точные данные о клеточной, генетической и молекулярной структуре нейронов и образуемых ими связях. Цель проекта — перевести эти данные (на данный момент это касается в основном клеточного уровня) на уровень цифрового моделирования на компьютере Blue Gene. На данный момент исследователи обработали результаты десятков тысяч экспериментов, сфокусированных на крохотном отделе головного мозга крыс, так называемой неокортикальной структуре, с целью разработки трёхмерной компьютерной симуляции примерно 10 000 нейронов, сообщающихся посредством около 10 миллионов связей. Сравнение реакции неокортикальной структуры живой крысы и компьютерной симуляции демонстрируют обнадёживающую уверенность в синтетической модели. Это далеко не 100 миллиардов нейронов в типичном человеческом мозге, но руководитель проекта, нейробиолог Генри Маркрам, говорит, что до 2020 года проект «Blue Brain», увеличив скорость обработки информации, которая по прогнозам вырастет более чем в миллион раз, позволит достичь полного компьютерного моделирования человеческого мозга. Цель проекта «Blue Brain» не в искусственном интеллекте, а в создании нового исследовательского инструмента для развития способов лечения различных форм психических расстройств; однако, Маркрам рискнул заявить, что после завершения проекта у «Blue Brain» появится способность говорить и чувствовать.
Независимо от результатов, подобные практические исследования крайне важны для теорий работы мозга; я совершенно уверен, что вопрос о том, какая из этих теорий окажется правильной, если такое случится, не может быть решён на основе лишь гипотетических умозаключений. На практике проблемы сразу выявляются. Предположим, что однажды компьютер открыто заявит, что стал разумным — каким образом мы сможем убедиться, что это действительно так? У меня нет никакой возможности убедиться в правильности подобных заявлений, даже если их делает моя жена. И наоборот, она не может убедиться, что я разумен. Всё очень сильно усложняется, поскольку сознание является личностным делом. Однако, так как человеческие отношения убедительно свидетельствуют о том, что другие тоже разумны, солипсизм быстро превращается в абсурд. Компьютерные отношения могут однажды достичь похожей точки. Общаясь с компьютерами, утешая и обихаживая их, в один прекрасный момент мы можем убедиться, что простейшее объяснение их проявившегося разумного компьютерного самосознания в том, что они действительно разумны и осознают себя.
Давайте примем точку зрения функционалистов и посмотрим, куда она нас приведёт.
Смоделированные вселенные
Если компьютерный разум когда-нибудь будет создан, то скорее всего возникнет желание поместить думающие машины в искусственные человеческие тела, создав механических существ — роботов, которые будут интегрированы в окружающую реальность. Но сейчас меня интересуют другие «существа» — те, кто является совокупностью электрических импульсов, возникающих при программировании смоделированных сред, населённых смоделированными существами, которые живут исключительно внутри компьютерного оборудования. Поэтому вместо персонажей «Звёздных войн» C-3PO или Дэйта перенесём наше внимание на виртуальный мир игр Sims или Second Life и представим, что их жители осознают себя и обладают чутким умом. История технологических достижений говорит, что, шаг за шагом, компьютерные симуляции будут достигать всё большего правдоподобия, позволяя физическим и опытным характеристикам смоделированных миров достичь убедительного уровня схожести и реализма. Тот, кто будет управлять данной симуляцией, будет решать, следует ли искусственным существам знать о том, что они существуют внутри компьютера; возможно, что те искусственные люди, которые заподозрят, что их мир является продвинутой компьютерной программой, будут схвачены искусственными медбратьями в белых халатах и помещены в искусственный госпиталь. А может быть, подавляющее большинство искусственных существ сочтут возможность своего существования внутри компьютерной симуляции слишком нелепой, чтобы об этом беспокоиться.
Возможно, что ваша реакция сейчас именно такая. Даже если вы допускаете возможность искусственного разума, вы, вероятно, склоняетесь к мнению, что компьютерное моделирование целой цивилизации или даже небольшого сообщества является архисложной задачей, требующей выходящего за рамки вычислительных возможностей мастерства. С этой точки зрения имеет смысл проанализировать следующие несколько чисел. Скорее всего, наши далёкие потомки не будут экономить материю при создании огромных вычислительных сетей. Тогда давайте дадим полёт фантазии. Будем мыслить широко. Учёные сделали оценку, что современный высокоскоростной компьютер размером с Землю будет выполнять от 1033 до 1042 операций в секунду. Для сравнения заметим, что если наша предыдущая оценка в 1017 операций в секунду для человеческого мозга точна, то в среднем человеческий мозг выполняет 1024 операций в течение ста лет жизни. Умножьте это примерно на 100 миллиардов людей, которые когда-либо ходили по этой планете, и полное число операций, выполненных всеми когда-либо существовавшими человеческими мозгами со времён Люси (мои друзья археологи утверждают, что правильно надо говорить об «Арди»), будет равно 1035. Взяв консервативную оценку в 1033 операций в секунду, мы видим, что коллективная вычислительная мощность человеческого рода может быть достигнута менее чем за две минуты на компьютере размером с Землю.
И это если брать за основу современные технологии. Квантовые вычисления используют совсем другие возможности, содержащиеся в волне квантовой вероятности, поэтому, при необходимости проводить одновременно много разных вычислений, они могут увеличить скорость процесса в невероятное число раз. Хотя мы по-прежнему далеки от создания такого приложения квантовой механики, исследователи оценили, что квантовый компьютер размером с лаптоп обладает потенциалом обработать помыслы всех людей с момента возникновения нашей расы за малую долю секунды.
Чтобы смоделировать не просто отдельные умы, но также их взаимодействия между собой и с окружающей средой, требование к вычислительному объёму вырастает на многие порядки величины. Однако хитроумная симуляция может изловчиться и срезать вычислительные углы с минимальной потерей качества. Смоделированные люди на смоделированной Земле совсем не будут скучать, если компьютер будет моделировать только то, что находится внутри космического горизонта. У нас нет возможности заглянуть за это расстояние, поэтому компьютер может спокойно проигнорировать его. Можно поступить ещё смелее и моделировать звёзды вокруг Солнца только во время смоделированных ночей, и только когда благодаря смоделированному ветру небо очищается от облаков. Когда никто не смотрит, небесный компьютерный симулятор может отдохнуть от создания соответствующих стимулов у всякого, кто мог бы взглянуть наверх. Достаточно хорошо структурированная программа будет следить за ментальным состоянием и намерениями своих смоделированных обитателей, и поэтому будет предугадывать и отвечать нужным образом на любое назревающее желание созерцать звёзды. То же самое справедливо для смоделированных клеток, молекул и атомов. По большей части, они будут необходимы для смоделированных специалистов той или иной научной дисциплины, и только тогда, когда эти специалисты непосредственно изучают эти экзотические миры. Таким образом, вычислительно менее затратная копия привычной реальности, которая выходит на требуемый уровень детализации симуляции по мере необходимости, будет вполне адекватной.
Такие смоделированные (или симулированные) миры будут убедительно подтверждать мнение Уилера о первичности информации. Создайте контуры, переносящие правильную информацию, и вы создадите параллельные реальности, которые столь же реальны для своих обитателей, как наша реальность для нас. Эти симуляции составляют восьмое множество вселенных, которое я буду называть смоделированной мультивселенной.
Вы живёте в симуляции?
Идея о компьютерном моделировании вселенных имеет долгую историю, уходящую корнями в идеи, выдвинутые в 1960-х годах пионером компьютеростроения Конрадом Цузе и цифровым гуру Эдвардом Фредкином. Я работал в IBM каждое лето на протяжении пяти лет учёбы в старших классах школы и колледжа; мой босс, не так давно почивший Джон Кок, сам был известным компьютерным специалистом и часто обсуждал идею Фредкина о том, что вселенная — это не что иное как гигантский компьютер, напряжённо считающий на чём-то вроде космического Фортрана. Эта идея поразила меня в плане того, как цифровая парадигма была доведена до абсурдного предела. За все эти годы я совсем не вспоминал о ней — до тех пор, пока мне не встретилось, совсем недавно, простое, но любопытное заключение оксфордского философа Ника Бострома.
Чтобы понять точку зрения Бострома (на которую также ссылается Моравец), сравним между собой степень трудности создания реальной вселенной и трудность создания смоделированных вселенной. Мы видели, что для создания реальной вселенной имеется множество препятствий. Если нам повезёт, мы не увидим плоды нашего труда, и это, в первую очередь, ставит вопрос о том, что побудило нас заняться этим.
Компьютерное моделирование вселенной — это совсем другое дело. Эволюция в направлении всё усложняющихся компьютеров со всё более увеличивающейся производительностью происходит неумолимо. Даже при современных рудиментарных технологиях мы не можем не поддаться искушению создавать смоделированные среды обитания; а если появятся ещё бо́льшие возможности — вообще трудно представить себе что-то более увлекательное. Вопрос не в том, создадут ли наши потомки смоделированные компьютерные миры. Мы уже делаем это. Но нам неведомо, насколько они будут реалистичными. Если возникнут внутренние препятствия для создания искусственного разума, то все вопросы снимаются. Однако Бостром, предполагая, что реалистичные симуляции возможны, приходит к следующему простому наблюдению.
Наши потомки будут готовы к созданию колоссального количества смоделированных вселенных, заполненных большим числом сознательных, разумных обитателей. Если вернувшись домой поздно вечером, можно будет расслабиться и запустить программу по созданию вселенных, то легко представить, что наши потомки будут делать это довольно часто. Давайте подумаем, к чему может привести подобный сценарий. В один прекрасный день космическая перепись, которая учитывает все разумные существа, может обнаружить, что число людей из плоти и крови бледнеет по сравнению с числом сделанных из чипов и байтов или их будущих аналогов. И, рассуждает Бостром, если отношение смоделированных людей к реальным людям станет колоссальным, то беспощадная статистика укажет, что мы не живём в реальной вселенной. Все цифры будут в пользу того, что вы, я и все остальные живут в симуляции, созданной, например, будущими историками, увлекающимися историей Земли XXI века.
Вы можете возразить, что сейчас мы стремглав несёмся в зыбучие пески, куда в самом начале договорились не ходить. Как только мы пришли к выводу, что существует высокая вероятность того, что мы живём в компьютерной симуляции, как можно доверять чему-то, в том числе тем самым рассуждениям, которые привели нас к этому заключению? Наша уверенность во многом пошатнётся. Взойдёт ли завтра Солнце? Возможно, если тот, кто управляет симуляцией, не станет выдёргивать шнур из розетки. Можно ли доверять нашим воспоминаниям? Наверное можно, если тот, кто стучит по клавиатуре, не склонен подправлять их время от времени.
Тем не менее Бостром замечает, что вывод о том, что мы живём в симуляции, не полностью обрубает возможность для понимания нами настоящей, основополагающей реальности. Даже если мы верим, что живём в симуляции, мы по-прежнему можем установить одно свойство, которым определённо обладает лежащая в основе реальность: она допускает реалистичные компьютерные симуляции. В конце концов мы верим, что мы в такой и находимся. Скептицизм, порождённый подозрением о смоделированном характере нашей природы, находится в одном ряду с самим этим знанием, и поэтому никак не может его пошатнуть. Хотя в самом начале нашего обсуждения было полезно бросить якорь и объявить реальным всё, что выглядит реальным, такой шаг не был необходимым. Одна только логика не может гарантировать, что мы не в компьютерной симуляции.
Единственный способ избежать заключения о том, что мы можем оказаться в симуляции, состоит в поиске внутренних противоречий в этих рассуждениях. Возможно, ощущения не поддаются симуляции — тогда на этом точка. Может быть, продолжает Бостром, цивилизации по пути к технологическому совершенству, необходимому для создания разумных симуляций, неизбежно обратят эту технологию против себя, что приведёт к саморазрушению. Может быть, когда наши далёкие потомки будут способны создавать смоделированные вселенные, они не станут этого делать, например, по этическим соображениям, или просто потому, что другие текущие невероятные дела окажутся гораздо более интересными и поэтому, как отмечалось в случае с созданием вселенной, интерес к симуляции вселенных окажется на обочине.
Есть и другие лазейки, но достаточно ли их, чтобы выйти из положения?[62] Если нет, то вам, возможно, захочется немножко разнообразить вашу жизнь, как-то отличиться. Кто бы ни управлял симуляцией, в какой-то момент он обязательно устанет от статистов. Быть звездой — наилучший путь к долговечности.{97}
Взгляд за пределы симуляции
Если бы вы жили в симуляции, то смогли бы это понять? Ответ во многом зависит от того, кто управляет вашей симуляцией — назовём его Симулятором — и от того, каким образом запрограммирована ваша симуляция. Симулятор, например, может раскрыть вам свой секрет. Однажды, принимая душ, вы можете услышать мягкое «динь-динь» и, промыв глаза от шампуня, увидите окно на парящем экране монитора, в котором возникнет улыбающийся Симулятор. Может быть, это откровение случится в мировом масштабе с гигантскими открывшимися окнами и гремящим на всю планету голосом, объявляющим, что на самом деле на небесах существует Всемогущий Программист. Но даже если ваш Симулятор не склонен к саморекламе, то существуют менее очевидные способы дать подсказку.
Симуляции, приводящие к разумным существам, определённо достигнут порога минимальной точности, но, как и в случае с дизайнерской одеждой и дешёвой подделкой, качество и самосогласованность будут скорее всего варьироваться. Например, один из подходов к программированию симуляций — назовём его «эмерджентной, или проявляющейся стратегией» — будет состоять в использовании массы накопленного человечеством знания с осмысленным привлечением разных научных положений в зависимости от контекста. Столкновения между протонами в ускорителях частиц будут смоделированы с помощью квантовой теории поля. Траектория футбольного мяча будет смоделирована с помощью законов Ньютона. Реакция матери, наблюдающей за первыми шагами своего ребёнка, будет смоделирована совместными достижениями биохимии, физиологии и психологии. Действия лидеров правительства будут заимствованы из политики, истории и экономики. Будучи кусочно-собранной из различных подходов, сфокусированных на различных аспектах смоделированной реальности, проявляющаяся стратегия потребует внутренней самосогласованности для переноса процессов, номинально сконструированных в одном мире, в другой мир. Психиатру не надо знать клеточные, химические, молекулярные, атомные и субатомные процессы, лежащие в основе активности человеческого мозга — и для психиатрии это несомненное благо. Но при симуляции личности перед эмерджентной стратегией будет стоять задача самосогласованным образом объединить грубые и тонкие уровни информации, обеспечив, например, что эмоциональные и познавательные функции будут оптимально скоординированы с психохимическими данными. Такой тип пограничного сплетения характерен для всех явлений и всегда подталкивал науку к поиску более глубоких объяснений.
Симуляторы, которые используют эмерджентные стратегии, должны устранить несоответствия, возникающие при применении различных методов, и должны гарантировать, что сплетение происходит гладким образом. Это может потребовать подкруток и поправок, которые для обитателя симуляции проявятся в виде неожиданных изменений в окружающей среде без каких-либо очевидных причин и объяснений. Сплетение может оказаться не совсем эффективным; возникающие нестыковки могут нарастать со временем, принимая угрожающие размеры, так что мир окажется непоследовательным, и симуляция разрушится.
Возможный способ обойти эти проблемы состоит в использовании другого подхода — назовём его «ультра-редукционистской стратегией» — когда симуляция выполняется согласно одному-единственному набору фундаментальных уравнений, что, как представляется физикам, имеет место в случае реальной вселенной. Роль исходных данных в таких симуляциях играет математическая теория материи и фундаментальных взаимодействий, а также выбор «начальных условий» (как всё устроено в начальный момент симуляции); затем компьютер просчитает всё вперёд во времени, избегая тем самым проблем сплетения характеристик из эмерджентной стратегии. Однако, симуляции этого типа столкнутся со своими собственными вычислительными проблемами, и даже не с непосильным симулированием «всего на свете», а уже при симуляции поведения отдельных частиц. Если уравнения, с которыми будут оперировать наши потомки, будут похожи на современные — с непрерывно изменяющимися числами — то симуляции неизбежно будут использовать приближённые методы. Чтобы точно отслеживать число при его непрерывном изменении, понадобится знать его значения с точностью до бесконечного числа знаков после запятой (например, если такая величина непрерывно изменяется, скажем, от 0,9 до 1, она будет принимать последовательно такие значения как 0,9, 0,95, 0,958, 0,9583, 0,95831, 0,958317 и так далее, вплоть до произвольного знака после запятой, для достижения абсолютной точности). Именно этого компьютер с ограниченным ресурсом не может себе позволить: ему просто не хватит времени и памяти. Поэтому, даже если использовать самые фундаментальные уравнения, всё равно возможно, что компьютерные вычисления будут приближёнными, что даст растущую со временем ошибку.[63]
Конечно же, под «ошибкой» я подразумеваю разницу между тем, что происходит в симуляции, и описанием, следующим из самых точных физических теорий, которые находятся в распоряжении симулятора. Но те, кто подобно вам находится внутри симуляции, будут считать математические правила, управляющие компьютером, законами природы. Тогда вопрос не в том, насколько точно используемые в компьютере математические законы моделируют внешний мир, ведь считается, что находясь внутри симуляции вы не видите внешнего мира. Проблема смоделированной вселенной в том, что когда компьютерные необходимые приближения начинают применяться к точным математическим уравнениям, вычисления быстро становятся нестабильными. Ошибки округления, накапливающиеся после большого количества вычислений, могут привести к противоречиям. Вы и другие смоделированные учёные окажутся свидетелями аномальных результатов в экспериментах; милые сердцу законы начнут приводить к неточным предсказаниям; измерения, которые всегда давали единственный и всеми подтверждаемый результат, начнут выдавать разные ответы. По прошествию времени, вы и ваши смоделированные коллеги начнёте думать, подобно вашим предкам из предыдущих столетий и тысячелетий, что ваша окончательная теория отнюдь не является окончательной. Все вместе вы тщательно перепроверите теорию, возможно, придумаете новые идеи, уравнения и принципы, более точно описывающие имеющиеся данные. Но, предполагая, что ошибки не приведут к таким противоречиям, которые обрушат программу, в какой-то момент вы упрётесь в стену.
После разностороннего поиска возможных объяснений, ни одно из которых не будет способно полностью объяснить произошедшее, дерзкий мыслитель может выдвинуть радикально иную идею. Если континуальные физические законы, развиваемые в течение многих тысячелетий, принять за цифровые начальные данные для мощного компьютера и использовать для создания смоделированной вселенной, то ошибки от неизбежных приближений приведут к аномалиям того же самого типа, что и наблюдаются. «Вы считаете, что мы живём в компьютерной симуляции?», — спросите вы. «Да», — ответит ваш дерзкий коллега. «Да вы с ума сошли!», — возмутитесь вы. «Да? А вы взгляните», — ответит он и развернёт к вам монитор с изображённым смоделированным миром, запрограммированным им с помощью тех же самых фундаментальных законов физики, и — затаив дыхание от первой встречи с смоделированным миром — вы увидите, как смоделированные учёные размышляют над теми же самыми странными данными, которые вызвали затруднения и у вас.{98}
Конечно, если Симулятор задумает замаскироваться более тщательно, он может выбрать более агрессивную тактику. Когда начнут возникать противоречия, он может перезапустить программу и стереть аномалии из памяти обитателей. Поэтому, скорее всего будет преувеличением утверждать, что смоделированная реальность проявит свою истинную природу посредством глюков и перебоев. И ещё сложнее утверждать, что противоречия, аномалии, вопросы без ответа и забуксовавший прогресс будут отражать нечто большее, чем наши собственные научные неудачи. Разумная интерпретация при обнаружении подобных явлений будет состоять в том, что мы, учёные, должны работать ещё упорнее и проявлять больше фантазии для поиска объяснений. Однако, из этого причудливого сценария напрашивается следующий серьёзный вопрос. Если мы когда-нибудь действительно создадим смоделированный мир с явно разумными обитателями, то уместно ли полагать, что мы занимаем особое место в истории научно-технического прогресса — что мы стали самыми первыми создателями разумных симуляций? Могли бы стать — но если стремиться учитывать все варианты, следует рассматривать альтернативные сценарии полной картины бытия, которые не выделяют человечество каким-то особенным образом. Причём уже имеется готовый сценарий, отвечающий всем требованиям. Как только мы убедимся, что разумные симуляции возможны, то руководящий принцип «заурядности», обсуждавшийся в главе 7, скажет, что такая симуляция не единственна, что их целый бурлящий океан под названием «смоделированная мультивселенная». Хотя созданная нами симуляция может стать знаменательным событием в той ограниченной области, к которой мы имеем доступ, в контексте всей смоделированной мультивселенной в этом нет ничего особого, и до нас такое происходило несметное количество раз. Как только мы примем эту идею, нам придётся допустить, что мы тоже можем находиться внутри симуляции, поскольку именно таков статус абсолютного большинства разумных существ в смоделированной мультивселенной.
Указания на искусственный разум и смоделированные миры дают почву для размышления о природе вашей собственной реальности.
Вавилонская библиотека
Во время моего первого семестра в колледже я записался на вводный курс по философии, который читал уже почивший Роберт Нозик. С самой первой лекции началось что-то невероятное. Нозик заканчивал писать свою объёмную книгу «Философские разъяснения» и использовал курс для отработки многих важных аргументов. Практически каждое занятие потрясало моё представление о мире, иногда весьма энергично. Для меня это стало неожиданным опытом — я думал, что сотрясение основ реальности исключительно прерогатива курсов по физике. Однако была существенная разница. Лекции по физике подрывали привычные взгляды на вещи посредством рассмотрения явлений, происходящих в совершенно незнакомых областях, когда объекты движутся быстро, либо являются очень тяжёлыми, либо имеют фантастически маленький размер. Лекции по философии ставили под сомнения привычные взгляды, раскачивая устои ежедневного опыта. Откуда нам знать, что существует реальный мир? Должны ли мы доверять нашим ощущениям? Что связывает молекулы и атомы, сохраняя нашу личность с течением времени?
Как-то раз после занятий Нозик спросил меня, чем я интересуюсь, и я браво заявил, что хочу изучать квантовую гравитацию и единые теории. Обычно на этом разговор и заканчивался, но Нозик использовал это как возможность раскрыть горизонты молодому человеку. «Что движет твоим интересом?» — спросил он. Я ответил, что хочу найти вечные истины, чтобы понять, почему всё устроено так, а не иначе. Наивно и хвастливо, конечно же. Но Нозик сначала внимательно меня выслушал, а потом развил эту идею дальше. «Допустим, что ты построил единую теорию, — сказал он. — Действительно ли она даст ответы на твои вопросы? Может, ты по-прежнему будешь задумываться, почему именно эта теория, а не другая, оказалась правильной теорией вселенной?» Конечно же, он был прав, но я ответил, что в процессе поиска объяснений может наступить момент, когда мы должны будем принять определённые вещи как данность. Именно этого и ждал от меня Нозик; в книге «Философские разъяснения» он развивал альтернативную точку зрения. Она основана на том, что он называл принципом изобилия, и является попыткой строить объяснения без «принятия определённых вещей как данности», без принятия чего-либо как истины сверху.
Стоящий за этой уловкой философский манёвр совершенно очевиден: следует ослабить вопрос. Если хотите избежать объяснения, почему одна теория чем-то выделена среди других, то тогда не выделяйте её. Нозик предлагает, чтобы мы считали, будто являемся частью мультивселенной, которая охватывает все возможные вселенные.{99} Эта мультивселенная будет включать в себя не только альтернативные эволюции, возникающие из квантовой мультивселенной, или множество пузырьков-вселенных из инфляционной мультивселенной, или возможные струнные миры ландшафтной мультивселенной. Такие мультивселенные сами по себе не будут удовлетворять идее Нозика, потому что вы по-прежнему будете спрашивать: почему квантовая механика? почему инфляция? почему теория струн? Наоборот, возьмите вообще любую возможную вселенную — она может состоять из обычных атомов, но столь же хорошо подойдёт и вселенная, сделанная исключительно из расплавленного сыра моцарелла — и у неё будет своё место в подходе Нозика.
Это будет последняя из рассматриваемых нами мультивселенных, потому что она самая необъятная из всех — настолько необъятная, насколько это возможно. Любая из когда-либо предложенных мультивселенных или тех, которые когда-нибудь будут предложены, сама состоит из возможных вселенных, и поэтому будет являться частью этого мегаконгломерата, который я буду называть окончательной мультивселенной. Если в рамках данного подхода вы зададитесь вопросом, почему наша вселенная управляется законами, открытыми нашими исследованиями, то ответ сведётся к антропности: там, дальше, существуют другие вселенные, всевозможные вселенные на самом деле, а мы живём в нашей вселенной, потому что она принадлежит к числу тех, которые поддерживают нашу форму жизни. В других вселенных, пригодных для жизни — а их достаточно много, поскольку мы, безусловно, сможем выжить при достаточно малых изменениях фундаментальных физических параметров — есть люди, похожие на нас, задающиеся тем же вопросом. Точно такой же ответ справедлив и для них. Смысл в том, что признак существования никак не выделяет вселенную, потому что в окончательной мультивселенной действительно существуют все возможные вселенные. Отпадает сам вопрос, почему один набор законов описывает реальную вселенную — нашу — а другие наборы являются бесплодными абстракциями. Бесплодных законов не существует. Любой набор законов описывает свою реальную вселенную.
Любопытно, что Нозик отметил, что внутри его мультивселенной существует вселенная, состоящая из ничего. Абсолютного ничего. Не пустое пространство, а ничто, о котором вопрошал Готфрид Лейбниц в знаменитой фразе «Почему существует нечто, а не ничто?». Нозик не мог знать, что для меня это утверждение имело особый смысл. Когда мне было лет десять или одиннадцать, я наткнулся на фразу Лейбница и сильно озаботился этим вопросом. Я расхаживал по своей комнате, пытаясь ухватить, что значит ничто, часто заложив при этом одну руку за голову, думая, что попытка сделать невозможное — увидеть свою руку — поможет мне понять смысл полного отсутствия. Даже теперь, пытаясь представить абсолютное истинное ничто, небытие, я падаю духом. Полное ничто, с привычной нам позиции существующего нечто, есть самое полное отсутствие чего бы то ни было. И поскольку кажется, что ничто — это настолько проще, чем нечто — никаких законов в действии, никакой материи в игре, никакого пространства для заселения, никакого времени в течении — вопрос Лейбница попадает как раз в точку. Почему бы небытию не существовать? Небытие было бы бесспорно превосходным.
В окончательной мультивселенной действительно существует вселенная, состоящая из ничего. Насколько можно судить, ничто являет собой совершенно логическую возможность, поэтому такая вселенная обязана быть включена в мультивселенную, охватывающую все вселенные. Тогда ответ Нозика на вопрос Лейбница таков, что в окончательной мультивселенной нет дисбаланса между нечто и ничто, требующего особого объяснения. Вселенные обоих типов являются частью этой мультивселенной. Вселенная из ничего ничем не привлекает к себе особого внимания. И только потому, что мы, люди, являем собой нечто, вселенная из ничего ускользает от нас.
Теоретик, приученный говорить на языке математики, понимает всеобъемлющую мультивселенную Нозика как вселенную, где все возможные уравнения реализуются физически. Это такая версия рассказа Хорхе Луиса Борхеса «Вавилонская библиотека», в которой книги Вавилона написаны на языке математики и поэтому содержат все возможные осмысленные, непротиворечивые строчки из математических символов.[64] Некоторые из книг содержат известные нам формулы, такие как уравнения общей теории относительности и квантовой механики в приложении к известным в природе частицам. Однако, узнаваемые строки математических символов будут встречаться крайне редко. Большинство книг содержит уравнения, никем до сих пор не написанные, уравнения, которые в обычных условиях будут считаться чистой абстракцией. Идея окончательной мультивселенной в том, чтобы отказаться от этой привычной точки зрения. Больше не будет ситуации, когда большинство уравнений бездействуют, лёжа в спячке, и лишь несколько удачливых соотношений каким-то чудесным образом встроены в жизнь посредством физической реализации. Наоборот, каждая книга в библиотеке математического Вавилона является реальной вселенной.
Предложение Нозика, если оформить его математически, даёт конкретный ответ на давно обсуждаемый вопрос. В течение столетий математики и философы задавались вопросом — математика изобретена или открыта? Витают ли математические понятия и законы где-то рядом, в ожидании отважного исследователя, который на них наткнётся? Или, поскольку этот исследователь скорее всего сидит за письменным столом, с карандашом в руках, быстро черкая заумные символы на бумаге, не являются ли полученные математические понятия и законы изобретением нашего разума в поиске порядка и системы?
На первый взгляд огромное количество математических достижений, нашедших своё применение в физических явлениях, убедительно свидетельствует в пользу того, что математика реальна. Примеров много. В широком диапазоне от общей теории относительности до квантовой механики физики обнаружили, что многочисленные математические открытия как будто по заказу изготовлены для физических приложений. Простой, но впечатляющий пример — это предсказание позитрона (античастицы электрона) Полем Дираком. В 1931 году при решении квантовых уравнений, описывающих движение электрона, Дирак обнаружил, что в математических выкладках возникает «постороннее» решение, которое описывает движение частицы, тождественной электрону, но с положительным электрическим зарядом (напомним, что у электрона заряд отрицательный). В 1932 году эта самая частица была обнаружена Карлом Андерсоном при тщательном изучении космических лучей, бомбардирующих Землю из космоса. То, что начиналось как манипуляции Дирака с математическими символами на бумаге, завершилось экспериментальным открытием первой частицы антиматерии в лаборатории.
Однако, скептик может возразить, что математику задаём именно мы. Мы сформировались в ходе эволюции таким образом, чтобы уметь находить закономерности в окружающей среде; чем лучше у нас это получается, тем выше наши шансы найти очередную порцию пищи. Математика как системный язык родилась из нашей биологической совместимости. С этим языком мы смогли систематизировать поиск новых закономерностей, выйдя за рамки тех, что обеспечивали просто банальное выживание. Но математика, подобно другим инструментам, развитым и освоенным нами в течение прошедших столетий, является человеческим изобретением.
Мой взгляд на математику периодически меняется. Когда я погружён в математическое исследование, которое хорошо продвигается, то часто чувствую, что этот процесс является открытием, а не изобретением. Я не знаю ничего более возбуждающего, чем наблюдать, как разрозненные кусочки математического паззла соединяются в единую непротиворечивую картину. Когда такое происходит, возникает чувство, что эта картина всегда там была, подобно тому как широкий простор выплывает из утреннего тумана. С другой стороны, когда я более объективно оцениваю математику, то моя уверенность пропадает. Математическое знание — это литературный продукт общения знающих людей на необычайно точном языке математики. И подобно литературе, написанной на одном из естественных мировых языков, математическая литература является продуктом человеческой изобретательности и фантазии. Это совсем не значит, что другие разумные формы жизни не могут прийти к такому же математическому результату, что и мы; очень даже могут. Однако, случись такое, это явилось бы отражением подобия нашего опыта (как необходимости считать, торговать, выживать и так далее), и поэтому вряд ли может считаться доказательством трансцендентного существования математики.
Несколько лет назад, в публичных дебатах по этому поводу, я сказал, что мог бы себе представить встречу с инопланетной формой жизни, во время которой, отвечая на вопрос о наших научных теориях, инопланетянин сказал: «А, математика… да, мы немного её поизучали. Сначала показалась многообещающей, но, в конце концов, завела в тупик. Давайте я покажу вам, как это на самом деле работает». Но, возвращаясь к моим собственным колебаниям, я на самом деле не знаю, как закончил бы своё предложение инопланетянин, а учитывая достаточно широкое определение математики (например, логические заключения, вытекающие из ряда предположений), я даже не уверен, ответы какого типа не свелись бы к математике.
Окончательная мультивселенная избавлена от двусмысленности в этом вопросе. Любая математика реальна в том смысле, что любая математика описывает какую-то реальную вселенную. Внутри этой мультивселенной любая математика так или иначе реализуется. Вселенная, управляемая уравнениями Ньютона и населённая исключительно твёрдыми бильярдными шарами (без какой-либо дополнительной внутренней структуры), является реальной вселенной; пустая вселенная с 666 пространственными измерениями, управляемая высокоразмерной версией уравнений Эйнштейна, тоже является реальной вселенной. Если окажется, что инопланетяне правы, то будут вселенные, описание которых не является математическим. Однако давайте пока оставим такой вариант в сторонке. Мультивселенной, реализующей все математические уравнения, будет достаточно, чтобы занять наше внимание; именно это и даёт нам окончательная мультивселенная.
Логическое обоснование мультивселенной
Отличие окончательной мультивселенной от других рассмотренных нами ранее проектов параллельных миров и является той причиной, которая привела нас к её рассмотрению. Теории мультивселенных из предыдущих глав не задумывались в качестве решения какой-то проблемы или как ответ на какой-нибудь вопрос. Некоторые из них дают ответы на вопросы или, по крайней мере, претендуют на ответы, но их не разрабатывали для этих целей. Как мы видели, некоторые теоретики полагают, что квантовая мультивселенная разрешает проблему квантовых измерений; некоторые полагают, что циклическая мультивселенная поднимает вопрос начала времени; некоторые полагают, что бранная мультивселенная проясняет, почему гравитация так сильно слабее других взаимодействий; некоторые полагают, что ландшафтная мультивселенная может объяснить наблюдаемое значение тёмной энергии; некоторые полагают, что голографическая мультивселенная объясняет данные по столкновениям тяжёлых атомных ядер. Но подобные приложения вторичны. Квантовая механика была разработана для описания микромира; инфляционная космология — для осмысления наблюдаемых свойств космоса; теория струн — для прокладки мостика между квантовой механикой и общей теорией относительности. Возникновение мультивселенных в этих теориях оказывается побочным продуктом.
Наоборот, окончательная мультивселенная не несёт никакой другой объяснительной нагрузки, помимо идеи о мультивселенной. Здесь преследуется только одна цель: выделить из нашего списка текущих дел задачу по поиску объяснения, почему наша вселенная привязана к такому набору математических законов, а не к другому. И совершается этот исключительный подвиг путём введения мультивселенной. Приготовленная специально для ответа на один-единственный вопрос, окончательная мультивселенная не имеет независимого смысла, присущего обсуждавшимся в предыдущих главах мультивселенным.
Такова моя точка зрения, и с ней можно не соглашаться. Есть философский взгляд на вещи (идущий от школы структурного реализма), согласно которому физики могут стать жертвой искусственного разделения между математикой и физикой. В теоретической физике принято считать, что математика является количественным языком описания физической реальности; я сам так делал почти на каждой странице этой книги. Но, возможно, говорит эта философская доктрина, математика — это нечто большее, чем просто описание реальности. Возможно, математика и есть реальность.
Это особенная идея. Мы не привыкли думать, что осязаемая реальность построена из эфемерной математики. Смоделированные вселенные из предыдущего раздела дают конкретный и поучительный способ думать об этом. Вспомним знаменитый исторический эпизод, когда во время философского разговора на природе епископа Беркли и Самюэля Джонсона последний пнул ногой придорожный камень, выразив тем самым свою спонтанную реакцию на утверждение Беркли, что материя — это плод воображения. Представьте, однако, что неведомо от д-ра Джонсона его пинок произошёл в гипотетической очень точной компьютерной симуляции. В этом смоделированном мире ощущение от пинка д-ра Джонсона будет таким же убедительным, как и в исторической версии. Но компьютерная симуляция — это не более чем цепочка математических манипуляций, которые берут состояние компьютерной памяти в один момент — сложную конфигурацию битов — и переводят эти биты, согласно установленным математическим правилам, в другие конфигурации.
Тогда если вы пристально изучите математические преобразования, выполняемые компьютером во время жеста д-ра Джонсона, вы увидите, прямо внутри самой математики, и пинок, и отскок ноги, а также мысль и знаменитую фразу «Вот как я это опровергаю!». Подключите компьютер к монитору (или к какому-нибудь футуристическому интерфейсу), и вы увидите, как математический танец битов изображает д-ра Джонсона и его пинок. Но не допускайте, чтобы смоделированные «бантики» — системный блок, прикольный интерфейс и так далее — затемнили важный факт: под капотом нет ничего кроме математики. Измените математические правила, и танцующие биты отчеканят другую реальность.
А почему бы не пойти дальше? Я поместил д-ра Джонсона внутрь симуляции только потому, что этот пример демонстрирует поучительную связь между математикой и реальностью д-ра Джонсона. Но более глубокий ответ в том, что компьютерная симуляция — это несущественный промежуточный шаг, всего лишь мысленный трамплин между опытом осязаемого мира и абстракцией математических уравнений. Математика сама по себе — посредством установленных ею отношений, образованных связей и вовлекаемых преобразований — содержит д-ра Джонсона, его движения и мысли. Вам не нужен компьютер. Вам не нужны танцующие биты. Д-р Джонсон сам находится внутри математики.{100}
Если вы принимаете идею, что математика сама может посредством своей внутренней структуры охватить все до одного аспекты реальности — интеллект, большие камни, решительные пинки, сбитые ноги — вы придёте к представлению о том, что наша реальность является ни чем иным как математикой. При таком взгляде на вещи всё, что вы осознаёте — ощущение от прикосновения к этой книге, ваши текущие мысли, планы на ужин — является проявлением математики. Реальность — это чувства, переживаемые математикой.
Разумеется, такая точка зрения требует концептуального прыжка, совершить который можно уговорить не каждого; что касается меня, то я на него не решусь. Но для тех, кто решится, математика в картине мира займёт место не просто «здесь вокруг», она станет единственным, что находится «здесь вокруг». Тело математики, будь то ньютоновские уравнения, или эйнштейновские, или любые другие уравнения, не становится реальным от того, что возникают физические сущности, в которых оно реализуется. Математика — вся целиком — уже реальна; она не требует реализации. Различные наборы математических уравнений — это различные вселенные. Таким образом, окончательная вселенная является побочным продуктом такой точки зрения на математику.
Макс Тегмарк из Массачусетского технологического института, активно продвигающий идею окончательной мультивселенной (которую он называет «математической гипотезой вселенной»), объясняет этот взгляд с помощью такого рассуждения. Фундаментальное описание вселенной не должно привлекать понятия, смысл которых основывается на человеческом опыте или интерпретации. Реальность выходит за рамки нашего опыта, поэтому никаким фундаментальным образом она не должна зависеть от выдвинутых человеком идей. Точка зрения Тегмарка такова, что именно математика — понимаемая как наборы операций (подобных сложению), действующих на абстрактные наборы объектов (подобных целым числам), давая различные соотношения между ними (типа 1 + 2 = 3) — является тем языком для выражения утверждений, который лишён вредного человеческого влияния. Однако, что тогда может отличить тело математики от той вселенной, которую она описывает? Тегмарк считает, что правильный ответ — ничто. Если бы существовало некоторое свойство, отличающее математику от вселенной, то оно должно было быть нематематическим; иначе его можно добавить в математическую картину, что приведёт к потере его смысла. Однако, если следовать этой линии рассуждений, если данное свойство не имеет математической природы, то оно несёт отпечатки человеческого вмешательства, поэтому не может являться фундаментальным. Таким образом, нет никакого различия между тем, что мы привычно называем математическим описанием реальности, и её физическим воплощением. Они одинаковы. Нет такого переключателя, который ставит математику на «вкл». Математическое существование — это синоним физического существования. Поскольку такое отождествление справедливо для любой математики, возникает ещё одна дорога, ведущая нас к окончательной мультивселенной.
Хотя над этими любопытными рассуждениями интересно поразмышлять, моё отношение к ним остаётся скептическим. При рассмотрении проекта любой мультивселенной, я предпочитаю думать, что существуют процессы, пусть даже гипотетические — например, флуктуирующее поле инфлатона, столкновение бранных миров, квантовое туннелирование сквозь струнный ландшафт, распространение волны согласно уравнению Шрёдингера — которые, как нам представляется, приводят к возникновению этой мультивселенной. Я предпочитаю опираться в своих размышлениях на последовательность событий, которые, по крайней мере в принципе, могут привести к развитию такой мультивселенной. Тяжело представить, каким может быть такой процесс для окончательной мультивселенной; он должен приводить к различным математическим законам в разных областях. Мы видели, что в инфляционной и ландшафтной мультивселенных детали того, как проявляются физические закономерности, могут варьироваться от вселенной к вселенной; это обусловлено различиями в окружающей среде, такими как значения определённых полей Хиггса или форма дополнительных измерений. При этом основополагающие математические уравнения, действующие во всех вселенных, одинаковы. Поэтому какой процесс, оперирующий с заданным набором математических законов, может изменить эти математические законы? Это кажется совершенно невозможным, подобно тому как число пять не может стать числом шесть, как бы отчаянно оно не старалось.
Однако, прежде чем остановиться на том выводе, обратим внимание, что могут существовать области, которые выглядят так, будто они управляются другими математическими правилами. Давайте снова представим смоделированные миры. В примере с д-ром Джонсоном компьютерная симуляция привлекалась как педагогический приём для объяснения того, как математика может охватывать суть восприятия. Однако, если рассмотреть такие симуляции сами по себе в рамках смоделированной мультивселенной, мы увидим, что здесь возникает процесс, за который мы боремся: хотя компьютерное оборудование, на котором выполняется симуляция, подчинено обычным законам физики, сам смоделированный мир будет основываться на математических уравнениях, выбранных пользователем. Математические законы могут и будут произвольно варьироваться от симуляции к симуляции.
Как мы сейчас увидим, это приводит к механизму образования некоторой привилегированной части окончательной мультивселенной.
Симуляция Вавилона
Ранее отмечалось, что для изучаемых в физике типов уравнений компьютерные методы дают только аппроксимацию к математике. Типично такая ситуация возникает, когда непрерывные числа «перевариваются» цифровым компьютером. Например, в классической физике (где предполагается, что пространство-время непрерывно) бейсбольный мяч проходит через бесконечное число различных точек, по мере того как он летит с домашней базы в левое поле.[65] Отслеживание бесконечных положений мяча и бесконечных возможностей для скоростей в этих положениях всегда будет недостижимо. В лучшем случае компьютеры могут осуществить высокоточные, но всё равно приближённые вычисления, отслеживая мяч на каждой миллионной, или миллиардной, или триллионной доле сантиметра. Это прекрасно подходит для большинства целей, но всё равно является аппроксимацией. Квантовая механика и квантовая теория поля, вводя различные формы дискретности, отчасти исправляют ситуацию. Однако обе эти теории интенсивно используют непрерывно меняющиеся числа (значения волн вероятности, значения полей и так далее). Такие же рассуждения справедливы для всех остальных стандартных уравнений в физике. Компьютер способен выполнить приближённые вычисления, но не может точно смоделировать уравнения.[66]
Однако, существуют типы математических функций, для которых компьютерная симуляция может быть абсолютно точной. Они принадлежат к классу так называемых вычислимых функций, являющихся функциями, которые могут быть вычислены на компьютере за конечное число дискретных шагов. Возможно, компьютеру понадобится циклически повторять этот набор шагов, но рано или поздно точный ответ будет получен. Каждый шаг вычислений не требует никакой оригинальности или новизны; это исключительно вопрос уточнения результата. Тогда на практике, для симуляции движения бейсбольного мяча компьютер программируется уравнениями, являющимися вычислимыми аппроксимациями к школьным законам физики. (Как правило, непрерывное пространство и время аппроксимируются на компьютере мелкой решёткой.)
Наоборот, компьютер, пытающийся просчитать невычислимую функцию, будет крутиться неопределённо долго, не приходя ни к какому ответу, независимо от его скорости и памяти. Так будет происходить при компьютерном вычислении точной непрерывной траектории бейсбольного мяча. В качестве более ощутимого примера представим смоделированную вселенную, в которой компьютер запрограммирован для создания поразительно работоспособного смоделированного повара, который готовит пищу для всех тех смоделированных обитателей — и только для них, — кто не готовит себе еду. Пока повар неистово печёт, жарит и парит, у него появляется аппетит. Вопрос: кого компьютер обяжет приготовить еду для повара?[67] Задумайтесь об этом, и голова у вас распухнет. Повар не может готовить для себя, потому что он готовит только для тех, кто не готовит для себя, но если повар не готовит для себя, то он относится к тем, для кого он должен готовить. Будьте уверены, компьютер справится не лучше вас. Невычислимые функции похожи на этот пример: они ставят в тупик способность компьютера завершить вычисление, и исполняемая компьютером симуляция зависает. Поэтому успешные вселенные, входящие в состав смоделированной мультивселенной, будут основываться на вычислимых функциях.
В этих рассуждениях предполагается, что существует пересечение между смоделированной и окончательной мультивселенными. Рассмотрим уменьшенную версию окончательной мультивселенной, включающую только те вселенные, которые возникают на основе вычислимых функций. Тогда, вместо того чтобы просто быть постулированной в виде ответа на один частный вопрос — почему эта вселенная реальна, а другие возможные вселенные нет? — уменьшенная версия окончательной мультивселенной может возникать как итог некоторого процесса. Армия компьютерных пользователей из будущего, возможно, не сильно отличающихся по темпераменту от сегодняшних энтузиастов игры Second Life, могла бы создать эту мультивселенную в результате своего ненасытного увлечения использованием симуляций, основанных каждый раз на новых уравнениях. Эти пользователи не смогут создать все смоделированные вселенные из математической библиотеки Вавилона, потому что те из них, которые основаны на невычислимых функциях, невозможно будет запустить. Но они будут непрестанно прокладывать себе дорогу сквозь вычисляемое крыло библиотеки.
Расширив первоначальные идеи Цузе, учёный-компьютерщик Юрген Шмидхубер пришёл к похожему заключению, но с другой точки зрения. Шмидхубер осознал, что на самом деле легче запрограммировать компьютер для создания сразу всех возможных вычислимых вселенных, чем индивидуально запрограммировать компьютеры для их создания одной за другой. Чтобы понять почему, представим программирование компьютера для симуляции игры в бейсбол. В каждой игре количество необходимой информации огромно: каждая деталь каждого игрока, физическая и ментальная, каждая деталь стадиона, арбитров, погоды и так далее. Каждая новая симуляция игры требует от вас задать новую груду данных. Однако, если вы решите смоделировать не одну или несколько игр, но вообще все мыслимые игры, объём программирования упростится. Потребуется всего лишь задать одну мастер-программу, которая будет систематически выполняться для каждой возможной переменной — определяющей игроков, окружение и другие существенные свойства, — после чего запустить симуляцию. Выудить какую-то определённую игру из получающейся кучи игр будет затруднительно, но можно быть уверенным, что рано или поздно любая возможная игра будет проиграна.
Суть в том, что для задания какой-либо одной составляющей из большого набора требуется большое количество информации, а задание всего набора в целом зачастую гораздо проще. Шмидхубер обнаружил, что это заключение применимо к смоделированным вселенным. Программист, приглашённый для симуляции набора вселенных, основанных на определённом наборе математических уравнений, может пойти простым путём: подобно бейсбольному фанату, он может предпочесть написать одну, относительно короткую программу, которая создаст все вычислимые вселенные, и предоставить компьютер самому себе. Где-то внутри гигантского набора смоделированных вселенных программист обнаружит те вселенные, ради которых его пригласили. Я бы не хотел платить за почасовое использование компьютера, потому что время для создания этих симуляций будет гигантским. Но я с удовольствием оплатил бы почасовой труд программиста, потому что набор команд для создания всех вычислимых вселенных будет гораздо менее объёмным, нежели требуемый для создания любой выделенной вселенной.[68]
Любой из этих сценариев — много пользователей, моделирующих много вселенных, или одна мастер-программа, моделирующая их все разом — пригоден для образования смоделированной мультивселенной. Поскольку возникающие вселенные будут основываться на широком наборе различных математических законов, можно эквивалентным образом считать, что эти сценарии генерируют часть окончательной мультивселенной — ту часть, что охватывает вселенные, основанные на вычислимых математических функциях.[69]
Недостаток генерации только части окончательной мультивселенной в том, что в уменьшенной версии не так ясно видна идея, которая изначально вдохновила Нозика на принцип изобилия. Если все возможные вселенные не существуют, если полная окончательная мультивселенная не генерируется, то опять всплывает вопрос, почему некоторые уравнения реализуются в природе, а другие нет. В частности, мы по-прежнему будем задаваться вопросом, почему вселенные, основанные на вычислимых уравнениях, занимают такое выделенное место под солнцем.
Продолжая крайне спекулятивную линию изложения этой главы, заметим, что разделение на вычислимые/невычислимые о чём-то нам говорит. Вычислимые математические уравнения позволяют обойти неудобные вопросы, которые были подняты в середине предыдущего столетия такими выдающимися мыслителями, как Курт Гёдель, Алан Тьюринг и Алонзо Чёрч. Знаменитая теорема Гёделя о неполноте показывает, что определённые математические системы с необходимостью допускают существование истинных утверждений, которые нельзя доказать, оставаясь в рамках этой системы. Физики давно интересовались возможными следствиями из рассуждений Гёделя для своих целей. Может быть, физика тоже обязана быть неполной в том смысле, что некоторые свойства реального мира никогда не будут доступны для математического описания? В контексте уменьшенной окончательной мультивселенной ответ на этот вопрос отрицательный. Вычислимые математические функции по определению находятся в границах вычислений. Это те самые функции, для которых есть процедуры, следуя которым, компьютер может их успешно просчитать. Поэтому, если бы все вселенные в мультивселенной были основаны на вычислимых функциях, они бы успешно преодолели теорему Гёделя; в это крыло библиотеки математического Вавилона, в эту версию окончательной мультивселенной вход для тени Гёделя будет закрыт. Может быть, именно это выделяет вычислимые функции.
Будет ли у нашей вселенной место в этой мультивселенной? То есть, если когда-нибудь мы сформулируем окончательные законы физики, будут ли они описывать космос с помощью вычислимых математических функций? Не просто приблизительно вычислимых функций, как в случае с современными физическими законами. Но точно вычислимых? Это никому не известно. Если так, то развитие физики должно привести нас к теориям, в которых непрерывность не играет никакой роли. Должна превалировать дискретность, ядро вычислительной парадигмы. Пространство, конечно, выглядит непрерывным, однако мы это протестировали до расстояний не глубже, чем миллиардная доля от миллиардной доли метра. Возможно, что однажды, с более точным оборудованием, мы установим, что пространство дискретно на фундаментальном уровне; но пока этот вопрос остаётся открытым. Подобное ограниченное понимание имеет место и в случае интервалов времени. Открытия, перечисленные в главе 9, согласно которым информационная ёмкость любой области пространства задаётся одним битом на единицу планковской площади, являются важным шагом в направлении дискретности. Однако вопрос о том, насколько далеко может продвинуться цифровая парадигма, ещё очень далёк от решения.{101} Независимо от того, появятся когда-нибудь разумные симуляции или нет, я думаю, что мы действительно придём к мнению, что этот мир фундаментально дискретен.
У корней реальности
В смоделированной мультивселенной нет никакой неоднозначности относительно того, какая вселенная «реальна» — то есть какая вселенная расположена у корней ветвящегося дерева смоделированных миров. Эта та вселенная, где находятся компьютеры, поломка которых приведёт к обрушению всей мультивселенной. Смоделированный обитатель может моделировать свой собственный набор смоделированных вселенных на смоделированных компьютерах, и также могут поступить обитатели этих симуляций, но всё же существуют реальные компьютеры, в которых все эти многоуровневые симуляции являются не более чем лавиной электрических импульсов. Нет никакой неопределённости насчёт того, какие факты, системы и законы являются реальными в традиционном смысле: именно по ним работает корневая вселенная.
Однако, типичный смоделированный учёный в смоделированной мультивселенной может иметь другую точку зрения. Если эти учёные обладают достаточной автономией — если симуляторы довольно редко подправляют (если вообще это происходит) память обитателей или вмешиваются в естественный ход событий — тогда, на основе нашего собственного опыта можно предвидеть, что эти учёные достигнут больших результатов в понимании математического кода, управляющего их миром. Они будут считать этот код законами природы. Тем не менее, их законы необязательно будут тождественны законам, управляющим реальной вселенной. Их законы должны быть достаточно хороши в том смысле, что при создании компьютерной симуляции должна возникать вселенная с разумными обитателями. Если есть много разных наборов математических законов, считающихся достаточно хорошими, то вполне может существовать всё пополняющееся сообщество смоделированных учёных, убеждённых в справедливости математических законов, которые совсем не являются фундаментальными, а просто были выбраны кем-то, кто запрограммировал симуляцию. Если мы являемся типичными обитателями такой мультивселенной, то из вышеприведённых рассуждений следует, что вера в науку как дисциплину, нацеленную на поиск фундаментальных истин относительно реальности — корневой реальности, расположенной у подножия дерева, — будет подорвана.
Такая возможность, конечно, не очень приятная, но не настолько, чтобы не дать мне уснуть. Пока у меня не перехватит дыхания от образа увиденной разумной симуляции, я не стану серьёзно рассматривать возможность того, что мы находимся в одной из них. Давайте забежим в будущее и допустим, что разумные симуляции однажды будут созданы (что само по себе под большим вопросом). Я хорошо могу себе представить, что когда технологические возможности цивилизации позволят впервые запустить подобные симуляции, они вызовут невероятный интерес. Но долго ли он продержится? Я подозреваю, что новизна создания искусственных миров, обитатели которых не в курсе своего смоделированного статуса, быстро сойдёт на нет; у нас уже так много реальности на телевидении, за которой мы можем наблюдать.
Но если отпустить нашу фантазию свободно полетать по этой спекулятивной территории, то мне кажется, что будущее за приложениями, которые устанавливают контакт между смоделированными и настоящими мирами. Возможно, смоделированные обитатели смогут переходить в реальный мир или в смоделированном мире к ним смогут присоединяться их настоящие биологические прототипы. Со временем различие между реальными и смоделированными существами может стать анахронизмом. Такие сращённые союзы мне представляются наиболее возможным вариантом. В этом случае смоделированная мультивселенная будет содействовать расширению реальности — нашей реальности, нашей реальной реальности — самым осязаемым способом. Это станет ещё одной характерной чертой того, что мы называем «реальностью».
Глава 11. Пределы исследования Будущее и мультивселенные
Исаак Ньютон существенно расширил научное познание. Он открыл, что несколько математических уравнений могут описать движения тел как здесь, на Земле, так и выше, в просторах космоса. Размышляя над силой и простотой его результатов, можно было бы подумать, что уравнения Ньютона отражают вечные истины, начертанные на своде космоса. Но сам Ньютон так не думал. Он полагал, что Вселенная значительно более сложна и загадочна, чем следует из его уравнений; позже он писал: «Я не знаю, каким меня воспринимает мир, но сам я ощущаю себя ребёнком, играющим на берегу и подбирающим камушки и ракушки, более гладкие и красивые, чем остальные, в то время как передо мной лежит необъятный и неисследованный океан истины». Прошедшие с тех пор столетия лишь подтвердили это ощущение.
Я рад этому. Если бы уравнения Ньютона обладали неограниченной применимостью, правильно описывая любые явления, на малых или больших расстояниях, с лёгкими или тяжёлыми массами, на больших и малых скоростях, последующая научная одиссея приобрела бы совершенно другой характер. Уравнения Ньютона учат многому об устройстве окружающего нас мира, но их неограниченная применимость означала бы, что во Вселенной нет ничего примечательного, ни там, ни здесь. Поняв, как устроена физика на обычном масштабе, можно было бы успокоиться и ничего больше не делать. Всё то же самое было бы здесь, там и в любом другом месте.
Продолжая исследования Ньютона, учёные ступили на земли далеко за пределами применимости его уравнений. Обнаруженное нами потребовало стремительного переосмысления наших представлений о реальности. Такое переосмысление даётся нелегко. Новые идеи тщательным образом изучаются научной общественностью и зачастую им оказывается резкое сопротивление; и лишь тогда, когда накапливается достаточное количество подтверждённых фактов, новая точка зрения принимается. Именно так и должно быть. Нет никакой необходимости в поспешной оценке. Реальность подождёт.
Центральный факт, находящий своё убедительное подтверждение на протяжении нескольких последних веков теоретического и экспериментального развития, состоит в том, что на обычный опыт нельзя полагаться при изучении явлений, выходящих за рамки обычного. И с какими бы радикальными явлениями не столкнулась новая физика в экстремальных условиях — описываемыми общей теорией относительности, квантовой механикой и теорией струн, — если она окажется правильной, тот факт, что это потребует радикально новых идей, совсем не удивителен. Основная гипотеза науки заключается в том, что на всех масштабах имеются закономерности и модели, но как предвидел сам Ньютон, нет никакой причины ожидать, что эти модели будут повторяться на всех масштабах.
Сюрприз будет в том, если сюрпризов не будет.
Безусловно, то же самое справедливо и для того, с чем физика столкнётся в будущем. Настоящее поколение физиков никогда не знает, как история науки оценит их труды — как приятное времяпрепровождение, как мимолётное увлечение, как трамплин для будущих открытий, или как достижения, которые пройдут испытания временем. Такая локальная неопределённость уравновешивается одной из самых приятных сторон физики — глобальной стабильностью; новые теории, как правило, не отбрасывают старые, на место которых они приходят. Как мы уже обсуждали, хотя новым теориям может потребоваться акклиматизация на новых гранях природы реальности, они почти никогда не оспаривают значимости предыдущих открытий. Наоборот, они их впитывают в себя и развивают далее. По этой причине, для истории физики характерна впечатляющая последовательность.
В этой книге мы рассмотрели нового кандидата, претендующего на роль стать новым главным открытием в развитии физики: мы рассмотрели возможность, что наша Вселенная является частью мультивселенной. На этом пути нам встретились девять вариаций на тему мультивселенной, сведённые вкратце в табл. 11.1. Хотя эти вариации сильно различаются в деталях, все они предполагают, что картина реальности, которую нам рисует здравый смысл, лишь часть чего-то большего. Все они отмечены гением человеческой изобретательности и творчества. Однако, для того чтобы установить, стоит ли за какой-нибудь из них нечто большее, чем просто математические размышления человеческого разума, нам потребуется гораздо больше знаний, вычислений, достижений, экспериментов и наблюдений, чем мы пока располагаем. Поэтому лишь будущее покажет, оправданно или нет делать ставку на то, что параллельные вселенные окажутся вписаны в следующую главу истории физики.
Таблица 11.1. Обзор различных версий параллельных вселенных
Модель параллельных вселенных Описание Лоскутная мультивселенная Условия в бесконечной вселенной обязательно повторяются на просторах космоса, что приводит к параллельным мирам. Инфляционная мультивселенная Вечная космологическая инфляция приводит к огромной цепочке пузырьков-вселенных, один из которых — это наша Вселенная. Бранная мультивселенная В бранном сценарии, основанном на теории струн, или M-теории, предполагается, что наша Вселенная существует на трёхмерной бране, которая находится внутри пространства с большей размерностью, возможно, населённого другими бранами — другими параллельными вселенными. Циклическая мультивселенная Столкновения между бранными мирами могут выглядеть как процесс рождения, подобный Большому взрыву, что приводит к вселенным, параллельным во времени. Ландшафтная мультивселенная При объединении инфляционной космологии и теории струн множество различных форм дополнительных измерений в теории струн приводят ко множеству различных пузырьков-вселенных. Квантовая мультивселенная Из квантовой механики следует, что каждое возможное событие, закодированное своей волной вероятности, реализуется в своей вселенной, одной из гигантского ансамбля параллельных вселенных. Голографическая мультивселенная Голографический принцип утверждает, что наша Вселенная является точным отражением явлений, происходящих на удалённой граничной поверхности, являющейся физически эквивалентной параллельной вселенной. Смоделированная мультивселенная Вполне возможно, что однажды технологический прогресс приведёт к созданию искусственных смоделированных вселенных. Окончательная мультивселенная Принцип изобилия утверждает, что каждая возможная вселенная реальна, поэтому снимается вопрос, почему одна из возможностей — наша — является выделенной. Такие вселенные служат реализацией всех возможных математических уравнений.Книга, которую вы сейчас держите, в чём-то похожа на метафорическую книгу природы. В этой последней главе я бы с радостью хотел свести всё воедино и ответить на самый главный здесь вопрос: вселенная или мультивселенная? Но я не могу. Таков характер исследований, происходящих на переднем крае науки. Вместо этого я предлагаю рассмотреть, в каком направлении могла бы далее развиваться идея мультивселенной, а также подчеркнуть её статус в настоящий момент. Для этого позвольте озвучить пять центральных вопросов, которые будут занимать внимание физиков в последующие годы.
Фундаментальна ли модель Коперника?
Закономерности и модели, проявляющиеся с очевидностью в наблюдениях и в математике, очень важны для формулировки физических законов. Также поучительны модели иного сорта, касающиеся природы физических законов, принимаемые каждым последующим поколением. Эти модели отражают то, как научное открытие меняет точку зрения человечества на его место в космическом мироустройстве. В течение приблизительно пяти столетий превалировала коперниканская точка зрения. Всё вокруг, от восхода и заката солнца, движения созвездий по ночному небу, до ведущей роли, которую каждый из нас играет в своём внутреннем мире, всё указывает на то, что мы являемся центром, вокруг которого вертится космос. Однако объективные методы научного исследования постоянно вносили коррективы в эту точку зрения. Раз за разом мы убеждались, что если бы человечество вдруг исчезло, то устройство Вселенной вряд ли бы изменилось. Нам пришлось отказаться от своей веры в то, что Земля занимает центральное место в обществе своих соседей, а Солнце находится в центре галактики, а Млечный Путь — в центре всех галактик, и даже отказаться от того, что протоны, нейтроны и электроны — то, из чего мы сделаны, — это центральные ингредиенты в космическом рецепте. Было время, когда выступления против укоренившейся коллективной мании величия рассматривались как прямая угроза человеческим ценностям. Но со временем просвещённость стала цениться более высоко.
На протяжении всей книги мы двигались к тому, что можно назвать апофеозом скорректированной системы Коперника. Наша Вселенная может и не быть центральным элементом в космическом мироустройстве. Так же как наша планета, звёзды и галактика, наша Вселенная может оказаться лишь одной из великого множества вселенных. Идея о том, что картина реальности, основанная на понятии мультивселенной, расширяет и, возможно, завершает коперниковскую систему, весьма любопытна. Но ключевой факт, который возвышает концепцию мультивселенной над пустыми спекуляциями, состоит в следующем. Нельзя сказать, что учёные целенаправленно работают над тем, чтобы расширить революционные взгляды Коперника. Они не вынашивают в своих затемнённых лабораториях планы по шлифовке картины Коперника. Вместо этого учёные занимаются тем, чем занимались всегда: на основе полученных данных и наблюдений они выдвигают математические теории для описания фундаментальных составляющих вещества и сил, которые контролируют их поведение, эволюцию и взаимодействия. Примечательно, что прилежно следуя логике этих теорий, исследователи наталкиваются то на одну возможную мультивселенную, то на другую. Прокатитесь по любой из наиболее оживлённых научных магистралей, будьте минимально бдительными — и вы увидите неплохой набор разнообразных потенциальных мультивселенных. Избежать их гораздо сложнее, чем с ними встретиться.
Возможно, в будущем исследователи по-другому расценят развитие коперниковских взглядов. Но пока дела обстоят так, что чем больше мы понимаем, тем менее центральным оказывается наше положение. Если научные исследования, которые мы обсуждали выше, будут и дальше указывать нам на мультивселенный сценарий, то это станет естественным шагом в завершении коперниковской революции спустя пятьсот лет развития.
Могут ли быть проверены научные теории мультивселенных?
Хотя концепция мультивселенной хорошо ложится на коперниковскую философию, она качественно отличается от нашего предыдущего отступления от центра. Привлекая миры, которые, возможно, нам никогда не удастся исследовать — либо с желаемой точностью, либо, в некоторых случаях, вообще никак, — мультивселенные воздвигают, по всей видимости, значительные барьеры для научного познания. Независимо от точки зрения на место человечества во Вселенной, мы придерживаемся того широко признанного предположения, что посредством аккуратно выполненных экспериментов, наблюдений и математических вычислений, наша способность к расширению границ познания неограниченна. Однако если мы являемся частью мультивселенной, то разумно ожидать, что в лучшем случае мы можем изучить нашу Вселенную, наш небольшой уголок космоса. Но более всего удручает то, что привлекая идею мультивселенной, мы попадаем в область непроверяемых теорий — теорий, основанных на историях из разряда «это так, потому что так», объясняющих всё, что мы наблюдаем, утверждениями типа «это случилось, потому что случилось».
Однако, как я уже излагал, концепция мультивселенной гораздо изящнее. Существуют различные способы получения проверяемых предсказаний в теории с мультивселенной. Например, хотя конкретные вселенные, составляющие некоторую мультивселенную, могут значительно различаться, у них могут быть общие свойства, поскольку они возникают из одной теории. Если нам не удастся обнаружить эти свойства с помощью измерений, проводимых здесь, во Вселенной, где мы живём, это покажет, что гипотеза мультивселенной неверна. Подтверждение этих свойств, особенно если они окажутся новыми, укрепит уверенность в правоте теории.
Есть и другой способ. Если общие для всех вселенных свойства отсутствуют, но есть корреляция между разными физическими свойствами, то это может привести к другому классу проверяемых предсказаний. Например, мы видели, что если во всех вселенных, где в списке частиц присутствует электрон, должны также присутствовать другие ещё не обнаруженные типы частиц, то неспособность обнаружить эти частицы экспериментально здесь, в нашей Вселенной, приведёт к тому, что гипотезу мультивселенной надо будет отбросить. Обнаружение неизвестных частиц укрепит уверенность в правоте теории. Аналогичным образом, более сложные корреляции, когда вселенные, список частиц которых включает, скажем, все известные частицы (электроны, мюоны, u-кварки, d-кварки и так далее), с необходимостью содержат новые типы частиц, приводят к проверяемым, фальсифицируемым предсказаниям.
Если такие тесные корреляции отсутствуют, то следует попытаться рассмотреть способ варьирования физических свойств от вселенной ко вселенной — это также может привести к предсказаниям. Например, на просторах рассматриваемой мультивселенной космологическая постоянная может иметь широкий диапазон значений. Но если для огромного большинства вселенных значения космологической постоянной согласуются с тем, что показывают проведённые здесь измерения (рис. 7.1), то наше доверие к такой мультивселенной заслуженно возрастает.
Наконец, даже если большинство вселенных в данной мультивселенной имеет свойства, отличные от наших, то можно привлечь ещё один способ диагностики. Можно опереться на антропный принцип и рассматривать только те вселенные в мультивселенной, которые благоприятствуют нашей форме жизни. Если значительное большинство в этом подклассе вселенных имеет общие с нами свойства — если наша Вселенная типична среди тех, условия в которых позволяют нам существовать, — то уверенность в этой мультивселенной будет крепнуть. Если же мы нетипичны, мы не можем отбросить эту теорию, но это является привычным ограничением при статистических рассуждениях. Маловероятные события могут происходить, и иногда они действительно происходят. И в этом случае чем менее мы типичны, тем менее убедительной будет данная теория с мультивселенной. Если среди всех поддерживающих жизнь вселенных в данной мультивселенной наша Вселенная будет выделяться, как белая ворона, это даст весомый аргумент, чтобы отказаться от этой модели мультивселенной.
Поэтому для того, чтобы рассмотреть модель мультивселенной количественно, необходимо определить демографию населяющих её вселенных. Недостаточно знать, какие возможные вселенные допускает данная мультивселенная; необходимо определить детальные свойства настоящих вселенных, к которым приводит теория. Для этого необходимо понимание космологического процесса, в результате которого возникают различные вселенные данной мультивселенной. Тогда проверяемые предсказания могут возникнуть на основе того, как варьируются физические свойства от вселенной ко вселенной на просторах мультивселенной.
Приведёт ли эта цепочка рассуждений к ярким результатам — станет понятно только при обстоятельном изучении мультивселенной за мультивселенной. Но вывод таков, что теории, включающие другие вселенные — миры, которые мы не можем исследовать сейчас, а возможно, вообще никогда не сможем, — всё равно могут приводить к проверяемым и, следовательно, фальсифицируемым предсказаниям.
Могут ли быть проверены рассмотренные нами теории мультивселенных?
В теоретических исследованиях физическая интуиция жизненно необходима. Теоретики должны как-то ориентироваться среди нагромождения различных вариантов. Следует рассмотреть это уравнение или то, применить эту схему или другую? Лучшие физики обладают острым чутьём на то, какие направления выглядят многообещающе, а какие скорее всего бесплодны. Но это происходит за кулисами. Когда научная гипотеза выдвинута, интуиция и чутьё уже не причём. Уместен лишь один стандарт — способность этой гипотезы объяснить или предсказать экспериментальные данные и астрономические наблюдения.
В этом состоит необыкновенная прелесть науки. По мере того как мы боремся за углубление нашего понимания, нашему творческому воображению необходимо давать всё больше пространства для размышлений. Нам требуется перешагнуть за пределы обычных идей и принятых рамок. Но в отличие от любой другой человеческой деятельности, наполненной творческим импульсом, наука даёт окончательный рецепт, встроенную оценку того, что считать правильным, а что — неправильным.
Усложнение научной жизни во второй половине двадцатого столетия и в начале двадцать первого заключается в том, что некоторые наши теоретические идеи превосходят имеющиеся наблюдательные или экспериментальные возможности. Долгое время таким примером была теория струн. Возможность того, что мы являемся частью мультивселенной, является ещё более ярким примером. Я привёл общее предписание того, как идея мультивселенной может быть проверена, но на нашем текущем уровне понимания ни одна из рассмотренных нами мультивселенных пока не удовлетворяет этому критерию. Однако исследования продолжаются, и ситуация может значительно улучшиться.
Например, наши исследования по ландшафтной мультивселенной находятся на начальном этапе. Набор возможных вселенных в теории струн — струнный ландшафт — схематически представлен на рис. 6.4, но подробные карты этого горного рельефа всё ещё предстоит нарисовать. Подобно древним мореплавателям, мы имеем слабое представление, что там за горизонтом, и для создания карт этих земель потребуется ещё много математических исследований. После получения таких знаний следующим шагом будет установление того, как эти возможные вселенные распределены по просторам ландшафтной мультивселенной. Мы хорошо понимаем на качественном уровне важный физический процесс образования пузырьков-вселенных посредством квантового туннелирования (рис. 6.6, и рис. 6.7), но нам ещё предстоит провести детальные вычисления в теории струн. Различные исследовательские группы (включая и мою группу) провели первую разведку, но перед нами лежат ещё огромные неизведанные территории. Как мы видели в предыдущих главах, и в других моделях мультивселенных имеется множество подобных неопределённостей.
Никто не знает, пройдут года или десятилетия и даже ещё больше, прежде чем экспериментальный и теоретический прогресс приведёт нас к детальным предсказаниям в рамках любой заданной мультивселенной. Если же текущая ситуация не изменится, то мы окажемся перед выбором. Как определить науку, «серьёзную науку» — как включающую только те идеи, миры и возможности, которые соответствуют текущим экспериментальным и наблюдательным возможностям людей на планете Земля? Или нам стоит придерживаться более широкой точки зрения и считать идеи «научными», если их можно будет проверить с помощью технологических достижений, появление которых мы прогнозируем в последующие сто лет? В последующие двести лет? Дольше? Или принять ещё более широкую точку зрения? Позволяем ли мы науке следовать всевозможными путями, идти дорогами, отклоняющимися от экспериментально подтверждённых идей, но которые могут привести нас в скрытые миры, находящиеся, возможно, навсегда, за пределами человеческих возможностей?
Чёткого ответа на эти вопросы не существует. Именно здесь начинает играть ведущую роль личный научный вкус каждого. Я хорошо понимаю привязанность к тем научным исследованиям, которые могут быть проверены незамедлительно или в ближайшем будущем; именно так, в конце концов, мы выстраиваем систему научных взглядов. Но было бы порочным загонять наши размышления в узкие рамки, определяемые тем, где мы есть, куда мы движемся и кто мы такие. Реальность выходит за эти рамки, и поэтому следует ожидать, что поиск глубоких истин также не застрянет на месте.
Я голосую за расширенную точку зрения. Но я не принимаю идей, которые невозможно осмысленно проверить на эксперименте или в наблюдениях, не в силу человеческой слабости и технологических ограничений, а по причине внутренней природы таких гипотез. Из всех рассмотренных нами мультивселенных только полномасштабная версия окончательной мультивселенной оказывается в таком положении. Если учитывается абсолютно каждая возможная вселенная, то тогда совершенно неважно, что мы наблюдаем и какие эксперименты проводим; окончательная мультивселенная кивнёт и одобрит наш результат. Другие восемь мультивселенных (табл. 11.1) лишены этого недостатка. Каждая из них возникает на основе хорошо обоснованной логической цепочки рассуждений и каждая открыта для тестирования. Если наблюдения дадут убедительное доказательство того, что пространство конечно, то лоскутная мультивселенная будет отброшена. Если пошатнётся наша уверенность в инфляционной космологии — возможно потому, что будут получены более точные данные по реликтовому излучению, для объяснения которых придётся предположить слишком крутую (и, следовательно, неубедительную) кривую потенциальной энергии инфлатона, — привлекательность инфляционной мультивселенной также уменьшится.[70] Если теория струн потерпит неудачу, если будет найден скрытый математический изъян, что приведёт к противоречивости теории (как казалось первым исследователям теории струн), то мотивация для изучения её разнообразных мультивселенных испарится. С другой стороны, если будут обнаружены характеристики в реликтовом излучении, ожидаемые при столкновениях пузырьков-вселенных, это станет прямым подтверждением инфляционной мультивселенной. Эксперименты, проводимые на ускорителях по поиску суперсимметричных частиц, потерянной энергии и чёрных мини-дыр, могут способствовать укреплению позиций теории струн и бранной мультивселенной, а подтверждение столкновений пузырьков-вселенных может также считаться указанием в пользу ландшафтного разнообразия. Обнаружение отпечатков гравитационных волн из ранней Вселенной (или их отсутствие) позволит сделать выбор между инфляционной парадигмой для космологии или циклической мультивселенной.
Квантовая механика, рассматриваемая с точки зрения многомирового подхода, приводит к квантовой мультивселенной. Если в будущем исследования покажут, что уравнения квантовой механики, сколь бы надёжными они ни были до сих пор, потребуют небольших модификаций для соответствия с более точными данными, то этот тип мультивселенной может быть отброшен. Так произойдёт, если при модификации потребуется отказаться от свойства линейности (на котором основывались все наши рассуждения в главе 8). Мы также отмечали, что в принципе существуют тесты на квантовую мультивселенную, эксперименты, результаты которых зависят от того, правилен ли подход Эверетта или нет. Эти эксперименты выходят за рамки того, что нам доступно сейчас, а может, и будет доступно когда-либо, но причина этого в том, что они фантастически сложны, а вовсе не в том, что они фундаментально невыполнимы из за каких-то внутренних свойств самой квантовой мультивселенной.
Голографическая мультивселенная возникает из рассмотрения хорошо установленных теорий — общей теории относительности и квантовой механики — и получает сильнейшую теоретическую поддержку со стороны теории струн. Вычисления, основанные на голографическом принципе, предварительно согласуются с экспериментальными результатами на ускорителе тяжёлых релятивистских ионов, и всё указывает на то, что такие экспериментальные связи в будущем будут только крепнуть. Рассматривать ли голографическую мультивселенную только как полезный математический инструмент или же как указание на голографичность реальности — является личным мнением каждого. Следует подождать дальнейших работ, теоретических и экспериментальных, чтобы иметь больше данных для физической интерпретации.
В основе смоделированной мультивселенной лежит не какая-то одна теоретическая структура, а непреклонный рост компьютерных мощностей. Ключевое допущение здесь состоит в том, что способность к ощущениям не привязана фундаментальным образом к какой-то выделенной основе — мозгу, — а является сопутствующей характеристикой определённого множества информационных процессов. Это весьма спорное предположение, и пылкие аргументы выдвигаются с обеих сторон. Возможно, что будущие исследования мозга и природы сознания развенчают идею о машинах, обладающих самосознанием. А может быть и нет. Впрочем, один способ тестирования этой модели мультивселенной вполне очевиден. Если наши потомки однажды увидят, или вступят в контакт, или виртуально посетят, или станут частью вполне убедительного смоделированного мира, то вопрос с практической точки зрения будет решён.
Смоделированная мультивселенная, по крайней мере теоретически, может быть также связана с урезанной версией окончательной мультивселенной, которая включает вселенные, основанные только на вычислимых математических структурах. В отличие от полной теории окончательной мультивселенной, генезис этой более ограниченной версии позволяет поднять её на ступень выше, чем просто гипотеза. Пользователи, реальные и виртуальные, стоящие за этой смоделированной мультивселенной, будут, по определению, моделировать вычислимые математические структуры и поэтому будут обладать способностью породить эту часть окончательной мультивселенной.
Получить экспериментальные и наблюдательные подтверждения справедливости любой из гипотез мультивселенных — это, конечно, непростая задача. Но в ней нет ничего невозможного. И понимая, каким огромным может быть вознаграждение, и если теоретические исследования естественно толкают нас на путь изучения мультивселенных, мы обязаны проследовать по этому пути и выяснить, куда он нас приведёт.
Как мультивселенная влияет на природу научного исследования?
Иногда наука направляет фокус на детали. Она говорит нам, почему планеты вращаются по эллиптическим орбитам, почему небо голубое, почему вода прозрачная, почему письменный стол твёрдый. Сколь бы привычными эти факты ни казались, поразительно, что мы можем их объяснить. Иногда наука расширяет фокус и смотрит на вещи более широко. Она обнаруживает, что мы живём внутри галактики, насчитывающей несколько сотен миллиардов звёзд, она устанавливает, что наша галактика — одна из сотен миллиардов других галактик, и утверждает, что существует невидимая тёмная энергия, пронизывающая каждый уголок этого огромного пространства. Оглядываясь всего лишь на сто лет назад, во время, когда считалось, что Вселенная статична, и в ней есть только галактика Млечный Путь, мы можем с удовлетворением окинуть взором величественную картину, которую наука нарисовала за это время.
Иногда наука делает ещё кое-что. Иногда она заставляет нас пересмотреть наши взгляды на саму науку. Устоявшаяся многовековая научная традиция говорит, что при описании физической системы учёному следует определить три момента. Мы уже встречались со всеми тремя в разных контекстах, но полезно собрать их все в одном месте. Во-первых, это математические уравнения, описывающие применяемые физические законы (например, это могут быть уравнения движения Ньютона, уравнения электромагнетизма Максвелла, уравнение Шрёдингера в квантовой механике). Во-вторых, это численные значения всех фундаментальных констант, входящих в математические уравнения (например, констант, определяющих силу гравитации или электромагнетизма, или констант, определяющих массу фундаментальных частиц). В-третьих, следует задать «начальные условия» для системы (например, когда бейсбольный мяч выбивается с домашней базы с определённой скоростью в определённом направлении или когда электрон отправляется в путь с вероятностью в 50 процентов быть обнаруженным в мемориале Гранта и с такой же вероятностью быть обнаруженным на Земляничных полях). Тогда уравнения определят, что произойдёт в любой последующий момент времени. Как классическая, так и квантовая физика следуют этой традиции; различие лишь в том, что классическая физика имеет цель сообщить нам, каким определённым образом всё будет устроено в данный момент времени, а квантовая механика задаёт вероятность того, что всё будет так или иначе.
Когда речь заходит о предсказании того, где упадёт бейсбольный мяч или как электрон пройдёт сквозь компьютерный чип (или модель Манхэттена), эта трёхшаговая процедура демонстрирует очевидную силу. Однако при описании реальности в целом, эти три шага наталкивают нас на более глубокие вопросы: можем ли мы объяснить начальные данные — то, как вещи устроены в самый начальный момент? Можем ли мы объяснить значения констант — массы частиц, силу взаимодействий и так далее, — от которых эти законы зависят? Можем ли мы объяснить, почему определённый набор математических уравнений описывает ту или иную грань физической вселенной?
Те модели мультивселенной, которые мы обсуждали, могут значительно повлиять на наше осмысление этих вопросов. В лоскутной мультивселенной мы имеем одинаковые физические законы внутри разных вселенных, но разные конфигурации частиц. Разные конфигурации частиц в настоящем отражают разные начальные условия в прошлом. Поэтому в рамках этой модели мультивселенной наш подход к вопросу, почему начальные условия в нашей Вселенной были такими или другими, меняется. Начальные условия могут и, как правило, действительно варьируются от вселенной к вселенной, поэтому нет какого-либо фундаментального объяснения того, что наблюдается та или иная конфигурация частиц. Требовать объяснения этому — это неправильно ставить вопрос; это привлекать логику одной единственной вселенной в контексте мультивселенной. Вопрос следует ставить так: есть ли где-нибудь на просторах мультивселенной вселенная, конфигурации частиц внутри которой и, следовательно, начальные условия, согласуются с теми, что мы здесь видим. А лучше всего спросить, можем ли мы показать, что таких вселенных много? Если да, то на глубокий вопрос о начальных условиях можно будет просто пожать плечами — в такой мультивселенной требовать объяснения начальных условий в нашей Вселенной — это всё равно что требовать объяснить то, что где-то в Нью-Йорке есть обувной магазин, в котором продаётся обувь вашего размера.
В инфляционной мультивселенной фундаментальные «константы» природы могут и, как правило, варьируются от одной дочерней вселенной, возникающей из пузырька, к другой. Вспомним из главы 3, что различие в условиях — разные значения поля Хиггса, пронизывающего каждый пузырёк, — приводят к различным массам частиц и свойствам взаимодействий. То же самое справедливо для бранной мультивселенной, циклической мультивселенной и ландшафтной мультивселенной, где разная форма дополнительных измерений в теории струн вместе с различиями в полях и потоках приводят ко вселенным с разными свойствами, такими как масса электрона, если он вообще существует, величина электромагнитного взаимодействия, если оно есть, значение космологической постоянной и так далее. В контексте этих мультивселенных вопрос об объяснении измеряемых свойств частиц и взаимодействий опять же является неправильным вопросом; это вопрос, порождённый логикой одной единственной Вселенной. Наоборот, следует задаться вопросом о том, есть ли в одной из этих мультивселенных такая вселенная, физические свойства которой совпадают с измеряемыми нами на опыте. А лучше было бы показать, что вселенных с нашими физическими свойствами много, или, по крайней мере, их много среди тех вселенных, которые поддерживают жизнь в известном нам виде. Но подобно тому, как бессмысленно спрашивать о том, каким единственным словом написана «Леди Макбет» Шекспира, также бессмысленно требовать от уравнений выделить те значения физических свойств, которые мы наблюдаем в нашей Вселенной.
Смоделированная и окончательная мультивселенные — это лошадки другой масти; эти мультивселенные не возникают из каких-либо определённых физических теорий. Однако у них тоже есть потенциал для изменения характера наших вопросов. Математические законы, управляющие отдельными вселенными в этих мультивселенных, варьируются. Таким образом, подобно варьированию начальных условий и фундаментальных констант, варьирование законов лишает смысла вопрос о том, почему здесь действует тот или иной закон. Разные вселенные имеют разные законы; у нас действуют те законы, которые действуют, потому что они среди тех, которые не противоречат нашему существованию.
В общем и целом мы видим, что модели мультивселенных, собранные в табл. 11.1, сводят к прозе три первостепенных вопроса стандартного научного подхода, которые кажутся глубоко мистическими в одновселенном подходе. Начальные условия, фундаментальные константы и даже математические законы в разных мультивселенных больше не нуждаются в объяснении.
Следует ли доверять математике?
Нобелевский лауреат Стивен Вайнберг однажды написал: «Наша ошибка не в том, что мы слишком серьёзно воспринимаем наши теории, а в том, что мы недостаточно серьёзно к ним относимся. Всегда тяжело осознавать, что числа и уравнения, с которыми мы играемся на письменном столе, имеют какое-то отношение к реальному миру».{102} Вайнберг имел в виду пионерские результаты Ральфа Альфера, Роберта Германа и Георгия Гамова по реликтовому излучению, описанные в главе 3. Хотя предсказанное излучение является прямым следствием общей теории относительности и принятой космологической физики, о нём стали говорить только после повторного теоретического открытия, через дюжину лет, и после его счастливого экспериментального наблюдения.
Разумеется, слова Вайнберга не следует воспринимать буквально. Хотя на его письменном столе лежат неординарные уравнения той математики, которая оказалась существенной для описания реального мира, но далеко не каждое уравнение, с которым мы, теоретики, возимся, поднимается до этого уровня. Определить, какая математика важна в отсутствие убедительных экспериментальных и наблюдательных результатов, — это столь же искусство, сколь и наука.
Действительно, этот вопрос является главным во всём, что мы обсуждали в этой книге; он также повлиял на выбор её названия. Широта выбора различных гипотез мультивселенных (табл. 11.1) может свидетельствовать о целой панораме скрытых реальностей. Однако в названии этой книги фигурирует реальность в единственном числе, что отражает уникальность исключительно глубокого смысла, стоящего за всеми ними: способность математики выявлять скрытые истины об устройстве мира. Научные открытия на протяжении нескольких столетий выявили это со всей очевидностью. Монументальные перевороты идей в физике неоднократно возникали только благодаря математике. То, как обхаживал математику сам Эйнштейн, как раз является показательным примером.
Когда в конце 1800-х годов Джеймс Клерк Максвелл осознал, что свет — это электромагнитная волна, его уравнения показали, что скорость света должна быть равной примерно 300 000 километров в секунду — очень близко к измеренному в экспериментах значению. Однако уравнения оставили без ответа следующий вопрос: 300 000 километров в секунду по отношению к чему? В качестве паллиативного решения было предложено, что существует невидимая субстанция — «эфир», — пронизывающая всё пространство, которая задаёт незримую систему координат. Но в самом начале двадцатого столетия Эйнштейн доказал, что учёным следует воспринимать уравнения Максвелла более серьёзно. Если уравнения Максвелла не используют систему координат, то в ней вообще нет никакой необходимости; скорость света, настойчиво утверждал Эйнштейн, составляет 300 000 километров в секунду по отношению к чему угодно. Хотя подробности этого уже имеют лишь исторический интерес, я привожу данный эпизод с важной целью: любому было доступно изучить уравнения Максвелла, но лишь гений Эйнштейна смог охватить их целиком. Осознав это свойство уравнений Максвелла, Эйнштейн сформулировал специальную теорию относительности, ниспровергнув многовековые размышления о пространстве, времени, материи и энергии.
В течение последующего десятилетия, развивая общую теорию относительности, Эйнштейн близко познакомился с многочисленными разделами математики, которые большинство физиков того времени знало плохо или не знало вообще. Нащупывая путь к окончательным уравнениям общей теории относительности, Эйнштейн проявил огромное мастерство в объединении разных математических конструкций твёрдой рукой физической интуиции. Спустя несколько лет, узнав хорошие новости о том, что наблюдения солнечного затмения 1919 года подтверждают предсказания общей теории относительности об искривлении траектории света от звёзд, Эйнштейн самоуверенно заявил, что если бы результаты наблюдений оказались другими, то ему «было бы очень жаль дорогого Господа, так как теория верна». Я уверен, что убедительные данные, противоречащие общей теории относительности, изменили бы настрой Эйнштейна, но это замечание хорошо отражает то, как набор математических уравнений, с их последовательной внутренней логикой, присущей им красотой и возможностью обширного применения, может излучать реальность.
Тем не менее, был предел тому, насколько сильно Эйнштейн желал следовать своим собственным математическим уравнениям. Эйнштейн не воспринимал общую теорию относительности «достаточно серьёзно», чтобы поверить в предсказанные ею чёрные дыры или в предсказанное расширение Вселенной. Как мы видели, другие, включая Леметра, Шварцшильда и Фридмана, восприняли уравнение Эйнштейна более глубоко, нежели он сам, и их достижения задали курс, которому следуют космологические исследования уже почти сто лет. Сам Эйнштейн, наоборот, в течение последних примерно двадцати лет своей жизни полностью погрузился в математические расчёты, увлечённо занимаясь построением единой теории физики. Оценивая эту работу на основе того, что нам известно теперь, трудно удержаться и не сделать вывод, что в течение этих лет Эйнштейн был слишком увлечён — можно сказать, был ослеплён — лесом уравнений, в которые он был постоянно погружён. Поэтому даже Эйнштейн в разные моменты его жизни принимал неверные решения относительно того, к каким уравнениям относиться серьёзно, а к каким нет.
Третья по счёту революция в современной теоретической физике, квантовая механика, является другим примером, прямо относящимся ко всему, что рассказано в этой книге. Шрёдингер выписал своё уравнение распространения квантовых волн в 1926 году. В течение десятилетий это уравнение считалось применимым только на малых расстояниях, к молекулам, атомам и частицам. Но в 1957 году Хью Эверетт воплотил напутствие Эйнштейна по оценке максвелловских уравнений, данное за пол века до этого: воспринимайте математику серьёзно. Эверетт доказал, что уравнение Шрёдингера должно быть применимо ко всему, потому что всё, что материально, независимо от размера, сделано из молекул, атомов и субатомных частиц. Как мы видели, это привело Эверетта к многомировому подходу к квантовой механике и квантовой мультивселенной. Более чем пятьдесят лет спустя мы по-прежнему не знаем, верен ли подход Эверетта. Но если воспринимать математический аппарат квантовой теории серьёзно — полностью серьёзно, — возможно, что Эверетт стал первооткрывателем одного из наиболее глубоких направлений научного исследования.
Другие модели мультивселенных также основываются на убеждении в том, что математика плотно вплетена в ткань реальности. В модели окончательной мультивселенной эта идея доведена до самого конца; согласно окончательной мультивселенной, математика является реальностью. Но даже при не столь радикальной точке зрения на характер взаимосвязи между математикой и реальностью другие модели мультивселенной (см. табл. 11.1) также были вызваны к жизни благодаря числам и уравнениям, над которыми колдуют теоретики за своими письменными столами — а также пишут в блокнотах, на досках, программируют на компьютерах. Даже если мы будем думать об общей теории относительности, квантовой механике, теории струн или математических методах в более широком контексте, то содержимое табл. 11.1 возникнет только в том случае, если мы допустим, что математические теоретизирования могут проявить скрытые истины. Только время покажет, воспринимаются ли на такой линии рассуждений соответствующие математические теории слишком серьёзно или, возможно, недостаточно серьёзно.
Если что-то или все из тех математических идей, которые толкнули нас на мысли о параллельных мирах, окажется важным для описания реальности, то мы сможем дать определённый ответ на знаменитый вопрос Эйнштейна о том, имеет ли Вселенная те свойства, какие имеет, просто потому, что другие вселенные невозможны? И ответ будет таков — нет. Наша Вселенная не является единственно возможной. Её свойства могли бы быть другими. Во многих моделях мультивселенных свойства других вселенных могут быть другими. В свою очередь, поиск фундаментальных объяснений того, почему определённые вещи таковы, каковы они есть, станет бессмысленным. Вместо этого в нашем понимании бескрайнего космоса прочное место займут статистическая вероятность или чистая случайность.
Я не знаю, так это будет или нет. Никто не знает. Но только благодаря дерзким усилиям мы сможем узнать свои собственные пределы. Только благодаря тщательному осмыслению теорий, даже тех, которые влекут нас в странные и неведомые просторы, у нас появится шанс осознать размах реальности.
Литература для дальнейшего чтения
Идея параллельных вселенных вызывает широкий научный интерес. Увеличивается количество литературы, в которой затрагиваются те или иные темы. В основном она предназначена для неспециалистов, хотя также подойдёт тем, кто уже имеет определённое образование в этом вопросе. В дополнение к процитированным в примечаниях источникам ниже приводится ряд книг — лишь некоторых из многих замечательных сочинений на эту тему, — с помощью которых читатель может продолжить изучение вопросов, обсуждавшихся в «Скрытой реальности».
Albert, David. «Quantum Mechanics and Experience». Cambridge, Mass.: Harvard University Press, 1994.
Alexander H. G. «The Leibniz — Clarke Correspondence». Manchester: Manchester University Press, 1956.
Barrow, John. «Pi in the Sky». Boston: Little, Brown, 1992.
Barrow, John. «The World Within the World». Oxford: Clarendon Press, 1988.
Barrow, John, and Frank Tipler. «The Anthropic Cosmological Principle». Oxford: Oxford University Press, 1986.
Bartusiak, Marcia. «The Day We Found the Universe». New York: Vintage, 2010.
Bell, John. «Speakable and Unspeakable in Quantum Mechanics». Cambridge, Eng.: Cambridge University Press, 1993.
Bronowski, Jacob. «The Ascent of Man». Boston: Little, Brown, 1973.
Byrne, Peter. «The Many Worlds of Hugh Everett III». New York: Oxford University Press, 2010.
Callender, Craig, and Nick Huggett. «Physics Meets Philosophy at the Planck Scale». Cambridge, Eng.: Cambridge University Press, 2001.
Carroll, Sean. «From Eternity to Here». New York: Dutton, 2010.
Clark, Ronald. «Einstein: The Life and Times». New York: Avon, 1984.
Cole, K. C. «The Hole in the Universe». New York: Harcourt, 2001.
Crease, Robert P., and Charles C. Mann. «The Second Creation». New Brunswick, N. J.: Rutgers University Press, 1996.
Davies, Paul. «Cosmic Jackpot». Boston: Houghton Mifflin, 2007.
Deutsch, David. «The Fabric of Reality». New York: Allen Lane, 1997. (Рус. пер.: Дойч Д. «Структура реальности». Ижевск: РХД, 2001.)
DeWitt, Bryce, and Neill Graham, eds. «The Many-Worlds Interpretation of Quantum Mechanics». Princeton: Princeton University Press, 1973.
Einstein, Albert. «The Meaning of Relativity». Princeton: Princeton University Press, 1988. (Рус. пер.: Эйнштейн А. «Сущность теории относительности». М.: Иностранная литература, 1955.)
Einstein, Albert. «Relativity». New York: Crown, 1961.
Ferris, Timothy. «Coming of Age in the Milky Way». New York: Anchor, 1989.
Ferris, Timothy. «The Whole Shebang». New York: Simon & Schuster, 1997.
Feynman, Richard. «The Character of Physical Law». Cambridge, Mass.: MIT Press, 1995. (Рус. пер.: Фейнман P. «Характер физических законов». М.: Наука, 1987.)
Feynman, Richard. «QED». Princeton: Princeton University Press, 1986. (Рус. пер.: Фейнман P. «КЭД — странная теория света и вещества». М.: Наука, 1988.)
Gamow, George. «Mr. Tompkins in Paperback». Cambridge, Eng.: Cambridge University Press, 1993.
Gleick, James. «Isaac Newton». New York: Pantheon, 2003.
Gribbin, John. «In Search of the Multiverse». Hoboken, N. J.: Wiley, 2010.
Gribbin, John. «Schrodinger’s Kittens and the Search for Reality». Boston: Little, Brown, 1995.
Guth, Alan H. «The Inflationary Universe». Reading, Mass.: Addison — Wesley, 1997.
Hawking, Stephen. «A Brief History of Time». New York: Bantam Books, 1988. (Рус. пер.: Хокинг С. «Краткая история времени: от Большого взрыва до чёрных дыр». СПб.: Амфора, 2010.)
Hawking, Stephen. «The Universe in a Nutshell». New York: Bantam Books, 2001. (Рус. пер.: Хокинг С. «Мир в ореховой скорлупке: Новейшие тайны Вселенной в кратком и красочном изложении». СПб.: Амфора, 2011.)
Isaacson, Walter. «Einstein». New York: Simon & Schuster, 2007.
Kaku, Michio. «Parallel Worlds». New York: Anchor, 2006. (Рус. пер.: Каку М. «Параллельные миры: Об устройстве мироздания, высших измерениях и будущем Космоса». М: София, 2008.)
Kirschner, Robert. «The Extravagant Universe». Princeton: Princeton University Press, 2002.
Krauss, Lawrence. «Quintessence». New York: Perseus, 2000.
Kurzweil, Ray. «The Age of Spiritual Machines». New York: Viking, 1999.
Kurzweil, Ray. «The Singularity Is Near». New York: Viking, 2005.
Lederman, Leon, and Christopher Hill. «Symmetry and the Beautiful Universe». Amherst, N. Y.: Prometheus Books, 2004.
Livio, Mario. «The Accelerating Universe». New York: Wiley, 2000.
Lloyd, Seth. «Programming the Universe». New York: Knopf, 2006.
Moravec, Hans. «Robot». New York: Oxford University Press, 1998.
Pais, Abraham. «Subtle Is the Lord». Oxford: Oxford University Press, 1982.
Penrose, Roger. «The Emperor’s New Mind». New York: Oxford University Press, 1989. (Рус. пер.: Пенроуз P. «Новый ум короля: О компьютерах, мышлении и законах физики». М.: URSS, 2011.)
Penrose, Roger. «Shadows of the Mind». New York: Oxford University Press, 1994. (Рус. пер.: Пенроуз P. «Тени разума. В поисках науки о сознании». Ижевск: РХД, 2005.)
Randall, Lisa. «Warped Passages». New York: Ecco, 2005. (Рус. пер.: Рэндалл Л. «Закрученные пассажи: Проникая в тайны скрытых размерностей пространства». М.: URSS, 2011.)
Rees, Martin. «Before the Beginning». Reading, Mass.: Addison — Wesley, 1997.
Rees, Martin. «Just Six Numbers». New York: Basic Books, 2001.
Schrodinger, Erwin. «What Is Life?» Cambridge, Eng.: Canto, 2000. (Рус. пер.: Шрёдингер Э. «Что такое жизнь с точки зрения физики?» М.: Римис, 2009.)
Siegfried, Tom. «The Bit and the Pendulum». New York: John Wiley & Sons, 2000.
Singh, Simon. «Big Bang». New York: Fourth Estate, 2004.
Susskind, Leonard. «The Black Hole War». New York: Little, Brown, 2008.
Susskind, Leonard. «The Cosmic Landscape». New York: Little, Brown, 2005.
Thorne, Kip. «Black Holes and Time Warps». New York: W. W. Norton, 1994.
Tyson, Neil deGrasse. «Death by Black Hole». New York: W. W. Norton, 2007.
Vilenkin, Alexander. «Many Worlds in One». New York: Hill and Wang, 2006.
von Weizsacker, Carl Friedrich. «The Unity of Nature». New York: Farrar, Straus and Giroux, 1980.
Weinberg, Steven. «Dreams of a Final Theory». New York: Pantheon, 1992. (Рус. пер.: Вайнберг С. «Мечты об окончательной теории: Физика в поисках самых фундаментальных законов природы». М.: URSS, 2008.)
Weinberg, Steven. «The First Three Minutes». New York: Basic Books, 1993. (Рус. пер.: Вайнберг С. «Первые три минуты». М.: ЭКСМО, 2011.)
Wheeler, John. «A Journey into Gravity and Spacetime». New York: Scientific American Library, 1990.
Wilczek, Frank. «The Lightness of Being». New York: Basic Books, 2008.
Wilczek, Frank, and Betsy Devine. «Longing for the Harmonies». New York: W. W. Norton, 1988.
Yau, Shing-Tung, and Steve Nadis. «The Shape of Inner Space». New York: Basic Books, 2010.
Комментарии
1
Возможность того, что наша Вселенная представляет собой лист, парящий в многомерном пространстве, восходит к статье двух знаменитых советских физиков В. А. Рубакова и М. Е. Шапошникова «Do We Live Inside a Domain Wall?» (V A. Rubakov and М. E. Shaposhnikov, «Physics Letters В» 125 (May 26, 1983): 136) и не использует теорию струн. Рассматриваемый в главе 5 сценарий возникает из теоретико-струнных построений середины 1990-х годов.
(обратно)2
Эта цитата взята из мартовского выпуска «Literary Digest» 1933 года. Следует отметить, что точность цитаты недавно была поставлена под сомнение датским историком науки Хельге Крагхом (см. его книгу: Helge Kragh, «Cosmology and Controversy». Princeton: Princeton University Press, 1999), который считает, что она может являться перефразировкой более ранней заметки в газете «Newsweek» того же года, где Эйнштейн высказывался о происхождении космических лучей. Однако доподлинно известно, что в этом же году Эйнштейн отрёкся от веры в статичную вселенную и принял динамичную космологию, возникающую из его исходных уравнений общей теории относительности.
(обратно)3
Этот закон определяет силу гравитационного притяжения F между двумя объектами с заданными массами m1 и m2 и расстоянием r между ними. Математически закон имеет вид F = Gm1m2/r2, где G обозначает константу Ньютона — экспериментально измеренное число, характеризующее силу гравитационного взаимодействия.
(обратно)4
Для математически подкованного читателя приведём уравнения Эйнштейна:
где g — это метрика пространства-времени, Rμν — тензор кривизны Риччи, R — скалярная кривизна, G — константа Ньютона, Tμν — тензор энергии-импульса.
(обратно)5
За десятилетия, прошедшие с момента этого знаменитого подтверждения общей теории относительности, возникли вопросы, касающиеся надёжности полученных результатов. Чтобы увидеть световой луч от удалённой звезды, огибающий Солнце, наблюдения должны были проводиться во время солнечного затмения; к сожалению, плохая погода затруднила получение чётких фотографий затмения 1919 года. Вопрос в том, могли ли Эддингтон и его сотрудники внести систематическую ошибку под влиянием ожидаемого результата: отбраковывая фотографии, кажущиеся ненадёжными по причине интерференции, вызванной погодными условиями, они могли бы исключить несоразмерное количество фотографий с данными, которые казались противоречащими теории Эйнштейна. Недавнее подробное исследование Даниэля Кеннефика (см.: , paper arXiv:0709.0685, в котором, помимо прочих рассмотрений, делается современная переоценка фотографических пластинок, сделанных в 1919 году) убедительно свидетельствует что подтверждение теории, сделанное в 1919 году, на самом деле является надёжным.
(обратно)6
Для заинтересованного читателя приведём уравнения Эйнштейна общей теории относительности, которые в рассматриваемом случае выглядят так:
Переменная a(t) является масштабным фактором вселенной — её значение, как указывает название, устанавливает масштаб расстояния между объектами (если значения a(t) в два разных момента времени отличаются, например, в 2 раза, то расстояние между двумя частными галактиками будет отличаться между этими временами также в 2 раза), G — это константа Ньютона, ρ — плотность материи/энергии, и k является параметром, значение которого может быть 1, 0 или −1, в зависимости от того, является ли форма пространства сферической, евклидовой («плоской») или гиперболической. Обычно считается, что вид этого уравнения был найден Александром Фридманом и, собственно, называется уравнением Фридмана.
(обратно)7
Внимательный читатель может отметить два момента. Во-первых, в общей теории относительности, как правило, мы определяем координаты, которые сами зависят от находящегося в пространстве вещества: мы используем галактики в качестве носителей координат (как будто на каждой галактике «нарисован» частный набор координат — так называемые движущиеся системы координат). Поэтому для задания определённой области пространства обычно ссылаются на присутствующую в ней материю. Тогда более точная перефразировка текста такова: область пространства, в которой находится некоторая группа из N галактик в момент времени t1, будет иметь больший объём в более поздний момент времени t2. Во-вторых, интуитивно понятное утверждение, касающееся плотности материи и энергии, изменяющиеся при расширении или сжатии пространства, содержит неявное предположение насчёт уравнения состояния материи и энергии. Есть ситуации и скоро мы столкнёмся с одной из них, когда пространство может расширяться или сжиматься, а плотность некоторого вклада энергии — плотность энергии так называемой космологической постоянной — остаётся неизменной. Действительно, есть даже более экзотические сценарии, в которых пространство расширяется а плотность энергии при этом растёт. Такое происходит, потому что при определённых обстоятельствах гравитация служит источником энергии. Важный момент этого параграфа состоит в том, что уравнения общей теории относительности в исходном виде противоречат статичной вселенной.
(обратно)8
Двумерный тор обычно изображается как пустой бублик. Двухшаговый процесс показывает, что эта картинка согласована с приведённым в тексте книги описанием. Когда, достигнув правого края экрана, вы попадаете назад на левый край, это равносильно отождествлению всего правого края с левым краем. Если бы экран был гибким (например, из тонкого пластика), то такое отождествление могло бы быть буквальным, если скатать экран в цилиндр и объединить вместе правый и левый края. Когда, ступив на верхний край, вы попадаете в нижний, то это тоже равносильно отождествлению этих краёв. Это достигается явным образом на втором шаге, в котором мы скручиваем цилиндр и соединяем верхний и нижний круговые края. Получившаяся фигура выглядит как обычный бублик. Обманчивый аспект этих манипуляций состоит в том, что поверхность бублика выглядит искривлённой; если его поверхность покрыть отражающей краской, то ваше отражение будет искажено. Это артефакт реализации тора в виде объекта, расположенного в объемлющем трёхмерном пространстве. В действительности, являясь двумерной поверхностью, тор не искривлён. Он плоский. Что очевидно, если его представить в виде плоского экрана для видеоигр. Именно поэтому в тексте книги я выбрал более фундаментальное описание в виде фигуры, края которой попарно отождествляются.
(обратно)9
Искушённый в математике читатель заметит, что под словами «подходящим образом нарезать и скомпоновать» я подразумеваю факторпространства, которые возникают при факторизации односвязных накрывающих пространств по дискретным группам изометрии.
(обратно)10
Образно говоря, можно считать, что в силу квантовой механики частицы всегда находятся в состоянии, которое мне нравится называть «квантовым дрожанием»: что-то вроде неизбежных случайных квантовых вибраций, что придаёт самому понятию частицы с определённым положением и скоростью (импульсом) приближённый смысл. В этом смысле изменения в положении/скорости, достаточно малые, чтобы быть на равных с квантовыми флуктуациями, являются квантово-механическим «шумом» и, следовательно, не имеют значения.
На более точном языке, если погрешность в измерениях положения умножить на погрешность в измерениях импульса, то результат — неопределённость — всегда больше, чем число, называемое постоянной Планка (в честь Макса Планка, одного из пионеров квантовой физики). Это, в частности, означает, что точное разрешение в процессе измерения положения частицы (небольшая погрешность) обязательно приведёт к большой неопределённости при измерении импульса частицы и, за компанию, её энергии. Поскольку энергия всегда ограничена, разрешение при измерении положения, таким образом, тоже является ограниченным.
Также отметим, что эти понятия всегда будут применяться в конечной пространственной области — как правило, в областях, размер которых сопоставим с современным космическим горизонтом (как в следующем разделе). Область конечного размера, пусть даже большая, подразумевает максимальную неопределённость при измерении положения. Если предполагается, что частица находится в данной области, то неопределённость её положения конечно же будет не больше размера самой области. Согласно принципу неопределённости, такая максимальная неопределённость в положении приводит к минимальной неопределённости при измерении импульса. Помимо ограниченного разрешения при измерении местоположения, мы видим редукцию от бесконечного к конечному числу возможных различных конфигураций положений и скоростей частицы.
Вы всё ещё можете задаваться вопросом о том, что препятствует построению прибора, способного измерять положения частицы с ещё большей точностью. Это также касается энергии. Как описано в книге, если вы хотите измерить положение частицы с большей точностью, необходимо использовать более точный прибор. Для определения местоположения мухи в комнате можно включить обычный верхний свет. Для определения положения электрона необходимо осветить его узким лучом мощного лазера. Для ещё более точного определения положения электрона надо использовать ещё более мощный лазер. Когда более мощный лазер бьёт по электрону, его скорость сильно искажается. Таким образом, ключевой момент здесь в том, что точность определения положения частицы достигается за счёт огромных изменений скорости частицы — и, следовательно, огромных изменений её энергии. Если есть предел того, сколько энергии может иметь частица, а такой предел есть всегда, то также есть предел того, насколько точно можно измерить её положение.
Таким образом, ограниченность энергии в ограниченной пространственной области приводит к конечному разрешению при измерении как положения, так и скорости.
(обратно)11
Наиболее прямой способ проделать это вычисление состоит в использовании результата, который без привлечения технических подробностей будет описан в главе 9: энтропия чёрной дыры — логарифм числа различных квантовых состояний — пропорциональна площади её поверхности, измеренной в единицах планковской площади. Заполняющая наш космический горизонт чёрная дыра будет иметь радиус примерно 1028 сантиметра, или примерно 1061 планковских длин. Таким образом, её энтропия будет примерно 10122 в единицах планковской площади. Следовательно, полное число различных состояний составляет примерно 10, возведённое в степень 10122, или 1010122.
(обратно)12
Можно поинтересоваться, почему не учитываются поля. Как мы увидим, описания частиц и полей дополнительны друг к другу — поле может описываться в терминах определённых частиц, из которых оно состоит, подобно тому как океанские волны могут описываться в терминах составляющих их молекул воды. Выбор описания в терминах частиц или полей является в основном вопросом удобства.
(обратно)13
Расстояние, проходимое светом за заданный промежуток времени, сильно зависит от скорости расширения пространства. В последующих главах мы обсудим доводы, указывающие на то, что темп пространственного расширения ускоряется. Если так, то существует предел того, насколько далеко свет может распространиться в пространстве, даже если ждать сколь угодно долго. Удалённые области пространства будут удаляться от нас так быстро, что излучаемый нами свет не сможет достичь их; аналогичным образом испущенный ими свет не сможет достичь нас. Это будет означать, что космические горизонты — та часть пространства, с которой можно обмениваться световыми сигналами, — не будут расти бесконечно. (Заинтересовавшийся читатель может найти соответствующие формулы в комментарии {49}.)
(обратно)14
Дж. Эллис и Дж. Бандрит исследовали повторяющиеся миры в бесконечной классической вселенной; Ж. Гаррига и А. Виленкин изучали такие миры в квантовом контексте.
(обратно)15
В ранних работах Дикке рассматривал идею осциллирующей Вселенной, которая многократно проходит через вереницу циклов Большой взрыв — расширение — сжатие — схлопывание и снова Большой взрыв. В любом цикле будет присутствовать заполняющее пространство остаточное излучение.
(обратно)16
Проблема горизонта довольно тонкая, и приведённое мной описание решения на основе инфляционной космологии несколько отличается от стандартного, поэтому, возможно, читателя заинтересует чуть более подробное обсуждение этого вопроса. Сначала опять постановка проблемы: рассмотрим две области в ночном небе, настолько удалённые друг от друга, что они никогда не вступали в контакт. Для определённости скажем, что в каждой области находится наблюдатель, который контролирует термостат, поддерживающий температуру в его области. Эти наблюдатели хотят, чтобы две данные области имели одинаковую температуру, но поскольку наблюдатели не имели возможности контактировать, они не знают на какую температуру устанавливать свои термостаты. Естественная идея состоит в том, что поскольку миллиарды лет назад наблюдатели находились гораздо ближе, то тогда им было проще установить контакт и сравнять температуры в своих областях. Однако, как отмечалось в основном тексте, в стандартной теории Большого взрыва эти рассуждения не проходят. И этому есть причины. В стандартной теории Большого взрыва Вселенная расширяется, но в силу гравитационного притяжения темп расширения со временем замедляется. Это очень похоже на подбрасывание мяча вверх. Во время подъёма он сначала быстро удаляется от вас, но в силу притяжения Земли постепенно замедляется. Замедление пространственного расширения имеет серьёзные последствия. Для пояснения я воспользуюсь аналогией с подброшенным мячом. Представьте, что мяч достигает верхней точки за шесть секунд. Поскольку изначально (после того как отрывается от вашей руки) он двигался быстро, он может пройти первую половину расстояния за две секунды, но из-за уменьшения скорости пройдёт четыре секунды, прежде чем он одолеет вторую половину пути. Таким образом, на половине временного интервала, через три секунды, он пролетел больше половины пути. Аналогичным образом происходит процесс замедляющегося во времени пространственного расширения: в середине космической истории два наших наблюдателя будут разделены расстоянием бо́льшим, чем половина современного расстояния между ними. Давайте подумаем, что это значит. Два наблюдателя будут ближе друг к другу, но им будет тяжелее — а не легче — установить контакт. Посылаемый одним из наблюдателей сигнал будет располагать половиной от прошедшего интервала времени для достижения второго наблюдателя, но расстояние, которое он должен будет преодолеть, больше половины от современного расстояния. Половина времени для взаимодействия на расстоянии, превышающем половину текущего расстояния между ними, осложняет установление контакта между наблюдателями.
Таким образом, расстояние между наблюдателями — лишь один из факторов при анализе возможности наблюдателей влиять друг на друга. Другой фактор — время, прошедшее с момента Большого взрыва, поскольку это ограничивает дальность распространения сигнала. В стандартной теории Большого взрыва, хотя в прошлом всё действительно располагалось ближе друг к другу, Вселенная также и расширялась быстрее, поэтому, пропорционально говоря, для распространения влияния было меньше времени.
Решение этого вопроса, предложенное в инфляционной космологии, состоит в добавлении некоторой фазы в самые ранние моменты космической истории, в которой темп расширения не замедляется, как скорость подброшенного вверх мяча; наоборот, пространственное расширение начинается неспешно, а затем постепенно наращивает скорость: расширение ускоряется. Согласно только что приведённым рассуждениям, на половине пути такой инфляционной фазы два наших наблюдателя будут разделены расстоянием меньшим половины расстояния между ними в момент завершения инфляционной фазы. А если есть половина времени для распространения сигнала на менее чем половину расстояния, это означает, что в ранние моменты времени контакт мог быть легче установлен. Можно сказать, что ускорение расширения в более ранние моменты времени означает, что для распространения сигнала было больше времени, а не меньше. Это позволяло удалённым на настоящий момент областям легко контактировать в ранней Вселенной, что объясняет их одинаковую температуру сейчас.
Поскольку по сравнению со стандартной теорией Большого взрыва ускоренное расширение приводит к ещё большему пространственному расширению, эти области будут гораздо ближе в начальный момент при инфляции, чем в аналогичный момент времени в стандартной теории Большого взрыва. Эта разница в расстоянии в ранней Вселенной является эквивалентным способом для понимания того, почему контакт между областями, невозможный при стандартном Большом взрыве, легко достигается в инфляционной теории. Если в некоторый момент после начала расстояние между двумя областями меньше, им легче обмениваться сигналами.
Применяя уравнения, описывающие расширение в произвольные ранние моменты времени (представьте, для определённости, что пространство имеет форму сферы), мы увидим, что две области в инфляционной модели будут удаляться друг от друга медленнее, чем при стандартном Большом взрыве: именно поэтому они удаляются на меньшее расстояние по сравнению с теорией Большого взрыва. В этом смысле в инфляционном подходе есть период времени, когда темп разлёта областей меньше, чем в картине обычного Большого взрыва.
При описании инфляционной космологии очень часто всё внимание целиком сосредоточено на фантастическом увеличении скорости расширения по сравнению со стандартными подходами, а не на уменьшении. Различие в описании возникает из того, какие физические свойства двух подходов сравниваются. Если сравнить траектории двух областей, расположенных в ранней Вселенной на некотором расстоянии друг от друга, то в инфляционной теории эти области разлетаются гораздо быстрее, чем в стандартной теории Большого взрыва; на сегодняшний день они находятся гораздо дальше друг от друга, чем после обычного Большого взрыва. Но если рассматривать области, расположенные на определённом расстоянии сегодня (подобно двум участкам в противоположных концах ночного неба), то становится важным приведённое мной описание. А именно: в определённый момент времени в очень ранней Вселенной эти области были гораздо ближе друг к другу, и в теории с инфляционным расширением разлетались гораздо медленнее, чем в теории без такового. Роль инфляционного расширения в том, чтобы компенсировать медленный старт, разгоняя затем эти области быстрее и быстрее, гарантируя, что они окажутся в тех же местах на небе как и в стандартной теории Большого взрыва.
Более полное обсуждение проблемы горизонта включало бы подробное рассмотрение условий возникновения инфляционного расширения, а также последующих процессов, которые, например, приводят к возникновению реликтового излучения. Однако цель приведённых выше рассуждений — подчеркнуть существенное различие между ускоряющимся и замедляющимся расширением.
(обратно)17
Отметим, что, сжимая пакет, вы добавляете в систему энергию, и поскольку масса и энергия приводят к гравитационному искривлению, то увеличение веса будет частично происходить благодаря увеличению энергии. Однако увеличение давления также даёт вклад в увеличение веса. (Точности ради заметим, что следует представлять этот «эксперимент» в вакуумной камере, поэтому нет необходимости рассматривать выталкивающую силу со стороны воздуха вокруг пакета.) В повседневных примерах обсуждаемое увеличение веса крайне мало. Однако на космических масштабах оно может оказаться весьма значительным. На самом деле, оно играет роль при объяснении того, почему в определённых ситуациях звёзды обязательно схлопываются в чёрные дыры. Как правило, равновесие в звёздах поддерживается благодаря балансу между давлением, направленным наружу, порождённым ядерными процессами в звёздном ядре, и направленной внутрь гравитацией, порождаемой массой звезды. По мере того как звезда расходует ядерное топливо, положительное давление падает, что приводит к её сжатию. При этом вещество внутри звезды сжимается плотнее, вследствие чего гравитационное притяжение возрастает. Для избежания дальнейшего сжатия, необходимо дополнительное давление наружу (что называется положительным давлением, как в следующем абзаце в основном тексте). Однако дополнительное положительное давление само создаёт дополнительную силу гравитационного притяжения и таким образом приводит к необходимости ещё большего дополнительного положительного давления. В определённых ситуациях это приводит к спиральной нестабильности, и положительное давление, на котором обычно держится противодействие звезды внутреннему гравитационному сжатию, настолько усиливает внутреннее притяжение, что становится неизбежным полный гравитационный коллапс. Звезда коллапсирует, и образуется чёрная дыра.
(обратно)18
В описанном только что подходе к инфляции нет фундаментального объяснения, почему значение поля инфлатона должно находиться на возвышенной части кривой потенциальной энергии, а также нет объяснения, почему кривая потенциальной энергии имеет именно такую форму. Всё это предположения теории. В последующих версиях теории инфляции, в особенности версии, разработанной Андреем Линде, которая называется хаотическая инфляция, более «обычная» кривая потенциальной энергии (параболическая форма без плоских участков, выводимая из простейших математических уравнений для потенциальной энергии) также может приводить к инфляции. Для запуска инфляционного расширения значение поля инфлатона также должно находиться высоко на этой кривой потенциальной энергии, однако неимоверно горячая среда в ранней Вселенной естественным образом создаёт для этого все условия.
(обратно)19
Внимательного читателя заинтересует следующая подробность. Быстрое расширение пространства в инфляционной космологии приводит к сильному остыванию (подобно тому как быстрое сжатие пространства, или чего-нибудь ещё, вызывает повышение температуры). Однако, когда инфляция подходит к завершению, поле инфлатона колеблется около минимума своей кривой потенциальной энергии, трансформируя свою энергию в газ частиц. Этот процесс называется «повторным разогревом», потому что порождённые таким образом частицы получают кинетическую энергию и, следовательно, могут характеризоваться температурой. По мере того как пространство продолжает расширяться обычным (не-инфляционным) способом, в сценарии Большого взрыва температура газа частиц постепенно снижается. Однако важный момент в том, что возникшая при инфляции однородность задаёт однородные условия для этого процесса, и поэтому приводит к однородным результатам.
(обратно)20
Значение поля инфлатона определяет количество энергии и отрицательное давление, которыми оно наполняет пространство. Чем больше энергия, тем быстрее темп расширения пространства. В свою очередь быстрое расширение пространства оказывает обратное влияние на само поле инфлатона: чем быстрее расширение пространства, тем сильнее флуктуации значений поля инфлатона.
(обратно)21
Давайте рассмотрим вопрос, который, возможно, уже возникал у вас, и к которому мы вернёмся в главе 10. Когда пространство испытывает инфляционное расширение, его полная энергия возрастает: чем больше объём пространства, заполненного полем инфлатона, тем больше полная энергия (если пространство бесконечно, энергия тоже бесконечна — в этом случае следует говорить об энергии, содержащейся в конечной области пространства, по мере того как эта область растёт). Что естественным образом приводит к следующему вопросу: где источник энергии? В аналогичной ситуации с бутылкой шампанского источник дополнительной энергии в бутылке обеспечивается усилиями ваших мускулов. Что играет роль мускулов в расширяющемся космосе? Ответ — гравитация. Подобно тому как ваши мускулы обеспечивают расширение доступного пространства в бутылке (путём вытаскивания пробки), гравитация является движущей силой расширения доступного пространства в космосе. При этом важно понимать, что энергия гравитационного поля может быть сколь угодно отрицательно большой. Рассмотрим две частицы, падающие друг на друга при взаимном гравитационном притяжении. Гравитация заставляет эти частицы приближаться друг к другу всё быстрее, при этом их кинетическая энергия становится всё более положительной. Гравитационное поле может обеспечить частицы такой положительной энергией за счёт расходования своего собственного энергетического резерва, который в таком процессе становится сколь угодно отрицательным: чем сильнее частицы сближаются, тем более отрицательной становится гравитационная энергия (эквивалентно, тем более положительна энергия, которую надо приложить, чтобы преодолеть силу гравитации и заново разнести частицы). Таким образом, гравитация подобна банку, который предоставляет безграничную кредитную линию и может давать бесконечное число денег; гравитационное поле может дать бесконечное количество энергии, потому что его собственная энергия может становиться при этом всё более отрицательной. Именно в этом состоит источник энергии, запускающий инфляционное расширение.
(обратно)22
Для математически подготовленного читателя отметим, что более точное описание горизонтальных осей на рис. 3.5 таково: рассмотрим двумерную сферу, состоящую из точек пространства в момент времени, когда реликтовое излучение начало свободно распространяться. Подобно любой двумерной сфере, удобный набор координат на этой поверхности — это угловые переменные сферической системы координат. Тогда температура реликтового излучения может рассматриваться как функция этих угловых переменных и, соответственно, может быть разложена в ряд Фурье по сферическим гармоникам Ylm(θ, ϕ). Вертикальная ось на рис. 3.5 отражает величину коэффициента каждой моды в этом разложении — перемещение вправо вдоль горизонтальной оси соответствует уменьшению углового разделения. Технические подробности могут быть найдены, например, в отличной книге Додельсона: Scott Dodelson, «Modern Cosmology». San Diego, Calif.: Academic Press, 2003.
(обратно)23
Напомним, что при обсуждении лоскутной мультивселенной предполагалось, что компоновки частиц варьируются случайным образом от лоскутка к лоскутку. Связь между лоскутной и инфляционной мультивселенными также позволяет прояснить это предположение. Пузырёк-вселенная образуется в данной области, когда падает значение поля инфлатона; когда это происходит, энергия инфлатона трансформируется в частицы. Точный набор этих частиц в любой момент времени определяется точным значением инфлатона во время процесса трансформации. Поскольку поле инфлатона испытывает квантовые флуктуации, при спускании оно начинает испытывать случайные колебания — такие же случайные колебания, которые приводят к образованию структуры из чуть более горячих и чуть более холодных пятнышек на рис. 3.4. Применительно к лоскуткам внутри пузырька-вселенной это будет соответствовать тому, что на значении инфлатона будут отражаться случайные квантовые колебания. Такая случайность обеспечит случайность получающихся распределений частиц. Именно поэтому мы ожидаем, что любая конфигурация частиц, например такая, которая отвечает за то, что мы видим вокруг нас прямо сейчас, будет повторяться так же часто, как любая другая.
(обратно)24
Я благодарен Вальтеру Исааксону за личное обсуждение этого и ряда других исторических вопросов, связанных с Эйнштейном.
(обратно)25
Давайте рассмотрим этот вопрос подробнее. Глэшоу, Салам и Вайнберг предположили, что электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия. Электрослабая теория была подтверждена в экспериментах на ускорителе в конце 1970-х и начале 1980-х годов. Глэшоу и Джорджи пошли дальше и предложили, что электрослабое и сильное взаимодействия являются проявлениями ещё более фундаментального взаимодействия, в рамках подхода, который был назван великим объединением. Однако простейшая версия великого объединения была отброшена, когда учёным не удалось экспериментально подтвердить одно из предсказаний — что протоны должны время от времени распадаться. Тем не менее есть много других вариантов великого объединения, которые пока экспериментально не отвергнуты, например потому, что предсказываемая ими скорость распада протона настолько мала, что чувствительность современного экспериментального оборудования недостаточна для обнаружения распада. Однако даже если великое объединение не подкрепляется экспериментальными данными, уже нет никаких сомнений, что три негравитационных взаимодействия могут быть описаны на едином математическом языке квантовой теории поля.
(обратно)26
Открытие теории суперструн дало толчок к развитию других, тесно связанных теоретических подходов, направленных на поиски единой теории фундаментальных взаимодействий. В частности, суперсимметричная квантовая теория поля и её гравитационное расширение (супергравитация) глубоко изучались в середине 1970-х годов. Суперсимметричная квантовая теория поля и супергравитация основаны на новом принципе суперсимметрии, который был открыт в рамках теории суперструн, но эти подходы подключают суперсимметрию к обычным теориям точечных частиц. Позже в этой главе мы кратко обсудим суперсимметрию, но для заинтересовавшихся читателей я здесь замечу, что суперсимметрия — это самая последняя из имеющихся симметрий (помимо вращательной симметрии, трансляционной симметрии, симметрии Лоренца и, в общем случае, симметрии Пуанкаре) в нетривиальной теории элементарных частиц. Она связывает частицы различных квантово-механических спинов и вскрывает глубокое математическое родство между частицами-переносчиками взаимодействий и частицами, из которых состоит материя. Супергравитация — это расширение суперсимметрии посредством включения гравитационного поля. В ранний период исследований по теории струн учёные осознали, что суперсимметрия и супергравитация возникают в низкоэнергетическом пределе теории струн. При низких энергиях протяжённость струны разглядеть нельзя, поэтому она выглядит как точечная частица. Соответственно, как будет обсуждаться в этой главе, применительно к низкоэнергетическим процессам математический аппарат теории струн преобразуется в аппарат квантовой теории поля. Учёные обнаружили, что поскольку суперсимметрия и гравитация выживают при таком преобразовании, то низкоэнергетические теории струн приводят к суперсимметричным квантовым теориям поля и супергравитации. Как будет обсуждаться в главе 9, связь между суперсимметричной теорией поля и теорией струн впоследствии стала ещё более глубокой.
(обратно)27
Осведомлённый читатель может не согласиться с моим утверждением, что каждое поле ассоциируется с частицей. Более точное утверждение звучит так: малые флуктуации поля около локального минимума его потенциала обычно интерпретируются как возбуждения частиц. Этого определения будет достаточно для наших обсуждений. К тому же осведомлённый читатель заметит, что локализация частицы в точке сама по себе является идеализацией, потому что для этого потребуется — из принципа неопределённости — бесконечный импульс и энергия. Опять же суть в том, что в квантовой теории поля нет, в принципе, предела того, как можно в конце концов локализовать частицу.
(обратно)28
Исторически математическая техника, известная как перенормировка (или ренормализация), была развита для устранения количественных проявлений жёстких (высокоэнергетичных) колебаний квантового поля на малых расстояниях. При применении к квантово-полевым теориям трёх негравитационных взаимодействий перенормировка устранила бесконечные величины, возникающие при различных вычислениях, что позволило физикам сделать фантастически точные предсказания. Однако, когда перенормировку применили к квантовым флуктуациям гравитационного поля, она оказалась неэффективной: метод не смог устранить бесконечности, возникающие при квантовых вычислениях с учётом гравитации.
С более современных позиций эти бесконечности рассматриваются несколько иначе. Физики осознали, что на пути к более глубокому пониманию законов природы разумно придерживаться той точки зрения, что любая теория приблизительна — если вообще значима — и скорее всего может описывать физические явления только вплоть до некоторого определённого масштаба (или только до некоторого энергетического масштаба). Явления за его пределами не могут описываться данной теорией. Согласно этой точке зрения, безрассудно применять данную теорию на расстояниях, меньших чем область применимости теории (или на энергиях, превышающих область применимости). С учётом таких встроенных отсеканий (подобно тем, что описаны в основном тексте) бесконечности никогда не будут возникать. Наоборот, все вычисления проводятся в теории, диапазон применимости которой обозначен с самого начала. Это означает, что предсказательная сила ограничена явлениями, находящимися в установленных теорией пределах, а на очень коротких расстояниях (больших энергиях) теория не работает. Окончательная цель полной теории квантовой гравитации состоит в устранении встроенных пределов и распространении предсказательной силы теории на произвольные масштабы.
(обратно)29
Чтобы понять, откуда берутся эти конкретные числа отметим, что квантовая механика (см. главу 8) сопоставляет частице волну, и чем тяжелее частица, тем короче длина волны (расстояние между последовательными гребнями). Общая теория относительности Эйнштейна также сопоставляет длину произвольному объекту — это размер, до которого надо сжать объект, чтобы он стал чёрной дырой. Чем тяжелее объект, тем больше этот размер. А теперь возьмите частицу, которая описывается квантовой механикой, и представьте, что её масса медленно растёт. При этом квантовая волна частицы укорачивается, а её «размер чёрной дыры» увеличивается. При некоторой массе квантовая длина волны и размер чёрной дыры совпадут, что задаст тот уровень массы и размера, при котором квантово-механические и гравитационные рассмотрения одновременно важны. При проведении численной оценки такого мысленного эксперимента масса и размер оказываются равными тем значениям, которые озвучены в основном тексте — планковской массе и планковской длине соответственно. Забегая вперёд, скажу, что в главе 9 мы будем обсуждать голографический принцип. Основываясь на общей теории относительности и физике чёрных дыр, этот принцип утверждает, что существует очень определённое ограничение на количество физических степеней свободы, которые могут существовать внутри произвольной области пространства (это более точная версия рассуждений из главы 2 относительно количества различных конфигураций частиц в заданном объёме пространства; это также обсуждается в комментарии {11}). Если этот принцип верен, то конфликт между общей теорией относительности и квантовой механикой может возникнуть прежде, чем расстояния станут малыми, а кривизны большими. Огромный объём пространства, заполненный газом частиц даже малой плотности, будет обладать, согласно квантовой теории, значительно бо́льшим количеством степеней свободы, чем позволяет голографический принцип (основанный на общей теории относительности).
(обратно)30
Квантово-механический спин является достаточно тонким понятием. Трудно представить, что значит «вращающийся», особенно в квантовой теории поля, где частицы считаются точками. На самом деле, из экспериментов следует, что частицы могут обладать внутренним свойством, очень похожим на постоянный угловой момент. Более того, из квантовой теории следует, и эксперименты это подтверждают, что частицы могут иметь угловой момент, который является только целым кратным некоторой фундаментальной величины (константы Планка, делённой на 2). Поскольку классические вращающиеся объекты обладают внутренним угловым моментом (который, однако, не является постоянным — он изменяется при изменении вращательной скорости объекта), теоретики заимствовали название «спин» и применили его к аналогичной квантовой ситуации. Отсюда название «спиновый угловой момент». Хотя выражение «вращающийся как волчок» создаёт подходящий зрительный образ, более точно будет представлять, что частицы характеризуются не только их массой, электрическим зарядом, зарядом ядра, а также внутренним неизменным спиновым угловым моментом. Подобно тому как электрический заряд частицы является одним из её фундаментальных определяющих свойств, эксперименты демонстрируют, что таким же свойством является её спиновый угловой момент.
(обратно)31
Напомним, что причиной напряжённости между общей теорией относительности и квантовой механикой являются мощные квантовые флуктуации гравитационного поля, которые сотрясают пространство-время настолько сильно, что традиционные математические методы перестают работать. Квантовая неопределённость говорит нам, что эти флуктуации становятся тем сильнее, чем меньше расстояние (именно поэтому эти флуктуации в обычной жизни не видны). Вычисления показывают, что именно энергичные флуктуации на расстояниях, меньше планковского масштаба, расстраивают наши математические инструменты (чем меньше расстояние, тем больше энергия флуктуаций). Поскольку в рамках квантовой теории поля частицы описываются как точки, не имеющие пространственного размера, расстояния, достижимые этими частицами, могут быть сколь угодно малыми, и, следовательно, ощущаемые ими квантовые флуктуации могут быть сколь угодно энергичными. В теории струн ситуация изменяется. Струны не являются точками — у них имеется пространственный размер. Это означает, что есть предел малости достижимого расстояния, даже в принципе, так как струна не может уместиться на расстоянии меньшем, чем её длина. В свою очередь самое малое достижимое расстояние задаёт предел того, насколько энергичными могут быть квантовые флуктуации. Этот предел оказывается достаточным, чтобы приручить неуправляемую математику, позволяя теории струн соединить квантовую механику и общую теорию относительности.
(обратно)32
«What Einstein never knew», NOVA documentary, 1985.
(обратно)33
Некоторые исследователи могут заметить, что хотя ни квантовая теория поля, ни текущее состояние теории струн не дают объяснения свойств частиц, этот вопрос более насущен для теории струн. Он достаточно сложен, но для заинтересованных читателей приведём краткое резюме. Свойства частиц в квантовой теории поля — например, их массы — задаются числами, которые подставляются в уравнения теории. Сам факт того, что уравнения квантовой теории поля допускают варьирование таких чисел, является математическим способом сказать, что квантовая теория поля не определяет массы частиц, а, наоборот, использует их в качестве начальных данных. В теории струн гибкость в выборе масс частиц имеет схожее математическое происхождение — уравнения допускают свободное варьирование некоторых чисел, — однако проявление этой гибкости более значимо. Свободно изменяющиеся числа — числа, которые могут изменяться без каких-либо затрат энергии — соответствуют наличию в теории безмассовых частиц. (Если вернуться к главе 3 к языку кривых потенциальной энергии, то представьте совершенно плоскую кривую, то есть горизонтальную линию. Подобно тому как прогулка по совершенно плоской поверхности не меняет вашей потенциальной энергии, изменение значения такого поля не приведёт к затратам энергии. Поскольку масса частицы соответствует кривизне кривой потенциальной энергии квантового поля вблизи её минимума, то кванты таких полей являются безмассовыми.) Избыточное число безмассовых частиц является особенно неприятным свойством любой предлагаемой теории, потому что есть строгие ограничения на такие частицы, вытекающие из экспериментальных данных, полученных на ускорителях, и космологических наблюдений. Чтобы теория струн была жизнеспособной, безмассовым частицам необходимо придать массу. В течение последних лет было предложено несколько механизмов генерации масс, основанных на потоках, пронизывающих дырки в пространствах Калаби — Яу дополнительных измерений. Я вернусь к этому в главе 5.
(обратно)34
Возможно, что в экспериментах будут получены данные, которые сильно пошатнут нашу веру в теорию струн. Структура теории струн гарантирует, что определённые базовые принципы должны соблюдаться во всех физических явлениях. Среди них унитарность (сумма вероятностей всех возможных результатов в данном эксперименте должна быть равна 1) и локальная Лоренц-инвариантность (в достаточно малой области справедлива специальная теория относительности), а также более технические свойства, такие как аналитичность и кроссинг-симметрия (результат столкновения частиц должен зависеть от импульсов частиц таким образом, чтобы удовлетворялся некоторый набор математических критериев). Если будет обнаружено — возможно, на Большом адронном коллайдере, — что любой из этих принципов нарушается, то примирить полученные данные с теорией струн станет трудной задачей. (Согласовать эти данные со Стандартной моделью физики частиц, которая также использует эти принципы, будет столь же проблематично; однако здесь спасает допущение, что при достаточно высоких энергиях Стандартная модель должна уступить место некой новой физике, поскольку она не включает в себя гравитацию. Но если мы получим данные, конфликтующие с любым из перечисленных выше принципов, это будет указывать на то, что новая физика — это не теория струн.)
(обратно)35
Первое указание на парность форм Калаби — Яу возникло в работе Ланса Диксона, а также в независимой работе Вольфганга Лерхе, Николаса Уорнера и Кумруна Вафы. В моей работе с Роненом Плессером был предложен метод построения первого конкретного примера таких пар, которые мы назвали зеркальными парами, а соотношение между ними — зеркальной симметрией. Плессер и я также показали, что трудная задача, такая как определение числа сфер, которые можно упаковать в данную форму, неподъёмная при использовании одного из партнёров по паре, может стать гораздо легче на зеркальной форме. Этот результат был подхвачен Филиппом Канделасом, Ксенией де ла Осой, Полом Грином и Линдой Паркерс — они развили технику вычислений, основанную на равенстве, которое Плессер и я установили между «трудными» и «простыми» формулами. С помощью простой формулы они получили информацию о трудном партнёре, включая числа, связанные с упаковкой сфер, приведённые в основном тексте книги. За последующие годы зеркальная симметрия стала отдельной областью исследований, где было получено много важных результатов. Детальная история этого вопроса приведена в книге Шин-Туна Яу и Стива Надиса: Shing-Tung Yau and Steve Nadis, «The Shape of Inner Space». New York: Basic Books, 2010.
(обратно)36
Классическая механика: Электромагнетизм: d*F = *J; dF = 0. Квантовая механика:
Общая теория относительности:
(обратно)37
Я имею в виду постоянную тонкой структуры, α = e2/ħc, численное значение которой (при характерных энергиях электромагнитных процессов) примерно равно 1/137, что приближённо составляет 0,0073.
(обратно)38
Согласно Виттену, когда константа связи в теории струн типа I становится большой, эта теория преобразуется в O-гетеротическую теорию с малой константой связи, и наоборот; теория типа IIB с большой константой связи преобразуется в себя, в теорию типа IIB, но с малой константой связи. В случае E-гетеротической и теории типа IIA ситуация более тонкая (более подробно см.: «Элегантная Вселенная», глава 12), но общая картина такова, что все пять теорий являются участниками целой сети взаимосвязей.
(обратно)39
Для подготовленного читателя отметим, что особенность струн — одномерных объектов — состоит в том, что описывающая их движение физика основана на некоторой бесконечномерной группе симметрии. Так как при движении струна заметает двумерную поверхность, то струнный функционал действия, на основе которого выводятся уравнения движения, определяет двумерную квантовую теорию поля. Классически, такие двумерные действия являются конформно-инвариантными (инвариантными относительно сохраняющих углы растяжений двумерной поверхности), и при наложении некоторых ограничений (таких как число измерений пространства-времени, в котором движется струна) конформная симметрия может сохраняться на квантовом уровне. Конформная группа преобразований симметрии бесконечномерная и это существенно для математической согласованности пертурбативного квантового анализа движущейся струны. Например, бесконечное число возбуждений движущейся струны, которые иначе имели бы отрицательную норму (возникающую из отрицательного знака временной компоненты пространственно-временной метрики), может быть устранено с помощью преобразований «вращения» из бесконечномерной группы симметрии. Более подробно можно прочитать в книге: М. Green, J. Schwarz, and Е. Witten, «Superstring Theory». Vol. 1. Cambridge: Cambridge University Press, 1988.
(обратно)40
Подобно истории многих открытий, заслуживают славы те, чьи идеи легли в основу, и те, кто указали на их важность. Большую роль в открытии бран в теории струн сыграли Майкл Дафф, Пол Хов, Такео Иннами, Келлог Стелле, Эрик Бергшофф, Эргин Жегин, Пол Таунсенд, Крис Халл, Крис Поп, Джон Шварц, Ашок Сен, Эндрю Строминджер, Куртис Калан, Джо Польчински, Петр Хоржава, Джин Дай, Роберт Лей, Герман Николаи и Бернард Девитт.
(обратно)41
Внимательный читатель может сказать, что в инфляционной мультивселенной время также было вплетено фундаментальным способом, потому что, в конце концов, граница нашего пузырька служит отметкой начала времени в нашей Вселенной; за пределами нашего пузырька означает за пределами нашего времени. Это безусловно так, но здесь идея носит более общий характер — все обсуждавшиеся до сих пор мультивселенные были основаны на анализе, сфокусированном на процессах, происходящих в пространстве. В обсуждаемой мультивселенной главную роль с самого начала играет время.
(обратно)42
Александр Фридман, «Мир как пространство и время», 1923.
(обратно)43
Потоки с большими значениями также приводят к дестабилизации заданной формы Калаби — Яу. То есть потоки стремятся заставить форму Калаби — Яу увеличиваться в размерах, что сразу приводит к противоречию с критерием малости дополнительных измерений.
(обратно)44
George Gamow, «My World Line». New York: Viking Adult, 1970; J. C. Pecker, Letter to the Editor, «Physics Today». May 1990, p. 117.
(обратно)45
Albert Einstein, «The Meaning of Relativity». Princeton: Princeton University Press, 2004, p. 127. Отметим, что вместо принятого сейчас названия «космологическая постоянная» Эйнштейн использовал термин «космологический член»; в процитированном тексте я воспользовался этой заменой для наглядности.
(обратно)46
«The Collected Papers of Albert Einstein», edited by Robert Schulmann et al. Princeton: Princeton University Press, 1998, p. 316.
(обратно)47
Есть одно усложнение, которое не влияет на основную идею, но которое начинает играть существенную роль при детальном научном анализе. При движении фотонов от сверхновой звезды к нам, плотность числа фотонов рассеивается описанным выше способом. Однако есть и другая причина для уменьшения. В следующем разделе будет рассказано, что растяжение пространства заставляет растягиваться длины волн фотонов, вследствие чего их энергии падают — эффект, называемый красным смещением. Астрономы используют данные по красному смещению для установления размера Вселенной в момент испускания этих фотонов — важный шаг в определении того, как расширение пространства меняется с течением времени. Но растяжение фотонов — уменьшение их энергии — проявляет себя ещё и другим способом: удалённый источник тускнеет. Поэтому для правильного определения расстояния до сверхновой путём сравнения видимой и собственной яркости астрономы должны учитывать не только рассеивание плотности числа фотонов (как описано в основном тексте), но дополнительно также и уменьшение энергии, вызванное красным смещением. (Если быть более точным, то дополнительный фактор уменьшения следует применить дважды; второй фактор красного смещения описывает степень растяжения длины фотона из-за космического расширения в момент приёма.)
(обратно)48
В определённом смысле и второй вариант ответа на то, какое расстояние измеряется, также может считаться правильным. В примере раздувающейся поверхности Земли, города Нью-Йорк, Остин и Лос-Анджелес удаляются друг от друга, но их географическое положение на Земле остаётся при этом неизменным. Города удаляются друг от друга, потому что поверхность Земли раздувается, а не потому, что их выкапывают гигантским ковшом, кладут на прицеп и перевозят на новое место. Аналогично, хотя галактики из-за космического расширения разлетаются, их положение в пространстве остаётся неизменным. Представим себе, что галактики — это блёстки на космической ткани. Если ткань растягивать, блёстки начинают разъезжаться, но каждая из них остаётся пришитой к тому же самому месту, что и ранее. Поэтому если на первый взгляд второй и третий варианты ответа и кажутся разными — во втором речь идёт о расстоянии между нами и положением удалённой галактики миллиарды лет назад, когда сверхновая излучила свет, дошедший до нас сейчас, а в третьем рассматривается расстояние в данный момент между нами и текущим положением галактики, — на самом деле это не так. Положение удалённой галактики в пространстве оставалось неизменным как в настоящий момент, так и в течение миллиардов лет. Только движение через пространство, а не свободный дрейф по волнам пространственного расширения может изменить её положение. В этом смысле второй и третий ответы действительно одинаковы.
(обратно)49
Поясним подготовленному читателю, как вычислить расстояние — сейчас, в момент времени tнаст, — которое свет прошёл с момента излучения во время tизл. Мы будем рассматривать модель, в которой пространственная часть пространства-времени является плоской, и поэтому метрика может быть записана в виде
ds2 = c2dt2 − a2(t)dx2,
где a(t) — это масштабный фактор Вселенной в момент времени t, а c — скорость света. Используемые координаты называются сопутствующими. На образном языке этой главы их можно рассматривать как координаты, соответствующие точкам на статичной карте, а масштабный фактор даёт информацию, приведённую в легенде карты.
Траектории светового луча характеризуется тем, что ds2 = 0 (это эквивалентно тому, что скорость света всегда равна c), откуда следует, что
или, выбирая конечный интервал времени между tизл и tнаст:
Левая часть этого уравнения задаёт расстояние, пройденное светом по статичной карте от момента излучения до настоящего момента. Чтобы перевести это в расстояние в реальном пространстве, необходимо перемасштабировать формулу с учётом современного масштабного фактора; поэтому полное расстояние, проходимое светом, будет равно
Если пространство не расширяется, полное пройденное расстояние будет
как и ожидалось. Таким образом, при вычислении расстояния, пройденного в расширяющейся Вселенной, мы видим, что каждый участок траектории светового луча умножается на фактор a(tнаст)/a(t), который характеризует то, как на настоящий момент увеличился участок траектории с того момента, как через него прошёл свет.
(обратно)50
Более точно примерно 7,12 × 10−30 грамма/кубический сантиметр.
(обратно)51
Пересчёт составляет 7,12 × 10−30 грамма/кубический сантиметр = (7,12 × 10−30 грамма/кубический сантиметр) × (4,6 × 104 планковская масса/грамм) × (1,62 × 10−33 сантиметр/планковская длина)3 = 1,38 × 10−123 планковская масса/кубический планковский объём.
(обратно)52
Гравитационное отталкивание при инфляции является кратким и интенсивным. Это объясняется огромной энергией и отрицательным давлением, обусловленными полем инфлатона. Однако если изменить форму кривой потенциальной энергии квантового поля, то количество энергии уменьшится и отрицательное давление снизится, что снизит интенсивность ускоренного расширения. Кроме того, при подходящей модификации кривой потенциальной энергии можно продлить период ускоренного расширения. А такой менее интенсивный и более продолжительный период ускоренного расширения — именно то, что требуется для объяснения данных по сверхновым. Однако за более чем десять лет с момента первого наблюдения ускоренного расширения, наиболее убедительным объяснением остаётся наличие у космологической постоянной небольшого отличного от нуля значения.
(обратно)53
Хотя утверждение о том, что изменения физических свойств нашей Вселенной не будут благоприятствовать жизни в привычном виде, широко признано научной общественностью, некоторые учёные полагают, что диапазон значений, совместимых с жизнью, может быть шире, чем принято думать. Эти вопросы широко обсуждались в литературе. См., например: John Barrow and Frank Tipler, «The Anthropic Cosmological Principle». New York: Oxford University Press, 1986; John Barrow, «The Constants of Nature». New York: Pantheon Books, 2003; Paul Davies, «The Cosmic Jackpot». New York: Houghton Mifflin Harcourt, 2007; Victor Stenger, «Has Science Found God?» Amherst, N. Y.: Prometheus Books, 2003; а также приведённые там ссылки.
(обратно)54
Опираясь на материал, изложенный в предыдущих главах, можно, казалось бы, легко заключить, что ответ, безусловно, да. Рассмотрим, говорите вы, стёганную мультивселенную, в бесконечном пространственном объёме которой находится бесконечно много вселенных. Однако вам следует быть осторожнее. Даже при бесконечном количестве вселенных список различных значений для космологических постоянных может оказаться коротким. Если, например, основные законы не допускают много различных значений для космологической постоянной, то тогда независимо от числа вселенных, будет реализовываться лишь малый набор возможных космологических постоянных. Поэтому задаваемый нами вопрос такой: (а) есть ли кандидаты на роль физических законов, которые приводят к мультивселенной, (б) содержит ли порождённая таким образом мультивселенная значительно больше, чем 10124 различных вселенных, (в) гарантируют ли эти законы, что значение космологической постоянной варьируется от вселенной к вселенной.
(обратно)55
Эти четыре автора были первыми, кто показал, что при разумном выборе пространств Калаби — Яу и пронизывающих их отверстия потоков, можно прийти к струнным моделям с небольшими положительными значениями космологической постоянной, сопоставимыми с наблюдаемыми данными. Впоследствии, совместно с Хуаном Малдасеной и Лайамом Макалистером, эта группа опубликовала крайне важную статью о том, как совместить инфляционную космологию с теорией струн.
(обратно)56
Если быть более точным, этот горный рельеф будет существовать внутри приблизительно 500-мерного пространства, независимые направления которого — координатные оси — будут соответствовать различным полевым потокам.
Рисунок 6.4 даёт приблизительную картину, но позволяет получить представление о взаимосвязях между различными формами дополнительных измерений. Помимо этого, говоря о струнном ландшафте, физики обычно подразумевают, что кроме возможных значений потоков этот горный рельеф отражает также все возможные размеры и формы (различные топологии и геометрии) дополнительных измерений. Долины струнного ландшафта — это те места (определённые формы дополнительных измерений и их потоков), где естественным образом располагаются пузырьки-вселенные, как расположился бы мяч, скатившийся в долину с реального горного ландшафта. С математической точки зрения долины — это (локальные) минимумы потенциальной энергии, ассоциированной с дополнительными измерениями. В классической теории, если пузырёк-вселенная обретёт форму дополнительных измерений, соответствующую долине, то это свойство останется навсегда неизменным. Однако в квантовой теории туннелирование может привести к изменению формы дополнительных измерений.
(обратно)57
Квантовое туннелирование на более высокий пик возможно, но согласно квантовым вычислениям, значительно менее вероятно.
(обратно)58
Продолжительность расширения пузырька-вселенной до столкновения определяет силу столкновения и последующие разрушения. Если вернуться к примеру с Трикси и Нортоном из главы 3, такие столкновения поднимают интересный вопрос о времени. При столкновении двух пузырьков-вселенных их внешние края — на которых энергия поля инфлатона имеет большие значения — соприкасаются. С точки зрения наблюдателя, находящегося внутри любого из сталкивающихся пузырьков, большое значение энергии поля инфлатона соответствует ранним моментам времени, близким к моменту Большого взрыва в этом пузырьке. Таким образом, столкновения пузырьков-вселенных происходят на заре их рождения, и потому образовавшиеся волны могут оказывать влияние на ещё один процесс, происходящий в ранней Вселенной, — на образование реликтового излучения.
(обратно)59
В главе 8 мы рассмотрим квантовую механику более подробно. Как мы увидим, моё утверждение «находятся за кулисами повседневной реальности» может быть интерпретировано разными способами. Здесь я имею в виду самый простой: уравнение квантовой механики подразумевает, что волны вероятности, как правило, отсутствуют в обычных пространственных измерениях. Наоборот, эти волны распространяются в другой среде, которая учитывает не только привычные пространственные измерения, но также число описываемых частиц. Эта среда называется конфигурационным пространством; его объяснение заинтересованный читатель может найти в комментарии {71}.
(обратно)60
Если наблюдаемое нами ускоренное расширение пространства не постоянно, тогда в некоторый момент в будущем расширение замедлится. Замедление позволит свету от объектов, находящихся в данный момент за пределами нашего космического горизонта, достичь нас; наш космический горизонт увеличится. В этом случае будет совсем странным считать, что миры за пределами нашего горизонта не являются реальными, поскольку в будущем к ним может появится доступ. (Вы можете вспомнить, что в конце главы 2 было отмечено, что показанные на рис. 2.1 космические горизонты будут увеличиваться с течением времени. Это верно для вселенной, в которой темп пространственного расширения не убыстряется. Однако, если расширение ускоряется, то существует расстояние, за которое мы никогда не сможем заглянуть, сколь долго мы не ждали бы. В ускоряющейся вселенной космический горизонт не может превзойти размер, который определяется математически темпом ускорения.)
(обратно)61
Приведём конкретный пример свойства, которое может быть общим для всех вселенных из некоторой мультивселенной. В главе 2 отмечалось, что современные наблюдательные данные строго указывают на то, что кривизна пространства равна нулю. Однако довольно сложные математические вычисления показывают, что все пузырьки-вселенные в инфляционной мультивселенной обладают отрицательной кривизной. Грубо говоря, пространственные формы с равными значениями инфлатона — формы, определяемые соединением равных чисел на рис. 3.8б, — больше похожи на картофельные чипсы, чем на плоскую поверхность стола. Но даже в этом случае инфляционная мультивселенная остаётся совместимой с наблюдениями, потому что при расширении любой формы её кривизна уменьшается (кривизна жемчужины всем очевидна, а кривизна поверхности Земли не замечалась тысячелетиями). Если наш пузырёк-вселенная продолжает испытывать значительное расширение, его кривизна может быть отрицательной и при этом настолько малой, что современные измерения не смогут уловить отличие от нуля. Отсюда следует возможный тест. Если более точные наблюдения в будущем покажут, что кривизна пространства очень мала, но положительна, это опровергнет гипотезу о том, что наша Вселенная является частью инфляционной мультивселенной, как было отмечено Б. Фрайфогелем, М. Клебаном, М. Родригез Мартинезом и Л. Сасскиндом в статье: B. Freivogel, M. Kleban, M. Rodriguez Martinez, and L. Susskind «Observational Consequences of a Landscape», «Journal of High Energy Physics» 0603, 039 [2006]; если измерения дадут положительное значение для кривизны, равное примерно 10−5, это станет сильным аргументом против квантово-туннельных переходов, которые согласно теории заполняют струнный ландшафт (см. главу 6).
(обратно)62
Список космологов и струнных теоретиков, внёсших значительный вклад в эту область, включает, помимо многих других, таких исследователей как Алан Гут, Андрей Линде, Александр Виленкин, Жауме Гаррига, Дон Пейдж, Сергей Виницки, Ричард Истер, Юджин Лим, Мэттью Мартин, Майкл Дуглас, Фредерик Денеф, Рафаэль Буссо, Бен Фрайфогель, И-Шен Янг, Делия Шварц-Перлов.
(обратно)63
Стоит ещё отметить, что описанные вычисления выполнялись без конкретизации типа мультивселенной. Наоборот, Вайнберг и его соавторы рассмотрели модель мультивселенной с изменяющимися характеристиками и вычислили густоту галактик в каждой из составляющих её вселенных. Чем больше галактик во вселенной, тем больший вес приписывается её свойствам при вычислении усреднённых свойств, с которыми столкнётся типичный наблюдатель. Однако, поскольку Вайнберг и его соавторы не конкретизируют модель мультивселенной, их вычисления не могут учесть вероятность нахождения в данной мультивселенной вселенных с теми или иными свойствами (те вероятности, которые обсуждались в предыдущем разделе). Возможно наличие вселенных с космологическими постоянными и флуктуациями, лежащими в определённом диапазоне, так что они готовы для запуска процесса образования галактик, но если такие вселенные редки в данной мультивселенной, то мы вряд ли обнаружим, что находимся в одной из них.
Для упрощения вычислений Вайнберг и его соавторы предположили, что поскольку рассматриваемый ими диапазон значений космологической постоянной очень узок (между 0 и 10−120), то вероятности существования таких вселенные в данной мультивселенной не будут, по всей видимости, сильно варьироваться (подобно как вероятность того, что вы встретите собаку весом в 26,99997 килограмма не сильно отличается от вероятности, что вы встретите собаку весом 26,99999 килограмма). Таким образом, они полагали, что любое значение космологической постоянной в том узком диапазоне, который совместим с образованием галактик, столь же вероятно, как и любое другое. На нашем рудиментарном уровне понимания механизма возникновения мультивселенной это кажется достаточно разумным предположением. Однако дальнейшие исследования поставили под вопрос справедливость данного допущения, требуя более полного анализа. Было показано, что для того чтобы продвинуться дальше, необходимо конкретизировать тип мультивселенной и задать распределение вселенных с разными свойствами. Вычисления, основанные на антропном принципе с самым минимальным набором допущений, являются единственным способом понять, сможет ли этот подход в будущем дать осмысленные плоды, обладающие предсказательной силой.
(обратно)64
Само слово «типичное» тоже добавляет проблем, поскольку его смысл зависит от того, как оно определяется и какие измерения за этим стоят. Если, например, мы используем в качестве критерия число детей и машин, то придём к одному виду «типичной» американской семьи. Если использовать другие критерии, такие как интерес к физике, любовь к опере или увлечение политикой, то характеристика «типичной» семьи изменится. Тот анализ, что верен для «типичной» американской семьи, по всей вероятности верен и для «типичных» наблюдателей в мультивселенной: рассмотрение других свойств помимо размера популяции приведёт к другому определению «типичного» наблюдателя. В свою очередь это будет влиять на предсказание вероятности наблюдения того или иного свойства в нашей Вселенной. Чтобы антропные вычисления стали по-настоящему убедительны, они должны учитывать этот аспект. В противном случае, как говорилось в основном тексте, распределения должны иметь очень резко выраженные пики, чтобы отклонения от одной населённой вселенной к другой были бы минимальными.
(обратно)65
Изучение наборов с бесконечным числом составляющих является богатым и хорошо изученным разделом математики. Любознательный читатель может быть знаком с тем фактом, что проводимые в XIX столетии исследования выявили, что есть различные «размеры» или, как принято говорить, «уровни» бесконечности. То есть одна бесконечная величина может быть больше, чем другая бесконечная величина. Уровень бесконечности, задающий размер множества, содержащего все целые числа, обозначается Ν0. Георг Кантор показал, что эта величина меньше, чем аналогичная величина для множества всех вещественных чисел. Грубо говоря, если попытаться сопоставить целые и вещественные числа, то первые обязательно закончатся раньше вторых. А если рассмотреть множество всех подмножеств вещественных чисел, то уровень бесконечности будет ещё больше.
Во всех обсуждавшихся выше примерах из основного текста речь шла о бесконечности типа Ν0, потому что мы рассматривали бесконечные наборы дискретных, или «счётных», объектов — то есть различные наборы целых чисел. Тогда в математическом смысле во всех примерах размер одинаков; полное число составляющих описывается одним и тем же уровнем бесконечности. Однако, как мы вскоре увидим, для физиков вывод такого сорта не особенно полезен, ибо цель состоит в том, чтобы найти физически обоснованную схему для сравнения бесконечных наборов вселенных, которая приведёт к более точной иерархии, той, что позволит объяснить относительное преобладание одного набора свойств во всей мультивселенной по сравнению с другим набором. Типичный для физиков подход при решении такого сорта задач состоит в следующем. Сперва следует сравнить между собой конечные подклассы рассматриваемых бесконечных наборов (потому что в конечном случае все непонятные вопросы снимаются), а затем добавлять в подклассы всё больше и больше элементов, так чтобы в конце концов включить полный бесконечный набор. Трудность в том, чтобы найти физически оправданный способ выбора конечных подклассов для сравнения, а также обосновать, что при увеличении выбранных подклассов сравнения остаются осмысленными.
(обратно)66
У теории инфляции есть и другие достижения, в частности решение проблемы магнитных монополей. При попытке объединить три негравитационных взаимодействия в одну теоретическую схему (известную под названием великое объединение) исследователи обнаружили, что Большой взрыв должен сопровождаться образованием большого количество магнитных монополей. Эти частицы представляют собой, по сути, северный полюс линейного магнита, в котором нет привычной пары — южного полюса (и наоборот). Однако до сих пор такие частицы не были обнаружены. Инфляционная космология объясняет отсутствие монополей тем, что быстрое колоссальное расширение пространства сразу после Большого взрыва разметало их по всему пространству, поэтому вероятность их присутствия в нашей Вселенной близка к нулю.
(обратно)67
В настоящее время есть разные точки зрения, насколько трудна эта задача. Некоторые рассматривают проблему измерения как хитроумный технический трюк, который в случае успешного решения станет важным дополнением инфляционной космологии. Другие (например, Пол Стейнхард) считают, что решение проблемы измерения потребует выхода далеко за рамки математического формализма инфляционной космологии, что приведёт к новому подходу, который должен будет рассматриваться как новая космологическая теория. Моя личная точка зрения, которую разделяют немногие, но их число постоянно растёт, состоит в том, что проблема измерения уходит корнями на самый глубокий фундаментальный уровень, и её решение может потребовать серьёзного пересмотра основополагающих идей.
(обратно)68
Оригинальную версию 1956 года и урезанную версию 1957 года диссертации Эверетта можно найти в книге Брайса ДеВитта: «The Many-Worlds Interpretation of Quantum Mechanics», edited by Bryce S. DeWitt & Neill Graham. Princeton: Princeton University Press, 1973.
(обратно)69
27 января 1998 года я обсуждал с Джоном Уилером аспекты квантовой механики и общей теории относительности, которые я собирался описать в «Элегантной Вселенной». Прежде чем углубиться в науку, Уилер отметил, насколько важно, особенно для молодых теоретиков, найти правильный способ представления своих результатов. В тот момент я воспринял это как не более чем мудрый совет, возможно, побуждённый его разговором с мной, «молодым теоретиком», проявившим интерес к описанию математических достижений на обычном языке. Однако, читая поучительную историю, изложенную в книге Питера Бирна: Peter Byrne, «The Many Worlds of Hugh Everett III». New York: Oxford University Press, 2010, я был поражён тем, что Уилер также акцентировал эту тему примерно сорок лет назад в его общении с Эвереттом, только в ситуации, где ставки были гораздо выше. Комментируя черновой вариант диссертации Эверетта, Уилер сказал, что надо «подчистить слова, не формализм», и предупредил о «сложности использования обычных слов для описания математического формализма, который удалён от обычной жизни настолько, насколько это вообще возможно; о противоречиях и недопониманиях, которые могут возникнуть; об очень и очень тяжёлой ноше ответственности, с которой следует делать все утверждения, так чтобы эти недопонимания не могли возникнуть». Бирн убедительно свидетельствует, что Уилер балансировал на тонкой грани между восхищением работой Эверетта и уважением к квантово-механическому подходу, над которым трудились Бор и много других знаменитых физиков. С одной стороны, он не хотел, чтобы идеи Эверетта бесцеремонно были принижены старой гвардией только потому, что Эверетт выбрал неудачную форму для презентации или потому что эмоциональные слова (вроде «расщепляющиеся» вселенные) могут резануть своей новомодностью. С другой стороны, Уилер не хотел, чтобы почтенное физическое сообщество подумало, будто он является инициатором ничем не оправданной атаки на успешный квантовый формализм. Относительно Эверетта и его диссертации Уилер предложил компромисс, что развитый математический формализм должен быть сохранён, но трактовка и приложения должны быть облечены в более мягкую форму. В то же время, Уилер настоятельно побуждал Эверетта съездить к Бору и изложить свои доводы лично, у доски. В 1959 году Эверетт так и поступил, однако то, что ему виделось как двухнедельные разносторонние обсуждения, свелось к нескольким непродуктивным разговорам. Никто не изменил своего мнения; позиции остались прежними.
(обратно)70
Позвольте пояснить одну неточность. Из уравнения Шрёдингера следует, что значения, которые может принимать квантовая волна (или, на языке полей, волновая функция) могут быть положительными и отрицательными; в общем случае, эти значения могут быть комплексными числами. Такие числа не могут быть напрямую интерпретированы как вероятности — что означает отрицательная или комплексная вероятности? Вероятности ассоциируются с квадратом амплитуды квантовой волны в данной точке. Математически это означает, что для определения вероятности нахождения частицы в данной точке мы перемножаем значение волны в этой точке с его комплексно сопряжённым значением. Это пояснение также важно для понимания следующего вопроса. Сокращения между перекрывающимися волнами необходимы для появления интерференционной картины. Но если бы волны действительно описывались как волны вероятности, такие сокращения не происходили бы, потому что вероятности являются положительными числами. Однако, как мы теперь знаем, квантовые волны принимают не только положительные значения; благодаря этому и происходят сокращения между положительными и отрицательными числами, а в общем случае, между комплексными числами. Поскольку нам важны только качественные свойства таких волн, для упрощения обсуждения в основном тексте я не буду различать квантовые волны и связанные с ними волны вероятности (получаемые путём возведением амплитуды в квадрат).
(обратно)71
Для математически подготовленного читателя заметим, что квантовая волна (волновая функция) одной частицы с большой массой будет описываться так, как это указано в основном тексте. Однако очень массивные объекты, как правило, состоят из многих частиц. В такой ситуации квантово-механическое описание более сложное. Вы могли бы подумать, что все частицы будут описываться квантовой волной, определённой на той же сетке координат, которая использовалась для одной частицы — с помощью тех же трёх пространственных осей. Но это не так. Волна вероятности использует в качестве начальных данных возможное положение каждой частицы и задаёт вероятность нахождения частиц в этих положениях. Следовательно, волна вероятности живёт в пространстве с тремя осями для каждой из частиц — то есть общее количество осей будет в три раза больше количества частиц (или в десять раз больше количества частиц, если учитывать дополнительные измерения теории струн). Это означает, что волновая функция составной системы, состоящей из n фундаментальных частиц, будет являться комплекснозначной функцией, определённой не на обычном трёхмерном пространстве, а на 3n-мерном пространстве; если число пространственных измерений не 3, а m, то число 3 в этом выражении будет заменено на m. Такое пространство называется конфигурационным. То есть в общем случае, волновая функция будет отображением . Когда мы говорим, что волновая функция имеет острый пик, мы имеем в виду, что это отображение определено на небольшом mn-мерном шаре внутри области определения. Отметим, в частности, что волновая функция, как правило, определена не в привычном пространстве. Конфигурационное пространство совпадает с привычным нам пространством только в идеализированном случае волновой функции одной, полностью изолированной, частицы. Ещё заметим, что когда говорится, что квантовые законы гарантируют распространение остролокализованной волновой функции массивного объекта по траектории, которую задают уравнения Ньютона, можно представлять себе, что волновая функция описывает движение центра масс данного объекта.
(обратно)72
Из этого описания вы можете сделать вывод, что существует бесконечно много местоположений, где может находиться электрон: для заполнения плавно меняющегося волнового профиля квантовой волны понадобится бесконечное число пикообразных форм, каждая из которых ассоциирована с возможным положением электрона. Как это стыкуется с главой 2, в которой мы обсуждали конечное число различных конфигураций частиц? Во избежание постоянных оговорок, не имеющих важного значения для основного изложения этой книги, я не стал заострять внимание на факте (указанном в главе 2), что для всё более точного определения положения электрона измерительный прибор будет тратить всё больше энергии. Поскольку в реальных ситуациях энергия ограничена, то разрешение прибора не идеально. Для пикообразных квантовых волн это означает, что при любой конечной энергии у пиков имеется отличная от нуля ширина. В свою очередь это означает, что в любой ограниченной области (например, внутри космического горизонта) существует конечное число различных измеряемых положений электрона. Более того, чем тоньше пик (более точное разрешение положения частицы), тем шире квантовая волна, описывающая энергию частиц, что демонстрирует обусловленный принципом неопределённости компромисс между характеристиками частицы.
(обратно)73
Для читателя с философским складом ума замечу, что описанная выше двухъярусная картина научного объяснения была предметом философских обсуждений и споров. Смежные идеи и обсуждения можно найти в работах: Frederick Suppe, «The Semantic Conception of Theories and Scientific Realism». Chicago: University of Illinois Press, 1989; James Ladyman, Don Ross, David Spurrett, & John Collier, «Every Thing Must Go». Oxford: Oxford University Press, 2007.
(обратно)74
Физики часто довольно свободно говорят о бесконечном количестве вселенных в контексте многомирового подхода к квантовой механике. Безусловно, существует бесконечно много форм возможных волн вероятности. Даже в одной и той же точке пространства можно непрерывным образом изменять значение волны вероятности, и поэтому число принимаемых ею значений будет бесконечным. Однако волны вероятности не являются физическими характеристиками системы, к которым у нас есть прямой доступ. Наоборот, волны вероятности содержат информацию о возможных различных исходах в заданной ситуации, а их не обязательно бесконечное число. В частности, подготовленный читатель заметит, что квантовая волна (волновая функция) находится в гильбертовом пространстве. Если данное гильбертово пространство конечномерно, то имеется конечное число разных возможных результатов измерений в физической системе, задаваемой этой волновой функцией (то есть любой эрмитов оператор имеет конечное число различных собственных значений). Это приведёт к конечному числу миров для конечного числа наблюдений или измерений. Считается, что гильбертово пространство, ассоциированное с физическими явлениями, происходящими внутри пространства конечного объёма и с ограниченной энергией, является с необходимостью конечномерным (мы остановимся на этом более подробно в главе 9), откуда следует, что число миров также будет конечно.
(обратно)75
См.: Peter Byrne, «The Many Worlds of Hugh Everett III». New York: Oxford University Press, 2010, p. 177.
(обратно)76
В разное время многие учёные, включая Нила Грахама; Брайса де Витта; Джеймса Хартли; Эварда Фархи, Джефри Голдстоуна и Сэма Гутмана; Дэвида Дойча; Сидни Коулмена; Дэвида Альберта и других, включая меня самого, независимо обнаружили удивительный математический факт, который, по видимому, является центральным для понимания природы вероятности в квантовой механике. Приведём его формулировку для математически подготовленного читателя: пусть ψ — волновая функция квантово-механической системы — вектор, являющийся элементом гильбертова пространства H. Волновая функция для n тождественных копий системы имеет, таким образом, вид . Пусть A — это произвольный эрмитов оператор с собственными значениями αk и собственными функциями . Пусть FK(A) — это оператор «частоты», который подсчитывает число раз, которое появляется в данном состоянии, принадлежащем . Тогда имеем следующий математический результат:
То есть при неограниченном росте числа тождественных копий системы волновая функция всей составной системы стремится к собственной функции оператора частоты с собственным значением . Это замечательный результат. Из самого определения собственной функции тогда следует, что в указанном пределе наблюдатель, измеряющий A, обнаружит αk дробное число раз, равное , что выглядит как самый прямой вывод знаменитого правила Борна для квантово-механической вероятности. С точки зрения многомирового подхода это означает, что миры, в которых число наблюдений αk не согласуется с правилом Борна, обладают нулевой нормой в гильбертовом пространстве в пределе произвольно больших n. В этом смысле кажется, будто квантово-механическая вероятность имеет прямую интерпретацию в рамках многомирового подхода. Все наблюдатели в многомировом подходе будут видеть результаты с частотами, которые соответствуют возникающим из стандартной квантовой механики, за исключением множества наблюдателей, норма которых в гильбертовом пространстве становится исчезающее мала при n, стремящемся к бесконечности. Хотя это выглядит многообещающим, но по зрелому размышлению возникают сомнения. В каком смысле можно говорить, что наблюдатель, норма которого в гильбертовом пространстве мала или норма которого стремится к нулю при n, стремящемся к бесконечности, неважен или не существует? Мы хотим сказать, что такие наблюдатели аномальны или «маловероятны», но как установить связь между нормой вектора в гильбертовом пространстве и этими характеристиками? Ситуацию можно разъяснить на примере. В двумерном гильбертовом пространстве с состояниями спин-вверх и спин-вниз рассмотрим состояние . При измерении это состояние даёт вероятность состояния спин-вверх примерно 0,98 и состояния спин-вниз примерно 0,02. Если рассмотреть n копий этой спиновой системы, , то при стремлении n к бесконечности подавляющее большинство членов в разложении этого вектора имеют примерно одинаковые количества состояний спин-вверх и спин-вниз. Поэтому подавляющее большинство наблюдателей (копий экспериментаторов) будут видеть состояния спин-вверх и спин-вниз в отношении, которое не согласуется с квантово-механическими предсказаниями. Лишь небольшое количество членов в разложении , у которых 98 процентов состояний спин-вверх и 2 процента состояний спин-вниз, будут согласованы с квантово-механическим ожиданием. Этот результат говорит нам, что только эти состояния и будут теми единственными, имеющими ненулевую норму при n, стремящемся к бесконечности. Тогда абсолютное большинство членов в разложении (абсолютное большинство копий экспериментаторов) следует рассматривать в некотором смысле как «несуществующие». Проблема состоит в том, чтобы понять, что всё это вообще значит.
Я независимо пришёл к описанному выше математическому результату во время подготовки к лекциям по курсу квантовой механики. Было бы полным восторгом получить вероятностную интерпретацию квантовой механики, напрямую следующую из математического формализма — я представляю как учащённо бились сердца всех физиков, которые, как и я, получили этот результат. Поражает, однако, сколь мало известен этот результат в физическом сообществе. Например, я не знаю ни одного стандартного учебника по квантовой физике, в котором он содержится. Я считаю, что этот результат можно осмыслить с нескольких ракурсов: во-первых, как сильную математическую мотивацию вероятностной интерпретации волновой функции Борном — если бы Борн не «угадал» эту интерпретацию, то кто-нибудь, в конце концов, вывел бы её прямо из математического формализма; во-вторых, как проверку совместимости вероятностной интерпретации — если бы этот математический результат не выполнялся, то встал бы вопрос о внутренней осмысленности вероятностной интерпретации волновой функции.
(обратно)77
Я использовал выражение «рассуждения закстарианского типа» для обозначения подхода, в котором понятие вероятности возникает благодаря неведению каждого обитателя из множества миров относительно того, какому конкретному миру он принадлежит. Лев Вайдман предложил отнестись более серьёзно к идее закстарианского сценария. Он говорит, что понятие вероятности возникает в многомировом подходе во временном промежутке между завершением измерения и считыванием полученного результата экспериментатором. Но, возражают скептики, ложка хороша к обеду: обязанность квантовой механики и науки вообще состоит в том, чтобы давать предсказания о том, что произойдёт, а не о том, что произошло. Более того, сомнительно, чтобы понятие квантовой вероятности основывалось на отсрочке во времени, которая легко поддаётся устранению: если учёный имеет немедленный доступ к результатам эксперимента, то возникает опасение, что квантовая вероятность может быть вообще вытеснена из формализма. (Подробное обсуждение содержится в работах: David Albert, Probability in the Everett Picture, «Many Worlds: Everett, Quantum Theory, and Reality», eds. Simon Saunders, Jonathan Barrett, Adrian Kent, David Wallace. Oxford: Oxford University Press, 2010; Peter Lewis, Uncertainty and Probability for Branching Selves, philsciarchive.pitt.edu/archive/00002636.) Окончательный вердикт о гипотезе Вайдмана и подобной вероятности неведения таков: если я подбрасываю монетку в контексте обычной, одной единственной Вселенной и говорю, что есть 50-процентная вероятность того, что выпадет орёл, то я говорю так по той причине, что хотя я и получил всего один результат, на самом деле существуют два результата, которые я мог бы получить. Однако давайте я закрою глаза и представлю, что я только что измерил положение нашего электрона. Я знаю, что монитор детектора показывает либо Земляничные поля, либо мемориал Гранта, но я не знаю, что именно. Тогда вы обращаетесь ко мне. «Брайан, — говорите вы, — какова вероятность того, что монитор показывает мемориал Гранта?» Чтобы ответить, я вспоминаю подбрасывание монетки, но как только я начинаю рассуждать в том же духе, меня одолевают сомнения. «Ммммм, — думаю я, — действительно ли есть два результата, которые я мог бы получить? Единственное, что отличает меня от другого Брайана, — это показание монитора. Представить, что на мониторе показана другая надпись, — это всё равно что представить, что я — это не я. Это представить, что я — другой Брайан». Поэтому, хотя я не знаю, что написано на мониторе, я — тот парень, который говорит сейчас в моей голове — не мог бы получить никакого другого результата; отсюда следует, что моё неведение не может быть причиной вероятностного мышления.
(обратно)78
Считается, что учёные должны быть объективны в своих оценках. Но я спокойно отношусь к тому, что мне хотелось бы, чтобы многомировой подход оказался верным, по причине его математической экономичности и далеко идущих последствий для понимания реальности. В то же время, я проявляю здоровый скептицизм, который исходит из трудностей, с которыми сталкивается включение понятия вероятности в этот подход, потому я полностью открыт альтернативным способам решения этого вопроса. Два из них являются хорошим материалом для обсуждения. В одном делается попытка доработать незавершённый копенгагенский подход до полной теории; другой можно рассматривать как многомировой подход, но без множественности миров.
В первом подходе, инициаторами которого являются Джанкарло Джирарди, Альберто Римини и Туллио Вебер, делается попытка придать смысл копенгагенской схеме путём подстройки математического аппарата теории, основанного на уравнении Шрёдингера, так чтобы он действительно приводил к схлопыванию волны вероятности. Но проще сказать, чем сделать. Подстроенный математический аппарат теории не должен изменять волны вероятности объектов микромира, таких как отдельные частицы или атомы, поскольку у нас нет причин вносить поправки в успешное описание явлений в этой области. Но подстройка обязательно требуется, когда в игру вступают объекты макромира, такие как лабораторное оборудование, что приводит к схлопыванию общей волны вероятности. Джирарди, Римини и Вебер развили соответствующий математический аппарат. Итог их работы таков, что с помощью предложенных ими подстроенных уравнений акт измерения действительно заставляет волну схлопнуться; это приводит к эволюции волны вероятности, показанной на рис. 8.6.
Второй подход, изначально развитый Луи де Бройлем в 1920-х годах и затем спустя десятилетия дополненный Дэвидом Бомом, начинается с математического предположения, перекликающегося с идеями Эверетта. Уравнение Шрёдингера при любых обстоятельствах обязано задавать эволюцию квантовых волн. Поэтому в теории де Бройля — Бома волны вероятности распространяются так же, как в многомировом подходе. Однако теория де Бройля — Бома основана на идее, которую я ранее охарактеризовал как ошибочную: в этом подходе все, кроме одного, из множества миров, содержащиеся в волне вероятности, являются лишь возможными мирами; только один мир считается реальным.
С этой целью в данном подходе перестают петь заученную квантовую песню о волне или частице (что до измерения электрон — это волна, а после измерения электрон превращается в частицу), а вместо этого предлагают одновременно рассматривать волны и частицы. В противоположность стандартной квантовой точке зрения, де Бройль и Бом считают частицы крошечными, локализованными сущностями, эволюция которых происходит вдоль определённых траекторий, что приводит к обычной, однозначной действительности, так же как и при классическом описании. Единственный «реальный» мир — это тот, в котором частицы находятся в своих единственных, определённых положениях. При этом квантовые волны играют совершенно другую роль. Вместо воплощения всей совокупности реальностей, роль квантовой волны сводится к руководству движением частиц. Квантовая волна толкает частицы в те положения, где высота волны большая, что делает вероятным обнаружение частиц в этих положениях, и отталкивает от положений, где высота волны мала, что делает обнаружение частиц в этих положениях маловероятным. Для описания этого процесса де Бройлю и Бому требуется дополнительное уравнение, описывающее действие квантовой волны на частицу, поэтому хотя от уравнения Шрёдингера не отказываются, но теперь на сцене появляется и другой математический исполнитель. (Заинтересованный читатель познакомится с этими уравнениями ниже.)
В течение многих лет бытовало мнение, что подход де Бройля — Бома не стоит того, чтобы на него тратить время, что он перегружен дополнительными вещами — не только вторым уравнением, но также, поскольку он вовлекает одновременно частицы и волны, удвоенным списком ингредиентов. Недавно, однако, стали раздаваться голоса, что этот критицизм надо вложить в контекст. Из работы Джирарди — Римини — Вебера совершенно ясно следует, что даже в версии флагмана квантовой механики, в копенгагенском подходе, требуется второе уравнение. Помимо этого, включение как частиц, так и волн приносит огромную выгоду: возрождается понятие объектов, движущихся вдоль определённых траекторий, происходит возвращение к базовому, привычному свойству реальности, от которого копенгагенцы несколько поспешно убедили всех отказаться. На более техническом уровне критицизм состоит в том, что этот подход является нелокальным (новое уравнение показывает, что воздействие в одной точке моментально переносится в удалённые точки), и его трудно совместить со специальной теорией относительности. Но важность первого критического замечания снижается, если заметить, что даже в копенгагенском подходе имеются нелокальные свойства, которые, к тому же, подтверждены экспериментально. Вопрос насчёт совместимости со специальной теорией относительности безусловно важен, и его ещё предстоит решить в полном объёме.
Частично неприятие теории де Бройля — Бома вызвано тем, что математический формализм теории не всегда представляется в отчётливом виде. Для математически настроенного читателя, приведём здесь прямой вывод этой теории.
Начнём с уравнения Шрёдингера для волновой функции частицы:
где плотность вероятности частицы в точке x, ρ(x) задаётся стандартным уравнением,
Теперь представьте, что частица движется по определённой траектории со скоростью, задаваемой функцией υ(x) в точке x. Какому физическому условию должна удовлетворять функция скорости? Определённо, она должна удовлетворять закону сохранения вероятности: если частица движется со скоростью υ(x) из одной области в другую, плотность вероятности должна меняться соответственно:
Теперь легко найти решение для υ(x), которое имеет вид
где m — это масса частицы.
Вместе с уравнением Шрёдингера это уравнение определяет теорию де Бройля — Бома. Отметим, что второе уравнение нелинейно, но это не влияет на уравнение Шрёдингера — оно по-прежнему остаётся полностью линейным. Тогда подходящая интерпретация такова, что этот подход для устранения недочётов копенгагенского подхода предлагает новое уравнение, зависящее от волновой функции нелинейным образом. Вся сила и красота основополагающего уравнения, то есть уравнения Шрёдингера, полностью сохраняется.
Можно также добавить, что уравнение непосредственно обобщается на случай многих частиц: в правую часть нового уравнения подставляется волновая функция многочастичной системы ψ(x1, x2, x3… xn), и при вычислении скорости k-й частицы производная берётся по отношению к k-й координате (рассматривается, для простоты, одномерное пространство; в старших измерениях, соответственно, увеличивается число координат). Это обобщённое уравнение явно нелокально: скорость k-й частицы мгновенным образом зависит от положений других частиц (поскольку волновая функция зависит от координат положения частиц).
(обратно)79
Приведём конкретный умозрительный эксперимент, демонстрирующий различия между копенгагенским и многомировым подходом. Электрон, подобно всем остальным элементарным частицам, обладает свойством, известным как спин. Электрон, подобно волчку, может вращаться вокруг некоторой оси, но с тем существенным отличием, что скорость его вращения — независимо от направления оси — всегда постоянна. Спин является внутренней характеристикой электрона, подобно массе или электрическому заряду. При этом значение имеет лишь то, вращается он по часовой стрелке или против часовой стрелки вокруг заданной оси. Если против часовой стрелки, мы говорим, что спин электрона вдоль этой оси направлен вверх; если по часовой стрелке, мы говорим, что спин электрона направлен вниз. Из квантово-механической неопределённости следует, что если спин электрона вдоль данной оси имеет определённое значение — например, со 100-процентной вероятностью спин электрона направлен вверх вдоль z-оси — то его спин вдоль x-оси и y-оси неопределён: вдоль x-оси спин будет с вероятностью 50 процентов направлен вверх и с вероятностью 50 процентов вниз; то же самое справедливо для y-оси.
Представьте теперь, что берётся электрон, спин которого вдоль z-оси с вероятностью 100 процентов направлен вверх, и затем требуется измерить его спин вдоль x-оси. Согласно копенгагенскому подходу, если спин окажется направленным вниз, это означает, что волна вероятности спина электрона схлопнулась: возможность «спин-вверх» была стёрта из реальности, остался единственный пик, соответствующий «спин-вниз». В многомировом подходе наоборот, имеют место оба результата, «спин-вниз» и «спин-вверх», поэтому, в частности, возможность «спин-вверх» полностью сохраняется.
Чтобы вынести решение в пользу того или иного подхода, вообразим следующее. Представим, что после измерения спина электрона вдоль x-оси, кто-то полностью обратил физическую эволюцию. (Фундаментальные уравнения физики, включая уравнение Шрёдингера, инварианты относительно обращения времени, что означает, в частности, что по крайней мере в принципе можно развернуть назад любую эволюцию. В моей книге «Ткань космоса» содержится полное обсуждение этого вопроса.) Этой инверсии подвергнется всё: электрон, приборы, всё что угодно, участвующее в эксперименте. Теперь, если многомировой подход верен, последующее измерение спина электрона вдоль z-оси должно привести, со 100-процентной вероятностью, к значению, с которого мы начали: «спин-вверх». Однако, если верен копенгагенский подход (под которым я подразумеваю математически самосогласованную версию, такую как формулировка Джирарди — Римини — Вебера), то мы получим другой ответ. Копенгагенский подход говорит, что при измерении спина электрона вдоль x-оси, где мы обнаружили «спин-вниз», возможность появления «спин-вверх» была аннулирована, полностью стёрта из регистра реальности. Поэтому при обращении измерения мы не возвратимся назад в начальное положение, потому что часть волны вероятности навсегда потеряна. При последующем измерении спина электрона вдоль z-оси нет 100-процентной вероятности получения того же самого результата, с которого мы начали. Наоборот, оказывается, что есть 50 процентов вероятности, что будет получен исходный результат, и 50 процентов вероятности, что будет получен другой. Если повторять этот эксперимент раз за разом и если доверять копенгагенскому подходу, то в среднем в половине случаев вы не получите исходного результата для спина электрона вдоль z-оси. Проблема, конечно же, в осуществлении полного обращения физической эволюции. Но в принципе, этот эксперимент может помочь выяснить, какая из двух теорий верна.
(обратно)80
Основываясь на общей теории относительности и проведя соответствующие вычисления, Эйнштейн математически доказал, что экстремальные конфигурации Шварцшильда — известные теперь как чёрные дыры — не могут существовать. Математически его вычисления были совершенно верными. Но он ввёл дополнительные предположения, которые, при экстремальной искривлённости пространства и времени, вызываемой чёрной дырой, оказались слишком ограничительными. Эти ограничения означали, что используемый Эйнштейном математический формализм не обладал достаточной свободой для обнаружения существования чёрных дыр. Но это всего лишь артефакт подхода Эйнштейна, а не указание на то, могут или нет образовываться чёрные дыры. При современном понимании очевидно, что в общей теории относительности есть место для решений, содержащих чёрные дыры.
(обратно)81
В 1972 году Джеймс Бардин, Брэндон Картер и Стивен Хокинг открыли математические законы, описывающие эволюцию чёрных дыр, и обнаружили, что эти уравнения выглядят точно так же, как уравнения термодинамики. Всё, что надо сделать для перевода из одного набора законов в другой, это заменить «площадь горизонта чёрной дыры» на «энтропию» (и наоборот), а «гравитацию на поверхности чёрной дыры» на «температуру». Поэтому, чтобы идея Бекенштейна сработала — чтобы сходство оказалось не просто совпадением, а свидетельством наличия энтропии у чёрных дыр, — температура чёрных дыр должна быть отлична от нуля.
(обратно)82
Причина, по которой энергия меняется, отнюдь не так очевидна; она основывается на внутренней связи между энергией и временем. Энергию частицы можно представлять как скорость вибраций квантового поля. Если заметить, что сам смысл скорости вовлекает понятие времени, взаимосвязь между энергией и временем становится очевидной. Чёрные дыры оказывают глубочайшее влияние на время. Для удалённого наблюдателя время при приближении объекта к горизонту чёрной дыры замедляется, а на горизонте останавливается совсем. При пересечении горизонта время и пространство меняются ролями — внутри чёрной дыры радиальное направление становится временем. Это означает, что внутри чёрной дыры понятие положительной энергии совпадает с движением вдоль радиального направления к центру сингулярности чёрной дыры. Когда партнёр с отрицательной энергией из пары рождённых из вакуума частиц пересекает горизонт, он действительно падает в центр чёрной дыры. Таким образом, отрицательная энергия, которая у него была с точки зрения удалённого наблюдателя, становится положительной энергией для наблюдателя внутри чёрной дыры. Поэтому такие частицы могут существовать во внутренности чёрной дыры.
(обратно)83
Из всех достижений, которые будут обсуждаться далее в этой главе, только вопрос о микроскопическом устройстве чёрной дыры пока не имеет полной ясности. Как упоминалось в главе 4, в 1996 году Эндрю Строминджер и Кумрун Вафа обнаружили, что если постепенно уменьшать (математически) силу гравитации, то чёрные дыры определённого типа превращаются в некоторые наборы струн и бран. Подсчитав возможные конфигурации всех составляющих, Строминджер и Вафа заново вывели, самым явным из когда либо имеющихся способов, знаменитую формулу Хокинга об энтропии чёрной дыры. Но даже при этом они не смогли описать эти составляющие в случае более сильного гравитационного поля, то есть в условиях, когда формируется чёрная дыра. Другие учёные, например Самир Матур и некоторые из его коллег, выдвинули другие идеи, в том числе возможную реализацию чёрных дыр в виде так называемых «пушистых шариков», места скопления вибрирующих струн, разбросанных по всей внутренности чёрной дыры. Пока эти идеи остаются гипотетическими. Далее в этой главе будут обсуждаться результаты (в разделе «Теория струн и голография»), наиболее внятно проясняющие вопрос микроскопического устройства чёрной дыры.
(обратно)84
Более точно, гравитация может быть выключена в некоторой области пространства, если перейти в состояние свободного падения. Размер этой области зависит от масштабов изменения гравитационного поля. Если гравитационное поле изменяется только на больших расстояниях (то есть если гравитационное поле однородно или почти однородно), свободное падение скомпенсирует гравитацию в большой области пространства. Но если гравитационное поле изменяется на малых расстояниях — например, на расстояниях порядка вашего роста — то гравитацию можно погасить на уровне ног, но при этом чувствовать её на уровне головы. Это будет особенно важно потом, при падении на чёрную дыру, потому что гравитационное поле усиливается по мере приближения к сингулярности чёрной дыры; сила гравитации резко возрастает при уменьшении расстояния до сингулярности. Быстрое изменение означает, что нет никакого способа скомпенсировать эффект наличия сингулярности, что в конце концов растянет ваше тело до точки полного разрыва, потому что гравитационное притяжение на уровне ваших ног будет сильнее (если вы падаете ногами вперёд), чем на уровне головы.
(обратно)85
Эти рассуждения иллюстрируют открытие, сделанное в 1976 году Вильямом Унру, в котором движение некоторого объекта связывается частицами, встреченными им на пути. Унру обнаружил, что если вы будете двигаться с ускорением сквозь пространство, вы окажетесь в газе частиц, температура которого задаётся вашим движением. Общая теория относительности указывает, что наличие ускорения определяется по сравнению с системой отсчёта, связанной с наблюдателем в состоянии свободного падения (см.: «Ткань космоса», глава 3). Поэтому если удалённый наблюдатель не находится в состоянии свободного падения, он видит излучение, испускаемое чёрной дырой; свободно падающий наблюдатель его не видит.
(обратно)86
Чёрная дыра образуется, если масса M, заключённая внутри сферы радиуса R, превышает c2R/2G, где c — скорость света и G — постоянная Ньютона.
(обратно)87
На самом деле, когда материя под давлением своего собственного веса сжимается и образуется чёрная дыра, горизонт событий будет, как правило, находиться внутри границы рассматриваемой области. Иными словами, мы ещё не максимизировали энтропию в данной области. Это легко поправить. Набросайте больше материи внутрь чёрной дыры, что приведёт к расширению горизонта событий до исходной границы области. Поскольку за счёт этого добавочного процесса энтропия снова увеличится, то энтропия материи внутри данной области окажется меньше энтропии чёрной дыры в этом объёме, то есть площади поверхности данной области в планковских единицах.
(обратно)88
G.’t Hooft, Dimensional Reduction in Quantum Gravity, «Salam Festschrift», eds. A. Ali, J. Ellis & S. Randjbar-Daemi. River Edge, N. J.: World Scientific, 1993, p. 284–296 (QCD161:C512:1993).
(обратно)89
Большинство самых важных научных открытий выросло из работ и достижений предшественников. Данный результат не является исключением. Помимо т’Хоофта, Сасскинда и Малдасены, среди исследователей, осветивших путь к этому результату и развивших его последствия, были Стивен Габсер, Джо Польчински, Александр Поляков, Ашок Сен, Эндрю Строминджер, Кумрун Вафа, Эдвард Виттен и многие другие.
Для подготовленного читателя приведём более точное описание результата Малдасены. Пусть N — это число три-бран в стопке бран и пусть g — это значение константы связи в теории струн типа IIB. Когда gN мало, много меньше единицы, физика хорошо описывается низкоэнергетическими струнами, движущимися в стопке бран. В свою очередь такие струны хорошо описываются некоторой четырёхмерной суперсимметричной конформно-инвариантной квантовой теорией поля. Но когда gN велико, теория поля попадает в режим сильной связи, что затрудняет её аналитическое рассмотрение. Однако в этом режиме мы можем применить результат Малдасены, который говорит, что можно перейти к описанию струн, движущихся на фоне геометрии, обусловленной близким расположением к горизонту стопки бран, что есть AdS5×S5 (пятимерное пространство анти-де Ситтера на пятимерную сферу). Радиус этого пространства контролируется gN (точнее, радиус пропорционален (gN)1/4), таким образом, при больших gN кривизна пространства AdS5×S5 мала, что гарантирует обозримость вычислений по теории струн (в частности, они хорошо аппроксимируются вычислениями в рамках модели, являющейся модификацией эйнштейновской гравитации). Поэтому при изменении gN от малых значений до больших физическое описание переходит от четырёхмерной суперсимметричной конформно-инвариантной квантовой теории поля к десятимерной теории струн на пространстве AdS5×S5. Это и есть так называемое АдС/КТП соответствие (анти-де Ситтер / конформная теория поля).
(обратно)90
Хотя полное доказательство гипотезы Малдасены пока неосуществимо, за последние годы связь между описаниями в балке и на границе значительно прояснилась. Например, был выделен класс вычислений, результаты которых справедливы для любых значений константы связи. Поэтому эти результаты можно явно проследить от малых значений константы связи до больших. Таким образом, можно подсмотреть процесс «трансформации», согласно которому описание физики в объёме переходит в граничное описание, и наоборот. Такие вычисления показали, например, как цепочки взаимодействующих частиц в граничной теории могут трансформироваться в струны в объёме — особенно убедительная интерполяция между двумя описаниями.
(обратно)91
Более точно, это некий изменённый вариант гипотезы Малдасены. Здесь на границе вместо изначальной квантовой теории рассматривается теория, приближённая к квантовой хромодинамике. Это изменение приводит к соответствующим модификациям теории в балке. В частности, следуя работе Виттена, высокая температура в граничной теории переходит в чёрную дыру в теории в балке. В свою очередь словарь по переводу между двумя описаниями показывает, что трудная задача вычисления вязкости кварк-глюонной плазмы переходит в задачу вычисления реакции горизонта чёрной дыры на определённые деформации — что трудоёмко, но вполне выполнимо.
(обратно)92
Другой подход к задаче полного определения теории струн, возникший из более ранних работ в этой области, называется Матричной теорией (что даёт ещё одно возможное объяснение для значения буквы «M» в M-теории). Этот подход был разработан Томом Бэнксом, Вили Фишлером, Стивом Шенкером и Леонардом Сасскиндом.
(обратно)93
Я указал число 1055 грамм, что соответствует содержимому наблюдаемой вселенной на современном этапе, но в более ранние времена температура содержимого вселенной была выше, и поэтому оно имело бо́льшую энергию. Поэтому 1065 грамм является более точной оценкой для той массы, которую вам потребуется собрать в крохотное зёрнышко для повторения эволюции нашей Вселенной с того момента, когда её возраст составлял примерно одну секунду.
(обратно)94
Можно подумать, что поскольку ваша скорость ограничена сверху скоростью света, то ваша кинетическая энергия также будет ограничена. Но это не так. По мере того как ваша скорость приближается к скорости света, ваша энергия увеличивается; из специальной теории относительности следует, что она не ограничена. Математически формула вашей энергии имеет вид:
где c — это скорость света, а υ — ваша скорость. Как можно видеть, когда υ стремится к c, энергия E неограниченно растёт. Отметим также, что это справедливо с точки зрения наблюдателя, который следит за вашим падением, например, кого-то, неподвижно стоящего на поверхности Земли. С вашей точки зрения, пока вы свободно падаете, вы неподвижны, а окружающая вас материя постоянно набирает скорость.
(обратно)95
На нашем текущем уровне понимания имеется значительный разброс в таких оценках. Величина в 10 грамм возникает из следующих рассуждений: считается, что энергетический масштаб инфляции составляет примерно 10−5 от планковской энергии, которая превышает примерно в 1019 энергию, эквивалентную массе протона. (Если бы инфляция происходила на бо́льших масштабах энергии, то по некоторым оценкам мы уже должны были бы наблюдать гравитационные волны, порождённые в ранней вселенной.) В более привычных единицах планковский масштаб составляет примерно 10−5 грамма (небольшая величина по обычным меркам, но на масштабе физики элементарных частиц, где говорится об энергии, переносимой отдельными частицами, она огромна). Таким образом, плотность энергии поля инфлатона будет составлять примерно 10−5 грамма на каждую кубическую единицу объёма, линейный размер которого определяется расстоянием, кратным планковской длине с множителем 105 (напомним, что из соотношения квантовой неопределённости следует, что энергия и длина обратно пропорциональны друг другу), что составляет примерно 10−28 сантиметра. Таким образом, полная масса-энергия поля инфлатона в объёме с ребром в 10−26 сантиметра равна 10−5 грамма/(10−28 сантиметра)3 × (10−26 сантиметра)3, что составляет примерно 10 грамм. Те, кто прочитал «Ткань космоса», возможно помнят, что там я использовал несколько иное значение. Различие возникло из предположения, что энергетический масштаб инфлатона был несколько выше.
(обратно)96
Hans Moravec, «Robot: Mere Machine to Transcendent Mind». New York: Oxford University Press, 2000. См. также: Ray Kurzweil, «The Singularity Is Near: When Humans Transcend Biology». New York: Penguin, 2006.
(обратно)97
См., например: Robin Hanson, «How to Live in a Simulation», «Journal of Evolution and Technology» 7, 1 (2001).
(обратно)98
Согласно тезису Чёрча — Тьюринга, любой компьютер так называемого универсального тьюрингова типа может моделировать действия другого компьютера, поэтому вполне справедливо, что находящийся внутри симуляции компьютер — он сам смоделирован основным компьютером, на котором выполняется общая симуляция — может решать определённые задачи, эквивалентные тем, что решаются на основном компьютере.
(обратно)99
Философ Дэвид Льюис развил похожую идею, названную им модальным реализмом. См.: Lewis David, «On the Plurality of Worlds». Malden, Mass.: Wiley-Blackwell, 2001. Однако, мотивация Льюиса для введения всех возможных вселенных отличается от мотивации Нозика. Льюису нужен был контекст, в котором, например, могли бы воплотиться нереализованные утверждения (такие как «если бы Гитлер выиграл войну, то мир был бы другим»).
(обратно)100
Джон Барроу высказывал похожее мнение в: John Barrow, «Pi in the Sky». New York: Little, Brown, 1992.
(обратно)101
При более детальном обсуждении вычислимых и невычислимых функций мы встретимся с функциями, вычислимыми с любой наперёд заданной точностью. Это функции, для которых имеется конечный алгоритм вычисления значений с растущей точностью. Например, это имеет место для вычисления числа π с точностью до определённого количества знаков: компьютер может вычислить в π каждый последующий знак после запятой, хотя никогда не достигнет конца вычислений. Поэтому, хотя π, строго говоря, не является вычислимым числом, оно вычислимо с любой наперёд заданной точностью. Однако большинство вещественных чисел непохожи на π. Они не просто невычислимы, они также невычислимы с любой наперёд заданной точностью.
При рассмотрении «успешных» симуляций мы должны рассматривать те, которые основаны на функциях, вычислимых с любой наперёд заданной точностью. В принципе, убедительная реальность может быть создана на основе частичного результата вычислений на компьютере функций, вычислимых с любой наперёд заданной точностью.
Чтобы законы физики были вычислимы, или даже вычислимы с любой наперёд заданной точностью, следует отказаться от традиции опираться на вещественные числа. Причём не только при описании пространства и времени, где обычно задействуются вещественнозначные координаты, но также для всех остальных математических составляющих законов природы. Например, величина силы электромагнитного поля не должна пробегать вещественные значения, а только принимать набор дискретных значений. То же самое должно выполняться для вероятности нахождения электрона в том или ином месте. Шмидхубер обращает внимание, что все когда-либо проделанные в физике вычисления вовлекают манипуляции с дискретными символами (на бумаге, на доске, на компьютере). Поэтому хотя всегда считалось, что эта часть научной работы использует вещественные числа, на практике оказывается, что это не так. То же самое справедливо для всех когда-либо проведённых измерений. Ни один из приборов не имеет абсолютной точности, поэтому наши измерения всегда выдавали дискретные численные результаты. В этом смысле все успехи в физике можно считать успехами цифровой парадигмы. Тогда возможно, что истинные законы сами являются вычислимыми (или вычислимыми с любой наперёд заданной точностью).
Есть много разных взглядов на «цифровую физику». См., например, книгу С. Вольфрама: Stephen Wolfram, «A New Kind of Science». Champaign, Ill.: Wolfram Media, 2002; и книгу С. Ллойда: Seth Lloyd, «Programming the Universe». New York: Alfred A. Knopf, 2006. Математик Роджер Пенроуз считает, что человеческий разум основывается на невычислимых процессах и, следовательно, Вселенная, в которой мы обитаем, обязана содержать невычислимые математические функции. С этой точки зрения наша Вселенная не соответствует цифровой парадигме. См., например: Penrose Roger, «The Emperor’s New Mind». New York: Oxford University Press, 1989; Penrose Roger, «Shadows of the Mind». New York: Oxford University Press, 1994.
(обратно)102
Steven Weinberg, «The First Three Minutes». New York: Basic Books, 1973, p. 131.
(обратно)Примечания
1
Изобразить искривлённое пространство легче, чем искривлённое время, поэтому во многих популярных изложениях теории гравитации Эйнштейна внимание уделяют только первому. Однако в действительности основной вклад в притяжение хорошо известных нам объектов, таких как Земля и Солнце, вносит кривизна времени, а не пространства. В качестве иллюстрации представьте себе двое часов: одни у земной поверхности, а вторые — на верхнем этаже Эмпайр-стейт-билдинг. Поскольку те часы, которые находятся внизу, расположены ближе к центру Земли, на них действует более мощная сила притяжения, чем на часы, которые размещены высоко над Манхэттеном. Общая теория относительности указывает, что из-за этого скорость течения времени для тех и других часов будет слегка различной: нижние часы будут идти чуть медленнее (на несколько миллиардных долей секунды в год), чем часы на высоте. Эта нестыковка во времени является примером того, что мы имеем в виду, когда говорим об искривлённом времени. Общая теория относительности утверждает, что объекты двигаются в те области пространства, где время течёт медленнее, — в каком-то смысле все объекты «хотят» стареть как можно медленнее. С точки зрения Эйнштейна, это объясняет, почему любой объект падает, когда вы его отпускаете.
(обратно)2
Вскоре мы увидим, что Эйнштейн отказался от статичной вселенной, столкнувшись с астрономическими данными, согласно которым вселенная расширяется. Однако, следует отметить, что его опасения насчёт статичной вселенной предшествовали получению этих данных. Физик Виллем де Ситтер указал Эйнштейну, что его статичная вселенная нестабильна: стоит её слегка толкнуть, и она начнёт расти или сжиматься. Физики избегают решений, которые могут существовать лишь в идеальных, неискажённых условиях.
(обратно)3
В модели Большого взрыва расширение пространства вовне во многом подобно движению вверх подброшенного мяча: сила притяжения гравитации тянет обратно движущийся вверх мяч, и тем самым замедляет его движение; аналогичным образом сила притяжения гравитации действует на разлетающиеся галактики и тем самым тормозит их движение. Ни в одном из случаев движение вперёд не требует отталкивающей силы. Однако вы всё равно можете спросить: мяч был запущен вверх рукой, а что «запустило» пространство и его расширение вовне? Мы вернёмся к этому вопросу в главе 3, где увидим, что современная теория постулирует непродолжительную вспышку гравитационного отталкивания, действующего в самые ранние моменты космической истории. Мы также увидим, что более точные данные свидетельствуют о том, что расширение пространства не замедляется со временем, что приводит к удивительному — и это станет ясно в последующих главах — воскрешению потенциально глубокого смысла космологической постоянной.
(обратно)4
С учётом предыдущего обсуждения того, что материя искривляет область пространства, в которую она погружена, читателя может удивить, что кривизны нет, хотя материя присутствует. Это объясняется тем, что равномерное распределение материи, как правило, искривляет пространство-время; в данном частном случае пространственная кривизна равна нулю, а пространственно-временная кривизна не нулевая.
(обратно)5
Приведённое количество справедливо для текущей эры. В более ранней Вселенной критическая плотность была выше.
(обратно)6
Если бы Вселенная была статична, то свет, путешествующий в течение последних 13,7 миллиардов лет и только сейчас достигший нас, действительно был бы излучён с расстояния в 13,7 миллиардов световых лет. В расширяющейся вселенной, в то время, пока свет находится в пути, испустивший его объект продолжает отдаляться миллиарды лет. Таким образом, на момент, когда мы принимаем этот свет, объект находится ещё дальше — значительно дальше, — чем 13,7 миллиардов световых лет. Вычисления с помощью общей теории относительности показывают, что этот объект (допустим, что он всё ещё существует и постоянно движется вместе с расширяющимся пространством) будет теперь находиться на расстоянии примерно 41 миллиарда световых лет. В этом смысле, наблюдаемая Вселенная имеет диаметр примерно 82 миллиарда световых лет. Свет от объектов, находящихся дальше, ещё не успел до нас дойти, и поэтому они находятся за пределами нашего космического горизонта.
(обратно)7
Более по́лно чёрные дыры я буду обсуждать в последующих главах. Здесь же будем придерживаться укоренившегося в популярной литературе представления о чёрной дыре как о некоторой пространственной области — можно представить себе шар в пространстве, — гравитационное притяжение которой настолько велико, что ничего из пересекающего её границу не может вырваться обратно. Чем больше масса чёрной дыры, тем больше её размер. Поэтому когда что-нибудь падает в чёрную дыру, то увеличивается не только масса, но и размер чёрной дыры.
(обратно)8
В отечественной литературе принят введённый И. С. Шкловским термин «реликтовое излучение», которым мы будем пользоваться в оставшейся части книги. (Прим. перев.)
(обратно)9
Следует отметить, что хотя у галактик нет реактивных двигателей, в общем случае они движутся чуть быстрее, чем ожидается из расширения пространства — как правило, это результат крупномасштабных межгалактических гравитационных сил, а также внутреннего движения вращающегося газового облака, из которого образуются звёзды в галактиках. Скорость такого движения называется пекулярной и, как правило, она достаточно мала, поэтому в космологическом анализе ею можно смело пренебречь.
(обратно)10
Аналогично, сверхбыстрое расширение пространства означает, что регионы, достаточно отдалённые друг от друга в настоящий момент, находились в ранней Вселенной гораздо ближе, чем предсказывает стандартная теория Большого взрыва, обеспечивая таким образом выравнивание температуры до того, как инфляция разметала эти регионы друг от друга.
(обратно)11
Вы можете подумать, что отрицательное давление втягивает вовнутрь и поэтому противоречит гравитационному отталкиванию, то есть выдавливанию наружу. На самом деле, однородное давление, независимо от знака, вообще не давит и не выталкивает. Барабанные перепонки лопаются, только если оказываемое на них давление неравномерно — с одной стороны меньше, чем с другой. Описываемое здесь отталкивание является гравитационной силой, порождённой однородным отрицательным давлением. Трудный, но ключевой момент для понимания. Я повторюсь: положительная масса или положительное давление приводят к гравитационному притяжению, а отрицательное давление приводит к менее привычному гравитационному отталкиванию.
(обратно)12
Так как быстрое расширение пространства называется инфляцией, то следуя исторической традиции придумывания названий, поле, обеспечивающее инфляцию, стали называть инфлатоном (по аналогии с фотоном, электроном, нейтроном, мюоном и так далее).
(обратно)13
Алан Гут осознал бесконечную природу инфляции; Пол Стейнхард предложил её математическую реализацию в определённом контексте; Александр Виленкин описал её в самых общих терминах.
(обратно)14
Термин «ячейка-вселенная» не менее наглядно изображает процесс возникновения Вселенной в объемлющей среде, заполненной инфлатоном (был предложен Аланом Гутом).
(обратно)15
Ведущую роль в этих исследованиях сыграли Вячеслав Муханов, Геннадий Чибисов, Стивен Хокинг, Алексей Старобинский, Алан Гут, Co-Янг Пи, Джеймс Бардин, Пол Стейнхард и Майкл Тернер.
(обратно)16
Аббревиатура от Cosmic Background Explorer. (Прим. ред.)
(обратно)17
Подчеркнём, что речь идёт о фундаментальных частицах, таких как электроны и кварки, потому что у составных частиц, таких как протоны и нейтроны (состоящих из 3 кварков), значительная часть массы возникает из-за взаимодействия между конституэнтами (энергия глюонов, связывающих кварки внутри протонов и нейтронов, даёт основной вклад в массу этих составных частиц).
(обратно)18
Если более точно, не сила гравитационного поля сама по себе определяет замедление времени, а величина гравитационного потенциала. Например, если вы зависните внутри сферической полости в центре массивной звезды, то не будете вообще чувствовать гравитационную силу, но поскольку вы находитесь глубоко внутри ямы гравитационного потенциала, время для вас будет течь медленнее, чем для того, кто находится за пределами звезды.
(обратно)19
Перевод М. Лозинского. (Прим. перев.)
(обратно)20
Этот результат (и родственные идеи) был получен рядом исследователей в различных контекстах и наиболее чётко выражен Александром Виленкиным, а также Сидни Коулменом и Фрэнком де Луччией.
(обратно)21
Если хотите знать, как теория струн преодолевает проблемы, препятствовавшие предыдущим попыткам объединить гравитацию и квантовую механику, смотрите главу 6 книги «Элегантная Вселенная»; краткий обзор вопроса представлен в комментарии {31}. Если совсем коротко, то причина в том, что в отличие от частицы, которая находится в одной единственной точке, струна обладает длиной, а потому чуть растянута вдоль некоторой области пространства. В свою очередь такое растяжение ослабляет силу квантовых флуктуаций на малых расстояниях, которые и блокировали предыдущие попытки. К концу 1980-х годов появились сильные аргументы в пользу успешного объединения общей теории относительности и квантовой механики под эгидой теории струн; более поздние исследования добавили значительной убеждённости в этом вопросе (см. главу 9).
(обратно)22
Если некий объект был бы по-настоящему одномерным, мы не смогли бы его видеть, потому что у него нет поверхности, от которой могли бы отражаться фотоны, и он не мог бы сам порождать фотоны посредством атомных переходов. Поэтому когда я говорю «увидеть», то подразумеваю все возможные способы наблюдения или экспериментирования, которые могли бы подтвердить пространственную протяжённость объекта. Тогда утверждение состоит в том, что любое пространственное измерение, меньшее чем разрешающая способность оборудования, не может быть обнаружено на эксперименте.
(обратно)23
Более точно, та составляющая компонента Вселенной, которая наиболее существенна для нашей формы жизни, была бы разительно другой. Поскольку известные частицы и объекты, из которых они состоят — звёзды, планеты, люди и так далее, — сводятся к менее чем 5 процентам массы Вселенной, такое нарушение не будет влиять на бо́льшую часть Вселенной, по крайней мере в том, что касается её массы. Однако, если рассматривать это влияние на жизнь в привычном нам виде, разница будет огромной.
(обратно)24
Существуют некоторые умеренные ограничения, которые квантовая теория поля накладывает на свои внутренние параметры. Во избежание определённых типов неприемлемого физического поведения (нарушения закона сохранения, нарушения определённых преобразований симметрии и так далее) могут накладываться ограничения на заряды (электрические, а также ядерные) частиц теории. Более того, поскольку сумма вероятностей во всех физических процессах обязана быть равной 1, массы частиц также не могут быть любыми. Но даже при этом допустимые значения характеристик частиц варьируются достаточно широко.
(обратно)25
Когда говорят о центре чёрной дыры, то часто создаётся впечатление, что это некое место в пространстве. Но это не так. Центром чёрной дыры следует считать определённый момент времени. При пересечении горизонта событий чёрной дыры время и пространство (радиальное направление) меняются ролями. Если вы падаете в чёрную дыру, ваше радиальное движение являет собой движение во времени. Таким образом, вас толкает в центр чёрной дыры точно так же, как вас толкает к следующему моменту времени. В этом смысле центр чёрной дыры похож на последний момент времени.
(обратно)26
По многим причинам энтропия является ключевым понятием в физике. В обсуждаемом случае энтропия используется как диагностика того, не упускает ли теория струн какую-нибудь существенную физику при описании чёрных дыр. Если бы так случилось, то результат вычислений беспорядка внутри чёрной дыры на основе струнной математики оказался бы неверным. Тот факт, что ответ точно совпадает с тем, что Бекенштейн и Хокинг вывели с помощью совсем других рассуждений, указывает на то, что теория струн успешно ухватила фундаментальное физическое описание. Это очень обнадёживающий результат. Более подробно об этом можно прочитать в книге «Элегантная Вселенная», глава 13.
(обратно)27
Утверждение теории струн об успешном соединении квантовой механики и общей теории относительности основывается на множестве вычислений, а также на убедительных результатах, описанных в главе 9.
(обратно)28
Можно считать это существенным обобщением результатов, затронутых в главе 4, когда различные формы дополнительных измерений могут приводить к тождественным физическим моделям.
(обратно)29
Такой результат не является таинственным математическим совпадением. Наоборот, в строгом математическом смысле струны обладают высокосимметричной формой, и именно эта симметрия позволяет устранить все противоречия. Более детальное изложение содержится в комментарии {39}.
(обратно)30
Первая революция началась с работ Джона Шварца и Майкла Грина 1984 года, в которых была дана современная формулировка теории струн.
(обратно)31
Внимательный читатель заметит, что ломтик хлеба на самом деле трёхмерен (у него есть ширина, длина и толщина), но пусть вас это не беспокоит. Толщина хлебного ломтика напоминает, что ломтики — это визуализация больших три-бран.
(обратно)32
Вы можете спросить, движется ли всё многомерное пространство. Но каким бы интересным не был этот вопрос, он, однако, не имеет отношения к нашему обсуждению.
(обратно)33
Для читателей, знакомых с проблемой стрелы времени, отметим, что я предполагаю, в согласии с наблюдательными данными, что энтропия уменьшается по направлению в прошлое. Более подробное описание дано в книге «Ткань космоса», глава 6.
(обратно)34
Отметим как интересную деталь, что авторы циклической модели с бранами нашли вполне утилитарное применение тёмной энергии (тёмная энергия будет подробно обсуждаться в главе 6). В последнюю фазу каждого цикла присутствие тёмной энергии в мирах на бранах гарантирует согласие с современными наблюдениями ускоряющегося расширения; в свою очередь, это ускоряющееся расширение разбавляет плотность энтропии, что даёт начало следующему космологическому циклу.
(обратно)35
Одно пояснение насчёт терминологии. Бо́льшей частью в этой книге термины «космологическая постоянная» и «тёмная энергия» равнозаменяемы. Если требуется большая точность, я говорю о значении космологической постоянной для обозначения количества тёмной энергии, заполняющей пространство. Как было отмечено ранее, физики часто используют термин «тёмная энергия» более свободно, для обозначения всего, что может выглядеть (или маскироваться) как космологическая постоянная на больших временны́х интервалах, однако может медленно меняться и, следовательно, не быть постоянной на самом деле.
(обратно)36
Именно так работает 3D-технология в кино: подходящим образом подбирая смещение для почти тождественных кадров, кинематографисты заставляют ваш мозг интерпретировать возникающие параллаксы как разные расстояния, создавая таким образом иллюзию ЗD-окружения.
(обратно)37
Конечно же, некоторые вещи действительно изменяются. Как отмечалось в примечаниях к главе 3, у самих галактик есть небольшие скорости, сверх скорости пространственного расширения. На космологическом масштабе времени такое дополнительное движение может изменить взаимное расположение; оно также может привести к разным интересным астрофизическим событиям, таким как столкновение и слияние галактик. Однако для объяснения космических расстояний эти усложнения можно благополучно проигнорировать.
(обратно)38
Если пространство бесконечно велико, то вы можете спросить, что подразумевают, когда говорят, что Вселенная сейчас больше, чем в прошлом. Ответ состоит в том, что «больше» относится к современным расстояниям между галактиками по сравнению с расстояниями между теми же галактиками в прошлом. Расширение пространства означает, что сейчас галактики более удалены друг от друга, что математически выражается возросшим масштабным фактором Вселенной. В случае бесконечной вселенной «больше» не указывает на общий размер пространства, так как бесконечное всегда остаётся бесконечным. Но для простоты мы будем продолжать говорить об изменении размера Вселенной даже в случае бесконечного пространства, подразумевая при этом изменение расстояния между галактиками.
(обратно)39
Вдумчивый читатель заметит, что каждая флуктуация даёт вклад в энергию, обратно пропорциональный её длине волны, откуда следует, что сумма по всем возможным длинам волн приводит к бесконечной энергии.
(обратно)40
Заметим, что сокращение происходит благодаря тому, что суперсимметрия спаривает бозоны (частицы с целым спином) и фермионы (частицы с полуцелым (нечётным) спином). Так как бозоны описываются коммутирующими переменными, а фермионы описываются антикоммутирующими переменными, это приводит к противоположным знакам их квантовых флуктуаций.
(обратно)41
Кембриджский астрофизик Джордж Эфстатиу также одним из первых выдвинул убедительные аргументы в поддержку ненулевой космологической постоянной.
(обратно)42
В главе 7 вопрос проверки теорий с мультивселенными будет рассматриваться более подробно; также более тщательно будет рассмотрена роль антропных рассуждений в получении потенциально проверяемых предсказаний.
(обратно)43
Поскольку есть различные взгляды на роль научных теорий в изучении природы, излагаемые мной утверждения могут допускать разную интерпретацию. Есть две выделенные позиции, одну из которых занимают реалисты, уверенные, что математические теории напрямую описывают устройство природы, и инструменталисты, которые верят, что теория является лишь удобным инструментом предсказания того, что измеряют приборы, но при этом ничего не говорит об устройстве самой реальности. В течение десятилетий изнурительных споров, философы от науки развили множество уточнённых вариантов этих направлений и связанных с ними взглядов. Несомненно, моя собственная позиция и подход, развиваемый в этой книге, принадлежат к лагерю реалистов. В этой главе, в которой рассматривается научная состоятельность теорий определённого типа и даётся оценка их значения для понимания природы, поднимаются вопросы, на которые различные философские школы предложили бы существенно разные точки зрения.
(обратно)44
В мультивселенной с огромным количеством разных вселенных возникает разумное опасение, что независимо от результатов экспериментов и наблюдений, среди гигантского количества вселенных теории найдётся некоторая вселенная, для которой подойдут полученные результаты. Если так, то не будет существовать никакого экспериментального свидетельства, способного доказать неправильность теории; в свою очередь, никакие данные не смогут быть интерпретированы подходящим образом как доказательства в поддержку теории. Мы ещё вернёмся к этому вопросу.
(обратно)45
Важно сделать оговорку, что хотя последствия небольших изменений нескольких констант можно достоверно просчитать, более значительные изменения значений большего числа констант значительно усложняют задачу. По крайней мере, нельзя исключить, что значительные отклонения разных фундаментальных констант скомпенсируют друг друга, или приведут к новым эффектам и таким образом окажутся совместимы с жизнью в обычном для нас виде.
(обратно)46
Более точно, если космологическая постоянная отрицательна и достаточно мала, процесс схлопывания будет продолжаться достаточно долго для того, чтобы смогли образоваться галактики. Простоты ради, мы будем игнорировать эту тонкость.
(обратно)47
Ради простоты мы не будем рассматривать положение электрона в вертикальном направлении, а целиком сосредоточимся на его положении на карте Манхэттена. Позвольте ещё раз подчеркнуть, что хотя из рассуждений этого раздела станет ясно, что уравнение Шрёдингера не позволяет волне мгновенно схлопнуться, как на рис. 8.6, тем не менее, экспериментатор может аккуратно придать волне пикообразную форму (или, более точно, очень близкую к ней форму).
(обратно)48
Математическое описание приведено в комментарии {71}.
(обратно)49
Такая точка зрения, отвергающая случайность, требует отказа от используемого мной разговорного выражения «волна вероятности» в пользу технического термина «волновая функция».
(обратно)50
Это не совсем точное определение, но оно вполне подходит для настоящих целей. Мы его скоро уточним.
(обратно)51
Как только система достигает конфигурации с максимальной энтропией (подобно пару при фиксированной температуре, однородно заполняющему контейнер), то все возможности для дальнейшего увеличения энтропии оказываются исчерпанными. Поэтому более точное утверждение таково, что энтропия возрастает, пока не достигнет наибольшего значения, допускаемого системой.
(обратно)52
В главе 3 мы обсуждали, что энергия гравитационного поля может быть отрицательной; однако, эта энергия является потенциальной. Энергия, которую мы обсуждаем сейчас, является кинетической, она обусловлена массой электрона и его движением. В классической физике она должна быть положительной.
(обратно)53
Когда чёрная дыра сжимается, поверхность её горизонта событий тоже сжимается, что противоречит утверждению Хокинга об увеличении площади полной поверхности. Напомним, однако, что теорема Хокинга о площади основана на классической общей теории относительности. Здесь мы учитываем квантовые процессы и приходим к более точному заключению.
(обратно)54
Помимо переворачивания монет можно также менять их расположение, но для демонстрации основных идей этим усложнением можно пренебречь.
(обратно)55
Если более точно, то это минимальное число «да или нет» вопросов, ответы на которые однозначно определяют устройство системы на микроскопическом уровне.
(обратно)56
Хокинг показал, что энтропия равна одной четвёртой от площади горизонта событий в планковских единицах.
(обратно)57
Если вас, читатель, это заинтересовало, я рекомендую вам отличную книгу Леонарда Сасскинда «Войны чёрных дыр».
(обратно)58
Читатель, знакомый с чёрными дырами, заметит, что даже без рассмотрения на квантовом уровне, которое приводит к излучению Хокинга, эти две точки зрения будут отличаться по течению времени. С помощью излучения Хокинга различие между двумя точками зрения становится ещё более очевидным.
(обратно)59
Как мы уже говорили, «уставший», или «измотанный» свет — это свет, у которого длина волны растянулась (испытала красное смещение), а частота колебаний уменьшилась из-за затрат энергии на удаление от чёрной дыры (или от любого источника гравитации). Подобно более привычным циклическим процессам (как, например, орбитальное движение Земли вокруг Солнца, вращение Земли вокруг своей оси и так далее), колебания света можно использовать для определения прошедшего времени. Собственно, колебания света, испущенного возбуждёнными атомами цезия-133, сейчас используются учёными для определения одной секунды. Таким образом, замедленные колебания уставшего света означают, что течение времени вблизи чёрной дыры — с точки зрения удалённого наблюдателя — также замедляется.
(обратно)60
Имеет смысл упомянуть историю, которую я обошёл в этой главе и которая касается давних споров о том, требуется ли из-за чёрных дыр пересмотреть квантовую механику — нарушают ли чёрные дыры, поглощая информацию, способность волн вероятности распространяться вперёд во времени. Если кратко подытожить, то результат Виттена об эквивалентности между чёрной дырой и физической ситуацией, в которой не происходит потери информации (разогретая квантовая теория поля), привёл к окончательному доказательству, что вся падающая в чёрную дыру информация в конечном счёте остаётся доступной внешнему миру. Не требуется никакого пересмотра квантовой механики. С помощью открытия Малдасены было установлено, что граничная теория даёт полное описание информации (энтропии), хранящейся на поверхности чёрной дыры.
(обратно)61
Забавно, но объяснение, почему магнитные монополи до сих пор не были обнаружены (хотя они предсказываются во многих вариантах единой теории), состоит в том, что они стали очень редкими, растворились в быстро расширяющемся пространстве, как это предписывает инфляционная космология. Гипотеза, которая выдвигается теперь, состоит в том, что магнитные монополи могут инициировать последующие инфляционные эпизоды.
(обратно)62
Другая лазейка возникает благодаря проблеме измерений, рассмотренной в главе 7. Если число реальных (не виртуальных) вселенных бесконечно (например, если мы часть лоскутной мультивселенной), то будет бесконечно много похожих на наш миров, в которых далёкие потомки смогут запускать симуляции, что приводит к бесконечному числу смоделированных миров. В этом случае снова может казаться, что число смоделированных миров сильно превышает число реальных миров, но, как мы видели в главе 7, сравнение бесконечностей является ненадёжным занятием.
(обратно)63
Теория с конечным числом состояний в конечном пространственном объёме (в соответствии, например, с ограничениями на энтропию, обсуждавшимися в предыдущей главе) всё равно может содержать непрерывные величины как часть математического аппарата теории. Именно так происходит, например, в квантовой механике: величина волны вероятности может непрерывно изменяться даже тогда, когда возможно лишь конечное число разных результатов.
(обратно)64
У Борхеса речь шла о книгах, строки в которых написаны любыми возможными символами, неважно со смыслом или нет.
(обратно)65
Как объяснялось в комментарии {65}, размер этой бесконечности превышает размер бесконечного набора целых чисел 1, 2, 3… и так далее.
(обратно)66
При обсуждении лоскутной мультивселенной (в главе 2) я подчеркнул, что квантовая физика утверждает, что в любой конечной области пространства существует лишь конечное число различных способов организации материи. Тем не менее, математический формализм квантовой механики вовлекает непрерывные характеристики, поэтому допустимых значений бесконечно много. Эти характеристики не являются непосредственно наблюдаемыми (подобно высоте волны вероятности в данной точке); конечное число возможностей возникает только по отношению к различным результатам проведённых экспериментов.
(обратно)67
Это вариация на тему знаменитого парадокса брадобрея из Севильи, в котором брадобрей бреет всех, кто не бреет самого себя. Отсюда вопрос: кто бреет брадобрея? (Предполагается, что брадобрей мужчина, ибо если брадобрей женщина, то ответ слишком прост.)
(обратно)68
Согласно Шмидхуберу, эффективной будет такая стратегия, при которой компьютер будет делать вычисления каждой смоделированной вселенной вперёд во времени способом типа «ласточкин хвост»: первая вселенная будет обновляться на каждом втором такте компьютера, вторая вселенная будет обновляться на каждом втором из оставшихся тактов, третья вселенная будет обновляться на каждом втором из тактов, незадействованных в первых двух вселенных, и так далее. Таким образом, каждая вычислимая вселенная будет моделироваться вперёд во времени в течение произвольно большого количества тактов.
(обратно)69
Макс Тегмарк отметил, что цельная симуляция, выполненная от начала и до конца, сама является набором математических соотношений. Таким образом, если считать, что вся математика реальна, то данный набор также будет реальным. С этой точки зрения нет нужды запускать на самом деле какие-либо компьютерные симуляции, поскольку математические соотношения, к которым они приведут, являются уже реальными. Отметим также, что установка на выполнение симуляции вперёд во времени, пусть даже интуитивная, является излишним ограничением. Вычислимость вселенной должна оцениваться на основе рассмотрения вычислимости математических соотношений, которые определяют полную историю эволюции вселенной, независимо от того, описывают или нет эти соотношения временную эволюцию симуляции.
(обратно)70
Отметим, как и в главе 7, что для убедительного наблюдательного опровержения инфляции потребуется сравнить бесконечные классы вселенных — а это пока недостижимо для теории. Однако большинство исследователей согласились бы, что если, скажем, данные по реликтовому излучению выглядели бы иначе, чем на рис. 3.4, то их уверенность в инфляции сильно бы уменьшилась, даже если бы теория допускала, что в инфляционной мультивселенной может существовать пузырёк-вселенная с такими данными.
(обратно)

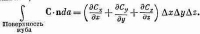
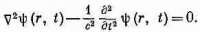

Комментарии к книге «Скрытая реальность», Брайан Рэндолф Грин
Всего 0 комментариев