Березовчук А.В. Физическая химия: конспект лекций
Введение
Физическая химия – наука, объясняющая химические явления и устанавливающая их закономерности на основе общих принципов физики.
Общая задача физической химии – предсказание временного хода химического процесса и конечного результата на основании данных о строении и свойствах молекул.
Термин «физическая химия» предложен М. В. Ломоносовым. Им же был прочитан первый курс по собственной книге «Введение в физическую химию». В 1860 г. Н. Н. Бекетов впервые вводит физическую химию в качестве особой учебной дисциплины, читает курс лекций в Харьковском университете, создает кафедру физической химии. В 1887 г. В. Оствальд в Лейпцигском университете организует кафедру физической химии. Он же выпускает первое периодическое издание по физической химии. Годом ранее И. А. Каблуков читает курс в Московском университете. К концу XIX в. определились три основных раздела физической химии: химическая термодинамика, химическая кинетика и электрохимия.
В настоящее время физическая химия полностью сформировалась как наука, включающая в себя химическую термодинамику (термохимию, фазовое равновесие), дополняющую химическую кинетику катализом, а также создала разнообразные физико-химические методы анализа.
ЛЕКЦИЯ № 1. Идеальный газ. Уравнение состояния реального газа
1. Элементы молекулярно-кинетической теории
Науке известно четыре вида агрегатных состояний вещества: твердое тело, жидкость, газ, плазма. Переход вещества из одного состояния в другое называют фазовым переходом. Вода, как известно, существует в трех агрегатных состояниях: в жидком (вода), твердом (лед), газообразном (пар). Это различие между тремя агрегатными состояниями определяется межмолекулярным взаимодействием и степенью сближения молекул.
Газ – агрегатное состояние вещества, в котором молекулы движутся хаотически, расположены на большом расстоянии друг от друга. В твердых телах расстояния между частицами малы, сила притяжения соответствует силе отталкивания. Жидкость – агрегатное состояние, промежуточное между твердым и газообразным. В жидкости частицы расположены близко одна к другой и могут перемещаться друг относительно друга; жидкость, как и газ, не имеет определенной формы.
Каждое из этих состояний можно описать набором некоторых параметров: например, состояние газа достаточно полно описывается тремя параметрами: объем, давление, температура.
Комбинация трех параметров, достаточно легко измеряемых, уже с середины ХVII века, когда были созданы барометры и термометры, хорошо описывает состояние газовой системы. Именно поэтому изучение сложных многоатомных систем началось с газов. У истоков наук химии и физики стоял Р. Бойль.
2. Уравнение состояния идеального газа
Изучение эмпирических газовых законов (Р. Бойль, Ж. Гей-Люссак) постепенно привело к представлению об идеальном газе, поскольку обнаружилось, что давление данной массы любого газа при постоянной температуре обратно пропорционально объему, занимаемому этим газом, и термические коэффициенты давления и объема с высокой точностью совпадают для различных газов, составляя, по современным данным, 1/273 град–1. Придумав способ графического представления состояния газа в координатах «давление – объем», Б. Клапейрон получил объединенный газовый закон, связывающий все три параметра:
PV = BT,
где коэффициент В зависит от вида газа и его массы.
Только через сорок лет Д. И. Менделеев придал этому уравнению более простой вид, записав его не для массы, а для единицы количества вещества, т. е. 1 кмоля.
PV = RT, (1)
где R – универсальная газовая постоянная.
Физический смысл универсальной газовой постоянной. R – работа расширения 1 кмоля идеального газа при нагревании на один градус, если давление не меняется. Для того, чтобы понять физический смысл R, представим себе, что газ находится в сосуде при постоянном давлении, и мы повысим его температуру на ΔT, тогда
PV1 = RT1, (2)
и
PV2 = RT2. (3)
Вычитая из (3) уравнение (2), получим
P(V2 – V1) = R(T2 – T1).
Если правая часть уравнения равна единице, т. е. мы нагрели газ на один градус, тогда
R = PΔV
Поскольку P = F/S, а ΔV равно площади сосуда S, умноженной на высоту подъема его поршня Δh, имеем
Очевидно, что справа получим выражение для работы, и это подтверждает физический смысл газовой постоянной.
3. Кинетическая теория газов
Очень плодотворным в середине XIX века оказалось представление о молекулярном строении вещества. Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 1026 кмоля = 6,02 x 1023 моля, поскольку молярная масса воды M(H2O) = 18 кг/кмоль , следовательно, в 18 литрах воды находится столько же молекул, сколько в 22,4 м3 водяного пара. Это позволяет легко понять, что расстояние между молекулами газообразной воды (пара) значительно больше, в среднем на один порядок, чем в жидкой воде. Можно предположить, что это выполняется для любого вещества. Считая, что в газах молекулы движутся хаотически, можно вывести так называемое основное уравнение кинетической теории:
где Na – 6,02 x 1026 кмоль = 6,02 x 1023 моль – число Авогадро;
VM – молекулярный объем = 22,4 м3;
m – масса одной молекулы;
v – скорость молекулы.
Преобразуем уравнение (4):
где Ek – энергия одной молекулы.
Видно, что справа стоит полная кинетическая энергия всех молекул. С другой стороны, сравнивая с уравнением Менделеева – Клапейрона, видим, что это произведение равно RT.
Это позволяет выразить среднюю кинетическую энергию молекулы газа:
где к = R / Na – постоянная Больцмана, равная 1,38 ґ 10–23 кДж/кмоль. Зная кинетическую энергию молекулы, можно рассчитать ее среднюю скорость
Около 1860 г. Д. К. Максвелл вывел функцию, описывающую распределение молекул газа по скоростям. Эта функция имеет на графике вид характерной кривой с максимумом около наиболее вероятной скорости примерно 500 м/с. Важно заметить, что существуют молекулы со скоростями, превышающими этот максимум. С другой стороны, уравнение (6) позволяет сделать вывод об увеличении доли молекул с большими скоростями при нагревании газа. Спустя почти 60 лет гениальная догадка Д. К. Максвелла была подтверждена в опытах О. Штерна.
4. Уравнение состояния реального газа
Исследования показали, что уравнение Менделеева – Клапейрона не очень точно выполняется при исследовании разных газов. Голландский физик Я. Д. Ван-дер-Ваальс первым понял причины этих отклонений: одна из них состоит в том, что вследствие огромного числа молекул, их собственный объем в целом сравним с объемом сосуда, в котором находится газ. С другой стороны, существование взаимодействия между молекулами газа слегка искажает показание манометров, с помощью которых обычно измеряют давление газа. В итоге Ван-дер-Ваальс получил уравнение следующего вида:
где а, в – постоянные величины для различных газов.
Недостаток этого уравнения в том, что а и в должны быть измерены для каждого газа эмпирически. Преимущество в том, что оно включает область перехода газа в жидкую фазу при высоких давлениях и низких температурах. Осознание этого сделало возможным получать любой газ в жидкой фазе.
ЛЕКЦИЯ № 2. Химическая термодинамика
Химическая термодинамика – наука, изучающая условия устойчивости систем и законы.
Термодинамика – наука о макросистемах.
Она позволяет apriori определить принципиальную невозможность того или иного процесса. Физические и химические явления в термодинамике исследуются с помощью основных законов термодинамики. Состояние рассматриваемых объектов в термодинамике определяется непосредственно измеряемыми величинами, характеризующими вещества; механизм процесса и сама структура вещества не рассматриваются.
В химической термодинамике изучается применение законов термодинамики к химическим и физико-химическим явлениям.
В ней рассматриваются главным образом:
1) тепловые балансы процессов, включая тепловые эффекты физических и химических процессов;
2) фазовые равновесия для индивидуальных веществ и смесей;
3) химическое равновесие.
Тепловые балансы составляют на основе первого закона термодинамики. На основе второго и третьего законов проводят анализ фазового и химического равновесий.
Изучение законов, которые описывают химические и физические равновесия, имеет огромное значение в химической термодинамике. Значение их позволяет решать задачи для производственной и научно-исследовательской работы. Рассмотрим основные задачи:
1) определение условий, при которых данный процесс становится возможным;
2) нахождение пределов устойчивости изучаемых веществ в тех или иных условиях;
3) устранение побочных реакций;
4) выбор оптимального режима процесса (давления, концентрации реагентов и т. д.).
Основные понятия и определения
1. Системы и их классификация
Система – тело или несколько тел, находящихся во взаимодействии между собой (диффузия, теплообмен, химическая реакция) и отделенных от окружающей среды.
Состояние системы в термодинамике определяется с помощью набора переменных, называемых параметрами состояния и характеризующих термодинамическое состояние при равновесии. Всякое изменение, происходящее в системе и связанное с изменением хотя бы одного из параметров состояния, называется термодинамическим процессом.
Системы имеют определенные границы, отделяющие их от внешней среды, и могут быть гомогенными или гетерогенными.
Гомогенная система – система, в которой все макроскопические свойства в любых ее частях имеют одно и то же значение или непрерывно меняются от точки к точке. Примеры: ненасыщенные растворы, пар, газовые смеси. Составленные части гомогенной системы не могут быть выделены из нее с помощью простых механических приемов (фильтрования, отбора и т. д.).
Гетерогенная система – система, составные части которой отделены друг от друга видимыми поверхностями раздела, на которых происходят резкие скачкообразные изменения какого-либо свойства. Примеры: насыщенный раствор какой-либо соли, находящийся в равновесии с кристаллами этой соли, две несмешивающиеся жидкости и т. д.). Составные части таких систем могут быть отделены друг от друга с помощью механических операций.
Совокупность тел, энергетически взаимодействующих между собой и с другими телами, обменивающихся с ними веществом, называется термодинамической системой.
Системы делят на изолированные (это те системы, которые не обмениваются энергией и веществом с другими системами), открытые (те системы, которые обмениваются с окружающей средой и веществом, и энергией), закрытые (системы, в которых есть только обмен энергией).
2. Термодинамические параметры. Термодинамические показатели. Баланс напряжений
Любая ТДС характеризуется параметрами: температура, давление, плотность, концентрация, мольный объем. В любой ТДС обязательно протекают процессы, и они могут быть равновесными, неравновесными, обратимыми и необратимыми.
Если в ТДС определенное свойство системы не будет изменяться во времени, т. е. оно будет одинаковым во всех точках объема, то такие процессы – равновесные.
В неравновесных процессах свойство системы будет изменяться во времени без воздействия окружающей среды.
Обратимые процессы – процессы, в которых система возвращается в первоначальное состояние.
Необратимые – когда система не возвращается в первоначальное состояние.
Функции могут зависеть от пути процесса. Функции, которые зависят от начального и конечного состояний системы и не зависят от пути процесса, – функции состояния; внутренняя энергия, энтальпия, энтропия и другие – полные дифференциалы.
Функции, которые зависят от начального и конечного состояний системы и зависят от пути процесса, не являются функциями состояния и не являются полными дифференциалами Q, A.
Функции можно разделить на две группы: экстенсивные и интенсивные.
Экстенсивное свойство системы прямо пропорционально массе системы и обладает аддитивностью (можно складывать): V, H, Uвн, S, G, F.
Интенсивное свойство системы не зависит от массы системы и не обладает свойством аддитивности: Q, A, T, P.
Давление – параметр состояния, определяемый силой, действующей в теле на единицу площади поверхности по нормали к ней. Оно характеризует взаимодействие системы с внешней средой.
Температура определяет меру интенсивности теплового движения молекул.
Значение градуса температуры и начало ее отсчета произвольны. В качестве эталона можно было бы выбрать не воду, а любое другое вещество (лишь бы его свойства однозначно изменялись с температурой, были воспроизводимы и легко поддавались измерению).
Такая произвольность исчезает, если пользоваться термодинамической (абсолютной) шкалой температур, основанной на втором законе термодинамики. Начальной точкой этой универсальной шкалы является значение предельно низкой температуры – абсолютный нуль, равный 273,15 оС.
Уравнение состояния
Уравнение, связывающее термодинамические параметры системы в равновесном состоянии, – уравнение состояния.
Вследствие взаимосвязи между свойствами системы для определения ее состояния достаточно указать лишь некоторое число свойств. Так, состояние газа можно считать заданным, если указаны два параметра, например, температура и объем, а значение третьего параметра – давления – можно определить из уравнения состояния
P = f(V, T ),
φ(P, V, T ) = 0.
Графически это уравнение является уравнением поверхности, построенной на трех взаимно перпендикулярных осях, каждая из которых соответствует одному термодинамическому параметру. Таким образом, термодинамическая поверхность – геометрическое место точек, изображающих равновесные состояния системы в функциях от термодинамических параметров.
Понятие теплоты
Пусть дан изолированный сосуд, который разделен полупроницаемой перегородкой (рис. 1). В первой части сосуда температура Т1, во второй – температура Т2; Т1 > Т2.
Рис. 1
Молекулы, ударяясь о полупроницаемую перегородку, будут отдавать часть энергии, а другие – принимать ее, без механического перемещения.
Форма передачи энергии от одной части системы к другой называется теплотой Q.
Мера переданной энергии от одной системы к другой – количество теплоты. Q не является функцией состояния и не является полным дифференциалом ΔQ.
Понятие работы
Работа процесса – это энергия, передаваемая одним телом другому при их взаимодействии, не зависящая от температуры этих тел и не связанная с переносом вещества от одного тела к другому.
Обмен энергией между системой и внешней средой обуславливается работой, совершаемой этой системой:
А = PdV.
Работа (А) определяется суммой произведений сил, действующих на систему сил (давления и изменения объема).
Работа не является полным дифференциалом, ΔА.
Если протекают равновесные процессы, то работа равновесного процесса будет максимальной величиной, по сравнению с неравновесным процессом
ΔAравн > ΔAнеравн.
Если телу сообщают определенное количество теплоты, то это значит, что тело надо нагреть, а охладить систему – произвести действие, обратное нагреванию, т. е. отвести энергию.
Работа и теплота являются количественными характеристиками двух форм обмена энергией между системой и окружающей средой.
Понятие внутренней энергии
Внутренняя энергия системы Uвнскладывается из энергии поступательного и вращательного движения молекул, энергии внутримолекулярного колебательного движений атомов и атомных групп, энергии, заключающейся в ядрах атомов, энергии межмолекулярного взаимодействия.
Uвнявляется полным дифференциалом, она не зависит от пути процесса, а зависит от начального и конечного состояний системы, она однозначно непрерывна и конечна. Абсолютное значение Uвнопределить нельзя, можно определить только ее изменения.
Q и А качественно и количественно характеризуют форму передачи энергии, взаимосвязь между Q, A, Uвнустанавливает первый закон термодинамики.
Термодинамические показатели
К термодинамическим показателям относятся те, которые можно рассчитать, используя законы термодинамики, исходя из условий, что система находится в равновесии. Напряжение разложения:
где ΔG – изменение термодинамического потенциала;
п – число электронов, участвующих в химической реакции;
F– число Фарадея.
где А – максимальная работа, которую способна совершить система в равновесном состоянии.
где Q – тепловой эффект реакций;
Up– термодинамическая характеристика электрохимической системы, которая мало зависит от условий электролиза.
Отклонение системы – поляризация. Электрохимическая реакция является гетерогенным процессом, и ее скорость может лимитироваться одной из стадий:
1) подвод реагирующего вещества к границе раздела фаз;
2) разряд и ионизация;
3) отвод продуктов реакции.
Поляризация, определяемая медленной стадией массопереноса – концентрационная. Если медленной стадией является стадия разряда ионизации, то поляризация называется перенапряжением. Природа и значение поляризации зависят от многих факторов: природа реагирующего вещества, материал электрода, состояние поверхности электрода, плотность тока, состав раствора и режим электролиза. Кинетический параметр – параметр, определяемый в реальных условиях электрохимической системы: ρ тока, ЕАКТИВ, коэффициент диффузии, коэффициент переноса α (на катод), β (на анод) – доля расхода на процесс:
1) сила тока в электрохимическом аппарате J= iKSед загрузки, A, Z, iK – в зависимости от электролита;
2) скорость электролиза – образование массы вещества за единицу времени
где q – электрохимический эквивалент, v электролиза – J тока,
если в 1 см2 – v – i тока.
Баланс напряжений. Напряжение на электрохимическом аппарате определяет расход электроэнергии при электролизе. Баланс напряжений на электрохимическом аппарате складывается из следующих составляющих:
UЭЛ-РЕ = Еa– Еk+ ηa+ ηk, + ΔUЭЛ-ТА+ ΔUДИФ+ ΔUКОН+ ΔUЭЛ,
где Еa– обратимый потенциал анода, В;
ЕК – обратимый потенциал катода, В;
ηa– поляризация анода, В;
ηk– поляризация катода, В;
ΔUЭЛ-ТА– падение напряжения в электролите, В;
ΔUДИФ– падения напряжения в диафрагме, В;
ΔUКОН– падение напряжения в контактах, В;
ΔUЭЛ – падение напряжения в электродах, В.
где i– плотность катодного тока;
ρ0 – удельное сопротивление электролита, ρ0 повышается при вводе газа;
l – расстояние между электродами;
S – площадь сечения электролита;
J – электропроводность.
Коэффициент газонаполнения k = ρ/ρ0.
Падение напряжения газозаполнения элемента определяется по формуле
ΔUЭЛ-ТА = ilρ0k.
Падение напряжения в диафрагме
ΔUДИФ= JRДИАФ.
Падение напряжения в контактах обычно принимают равным 5 – 10% от общего напряжения.
Падение напряжения в электродах:
Снижение напряжения на электрохимическом аппарате – оптимальное расстояние между электродами, максимальной электропроводностью.
Рис. 2
К энергетическим характеристикам относятся:
1) напряжение на электрохимическом аппарате;
2) отдача по напряжению.
3) отдача по емкости
4) отдача по энергии
5) производительность электрохимического аппарата оценивается количеством продукта на одной затраченной энергии.
Расход электрической энергии на 1 тонну произведенного продукта определяется так:
ВT – выход по току в долях единицы.
Энергетический баланс – устанавливает соотношение между видом энергии, поступающей в электролизер, и энергией, уходящей из него, демонстрируя равенство статей прихода и расхода. Электроэнергия const тока, подводимая к электролизеру, составляет:
WЭЛ= UJt.
Общее уравнение энергетического баланса имеет следующий вид:
Wэ + ∑Qприхода = Wэл.хим.р-ии + Wтока + ∑Qрасх,
где ∑Qприхода – тепловая энергия, поступающая в электролизер с электролитом и электродами за счет вторичных процессов;
Wэл.хим.р-ии – энергия тока, затраченная на электрохимическую реакцию;
Wтока – энергия тока, перешедшая в тепловую энергию; ∑Qрасх– тепловая энергия, уносимая электролитом, электродами, газами при испарении Н2О, излучении и конвекции.
3. Первый закон термодинамики. Калорические коэффициенты. Связь между функциями CP и Cv
Формулировки первого закона термодинамики.
1. Общий запас энергии в изолированной системе остается постоянным.
2. Разные формы энергии переходят друг в друга в строго эквивалентных количествах.
3. Невозможно построить вечный двигатель первого рода, который бы давал механическую энергию, не затрачивая на это определенное количество молекулярной энергии.
4. Количество теплоты, подводимое к системе, расходуется на изменение Uвн и совершаемую работу.
5. Uвн– функция состояния, т. е. она не зависит от пути процесса, а зависит от начального и конечного состояния системы.
Доказательство:
Пусть ТДС рассматривается при двух параметрах давления и объема, имеется два состояния системы I и II. Нужно перевести систему из состояния I в состояние II либо по пути А, либо по пути В (рис. 3).
Рис. 3
Предположим, что по пути А изменение энергии будет ΔUA, а по пути В – ΔUB. Внутренняя энергия зависит от пути процесса
ΔUA = ΔUB,
ΔUA – ΔUB ≠ 0.
Согласно пункту 1 из формулировок первого закона термодинамики, общий запас энергии в изолированной системе остается постоянным
ΔUA = ΔUB ,
Uвн – функция состояния не зависит от пути процесса, а зависит от состояния системы I или II. Uвн – функция состояния, является полным дифференциалом
Q = ΔU + А –
интегральная форма уравнения первого закона термодинамики.
δQ = dU + δA–
для бесконечно малого процесса, δA– сумма всех элементарных работ.
Калорические коэффициенты
Теплота изотермического расширения:
Уравнение первого закона термодинамики в калорических коэффициентах
δQ = ldv + CvdT,
где l– коэффициент изотермического расширения;
Сv– теплоемкость при постоянном объеме.
теплоемкость при const давлении,
δQ = hdp + СpdT,
δQ = χdP + ψpdv.
Связь между функциями CP и Cv
δQ = hdp + СpdT = ldv + CvdT,
для реального газа.
Для идеального газа l= р
Ср– СV= R,
к = (δQ/дv)ρ– теплота изохорного расширения;
m = (δQ/дP)v– теплота изобарного сжатия.
4. Изопроцессы в термодинамике. Энергия Гельмгольца
1. Изотермический – Т= const
так как
2. Изохорный – V = const
δА = 0,
δА = pdυ = 0,
δQ = dU + pdυ,
δQ = CvdT.
3. Изобарный – P = const
δА = pdυ,
A = pV2 – pV1.
4. Адиабатический – δQ = 0
1) δA = –dU,
A = –CV(T2 – T1), T2 > T1;
2) pdδ= –CvdT,
действие, обратное логарифму – потенцирование
Уравнение первого закона термодинамики в калорических коэффициентах
δQ = ldυ + CVdT,
где l– коэффициент изотермического расширения;
CV – теплоемкость при постоянном объеме.
теплоемкость при const давлении,
δQ = hdP + CpdT ,
δQ = χdP + ψdυ.
Связь между функциями CPи CV
5. Процессы. Второй закон термодинамики
Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.
Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.
Самопроизвольные процессы делятся на обратимые и необратимые. Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Слово «энтропия» создано в 1865 г. Р. Ю. Э. Клаузиусом – «тропе» с греческого означает превращение. В 1909 г. профессор П. Ауербах назвал царицей всех функций внутреннюю энергию, а S – тенью этой царицы. Энтропия – мера неупорядоченности системы.
Обратимые и необратимые процессы
Необратимые процессы идут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:
1) теплопроводность при конечной разности температур;
2) расширение газа при конечной разности давлений;
3) диффузия при конечной разности концентраций.
Обратимыми процессами в изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.
Обратимые: механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Na с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – не может быть перехода тепла от менее нагретого к более нагретому телу.
2. Постулат Томсона – теплота наиболее холодного тела не может служить источником работы.
Теорема Карно – Клаузиуса: все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела.
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики
Q1 /Т1– приведенное тепло нагревателя;
Q2 / T2 – приведенное тепло холодильника;
Q1 /Т1= Q2 /Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то
Это четвертое уравнение второго закона термодинамики Если процесс является замкнутым, то
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Это шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
S = klnW.
Действие, обратное логарифму – потенцирование:
Первый закон термодинамики определяется постоянством функции U в изолированной системе. Найдем функцию, выражающую содержание второго закона, а именно, одностороннюю направленность протекающих в изолированной системе процессов. Изменение искомой функции должно иметь для всех реальных, т. е. необратимых процессов, протекающих в изолированных системах, один и тот же знак. Второй закон термодинамики в приложении к некруговым необратимым процессам должен выражатся неравенством. Вспомним Цикл Карно. Так как любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, то выражение:
справедливо для любого обратимого цикла. Считая на каждом элементарном участке теплообмена Т = const, найдем, что:
и для всего цикла
или
Энергия Гельмгольца Изохорно-изотермический потенциал
F = U – TS
Величина (V – TS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.
dF = dU – TdS – SdT,
U = F + TS,
dF = TdS – pdV – SdT,
F – полный дифференциал.
Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.
δАравн > δАнеравн
Q = ΔU + A,
A = Q – ΔU,
A = T(S2 – S1) – (U2 – U1),
А = F1 – F2 = –ΔF,
Аравн = –ΔF –
физический смысл изохорно-изотермического потенциала.
Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: AFT г< 0.
Для несамопроизвольного процесса: ΔFT,V > 0. Для равновесного процесса: ΔFT,V = 0.
ΔFV,T ≤ 0.
Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).
Рис. 4
где 1 – самопроизвольный процесс;
2 – несамопроизвольный процесс;
3 – равновесный процесс.
Изобарно-изотермический потенциал.
1) G (P, Т= cоnst), энергия Гиббса
G = U – TS + PV = H – TS = F + PV,
δQ = dU – Pdv + A′,
δA′ = Q – dU – pdv,
δA′max = T(S2 – S1) – (U2 – U1) – p(V2 – V1),
δA′max = (U1 – TS1 + PV1) – (U2 – TS2 + PV2) = G1 – G2 = –ΔG,
U – TS + pV = G,
A′max = –ΔG.
Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;
2) функция – полный дифференциал, однозначна, конечна, непрерывна.
G = U – TS + pV,
dG = dU – TdS – SdT + pdv + vdp,
dG = TdS – pdV – TdS – SdT + pdv + vdp,
dG = –SdT + Vdp,
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;
3) G как критерий направленности процесса в изолированной системе.
Для самопроизвольного процесса: (ΔG)P,T < 0. Для несамопроизвольного процесса: (ΔG)P,T > 0. Для равновесного процесса: (ΔG)P,T = 0
ΔG(P,T)≤ 0.
Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.
Рис. 5
где 1 – самопроизвольный процесс;
2 – равновесный процесс;
3 – несамопроизвольный процесс.
Совершается работа за счет ΔU и ΔH.
Противодействующие факторы. Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.
Энтальпия – Н Внутренняя энергия – U.
H = U + PV,
dH = dU + pdv + vdp,
U = TS – PV,
dU = TdS – SdT + pdV + Vdp,
dH = –pdV + pdV + Vdp; U = TdS + VdP.
Рис. 6
где 1 – самопроизвольный процесс,
2 – несамопроизвольный процесс,
3 – равновесный процесс,
(dH)P,T ≤ 0,
(dU)S,T ≤ 0.
Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.
Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).
Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.
Уравнение Клаузиуса-Клапейрона
Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии
U2 – U1 = T(S2 – S1) – P(V2 – V1),
(U1 – TS1 + PV1) = (U2 – TS2 + PV2),
G1 = G2 – в условиях равновесия.
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
I фаза => dG1 = V1dp – S1dT.
II фаза => dG2= V2dp – S2dT, при равновесии dG2 – dG1 = 0
dG2 – dG1 = dp(V2 – V1) – dT(S2 – S1) –
нет условного равновесия,
где dP/dT – температурный коэффициент давления,
где λфп – теплота фазового перехода.
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.
эмпирическая форма уравнения Клаузиуса-Клапейрона.
Рис. 7
Рис. 8
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
I рода – ΔG = 0, ΔS ≠ 0, ΔV ≠ 0.
II рода – ΔG = 0, ΔS = 0, ΔV = 0.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Tи других свойств.
Итак, энтропия выражается уравнением:
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться UВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni;
3) внутренняя энергия при независимых переменных: S, V, ni;
4) энтальпия при независимых переменных: S, Р, пi;
5) энтропия при независимых переменных Н, Р, ni..
В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Связь энтропии с другими термодинамическими параметрами
Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δQ/T в сочетании с δQ = dU + PdV и δQ = dH – VdP дает уравнения:
dU = TdS – PdV,
dH = TdS + VdP.
Записав уравнение:
применительно к функциональной зависимости φ(Т, V, S) = 0, получим
т. е.
Теперь найдем зависимость энтропии от температуры из уравнений:
и
Вот эти зависимости:
и
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:
TdS = CdT.
Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».
2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».
Теорема Карно-Клаузиуса: «Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики
где Q /Т – приведенное тепло;
Q1 /Т1– приведенное тепло нагревателя;
Q2 / T2 – приведенное тепло холодильника;
Q1 /Т1= Q2 / T2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то
Это четвертое уравнение второго закона термодинамики
Если процесс является замкнутым, то
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
S = klnW.
Термодинамическая вероятность
S = klnW –
это формула Больцмана,
где S – энтропия – степень разупорядоченности системы;
k– постоянная Больцмана;
W – термодинамическая вероятность системы макросостояний.
Термодинамическая вероятность – число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).
Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.
Термодинамическая вероятность – это число способов, которыми атомы и молекулы можно распределить в объеме.
6. Цикл Карно
Цикл Карно – круговой тепловой процесс, в результате которого некоторое количество тепла термодинамически обратимым способом переносится от горячего тела к холодному. Процесс должен совершаться таким образом, чтобы тела, между которыми происходит непосредственный обмен энергией, находились при постоянной температуре, т. е. и горячее и холодное тела считаются настолько большими тепловыми резервуарами, что температура первого при отнятии и температура второго при прибавлении рассматриваемого количества тепла ощутимо не изменяются. Для этого необходимо «рабочее тело». Рабочим телом в этом цикле является 1 моль идеального газа. Все процессы, составляющие цикл Карно, являются обратимыми. Рассмотрим их. На рисунке 9 показано:
АВ – изотермическое расширение газа от V1 до V2 при температуре T1, количество теплоты Q1 поглощается;
ВС – адиабатическое расширение от V2 до V3, температура снижается от Т1 до Т2;
CD – сжатие изотермическое от V3до V4 осуществляется при температуре Т2, количество теплоты Q отдается;
DA – сжатие адиабатическое от V4 до V1, температура увеличивается от Т2 до T1.
Puc. 9
Проанализируем его подробно. Для процесса необходимо «рабочее тело», которое сначала при более высокой температуре Т1 приводится в соприкосновение с горячим телом и изотермически получает от него указанное количество тепла. Затем оно адиабатически охлаждается до температуры Т2, отдавая при этой температуре тепло холодному телу с температурой Т2, а затем адиабатически возвращается в начальное состояние. В цикле Карно ΔU = 0. При проведении цикла «рабочее тело» получило количество теплоты Q1 – Q2 и произвело работу А, равную площади цикла. Итак, в соответствии с первым законом термодинамики Q1 – Q2 = А, получаем:
Для адиабатических процессов можно записать:
Поделим первое уравнение на второе. В результате имеем:
Получаем уравнение для работы:
Теперь получим КПД:
Итак, КПД цикла Карно зависит от температуры теплоотдатчика и теплоприемника. Эта величина имеет тем большее значение, чем выше T1 и ниже T2. Цикл Карно необходим при разрешении вопроса о КПД тепловых машин.
7. Невозможность вечного двигателя
Даже в самой современной высокопроизводительной машине часть теплоты не может быть превращена в работу. Чтобы это осуществить, нужна машина, работающая в пределах температуры теплоприемника и более низкой температуры теплоотдатчика.
Значит, невозможно построить двигатель, в котором рабочее тело совершало бы работу, вступая в теплообмен с одним только, и при-чем единственным, источником теплоты, то есть нельзя осущест-вить вечный двигатель второго рода. Из этой формулировки логически вытекает следующая: нельзя превратить теплоту какого-либо тела в работу, не производя никакого другого изменения, кроме охлаждения этого тела. Это доказывает одно: что невозможно при помощи кругового изотермического процесса произвести работу. Попробуем сформулировать неосуществимость вечного двигателя первого рода. Ее можно рассматривать двояко: с одной стороны, «работу нельзя создать из ничего», с другой стороны, «работу нельзя превратить в ничто». Хаотическое тепловое движение частиц более вероятно, чем их направленное движение. «Появление» теплоты всегда знаменуется превращением энергии в малоэффективную форму. Вероятность того, что молекулы, движущиеся хаотично, получат определенную ориентацию, ничтожна. Если бы это существовало на самом деле, то привело бы к появлению направленной силы, способной совершать работу. Поэтому переход без ограничений теплоты в работу невозможен, хотя работа может перейти в теплоту целиком. Итак, при отсутствии теплоприемника запас энергии теплоотдатчика не может быть использован. Нельзя использовать безграничные запасы энергии воздуха, морей, океанов и т. д.
ЛЕКЦИЯ № 3. Растворы
1. Общая характеристика растворов
Растворы – термодинамически устойчивые системы переменного состава, состоят не менее чем из двух компонентов и продуктов их взаимодействия. Это дисперсные системы, состоящие из дисперсной фазы и дисперсионной среды. Различают девять систем (табл. 1):
Таблица 1
Дисперсные системы
где Г – газ;
Т – твердое тело;
Ж – жидкость.
Существуют жидкие, газовые и твердые растворы. Растворы отличаются от химических соединений тем, что их состав может изменяться непрерывно. Как и любая химически равновесная в данных условиях система, растворы должны обладать минимумом свободной энергии Гиббса. По своему агрегатному состоянию дисперсные системы могут быть: газообразными, жидкими, твердыми; по степени дисперсности – взвесями, коллоидными и истинными растворами. Взвеси – гетерогенные системы, нестабильные во времени. Частицы их очень малы и сохраняют все свойства фазы. Взвеси расслаиваются, причем диспергированная фаза или выпадает в виде осадка, или всплывает в зависимости от соотношения плотностей. Примеры: туман (жидкость распределена в газе), суспензия (твердое тело – жидкость), эмульсия (жидкость – жидкость, C2H5OH + H2O – этиловый спирт и вода).
В истинном растворе распределенное в среде вещество диспергировано до атомного или молекулярного уровня. Примеры многочисленны: газообразный раствор – воздух, состоящий из главного компонента азота – 78% N2; сплавы, представляющие собой твердые растворы, например, медные Cu – Zn, Cu – Cd, Cu – Ni и др.
Коллоидные растворы – микрогетерогенные системы, занимают промежуточное положение между истинными растворами и взвесями. Растворы состоят из растворенного вещества и растворителя. Растворителем считают тот компонент, который преобладает в растворе. Свойства растворов зависят от концентрации. Рассмотрим способы выражения концентрации растворов.
2. Концентрация и способы ее выражения
Концентрация – количество растворенного вещества, содержащееся в определенном количестве раствора или растворителя. При определении концентрации растворов используются различные методы аналитической химии: весовые, объемные, а также методы, основанные на измерении плотности, показателя преломления и других физико-химических свойств.
Виды концентрации
Массовая доля растворенного вещества в растворе ω, % – отношение массы вещества к массе раствора:
Пример: пусть m(CaCl2) = 10 г, тогда ω(CaCl2) = (10/100) ґ 100% = 10%.
Молярность раствора – число молей растворенного вещества в одном литре раствора.
Пример: 1 моль H2SO4 – 98 г, до одного литра надо добавить воду.
Моляльность – число молей растворенного вещества на 1000 г растворителя. Пример:
H2SO4 – 98 г/моль+1000 г H2O.
Мольная доля растворенного вещества в растворе, N
где n1 – растворенное вещество (моль);
n2 – растворитель (моль).
Пример: имеем 20% NaOH (едкий натр).
Титр – число растворенного вещества в одном миллилитре раствора. Существует титриметрический анализ – метод количественного анализа, при котором содержание определяемого вещества Х рассчитывают на основании измерения количества реактива, затраченного на взаимодействие с Х, выполнение реакции в титриметрическом анализе является конечной стадией анализа. Пример: объем кислоты оттитруем щелочью каплями до исчезновения окрас-ки – полная нейтрализация. При титровании
где Н – нормальность – число моль-эквивалентов растворенного вещества в одном литре раствора.
Основной характеристикой растворов является их растворимость – масса вещества, способная раствориться в ста граммах растворителя при данной температуре; этот процесс сопровождается тепловым эффектом. Количественно растворимость твердого тела, газа, жидкости в жидком растворителе определяется концентрацией насыщенного раствора при данной температуре, т. е. сколько вещества по массе (объему) в данном растворителе. Пример: m(NaCl) – 58,5 г на 100 г H2O при данной температуре. Насыщенный раствор – раствор, находящийся в равновесии, с избытком растворяемого вещества. Пересыщенный – неустойчивый раствор, содержащий больше вещества, чем это определяется его растворимостью.
Качественная характеристика состоит в способности растворяться или не растворяться, например, сера в воде не растворяется, йод в воде практически нерастворим. Процесс растворения состоит из двух стадий:
1. Растворимость в воде твердых веществ (разрушение кристаллов – эндотермическая реакция, т. е. тепло поглощается –q1).
2. Отдельные частицы взаимодействуют с водой, этот процесс носит название – гидратация, при ней тепло выделяется +q2
Qраствореия = –q1 + q2.
Если –q1 > q2, то суммарный эффект отрицателен (–Q), если наоборот, то положителен (+Q).
ΔH = 0 – одинаковые эффекты, ΔH < 0 – тепло выделяется, ΔH > 0 – тепло поглощается.
Тепловой эффект растворения – количество тепла одного моля вещества.
вещество + растворитель ↔ насыщенный раствор + Q.
То вещество, которое растворяется с понижением температуры, увеличивает свою растворимость. Рассмотрим растворимость некоторых веществ. Пример, NH4NO3 – нитрат аммония, растворимость падает до нуля, эндотермический эффект реакции. Рассмотрим стадии подробно: на первой стадии – эффект разрушения кристаллической решетки, эндотермический. На второй – равномерное распределение по объему с водой, гидратация – экзотермический.
q1 > q2 → – Q – тепло поглощается,
ΔH > 0.
Другой пример, NaOH – едкий натр, экзотермический эффект реакции,
q1 < q2 → +Q – тепло выделяется.
Значит, растворимость определяется природой соли вещества и растворителя.
Другой характеристикой растворов является диэлектрическая проницаемость – во сколько раз сила взаимодействия между двумя зарядами меньше, чем в вакууме.
Если растворить в ста миллилитрах водопроводной воды 10 г едкого натра NaOH, то температура резко повышается до 60 oС (температура воды из водопроводного крана +20 oС).
Если растворить 40 г нитрата аммония NH4NO3 в 100 мл этой же воды, то температура резко понижается от +20 oС до –7 oС.
Если растворить хлорид натрия NaCl в 100 мл водопроводной воды, то температура не изменяется.
3. Растворимость газов в жидкостях
Она зависит от давления и температуры. Растворимость газов неодинакова из-за различной химической природы.
Пример:
N2, H2 – мало растворимы в воде, растворимость NH3, HCl очень велика, в одном объеме H2O растворяется 700 объемов аммиака NH3.
Газ + H2O → 3,5 объема О2 в одном объеме Н2О экзотермический процесс. С повышением температуры растворимость некоторых газов уменьшается. При постоянной температуре и невысоком давлении растворимость газов, не вступающих в химическое взаимодействие с растворителем, подчиняется закону Генри – Дальтона, который состоит из нескольких частей.
1 часть: масса газа, растворяющаяся в данном объеме жидкости, пропорциональна давлению, которое газ производит на жидкость.
Например, CO2 под давлением загоняем в бутылку.
2 часть: объем газа не зависит от давления.
3 часть: если смесь газов растворять, то растворимость каждой составной части пропорциональна своему парциальному давлению.
Газы, реагирующие с водой, не подчиняются закону Генри – Дальтона.
4. Растворы неэлектролитов. Закон Рауля и его следствия
Рассмотрим модель идеального раствора. Раствор называется идеальным, если в нем отсутствует взаимодействие между частицами (молекулами, атомами, ионами). Растворы неэлектролитов – частицы, плохо растворимые в воде, так как нет носителя электрического заряда. Закон Рауля справедлив только для разбавленных растворов неэлектролитов.
Пусть PBO – давление пара над чистым растворителем, при постоянной температуре T1; PB – давление пара растворителя при этой же температуре, но над раствором, состоящим из нелетучего компонента А (сахар), и чистым жидким растворителем В:
PB = f (T).
Разность PBO – PB равна понижению давления пара.
Величина (PBO – PB) /PBO – относительное понижение упругости пара = XA = ΔP/PBO, где XA – мольная доля, PBO > PB, ΔP = PBO – PB – абсолютное понижение упругости пара.
Закон Рауля. Относительное понижение упругости пара растворителя над раствором равно мольной доле растворенного нелетучего компонента.
барометрическая формула Больцмана.
Следствия из закона Рауля:
1. Растворение нелетучего компонента в растворителе приводит к расширению температурной области существования жидкой фазы.
2. Понижение температуры замерзания и повышение температуры кипения прямо пропорциональны моляльной концентрации растворенного вещества.
3. Растворы, содержащие одинаковое число молей растворенных веществ в одинаковых молях растворителя, обнаруживают одно и то же понижение температуры замерзания и одно и то же повышение температуры кипения.
Δtкип=Э x Смоляльн,
где Э – эбуллиоскопическая константа, +0,52.
Δtзам=К x Смоляльн,
где К – криоскопическая константа, равная –1,86.
Эбуллиоскопическая константа – разница между температурой кипения раствора и температурой чистого растворителя.
Криоскопическая константа – разница между температурой замерзания раствора и температурой чистого растворителя.
Для решения задач об этих константах необходимо знать массу растворенного вещества и массу раствора. Например, масса хлороформа (трихлорметан CHCl3) рассчитывается по формуле:
где m1 – масса растворенного вещества;
m2 – масса растворителя;
Δt – величина, показывающая на сколько градусов понизилась температура;
К – криоскопическая константа.
5. Осмос
Осмос – явление селективной диффузии определенного сорта частиц через полупроницаемую перегородку. Это явление впервые описал аббат Нолле в 1748 г. Перегородки, проницаемые только для воды или другого растворителя и непроницаемые для растворенных веществ, как низкомолекулярных, так и высокомолекулярных, могут быть изготовлены из полимерных пленок (коллодия) или гелеобразных осадков, например, ферроцианида меди Cu2[Fe(CN)6]; этот осадок образуется в порах перегородки стеклянного фильтра при погружении пористого материала сначала в раствор медного купороса (CuSO4 x 5H2O), а затем желтой кровяной соли K2[Fе(CN)6] . Вещества диффундируют через такую перегородку, что является важным случаем осмоса, позволяющим измерять осмотическое дав-ление, т. е. осмотическое давление – мера стремления растворенного вещества перейти вследствие теплового движения в процессе диффузии из раствора в чистый растворитель; распределяется равномерно по всему объему растворителя, понизив первоначальную концентрацию раствора.
За счет осмотического давления сила заставляет жидкость подниматься вверх, это осмотическое давление уравновешивается гидростатическим давлением. Когда скорости диффундирующих веществ станут равны, тогда осмос прекратится.
Закономерности:
1. При постоянной температуре осмотическое давление раствора прямо пропорционально концентрации растворенного вещества.
2. Осмотическое давление пропорционально абсолютной температуре.
В 1886 г. Я. Г. Вант-Гофф показал, что величина осмотического давления может быть выражена через состояние газа
PоснV = RT.
Закон Авогадро применим к разбавленным растворам: в равных объемах различных газов при одинаковой температуре и одинаковом осмотическом давлении содержится одинаковое число растворенных частиц. Растворы различных веществ, имеющие одинаковые молярные концентрации при одинаковой температуре, имеют одинаковое осмотическое давление. Такие растворы называются изотоническими.
Осмотическое давление не зависит от природы растворяемых веществ, а зависит от концентрации. Если объем заменить на концентрацию, получим:
Рассмотрим закон Вант-Гоффа: осмотическое давление раствора численно равно тому давлению, которое производило бы данное количество растворенного вещества, если бы оно в виде идеального газа занимало при данной температуре объем, равный объему раствора.
Все описанные законы относятся к бесконечно разбавленным растворам.
Парциальное давление
Парциальное давление – то давление, которое оказывал бы газ, входящий в газовую смесь, если бы из нее были удалены все остальные газы при условии сохранения постоянными температуры и объема.
Общее давление газовой смеси определяется законом Дальтона: общее давление смеси газов, занимающих определенных объем, равно сумме парциальных давлений, которыми обладал бы каждый отдельно взятый газ, если бы он занимал объем, равный объему смеси газов.
Р = Р1 + Р2 + Р3 + … + Рк,
где Р – общее давление;
Рк – парциальное давление компонентов.
6. Фугитивность
Фугитивность – функция, характеризующая состояние данного вещества в чистом виде или в смеси с другими веществами при заданных температуре и давлении. По-другому она называется термодинамическая летучесть; является величиной, количественно характеризующей способность вещества к выходу из данной фазы, но выражающей эту характеристику в единицах давления. Для жидкостей и твердых тел она связана с давлением насыщенного пара и становится равной ему, когда к пару применимы законы идеальных газов. Для идеального газа, чтобы найти, например, изменение энергий Гиббса при изотермическом процессе, надо просто решить задачу в соответствии с уравнением Менделеева – Клапейрона:
Для упрощения расчета Г. Льюисом в 1901 г. была введена функция f от Р – фугитивность. Заменяя давление фугитивностью, мы сохраняем простую математическую форму, которую имеют термодинамические зависимости для идеального газа.
Итак, новая функция определяется уравнением:
или
Значения фугитивности при больших давлениях (и низких температурах) сильно отличаются от Р. Так, при t = 0 и Р = 1200, fco = 2663, при t = 0, P = 100, fNH3 = 204, а для N2 при t = –75, P = 6000, f – 2 x 106, то есть фугитивность становится несоизмеримой с давлением.
Фугитивность можно определить как давление, которое должна производить данная реальная система, чтобы оказывать такое же действие, как и идеальная. Она характеризует отклонение от идеального состояния и, подобно давлению для идеального газа, может рассматриваться как мера рассеиваемости вещества. С приближением реального газа к идеальному состоянию/по величине приближается к Р, так что для идеального газа при всех давлениях обе величины становятся равными, то есть:
Видно, что размерность/совпадает с размерностью Р. Следует подчеркнуть, что замена Р на/в уравнениях идеального газа при переходе к реальному справедлива только для изотермического процесса, так как в соответствии с (2) фугитивность является специфической изотермической функцией. Для характеристики степени отклонения газа от идеального состояния вводят также величину
где γ – коэффициент фугитивности.
7. Закон Генри
Фугитивность растворителя в разбавленном растворе не зависит от природы растворенного вещества и вычисляется по закону Рауля, то есть:
Так как фугитивность жидкости или твердого раствора равна фугитивности насыщенного пара, когда растворитель в парообразном состоянии ведет себя как идеальный газ, уравнение (4) переходит в
Зная зависимостьf1 от состава, можно найти зависимость f2 от N2 по уравнению:
N1dRT ln (f1N1) + N2dRT ln f2 = 0
или
откуда
ln f2 = ln N2 + const.
Переписывая это уравнение в виде
ln f2 = ln N2+ ln K(P, T),
получим при P,T= const
f2 = KN2
или
Если в последнем уравнении рассматривать f2 как фугитивность растворенного вещества в газовой фазе, сосуществующей жидкой (твердой), то она является точной термодинамической формой закона Генри.
Его формулировка: зависимость растворимости газа в жидкости от давления, заключается в том, что при постоянной температуре газа, растворенного в данной жидкости, растворимость газа пропорциональна его давлению над раствором.
Краткая формулировка: растворимость газа пропорциональна давлению. Этот закон установлен в 1803 г. Ему отвечает уравнение:
где Р2 – парциальное давление растворенного газа.
Газовый закон Генри точно соблюдается только для идеальных растворов и применим лишь в области невысоких давлений к газам, достаточно хорошо подчиняющимся законам Бойля – Мариотта и Гей-Люссака.
Таким образом, для разбавленного раствора фугитивность растворителя вычисляется по закону Рауля, а фугитивность растворенного вещества – по закону Генри. Константа Генри приобретает смысл фугитивности (давления) чистого растворенного вещества при давлении, равном общему давлению над раствором.
ЛЕКЦИЯ № 4. Катализ
1. История открытия явления катализа
Катализ – изменение скорости химической реакции в присутствии катализаторов. Самые простые научные сведения о катализе были известны уже к началу XIX в. Знаменитый русский химик, академик К. С. Кирхгоф, открыл в 1811 г. каталитическое превращение крахмала в сахар под действием разбавленных кислот. Эта реакция лежит в основе крахмалопаточного производства. А в 1814 г. он открыл фермент – амилазу, и им же было установлено, что эту реакцию может катализировать диастаза из ячменного солода, чем было положено начало изучению биологических катализаторов – ферментов. Четыре года спустя Г. Деви открыл способность паров спирта и эфира окисляться кислородом на платине. В 1822 г. И. Деберейнер установил, что при обычной температуре можно соединять водород и кислород на платине. Вскоре эти и многие другие открытия привели к установлению существования явлений, в 1833 г. названных Э. Митчерлихом контактными, а в 1835 г. И. Берцелиусом – каталитическими. В органической химии успехи катализа связаны с развитием теории строения органических соединений Бутлерова.
Катализ в промышленности и живой природе
Большую роль сыграли каталитические методы в развитии процессов органического синтеза. Следующим направлением использования катализатора является каталитическая очистка технологических газов, а также очистка сточных вод, загрязненных органическими веществами. В живой природе вся система управления жизненными процессами в организмах основана на катализе. Такие процессы, как брожение, дыхание, пищеварение, синтез белков и других соединений и т. п. осуществляется с помощью ферментов, называемых энзимами.
2. Механизм каталитического взаимодействия. Виды катализаторов
Различают гомогенный и гетерогенный катализ. При однородном (гомогенном) катализе катализатор и реагенты образуют однородную систему.
Пример:
представляют однородную газовую фазу. Границы раздела между катализатором и реагентом отсутствуют. При гетерогенном – катализатор и реагирующие вещества находятся в разных фазах и отделены границей раздела. При этом катализатором является твердое тело, а реагенты находятся либо в газовой, либо в жидкой фазе. Пример:
N2(г) + 3H2(г) → 2NH3(г).
Существует еще микрогетерогенный катализ, при котором катализатор находится в коллоидном или в высокомолекулярном состоянии.
Пример – биокаталитический процесс, катализаторами служат ферменты (энзимы). Есть еще автокаталитические процессы, когда катализатор – продукт самой реакции.
Рассмотрим механизм каталитического взаимодействия в общих чертах. Пусть дана некая химическая реакция
А + В = АВ.
Без катализатора она протекает медленно. Как же она будет протекать с катализатором, по какой схеме? Ответим на данные вопросы. Катализатор взаимодействует с одним из реагентов, образуя промежуточные соединения по реакции
А + К = АК.
Затем уже это соединение реагирует с другим исходным веществом, при этом образуется продукт реакции АВ и выделяется еще катализатор. Напомним, катализатор – вещество, активно участ-вующее в химической реакции, но регенерирующееся (восстанав-ливающееся) после ее завершения, что мы и наблюдаем в ходе реакции
АК + В = АВ + К.
Главное преимущество катализатора в том, что он уменьшает энергию активации, увеличивая скорость реакции, но не влияет на термодинамические величины: ΔU, ΔH, ΔS, ΔG, ΔF.
ЛЕКЦИЯ № 5. Химическое равновесие
1. Понятие химического равновесия. Закон действующих масс
При протекании химической реакции через некоторое время устанавливается химическое равновесие. Существует два признака химического равновесия: кинетический, термодинамический. В кинетическом – υпр = υобр, в термодинамическом – характеризует химическую реакцию при условиях P, t – const (ΔG = 0); при условиях V, Т – const (ΔF = 0).
Химический потенциал – функция, которая характеризует состояние i-го компонента при определенных внешних условиях.
где n1 – число молей i-го компонента.
Если к бесконечно большому количеству раствора прибавить определенное количество какого-нибудь компонента, то химический потенциал системы определяется изменением изобарного потенциала при изобарных условиях или изменением изохорного потенциала при изохорных условиях.
Химический потенциал зависит от концентрации данного компонента
μi = μ0 + RTLnPi– (для идеального газа),
где Рi– парциальное давление – вклад каждого компонента в общее давление или давление, которое компонент имел бы, если бы находился в смеси.
Парциальное давление – элементарная функция (можно складывать). Пример (O2, N2, H2) – их общее давление
μi= μ0+ RTLnCi – (для раствора),
μ0– значение химического потенциала при стандартных условиях.
Химический потенциал характеризует способность данного компонента выходить из данной фазы путем испарения, растворения, кристаллизации и т. д. Переход этот происходит произвольно.
В результате химического равновесия скорость прямой реакции уменьшается, а скорость обратной реакции увеличивается.
Концентрации, которые соответствуют химическому равновесию, называются равновесными концентрациями. Связь между равновесными концентрациями устанавливается законом действующих масс (ЗДМ). Этот закон в 1867 г. вывели К. М. Гульберг и П. Вааге.
Кинетический вывод ЗДМ
f – фугитивность – парциальное давление для реальных газов. Возникает вопрос, будут ли равняться Кpи Кс.
Кpи Кc– отличаются на RT ∑vi в сумме стехиометрических коэффициентов.
Связь между Кpи Кс
если ∑vi = 0, то Kp = Kc. ∑vi = 1 + 1 – 1 – 1 =0 – когда стехиометрический коэффициент = 1.
2. Уравнение изотермы химической реакции
Если реакция протекает обратимо, то ΔG= 0.
Если реакция протекает необратимо, то ΔG≤ 0 и можно рассчитать изменение ΔG.
где χ – пробег реакции – величина, которая показывает, сколько молей изменилось в ходе реакции. I сп – характеризует равновесное и неравновесное состояние реакции, II сп – характеризует только неравновесные состояния.
Если
дχ = 1,
то
это уравнение изотермы химической реакции.
С помощью уравнения изотермы химической реакции можно судить о направлении протекания реакции.
1) Пp< Кp, ΔG < 0, слева направо;
2) Пp> Кp, ΔG > 0, справа налево;
3) Пp= Кp, ΔG = 0, химическое равновесие.
3. Уравнения изохоры, изобары химической реакции
Зависимость К от температуры
Уравнение изобары:
Уравнение изохоры:
По ним судят о направлении протекания реакции:
4. Расчет KP (метод Темкина-Шварцмана)
1-й способ:
термодинамический метод расчета Kp.
2-й способ:
Пример. Расчет Kp для реакции PbS04 распадается на РbО и S03.
Результаты вычислений занесены в таблицу 2.
Таблица 2
Результаты вычислений
5. Расчет равновесного состава химического равновесия
Равновесный состав можно рассчитать только для газовой системы
равновесная концентрация.
Исходная концентрация всех компонентов
Изменение каждого компонента по числу молей (или стехиометрическому коэффициенту):
ξγ– (пробег реакции) – химическая переменная.
Она показывает изменение количества вещества по числу молей. Если реакция не началась, то ξγ = 0. Если количество исходных веществ превратилось в такое же количество продуктов реакции, то ξγ = 1.
3H2 + N2 = 2NH3; ξγ= 1,
1,5H2 + 0,5N2 = NH3; ξγ= 0,5,
v1 А 1 + v2А2 = v3А3+ v4А4, – газовая реакция.
Рассчитать равновесный состав по третьему компоненту при условии, что А = а моль/л; В = в моль/л.
Рассчитываем по 4 компоненту:
Задача.
Газообразные вещества реагируют по уравнению:
Общее давление в газовой смеси – Робщ, общий объем – Vоб . Рассчитать KP и Kс.
Найти парциальное давление каждого компонента.
Вещества А и В превращаются в С в количестве Х. Исходные вещества А= 2 моль, В= 1 моль.
Для того, чтобы найти парциальное давление, мы должны Роб умножить на мольную долю. Мольная доля определяется отношением числа молей каждого компонента, отнесенного к общему числу молей всех компонентов.
где En – общее число молей, участвующих в этой газовой смеси.
где NA – мольная доля А.
где РА – парциальное давление.
Расчет Kc:
Δv= l – 0,5 – 2 = – 1,5,
где Δv– изменение количества молей.
ЛЕКЦИЯ № 6. Химическая кинетика
1. Понятие химической кинетики
Кинетика – наука о скоростях химических реакций.
Скорость химической реакции – число элементарных актов химического взаимодействия, протекающих в единицу времени в единицу объема (гомогенные) или на единице поверхности (гетерогенные).
Истинная скорость реакции:
2. Факторы, влияющие на скорость химической реакции
Для гомогенных, гетерогенных реакций:
1) концентрация реагирующих веществ;
2) температура;
3) катализатор;
4) ингибитор.
Только для гетерогенных:
1) скорость подвода реагирующих веществ к поверхности раздела фаз;
2) площадь поверхности.
Главный фактор – природа реагирующих веществ – характер связи между атомами в молекулах реагентов.
Пример:
NO2 – оксид азота (IV) – лисий хвост, СО – угарный газ, монооксид углерода.
Если их окислить кислородом, то в первом случае реакция пойдет мгновенно, стоит приоткрыть пробку сосуда, во втором случае реакция растянута во времени.
Концентрация реагирующих веществ будет рассмотрена ниже.
Пример:
Голубая опалесценция свидетельствует о моменте выпадения серы, чем выше концентрация, тем скорость выше.
Рис. 10
Чем больше концентрации Na2S2O3, тем меньше времени идет реакция. На графике (рис. 10) изображена прямо пропорциональная зависимость. Количественная зависимость скорости реакции от концент-рации реагирующих веществ выражается ЗДМ (законом действующих масс), который гласит: скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ.
Итак, основным законом кинетики является установленный опытным путем закон: скорость реакции пропорциональна концентрации реагирующих веществ, пример: (т.е. для реакции)
Для этой реакции Н2 + J2 = 2НJ – скорость можно выразить через изменение концентрации любого из веществ. Если реакция протекает слева направо, то концентрация Н2 и J2 будет уменьшаться, концентрация НJ – увеличиваться по ходу реакции. Для мгновенной скорости реакций можно записать выражение:
квадратными скобками обозначается концентрация.
Физический смысл k– молекулы находятся в непрерывном движении, сталкиваются, разлетаются, ударяются о стенки сосуда. Для того, чтобы произошла химическая реакция образования НJ, молекулам Н2 и J2 надо столкнуться. Число же таких столкновений будет тем больше, чем больше молекул H2 и J2 содержится в объеме, т. е. тем больше будут величины [Н2] и [J2]. Но молекулы движутся с разными скоростями, и суммарная кинетическая энергия двух сталкивающихся молекул будет различной. Если столкнутся самые быстрые молекулы Н2 и J2, энергия их может быть такой большой, что молекулы разобьются на атомы йода и водорода, разлетающиеся и взаимодействующие затем с другими молекулами Н2 + J2 →2H+2J, далее будет H + J2 →HJ + J. Если энергия сталкивающихся молекул меньше, но достаточно велика для ослабления связей H – H и J – J, произойдет реакция образования йодоводорода:
У большинства же сталкивающихся молекул энергия меньше необходимой для ослабления связей в Н2 и J2. Такие молекулы «тихо» столкнутся и также «тихо» разойдутся, оставшись тем, чем они были, Н2 и J2. Таким образом, не все, а лишь часть столкновений приводит к химической реакции. Коэффициент пропорциональности (k) показывает число результативных, приводящих к реакции соударений при концентрациях [Н2] = [J2] = 1моль. Величина k– const скорости. Как же скорость может быть постоянной? Да, скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка. Но молекулы движутся хаотически, тогда как же может быть скорость – const? Но постоянная скорость может быть только при постоянной температуре. С ростом температуры увеличивается доля быстрых молекул, столкновения которых приводят к реакции, т. е. увеличивается константа скорости. Но увеличение константы скорости не безгранично. При какой-то температуре энергия молекул станет столь большой, что практически все соударения реагентов будут результативными. При столкновении двух быстрых молекул будет происходить обратная реакция.
Настанет такой момент, когда скорости образования 2НJ из Н2 и J2 и разложения будут равны, но это уже химическое равновесие. Зависимость скорости реакции от концентрации реагирующих веществ можно проследить, пользуясь традиционной реакцией взаимодействия раствора тиосульфата натрия с раствором серной кислоты.
Na2S2O3 + H2SO4 = Na2SO4 + H2S2O3, (1)
H2S2O3 = S↓+H2O+SO2↑. (2)
Реакция (1) протекает практически мгновенно. Скорость реакции (2) зависит при постоянной температуре от концентрации реагирующего вещества H2S2O3. Именно эту реакцию мы наблюдали – в этом случае скорость измеряется временем от начала сливания растворов до появления опалесценции. В статье Л. М. Кузнецовой описана реакция взаимодействия тиосульфата натрия с соляной кислотой. Она пишет, что при сливании растворов происходит опалесценция (помутнение). Но данное утверждение Л. М. Кузнецовой ошибочно так как опалесценция и помутнение – это разные вещи. Опалесценция (от опал и латинского escentia – суффикс, означающий слабое действие) – рассеяние света мутными средами, обусловленное их оптической неоднородностью. Рассеяние света – отклонение световых лучей, распространяющихся в среде во все стороны от первоначального направления. Коллоидные частицы способны рассеивать свет (эффект Тиндаля – Фарадея) – этим объясняется опалесценция, легкая мутноватость коллоидного раствора. При проведении этого опыта надо учитывать голубую опалесценцию, а затем коагуляцию коллоидной суспензии серы. Одинаковую плотность суспензии отмечают по видимому исчезновению какого-либо рисунка (например, сетки на дне стаканчика), наблюдаемого сверху через слой раствора. Время отсчитывают по секундомеру с момента сливания.
Растворы Na2S2O3 x 5H2O и H2SO4.
Первый готовят путем растворения 7,5 г соли в 100 мл H2O, что соответствует 0,3 М концентрации. Для приготовления раствора H2SO4 той же концентрации отмерить надо 1,8 мл H2SO4(к), ρ = = 1,84 г/см3 и растворить ее в 120 мл H2O. Приготовленный раствор Na2S2O3 разлить в три стакана: в первый – 60 мл, во второй – 30 мл, в третий – 10 мл. Во второй стакан добавить 30 мл H2O дистиллированной, а в третий – 50 мл. Таким образом, во всех трех стаканах окажется по 60 мл жидкости, но в первом концентрация соли условно = 1, во втором – Ѕ, а в третьем – 1/6. После того, как будут подготовлены растворы, в первый стакан с раствором соли прилейте 60 мл раствора H2SO4 и включите секундомер, и т. д. Учитывая, что скорость реакции падает с разбавлением раствора Na2S2O3, ее можно определить как величину, обратно пропорциональную времени v = 1/τ и построить график, отложив на оси абсцисс концентрацию, а на оси ординат – скорость реакции. Из этого вывод – скорость реакции зависит от концентрации веществ. Полученные данные занесены в таблицу 3. Можно этот опыт выполнить с помощью бюреток, но это требует от выполняющего большой практики, потому что график бывает неправильным.
Таблица 3
Скорость и время реакции
Подтверждается закон Гульдберга-Вааге – профессора химии Гульдерга и молодого ученого Вааге).
Рассмотрим следующий фактор – температуру.
При увеличении температуры скорость большинства химических реакций повышается. Эта зависимость описана правилом Вант-Гоффа: «При повышении температуры на каждые 10 °C скорость химических реакций увеличивается в 2 – 4 раза».
где γ – температурный коэффициент, показывающий, во сколько раз увеличивается скорость реакции при повышении температуры на 10 °C;
v1 – скорость реакции при температуре t1;
v2 – скорость реакции при температуре t2.
Например, реакция при 50 °С протекает за две минуты, за сколько времени закончится процесс при 70 °С, если температурный коэффициент γ= 2?
Решение:
t1 = 120 с = 2 мин; t1 = 50 °С; t2 = 70 °С.
Даже небольшое повышение температуры вызывает резкое увеличение скорости реакции активных соударений молекулы. Согласно теории активации, в процессе участвуют только те молекулы, энергия которых больше средней энергии молекул на определенную величину. Эта избыточная энергия – энергия активации. Физический смысл ее – это та энергия, которая необходима для активного столкновения молекул (перестройки орбиталей). Число активных частиц, а следовательно, скорость реакции возрастает с температурой по экспоненциальному закону, согласно уравнению Аррениуса, отражающему зависимость константы скорости от температуры
где А – коэффициент пропорциональности Аррениуса;
k– постоянная Больцмана;
ЕА – энергия активации;
R – газовая постоянная;
Т– температура.
Катализатор – вещество, ускоряющее скорость реакции, которое само при этом не расходуется.
Катализ – явление изменения скорости реакции в присутствии катализатора. Различают гомогенный и гетерогенный катализ. Гомогенный – если реагенты и катализатор находятся в одном агрегатном состоянии. Гетерогенный – если реагенты и катализатор в различных агрегатных состояниях. Про катализ см. отдельно (дальше).
Ингибитор – вещество, замедляющее скорость реакции.
Следующий фактор – площадь поверхности. Чем больше поверхность реагирующего вещества, тем больше скорость. Рассмотрим на примере влияние степени дисперсности на скорость реакции.
CaCO3 – мрамор. Плиточный мрамор опустим в соляную кислоту HCl, подождем пять минут, он растворится полностью.
Порошкообразный мрамор – с ним проделаем ту же процедуру, он растворился через тридцать секунд.
Уравнение обоих процессов одинаково.
CaCO3(тв) + HCl(г) = CaCl2(тв) + H2O(ж) + CO2(г) ↑.
Итак, при добавлении порошкообразного мрамора время меньше, чем при добавлении плиточного мрамора, при одинаковой массе.
С увеличением поверхности раздела фаз скорость гетерогенных реакций увеличивается.
ЛЕКЦИЯ № 7. Коррозия металлов
1. Основные понятия и терминология
Коррозия – самопроизвольное окисление металлов, вредное для промышленной практики (уменьшающее долговечность изделий). Это слово произошло от латинского corrodere – разъедать. Среда, в которой металл подвергается коррозии (корродирует), называется коррозионной или агрессивной. При этом образуются продукты коррозии: химические соединения, содержащие металл в окисленной форме. В тех случаях, когда окисление металла необходимо для осуществления какого-либо технологического процесса, термин «коррозия» употреблять не следует. Например, нельзя говорить о коррозии растворимого анода в гальванической ванне, поскольку анод должен окисляться, посылая свои ионы в раствор, чтобы протекал нужный процесс. Нельзя также говорить о коррозии алюминия при осуществлении алюмотермического процесса. Но физико-химическая сущность изменений, происходящих с металлом во всех подобных случаях, одинакова: металл окисляется. Следовательно, термин «коррозия» имеет не столько научное, сколько инженерное значение. Правильнее было бы употреблять термин «окисление» независимо от того, вредно или полезно оно для нашей практики. В системе стандартизации (ГОСТ 5272-68) коррозия металлов определена как разрушение металлов вследствие химического и электрохимического взаимодействия их с коррозионной средой. В системе ИСО (международной стандартизации) это понятие несколько шире: физико-химическое взаимодействие между металлом и средой, в результате которого изменяются свойства металла, и часто происходит ухудшение функциональных характеристик металла, среды или включающей их технической системы.
Объекты воздействия коррозии – металлы, сплавы (твердые растворы), металлопокрытия, металлоконструкции машин, оборудования и сооружений. Процесс коррозии представляют как коррозионную систему, состоящую из металла и коррозионной среды. Коррозионная среда содержит одно или несколько веществ, вступающих в реакцию с металлом. Она может быть жидкой и газообразной. Газообразная среда, окисляющая металл, называется окислительной газовой средой. Изменение в любой части коррозионной системы, вызванное коррозией, называется коррозионным эффектом. Коррозионный эффект, ухудшающий функциональные характеристики металла, покрытия, среды или включающих их технических систем, расценивают как эффект повреждения или как коррозионную порчу (по системе ИСО). В результате коррозии образуются новые вещества, включающие окислы и соли корродирующего металла, это – продукты коррозии. Видимые продукты атмосферной коррозии, состоящие в основном из гидратированных оксидов железа, называют ржавчиной, продукты газовой коррозии – окалиной. Количество металла, превращенного в продукты коррозии за определенное время, относят к коррозионным потерям. Коррозионные потери единицы поверхности металла в единицу времени характеризуют скорость коррозии. Эффект повреждений, связанный с потерями механической прочности металла, определяют термином – коррозионное разрушение, глубину его в единицу времени называют скоростью проникновения коррозии. Важнейшее понятие – коррозионная стойкость. Она характеризует способность металла сопротивляться коррозионному воздействию среды. Коррозионную стойкость определяют качественно и количественно – скоростью коррозии в данных условиях, группой или баллом стойкости по принятой шкале, с помощью оптических приборов. Металлы, обладающие высокой коррозионной стойкостью, называют коррозионно стойкими. Факторы, влияющие на скорость, вид, рас-пределение коррозии и связанные с природой металла (состав, структура, внутренние напряжения, состояние поверхности), называют внутренними факторами коррозии. Факторы, влияющие на те же параметры коррозии, но связанные с составом коррозионной среды и условиями процесса (температура, влажность, обмен среды, давление и т. п.), называют внешними факторами коррозии. В ряде случаев факторы коррозии целесообразно делить в соответствии с таблицей 4.
Таблица 4
Факторы коррозии
2. Классификация процессов коррозии металлов
Классифицировать коррозию принято по механизму, условиям протекания процесса и характеру разрушения. По механизму протекания коррозионные процессы, согласно ГОСТ 5272-68, подразделяются на два типа: электрохимические и химические. К электрохимической коррозии относят процесс взаимодействия металла с коррозионной средой, при котором ионизация атомов металла и восстановление окислительных агентов среды протекают не в одном акте и зависят от электронного потенциала (наличия проводников второго рода). Рассмотрим несколько видов электрохимической коррозии:
1) атмосферная – характеризует процесс в условиях влажной воздушной среды. Это наиболее распространенный вид коррозии, так как большинство конструкций эксплуатируют в атмосферных условиях. Ее можно разделить следующим образом: на открытом воздухе, с возможностью попадания на поверхность машин осадков, или с защитой от них в условиях ограниченного доступа воздуха и в замкнутом воздушном пространстве;
2) подземная – разрушение металла в почвах и грунтах. Разновидность этой коррозии – электрохимическая коррозия под воздействием блуждающих токов. Последние возникают в грунте вблизи источников электрического тока (систем передачи электроэнергии, электрифицированных транспортных путей);
3) жидкостная коррозия, или коррозия в электролитах. Ее частным случаем является подводная коррозия – разрушение металлических конструкций, погруженных в воду. По условиям эксплуатации металлоконструкций, этот вид подразделяют на коррозию при полном и неполном погружении; при неполном погружении рассмотрен процесс коррозии по ватерлинии. Водные среды могут отличаться коррозийной активностью в зависимости от природы растворенных в них веществ (морская, речная вода, кислотные и щелочные растворы химической промышленности и т. п.). При подводной коррозии возможны процессы коррозии оборудования в неводных жидких средах, которые подразделяют на неэлектропроводящие и электропроводящие. Такие среды специфичны для химической, нефтехимической и других отраслей промышленности. К химической коррозии относят процесс, в котором окисление металла и восстановление среды представляют единый акт (отсутствие проводников второго рода). Химическая коррозия – это разрушение металлов в окислительных средах при высоких температурах. Различают два вида: газовая (т. е. окисление металла при нагреве) и коррозия в неэлектролитах:
а) характерной особенностью газовой коррозии является отсутствие влаги на поверхности металла. На скорость газовой коррозии влияет, прежде всего температура и состав газовой среды. В промышленности часто встречаются случаи этой коррозии: от разрушения деталей нагревательных печей до коррозии металла при термической обработке.
б) коррозия металлов в неэлектролитах, независимо от их природы, сводится к химической реакции между металлом и веществом. В качестве неэлектролитов используют органические жидкости.
В особую группу следует выделить виды коррозии в условиях воздействия механических напряжений (механическая коррозия). Эта группа включает: собственно коррозию под напряжением, характеризуемую разрушением металла при одновременном воздействии коррозионной среды и постоянных или переменных механических напряжений; коррозионное растрескивание – при одновременном воздействии коррозионной среды и внешних или внутренних механических напряжений растяжения с образованием транскристаллитных трещин.
Различают самостоятельные виды коррозии:
1) коррозия при трении – разрушение металла, вызываемое одновременным воздействием коррозионной среды и трения;
2) фреттинг-коррозия – разрушение при колебательном перемещении двух поверхностей относительно друг друга в условиях воздействия коррозионной среды;
3) коррозионная кавитация – разрушение при ударном воздействии среды;
4) коррозионная эрозия – при истирающем воздействии среды;
5) контактная коррозия – разрушение одного из двух металлов, находящихся в контакте и имеющих разные потенциалы в данном электролите.
Следует различать коррозию и эрозию. Эрозия о латинского слова erodere (разрушать) – постепенное механическое разрушение металла, например при истирании трущихся частей механизмов.
Самостоятельный вид коррозии – биокоррозия – это разрушение металла, при котором в качестве значимого выступает биофактор. Биоагенты – микроорганизмы (грибы, бактерии), которые являются инициаторами или стимуляторами процесса коррозии.
По характеру разрушения коррозия делится на сплошную (или общую) и местную (локальную). Сплошная коррозия охватывает всю поверхность металла, при этом она может быть равномерной или неравномерной. Местная коррозия происходит с разрушением отдельных участков поверхности металлов. Разновидность этой коррозии: точечная (питтинг), коррозия пятнами и сквозная коррозия.
Подповерхностная коррозия начинается с поверхности, но развивается преимущественно под ней таким образом, что продукты коррозии сосредоточены внутри металла. Ее разновидность – послойная коррозия, распространяющаяся преимущественно в направлении пластической деформации металла.
Структурная коррозия связана со структурной неоднородностью металла. Ее разновидность – межкристаллитная – разрушение металла по границам кристаллитов (зерен) металла; внутрикристаллитная – разрушение металла по зернам кристаллитов. Наблюдается при коррозийном растрескивании, протекающем под влиянием внешних механических нагрузок или внутренних напряжений.
Ножевая коррозия – локализованное разрушение металла в зоне сплавления сварных соединений в жидких средах с высокой коррозионной активностью.
Щелевая коррозия – усиление процесса разрушения металла в зазорах между двумя металлами.
Избирательная коррозия – разрушение одной структурной составляющей или одного компонента металла в высокоактивных средах. Существует ряд разновидностей: графитизация чугуна (растворение ферритных или перлитных составляющих) и обесцинкование (растворение цинковой составляющей) латуней.
3. Виды коррозионных разрушений
Коррозия, в зависимости от природы металла, агрессивной среды и других условий, приводит к различным видам разрушений. На рисунке 13 представлены разрезы через прокорродировавший образец металла, показывающие возможные изменения рельефа поверхности в результате коррозии.
Рис. 11. Схематическое изображение различных видов коррозии: а – равномерная коррозия; б – коррозия пятнами; в, г – коррозия язвами; д – точечная коррозия (питтинг); е – подповерхностная коррозия; НН – исходная поверхность металла; КК – рельеф поверхности, измененный вследствие коррозии.
Иногда коррозия протекает со скоростью, одинаковой по всей поверхности; в таком случае поверхность становится только немного более шероховатой, чем исходная (а). Часто наблюдается различная скорость коррозии на отдельных участках: пятнами (б), язвами (в, г). Если язвы имеют малое сечение, но относительно большую глубину (д), то говорят о точечной коррозии (питтинг). В некоторых условиях небольшая язва распространяется вглубь и вширь под поверхностью (е). Неравномерная коррозия значительно более опасна, чем равномерная. Неравномерная коррозия, при сравнительно небольшом количестве окисленного металла, вызывает большое уменьшение сечения в отдельных местах. Язвенная или точечная коррозия могут привести к образованию сквозных отверстий, например, в листовом материале, при малой потере металла.
Приведенная классификация, конечно, условна. Возможны многочисленные формы разрушения, лежащие между характерными типами, показанными на данном рисунке.
Некоторые сплавы подвержены своеобразному виду коррозии, протекающей только по границам кристаллитов, которые оказываются отделенными друг от друга тонким слоем продуктов коррозии (межкристаллитная коррозия). Здесь потери металла очень малы, но сплав теряет прочность. Это очень опасный вид коррозии, который нельзя обнаружить при наружном осмотре изделия.
4. Методы защиты от коррозии
Для ослабления коррозионного процесса требуется повлиять либо на сам металл, либо на коррозионную среду. Выделяют основные направления для борьбы с коррозией:
1) легирование металла, либо замена его другим, более коррозионностойким;
2) защитные покрытия (металлические и неметаллические) органического или неорганического происхождения;
3) электрохимическая защита, различают катодную, анодную и протекторную как вариант катодной защиты.
Например, при атмосферной коррозии применяют покрытия органического и неорганического происхождения; от подземной коррозии эффективна электрохимическая защита;
4) введение ингибиторов (веществ, замедляющих скорость реакции).
ЛЕКЦИЯ № 8. Физико-химический анализ
1. Суть физико-химического анализа
Задача физико-химического анализа состоит в установлении зависимости свойств равновесной системы от параметров состояния. Под параметрами состояния обычно понимают: состав, давление, температуру. Зависимости выражаются в виде различных диаграмм «параметр состояния – свойство». На практике большое значение имеет диаграмма «состав – свойство». Анализ именно такой диаграммы позволяет получать сведения о характере взаимодействия компонентов, о давлении и концентрации компонентов, о составе и устойчивости образующихся в системе химических соединений. Совокупность зависимостей всех свойств равновесной системы от параметров состояния позволяет изобразить в виде графика фазовую диаграмму – диаграмму состояния. Чтобы рассмотреть каждую диаграмму состояния систем, пользуются понятиями: фаза, система, степень свободы, компонент, составляющее вещество, термодинамическое равновесие. Раскроем суть этих понятий.
Компонент – химически индивидуальные вещества, наименьшего числа которых достаточно для образования всех фаз, т. е. гомогенных частей данной системы.
Система – совокупность тел, находящихся во взаимодействии между собой и отделенных от окружающей среды. Различают физическую и химическую системы. Если составные части системы не вступают друг с другом в химические реакции, то такая система называется физической. Если составные части системы реагируют друг с другом, то она называется химической.
Составляющее вещество – вещество, которое может быть выделено из системы и существовать вне ее.
Степень свободы (вариантность) – число независимых параметров системы, которые можно произвольно менять в некотором интервале без изменения вида и числа фаз системы.
Термодинамическое равновесие – состояние, к которому самопроизвольно стремится система. Она находится в состоянии термодинамического равновесия в том случае, когда изменение свободной энергии Гиббса равно нулю.
Фаза – гомогенная часть гетерогенной системы, ограниченная поверхностью раздела от других частей.
Раскрыв суть важнейших понятий физико-химического анализа, рассмотрим правила и принципы, лежащие в его основе.
Правило фаз – число степеней свободы равновесной системы, на которую из внешних факторов влияют только давление и температура, равно числу независимых компонентов системы плюс два минус число фаз, т. е.
F = k + 2 – z,
где F – число степеней свободы;
k – число компонентов;
z – число фаз;
число 2 – два независимых параметра системы: давление и температура.
Применим правило фаз к однокомпонентной системе:
F = 1 + 2 – z.
Итак, в этой системе максимальное число фаз, одновременно находящихся в равновесии, равно трем. Состояние равновесия однокомпонентной системы определяется ее объемом, температурой, давлением:
f(P, T, V ) = 0.
Рассмотрим возможные состояния однокомпонентной системы, сведенные в таблицу 5.
Таблица 5
Фазовые состояния однокомпонентной системы
Рассмотрим зависимость между числом фаз и числом степеней свободы в двухкомпонентной системе.
F = 2 + 2 – z.
Из этого видно, что максимальное число фаз, находящихся одновременно в равновесии, равно четырем. Состояние равновесия двухкомпонентной системы определяется давлением, температурой и концентрацией компонентов. В некоторых случаях возможны и другие состояния (табл. 6).
Таблица 6
Фазовые состояния двухкомпонентной системы
Из этого можно сделать вывод, что в двухкомпонентных системах число независимых переменных достигает пяти: температура, давление, мольный объем, концентрация первого компонента, концентрация второго компонента, т. е. уравнение состояния будет:
f(P, T, V, XA, XB) = 0.
Из пяти параметров независимы только три, потому что мольный объем является функцией температуры и давления, и при заданной концентрации одного компонента XA концентрация другого будет 1 – XA. Итак, для характеристики двухкомпонентной системы нужны: давление, температура, концентрация одного из компонентов. Изменение состояния системы, при котором давление, температура и состав фаз остаются постоянными, а масса одних фаз увеличивается за счет массы других фаз, носит название фазовой реакции.
Фазовое превращение или фазовый переход – переход вещества из одной фазы в другую. Итак, правило фаз Гиббса имеет большое значение в гетерогенных системах, в учении о равновесии, является теоретической основой для физико-химического анализа, который проанализировав его задачи, понятия и принципы заключается в следующем: измеряют любое физическое свойство расплава или раствора (плотность, температуру плавления, давление пара и т. п.) и, изменяя состав, получают числовые данные свойства и сводят в таблицу, а затем строят диаграмму «состав – свойство», анализируют зависимость между геометрическими особенностями диаграммы и природой раствора. Плавное изменение, минимум или максимум на кривых, излом и другое, т. е. любая геометрическая форма кривой и диаграммы в целом, характеризует взаимодействия между компонентами раствора. Эти диаграммы решают задачи об установлении числа, химической природы и границах существования фаз.
С помощью метода физико-химического анализа изучают сплавы, минералы и т. п. Огромная заслуга в этом принадлежит И. С. Курнакову, Х. В. Розебому, Г. Г. Тамману и др.
2. Однокомпонентные системы
Пример такой системы – диаграмма состояния воды. В такой системе тройную точку О, координаты которой определяют условия сосуществования трех фаз: лед, вода, пар, – можно рассматривать как геометрический образ с нулевым числом измерений. Число степеней свободы этой системы равно нулю. Если изменить хотя бы один из параметров (давление или температуру), то сразу же изменится число сосуществующих фаз. Кривые, описывающие условия равновесия двух фаз (лед – пар, лед – вода, вода – пар), имеют число степеней свободы, равное единице. Можно менять как угодно любой параметр, сохраняя равновесие двух фаз, но величина второго будет строго определенна. Итак, линия двухфазного равновесия – это функция одного параметра, зависящая от другого:
P = f(T ) или I = z(P).
Тройная точка в этой системе представляет собой нонвариантное равновесие.
3. Физико-химические методы анализа состава сплавов
Различают термический и рентгеноструктурный анализ.
Физико-химический анализ – область химии, изучающая посредством сочетания физических и геометрических методов превращения, происходящие в равновесных системах.
Рентгеноструктурный анализ – метод исследования строения тел, использующий явление дифракции рентгеновских лучей. Дифракция рентгеновских лучей – один из видов рассеяния рентгеновский лучей.
Рентгеноструктурный анализ является основным методом определения структуры кристалла. Исследуемый образец помещают на пути рентгеновских лучей и регистрируют дифракционную картину, возникающую в результате взаимодействия лучей с веществом.
Задача физико-химического анализа – установить зависимость свойств равновесной системы от параметров состояния (Т, P, состава).
Термический анализ позволяет исследовать всевозможные превращения простых и сложных систем по тепловым эффектам.
Термический анализ проводится с визуальным наблюдением за температурой появления и исчезновением кристаллов. Наблюдения за исчезновением и появлением кристаллической фазы при нагревании и охлаждении расплава проводят до получения близких по значению температурных данных. Термический анализ применим, если сплав прозрачен.
Хронопотенциометрия в некоторых расплавах. Особенность – постоянная скорость подачи титранта в анализируемый расплав и непрерывная запись показателей рН-метра в процессе титрования. О количестве вещества судят по соответствующей длине диаграммной ленты самописца.
Применение хронопотенциометрии для физико-химического исследования расплавов
Определение коэффициента диффузии в расплавах:
где m0 – концентрация ионов % масс;
М0 – молекулярная масса, г/моль;
ρ– плотность электролита, г/см3.
Определение толщины диффузного слоя
В условиях принудительного перемешивания у поверхности электрода существует ограниченный диффузный слой. Для определения толщины используется уравнение хронопотенциограммы:
где φ∞– величина установившегося потенциала при заданном токе. По наклону прямой, выражающей зависимость (1), находят величину 4δ2/π 2D0.Отношение D0 / δопределяют из значения установившегося потенциала
По величинам 4δ2/π 2D0и D0 / δлегко найти δи D0.
Определение растворимости Н2, Cl2, O2 в расплаве. Электродные процессы в расплавах с участием Н2, Cl2, O2 привлекают внимание исследователей в связи с развитием электрохимии топливных элементов. Растворимость газообразных веществ в расплавах находят по уравнению Сэнда. Величина произведения i x τ1/2 однозначно связана с величиной растворимости Н2, Cl2, O2 в расплаве, если между газами и компонентами расплава отсутствует какое-либо химическое взаимодействие. В двойной эвтектике CuCN и Cd(CN)2 растворимость Н2 подчиняется закону Генри. Для оценки абсолютного значения растворимости газов необходимо знать величину коэффициента диффузии. Если в исходном расплаве содержатся ионы О2-, то между i x τ1/2 и концентрацией ионов О2- наблюдается линейная зависимость, на основании которой можно судить о содержании О2- .
ЛЕКЦИЯ № 9. Термохимия
1. Понятие термохимии
Раздел физической химии и химической термодинамики, изучающий тепловые процессы теплоемкости веществ, называется термохимией.
δQ = dU + δA– первый закон термодинамики. δQ – не является функцией состояния. P = const || V = const – функции состояния при этих условиях. δQP = dH || δQV= dUвн– функции состояния при этих условиях.
2. Закон Гесса
При изобарных и изохорных условиях теплота является функцией состояния.
В 1840 г. Г. Н. Гесс формулирует закон: «Тепловой эффект химической реакции не зависит от промежуточных стадий, а зависит только от начального и конечного состояния системы».
δQP = dH,
δQV = dUвн,
QP = ΔH,
QV = ΔUвн.
Современная формулировка закона Гесса – общие приращения энтальпии при переходе начальных веществ в продукты реакции не зависят от того, через какие промежуточные стадии прошла реакция.
Закон Гесса позволяет рассчитать тепловые эффекты или приращение энтальпии только при стандартных условиях (р = 1 атм = 105 Па, Т = 273 К + 25 = 298 К).
Теплоты при стандартных условиях сведены в таблицу (справочник под редакцией Нищенко). Для индивидуальных веществ: С, Н2, Fe и др. – ΔН = 0.
Следствия из закона Гесса:
1) энтальпия образования 1 моля соединения из простых веществ не зависит от способа получения;
2) теплоты сгорания – «теплота реакции равна сумме теплот сгорания исходящих веществ за вычетом теплот сгорания продуктов реакции с учетом стехиометрических коэффициентов»
где r – реакции;
c – композиция;
3) теплоты образования – «тепловой эффект реакции равен разности между теплотами образования всех веществ, указанных в правой части уравнения (продукт реакции), и теплотами образования всех веществ, указанных в левой части уравнения».
где f – формация.
Пример 1. Рассчитать тепловой эффект реакции этерификации спирта.
Пример 2. Рассчитать тепловой эффект реакции, протекающей по уравнению:
3. Закон Кирхгоффа. Интегральная форма уравнений Кирхгоффа
3акон Кирхгоффа
Это уравнения Кирхгоффа в дифференциальной форме.
Когда идет изменение функции по t – температурный коэффициент:
Закон Кирхгоффа: температурный коэффициент теплового эффекта равен изменению теплоемкости данного процесса.
Интегральная форма уравнений Кирхгоффа:
интегральная форма уравнений Кирхгоффа, Т1 = 298 К.
1) ΔСР ≠ f(T)
усредненное ΔН при Т1 – по закону Гесса;
2) ΔСР = f(T)
Пример 3. Рассчитать тепловой эффект химической реакции при Т= 1000 К (реакция сгорания С2Н5ОН).
С2Н5ОН + 302 = 2С02 + ЗН20 (самостоятельно).
Все реакции – как реакции образования:
Т = 1000 к.
ЛЕКЦИЯ № 10. Гальванические элементы
1. Понятие гальванического элемента
Гальванический элемент – прибор, который преобразовывает химическую энергию в электрическую. Одним из таких элементов является элемент Даниэля – Якоби. Этот элемент состоит из двух электродов: цинкового и медного, – погруженных в соответствующие сульфатные растворы, между которыми пористая перегородка:
При замыкании внешней цепи электроны переходят от Zn к Cu, происходит диффузия цинка в медь:
Образуем электрохимическую схему:
Анод – отрицательный электрод (слева). Катод – положительный электрод.
Для определения ЭДС этого элемента нужно сравнить стандартные электродные потенциалы обоих электродов. При записи электродных реакций принято, что окисленная форма находится в левой части, а восстановленная – в правой части уравнения.
где E0 – электродвижущая сила (ЭДС) гальванического элемента, когда все реагенты в стандартном состоянии.
ЭДС элемента вычисляется вычитанием из потенциала катода потенциала анода.
ЭДС элемента равна +0,34 – (–0,76) = 1,1 В; чем больше электродные потенциалы отличаются друг от друга, тем больше ЭДС. Если погрузить металл в раствор соли большей концентрации, то потенциал нестандартный. Значит, на величину электродного потенциала влияет концентрация и температура. Такая зависимость выражается уравнением В. Нернста.
где п – число ионов;
R – универсальная газовая постоянная;
Т – температура;
С – концентрация активных ионов в растворе;
F – число Фарадея = 96500 В.
2. Химические источники тока
ХИТы – устройства, которые применяют для непосредственного преобразования энергии химической реакции в электрическую. ХИТы применяются в различных областях техники. В средствах связи: радио, телефон, телеграф; в электроизмерительной аппаратуре; они служат источниками электропитания для автомобилей, самолетов, тракторов; применяются для приведения в действие стартеров и др.
Недостатки ХИТ:
1) стоимость веществ, необходимых для работы: Pb, Cd, – высока;
2) отношение количества энергии, которую может отдать элемент, к его массе, мало.
Преимущества ХИТ:
1) ХИТы делятся на две основные группы: обратимые (аккумуляторы), необратимые (гальванические элементы). Аккумуляторы можно использовать многократно, так как их работоспособность может быть восстановлена при пропускании тока в обратном направлении от внешнего источника, а в гальванических элементах допускают лишь однократное использование, поскольку один из электродов (Zn в элементе Даниэля – Якоби) необратимо расходуется;
2) применяются электролиты, поглощенные пористыми материалами, они имеют большее внутреннее сопротивление;
3) создание топливных элементов, при работе которых расходовались бы дешевые вещества с малой плотностью (природный газ, водород);
4) удобство в работе, надежность, высокие и стабильные напряжения.
Рассмотрим процесс технологии на основе свинцово-кислотного аккумулятора с намазными электродами.
Общая схема: (–) активное вещество | электролит | активное вещество (+).
Активным веществом отрицательного электрода служит восстановитель, отдающий электроны. При разряде отрицательный электрод является анодом, т. е. электродом, на котором протекают окислительные процессы. Активное вещество положительного электрода – окислитель. Активные вещества – окислитель и восстановитель – участвуют в электрохимической реакции.
Электрохимическая схема свинцово-кислотного аккумулятора
Активными веществами свинцового аккумулятора являются: губчатый свинец и PbO2. Создание активных масс в электродах заключается в следующем: на электропроводящий каркас конструкции наносят пасту или смесь оксидов Pb; при последующем формировании пластин оксиды Pb превращаются в активные вещества. Формирование – перевод незаряженной массы в заряженную. Такого рода пластины подразделяются в зависимости от типа каркаса на намазные и решетчатые. Большинство аккумуляторов собирают из намазных пластин. При их изготовлении пасту из оксидов свинца вмазывают в ячейки профилированных решеток толщиной 1 – 7 мм, отлитых из Pb – Sb сплава. После затвердевания паста удерживается на решетке, гарантия такого аккумулятора – 2 – 3 года. При выборе материалов токоотводов положительных электродов аккумуляторов важно обеспечить их практическую пассивность (при сохранении электрической проводимости) в условиях заряда (до весьма высоких потенциалов при анодной поляризации). Для этой цели в растворах H2SO4 применяют Pb или его сплавы. Корпус и крышка ХИТ могут быть изготовлены из стали, либо из различных диэлектриков, но в свинцово-кислотных аккумуляторах корпус выполняют из эбонита, полипропилена, стекла. Электролит в свинцово-кислотном аккумуляторе может участвовать в суммарной токообразующей реакции. Для токоведущих отводов отрицательного электрода применяют Cu, Ti, Al.
3. Регенерация и утилизация ХИТов
Срок службы гальванических элементов кончается (разряд ХИТ) после полного или частичного использования активных материалов, работоспособность которых после разряда может быть восстановлена путем заряда, то есть пропусканием тока в направлении, обратном направлению тока при разряде: такие гальванические элементы называются аккумуляторами. Отрицательный электрод, который при разряде аккумулятора был анодом, при заряде становится катодом. Условиями лучшего использования активных материалов являются низкие плотности тока, высокие температуры до нормы. Обычно причиной нарушения работы ХИТов является пассивация электродов – резкое уменьшение скорости электрохимического процесса при разряде, вызванное изменением состояния поверхности электродов при разряде из-за образования оксидных слоев или солевых пленок. Способ борьбы с пассивацией – уменьшение истинных плотностей тока разряда путем применения электродов с развитыми поверхностями. Производство ХИТ отличается применением разнообразных токсичных веществ (сильных окислителей, соединений Pb, Hg, Zn, Cd, Ni, применяемых в мелкодисперсном состоянии; кислот, щелочей, органических растворителей). Для обеспечения нормальных условий труда предусмотрена автоматизация производственных процессов, рациональные системы вентиляции, включающие применение местных отсосов от аппаратов с токсичными выделениями, герметизация оборудования, замена сухих способов переработки пылящих материалов мокрыми, очистка загрязненного воздуха и газов от аэрозолей, очистка промышленных сточных вод. Массовое использование ХИТ в народном хозяйстве связано с проблемами экологии. Если свинец из аккумуляторов в основном может быть возвращен потребителями на заводы по его переработке, то утилизация небольших бытовых первичных ХИТ экономически нецелесообразна.
Каждая батарея Hg – Zn обеспечивает работу слухового аппарата в течение 5 – 7 дней.
Проводится разработка электромобилей с использованием ХИТ вместо двигателей внутреннего сгорания, которые отравляют атмосферу городов выхлопными газами. По степени отрицательного воздействия на окружающую среду гальваническое производство стоит на первом месте. Причина крайне негативного воздействия гальванического производства заключается в том, что на подавляющем большинстве предприятий в технологических процессах нанесения покрытий полезно расходуется только 10 – 30% солей тяжелых металлов, остальная же часть при неудовлетворительной работе попадает в среду. Выход – максимально сократить потери солей цветных металлов, то есть уменьшить вынос деталями электролитов из гальванических ванн. Это приведет к уменьшению концентраций и объемов сточных вод и создаст тем самым необходимые условия для ведения малоотходной (МОТ) и безотходной (БОТ) технологий нанесения гальванических покрытий. Надо первоначально правильно подобрать электролит. Основополагающий принцип МОТ и БОТ – уменьшать расход химикатов на входе и меньше поставлять ядов на выходе процесса.
ЛЕКЦИЯ № 11. Электрохимия
1. Понятие электрохимии
Электрохимия – раздел физической химии, который рассматривает системы, содержащие ионы (растворы или расплавы электролитов) и процессы, протекающие на границе двух фаз с участием заряженных частиц.
Первые представления о взаимосвязи химических и электрических явлений были известны в XVIII веке, так как было выполнено огромное количество физико-химических экспериментов с электрическим и грозовыми разрядами, с зарядами, находящимися в лейденских банках, но все они имели случайный характер из-за отсутствия постоянного мощного источника электрической энергии. Зарождение электрохимии связано с именами Л. Гальвани и А. Вольта. Занимаясь исследованием физиологических функций лягушки, Гальвани случайно создал электрохимическую цепь. Она состояла из двух различных металлов и препарированной лапки лягушки. Лапка одновременно являлась электролитом и индикатором электрического тока, но вывод был дан неправильный, т. е., согласно Гальвани, этот электрический ток, который возникал в цепи, имел животное происхождение, т. е. был связан с функциональными особенностями организма лягушки (теория «животного электричества»). Правильное толкование опытам Гальвани дал А. Вольта. Он создал первую батарею гальванических элементов – вольтов столб. Элементы батареи состояли из медных и цинковых дисков, а электролитом служил пропитанный соленой водой или кислотой губчатый материал. Именно такое соединение позволило получить электрический ток. Вскоре трудами великих ученых А. Вольта, Дж. Даниэля, Б. С. Якоби, П. Р. Багратиона, Г. Плантэ и др. появились удобные в работе мощные гальванические элементы и аккумуляторы. Затем А. Вольта разработал ряд напряжений металлов. Если два различных металла привести в соприкосновение, а затем разъединить, то при помощи физических средств, например, электроскопа, можно увидеть, что один металл приобрел положительный заряд, а другой – отрицательный. Этот ряд металлов, в котором каждый предшествующий металл заряжается положительно, но после контакта с любым последующим, т. е. ряд Вольта, оказался аналогичным ряду напряжений. Далее, в начале XIX века, был разработан электролиз, а М. Фарадей установил количественные законы электролиза. Большой вклад в развитие электрохимии внесли ученые: С. А. Аррениус, В. Ф. Оствальд, Р. А. Колли, П. Дебай, В. Нернст, Г. Гельмгольц и др. Сейчас электрохимия делится на теоретическую и прикладную. Благодаря использованию электрохимических методов, она связана с другими разделами физической химии, а также с аналитической химией и другими науками.
2. Электродные процессы
Электродные процессы – процессы, связанные с переносом зарядов через границу между электродом и раствором. Катодные процессы связаны с восстановлением молекул или ионов реагирующего вещества, анодные – с окислением реагирующего вещества и с растворением металла электрода.
Возможность протекания того или иного электродного процесса в общем случае определяется изменением ΔH и ΔS в ходе соответствующей химической реакции. Зная эти изменения, по уравнению Гельмгольца можно рассчитать минимальную величину напряжения, которое необходимо наложить на электроды для протекания данного электродного процесса. Например, на основании термодинамических данных для реакции 2Н2 + О2 = 2Н2О было установлено, что минимальное напряжение, необходимое для электрохимического разложения Н2О на Н2 и О2 =1,23В. Однако при таком напряжении между Hg катодом и Pt анодом для получения всего 1 см3 Н2 потребовалось бы около 400 тыс. лет. Чтобы увеличить скорость электродных процессов, не изменяя природы электродов, необходимо наложить на электроды значительно большую разность потенциалов. Например, для прохождения в рассмотренной системе электрического тока плотностью 1 А/см2 разность потенциалов между электродами должна составить 3,5 В. При этом только 35% электрической энергии затрачивается на реализацию электродного процесса, остальные 65% расходуются на нагревание электролита. Однако коэффициент полезного действия электрической энергии можно резко увеличить, если Hg катод заменить на Pt. Приведенный пример показывает, что термодинамический подход к изучению электродного процесса недостаточен.
Значительно большее значение имеет исследование кинетики электродных процессов. С помощью меченых атомов можно показать, что электродные процессы всегда идут в двух направлениях. Например, при восстановлении Cu2+ на медном электроде одновременно с реакцией Cu2+ + 2e- →Cu0 идет, хотя и с меньшей скоростью, ионизация Cu. При отсутствии внешнего тока скорости прямого и обратного электродного процесса равны между собой и равны плотности тока обмена, которая характеризует собственную скорость электродного процесса. При пропускании внешнего тока скорости электродного процесса в прямом и обратном направлениях различаются на величину плотности тока i. В этих условиях потенциал электрода отличается от своего равновесного значения. Сдвиг потенциала электрода от его равновесного значения при электродном процессе – поляризация. Абсолютная величина поляризации – η(перенапряжение). Чем больше плотность тока обмена, тем меньше при заданном значении iотклонение электрохимической системы от равновесия, и тем меньше перенапряжение. Таким образом, при заданном значении iвеличина ηхарактеризует собственную скорость данного электродного процесса. Поэтому задача электрохимической кинетики заключается в том, чтобы связать уравнением величину ηс плотностью тока и с другими параметрами электрохимической системы. Зная эту закономерность, можно сознательно регулировать скорость исследуемых электродных процессов. Электродные процессы – гетерогенные, и поэтому состоят из ряда последовательных стадий. Суммарная скорость электродного процесса в этих условиях определяется скоростью самой медленной стадии. Это означает, что суммарная величина ηскладывается из значений ηдля различных стадий: самая медленная стадия при заданной i даст самую большую составляющую η, по сравнению с которой другими составляющими ηпренебрегают.
Пример. Рассмотрим стадии электродного процесса на примере разряда ионов Н3О с образованием Н2 (газ).
Стадия I – перенос ионов Н3О+ из объема раствора к поверхности электрода за счет диффузии под действием электрического поля (миграция) или за счет перемешивания раствора (конвекция). Если максимально возможная в данных условиях скорость переноса ионов Н3О+ соответствует плотности тока iд, то для стадии I:
Стадия II – вхождение иона Н3О+ в ДЭС. Химические закономерности этой стадии были впервые рассмотрены В. Г. Левичем в 1949 г. Как показали более поздние исследования П. Делахея, скорость стадии II может существенно отразиться на общей скорости электродного процесса, лишь в случае электростатического отталкивания реагирующей частицы от электрода в условиях очень быстрой последующей стадии разряда (например, при разряде ионов Hg2+ на положительно заряженной поверхности Hg).
Стадия III – собственно электрохимическая стадия разряда. Медленность этой стадии в рассматриваемом примере обусловлена очень большой энергией связи протона с молекулой Н2О в разряжающемся ионе Н3О+. Согласно теории замедленного разряда, впервые предложенной М. Фольмероми Т. Эрдей-Грузомв 1930 г., а затем развитой А. Н. Фрумкиным в 1932 г. с учетом строения ДЭС для стадии III:
где α– const 0 < a <1;
ψ1 – потенциал на расстоянии среднего ионного радиуса от
поверхности электрода;
Wadc – энергия адсорбции атомов Н на поверхности металла.
Приведенное уравнение дает зависимость перенапряжения от плотности тока, состава раствора и природы металла (через Wadc) и в большинстве случаев хорошо согласуется с экспериментальными данными. В частности, стадия III определяет общую скорость электрохимической реакции при использовании в качестве электрода: Hg, Pb, Sn, Zn, Tl.
Стадия IVa – рекомбинация адсорбированных атомов водорода в молекулы Н2. Впервые выражение для этой стадии получил Ю. Тафель в 1905 г. В 1930 г. эта теория развилась в работе Н И. Кобозева и Н И. Некрасова, которые учли энергию адсорбции атомов Н на поверхности электрода. Стадия IVa:
где п > 1 – const.
Одновременно Н И. Кобозевым и Н И. Некрасовым была рассмотрена возможность удаления адсорбции Н путем эмиссии атомов Н в раствор. Стадия IVa является заметным вкладом в суммарную величину ηпри использовании в качестве электродов металлов, которые хорошо адсорбируют водород: Pt, Fe, Ni.
Механизм удаления ад.Н, соответствует стадии IVб, был предложен Я. Гейровским в 1925 г. – электрохимическая десорбция. Поскольку в стадии IVб применяют участие ионы Н3О+ и электроны металла, то зависимость скорости этой стадии от состава раствора и от потенциала электрода такая же, как и в стадии III. Экспериментально существование стадии IVб было доказано для электродов из Fe и Ni.
3. Катодные и анодные процессы в гальванотехнике
Основными процессами в гальванотехнике являются восстановление и снижение.
На Kat – восстановление, где Kat – катод. На An – снижение, где An – анод.
Электролиз H2O:
Катодные реакции
Последняя реакция протекает свыделением водорода.
4. Современные направления в развитии термодинамической и прикладной электрохимии
Наиболее важная стадия любого электрохимического процесса – стадия переноса заряда, она протекает на межфазной границе электрод-электролит в пределах ДЭС, в его плотной части (слой Гельмгольца). Особенностью стадии переноса зарядов является обязательное участие электронов в процессе, источник электронов – металл или электрод; ионы раствора в свободном виде или в виде комплексов диффундируют (перемещаются посредством диффузии к межфазной границе), входят в плотный слой Гельмгольца, то есть адсорбируются на поверхности электрода за счет электростатических сил; в слое Гельмгольца ионы принимают или отдают электрон; процесс переноса электронов, степень переноса заряда с электрода на реагирующую частицу или обратно определяется или зависит от электрического поля ДЭС. Образующиеся продукты реакции уходят в раствор (десорбируются с поверхности) или образуют на поверхности новую фазу, такой новой фазой являются: металлопокрытия (осадки металла), осадки оксидов или нерастворимых солей. С образованием новой фазы дальнейшее протекание процесса будет зависеть от свойств в этой фазе, в частности от диффузии образующихся частиц через слой фазы. В зависимости от соотношения коэффициента диффузии реагирующих частиц в слое фазы, дальнейшее протекание электродного процесса может концентрироваться или на внешней границе новой фазы (раствор электролита), или на внутренней границе, где образовавшаяся фаза соприкасается с электродом. В связи с этим любой электрохимический процесс включает стадии диффузии, адсорбции, переноса заряда, кристаллизации новой фазы. Скорость суммарного процесса будет определяться скоростью самой медленной стадии. Соответственно этому различают электрохимические процессы, протекающие с перенапряжением диффузии, с перенапряжением переноса заряда, перенапряжением кристаллизации. Процесс кристаллизации – частный случай гетерогенной химической реакции. Возможны реакции, скорость которых лимитируется химической реакцией, протекающей у поверхности электрода (перенапряжение гомогенной химической стадии). Кинетические характеристики каждой из лимитирующих стадий можно определить с помощью следующих электрохимических методов: метод гальваностатической кривой – потенциал, время (хронопотенциометрия); метод потенциостатических кривых – плотность тока, время (хроноамперометрия); метод потенциодинамических кривых (хроновольтамперометрия): особенностью метода является то, что изменение ρToка во времени регистрируется параллельно с изменением потенциала. Потенциал на электрод подается с определенной линейной скоростью.
Все эти методы могут использоваться в ячейках с вращающим дисковым электродом. Кинетические характеристики любого электрохимического процесса: ρтoкообмена – i0; константа скорости в стадии переноса заряда – к; энергия активации А; iд – предельный ток диффузии (гетеро); iд – предельный ток реакции (гомо); iкр – предельный ток кристаллизации.
Для них можно использовать метод переменного тока, который позволяет проводить измерения С – емкостной, R – омической составляющей импеданса электрода в условиях, близких к равновесным, в отсутствии внешней поляризации постоянным током, вблизи равновесного потенциала. Твердофазные процессы также характеризуются сложным механизмом, то есть включают несколько стадий: поверхностная диффузия (диффузия в твердой фазе), взаимодействие диффундирующих частиц на поверхности, с образованием зародышей новой фазы, участие их в процессе кристаллизации.
В последние годы накоплен большой экспериментальный материал, который показывает, что электроны могут переходить в раствор и там существовать длительное время в виде самостоятельных частиц. Присутствие электронов в растворе в сольватированном виде может значительно изменять структуру раствора и оказывать влияние на механизм поведения компонентов раствора в ДЭС. Это направление широко развивается, так как открывает возможности для создания принципиально новых технологий, получения новых материалов. Это направление – электронная электрохимия. В настоящее время с помощью различных физико-химических методов достаточно подробно изучена диффузия водорода в металлах и сплавах. Полученные данные способствуют развитию применения водорода в энергетике (топливные элементы и солнечные батареи), а так же радиотехнике и оптоэлектронике. Открытие металлической связи в водородном соединении металлов используется для разработки «элементов памяти», которые способны реагировать на внешние воздействия и восстанавливать свою форму после прекращения такого воздействия. Кроме того, благодаря открытию металлической связи развиваются «аккумуляторы Н2», которые представляют собой металлические сплавы, способные поглощать большие количества Н2, а при каком-либо внешнем воздействии выделять этот Н2 для практического применения (металлогидридные аккумуляторы).
ЛЕКЦИЯ № 12. Теоретическая электрохимия
1. Ассоциации в растворах электролитов. Понятие о теории сильных электролитов. Активность
При увеличении концентрации растворов электролитов создаются условия, когда за счет электростатического взаимодействия становится возможным образование новых соединений – ассоциатов. На вероятность образования ассоциатов указал Н. Бьеррум, им определено то минимальное расстояние между ионами, при котором становится возможным образование ассоциатов. В симметричных электролитах образуются нейтральные ионные пары. Эти ионные пары имеют определенное время жизни, т. е. можно говорить об ионном равновесии между ионной парой и теми ионами, которые составляют эти ионные пары. Различают несколько видов ионных пар, находящихся в растворе:
1) константная K+, An–;
2) гидратно (сольватно)-ионная пара K+(H2O)An–;
3) гидратно (сольватно)-разделенная пара K+(H2O)N An–;
4) ионные тройники K+An–K+, An–K+An–.
Образование ионных пар в растворе сказывается на величине проводимости раствора, причем появление и образование нейтральных ассоциатов снижает проводимость растворов электролитов.
Для сильных электролитов, когда степень ионизации велика, константа ионизации зависит от концентрации, так как при накоплении в растворе большого числа ионов сказывается их взаимное влияние. Когда растворитель обладает малой диэлектрической проницаемостью (величина, показывающая, во сколько раз ослабевают силы взаимодействия электрических зарядов при расположении этих зарядов в диэлектрике по сравнению с силами в вакууме), создаются условия для электростатического взаимодействия сольватированных ионов противоположного знака. При этом последние подходят друг к другу на близкое расстояние и образуют ионную пару – сложный агрегат, состоящий из двух противоположно заряженных ионов, окруженных молекулами растворителя, в котором электрические заряды взаимно компенсированы, это – ассоциация.
Параметр Бьеррума
где е – заряд электрона –16 x 10–19Кл;
к – константа Больцмана = 1.38 x 10–23Кдж/к;
Т – абсолютная температура;
Е – диэлектрическая проницаемость.
Ассоциация ионов – образование из противоположно заряженных ионов (в растворах электролитов) особого рода частиц-ассоциатов, в которых ионы удерживаются за счет электростатического взаимодействия их электрических зарядов в соответствии с законом Кулона. Процессы ассоциации ионов подчиняются закону действующих масс, термодинамическим соотношениям.
Простейшие ассоциаты – ионные пары, нейтральные или электрически заряженные, термодинамически устойчивые частицы, находящиеся в равновесии с простыми ионами.
Степень ассоциации ионов зависит от природы растворителя, электролита, температуры, концетрации раствора. Она возрастает с уменьшением диэлектрической проницаемости растворителя вследствие увеличения кулоновского притяжения ионов.
Ассоциация – объединение однородных частиц в растворе.
Сольватация – взаимодействие растворенного вещества с растворителем. Молекулярные группы, сольваты, образовавшиеся в результате взаимодействия, слой молекул растворителя, связанный с центральной частицей сольвата силами притяжения – сольватная оболочка. Наименьшее число молекул, удерживаемых в непосредственной близости от сольватированной частицы – координационное число сольватации. В зависимости от природы растворенного вещества, сольваты могут образовываться различными путями. Ион-дипольное взаимодействие – при растворении веществ с ионной структурой молекулы растворителя удерживаются около иона силами электростатического притяжения. Процесс гидратации – взаимодействие веществ с водой.
2. Термодинамика растворов электролитов. Типы ДЭС
На границе раздела фаз электрод – раствор происходит перераспределение зарядов, в результате которого у поверхности электрода накапливается избыток ионов какого-либо одного знака, в результате на поверхности возникает избыток зарядов противоположного знака. Такое пространство разделения избыточных зарядов позволяет ввести понятие ДЭС. Условно можно представить две воображаемые плоскости, которые проходят через центры тяжести избыточных зарядов в поверхностном слое на электроде и раствора у поверхности электрода.
Расстояние между плоскостями равно диаметру сольватированного комплекса (d). Таким образом, ДЭС можно рассматривать как плоский конденсатор:
D – диэлектрическая проницаемость, для Н2О = 80, d = 10–8 – расстояние между обкладками. Перераспределяемый заряд на границе раздела фаз имеет динамическое преобладание.
Согласно закону термодинамики, перенос вещества из одной фазы в другую характеризуется химическим потенциалом
μ = ΔGхим
μ зависит от концентрации частиц.
μ = μ0 +RTlnС,
где С – концентрация частиц, участвующих в реакции переноса;
μ0– стандартное значение потенциала при С= 1.
Согласно термодинамике, перенос вещества из одной фазы в другую происходит таким образом, что химический потенциал вещества действует до тех пор, пока μ1 = μ2 в обеих фазах.
Определяющимися ионами являются ионы Ag+, следовательно, если химический μ ионов Ag (Ме),
то, согласно уравнению Ле-Шателье, перенос ионов Ag+, в сторону раствора будет происходить с большей скоростью, чем в обратном направлении, в результате количество ионов Ag у поверхности будет увеличиваться, так как концентрация в растворе растет.
μAg+ = μ0 + RT lnCAg+.
Перенос происходит до тех пор, пока
Когда наступит равенство μ, скорость переноса в обоих направлениях через границу раздела фаз становится одинаковой.
Наступает равновесие; так как в переносе принимают участие заряженные частицы, то в этом случае говорят об электрохимическом равновесии. При установлении равновесия поверхность, с которой ушли Ag+, приобретает избыток отрицательного заряда, под действием его избыток положительных зарядов собирается в растворе у поверхности.
Возникновение избытка заряда приводит к возникновению скачка μна границе раздела фаз. Согласно представлению о плоском конденсаторе, скачок потенциала изменяется линейно с расстоянием от поверхности электрода. Емкость такого плоского конденсатора, когда ионная обкладка ДЭС состоит из катионов, составляет С = 20 МКФ/см2.
3. Современные подходы к описанию термодинамических свойств растворов электролитов
При теоретическом подходе к концентрированным растворам электролитов предпринимались попытки уточнить классическую модель теории Дебая – Хюккеля за счет учета следующих эффектов:
1) собственного объема ионов;
2) изменения диэлектрической проницаемости вблизи ионов вследствие диэлектрического насыщения растворителя;
3) изменения макроскопической диэлектрической проницаемости в объеме раствора в зависимости от концентрации и т. д.
Общий недостаток работ этого направления состоит в том, что в каждой из них учитывают только один или два из перечисленных эффектов.
Расхождение современных статических теорий наблюдается, в основном, в ходе функций распределения на малых расстояниях. Теоретический расчет потенциала взаимодействия частиц на малых расстояниях сложен и не может быть пока проведен однозначно, так как на таких расстояниях, наряду с кулоновскими силами, играют роль квантово-механические, дисперсионные и другие силы.
Г. Кеселером было развито специфическое взаимодействие ионов в растворах и показано, что некулоновские эффекты при сближении ионов проявляются вследствие десольватации ионов (при перекрытии сфер сольватации) и сольватации ионных пар как целого.
Термодинамические характеристики ион-молекулярных взаимодействий в растворах
Теория Дебая и Хюккеля позволила предсказать эффект выделения тепла при разбавлении растворов электролитов, вызванный тем, что при разбавлении уменьшается взаимодействие между ионами.
Характеристики
Химический потенциал
Средняя активность
Коэффициент активности характеризует работу перенесения иона из идеального газа в реальный.
Абсолютная активность
где МS– молярная масса растворенного вещества.
4. Термодинамические характеристики ионов в растворах электролитов
μi– химический потенциал иона.
где Δχизменение поверхностного потенциала данного раствора по сравнению с поверхностным потенциалом стандартного раствора;
аi– «реальная» активность иона.
где lnγi– экспериментально определенный реальный коэффициент активного иона.
ai = γi mi.
Поверхностная активность – способность вещества при абсорбции на границе раздела фаз понижать поверхностное натяжение. Адсорбция Г вещества и вызванное ею понижение поверхностного натяжения δсвязаны с концентрацией с вещества в фазе, из которой вещество абсорбируется на межфазовую поверхность, – уравнение Гиббса.
где дδ/ дC– мера способности вещества понижать поверхностное натяжение на данной межфазной границе, называется также поверхностной активностью.
5. Неравновесные явления в ионной системе
Равновесие в растворах электролитов всегда является динамическим, усредненным по времени, объему. Частицы раствора совершают хаотические движения, которые осуществляются периодическими перескоками с одного места на другое. В среднем эти перемещения частиц скомпенсированы так, что направленного макроскопического перехода ионов и диполей в условиях равновесия не происходит. Вызвать в растворе электролита неравновесные явления можно:
1) изменением активности растворенного вещества в одной части раствора по отношению к другой без изменения химического состава раствора;
2) наложением электрического поля, которое вызовет направленное перемещение заряженных частиц;
3) изменением состава раствора по отношению к равновесной концентрации возможных для данной системы веществ.
В первом способе количество перескоков данной частицы iв направлении уменьшения ее концентрации оказывается больше, чем количество перескоков этой частицы в обратном направлении. В результате этого возникает поток диффузии.
Во втором способе наложение электрического поля изменяет вероятность перескоков заряженных частиц по полю и против поля: у катионов количество перескоков по полю превышает количество перескоков против поля, у анионов – наоборот. Таким образом, в результате наложения электрического поля возникают потоки миграции катионов и анионов. Миграция ионов, составляющая основу электропроводности электролитов, сопровождает работу электрохимических систем.
Общий поток ионов j = jд + jм, jд – поток диффузии, jм– поток миграции.
Диффузионный потенциал – разность потенциалов, возникающая на границе двух растворов разных электролитов или двух растворов одного электролита, но разной концентрации.
Диффузия в твердых электролитах характеризуется тем, что с повышением температуры скорость диффузии возрастает.
Диффузия связана с механизмом образования вакансий и дислоцированных атомов. В результате колебаний около положения равновесия атомов, ионов, расположенных в узлах кристаллической решетки, некоторые из них, обладающие в данный момент избыточной энергией, могут покинуть свое положение равновесия и переместиться в соседние междоузлия. Ранее занимаемые ими места в решетке окажутся вакантными, кроме того, образуется соответствующее число дислоцированных атомов, такой процесс по Френкелю следует рассматривать как внутреннее испарение атомов твердого тела. Число вакансий, т. е. пустых мест в решетке, вообще может и не соответствовать числу дислоцированных атомов (атомов, расположенных в междоузлиях), так как вакансии могут образовываться на поверхности твердого тела в результате полного или неполного «испарения» поверхностных атомов. Каждой данной температуре соответствует определенное равновесное число вакансий, тем больше, чем выше температура. Наличие пустых мест в кристаллической решетке реального кристалла обеспечивает возможность процесса диффузии в твердых телах. Зависимость коэффициента диффузии от температуры:
D = D0(–EaRT),
где и – энергия активации процесса диффузии.
Диффузия в полупроводниках. С понижением температуры проводимость убывает, при высоких температурах проводимость приближается к проводимости металла. Концентрация носителей тока (электронов проводимости) в металле практически не зависит от температуры, а в полупроводниках носители тока сами возникают в результате теплового движения. В полупроводниках, благодаря сильной связи валентных электронов с ядрами, положение атомов такое, что нужно сообщить энергию ионизации. Такая энергия поставляется тепловыми колебаниями атомов решетки. Число атомов с энергией, равной или превышающей энергию ионизации, мало.
6. Равновесие в системе жидкость – жидкость
Равновесие жидкость – жидкость
В случае ограниченной взаимной растворимости компонентов в жидком состоянии в двухкомпонентной системе осуществляется равновесие двух жидких фаз. Явление образования двух жидких фаз называется расслаиванием или расслоением. Типы диаграмм состояния систем с расслаиванием приведены в литературе по физико-химическому анализу.
Взаимная растворяемость жидкостей при постоянном давлении зависит только от температуры. Рассмотрим случай возрастания растворимости с ростом температуры. При температуре больше критической обе жидкости смешиваются в любых соотношениях. Критические явления часто сопровождаются в момент перехода из двухфазного состояния в гомогенное образованием голубой опалесценции.
Согласно правилу В. Ф. Алексеева (1886 г.), при разделении соединительных линий фазовой диаграммы пополам точки деления ложатся на общую прямую, которая заканчивается в критической точке растворения (прямая еК). Это правило позволяет дополнить экспериментальные данные о взаимной растворимости жидкостей, а также найти состав в критической точке по известным значениям tкр. Правило Алексеева приближенно, наиболее точно оно при выражении состава в процентах.
Рассмотрим подробно наиболее распространенный тип систем с верхней критической температурой растворимости (ВКТР). Взаимную растворимость таких двухфазных систем изучают обычно визуально-политермическим методом, предложенным В. Ф. Алексеевым. Суть метода заключается в определении температуры перехода из расслоения в гомогенное состояние и обратно. Заготавливают ряд смесей определенного состава, помещают их по очереди в термостат (термостойкий стакан с водой или глицерином, снабженный термометром) и наблюдают изменение фазовых состояний системы с изменением температуры. При непрерывном встряхивании отмечают температуру, при которой мутноватая смесь становится прозрачной. Затем, охлаждая жидкость, отмечают температуру, при которой она вновь становится мутной (появление первых капелек второй фазы). Для удобства наблюдения за происходящими в смеси изменениями пользуются лампой-осветителем.
Повторяют опыт с той же смесью несколько раз, причем добиваются, чтобы температуры появления и исчезновения мути были достаточно близки (расхождения не превышали 0,5о). Среднее значение между ними считают за температуру перехода. Этот простой метод позволяет по полученным экспериментальным данным построить бинодальную кривую и, следовательно, определить составы равновесных фаз.
7. Понятие ДЭС. Модельные представления о строении ДЭС на границе раздела фаз
ДЭС – двойной электрический слой – тонкий поверхностный слой из пространственно разделенных электрических зарядов противоположного знака, образующихся на границе двух фаз.
Если погрузить металлическую пластину (электрод) в раствор соли данного металла, то может произойти один из двух процессов.
1. Пусть металл является активным восстановителем, т. е. окисляется, тогда из-за диполей воды, содержащихся в данном растворе, какая-то часть атомов металла оставляет свои электроны на электроде и из-за процесса гидратации в виде гидратированных ионов переходит в раствор по реакции.
Общий вид реакции
или, без учета гидратации ионов,
Этот процесс называется окислением. В результате него металлическая пластинка заряжается отрицательно, а катионы металла притягиваются к ней, и прилегающий к пластинке слой раствора заряжается положительно. На границе металл-раствор возникает ДЭС. Химически активные металлы как: Na, Mg, Al, Zn и др. имеют большие концентрации поверхностного раствора, состоящего из гидратированных катионов металла. При погружении в раствор своей соли любой концентрации происходит дополнительное растворение металла с образованием ДЭС, так как всегда концентрация поверхностного раствора всегда больше концентрации соли металла, и металл заряжается отрицательно.
2. Пусть металл является слабым восстановителем, тогда его ионы, содержащиеся в растворе соли, являются сильными окислителями. Некоторая часть ионов подходит к металлической поверхности и восстанавливается за счет свободных электронов, присутствующих в ней по реакции:
В результате процесса восстановления металлическая пластинка заряжается положительно и притягивает отрицательно заряженные частицы. При погружении малоактивных благородных металлов (Cu, Ag, Au и др.) в раствор соли наблюдается обратная картина, от первой: при любой достижимой концентрации, концентрация поверхностного раствора меньше концентрации соли металла, поэтому ионы металлов осаждаются на электроде, а в приэлектродном пространстве накапливается избыточный отрицательный заряд за счет анионов соли или ионов гидроксидной группы OH–. После достижения равновесной разницы потенциалов между металлом и раствором переход ионов в раствор прекращается.
Модельные представления о строении ДЭС на границе раздела фаз:
1) модель Гельмгольца;
2) модель Гуи, Чапмена;
3) модель Штерна;
4) модель Грэма;
5) модель современная.
Первая модель ДЭС открыта Гельмгольцем, он представлял ДЭС в виде двух обкладок плоского конденсатора, одна обкладка расположена непосредственно на поверхности электрода, вторая – в электролите.
d = диаметру молекул Н2О.
Так как все заряды сконцентрированы в двух плоскостях, то изменение потенциала по мере удаления от поверхности электрода Е0 будет описываться прямой линией.
Еа – величина электродного удаления от поверхности электрода потенциала.
Используя теорию конденсатора, Гельмгольц рассчитал величину заряда ДЭС и величину дифференциальной емкости ДЭС.
q – величина заряда = (D/4π2)Е0, С – дифференциальная емкость ДЭС = D/4π2, D – диэлектрическая проницаемость раствора, d – расстояние между обкладками конденсатора.
Теория Гельмгольца позволила объяснить ход электрокапиллярной кривой, рассчитать величину дифференциальной емкости ДЭС, хорошо совпадающую с экспериментально полученными данными. Наилучшая сходимость была получена для концентрированных растворов элементов, однако данная теория не объясняла зависимость плотности заряда и дифференциальной емкости ДЭС от состава электролита и концентрации компонента.
Недостатки теории Гельмгольца:
1) не учитывалось тепловое движение ионов в растворе;
2) не учитывался размер ионов;
3) не рассматривались процессы адсорбции на границе раздела фаз (электрод – электролит).
Ее применяют только к концентрированным растворам, не содержащим поверхностно-активные вещества (ПАВ).
Б. Гуи, Д. Чапмен учли тепловое движение в растворах электролитов.
Эта теория позволяет рассчитать плотность ρзаряда ДЭС и величину дифференциальной емкости С, они учли влияние концентрации, но рассчитанные значения дифференциальной емкости С, но они меньше сходятся с экспериментально полученными результатами. Теория Гуи, Чапмена применима к разбавленным растворам электролитов.
Недостатки:
1) не учитываются размеры ионов;
2) не учитывается явление адсорбции на границе раздела фаз.
В. Штерн учел, что в электролитах наблюдается электростатическое взаимодействие между ионами, тепловое движение компонентов электролита и возможное специфическое взаимодействие компонентов электролита с поверхностью электрода.
Он соединил теорию Гельмгольца с теорией Гуи, Чапмен, в результате ДЭС представлялся состоящим из двух частей:
1) плотной части Гельмгольца;
2) диффузной части по модели Гуи, Чапмена.
За счет адсорбции ПА компонента может происходить перезаряд поверхности. Штерн считал, что адсорбция происходит на границе плотной и диффузной части ДЭС. Эта граница называется плоскостью Гельмгольца.
Теория Штерна легла в основу современных представлений и развивалась в работах Грема, Фрумкина, Эршлера, Есина и др.
Недостатки:
1) не учитывал дискретность зарядов;
2) величина емкости, рассчитанная по модельным представлениям Штерна, не соответствовала экспериментально полученным результатам.
Г. Греем рассмотрел возможность адсорбции ПА анионов внутри плотной части ДЭС, он ввел понятие внутренней и внешней плоскости Гельмгольца.
Адсорбция анионов происходит на внутренней плоскости Гельмгольца.
Недостаток: рассматривал адсорбцию только анионов и не учитывал дискретность зарядов.
О. А. Есин рассмотрел дискретность зарядов и показал, что ионы, образующие внутреннюю и внешнюю плоскости Гельмгольца, взаимодействуют между собой, образуя диполи.
Указанное взаимодействие влияет на величину диффузной емкости с ДЭС. О. А. Есин рассмотрел возможность адсорбции на внутренней плоскости Гельмгольца как катионов, так и анионов.
8. Проводники первого и второго рода
Проводники – вещества, проводящие электрический ток благодаря наличию в них большого количества зарядов, способных свободно перемещаться (в отличие от изоляторов). Они бывают I (первого) и II (второго) рода. Электропроводность проводников I рода не сопровождается химическими процессами, она обусловлена электронами. К проводникам I рода относятся: чистые металлы, т. е. металлы без примесей, сплавы, некоторые соли, оксиды и ряд органических веществ. На электродах, выполненных из проводников I рода, происходит процесс переноса катиона металла в раствор или из раствора на поверхность металла. К проводникам II рода относятся электролиты. В них прохождение тока связано с химическими процессами и обусловлено движением положительных и отрицательных ионов.
Электроды первого рода. В случае металлических электродов первого рода такими ионами будут катионы металла, а в случае металлоидных электродов первого рода – анионы металлоида. Серебряный электрод первого рода Ag+/Ag. Ему отвечает реакция Ag+ + e- = Ag и электродный потенциал
EAg+ /Ag = Ag+ / Ag+b0lg a Ag+.
После подстановки численных значений Е 0 и b0 при 25 oС:
Примером металлоидных электродов первого рода может служить селеновый электрод Se2–/Se, Se + 2e- = Se2; при 25 oС ESe2–/Se0 = –0,92 – 0,03lg a Se2–.
Электроды второго рода – полуэлементы, состоящие из металла, покрытого слоем труднорастворимого соединения (соли, оксида или гидроксида) и погруженного в раствор, содержащий тот же анион, что и труднорастворимое соединение электродного металла. Схематически электрод второго рода можно представить так: АZ–/MA, M, а протекающую в нем реакцию – МА + ze = М + АZ–. Отсюда уравнением для электродного потенциала будет:
Каломельные электроды – это ртуть, покрытая пастой из каломели, и ртуть, находящаяся в контакте с раствором KCl.
Cl– / Hg2Cl2, Hg.
Электродная реакция сводится к восстановлению каломели до металлической ртути и аниона хлора:
Потенциал каломельного электрода обратим по отношению к ионам хлора и определяется их активностью:
При 25 оС потенциал каломельного электрода находят по уравнению:
Ртутно-сульфатные электроды SO42 –/Hg2SO4, Hg аналогичны каломельным с той лишь разницей, что ртуть здесь покрыта слоем пасты из Hg и закисного сульфата ртути, а в качестве раствора используется H2SO4. Потенциал ртутно-сульфатного электрода при 25 oС выражается уравнением:
Хлорсеребряный электрод представляет собой систему Cl–/AgCl, Ag, а его потенциалу отвечает уравнение:
ECl– /AgCl, Ag = E0Cl–/AgCl, Ag –b lg aCl–
или при 25 оС:
ECl–/AgCl, Ag = 0,2224 – 0,0592 lg a Cl–.
9. Электроды сравнения
Электроды сравнения – электроды, используемые при измерении электродных потенциалов в паре с используемым электродом. Электродный потенциал – скачок потенциала на границе металл-раствор. Он определяется: природой металла, раствора, концентрацией, температурой. Для сравнения электродных потенциалов нужны стандартные условия: t = 25 °С = 298 К; Р – 1 атм, одномолярный раствор. Абсолютное значение электродного потенциала измерить нельзя. Поэтому измеряют разность потенциалов между данным электродом и электродом сравнения, потенциал которого принимают равным нулю. Часто используют водородный электрод, изготовленный из губчатой платины с сильно развитой поверхностью (платиновая чернь), опускают в раствор H2SO4 – серной кислоты с активностью ионов водорода, равной единице. При этом через раствор пропускается газообразный водород под давлением, который затем адсорбируется платиной. Относительно потенциала водородного электрода все металлы располагают в ряд напряжений, установленный электрически Н. Н. Бекетовым, взаимному вытеснению металлов в зависимости от величины и знака стандартного электродного потенциала. Существуют и другие электроды сравнения: каломельный, хлорсеребряный и другие, в зависимости от различных методов. Конструктивное оформление электрода сравнения разнообразно. Например, для полярографического метода электроды сравнения должны иметь большую поверхность во избежание поляризации их при работе под током.
ЛЕКЦИЯ № 13. Электрохимическая кинетика
1. Основные кинетические характеристики и методы их расчетов
i0 – ток обмена – кинетическая характеристика равновесия между электродом и раствором при равновесном значении электродного потенциала. Токи обмена относят к 1 см2 поверхности раздела электрод-раствор.
α– коэффициент переноса заряда – характеризует степень влияния электрического поля электрода на энергию активации электрохимической стадии и определяет симметрию катодного и анодного процессов, зависит от формы потенциальных кривых.
α≈ 0,5.
При одном и том же отклонении потенциала электрода от равновесного значения скорости реакции результативная плотность тока будет тем больше, чем выше i0. Ток обмена i0 зависит от природы электрохимической реакции, материала электрода и состава раствора.
Константа скорости – скорость реакции при единичных концентрациях.
Скорость прямой реакции:
где k – константа, зависящая от свойств системы и способа выражения скорости процесса;
Cox – концентрация реагирующих частиц;
Ea – энергия активации разряда в отсутствии скачка потенциала между металлом и раствором.
Скорость обратной реакции
где CRed – концентрация частиц Red (восстановление продуктов);
Еa– энергия активации реакции ионизации при скачке потенциала между металлом и раствором, равным нулю.
Энергия активации электрохимического процесса зависит от величины электродного потенциала, природы ее непосредственных участников и электрода.
Энергия активации при постоянном перенапряжении η – эффективная энергия активации. Если энергия активации не зависит от перенапряжения, то ее появление замедляет диффузию.
Метод расчета величин αи i0 основан на явлении редоксикинетического эффекта заключается в том, что при наложении переменного тока на электрод его потенциал смещается в ту или иную сторону на некоторую величину от первоначального значения. Это смещение – редоксикинетический потенциал ψ. Связь редоксикинетического потенциала ψ с кинетическими параметрами а и i0 такая: если наложить переменный ток на электрод, находящийся в равновесии с соответствующими ионами в растворе, то за время катодного полупериода он окажется заполяризованным катодно, причем зависимость между ηи iпри условии замедленности стадии разряда будет передаваться уравнением
При достаточном удалении от состояния равновесия
Из последнего выражения следует, если α= 0,5, то ψ = 0, чем сильнее αотклонена от 0,5, тем больше ψ.
Энергия активизации – энергия, представляющая собой минимальную энергию, достаточную для осуществления акта химической реакции.
2. Уравнения электрохимической кинетики, пределы их применимости
1-й закон Фарадея устанавливает прямую пропорциональность между количеством прошедшего через систему электричества и количеством прореагировавшего вещества.
Δm = kэJt = kэq, (1)
где Δm – количество прореагировавшего вещества;
k – коэффициент пропорциональности;
q – количество электричества, равное произведению силы тока I на время t.
Если q = Jt = 1, то Δm = kэ – количество вещества, прореагировавшего в результате протекания единицы количества электричества.
kэ – электрохимический эквивалент.
2-й закон Фарадея устанавливает связь между количеством прореагировавшего вещества при пропускании данного количества электричества и его природой.
По этому закону, при постоянном количестве прошедшего электричества массы прореагировавших веществ относятся между собой, как их химические эквиваленты А:
Если количество электричества равно F, числу Фарадея, то Δm1 = Fkэ1 = A1, Fkэ при q = 1F, то
Уравнение (3) позволяет объединить оба закона Фарадея в виде одного общего закона, по которому количество электричества (1F = 96500k) всегда изменяет электрохимически массу любого вещества, независимо от его природы.
Законы Фарадея – основные законы электролиза, согласно которых, количество вещества, выделившегося при электролизе, прямо пропорционально его химическому эквиваленту и количеству прошедшего электричества.
Уравнение Нернста
Е0 – равновесный стандартный потенциал.
где С0 – стандартная концентрация раствора;
С – любая концентрация в нестандартных условиях, С = С0 x Е = Е0 , т. е. в стандартных условиях С = C0 = 1 моль.
Для окислительных веществ
1-й закон Фика:
где dc/dx – градиент концентрации;
s – площадь, через которую происходит диффузия.
Δ – коэффициент диффузии cм2 x c-1, показывает число частиц, продиффундировавших за 1 с через поперечное сечение раствора площадью 1 см2, dt – время диффузии, dm – число продиффундировавших частиц.
где Тк – коэффициент внутреннего трения;
D – коэффициент диффузии.
Первый закон Фика относится к процессу стационарной диффузии, сходен с закономерностями переноса тепла из электричества.
Если диффузионный поток не изменяется с течением времени, это называется стационарной диффузией.
Диффузия – самопроизвольно протекающий в системе процесс выравнивания концентрации молекул, ионов, частиц под влиянием теплового хаотического движения.
Основное уравнение электрохимической кинетики
ik = ia = i0,
где i0 – ток обмена,
(окислительно-восстановительные реакции).
При катодной поляризации на электроде через систему протекает ik преимущественно, если поляризация не слишком велика, то суммарная скорость процесса равна:
i = ik – ia,
для реакции (1) катодные и анодные токи будут равны:
где Z – количество электронов, участвующих в реакции;
F – число Фарадея;
к – const скорости;
Сox, Cred – концентрация окислительной и восстановленной форм реагентов;
ΔGK – энергия активации катодного процесса;
ΔGA – энергия активации анодного процесса.
Энергия активации зависит от величины накладываемого потенциала, в то же самое время эта энергия распределяется между прямой и обратной реакцией в соответствии с коэффициентом переноса – а, т. е.
υ = υпр – υоб.
Коэффициент переноса α– доля энергии электрического поля в ДЭС, которая приходится на прямую и обратную реакции.
α– коэффициент переноса для катодной реакции;
(1 – α) – для анодного процесса (коэффициент переноса).
ΔGk = ZFE α, (4)
ΔGA = ZFE(1 – α) (5)
С учетом уравнений (4), (5) уравнения (2), (3) примут следующий вид:
Различие знаков у электрона объясняется тем, что катодная поляризация («–») ускоряет прямую реакцию и замедляет обратную реакцию.
Введем в уравнение (8) плотность тока обмена – i0.
Вместо потенциала введем перенапряжение:
полное уравнение поляризационной кривой.
Вывод из уравнения (10):
1) при равновесном потенциале, когда ток равен нулю, уравнение (10) преобразуется в уравнение Нернста:
2) при малых величинах η:
При сдвижении потенциала от равновесного (59 mВ);
η = a + b ln i– уравнение Тафеля в простом виде при замедлении стадии переноса заряда.
Величина i0 (тока обмена) и α(коэффициента переноса) – основные кинетические параметры стадии переноса заряда (q). Они могут быть определены из экспериментальных измерений, для этого на исследуемом электроде снимают зависимость η– i или Ei – i.
Поляризационная кривая судит о коррозионной стойкости металлов.
Перестраиваем поляризационную кривую в координаты:
Определяем const а и bв уравнении Тафеля, определяем b:
Из коэффициента bнайдем а, после подставим в а и найдем i0.
Перенапряжение Н2 (водорода).
Источник выделения Н2 – Н2SO4 →Н++ НSO4–
Источник выделения Н2 – Н2О → Н++ ОН-.
В рН < 7 Н2 выделяется по реакции.
Н2 всегда выделяется в потенциалах более отрицательных, чем равновесный потенциал, то есть с перенапряжением.
Суммарный процесс выделения водорода состоит из следующих стадий:
1) доставка к поверхности катода реагирующих частиц Н3О+;
2) разряд Н3О+ с образованием Надс
3) удаление выделяющегося Надс с поверхности электрода может происходить тремя путями:
а) каталитическая рекомбинация
где Кat – материал катода;
б) электрохимическая десорбция – удаление Н2 происходит на уже адсорбированных атомах
в) эмиссия включает две стадии:
Для Pt замедлена стадия а), для других металлов (Hg, Pb) – стадия разряда, Н+ – самый подвижный.
3. Кинетические особенности электроосаждения металлов и сплавов
Процесс электроосаждения металлов, сплавов протекает через последовательность стадий: диффузия катионов металлов к поверхности электрода из объема раствора, вхождение катионов в ДЭС (двойной электрический слой), потери сольватной оболочки, переход катионов в состояние адсорбции атома, полный перенос заряда с поверхности электрода на разряжающийся ион или адсорбированного атома (ад. атома) и образование зародышей металлов, рост зародышей и заполнение поверхности новой фазы в виде сплошного слоя, рост слоя осадка в толщину.
Процесс электровыделения не зависит от состояния поверхности электрода, в частности, большое влияние на η(перенапряжение) процесса оказывает концентрация вакансий на поверхности электрода. Кристаллическая решетка каждого металла содержит определенное количество равновесных вакансий (свободных незанятых узлов в кристаллической решетке). Наличие таких пустот в структуре поверхностного слоя облегчает образование ад.атомов, так как в местах вакансий имеет место более сильное энергетическое воздействие кристаллической решетки на образующиеся атомы новой фазы. После заполнения этих активных мест начинается рост зародышей, т. е. образование скоплений атомов, которые постепенно заполняют всю поверхность. С другой стороны, скорость реакции электровыделения металлов зависит от состояния катионов этого металла в растворе. В растворе катионы находятся в сольватированном виде или в виде комплексов. Разрушение сольватной оболочки происходит на границе плотного слоя Гельмгольца с диффузной частью ДЭС. Таким образом, реакции разряда, протекающие в плотном слое Гельмгольца, энергетически возможны только в том случае, если ионы металла преодолевают потенциальный барьер. Высота потенциального барьера, т. е. величина энергии, которую ионам в растворе нужно преодолеть, чтобы попасть из раствора в плотный слой Гельмгольца, может быть различной, и определяется она природой растворителя, лигандов, прочностью связей в комплексах.
Пример:
(заряд комплекса не меняется, так как молекула нейтральна).
Сама стадия переноса зарядов также протекает стадийно
Анионные комплексы наиболее прочные, и последняя стадия состоит из процесса распада до свободного иона на поверхности электрода в слое Гельмгольца. Это обусловлено тем, что анионы, обладающие высокой поверхностной активностью, связываются с поверхностью электрода и оказывают влияние на распределение заряда в ДЭС.
Итак, помимо диффузии в объеме раствора, диффузии ад. ионов, ад. атомов по поверхности, стадий переноса заряда, образования зародышей и роста зародышей в сплошной слой (стадия кристаллизации), на скорость реакции могут оказывать влияние также реакции разложения комплексов в растворе, гомогенная химическая стадия, предшествующая стадии разрядов, и гетерогенная химическая стадия на поверхности электродов. Скорость реакции определяется концентрацией потенциал-определяющих частиц в растворе; концентрация потенциал-определяющих частиц зависит от состояния ионов. Состояние ионов в растворе определяется энергией взаимодействия с молекулами растворителя и лигандами. Потенциал электрода определяется активностью ионов раствора. В случае твердых металлических электродов активность самого металлического электрода не сказывается на длительности процесса и на величине скорости потенциала электродов (принято считать α твердой фазы = 1). Если металл растворен в ртути (Hg), то в этом случае i зависит от α металла фазы в матрице электрода
Анодные процессы
Ионизация металла (с растворимыми анодами)
С нерастворимыми анодами – реакция выделения кислорода.
При повышенных анодных плотностях тока растворимые аноды могут пассивироваться, на поверхности этих анодов образуются фазовые пленки, которые могут быть как токопроводящими, так и непроводящими, в последнем случае ток будет проходить через поры, если пленка не сплошная. Во всех случаях при пассивации анода анодный потенциал будет повышаться, что приведет к изменению анодных реакций и к изменению валентности металла.
4. Влияние природы растворителя на скорость электрохимических реакций
Замена одного растворителя на другой скажется на каждой из стадий электрохимического процесса. В первую очередь это отразится на процессах сольватации, ассоциации и комплексообразования в растворах, скажется на стадии диффузии, на скорости процесса разряда ионизации. Изменения в объеме раствора электролита, связанные с процессами сольватации, ассоциации, скажутся на скорости доставки вещества к поверхности электрода и на скорости разряда ионизации. Влияние природы растворителя на стадии разряда ионизации проявляется изменениями константы скорости реакции, коэффициента переноса. Например, при электровосстановлении кадмия из растворов с различными растворителями были получены следующие величины для константы скорости и коэффициента переноса α– доли энергии (табл. 7).
Таблица 7
Получение величины для константы скорости и коэффициента переноса
Объяснение изменений кинетических параметров процесса состоит в следующем:
1) изменяется строение ДЭС;
2) изменяется адсорбционная способность разряжающихся частиц;
3) разряжающиеся ионы имеют различную сольватную оболочку.
Для объяснения влияния природы растворителя на скорость реакции в объеме раствора была использована теория «Абсолютных скоростей реакции». Основным моментом данной теории является введение понятия «активированный комплекс». Рассмотрим изменение ΔG (свободная энергия Гиббса) при замене одного растворителя на другой (рис. 12).
Рис. 12. Энергетические профили реакции. А – исходное энергетическое состояние для реагента, участвовавшего в реакции, В – энергетическое состояние продуктов реакции, ≠– активированный комплекс.
Для того чтобы прошла реакция в исходное состояние и перешла в состояние активированного комплекса, требуются затраты энергии – Еа. Энергетический профиль, описанный кривой I, соответствует состоянию, когда исходное вещество и активированный комплекс не сольватированы. Энергия, необходимая для превращения вещества А в вещество В для реакции: F = ΔGI≠. При замене растворителя допустим вариант (а): происходит сольватация активированного комплекса – кривая II. В этом случае наблюдается уменьшение Еа процесса на величину ΔGII≠. При сольватации исходного реагента (вариант б) – кривая III, происходит увеличение Еа процесса на величину ΔGIII≠.
5. Электроосмос
Электроосмос – перенос жидкости по отношению к граничащей с ней неподвижной твердой поверхностью при приложении ЭДС (электродвижущей силы). Электроосмос возможен только в системах с твердой дисперсной фазой.
Электрокинетические процессы происходят в тех случаях, когда одна фаза диспергирована в другой; к их числу относится электрофорез – движение взвешенных твердых частиц внутри жидкости. При наложении электрического поля наблюдается электроосмос – движение жидкости относительно твердого тела. Электрокинетические явления – эффекты, связанные с относительным движением двух фаз под действием электрического поля, а также с возникновением разности потенциалов при относительном смещении двух фаз, на границе между которыми существует ДЭС. Чаще всего электрокинетические явления наблюдаются в диспергированных системах.
Электроосмос (электроэндоосмос) – движение жидкостей (или газов) через капилляры, твердые пористые диафрагмы и мембраны, а также через слои очень мелких частиц под действием внешнего электрического поля. Все электрокинетические явления имеют общий механизм и связаны с существованием на границе раздела фаз ДЭС. Под действием внешнего электрического поля, направленного вдоль границ раздела, возникает относительное перемещение противоположно заряженных обкладок ДЭС, что и приводит к относительному движению фаз. С другой стороны, движение одной из фаз по отношению к другой, вызванное механической силой, приводит в относительное движение также обкладки ДЭС и тем самым вызывает появление разности потенциалов в направлении движения фаз. Электроосмос при экспериментальном исследовании обычно осуществляют наложением разности потенциалов на жидкость с двух сторон капилляра или пористой диафрагмы. Поддерживая давление с обеих сторон одинаковым и измеряя в этих условиях количество протекающей в единицу времени жидкости, легко определить скорость электроосмоса.
Электроосмос и электрофорез используются при обезвоживании и очистке различных материалов, нанесении на непроводящие материалы покрытий из каучука, отходов кожи и т. п., также при пропитке тканей огнестойкими веществами, определении состава и разделении энзимов, белков, вирусов и других сложных систем. Исследованиями Г. Видемана в 1852 г. было установлено, что количество жидкости, прошедшей через капилляры пористой диафрагмы, пропорционально силе тока и при постоянной силе тока не зависит от площади сечения или толщины диафрагмы. Это явление было названо электроосмосом.
Наличие у частиц дисперсных систем электрического заряда открыто в 1808 г. Ф. Ф. Рейсом в МГУ. Он показал, что при наложении разности электрических потенциалов на электроды, опущенные в заполненные водой стеклянные трубки, воткнутые в кусок сырой глины, жидкость в трубке с положительным полюсом мутнела, а в трубке с отрицательным полюсом вода оставалась прозрачной. Это указывало на то, что частицы глины переносятся к положительному полюсу с постоянной скоростью. Эта скорость тем больше, чем выше приложенная разность потенциалов и диэлектрическая проницаемость среды, и тем меньше, чем больше вязкость среды. Перенос частиц в электрическом поле – электрофорез.
6. Электрокапиллярные кривые
Изменение состава электролита и изменение компонентов в электролите изменяют электрокапиллярные кривые. Форма электрокапиллярной кривой зависит от состава электролита и концентрации активных компонентов в составе электролита. Зависимость формы электрокапиллярной кривой от состава электролита связана с процессами адсорбции на границе раздела фаз (рис. 13). Присутствие в электролите ПА (поверхностно-активные) анионов приводит к смещению потенциала точки нулевого заряда в область более отрицательного значения и некоторому снижению max электрокапиллярной кривой.
В присутствии NaJ, NaCl происходит изменение хода электрокапиллярной кривой.
Кривые 2 и 3 – электрокапиллярные кривые, снятые в электролитах, содержащих ПА анионы: J-, Cl–. В области наиболее низких электродных потенциалов все три электрокапиллярные кривые совпадают, так как при указанных потенциалах наблюдается десорбция ПА анионов. В присутствии ПА катионов электрокапиллярные кривые имеют вид:
Рис. 13. Кривые 2, 3 в присутствии ПА катионов.
Наличие в элементе ПА органических веществ приводит к снижению max электрокапиллярной кривой (рис. 14).
Рис. 14. Кривая 2 – с добавками ПАВ (поверхностно-авктивныхвеществ).
Молекулярный тип – не дипольные молекулы 2 – с добавками ПА органическими.
Электрокапиллярная кривая – исходная кривая, дифференцируя ее, определяем емкость ДЭС.
7. Электрохимическое перенапряжение (перенапряжение переноса заряда)
1. Вывод уравнения полной поляризационной кривой.
2. Перенапряжение при выделении Н2.
3. Перенапряжение при выделении О2.
Если на электроде замедлена стадия присоединения или отдачи электронов, то возникающее перенапряжение – перенапряжение переноса заряда (перенапряжение перехода – электрохимическое перенапряжение).
Теория разряжения для реакции выделения Н2 на катоде:
Стадия переноса электрона из-за построения новой кристаллической решетки затруднена.
8. Факторы, влияющие на перенапряжение водорода. Перенапряжение кислорода
Факторы, влияющие на ηН2:
1) ρтока (плотность тока). Зависимость от плотности тока описывается уравнением Тафеля;
2) природа материала катода – ряд по возрастанию η, η– перенапряжение.
В уравнении Тафеля const a характеризует зависимость ηот природы материала катода, а константа b отражает зависимость от плотности тока.
В классическом варианте b – 0,12В, а – меняется в широких пределах, из-за разных металлов и разных катодных взаимодействий с Н2.
а – 0,01…1,0 В, чем больше а, тем большеη Н2. Большим η Н2 обладают: Hg, Pb, Zn, низким ηН2 – Pt, средним ηН2 – Fe, Co, Ni;
3) состав раствора. Наибольшее ηв рН = 7, а в рН < 7 η меньше. В растворе могут быть ПАВ, они влияют на величинуη, включаются в плотную часть ДЭС.
Уравнение ηв присутствии ПАВ:
где ψ– потенциал плотной части ДЭС;
4) температура. С ростом температуры ηуменьшается.
Перенапряжение кислорода
Кислород выделяется на аноде при потенциалах более положительных, чем равновесный.
в щелочном растворе,
в нейтральном, кислом растворе.
Перенапряжение О2 зависит от ρт (плотность тока), в соответствии с уравнением Тафеля. В ряду металлов, расположенных по мере возрастания перенапряжения Н2, перенапряжение О2, наоборот, уменьшается. При увеличении температуры ηО2 снижается.
Когда на металле выделяется кислород, то он сразу же окисляет металл, и поэтому дальнейшее выделение кислорода уже проходит на окисленной поверхности.
ЛЕКЦИЯ № 14. Применение теоретической и прикладной электрохимии
1. Прикладная электрохимия
Прикладная электрохимия – часть электрохимии, которая рассматривает электрохимические реакции с точки зрения применения их для практических целей – получения электрической энергии, нанесения металлических покрытий или получения целевых продуктов.
По современным прогнозам, электрохимия должна играть важную роль в энергетике будущего. После овладения управляемой термоядерной реакцией возникает проблема разумного использования получаемой энергии, в связи с этим большое значение отводится водородной энергетике. Энергия термоядерных электростанций будет, в основном, расходоваться на разложение Н2О. Получаемый таким путем Н2 может быть использован как экологически чистый теплоноситель для отопления городов, для приведения в движение автомобилей. Электрохимический метод используют для очистки сточных вод с выделением Cu, Zn, Ag и других, процесс электродиализа – для опреснения вод.
2. Электрохимия углерода
В настоящее время углерод, благодаря своей слоистой структуре в виде графита, широко используется для синтеза соединения внедрения графита, который, в свою очередь, нашел применение в литиевом источнике тока (аккумуляторе), используется в науке, технике. Наряду с Сгр и его производными, в последние годы ученые и техники занялись разработкой и получением фуллерена (С60, С70). С60 – имеет шарообразную полую структуру, С70 – эллипсообразную. Они построены из гексогональных и пентагональных ячеек.
Эти соединения способны поглощать щелочные, редкоземельные металлы, фторопроизводные. Эти вещества исследуются сейчас во всех отраслях науки и техники, оказывают активирующее действие.
3. Биоэлектрохимия
Изучает структуру и свойства мембран живых клеток, механизм переноса ионов через мембрану, природу скачка потенциала на мембране живой клетки, механизм передачи потенциала вдоль нервного волокна. Знания механизма работы клеточной мембраны позволят разработать различные приборы, работающие по принципу работы живой клетки. В настоящее время известны различные искусственные органы. Электрические угри – микроэлектростанции со скоростью, большей в 1000 раз (чтобы заменить атомные электростанции), бионика (особенности безошибочных перелетов птиц, сверхчувствительного слухового, зрительного нерва).
4. Стохастические процессы и самоорганизующиеся системы
Стохастические процессы и самоорганизующиеся системы являются предметом изучения электрохимической синергетики. Такие процессы имеют место во всех областях: переход от ламинарного к турбулентному процессу, электроосаждение металлов, колебательное явление с пассивацией металла. В основе синергетики лежат законы неравновесной термодинамики, так как колебательные явления обнаруживаются все больше.
5. Исследование явления высокотемпературной сверхпроводимости в оксидах сложного состава
В настоящее время наиболее изучены оксиды на основе Cu и Bi, в состав оксидов, помимо Cu, Bi, входят щелочно-земельные металлы – B a, C a, Sr, р.з.м. (редкоземельные) – лантаниды, Ir, известны соединения, содержащие Tl, (Cu, Bi, Tl, Pb) – металлы, способные проявлять переменную валентность. Переход этих металлов из одного валентного состояния в другое в структуре оксидов может привести к тому, что при некоторой критической температуре, близкой к температуре жидкого азота, вещества подобного типа теряют способность сопротивляться пропусканию электрического тока. Электрический ток может мгновенно возрастать в тысячи и десятки тысяч раз. Это явление получено в настоящее время при изготовлении проводов для высоковольтных передач, на транспорте. Широкое практическое использование явления сверхпроводимости затруднено в связи с тем, что эти вещества гигроскопичны и легко теряют свое свойство при поглощении воды. В связи с этим ведутся поиски новых технологий получения этих веществ. Открытие ВТСП послужило началом для развития нового направления низкотемпературной электрохимии – криоэлектрохимии.
6. Моделирование электрохимических процессов
Моделирование электрохимических процессов состоит в следующем. На основе системы уравнений, лежащих в основании какого-либо электрохимического металлического исследования, составляется программа для исследуемого электрохимического процесса с учетом предполагаемого механизма этого процесса и лимитирующих стадий. Задаются исходные параметры (i, потенциал, t, c, η, коэффициент переноса заряда) и с помощью компьютера проводится расчет.
7. Метод гальваностатических кривых
В этом методе анализируется зависимость Е, t при заданной i.
Рис. 15.1, 3 – резкое изменение потенциала, где наступает заряжение ДЭС (изменение заряда поверхности); ΔE/Δt– угловой коэффициент наклона, по нему можно рассчитать емкость ДЭС.
Для этого необходимо кривую записывать с помощью осцилирования, так как заряжение ДЭС происходит в течение тысячных долей секунды. В обычных условиях прибора КСП-4 кривую можно зарегистрировать с точностью до 0,1 с, определяемую по угловому коэффициенту; емкость является поляризационной емкостью (псевдоемкость). Она характеризует количество адсорбированных частиц на электроде, которые вступают в электрохимическую реакцию. Потенциал начала реакции, где первая дуга переходит во вторую – Еa. Участок 2 характеризует время протекания электрохимической реакции. Из точек пересечения касательных опускаем перпендикуляр и находим отрезок, τ – переходное время процесса, i x τ = Q– количество образовавшегося продукта. Можно на основе определения переходного времени процесса при различных плотностях тока анализировать зависимость τ от i. Для замедленной стадии диффузии, лимитирующей скорость суммарного электрохимического процесса, зависимость между переходным временем и плотностью тока:
F – число Фарадея;
С0 – объемная концентрация ионов в растворе;
D – коэффициент диффузии.
В случае замедленной диффузии
(зависит только от концентрации раствора) по угловому коэффициенту наклона прямой можно рассчитать коэффициент диффузии.
Знание зависимости переходного времени от i позволяет определить const скорости химической стадии и Кр; если электрохимическая реакция лимитируется замедленной предшествующей химической стадией то например: при катодном выделении Н2
k2 – const молизации, kр = k1/k2.
τ в химической стадии будет меньше ∑τ на величину, определяемую const скорости замедленной химической стадии.
Кроме того, определение переходного времени позволяет графически находить адсорбцию веществ, участвующих в процессе. Количество электричества, определяемое длиной задержки на Е, t кривых, складывается из количества электричества, которое идет на протекание электрохимической реакции и может быть определено через долю τ, связанную с диффузией вещества к поверхности элект-рода и с адсорбцией вещества на электроде
iτ = iτд+ iτадс.
При высоких плотностях тока доля электричества, которое тратится на электрохимическое превращение диффундирующих частиц, → 0.
iτ ≈ iτадс, iτадс = Г
где Г – величина адсорбции.
Существует несколько механизмов протекания электрохимических реакций с участием адсорбированных частиц:
1) сначала в реакцию вступают частицы, адсорбированные на поверхности электрода, а потом те, которые подходят к поверхности за счет диффузии – «сначала адсорбат»;
2) «адсорбат потом» – сначала электрохимическому превращению подвергаются диффузионные частицы, а затем те, которые адсорбируются на поверхности;
3) выполняется в тех случаях, когда поверхностная концентрация реагирующих частиц и их концентрация у поверхности подчиняется уравнению линейной изотермы адсорбции;
4) когда соотношения скоростей восстановления адсорбированных частиц и частиц диффундирующих из объема раствора, их концентрация не зависит от времени:
ЛЕКЦИЯ № 15. Третий закон термодинамики
Понятие химического сродства. Известно, что многие вещества реагируют друг с другом легко и быстро, другие вещества реагируют с трудом, а третьи – не реагируют. Исходя из этого, вывели предположение, что между веществами существует какое-то химическое сродство.
1-е предположение – мерой химического сродства была скорость реакции.
2-е предположение – М. Бертло и Х. Томсон высказали, что мерой химического сродства является тепловой эффект.
3-е предположение – max А (Вант-Гофф). Если max А > 0, то химическое сродство между веществами существует, и реакция протекает слева направо. Если Аmax< 0 →, то химического сродства между веществами нет, и реакция протекает справа налево. Если Аmax= 0, то реакция протекает и туда, и обратно. На основе этого создавался третий закон термодинамики; М. Бертло и Х. Томсон, изучая поведение термодинамических систем при низких температурах, в 1906 г. обнаружили, что при низких температурах между веществами существует так называемое химическое сродство, которое они определили как тепловой эффект, ими было установ-лено, что тепловой эффект Qv – Аmax в конденсированных системах при низких температурах, где Аmax – максимальная работа.
но на самом деле это не max, если исходить из уравнения Гельмгольца.
Для того, чтобы работа была max, она должна равняться тепловому эффекту Amax = Qv, надо вычислить:
ΔF = Qv.
Аналитические выражения третьего закона термодинамики:
это изохорно-изотермические условия.
Если Аmax = QP, ΔG, Qp, ΔH – функции
это изобарно-изотермические условия.
Тепловая теорема Нернста (третий закон термодинамики)(рис. 16)
Рис. 16
Энергии (ΔU, ΔH, QV, QP, ΔF, ΔG), tgαугла наклона прямой – дает температурный коэффициент любой функции.
Для реакций, протекающих в конденсированных системах при приближении температуры к абсолютному нулю, кривые max работы и теплового эффекта соединяются и имеют одну большую касательную, параллельную оси температур.
Следствия из третьего закона термодинамики:
1. Свойства энтропии вблизи абсолютного нуля – постулат Планка:
ΔF = ΔU – TΔS.
абсолютная энтропия.
2. Теплоемкость Сp, Сv
3. Коэффициент термического расширения тела и термического давления.
Идеальные газы не подчиняются третьему закону термодинамики, так как газ вблизи абсолютного нуля называется вырожденным.
CP – CV ≠ R вблизи абсолютного нуля – уравнение Майера не работает.
4. О невозможности достижения абсолютного нуля. Третий закон термодинамики – приближенный закон. Используется для совершенного кристалла любого вещества.


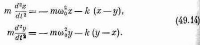

Комментарии к книге «Физическая химия: конспект лекций», А. В. Березовчук
Всего 0 комментариев