«Сборка кубика Рубика»

СОБРАТЬ КУБИК? ЭТО НЕСЛОЖНО!

Головоломка «Кубик Рубика» («Волшебный кубик», «Венгерский кубик» и даже просто «Рубик») привлекла внимание, как говорится, «всех групп населения» и получила широчайшее распространение, О достоинствах этой замечательной головоломки, в которую с удовольствием стали играть и школьники и академики, находя в ней достоинства, сообразные уровню учености, образования и склонности к исследованиям, мы уже писали (см. «Наука и жизнь» № 3, 1981 г. и № 2, 1982 г.) и даже приводили методы решения.

Но читательская почта заставляет нас вновь вернуться к опубликованным материалам. И не только к задачам-пасьянсам на кубике, ответов на которые мы еще не давали, но и к методу сборки.

Мы не будем касаться ни математической теории групп, ни квантовой физики, для определенных разделов которых кубик Рубика служит оригинальным наглядным пособием. Попытаемся рассказать о том, как привести в порядок перепутанный кубик, и тем читателям и читательницам, которые весьма и весьма далеки от математики и от физики вообще. Возможно, будет и некоторая польза в самообразовании, в расширении кругозора: ведь здесь придется познакомиться и с математическими символами и с чертежами, хотя и очень простыми. Надеемся, что желание собрать кубик пересилит их нелюбовь к точным наукам

Поэтому мы заранее просим прощения у более подготовленных читателей за «излишние» подробности в описании: уж очень много пришло писем с просьбой «рассказать так. чтобы было понятно всем, всем…».

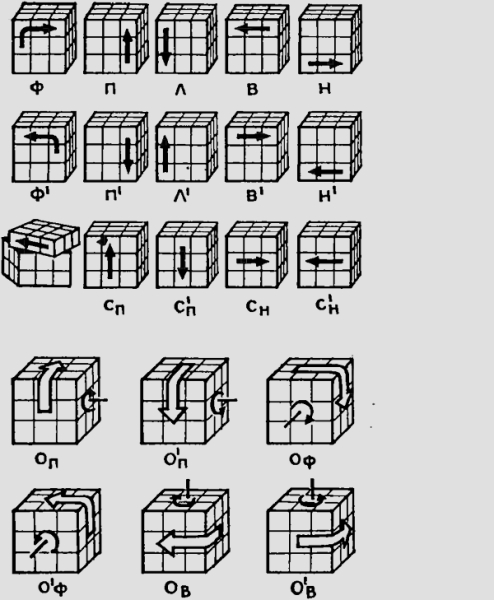
Прежде всего напомним принятую в журнале систему обозначений. Грани куба обозначаются буквами Ф, Т, П, Л, В, Н — начальными буквами слов фасад, тыл, правая, левая, верх, низ. Какую грань куба посчитать фасадной — синюю, зеленую и т. п. — зависит от вас и от получившейся ситуации. В процессе сборки вам придется несколько раз принимать за фасадную ту или иную грань, удобную для данного случая. Центральные кубики определяют цвет грани, то есть можно сказать, что даже в полностью перепутанном кубике центральные кубики уже подобраны и к каждому из них остается присоединить по 8 кубиков того же цвета. Центральные кубики обозначаются одной буквой: ф, п. л, в, т, н.

Реберные кубики (их 12 штук) принадлежат двум граням и обозначаются двумя буквами, например фп, пв, фн и т. д.

Угловые кубики — тремя буквами по наименованию граней, например, фпв, флн и т. д.

Прописными буквами Ф, Т, П, Л, В, Н обозначаются элементарные операции поворота соответствующей грани (слоя, ломтика) куба иа 90° по часовой стрелке. Обозначения Ф', Т', П', Л', В', Н' соответствуют повороту граней на 90° против часовой стрелки. Обозначения Ф², П² и т. д. говорят о двойном повороте соответствующей грани (Ф²= ФФ).

Буквой С обозначают поворот среднего слоя. Подстрочный индекс показывает, со стороны какой грани следует проделать этот поворот. Например Сп— со стороны правой грани, Сн—со стороны нижней, С'л— со стороны левой, против часовой стрелки и т. д. Буква О— поворот (оборот) всего куба. Оф — со стороны фасадной грани по часовой стрелке и т. д.

Запись процесса (Ф' П') Н² (ПФ) означает: повернуть фасадную грань против часовой стрелки на 90°, то же — правую грань, повернуть нижнюю грань дважды (то есть на 180°), повернуть правую грань на 90° по часовой стрелке, повернуть фасадную грань.

Наряду с буквенной записью процессов применяется и матричная форма записи, где элементарные операции изображаются рисунком фасадной грани с соответствующими стрелками, обозначающими направления поворотов соответствующей грани (см. рис.).

Теперь перейдем собственно к сборке куба. Есть несколько разных систем, но нам больше всего нравится послойная сборка, когда собирают сначала один слой, затем второй и, наконец, третий. Всего получается семь этапов.

Первый этап

Крест верхней грани. Нужный кубик опускается вниз поворотом соответствующей боковой грани (П, Т, Л) и выводится на фасадную грань операцией Н, Н' или Н². Заканчивается операция выведения зеркальным поворотом (обратным) той же боковой грани, восстанавливающим первоначальное положение затронутого реберного кубика верхнего слоя После этого проводится операция а) или б) первого этана. В случае а) кубик вышел на фасадную грань так, что цвет его передней грани совпадает с цветом фасада. В случае б) кубик надо не только переместить наверх, но и развернуть его, чтобы он был правильно сориентирован, став на свое место. На рисунках точками отмечено место, на которое должен встать нужный кубик, выведенный предварительно на фасад нижней грани. Результат: собран крест верхней грани.

Второй этап

Отыскивается нужный угловой кубик (имеющий цвета граней Ф, В, Л) и тем же приемом, который описан для первого этапа, выводится в левый угол избранной вами фасадной грани. Здесь могут быть три случая ориентации этого кубика. Сравните свой случай с рисунком и примените одну из операций второго этапа а), б) или в). Точками отмечено место, на которое должен стать нужный вам кубик. Отыщите на кубе остальные три угловых кубика и повторите описанный прием для перемещения их на свои места верхней грани. Результат: верхний слой подобран. Первые два этапа почти ни у кого не вызывают затруднений: довольно легко можно следить за своими действиями, так как все внимание обращено на один слон, а что делается в двух оставшихся — совсем неважно.

Третий этап

Пояс. Процессы, приведенные на рисунках, легко запоминаются, если применить мнемоническое правило. Для перемещения кубика, выведенного на фасадную грань, налево начало процесса совпадает с начальными буквами НЛ — НаЛево, а направо с начальными буквами НаП'раво. И здесь, как вы видите, нужный кубик отыскивается и сначала выводится вниз на фасадную грань. Если он внизу — простым поворотом нижней грани до совпадения с цветом фасада, а если он в среднем поясе, то его нужно сначала опустить вниз любой из операций а) или б), а потом совместить по цвету с цветом фасадной грани и проделать операцию третьего этапа а) или б). Результат: собрано два слоя.

Четвертый этап

Крест нижней грани. К цели приводят операции, перемещающие бортовые кубики одной грани, не нарушающие в конечном счете порядка в собранных слоях. Один из процессов, позволяющий подобрать все бортовые кубики грани, дан на рисунке. Там же показано и что происходит при этом с другими кубиками грани Повторяя процесс, выбрав другую фасадную грань, можно поставить на место все четыре кубика. Результат: реберные кубики стоят на своих местах, но, как правило, два из них неверно ориентированы.

Пятый этап

Ориентирование двух бортовых кубиков по Д. Конвею. Очень простой, легко запоминающийся процесс, но именно здесь у некоторых читателей возникли трудности. Здесь следует учесть: разворачиваемый кубик должен быть на правой грани, на рисунке он помечен стрелками. На рисунках а), б), и в представлены возможные случаи расположения неверно ориентированных кубиков (помечены точками). Используя общую формулу в случае а), потребуется выполнить промежуточный поворот В, чтобы вывести второй кубик на правую грань, а в случаях б) и в) соответственно В' и В².

Многих смущало то, что после первой части процесса (ПСн)4 нужный кубик разворачивался как надо, но порядок в собранных слоях нарушался. Это сбивало с толку и заставляло бросать на полпути почти собранный куб. Выполнив промежуточный поворот, не обращая внимания на поломку нижних слоев, проделайте операции (ПСн)4 второй части процесса, и все станет на свои места. Результат: собран крест.

Шестой этап

Углы последней грани возможно поставить на свои места, используя не 22-ходовый процесс, описанный в № 2, 1982 года, а 8-ходовый, удобный для запоминания, — прямой, переставляющий три угловых кубика в направлении по часовой стрелке, и обратный, переставляющий три кубика в направлении против часовой стрелки.

После пятого этапа, как правило, хотя бы одни кубик да сядет на свое место, пусть и неправильно ориентированно. Поверните куб так, чтобы этот кубик оказался в левом дальнем углу, и повторите процесс еще раз-два, пока все кубики не станут на свои места. Результат: все угловые кубики заняли свои места, но два из них (а может, и четыре) ориентированы неправильно.

Седьмой этап

Ориентация угловых кубиков последней грани. Процесс тоже очень легко запомнить — это многократно повторяемая последовательность поворотов ПФ'П'Ф.

Поверните куб так, чтобы кубик, который вы хотите развернуть, был в правом верхнем углу фасада. 8-ходовый процесс (2x4 хода) повернет его на ¹/з оборота но часовой стрелке. Если при этом кубик еще не сориентировался, повторите 8-ходовку еще раз (в формуле это отражено индексом «п»).

Не обращайте внимания на то, что нижние слои при этом придут в беспорядок: ситуации аналогична проделанной на пятом этапе, она тоже парная, разбивается на дпе идентичные половники с промежуточной операцией поворота верхней грани Выполнение лраной части процесса автоматически приводит в порядок нарушенную гармонию

На рисунке показаны трн случая расположения «плохих» кубиков (они помечены точками). В случае а) требуется промежуточный поворот В, а в случае б) — поворот В' и в случае в) — поворот В2. Результат: последняя грань собрана.

Теперь остается лишь повернуть ее, и все — куб собран, хлопайте в ладошки!

ПАСЬЯНСЫ НА КУБИКЕ

Первоначальная ориентация куба: верх — синий, фасад — красный, справа — зеленый, слева — желтый, низ — белый, тыл — оранжевый

Ослиный мостик (шахматный кубик 2-го порядка) (№ 4) — С²пС²нС²ф.

Точки — С'нС'пСнСп.

Крест Кристмана (№ 2) — П'(С²пС²фВ²С²пС²ФН²)П.

Крест Пламмера (№ 3) — О²ф[Оф (В²С²ПВ С²пВ²С²фН'С²ф)]².

Шахматный кубик 3-го порядка (№ 5) — [(С²фНС²фВ²С²пВ'С²пВ²)О'ф]²О²ф•(С'пС'нСпСн) • ОпОв•С²пС²фС²н.

Эта фигура представляет собой сочетание фигур «Крест Пламмера» и «Точки».

Шахматный кубик 6-го порядка — сочетание алгоритмов шахматного кубика 3-го порядка и «Ослиного мостика» (№ 6) —

[(С²фНС²фВ²С²ПВ'С²пВ²)О'ф]² О²Ф С'пС'Н СпСп•ОпОв•С²пС²фС²н

Фигура «6Н» (№ 7) — Н²СпС²фС'пВ² О²в.

Фигура «6 минусов» (№ 8) — П²Ф²С²пТ²Л²Оп²СпО'п

6 флагов (№ 9) — В'Т²Л²ВС²пВ'П²Ф²НФТПСпП'Т'П'СнП²С'нП'Ф' Т²П²Т²Ф²Сф ОфОв (Г. Галл).

Мезон («кварк — антикварк») (№ 10)

Л²П'НП ФНФ' В' • ФН'Ф' • П'Н'П • В • Л².

Гигантский мезон — Ф'В'ТВ²ВПВ²П'Ф ТНФ'Н²ФН'Л'Н²ЛТ' (Д. Сингмайстер).

Гигантский мезон с вишнями (№ 11) — П'В²НТ'СнТ²С'нТ'В²Н'П ЛН²В'ФСнФ²С'нФН²ВЛ'С'нС'пСпСп.

Глобус (№ 12) — (ФТЛП)²ЛП. Фигура, придуманная Д. Максвеллом, представляет собой «глобус»», на котором расположены 54 страны, и ни одна из иих не соприкасается протяженными границами со страной, совпадающей по цвету иа глобусе.

Редакция благодарит И. Белова (г. Москва), В. Гаврилец (г. Калинин), М. Ганшина (г. Москва), В. Гурина (г. Севастополь), А. Ев-сюкова (г. Калининград), И. Индриксона (г. Рига), Е. Клиссанича (г. Ленинград), Ю. и Д. Кошелевых (г. Москва), А Кура (г. Ленинград), Р. Терехова (г. Уфа), А. Чува-сова (г. Тула) и других читателей, приславших интересные сообщения о придуманных ими алгоритмах сборки кубика и решивших предложенные аадачи-пасьянсы

Оглавление